Randomization tests as alternative analysis methods for behavior-analytic data

Abstract

Randomization statistics offer alternatives to many of the statistical methods commonly used in behavior analysis and the psychological sciences, more generally. These methods are more flexible than conventional parametric and nonparametric statistical techniques in that they make no assumptions about the underlying distribution of outcome variables, are relatively robust when applied to small-n data sets, and are generally applicable to between-groups, within-subjects, mixed, and single-case research designs. In the present article, we first will provide a historical overview of randomization methods. Next, we will discuss the properties of randomization statistics that may make them particularly well suited for analysis of behavior-analytic data. We will introduce readers to the major assumptions that undergird randomization methods, as well as some practical and computational considerations for their application. Finally, we will demonstrate how randomization statistics may be calculated for mixed and single-case research designs. Throughout, we will direct readers toward resources that they may find useful in developing randomization tests for their own data.

Introduction

“… [S]tatistics are merely tools, and like most tools, they are morally neutral; it is how one uses such tools that determines whether they are good or evil, helpful or harmful.”

(Fisher & Lerman, 2014, p. 243).

Zimmermann, Watkins, and Poling (2015) compiled a list of all 3,084 original research articles published in the Journal of the Experimental Analysis of Behavior (JEAB) from its inception in 1958 through 2013. The authors semirandomly selected about one third of these articles (n = 1,048, 524 of which used only human participants, and 524 of which used only nonhuman subjects) for analysis. They coded study characteristics including the studied species, the number and sex of participants/subjects, and the type of experimental design (i.e., within-subject, between-group, or mixed designs) used to address the question under study. Importantly for present purposes, they also collected data on whether or not these studies reported inferential statistics as a component of data analysis. When they regressed the percentage of studies in each year that reported inferential statistics onto year of publication, Zimmermann and colleagues found that the relation was reasonably well described by a linear model (i.e., R² = .82; see also their Fig. 4) with a slope coefficient of 1.08 (see also Foster, Jarema, & Poling, 1999, for similar findings). That is, the number of articles published in JEAB that included inferential statistics increased by roughly 1.08% each year over this time frame.

Zimmermann and colleagues’ (2015) findings demonstrate that inferential statistics have become common components of data analysis in behavior-analytic research. Whether this shift toward embracing statistical methods is a good thing or a bad thing for the science is up to debate (for contrasting views, interested readers may see, e.g., Branch, 1999; 2014; Hopkins, Cole, & Mason, 1998; Huitema, 1986; Kratochwill & Levin, 2014; Michael, 1974; Shadish, Hedges, & Pustejovsky, 2014). Nevertheless, there are circumstances under which it may be particularly beneficial for researchers to conduct statistical analyses of their results.

For example, though within-subject designs remain the most popular study design in experimental and applied analyses of behavior, between-subjects and mixed designs are becoming more common (see, e.g., Kyonka, in press; Zimmermann et al., 2015). On the one hand, these latter designs offer researchers the ability to study behavioral outcomes that may be affected by repeated testing (e.g., extinction learning or relapse of previously eliminated behavior; see Baum, 2012; Lieving & Lattal, 2003; Sweeney & Shahan, 2013; Wacker et al., 2011) or that are not reversible within subjects (e.g., acquisition of novel skills; see Roane, Ringdahl, Kelley, & Glover, 2011). On the other hand, between-subjects designs are limited in that they introduce an additional source of uncontrolled variability (i.e., variability between subjects) that might complicate interpretation of between-group differences in a behavioral outcome (for discussion, see Charness, Gneezy, & Kuhn, 2012). Inferential statistics can help to clarify relations between variables while accounting for these sources of additional variance. Statistical methods also add to the set of tools that a researcher may use when making decisions about data when the functional relations between independent and dependent variables are not immediately clear through means of visual inspection alone (for discussion, see Weaver & Lloyd, 2018). Further, Huitema (1986) cogently argued that statistical analysis of behavior-analytic data could increase the visibility of the science to other disciplines (e.g., neuroscience, pharmacology, medicine) that place stronger emphasis on statistical outcomes when evaluating a study’s results. Finally, standards of evidence for empirically supported procedures rely heavily on the outcomes of meta-analyses that summarize the statistical effect sizes reported in a defined body of empirical investigation (APA Presidential Task Force on Evidence-Based Practice, 2006; Oxford Center for Evidenced-Based Medicine, 2011). Meta-analysis researchers have generally excluded behavior-analytic research from their analyses in large part due to the absence of the relevant statistical data required for inclusion in meta-analyses. Conducting and reporting appropriate statistical analysis of behavior-analytic findings should increase the likelihood that those findings will be included in future meta-analyses (Fisher & Lerman, 2014).

Despite the potential utility of inferential statistics for behavioral research described above, the opening quote from Fisher and Lerman (2014) expresses a dimension of statistical methods that is important to bear in mind. Inferential statistics may help researchers interpret and make decisions about complex data sets, provided that the data are reasonably well suited for the statistical test that is applied. If the data are poorly suited for a test, however, the output from a statistical test may be misleading. Inasmuch, behavioral researchers must consider practical barriers when selecting statistical methods to apply to their data.

Determining how well suited a specific set of data is for a specific statistical test can be a challenge, as Perone (1999) noted in his critique of statistics for the behavioral sciences. In the case of study designs that include multiple subjects or participants, specifics of the study and the type of data to be analyzed will help to guide researchers toward an appropriate constellation of statistical methods (see, e.g., Nayak & Hazra, 2011, for a reduced decision-making process based on these considerations). Inferential statistical methods, however, are packaged with assumptions that must be met (or at least not grossly violated) for the outcomes of those tests to be valid. For example, the t and F family of tests, two of the most common analytic strategies for comparing mean differences in the psychological sciences, require that residuals (i.e., the difference between obtained values of the dependent variable and values of this variable that are predicted by the statistical model) are normally distributed. That is, these tests are parametric methods because they assume that data are sampled from a population whose distribution of scores may be characterized by a fixed number of parameters (in the case of the normal distribution, these parameters are the mean and standard deviation; we will return to this issue in more detail in the “Advantages of Randomization” section below). It may be difficult to visually or statistically assess the extent to which this assumption is met with the relatively small-n sample sizes often used in behavior-analytic research (Geng, Wang, & Miller, 1979; Ghasemi & Zahediasl, 2012).

When single-case research designs are used, researchers’ statistical options are further limited. Because only a single subject or participant is observed, methods like t and F tests, which require samples of independent observations, are inappropriate (see Bulté & Onghena, 2008; Weaver & Lloyd, 2018). Further, autocorrelation between data points is a serious concern in single-case research designs because of the time-series nature of the data that they produce. That is, data points that are close together in time tend to be more highly correlated than data points that are temporally further apart. Autocorrelation may strongly bias parametric statistics (see Busk & Marascuilo, 1988; Sharpley & Alavosius, 1988; Wilkinson & Task Force on Statistical Inference, 1999), though sophisticated methods for analyzing time-series data certainly exist (see, e.g., Brockwell & Davis, 2016, for a thorough introduction).

Additional complications with statistical inference when applied to behavior-analytic data arise from their conceptual underpinnings. Sir Ronald Fisher’s (1954; 1955) general approach to statistical inference, which undergirds the lion’s share of modern statistical-significance testing (see, for discussion, Perezgonzalez, 2015), relies on estimation of population parameters based on sample statistics. In effect, these methods help to answer questions like: “Given that the experimenter drew subjects or participants from a specific population with mean = μ and variance = σ for the outcome of interest, what is the probability that the researcher randomly would have drawn a sample with scores on the outcome of interest as extreme or more extreme than the observed scores?” These are not always the types of research questions in which behavior analysts are interested (see, e.g., Branch, 1999). That is, behavior analysts generally direct their hypotheses toward demonstrating behavior change in the face of one set of contingencies relative to behavior under another set of contingencies, not relative to the behavior of a hypothesized population of individuals.

In light of these practical and conceptual limitations of popular statistical methods like t and F tests when applied to behavior-analytic data, alternative analysis methods are desirable. An increasing number of researchers have come to embrace randomization statistics (e.g., Adams & Anthony, 1996; Ferron & Ware, 1994; Wampold & Furlong, 1981; Weaver & Lloyd, 2018; for review, see Huo, Heyvaert, Van den Noortgate, & Onghena, 2014), as such methods may be particularly well suited for use in behavioral research. The purpose of this article is to introduce readers to randomization methods. We first will provide a brief historical overview of randomization methods. Next, we will present some of the advantages of randomization over other statistical methods when applied to behavioral data. We will describe some practical limitations of these tests, as well as the assumptions that must be met for their application. Finally, we will apply randomization methods to analyze hypothetical behavioral data sets to provide examples of their potential utility for the science.

A Brief History of Randomization Methods

Randomization tests are not a new statistical methodology. In fact, they are quite old, having been described initially by Sir Ronald Fisher in his influential 1935 text, The Design of Experiments. Fisher acknowledged the usefulness of testing a “wider hypothesis [relative to that of the t-test] which merely asserts that two series [of data] are drawn from the same population, without specifying that this is a normal distribution” (p. 51). He then went on to describe a method for testing such a hypothesis using data from an experiment conducted by Charles Darwin (1876). In this experiment, Darwin planted 15 pairs of corn plants, one of which was produced through cross pollination, and the other of which was produced through self-pollination. Within each pair of plants, Darwin controlled variables such as type of soil, time of planting, and other growing conditions. Darwin wanted to know whether pollination method affected the height of his mature corn plants.

The logic of Fisher’s (1935) “wider hypothesis” test was as follows. If pollination method had no effect on the height of Darwin’s (1876) corn plants, it should have been equally likely for cross-pollinated plants to be taller than self-pollinated plants within each matched pair as it was for cross-pollinated plants to be shorter than self-pollinated plants. This was the null hypothesis, H₀, for Fisher’s test. Fisher reasoned that randomly switching pairs of plants between groups would not alter the expected value for the mean of each group under the H₀, so he calculated every possible rearrangement of plants between groups while keeping pairs of plants matched.¹ He retained the matched pairs because Darwin controlled growing factors within pairs but these factors varied between pairs.

For each of these rearrangements, Fisher (1935) calculated absolute differences in the heights of plants between groups by summing the heights of all plants in each group and then subtracting this sum for the self-pollinated group from that of the cross-pollinated group. Fisher then determined the probability of obtaining a between-group height difference that was as or more extreme than the actual difference that Darwin (1876) obtained (i.e., a difference of 39.25 inches between groups, in favor of cross-pollinated plants being taller than self-pollinated plants). Fisher also may have examined mean differences between groups and calculated the probability of obtaining a mean difference between groups as or more extreme than the mean difference Darwin obtained (i.e., D = 2.62 inches [where D stands for “difference”] in favor of cross-pollinated plants, SD of the difference = 4.72 inches)—his outcomes would have been identical. We will focus on mean differences below because this practice aligns with contemporary practices in randomization methods.

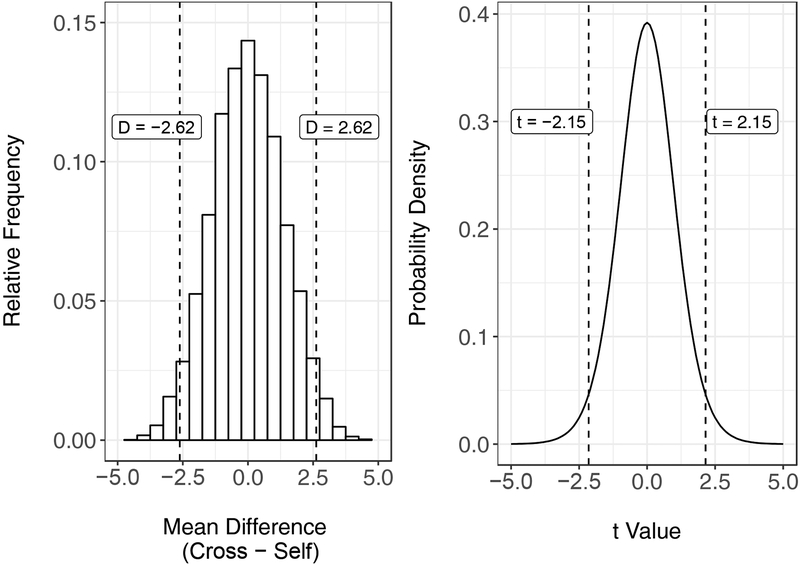
Panel A on the left side of Figure 1 shows a relative frequency distribution of mean differences (heights of cross-pollinated plants – heights of self-pollinated plants) from the rearrangements of plants between groups.² (An empirical distribution that shows the frequency of outcomes derived from randomly rearranging obtained data a large number of times, like the one shown in Panel A, is sometimes called a “reference,” “resampling,” or “permutation” distribution to distinguish it from the theoretical “sampling” distribution germane to many contemporary statistical methods [see, e.g., Ludbrook & Dudley, 1998; Yu, 2003]. Both of these types of distributions, however, serve a similar purpose in that they act as a frame of reference for researchers to determine p-values for obtained outcomes.) Of these possible rearrangements, Fisher (1935) observed that about 5.3% of cases produced differences in plant heights that were as extreme or more extreme than those observed by Darwin (1876). Thus, the probability of Darwin’s findings, given the data that he collected, was p = .053. This probability is represented by the portions of the distribution to the left and right of the dashed lines labeled D = −2.62 and D = 2.62 in Panel A, respectively.

Fig. 1.

Panel A: Relative-frequency histogram showing mean differences from rearrangements of Darwin’s (1876) experiment on the heights of corn plants. The dashed lines labeled “D = −2.62” and “D = 2.62” represent the mean difference in height between plants that received different pollination methods that Darwin (1876) obtained. Panel B: Probability density for the t distribution with 14 degrees of freedom. The dashed lines labeled “t = −2.15” and “t = 2.15” represent the two-sided t-values derived from Darwin’s data.

As Fisher (1935) noted, this p-value is virtually identical to the outcome of a two-tailed, paired-samples t-test performed on Darwin’s data, t(14) = 2.15, p = .050. For illustrative purposes, Panel B on the right side of Figure 1 shows the probability density function (PDF) for t with 14 degrees of freedom. Researchers may use a PDF to determine the probability that an outcome would fall within a specified range of values by examining the area under the curve (AUC) between those values. In this case, the sum of the AUC that falls below t = −2.15 and above t = 2.15 gives us the p-value for our test, p = .050. Thus, the proportions of the PDF that are more extreme than t = −2.15 and t = 2.15 are roughly equal to the proportions of the empirical reference distribution in Panel A that are more extreme than D = −2.62 and D = 2.62.

The test that Fisher (1935) conducted is termed a “permutation test” because he compared obtained data to every possible rearrangement of scores between groups (see Ludbrook & Dudley, 1998). This early example of randomization-based data analysis set the stage for researchers to generalize the approach to other experimental designs, types of data, and purposes of analysis (see, e.g., Box & Anderson, 1955; Pesarin, 2001; Westfall & Young, 1993). Shortly after publication of Fisher’s The Design of Experiments, for example, E. J. G. Pitman (1937a; 1937b; 1938) demonstrated how researchers might apply this approach to other relatively simple comparisons (e.g., tests of mean differences between two or more independent groups and the correlations between two paired sets of scores). More recently, researchers have extended randomization methods to describe simple and complex linear models (see, for discussion, Nyblom, 2015). They have also used randomization methods to describe simultaneous effects of multiple independent variables on a dependent variable (i.e., “interaction effects” in regression and analyses of variance [ANOVA]), though these tests are complex and statisticians have not reached clear consensus concerning best practices for their application (see Anderson, 2001; Anderson & Ter Braak, 2003). We will return to some of these analyses in the section titled “Applications to Behavior-Analytic Data” below.

To summarize, Ronald Fisher first developed randomization methods in the mid-1930s. The general premise of randomization methods is that, under the H₀, scores from different groups should be interchangeable. Thus, researchers can determine the probability of obtaining a statistic from a given set of data by (a) repeatedly rearranging data between groups, (b) calculating the statistic of interest for each set of rearranged data (e.g., a mean difference or t-value), (c) determining how many of those statistics are as extreme or more extreme than the statistic obtained from an experiment, and (d) dividing that number of extreme statistics by the total number of statistics obtained by rearranging the data. Following this basic logic, randomization-based alternatives have been developed for many of the statistical analyses that are common in the behavioral sciences.

Advantages of Randomization

Randomization-based methods differ from other methods for drawing statistical inferences like the t and F family of tests in several major ways that make their application considerably more flexible (see Edgington & Onghena, 2007). Below, we will describe these differences. In so doing, we will emphasize some of the potential advantages of randomization methods over other inferential statistics when analyzing behavior-analytic data.

Many inferential statistical techniques require that residuals of scores on an outcome variable be normally distributed in a researcher’s sample. The exact reason this assumption exists is rather complicated, but we will provide a brief explanation (see Lumley, Diehr, Emerson, & Chen, 2002, for an additional and very helpful treatment). Statistical tests like the t-test and ANOVA are used to determine the extremity of mean differences, and they do so by comparing these differences to the sampling distribution of the mean for a given population. The sampling distribution of the mean is exactly what it sounds like: If one were to draw samples of size n from the population over and over again and measure the outcome variable of interest in each one of those samples, the histogram of mean scores from all of the samples would be the sampling distribution of the mean. The problem is that researchers usually do not have access to a large number of samples from the overall population; they have only one sample of scores on an outcome variable. Fortunately, the central limit theorem can be applied to help researchers render an informed guess about what this distribution would look like. This theorem states that, as the sample size (n) increases, the sampling distribution of the mean on an outcome will approach normality regardless of the distribution of scores in the population. That is, for relatively large samples (e.g., n > 30; see Ghasemi & Zahediasl, 2012), it is likely that the sampling distribution of the mean, if empirically constructed, would be normal. With smaller sample sizes, however, it becomes less certain what the sampling distribution of the mean would look like. If the distribution of scores is normal in the population (as would likely be the case if the researcher obtains a sample with normally distributed residuals), then the sampling distribution of the mean will be normal regardless of the sample size. Thus, statistics like t- and F-tests assume normality of residuals in the sample because that helps to ensure that the sampling distribution of means is likely to be normally distributed regardless of the size of a researcher’s sample.

As Fisher (1935) alluded to in his quote above (i.e., “… without specifying that this is a normal distribution,” [p. 51, italics added for emphasis]), randomization tests are nonparametric, meaning that they do not require any distributional assumptions for the outcome of the test to be valid. Nonparametric tests may be particularly useful for behavior-analytic data because the science tends to use small-n research designs. Not only is the normality assumption of t and F statistics particularly important with small sample sizes (because the sampling distribution of the mean cannot be assumed to be normal when n is small), but it may be difficult if not impossible to tell whether or not residuals of data within a sample are normally distributed with small ns. Under these circumstances, visual assessments of normality (e.g., plotting a histogram of residuals or a quantile–quantile [q–q] plot of these data) may not be particularly informative, and formal tests for normality (e.g., tests for skewness or kurtosis; linear regression of obtained quantiles onto quantiles from a hypothetical, normal distribution in a q–q plot) may be underpowered to detect deviations from normality. As a result, researchers may be led to believe residuals of their data are normally distributed when they are not, possibly leading to unreliable statistical outcomes. Randomization tests are nonparametric because the obtained data themselves are used to create an empirical reference distribution that serves the same purpose as the sampling distribution of the mean in parametric statistics.

Randomization tests are, of course, not the only statistical tests that are applicable to data for which the residuals are distributed nonnormally. For example, the Mann-Whitney U-test (Mann & Whitney, 1947) may be used to analyze differences between two independent groups, and Wilcoxon’s sign-rank test (Wilcoxon, 1945) is a common method for analyzing differences between two paired groups, when the normality assumption of t-tests is violated. It is important to note, however, that these tests tend to be considerably less powerful than their parametric counterparts (Colquhoun, 1971). By “powerful,” we refer here to statistical power, which is the probability of rejecting the null hypothesis when it is, in fact, false (see Kyonka, in press, for discussion and a very helpful tutorial on statistical power with small-n samples). Simulation studies have demonstrated that randomization tests are often more powerful than other nonparametric tests and, in some cases, may be even more powerful than parametric statistics (see Ludbrook & Dudley, 1998; Nuzzo, 2017).

As an important aside, we alluded in the Introduction that the term parametric in statistics does not necessarily entail that the parametric statistical model deals with the normal distribution. Generalized linear models are a class of parametric statistics that was developed to describe data whose distributional properties are better described by a variety of distributions like the binomial, Poisson, and gamma (see, for review, Dunn & Smyth, 2018; Nelder & Wedderburn, 1972). We encourage readers to become familiar with this family of statistical tests, too, in the case that their data are well suited for analyses using these methods.

A second advantage of randomization statistics is that these methods do not require random sampling from a specific population. Random sampling is important for many contemporary statistical methods because sample statistics (e.g., sample means and standard deviations) are used to draw inferences about population parameters. When researchers select samples using methods other than random selection (e.g., selecting a sample of convenience; Freedman, 2010), estimates of the population parameters may be biased, or interpretation of statistical outcomes may be strongly limited. Fisher (1935) initially considered randomization tests as an alternative method for estimating population parameters based on a sample of data. Inasmuch, he considered that random sampling from the population was a requirement of randomization tests (for discussion, see Edgington & Onghena, 2007). Pitman (1937a; 1937b; 1938) later demonstrated that randomization tests could be used to draw inferences specifically about the sample without knowing anything about the parameters at the level of the population. Often, behavior-analytic research does not entail random sampling of subjects or participants from a population of interest.

In clinical settings, for example, geographic location, socioeconomic status, and disorder severity all play a role in determining whether participants are able to access services in the context of which research is conducted (see, e.g., Pickard & Ingersoll, 2016). Thus, some subpopulations of participants may be more likely to be included in clinical research than others. Inasmuch, samples of participants may not be representative of the population of those participants. For example, data on the treatment of severe problem behavior generated from samples in inpatient or day-treatment settings (e.g., Greer, Fisher, Saini, Owen, & Jones, 2016; Rooker, Jessel, Kurtz, & Hagopian, 2013) may differ substantially from data generated in routine outpatient settings (e.g., Jessel, Hanley, & Ghaemmaghami, 2016). Further, in laboratory research, animal subjects usually are not randomly selected from the population of all possible subjects. One may protest this statement by arguing that ordering, for example, rats from a breeder simulates random selection because (a) environmental variables are kept as constant as possible for all subjects prior to shipment and (b) most suppliers use outbreeding to keep the genotype of each rat strain as uniform as possible. Startling new genetic data (see Gileta et al., 2018), however, demonstrates that the genotype of rat strains varies widely between popular breeders. Thus, unless researchers select their samples of animals from all breeders, their samples may not be representative of the entire population of animals. Randomization tests are an ideal alternative to statistics like t and F tests for analyzing data from such samples. Randomization tests help to determine the significance of the findings within each sample, whereas generalization to the broader population requires multiple replications across samples (Kazdin, 2011). To the extent that conventional practices in behavior analysis rely on sampling from a subset of the population, the generality of statistical methods that draw inferences about the population at large are strongly limited—they may tell the readers little more than the sample-specific inferences drawn using randomization statistics.

Within-subject research poses a unique challenge to the random-sampling assumption that exists for several popular statistical methods like regression, ANOVA, and t-tests. If the data to be analyzed consist of scores from the same participant across more than one time point (e.g., preintervention and postintervention rates of some target behavior), it is clear that these data points were not obtained from different, randomly sampled participants. Among other methods, multilevel regression models, repeated-measure ANOVA, and paired-sample t-tests may be used to analyze data from such designs (see, e.g., Gelman & Hill, 2007; Girden, 1992), as may randomization tests (as we will demonstrate in the “Applications to Behavior-Analytic Data” section below).

Randomization tests’ focus on the sample instead of the population offers an additional benefit to behavior analysts: The hypotheses that are tested through randomization methods align more closely with the research questions behavior analysts tend to ask than do those tested by population-based statistics. Behavior-analytic research often demonstrates experimental control of behavior using single-case research methods (e.g., reversal, multiple-baseline, and multielement designs; see Kazdin, 2011) to answer questions like, “Did the participant respond more or less in this condition than in the other?” or, “Was this treatment effective for a participant?” These questions are more concerned with data collected from a specific individual or group of individuals than they are about estimating population parameters. That is not to say that the specific hypotheses tested by randomization-based statistics are more appropriate than those tested by population-based statistics for all behavior-analytic data. Researchers more often use single-case research designs than group or mixed designs in behavior analysis (for discussion, see Foster et al., 1999; Kyonka, in press; Zimmermann et al., 2015), and it is for single-case designs that hypotheses under randomization tests tend to be more logically consistent than those under other statistical tests. For studies that use group or mixed designs, however, it makes sense to ask whether observed group differences could have resulted from sampling error.

As we hope the above discussion illustrates, randomization statistics differ from statistical techniques like t and F tests in almost every respect. Randomization tests (a) do not require residuals of sampled data to adhere to any specific (e.g., normal) distribution, (b) are applicable when data violate many of the specific assumptions of other statistical techniques, (c) test hypotheses that are based on the obtained data without reference to their relation to any specific population, and (d) are flexible enough to analyze data from individual subjects/participants and groups of subjects/participants. Despite the strengths of randomization statistics described above, researchers will need to consider several technical aspects of these methods before using them to analyze obtained data. These are described in the following section.

Some Important Considerations

Randomization tests trade flexibility for computational intensiveness. For example, consider the permutation test that Fisher (1935) conducted on data from Darwin’s (1876) corn-breeding experiment. For paired-sample permutation tests, there are 2ⁿ possible combinations of group assignments, where n is the number of pairs in the data set. In Fisher’s reanalysis, then, 2¹⁵ = 32,768 distinct rearrangements of pairs of corn plants between groups contributed to the reference distribution shown in Figure 1. The fact that Fisher was able to determine each of these rearrangements with the technology at the time truly is impressive (though he technically calculated only a subset of these combinations; see Footnote 1 for more information). He acknowledged the difficulty he faced, though, stating that, “The arithmetical procedure of such an examination is tedious, and we shall only give the results of its application in order to show the possibility of an independent check on the more expeditious methods in common use [i.e., the t test]” (p. 51; see also Bradley, 1968). What if Darwin’s experiment used nonpaired samples of 15 corn plants apiece? When data in two groups or two sets of observations are independent, the reference distribution is created by randomly shuffling data between groups until each possible combination is sampled, without regard to any matching between observations. For n overall observations with r observations per group, there are n!/([n - r]! * r!) possible combinations. In this case, the reference distribution would be composed of 30!/([30 – 15]! * 15!) = 155,117,520 possible combinations!

Calculating these many combinations by hand is prohibitive. Modern computing, however, allows researchers to automate these calculations to make them more tractable. Still, calculating all possible combinations of data from a given sample may be time intensive. Dwass (1957) described an approach to randomization tests that helped to address this issue. Instead of examining all possible combinations of data rearranged between groups, Dwass suggested that researchers could instead sample a large but nonexhaustive subset of these combinations. This method of sampling from all possible combinations is common in modern randomization tests because it is less computationally intensive than, and asymptotically equivalent to, randomization tests that use all possible combinations if the sample of combinations is large enough (for review, see Kabacoff, 2015; see also Hothorn, Hornik, van De Wiel, & Zeileis, 2008; Wheeler, 2010).

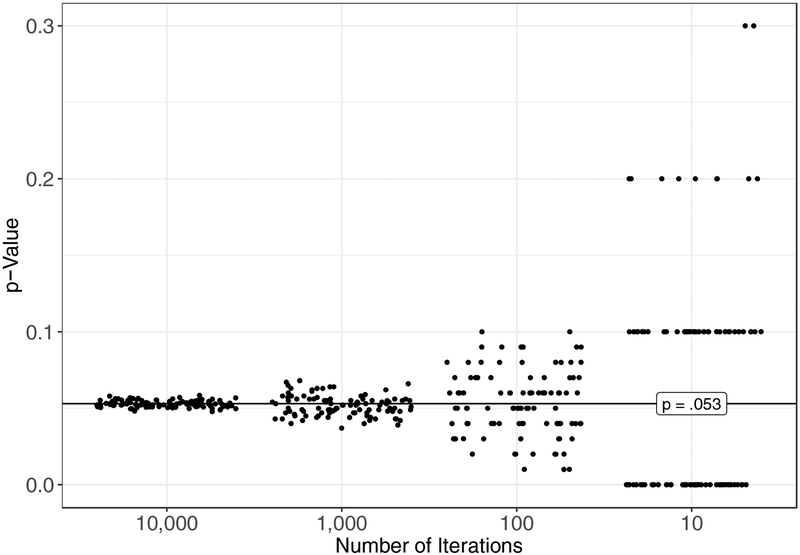
How does one know if a sample is large enough to approximate the outcome of an exhaustive permutation test? Generally speaking, a sample between n = 1,000 and n = 10,000 is sufficient to obtain a precise estimate of the exact p-value that would be derived from a permutation test (see, e.g., Marozzi, 2004). To illustrate why this range of sample sizes is recommended, we sampled from possible combinations of data from Darwin’s (1876) corn-height experiment using Monte Carlo sampling. That is, we randomly generated combinations of group assignments in this experiment with replacement, meaning that it was in principle possible to generate the same combination more than once. (Generating large samples of combinations with replacement is faster and more convenient than generating samples without replacement because, whenever it draws a sample, the computer does not need to check its memory to determine whether that particular sample had been generated before.) In four separate simulations, we drew samples of n = 10,000, n = 1,000, n = 100, and n = 10 from all possible combinations. For each of these sample sizes, we calculated the p-value associated with Darwin’s data by dividing the number of obtained samples with mean differences that were as or more extreme than the difference Darwin obtained by the total number of samples drawn. We repeated this process 100 times to generate 100 p-values for each sample size. Figure 2 shows the resulting p-values for each Monte Carlo sample size. For samples of n = 10,000 and n = 1,000, estimates were reasonably precise (range_10,000: .048 - .058; range_1,000: .037 - .068) and approximated the exact p-value that Fisher (1935) obtained in his reanalysis of the same data (i.e., p = .053; see the horizontal line that bisects the y-axis in Fig. 2). Obtained p-values for samples of n = 100 and n = 10, however, spanned ≥ an order of magnitude around the exact p-value (range₁₀₀: .010 - .100; range₁₀: .000 - .300). Using R software (v. 3.4.1; R Core Team, 2017), it took us an average of 5.49 s per iteration, range: 5.10 – 7.66 s, to calculate p-values using a Monte Carlo sample size of n = 10,000 while generating the data in Figure 2. Thus, interested readers may wish to explore Monte Carlo methods with ns between 1,000 and 10,000 for approximating exact tests if the number of possible combinations of their data is intractably large.

Fig. 2.

p-values from randomization tests that were generated using Monte Carlo sampling from possible permutations of group assignment from Darwin’s (1876) corn-height experiment. Individual p-values were generated using Monte Carlo samples of n = 10,000, n = 1,000, n = 100, and n = 10. For each of these sample sizes, 100 p-values were generated. The horizontal line that bisects the y-axis is the exact p-value from Fisher’s (1935) reanalysis of the same data.

Researchers who are interested in using randomization methods also must consider the minimum sample sizes needed to achieve statistically meaningful p-values. Thus far, we have described randomization methods for mean comparisons between two independent groups and two matched groups. Recall that the total number of combinations for these tests may be calculated using the equations n!/([n! - r!] * r!), where n is the total sample size and r is the size of the individual groups, and 2ⁿ, where n is the number of pairs, respectively. To obtain a p-value of at least .05, the total number of possible combinations needs to be at least 40. That is, if obtained data produce the most extreme possible mean difference between groups, then there will be only two combinations with mean differences as extreme or more extreme than the obtained one: the original data and the combination of the original data where group assignments are perfectly swapped between groups (and p = 2/40 = .05). In the independent-groups case, the required sample size is eight, with four subjects or participants per group. In the paired-groups case, the required number of pairs is six with 12 total observations. (For one-tailed tests, the required sample sizes for paired- and independent-group cases are six total subjects or participants [with three per group] and five total pairs of observations [10 total observations], respectively. Two-tailed tests are more common, however, because they are more conservative than one-tailed tests.)

Finally, the logic of randomization tests requires that, under the null hypothesis, data are exchangeable between the groups or treatments that are being compared. Data are said to be exchangeable if the variance between two sets of data are independent and identically distributed (for discussion, see Anderson, 2001; Good, 2002). Practically, the assumption of exchangeability places two limits on randomization statistics. First, participants/subjects must be randomly assigned to groups, or experimental conditions must be presented in a random order, so as to control for all extraneous factors that might affect the dependent variable. In the case that the independent variable under investigation is an organismic factor (e.g., sex, age, strain, etc.), subjects or participants clearly cannot be randomly assigned to groups. Under these circumstances, though, researchers must be able to assume that no other relevant variables moderate putative between-group differences in the dependent variable. Second, the variance of data from whichever groups or treatment conditions a researcher might like to compare must be homogenous. If variances are heterogeneous between the two groups or treatments, randomization tests may generate inaccurate or misleading results (see, for empirical examples, Boik, 1987; Huang, Xu, Calian, & Hsu, 2006). Dean and Voss (1999) suggested that researchers may assess whether homogeneity of variance is present in their data by dividing the largest group variance (i.e., variance from whichever treatment group demonstrates the largest amount of variability on the outcome of interest) by the smallest group variance: If this ratio is < 3, researchers are unlikely to violate this assumption. Alternatively, researchers may formally test for homogeneity of variance using methods like Levene’s F-test (Levene, 1960). As others have pointed out (e.g., Anderson, 2001; Boik, 1987), the exchangeability assumption of randomization tests often is overlooked, much to the detriment of data analysis. Given the importance of this assumption for the fidelity of randomization-based statistics, we direct readers to the writings of Anderson (2001) and Good (2002) for thorough treatments.

Applications to Behavior-Analytic Data

In the previous sections, we provided a brief historical overview of randomization tests, some advantages of these tests over other statistical methods, and some of the computational and conceptual baggage researchers must consider when applying randomization tests to their data. With this context in mind, we will next provide two examples of how randomization tests may be used to analyze hypothetical data similar to those generated in behavior-analysis laboratories. We will describe two tests that examine mean differences in outcomes between hypothetical treatments. One will consider data from a mixed within-subjects and between-groups design, and the second will demonstrate analysis of data from an individual participant.

Mixed-design Example

“Resurgence” refers to the recurrence of previously extinguished operant behavior when an alternative source of reinforcement is suspended or otherwise reduced in quality (for review, see Lattal & Wacker, 2015; Shahan & Craig, 2017). This topic of study is a hot button in behavior analysis at present: A quick search of Google Scholar with the terms “resurgence” and “behavior analysis” returned well over 500 articles and other scholarly works published since 2014. Accordingly, it seems appropriate to demonstrate how randomization methods might be applied to data from a resurgence experiment.

Typically, resurgence is studied in a three-phase arrangement. During baseline, a target behavior is reinforced. Next, the target behavior is extinguished while an alternative behavior is reinforced. Finally, alternative reinforcement is either reduced (Craig, Browning, Nall, Marshall, & Shahan, 2017; Craig, Browning, & Shahan, 2017; Lieving & Lattal, 2003) or eliminated altogether (Craig, Cunningham, Sweeney, Shahan, & Nevin, 2018; Craig & Shahan, 2016; Fisher et al., 2018; Fisher et al. (in press); Leitenberg, Rawson, & Mulick, 1975; Nevin et al., 2016). Resurgence occurs if target behavior returns in this last phase. Typically, researchers are most interested in comparing rates of target behavior during the final session of the alternative-reinforcement treatment phase (where responding often is lowest during treatment) and the first session of the resurgence test (where responding often is highest during the test).

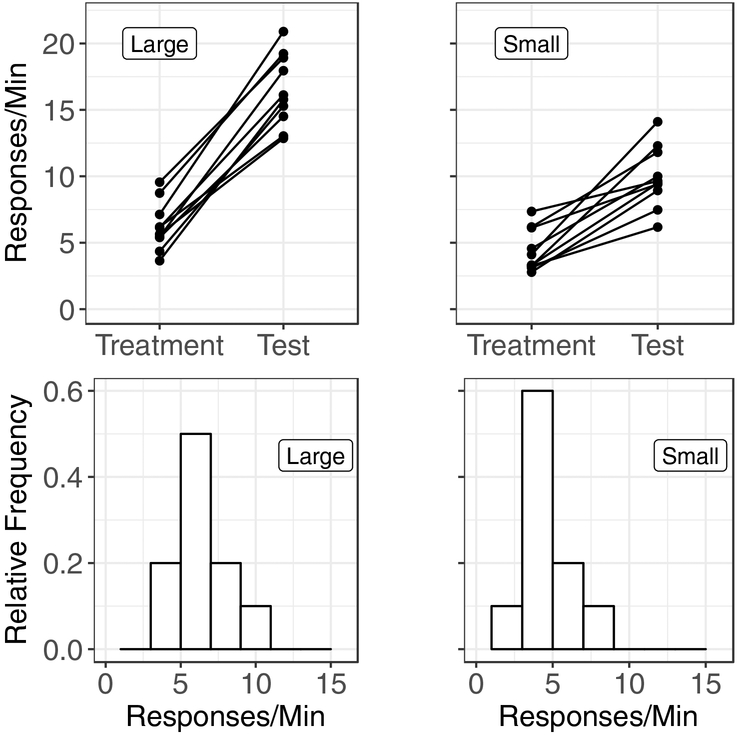
We generated data for a hypothetical experiment that examined resurgence in two groups of subjects (for the sake of argument, let’s say they were rats; n = 10 in both groups): One group experienced a set of contingencies that we hypothesized would produce a relatively large resurgence effect (we will call this the “Large” group), and the other group experienced contingencies that we hypothesized would produce a relatively small resurgence effect (the “Small” group). Hypothetical data from the last session of treatment and the first session of the resurgence test for these groups are shown in the top two panels of Figure 3.

Fig. 3.

Top panels: Hypothetical response-rate data from the last session of an alternative-reinforcement treatment and the first session of a resurgence test for the treatments that we hypothesized should produce a large amount of resurgence (left panel) and a small amount of resurgence (right panel). Bottom panels: Histograms showing the distribution of response rates from the last session of the alternative-reinforcement treatment phase for the treatments we hypothesized should produce a large amount of resurgence (left panel) and a small amount of resurgence (right panel). The bin width for these histograms is two responses per minute.

Visual analysis suggests our initial hypothesis might have some support: The increase in responding during the resurgence test tended to be higher in the Large group than in the Small group, but there is quite a bit of variability in both groups. How should we go about analyzing these data to provide a second (statistical) opinion? A mixed ANOVA with a within-subject factor of Phase and a between-groups factor of Group might do the trick, but we sampled these data from a distribution with a strong positive skew (generated using the “sn” package in R; Azzalini, 2018), so the distribution of response rates at each combination of the Phase and Group are distributed nonnormally. Because nonnormality of the outcome variable at any specific level of the predictor variable is equivalent to nonnormality of the residuals of obtained scores around predicted scores, we can be certain that the assumption of normality that is critical for ANOVA has been violated. To illustrate, the bottom two panels of Figure 3 show the distribution of response rates during the final session of the alternative-reinforcement treatment phase for the Large and Small groups. Even with a relatively small sample size of n = 10 in both groups, these histograms demonstrate that most of our hypothetical rats responded at a relatively low rate, but a few responded at a high rate (this is especially clear in the “Small” group). These data show that the assumption of normality has been violated to a substantial degree, and thus, an ANOVA may produce spurious results. By contrast, this deviation from the normality assumption will not adversely affect the results of a randomization-based analysis. We randomly assigned our hypothetical animals to groups, and the groups showed roughly equal variability between groups, and between time points within groups, on our dependent variable, so our data meet the exchangeability assumption for randomization.

To address our research question, we are most interested in the interaction between Group and Phase, because that will tell us whether response rates increased more in one group than in the other between phases. As we described above in the “A Brief History of Randomization Methods” section, the correct method for assessing interactions between independent variables in randomization tests is up for debate (see Anderson, 2001; Howell, 2015), but for demonstrative purposes we will adopt Edgington and Onghena’s (2007) approach. Briefly, Edgington and Onghena suggested reshuffling data between both factors of the two-way ANOVA and calculating an interaction F statistic for each set of reshuffled data a large number of times to create a reference distribution against which the researcher can compare the interaction F statistic from the original, unshuffled data. Violation of the assumption of normality inflates the rate of Type-I errors (i.e., of obtaining a false positive; rejecting the H₀ when, in reality, no difference exists) for individual F statistics, but this should be true for each reshuffled F statistic in the reference distribution. Thus, randomization should control for the inflated Type-I error rate, because the resulting p-value is derived from comparison of the original F statistic to all of the F statistics in the reference distribution.

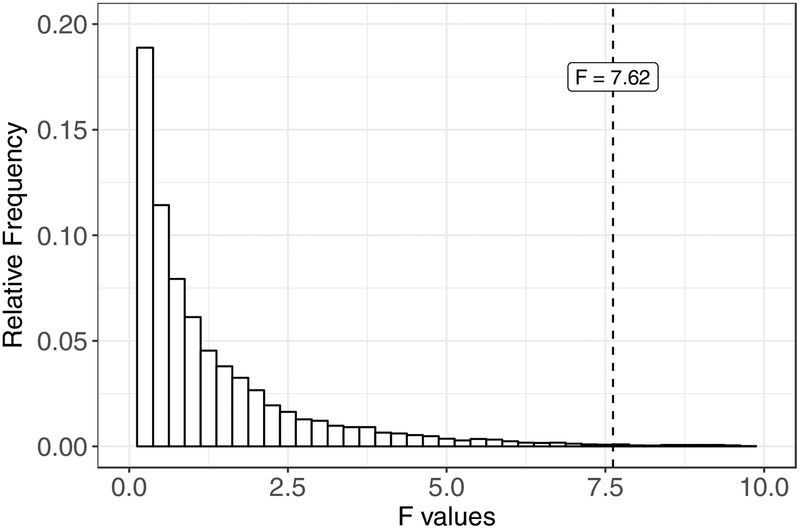
Table 1 shows the four cells for the present ANOVA. Our first step in randomizing these data was to reshuffle data across the within-subjects measure, Phase. As in Fisher’s (1935) randomization test, we did not separate measures of individual rats’ response rate during the treatment phase and the test phase but instead simply randomized each individual’s response rate between phases (e.g., we may switch scores between G₁P₁ and G₁P₂, but we will not switch scores between G₁P₁ and G₂P₁). Next, we reshuffled data across the between-groups measure, Group. To do this, we randomly distributed subjects across the two groups while maintaining the paring between individuals’ treatment and test response rates. After each randomization (n = 10,000 in total), we conducted a 2 X 2 (Group X Phase) mixed ANOVA to obtain an F-value for the interaction. The reference distribution of interaction F-values that we obtained is shown in Figure 4. To calculate the p-value for our interaction term: (a) we summed the number of F statistics in our reference distribution that were equal to or larger than the interaction F value derived from a 2 X 2 (Group X Phase) mixed ANOVA conducted on our obtained data, F(1, 34) = 7.62, p = .009 (see the vertical line that bisects the x-axis of Fig. 4), and (b) divided by 10,000 (we use a one-tailed hypothesis test here because F tests invariably are one-tailed tests). The resulting p-value from the randomization test was identical to the p-value obtained from the original ANOVA conducted on our obtained data to three decimal places. Thus, we may conclude that violating the normality assumption had a relatively minor impact on the fidelity of our test statistic, but we would not have known that had we not conducted the randomization-based F-test. Thus, based on these results, we would reject the null hypothesis of no difference and conclude that the difference in levels of resurgence obtained between the “Large” and “Small” groups is unlikely to have resulted from chance.

Table 1.

Factorial ANOVA table for our hypothetical resurgence experiment

	Phase
Group	Treatment	Test
Large	G1P1	G1P2
Small	G2P1	G2P2

Fig. 4.

Reference distribution of F values for the interaction term in our hypothetical relapse experiment. The vertical line that bisects the x-axis represents F = 7.62, the resulting interaction F value from a 2 X 2 (Group X Phase) mixed ANOVA on the data shown in the top two panels of Fig. 3. The bin width for this histogram was F = 0.25.

At this point in the analysis, it is unnecessary to test the main effects of Group or Phase individually. These effects would provide no information beyond what is provided by the interaction between them. We will, however, describe one method to test for these effects in a randomization framework for the sake of clarity. In a factorial ANOVA, Edgington and Onghena (2007) suggested to test for the effects of one factor by permuting obtained data across levels of that factor while holding levels of the other factor constant (this method is sometimes referred to as “restricted randomization between factors”).³ That is, to test for the main effect of Phase in the present hypothetical experiment, we randomly reassigned data between the treatment phase and the test phase while maintaining group assignments for all subjects. For each rearrangement of data, we calculated the F statistic for the main effect of Phase, against which we compared the F statistic for Phase calculated for our obtained data, F(1, 34) = 57.73, p < .001, to obtain a randomization p-value. To test for the main effect of Group, we randomly assigned group labels to each subject, but we did not randomize data between the phases of the experiment. We then created the reference distribution by calculating the F-value for Group for each rearrangement of data and compared our original obtained F-value for Group, F(1, 34) = 9.14, p = .005, against this distribution to obtain a p-value. The resulting p-value from the randomization test for Group was p = .043, whereas the p-value for the test of Phase was p < .001. This outcome for Phase was a foregone conclusion, because responding increased across phases for every subject in both groups, so no possible rearrangement of data across phases could produce a larger effect of Phase.

Single-case Example

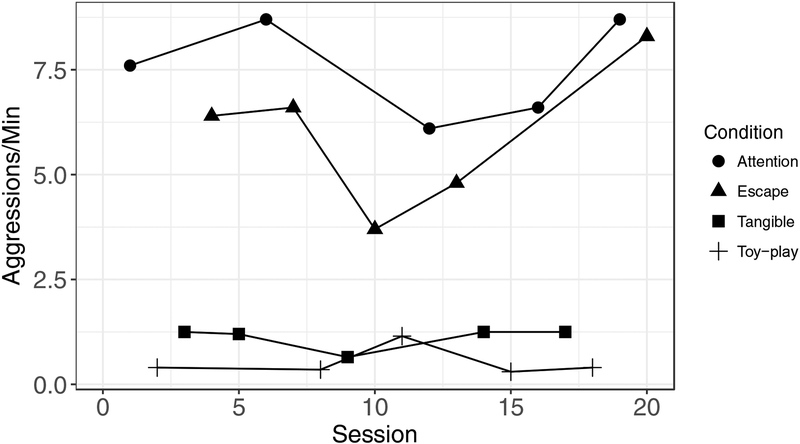
Applied researchers and practitioners often use functional analyses (Iwata, Dorsey, Slifer, Bauman, & Richman, 1982/1994) to identify the environmental variables that evoke and reinforce participants’ problem behavior. These assessments consist of several conditions with a different set of contingencies in place in each. To determine whether a participant engages in problem behavior to gain access to attention or tangible items, a therapist typically withdraws his or her attention or restricts access to preferred tangibles and delivers attention or tangibles again only if the participant engages in problem behavior. To determine whether escape from demands reinforces problem behavior, a therapist typically delivers instructions and provides a break from instructions only if the participant engages in problem behavior. Functional analyses often include a control condition in which the purported establishing operations in the test conditions described above are absent. For example, a therapist typically delivers attention on a dense schedule, provides access to tangibles freely and continuously, and abstains from delivering instructions during the control condition. Applied researchers often refer to this condition as “toy play”.

Despite the utility of skilled visual assessment in determining functions of behavior from functional-analysis outcomes and the development of structured, formal visual-analysis protocols for functional analyses (e.g., Hagopian et al., 1997; Roane, Fisher, Kelley, Mevers, & Bouxsein, 2013; Saini, Fisher, & Retzlaff, 2018), assessment of differences in levels of problem behavior between conditions is not always straightforward. Figure 5, for example, shows aggressions per minute from a hypothetical multielement functional analysis. We presented attention, escape, tangible, and toy-play (or control) conditions in a randomized order across sessions so that each condition was arranged in five sessions with the caveat that each condition needed to be presented within successive four-session series. Aggression occurred at relatively high rates in the attention condition during the initial two sessions, but it occurred at rates similar to those observed in the escape condition in the remaining three sessions. The escape condition evoked moderate-to-high rates of aggression in three sessions, but relatively low rates in two sessions. Finally, aggression occurred at relatively low rates in the tangible condition, but it occurred at higher rates than in the toy-play condition in four of five sessions. Based solely on visual inspection, it is reasonably clear that the attention and escape conditions evoked problem behavior, but it is less clear for the tangible condition. Inasmuch, for the tangible condition it is reasonable for the behavior analyst to ask, “How often might the observed or larger differences between the tangible and the toy-play conditions occur by chance?” If the observed differences between the tangible and toy-play conditions are unlikely to have occurred by chance, then it would be important for the behavior analyst to address the tangible function during treatment. In addition, with regard to the attention and escape conditions, it is reasonable for the behavior analyst to ask, “Which one of these conditions produced the more evocative effect?” If one condition produced more evocative effects than the other, and the differences are unlikely to have occurred by chance, then the behavior analyst might decide to address the more evocative function of problem behavior first during treatment.

Fig. 5.

Aggressive behaviors per minute from a hypothetical multielement functional analysis.

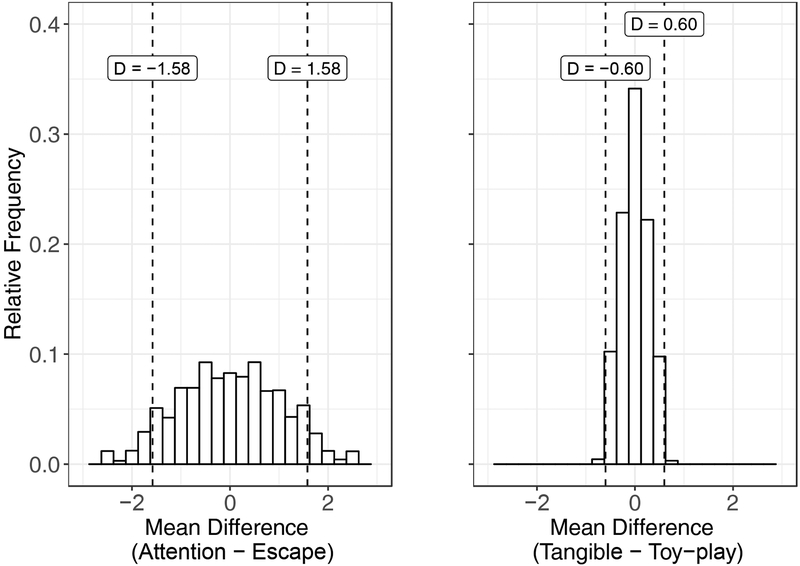
Randomization analyses may provide a helpful tool in making decisions about these types of outcomes. Because we randomized the presentation of conditions in each series and variability is at least roughly proportional between the conditions that we wish to compare, data are exchangeable between conditions. The H₀ is that the conditions of the functional analysis had no effect on rates of aggression. That is, the data obtained from one condition should be equally likely to appear in another condition. Using randomization analyses, we performed pairwise comparisons of aggression between the pairs of conditions about which we had remaining questions following visual inspection (i.e., attention vs. escape and tangible vs. toy play). To begin, we calculated the differences in mean rates of aggression between each pair of conditions (attention vs. escape: D = 1.58 aggressions per minute; tangible vs. toy play: D = 0.60 aggressions per minute). Next, for each pairwise comparison, we rearranged response rates randomly between the two conditions 10,000 times. For each rearrangement, we calculated the difference in the mean rates of aggression between conditions and used those rearranged data to create reference distributions for each pairwise comparison.

Figure 6 shows the reference distributions for each of these pairwise comparisons, with the distribution of attention—escape difference scores on the left and the distribution of the tangible–toy-play difference scores on the right. The vertical dashed lines that bisect the x-axes in each panel represent the mean differences between conditions calculated from the original data. Out of 10,000 randomly generated samples per distribution, 1,461 samples produced mean differences that were as extreme as, or more extreme than the obtained mean difference for the comparison between the attention and escape conditions, corresponding to a p-value of .146. For the comparison between the tangible and toy-play conditions, we obtained 160 difference scores that were as or more extreme than the original, obtained mean difference, corresponding to a p-value of .016.

Fig. 6.

Reference distributions for mean differences comparing the attention and escape (left panel) and tangible to toy-play (right panel) conditions from the hypothetical functional analysis results shown in Fig. 5. The vertical dashed lines that bisect the x-axes in each panel represent the between-condition mean differences observed in the obtained data. The bin width for these histograms was D = 0.25.

Because we conducted multiple comparisons in the examples above, we should adjust our α-level (e.g., using the conservative Bonferroni correction, which divides the α-level by the number of comparisons made; α = .050 / 2 = .025). This correction holds constant the experiment-wise error rate. After calculating this correction, we can reasonably conclude that the original, obtained difference between the attention and escape conditions failed to meet our criterion for statistical significance and easily could have occurred by chance. Thus, the behavior analyst could decide which function of aggression to address first based on practical or other considerations rather than based on the observed differences between the attention and escape conditions. By contrast, the original, obtained difference between the tangible and toy-play condition met our criterion for statistical significance and was unlikely to have occurred by chance. This finding suggests that it would be important for the behavior analyst to address the observed tangible function during treatment.

We generated the data for our hypothetical functional analysis by randomly sampling from normal distributions. Accordingly, we had no reason to be concerned about autocorrelation between our generated data points, though a case might be made that data in the attention and escape conditions tended to covary despite the random nature of the underlying process used to generate these data. Some authors have argued that autocorrelation between data points is not problematic for application of basic randomization techniques, while others have suggested that autocorrelation violates the assumption of exchangeability required for these statistics (for review, see Sierra, Solanas, & Vincenç, 2005).

The problem of autocorrelation affects certain single-case designs more so than other designs. As mentioned previously, data points that are closer together in a data series tend to show greater correlation than data points that are further apart in the series. As such, single-case designs that rapidly alternate between comparison conditions (e.g., multielement or multiple-schedule designs) tend to be less susceptible to p-value inflation due to autocorrelation because a given data point from a given condition occurs closer in time to data points from different conditions than to data points from the same condition. For example, an attention session in a multielement functional analysis tends to occur closer in time to sessions from other conditions (e.g., an escape or tangible session) than to the next attention session. Thus, in this case, autocorrelation is likely to result in p-value deflation rather than inflation because autocorrelation due to the temporal proximity of data points in the series will decrease the observed difference between a given test condition and its comparison condition(s). By contrast, single-case designs that infrequently alternate between comparison conditions (e.g., reversal or multiple-baseline designs) tend to be more susceptible to p-value inflation due to autocorrelation because data points within a given condition tend to be closer to one another than to data points from the comparison condition(s). Readers should consider the potential effects of autocorrelation when choosing a single-case design and corresponding statistical analysis with which to evaluate their experimental question. In general, randomization tests are best suited for single-case designs that randomly and rapidly alternate experimental conditions over the course of a data series.

Conclusions

Randomization-based statistical techniques offer flexible, powerful, nonparametric alternatives to the statistical techniques often used in psychological research (e.g., t- and F-tests). These methods draw inferences based on obtained data rather than hypothetical populations. The same basic approach can accommodate data from just about all of the experimental designs commonly used in behavior-analytic research, including between-groups, within-subjects, mixed, and single-case research designs (even when there is just one participant). That is, outside of the sample-size requirements to make achievement of desired p-values analytically possible (e.g., n = 8 in independent-sample tests, with four participants or subjects in each of two groups; n = 6 pairs of observations for a total of 12 observations in paired-sample tests), randomization tests are well suited for analysis of data from experiments with relatively few participants, subjects, or observations. Because of the advantages that randomization tests offer over their parametric and nonparametric counterparts, behavior analysts may wish to incorporate these methods for data analysis into their repertoires.

For readers who are interested in conducting randomization tests, we suggest they become acquainted with R software (R Core Team, 2017). This free-to-use statistical-computing software allows users to create flexible programs for performing these analyses. Howell (2015) provides an approachable overview of randomization tests for various research designs and provides example R code that may be helpful to readers. Furthermore, downloadable, user-created software may help users to conduct these analyses without writing custom functions. For example, the “coin” package (Hothorn et al., 2008) offers routines for conducting permutation tests on many types of data and for many types of research questions.

Our motivation for writing this article was not to imply that randomization methods always are preferable relative to other methods for statistically analyzing obtained behavior-analytic data. If collected data meet the assumptions of t- or F-tests, or their nonparametric counterparts, randomization may not be the most desirable method for data analysis. For example, Peres-Neto and Olden (2001) conducted a simulation study to compare parametric, nonparametric, and randomization-based methods in terms of their associated Type-I error rates and statistical power for various statistical questions (i.e., comparing mean differences between multiple groups and determining the degree of relatedness between sets of variables). These authors observed that, under many circumstances, randomization-based methods were superior to other methods in that they reduced Type-I error rates while maintaining high levels of statistical power. Under other circumstances, however, randomization methods were outperformed by their competitors. Peres-Neto and Olden concluded, “… although randomization tests appear to be a powerful alternative to parametric and classic nonparametric statistics, this is not a general rule and their appropriateness should be judged and compared to alternatives” (p. 85).

Unfortunately, short of conducting a simulation study to evaluate and compare Type-I error rates and statistical power between different tests, it may not be possible to judge which specific statistical method is the most appropriate for a specific set of data in an a priori manner. Many factors play into that determination, including the distributional properties of the data in question, the extent to which properties of the data violate assumptions of alternative statistical methods, the amount of variation in the data, and so on. Thus, we encourage readers to become familiar with diverse statistical methods and to view randomization statistics as one of many potential tools that they may use to supplement analysis of their data.