Does evidence support the high expectations placed in precision medicine? A bibliographic review

Jordi Cortés; José Antonio González; María Nuncia Medina; Markus Vogler; Marta Vilaró; Matt Elmore; Stephen John Senn; Michael Campbell; Erik Cobo

doi:10.12688/f1000research.13490.3

. 2018 Nov 15;7:30. Originally published 2018 Jan 9. [Version 3] doi: 10.12688/f1000research.13490.3

Does evidence support the high expectations placed in precision medicine? A bibliographic review

Jordi Cortés ^1,^a, José Antonio González ¹, María Nuncia Medina ², Markus Vogler ³, Marta Vilaró ⁴, Matt Elmore ¹, Stephen John Senn ⁵, Michael Campbell ⁶, Erik Cobo ¹

PMCID: PMC6524747 PMID: 31143439

Version Changes

Revised. Amendments from Version 2

The following major changes have been introduced in the manuscript: 1) Three references have been added that aim to clarify some issues related to the constant effect assumption. 2) A broader explanation of the statistical methods used in the analysis has been incorporated. 3) The interpretation of the constant effect assumption by the authors of the articles included in the bibliographic review has been softened. 4) A new section has been added to the supplementary material dealing with the conditions for having a constant effect in an additive effect model.

Abstract

Background: Precision medicine is the Holy Grail of interventions that are tailored to a patient’s individual characteristics. However, conventional clinical trials are designed to find differences with the implicit assumption that the effect is the same in all patients within the eligibility criteria. If this were the case, then there would be no grounds for treating different patients differently. One consequence of the assumption is that the variance in the outcome variable would be the same in treated and control arms. We reviewed the literature to see if this were the case and so to see how often precision medicine would not be useful.

Methods: We reviewed parallel trials with quantitative outcomes published in 2004, 2007, 2010 and 2013. We collected baseline and final standard deviations of the main outcome. We assessed homoscedasticity by comparing the variance of the primary endpoint between arms through the outcome variance ratio (treated to control group).

Results: The review provided 208 articles with enough information to conduct the analysis. One out of seven studies (n = 30, 14.4%) had statistically different variances between groups, leading a non-constant-effect. The adjusted point estimate of the mean outcome variance ratio (treated to control group) is 0.89 (95% CI 0.81 to 0.97).

Conclusions: We found that the outcome variance was more often smaller in the intervention group, suggesting that treated patients may end up pertaining more often to reference or “normality” values and thus would not require further precision medicine. However, this result may also be compatible with a reduced effect in some patients, which would require studying whether the effect merits enduring the side effects as well as the economic costs. We have shown that the comparison of variances is a useful but not definitive tool to asses if the design assumption of a constant effect holds.

Keywords: Constant Effect, Precision medicine, Homoscedasticity, Clinical Trial, Variability, Standard deviation, Review

Introduction

The idea behind precision medicine is to develop prevention and treatment strategies that take into account individual characteristics. With this strong endorsement “The prospect of applying this concept broadly has been dramatically improved by recent developments in large-scale biologic databases (such as the human genome sequence), powerful methods for characterizing patients (such as proteomics, metabolomics, genomics, diverse cellular assays, and mobile health technology), and computational tools for analyzing large sets of data.”, US President Obama launched the Precision Medicine initiative in 2015 to capitalize on these developments ^1,
2. However, we aim to quantify the proportion of interventions that may benefit from this idea.

The variability of a clinical trial outcome measure should interest researchers because it conveys important information about whether or not there is a need for precision medicine. Does variance come only from unpredictable and ineluctable sources of patient variability? Or should it also be attributed to a different treatment effect that requires more precise prescription rules ^3–
5? Researchers assess treatment effect modifications (“interactions”) among subgroups based on relevant variables. The main problem with that methodology is that, by the usual standards of a classical phase III trial, the stratification factors must be known in advance and be measurable. This in turn implies that when new variables are discovered and introduced into the causal path, new clinical trials are needed. Fortunately, one observable consequence of a constant effect is that the treatment will not affect variability, and therefore the outcome variances in both arms should be equal (“homoscedasticity”). If this homoscedasticity holds, there is no evidence that the clinical trial should be repeated once a new possible effect modifier becomes measurable.

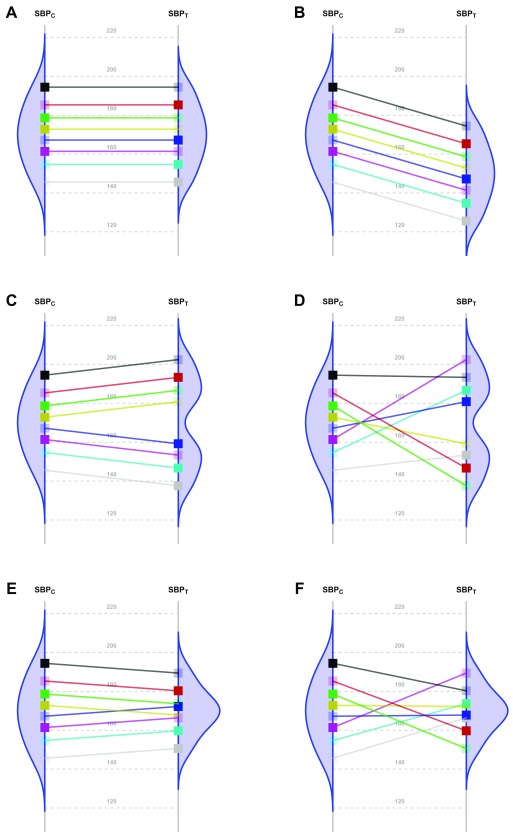
Nevertheless, the fundamental problem of causal inference is that for each patient in a parallel group trial, we can know the response for only one of the interventions. That is, we observe their response to either the new Treatment or to the Control, but not both. By experimentally controlling unknown confounders through randomization, a clinical trial may estimate the averaged causal effect. In order to translate this population estimate into effects for individual patients, additional assumptions are needed. The simplest one is that the effect is constant. Panels A and B in Figure 1 ^6–
15 represent two scenarios with a common effect in all patients, although the effect is null in the first case. Following Holland ¹⁶, this assumption has the advantage of making the average causal effect relevant to each patient. All other scenarios ( Figure 1, Panels C to F) require additional parameters to fully specify the treatment effect.

Figure 1. — Because of the random allocation to one of two treatment arms, we will observe only one of the two potential outcomes for each patient: either under T or under C. Fully saturated colors represent observed Systolic Blood Pressure (SBP) values, and transparent squares represent missing potential values. The line slope indicates the individual non-observable effect for each patient. Densities are the potential distributions of the outcome in each group: As both random samples come from the same target population, the average causal effect is estimable without bias. **Panel A** shows the potential outcome values that we could obtain if there were not any treatment effect; as the intervention has no effect at all, both groups have the same distribution (i.e., mean and variance). **Panel B** shows the scenario of a constant effect, meaning that the intervention lowers the SBP by a single value in every patient and thus implying the same variability in both arms. For instance, the study from Duran-Cantolla *et al.* ⁶ compared the 24-hour systolic blood pressure among 340 patients randomized to either Continuous Positive Airway Pressure (CPAP) or sham–CPAP, and it showed a greater decrease of 2.1 mmHg (95% CI from 0.4 to 3.7) in the intervention group compared to the control group. Furthermore, baseline standard deviations (SDs) were 12 and 11; and final SDs were 13 for both groups. Therefore, their results fully agree with the trial design’s assumption of a constant effect (scenario B) and nothing contradicts the inference that each patient exhibits a constant reduction of 2.1mmHg, although the uncertainty of random allocation makes the results compatible with a constant effect that lies anywhere between 0.4 and 3.7. **Panel C** represents a situation with 2 different effects in 2 subpopulations (“treatment by subgroup interaction”). Although the effects are identical within them, the observable distribution in the treated arm would have higher variability. Here, we need to find finer eligibility criteria for classifying patients in those subpopulations so that a constant effect could be assumed again. In **Panel D**, the treatment has a variable effect in each patient, resulting also in greater variability within the treated arm but without any subgroup sharing a common effect. The results are poorly predictive about the effects on future patients. In the study by Kojima *et al.* ⁷, the primary outcome measure was the 3-hour postprandial area under the curve of apolipoprotein B48, with outcome SDs being 0.78 and 0.16 in the treated and reference arms, respectively, and thus showing an outcome variance ratio of 23.77. This is compatible with different treatment effects that could need additional refinements through precision medicine, since a greater variance in the treated arm indicates that “ *the interpretation of the main treatment effect is controversial”* ⁸. In that case, guidelines for treating new patients should be based either on additional eligibility criteria (“precision medicine”, panel C) or on n-of-1 trials (“individualized medicine”, panel D) ^9–
13. This “treatment by patient interaction” was already highlighted by W. S. Gosset in the data of his 1908 paper proposing the Student t-distribution ¹⁴. Alternatively, interactions can result in smaller variances in the treated arm. **Panel E** shows a different effect in 2 subgroups; but the variability is now reduced indicating that the best solution would be to identify the subpopulations in order to refine the selection criteria. In **Panel F**, the treatment again has a variable effect on each patient; but unlike Panel D, in this case the result is less variability within the treated arm. In the study from Kim *et al.* ¹⁵, the primary endpoint was the PTSD Checklist–Civilian version (PCL-C). This scale is based on the sum of 17 Likert symptoms, ranging from 17 (perfect health) to 85 (worst clinical situation). At the end of the trial, the respective outcome SDs were 16 and 3 for the control and treated arms, meaning that variance was reduced around 28 times. This situation can correspond to scenarios E or F, and it merits much more statistical consideration, which is beyond the scope of this paper.

As an example, the 10 clinical trials published in the journal Trials in October 2017 ( Supplementary File 1: Table S1) were designed without explicitly mentioning that the effect was not constant within the study population. Furthermore, all their analyses were designed to estimate just an average effect with no mention of any possible interaction with baseline variables ( Figure 1, Panels C and E), nor did they discuss any random variability for the treatment effect ( Figure 1, Panels D and F). In those scenarios, the authors should take these factors into account when designing their trials. For example, Kim et al. ¹⁷ designed their trial to test the intervention for non-inferiority in the overall population and for superiority in the subgroup of patients with high epidermal growth factor receptor. So, without further specifications, it seems that they were hoping for the treatment effect to be the same for all patients.

Below, we will elucidate whether the comparison of observed variances may shed some light on the non-observable individual treatment effect.

Our objectives were, first, to compare the variability of the main outcome between arms in clinical trials published in medical journals; and, second, to provide a rough estimate of the proportion of studies that could potentially benefit from precision medicine. To assess the consistency of results, we explore the changes in the variability of the experimental arm over time (from baseline to the end of the study).

Methods

Population

Our target population was parallel randomized clinical trials with quantitative outcomes (not including time-to-event studies). The trials needed to provide enough information to assess two homoscedasticity assumptions in the primary endpoint: between arms at trial end; and baseline to outcome over time in the treated arm. Therefore, baseline and final SDs for the main outcome were necessary or, failing that, we needed at least one measure that would allow us to calculate them (variances, standard errors or mean confidence intervals).

Data collection

Articles on parallel clinical trials from the years 2004, 2007, 2010 and 2013 were selected from the Medline database with the following criteria: “ AB (clinical trial* AND random*) AND AB (change OR evolution OR (difference AND baseline)” [The word “difference” was paired with “baseline” because the initial purpose of the data collection, subsequently modified, was to estimate the correlation between baseline and final measurements]. The rationale behind the selection of these years was to have a global view of the behavior of the studies over a whole decade. For the years 2004 and 2007, we selected all papers that met the inclusion criteria; however, we retrieved a greater number of articles from our search for the years 2010 and 2013 (478 and 653, respectively) and therefore chose a random sample of 300 papers (Section II in Supplementary File 1).

Data were collected by two different researchers (NM, MkV) in two phases: 2004/2007 and 2010/2013. Later, two statisticians (JC, MtV) verified the data and made them accessible to readers through a shiny application and through the Figshare repository ¹⁸.

Variables

Collected variables were: baseline and outcome SDs; experimental and reference interventions; sample size in each group; medical field according to Web of Science (WOS) classification; main outcome; patient’s disease; kind of disease (chronic or acute); outcome type (measured or scored); intervention type (pharmacological or not); improvement direction (upwards or downwards) and whether or not the main effect was statistically significant.

For studies with more than one quantitative outcome, the primary endpoint was determined according to the following hierarchical criteria: (1) objective or hypothesis; (2) sample size determination; (3) main statistical method; (4) first quantitative variable reported in results.

In the same way, the choice of the "experimental" arm was determined depending on the role in the following sections of the article: (1) objective or hypothesis; (2) sample size determination; (3) rationale in the introduction; (4) first comparison reported in results (in the case of more than two arms).

Statistical analysis

We assessed homoscedasticity between treatments and over time. For the former, our main analysis compared, the outcome variability between Treated (T) and Control (C) arms at the trial end. For the latter, we compared the variability between Outcome (O) and its Baseline (B) value for the treated arm.

Two different methods were used to compare the variances: a random-effects model and a classical variance comparison test.

To distinguish between the random sampling variability and heterogeneity, we fitted a random-effects model. The response was the logarithm of the outcome variance ratio at the end of the trial. The covariates were the study as a random effect and the logarithm of the variance ratio at baseline served as a fixed effect ¹⁹.

The main fitted model for between-arm comparison was:

\log {(\frac{V_{O T}}{V_{O C}})}_{i} = μ + S_{i} + β . \log {(\frac{V_{B T}}{V_{B C}})}_{i} + e_{i}

w i t h S_{i} \sim N (0, τ^{2}) a n d e_{i} \sim N (0, v_{i}^{2})

where V _XX represent the variances of the outcome in each arm (V _XT, V _XC) at the end of the study (V _OT, V _OC) and at baseline (V _BT, V _BC). The parameter μ is the logarithm of the average variance ratio across all the studies; s _i represents the heterogeneity between-study effect associated with study i with variance τ ²; β is the coefficient for the linear association with the baseline variance ratio; and e _i represents the intra-study random error with variance $v_{i}^{2}$ .

The parameter μ represents a measure of the imbalance between the variances at the end of the study, which we call heteroscedasticity.

The estimated value of τ ² provides a measure of heterogeneity, that is, to what extent the value of μ is applicable to all studies. The larger τ ² is, the less the homogeneity.

The percentage of variance explained by the differences among studies in respect to the overall variance is measured by the I ² statistic ²⁰. That is:

I^{2} = \frac{τ^{2}}{τ^{2} + v^{2}}

v ² is the expected value of the error variance.

An analogous model was employed to assess the homoscedasticity over time. As there is only one available measure for each study, it is not possible to differentiate both sources of variability: (i) within-study or random variability; and (ii) heterogeneity. To isolate the second, the first was estimated theoretically using either the Delta method in the case of comparison between arms or some approximation in the case of comparison over time (see details in Sections VI and VII of Supplementary File 1):

V [l o g (\frac{V_{O T}}{V_{O C}})] = \frac{2}{n_{O T} - 2} + \frac{2}{n_{O C} - 2} (b e t w e e n a r m s)

V [l o g (\frac{V_{O T}}{V_{B T}})] = \frac{4}{n - 1} - 2 \cdot l o g [1 + \frac{2 \cdot C o r r {[Y_{O T}, Y_{B T}]}^{2}}{n^{2} / (n - 1)}] (o v e r t i m e)

In order to obtain a reference in the absence of treatment effect, we first modeled the baseline variance ratio as a response that is expected to have heterogeneity equal to 0 due to randomization – so long as no methodological impurities are present (e.g., considering the outcomes obtained 1 month after the start of treatment to be the baseline values). This reference model allows us to know the proportion of studies in the previous models that could have additional heterogeneity and which cannot be explained by the variability among studies (Section III in Supplementary File 1). Specifically, studies with larger discrepancies in variances were removed one by one until the estimated value of τ was as close as possible to that of the reference model. These deleted studies were considered to be those that had significantly different variances, perhaps because the experimental treatment either increased or decreased the variance.

Centered at zero, funnel plots for the measurement of interest as a function of its standard error are reported in order to help investigate asymmetries.

In addition, we also assessed homoscedasticity in each single study using pre-specified tests: (a) between outcomes in both arms with an F-test for independent samples; and (b) between baseline and outcome in the treated arm with a specific test for paired samples ²¹ when the variance of the paired difference was available. All tests were two-sided (α=5%).

Several subgroup analyses were carried out according to the statistical significance of the main effect of the study and to the different types of outcomes and interventions.

All analyses were performed with the R statistical package version 3.2.5. (The R code for the main analysis is available from https://doi.org/10.5281/zenodo.1239539 ²²)

Results

Population

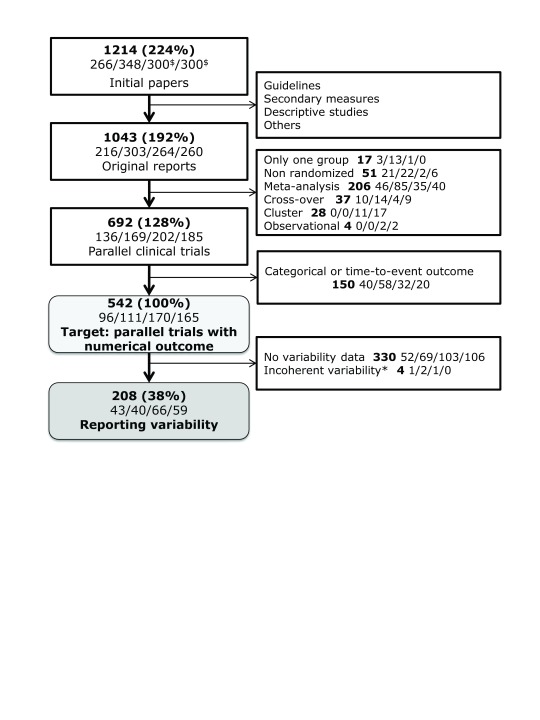
A total of 1214 articles were retrieved from the search. Of those papers, 542 belong to the target population and 208 (38.4%) contained enough information to conduct the analysis ( Figure 2).

Figure 2. — Percentages represent the quantity of papers in the target population. The number of articles for each year (2004/2007/2010/2013) is specified in the second line of each box (separated by slashes). ^$300 papers were randomly selected for years 2010 and 2013. *Four papers were excluded because the variance of the change over time was inconsistent with both the baseline and final variances, which would lead to impossible absolute correlation estimates greater than 1.

Overall, the selected studies were non-pharmacological (122, 58.6%), referred to chronic conditions (101, 57.4%), had an outcome measure with units (132, 63.8%) instead of a constructed scale, had an outcome that was measured (125, 60.1%) rather than assessed; and had better responses corresponding to lower values (141, 67.8%). Regarding the primary objective of each trial, the authors found statistically significant differences between arms (all of which favoring the experimental group) in 83 (39.9%) studies. Following the WOS criteria, 203 articles (97.6%) belonged to at least one medical field. The main areas of study were: General & Internal Medicine (n=31, 14.9%), Nutrition & Dietetics (21, 10.1%), Endocrinology & Metabolism (19, 9.1%), and Cardiovascular System & Cardiology (16, 7.7%).

Homoscedasticity

On average, the outcome variance ratio is close to one, with evidence of smaller variability in the treated arm. At the end of the study, 113/208 (54%, 95% CI, 47 to 61%) papers showed less variability in the treated arms ( Supplementary File 1 : Figure S1 and Figure S2). Among the treated arms, 111/208 (53%, 95% CI, 46 to 60%) had less or equal variability at the end of follow-up than at the beginning ( Supplementary File 1 : Figure S3 and Figure S4).

Regarding the comparison between arms and according to the random-effects model ( Supplementary File 1 : Table S4, model 3), the adjusted point estimate of the mean outcome variance ratio (Treated to Control group) is 0.89 (95% CI 0.81 to 0.97), indicating that treatments tend to reduce the variability of the patient's response by about 11% on average. As for the comparison over time ( Supplementary File 1 : Table S4, model 6), the average variability at the end of the study is 14% lower than that at the beginning.

The estimated baseline heterogeneity (τ ²) was 0.31 ( Supplementary File 1 : Table S4, model 1), which is a very high value that could be explained by methodological flaws similar to those presented by Carlisle ²³. Fortunately, the exclusion of the four most extreme papers reduced it to 0.07 ( Supplementary File 1 : Table S4, model 2); one of these was the study by Hsieh et al. ²⁴ whose “baseline” values were obtained 1 month after the treatment started. When we modeled the outcome instead of the baseline variances as the response, estimated heterogeneity (

\hat{τ}

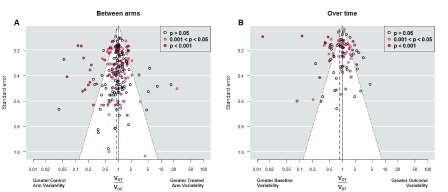
) was approximately doubled ( Supplementary File 1 : Table S4, model 6). We found 30 studies that compromised homoscedasticity: 11 (5.3%) with higher variance in the treated arm and 19 (9.1%), with lower variance. These figures were slightly higher in the analysis based on the classical variance comparison tests: In 41 studies (19.7%) we found statistically significant differences between outcome variances, 15 (7.2%) were in favor of greater variance in the treated arm; and 26 (12.5%) were in the opposite direction. Larger proportions were obtained from the comparisons over time of 95 treated arms: 16.8% had significantly greater variability at the end of the study and 23.2% at the beginning ( Table 1). Figure 3 shows the funnel plots for both between-arm and over-time comparisons.

Figure 3. — Funnel plots of outcome variance ratio between arms ( **Panel A**) and of outcome variance ratio over time ( **Panel B**). The first shows all 208 studies while the second shows the only 95 studies in which the variance of the difference between the baseline and final response was available. Vertical axis indicates precision for the comparison of variances; with points outside the triangle being statistically significant. Additionally, red points mark significant differences between the means, which correspond each study’s objective to assess main treatment effects. In **Panel A**, points on the right indicate higher outcome variability for the treated individuals, as expected if there is patient-by-treatment interaction; similarly, points on the left correspond to lower variability, although this is compatible with traditional Evidence-Based Medicine. Eleven (5.2%) out of 208 studies reported exactly the same outcome variability in both arms. We observe more red points on the left, indicating that changes in the average come with reductions in the variance. In **Panel B**, points on the right indicate higher variability in the experimental arm at the end of the study, as expected in a scenario of heterogeneous treatment effect; points on the left correspond to lower variability at the end, which implies a more homogenous response after treatment. The largest number of points on the left side indicates a majority of experimental interventions that reduce variability. In addition, several of these interventions yielded significant results in the main endpoint. V _OT: Variance of the Outcome in the Treated arm. V _OC: Variance of the Outcome in the Control arm. V _BT: Variance of the Outcome at baseline in the Treated arm.

Table 1. Variance comparison.

Alternative possible methods to estimate the number and percentage of studies with different variances on comparisons between arms and over-time. Limits for declaring different variances come from different statistical methods: (1) either pre-specified statistical tests (F for independent outcomes or Sachs’ test ²¹ for related samples); or (2) number of studies that have to be deleted from the random-effects model in order to achieve a negligible heterogeneity (studies with larger discrepancies in variances were removed one by one until the estimated value of τ was as close as possible to that of the reference model – the one that compares the variances of the response at baseline. See Methods for details). ^¥ This comparison was performed in studies reporting enough information to obtain the variability of the change from baseline to outcome, for example because they provide the correlation between outcome and baseline values.

Comparing variances	N	Method	After treatment, variability is…
Comparing variances	N	Method	Increased n (%)	Decreased n (%)	Not changed n (%)
Outcome between treatment arms	208	F test	15 (7.2%)	26 (12.5%)	167 (80.3%)
Outcome between treatment arms	208	Random model	11 (5.3%)	19 (9.1%)	178 (85.6%)
Outcome versus baseline in treated arm	95 ^¥	Paired test	16 (16.8%)	22 (23.2%)	57 (60.0%)
Outcome versus baseline in treated arm	95 ^¥	Random model	13 (13.7%)	19 (20.0%)	63 (66.3%)

Open in a new tab

Subgroup analyses suggest that significant interventions had an effect on reducing variability ( Supplementary File 1 : Figures S5–S7), which has already been observed in other studies ^25,
26. Even more important, lower variances in experimental arm occur only in outcomes that require low values for a better response; this is in line with other works that have found a positive correlation between the effect size and its heteroscedasticity ^27,
28: The fact is that difficult to find heteroscedasticity when there is no overall treatment effect. The remaining subgroup analyses did not raise concerns (section V in Supplementary File 1).

Discussion

Our main objective was to show that comparing variances can provide some evidence about how much precision medicine is needed. We found that variability seems to decrease for treatments that perform significantly better than the reference; otherwise, it remains similar. Therefore, the treatment seems to be doing what medicine should do –having larger effects in the most ill patients. Two considerations may be highlighted here: (1) as the outcome range becomes reduced, we may interpret that, following the intervention, this population is under additional control; but also, (2) as subjects are responding differently to treatment, this opens the way for not treating some (e.g. those subjects who are not very ill, and thus lack the scope to respond very much), which subsequently incurs savings in side effects and costs.

This reduced variability could also be due to methodological reasons. One is that some measurements may have a “ceiling” or “floor” effect (e.g., in the extreme case, if a treatment heals someone, no further improvement is possible). In fact, according to the subgroup analysis of the studies with outcomes that indicate the degree of disease (high values imply greater severity; e.g., pain), a greater variance (25%) is obtained in the experimental arm (see Figure S5). However, in the studies with outcomes that measure the degree of healthiness (high values imply better condition; e.g., mobility), the average variances match between arms and this does not suggest a ceiling effect. Another reason might be that the treatment effect is not additive, suggesting that it would be suitable to explore other metricsand transformations. For example, if the treatment acts proportionally rather than linearly, the logarithm of the outcome would be a better scale.

When both arms have equal variances, then the simplest interpretation is that the treatment effect is constant, thus rendering futile any search for predictors of differential response. This means that the average treatment effect can be seen as an individual treatment effect (not directly observable), which supports the use of a unique protocol for all patients within the eligibility criteria, thus in turn also supporting evidence-based medicine.

Our second objective was to provide a rough estimate of the proportion of interventions with different variability that would require more precise medicine: Considering the most extreme result from Table 1 for comparison between arms, 1 out of 14 interventions (7.2%) had greater variance in the experimental arm while 1 out of 8 interventions (12.5%) had lower variance. Even if there are no differences in means, lower variance implies a larger proportion of patients within the reference range. However, the non-constant effect indicates that trials with n=1 are needed to estimate different treatment effects on those individuals.

Our sensitivity analysis of the change over time in the experimental arm agreed with the findings in the comparison between arms, although this comparison is not protected by randomization. For example, the existence of eligibility criteria at baseline may have limited the initial variance (a hypertension trial might recruit patients with baseline SBP between 140 and 159 mm Hg), leading to the variance naturally increasing over time.

There are three reasons why these findings do not invalidate precision medicine in all settings. First, there are studies where the variability in the response is glaringly different, indicating the presence of a non-constant effect. Second, the outcomes of some type of interventions such as surgeries, for example, are greatly influenced by the skills and training of those administering the intervention; and these situations could have some effect on increasing variability. And third, we focus on quantitative outcomes, which are neither time-to-event nor binary, meaning that the effect in these cases could take a different form, such as all-or-nothing.

The results rely on published articles, which raises some relevant issues. First, some of our analyses are based on Normality assumptions for the outcomes that are unverifiable without access to raw data. Second, a high number of manuscripts (61.6%, Figure 2) act contrary to CONSORT ²⁹ advice in that they do not report variability. Thus, the trials of this study may not be representative of trials in general. Third, trials are usually powered to test constant effects and thus the presence of greater variability would lead to underpowered trials, non-significant results and unpublished papers. Fourth, the heterogeneity observed in the random-effects model may be the result of methodological inaccuracies ²³ arising from typographical errors in data translation, inadequate follow-up, insufficient reporting, or even data fabrication. On the other hand, this heterogeneity could also be the result of relevant undetected factors interacting with the treatment, which would indeed justify the need for precision medicine. A fifth limitation is that many clinical trials are not completely randomized. For example, multicenter trials often use a permuted blocks method. This means that if variances are calculated as if the trial were completely randomized (which is standard practice), the standard simple theory covering the random variation of variances from arm to arm is at best approximately true ²⁵

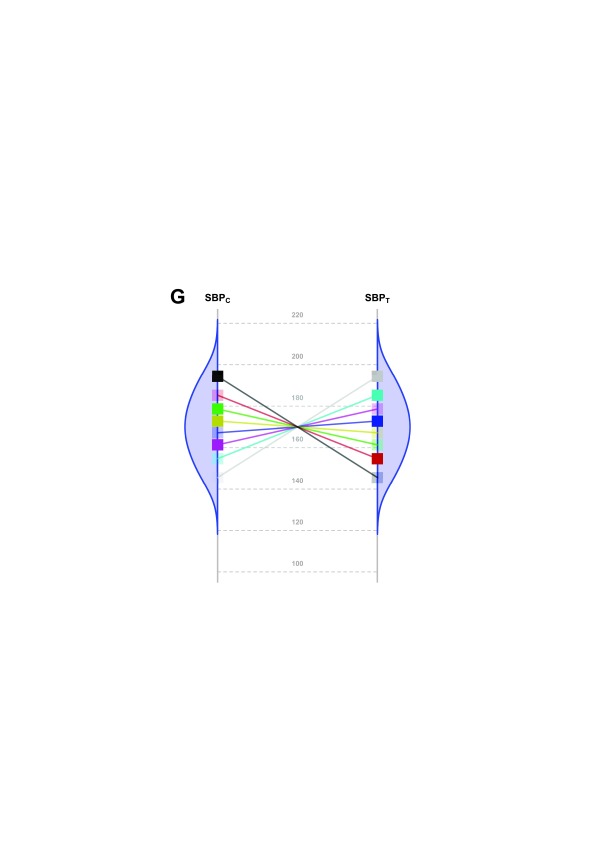
The main limitation of our study arises from the fact that, although a constant effect always implies homoscedasticity on the chosen scale, the reverse is not true; i.e., homoscedasticity does not necessarily imply a constant effect. Nevertheless, a constant effect is the simplest explanation for homoscedasticity. For example, the highly specific and non-parsimonious situation reflected in Figure 4 indicates homoscedasticity but without a constant effect (Section VIII of Supplementary File 1: Conditions for homoscedasticity to hold without a constant effect under an additive model).

Figure 4. — SBP potential values of each patient in both groups (C: Control; T: Treated) under a highly hypothetical scenario: the treatment effect has no value if systematically applied to the whole population; but if n-of-1 trials could be performed in this situation, the best treatment strategy would be chosen for each patient and the overall health of the population would be improved.

Heteroscedasticity may suggest the need for further refinements of the eligibility criteria or for finding an additive scale ^25,
30. Because interaction analyses cannot include unknown variables, all trials would potentially need to be repeated once any new potential interaction variable emerges (e.g., a new biomarker) as a candidate for a new subgroup analysis. Nevertheless, we have shown how homoscedasticity can be assessed when reporting trials with numerical outcomes, regardless of whether every potential effect modifier is known.

For most trials, the variability of the response to treatment changes scarcely or even decreases, which suggests that precision medicine’s scope may be less than what is commonly assumed – while always taking into account the limitation previously explained in Figure 4. Evidence-Based Medicine operates under the paradigm of a constant effect assumption, by which we learn from previous patients in order to develop practical clinical guides for treating future ones. Here, we have provided empirical insights for the rationale behind Evidence-Based Medicine. However, even where one common effect applies to all patients fulfilling the eligibility criteria, this does not imply that the same decision is optimal for all patients, specifically because different patients and stakeholders may vary in their weighting not only of efficacy outcomes, but also of the harm and cost of the interventions – thus bridging the gap between common evidence and personalized decisions.

Nevertheless, there is evidence of effect variation in around 1 out of 7 trials, suggesting a limited role for tailored interventions: either with finer selection criteria (common effect within specific subgroups), or with n-of-1 trials (no subgroups of patients with a common effect). By identifying indications where the scope for precision medicine is limited, studies such as ours may free up resources for situations with a greater scope.

Our results uphold the assertion by Horwitz et al. that there is a “need to measure a greater range of features to determine [...] the response to treatment” ³¹. One of these features is an old friend of statisticians, the variance. Looking only at averages can cause us to miss out on important information.

Data availability

Data associated with the article are available under the terms of the Creative Commons Zero "No rights reserved" data waiver (CC0 1.0 Public domain dedication). http://creativecommons.org/publicdomain/zero/1.0/

Data is available through two sources:

- A shiny app that allows the user to interact with the data without any need to download it: http://shiny-eio.upc.edu/pubs/F1000_precision_medicine/
The Figshare repository: https://doi.org/10.6084/m9.figshare.5552656 ¹⁸

In both sources, the data can be downloaded under a Creative Commons License v. 4.0.

The code for the main analysis is available in the following link: https://doi.org/10.5281/zenodo.1239539 ²²

Supplementary material

Supplementary File 1: The supplementary material contains the following sections:

Click here for additional data file.^{(402KB, tgz)}

- Section I: Constant effect assumption in sample size rationale

- Section II: Bibliographic review

- Section III: Descriptive measures

- Section IV: Random-effects models

- Section V: Subgroup analyses

- Section VI: Standard error of log(V _OT/V _OC) in independent samples

- Section VII: Standard error of log(V _OT/V _BT) in paired samples

- Section VIII: Conditions for homoscedasticity to hold without a constant effect under an additive model

Funding Statement

Partially supported by Methods in Research on Research (MiRoR, Marie Skłodowska-Curie No. 676207); MTM2015-64465-C2-1-R (MINECO/FEDER); and 2014 SGR 464.

The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

[version 3; peer review: 3 not approved]

References

1. Collins FS, Varmus H: A new initiative on precision medicine. N Engl J Med. 2015;372:793–5. 10.1056/NEJMp1500523 [DOI] [PMC free article] [PubMed] [Google Scholar]
2. Kohane IS: HEALTH CARE POLICY. Ten things we have to do to achieve precision medicine. Science. 2015;349(6243):37–8. 10.1126/science.aab1328 [DOI] [PubMed] [Google Scholar]
3. Schork NJ: Personalized medicine: Time for one-person trials. Nature. 2015;520(7549):609–11. 10.1038/520609a [DOI] [PubMed] [Google Scholar]
4. Willis JC, Lord GM: Immune biomarkers: the promises and pitfalls of personalized medicine. Nat Rev Immunol. 2015;15(5):323–29. 10.1038/nri3820 [DOI] [PubMed] [Google Scholar]
5. Wallach JD, Sullivan PG, Trepanowski JF, et al. : Evaluation of Evidence of Statistical Support and Corroboration of Subgroup Claims in Randomized Clinical Trials. JAMA Intern Med. 2017;177(4):554–60. 10.1001/jamainternmed.2016.9125 [DOI] [PMC free article] [PubMed] [Google Scholar]
6. Durán-Cantolla J, Aizpuru F, Montserrat JM, et al. : Continuous positive airway pressure as treatment for systemic hypertension in people with obstructive sleep apnoea: randomised controlled trial. BMJ. 2010;341:c5991. 10.1136/bmj.c5991 [DOI] [PubMed] [Google Scholar]
7. Kojima Y, Kaga H, Hayashi S, et al. : Comparison between sitagliptin and nateglinide on postprandial lipid levels: The STANDARD study. World J Diabetes. 2013;4(1):8–13. 10.4239/wjd.v4.i1.8 [DOI] [PMC free article] [PubMed] [Google Scholar]
8. International conference on harmonisation: statistical principles for clinical trials ICH-E9.1998. Accessed September 14 2017. Reference Source [Google Scholar]
9. Shamseer L, Sampson M, Bukutu C, et al. : CONSORT extension for reporting N-of-1 trials (CENT) 2015: Explanation and elaboration. BMJ. 2015;350:h1793. 10.1136/bmj.h1793 [DOI] [PubMed] [Google Scholar]
10. Araujo A, Julious S, Senn S: Understanding Variation in Sets of N-of-1 Trials. PLoS One. 2016;11(12):e0167167. 10.1371/journal.pone.0167167 [DOI] [PMC free article] [PubMed] [Google Scholar]
11. Senn S: Individual response to treatment: is it a valid assumption? BMJ. 2004;329(7472):966–68. 10.1136/bmj.329.7472.966 [DOI] [PMC free article] [PubMed] [Google Scholar]
12. Senn S: Mastering variation: variance components and personalised medicine. Stat Med. 2016;35(7):966–77. 10.1002/sim.6739 [DOI] [PMC free article] [PubMed] [Google Scholar]
13. Wang R, Lagakos SW, Ware JH, et al. : Statistics in medicine--reporting of subgroup analyses in clinical trials. N Engl J Med. 2007;357(21):2189–94. 10.1056/NEJMsr077003 [DOI] [PubMed] [Google Scholar]
14. Senn S, Richardson W: The first t-test. Stat Med. 1994;13(8):785–803. 10.1002/sim.4780130802 [DOI] [PubMed] [Google Scholar]
15. Kim SH, Schneider SM, Bevans M, et al. : PTSD symptom reduction with mindfulness-based stretching and deep breathing exercise: randomized controlled clinical trial of efficacy. J Clin Endocr Metab. 2013;98(7):2984–92. 10.1210/jc.2012-3742 [DOI] [PMC free article] [PubMed] [Google Scholar]
16. Holland P: Statistics and Causal Inference. J Am Stat Assoc. 1986;81(396):945–60. 10.2307/2289064 [DOI] [Google Scholar]
17. Kim ES, Hirsch V, Mok T, et al. : Gefitinib versus docetaxel in previously treated non-small-cell lung cancer (INTEREST): a randomised phase III trial. Lancet. 2008;372(9652):1809–1818. 10.1016/S0140-6736(08)61758-4 [DOI] [PubMed] [Google Scholar]
18. Cortés J: ‘review_homoscedasticity_clinical_trials’.[Data set].2017. 10.6084/m9.figshare.5552656 [DOI] [Google Scholar]
19. Bartlett MS, Kendall DG: The statistical analysis of variance-heterogeneity and the logarithmic transformation. J R Stat Soc. 1946;8(1):128–38. 10.2307/2983618 [DOI] [Google Scholar]
20. Higgins JP, Thompson SG, Deeks JJ, et al. : Measuring inconsistency in meta-analyses. BMJ. 2003;327(7414):557–560. 10.1136/bmj.327.7414.557 [DOI] [PMC free article] [PubMed] [Google Scholar]
21. Sachs L: Applied Statistics: A Handbook of Techniques.2nd ed. New York: Springer-Verlag,1984. 10.1007/978-1-4612-5246-7 [DOI] [Google Scholar]
22. Cortés J: R code for analysis of homoscedasticity in clinical trials. Zenodo. 2017. 10.5281/zenodo.1133609 [DOI] [Google Scholar]
23. Carlisle JB: Data fabrication and other reasons for non-random sampling in 5087 randomised, controlled trials in anaesthetic and general medical journals. Anaesthesia. 2017;72(8):944–952. 10.1111/anae.13938 [DOI] [PubMed] [Google Scholar]
24. Hsieh LL, Kuo CH, Yen MF, et al. : A randomized controlled clinical trial for low back pain treated by acupressure and physical therapy. Prev Med. 2004;39(1):168–76. 10.1016/j.ypmed.2004.01.036 [DOI] [PubMed] [Google Scholar]
25. Senn S: Controversies concerning randomization and additivity in clinical trials. Stat Med. 2004;23(24):3729–53. 10.1002/sim.2074 [DOI] [PubMed] [Google Scholar]
26. Jamieson J: Measurement of change and the law of initial values: A computer simulation study. Educ Psychol Meas. 1995;55(1):38–46. 10.1177/0013164495055001004 [DOI] [Google Scholar]
27. Senn S: Trying to be precise about vagueness. Stat Med. 2007;26(7):1417–30. 10.1002/sim.2639 [DOI] [PubMed] [Google Scholar]
28. Greenlaw N: Constructing appropriate models for meta-analyses. University of Glasgow,2010. Accessed September 14, 2017. Reference Source [Google Scholar]
29. Schulz KF, Altman DG, Moher D, et al. : CONSORT 2010 statement: updated guidelines for reporting parallel group randomised trials. BMJ. 2010;340:c332. 10.1016/j.jclinepi.2010.02.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
30. Rothman KJ, Greenland S, Walker AM: Concepts of interaction. Am J Epidemiol. 1980;112(4):467–70. 10.1093/oxfordjournals.aje.a113015 [DOI] [PubMed] [Google Scholar]
31. Horwitz RI, Cullen MR, Abell J, et al. : Medicine. (De)personalized medicine. Science. 2013;339(6124):1155–6. 10.1126/science.1234106 [DOI] [PubMed] [Google Scholar]

F1000Res. 2018 Dec 19. doi: 10.5256/f1000research.17220.r40679

Reviewer response for version 3

Ian R White ¹

I consider each of the points in turn.

1. We are debating whether “conventional clinical trials are designed to find differences with the implicit assumption that the effect is the same in all patients within the eligibility criteria”.

The authors quote Paul Holland. The passage quoted is a careful definition of the “constant effect assumption”, but it does not support the authors’ argument - it does not claim that this assumption is required in randomised trials. Indeed elsewhere in his paper, Holland points out the value of an average causal effect:

“The value of the average causal effect T is of potential interest for its own sake in certain types of studies. It would be of interest to a state education director who wanted to know what reading program would be the best to give to all of the first graders in his state. The average causal effect of the best program would be reflected in increases in statewide average reading scores.”

I entirely agree with the authors that

“Without this [constant effect] assumption, the value of the “average causal effect” is not enough to convey all the information about the treatment effect.”

but I don’t agree that

“If the effect randomly varies among the different units (as shown in panel D of Figure 1), we need to characterize its distribution: for example, by a normal distribution with its mean (delta) and standard deviation (SD).”

My disagreement is over the word “need”. It would be really useful to characterize the distribution. But we usually can’t do that in RCTs (cross-over trials and n-of-1 trials being notable exceptions). If we can’t characterize the distribution, the mean is still useful, as in the reading program example above, or as in treatment of a group of patients. As I said in my original review:

“This is why the trials community worries so much about external generalisability: for example, if a trial treated 60% women and 40% men and showed a benefit of treatment, then a clinician treating women and men in the same ratio can be confident of giving a benefit overall, but a clinician treating women and men in a different ratio cannot be so confident.”

2. Here we are debating whether the authors’ conclusions follow validly from the observed reduction in variance in the treated arm. The authors have included plenty of caveats. But their primary statement (in the abstract) remains “treated patients … would not require further precision medicine”: I still disagree with this. Other over-statements in the discussion are

“When both arms have equal variances, then the simplest interpretation is that the treatment effect is constant, thus rendering futile any search for predictors of differential response.” (p9)

“For most trials, the variability of the response to treatment changes scarcely or even decreases, which suggests that precision medicine’s scope may be less than what is commonly assumed” (p10)

“There is evidence of effect variation in around 1 out of 7 trials, suggesting a limited role for tailored interventions” (p10)

3. I find the presentation of the methods and results clearer now, though some parts remain poorly explained:

In the formula for I^2, nu^2 is not the expected value of the error variance, since the latter is not a random variable.
The formulae for V[log(V_OT/V_OC)] and V[log(V_OT/V_BT)] are in fact formulae for their within-study variances nu_i^2: this should be made clear. As written, they wrongly appear to be the total variances, which also involve tau^2
In Table 1, “Random model” is an inadequate description of the complex procedure described in the caption.

4. I fully apologise for not seeing the authors’ response to Erica Moodie’s comments. I agree that they did respond.

For the above reasons 1 and 2, I do not approve the paper as a whole. I do approve the methods and results, which provide useful insights. It is only the author’s interpretation of their results that I do not approve. An advantage of the open reviewing platform is that the paper remains available and those who disagree with my opinions remain able to read it.

I am still learning how to review papers in non-conventional journals like this one. Usually I would not expect to review a 2 ^nd submission (such as this). I will not review a 3 ^rd submission.

I have read this submission. I believe that I have an appropriate level of expertise to state that I do not consider it to be of an acceptable scientific standard, for reasons outlined above.

F1000Res. 2019 Mar 1.

Jordi Cortés ¹

We are thankful for the comments from Prof. Ian White, which have helped us greatly in rethinking our paper.

We agree that Holland is using the concept of Average Causal Effect (ACE); however, he also mentions that " The assumption of constant effect makes the value of the average causal effect relevant to every unit, and therefore, allows T to be used to draw causal inferences at the unit level ". However, we wonder to whom this quote is relevant: to health managers?; or to doctors giving specific advice to individual patients? In any case, our statement will still remain valid: health managers would like to know the amount of variability added by the treatment; or, even better, they would like to know any additional measure of the amount of deviations from the causal effect assumption.

I entirely agree with the authors that

“Without this [constant effect] assumption, the value of the “average causal effect” is not enough to convey all the information about the treatment effect.”

but I don’t agree that

Thank you for this observation; however, we disagree. While it is certainly true that science currently cannot provide this information; that does not mean that we don’t need this information in order to provide individualized advice. For us, “need” is the correct word. Perhaps our disagreement is simply a question of nuance, for example, maybe Prof. White would prefer “need to be able to” or something similar.

As I said in my original review:

Thank you, although we disagree. As stated before: maybe some patients may rely on an average treatment. However, the best clinicians would like to know the effect on both subgroups: this is why we “need” to know the “distribution” of the effect size among the population.

Thank you, although we still disagree with Prof. Ian White’s interpretation.

If the constant effect assumption does not hold, new paradoxes may appear. For example, we agree that a different effect in some units may justify a tailored recommendation. However, in the case of a reduced variance with a similar mean (as in panel E, Figure 1), more patients would finish within reference or “normality” values, which may be interpreted as the goal of interventions.

Other over-statements in the discussion are

“When both arms have equal variances, then the simplest interpretation is that the treatment effect is constant, thus rendering futile any search for predictors of differential response.” (p9)

Again, thank you, although we disagree. As a constant ( effect) is independent of any variable, we wonder why this should be considered an “over-statement”

As before.

“There is evidence of effect variation in around 1 out of 7 trials, suggesting a limited role for tailored interventions” (p10)

Again, “idem”: we also disagree with Prof. Ian White’s interpretation.

3. I find the presentation of the methods and results clearer now, though some parts remain poorly explained:

In the formula for I^2, nu^2 is not the expected value of the error variance, since the latter is not a random variable.

Thank you. We have corrected it: “nu^2 is the mean of the error variances nu_i^2”

The formulae for V[log(V_OT/V_OC)] and V[log(V_OT/V_BT)] are in fact formulae for their within-study variances nu_i^2: this should be made clear. As written, they wrongly appear to be the total variances, which also involve tau^2

Thank you. We have clarified this issue adding this sentence before the formulas.

“Thus, the within-study variance was estimated using the following formulas:”

In Table 1, “Random model” is an inadequate description of the complex procedure described in the caption.

Thank you. As a consequence of your suggestions, we have decided to expand the table by specifying the 3 performed analyses based on: 1) the random effects model; 2) the heuristic method of eliminating one-to-one studies (what we previously called "random model" and now we call "heuristic method"); 3) the classic tests of variance comparison.

4. I fully apologise for not seeing the authors’ response to Erica Moodie’s comments. I agree that they did respond.

Thank you.

Thank you. We are happy Prof White thinks it “provides useful insights” and that he likes that it should “remain available”. As we interpret his comments, he appears to believe that the paper is now a worthwhile contribution to science. Anyway, we wonder if a non-indexed paper could be considered as “available”

I am still learning how to review papers in non-conventional journals like this one. Usually I would not expect to review a 2nd submission (such as this). I will not review a 3rd submission.

Competing Interests: No competing interests were disclosed. I have read this submission. I believe that I have an appropriate level of expertise to state that I do not consider it to be of an acceptable scientific standard, for reasons outlined above.

It seems to us that we agree more than we disagree with Prof. Ian White. We agree that the assumption of a constant effect is as unrealistic as some statements from the Normal Gauss-Laplace distribution. However, the constant effect has nevertheless served as a useful assumption for facilitating medical and social decisions arrived at on the basis of evidence-based medicine. The relevant question is not whether or not the assumption is true, but how much the effects deviate from a constant model. This is the point of our proposal, namely that it is necessary to quantify how much variability is added by the treatment.

In any case, we would like to thank again Prof. Ian White. Despite having different interpretations, he has helped us to significantly improve the article.

F1000Res. 2018 Jul 27. doi: 10.5256/f1000research.16548.r34991

Reviewer response for version 2

Saskia le Cessie ^1,²

Although the paper has been improved, there are still important shortcomings in the abstract, introduction, description of the methods and the discussion.

I completely agree with Ian White. The statement in the abstract: “However, conventional clinical trials are designed to find differences with the implicit assumption that the effect is the same in all patients within the eligibility criteria”, is definitely not true. Trials are designed to answer questions about average effects in populations: what would happen if everyone would be treated with treatment A versus treatment B. This does not imply that the effect in all subgroups or in all individuals is the same. This also apply to the discussion with statements like "Evidence-Based Medicine operates under the paradigm of a constant effect assumption"
The description of the methods is insufficient. The main fitted model has two random effect S_i and e_i, and the model is therefore not estimable. You do not clearly state that you circumvent this problem by estimating the variance nu_i from the sample sizes in the two trial arms.
The parameter mu is not the average variance ratio, it is the logarithm of it. And the notation should be s_i ~N(0, tau^2) instead of s_i ~N(0, tau), idem e_i ~N(0, nu_i^2).
The definition of I^2 is not clear, it is unclear what nu^2 is.
I am uncertain about the added value of using I^2. Why not just look at the size of tau, and use it to determine the prediction interval for the ratio of variances?
It is unclear how the model to assess homoscedasticity over time is formulated.
In the heading of Table 1 it is now explained how the distinction between increased variability, decreased variability and not changed is made. Please add this information to the methods section.
I can see how the distinction between increased, decreased and not changed stability based on the F-tests is made (although the term masked tests is unknown to me). However the random model method is rather heuristic. What is meant by a “neglectable heterogeneity”? And what is meant by” studies are removed one by one until achieving an estimated value of tau, similar to the reference model”. Which reference model? What difference is considered to be similar?
The presentation of the results is in some parts unclear. e.g. “The estimated baseline heterogeneity”. I assume that this is the estimate of the between study variance of an analysis with the log variance-ratio at baseline as dependent variable. Is that correct? Page 6. “heterogeneity was almost doubled”. Do you mean that tau is doubled? Or tau^2? “The sensitive analysis” To which analysis do you refer here?
The word “outcome” has multiple meanings. Sometimes it is the outcome variable, sometimes it is outcome variable, measured at end of the study. See for example the legend of Figure 3: the terms “variance of outcome” and “variance of outcome at baseline” are not very clear. Please reword.
In the discussion, you still equate heteroscedastic with precision medicine e.g. sentences like “a rough estimate of the proportion of interventions with different variability that would require more precise medicine”.
Page 7 The part starting with "Considering the most" until "Provided there are no differences in means, the latter implies a larger proportion of “cured” patients, within the normality range.” I did not understand this part. Why do you assume that there are no differences in means? And what do you mean with normality range?
Page 9: “First, the heterogeneity found in our analysis indicates that the observed lower variability in the experimental arm cannot be extrapolated to all individual studies.” This remark is unclear.

I have read this submission. I believe that I have an appropriate level of expertise to state that I do not consider it to be of an acceptable scientific standard, for reasons outlined above.

F1000Res. 2018 Nov 6.

Jordi Cortés ¹

We are sincerely thankful for the critical review from Prof. Saskia le Cessie. Next, we will try to clarify the raised issues.

Although the paper has been improved, there are still important shortcomings in the abstract, introduction, description of the methods and the discussion.

1. I completely agree with Ian White. The statement in the abstract: “However, conventional clinical trials are designed to find differences with the implicit assumption that the effect is the same in all patients within the eligibility criteria”, is definitely not true. Trials are designed to answer questions about average effects in populations: what would happen if everyone would be treated with treatment A versus treatment B. This does not imply that the effect in all subgroups or in all individuals is the same. This also apply to the discussion with statements like "Evidence-Based Medicine operates under the paradigm of a constant effect assumption"

As this question deals with the same issue posed by Professor Ian White, we use more or less the same answer:

Paul Holland [1], in his paper about statistics and causal inference, stated: “ The assumption of constant effect is that the effect of t on every unit is the same […]. [It] makes the value of the average causal effect relevant to every unit.”

Without this assumption, the value of the “average causal effect” is not enough to convey all the information about the treatment effect. If the effect randomly varies among the different units (as shown in panel D of Figure 1), we need to characterize its distribution: for example, by means of a normal distribution with its mean (delta) and standard deviation (SD). Depending on the value of this SD, we may consider applying the intervention to the full population or not. In the case of an interaction with measurable baseline characteristics (as shown in panel C of Figure 1), we need to specify the different delta values for each group.

Without specification of the further parameters required to characterize a non-constant effect, the reader cannot distinguish whether: (a) the authors were looking for a non-constant effect, but they erroneously omitted those further details required to specify this sophisticated effect; or (b) they were just assuming a constant effect (perhaps unconsciously). We agree with Prof. White that authors should be fully transparent about those assumptions; and with Grissom and Kim [2] in the sense that those further sophisticated situations may require a broader approach than just looking at the means.

[1] HOLLAND, P & PAUL, W. (1986). Statistics and Causal Inference. Journal of the American Statistical Association, 81(396), 945-960.

[2] GRISSOM, R. J. & KIM, J. J. (2005). Effect Sizes for Research: a Broad Practical Approach. Lawrence Erlbaum Associates, Mahwah, NJ

2.The description of the methods is insufficient. The main fitted model has two random effect S_i and e_i, and the model is therefore not estimable. You do not clearly state that you circumvent this problem by estimating the variance nu_i from the sample sizes in the two trial arms.

You are right. Although we have extensively explained it in sections VI and VII of the supplementary material, we have clarified it in a new version of the manuscript:

Before: “As there is only one available measure for each study, both sources of variability cannot be empirically differentiated: (i) within study or random or that one related to sample size; and (ii) heterogeneity. In order to isolate the second, the first was theoretically estimated using the Delta method –as explained in Sections V and VI in Supplementary File 1.”

After: “As there is only one available measure for each study, both sources of variability cannot be empirically differentiated: (i) within study or random variability; and (ii) heterogeneity. To isolate the second, the first was estimated theoretically using either the Delta method in the case of comparison between-arm or using some approximation in the case of comparison over time (see details in Sections VI and VII of Supplementary File 1):

V[log(V_OT/V_OC )]=2/(n_OT-2)+2/(n_OC-2) (between arms)

V[log(V_OT/V_BT )]= 4/(n-1) - 2·log [1+(2·Corr[Y_OT,Y_BT ]^2)/(n^2/(n-1))] (over time)”

3. The parameter mu is not the average variance ratio, it is the logarithm of it. And the notation should be s_i ~N(0, tau^2) instead of s_i ~N(0, tau), idem e_i ~N(0, nu_i^2).

Thanks. We have corrected it.

4. The definition of I^2 is not clear, it is unclear what nu^2 is.

Thank you for the suggestion. Regarding the definition of I^2, we have added a new reference [1] that contains a broader explanation of its meaning. Regarding nu^2, we have removed the second definition (“the expected value of the error variance”), since it had already been previously defined.

[1] Higgins JPT, Thompson SG, Deeks JJ, et al.: Measuring inconsistency in meta-analyses. BMJ. 2003;327(7414):557-560.

5. I am uncertain about the added value of using I^2. Why not just look at the size of tau, and use it to determine the prediction interval for the ratio of variances?

In fact, although we define the measure of I^2, our explanations always underlie the interpretation of tau.

The question about why we do not use the prediction intervals is very appropriate. This was our initial idea, but Carlisle's paper [1] made us think that there could be some methodological deficiencies in the random assignments that involve artificially different variances between arms. However, after making the decision, we found that the number of studies with statistically different variances using our "heuristic" method or using the prediction intervals was very similar. This can be checked by comparing the results shown in Table 1 with the points outside the triangle in Figure 3.

[1] Carlisle JB: Data fabrication and other reasons for non-random sampling in 5087 randomised, controlled trials in anaesthetic and general medical journals. Anaesthesia. 2017;72(8):944–952. 28580651 10.1111/anae.13938

6. It is unclear how the model to assess homoscedasticity over time is formulated.

The methodology is explained in Section IV of the supplementary file. As the methodology was relatively similar to the comparison between groups, we decided to omit the details in the statistical analysis section so as not to wear down the reader.

7. In the heading of Table 1 it is now explained how the distinction between increased variability, decreased variability and not changed is made. Please add this information to the methods section.

Thank you for your advice. We have introduced two modifications.

First, just to clarify, we have added an additional introductory paragraph in the statistical analysis section mentioning the 2 methods before explaining them:

To compare the variances, two different methods have been used: one based on a random-effects model and the other based on classical variance comparison tests.

Second, it is our opinion that doubts arise in regard to how the random-effects model determines which studies have significantly different variances (since we believe it is obvious with variance comparison tests), therefore we have added the following explanatory text in the statistical analysis section:

Specifically, studies with more extreme outcomes were removed one by one until achieving an estimated value of τ similar to the one obtained from the reference model. These deleted studies were considered to be those that had significantly different variances, because the experimental treatment either increased or decreased the variance.

8. I can see how the distinction between increased, decreased and not changed stability based on the F-tests is made (although the term masked tests is unknown to me). However the random model method is rather heuristic. What is meant by a “neglectable heterogeneity”? And what is meant by” studies are removed one by one until achieving an estimated value of tau, similar to the reference model”. Which reference model? What difference is considered to be similar?

The term "masked" refered to the fact that this analysis was defined without looking at the data previously. To clarify, we have changed "masked specified" to "pre-specified". We agree that the method which obtains the studies with significantly different variances is heuristic. However, it provides almost the same number of significant studies as when using the limits defined by the funnel-plots in Figure 3.

The reference model is the one in which the variances of the two groups are compared at the baseline: It is the first model of Table S4 of the supplementary file. To clarify, we have added an additional sentence in the legend of Table 1:

“Reference model – the one that compares the variances of the response at baseline”.

Also, we have slightly modified the explanation of this heuristic method to clear up doubts:

Before: “studies with more extreme outcomes were removed one by one until achieving an estimated value of tau similar to the one obtained from the reference model.”

After: “studies with larger discrepancies in variances were removed one by one until the estimated value of tau was as close as possible to that of the reference model.”

9. The presentation of the results is in some parts unclear. e.g. “The estimated baseline heterogeneity”. I assume that this is the estimate of the between study variance of an analysis with the log variance-ratio at baseline as dependent variable. Is that correct? Page 6. “heterogeneity was almost doubled”. Do you mean that tau is doubled? Or tau^2? “The sensitive analysis” To which analysis do you refer here?

You are right in all the matters you mention.

Baseline heterogeneity refers to the model that uses the logarithm of the baseline variances ratio as response.

In the new version of the manuscript, we have clarified that when we say that “heterogeneity is approximately doubled”, we refer to the estimated tau.

Before: “Heterogeneity was approximately doubled.”

After: “Estimated heterogeneity (hat_tau) was approximately doubled.”

Also, instead of using the term "sensitivity analysis", which is not very specific, we now specifically mention what analysis we are referring to.

Before: “These figures were slightly higher in the sensitive analysis.”

After: “These figures were slightly higher in the analysis based on the classical variance comparison tests.”

10. The word “outcome” has multiple meanings. Sometimes it is the outcome variable, sometimes it is outcome variable, measured at end of the study. See for example the legend of Figure 3: the terms “variance of outcome” and “variance of outcome at baseline” are not very clear. Please reword.

We have modified the legend of Figure 3.

Before: “V_BT: Variance of the Outcome at baseline in the Treated arm”.

After: “V_BT: Variance at Baseline in the Treated arm”.

In the rest of the document, we think that there is no ambiguity in the use of the term "Outcome", since it is always explicit when we refer to the baseline value.

11. In the discussion, you still equate heteroscedastic with precision medicine e.g. sentences like “a rough estimate of the proportion of interventions with different variability that would require more precise medicine”.

It is not our intention in this statement to make an equivalence between heteroscedasticity and personalized medicine, i.e.:

Heteroscedasticity <-> Precision medicine

With the use of a conditional in the sentence, we want to highlight that the studies where personalized medicine has more room are those in which different variability has been observed and, therefore, they are those of which we are sure that the effect of the treatment is not constant:

Heteroscedasticity -> Precision medicine

12. Page 7 The part starting with "Considering the most" until "Provided there are no differences in means, the latter implies a larger proportion of “cured” patients, within the normality range.” I did not understand this part. Why do you assume that there are no differences in means? And what do you mean with normality range?

We wanted to emphasize that a treatment that is not effective because it does not modify the mean of the outcome could be beneficial by decreasing the variance, since this implies that there is a greater number of patients within the reference range (we have changed the terminology “normality range” to “reference range” in order to avoid ambiguities). We have changed the text in the following way:

Before: “Provided there are no differences in means, the latter implies a larger proportion of “cured” patients within the normality range.”

After: “Even if there are no differences in means, lower variance implies a larger proportion of patients within the reference range.”

13. Page 9: “First, the heterogeneity found in our analysis indicates that the observed lower variability in the experimental arm cannot be extrapolated to all individual studies.” This remark is unclear.

Thank you. We have tried clarified this sentence.

Before: “First, the heterogeneity found in our analysis indicates that the observed lower variability in the experimental arm cannot be extrapolated to all individual studies.”

After: “First, there are studies where the variability in the response is glaringly different, indicating the presence of a non-constant effect.”

We sincerely thank the referee for the time devoted to her comments, because despite not having considered the manuscript acceptable, she has helped us to considerably improve the manuscript.

F1000Res. 2018 Jun 20. doi: 10.5256/f1000research.16548.r35299

Reviewer response for version 2

Ian R White ¹

I appreciate the authors’ careful response to my review. They have made a number of changes which have improved the manuscript. However, a number of errors remain which leave me unable to approve the manuscript. The key errors are:

I still do not accept the authors’ argument (stated in the abstract) that “conventional clinical trials are designed to find differences with the implicit assumption that the effect is the same in all patients within the eligibility criteria”. Their response document does not make a convincing case. I think the authors see that standard procedures - the Neyman-Pearson lemma, a sample size calculation - use a single parameter, and infer that these procedures assume a common treatment effect. But this single parameter is the between-group difference of means, which equates to the average treatment effect. There is no assumption that the treatment effect is the same for all individuals.
The observed reduction in variance does not imply that “treated patients … would not require further precision medicine” (abstract). If for example there is a subgroup of less ill patients who derive no benefit, then this would explain the observed data, but excluding this subgroup would leave us in the setting of equal variances, which as already argued does not imply no role for precision medicine.
The reporting, though much improved, is still unclear in some ways. For example,
1. what is the “baseline heterogeneity (τ2)” that is estimated as 0.31 (p6)?
2. what does this mean: “both sources of variability cannot be empirically differentiated: (i) within study or random or that one related to sample size; and (ii) heterogeneity”?
3. Table 1 remains unclear to me.

I am also disappointed that the authors have not replied to Erica Moodie’s critical comments.

I have read this submission. I believe that I have an appropriate level of expertise to state that I do not consider it to be of an acceptable scientific standard, for reasons outlined above.

F1000Res. 2018 Jul 26.

Jordi Cortés ¹

We are honestly thankful for the critical review from Prof. Ian White, especially for highlighting the discrepancies between his and our interpretation regarding the average treatment effect (ATE) and the constant effect.

Nevertheless, we have the deep conviction that, by some honest mistake, Prof. White did not see our separate responses to each reviewer. Based on his comment that we did not answer Erica Moodie, which we had done as well as some other comments.

From here, we’ll answer specific issues of this report.

1. I still do not accept the authors’ argument (stated in the abstract) that “conventional clinical trials are designed to find differences with the implicit assumption that the effect is the same in all patients within the eligibility criteria”. Their response document does not make a convincing case. I think the authors see that standard procedures - the Neyman-Pearson lemma, a sample size calculation - use a single parameter, and infer that these procedures assume a common treatment effect. But this single parameter is the between-group difference of means, which equates to the average treatment effect. There is no assumption that the treatment effect is the same for all individuals.

Paul Holland [1], in his paper about statistics and causal inference, stated: “ The assumption of constant effect is that the effect of t on every unit is the same (…). (It) makes the value of the average causal effect relevant to every unit.”

Without this assumption, the value of the “average causal effect” is not enough to convey all the information about the treatment effect. If the effect randomly varies among the different units (as shown in panel D of Figure 1), we need to characterize its distribution: for example, by a normal distribution with its mean (delta) and standard deviation (SD). Depending on the value of this SD, we may consider applying the intervention to the full population or not. In the case of an interaction with measurable baseline characteristics (as shown in panel C of Figure 1), we need to specify the different delta values for each group.

Without specification of the further parameters required to characterize a non-constant effect, the reader cannot differentiate between: (a) the authors were looking for a non-constant effect, but they erroneously omitted those further details required to specify this sophisticated effect; or (b) they were just assuming a constant effect (perhaps subconsciously). We agree with Prof. White that authors should be fully transparent about those assumptions; and with Grissom and Kim [2] in the sense that those further sophisticated situations may require a broader approach than just looking at the means.

[1] HOLLAND, P & PAUL, W. (1986). Statistics and Causal Inference. Journal of the American Statistical Association, 81(396), 945-960.

[2] GRISSOM, R. J. & KIM, J. J. (2005). Effect Sizes for Research: a Broad Practical Approach. Lawrence Erlbaum Associates, Mahwah, NJ.

2. The observed reduction in variance does not imply that “treated patients … would not require further precision medicine” (abstract). If for example there is a subgroup of less ill patients who derive no benefit, then this would explain the observed data, but excluding this subgroup would leave us in the setting of equal variances, which as already argued does not imply no role for precision medicine.

This is the essential criticism. It was raised (and answered) in points 1 to 3 of the previous review from Prof White. We have added a new section to the supplementary file 1 ( Conditions for homoscedasticity to hold without a constant effect under an additive model) showing the conditions required for V[Y(1)]=V[Y(0)] under the additive model.

Essentially, if the effect was random, we need the correlation between the effect and V[Y(0)] to be exactly:

- ½ * Sigma_effect/Sigma_Y(0).

In the Discussion section of the 2 ^nd version of the paper, we did already include an extended explanation:

“Our second objective was (...) the remaining 80% of the studies agrees with the design assumption of a constant effect.”

3. The reporting, though much improved, is still unclear in some ways. For example,

a) what is the “baseline heterogeneity (τ2)” that is estimated as 0.31 (p6)?

This was previously raised by Prof. Ian White in the first revision (“Methods, point 2”), which offered us the opportunity to improve our presentation (see our previous answer).

It is an estimate of the variability of the logarithm of the ratio of variances at baseline. All the models are specified in the legend of Table S4 in Supplementary File 1.

Randomization should lead to this tau^2 being close to 0; and, in fact, by removing only the 4 most extreme studies reduces tau from 0.31 to 0.07, indicating that these 4 studies have some problems, such as in one study using outcomes that were obtained 1 month after the start of treatment as the baseline values [3].

[3] Hsieh LL, Kuo CH, Yen MF, et al.: A randomized controlled clinical trial for low back pain treated by acupressure and physical therapy. Prev Med. 2004; 39(1): 168–76

b) what does this mean: “both sources of variability cannot be empirically differentiated: (i) within study or random or that one related to sample size; and (ii) heterogeneity”?

The model can be defined without using scientific notation:

Response = Mean + Inter-study variability + Intra-study variability

By having a single measure per study, we do not have enough information to distinguish between intra-study variability and inter-study variability of the measure of interest. For this reason, the delta method was used to estimate the first and distinguish between them.

c) Table 1 remains unclear to me.

[See also our previous answer to Saskia Le Cessie comment 11.]

The white rows in Table 1 are the direct result obtained from a statistical test for comparing the variances between groups (F test) or before-after (paired test) in the experimental arms. From here, the studies are divided into not significant or significant in one or the other direction.

In the gray rows, the significant studies are those that should be removed in order to obtain a heterogeneity as close as possible to the baseline (which supposedly should be zero by randomization). All those details were explained in either the text or the legend labels.

I am also disappointed that the authors have not replied to Erica Moodie’s critical comments.

Our reply to Erica Moodie was published on the F1000 website at the same time as the other two. We gave our best efforts in responding to her comments. We are grateful for her contribution even if we of course refuted any statements that we considered erroneous.

F1000Res. 2018 Apr 3. doi: 10.5256/f1000research.14648.r31692

Reviewer response for version 1

Saskia le Cessie ^1,²

Review report. Does evidence support the high expectations placed in precision medicine? A bibliographic review. By J Cortés et al,

Summary: a review of randomised trials with continuous outcomes, measured at baseline and at follow up has been conducted. The aim was to compare the variance of the outcome measure at baseline and follow-up and to compare the variances at follow-up between the treated and the control group. The authors argue that a difference in variances may indicate a heterogeneous treatment effect.

General impression. The paper is well written and the results are of interest. The interpretation of the results is somewhat speculative but the authors discuss adequately the limitations.

Remarks

Abstract, Background : “However, the conventional design of randomized trials assumes that each individual benefits by the same amount.” This is not a correct statement. In a randomised trial, the average treatment effect in the population is estimated, and no assumptions about homogeneity of treatment effects are made here. The authors probably mean that many researchers implicitly assume a homogeneous treatment effect when conducting a randomised trial, interpreting the average treatment effect in the population as treatment effect at an individual level.
Introduction. I liked Figure 1 with the different explanations.
Methods and flow chart. The target population was parallel randomized clinical trials with quantitative/numerical outcomes. This is not true: trials with a survival time as outcome are also trials with a numerical (sometimes censored) outcome, but are not into the scope of your paper. So please mention that you are interested in trials with a numerical response variable which are measured both at baseline and at followup. In the Flow-chart, please check whether there were indeed 150 trials with a qualitative outcome, or whether there were 150 trials which did not satisfy the requirement of both having a baseline and a followup numerical measurement.
Statistical analysis. Here I got lost, the random mixed effects models should distinguish between random variability and heterogeneity, but how was unclear to me. Is adding the variance ratio at baseline needed to correct for the random variability? More details of the models and explanation of the different estimates of the model is needed, and should not only be given in the supplementary material.
Did you compare the Var(change) between the treated and control group? Power to detect differences here would be larger.
It may be of interest to perform a subgroup analysis in the studies where control is placebo
Supplementary material, section 4. The model has two random effects: s_i, the heterogeneity between-study effect and e_i the within sample error with variance nu^2 . I guess this should be nu_i, as each study has its own within sample error variance, estimated form the sample sizes in the two groups (as described in the material)?
The supplementary material did not clearly described which parameter(s) from the models reflected the heterogeneity. From the main text I derived that you used the mean effect mu to indicate the amount of heterogeneity. But then how to interpret the parameter tau?
Supplementary Table S4. Why not put this Table in Section 4, and make one overview of all the models fitted? And I guess that e_ij should be e_i here.
Results: I did not find Figure S1 and Figure S2 very informative. Why not just give a histogram of log(var_OT/var_CT) etc.
Table 1: How were the results from the random model obtained (the 11 increased, 19 decreased etc)?
Figure 3. Please explain what V_OT, V_OC etc is, as Figures should be self-explained.
I did not understand the second paragraph of the discussion. I guess that you want to say that the average treatment effect can be interpreted as an individual treatment effect, but I was confused at first by the words “non-observable patient treatment effect”.
Shocking to see that so many studies do not report measures of variability.
The fourth limitation: “the random effect model reveals additional heterogeneity”. To which result are you referring here, comparisons at baseline, followup or over time? The estimate of tau? Why should this be the result of methodological accuracies?
Figure G is of interest because this is a situation where precision medicine is of interest: for some patients treatment T would be a better choice, for others treatment C and by performing precision medicine the subgroups with different responses could be detected and tailored prescriptions could be given. This indicates that observed homoscedasticity in a study should be interpreted with care and background knowledge of a study is needed to assess whether a situation as in Figure 4 is plausible.

I have read this submission. I believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

F1000Res. 2018 Jun 3.

Jordi Cortés ¹

JOINT ANSWER to Ian White and Saskia le Cessie

This is a general response to Ian White and Saskia Le Cessie on why we stated that the standard clinical trial design and analysis assume a constant effect.

In the following, (1) we update the standard sample size rationale; and (2) we explain why inflated variances may require precision medicine in just two general cases: (a) interaction, as represented in Fig. 1, panel C; and (b) random treatment effect, Fig. 1, panel D.

Under the Neyman-Pearson framework to determine sample size, a single effect size value Δ is specified under the alternative hypothesis H1, assuming in that way a constant effect, as in Fig. 1, panels A (H0) and B (H1).
We devise two situations that, because they result in higher variance, they would need personalized medicine:
- Interaction between treatment and a baseline variable such us, for example, gender (Fig. 1, panel C). In this scenario there are two subpopulations (e.g., men and women) with different treatment effects that require the effect to be made further “precise”.
- Random treatment effect on each patient (Fig. 1, panel D). In this scenario, the effect size does not depend on a known patient baseline characteristic and the only way to estimate the individual patient effect is by means of individualized trials (“n of 1” trials).

Those 2 hypothetical scenarios, lead to an increased variance. Conversely, scenarios E and F represent two similar situations (interaction and random effect) but result in reduced variance –without relevant changes on the average. Although we agree that in those two last scenarios leading to reduced variability the specific patient treatment effect may still be unknown because the outcome has reduced variability with a similar central overall position, we argue that patients in those situations were subject to “further control” (having more stable values within the boundaries of “normality”).

So, the usual sample size rationale specified by statisticians in trials assumes a constant, unique effect that agrees with the clinical and legal interpretation that the effect is the same – or at least similar enough to be considered homogeneous – for all the patients fulfilling the eligibility criteria.

To illustrate this secondary “argument”, we reviewed the sample size rationale for the last (at that time) 10 protocols published in Trials, and we found that all of them defined a single effect size (100%, two-sided 95% confidence interval from 69% to 100%). In addition, we have included a new column in Table S1 with the main analysis showing that the SAP in all those cases (10 out of 10, 95%CI from 69 to 100%) was also designed to estimate a single, constant effect.

We have modified Fig. 1 (panels E and F) to show decreasing variance treatment effects, but now without affecting the average. We have also improved the 2 following sentences:

Before [Abstract]: However, the conventional design of randomized trials assumes that each individual benefits by the same amount.

After [Abstract]: However, conventional clinical trials are designed to find differences with the implicit assumption that the effect is the same in all patients within the eligibility criteria.

Before [Introduction]: The assumption that the average effect equals the single unit effect underlies the rationale behind the usual sample size calculation, where only a single effect is specified. As an example, the 10 clinical trials published in the Trials Journal in October 2017 (see Supplementary material: Table S1) were designed under this scenario of a fixed, constant or unique effect in the sample size calculation.

After [Introduction]: The assumption of homoscedasticity in the usual calculations of sample size is better interpreted under the constant effect model (Figure 1, panels A, H ₀; and B, H ₁). As an example, the 10 clinical trials published in the Trials Journal in October 2017 (Table S1 of Supplementary material) were designed with only a constant for the effect size. Furthermore, all their analyses were designed to test (and estimate) a single constant for the effect size. In other words, there was mention of neither any possible interaction with baseline variables (Figure 1, scenarios C and E), nor of any random variability for the treatment effect (Figure 1, scenarios D and F); and thus, all those trials were designed to test a constant effect.

We have also updated the legend of Figure 1 to highlight that now panels C to F show only possible individual treatment effects on variances but not on means.

We are deeply grateful to Ian White and Saskia le Cessie for highlighting the need to clarify this crucial issue.

Saskia le Cessie

From here, we’ll answer specific issues

General impression. The paper is well written and the results are of interest. The interpretation of the results is somewhat speculative but the authors discuss adequately the limitations.

Remarks

We are grateful to Prof. Saskia le Cessie for her suggestions, which definitively help us to improve our manuscript.

1. Abstract, Background : “However, the conventional design of randomized trials assumes that each individual benefits by the same amount.” This is not a correct statement. In a randomised trial, the average treatment effect in the population is estimated, and no assumptions about homogeneity of treatment effects are made here. The authors probably mean that many researchers implicitly assume a homogeneous treatment effect when conducting a randomised trial, interpreting the average treatment effect in the population as treatment effect at an individual level.

Yes, our impression is that at least some trialists are not aware of these assumptions. But the fact that we wanted to highlight is that trials are usually designed to provide evidence for just one parameter (in our context the “effect size” collected by the difference of means) without further specification, neither in the sample size rationale nor in the analysis of the further parameters required by precision medicine. We have addressed this point in the joint answer above.

2. Introduction. I liked Figure 1 with the different explanations.

Thank you. Please note that we have now updated panels C to F to isolate changes just in variance.

3. Methods and flow chart. The target population was parallel randomized clinical trials with quantitative/numerical outcomes. This is not true: trials with a survival time as outcome are also trials with a numerical (sometimes censored) outcome, but are not into the scope of your paper. So please mention that you are interested in trials with a numerical response variable which are measured both at baseline and at follow-up. In the Flow-chart, please check whether there were indeed 150 trials with a qualitative outcome, or whether there were 150 trials which did not satisfy the requirement of both having a baseline and a follow-up numerical measurement.

Thanks. We fully agree that discussion was introduced too late, and we have further clarified it in the Methods section and in the flow chart. The modifications are described below.

Before [Methods]: Our target population was parallel randomized clinical trials with quantitative outcomes

After [Methods]: Our target population was parallel randomized clinical trials with quantitative outcomes (not including time-to-event studies)

Before [Flow chart]: Qualitative outcome

After [Flow chart]: Categorical or time-to-event outcome

4. Statistical analysis. Here I got lost, the random mixed effects models should distinguish between random variability and heterogeneity, but how was unclear to me. Is adding the variance ratio at baseline needed to correct for the random variability? More details of the models and explanation of the different estimates of the model is needed, and should not only be given in the supplementary material.

Thanks. The model includes the (logarithm of the) baseline variances ratio because some imbalances in the initial variability between groups (after randomization) can occur simply by chance. It is foreseeable that these baseline differences in variability may influence the final differences in variability. This baseline log-ratio was highly significant (p < 0.0001) in the model.

All your suggestions related to the statistical analysis (4, 7, 8, 9 and 11) and the random effects model have been addressed through a clearer and longer explanation of the model in the statistical analysis section (detailed here and in the manuscript)

Nevertheless, we provide the following rule of thumb for interpreting the parameters μ (heteroscedasticity) and I ² (heterogeneity) of the random-effects model.

mu < 0 --> On average, studies have lower variability in the experimental arm.

mu > 0 --> On average, studies have greater variability in the experimental arm.

I^2 < 25% --> As the point estimate of heterogeneity is not high enough, mu is constant throughout all the studies.

I^2 < 25% --> As the point estimate of heterogeneity is high, mu does not apply to every single study.

mu < 0 & I^2 < 25% --> Not one study requires precision medicine.

mu < 0 & I^2 > 25% --> Some studies require precision medicine.

mu > 0 & I^2 < 25% --> All studies require precision medicine.

mu > 0 & I^2 > 25% --> Most studies require precision medicine.

[The threshold of 25% for I^2 is based on PRISMA Statement [1] that considers values under this cutpoint as low.]

The estimates of these parameters in our data were mu = -0.12 and I^2 = 80.8%, which implies that some studies require precision medicine.

Liberati A, Altman DG, Tetzlaff J, Mulrow C, Gøtzsche P, et al. (2009) The PRISMA statement for reporting systematic reviews and meta-analyses of studies that evaluate health care interventions: Explanation and elaboration. PLoS Med 6: e1000100.

5. Did you compare the Var(change) between the treated and control group? Power to detect differences here would be larger.

Strongly agree. For high correlations between baseline and outcome, it follows that V (log (V _Ox/V _Bx)) < V (log (V _Ox)), as can be seen in Appendix VII of the supplementary material. However, just 95 out of 208 studies provide the Var(change) or the baseline-final correlation that would allow this analysis.

6. It may be of interest to perform a subgroup analysis in the studies where control is placebo

In fact, we performed this subgroup analysis beforehand without obtaining relevant results. We decided not to include or mention it because the distinction between a treatment called "placebo" and an "active" treatment is not clear. “Placebo” is defined as a simulator of the experimental treatment that tries to emulate its characteristics; but in some studies “control” may equal “best medical treatment”, which is also provided to “treated” patients, such that “Placebo” is complemented by the standard intervention. Because of this ambiguity in the classification, we decided to omit this information. As illustrative examples, we mention the following included studies:

- Ghaleiha A, Mohammadi E, Mohammadi M, et al. Riluzole as an adjunctive therapy to risperidone for the treatment of irritability in children with autistic disorder: a doubleblind, placebocontrolled, randomized trial. Paediatr Drugs 2013; 15:505–514. The patients in the reference group took placebo in addition to risperidone (titrated up to 2 or 3 mg/day based on bodyweight) for 10 weeks.

- Carroll MW, Jeon D, Mountz JM, et al. Efficacy and safety of metronidazole for pulmonary multidrug-resistant tuberculosis. Antimicrob Agents Chemother 2013; 57:3903-9. The patients in the reference group took placebo for 8 weeks in addition to an individualized background regimen.

7. Supplementary material, section 4. The model has two random effects: s_i, the heterogeneity between-study effect and e_i the within sample error with variance nu^2 . I guess this should be nu_i, as each study has its own within sample error variance, estimated form the sample sizes in the two groups (as described in the material)?

Thank you. We have corrected the typo including the subscript both in the Methods section and in the supplementary material: “nu_i”

8. The supplementary material did not clearly describe which parameter(s) from the models reflected the heterogeneity. From the main text I derived that you used the mean effect mu to indicate the amount of heterogeneity. But then how to interpret the parameter tau?

Thanks. Tau reflects the heterogeneity in the assessment of the heteroscedasticity throughout the studies. Following this suggestion and similar comment of Professor Ian White, we have tried to clarify that mu is a measure of heteroscedasticity and tau is a measure of the heterogeneity of the former throughout all the studies. See also the answer to question 4 for more clarification.

9. Supplementary Table S4. Why not put this Table in Section 4, and make one overview of all the models fitted? And I guess that e_ij should be e_i here.

Thank you, we have corrected the subscript typo: “e_i”

And yes, your suggestion facilitates readability. We have interspersed all the tables and figures of the supplementary material in their respective sections.

10. Results: I did not find Figure S1 and Figure S2 very informative. Why not just give a histogram of log(var_OT/var_CT) etc.

We have kept Figures S1 and S2 because we believe that they provide additional information about whether or not the increase (or decrease) in the variability in the outcome of the experimental arm depends on the outcome variability of the control arm (or on the baseline variability of the experimental group). However, we have also added the histograms you mention in order to summarize the essential information. The histograms can be seen here or in the Supplementary material.

11. Table 1: How were the results from the random model obtained (the 11 increased, 19 decreased etc)?

We have obtained them as the studies that had to be removed in order to obtain heterogeneity (i.e., tau) similar to the baseline (which we expect to be null by randomization). We have tried to clarify this point in the legend of the table:

“…or (2) number of studies that have to be deleted from the random-effects model in order to achieve a negligible heterogeneity (studies with more extreme outcome were removed one by one until achieving an estimated value of τ similar to the one obtained from the reference model. See Methods section for more details…)”

12. Figure 3. Please explain what V_OT, V_OC etc is, as Figures should be self-explained.

Thanks. We have included a legend in this figure explaining these abbreviations:

V_OT: Variance of the Outcome in the Treated arm

V_OC: Variance of the Outcome in the Control arm

V_BT: Variance of the Outcome at baseline in the Treated arm

13. I did not understand the second paragraph of the discussion. I guess that you want to say that the average treatment effect can be interpreted as an individual treatment effect, but I was confused at first by the words “non-observable patient treatment effect”.

You are right. We say “non-observable” for the fundamental problem of causal inference (both potential responses are not observable in the same patient), which avoids seeing the treatment effect at the individual level. We have clarified this point:

Before: This means that treatment effects obtained by comparing the means between groups can be used to estimate both the averaged treatment effect and the non-observable patient treatment effect.

After: This means that the average treatment effect can be interpreted as an individual treatment effect (not directly observable).

14. Shocking to see that so many studies do not report measures of variability.

Yes. It is really surprising that 61.6% of studies do not report the variability either at baseline or at the end of the study. Although CONSORT advises it, this guideline does not provide the historical data on this practice with which it can be compared.

15. The fourth limitation: “the random effect model reveals additional heterogeneity”. To which result are you referring here, comparisons at baseline, followup or over time? The estimate of tau? Why should this be the result of methodological accuracies?

We are referring to the main analysis: comparison between arms. Nevertheless, this sentence could be applied to all analyses. Heterogeneity among studies is measured by tau (see response to question 4).

We stated that methodological inaccuracies can be derived in the presence of heterogeneity. In an ideal scenario of constant treatment effect in all the studies, the only thing that could lead to heterogeneity in the model would be methodological inaccuracies such as those mentioned in the manuscript or in the referenced paper of Carlisle: transcription errors, insufficient follow-up time for being able to observe this constant effect, or the manipulation of the results in order to achieve greater impact.

16. Figure G is of interest because this is a situation where precision medicine is of interest: for some patients treatment T would be a better choice, for others treatment C and by performing precision medicine the subgroups with different responses could be detected and tailored prescriptions could be given. This indicates that observed homoscedasticity in a study should be interpreted with care and background knowledge of a study is needed to assess whether a situation as in Figure 4 is plausible.

Fully agree, although this is a highly sophisticated scenario that we hope will not be viewed as a frequent scenario.

Of course, we think that personalized medicine has already been demonstrated to be effective in some areas. Our point is that unless those demonstrations exist, most interventions should be routinely administrated to all patients fulfilling eligibility criteria.

F1000Res. 2018 Mar 23. doi: 10.5256/f1000research.14648.r31694

Reviewer response for version 1

Erica EM Moodie ¹

The authors have performed a review of a sample of clinical trials conducted every three years from 2004-2013 to examine whether there exists post-treatment heterogeneity in participants responses with premise that lack of heterogeneity suggests that precision medicine is not warranted.

While the question is one that should be asked. However, the study carried out is not suited to answering the question as it has been conducted in randomized trials where there is typically little heterogeneity. That is, the authors have performed a perfectly reasonable analysis that cannot answer the pertinent question. It is well known that randomized trials tend to be populated by homogenous population (more white, more male, etc.) – see, for example Oh et al. (2015) Diversity in Clinical and Biomedical Research: A Promise Yet to Be Fulfilled. PLoS Med 12(12): e1001918, Caplan & Friesen P (2017) Health disparities and clinical trial recruitment: Is there a duty to tweet? PLoS Biol 15(3): e2002040 and the references therein – or indeed many other papers on this topic. This may be in part a function of recruitment strategies and also by design, as trialists (particularly those testing new therapies) often determine inclusion criteria to target the (potentially homogeneous) segment of the population who might show the greatest response to the treatment. Thus, the authors have chosen to study a population that is likely to be homogeneous and not reflective of real-world clinical care. There are numerous examples covariate-tailored treatment algorithms, from the choice of hormonal therapies for women diagnosed with estrogen-receptor-positive, HER2-negative breast cancer to the choice of ACE inhibitors vs. calcium channel blockers for hypertension, that the authors choose to overlook as cases where we have learned about previous patients with particular characteristics to learn about future similar patients.

I have read this submission. I believe that I have an appropriate level of expertise to state that I do not consider it to be of an acceptable scientific standard, for reasons outlined above.

F1000Res. 2018 Jun 3.

Jordi Cortés ¹

The referee’s objections can be summarized in two points:

(1) “There are numerous examples of covariate-tailored treatment algorithms.”

(2) “Randomized trials tend to be populated by homogenous populations”, which in turn does not reflect a real population’s existing variability.

We understand the reviewer’s comments, but we disagree with the reviewer’s conclusions:

(1) Our work does not intend to completely invalidate precision medicine. We are not stating that there are not “examples of covariate-tailored treatments”; rather that (Abstract): “We found that the outcome variance was more often smaller in the intervention group, suggesting that treated patients may end up pertaining more often to reference or normality values and thus would not require further precision medicine”. This was already stated in the discussion: “these findings do not invalidate precision medicine in all settings.” Thus in the quite wide settings of our trials, we found little evidence that precision medicine would be of any use.

(2) The referee argues that trials have “too many” selection criteria to reflect “a real population”. This is a standard criticism of explanatory clinical trials, suggesting that the selection criteria are usually “too many”. And we agree, because our point is that most trials have “enough” selection criteria to provide a homogeneous effect. Furthermore, we also agree that we can only talk about “published trials with eligibility criteria”. As for whether those selection criteria should be used to define the target population in clinical guidelines, there is no further need to tailor precision medicine.

Dr. Moodie argues that our results do not answer the question that is posed. We also disagree. The issue of heterogeneity is obviously one that bedevils the generalizability of clinical trials. However, these are randomized comparisons; so, in the absence of a treatment effect we would expect the two arms to be comparable, no matter how heterogeneous the underlying population. The fact that even in the presence of a treatment effect there was little evidence of heterogeneity suggests there will be little scope for precision medicine in these populations. One might argue that with a more heterogeneous population, there is more scope to detect the few non-responders who would not form part of a general trial population. This does not invalidate our results; rather it argues for much larger trials with a more heterogeneous population. The point is that in the absence of these the evidence base for precision medicine is weak.

F1000Res. 2018 Mar 2. doi: 10.5256/f1000research.14648.r30604

Reviewer response for version 1

Ian R White ¹

This paper considers randomised trials (RCTs) of treatment versus control with a quantitative outcome. It observes that if treatment effects are homogeneous (the same for all trial participants) then the outcome variance will be the same in both trial arms. It therefore reviews the extent to which the outcome variance is the same across trial arms in 208 published RCTs. It finds 41 RCTs with significant differences in outcome variance, and that it is more common for the outcome variance to be smaller in the treatment arm rather than larger.

My overall comment is that the analysis results are useful, but they need to be made clearer, and the interpretation should be much more cautious. Points marked * must be addressed to make the article scientifically sound (with ** the top priority).

Background

*Abstract, background: “The conventional design of randomized trials assumes that each individual benefits by the same amount.” This is also asserted elsewhere in the paper, but it is not true. From a causal inference perspective, a RCT estimates the average causal effect, which is well defined in the presence of treatment effect heterogeneity. This is why the trials community worries so much about external generalisability: for example, if a trial treated 60% women and 40% men and showed a benefit of treatment, then a clinician treating women and men in the same ratio can be confident of giving a benefit overall, but a clinician treating women and men in a different ratio cannot be so confident. This point (repeated elsewhere) is not essential to the paper’s argument, so should be removed.
*Similarly, the argument “The assumption that the average effect equals the single unit effect underlies the rationale behind the usual sample size calculation, where only a single effect is specified” (Introduction) is false. Sample size calculations relate only to comparisons of group averages.

Methods

The methods used appear entirely appropriate. However they are not well described.

*Terminology must be improved. For example, the key outcome in this study is the ratio of variances between treatment and control arms, and this (or its opposite) is variously called “homoscedasticity”, “heterogeneity”, even “concordance”. The authors should choose a term and stick with it. Similarly for the “random mixed effects model” which later becomes the “random model”. (I’m going to use “homoscedasticity” and “random-effects model”.)
The authors are doing a meta-analysis, even though they don’t call it that, so the term “heterogeneity” should be reserved for “variation between studies”, i.e. tau^2 in the random effects models.
*It’s not clear to me what the “random model” results in Table 1 are. Since this is a model across studies, how can it count individual studies? If empirical Bayes estimates of study-specific effects are being tested, this must be explained.
Trials that are “significant” are combined - “Subgroup analyses suggest that only significant interventions had an effect on reducing variability” - but interventions that increase the mean should be separated from those that decrease the mean. The later conclusion that “The variability seems to decrease for treatments that perform significantly better than the reference” suggests a different distinction (better/worse is not the same as larger/smaller because outcomes may be positive or negative) and is not supported by the results presented.
Abstract, Results: “The adjusted point estimate of the mean ratio (treated to control group) of the outcome variances” is not clear without reading the whole text. Again, defining a term (“outcome variance ratio”?) will help.
*Table 1, “variability is… increased”: from the text, this means “significantly increased”, which should be clarified.

Interpretation

The results may be interpreted in many ways, which are sensibly discussed by the authors.

Homoscedasticity is scale-dependent: for example, it may be removed (or created) by a log transformation (mentioned in the Discussion).

*The authors omit one alternative explanation of homoscedasticity over time: clinical trial populations have eligibility criteria at baseline which may limit baseline variance. For example, a hypertension trial might recruit patients with baseline SBP between 140 and 159 mm Hg. In this case, variance is very likely to naturally increase over time.
**The authors’ conclusions ignore the alternative interpretations noted above. Here are some examples which are illogical:
- Abstract, Conclusions: “the variance was more often smaller in the intervention group, suggesting, if anything, a reduced role for precision medicine”, and Discussion: “variability tends to be reduced on average after treatment, thus making precision medicine dispensable in most cases”. This is actually false. If a study finds smaller variance in the treated group then we DO have evidence of treatment effect heterogeneity, and indeed the treatment may be doing exactly what medicine should do - making the sickest better while not harming the less sick.
- Introduction: “If this homoscedasticity holds, there is no need to repeat the clinical trial once a new possible effect modifier becomes measurable” - again, this wrongly assumes the converse stated above.
- Discussion: “When both arms have equal variances, then an obvious default explanation is that the treatment is equally effective for all, thus rendering the search for predictors of differential response futile”: this is illogical.
- Discussion: “For most trials, subjects vary little in their response to treatment, which suggests that precision medicine’s scope may be less than what is commonly assumed.” : this is also illogical.
*In the light of the above arguments, I find the statement (Abstract, Conclusions) that “Homoscedasticity is a useful tool for assessing whether or not the premise of constant effect is reasonable” to be highly debatable. Logic suggests it gives a lower bound on the extent of usefulness of precision medicine, and the results of this study do not add any more to this.
*The objectives in the Discussion should be the same as those stated in the Introduction.

Source data

I had trouble opening the source data both in Excel (since the csv file is in fact semi-colon-delimited) and in Stata (which was thrown by line 80). Could it be provided in a more convenient format or with some notes?

F1000Res. 2018 Jun 3.

Jordi Cortés ¹

JOINT ANSWER to Ian White and Saskia le Cessie

This is a general response to Ian White and Saskia Le Cessie on why we stated that the standard clinical trial design and analysis assume a constant effect.

Under the Neyman-Pearson framework to determine sample size, a single effect size value Δ is specified under the alternative hypothesis H1, assuming in that way a constant effect, as in Fig. 1, panels A (H0) and B (H1).
We devise two situations that, because they result in higher variance, they would need personalized medicine:
- Interaction between treatment and a baseline variable such us, for example, gender (Fig. 1, panel C). In this scenario there are two subpopulations (e.g., men and women) with different treatment effects that require the effect to be made further “precise”.
- Random treatment effect on each patient (Fig. 1, panel D). In this scenario, the effect size does not depend on a known patient baseline characteristic and the only way to estimate the individual patient effect is by means of individualized trials (“n of 1” trials).

We have modified Fig. 1 (panels E and F) to show decreasing variance treatment effects, but now without affecting the average. We have also improved the 2 following sentences:

Before [Abstract]: However, the conventional design of randomized trials assumes that each individual benefits by the same amount.

After [Abstract]: However, conventional clinical trials are designed to find differences with the implicit assumption that the effect is the same in all patients within the eligibility criteria.

We have also updated the legend of Figure 1 to highlight that now panels C to F show only possible individual treatment effects on variances but not on means.

We are deeply grateful to Ian White and Saskia le Cessie for highlighting the need to clarify this crucial issue.

Ian White

From here, we’ll answer specific issues

We are grateful to Prof. Ian White for his suggestions, which will definitively help us to improve our manuscript.

Background

1.*Abstract, background: “The conventional design of randomized trials assumes that each individual benefits by the same amount.” This is also asserted elsewhere in the paper, but it is not true. From a causal inference perspective, a RCT estimates the average causal effect, which is well defined in the presence of treatment effect heterogeneity. This is why the trials community worries so much about external generalisability: for example, if a trial treated 60% women and 40% men and showed a benefit of treatment, then a clinician treating women and men in the same ratio can be confident of giving a benefit overall, but a clinician treating women and men in a different ratio cannot be so confident. This point (repeated elsewhere) is not essential to the paper’s argument, so should be removed.

2. *Similarly, the argument “The assumption that the average effect equals the single unit effect underlies the rationale behind the usual sample size calculation, where only a single effect is specified” (Introduction) is false. Sample size calculations relate only to comparisons of group averages.

Thanks again for highlighting this hugely important issue. We have addressed these two comments in the previous common answer.

Methods

The methods used appear entirely appropriate. However they are not well described.

1. *Terminology must be improved. For example, the key outcome in this study is the ratio of variances between treatment and control arms, and this (or its opposite) is variously called “homoscedasticity”, “heterogeneity”, even “concordance”. The authors should choose a term and stick with it. Similarly for the “random mixed effects model” which later becomes the “random model”. (I’m going to use “homoscedasticity” and “random-effects model”.)

Thanks. To simplify the notation, we have deleted the term “concordance”. We also reserved the term heterogeneity for the tau^2 statistic resulting from the mixed-effects model (see next answer). Furthermore, we have homogenized the terms for referring to the “random-effects model” throughout the text.

2. The authors are doing a meta-analysis, even though they don’t call it that, so the term “heterogeneity” should be reserved for “variation between studies”, i.e. tau^2 in the random effects models.

We appreciate this insightful observation. In the random-effects model, we measured heteroscedasticity with the mu parameter, and heterogeneity between studies, through tau^2. In order to clarify this as much as possible, we have specified in the Methods section that tau^2 is used for measuring heterogeneity; and this has also been included between brackets in the Results section:

“The estimated value of tau^2 provides a measure of heterogeneity, that is, to what extent the value of mu is applicable to all studies. The larger tau^2 is, the less the homogeneity”

3. *It’s not clear to me what the “random model” results in Table 1 are. Since this is a model across studies, how can it count individual studies? If empirical Bayes estimates of study-specific effects are being tested, this must be explained.

We used the Delta method to estimate the within study variability (specifically, the variance of the logarithm of the outcome variance ratio). We have included this explanation in the Methods section: “As there is only one available measure for each study, both sources of variability cannot be empirically differentiated: (i) within study or random or that one related to sample size; and (ii) heterogeneity. In order to isolate the second, the first was theoretically estimated using the Delta method –as explained in Sections V and VI of Supplementary material“

4. Trials that are “significant” are combined - “Subgroup analyses suggest that only significant interventions had an effect on reducing variability” - but interventions that increase the mean should be separated from those that decrease the mean. The later conclusion that “The variability seems to decrease for treatments that perform significantly better than the reference” suggests a different distinction (better/worse is not the same as larger/smaller because outcomes may be positive or negative) and is not supported by the results presented.

Thanks for this great contribution. Following your suggestion, we have sought in each primary endpoint for whether improvements in the response correspond to higher (e.g., mobility) or lower (e.g., pain) values. This new factor has been included in the subgroup analysis (see new figures S5-S7 clicking here or in the Supplementary Material), thus providing an argument for the existence of a "floor" effect in those studies where a lower value corresponds to a better condition. We have added an interpretation of this finding in the Discussion:

“This reduced variability could also be due to methodological reasons. One is that some measurements may have a “ceiling” or “floor” effect (e.g., in the extreme case, if a treatment heals someone, no further improvement is possible). In fact, according to the subgroup analysis of the studies with outcomes that indicate the degree of disease (high values imply greater severity; e.g., pain), a greater variance (25%) is obtained in the experimental arm (see Figure S5). However, in the studies with outcomes that measure the degree of healthiness (high values imply better condition; e.g., mobility), the average variances match between arms and do not suggest a ceiling effect.”

In addition, we have included this new factor (direction of the improvement) in the Shiny app .

On the other hand, all the significant studies were in favor of the experimental group; therefore, in our context, "statistically significant" is equivalent to "better response in the experimental group". We have specified this statement in the manuscript and we have kept the sentence: "the authors found statistically significant differences between the arms (all of them in favor of the experimental group) in 83 (39.9%) studies"

5. Abstract, Results: “The adjusted point estimate of the mean ratio (treated to control group) of the outcome variances” is not clear without reading the whole text. Again, defining a term (“outcome variance ratio”?) will help.

Thanks. Corrected both in the Abstract and the main text:

Before [Abstract]: We assessed homoscedasticity by comparing the outcome variability between treated and control arms

After [Abstract]: We assessed homoscedasticity by comparing the variance of the primary endpoint between arms through the outcome variance ratio (treated to control group).

Before [Abstract]: The adjusted point estimate of the mean ratio (treated to control group)

After [Abstract]: The adjusted point estimate of the mean outcome variance ratio (treated to control group) …

Before [Methods]: … we fitted a random-mixed effects model using the logarithm of the variance ratio at the end of the trial…

After [Methods]: … we fitted a random-effects model using the logarithm of the outcome variance ratio at the end of the trial …

6. *Table 1, “variability is… increased”: from the text, this means “significantly increased”, which should be clarified.

Thanks. We have corrected it:

Before [Table 1]: increased/decreased

After [Table 1]: significantly increased / significantly decreased

Interpretation

The results may be interpreted in many ways, which are sensibly discussed by the authors.

Most importantly, treatment effect homogeneity implies homoscedasticity, but the converse (“homoscedasticity implies treatment effect homogeneity”) is not true: this is demonstrated very nicely in Figure 4. Homoscedasticity is scale-dependent: for example, it may be removed (or created) by a log transformation (mentioned in the Discussion).

1. *The authors omit one alternative explanation of homoscedasticity over time: clinical trial populations have eligibility criteria at baseline which may limit baseline variance. For example, a hypertension trial might recruit patients with baseline SBP between 140 and 159 mm Hg. In this case, variance is very likely to naturally increase over time.

Thanks again. We have dealt with this in the Discussion:

“…it has been observed that the variability in the experimental arm also decreases from baseline to the end of the study, although this comparison is not protected by randomization; for example, the existence of eligibility criteria at baseline may have limited the initial variance (a hypertension trial might recruit patients with baseline SBP between 140 and 159 mm Hg), leading to the variance naturally increasing over time”

2. **The authors’ conclusions ignore the alternative interpretations noted above. Here are some examples which are illogical:

Abstract, Conclusions: “the variance was more often smaller in the intervention group, suggesting, if anything, a reduced role for precision medicine”, and Discussion: “variability tends to be reduced on average after treatment, thus making precision medicine dispensable in most cases”. This is actually false. If a study finds smaller variance in the treated group then we DO have evidence of treatment effect heterogeneity, and indeed the treatment may be doing exactly what medicine should do - making the sickest better while not harming the less sick.

Thanks. We agree. We have addressed this point in the general response above. We provide here further specific comments.

There is heteroscedasticity of effect leading to reduced outcome variability, such as the one shown in examples E and F of Figure 1. Those cases with reduced variability show situations in which the outcome is “under additional control” at the end. The only mathematical model that we can imagine here is the one with an effect correlated with baseline values: higher effects for higher (worse) baseline values. We can imagine this situation for the “ideal” training program: worse participants at the beginning, which further increases or reduces variability. So, although we agree that this is a theoretical heterogeneity, we do not think that it has any practical implication for “individualizing” the treatment: all patients benefit (although to a different degree) from the intervention; and at the end, all patients are “under additional control”.

We have performed some changes in the manuscript in order to clarify this point:

Before [Abstract]: the variance was more often smaller in the intervention group, suggesting, if anything, a reduced role for precision medicine

After [Abstract]: We found that the outcome variance was more often smaller in the intervention group, suggesting that treated patients may end up pertaining more often to reference or “normality” values and thus would not require further precision medicine. However, this result may also be compatible with a reduced effect in some patients, which would require studying whether the effect merits enduring the side effects as well as the economic costs.

Before [Discussion]: variability tends to be reduced on average after treatment, thus making precision medicine dispensable in most cases

After [Discussion]: We found that variability seems to decrease for treatments that perform significantly better than the reference; otherwise, it remains similar. Therefore, the treatment seems to be doing what medicine should do –having larger effects in the most ill patients. Two considerations may be highlighted here: (1) as the outcome range becomes reduced, we may interpret that, following the intervention, this population is under additional control; but also, (2) as subjects are responding differently to treatment, this opens the way for not treating some (e.g. those subjects who are not very ill, and so have no scope to respond very much), with obvious savings in side effects and costs

Introduction: “If this homoscedasticity holds, there is no need to repeat the clinical trial once a new possible effect modifier becomes measurable” - again, this wrongly assumes the converse stated above.

In this case, we have softened the sentence by changing the term "need" to "evidence".

Before [Introduction]: If this homoscedasticity holds, there is no need to repeat the clinical trial once a new possible effect modifier becomes measurable

After [Introduction]: If this homoscedasticity holds, there is no evidence that the clinical trial should be repeated once a new possible effect modifier becomes measurable

Discussion: “When both arms have equal variances, then an obvious default explanation is that the treatment is equally effective for all, thus rendering the search for predictors of differential response futile”: this is illogical.

We are not sure that we understood why this is illogical. Anyway, we have softened the sentence by changing "an obvious default explanation" to "the simplest explanation".

Before [Discussion]: When both arms have equal variances, then an obvious default explanation is that the treatment is equally effective for all, thus rendering the search for predictors of differential response futile

After [Discussion]: When both arms have equal variances, then the simplest explanation is that the treatment is equally effective for all, thus rendering the search for predictors of differential response futile.

Discussion: “For most trials, subjects vary little in their response to treatment, which suggests that precision medicine’s scope may be less than what is commonly assumed”: this is also illogical.

Again, we are not sure that we understood why this is illogical. Nevertheless, we have referred to the limitations derived from Figure 4.

Before [Discussion]: For most trials, subjects vary little in their response to treatment, which suggests that precision medicine’s scope may be less than what is commonly assumed

After [Discussion]: For most trials, variability of the response to treatment changes scarcely or even decreases, which suggests that precision medicine’s scope may be less than what is commonly assumed – while always taking into account the limitation previously explained in Figure 4.

3. *In the light of the above arguments, I find the statement (Abstract, Conclusions) that “Homoscedasticity is a useful tool for assessing whether or not the premise of constant effect is reasonable” to be highly debatable. Logic suggests it gives a lower bound on the extent of usefulness of precision medicine, and the results of this study do not add any more to this.

We have reduced the ostentatious nature of this phrase, warning the reader that there are limitations to this methodology:

“We have shown that the comparison of variances is a useful but not definitive tool to asses if the design assumption of a constant effect holds.”

4. *The objectives in the Discussion should be the same as those stated in the Introduction.

Thanks. We have simplified the objectives in the introduction:

Before: Our objectives were, first, to compare the variability of the main outcome between different arms in clinical trials published in medical journals and, second, to provide a first, rough estimate of the proportion of studies that could potentially benefit from precision medicine. As sensitivity analysis, we explore the changes in the experimental arm’s variability over time (from baseline to the end of the study). We also fit a random- effects model to the outcome variance ratio in order to isolate studies with a variance ratio outside their expected random variability values (heterogeneity).

After: Our objectives were, first, to compare the variability of the main outcome between different arms in clinical trials published in medical journals using a random-effects model; and, second, to provide a rough estimate of the proportion of studies that could potentially benefit from precision medicine. Finally, we explore the changes in the experimental arm’s variability over time (from baseline to the end of the study).

Also, we have reordered the whole Discussion section according to these objectives:

1) Variability comparison between arms and explanation

2) Rough estimate of the studies that potentially benefit from precision medicine (greater variability in experimental arms)

3) Variability comparison between arms and explanation provided in your first suggestion of this section.

Source data

1. I had trouble opening the source data both in Excel (since the csv file is in fact semi-colon-delimited) and in Stata (which was thrown by line 80). Could it be provided in a more convenient format or with some notes?

We have changed the format (now, columns are comma-delimited) both in the Shiny app and in the Figshare repository. We also solved the problem with line 80, which included some unnecessary quotation marks (“) in the Title field.

F1000Res. 2018 Nov 6.

Jordi Cortés ¹

Following your suggestions together with those of the other reviewers, we have updated the manuscript with a new version that aims to emphasize the fact that researchers’ assumption of a constant effect is not clear as long as they do not mention it explicitly. Admittedly, in those studies whose sample size calculation considers some variability in the treatment effect, there is no doubt that this premise has not been considered.

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Click here for additional data file.^{(402KB, tgz)}

Data Availability Statement

Data is available through two sources:

- A shiny app that allows the user to interact with the data without any need to download it: http://shiny-eio.upc.edu/pubs/F1000_precision_medicine/
The Figshare repository: https://doi.org/10.6084/m9.figshare.5552656 ¹⁸

In both sources, the data can be downloaded under a Creative Commons License v. 4.0.

The code for the main analysis is available in the following link: https://doi.org/10.5281/zenodo.1239539 ²²

[ref-1] 1. Collins FS, Varmus H: A new initiative on precision medicine. N Engl J Med. 2015;372:793–5. 10.1056/NEJMp1500523 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-2] 2. Kohane IS: HEALTH CARE POLICY. Ten things we have to do to achieve precision medicine. Science. 2015;349(6243):37–8. 10.1126/science.aab1328 [DOI] [PubMed] [Google Scholar]

[ref-3] 3. Schork NJ: Personalized medicine: Time for one-person trials. Nature. 2015;520(7549):609–11. 10.1038/520609a [DOI] [PubMed] [Google Scholar]

[ref-4] 4. Willis JC, Lord GM: Immune biomarkers: the promises and pitfalls of personalized medicine. Nat Rev Immunol. 2015;15(5):323–29. 10.1038/nri3820 [DOI] [PubMed] [Google Scholar]

[ref-5] 5. Wallach JD, Sullivan PG, Trepanowski JF, et al. : Evaluation of Evidence of Statistical Support and Corroboration of Subgroup Claims in Randomized Clinical Trials. JAMA Intern Med. 2017;177(4):554–60. 10.1001/jamainternmed.2016.9125 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-6] 6. Durán-Cantolla J, Aizpuru F, Montserrat JM, et al. : Continuous positive airway pressure as treatment for systemic hypertension in people with obstructive sleep apnoea: randomised controlled trial. BMJ. 2010;341:c5991. 10.1136/bmj.c5991 [DOI] [PubMed] [Google Scholar]

[ref-7] 7. Kojima Y, Kaga H, Hayashi S, et al. : Comparison between sitagliptin and nateglinide on postprandial lipid levels: The STANDARD study. World J Diabetes. 2013;4(1):8–13. 10.4239/wjd.v4.i1.8 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-8] 8. International conference on harmonisation: statistical principles for clinical trials ICH-E9.1998. Accessed September 14 2017. Reference Source [Google Scholar]

[ref-9] 9. Shamseer L, Sampson M, Bukutu C, et al. : CONSORT extension for reporting N-of-1 trials (CENT) 2015: Explanation and elaboration. BMJ. 2015;350:h1793. 10.1136/bmj.h1793 [DOI] [PubMed] [Google Scholar]

[ref-10] 10. Araujo A, Julious S, Senn S: Understanding Variation in Sets of N-of-1 Trials. PLoS One. 2016;11(12):e0167167. 10.1371/journal.pone.0167167 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-11] 11. Senn S: Individual response to treatment: is it a valid assumption? BMJ. 2004;329(7472):966–68. 10.1136/bmj.329.7472.966 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-12] 12. Senn S: Mastering variation: variance components and personalised medicine. Stat Med. 2016;35(7):966–77. 10.1002/sim.6739 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-13] 13. Wang R, Lagakos SW, Ware JH, et al. : Statistics in medicine--reporting of subgroup analyses in clinical trials. N Engl J Med. 2007;357(21):2189–94. 10.1056/NEJMsr077003 [DOI] [PubMed] [Google Scholar]

[ref-14] 14. Senn S, Richardson W: The first t-test. Stat Med. 1994;13(8):785–803. 10.1002/sim.4780130802 [DOI] [PubMed] [Google Scholar]

[ref-15] 15. Kim SH, Schneider SM, Bevans M, et al. : PTSD symptom reduction with mindfulness-based stretching and deep breathing exercise: randomized controlled clinical trial of efficacy. J Clin Endocr Metab. 2013;98(7):2984–92. 10.1210/jc.2012-3742 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-16] 16. Holland P: Statistics and Causal Inference. J Am Stat Assoc. 1986;81(396):945–60. 10.2307/2289064 [DOI] [Google Scholar]

[ref-17] 17. Kim ES, Hirsch V, Mok T, et al. : Gefitinib versus docetaxel in previously treated non-small-cell lung cancer (INTEREST): a randomised phase III trial. Lancet. 2008;372(9652):1809–1818. 10.1016/S0140-6736(08)61758-4 [DOI] [PubMed] [Google Scholar]

[ref-18] 18. Cortés J: ‘review_homoscedasticity_clinical_trials’.[Data set].2017. 10.6084/m9.figshare.5552656 [DOI] [Google Scholar]

[ref-19] 19. Bartlett MS, Kendall DG: The statistical analysis of variance-heterogeneity and the logarithmic transformation. J R Stat Soc. 1946;8(1):128–38. 10.2307/2983618 [DOI] [Google Scholar]

[ref-20] 20. Higgins JP, Thompson SG, Deeks JJ, et al. : Measuring inconsistency in meta-analyses. BMJ. 2003;327(7414):557–560. 10.1136/bmj.327.7414.557 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-21] 21. Sachs L: Applied Statistics: A Handbook of Techniques.2nd ed. New York: Springer-Verlag,1984. 10.1007/978-1-4612-5246-7 [DOI] [Google Scholar]

[ref-22] 22. Cortés J: R code for analysis of homoscedasticity in clinical trials. Zenodo. 2017. 10.5281/zenodo.1133609 [DOI] [Google Scholar]

[ref-23] 23. Carlisle JB: Data fabrication and other reasons for non-random sampling in 5087 randomised, controlled trials in anaesthetic and general medical journals. Anaesthesia. 2017;72(8):944–952. 10.1111/anae.13938 [DOI] [PubMed] [Google Scholar]

[ref-24] 24. Hsieh LL, Kuo CH, Yen MF, et al. : A randomized controlled clinical trial for low back pain treated by acupressure and physical therapy. Prev Med. 2004;39(1):168–76. 10.1016/j.ypmed.2004.01.036 [DOI] [PubMed] [Google Scholar]

[ref-25] 25. Senn S: Controversies concerning randomization and additivity in clinical trials. Stat Med. 2004;23(24):3729–53. 10.1002/sim.2074 [DOI] [PubMed] [Google Scholar]

[ref-26] 26. Jamieson J: Measurement of change and the law of initial values: A computer simulation study. Educ Psychol Meas. 1995;55(1):38–46. 10.1177/0013164495055001004 [DOI] [Google Scholar]

[ref-27] 27. Senn S: Trying to be precise about vagueness. Stat Med. 2007;26(7):1417–30. 10.1002/sim.2639 [DOI] [PubMed] [Google Scholar]

[ref-28] 28. Greenlaw N: Constructing appropriate models for meta-analyses. University of Glasgow,2010. Accessed September 14, 2017. Reference Source [Google Scholar]

[ref-29] 29. Schulz KF, Altman DG, Moher D, et al. : CONSORT 2010 statement: updated guidelines for reporting parallel group randomised trials. BMJ. 2010;340:c332. 10.1016/j.jclinepi.2010.02.005 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-30] 30. Rothman KJ, Greenland S, Walker AM: Concepts of interaction. Am J Epidemiol. 1980;112(4):467–70. 10.1093/oxfordjournals.aje.a113015 [DOI] [PubMed] [Google Scholar]

[ref-31] 31. Horwitz RI, Cullen MR, Abell J, et al. : Medicine. (De)personalized medicine. Science. 2013;339(6124):1155–6. 10.1126/science.1234106 [DOI] [PubMed] [Google Scholar]

PERMALINK

Does evidence support the high expectations placed in precision medicine? A bibliographic review

Jordi Cortés

José Antonio González

María Nuncia Medina

Markus Vogler

Marta Vilaró

Matt Elmore

Stephen John Senn

Michael Campbell

Erik Cobo

Roles

Version Changes

Revised. Amendments from Version 2

Abstract

Introduction

Figure 1. Scenarios representing fictional trials using 8 participants with Systolic Blood Pressure as the primary endpoint.

Methods

Population

Data collection

Variables

Statistical analysis

Results

Population

Figure 2. Flow-chart of the articles in the study.

Homoscedasticity

Figure 3. Funnel plots of variance ratio.

Table 1. Variance comparison.

Discussion

Figure 4. Scenario representing a fictional trial with 8 participants with homoscedasticity but non constant effect.

Data availability

Supplementary material

Funding Statement

References

Reviewer response for version 3

Ian R White

Roles

Jordi Cortés

Reviewer response for version 2

Saskia le Cessie

Roles

Jordi Cortés

Reviewer response for version 2

Ian R White

Roles

Jordi Cortés

Reviewer response for version 1

Saskia le Cessie

Roles

Jordi Cortés

Reviewer response for version 1

Erica EM Moodie

Roles

Jordi Cortés

Reviewer response for version 1

Ian R White

Roles

Jordi Cortés

Jordi Cortés

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases