Abstract
Optical trapping of (sub)micron-sized particles is broadly employed in nanoscience and engineering. The materials commonly employed for these particles, however, have physical properties that limit the transfer of linear or angular momentum (or both). This reduces the magnitude of forces and torques, and the spatiotemporal resolution, achievable in linear and angular traps. Here, we overcome these limitations through the use of single-crystal rutile TiO2, which has an exceptionally large optical birefringence, a high index of refraction, good chemical stability, and is amenable to geometric control at the nanoscale. We show that rutile TiO2 nanocylinders form powerful joint force and torque transducers in aqueous environments by using only moderate laser powers to apply nN·nm torques at kHz rotational frequencies to tightly trapped particles. In doing so, we demonstrate how rutile TiO2 nanocylinders outperform other materials and offer unprecedented opportunities to expand the control of optical force and torque at the nanoscale.
Keywords: dielectric crystals, rutile titanium dioxide, optical trapping, force spectroscopy, torque spectroscopy, optical torque wrench
The ability of optical tweezers to apply torque to, and thereby control the rotation of, micron-scale (or smaller) particles1,2 complements their well-known control of force and position and provides the opportunities for diverse novel applications at the nanoscale. For example, in biological physics, angular optical tweezers have been utilized in single-molecule torque spectroscopy,3,4 rotational microrheology,5 and in the manipulation of cellular growth dynamics.6 In quantum physics, rotational optomechanical effects within angular optical traps7 are under active investigation. And in engineering applications, angular optical tweezers enable optically driven microfluidic actuators such as microgears8 and fluidic pumps.9
Linear optical tweezers achieve stable 3D trapping of either dielectric or metal particles using Gaussian (TEM00) beams and have been extensively described.10 To achieve additional angular optical control, specialized forms of laser beams or trapping particles (or both) are required.4 One of the most practical implementations for angular optical tweezers makes use of a linearly polarized Gaussian beam together with optically anisotropic (i.e., birefringent) dielectric particles.11−15 This choice of beam enables straightforward control of torque and angle12,15 while obviating mode changes (e.g., into the Laguerre-Gaussian mode)16 or modulation of the laser beam power.17 While metal particles have been successfully trapped and rotated,18,19 the use of dielectric particles presents several advantages. First, torque detection is direct because only dielectric materials have transmitted light components that are proportional to the transfer of angular momentum.14 Second, highly transparent dielectric materials do not suffer from the extreme heating of absorptive metals.20 Third, the reduced light scattering from dielectric materials relative to metals is more favorable for three-dimensional (3D) trapping. Extensive scattering from metals destabilizes axial trapping, and hence, metal particles with dimensions exceeding a few hundred nanometers support only two-dimensional (2D) trapping.18,19 Finally, unlike inherently isotropic metals, optically anisotropic dielectric crystals make it possible to simultaneously confine all three rotational degrees of freedom (RDOF), which is advantageous for high-accuracy sensing applications. Among the wide range of dielectric materials, uniaxial crystals such as quartz SiO2 have been popular choices due to their well-defined refractive index (n), birefringence (Δn), and optic axis.4
Nonetheless, the full potential of combined linear and angular optical manipulation using dielectric force and torque transducers has not been achieved due to the limited performance offered by conventional dielectric materials. For example, quartz SiO2 has a relatively low index of refraction (n = 1.54) that limits the efficient transfer of linear momentum (and, hence, the achievable maximum force21,22), as well as a low birefringence (Δn = 0.009) that prohibits the efficient transfer of angular momentum (limiting the achievable maximum torque4). Other materials, for example, vaterite CaCO3, calcite CaCO3, and liquid crystal RM257, have higher birefringence (Δn = 0.1, |Δn| = 0.16, and Δn = 0.18, respectively), but a similarly low refractive index (n = 1.6, n = 1.56, and n = 1.6, respectively).2,23,24 Attempts to overcome these material limitations have come with adverse side effects. For example, one may compensate for inefficient momentum transfer by increasing the power (and, hence, the momentum) in the input beam, but this enhances the risk of photodamage in biological applications.25 Alternatively, one may employ larger particles to achieve higher force and torque, but the increased frictional drag will decrease the achievable spatiotemporal resolution in these parameters (and their conjugate variables, position and angle).26
Rutile TiO2 has several key features that make it a highly propitious candidate for overcoming these drawbacks. To start, rutile TiO2 exhibits the highest birefringence (Δn = 0.26)27 of all known naturally occurring dielectric crystals, ∼29-fold larger than that of quartz SiO2. Next, its refractive index (n = 2.6)27 is one of the largest among dielectric crystals, comparable to that of anatase TiO2 (n = 2.5),27 previously selected to demonstrate the generation of very large optical forces22 and, again, much larger than that of quartz SiO2. Furthermore, rutile TiO2 in its pure single-crystalline form can be maintained at the nanoscale level via top-down fabrication.28 This makes it possible to harness its full nominal birefringence and optical index, without any of the reduction observed in porous polycrystalline structures prepared by bottom-up processes.29,30 Lastly, rutile TiO2 has demonstrated biocompatibility and biofunctionalizability and is chemically, mechanically, and thermally stable.28 This means that it may be employed under tougher conditions (e.g., high pressure, high temperature, or prolonged exposure to aqueous and biological environments) relative to other birefringent materials such as CaCO3 (which dissolves in aqueous environments23).
Here, we demonstrate how these favorable properties collectively render rutile TiO2, when shaped into nanocylinders, into an ideal, joint transducer of optical force and torque. To do so, we show that single-crystal rutile TiO2 nanocylinders, even those with larger volumes, can be trapped in 3D using moderate laser powers, with no need for secondary antireflection coatings22 or modified optics.21,31 We then perform measurements of differently sized nanocylinders in an optical torque wrench (OTW)13 to quantify the applied forces and torques, which show excellent agreement with numerical calculations based on finite element methods (FEM). This allows us to show that tightly trapped rutile TiO2 nanocylinders outperform other available dielectric materials by sustaining nN·nm torques at kHz rotational frequencies in aqueous environments. This, together with the excellent joint resolution in force, torque, and their conjugate variables (exceeding 1 pN and 1 nm; 1 pN·nm and 1 degree) achieved, expands our control of forces and torques at the nanoscale.
Results and Discussion
Optimization of Rutile TiO2 Particle Geometry
In this section, we describe the optimization of rutile TiO2 nanoparticle geometry for optical trapping. First, we describe how particle selection based on height can maximize the efficiency of birefringence-based torque transfer, for which the exceptionally high birefringence of rutile TiO2 is advantageous. Then we discuss how the high refractive index of rutile TiO2 enhances the applied force compared to other commonly used dielectric materials. Finally, we show that a cylindrical geometry permits improved 3D trapping and full RDOF confinement.
Large Birefringence for Optimal Angular Momentum Transfer
The optical torque τ around the z-axis that a linearly polarized plane wave propagating in the z-direction can apply to a birefringent particle with uniform thickness, when its optic axis lies in the polarization plane (i.e., xy-plane), is given by
| 1 |
where the negative sign implies that the resulting optical torque acts as a restoring torque as if it is a torsional spring, A = Sεonc(Eo)2/(2ω), S is the particle cross-sectional area, εo is the vacuum permittivity, n = (ne + no)/2 is the mean of the particle’s optical indices along the extraordinary (ne) and ordinary (no) axes, c is the speed of light in vacuum, Eo is the electric field amplitude of light in the particle, and ω is the angular frequency of the input beam. In the first sine term, h is the particle height along the direction of beam propagation, ko = 2π/λo is the wavenumber of the input laser beam in vacuum (here, λo is the wavelength of the beam in vacuum, which is 1064 nm in our setup), and Δn = ne – no is the particle’s birefringence. The torque is modulated according to the offset angle θ between the linear polarization direction of the input beam and the particle optic axis as described by the second sine term, and thus, the maximal torque τo = A sin(hkoΔn) appears at θ = ±45°. Note that eq 1 does not precisely describe the torque experienced by nanoparticles trapped at a beam focus (Supporting Information, Figure S1), as it is derived in the context of a plane wave that imparts angular momentum to an infinitely wide plate (Supporting Information, Text S1). Nonetheless, eq 1 provides a reasonable starting point for torque transducer design.
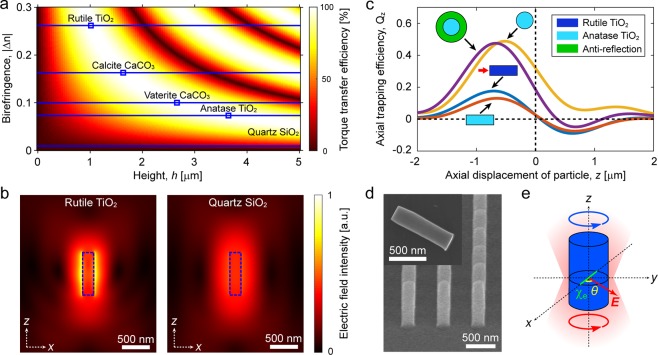
As eq 1 shows, for a given particle material, the particle height h can be optimized to maximize the torque transfer efficiency. For materials with low birefringence, the optimal particle height is excessively large (e.g., ∼30 μm for quartz SiO2). This size scale not only presents a challenge to fabrication but also far exceeds the favorable particle size range for stable 3D trapping in typical single-beam optical tweezers, that is, <∼1 μm, below the size of a tightly focused beam. The conventional torque transducers of heights of ∼1 μm11,13,23 are made of low birefringence materials and cannot transfer the full angular momentum carried by the laser beam (Figure 1a). However, in the case of rutile TiO2, with its exceptionally large birefringence, a torque transfer efficiency of 100% should be achievable for 1 μm particles (Figure 1a).
Figure 1.
Design principles for force and torque transducers in optical tweezers. (a) Map of the torque transfer efficiency (|sin(hkoΔn)| × 100; derived from eq 1) as a function of particle height (h) and birefringence (|Δn|) of different dielectric materials. The blue squares indicate the smallest particle heights at which 100% torque transfer efficiency can be achieved (∼30 μm for quartz SiO2). (b) FEM-calculated electric field intensity around nanocylinders (blue dashed line) made of different materials, located at the laser beam focus (z = 0) in water. (c) FEM-calculated axial trapping efficiency (Qz) curves for various TiO2 nanoparticle geometries at fixed volumes. An anatase TiO2 (n = 2.3; light blue) sphere (d = 430 nm) cannot be trapped in 3D, but it becomes trappable upon the addition of an antireflection coating (green) or when reshaped (at constant volume) into a cylinder (d = 220 nm, AR = 5). A rutile TiO2 (n = 2.6; dark blue) cylinder with the same dimensions is also trappable. The trapping orientation of each cylinder with respect to the beam propagation direction (red arrow) is as drawn. (d) SEM micrograph (60° tilted view) of a fabricated rutile TiO2 nanocylinder batch prior to mechanical cleaving. The inset shows a cleaved single nanocylinder. (e) Experimental scheme of the OTW. The x-, y-, and z-axes are in the reference frame of the nanocylinder, which has the optic axis along the x-axis (as indicated by the extraordinary electric susceptibility χe). The laser beam propagates along the z-axis, and the optical gradient force traps the nanocylinder in 3D. When a nonzero offset angle θ exists between the optic axis and the linear polarization direction of the input beam (electric field vector E in the xy-plane), the optical torque is applied on the nanocylinder.
The ability to reach larger maximal torques (τo) for smaller particles (i.e., particles with lower rotational drag γθ) has several implications for optical torque transducers. (i) The faster maximal rotation speed (fo = τo/(2πγθ)) allows access to a larger torque-speed space. (ii) The increased angular trap stiffness (κθ = 2τo) and low drag improve measurement precision for both torque and angle, as they are proportional to (γθ)1/2 and (γθ)1/2/κθ, respectively.26 (iii) The shorter angular trap relaxation time (tc,θ = γθ/κθ) results in enhanced temporal resolution.26
Large Refractive Index Results in Enhanced Linear Momentum Transfer
Compared to conventional dielectric materials employed in angular trapping, such as quartz SiO2, vaterite CaCO3, and calcite CaCO3 (n = 1.5–1.6), rutile TiO2 possesses a substantially larger optical index (n = 2.6 on average).27 This implies a larger index difference with the surrounding medium (e.g., water, n = 1.33) and correspondingly stiffer linear trapping.21,22 This can be visualized through FEM calculations (Figure 1b), which show more intense scattering at the interface between the particle and the medium that leads to a higher field gradient and, hence, an enhanced trapping force. Thus, the use of rutile TiO2 enhances the transfer of not only angular, but also linear momentum. This simultaneous enhancement is unique to rutile TiO2, as other materials that have high birefringence possess only low refractive indices (e.g., calcite CaCO3).
Cylindrical Shape for Stable 3D Trapping
The advantage of being able to generate high gradient forces comes at a cost, as a higher index mismatch leads to increased scattering. This implies that radiation pressure from the incident laser beam is more likely to perturb axial trapping. Therefore, 3D trapping of high-index particles in single-beam optical traps is limited to those smaller than a certain threshold size, which is determined by the material and the particle geometry. To compensate for the adverse effect of scattering on trapping, diverse solutions have been developed. One solution is to alter the optical configuration by implementing counter-propagating beams21 or a donut-shaped beam31 for trapping. Another solution is to modify the particle by introducing an antireflection coating.22 However, this increased sophistication in optical configuration or fabrication prevents its straightforward widespread implementation.
Instead, we can overcome the adverse effects of scattering by using a cylindrical shape for rutile TiO2 nanoparticles, as shown for previously described dielectric torque transducers.11−15 This geometry decreases light scattering for a fixed volume of a particle by reducing the surface area encountered by the input laser beam. This effect is explicitly demonstrated by our numerically calculated trapping force curves comparing differently shaped high-index particles (Figure 1c). Our FEM calculations show that rutile TiO2 spheres cannot be trapped in 3D if their diameter exceeds ∼346 nm (Supporting Information, Figure S2), in agreement with previously reported calculations.32 However, as we describe in detail below, we use an OTW to demonstrate stable 3D trapping of fabricated rutile TiO2 nanocylinders (Figure 1d,e) with volumes that exceed the volume threshold for the trappability of spheres. Having an increased range of trappable particle volumes available allows the application of increased force or torque. Furthermore, the omission of antireflection coatings reduces drag and, thus, improves the achievable maximum angular speed, temporal resolution, and measurement precision.
The use of cylindrically shaped rutile TiO2 nanoparticles includes another important advantage, namely the full confinement of the three RDOF. For a positive or negative uniaxial birefringent sphere, the birefringence-originated torque constrains only two or one RDOF. This has the drawback that unconstrained RDOF may introduce unexpected angular fluctuations into torque and angle signals. The geometrical anisotropy provided by a nonspherical particle shape such as a cylinder can avoid these complications (Supporting Information, Figure S3) and is, hence, a requirement for certain applications, for example, high-precision single-molecule torque spectroscopy.
Linear and Angular Trapping of TiO2 Nanoparticles
Dimensions of Rutile TiO2 Nanocylinders Trappable in 3D
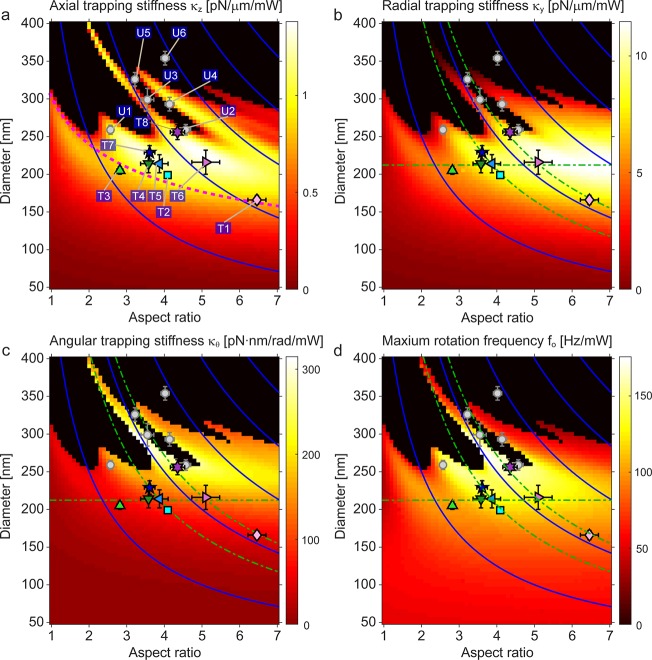
We fabricated multiple rutile TiO2 nanocylinder batches (Methods) with different diameters d = 150–400 nm and heights h = 0.5–1.5 μm, with resulting aspect ratios (AR = h/d) ranging from 2.5 to 6.5 (Supporting Information, Figure S4; precise dimensions measured by scanning electron microscopy (SEM) are shown in Figure 2 and Supporting Information, Table S1). We first tested whether these particles could be optically trapped in 3D in an aqueous environment (Methods), because stable 3D trapping is a prerequisite for the application of force and torque. We experimentally observed that rutile TiO2 cylinders with small diameters (160–230 nm) could be stably trapped (T1–T7 in Figure 2), even though their volumes are similar to or larger than that of the largest rutile TiO2 sphere predicted to be trappable. In contrast, cylinders with diameters exceeding ∼260 nm (U1–U6 in Figure 2) were not trappable in 3D, but rather scattered away from the trap. Therefore, we defined an experimental threshold diameter dexp* for the trappability of the rutile TiO2 cylinders as a function of their AR. For each AR, dexp* falls within the range 230–260 nm.
Figure 2.
Calculated maps of linear and angular stiffness for rutile TiO2 nanocylinders of varying dimensions, with experimentally assessed trappability per cylinder batch superimposed. (a–c) FEM-calculated (a) axial (κz), (b) radial (κy), and (c) angular (κθ) stiffness maps of rutile TiO2 nanocylinders. The stiffness values are calculated with the zero-taper angle for each cylinder dimension and the measured aperture filling ratio (α = 1.7) from our OTW setup, and normalized by the input beam power. (d) Maximum rotation frequency (fo = τo/(2πγθ)) map of rutile TiO2 nanocylinders obtained from FEM-calculated maximum torque (τo = κθ/2; derived from data in panel (c)) and drag (γθ; Supporting Information, Figure S7). In panel (a), the region above the dashed magenta curve includes nanocylinders with volumes exceeding that of the largest trappable rutile TiO2 sphere with d ≈ 346 nm. In panels (b)–(d), dimensions relevant for the analysis in Figure 3 are displayed: the horizontal dash-dotted green line represents d ≈ 213 nm; the leftmost dash-dotted green curve represents h ≈ 825 nm; and the rightmost dash-dotted green curve represents h ≈ 1096 nm. In all panels, the maps are plotted as a function of the cylinder aspect ratio (AR = 1–7, with step size 0.1) and the cylinder diameter (d = 100–400 nm, with step size 5 nm). The black pixels indicate cylinders with untrappable dimensions (for which axial stiffnesses cannot be calculated). The solid blue curves are iso-height contours (500–2500 nm from left to right, with a step size of 500 nm). Trappable fabricated cylinder batches (labeled as T1–T8) are indicated by distinct symbols and colors. Untrappable fabricated cylinder batches (labeled as U1–U6) are shown as gray filled circles. Symbols and error bars denote the averages and standard deviations of the SEM-measured cylinder dimensions, respectively (N = 5–10; Supporting Information, Table S1).
The behavior of individual particles within cylinder batches is consistent with this transition. For example, the mean diameter of cylinder batch T8 (AR = 4.4) is 256 nm ±10 nm (Figure 2a). While most cylinders from this batch were not trappable or could be trapped only temporarily (with particles exiting the trap within seconds or minutes), a few were stably trapped for hours. Such behavior is expected if a small fraction of the batch has diameters that fall below dexp*.
We compare these and subsequent findings with FEM calculations (Methods). The calculated axial stiffness (κz) map (Figure 2a; other calculated linear trapping parameters are described in Supporting Information, Figure S5), where black pixels indicate untrappable cylinder dimensions, reveals a higher threshold range for trappability, dcal* ≈ 255–315 nm, defined as the minimum diameter which results in a black pixel for each AR. A few experimental factors that have not been considered in the calculations could explain the mismatch between the trappable cylinder dimensions found by experimental and numerical approaches. For example, cylinder batch U1 lies in a trappable regime of the calculated map but is experimentally untrappable. The calculations for the maps shown in Figure 2 incorporate the objective lens aperture filling ratio (α = 1.7; Methods and Supporting Information, Figure S6). However, they do not account for optical aberrations (see also Rutile TiO2Nanocylinders Optimized for High Stiffness, Low Drag, and Rapid Response Time) and, for a given cylinder geometry, they assume zero taper angle, whereas trapping behaviors are largely dependent on taper angle (Supporting Information, Figure S6).
We have also calculated maps of the radial stiffness (κy; Figure 2b), the angular stiffness (κθ; Figure 2c), and the maximal rotation frequency (fo = (κθ/2)/(2πγθ); Figure 2d, obtained using FEM-calculated drag coefficients (γθ; Supporting Information, Figure S7) and angular stiffnesses (κθ; Figure 2c)), which we compare to our experimental results in the next subsections.
Rutile TiO2 Nanocylinders Optimized for High Stiffness, Low Drag, and Rapid Response Time
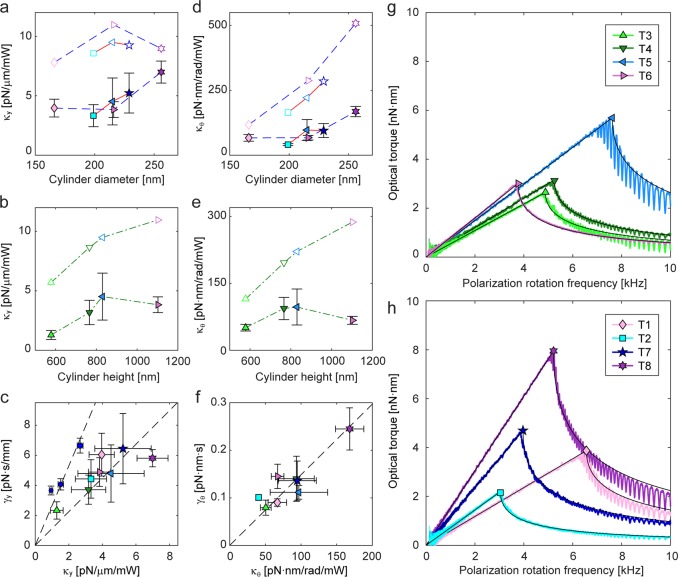
The stiffness and drag are the two primary physical parameters that describe the behavior of optically trapped particles.26 Therefore, we experimentally determined the trap stiffness (linear and angular) and the corresponding drag coefficient for each trappable rutile TiO2 cylinder batch, with the results summarized in Figure 3. We used laser powers less than 100 mW to demonstrate the high performance of rutile TiO2 cylinders even in the low-power regime. However, we present the trapping stiffness normalized by laser power for comparison with other studies. The laser power values are precisely calibrated as if they are measured at the focal plane in the flow cell (Methods). To highlight the effect of geometrical parameters, the experimental stiffness values are plotted as a function of diameter or height at a fixed height or diameter in Figure 3a,b,d,e. In Figure 2b–d, the dash-dotted green lines represent the fixed heights h ≈ 1096 and ≈ 825 nm, and the fixed diameter d ≈ 213 nm. The results of FEM calculations based on mean particle geometries (with actual sidewall profiles as quantified by SEM and displayed in Supporting Informtion, Figure S4) are coplotted in Figure 3a,b,d,e for comparison. In the case of linear trapping, we display the trapping parameters as measured in the y-dimension. Because the input beam is polarized along the x-dimension (Methods), trapping is strongest along the y-dimension (2- and 10-fold stronger than trapping in the x- and z-dimensions, respectively; Supporting Information, Figure S5). Overall, increases in either cylinder diameter (Figure 3a,d) or height (Figure 3b,e) that enhance the light–matter interaction volume tend to result in greater linear and angular trap stiffnesses. Particularly, for angular trapping, an increased cylinder diameter at a fixed height corresponds to a wider cross-sectional area S in eq 1, and hence, also a higher value of the angular stiffness (Figure 3d). For a fixed diameter, taller cylinders yield increased angular stiffness, until saturation occurs close to the height h in eq 1 for optimal torque transfer (Figure 3e). These trends agree very well with the FEM-based predictions. Exact quantitative agreement between the experimental observations and FEM predictions is achieved upon scaling the calculated stiffnesses by 42% ± 14% (Supporting Information, Figure S8), which we attribute to optical aberrations that distort the electric field distribution at the beam focus,33 an experimental limitation that is challenging to include in calculations. The measured drag coefficients, which are not similarly influenced by aberrations, equal 104% ± 17% of the values calculated by FEM (Supporting Information, Figure S8), implying high accuracy of our calibrated measurements.
Figure 3.
Experimentally measured linear and angular trapping performances of rutile TiO2 nanocylinders. (a, b, d, e) Measured stiffness (κy, κθ) values plotted vs cylinder diameter or height, together with calculated values for comparison. The OTW-measured values are represented by filled symbols and associated error bars. The FEM-calculated values (which make use of SEM-measured cylinder geometries with actual sidewall profiles) are represented by empty symbols. For ease of visualization, in panel (a, d), data points from the cylinders of similar height h ≈ 1096 nm (825 nm) are connected with dashed blue lines (solid red lines), and in panel (b, e), data points from the cylinders of similar diameter d ≈ 213 nm are connected with dash-dotted green lines. (c, f) Measured drag coefficients (γy, γθ) plotted vs measured stiffness values (κy, κθ). The slope of a linear fit (dashed black line, forced through the origin) reports on the trap relaxation time (tc,y = 11 μs at 100 mW, tc,θ = 15 μs at 100 mW). The measurement results from PS spheres are overlaid in panel (c) for comparison (filled blue circles; the mean diameters of batches P1, P2, and P3 are 370, 505, and 746 nm, respectively). A linear fit to PS data results in tc,y = 26 μs at 100 mW. (g, h) Moving-averaged optical torque as a function of input beam polarization rotation frequency (PRF), measured at 92 mW. Each curve represents the data obtained from a single cylinder, and its fit to the theory15 is overlaid (black line). When the PRF exceeds the maximum rotation frequency of a cylinder (denoted by the corresponding colored symbol), the particle begins to slip and thus exhibits a decreased torque.15 The cylinders with similar diameters (d ≈ 213 nm, T3–T6) are compared in panel (g), and those with similar heights (h ≈ 1096 nm, T1 and T8; h ≈ 825 nm, T2 and T7) are compared in panel (h). For the symbols employed in panels (a)–(h), the shape and color coding are as in Figure 2.
The ratio of the measured drag (Methods) and stiffness reports on the response times of trapped rutile TiO2 cylinders. When the measured translational or rotational drag is plotted against the corresponding trap stiffness, a linear relationship is observed (Figure 3c,f). Within the range of cylinder dimensions tested, this reflects the above-mentioned trend of increased stiffness with increased diameter or height (corresponding to increased drag). The slope of the fitted lines yields the overall trap relaxation time (tc,y = γy/κy or tc,θ = γθ/κθ), with a shorter tc reflecting a more rapid response time and increased temporal resolution.
For linear trapping, we compare the results obtained with rutile TiO2 cylinders to those obtained with standard polystyrene (PS) spheres (representative of low-index force transducers). The linear trap stiffness of rutile TiO2 nanocylinders is approximately 2-fold higher than that of PS spheres of comparable drag, a direct consequence of the higher refractive index of rutile TiO2 (n = 2.6) compared to PS (n = 1.57). Correspondingly, rutile TiO2 nanocylinders enable a nearly 2-fold increase in temporal response (tc,y = 11 μs for rutile TiO2 vs tc,y = 26 μs for PS at 100 mW; Figure 3c). These effects can be appreciated by comparing the rutile TiO2 cylinder batch T2 with the PS sphere batch P2 (d = 505 nm), which both have drag coefficients of ∼4 pN·s/mm (Figure 3c). For angular trapping, the trap relaxation time of rutile TiO2 nanocylinders (tc,θ = 15 μs at 100 mW; Figure 3f) is again considerably shorter due to the high angular trap stiffness (Figure 2c, deriving from the large birefringence) achievable with such low rotational drag (Supporting Information, Figure S7). As the trap relaxation time is inversely proportional to the laser beam power, it can be further tuned using this parameter.
Rutile TiO2 Nanocylinders Transmit nN Forces and nN·nm Torques with Excellent Measurement Precision
To deduce the range of applicable forces using trapped rutile TiO2 nanocylinders, we examine their measured linear stiffnesses and estimate the range of their harmonic regime. The high radial trapping stiffness of rutile TiO2 nanocylinders should permit the application of large forces up to ∼nN, as demonstrated for antireflection coated anatase TiO2 spheres.22 For example, a rutile TiO2 nanocylinder with radial trap stiffness κy = ∼7 pN/μm/mW (cylinder batch T8) should experience a ∼1 nN restoring force at ∼1.4 W laser power (not measured due to the limitation of available power in our setup) upon displacement of ∼100 nm from the trap center, well within the estimated harmonic potential regime (Supporting Information, Figure S5). This represents an order of magnitude improvement over the typical ∼100 pN limit of optical tweezers.34
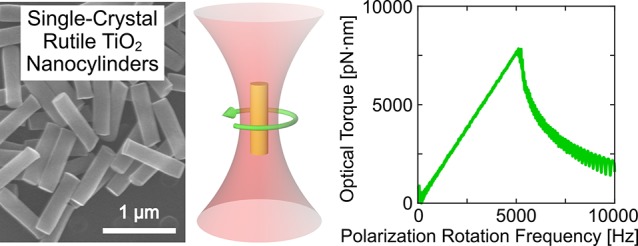
The exceptionally large birefringence of rutile TiO2 makes it possible to simultaneously achieve very high torques (1–10 nN·nm) and rotational speeds (1–10 kHz) at only moderate laser powers (<100 mW) in aqueous solution (Figure 3g,h). Such an expansive torque-speed range is not achievable in similar measurement conditions using other dielectric particles with much lower birefringence.11,13 To provide a guideline for selecting cylinder dimensions, we compare the torque-speed curves of differently sized nanocylinders (Figure 3g,h). We first compare cylinders with similar diameters (d ≈ 213 nm, batches T3–T6) but different heights (Figure 3g). Here, the rotational drag coefficients are similar, as observable from the slopes (γθ = τo/ωo) in the linear part of the torque-speed curves. Using a cylinder with an optimal height for torque transfer efficiency (within this data set, batch T5) results in a higher maximum torque and increased rotational frequency. Differently stated, for a fixed cylinder diameter, the height provides a means to tune the torque transfer efficiency. We next compare two groups of cylinders with similar heights (h ≈ 1096 nm, batches T1 and T8; h ≈ 825 nm, batches T2 and T7), but different diameters (Figure 3h). Within each group of cylinders, the torque transfer efficiencies are similar, but the drag coefficients differ substantially. A smaller drag coefficient is preferable in general for a higher rotation frequency (e.g., compare batches T1 and T8 in Figure 3h). However, a reduction in drag does not always guarantee an increased rotation frequency even if torque transfer efficiency is maintained (e.g., compare batches T2 and T7 in Figure 3h). This is because the resulting rotation frequency (fo ∝ κθ/γθ) is dependent on the relative rates of change between stiffness and drag, which are distinct functions of particle dimensions. Hence, for a fixed cylinder height, one should select the suitable cylinder diameter to access the desired torque-speed regime.
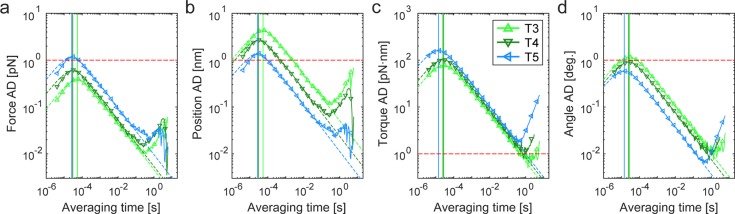
Utilizing the high linear and angular stiffnesses achievable with low-drag rutile TiO2 nanocylinders, we employ Allan deviation (AD) analysis26 to demonstrate the ensuing improvements in measurement precision. For the primary quantities of physical interest, force, torque, position, and angle, we demonstrate in Figure 4 that one can achieve excellent precisions below 1 pN, 1 pN·nm, 1 nm, and 1 degree, respectively, on short time scales between (sub)milliseconds and seconds. To quantify trapping, signal averaging times longer than the time at which the AD peak (colored vertical lines in Figure 4) occurs are appropriate. This regime corresponds to the thermal limit, that is, the harmonic trapping regime. AD values within this region determine the measurement precision as a function of the averaging time. Theoretically, longer averaging times increase the measurement precision, but there is a practical lower bound on the measurement precision because of long-term drift or other measurement noise.26 In our setup, this lower bound occurs at an averaging time between ∼0.1 and ∼10 s.
Figure 4.
Temporal resolution and measurement precision in force, position, torque, and angle, achieved with rutile TiO2 nanocylinders. (a–d) Allan deviation (AD) as a function of averaging time for three selected rutile TiO2 cylinder batches (T3–T5, in order of increasing linear and angular stiffness; the same symbols and colors as in Figure 2). AD plots for four different physical quantities are shown: (a) force, (b) position, (c) torque, and (d) angle. Each colored solid curve represents the normal AD obtained from a single cylinder measured at 92 mW. Colored symbols reflect the octave-sampled overlapping AD, and their fit to the theory26 is overlaid as a dashed curve. The AD values report on the achievable measurement precision for a given averaging time, and the horizontal dashed red lines indicate the typical precisions required for measurements of individual biomolecules. For each cylinder, the trap relaxation time (tc) can be deduced from the time scale at which the AD curve peaks (1.8926tc; designated by the colored vertical lines).26 This relaxation time forms the lower bound of the achievable temporal resolution.
We illustrate here how the main trapping parameters affect the magnitude of the AD curve, in turn, increasing or decreasing the achievable measurement precision. As an example, we selected a subset of the cylinder batches, that is, T3–T5, that exhibits the order of increasing linear and angular stiffnesses. The force AD (Figure 4a) and torque AD (Figure 4c) are functions of drag only (∝ γ1/2). Therefore, the best force and torque precisions are obtained from the cylinder with the smallest linear and angular drag coefficients (batch T3). However, the position AD (Figure 4b) and angle AD (Figure 4d) are functions of both drag and stiffness (∝ γ1/2/κ). As differences in stiffness values are more significant in the chosen data set, the best position and angle precisions are achieved with the highest linear and angular stiffnesses (batch T5).
We compare the stiffness, torque-speed regime, measurement precision, and temporal resolution between rutile TiO2 and other common dielectric crystals, that is, quartz SiO2 and calcite CaCO3. We chose to compare only calculated results because of the difficulty of fabricating different materials into an identical geometry. As experimentally demonstrated here (Figure 3 and Supporting Information, Figure S8), we can reliably predict the overall trends in both linear and angular trapping parameters by numerical modeling. This comparison shows that rutile TiO2 is indeed the most competent material as a combined force and torque transducer (Supporting Information, Figure S9).
Finally, the simultaneous measurement of linear and angular physical quantities is of interest in diverse applications including single-molecule biophysics research.24,35 Here, for a more precise calibration, we record only one physical quantity at a time, either force or torque, while the variations of the other quantity is influenced only by thermal fluctuations. However, if larger variations in force and torque exist simultaneously, the potential crosstalk between translational and rotational degrees of freedom needs to be characterized. When considering such crosstalk, one should consider both the inherent dynamics of the rutile TiO2 cylinders as well as the measurements performed on them (Supporting Information, Text S2).
Conclusions
In this work, we have employed experimental measurements and numerical calculations based on finite-element methods to demonstrate how the collective optical properties of single-crystalline rutile TiO2 (including high refractive index and exceptionally large birefringence), together with its shaping into nanocylinders of appropriate dimensions, make it possible to develop joint optical force and torque transducers with outstanding properties. We show that rutile TiO2 nanocylinders exhibit high stiffness in both linear and angular domains, allowing for the application of ∼nN-scale forces and unprecedentedly high 1–10 nN·nm torques. Given their low drag coefficients, our fabricated rutile TiO2 nanocylinders should exhibit excellent time response, which we have verified experimentally and exploited to highlight how rutile TiO2 torque transducers can sustain high 1–10 kHz rotation frequencies in aqueous solution, even at a moderate trapping laser power not exceeding 100 mW. Furthermore, we show how optically trapped rutile TiO2 nanocylinders enable high measurement precision in the key physical parameters of force, torque, position, and angle.
We expect that this coalescence of exceptional trapping properties into single rutile TiO2 particles will open up opportunities for micro- and nanoscale applications. For example, the ability to transmit ∼nN·nm torques at ∼kHz rotation frequency will render measurements on systems with a wide torque-speed regime, for example, the bacterial flagellar motor,36 accessible. Similarly, the high temporal resolution and excellent measurement precision will permit investigations of fast dynamics in other biomolecules.3,37 Moreover, the small size, biocompatibility, and chemical inertness of rutile TiO2 nanocylinders, together with their low laser power requirements compared to other materials, will facilitate their usage in cellular manipulation6,39 or in vivo microrheology.38 Alternatively, these force and torque transducers could provide an enhanced platform for studies of quantum phenomena such as cavity cooling7 and Casimir effects.40 Finally, we foresee potential applications for rutile TiO2 nanocylinders in engineering applications such as optically driven nanomachines,8,9 excitability-based sensors,13 or photonic force microscopy.41
Methods
Fabrication and Surface Functionalization of Rutile TiO2 Nanocylinders
To produce rutile TiO2 nanocylinders (Figure 1d), we use our developed top-down fabrication protocol (more details can be found in ref (28)). We use a high-quality (100) single-crystal rutile TiO2 substrate (1 cm × 1 cm, ∼500 μm thickness, MTI Corp.). The optic axis is precisely aligned in every produced nanocylinder, using the (100) crystal orientation in which the optic axis is perpendicular to the substrate surface normal. This configuration allows the precise angular manipulation around z-axis, with a trapping beam linearly polarized in xy-plane (as depicted in Figure 1e). Compared to our previously reported fabrication protocol,28 we further optimized the chromium mask shape and thickness to obtain more circular cross sections and smaller taper angles (see details in Supporting Information, Figure S10). The steps in the nanofabrication protocol that control nanocylinder diameter and height are electron-beam lithography (EBPG 5000 or EBPG 5200, Vistec) and plasma etching (Fluor Z401S, Leybold Heraeus or Plasmalab System 100, Oxford Instr.), respectively. As shown in Supporting Information, Table S1, this optimization leads to excellent structural uniformity among the fabricated TiO2 nanocylinders (relative standard deviation 2–8% for diameters and 0.1–1.5% for heights, measured for 5–15 particles per batch), as deduced from the SEM images (S4800 FESEM, Hitachi; Supporting Information, Figure S4). As a result, our nanoparticles more closely resemble ideal cylinders and display more reproducible behavior. Otherwise, for example, deviations in the taper angle can lead to a substantial change in the trap stiffness (Supporting Information, Figure S6).
To increase the probability of trapping single isolated nanocylinders in OTW measurements, it is crucial to prolong the monodispersed status of the nanocylinders in aqueous solution. For this purpose, the nanocylinders are coated with amino-terminated monofunctional polyethylene glycol (NH2–PEG) molecules (MW 5000, PEG1154, Iris Biotech) via epoxysilane linkers (3-glycidoxypropyldimethylethoxysilane, 539260, Sigma-Aldrich) using our previously developed TiO2 surface functionalization protocol.28 The PEGylated nanocylinders are mechanically cleaved in phosphate buffered saline (PBS) buffer (pH 7, Sigma-Aldrich) droplets by scratching the substrate surface with a sharpened homemade plastic blade. The plastic blade is softer than the TiO2 substrate and minimizes the production of TiO2 dust particles. We note that the presence of short PEG molecules does not affect the trapping and rotational dynamics of our nanocylinders20 and have observed that the monodispersity of PEGylated TiO2 particles is maintained upon sonication and vortexing, even after year-long storage (in plastic tubes at 4 °C). Meanwhile, for biological applications, the same epoxysilane linker-based protocol can be utilized to specifically tether biomolecules. For example, the monofunctional PEG can be (partially) replaced with heterobifunctional PEG.42 Also, biomolecules with primary amino groups can be directly coupled to epoxysilane layer in the absence of PEG, as previously demonstrated.28
OTW Setup and Measurements
We conducted OTW experiments with our home-built setup (1064 nm-wavelength single-beam optical trap with polarization control; more details can be found in refs (13, 14, and 28)). We use a custom-made flow cell assembled with two borosilicate glass coverslips (No. 1.5H, Marienfeld) separated by a single-layer Parafilm spacer of ∼100 μm thickness. The use of coverslips with high-precision thickness (170 μm ± 5 μm for No. 1.5H) reduces possible variations in optical trap quality that might occur when the conventional coverslips with large thickness variation (e.g., 160–190 μm for No. 1.5) are used.43 As the objective and condenser lenses are identical in our OTW setup, we employed the dual-objective method44 to precisely calibrate the laser beam power delivered at the focal plane within the flow cell, revealing a 51% transmittance of laser power through the objective lens to the flow cell center. The measured input beam radius and the effective objective back-aperture radius are 6.9 and 4.0 mm, respectively, resulting in the objective lens back-aperture filling ratio of ∼1.7. Based on these, the laser power at the focal plane can be obtained from the power measured at the objective lens back-aperture. The PBS buffer containing the nanocylinders are injected into the flow cell channel and both input and output of the channel are sealed by vacuum grease (18405, Sigma-Aldrich). After ∼1 h, most of the nanocylinders in the solution are sedimented to the bottom of the flow cell. Among these nanocylinders, only a chosen nanocylinder can be lifted from the bottom by focusing the laser beam on the particle to generate a pushing force via light scattering. Using rutile TiO2 is beneficial in this lifting process because its large refractive index induces stronger scattering for a given laser power. Afterward, we can trap and measure the freed nanocylinder without any hydrodynamic coupling effect that can occur if the particle concentration is too high.45 Also, it is possible to measure for extended times (tested up to ∼3 h) without losing the particle by collision with other particles entering the optical trap. The nanocylinder trapping position is kept as 18–20 μm above the bottom surface of the flow cell channel to effectively avoid any hydrodynamic interaction with the flow cell.
We measured 14 different rutile TiO2 nanocylinder batches (Supporting Information, Table S1), and 3–10 particles were recorded for each trappable batch (Figure 3, Supporting Information, Figure S8 and Table S2). For calibration of linear and angular trapping properties, we adapted the previously developed methods.14,46 For measurement of linear and angular fluctuations of a trapped cylinder, we employed an input beam which is linearly polarized along the x-axis. The large radial stiffnesses of the rutile TiO2 particles lead to hydrodynamic effects, which contribute colored noise to the power spectrum.22,47 We have considered this in our analysis (Supporting Information, Figure S10). The linear and angular fluctuation data are acquired at 250 kHz sampling frequency. For a more precise linear calibration, we employed an enhanced method in which radial and axial position detectors are separated (Supporting Information, Figure S10). We also developed an improved method to more precisely measure torque-speed curves (Supporting Information, Figure S10). In our method, each curve is measured by continuously scanning the polarization rotation frequency (PRF) in the range of 0–15 kHz for a few seconds using a waveform generator (33120A, Agilent), with 100 kHz sampling frequency. Compared to the conventional time-consuming method in which separate torque traces are recorded at multiple different frequency values, this high-speed recording over a wide frequency range avoids the distortion of the measured curve caused by setup drift. The downward spikes shown at high PRF in Figure 3g,h are attributed to the peculiarities of the setup, such as the finite time required for the polarization reversal of electro-optic modulator (EOM) voltage,12,15 and appear regardless of the chosen torque-speed measurement method.
In addition, we measured linear trapping properties of PS microspheres (Polybead Microspheres, Polysciences; Figure 3c, Supporting Information, Figure S8 and Table S3) since they are one of the de facto standards among optical trapping community. In general, the characteristics of optical traps are not identical among different optical tweezers due to the difference in the specifications of the laser beam, objective lens, immersion medium, and flow cell design. Therefore, comparing the results from the standard commercial PS beads with high compositional and geometrical uniformity provides a means with which experimentalists can estimate the expected trapping properties of rutile TiO2 nanocylinders in their own instruments.
Numerical Calculation of Optical Momentum Transfer and Hydrodynamic Drag
The cylindrical geometry and anisotropic optical property of our rutile TiO2 particles require a numerical approach to precisely estimate their viscous drag coefficients and optical trapping force and torque. It is because the exact analytical solutions do not exist for anisotropic cylinders with arbitrary aspect ratios, unlike the commonly used isotropic spherical probes. We utilize FEM48 with one of its commercial implementations (COMSOL Multiphysics v5.2a, COMSOL Inc.). In general, FEM is more computationally demanding than other approaches such as T-matrix formulations.32 However, it is more flexible and versatile in the aspect of modeling anisotropic material and irregular geometry. Using FEM is straightforward even with cylinders of small aspect ratio and exotic shapes such as tapered cylinders (Supporting Information, Figure S6), cones, and hourglass shapes. The validations of our numerical models are shown in Supporting Information, Figure S10. We note that the properties (size, density, quality, etc.) of geometry meshing in FEM models should be optimized properly to obtain precise results.
To calculate linear and angular optical trapping properties, we locate a rutile TiO2 nanocylinder at the center of the calculation domain. The cylinder is enclosed by a uniform medium (water, n = 1.33) of spherical shape, and the medium is terminated with a perfect matching layer to treat the size of the medium as infinite by coordinate transformation. We use the exact focus beam equation without any approximations to calculate the input background field.49 The beam shape is defined by the vacuum wavelength (λ = 1064 nm), objective lens numerical aperture (NA = 1.2), filling ratio (α = ∞ or 1.7), linear polarization direction (along x-axis), and index of medium (n = 1.33). Here, the filling ratio α (= wo/ro) is defined as the ratio of the 1/e2 radius of input beam wo and effective input aperture radius of objective lens ro (= f NA, where f is the focal length of the objective lens). We use α = ∞ as an ideal configuration in which input beam is a plane wave and α = 1.7 as the measured value in our OTW setup. The time-averaged optical force and torque on the cylinder is obtained by integrating the Maxwell stress tensor over the surface of a virtual sphere enclosing the cylinder.50 We first obtain the axial force (Fz) curves, from which the axial equilibrium trapping positions (zeq) are derived (Supporting Information, Figure S5). Then we calculate radial force (Fx, Fy) and maximal torque (τo) at zeq. The optical force is calculated at the zero-torque condition (θ = 0° in eq 1), while the torque is calculated at the maximum torque transfer condition (θ = 45° in eq 1).
To calculate hydrodynamic drag coefficients, the surrounding medium (water at 23 °C, dynamic viscosity of 0.933 mPa·s) is set to flow translationally (rotationally), inducing viscous drag force (torque) on the nanocylinder. The solutions of Navier–Stokes equations51 result in force and torque as a function of the speed of medium flow, from which the drag coefficients can be extracted. We calculated two translational (axial, radial) and one rotational (around z-axis) drag coefficients: (i) for each ideal cylinder (Supporting Information, Figure S7) to use in calculations of angular speeds (Figure 2d and Supporting Information, Figure S9) and AD values (Supporting Information, Figure S9), (ii) for each fabricated nanocylinder batch (Supporting Information, Figure S8) to compare with our experimentally obtained values. For the case of ideal cylinders, like ideal spheres,52 analytical expressions for the translational53 and rotational54 viscous drag exist. However, these are valid for only a limited range of aspect ratios, and hence, we used our numerical approach.
Acknowledgments
We thank Zhuangxiong Huang for suggesting single-crystal rutile TiO2 for use in the OTW; Paul Urbach and Joseph Braat for advice on optical modeling; Daniel Tam for advice on developing numerical models for cylinder drag calculation; Charles de Boer, Marco van der Krogt, Marc Zuiddam, and Arnold van Run for technical advice on nanofabrication; Margreet Docter and Jacob Kerssemakers for technical advice on the OTW setup; Dimitri de Roos for the production of custom-made mechanical parts for the OTW setup; Theo van Laar, Sacha Khaiboulov, and Josko de Boer for help with laboratory infrastructure; and Kaley McCluskey for reviewing the manuscript. This work is supported by funding provided by the Faculty of Applied Sciences at Delft University of Technology (scienceDATE grant 2017; to S.H. and Y.T.); by the China Scholarship Council under Grant Number 201306160089 (to Y.T.); by NanoNextNL, a micro- and nanotechnology consortium of the Government of The Netherlands and 130 partners (to N.H.D.); by the Department of Bionanoscience at Delft University of Technology (to N.H.D.); by the Foundation for Fundamental Research on Matter (FOM), part of The Netherlands Organisation for Scientific Research (NWO; to N.H.D); and by the European Research Council (ERC) Consolidator Grant under Grant Number 312221 (DynGenome; to N.H.D.).
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsphotonics.9b00220.
Derivation of the analytical equation (eq 1) for optical torque transfer (Text S1); potential crosstalk between translational and rotational degrees of freedom of an optically trapped birefringent nanocylinder (Text S2); FEM-calculated rutile TiO2 nanocylinder height for maximal torque transfer efficiency at different fixed diameters (Figure S1); FEM-calculated optical trappability of rutile TiO2 spheres and cylinders (Figure S2); FEM-calculated RDOF confinement torque of rutile TiO2 spheres and cylinders (Figure S3); SEM micrographs of top-down fabricated rutile TiO2 nanocylinder batches (Figure S4); FEM-calculated parameters describing the linear optical trapping behavior of rutile TiO2 nanocylinders (Figure S5); FEM-calculated maps of axial stiffness and curves of axial trapping efficiency for rutile TiO2 nanocylinders with different objective lens aperture filling ratios and taper angles (Figure S6); FEM-calculated translational and rotational hydrodynamic drag coefficients of nanocylinders (Figure S7); comparison of experimentally and theoretically obtained stiffnesses and drag coefficients for trapping of rutile TiO2 cylinders and PS spheres (Figure S8); FEM-calculated linear and angular trapping parameters for different birefringent crystals (Figure S9); improved methods for nanocylinder fabrication and trap calibration, and validation of FEM numerical models (Figure S10); SEM-measured dimensions of rutile TiO2 nanocylinders (Table S1); OTW-measured and FEM-calculated optical trapping parameters of the 3D-trappable rutile TiO2 nanocylinders (Table S2); dimensions and linear optical trapping parameters of the PS spheres (Table S3) (PDF)
Author Contributions
S.H. and N.H.D. designed the research. A.J.L.A. and N.H.D. directed the research. S.H. fabricated TiO2 nanocylinders and conducted their geometrical characterization. S.H. built the OTW setup, performed OTW measurements, and analyzed OTW data sets. Y.T. and S.H. developed FEM numerical models and conducted calculations. M.M.v.O. advised on OTW setup, measurements, data analysis, and FEM calculations. R.J. and S.H. developed and optimized the nanocylinder surface functionalization protocol. R.M.D. and B.S. assisted with the OTW setup. S.H., Y.T., A.J.L.A., and N.H.D. discussed the data. S.H., Y.T., B.S., A.J.L.A., and N.H.D. wrote the manuscript.
Author Contributions
§ These authors are equally contributed to this work.
The authors declare no competing financial interest.
Supplementary Material
References
- Beth R. A. Mechanical detection and measurement of the angular momentum of light. Phys. Rev. 1936, 50, 115–125. 10.1103/PhysRev.50.115. [DOI] [Google Scholar]
- Friese M. E. J.; Nieminen T. A.; Heckenberg N. R.; Rubinsztein-Dunlop H. Optical alignment and spinning of laser-trapped microscopic particles. Nature 1998, 394, 348–350. 10.1038/28566. [DOI] [Google Scholar]
- Forth S.; Sheinin M. Y.; Inman J.; Wang M. D. Torque measurement at the single-molecule level. Annu. Rev. Biophys. 2013, 42, 583–604. 10.1146/annurev-biophys-083012-130412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipfert J.; van Oene M. M.; Lee M.; Pedaci F.; Dekker N. H. Torque spectroscopy for the study of rotary motion in biological systems. Chem. Rev. 2015, 115, 1449–1474. 10.1021/cr500119k. [DOI] [PubMed] [Google Scholar]
- Arita Y.; McKinley A. W.; Mazilu M.; Rubinsztein-Dunlop H.; Dholakia K. Picoliter rheology of gaseous media using a rotating optically trapped birefringent microparticle. Anal. Chem. 2011, 83, 8855–8858. 10.1021/ac2024365. [DOI] [PubMed] [Google Scholar]
- Wu T.; Nieminen T. A.; Mohanty S.; Miotke J.; Meyer R. L.; Rubinsztein-Dunlop H.; Berns M. W. A photon-driven micromotor can direct nerve fibre growth. Nat. Photonics 2012, 6, 62–67. 10.1038/nphoton.2011.287. [DOI] [Google Scholar]
- Arita Y.; Mazilu M.; Dholakia K. Laser-induced rotation and cooling of a trapped microgyroscope in vacuum. Nat. Commun. 2013, 4, 2374. 10.1038/ncomms3374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neale S. L.; MacDonald M. P.; Dholakia K.; Krauss T. F. All-optical control of microfluidic components using form birefringence. Nat. Mater. 2005, 4, 530–533. 10.1038/nmat1411. [DOI] [PubMed] [Google Scholar]
- Leach J.; Mushfique H.; di Leonardo R.; Padgett M.; Cooper J. An optically driven pump for microfluidics. Lab Chip 2006, 6, 735–739. 10.1039/b601886f. [DOI] [PubMed] [Google Scholar]
- Jones P. H.; Maragò O. M.; Volpe G.. Optical Tweezers: Principles and Applications; Cambridge University Press: Cambridge, 2015. [Google Scholar]
- La Porta A.; Wang M. D. Optical torque wrench: angular trapping, rotation, and torque detection of quartz microparticles. Phys. Rev. Lett. 2004, 92, 190801. 10.1103/PhysRevLett.92.190801. [DOI] [PubMed] [Google Scholar]
- Gutiérrez-Medina B.; Andreasson J. O. L.; Greenleaf W. J.; LaPorta A.; Block S. M., An optical apparatus for rotation and trapping. In Methods in Enzymology; Walter N. G., Ed.; Academic Press: San Diego, CA, 2010; Vol. 475, pp 377–404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedaci F.; Huang Z.; van Oene M.; Barland S.; Dekker N. H. Excitable particles in an optical torque wrench. Nat. Phys. 2011, 7, 259–264. 10.1038/nphys1862. [DOI] [Google Scholar]
- Pedaci F.; Huang Z.; van Oene M.; Dekker N. H. Calibration of the optical torque wrench. Opt. Express 2012, 20, 3787–3802. 10.1364/OE.20.003787. [DOI] [PubMed] [Google Scholar]
- Santybayeva Z.; Pedaci F., Optical torque wrench design and calibration. In Optical Tweezers: Methods and Protocols, Methods in Molecular Biology; Gennerich A., Ed.; Springer: New York, NY, 2017; Vol. 1486, pp 157–181. [DOI] [PubMed] [Google Scholar]
- Allen L.; Beijersbergen M. W.; Spreeuw R. J. C.; Woerdman J. P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A: At., Mol., Opt. Phys. 1992, 45, 8185–8189. 10.1103/PhysRevA.45.8185. [DOI] [PubMed] [Google Scholar]
- Funk M.; Parkin S. J.; Stilgoe A. B.; Nieminen T. A.; Heckenberg N. R.; Rubinsztein-Dunlop H. Constant power optical tweezers with controllable torque. Opt. Lett. 2009, 34, 139–141. 10.1364/OL.34.000139. [DOI] [PubMed] [Google Scholar]
- Lehmuskero A.; Ogier R.; Gschneidtner T.; Johansson P.; Kall M. Ultrafast spinning of gold nanoparticles in water using circularly polarized light. Nano Lett. 2013, 13, 3129–3134. 10.1021/nl4010817. [DOI] [PubMed] [Google Scholar]
- Shao L.; Yang Z.-J.; Andrén D.; Johansson P.; Käll M. Gold nanorod rotary motors driven by resonant light scattering. ACS Nano 2015, 9, 12542–12551. 10.1021/acsnano.5b06311. [DOI] [PubMed] [Google Scholar]
- Jauffred L.; Taheri S. M.; Schmitt R.; Linke H.; Oddershede L. B. Optical trapping of gold nanoparticles in air. Nano Lett. 2015, 15, 4713–4719. 10.1021/acs.nanolett.5b01562. [DOI] [PubMed] [Google Scholar]
- van der Horst A.; van Oostrum P. D. J.; Moroz A.; van Blaaderen A.; Dogterom M. High trapping forces for high-refractive index particles trapped in dynamic arrays of counterpropagating optical tweezers. Appl. Opt. 2008, 47, 3196–3202. 10.1364/AO.47.003196. [DOI] [PubMed] [Google Scholar]
- Jannasch A.; Demirörs A. F.; van Oostrum P. D. J.; van Blaaderen A.; Schäffer E. Nanonewton optical force trap employing anti-reflection coated, high-refractive-index titania microspheres. Nat. Photonics 2012, 6, 469–473. 10.1038/nphoton.2012.140. [DOI] [Google Scholar]
- Arita Y.; Richards J. M.; Mazilu M.; Spalding G. C.; Skelton Spesyvtseva S. E.; Craig D.; Dholakia K. Rotational dynamics and heating of trapped nanovaterite particles. ACS Nano 2016, 10, 11505–11510. 10.1021/acsnano.6b07290. [DOI] [PubMed] [Google Scholar]
- Ramaiya A.; Roy B.; Bugiel M.; Schäffer E. Kinesin rotates unidirectionally and generates torque while walking on microtubules. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, 10894. 10.1073/pnas.1706985114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neuman K. C.; Chadd E. H.; Liou G. F.; Bergman K.; Block S. M. Characterization of photodamage to Escherichia coli in optical traps. Biophys. J. 1999, 77, 2856–2863. 10.1016/S0006-3495(99)77117-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Oene M. M.; Ha S.; Jager T.; Lee M.; Pedaci F.; Lipfert J.; Dekker N. H. Quantifying the precision of single-molecule torque and twist measurements using Allan variance. Biophys. J. 2018, 114, 1970–1979. 10.1016/j.bpj.2018.02.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polyanskiy M. N.Refractive Index Database; https://refractiveindex.info/.
- Ha S.; Janissen R.; Ussembayev Y. Y.; van Oene M. M.; Solano B.; Dekker N. H. Tunable top-down fabrication and functional surface coating of single-crystal titanium dioxide nanostructures and nanoparticles. Nanoscale 2016, 8, 10739–10748. 10.1039/C6NR00898D. [DOI] [PubMed] [Google Scholar]
- Parkin S. J.; Vogel R.; Persson M.; Funk M.; Loke V. L. Y.; Nieminen T. A.; Heckenberg N. R.; Rubinsztein-Dunlop H. Highly birefringent vaterite microspheres: production, characterization and applications for optical micromanipulation. Opt. Express 2009, 17, 21944–21955. 10.1364/OE.17.021944. [DOI] [PubMed] [Google Scholar]
- Demirors A. F.; Jannasch A.; van Oostrum P. D.; Schaffer E.; Imhof A.; van Blaaderen A. Seeded growth of titania colloids with refractive index tunability and fluorophore-free luminescence. Langmuir 2011, 27, 1626–1634. 10.1021/la103717m. [DOI] [PubMed] [Google Scholar]
- Simpson N. B.; McGloin D.; Dholakia K.; Allen L.; Padgett M. J. Optical tweezers with increased axial trapping efficiency. J. Mod. Opt. 1998, 45, 1943–1949. 10.1080/09500349808231712. [DOI] [Google Scholar]
- Nieminen T. A.; Loke V. L. Y.; Stilgoe A. B.; Knoner G.; Branczyk A. M.; Heckenberg N. R.; Rubinsztein-Dunlop H. Optical tweezers computational toolbox. J. Opt. A: Pure Appl. Opt. 2007, 9, S196–S203. 10.1088/1464-4258/9/8/S12. [DOI] [Google Scholar]
- Rohrbach A.; Stelzer E. H. K. Trapping forces, force constants, and potential depths for dielectric spheres in the presence of spherical aberrations. Appl. Opt. 2002, 41, 2494–2507. 10.1364/AO.41.002494. [DOI] [PubMed] [Google Scholar]
- Neuman K. C.; Nagy A. Single-molecule force spectroscopy: optical tweezers, magnetic tweezers and atomic force microscopy. Nat. Methods 2008, 5, 491–505. 10.1038/nmeth.1218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma J.; Tan C.; Gao X.; Fulbright R. M.; Roberts J. W.; Wang M. D. Transcription factor regulation of RNA polymerase’s torque generation capacity. Proc. Natl. Acad. Sci. U. S. A. 2019, 116, 2583. 10.1073/pnas.1807031116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beeby M.; Ribardo D. A.; Brennan C. A.; Ruby E. G.; Jensen G. J.; Hendrixson D. R. Diverse high-torque bacterial flagellar motors assemble wider stator rings using a conserved protein scaffold. Proc. Natl. Acad. Sci. U. S. A. 2016, 113, E1917–E1926. 10.1073/pnas.1518952113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Capitanio M.; Pavone F. S. Interrogating biology with force: single molecule high-resolution measurements with optical tweezers. Biophys. J. 2013, 105, 1293–1303. 10.1016/j.bpj.2013.08.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Craig D.; McDonald A.; Mazilu M.; Rendall H.; Gunn-Moore F.; Dholakia K. Enhanced optical manipulation of cells using antireflection coated microparticles. ACS Photonics 2015, 2, 1403–1409. 10.1021/acsphotonics.5b00178. [DOI] [Google Scholar]
- Daniels B. R.; Masi B. C.; Wirtz D. Probing single-cell micromechanics in vivo: the microrheology of C. elegans developing embryos. Biophys. J. 2006, 90, 4712–4719. 10.1529/biophysj.105.080606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu Z.; Li T. Detecting Casimir torque with an optically levitated nanorod. Phys. Rev. A: At., Mol., Opt. Phys. 2017, 96, 033843. 10.1103/PhysRevA.96.033843. [DOI] [Google Scholar]
- Phillips D. B.; Grieve J. A.; Olof S. N.; Kocher S. J.; Bowman R.; Padgett M. J.; Miles M. J.; Carberry D. M. Surface imaging using holographic optical tweezers. Nanotechnology 2011, 22, 285503. 10.1088/0957-4484/22/28/285503. [DOI] [PubMed] [Google Scholar]
- Janissen R.; Berghuis B. A.; Dulin D.; Wink M.; van Laar T.; Dekker N. H. Invincible DNA tethers: covalent DNA anchoring for enhanced temporal and force stability in magnetic tweezers experiments. Nucleic Acids Res. 2014, 42, e137. 10.1093/nar/gku677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reihani S. N. S.; Mir S. A.; Richardson A. C.; Oddershede L. B. Significant improvement of optical traps by tuning standard water immersion objectives. J. Opt. 2011, 13, 105301. 10.1088/2040-8978/13/10/105301. [DOI] [Google Scholar]
- Viana N. B.; Rocha M. S.; Mesquita O. N.; Mazolli A.; Neto P. A. M. Characterization of objective transmittance for optical tweezers. Appl. Opt. 2006, 45, 4263–4269. 10.1364/AO.45.004263. [DOI] [PubMed] [Google Scholar]
- Meiners J.-C.; Quake S. R. Direct measurement of hydrodynamic cross correlations between two particles in an external potential. Phys. Rev. Lett. 1999, 82, 2211–2214. 10.1103/PhysRevLett.82.2211. [DOI] [Google Scholar]
- Tolić-Nørrelykke S. F.; Schäffer E.; Howard J.; Pavone F. S.; Jülicher F.; Flyvbjerg H. Calibration of optical tweezers with positional detection in the back focal plane. Rev. Sci. Instrum. 2006, 77, 103101. 10.1063/1.2356852. [DOI] [Google Scholar]
- Franosch T.; Grimm M.; Belushkin M.; Mor F. M.; Foffi G.; Forro L.; Jeney S. Resonances arising from hydrodynamic memory in Brownian motion. Nature 2011, 478, 85–88. 10.1038/nature10498. [DOI] [PubMed] [Google Scholar]
- Wei X.; Wachters A. J.; Urbach H. P. Finite-element model for three-dimensional optical scattering problems. J. Opt. Soc. Am. A 2007, 24, 866–881. 10.1364/JOSAA.24.000866. [DOI] [PubMed] [Google Scholar]
- Novotny L.Principles of Nano-Optics, 2nd ed.; Cambridge University Press: Cambridge, 2012. [Google Scholar]
- Chen J.; Ng J.; Lin Z.; Chan C. T. Optical pulling force. Nat. Photonics 2011, 5, 531–534. 10.1038/nphoton.2011.153. [DOI] [Google Scholar]
- White F. M.Fluid Mechanics, 7th ed.; McGraw-Hill: New York, NY, 2011. [Google Scholar]
- Leach J.; Mushfique H.; Keen S.; Di Leonardo R.; Ruocco G.; Cooper J. M.; Padgett M. J. Comparison of Faxen’s correction for a microsphere translating or rotating near a surface. Phys. Rev. E 2009, 79, 026301. 10.1103/PhysRevE.79.026301. [DOI] [PubMed] [Google Scholar]
- Khatibzadeh N.; Stilgoe A. B.; Bui A. A.; Rocha Y.; Cruz G. M.; Loke V.; Shi L. Z.; Nieminen T. A.; Rubinsztein-Dunlop H.; Berns M. W. Determination of motility forces on isolated chromosomes with laser tweezers. Sci. Rep. 2014, 4, 6866. 10.1038/srep06866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ortega A.; Garcıa de la Torre J. Hydrodynamic properties of rodlike and disklike particles in dilute solution. J. Chem. Phys. 2003, 119, 9914–9919. 10.1063/1.1615967. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.