Histologically derived fiber response functions for diffusion MRI vary across white matter fibers – an ex vivo validation study in the squirrel monkey brain

Abstract

Understanding the relationship between the diffusion-weighted MRI signal and the arrangement of white matter fibers is fundamental for accurate voxel-wise reconstruction of the fiber orientation distribution (FOD) and subsequent fiber tractography. Spherical deconvolution reconstruction techniques model the diffusion signal as the convolution of the FOD with a response function that represents the signal profile of a single fiber orientation. Thus, given the signal and a fiber response function, the FOD can be estimated in every imaging voxel by deconvolution. However, the selection of the appropriate response function remains relatively under-studied, and requires further validation. In this work, using 3D histologically-defined FODs and the corresponding diffusion signal from three ex vivo squirrel monkey brains, we derive the ground truth response functions. We find that the histologically-derived response functions differ from those conventionally used. Next, we find that response functions statistically vary across brain regions, which suggests that the practice of using the same kernel throughout the brain is not optimal. We show that different kernels lead to different FOD reconstructions, which in turn can lead to different tractography results depending on algorithmic parameters, with large variations in the accuracy of resulting reconstructions. Together, these results suggest there is room for improvement in estimating and understanding the relationship between the diffusion signal and the underlying FOD.

Graphical Abstract

Using 3D histologically defined fiber orientation distributions and the corresponding signal, we empirically derive the ground truth response functions. We find significant variation in response functions within and between brains.

Introduction

Diffusion MRI fiber tractography has been widely adopted in clinical and basic neuroscience studies to probe the structural connectivity of the brain^1–3. A key requirement for anatomically correct tractography is the accurate reconstruction of the distribution of neuronal fiber orientations in each voxel, an object often referred to as the fiber orientation distribution (FOD)^4,5. A large number of reconstruction strategies have been proposed with the aim to estimate, model, or infer the structure of the FOD. Among them, spherical deconvolution (SD)^6–9 has emerged as one of the most commonly implemented in neuroscience research.

Although there are many versions and derivations of this technique^6–23 most spherical deconvolution methods are based on the idea that the diffusion MRI signal, S, can be modelled as the convolution of the fiber orientation distribution, with a kernel (called the fiber response function, R) that represents the signal attenuation that would be measured from a single (parallel) fiber population:

$$S\left(\text{Θ},\text{Φ}\right)=R\left(\text{Θ}\right)\otimes FOD\left(\text{Θ},\text{Φ}\right)$$ 1

where Θ and Φ are the polar and azimuthal angle in spherical coordinates (the response function is defined as the signal from fibers perfectly aligned along the vertical z-axis). The FOD can then be calculated by a deconvolution of the signal with the response function. Thus, an appropriate response function is required for accurate reconstruction of the FOD.

Several methods have been proposed to estimate the response function. Most derive the kernel from the diffusion data itself. For example, the response function can be estimated from the signal from voxels (typically 100+ voxels) with the highest fractional anisotropy values – voxels that are typically assumed to contain coherently oriented fibers²⁴. Due to relying only on FA values, this family of algorithms is susceptible to artifacts (for example, Gibbs ringing near ventricles). To overcome this limitation, several strategies have been proposed which iterate between performing SD and estimating the response function from a set of voxels most likely to contain only a single fiber population^25,26. Alternatively, one can assume that a single fiber bundle gives rise to a spin displacement distribution that can be described with a single diffusion tensor model, and derive the response function as the signal that would be obtained from the tensor with given shape properties^10,14.

In addition to its use for FOD reconstruction and subsequent tractography, the response function is also relevant to the field of microstructural modeling^{19,21,22,27–31}. Here, quantifying brain microstructure with diffusion MRI requires an accurate representation of the relationship between the diffusion signal and relevant tissue parameters. In addition to the FOD, it is expected that the diffusion signal (and hence the response kernel) is dependent on intra-neurite, extra-neurite, and CSF volume (or signal) fractions and intrinsic diffusivities, axon packing and diameters, and myelination, as well as acquisition parameters including the diffusion times and diffusion weightings (b-value) (see equation 60 from³²).

Despite evidence that the diffusion signal is dependent on an array of microstructural parameters, a major limitation in both the field of tractography and microstructural modeling is that in most cases the same response function is used in the deconvolution throughout the entire brain³². There are some exceptions, where the response function varies based on tissue (i.e. white matter and gray matter)^33,34, however, these kernels still remain the same throughout the entire tissue type volume (for example, all white matter—an exception is the FORECAST method [8]). Despite the large number of approaches for response function estimation, little work has been done to validate the accuracy of these techniques and subsequent effects on tractography, or to question the validity of a brain-wide fiber response function.

In this study, we aim to use histology to derive the linear relationship (i.e., the response function) between the diffusion signal and the underlying FOD. Instead of the traditional approach of deconvolving the signal with an empirical response function in order to estimate the fiber distribution, we do the opposite – deconvolve the signal with the histologically-derived FOD to derive the response function. In essence, we ask, “what is the true response function, given the diffusion signal and the FOD”? To do this, we perform diffusion MRI on three fixed ex vivo squirrel monkey brains, followed by 3D confocal microscopy to derive the “ground truth” FOD. We begin by testing the validity of utilizing the same response function throughout the entire brain. Next, we assess the effects of varying response functions on both the voxel-wise reconstruction and tractography results. Finally, the anatomical accuracy of tractography using different response functions is assessed by comparing tracking results to known connections from an existing squirrel monkey atlas.

Methods

Overview

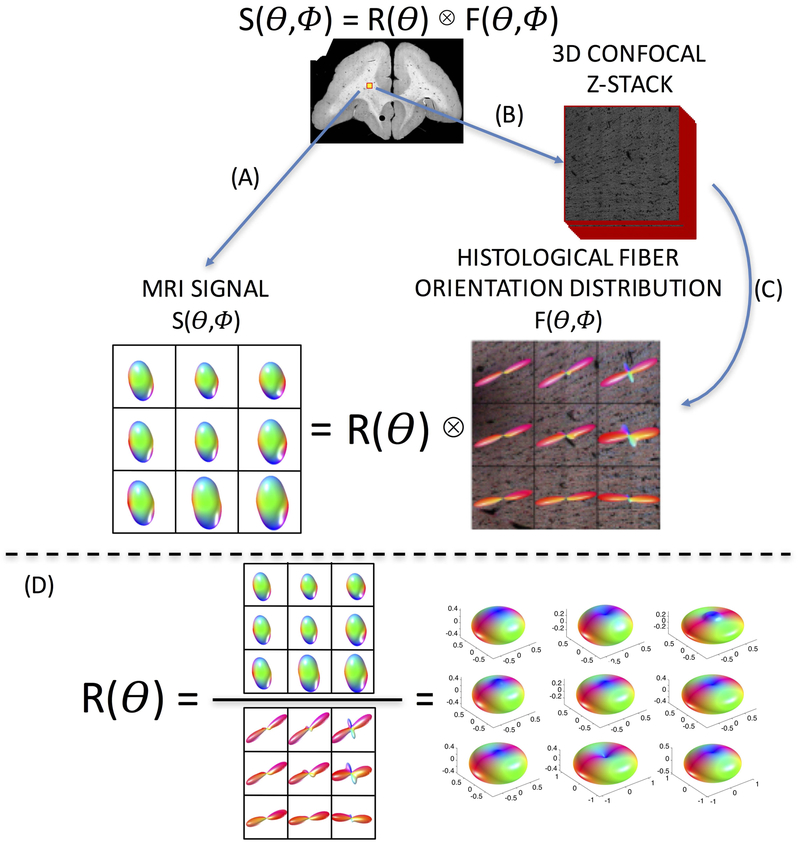
An overview of the study methodology is shown in Figure 1. Briefly, each ex vivo brain was first scanned using MR imaging to acquire the diffusion signal (Figure 1A; see MRI Acquisition). After sectioning, the tissue was imaged using confocal microscopy and multiple 3D confocal z-stacks were acquired (Figure 1B, see Histological Procedures). These z-stacks were processed using a pipeline previously developed to analyze 3D histology^35,36, which resulted in voxel-wise histological ground truth 3D FODs (Figure 1C, see Histological Procedures). Because we want to estimate the response function, the diffusion signal can be deconvolved with the corresponding FODs, resulting in voxel-wise reconstructions of the response functions (Figure 1D, see Response Function Estimation). All animal procedures were approved by the Vanderbilt University Animal Care and Use Committee.

Figure 1.

Overview of study methodology. Spherical deconvolution models the diffusion signal, S, as the convolution of the fiber response function, R, with the fiber orientation distribution, F. The brain is scanned (A) resulting in an MRI signal. Next, 3D confocal microscopy is acquired (B), followed by image processing (C), resulting in the ground truth histological FOD. Estimating the voxel-wise response function (D) is done through deconvolution of the signal with the corresponding FOD.

MRI acquisition

Diffusion MRI experiments were performed on three adult squirrel monkey brains that had been perfused with physiological saline followed by 4% paraformaldehyde. The brain was then immersed for 3 weeks in phosphate-buffered saline (PBS) medium with 1 mM Gd-DTPA in order to reduce longitudinal relaxation time³⁷. The brain was placed in liquid Fomblin (California Vacuum Technology, CA) and scanned on a Varian 9.4 T, 21 cm bore magnet using a quadrature birdcage volume coil (inner diameter = 63 mm).

Diffusion data were acquired with a 3D spin-echo diffusion-weighted EPI sequence (TR = 410 ms; TE = 41 ms; NSHOTS = 4; NEX = 1; Partial Fourier k-space coverage = 0.75) at 300 μm isotropic resolution. Diffusion gradient pulse duration and separation were 8 ms and 22 ms, respectively, and the b-value was set to 6000 s/mm2. This value was chosen due to the decreased diffusivity of ex vivo tissue, which is approximately a fourth of that in vivo^38,39, and is expected to closely replicate the signal attenuation profile for in vivo tissue with a b-value of approximately 1500 s/mm². A gradient table of 107 uniformly distributed directions⁴⁰ was used to acquire 107 diffusion-weighted volumes with four additional image volumes collected at b = 0.

Histological Procedures

Here, we aim to extract the histological FOD from 3D confocal z-stacks in areas equivalent to the size of an MRI voxel. To do this, we implement the methodology described in³⁶, which consisted of tissue sectioning and staining, confocal acquisition, and confocal pre-processing, followed by an image processing technique – structure tensor analysis – which resulted in an orientation estimate for every pixel in the 3D z-stack that is occupied by a fiber. The FOD is defined as the distribution of these orientation estimates. This procedure has been validated against manually traced fibers³⁶, and has been used to assess the accuracy of diffusion MRI reconstruction techniques³⁵.

Briefly, the tissue was sectioned at a thickness of 50um in the coronal plane. During sectioning, the frozen tissue block was digitally photographed prior to cutting every third section, resulting in a 3D “block-face” volume, which was used for inter-modality registration (see Image Registration).

Tissue sections were stained with the fluorescent lipophilic dye “DiI” (1, 10-dioctadecyl-3,3,30 30-tetramethylindocarbocyanine perchlorate) and imaged using an LSM 710 confocal microscope (Carl Zeiss, Inc. Thornwood, NY. USA). For all slices, acquisition began with a 2D confocal montage (0.8×0.8um resolution), used for image registration and for localizing the 3D high resolution region of interest. A 3D z-stack was then collected (0.2×0.2×0.42um resolution) with an in-plane field of view of 900×900um (equivalent to 9 MRI voxels). Confocal data were converted from the LSM file format to TIFF images and imported into MATLAB for image processing.

Image pre-processing consisted of attenuation correction, anisotropy correction, and interpolation to isotropic resolution. Next, pixel-wise fiber orientations in the 3D z-stack were obtained via structure tensor analysis⁴¹. The histological FOD was then computed as the histogram of the extracted fiber orientations, and fit to high order (l_max=20) spherical harmonic coefficients (SH). Throughout this paper, the histological-FODs are displayed as 3D glyphs in the same way that MRI-FOD’s are typically displayed in the literature.

Image Registration

In order to derive voxel-wise response functions, it is important that the diffusion MRI signal and the histological FODs are aligned and oriented appropriately. A multi-step registration procedure⁴² was used to align histology to MRI data. The first step is registration of the 2D confocal montage to the corresponding block face image using mutual information based 2D linear registration followed by 2D nonlinear registration using the adaptive bases algorithm (ABA)⁴³. Next, all block face photographs were assembled into a 3D block volume, and registered to the MRI b = 0 image using a 3D affine transformation followed by 3D nonlinear registration with ABA. Given the location of the 3D z-stack in the 2D confocal montage, we can use the combined deformation fields to determine the MRI signal from the same tissue volume. We then implemented the preservation of principle directions strategy⁴⁴ to the diffusion weighting vectors (b-vectors) in order to take into account rotation, scaling, and shearing effects of the spatial transformations. At this point, for each histological FOD, we have the corresponding diffusion signal – which was then fit to SH coefficients to facilitate deconvolution.

This multi-step registration procedure was validated in an earlier study⁴², which showed that the accuracy of the overall registration was approximately one MRI voxel (~0.3 mm) by comparing position errors between manually chosen landmarks in histological and MRI space. Further, the combination of registration and histological procedures is similar to those utilized in³⁶, which showed an angular accuracy of approximately 5° in single fiber regions when compared to manually defined ground truth fiber orientations.

Response Function Estimation

As described in Equation 1, the diffusion signal is assumed to be the convolution of the fiber distribution with the response function. Thus, to derive the response function, we deconvolved the signal with the histological FOD.

If the signal, response function, and FOD are expanded in terms of spherical harmonic coefficients s_lm, r_lm, and p_lm, respectively (where l is the SH order and m is the phase index), it can be shown that the deconvolution leads to a simple relationship⁸:

$$s_{lm}=S_0\sqrt{\frac{4\pi }{2l+1}}{p}_{lm}{r}_l$$ 2

where S₀ represents the non-diffusion weighted signal (assumed to equal 1, as long as the diffusion weighted signal is normalized to S₀ before SH fitting). We note that here we assume a single q-space shell, or single b-value, acquisition (as the signal and response are also dependent on acquisition parameters including b-value³²). Inverting this gives:

$$r_l=\sqrt{\frac{2l+1}{4\pi }}\frac{s_l}{S_0{p}_l}$$ 3

where r_l is only defined for m=0 (for axial symmetry of the response function around the z-axis^27,32,45), and p_l and s_l are vectors of coefficients (one element for each m value), for each order. Alternately, by multiplying both sides of Eq. (2) by p_lm and summing over m, the response function can be estimated from:

$$r_l=\sqrt{\frac{2l+1}{4\pi }}\frac{p_{l\cdot }{s}_l}{S_0{|p_l|}^2}$$ 4

We performed this procedure for 6 z-stacks on each brain, resulting in 18 independent confocal z-stacks, equivalent in size to 162 MRI voxels, resulting in 162 individual response function derivations. For quantitative analysis, we have chosen to focus only on voxels in the white matter which contain a single fiber population – defined to have only a single local maximum in the histological FOD. For this reason, voxels containing gray matter or crossing fibers were excluded, resulting in 153 total samples.

For response functions derived from MRI data, we used three conventional methods to estimate the response function (separately for each individual brain). The first algorithm is an implementation of the strategy developed in²⁶, which estimates the response function from the 300 voxels with the highest FA value in an eroded brain mask. This algorithm is referred to as “FA response” in the rest of the manuscript. Second, the “Iterative response” is an implementation also described in²⁶ which starts with an initial estimate of a response function, then performs CSD reconstruction to estimate FODs. From these, the voxels that are most likely to contain single-fiber populations are detected, and their signal is used to compute the next iteration of the procedure. The first two algorithms are implemented in MRTrix3 software²⁴, and described in detail at (http://www.mrtrix.org, Response Function documentation). Finally, the “Tensor Response” is created assuming an axially-symmetric tensor^8,10 with an FA of .70 and trace diffusivity of 0.7×10⁻³ mm²/s (note that ex vivo specimens have a diffusivity of approximately ¼ to ½ that of in vivo^38,39). Importantly, these conventionally derived response functions do not correspond to any particular single voxel(s) as they are assumed to be applicable to white matter fiber populations throughout the entire brain.

Tractography and Tracking Accuracy

We next assessed the effects of various response functions on both FOD reconstruction and tractography results. As a well-studied system with known connections in the squirrel monkey brain^46,47, we chose to perform tractography of the motor system, with a seed region in the primary motor cortex. Both the seed region, as well as white matter and gray matter anatomical labels, are propagated from the Validate29 squirrel monkey atlas⁴⁶ to each individual subject’s brain.

All reconstruction and tractography was performed using the MRtrix3 software toolkit²⁴. Given a response kernel of interest, we first estimated the FOD from diffusion data using spherical deconvolution⁷ (command dwi2fod). From a field of FOD estimates, we performed whole brain fiber tractography (iFOD2 algorithm) and used the primary motor cortex seed as an inclusion region of interest.

The anatomical accuracy of tractography connections to labelled regions of interest was assessed by comparing results to known connections derived from histology and defined in the squirrel monkey atlas^46,47. The atlas contains 71 white matter and gray matter ROIs, 44 of which are known to be connected to the left hemisphere primary motor cortex and 27 of which are not connected (i.e., do not show evidence of tracer after injection into the primary motor cortex). Following procedures similar to^48,49, tractography results were binarized, and the presence or absence of streamlines in each ROI (both white and gray matter) was determined. We measured the sensitivity (the ability to detect true connections) and specificity (the ability to avoid false connections) of the various tractographic implementations derived using different response kernels.

Results

Histologically Derived Average Response Functions

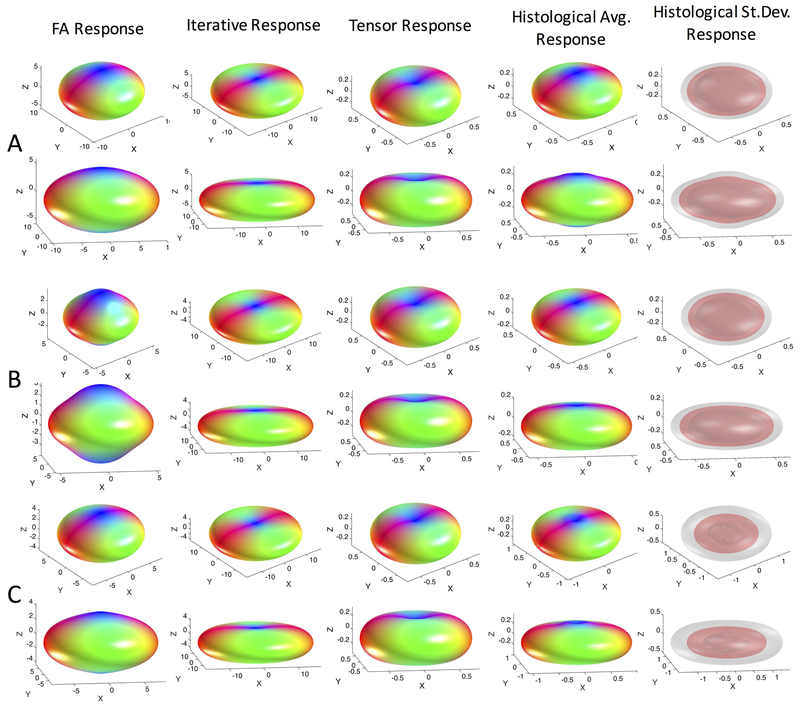
Response functions derived using standard practice methods for estimation are visualized in Figure 2 for all three subjects (A-C). Estimation using the signal from the voxels with the highest FA²⁴ (“FA Response”), using an iterative estimation method²⁶ (“Iterative Response”), and assuming a cylindrically symmetric diffusion tensor model¹⁰ (“Tensor Response”) show the standard, expected, oblate shape, where the signal is lowest in the direction of fibers (along the z-axis in the response function space) and highest perpendicular to them. Qualitatively, there are differences in the “flatness” of these functions within the same brain, suggesting fairly large variation between techniques.

Figure 2.

Response functions estimated using conventional methods differ from the histologically-derived response functions. Kernels estimated using the highest FA voxels, the iterative calibration method, and modelled from the diffusion tensor are shown in two views. The average histologically-derived response function for each monkey (across 6 z-stacks) is shown (monkeys #1–3 correspond to A-C) along with the mean (red) and mean +/− one standard deviation (gray) surfaces to highlight variability. Note differences in magnitude are due to differing normalization in our work and in MRTrix3. Shape, and not magnitude, determines the final FOD shape.

The average response function across all histology (i.e., 6 z-stacks) is shown in Figure 2 for each subject. Qualitatively, in all cases, the histologically-derived average response functions share similarities to standard-practice methods, and are somewhat intermediate in shape between the iterative estimation methods and the tensor and FA-derived shapes. Finally, visualizing the mean and standard deviation across the brain suggests that there is some deviation in response within white matter.

Variation across the brain

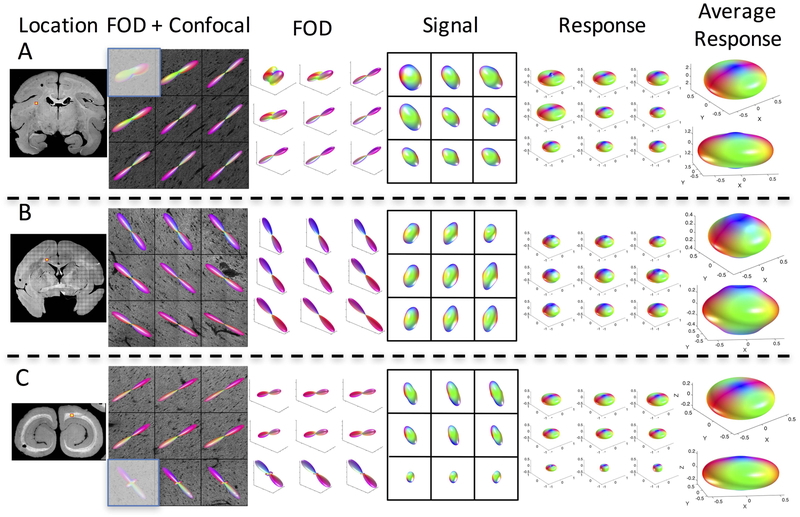
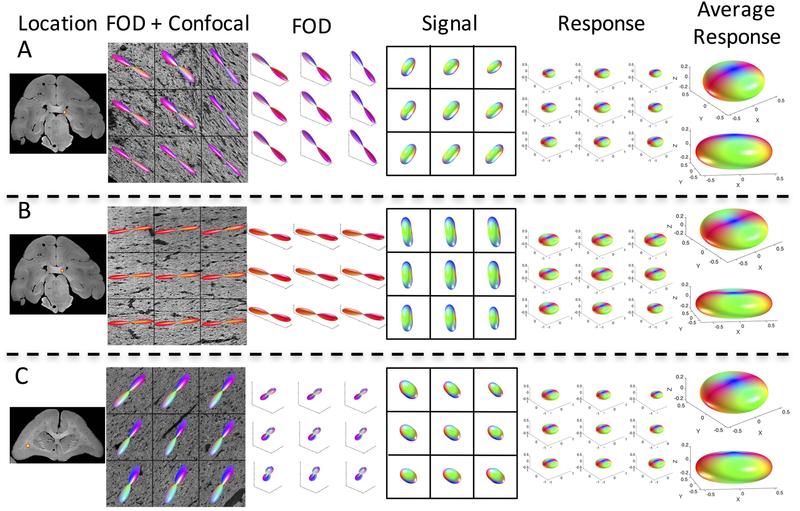
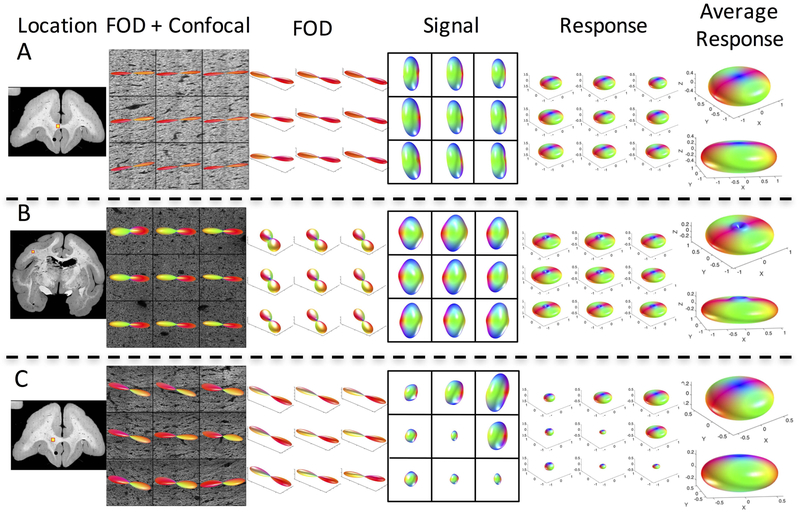
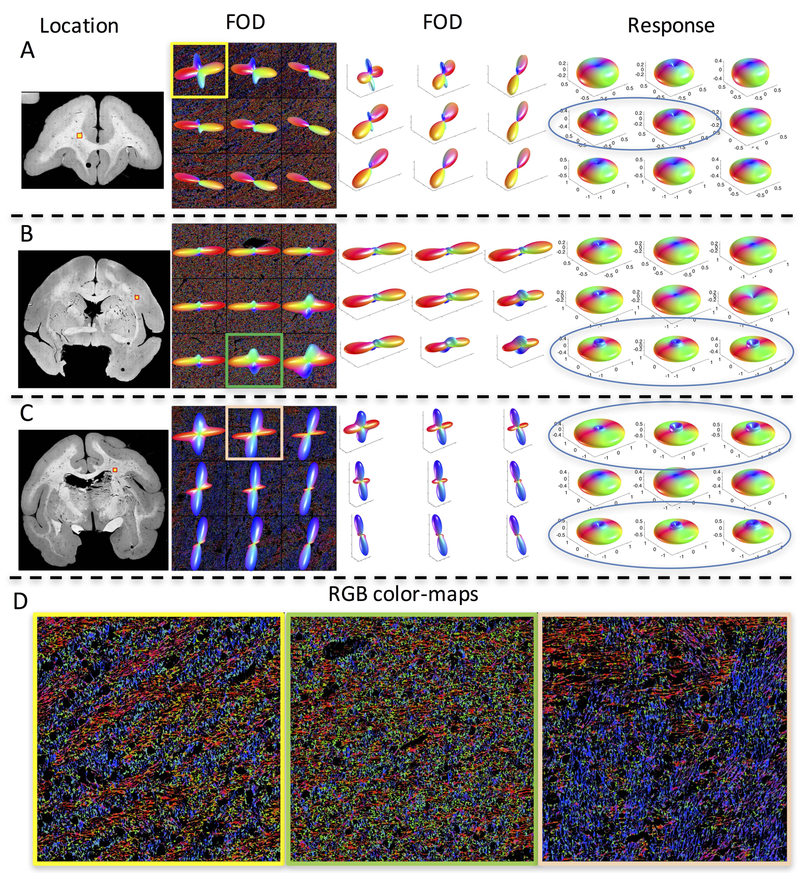
The variation in histologically derived response leads us to ask whether the use of a single response function across the entire brain is appropriate. For each monkey, we visualize the results of three (of the six) z-stacks (Figures 3, 4, and 5, for monkeys 1, 2, and 3, respectively), showing the z-stack location, the voxel-wise histological FOD, diffusion signal, and derived response functions, along with two views of the average response function at each location. Differences in shape, flatness, and radial and axial attenuations are apparent both within and across monkeys.

Figure 3.

The response function varies across brain regions. Three locations in the same monkey brain (monkey #1) are shown, along with the histological fiber orientation distribution, signal, and derived response function for all 9 voxels. In addition, the average response function for each z-stack is shown in two views. Grayed-out voxel contained some gray matter and hence was not included in the study (or in derivation of average response).

Figure 4.

The response function varies across brain regions. Three locations in the same monkey brain (monkey #2) are shown, along with the histological fiber orientation distribution, signal, and derived response function for all 9 voxels. In addition, the average response function for each z-stack is shown in two views.

Figure 5.

The response function varies across brain regions. Three locations in the same monkey brain (monkey #3) are shown, along with the histological fiber orientation distribution, signal, and derived response function for all 9 voxels. In addition, the average response function for each z-stack is shown in two views.

A multivariate analysis of variance (MANOVA) of the (n=4) spherical harmonic coefficients representing the response functions indicates that the response functions vary significantly across white matter locations within a brain (monkey #1: dimensionality = 3, p<.001; monkey #2: dimensionality = 3, p<.001; monkey #4: dimensionality = 4, p<.001 – here dimensionality is an estimate of the dimension of the space spanned by the group means, if the response functions were the same, the dimension would be 0). Additionally, a MANOVA also indicates that the response functions show significant differences across brains (dimensionality = 2; p<.001, indicating that the mean response function is not the same). Thus, there are statistically significant variations in response function within brains.

Fiber orientation distribution estimation

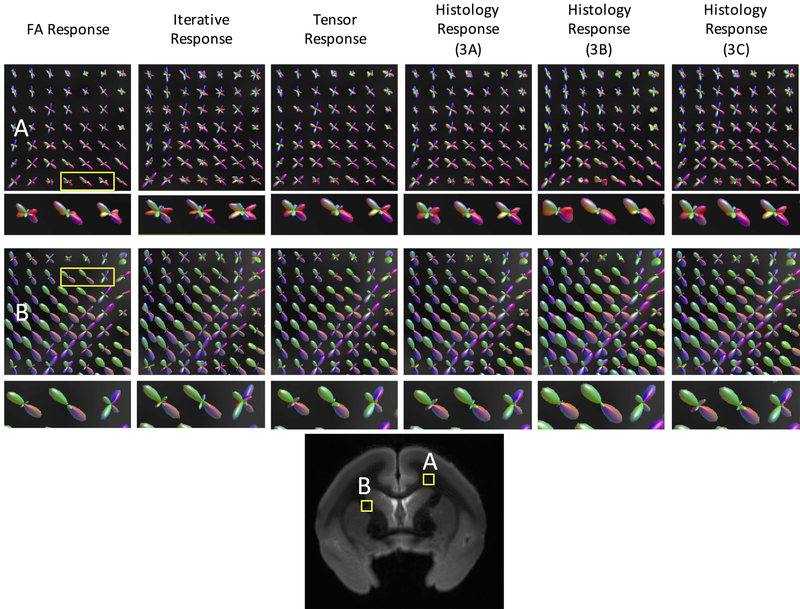
The standard-practice kernels, as well as three histologically defined kernels from the same monkey (Monkey #1 from Figure 3) are used to perform spherical deconvolution, and the resulting FODs are shown in Figure 6 for two white matter locations. It is clear that different response functions lead to different FODs. The most obvious differences are the amplification of smaller peaks in some of the methods utilizing the “flatter” kernels (for example, the Iterative Response). Our results are in agreement with the literature^7,8, where different response functions result in FODs with peaks in the same orientations, and only differ in relative volume fractions of different fiber populations. Given that the peak orientations are the same, the question then becomes whether this affects subsequent tractography.

Figure 6.

Different response functions lead to different FOD reconstructions. Fiber reconstruction in two regions of interest (A and B) using three commonly implemented response functions (FA Response, Iterative Response, Tensor Response), and three histologically derived response functions (those from Figure 3A, 3B, and 3C) from the same monkey. Reconstructed fiber orientation distributions retain similar shape and orientations, but contain different volume fractions of fiber populations. A zoomed-in region of 3 voxels is shown for each reconstruction to highlight differences/similarities.

Tractography

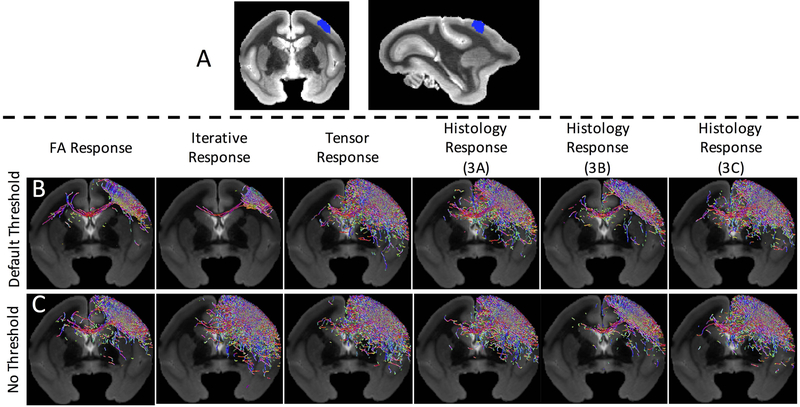
Tractography from a region of the primary motor cortex (Figure 7A) was performed using the FOD reconstructions from the standard kernels, and the individual kernels from three z-stacks (the same from Figure 6). Differences in spatial extent and path representation are apparent across different response functions (Figure 7B).

Figure 7.

Different response functions can lead to different tractography results. Whole-brain tractography is performed with an inclusion region in the primary motor cortex (A) using the FODs described in Figure 6, using standard tractography parameters and settings (i.e., the FOD amplitude threshold) (B). Tractography is repeated using no threshold on FOD amplitude, resulting in qualitatively similar streamlines (C). Note that only streamlines within a single coronal slice are visualized.

Because the only differences in reconstructed FODs are the amplitude of the peaks (and not orientation), we hypothesized that differences in tractographic reconstructions are due to the amplitude threshold on the FOD used in the fiber tracking algorithms. Given a number of “peaks” or local maxima of the FOD, the “FOD threshold” determines an amplitude below which the peak is considered negligible, and is not used to propagate streamlines. For Figure 7B, this threshold was set at a typical value of 0.05 of the maximum peak amplitude. To investigate whether the threshold affected tractography, we set the threshold to zero (no threshold on peak amplitude) and re-ran tractography (Figure 7C). Qualitatively, reconstructions appear much more similar despite differences in response functions.

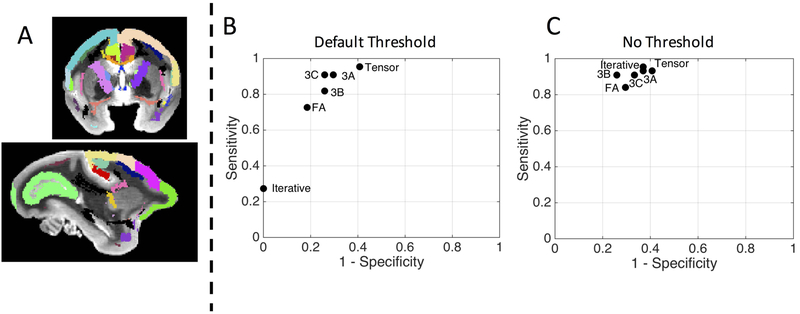
Connectivity to the motor cortex is compared to known connections from tracer studies, with white matter and gray matter ROIs shown in Figure 8A. Sensitivity and specificity of all tracking strategies from Figure 7 are computed and shown in Figure 8B for standard tracking parameters, and Figure 8C for the non-thresholded tracking. With default tracking parameters, not only do different response functions lead to qualitatively different tractography results, they can lead to a fairly wide variation in the true positive rate and true negative rate of tractography connections (Figure 8B). However, this variation is largely caused by the amplitude threshold and the differences in amplitude when using different kernels for FOD reconstructions. Eliminating this amplitude threshold results in very similar sensitivity/specificity results (Figure 8C). These findings generalize to the additional two subjects (results not shown) with notable variation of sensitivity/specificity across response functions, and algorithms resulting in similar sensitivity/specificity after eliminating peak-amplitude thresholds.

Figure 8.

Different response functions can lead to different tractography results. Tractography is compared to an atlas of known connections (atlas and histology described in^46,63, see Figure 2 from⁵³ and Figure 1B from⁴⁹ for visualization of the ground truth pathways), by calculating the true positive and true negative rate of connections to various regions of interest (A). The sensitivity and specificity of the tractography results from Figure 7 are plotted in an ROC curve using the default FOD threshold (B) and no FOD threshold (C). Method abbreviations: FA: average FA response; ITER: iterative response; Tensor: tensor-derived response; 3A-C: histological-derived response from z-stacks A-C from Figure 3.

Discussion

Understanding the relationship between the diffusion MRI signal and tissue microstructure is a fundamental goal in the field of diffusion MR imaging. Here, we study one aspect of the microstructure, the geometric distribution of fibers in each imaging voxel (i.e., the FOD), a function that is fundamental in creating maps of the human brain using tractography. In this work, we use histology to derive the linear relationship between the diffusion signal and the underlying FOD – the response function (Figure 1).

We first observe that the histologically-derived response functions can differ in shape from conventional methods of estimating this kernel from the diffusion data itself or by assuming signal profiles (Figure 2). Differences are critical, because tractography results not only depend on tracking parameters, algorithms, and constraints (i.e. step size, curvature threshold, FA threshold)^48,50,51, but spherical deconvolution results depend on the derivation and shape of the response function. Next, we show both qualitatively and quantitatively that the histologically derived response function varies within brains and between brains (Figure 3–5). Variation across white matter is expected, as the diffusion process is known to be dependent on local anatomy and microstructural properties. Despite this knowledge, a brain-wide response function is still the most prevalent method of performing SD today. Our results demonstrate that this practice is likely not adequate for accurate reconstruction of FODs across the brain, especially with varying tissue properties. It would be useful to extract other microstructural measures, for example axon diameters, volume fraction, or fiber dispersion, possibly from the confocal data itself, to study the response functions’ dependencies on the microstructure. Structure tensor analysis provides estimates of the fiber orientation distribution, but does not give information on other biophysical properties (e.g., the distribution of axonal diameters, net axonal volume fraction, myelination, or tortuosity of the extra-axonal space) that could be useful in relating the local response function to tissue microstructure. Other algorithms, and possibly multi-channel fluorescence microscopy data, will be required to identify the biophysical changes that account for the observed spatial variation of response functions in the brain. In principle, knowledge of the relevant biophysical parameters would allow calculation of the local response function—see⁵² for a review of the challenges and recent progress in diffusion MRI modeling.

In this study, we have assumed an axially symmetric response function, which is a common assumption in the diffusion literature (we are aware of no studies that have investigated, or utilized, an asymmetric response function). While axially symmetric response functions are simple and intuitive, it is possible that more complex geometries (e.g., sheet-like microstructure) of tissue could produce non-axially-symmetric response functions. Investigating the organization of fiber structure (in addition to simple orientation distributions) as well as non-symmetric response functions could be an avenue of future exploration. We note that the histologically-derived FODs can be asymmetric, which should simply result in an asymmetric signal.

While the focus of this manuscript is to show that the response function varies across white matter, we further show the effects of using different response functions on both FOD reconstruction and tractographic results. Unsurprisingly, different response functions lead to different FOD reconstruction estimates (Figure 6). Despite differences in the apparent volume fractions of fiber bundles, the peak orientation remains the same (given that the response functions used are axially symmetric). Because of this, it was surprising that different response functions can lead to different tractography results (Figures 7 and 8). This variation in tractography is almost certainly dependent on the algorithmic parameters as well; for example, the threshold below which peaks are deemed “spurious” as well as how the propagation steps are determined. To confirm this, tractography with no threshold resulted in very similar qualitative and quantitative results for all response functions, and subsequent FOD estimations. It is important to point out that we are not suggesting the use of no-thresholds for tractography, as it actually causes a distinct loss of specificity, and only use this as an example to show removing this threshold results in similar tracts for all tested response functions. In fact, no algorithmic parameters have both high specificity and sensitivity, in agreement with tractography validation studies^48,49,53, and in practice it is important to have some threshold to control the number of false positive bundles. While different choices of tracking parameters can produce large variations, it is important to point out that, with typical usage (i.e., typical parameters), different response functions also lead to different tractography results.

It is also important to point out that there are a large number of spherical deconvolution methods in the literature^{6–9,11–20}, each with slightly different derivations, modifications, or assumptions on the response kernels and models^54,55. Here, we have chosen to assess what we believe to be the most commonly utilized in the field, implemented using common or open-sourced platforms, and do not intend to compare or rank the different methodologies, instead highlighting a difference between these and histologically derived kernels. More importantly, with histological analysis alone, we find that the response functions vary across different white matter regions, and can potentially (depending upon tracking parameters) result in different tractography reconstructions, as well as reconstructions different from existing reconstruction methods. This does not mean that the histologically informed tractography is actually “better”. In fact, the histological response may only be appropriate for FOD reconstruction in certain anatomical locations and not others, and no method was perfect (Figure 8), all exhibiting a sensitivity/specificity tradeoff previously described in the validation literature^{48,50,51,53,56}. The tractographic analysis serves to emphasize that different response functions can lead to different connectivity results.

Limitations

This study has several potential limitations. First, because of the ex vivo nature of the tissue, and reduced ex vivo diffusivity³⁹, the derived response function is not the response function that should be used for in vivo data (or human data). However, studying ex vivo tissue is the only way in which the true fiber orientation distribution can be obtained, and our goal is simply to determine the linear relationship between this and the signal, and compare these data-driven methods of estimating the response function. Although these subjects did not have an in vivo acquisition, future studies should include both in vivo and ex vivo imaging, as well as multiple diffusion shells or diffusion times, followed by histological analysis, in order to better understand the response function, the signal, and the fiber distribution. Because of the ex vivo nature of the study, our results may not hold for in vivo human studies, although we expect the response function variation across brain regions, and across brains, to be largely generalizable to humans.

The second limitation is sample size. Only 6 z-stacks (containing predominantly single fiber populations) were analyzed per monkey. These regions covered multiple brains, with multiple slices per brain, and a variety of white matter locations (demonstrating a wide range of fiber orientations) across monkeys, further highlighting differences in response functions within and across brains. Additionally, only one connection was tested to assess differences in tractography. The primary motor system in the non-human primate has been studied extensively^57,58 with well characterized connections. Our approach highlights the effects of the response function on tracking accuracy, and the resulting tradeoff in tractography sensitivity and specificity is likely to exist in all pathways of interest. However, the focus of the study is on variation in the response function themselves, rather than a thorough validation of tractography⁵³.

Most importantly, for these results to be valid, it is important that the FODs derived from histology can actually be considered ground truth. The pipeline to extract 3D FODs from 3D confocal z-stacks is described thoroughly in³⁶, where the technique was validated to ensure directional accuracy on the order of 5°. Importantly, this pipeline both thresholds the image to ensure that orientation estimates are extracted only from voxels occupied by fibers, excluding directions estimated from non-tissue pixels, and also excludes pixels with poor, or uncertain, directional information. In this way, we excluded extra-axonal compartments in the FOD estimate, and FOD estimates are weighted by the volume fraction of the axons (i.e. big axons have more fiber-occupying voxels than small axons), in the same way that dMRI is sensitive to the volumes of various compartments.

Confocal microscopy has its own disadvantages. For example, while the in-plane field of view covers 900um², the through-plane thickness of the tissue is only 50um. We assume that the 50um thick tissue is representative of the fiber orientations throughout the sampled voxel, and un-sampled orientations can certainly cause erroneous fiber orientation estimates. Additionally, sources of anisotropy are present in acquisition, including anisotropic voxel sizes (0.2×0.2×0.42um) and anisotropic point spread functions, which we attempt to correct through interpolation and deconvolution, respectively³⁶. Despite this, the FOD derivation could possibly be less sensitive to through-plane fiber orientations, possibly biasing results (although obliquely-oriented fibers are detected and visible in 3D views). Together, these considerations may limit conclusions of the study, although we believe the primary conclusion – that the response function varies across the brain – to be supported by the results presented. Nevertheless, It is important to fully validate the histological techniques and image processing procedures. While we have previously manually traced fibers in individual z-stacks and found good agreement with the automated structure tensor analysis³⁶ (with agreement on the order of ~5 degrees), additional validation could include sectioning and imaging in orthogonal planes, and providing supporting evidence or complementary information in the form of alternative histological contrast. For example, Brightfield microscopy can cover large fields of view and has been used to extract FODs⁵⁹, however, this has so far been limited to 2D analysis (although extracting 3D microstructure from 2D histology may prove feasible⁶⁰). Recent work also shows the ability to exactly trace axons in 3D (on the scale of nm) using electron microscopy^52,61,62, although with limited fields of view that would likely prohibit direct comparison with MRI data from the same tissue volume.

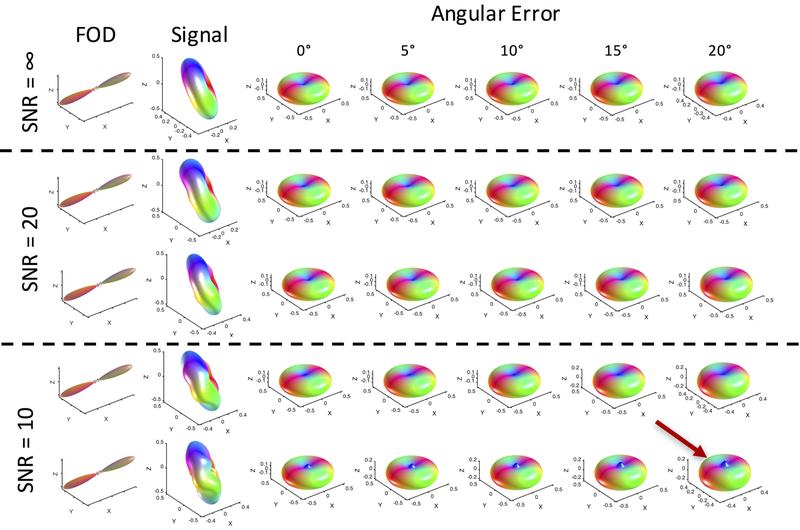
Estimates of the response function can be corrupted by two sources, noise and misalignment. We do expect some misalignment of the FOD and signal due to tissue distortions and registration errors, as well as noise in the MRI signal – our ex vivo acquisitions resulted in an SNR of the b0 images in the WM of approximately 25, 29, and 22 for monkeys #1–3, typical of that in research studies. Figure 9 shows the results of simulations investigating both misalignment and noise. Here, misalignment refers to a rotational error between the FOD and simulated signal (i.e., the peak of the simulated FOD no longer perfectly aligns with the minimum of the simulated signal), in order to simulate a histological stack that possibly underwent improper deformation or rotation. After misalignment and noise corruption, the response function is recomputed from Equation 4. In this case, with uncorrupted data (SNR=∞) misalignment between FOD and signal results in very little change to the derived response function (decreased radial and increased axial signal) with rotation as much as 20° of misalignment. In addition, with SNR as low as 10, the overall shape of the response function is qualitatively in agreement with the true function – noise causes a “blurring” of the true FOD, again decreasing radial signal and increasing axial signal. Additionally, spurious peaks frequently occurred axially in the direction where lowest signal is expected. Further analysis indicated that this peak occurs when noise samples are large specifically along, or near, the peak direction of the FOD, and becomes more prominent as the noise level in that direction increases (Supplementary Figure 1). Noise in other directions is more regularized due to the increased density of sampling at varying polar angles (i.e., longitudinal planes). In our data, these peaks were infrequent (for example, this could be observed in Figure 3A), and if they occurred, were not as prominent as in simulations.

Figure 9.

Noise and rotational misalignment can cause errors in estimating the response functions in single fiber regions. FODs and signal at varying noise levels (SNR = ∞, 10, and 20) and misalignments (angular errors between the FOD and diffusion signal of 0–20 degrees) were used to derive response functions. Response functions are relatively robust to angular error, but noise can cause spurious peaks axially (red arrow). Here, signal is generated from an axially symmetric diffusion tensor model with λ₁=1.6E-3 mm²/s, λ₂=λ₃=1.6E-3 mm²/s, FA=0.7. Two simulations are shown for each noise level. Noise is added in quadrature.

Crossing Fibers

This study focused on single fiber voxels in the white matter, in order to avoid contamination or partial volume effects from other compartments – including gray matter or multiple intra-voxel fiber populations. However, the dataset collected in³⁵ additionally contains a number of z-stacks that contain crossing fibers (defined as voxels having multiple local maxima in the FOD). Figure 10 shows example z-stacks with crossing fibers (which were not used in the current study), highlighting location, shape of the FOD shown in two views (to highlight crossing and show both in-plane and through-plane fiber orientations), and the derived response function. We also show RGB colormaps (Figure 10D) for visualizing crossing fiber patterns.

Figure 10.

Histologically-derived response functions in crossing fiber regions display unconventional shapes. Three locations determined to contain crossing fiber populations (A-C) are shown, along with the FOD (viewed along the normal to the tissue section) overlaid on RGB color-maps, the FOD shown at an alternate angle (to highlight both in-plane and through plane fibers), and the derived response functions. Many response functions show a “cusp-like” shape axially (indicated by blue ellipses). RGB color-maps of individual voxels (D) highlight orientation estimates (Red: right/left, Green: anterior/posterior, Blue: superior/inferior) of every pixel in the 3d z-stack volume occupied by a fiber and show complex, interwoven, crossing fiber patterns.

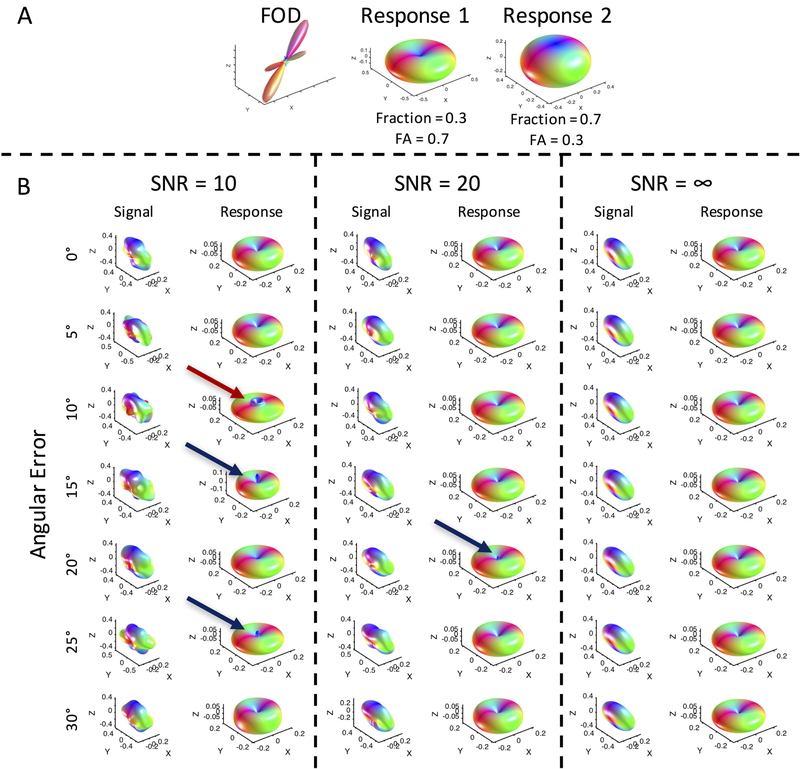
An interesting observation across many of the crossing fiber regions is the presence of a “cusp-like” shape axially, instead of a simple monotonically decreasing function at decreasing polar angles (towards the z-axis). There are several potential explanations. First, this could be a genuine effect of the diffusion process due to multiple compartments, boundaries and restrictions, especially at angles close to (within 5–20 degrees) of the main fiber orientation. This could be caused by a combination of multiple diffusion pools (for example, one or more for each fiber population), where the process cannot be adequately explained by a single axial and radial diffusivity.

Alternatively, this could be an artifact. Investigating the effects of noise and misalignment through simulations on crossing fibers (Figure 11) shows that noise can, indeed, cause a cusp-like shape (red arrow), in addition to the spurious peaks directly along the z axis (blue arrows). However, this generally happened at an SNR lower than in our acquired data, and was relatively infrequently observed in simulations. While we found that this “cusp” did in fact appear in simulations when two different response functions exist within an imaging voxel (Figure 11; also see Supplementary Figure 2 for 100 response function estimations at an SNR=10 when two different response functions exist), the cusp did not appear in simulations when the same response function describes the two crossing fiber populations (see Supplementary Figure 2 for 100 estimations at an SNR=10 when one response function describes both fiber populations). When the signal is generated with two fibers with inherently different response kernels, we believe that the deconvolution procedure can result in erroneous high order coefficient estimates (giving rise to the sharp cusp), and an overall estimate that differs from the two true kernels. With the same response function, the estimate is stable, and noise produces a uniform blurring of the estimate (as in single fiber populations). Thus, the “cusp” is not an artifact of (or exclusive to) histological analysis - appearing in (noisy) simulations when fiber populations exhibit different response functions – but rather an artifact of assuming a single response function within a voxel.

Figure 11.

Noise and misalignment can cause errors in estimating the response functions in crossing fiber regions. FODs and signal at varying noise levels (SNR = ∞, 10, and 20) and misalignments (angular errors of 0–30 degrees) were used to derive response functions. Noise can cause spurious peaks axially (blue arrows), and can result in “cusp-like” shapes near the poles.

Although the focus of this study is not on crossing fibers, we believe that these simulations suggest that in addition to variation within and across brains, response functions can vary within voxels. This is an effect not described or seen in the diffusion literature, as it is not common to assume multiple response functions within a voxel, or assume multiple response functions across a brain. Additionally, the cusp shape was seen (although only in one z-stack, Figure 5B) in single fiber populations, which may suggest that there are indeed two fiber populations with two different response functions, which share the same or similar orientation (a phenomenon expected in the brain⁵⁶), although only one local maximum is identified in the FOD. These results suggest that response functions can vary within a voxel, as well as between voxels.

Conclusion

Here, for the first time, we have empirically estimated the linear relationship (i.e., the fiber response function) between the diffusion signal and the underlying FOD using 3D histological analysis. We find statistically significant differences in response functions between brain regions, which suggests that a single response function may not be appropriate for use throughout the entire brain, and instead a region-wise, or fiber-wise, response may be more appropriate. Additionally, we find different response functions across different brains, as well as evidence that response functions may vary within voxels due to multiple fiber populations. Differences in response functions lead to different FOD reconstructions, which in turn can lead to different tractography results, even though peaks in the FOD retain the same orientation.

Supplementary Material

Supp FigS1

Supplementary Figure 1. Noise in the direction of the FOD peak causes axial spikes in the estimated response function. Signal was corrupted with varying levels of noise (−2 to 10 standard deviations) along the direction of the FOD peak (minimum signal) and at varying angles from the peak (0 to 20 degrees off axis).

Supp figS2

Supplementary Figure 2. Cusps in the estimated response function only appear if the true signal is composed of 2 different true response functions. With two different response functions (A1), and an SNR of 10, cusps in the estimated response function appear frequently (A2, black boxes). Each glyph represents a separate simulation in the presence of noise. However, with the same response function (B1), and an SNR of 10, no cusps are apparent in the estimated response function.

Abbreviations:

FOD

fiber orientation distribution

SD

spherical deconvolution