Significance
For living cells to function, proteins must efficiently navigate the densely packed cytosol. Protein diffusion is slowed down by high viscosity and can come to a complete halt because of nonspecific binding and aggregation. Using molecular dynamics simulations, we develop a detailed description of protein diffusion in concentrated protein solution. We confirm that soluble proteins in concentrated solutions diffuse not as isolated particles, but as members of transient clusters between which they constantly exchange. Nonspecific protein binding and the formation of dynamic clusters nearly quantitatively account for the high viscosity and slow diffusivity in concentrated protein solutions, consistent with the Stokes–Einstein relations.
Keywords: MD simulation, protein crowding, diffusion, viscosity, dynamic clusters
Abstract
We develop a detailed description of protein translational and rotational diffusion in concentrated solution on the basis of all-atom molecular dynamics simulations in explicit solvent. Our systems contain up to 540 fully flexible proteins with 3.6 million atoms. In concentrated protein solutions (100 mg/mL and higher), the proteins ubiquitin and lysozyme, as well as the protein domains third IgG-binding domain of protein G and villin headpiece, diffuse not as isolated particles, but as members of transient clusters between which they constantly exchange. A dynamic cluster model nearly quantitatively explains the increase in viscosity and the decrease in protein diffusivity with protein volume fraction, which both exceed the predictions from widely used colloid models. The Stokes–Einstein relations for translational and rotational diffusion remain valid, but the effective hydrodynamic radius grows linearly with protein volume fraction. This increase follows the observed increase in cluster size and explains the more dramatic slowdown of protein rotation compared with translation. Baxter’s sticky-sphere model of colloidal suspensions captures the concentration dependence of cluster size, viscosity, and rotational and translational diffusion. The consistency between simulations and experiments for a diverse set of soluble globular proteins indicates that the cluster model applies broadly to concentrated protein solutions, with equilibrium dissociation constants for nonspecific protein–protein binding in the Kd ≈ 10-mM regime.
The interior of cells is a densely crowded medium, in which macromolecular concentrations range from 90 mg/mL in red blood cells to 300 mg/mL in the mitochondrial matrix (1, 2). Macromolecular crowding influences the stability of proteins, reaction rates, the catalytic activity of enzymes, protein–protein association, and diffusion (3–13). Excluded volume through steric repulsion (14) and attractive protein–protein interactions as well as hydrodynamic interactions affect protein diffusion (6, 15–19). To address the influence of specific protein–protein interactions on protein diffusion (20), crowded solutions with proteins serving as both agents and readout have been studied (5, 14, 16, 21–30).
Experimental techniques to study the effects of macromolecular crowding on diffusion (15) include tracer boundary spreading (14), light scattering spectroscopy (31), fluorescence recovery after photobleaching (FRAP) (32–34), electron spin resonance (35), single-particle tracking (36), fluorescence correlation spectroscopy (FCS) (37–39), quasielastic neutron backscattering (27, 40), and NMR spectroscopy (24, 41, 42). Particle-based simulations complement these experiments (15), treating the proteins as spheres or ellipsoids (20, 43, 44), with residue-level coarse graining (45–47), or as rigid all-atom models (16, 48). Hydrodynamic interactions contribute significantly to the slowdown of protein diffusion in crowded environments (19). In implicit solvent, they are ignored or approximated via the diffusion tensor (16, 19, 44, 49).
Rapid advances in computing hardware and simulation algorithms have opened up the opportunity to study macromolecular crowding using atomistic molecular dynamics (MD) simulations. Explicit solvent accounts directly for excluded volume effects and hydrodynamic interactions and mediates short-range attractive and long-range electrostatic protein–protein interactions (5, 28–30, 50–52). Here, we use atomistic MD simulations of dense protein solutions to calculate the viscosity and protein diffusion coefficients as a function of protein concentration (Fig. 1). Ubiquitin (UBQ), the third IgG-binding domain of protein G (GB3), hen egg white lysozyme (LYZ), and villin headpiece (VIL) are used as model proteins.
Fig. 1.
Representative simulation snapshots of dense UBQ solution (200 mg/mL, ) and GB3 solution (100 mg/mL, ). Blue lines indicate the periodically replicated simulation boxes. Proteins are depicted as green surface (UBQ) or green ribbons (GB3); and ions as blue and cyan balls, respectively; and TIP4P-D water as red sticks.
Soluble proteins self-associate in concentrated solution to form transient and dynamic clusters (19, 24, 53–58). Clustering has also been reported for membrane proteins (59). The influence of cluster formation on the protein translational and rotational diffusivity has recently been addressed by atomistic simulation studies (29, 30). Here, we build on these findings and put cluster formation in the framework of the Stokes–Einstein relations connecting viscosity, cluster size, and diffusion. Central questions are (i) whether the Stokes–Einstein relations remain valid in concentrated protein solutions (60), (ii) how transient protein interactions affect the diffusivity and apparent hydrodynamic radii of proteins in concentrated solutions (42), (iii) how viscosity depends on protein concentration (39, 61, 62), and (iv) whether colloid models apply to concentrated protein solutions.
To address these questions, we perform extensive MD simulations, develop a cluster model of concentration-dependent protein diffusion, and compare our results to the theoretical predictions for hard-sphere (HS) colloidal suspensions without and with attractive interactions. We put our findings in the context of a wide range of experimental and simulation studies and obtain a remarkably consistent picture of the diffusive dynamics in concentrated solutions of soluble globular proteins.
Results
Shear Viscosity Increases Strongly with Protein Volume Fraction.
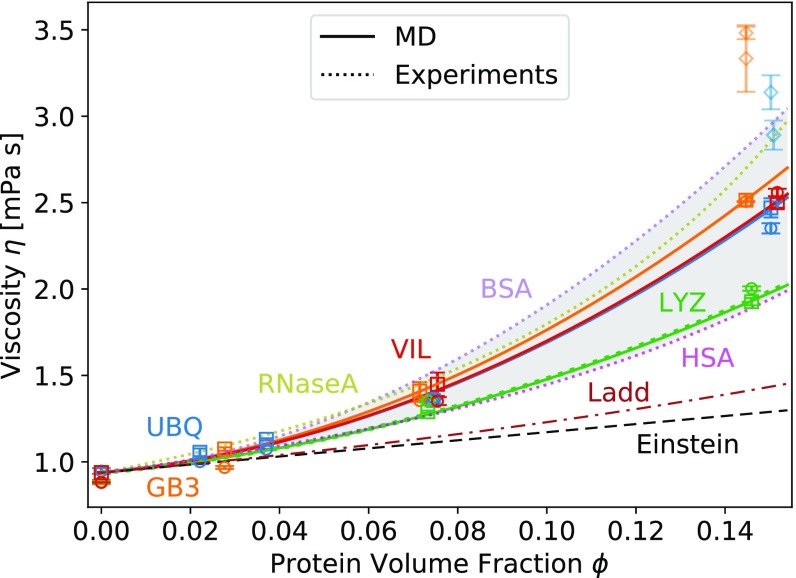
The viscosity of concentrated protein solutions and of TIP4P-D solvent at different ion concentrations was calculated from the pressure tensor fluctuations (SI Appendix, Fig. S5). The quadratic function Eq. 3 fits well over the simulation range, (Fig. 2, squares). We obtained similar fit parameters for UBQ, GB3, and VIL solutions, whereas of the LYZ solutions is significantly lower (Table 1). We calculated mPas from the average viscosity of solutions of TIP4P-D (65) water with 120 mM, 157 mM, and 200 mM NaCl. The values of the calculated LYZ viscosities are in remarkably good agreement with experimentally determined viscosities of the same protein (61). For all four proteins, the viscosities calculated from the pressure tensor fluctuations are bracketed by the experimental values for BSA (62), human serum albumin (HSA), and ribonuclease A (RNaseA) (39) solutions (Fig. 2).
Fig. 2.
Viscosity of concentrated protein solutions as a function of protein volume fraction from all-atom MD simulations (symbols), experiments (dotted lines and gray shading), and HS colloid theory (dashed lines). Blue, UBQ; orange, GB3; green, LYZ; red, VIL. The viscosity was calculated from MD using fluctuations in the pressure tensor (SI Appendix, Eq. S3, squares; fit of Eq. 3, solid lines) and the Stokes–Einstein (SE) relations (Eq. 6; small systems , circles; large systems , diamonds). Green and purple dotted lines: fits of Eq. 3 to experimental data on concentrated LYZ (61) and BSA (62) solutions. Magenta and olive dotted lines: exponential fit [equation 4 in Zorrilla et al. (39)] to the experimental data on HSA and RNaseA solutions (39). Black dashed line: Einstein expression for HS colloidal suspensions (Eq. 4). Brown dashed-dotted line: Ladd expression (63, 64) for HSs (Eq. 5).
Table 1.
Viscosity coefficient , clustering propensity , Baxter parameter , and effective dissociation constant for nonspecific protein–protein binding in concentrated solutions of UBQ, GB3, LYZ, and VIL
| Protein | ,mPas | , mM | , mM | , mM | , mM | , mM | ||||||
| UBQ | 55.3 | 8.2 | 0.12 | 19 | 0.13 | 21 | 0.13 | 21 | 0.49 | 80 | 0.038 | 6.1 |
| GB3 | 63.1 | 8.8 | 0.11 | 26 | 0.19 | 44 | 0.13 | 30 | 0.34 | 80 | 0.033 | 7.6 |
| LYZ | 32.5 | 3.6 | 0.27 | 26 | — | — | — | — | 0.80 | 80 | 0.071 | 6.9 |
| VIL | 56.2 | 11.6 | 0.09 | 28 | — | — | 0.13 | 43 | 0.24 | 80 | 0.037 | 12.2 |
and are from cluster sizes, and are from radial distribution function g(r), and are from (ɸ) at low protein concentration, and are from binding off rates, and and are from viscosity term b.
The viscosity of dense protein solutions exceeds the Einstein prediction for noninteracting HS colloids (66) even after correction for high concentration (63). The pronounced increase in the viscosity with protein concentration beyond the nonlinear HS viscosity model (63) indicates that short-range attractive interactions between the proteins cannot be ignored. For colloids, the second-order term in Eq. 3 for the viscosity is related to the attraction strength, as measured by the osmotic virial coefficient (67–69). In the following, we use in Eq. 3 with values of listed in Table 1 to account for the dependence of the viscosity on the protein volume fraction.
Translational Diffusion Slows Down at High Protein Density.
As shown in Movie S1 for GB3 at 200 mg/mL with proteins, translational and rotational diffusion in concentrated solution is strongly impacted by protein interactions. For each protein in the simulation box, mean-squared displacement (MSD) curves were calculated and fitted to the Einstein relation in SI Appendix, Eq. S5 (SI Appendix, Fig. S6). The MSD curves of the dense protein solutions averaged over starting times and proteins are linear at times exceeding 10 ns. The translational diffusion coefficients obtained by fitting the Einstein relation to the MSD from 10 ns to 30 ns are therefore long-time diffusion coefficients. The MSD curves of the dilute solutions (one protein in the simulation box) are linear at small delays and were fitted to the Einstein relation from 0 ns to 5 ns. We corrected for large finite-size effects using Eq. 7, where we used from the quadratic fit, Eq. 3. The values before finite-size correction are listed in SI Appendix, Table S3.
After finite-size correction, the translational diffusion coefficient of dilute UBQ is consistent with results of NMR spectroscopy (71, 72) in dilute solution. Our calculated values of LYZ are bracketed by measurements in dilute and dense solutions (21, 24, 25, 71–76). The spread in the measured diffusion coefficients of LYZ is possibly due to differences in pH value, ionic strength, and temperature in the different experiments. All simulation values of in the dilute solution are very close to Hydropro (70) predictions (Fig. 3A). The translational diffusion coefficients calculated for the large systems (with proteins) at 200 mg/mL concentration are similar to the values for the small systems () at the same concentration, decreasing slightly with increasing box sizes (number of ). For all proteins, our dynamic cluster model Eq. 8, developed below, accounts nearly quantitatively for the slowdown of translational diffusion with increasing concentration.
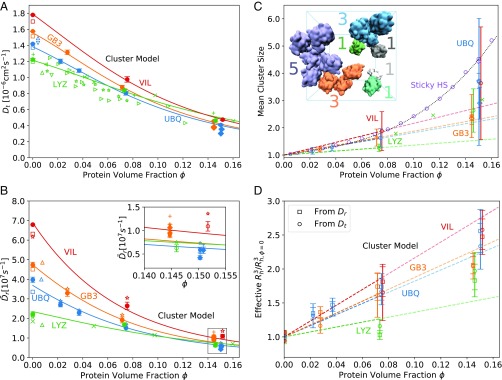
Fig. 3.
Protein diffusion and clustering. (A and B) Concentration-dependent translational (A) and rotational (B) protein diffusion. (A) Dependence of the translational diffusion coefficient on protein volume fraction . Solid circles and diamonds show the finite-size corrected diffusion coefficients of the small systems () and large systems (), respectively. Open squares show Hydropro calculations (70), and other open symbols show experimental data. UBQ data: (71), (72). LYZ data: (73), (74), (75), (21), (76), (24), (25). Lines show the predictions from the dynamic cluster model Eq. 8 with fitted . (B) Dependence of the rotational diffusion coefficients on protein volume fraction . Solid circles and diamonds show the diffusion coefficients obtained from the anisotropic diffusion tensor and corrected for finite-size effects () for the small systems () and large systems (), respectively. Stars () and plus signs () show the finite-size corrected diffusion coefficients from integration of for the small and large systems, respectively. Triangles () represent NMR data for dilute UBQ (blue) (77), dilute GB3 (orange) (78), and dilute LYZ (green) (73) solution. Green crosses () show NMR data for LYZ (25). Open squares show results from Hydropro (70) calculations. Lines show the predictions from the dynamic cluster model Eq. 9 with fitted . B, Inset shows a zoom-in at high protein volume fraction. (C and D) Protein-cluster model. (C) Dependence of mean cluster size on protein volume fraction [circles for small systems (), diamonds for large systems ()]. The dashed line shows a linear fit to the data at 0–100 mg/mL with binding propensity listed in Table 1. Purple circles and diamonds are results from a Monte Carlo simulation of Baxter’s sticky HSs with and particles in the box, respectively, using and finite-range attractive interactions up to 1.05 . The dotted curve shows the fit to the MC data up to . Green crosses show experimental data on LYZ cluster formation (79). (C, Inset) Representative simulation snapshot of dense UBQ solution (100 mg/mL). Blue lines indicate the periodically replicated simulation boxes. Colors and colored labels indicate transient UBQ protein clusters and cluster size , respectively (solvent not shown). (D) Dependence of reduced hydrodynamic radii cubed, , on protein volume fraction . The effective is calculated from the Stokes–Einstein relations for translation, Eq. 10 (circles), and for rotation, Eq. 11 (squares). The dashed lines show the prediction from C with values from Table 1.
Crowding Strongly Affects Rotational Diffusion.
Rotational diffusion coefficients and of the dense protein solutions were obtained by fitting quaternion correlations (80) and by integrating the orientational correlation function , respectively, over the time range 0–100 ns (SI Appendix). Fits to elements of the quaternion covariance matrix are shown in SI Appendix, Fig. S7. The resulting rotational diffusion coefficients – are shown in SI Appendix, Fig. S8. Fits to the orientational correlation function are shown in SI Appendix, Fig. S9.
Orientationally averaged diffusion coefficients and after finite-size correction (81) decrease strongly with increasing (Fig. 3B). At infinite dilution, the UBQ and GB3 results are bracketed by the rotational diffusion coefficients obtained from Hydropro (70) calculations and from NMR spectroscopy (77, 78). The experimental rotational diffusion coefficient in dilute LYZ solution reported in ref. 73 is slightly lower than the calculated values, whereas the rotational diffusion coefficients reported in ref. 25 agree well with our data at all protein concentrations. The calculated rotational diffusion coefficients of dilute LYZ and VIL are in fair agreement with Hydropro (70) predictions. As for the translational diffusion, the rotational diffusion coefficients calculated for the large systems () at 200 mg/mL concentration are close to the values of the small systems () at the same concentration, being slightly lower for UBQ and slightly higher for GB3. The dynamic cluster model Eq. 9 predicts the rotational diffusion coefficients of UBQ, GB3, VIL, and LYZ accurately over the entire concentration range, except for the LYZ solution at 100 mg/mL concentration, where the effect of the weak clustering (Fig. 3C) is somewhat overestimated.
Diffusion in Dense Protein Solutions Follows the Stokes–Einstein Relation.
Given translational and rotational diffusion coefficients, the viscosity can be estimated from the Stokes–Einstein relations (Eq. 6). For all small systems (), we observe excellent agreement between the viscosity calculated from the autocorrelation of the pressure tensor fluctuations and from the diffusion coefficients (Fig. 2), indicating that the dense protein solutions show normal (Stokes–Einstein) diffusion for all protein volume fractions considered here. For the large systems (), slight deviations in and (Fig. 3) lead to strongly overestimated viscosity (diamonds in Fig. 2). Therefore, in practical calculations we advise against calculating the viscosity via the Stokes–Einstein relation, Eq. 6, because the results are quite sensitive to the uncertainties in and .
Hydrodynamic Radius, Cluster Size, and Diffusion Are Related.
We obtained very similar hydrodynamic radii from the Stokes–Einstein relations for translation and rotation, Eqs. 10 and 11, respectively (Fig. 3D). Therefore, after correcting for finite-size effects with actual shear viscosities , both translational diffusion and rotational diffusion follow Stokes–Einstein theory even at high protein volume fractions. Only values for the small systems () are shown, because only for these systems was the computationally expensive calculation of the viscosity from the pressure fluctuation autocorrelation function performed.
If the increase in viscosity were to capture all factors that contribute to the concentration-dependent slowdown of protein diffusivity, then the hydrodynamic radius, calculated from the Stokes–Einstein relations, Eqs. 10 and 11, should remain constant at all concentrations. Instead, we observe that the effective hydrodynamic radius cubed, , increases with protein volume fraction . This dependence is consistent with protein cluster formation (Fig. 3C). Indeed, when calculating the cluster size distribution based on an -carbon distance cutoff criterion, the cluster size distribution shifts to larger clusters at increasing protein volume fraction (SI Appendix, Fig. S10). For protein concentrations up to 100 mg/mL, the mean number of proteins in a cluster grows linearly as , with clustering propensity listed in Table 1 (Fig. 3C). The highest concentration (200 mg/mL) was not included in the fit, because the close proximity of proteins causes a significant dependence of the calculated mean cluster size on the cutoff criterion (SI Appendix, Fig. S11). Given the linear increase of cluster size with protein volume fraction , the effective hydrodynamic radius cubed should likewise increase linearly with , , where we assumed that the hydrodynamic radius cubed is proportional to the cluster volume. Remarkably, the dynamic cluster model accounts nearly quantitatively for the relative increase of (Fig. 3D).
As shown in SI Appendix, the clustering propensity is related to an effective dissociation constant via the protein volume , . Given protein volumes , , , and (SI Appendix, Fig. S12), we obtain dissociation constants of mM, mM, mM, and mM with Avogadro’s constant (Table 1).
Effective Viscosity Accounts for Hydrodynamic Interactions.
We investigated whether the effective viscosity captures the indirect (hydrodynamic) effects of increased protein concentration and cluster formation, i.e., all of the effects that are not accounted for by an increased effective hydrodynamic radius. For each protein, we recorded the times at which it is free, i.e., not in any cluster (SI Appendix, Fig. S13). For these trajectory segments, we calculated MSD curves (SI Appendix, Fig. S14) and translational diffusion coefficients . could not be reliably determined for the proteins at the highest concentration (200 mg/mL) due to insufficient sampling of unbound proteins. For all four protein species, the product is approximately constant as a function of concentration (SI Appendix, Fig. S15). We conclude that the effective viscosity indeed accounts for the hydrodynamic contributions to the diffusivity slowdown.
Displacement Pair Correlation Shows Contribution from Direct and Hydrodynamic Interactions.
We calculated the displacement pair correlation introduced by Ando and Skolnick (19) (SI Appendix). We analyzed the protein pair correlation for pairs at distances 0.6–3 nm. At distances corresponding to cluster formation, we observed highly correlated motion for all protein pairs at all concentrations and time delays (SI Appendix, Fig. S16). At increasing pair distance (∼2–3 nm), the pair correlation decreased gradually.
Protein Binding Interfaces.
The interactions between the proteins in clusters were loose but not entirely random in their orientation (SI Appendix, Fig. S17). For UBQ, the preferred binding interface coincides remarkably well with the noncovalent dimer interface reported from NMR measurements (82), more or less independent of protein concentration (Fig. 4). It includes residues 8–11, 20, 24, 25, 28, 31–42, 46–49, 54–60, and 71–76. The C-terminal tail (residues 71–76) and an adjacent relatively hydrophobic surface patch show strong involvement, in line with experimental evidence (82). In dense LYZ solutions, we observed that residues Asp48 and Arg73 contribute most to LYZ–LYZ interaction (SI Appendix, Fig. S17). In a Brownian dynamics study (83), these residues were found to play crucial roles in the formation of a LYZ–LYZ encounter complex.
Fig. 4.
UBQ protein–protein interaction interfaces. Red, white, and blue indicate strong, intermediate, and weak involvement in UBQ–UBQ contacts. The NMR experimental noncovalent dimer interface is derived from Liu et al. (82). The rightmost view indicates hydrophobic (white), polar (green), acidic (red), and basic (blue) surface residues. C indicates the C terminus.
Colloidal Suspension Model.
Baxter’s attractive (sticky) HSs (68, 69, 84–86) are widely used as a model for suspensions of interacting colloidal particles. Their association constant is related to the dimensionless Baxter parameter as (derived in SI Appendix), where is the HS volume. Low indicates high protein stickiness. We conducted Monte Carlo (MC) simulations of Baxter sticky HSs with and finite-range attractive interactions up to 1.05 of and particles in a simulation box. The mean cluster size grows linearly at low protein concentrations, deviating for (Fig. 3C). Considering the rough approximations of this model, the cluster sizes of MC simulations of sticky HSs are in surprisingly good agreement with those of the atomistic MD simulations. We can also relate and to the second virial coefficient (69) . Integration of the radial distribution function of the UBQ centers at 30 mg/mL and GB3 centers at 39 mg/mL over the first peak gives us values of and , respectively (SI Appendix, Fig. S18) (no data for LYZ and VIL, as we did not conduct simulations at low concentrations for these proteins). With and and under the assumption of the sticky HS model, we thus obtain mM and mM, in good agreement with the values from the cluster model (Table 1).
For the sticky HS model, Cichocki and Felderhof (68) derived a low-density expansion of the long-time single-particle diffusion coefficient in terms of the volume fraction,
| [1] |
We determined the slope (Fig. 5A, dashed-dotted line) from a fit to our protein simulation data for UBQ and GB3 at low , which gives us a value of . From , , and , we obtain apparent dissociation constants of mM and mM that are in good agreement with the values obtained directly from the cluster model and by integration of (Table 1). Since the relative concentration-dependent slowdown of VIL diffusivity is similar to that of UBQ and GB3 (Fig. 5A), we also calculated mM using the same . This does not apply for LYZ solutions.
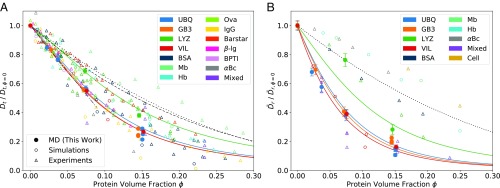
Fig. 5.
Concentration-dependent protein diffusion. (A) Dependence of the normalized translational diffusion coefficient on protein volume fraction . Solid circles show MD data from this study. Open circles show data from simulation studies (16, 26, 29, 87). Open triangles denote data from experimental studies (21–27, 75, 76, 88–93). Hb, hemoglobin; Mb, myoglobin; “Mixed,” CI2 in different dense protein solutions; Ova, ovalbumin. The solid curves show the prediction of the dynamic cluster model (Eq. 8, no adjustable parameters) for UBQ, GB3, LYZ, and VIL solutions, indicated by corresponding colors. The dashed and dotted curves show the slowdown of predicted from colloid theory on noninteracting HSs by van Blaaderen et al. (94) and Tokuyama and Oppenheim (95), respectively (SI Appendix). The dashed-dotted line shows a linear fit to of UBQ and GB3 at . A plot with experimental studies resolved by symbols is shown in SI Appendix, Fig. S20A. (B) Dependence of the normalized rotational diffusion coefficient on protein volume fraction . Solid circles show MD data from this study. Open circles show data from simulation studies (16, 29). Open triangles denote data from experimental studies (22, 25, 96). “Cell”: Hb or Mb in different cell types. The solid curves show the prediction of the dynamic cluster model (Eq. 9, no adjustable parameters) for UBQ, GB3, LYZ, and VIL solutions, indicated by corresponding colors. The dashed curve shows the slowdown of predicted from colloid theory for noninteracting HSs (97) (SI Appendix). A plot with experimental studies resolved by symbols is shown in SI Appendix, Fig. S20B.
Cichocki and Felderhof (68) also evaluated the quadratic term in the viscosity expansion,
| [2] |
Equating with the coefficient from the term in the viscosity expansion fitted to MD data (Eq. 3 and Table 1), we obtain values of and (Table 1), which are again close to those obtained from the cluster model, , and (Table 1).
Dissociation Constant from Off Rate of Nonspecific Complexes.
The cumulative distribution functions of the lifetimes of protein pairs (SI Appendix, Fig. S19) show that most pairs stay together for 1–50 ns, indicating dynamic clustering according to Liu et al.’s (24) terminology. The lifetimes of protein pairs are independent of the protein concentration, supporting the presence of dynamic protein clusters rather than protein aggregation. From the cumulative distribution function, we obtained the same median protein pair lifetime of ns for all proteins and concentrations and defined an off rate for nonspecific complexes as s−1, assuming exponential kinetics. Assuming in addition a Smoluchowski on rate, , and substituting the Stokes–Einstein relation for translational diffusion, we expect an on rate for nonspecific complexes of s−1. The resulting “kinetic” dissociation constant mM agrees well with those obtained from the other methods (Table 1).
Discussion
Relative Slowdown in Diffusion Is Consistent with Experiment and Cluster Model.
The relative slowdown of translational and rotational diffusion of UBQ, GB3, LYZ, and VIL at increasing protein volume fraction is within the range of published experimental and simulation results. Literature data on the protein-concentration dependence of were normalized to . If only protein mass concentrations were given, protein volume fractions were approximated according to the dependence of UBQ volume fraction on UBQ mass concentration.
The dependence of on protein crowding is surprisingly consistent across the different studies (Fig. 5A and SI Appendix, Fig. S20A), considering that they cover both experiments and simulations and report results for proteins of different size, shape, and charge, for different model resolution and different experimental conditions (temperature, pH value). In particular, our simulation results for of dense VIL solutions are in line with a recent study by Nawrocki et al. (29). Likewise, the slowdown of of dense LYZ solutions agrees with the majority of experimental data on LYZ diffusion (green triangles in Fig. 5A and open green symbols in SI Appendix, Fig. S20A). We conclude that the slowdown of translational diffusion in concentrated protein solutions is a general feature of soluble proteins and that the extent of the slowdown is governed by the clustering propensity of the protein (notwithstanding additional shape effects, which may not be captured by our choice of globular proteins). We also conclude that the colloidal models of noninteracting HSs (94, 95) (SI Appendix and dashed and dotted lines in Fig. 5) significantly underestimate the slowdown of translational diffusion of most proteins studied.
We collected data on the slowdown of the rotational diffusion from experimental and simulation studies and normalized the diffusion coefficients to . The slowdown of is less consistent in the considered studies (Fig. 5B and SI Appendix, Fig. S20B) than the slowdown of . We suggest that the greater variability in the slowdown of is due to the dependence of compared with the dependence of in the Stokes–Einstein relations. Up to intermediate concentration (100 mg/mL), the slowdown of in LYZ solutions, although in line with experiment (25), does not abide by the cluster model prediction, even though the model takes into account the reduced clustering propensity of the LYZ protein, possibly from its high positive charge (+9) (Fig. 3C and in Table 1). Indeed, the slowdown of at low LYZ concentrations appears to be better represented by a noninteracting HS model. In our simulations, LYZ forms very few clusters at intermediate (100 mg/mL) concentration. At higher concentration (200 mg/mL), we find a significant contribution of higher cluster numbers () (SI Appendix, Fig. S10). From small-angle X-ray scattering data, Stradner et al. (79) inferred slightly larger LYZ clusters (green crosses in Fig. 3C) compared with our simulations. However, the higher pH in their experiments may have reduced the net protein charge and increased cluster formation. Scattering data were subsequently found to be compatible with lysozyme being largely repulsive (98).
We stress that our dynamic cluster model (Eqs. 8 and 9 and solid lines in Figs. 3 A and B and 5) predicts the relative slowdown in diffusion based on protein cluster size and viscosity. In light of this, the prediction of the model represents the observed and calculated slowdown in diffusion strikingly well. Our cluster model relates differences in the relative diffusivities of different proteins to differences in their nonspecific interactions. This observation provides a physical basis for the protein-dependent concentration scaling factor introduced by ref. 21 to establish consistency with a HS diffusion model (95).
Separating the Effects of Clustering and Hydrodynamics.
Using an elegant MD simulation setup, Nawrocki et al. (30) found that direct protein interactions are the dominant contributors to the slowdown of rotational diffusivity, whereas hydrodynamics play only a minor role. Here, we could show that the effective viscosity accounts for the indirect, hydrodynamic effects of dense solutions on the diffusivity slowdown (SI Appendix, Fig. S15). In dense UBQ, GB3, and VIL solutions at 200 mg/mL, the viscosity is ∼2.5-fold increased compared to the solvent viscosity (Fig. 2). The translational diffusion decreases by a factor of ∼4, whereas the rotational diffusion decreases by a factor of ∼6 (Fig. 3 A and B). The direct effect of protein clustering (i.e., the increase in the effective hydrodynamic radius) accounts for an additional factor ∼ on translational diffusion and a factor ∼ on rotational diffusion. We therefore find that direct clustering interactions contribute to ∼40% and 50% of the total slowdown in translational and rotational diffusivity, respectively, of dense UBQ, GB3, and VIL solutions.
The displacement pair correlation function assesses concerted protein motion and is used to distinguish short-range and long-range interactions in simulations of crowded systems (19). At short distances, the proteins form clusters, and their motion is highly correlated (SI Appendix, Fig. S16). The pair correlation decreases at larger protein pair distances, because the short-range interactions fade out and only contributions from long-range effects (electrostatics, hydrodynamics) remain. Interestingly, at low protein concentrations (30–50 mg/mL), the protein motions are correlated up to high distances, whereas the correlation decreases quickly with increasing distance at high protein concentration. This suggests that the motion of proteins at low concentration is more effectively coupled by hydrodynamic and electrostatic forces. At high concentrations, the coupled motion of a protein pair at short distances appears to be effectively quenched by interference of competing proteins. This trend is surprising, because proteins may serve as bridging intermediates at high concentrations, which should effectively increase the pair correlation for the distances considered.
Protein Solutions as Colloidal Suspensions with Attractions.
The effective dissociation constants and Baxter parameters were derived according to the low-concentration behavior of the sticky-HS model for attractive colloidal particles. The values for nonspecific protein–protein binding derived from the structure, dynamics, and viscosity of the protein solutions are fairly consistent with each other (Table 1). As listed in Table 1, estimates from , , , , and vary within about one order of magnitude for a given protein. The corresponding values of also agree well with each other. Interestingly, the decreased clustering propensity of LYZ solutions compared with UBQ, GB3, and VIL solutions is reflected only by a higher , but not by an increase in the effective dissociation constant , because the increased value of LYZ is compensated by its larger volume . In turn, this results in a relatively small for LYZ. For our limited set of four proteins, protein stickiness decreases with size, thereby ameliorating the aggregation problem for large proteins pointed out by Ando and Skolnick (19).
The formation of 3D clusters explains the strong increase of the mean cluster size in sticky-HS solutions at large (Fig. 3C). Sticky spheres have no orientational preference, which allows the formation of compact clusters. By contrast, protein–protein interactions are directional and only some protein orientations result in favorable interactions (SI Appendix, Fig. S17). The orientational preference disfavors the formation of compact clusters, as can be seen in the formation of only protein connections for a cluster of size up to intermediate (100 mg/mL) protein concentration (SI Appendix, Fig. S21). In consideration of these differences, should be considered an effective parameter whose value depends on the property that is fitted and on the fit range. Therefore, we emphasize that the sticky HS model is only a rough approximation of a complex protein solution, which nonetheless explains the behavior of the complex protein systems surprisingly well up to intermediate protein concentration.
From light-scattering experiments, Scherer et al. (57) estimated for concentrated monoclonal antibody mAB2 solution (150 mM NaCl concentration), which is of the same order of magnitude as our simulation results (Table 1). They observed a strong dependence of on the ionic strength, ranging from ∼1,000 to ∼0.5 when increasing the ion concentration from 40 mM to 600 mM. It will be interesting to study the effect of varying ionic strengths on by MD simulations. In contrast to mAB2 solutions, the scattering data for antibody mAB1 solutions could not be represented by Baxter’s sticky HS model due to stronger (and possibly long-range) interactions, whereas an alternative model based on two oligomeric species (57, 58) fitted the data well. This suggests that only weakly interacting proteins are well described by the attractive HS model (57).
Limitations.
The generality of our findings on the connection of cluster size, viscosity, and diffusion is subject to several limitations.
All four proteins studied here are small and globular. This justifies the use of averaged rotational diffusion coefficients and facilitates the comparison with colloid theory, but does not consider the effects of different shapes on the concentration dependence of diffusion. Dense solutions of larger proteins and proteins with varying degree of anisotropy will have to be simulated atomistically to address these issues.
Slight finite-size effects on protein clustering and diffusivity were observed. In the smallest simulation of dense protein solutions (UBQ at 200 mg/mL with proteins), occasional formation of a box-spanning cluster was observed, as seen in the contribution of cluster sizes to the cluster size distribution for this system (SI Appendix, Fig. S10). This artifact was not seen in any of the other simulations and does not appear to strongly affect the diffusivity and viscosity of the UBQ solution (Figs. 2 and 3). The translational and rotational diffusion coefficients at high concentration (200 mg/mL) vary slightly for higher protein numbers in the simulation box. The absolute deviations in and between small and large systems are small. However, the relative deviations in and are substantial, overestimating the viscosity calculated from the Stokes–Einstein relations (Fig. 2, circles). On the one hand, we attribute these deviations to incomplete sampling of the extremely large simulation systems. We expect that the simulations with large system size () take more time to equilibrate, thus introducing a bias on the diffusion coefficients, which is not accounted for by the current finite-size corrections (Eq. 7 and SI Appendix, Eq. S10). On the other hand, we observe a significant tail to high cluster numbers in the cluster distribution in these systems (SI Appendix, Fig. S10). Whereas the mean cluster sizes in the small and large systems are similar (Fig. 3C), occasional large clusters in the large systems appear to slightly suppress diffusion in a way not captured by the smaller simulation systems. Assessing and quantifying both effects in detail would merit a separate study.
Based on the clustering data for UBQ and GB3 solutions, we assume that the cluster size increases linearly with protein concentration up to intermediate (100 mg/mL) protein concentration. Although this simple model works surprisingly well in explaining our calculated diffusion data even at higher concentrations (Fig. 3 A and B), the actual functional dependence of cluster size on protein concentration may be nonlinear and depend on the specifics of the system (protein type, pH, ionic strength, temperature). Much longer simulations would be needed to precisely determine the cluster distribution and mean cluster size at high protein concentration.
The representation of dense protein solutions by Baxter’s sticky HS suspensions is limited to weak, short-range protein–protein interactions. As scattering data show (57), the sticky HS model does not represent experimental data well for strongly interacting particles or particles with significant attractive long-range (electrostatic) interactions. In our simulations and in cellular conditions, these interactions are effectively shielded by the ions in the solution, making this limitation less relevant in vivo. Nevertheless, it would be interesting to test the applicability of the cluster model for these cases.
Conclusions
By performing all-atom molecular dynamics simulations of dense protein solutions, we found an increase in the viscosity of the solutions at higher protein volume fractions, consistent with experimental results (39, 61, 62). This increase is considerably higher than predicted by colloidal models of noninteracting HSs, stressing the importance of measuring or calculating rather than approximating the viscosity at protein volume fractions approaching cellular crowding conditions. We calculated translational and rotational diffusion coefficients and corrected them for finite-size effects using the respective viscosity of the solution. Translational diffusion and rotational diffusion are strongly affected by protein crowding. For LYZ solutions, experimentally measured diffusion coefficients are available also at high concentration and are in excellent agreement with our simulation data (Fig. 3 A and B). We calculated effective hydrodynamic radii using the Stokes–Einstein relations and found that a similar increase in the effective hydrodynamic radius can be inferred from the slowdown of translational and rotational diffusion caused by the formation of dynamic protein clusters. Indeed, establishing consistency with the Stokes–Einstein relations requires accounting for protein cluster formation (42) as a result of attractive interactions (60). Overall, we conclude that the concentration dependence of protein cluster size, the translational and rotational diffusion coefficient, and viscosity are consistent with each other (exception: LYZ at 100 mg/mL) and—for the proteins studied here—are explained well by Baxter’s sticky HS model of colloidal suspensions.
Representing the diffusion data in reduced form as a function of protein volume fraction showed that the relative slowdown in translational diffusion is consistent with results from previous studies. The relative slowdown in rotational diffusion shows a larger spread, consistent with the notion that rotational diffusivity depends more sensibly on clustering propensity and thus on the specifics of the protein interactions. Dynamic cluster formation has recently been observed also for membrane proteins (59) and shown to slow down rotational diffusion. In light of our analysis in terms of the cluster and colloidal models, we would expect similar affinities mM for other abundant, soluble proteins with similar size and shape. It will be interesting to explore the limits of our cluster model, i.e., if the cluster model remains valid for large, anisotropic, and more sticky proteins. In this context, the effect of liquid–liquid phase separation (99) on protein diffusivity is an exciting question to address.
We find that the proteins favor certain orientations for interactions and our findings on UBQ contact interfaces are consistent with experiments (82). The protein interactions lead to highly correlated motion at short distances and the correlation is sustained up to larger distances at low concentration. At high concentration, despite increased protein cluster formation, the pair correlation (19) at similar distances is decreased.
In the cellular environment, the situation is complicated by molecular heterogeneity, reactions, partitioning in microenvironments by phase separation, interactions with membranes and structural proteins, and other factors (99–102). Nevertheless, the findings here and in earlier work (103), as well as the observation that diffusion in cell lysates is similar to diffusion in crowded protein solutions (22), suggest that both in concentrated solution and in cells, proteins appear to diffuse not as isolated particles, but as members of dynamic clusters between which they constantly exchange. From the consistency of our diffusivity results with experiments in solution and on the basis of our cluster model, we conclude that—in crowded conditions corresponding to the cellular concentration—the strength of nonspecific protein–protein interactions for abundant proteins such as UBQ should correspond to low-millimolar binding.
We can now carry out atomistic MD simulations of crowded simulations at an unprecedented scale (29), here with up to 540 proteins and 3.6 million atoms in the box simulated over microseconds. Atomistic simulations of solutions of protein mixtures, possibly reflecting the distribution of proteins in the cell, no longer seem out of reach (52). Developments in nucleic acid force fields (104–109) will make it attractive to test the above findings on dense nucleic acid solutions and dense protein–nucleic acid mixtures. Ultimately, the macromolecular diversity in the cell will have to be considered (101) to predict passive diffusion in vivo.
SI Appendix.
SI Appendix contains supplementary text; SI Appendix, Figs. S1–S21; SI Appendix, Tables S1–S3; Movie S1; and SI references.
Movie S1.
Shown is an atomistic MD simulation of 540 GB3 proteins in concentrated solution (200 mg/mL) at simulation time 0–500 ns. The fully flexible proteins are shown in surface representation and differentiated by color. For clarity, water and ions are omitted. Proteins that seem to appear and disappear traverse the periodic boundaries.
Materials and Methods
MD Simulations of Dense Protein Solutions.
We performed all-atom MD simulations of solutions of human UBQ [PDB code 1UBQ (110)], GB3 [PDB code 1P7F (111)], LYZ [PDB code 1E8L (112)], and VIL [PDB code 1VII (113)] at up to five different densities with (UBQ) and (GB3, LYZ, VIL) proteins in the simulation box. In addition, the most concentrated UBQ and GB3 solutions (200 mg/mL) were simulated with large simulation boxes containing from to proteins (SI Appendix, Table S1). To mimic an infinitely dilute system, MD simulations with a single protein copy were carried out. The simulation procedures are detailed in SI Appendix.
Viscosity Calculation and Approximations.
The low-frequency, low-shear viscosity of dense protein solutions differs from the viscosity of the pure solvent consisting of only water and ions. We determined and from MD simulations by integration of the autocorrelation functions of the pressure tensor fluctuations (114), as detailed in SI Appendix. The dependence of on the protein volume fraction is well captured by a quadratic function,
| [3] |
with parameter fitted to the calculated viscosities, the solvent viscosity averaged over the NaCl concentrations used in this study, and the coefficient 2.5 adopted from Einstein’s colloid theory (66). The experiments of Woutersen and De Kruif (69) have shown that the coefficient increases with the strength of attractions between colloidal particles.
We compared the calculated viscosities to predictions from colloid theory. At low solute volume fractions , Einstein (66) predicted a linear dependence of the viscosity of HS suspensions on ,
| [4] |
For higher solute volume fractions, this expression was modified by Ladd (63, 64) to
| [5] |
with .
In addition, we also estimated the viscosity by assuming that the Stokes–Einstein relations for rotational diffusion, , and for translational diffusion, , are exactly satisfied, such that
| [6] |
where the bar indicates that we average over orientational asymmetries.
Translational Diffusion.
Translational diffusion coefficients were obtained for each protein density by fitting the Einstein relation to the MSD, as detailed in SI Appendix. The diffusion coefficients were corrected for finite-size effects using (115)
| [7] |
with and the edge length of the cubic simulation box. In the simulations of dilute proteins, where the protein radius is comparable to the box dimension , we used the expanded correction, (115).
We compared the calculated translational diffusion coefficients to the predictions of a dynamic cluster model without any free parameters,
| [8] |
where is the mean cluster size, as defined in SI Appendix and calculated directly from the MD structures. This model is based on the assumption that the slowdown in translational diffusion is linked to the increase in the effective hydrodynamic radius and in the viscosity via the Stokes–Einstein relation for translational diffusion. We also compared the reduced translational diffusion coefficients to the approximate form for monodisperse noninteracting HS colloidal suspensions (94, 95) (SI Appendix).
Rotational Diffusion.
Rotational diffusion coefficients were calculated following the procedure by Linke et al. (80, 116), as detailed in SI Appendix. Additionally, an effective rotational diffusion coefficient was obtained from fits to the orientational correlation function (117, 118), as detailed in SI Appendix.
We compared the calculated rotational diffusion coefficients to the predictions of the dynamic cluster model,
| [9] |
where we again assumed the Stokes–Einstein relation to apply with a hydrodynamic radius cubed proportional to the mean cluster size . We also compared the reduced rotational diffusion coefficients to predictions from colloidal models of noninteracting HSs (97) (SI Appendix).
Hydrodynamic Radius.
We solved the Stokes–Einstein relations for translational and rotational diffusion to define effective hydrodynamic radii for translation,
| [10] |
and for rotation,
| [11] |
Gaussian error propagation of , , and was employed to estimate the errors of and .
Supplementary Material
Acknowledgments
We thank Jürgen Köfinger and Martin Vögele for helpful discussions and technical assistance and Kara Grotz for help with the simulation setup. This research was supported by the Max Planck Society (S.v.B., M.S., M.L., and G.H.), the Human Frontier Science Program RGP0026/2017 (S.v.B. and G.H.), and the Landes-Offensive zur Entwicklung Wissenschaftlich-ökonomischer Exzellenz (LOEWE) Dynamem program of the state of Hesse (M.S. and G.H.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. H.-X.Z. is a guest editor invited by the Editorial Board.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1817564116/-/DCSupplemental.
References
- 1.Zimmerman SB, Trach SO. Estimation of macromolecule concentrations and excluded volume effects for the cytoplasm of Escherichia coli. J Mol Biol. 1991;222:599–620. doi: 10.1016/0022-2836(91)90499-v. [DOI] [PubMed] [Google Scholar]
- 2.Ellis RJ. Macromolecular crowding: Obvious but underappreciated. Trends Biochem Sci. 2001;26:597–604. doi: 10.1016/s0968-0004(01)01938-7. [DOI] [PubMed] [Google Scholar]
- 3.Zimmerman SB, Minton AP. Macromolecular crowding: Biochemical, biophysical, and physiological consequences. Annu Rev Biophys Biomol Struct. 1993;22:27–65. doi: 10.1146/annurev.bb.22.060193.000331. [DOI] [PubMed] [Google Scholar]
- 4.Minton AP. The influence of macromolecular crowding and macromolecular confinement on biochemical reactions in physiological media. J Biol Chem. 2001;276:10577–10580. doi: 10.1074/jbc.R100005200. [DOI] [PubMed] [Google Scholar]
- 5.Feig M, Sugita Y. Variable interactions between protein crowders and biomolecular solutes are important in understanding cellular crowding. J Phys Chem B. 2012;116:599–605. doi: 10.1021/jp209302e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mittal S, Chowhan RK, Singh LR. Macromolecular crowding: Macromolecules friend or foe. Biochim Biophys Acta Gen Subj. 2015;1850:1822–1831. doi: 10.1016/j.bbagen.2015.05.002. [DOI] [PubMed] [Google Scholar]
- 7.Ellis RJ, Minton AP. Protein aggregation in crowded environments. Biol Chem. 2006;387:485–497. doi: 10.1515/BC.2006.064. [DOI] [PubMed] [Google Scholar]
- 8.Zhou HX. Influence of crowded cellular environments on protein folding, binding, and oligomerization: Biological consequences and potentials of atomistic modeling. FEBS Lett. 2013;587:1053–1061. doi: 10.1016/j.febslet.2013.01.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Park S, Agmon N. Theory and simulation of diffusion-controlled Michaelis-Menten kinetics for a static enzyme in solution. J Phys Chem B. 2008;112:5977–5987. doi: 10.1021/jp075941d. [DOI] [PubMed] [Google Scholar]
- 10.Guseman AJ, Perez Goncalves GM, Speer SL, Young GB, Pielak GJ. Protein shape modulates crowding effects. Proc Natl Acad Sci USA. 2018;115:10965–10970. doi: 10.1073/pnas.1810054115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Blanco MA, Perevozchikova T, Martorana V, Manno M, Roberts CJ. Protein-protein interactions in dilute to concentrated solutions: -Chymotrypsinogen in acidic conditions. J Phys Chem B. 2014;118:5817–5831. doi: 10.1021/jp412301h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kekenes-Huskey PM, Eun C, McCammon JA. Enzyme localization, crowding, and buffers collectively modulate diffusion-influenced signal transduction: Insights from continuum diffusion modeling. J Chem Phys. 2015;143:94103. doi: 10.1063/1.4929528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Benton LA, Smith AE, Young GB, Pielak GJ. Unexpected effects of macromolecular crowding on protein stability. Biochemistry. 2012;51:9773–9775. doi: 10.1021/bi300909q. [DOI] [PubMed] [Google Scholar]
- 14.Muramatsu N, Minton AP. Tracer diffusion of globular proteins in concentrated protein solutions. Proc Natl Acad Sci USA. 1988;85:2984–2988. doi: 10.1073/pnas.85.9.2984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Dix JA, Verkman A. Crowding effects on diffusion in solutions and cells. Annu Rev Biophys. 2008;37:247–263. doi: 10.1146/annurev.biophys.37.032807.125824. [DOI] [PubMed] [Google Scholar]
- 16.Mereghetti P, Wade RC. Atomic detail Brownian dynamics simulations of concentrated protein solutions with a mean field treatment of hydrodynamic interactions. J Phys Chem B. 2012;116:8523–8533. doi: 10.1021/jp212532h. [DOI] [PubMed] [Google Scholar]
- 17.Ansari A, Jones CM, Henry ER, Hofrichter J, Eaton WA. The role of solvent viscosity in the dynamics of protein conformational changes. Science. 1992;256:1796–1798. doi: 10.1126/science.1615323. [DOI] [PubMed] [Google Scholar]
- 18.Elcock AH. Models of macromolecular crowding effects and the need for quantitative comparisons with experiment. Curr Opin Struct Biol. 2010;20:196–206. doi: 10.1016/j.sbi.2010.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ando T, Skolnick J. Crowding and hydrodynamic interactions likely dominate in vivo macromolecular motion. Proc Natl Acad Sci USA. 2010;107:18457–18462. doi: 10.1073/pnas.1011354107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Trovato F, Tozzini V. Diffusion within the cytoplasm: A mesoscale model of interacting macromolecules. Biophys J. 2014;107:2579–2591. doi: 10.1016/j.bpj.2014.09.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Nesmelova IV, Skirda VD, Fedotov VD. Generalized concentration dependence of globular protein self-diffusion coefficients in aqueous solutions. Biopolymers. 2002;63:132–140. doi: 10.1002/bip.10023. [DOI] [PubMed] [Google Scholar]
- 22.Wang Y, Li C, Pielak GJ. Effects of proteins on protein diffusion. J Am Chem Soc. 2010;132:9392–9397. doi: 10.1021/ja102296k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Porcar L, et al. Formation of the dynamic clusters in concentrated lysozyme protein solutions. J Phys Chem Lett. 2010;1:126–129. [Google Scholar]
- 24.Liu Y, et al. Lysozyme protein solution with an intermediate range order structure. J Phys Chem B. 2011;115:7238–7247. doi: 10.1021/jp109333c. [DOI] [PubMed] [Google Scholar]
- 25.Roos M, et al. Coupling and decoupling of rotational and translational diffusion of proteins under crowding conditions. J Am Chem Soc. 2016;138:10365–10372. doi: 10.1021/jacs.6b06615. [DOI] [PubMed] [Google Scholar]
- 26.Balbo J, Mereghetti P, Herten DP, Wade RC. The shape of protein crowders is a major determinant of protein diffusion. Biophys J. 2013;104:1576–1584. doi: 10.1016/j.bpj.2013.02.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Grimaldo M, Roosen-Runge F, Zhang F, Seydel T, Schreiber F. Diffusion and dynamics of -globulin in crowded aqueous solutions. J Phys Chem B. 2014;118:7203–7209. doi: 10.1021/jp504135z. [DOI] [PubMed] [Google Scholar]
- 28.Feig M, Sugita Y. Reaching new levels of realism in modeling biological macromolecules in cellular environments. J Mol Graph Model. 2013;45:144–156. doi: 10.1016/j.jmgm.2013.08.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Nawrocki G, Wang PH, Yu I, Sugita Y, Feig M. Slow-down in diffusion in crowded protein solutions correlates with transient cluster formation. J Phys Chem B. 2017;121:11072–11084. doi: 10.1021/acs.jpcb.7b08785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Nawrocki G, Karaboga A, Sugita Y, Feig M. Effect of protein–protein interactions and solvent viscosity on the rotational diffusion of proteins in crowded environments. Phys Chem Chem Phys. 2019;21:876–883. doi: 10.1039/c8cp06142d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Phillies GD, Ullmann GS, Ullmann K, Lin TH. Phenomenological scaling laws for “semidilute” macromolecule solutions from light scattering by optical probe particles. J Chem Phys. 1985;82:5242–5246. [Google Scholar]
- 32.Gorti S, Ware BR. Probe diffusion in an aqueous polyelectrolyte solution. J Chem Phys. 1985;83:6449–6456. [Google Scholar]
- 33.Konopka MC, et al. Cytoplasmic protein mobility in osmotically stressed Escherichia coli. J Bacteriol. 2009;91:231–237. doi: 10.1128/JB.00536-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Verkman AS. Diffusion in cells measured by fluorescence recovery after photobleaching. Methods Enzymol. 2003;360:635–648. doi: 10.1016/s0076-6879(03)60132-1. [DOI] [PubMed] [Google Scholar]
- 35.Mastro AM, Babich MA, Taylor WD, Keith AD. Diffusion of a small molecule in the cytoplasm of mammalian cells. Proc Natl Acad Sci USA. 1984;81:3414–3418. doi: 10.1073/pnas.81.11.3414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Jin S, Verkman AS. Single particle tracking of complex diffusion in membranes: Simulation and detection of barrier, raft, and interaction phenomena. J Phys Chem B. 2007;111:3625–3632. doi: 10.1021/jp067187m. [DOI] [PubMed] [Google Scholar]
- 37.Dauty E, Verkman AS. Molecular crowding reduces to a similar extent the diffusion of small solutes and macromolecules: Measurement by fluorescence correlation spectroscopy. J Mol Recognit. 2004;17:441–447. doi: 10.1002/jmr.709. [DOI] [PubMed] [Google Scholar]
- 38.Szymański J, Patkowski A, Wilk A, Garstecki P, Holyst R. Diffusion and viscosity in a crowded environment: From nano- to macroscale. J Phys Chem B. 2006;110:25593–25597. doi: 10.1021/jp0666784. [DOI] [PubMed] [Google Scholar]
- 39.Zorrilla S, Hink MA, Visser AJ, Lillo MP. Translational and rotational motions of proteins in a protein crowded environment. Biophys Chem. 2007;125:298–305. doi: 10.1016/j.bpc.2006.09.003. [DOI] [PubMed] [Google Scholar]
- 40.Roosen-Runge F, et al. Protein self-diffusion in crowded solutions. Proc Natl Acad Sci USA. 2011;108:11815–11820. doi: 10.1073/pnas.1107287108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Li C, Liu M. Protein dynamics in living cells studied by in-cell NMR spectroscopy. FEBS Lett. 2013;587:1008–1011. doi: 10.1016/j.febslet.2012.12.023. [DOI] [PubMed] [Google Scholar]
- 42.Rothe M, et al. Transient binding accounts for apparent violation of the generalized Stokes-Einstein relation in crowded protein solutions. Phys Chem Chem Phys. 2016;18:18006–18014. doi: 10.1039/c6cp01056c. [DOI] [PubMed] [Google Scholar]
- 43.Geyer T. Mixing normal and anomalous diffusion. J Chem Phys. 2012;137:115101. doi: 10.1063/1.4753804. [DOI] [PubMed] [Google Scholar]
- 44.Kondrat S, Zimmermann O, Wiechert W, Lieres EV. The effect of composition on diffusion of macromolecules in a crowded environment. Phys Biol. 2015;12:46003. doi: 10.1088/1478-3975/12/4/046003. [DOI] [PubMed] [Google Scholar]
- 45.Kim YC, Best RB, Mittal J. Macromolecular crowding effects on protein-protein binding affinity and specificity. J Chem Phys. 2010;133:205101. doi: 10.1063/1.3516589. [DOI] [PubMed] [Google Scholar]
- 46.Kim YC, Mittal J. Crowding induced entropy-enthalpy compensation in protein association equilibria. Phys Rev Lett. 2013;110:208102. doi: 10.1103/PhysRevLett.110.208102. [DOI] [PubMed] [Google Scholar]
- 47.Kang H, Pincus PA, Hyeon C, Thirumalai D. Effects of macromolecular crowding on the collapse of biopolymers. Phys Rev Lett. 2015;114:68303. doi: 10.1103/PhysRevLett.114.068303. [DOI] [PubMed] [Google Scholar]
- 48.McGuffee SR, Elcock AH. Atomically detailed simulations of concentrated protein solutions: The effects of salt, pH, point mutations, and protein concentration in simulations of 1000-molecule systems. J Am Chem Soc. 2006;128:12098–12110. doi: 10.1021/ja0614058. [DOI] [PubMed] [Google Scholar]
- 49.Frembgen-Kesner T, Elcock AH. Striking effects of hydrodynamic interactions on the simulated diffusion and folding of proteins. J Chem Theory Comput. 2009;5:242–256. doi: 10.1021/ct800499p. [DOI] [PubMed] [Google Scholar]
- 50.Cossins BP, Jacobson MP, Guallar V. A new view of the bacterial cytosol environment. PLoS Comput Biol. 2011;7:e1002066. doi: 10.1371/journal.pcbi.1002066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Lu C, Prada-Gracia D, Rao F. Structure and dynamics of water in crowded environments slows down peptide conformational changes. J Chem Phys. 2014;141:45101. doi: 10.1063/1.4891465. [DOI] [PubMed] [Google Scholar]
- 52.Yu I, et al. Biomolecular interactions modulate macromolecular structure and dynamics in atomistic model of a bacterial cytoplasm. Elife. 2016;5:e19274. doi: 10.7554/eLife.19274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Minton AP. Excluded volume as a determinant of protein structure and stability. Biophys J. 1980;32:77–79. doi: 10.1016/S0006-3495(80)84917-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Minton AP. The effect of volume occupancy upon the thermodynamic activity of proteins: Some biochemical consequences. Mol Cell Biochem. 1983;55:119–140. doi: 10.1007/BF00673707. [DOI] [PubMed] [Google Scholar]
- 55.Muramatsu N, Minton AP. Hidden self-association of proteins. J Mol Recognit. 1989;1:166–171. doi: 10.1002/jmr.300010404. [DOI] [PubMed] [Google Scholar]
- 56.Stradner A, et al. Equilibrium cluster formation in concentrated protein solutions and colloids. Nature. 2004;432:492–495. doi: 10.1038/nature03109. [DOI] [PubMed] [Google Scholar]
- 57.Scherer TM, Liu J, Shire SJ, Minton AP. Intermolecular interactions of IgG1 monoclonal antibodies at high concentrations characterized by light scattering. J Phys Chem B. 2010;114:12948–12957. doi: 10.1021/jp1028646. [DOI] [PubMed] [Google Scholar]
- 58.Lilyestrom WG, Yadav S, Shire SJ, Scherer TM. Monoclonal antibody self-association, cluster formation, and rheology at high concentrations. J Phys Chem B. 2013;117:6373–6384. doi: 10.1021/jp4008152. [DOI] [PubMed] [Google Scholar]
- 59.Paulino J, et al. Influenza A M2 channel clustering at high protein/lipid ratios: Viral budding implications. Biophys J. 2019;116:1075–1084. doi: 10.1016/j.bpj.2019.01.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Turton DA, Wynne K. Stokes-Einstein-Debye failure in molecular orientational diffusion: Exception or rule? J Phys Chem B. 2014;118:4600–4604. doi: 10.1021/jp5012457. [DOI] [PubMed] [Google Scholar]
- 61.Godfrin PD, et al. Short-time glassy dynamics in viscous protein solutions with competing interactions. Phys Rev Lett. 2015;115:228302. doi: 10.1103/PhysRevLett.115.228302. [DOI] [PubMed] [Google Scholar]
- 62.Heinen M, et al. Viscosity and diffusion: Crowding and salt effects in protein solutions. Soft Matter. 2012;8:1404–1419. [Google Scholar]
- 63.Ladd AJC. Hydrodynamic transport coefficients of random dispersions of hard spheres. J Chem Phys. 1990;93:3484–3494. [Google Scholar]
- 64.Bedeaux D. The effective viscosity for a suspension of spheres. J Colloid Interf Sci. 1987;118:80–86. [Google Scholar]
- 65.Piana S, Donchev AG, Robustelli P, Shaw DE. Water dispersion interactions strongly influence simulated structural properties of disordered protein states. J Phys Chem B. 2015;119:5113–5123. doi: 10.1021/jp508971m. [DOI] [PubMed] [Google Scholar]
- 66.Einstein A. Eine neue bestimmung der moleküldimensionen [A new determination of molecule dimensions] Ann Phys. 1906;19:289–306. [Google Scholar]
- 67.Russel WB. The Huggins coefficient as a means for characterizing suspended particles. J Chem Soc Faraday Trans 2 Mol Chem Phys. 1984;80:31–41. [Google Scholar]
- 68.Cichocki B, Felderhof BU. Diffusion coefficients and effective viscosity of suspensions of sticky hard spheres with hydrodynamic interactions. J Chem Phys. 1990;93:4427–4432. [Google Scholar]
- 69.Woutersen ATJM, De Kruif CG. The rheology of adhesive hard sphere dispersions. J Chem Phys. 1991;94:5739–5750. [Google Scholar]
- 70.Ortega A, et al. Prediction of hydrodynamic and other solution properties of rigid proteins from atomic- and residue-level models. Biophys J. 2011;101:892–898. doi: 10.1016/j.bpj.2011.06.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Altieri AS, Byrd RA, Hinton DP. Association of biomolecular systems via pulsed field gradient NMR self-diffusion measurements. J Am Chem Soc. 1995;117:7566–7567. [Google Scholar]
- 72.Mayo KH, Ilyina E, Park H. A recipe for designing water-soluble, beta-sheet-forming peptides. Protein Sci. 1996;5:1301–1315. doi: 10.1002/pro.5560050709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Dubin SB, Clark NA, Benedek GB. Measurement of the rotational diffusion coefficient of lysozyme by depolarized light scattering: Configuration of lysozyme in solution. J Chem Phys. 1971;54:5158–5164. [Google Scholar]
- 74.Mikol V, Hirsch E, Giegé R. Diagnostic of precipitant for biomacromolecule crystallization by quasi-elastic light-scattering. J Mol Biol. 1990;213:187–195. doi: 10.1016/S0022-2836(05)80130-5. [DOI] [PubMed] [Google Scholar]
- 75.Price WS, Tsuchiya F, Arata Y. Lysozyme aggregation and solution properties studied using PGSE NMR diffusion measurements. J Am Chem Soc. 1999;121:11503–11512. [Google Scholar]
- 76.Coffman J, Lightfoot E, Root T. Protein diffusion in porous chromatographic media studied by proton and fluorine PFG-NMR. J Phys Chem B. 1997;101:2218–2223. [Google Scholar]
- 77.Tjandra N, Bax A, Feller SE, Pastor RW. Rotational diffusion anisotropy of human ubiquitin from 15N NMR relaxation. J Am Chem Soc. 1995;117:12562–12566. [Google Scholar]
- 78.Hall JB, Fushman D. Characterization of the overall and local dynamics of a protein with intermediate rotational anisotropy: Differentiating between conformational exchange and anisotropic diffusion in the B3 domain of protein G. J Biomol NMR. 2003;27:261–275. doi: 10.1023/a:1025467918856. [DOI] [PubMed] [Google Scholar]
- 79.Stradner A, Cardinaux F, Schurtenberger P. A small-angle scattering study on equilibrium clusters in lysozyme solutions. J Phys Chem B. 2006;110:21222–21231. doi: 10.1021/jp0639804. [DOI] [PubMed] [Google Scholar]
- 80.Linke M, Köfinger J, Hummer G. Fully anisotropic rotational diffusion tensor from molecular dynamics simulations. J Phys Chem B. 2018;122:5630–5639. doi: 10.1021/acs.jpcb.7b11988. [DOI] [PubMed] [Google Scholar]
- 81.Linke M, Köfinger J, Hummer G. Rotational diffusion depends on box size in molecular dynamics simulations. J Phys Chem Lett. 2018;9:2874–2878. doi: 10.1021/acs.jpclett.8b01090. [DOI] [PubMed] [Google Scholar]
- 82.Liu Z, et al. Noncovalent dimerization of ubiquitin. Angew Chem Int Ed. 2012;51:469–472. doi: 10.1002/anie.201106190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Ermakova E. Lysozyme dimerization: Brownian dynamics simulation. J Mol Model. 2005;12:34–41. doi: 10.1007/s00894-005-0001-2. [DOI] [PubMed] [Google Scholar]
- 84.Baxter RJ. Percus-Yevick equation for hard spheres with surface adhesion. J Chem Phys. 1968;49:2770–2774. [Google Scholar]
- 85.Kranendonk WGT, Frenkel D. Simulation of the adhesive-hard-sphere model. Mol Phys. 1988;64:403–424. [Google Scholar]
- 86.Verduin H, Dhont JK. Phase diagram of a model adhesive hard-sphere dispersion. J Colloid Interf Sci. 1995;172:425–437. [Google Scholar]
- 87.Mereghetti P, Gabdoulline RR, Wade RC. Brownian dynamics simulation of protein solutions: Structural and dynamical properties. Biophys J. 2010;99:3782–3791. doi: 10.1016/j.bpj.2010.10.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Keller KH, Canales ER, Yam S. Tracer and mutual diffusion coefficients of proteins. J Phys Chem. 1971;75:379–387. doi: 10.1021/j100673a015. [DOI] [PubMed] [Google Scholar]
- 89.Gibbs SJ, Chu AS, Lightfoot EN, Root TW. Ovalbumin diffusion at low ionic strength. J Phys Chem. 1991;95:467–471. [Google Scholar]
- 90.Le Bon C, Nicolai T, Kuil ME, Hollander JG. Self-diffusion and cooperative diffusion of globular proteins in solution. J Phys Chem B. 1999;103:10294–10299. [Google Scholar]
- 91.Longeville S, Doster W, Diehl M, Gähler R, Petry W. 2003. Neutron resonance spin echo: Oxygen transport in crowded protein solutions. Neutron Spin Echo Spectroscopy: Basics, Trends and Applications, eds Mezei F, Pappas C, Gutberlet T (Springer, Berlin), pp 325–335.
- 92.Doster W, Longeville S. Microscopic diffusion and hydrodynamic interactions of hemoglobin in red blood cells. Biophys J. 2007;93:1360–1368. doi: 10.1529/biophysj.106.097956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Longeville S, Stingaciu LR. Hemoglobin diffusion and the dynamics of oxygen capture by red blood cells. Sci Rep. 2017;7:1–10. doi: 10.1038/s41598-017-09146-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.van Blaaderen A, Peetermans J, Maret G, Dhont JKG. Long-time self-diffusion of spherical colloidal particles measured with fluorescence recovery after photobleaching. J Chem Phys. 1992;96:4591–4603. [Google Scholar]
- 95.Tokuyama M, Oppenheim I. Dynamics of hard-sphere suspensions. Phys Rev E–Stat Nonlinear Soft Matter Phys. 1994;50:R16–R19. doi: 10.1103/physreve.50.r16. [DOI] [PubMed] [Google Scholar]
- 96.Wang D, Kreutzer U, Chung Y, Jue T. Myoglobin and hemoglobin rotational diffusion in the cell. Biophys J. 1997;73:2764–2770. doi: 10.1016/S0006-3495(97)78305-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Zuzovsky M, Adler PM, Brenner H. Spatially periodic suspensions of convex particles in linear shear flows. III. Dilute arrays of spheres suspended in Newtonian fluids. Phys Fluids. 1983;26:1714. [Google Scholar]
- 98.Shukla A, et al. Absence of equilibrium cluster phase in concentrated lysozyme solutions. Proc Natl Acad Sci USA. 2008;105:5075–5080. doi: 10.1073/pnas.0711928105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Hyman AA, Weber CA, Jülicher F. Liquid-liquid phase separation in biology. Annu Rev Cell Dev Biol. 2014;30:39–58. doi: 10.1146/annurev-cellbio-100913-013325. [DOI] [PubMed] [Google Scholar]
- 100.Luby-Phelps K. The physical chemistry of cytoplasm and its influence on cell function: An update. Mol Biol Cell. 2013;24:2593–2596. doi: 10.1091/mbc.E12-08-0617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Feig M, Yu I, Wang PH, Nawrocki G, Sugita Y. Crowding in cellular environments at an atomistic level from computer simulations. J Phys Chem B. 2017;121:8009–8025. doi: 10.1021/acs.jpcb.7b03570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Rivas G, Minton AP. Toward an understanding of biochemical equilibria within living cells. Biophys Rev. 2018;10:241–253. doi: 10.1007/s12551-017-0347-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Johnson ME, Hummer G. Nonspecific binding limits the number of proteins in a cell and shapes their interaction networks. Proc Natl Acad Sci USA. 2011;108:603–608. doi: 10.1073/pnas.1010954108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Ivani I, et al. Parmbsc1: A refined force field for DNA simulations. Nat Methods. 2015;13:55–58. doi: 10.1038/nmeth.3658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Zgarbová M, et al. Refinement of the sugar-phosphate backbone torsion beta for AMBER force fields improves the description of Z- and B-DNA. J Chem Theory Comput. 2015;11:5723–5736. doi: 10.1021/acs.jctc.5b00716. [DOI] [PubMed] [Google Scholar]
- 106.Pérez A, et al. Refinement of the AMBER force field for nucleic acids: Improving the description of / conformers. Biophys J. 2007;92:3817–3829. doi: 10.1529/biophysj.106.097782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Bana P, et al. Performance of molecular mechanics force fields for RNA simulations: Stability of UUCG and GNRA hairpins. J Chem Theory Comput. 2010;6:3836–3849. doi: 10.1021/ct100481h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Zgarbová M, et al. Refinement of the Cornell, et al. nucleic acids force field based on reference quantum chemical calculations of glycosidic torsion profiles. J Chem Theory Comput. 2011;7:2886–2902. doi: 10.1021/ct200162x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Tan D, Piana S, Dirks RM, Shaw DE. RNA force field with accuracy comparable to state-of-the-art protein force fields. Proc Natl Acad Sci USA. 2018;115:201713027. doi: 10.1073/pnas.1713027115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Vijay-Kumar S, Bugg CE, Cook WJ. Structure of ubiquitin refined at 1.8 A resolution. J Mol Biol. 1987;194:531–544. doi: 10.1016/0022-2836(87)90679-6. [DOI] [PubMed] [Google Scholar]
- 111.Ulmer TS, et al. Evaluation of backbone proton positions and dynamics in a small protein by liquid crystal NMR spectroscopy. J Am Chem Soc. 2003;125:9179–9191. doi: 10.1021/ja0350684. [DOI] [PubMed] [Google Scholar]
- 112.Schwalbe H, et al. A refined solution structure of hen lysozyme determined using residual dipolar coupling data. Protein Sci. 2001;10:677–688. doi: 10.1110/ps.43301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.McKnight CJ, Matsudaira PT, Kim PS. NMR structure of the 35-residue villin headpiece subdomain. Nat Struct Biol. 1997;4:180–184. doi: 10.1038/nsb0397-180. [DOI] [PubMed] [Google Scholar]
- 114.Hess B. Determining the shear viscosity of model liquids from molecular dynamics simulations. J Chem Phys. 2002;116:209. [Google Scholar]
- 115.Yeh IC, Hummer G. System-size dependence of diffusion coefficients and viscosities from molecular dynamics simulations with periodic boundary conditions. J Phys Chem B. 2004;108:15873–15879. [Google Scholar]
- 116.Linke M. 2018 Pydiffusion–A python software implementation to calculate the quaternion covariances from simulations, fit the rotational diffusion tensor, and run rotational Brownian dynamics simulations. Available at https://github.com/bio-phys/. Accessed April 10, 2018.
- 117.Favro LD. Theory of the rotational Brownian motion of a free rigid body. Phys Rev. 1960;119:53–62. [Google Scholar]
- 118.Woessner DE. Nuclear spin relaxation in ellipsoids undergoing rotational Brownian motion. J Chem Phys. 1962;37:647–654. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.