Abstract
Molecules with conjugated π-systems often feature strong electron correlation and therefore require multireference methods for a reliable computational description. A key prerequisite for the successful application of such methods is the choice of a suitable active space. Herein the automated π-orbital space (PiOS) method for selecting active spaces for multireference calculations of conjugated π-systems is presented. This approach allows the construction of small but effective active spaces based on Hückel theory. To demonstrate its performance, π→π* excitations for benzene, octatetraene, and free-base porphin are computed. In addition, this technique can be combined with the automated atomic valence active space method to compute excitations in complex systems with multiple conjugated fragments. This combined approach was used to generate two-dimensional potential energy surfaces for multiple electronic states associated with photoinduced electron-coupled double proton transfer in the blue light-using flavin photoreceptor protein. These types of methods for the automated selection of active space orbitals are important for ensuring consistency and reproducibility of multireference approaches for a wide range of chemical and biological systems.
Graphical Abstract
I. Introduction
Conjugated π systems have attracted considerable attention in the field of chemistry. Organic polymers with conjugated π-bonds often exhibit properties of semiconductors or superconductors1–4 and therefore serve as valuable components of organic photovoltaic devices5–6 and organic light-emitting diodes.7–8 Many biologically important molecular complexes containing conjugated π-bonds, including chlorophyll, hemoglobin, vitamin B12, β-carotene, and cytochromes, are responsible for vital functions in living organisms. The electronic structure characteristics of conjugated π-systems that are responsible for this rich chemistry also complicate the theoretical study of such systems. In particular, these systems often exhibit strong electron correlation, with multiple near-degenerate electronic states and multiconfigurational character. Therefore, a reliable computational description of such systems requires multiconfigurational and/or multireference methods.9–39 A major challenge in applying such methods in practice is the choice of a suitable active space, which strongly impacts the quality of the results.
The traditional methods of active space selection are accompanied by several problems, including difficulties in identifying the molecular orbitals (MOs) responsible for the principal chemical properties and the necessity of manual selection of the active orbitals. While the manual selection of an active space following general guidelines40 is still a feasible task in the case of small molecules or single geometries, it becomes impractical in studies of potential energy surfaces of large complex systems. To ensure a consistent active space (i.e., the same size and same atomic orbital character) along various reaction coordinates and while exploring multidimensional potential energy surfaces, a more systematic, and preferably automated, approach is desirable. This issue is even more amplified by the recent surge in novel electronic structure methods that allow the efficient treatment of large active spaces.29, 31, 37, 41–43
Recently several efforts44–47 have been directed toward the development of automated active space selection algorithms. These efforts aim to turn the selection procedure into black-box routines, thus avoiding the extensive user input still required for most calculations. In addition, such methods also improve the reproducibility of calculations by other researchers, which is often a challenge. Ref. 46 describes the atomic valence active space (AVAS) method, an automated active space selection scheme based on the projection of occupied and virtual molecular orbitals onto the target valence atomic orbitals. This technique is related to other techniques of constructing valence virtual orbital spaces48–49 but differs in both purpose and mathematical construction. The AVAS method has been shown to be general and flexible for constructing active spaces for many types of systems. In the case of conjugated π-systems, however, the active spaces generated from projecting the MOs onto all valence atomic orbitals of the target atoms will generally be much larger than required because only projection onto the valence atomic orbitals contributing to the π-system is necessary.
To alleviate this problem, herein we describe an automated approach based on Hückel MO theory,50–52 which is particularly well-suited for conjugated π-systems. This π-orbital space (PiOS) method first builds initial π-orbitals from a single-reference wavefunction, using a projection approach similar to that presented in Ref. 46. In this initial π-space, an effective Hamiltonian is diagonalized to obtain a set of energy-ordered π MOs that span the space. Depending on the specific application, the user can either select a small active space consisting of only a few of the highest-occupied molecular orbitals (HOMOs) and lowest-unoccupied molecular orbitals (LUMOs) of this space, or a larger active space consisting of more MOs, up to the entire π-orbital space if this is required. On the basis of classical MO theory, we expect this procedure to allow the selection of the minimal set of the most important π-orbitals. We examined the performance of this proposed method on typical π-conjugated systems, such as benzene, octatetraene, and free-base porphine. We also demonstrated how this approach can be combined with the AVAS method to study the large active site of the blue light-using flavin (BLUF) photoreceptor protein. This approach is thereby shown to enable chemically and biologically relevant calculations with quantitative multi-reference techniques even for multidimensional potential energy surfaces of complex systems, a task that currently would be difficult to execute without such methods.
II. Theory
This section explains how to construct π-orbitals from a single-reference wavefunction obtained from self-consistent field (SCF) calculations using linear algebraic transformations and Hückel theory. We first explain how to determine the plane that acts as the effective nodal surface of the π-system by considering the positions of the atoms comprising the π-system. Then we describe how to determine the number of π-electrons and the number of π-orbitals for a given system. Finally, we show how to obtain the molecular π-orbitals for an effective active space.
A. Determining spatial orientation of the π-system
Molecular systems with conjugated π-bonds typically have a planar structure. Herein M denotes the set of main group atoms A that contribute to the π-system within a molecule or complex. If these atoms lie in the xy plane at z ≈ 0, then the corresponding π-system is spanned by their valence pz orbitals. However, in an arbitrary molecular system, the molecule can be oriented differently. In this case, we need to first identify the spatial direction aligned with the direction of the local orbitals of M.
If the molecule were exactly planar, this vector n would be the normal of the plane in which all atoms comprising the π-system lie. If the molecule is not exactly planar, an approximate n must be determined. For this purpose, let {RA;A ∈ M} denote the three-dimensional column vectors denoting the positions of the atoms A of M contributing to the π-system. We first determine the “center of local π-system coordinates” (i.e., its centroid, which is an analogue of the center of mass but without mass weighting), represented by a 3-dimensional column vector as:
| (1) |
Here | M | denotes the number of atoms comprising the π-system. Then the system’s 3×3 inertial tensor matrix T around Rc is formed as
| (2) |
Diagonalization of this positive definite matrix T. yields the principal axes for the local π-system coordinates. The (normalized) eigenvector with the smallest eigenvalue is selected as the direction n. Note that this eigenvalue will be exactly zero if the molecule is exactly flat and is typically very close to zero for approximately planar structures.
B. Generating spatially oriented atomic orbitals
Once the direction n is determined, the local molecule-oriented orbital of each atom A is then obtained as a linear combination of the three valence px,A, py,A., pz,A atomic orbitals (AOs) of the atom A in the global Cartesian coordinate system as:
| (3) |
In general, basis functions of an arbitrary computational basis set have more variational degrees of freedom than atomic orbitals and do not necessarily correspond to the s-, p-, d-type atomic orbitals in a chemically intuitive sense. Therefore, a second auxiliary AO basis should be employed. A minimal basis set of tabulated free-atom AOs, denoted MINAO,53 or subsets of atomic natural orbital basis sets, such as ANO-RCC,54–55 ano-pVnZ,56 or ANO-VT-XZ,57 can be used for this purpose.
To simplify notation, we will assume that the set of locally oriented, orbitals is collected in a single matrix O with the dimension of NMINAO × Nπ-AO, where NMINAO. denotes the number of basis functions in a suitable minimal AO basis set of the entire molecule or complex (see also Sec. D), and Nπ-AO denotes the number of valence π-orbitals on M. Typically, each main group atom in M will contribute exactly one valence orbital to the π system, such that | M | = Nπ–AO. Each column of matrix O then represents one of the functions in Eq. (3) on a given main group atom. Specifically, it contains the coefficients nx, ny, nz in rows corresponding to atom A’s valence px, py, pz. AOs, respectively, and 0 for all other rows.
C. Determining the number of occupied and virtual π MOs
For a given molecule, the number of electrons Nπ,e its π-system is supposed to contain must be determined. For example, a neutral benzene molecule, as well as an anionic Cp− ligand, has six π electrons. The PiOS method finds the number of π-electrons automatically based on atomic connectivity using the following algorithm. First, the method determines the bond order for each atom of a given π-system, assuming two atoms i and j with covalent radii Ri and Rj., respectively, (see Ref. 58, for example) are bonded if rij < 1.3(Ri + Rj). Based on this information, the scheme identifies the number of electrons each atom in M normally contributes to the π-system. For example, each sp2 carbon atom in M typically contributes one π-electron regardless of connectivity, while each N or P atom in the aromatic system M will typically contribute one or two π-electrons if it is connected by two or three σ-bonds, respectively, to the rest of the system. If necessary, for individual atoms, the number of contributed π-electrons can be fixed manually based on user input, and the total number of π-electrons, as obtained via the sum of atomic contributions, can be adjusted up for anionic or down for cationic systems. This procedure allows for a simple and yet flexible way of fixing the number of π-electrons. Note that the validity and accuracy of these user choices can be easily established based on the projection eigenvalues discussed below.
Based on Nπ,e., the total number of π-electrons in M, and Nπ-AO, the number of locally-oriented orbitals in the π-system of M, the number of the full molecular system’s occupied and virtual MOs representing occupied and virtual π spatial MOs on M can be determined. Specifically, these numbers are
| (4) |
| (5) |
D. Representation of the full molecule’s core and valence atomic orbitals
To describe the core and valence atomic orbitals of the molecular system, we use Intrinsic Atomic Orbitals (IAOs),53 rather than using the MINAO directly. The IAOs represent polarized AOs and describe the occupied orbitals of the molecular SCF wavefunction | Φ〉 exactly, i.e., they correspond to chemical atomic orbitals. While the basis functions of an arbitrarily chosen computational basis set do not correspond directly to the AOs, the MINAO or ANO basis sets account for the molecular environment. Thus, it is advantageous to obtain the IAOs for a given molecular system and use them to describe the AOs. [Note that for cases in which users wish to create a “double-shell” π-space,59–60 they would need to use an ANO basis set from which to draw reference AOs, rather than the MINAO or IAOs described here, and then include both valence shell n and (n+1) pz AOs in the PiOS construction. This procedure is fully analogous to that used to include such effects in the AVAS method.46]
Let B1 denote the main computational basis set (e.g., cc-pVTZ) and B2. denote the auxiliary basis set (e.g., MINAO). S1. and S2 represent the overlap matrices for the basis functions μ ∈ B1 and ν ∈ B2, respectively. S12 denotes the overlap matrix between functions of the two bases with elements [S12]μν = 〈μ | ν〉. Herein we employ the updated IAO construction approach,61 in which the | B1 |× | B2 | coefficient matrix R of the IAOs in the B1 basis set is given as:
| (6) |
| (7) |
| (8) |
where Cocc denotes the occupied MO matrix of the molecular system. Note that the IAOs are not orthogonalized.
E. Isolation of the MOs corresponding to the π-system
Let | Φ〉 denote a closed-shell Slater determinant with Nocc occupied MOs describing the electronic structure of the system at the SCF level (i.e., Hartree-Fock or Kohn-Sham formulation of density functional theory). Its occupied and virtual MOs are expressed as:
| (9) |
| (10) |
where μ are basis functions from the employed computational basis set B1, and and are the coefficients of the basis function μ in the expansion of the occupied orbital i and virtual orbital a MOs, respectively. Cocc and Cvir denote the | B1 | × Nocc occupied and | B1 | × Nvir virtual sub-matrices of the | B1 | × | B1 | SCF orbital matrix C. Note that Nocc + Nvir = | B1 | because each orbital is either occupied or virtual.
Let SAO,π denote the overlap matrix of M’s selected and locally-oriented orbitals, given as
| (11) |
where O denotes the selection-and-orientation matrix from Sec. IIB and R denotes the | B1 | × | B2 | matrix of IAO coefficients from Sec. IID. With this, we can compute the Nocc × Nocc overlap matrix of the occupied orbitals with the locally-oriented orbitals (i.e., the overlap matrix of the occupied orbitals projected onto the π-space) as:
| (12) |
| (13) |
Diagonalizing Socc,π. yields a set of eigenvalues σi; i = 1,…,Nocc and an Nocc × Nocc (orthogonal) matrix of eigenvectors U, which define a rotation of the occupied orbitals. The unitarily transformed occupied orbital matrix
| (14) |
contains as the ith column the coefficients of a unitarily transformed occupied orbital with an overlap σi with the molecule M’s π-subspace:
| (15) |
The MOs with σi = 0 have no overlap with the π-system, and the MOs with σi ≠ 0 have an overlap with the π-system and thus should be selected into the π-active space. In total we need to select the subset of the Nπ,occ columns corresponding to the largest eigenvalues σi for the occupied MO part of the π-space. As a result, we obtain a | B1 | × Nπ,occ matrix Cocc,π.
Once determined, the occupied π-orbitals are semi-canonicalized by computing
| (16) |
where f is the full molecular system’s Fock matrix, diagonalizing focc,π, and using the resulting unitary transformation (given by the eigenvector matrix) to transform Cocc,π again. This procedure provides a set of energy-ordered occupied orbitals representing the occupied part of the π-system of M.
The entire procedure in this section is then repeated with the virtual orbitals to yield the virtual part of the π-system of M. The resulting occupied and virtual orbitals together span the same space as the orbitals from Sec. IIB.
F. Inactive orbitals
This subsection describes how the inactive orbitals are generated. In the simplest case of a molecular complex with one π-system, the inactive occupied orbitals are formed by the MOs from Eqs. (14) and (15) with σi = 0, and the inactive virtual orbitals are obtained in a similar manner from the subspace of virtual orbitals. In the case of a molecular complex with multiple π-systems, the active orbitals are obtained for each of the π-systems as described in Sec. IIE. After forming the entire active space, the inactive occupied and inactive virtual orbitals are obtained by constructing the subspace of the full system of occupied and virtual orbitals, respectively, that are orthogonal to the active orbitals.
For the case with multiple π-systems, let Cact denote the active orbital matrix containing the coefficients of the occupied and virtual active orbitals as the columns. First, the active orbitals should be orthogonalized, as the active orbitals obtained from different π-systems are not necessarily orthogonal:
| (17) |
where is the overlap matrix of the active orbitals. Then the matrix representation of the projector to the active orbitals in the basis of occupied orbitals is computed as
| (18) |
Diagonalizing the Pact,occ matrix yields a set of eigenvalues λi; i = 1,…,Nocc and an Nocc × Nocc orthogonal matrix of eigenvectors Uact,occ, which define a rotation of the occupied orbitals:
| (19) |
Now the columns of the unitarily transformed occupied orbital matrix
| (20) |
that correspond to eigenvalues λi = 0 (i.e., that have no overlap with the active space) define the new inactive occupied (core) orbitals. The inactive virtual orbitals are obtained through the same set of transformations performed on the virtual orbitals. As for the active orbitals, in practice the inactive occupied and virtual orbitals are semi-canonicalized after construction to improve the convergence behavior of subsequent calculations using a similar procedure as in Eq. 16.
G. Differences between AVAS and PiOS methods
The spirit of the PiOS method is similar to the AVAS method, but there are several key differences with important practical consequences. First, as the PiOS method is targeted at π-systems, we employ only locally-oriented orbitals as target orbitals for the projector, instead of all valence atomic orbitals as used in the AVAS method. This difference leads to a smaller initial active space that does not include the electronic degrees of freedom associated with the σ-system, which is typically unreactive, from the outset. For conjugated systems in which σ bonds break along a reaction coordinate of interest, the PiOS and AVAS methods can be combined to describe both cases.
Second, the AVAS scheme does not contain any kind of canonicalization or semi-canonicalization of the orbitals generated by the projection onto the target AO space. This additional procedure allows the selection of the most important orbitals based on energy criteria. In the general systems for which AVAS is designed, the single-particle orbital energies computable from Hartree-Fock or Kohn-Sham wave functions are often not meaningful for identifying what needs to be included in an active space to describe chemistry (e.g., bond dissociations), and therefore AVAS employs only overlap criteria. In the PiOS scheme, however, we obtain an essentially complete characterization of the molecular π-system at the Hückel MO level because all occupied and unoccupied π-orbitals of the π-system are constructed. Thus, semi-canonicalizing this full set of MOs in the PiOS method generates a meaningful energy ordering of the π-orbitals. This procedure allows a user to select, for example, only π-HOMOs and π-LUMOs, instead of all orbitals on the target fragment as in the AVAS method. In contrast to the general case treated by the AVAS method, the energy ordering of orbitals for π-systems is often highly relevant for characterizing the π-system’s electronic states and transitions (e.g., in π-systems, the lowest excited state is typically characterized by the HOMO→LUMO excitation).
Finally, the PiOS scheme can be applied to multiple fragments (e.g., on different monomers of a complex), by building a projector for each π-space, whereas the AVAS method can be applied only once with a single projector combining all AOs for a given system. Thus, the PiOS method can be used to describe phenomena such as singlet splitting or exciton recombination, which can often be expressed in terms of HOMOs and LUMOs of π-systems associated with different monomers.
III. Computational Details
The only user-defined input parameter in the PiOS method is the set of main-group atoms contributing to the π-system. In addition, the user can choose between the options of selecting the entire π-orbital space or selecting the number of π-orbitals in the active space from the generated occupied and unoccupied MO subspaces. For some systems, not all π-orbitals need to be included in the active space to capture most of the essential chemistry, particularly the aspects related to the lowest lying electronic states and their transitions. In this case, the user can decide to choose only the HOMO and LUMO π-orbitals, or some additional low-lying virtual or high-lying occupied orbitals, as the chemistry demands. In any case, these orbitals can be directly identified with the method described above.
In addition to comparing to high-level reference calculations and experimental data, we also employed an internal criterion to assess the quality of the obtained active spaces. Specifically, we computed the overlap matrix between the initial guess and the optimized final active space orbitals and then computed its singular value decomposition (SVD). An overlap of the optimized active space with the initial active space equal to 1.0 indicates a complete coincidence. If all singular values are close to 1.0, the active space remains mostly unchanged during the optimization. A singular value close to 0.0 for a given initial active orbital indicates that this orbital had to be completely replaced by a different orbital. This combination has been successfully used before to validate other active space construction methods.46
All complete active space self-consistent field (CASSCF) and strongly-contracted N-electron valence state perturbation theory (NEVPT2)21, 62 calculations presented in this paper were carried out using the PYSCF package.63 All geometries, computed electronic states, and other technical details are provided in the Supporting Information.
IV. Results and Discussions
A. Benzene
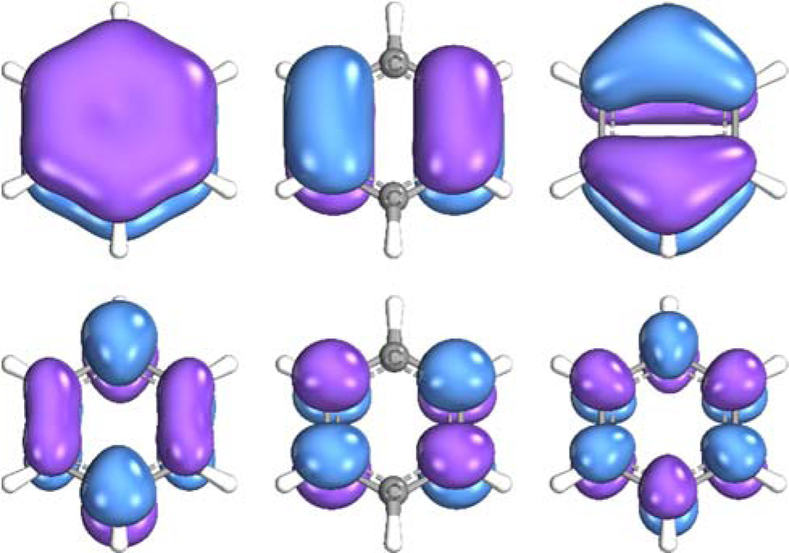
We begin by considering the electronic structure of benzene, one of the simplest conjugated systems that is studied for illustrative purposes. We carried out an initial restricted Hartree-Fock (RHF) calculation using the aug-cc-pVTZ64 basis set for the singlet ground state at the geometry optimized with the UB3LYP/cc-pVTZ basis set in Gaussian 09.65 The PiOS method generated the π-orbital space with six orbitals: three bonding and three antibonding type orbitals, as expected (Fig. 1). The singlet π→π* excitations were computed using the state-averaged CASSCF method (state-averaged over 7 states, the ground state and 6 excited states with two pairs of degenerate states) and the NEVPT2 method with this (6e, 6o) active space. Table 1 provides the singlet excited states obtained in this work and from multireference calculations with the manually chosen (6e, 6o) active space, as available from the literature. As shown from these data, the computed π→π* excitations are in good agreement with available computed and experimental values,66–69 and small differences can be explained by the use of different geometries, basis sets, and methodologies (see Table 1). Specifically, in Ref. 66 each electronic state was obtained by a separate CASSCF optimization, while in this work all states were obtained in a state-averaged manner; thus, the CASSCF reference wavefunctions for the dynamic correlation treatment were different. Additionally, different methods were used for the dynamic correlation correction (i.e., NEVPT2 is based on the bielectronic Dyall Hamiltonian and CASPT2 is based on the one-electron Fock-like zero-order Hamiltonian), explaining the more significant discrepancies observed for PT-corrected energies than for the CASSCF energies.
Figure 1.
Six π orbitals generated for benzene by PiOS before CASSCF optimization.
Table 1.
Excitation Energies (eV) of the Singlet States for Benzene with Six Active π-orbitals
| State | CASSCF | CASSCF/NEVPT2 | CASSCFa | CASPT2a | CASSCFb | MRMPb | Exp. |
|---|---|---|---|---|---|---|---|
| 11 B2u | 4.87 | 5.34 | 4.97 | 4.58 | 4.82 | 4.71 | 4.90c |
| 11 B1u | 7.81 | 6.07 | 7.85 | 5.90 | 7.91 | 5.83 | 6.20c |
| 11 E1u | 9.21 | 6.91 | 9.29 | 6.54 | 9.29 | 6.33 | 6.95c |
| 21 E2g | 8.11 | 8.54 | 8.11 | 7.65 | 8.01 | 7.74 | 7.80d |
State-specific (6e,6o) CASSCF and CASPT2 calculations with the ANO basis set and the C [4s3p2d]/H [3s2p] contraction scheme from Ref. 66.
MRMP calculations with state-averaged (6e,6o) CASSCF with the cc-pVTZ and cc-pVDZ basis sets for carbon and hydrogen, respectively, from Ref. 67.
Experimental values from Ref. 68.
Experimental value from Ref. 69.
The SVD eigenvalues for the overlap between the CASSCF-optimized active space and the initial guess active space were 0.9708, 0.9709, 0.9875, 0.9998, 0.9998, and 1.0. This analysis indicates that the π-orbitals generated by the algorithm require only minimal optimization by the CASSCF procedure, as they are near-optimal from the outset, and they can be used in multireference methods without orbital optimization, such as CASCI.
B. Octatetraene
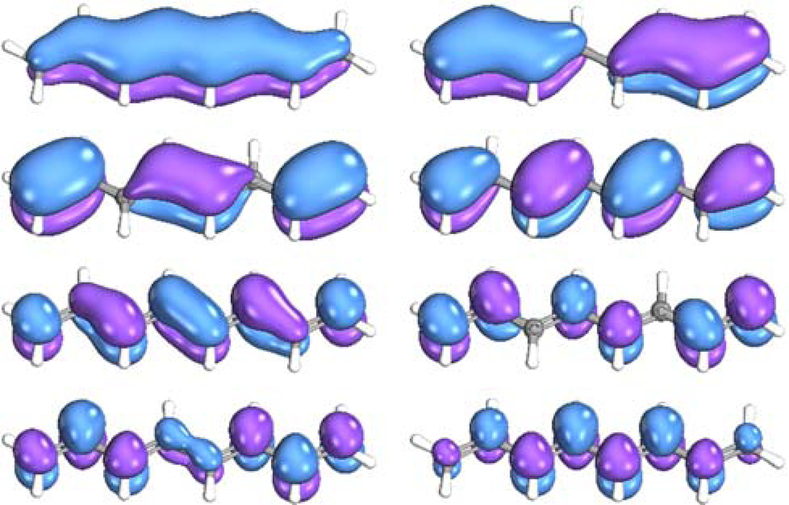
The next example is the (E,E)-1,3,5,7-octatetraene molecule, where the geometry was obtained from Ref. 70. As in the previous example, we started with an RHF calculation for the singlet ground state with the aug-cc-pVTZ64 basis set. The algorithm generated four π-orbitals from the occupied orbital subspace and another four π-orbitals from the unoccupied orbital subspace (Fig. 2). This (8e,8o) active space was used to obtain the five lowest singlet states (including the ground state) in the state-averaged CASSCF and subsequent NEVPT2 calculations. The singlet π→π* excitations obtained for octatetraene with this active space were compared with the computations of the electronic states performed with manual selection of the analogous active space (e.g., canonical orbitals from the RHF calculation) of the same size70–71 (Table 2). The states computed at the CASSCF/NEVPT2 level are identical to those computed at this level with the same size, but manually chosen, active space using the same basis set and geometry as used in Ref. 70. The SVD eigenvalues for the overlap between the active spaces before and after orbital optimization by CASSCF ranged from 0.9876 to 0.9999. This analysis implies that the algorithm provides a very accurate initial π-orbital active space for the CASSCF calculations of the octatetraene molecule as well.
Figure 2.
Eight π orbitals generated for octatetraene by PiOS before CASSCF optimization.
Table 2.
Lowest Excitation Singlet States (eV) for Octatetraene with Eight Active π-orbitals
C. Free-base porphine
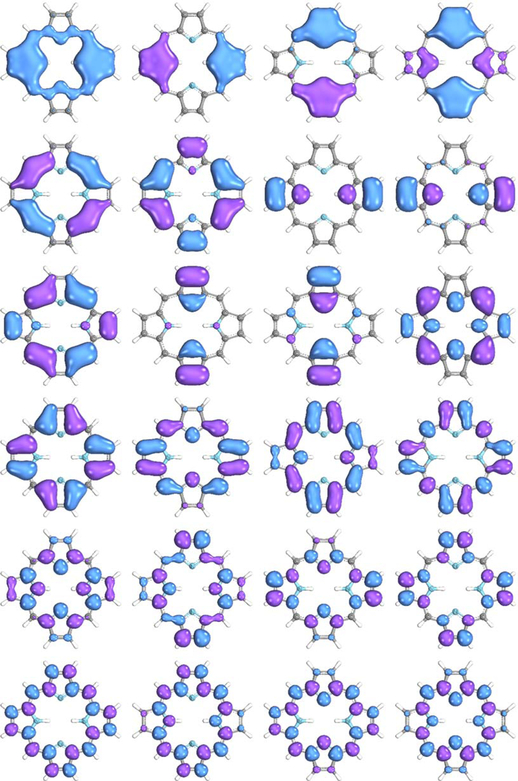
Free-base porphine is an example of an extended π-conjugated system that has 24 valence π- and π*-orbitals with 26 electrons. The geometry was obtained from Ref. 72. The RHF calculation for the singlet ground state, as well as the subsequent CASSCF and NEVPT2 calculations, were performed using the cc-pVDZ64 basis set. The PiOS algorithm built 13 π-orbitals from the occupied orbital subspace and another 11 π-orbitals from the unoccupied orbital subspace to yield a (26e, 24o) active space. Figure 3 shows all π-orbitals generated by the algorithm. This active space could be used to compute comprehensive electronic absorption spectra with modern methods supporting large active spaces, such as density matrix renormalization group (DMRG) or restricted active space self-consistent field (RASSCF) methods. Here, however, we set the algorithm to select only two HOMOs and two LUMOs to compute the Soret or B-band and the Q-bands of the porphine. All generated π-orbitals are sorted within their occupied and unoccupied subspaces based on the MO energies obtained through the Fock matrix and coefficients of the basis functions in the expansion of the generated π-orbital to compute the Soret or B-band and the Q-bands of the porphine.
Figure 3.
24 π orbitals generated for porphine by PiOS before CASSCF optimization.
The ground state and four excited states, corresponding to the Soret bands (Table 3), were computed using state-averaged CASSCF over five states with equal weights, followed by NEVPT2. The SVD eigenvalues for the overlap between the initial and optimized active spaces are 0.9835, 0.9835, 0.999, and 1.0. The computed CASSCF/NEVPT2 states are in good agreement with available theoretical and experimental values. The ability to easily select only the relevant highest-lying occupied and lowest-lying unoccupied orbitals even in complex and extended π-systems is one of the major advantages of the PiOS method, as it will often allow a massive reduction in computational cost via a decrease in the active space size.
Table 3.
Lowest Excitation Singlet States (eV) of Free-Base Porphine
D. Two-dimensional potential energy surfaces for the active site of the BLUF photoreceptor protein
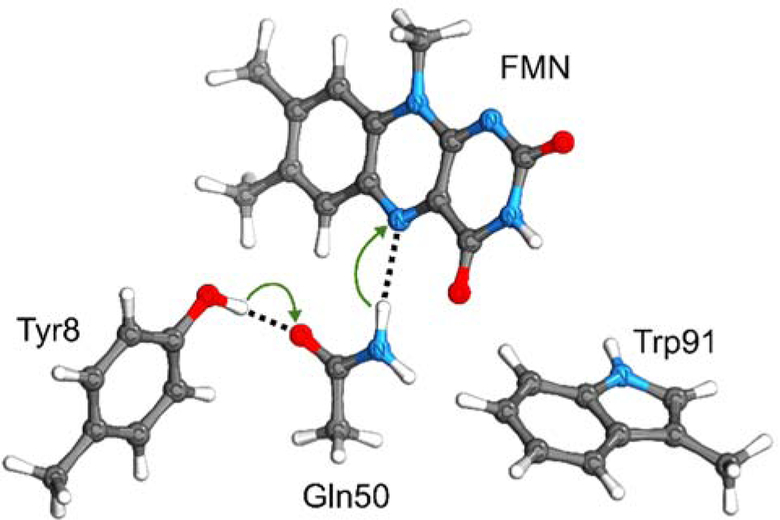
Now we consider a more complex system, namely the blue light-using flavin (BLUF) photoreceptor protein, which transmits a long-range signal to control cellular processes upon activation by light. In particular, we focus on the active site of the Slr1694 BLUF photoreceptor, which controls phototaxis in the cyanobacterium Synechocystis sp. PCC 6903. The active site consists of flavin adenine mononucleotide (FMN), conserved Gln and Tyr residues in the flavin binding pocket, and a semiconserved Trp. Upon photoexcitation of the flavin to its locally-excited (LE) state, the anionic semiquinone radical (FMN•−) is formed after charge transfer (CT) from Tyr8 to the flavin (FMN), and the neutral flavin semiquinone radical (FMNH•) is formed after the subsequent proton transfer from Tyr8 to the flavin via Gln50 (Figure 4). These two intermediates have been observed experimentally.77–83 However, many questions remain open, such as the nature of the double proton transfer reaction, which is presumed to occur in the CT state based on the experimental data but could occur either sequentially or concertedly. We used our PiOS approach in combination with the AVAS algorithm to compute two-dimensional potential energy surfaces along the two proton transfer coordinates for four different electronic states. Here we demonstrate such computations for a single conformation of the active site. The full study of this Slr1694 BLUF photoreceptor is beyond the scope of this work and will be presented in a separate paper.84 Herein we describe the core procedure and demonstrate how the active space selection method makes such calculations computationally tractable.
Figure 4.
The active site of the Slr1694 BLUF photoreceptor protein at the geometry with two protons positioned near their donor atoms. The two proton transfer reactions are indicated by green arrows, and the two proton transfer coordinates correspond to the axes connecting the heavy atoms in each of the two hydrogen bonds.
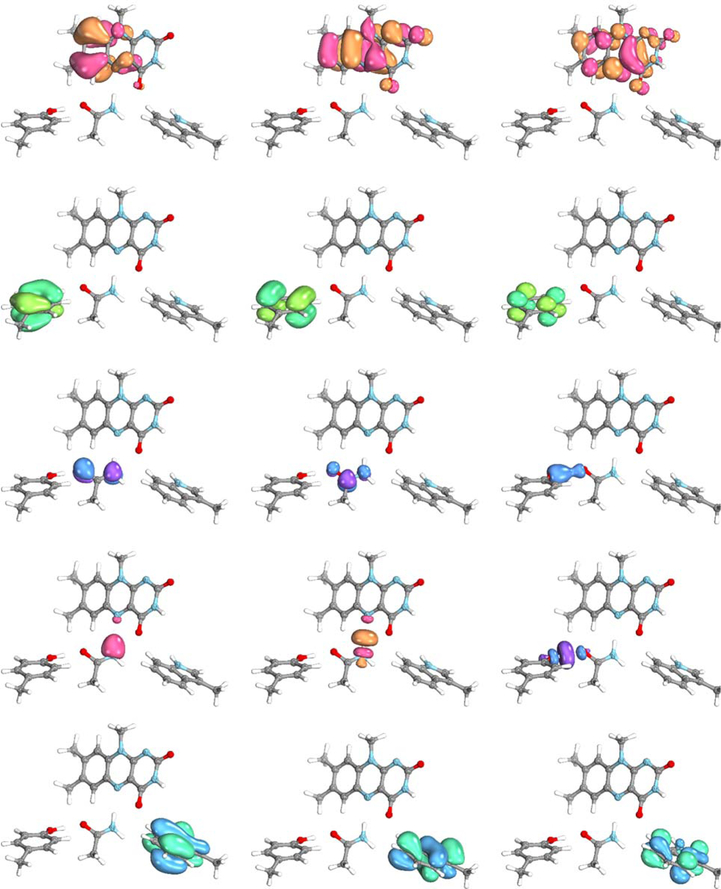
For a fixed conformation of the active site, we generated a two-dimensional grid by varying the positions of the two transferring protons along the lines connecting their respective donor and acceptor atoms (Figure 4) with a 0.1 Å step size. Our goal was to compute the two-dimensional potential energy surfaces for the ground state (GS) and the relevant excited states, namely the LE state within the flavin and the CTTyr and CTTrp states associated with electron transfer from Tyr8 or Trp91 to the flavin. To obtain the active orbitals (both bonding and antibonding types) associated with the two transferring protons, we used the AVAS algorithm, and to obtain the four π-conjugated fragments associated with FMN, Tyr8, Gln50, and Trp91, we used the PiOS method. This application utilizes the advantage of the PiOS method over the AVAS method for treating multiple π-systems within a molecular complex separately (i.e., selecting the HOMO and LUMO from each π-system individually) and subsequently combining them. In this case, the active space obtained in this manner is also combined with additional orbitals obtained with the AVAS method for modeling the bond formation and bond breaking associated with the two transferring hydrogen atoms.
We performed preliminary tests on a few geometries corresponding to different proton positions to determine the active space that is a reasonable size but also suitable for the description of all electronic states of interest, namely the GS, LE state, and two charge transfer states, CTTyr and CTTrp. The (18e, 15o) active space used for this system consists of two HOMOs and one LUMO for each of the FMN, Tyr8, and Trp91 (Figure 4), one HOMO and one LUMO for Gln50, and a pair of orbitals for each transferring proton (Figure 5). To obtain the complete twodimensional potential energy surfaces, we computed six electronic states in a state-averaged manner with CASSCF, followed by the NEVPT2 calculations. All of these calculations were performed with the 6–31++G**85–87 basis set.
Figure 5.
(18e,15o) active space generated for the active site of the Slr1694 BLUF photoreceptor protein at the geometry with two protons positioned near their donor atoms.
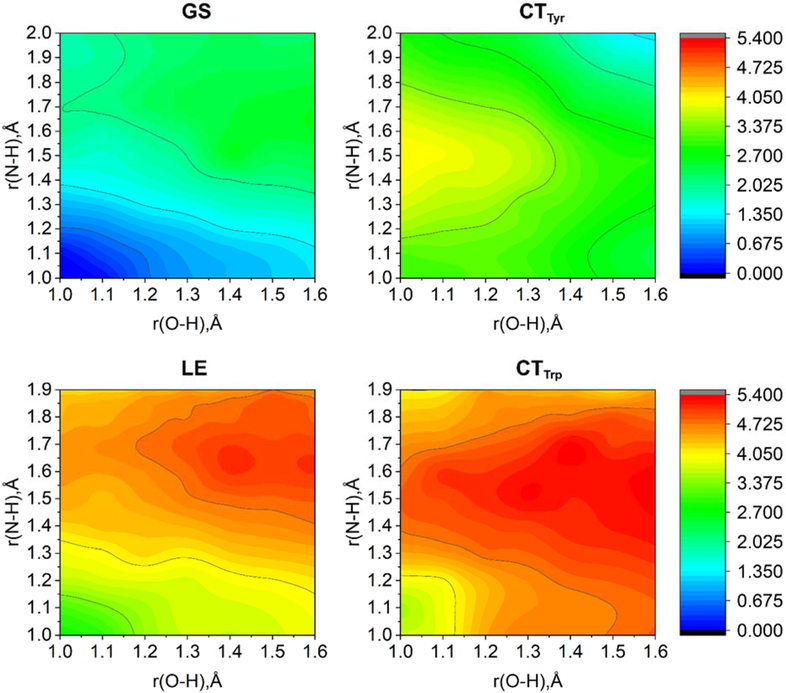
Figure 6 shows the computed potential energy surfaces as a function of the two proton transfer coordinates. Based on these potential energy surfaces and the analogous surfaces generated for other active site conformations, we discovered that double proton transfer can occur in the CTTyr state but not in the other states studied, corroborating the experimental data suggesting that electron transfer occurs prior to the double proton transfer reaction. In addition, the calculations suggest that the double proton transfer reaction is sequential, with proton transfer from Tyr8 to Gln50 occurring prior to proton transfer from Gln50 to the FMN. These conclusions are discussed more extensively elsewhere.84 Using the automated approach allowed us to compute excited electronic states at the CASSCF/NEVPT2 level with a (18e,15o) active space for more than 500 geometries with different protein active site conformations. This number of high-level calculations using a consistent active space for all geometries studied would not currently be computationally practical with a manual selection approach.
Figure 6.
Two-dimensional potential energy surfaces as a function of the two proton transfer coordinates in the GS, LE state, CTTrp state, and CTTyr state. These potential energy surfaces were computed with the CASSCF(18e,15o)+NEVPT2 method in the gas phase.
V. Conclusions
The automated π-orbital space (PiOS) method for selecting active spaces for multireference calculations of conjugated π-systems was presented. This approach is based on linear algebraic transformations of a single-reference wavefunction and Hückel theory for systems with conjugated π-bonds. This algorithm can be used alone to study π→π* excitations in conjugated systems such as aromatic hydrocarbons, polyenes, and porphyrins or, alternatively, can be combined with other active space selection approaches to study excitations in complex systems with multiple conjugated fragments. This work represents a continuation of efforts to advance the automated selection of active space orbitals to render multireference calculations of complex systems computationally practical. Such efforts are important for ensuring consistency, reproducibility, and broad applicability of multireference approaches for chemical and biological systems.
Supplementary Material
Acknowledgements
We thank Gerald Knizia for useful discussions and Josh Goings for providing the BLUF active site structures. This material is based upon work supported by the National Institutes of Health Grant GM056207 and by the Air Force Office of Scientific Research under AFOSR Award No. FA9550-18-1-0134. This work used the Extreme Science and Engineering Discovery Environment (XSEDE),88 which is supported by National Science Foundation grant number ACI-1548562. We used the Extreme Science and Engineering Discovery Environment (XSEDE) Stampede2 at the Texas Advanced Computing Center (TACC) at the University of Texas at Austin and Comet operated by the San Diego Supercomputer Center at UC San Diego through allocation TG-MCB120097. We also used the computational resources which were provided by the Yale Center for Research Computing.
Footnotes
Supporting Information
The Supporting Information is available free of charge on the ACS Publications website. Geometric structures of the studied systems, computed energies, additional details on identification of states for the active site of the BLUF photoreceptor.
References
- 1.Kallmann H; Pope M, Bulk conductivity in organic crystals. Nature 1960, 186, 31–33. [Google Scholar]
- 2.Ferraris J; Cowan DO; Walatka V; Perlstein JH, Electron transfer in a new highly conducting donor-acceptor complex. J. Am. Chem. Soc 1973, 95, 948–949. [Google Scholar]
- 3.Coleman LB; Cohen MJ; Sandman DJ; Yamagishi FG; Garito AF; Heeger AJ, Superconducting fluctuations and the peierls instability in an organic solid. Solid State Commun. 1973, 12, 1125–1132. [Google Scholar]
- 4.Ishiguro T; Yamaji K; Saito G, Organic Superconductors. 1998. [Google Scholar]
- 5.Hösel M; Angmo D; Krebs FC, Organic solar cells (OSCs). In Handbook of Organic Materials for Optical and (Opto)electronic Devices, 2013; pp 473–507. [Google Scholar]
- 6.Gunes S; Neugebauer H; Sariciftci NS, Conjugated polymer-based organic solar cells. Chem. Rev 2007, 107, 1324–38. [DOI] [PubMed] [Google Scholar]
- 7.Nguyen T-P; Molinie P; Destruel P, Organic and polymer-based light-emitting diodes. In Handbook of Advanced Electronic and Photonic Materials and Devices, 2001; pp 151. [Google Scholar]
- 8.Schwab T; Lüssem B; Furno M; Gather MC; Leo K, Organic light-emitting diodes (OLEDs). In Handbook of Organic Materials for Optical and (Opto)electronic Devices, 2013; pp 508–534. [Google Scholar]
- 9.Roos BO; Taylor PR; Siegbahn PEM, A complete active space SCF method (CASSCF) using a density matrix formulated super-CI approach. Chem. Phys 1980, 48, 157173. [Google Scholar]
- 10.Werner H-J; Meyer W, A quadratically convergent multiconfiguration–self-consistent field method with simultaneous optimization of orbitals and CI coefficients. J. Chem. Phys 1980, 73, 2342–2356. [Google Scholar]
- 11.Werner H-J; Meyer W, A quadratically convergent MCSCF method for the simultaneous optimization of several states. J. Chem. Phys 1981, 74, 5794–5801. [Google Scholar]
- 12.Werner H-J; Knowles PJ, A second order multiconfiguration SCF procedure with optimum convergence. J. Chem. Phys 1985, 82, 5053–5063. [Google Scholar]
- 13.Werner H-J; Knowles PJ, An efficient internally contracted multiconfiguration–reference configuration interaction method. J. Chem. Phys 1988, 89, 5803–5814. [Google Scholar]
- 14.Olsen J; Roos BO; Jorgensen P; Jensen HJA, Determinant based configuration interaction algorithms for complete and restricted configuration interaction spaces. J. Chem. Phys 1988, 89, 2185–2192. [Google Scholar]
- 15.Bofill JM; Pulay P, The unrestricted natural orbital–complete active space (UNO–CAS) method: An inexpensive alternative to the complete active space–self-consistent-field (CAS–SCF) method. J. Chem. Phys 1989, 90, 3637–3646. [Google Scholar]
- 16.Malmqvist PA; Rendell A; Roos BO, The restricted active space self-consistent-field method, implemented with a split graph unitary group approach. J. Phys. Chem 1990, 94, 5477–5482. [Google Scholar]
- 17.Andersson K; Malmqvist PA; Roos BO; Sadlej AJ; Wolinski K, Second-order perturbation theory with a CASSCF reference function. J. Phys. Chem 1990, 94, 5483–5488. [Google Scholar]
- 18.Andersson K; Malmqvist PÅ; Roos BO, Second-order perturbation theory with a complete active space self-consistent field reference function. J. Chem. Phys 1992, 96, 12181226. [Google Scholar]
- 19.Hirao K, Multireference Møller—Plesset method. Chem. Phys. Lett 1992, 190, 374380. [Google Scholar]
- 20.White SR; Martin RL, Ab initio quantum chemistry using the density matrix renormalization group. J. Chem. Phys 1999, 110, 4127–4130. [Google Scholar]
- 21.Angeli C; Cimiraglia R; Evangelisti S; Leininger T; Malrieu JP, Introduction of n-electron valence states for multireference perturbation theory. J. Chem. Phys 2001, 114, 1025210264. [Google Scholar]
- 22.Mitrushenkov AO; Fano G; Ortolani F; Linguerri R; Palmieri P, Quantum chemistry using the density matrix renormalization group. J. Chem. Phys 2001, 115, 6815–6821. [Google Scholar]
- 23.Chan GK-L; Head-Gordon M, Highly correlated calculations with a polynomial cost algorithm: A study of the density matrix renormalization group. J. Chem. Phys 2002, 116, 44624476. [Google Scholar]
- 24.Moritz G; Reiher M, Decomposition of density matrix renormalization group states into a Slater determinant basis. J. Chem. Phys 2007, 126, 244109. [DOI] [PubMed] [Google Scholar]
- 25.Malmqvist PA; Pierloot K; Shahi AR; Cramer CJ; Gagliardi L, The restricted active space followed by second-order perturbation theory method: theory and application to the study of CuO2 and Cu2O2 systems. J. Chem. Phys 2008, 128, 204109. [DOI] [PubMed] [Google Scholar]
- 26.Booth GH; Thom AJ; Alavi A, Fermion Monte Carlo without fixed nodes: a game of life, death, and annihilation in Slater determinant space. J. Chem. Phys 2009, 131, 054106. [DOI] [PubMed] [Google Scholar]
- 27.Kurashige Y; Yanai T, Second-order perturbation theory with a density matrix renormalization group self-consistent field reference function: theory and application to the study of chromium dimer. J. Chem. Phys 2011, 135, 094104. [DOI] [PubMed] [Google Scholar]
- 28.Ma D; Li Manni G; Gagliardi L, The generalized active space concept in multiconfigurational self-consistent field methods. J. Chem. Phys 2011, 135, 044128. [DOI] [PubMed] [Google Scholar]
- 29.Sharma S; Chan GK-L, Spin-adapted density matrix renormalization group algorithms for quantum chemistry. J. Chem. Phys 2012, 136, 124121. [DOI] [PubMed] [Google Scholar]
- 30.Li Manni G; Ma D; Aquilante F; Olsen J; Gagliardi L, SplitGAS method for strong correlation and the challenging case of Cr2. J. Chem. Theory Comput 2013, 9, 3375–84. [DOI] [PubMed] [Google Scholar]
- 31.Evangelista FA, A driven similarity renormalization group approach to quantum many-body problems. J. Chem. Phys 2014, 141, 054109. [DOI] [PubMed] [Google Scholar]
- 32.Evangelista FA, Adaptive multiconfigurational wave functions. J. Chem. Phys 2014, 140, 124114. [DOI] [PubMed] [Google Scholar]
- 33.Li Manni G; Carlson RK; Luo S; Ma D; Olsen J; Truhlar DG; Gagliardi L, Multiconfiguration pair-density functional Theory. J. Chem. Theory Comput 2014, 10, 3669–80. [DOI] [PubMed] [Google Scholar]
- 34.Li C; Evangelista FA, Multireference driven similarity renormalization group: a second-order perturbative analysis. J. Chem. Theory Comput 2015, 11, 2097–108. [DOI] [PubMed] [Google Scholar]
- 35.Guo S; Watson MA; Hu W; Sun Q; Chan GK, N-electron valence state perturbation theory based on a density matrix renormalization group reference function, with applications to the chromium dimer and a trimer model of poly(p-phenylenevinylene). J. Chem. Theory Comput 2016, 12, 1583–91. [DOI] [PubMed] [Google Scholar]
- 36.Fosso-Tande J; Nguyen TS; Gidofalvi G; DePrince AE 3rd, Large-scale variational two-electron reduced-density-matrix-driven complete active space self-consistent field methods. J. Chem. Theory Comput 2016, 12, 2260–71. [DOI] [PubMed] [Google Scholar]
- 37.Holmes AA; Tubman NM; Umrigar CJ, Heat-bath configuration interaction: an efficient selected configuration interaction algorithm inspired by heat-bath sampling. J. Chem. Theory Comput 2016, 12, 3674–80. [DOI] [PubMed] [Google Scholar]
- 38.Gomez JA; Henderson TM; Scuseria GE, Singlet-paired coupled cluster theory for open shells. J. Chem. Phys 2016, 144, 244117. [DOI] [PubMed] [Google Scholar]
- 39.Sharma S; Holmes AA; Jeanmairet G; Alavi A; Umrigar CJ, Semistochastic Heat-Bath Configuration Interaction Method: Selected Configuration Interaction with Semistochastic Perturbation Theory. J. Chem. Theory Comput 2017, 13, 1595–1604. [DOI] [PubMed] [Google Scholar]
- 40.Veryazov V; Malmqvist PÅ; Roos BO, How to select active space for multiconfigurational quantum chemistry? Int. J. Quant. Chem 2011, 111, 3329–3338. [Google Scholar]
- 41.Vogiatzis KD; Ma D; Olsen J; Gagliardi L; de Jong WA, Pushing configuration-interaction to the limit: Towards massively parallel MCSCF calculations. J. Chem. Phys 2017, 147, 184111. [DOI] [PubMed] [Google Scholar]
- 42.Sun Q; Yang J; Chan GK-L, A general second order complete active space self-consistent-field solver for large-scale systems. Chem. Phys. Lett 2017, 683, 291–299. [Google Scholar]
- 43.Smith JET; Mussard B; Holmes AA; Sharma S, Cheap and near exact CASSCF with large active spaces. J. Chem. Theory Comput 2017, 13, 5468–5478. [DOI] [PubMed] [Google Scholar]
- 44.Stein CJ; Reiher M, Automated selection of active orbital spaces. J. Chem. Theory Comput 2016, 12, 1760–71. [DOI] [PubMed] [Google Scholar]
- 45.Stein CJ; Reiher M, Automated identification of relevant frontier orbitals for chemical compounds and processes. Chimia (Aarau) 2017, 71, 170–176. [DOI] [PubMed] [Google Scholar]
- 46.Sayfutyarova ER; Sun Q; Chan GK-L; Knizia G, Automated construction of molecular active spaces from atomic valence orbitals. J. Chem. Theory Comput 2017, 13, 40634078. [DOI] [PubMed] [Google Scholar]
- 47.Bao JJ; Dong SS; Gagliardi L; Truhlar DG, Automatic selection of an active space for calculating electronic excitation spectra by MS-CASPT2 or MC-PDFT. J. Chem. Theory Comput 2018, 14, 2017–2025. [DOI] [PubMed] [Google Scholar]
- 48.Schmidt MW; Hull EA; Windus TL, Valence Virtual Orbitals: An unambiguous ab initio quantification of the LUMO Concept. J Phys Chem A 2015, 119, 10408–27. [DOI] [PubMed] [Google Scholar]
- 49.Derricotte WD; Evangelista FA, Localized intrinsic valence virtual orbitals as a tool for the automatic classification of core excited states. J. Chem. Theory Comput 2017, 13, 59845999. [DOI] [PubMed] [Google Scholar]
- 50.Hückel E, Zur Quantentheorie der Doppelbindung. Z. Physik 1930, 60, 423–456. [Google Scholar]
- 51.Hückel E, Quantentheoretische Beiträge zum Benzolproblem. Z. Physik 1931, 70, 204286. [Google Scholar]
- 52.Hückel E, Quantentheoretische Beiträge zum Problem der aromatischen und ungesättigten Verbindungen. III. Z. Physik 1932, 76, 628–648. [Google Scholar]
- 53.Knizia G, Intrinsic Atomic Orbitals: An unbiased bridge between quantum theory and chemical concepts. J. Chem. Theory Comput 2013, 9, 4834–43. [DOI] [PubMed] [Google Scholar]
- 54.Widmark P-O; Malmqvist P-Å; Roos BO, Density matrix averaged atomic natural orbital (ANO) basis sets for correlated molecular wave functions. Theoretica Chimica Acta 1990, 77, 291–306. [Google Scholar]
- 55.Roos BO; Lindh R; Malmqvist PA; Veryazov V; Widmark PO, Main group atoms and dimers studied with a new relativistic ANO basis set. J Phys Chem A 2004, 108, 28512858. [DOI] [PubMed] [Google Scholar]
- 56.Neese F; Valeev EF, Revisiting the atomic natural orbital approach for basis sets: robust systematic basis sets for explicitly correlated and conventional correlated ab initio methods? J. Chem. Theory Comput 2011, 7, 33–43. [DOI] [PubMed] [Google Scholar]
- 57.Claudino D; Gargano R; Bartlett RJ, Coupled-cluster based basis sets for valence correlation calculations. J. Chem. Phys 2016, 144, 104106. [DOI] [PubMed] [Google Scholar]
- 58.Cordero B; Gomez V; Platero-Prats AE; Reves M; Echeverria J; Cremades E; Barragan F; Alvarez S, Covalent radii revisited. Dalton Trans 2008, 2832–8. [DOI] [PubMed] [Google Scholar]
- 59.Hachmann J; Dorando JJ; Aviles M; Chan GK, The radical character of the acenes: a density matrix renormalization group study. J. Chem. Phys 2007, 127, 134309. [DOI] [PubMed] [Google Scholar]
- 60.Angeli C; Pastore M, The lowest singlet states of octatetraene revisited. J. Chem. Phys 2011, 134, 184302. [DOI] [PubMed] [Google Scholar]
- 61.Knizia G. http://sites.psu.edu/knizia/software/.
- 62.Angeli C; Cimiraglia R; Malrieu JP, n-electron valence state perturbation theory: A spinless formulation and an efficient implementation of the strongly contracted and of the partially contracted variants. J. Chem. Phys 2002, 117, 9138–9153. [Google Scholar]
- 63.Sun Q; Berkelbach TC; Blunt NS; Booth GH; Guo S; Li Z; Liu J; McClain JD; Sayfutyarova ER; Sharma S; Wouters S; Chan GK-L, PySCF: the Python-based simulations of chemistry framework. WIREs: Comput. Mol. Sci 2018, 8. [Google Scholar]
- 64.Dunning TH, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys 1989, 90, 1007–1023. [Google Scholar]
- 65.Frisch MJ; Trucks GW; Schlegel HB; Scuseria GE; Robb MA; Cheeseman JR; Scalmani G; Barone V; Petersson GA; Nakatsuji H; Li X; Caricato M; Marenich A; Bloino J; Janesko BG; Gomperts R; Mennucci B; Hratchian HP; Ortiz JV; Izmaylov AF; Sonnenberg JL; Williams-Young D; Ding F; Lipparini F; Egidi F; Goings J; Peng B; Petrone A; Henderson T; Ranasinghe D; Zakrzewski VG; Gao J; Rega N; Zheng G; Liang W; Hada M; Ehara M; Toyota K; Fukuda R; Hasegawa J; Ishida M; Nakajima T; Honda Y; Kitao O; Nakai H; Vreven T; Throssell K; M. JA Jr; Peralta JE; Ogliaro F; Bearpark M; Heyd JJ; Brothers E; Kudin KN; Staroverov VN; Keith T; Kobayashi R; Normand J; Raghavachari K; Rendell A; Burant JC; Iyengar SS; Tomasi J; Cossi M; Millam JM; Klene M; Adamo C; Cammi R; Ochterski JW; Martin RL; Morokuma K; Farkas O; Foresman JB; Fox DJ, Gaussian 09 Revision D.01. 2013. [Google Scholar]
- 66.Roos BO; Andersson K; Fülscher MP, Towards an accurate molecular orbital theory for excited states: the benzene molecule. Chem. Phys. Lett 1992, 192, 5–13. [Google Scholar]
- 67.Hashimoto T; Nakano H; Hirao K, Theoretical study of the valence π→π* excited states of polyacenes: Benzene and naphthalene. J. Chem. Phys 1996, 104, 6244–6258. [Google Scholar]
- 68.Lassettre EN; Skerbele A; Dillon MA; Ross KJ, High-Resolution Study of Electron-Impact Spectra at Kinetic Energies between 33 and 100 eV and Scattering Angles to 16°. J. Chem. Phys 1968, 48, 5066–5096. [Google Scholar]
- 69.Nakashima N; Inoue H; Sumitani M; Yoshihara K, Laser flash photolysis of benzene. III.Sn←S1absorption of gaseous benzene. J. Chem. Phys 1980, 73, 5976–5980. [Google Scholar]
- 70.Sokolov AY; Guo S; Ronca E; Chan GK-L, Time-dependent N-electron valence perturbation theory with matrix product state reference wavefunctions for large active spaces and basis sets: Applications to the chromium dimer and all-trans polyenes. J. Chem. Phys 2017, 146, 244102. [DOI] [PubMed] [Google Scholar]
- 71.Li C; Evangelista FA, Driven similarity renormalization group for excited states: A state-averaged perturbation theory. J. Chem. Phys 2018, 148, 124106. [DOI] [PubMed] [Google Scholar]
- 72.Perun S; Tatchen J; Marian CM, Singlet and triplet excited states and intersystem crossing in free-base porphyrin: TDDFT and DFT/MRCI study. Chem. Phys. Chem 2008, 9, 28292. [DOI] [PubMed] [Google Scholar]
- 73.Sauri V; Serrano-Andres L; Shahi AR; Gagliardi L; Vancoillie S; Pierloot K, Multiconfigurational Second-Order Perturbation Theory Restricted Active Space (RASPT2) Method for Electronic Excited States: A Benchmark Study. J. Chem. Theory Comput 2011, 7, 153–68. [DOI] [PubMed] [Google Scholar]
- 74.Edwards L; Dolphin DH; Gouterman M; Adler AD, Porphyrins XVII. Vapor absorption spectra and redox reactions: Tetraphenylporphins and porphin. J. Mol. Spect 1971, 38, 16–32. [Google Scholar]
- 75.Nagashima U; Takada T; Ohno K, Ab initio SCF-CI calculation on free base porphin and chlorin; theoretical analysis on intensities of the absorption spectra. J. Chem. Phys 1986, 85, 4524–4529. [Google Scholar]
- 76.Rimington C; Mason SF; Kennard O, Porphin. Spectrochim. Acta 1958, 12, 65–77. [Google Scholar]
- 77.Lukacs A; Brust R; Haigney A; Laptenok SP; Addison K; Gil A; Towrie M; Greetham GM; Tonge PJ; Meech SR, BLUF domain function does not require a metastable radical intermediate state. J. Am. Chem. Soc 2014, 136, 4605–4615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Mathes T; van Stokkum IHM; Stierl M; Kennis JTM, Redox modulation of flavin and tyrosine determines photoinduced proton-coupled electron transfer and photoactivation of BLUF photoreceptors. J. Biol. Chem 2012, 287, 31725–31738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Laptenok SP; Lukacs A; Brust R; Haigney A; Gil A; Towrie M; Greetham GM; Tonge PJ; Meech SR, Electron transfer quenching in light adapted and mutant forms of the AppA BLUF domain. Faraday Discuss. 2015, 177, 293–311. [DOI] [PubMed] [Google Scholar]
- 80.Gil AA; Laptenok SP; Iuliano JN; Lukacs A; Verma A; Hall CR; Yoon GE; Brust R; Greetham GM; Towrie M; French JB; Meech SR; Tonge PJ, Photoactivation of the BLUF protein PixD probed by the site-specific incorporation of fluorotyrosine residues. J. Am. Chem. Soc 2017, 139, 14638–14648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Gauden M; van Stokkum IHM; Key JM; Lührs DC; van Grondelle R; Hegemann P; Kennis JTM, Hydrogen-bond switching through a radical pair mechanism in a flavin-binding photoreceptor. Proc. Natl. Acad. Sci. U. S. A 2006, 103, 10895–10900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Bonetti C; Stierl M; Mathes T; van Stokkum IHM; Mullen KM; Cohen-Stuart TA; van Grondelle R; Hegemann P; Kennis JTM, The role of key amino acids in the photoactivation pathway of the Synechocystis Slr1694 BLUF domain. Biochemistry 2009, 48, 11458–11469. [DOI] [PubMed] [Google Scholar]
- 83.Bonetti C; Mathes T; van Stokkum IHM; Mullen KM; Groot M-L; van Grondelle R; Hegemann P; Kennis JTM, Hydrogen bond switching among flavin and amino acid side chains in the BLUF photoreceptor observed by ultrafast infrared spectroscopy. Biophys. J 2008, 95, 4790–4802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Sayfutyarova ER; Goings JJ; Hammes-Schiffer S, Double proton transfer coupled to electron transfer in the Slr1694 BLUF photoreceptor: a multireference electronic structure study. J. Phys. Chem. B, 2019, 123, pp 439–447. [DOI] [PubMed] [Google Scholar]
- 85.Hehre WJ; Ditchfield R; Pople JA, Self-consistent molecular orbital methods. XII. Further extensions of Gaussian—type basis sets for use in molecular orbital studies of organic molecules. J. Chem. Phys 1972, 56, 2257–2261. [Google Scholar]
- 86.Clark T; Chandrasekhar J; Spitznagel GW; Schleyer PVR, Efficient diffuse function-augmented basis sets for anion calculations. III. The 3–21+G basis set for first-row elements, Li–F. J. Comput. Chem 1983, 4, 294–301. [Google Scholar]
- 87.Hariharan PC; Pople JA, The influence of polarization functions on molecular orbital hydrogenation energies. Theor. Chim. Acta 1973, 28, 213–222. [Google Scholar]
- 88.Towns J; Cockerill T; Dahan M; Foster I; Gaither K; Grimshaw A; Hazlewood V; Lathrop S; Lifka D; Peterson GD; Roskies R; Scott JR; Wilkens-Diehr N, XSEDE: accelerating scientific discovery. Computing in Science & Engineering 2014, 16, 62–74. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.