Kinetics of Transient Protein Complexes Determined via Diffusion-Independent Microfluidic Mixing and Fluorescence Stoichiometry

Abstract

Low-affinity protein complexes and their transient states are difficult to measure in single-molecule experiments because of the requirement of low concentrations. A prominent solution to this problem is the use of microfluidic mixing devices, which rely on diffusion-based mixing of fluorescently labeled proteins. This is not ideal for multi-protein complexes, as the fluorescence signal is dominated by the already dissociated species. Here, we designed a microfluidic device for measuring structural properties and stoichiometries of transient states of diverse protein complexes with large equilibrium dissociation constants (K_D's) of 5 μM and above. It enables direct measurement of dissociation rates at a broad range of time scales from a few milliseconds to several minutes. This became possible by utilizing mixing structures for fast and homogenous mixing of components with varying diffusion coefficients and a design that enables fluorescence measurements at a defined single-molecule concentration. We used the platform to measure structural properties and dissociation rates of heat shock protein 90 (Hsp90) dimers and found at least two dissociation rates which depend on the nucleotide state. Finally, we demonstrate the capability for measuring also equilibrium dissociation constants, resulting in the determination of both the kinetics and thermodynamics of the system under investigation.

Introduction

Protein complexes and protein multimers are the basis for signaling and higher-level architectures in the cell. Their detection and characterization are still at the beginning. Standard methodologies such as immunoprecipitation (IP) assays measure the composition of stable complexes whereas low-affinity complexes or transient states of higher-affinity complexes are difficult or impossible to detect. Cryo-EM is able to capture transient complexes, but gives static snapshots and requires large efforts in sample preparation. On the other hand, single-molecule approaches have been often used to measure transient states, protein dynamics and dissociation kinetics ^1–3. Most prominent are fluorescence-based approaches, where the complexes are immobilized and their time-resolved single-molecule fluorescence is determined. However, this necessitates the introduction of cross-linkers or coil-coiled motives for artificially increasing the binding affinities as sub-nanomolar concentrations are usually needed for these measurements. Such elaborate biochemical engineering can modify the native function of the protein complex and prevents determination of dissociation rates and transient equilibrium dissociation constants (K_D's). Another approach for increasing the association rates for a small number of proteins is their encapsulation into vesicles^4–6.

In the past, several microfluidic mixing devices were designed to enable ultra-fast protein reactions or dilutions ^3,7,8. Such devices also satisfy the necessity of high concentrations for natural protein association and the necessity of low concentrations for single-molecule detection. These devices rely on diffusion-based mixing and can reach ultra-low dead times of microseconds. They take advantage of the broadening of the concentration profile due to diffusion of the analyte into the buffer region after dilution. Placing the confocal laser focus at the edge of this Gaussian concentration profile, allows us to measure the quasi-diluted sample. This concept has been used to study for example the folding kinetics of a protein which is labelled with a FRET dye pair at two different positions ^3,8.

This concept, however, is not suited for measuring the dissociation of protein complexes or multi-component protein complexes because the diffusion time depends on the particle size. The dissociated complex diffuses faster into the measurement region, so that the dissociation rate is altered; and structural analysis of the complex becomes difficult because the signal is dominated by the dissociated species. Besides, this approach can be prone to concentration fluctuations. Other designs relying on cascaded small dilution steps have very large dead times of seconds ^9–11.

In this work, we realized a single-step 50000-fold dilution and a subsequent diffusion-independent mixing within 10 ms that overcomes the mentioned challenges. We demonstrate the power of this device by measuring the nucleotide dependent dissociation kinetics of the Hsp90 dimer. The molecular chaperone heat shock protein 90 (Hsp90) is one of the most abundant proteins in eukaryotic cells. It is involved in the folding, activation and stabilization of various client proteins ¹². The function of Hsp90 depends on C-terminal dimerization, an exceptionally slow ATP hydrolysis and includes large conformational changes, e.g. a transient N-terminal dimerization mediated via a strand-exchange reaction ^13,14. While Hsp90’s N-terminal domain is known to bind and hydrolyse ATP, the isolated N-terminal domain has negligible ATPase activity, and the C-terminal association is known to be necessary for efficient ATP hydrolysis by Hsp90 ¹⁵. These dynamic structural changes and ATP hydrolysis are crucial for the functional cycle of Hsp90 and the concomitant processing of client proteins¹⁶. The N-terminal dynamics has been investigated in great detail during the last years and has led to a structural ensemble of the N-terminal dissociated (open) state of yeast Hsp90 ². The overall stability of the dimer has also been determined and resulted in a low K_D value of 60 nM for the yeast Hsp90 ¹⁵, but the C-terminal dynamics itself is hardly understood. A few studies with N-terminal stabilized constructs indicate C-terminal dynamics^17,18, but the artificial N-terminal stabilization prevents statements on the interplay between C-terminal dynamics and dissociation of the dimer. Finally, the role of Hsp90’s ATPase is one of the big questions in Hsp90 research and anti-cancer drug discovery. Dimer formation impacts the ATP hydrolysis rate and client binding ^15,16, while the release of ATP and clients might be coupled to dissociation. To scrutinize such a coupling and improve the mechanistic understanding of the Hsp90 machinery, it is important to study the dissociation rates of Hsp90 in a nucleotide-dependent manner from the closed and from the open dimer conformation, respectively. Such conformation-specific dissociation measurements will also be crucial for future studies of dynamic Hsp90 complexes including cochaperones and client proteins.

Experimental and Theoretical Methods

Single-molecule fluorescence measurements

The measurements were performed on a confocal microscope with pulsed interleaved excitation (PIE) ¹⁹. The fluidic device built on a precision 170μm-coverslip was placed on top of the objective, so that the lasers were focussed in the measurement channel. Buffer and sample volume flow were controlled by a neMESYS System (Cetoni) with two 50 ml glass syringes for buffer and one 100 μl glass syringe for the sample of interest. The measurement points were sampled with a stepper motor driven stage (Mad City Labs). At each point, microsecond-resolved fluorescence intensities were recorded for 3-5 min. For single-molecule analysis, dilution factors were adjusted via sample flow rate and the final concentration was checked via FCS (Fluorescence Correlation Spectroscopy) measurements. Donor dyes were excited with 532 nm and acceptor dyes with 640 nm. Sample fluorescence was separated from laser excitation (F53-534 Dual Line beam splitter z 532/633) and then split at 640 nm to separate donor and acceptor fluorescence (F33-647 beam splitter 640 DCXR) and sent through a pinhole of 150 μm diameter and recorded via single-photon detectors (two SPCM-AQR-14, Perkin Elmer and two PDM series APDs, Micro Photon Devices). For recording the photon stream, we used the HydraHarp 400 (Picoquant) capable of time-correlated single photon counting (TCSPC) and the Symphotime 32 software (Picoquant). Data was analysed in Symphotime, Matlab and LabView.

Fabrication of microfluidics

The design of the microfluidic device (see Figure S1) was printed as a negative film mask for curing spin coated photo resin SU-8 on a silicon wafer with UV light. Uncured resin was removed. The wafer with the cured resin was used as master for fabricating PDMS-based microfluidics (Sylgard 184, Dow Corning). Using the following parameters in the following order, we obtained a channel height of about 160 μm for SU-8 3050: spin coating at 30 s at 1300 rpm, baking at 45 min at 95°C (3 °C/min), spin coating at 30 s at 2900 rpm, baking at 30 min at 95 °C (3 °C/min), exposure at 70 s at 5.5 mW/cm² with I-line-filter and finally developing. PDMS oligomers were mixed 10:1, degassed and poured on the microfluidic wafer, and then degassed again. The PDMS was cured over night at 70 °C removed from the wafer and cut in shape. PDMS blocks can be stored at 70 °C for further crosslinking. Non-crosslinked PDMS oligomers that can cause green fluorescence background were removed by treating the PDMS block with triethylamine (2h), ethyl acetate (2h) and finally acetone (8h). During this process, the PDMS swells in triethylamine and then slowly reduces its size again, while the oligomers are removed subsequently. To remove residual acetone, the fluidic is blown dry with nitrogen and further dried at 70 °C for at least 1h.

Holes for connecting tubing are punched with a 1 mm biopsy punch. A cover slip was cleaned alternately with isopropanol and purified water, isopropanol being the last step, blown dry with nitrogen and then dehydrogenated at 70 °C for a few minutes. The PDMS block was covalently bound to the cleaned cover slip by activating the PDMS block and the cover slip in a plasma chamber (Diener) at 1 mbar for 1 min²⁰. The PDMS block was then quickly pressed on the cover slip and heated up for 5 min at 70 °C. After removing the fluidic device from the oven, a 6mM-solution of 500 Da PEG was incubated in the fluidic channels. The incubated device can be stored in the cold room for a few weeks, provided the inlets and outlets are closed. Shortly before measurement, the device is blown dry with nitrogen, flushed with measurement buffer and blown dry again several times to remove unbound PEG. The tubing material for the inlets was inert PTFE. For the outlets, more flexible tubings (Tygon) were used.

Biochemistry and sample preparation

A point mutation of Hsp90 was introduced – changing the aspartic acid residue at position 452 to a cysteine residue – to enable cysteine-maleimide labelling. Hsp90 was then expressed and purified using standard methods as described before ². Dyes used in this study were ATTO550 as donor and ATTO647N as acceptor (both AttoTec). Labelling efficiencies were between 90 % and 100 %.

Donor-labelled homodimers (i.e., Hsp90 dimers with the same dye at the same position on each monomer) were incubated together with acceptor-labelled homodimers for about 30 min at 37 °C for monomer exchange. We obtained about 50 % heterodimers that have exactly one acceptor dye at one monomer and one donor dye at the other monomer. Possible aggregates are removed by spinning the sample with a cooled centrifuge for about 30 min at 4 °C at 15000 rcf.

Hydrodynamic resistance network for calculating dilution factor and velocity in measurement channel

The Navier-Stokes equation can be simplified to the Hagen-Poiseuille equation for laminar and steady-state flow:

$$\eta \Delta v-\nabla p=0$$ (1)

For rectangular cross section of the microfluidic channels the volume flow rate Q can be simplified in case of h<<b with errors of 13 % for h=b and 0.2 % for h=b/2²¹.

$$Q\approx \frac{h^{3}b\Delta p}{12\eta L}\left(1-0.63\frac{h}{b}\right)$$ (2)

Here, h is the channel height, b the channel width, L the channel length, η the viscosity, and Δp the pressure difference. Combining all constants to the hydrodynamic resistance R_hyd leads to the following relation, which allows calculating the volume flow rates in each microfluidic channel depending on the effective resistance R_hyd,eff (analogous to an electrical resistance network):

$$\Delta p=R_{hyd,eff}Q$$ (3)

Widths and heights of the device channels were chosen so that fast mixing, sufficient large passage time through the confocal lasers and a broad observation time window were obtained. The dilution factor f was additionally controlled by the inlet pressures:

$$f=\frac{Q_{buffer}}{Q_{protein}}=\frac{\Delta p_{buffer}{R}_{hyd,protein}}{\Delta p_{protein}{R}_{hyd,buffer}}$$ (4)

Notably, the flow rate in the center of a laminar flow is twice as a high as the average flow rate assuming a quadratic velocity profile, so that the input flow rates need to be multiplied by a factor of two for calculating the dead time of the mixing structures.

Calculation of flow velocity and time points from FCS experiments

For each measurement point in the flow chamber, an FCS curve from the donor fluorescence (autocorrelation of donor time-resolved fluorescence intensity after donor excitation) was calculated (see Figure S2). This curve was fitted with a modified FCS function including a term for a moving fluid as described in ref. 22 (see also Supplementary Note 1). To obtain the velocity of the fluid, we divide the diameter of the focus by the passage time τ_F from the FCS fit. The focus diameter was determined via FCS diffusion measurement (without flow) with a dye with known diffusion coefficient (Rhodamine B). As can be seen in Figure S3, the flow velocity nicely correlates with the channel width. The absolute time is calculated by integrating the inverse flow velocity over the distance travelled in the measurement channel. Finally, the dead time for passing the Tesla mixing structures is added. This dead time is estimated by dividing the volume of the Tesla structures by the volume flow rate divided by a factor of two assuming a quadratic velocity profile for laminar flow. A typical dead time is 11 ms for three Tesla structures, a channel height of 160 μm and a total volume flow rate of 16 μL/s.

Calculation of homo dimer dissociation

Our ansatz assumes the following simple association and dissociation kinetics for the Hsp90 homo dimer:

$$M+M\underset{k_{dis}}{\overset{k_{ass}}{\rightleftarrows }}D$$ (5)

Here M is a monomer and D a dimer. Because of the fast concentration decrease from a concentration above the equilibrium dissociation constant K_D = k_dis/k_ass to a concentration of more than 100 times below the dissociation constant, the association rate k_ass can be neglected in comparison to the dissociation rate k_dis:

$$\frac{d\left[D\right]}{dt}=k_{ass}{\left[M\right]}^2-k_{dis}\left[D\right]\approx -k_{dis}\left[D\right]$$ (6)

This leads to a simple exponential decay with the starting concentration of dimers D₀:

$$[D]\approx D_0{e}^{-k_{dis}t}$$ (7)

If several dissociating species are present in the sample, the total decay curve can be described with a linear combination of exponential decays.

Calculation of dimer fraction

See supplementary Table S1 for an overview of all quantities introduced in this chapter.

The dissociation of the Hsp90 dimer does not result in a population with a different FRET efficiency, but in an increase in the donor-only (D) and acceptor-only (A) population and decrease in FRET population (F). Therefore, we use histograms of stoichiometry, where the different populations can be well separated (see Fig. 2B). The fully corrected stoichiometry can be determined using the equation (21) in ²³. The ratio between the FRET population (species with donor + acceptor dye) and the acceptor population (species with one or two acceptor dyes) can be used as a measure to calculate the fraction of associated dimers independently from the protein concentration. For randomly exchanging homo dimers (two identical monomers), there are already doubly-labelled donor- and acceptor-only populations at the very beginning of the measurement. These doubly-labelled single-color species also contribute to the dimer dissociation. Therefore, we derive a formula to calculate the real dimer fraction on the basis of the apparent single-color population. The following calculations are done for the apparent (total) acceptor-only population A_app, but can be analog done for the apparent donor-only population D_app.

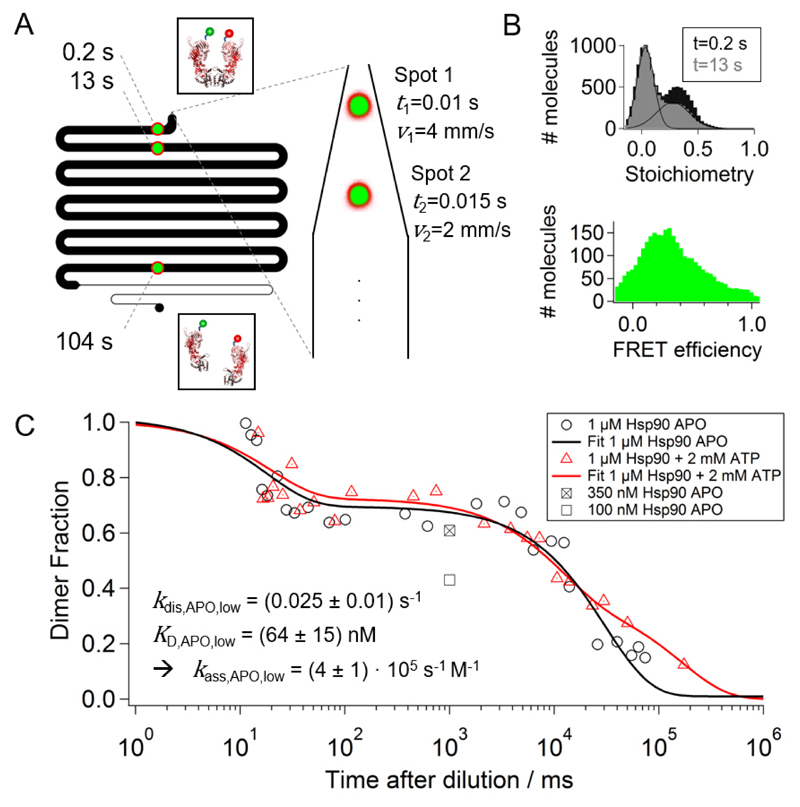
Figure 2.

Dissociation of the Hsp90 dimer. (A) The confocal laser foci are placed at different positions in the measurement chamber representing different times after dilution. The design of the measurement channel allows us to measure dissociation rates between 5 ms 100 s (B) Stoichiometry histograms are shown for two different measurement positions, i.e. dilution times. The corrected dimer fraction at each time point is calculated from the acceptor-only (S < 0.2) and the FRET population (0.2 < S < 0.8) using equation (14). A FRET efficiency histogram is shown for a time point of 1 s after dilution indicating that Hsp90 is mainly populated in an N-terminally open conformation. (C) The corrected dimer fractions for two measurement series, namely 1 μM Hsp90 APO (black circles) and 1 μM Hsp90 + 2mM ATP (red triangles), are plotted on a logarithmic timescale. The data is fitted with two- or three-exponential decays. Optimal fits result in two dissociation rates for Hsp90 APO, k_dis,APO,high=52 s^-1 with amplitude A_APO,high=32 % and k_dis,APO,low=0.025 s^-1 with A_APO,low=68 %, and three dissociation rates for Hsp90+ATP, k_dis,ATP,high=51 s^-1 with A_ATP,high=28 %, k_dis,ATP,mid=0.09 s^-1 with A_ATP,mid=36 %, and k_dis,ATP,low=0.006 s^-1 with A_ATP,low=36 %. The square marks represent average dimer fractions for different Hsp90 APO concentrations in the incubation chamber. This enables determination of the equilibrium dissociation constant K_D and the association rate k_ass. The uncertainties are the standard deviation of three separate measurements.

The fraction of dimers that are still present at a defined position, i.e. time, is:

$$P_D=\frac{F}{F+A^{\prime }}$$ (8)

A′ is the number of acceptor-only molecules of interest arising from the dissociation of FRET dimers, but we do also have dimers labelled with two acceptors (AA) and their dissociation products (A_AA→A). We get:

$$A^{\prime }=A_{\text{app}}-AA-A_{\text{AA}\to \text{A}}$$ (9)

A_AA→A is related to A′ by a factor C_AA/F that is defined by the ratio of the doubly-labelled acceptor-only population AA and the FRET population F at time zero (when no dimer is dissociated yet). This factor depends on the initial concentration ratio of donor-labelled and acceptor-labelled species and is 0.5 for an ideal 50%/50% mixture (binominal distribution). The time zero is practically not accessible and after the dead time of a few milliseconds the dimer might be already partially dissociated. That is why we describe the concentration ratio C_AA/F by means of the concentration ratio C_AA/DD = AA/DD which remains constant even after partial dissociation:

$$C_{\text{AA}/\text{F}}=\frac{AA}{F}=\frac{\frac{A}{D+A}\frac{A}{D+A}}{2\frac{D}{D+A}\frac{A}{D+A}}=\frac{AA}{2\sqrt{DD\cdot AA}}=0.5\sqrt{\frac{AA}{DD}}$$ (10)

Please note that the acceptor-only population AA, the donor-only population DD and the FRET population F are only correctly determined when normalizing the burst intensities with the beta factor. After correction, the FRET population should be located at S = 0.5. Then:

$$A_{\text{AA}\to \text{A}}=A^{\prime }\cdot 2\cdot C_{\text{AA}/\text{F}}$$ (11)

Next, we introduce the factor C_th which corrects for the different brightness levels of double labelled species AA compared to singly labelled species A’ for a certain threshold th. The factor describes the ratio of the number of AA bursts divided by the number of A’ bursts for the same fixed threshold th. This ratio is difficult to obtain, but it can be also described by the ratio of the FRET population F for donor and acceptor burst selection divided by the FRET population F for acceptor burst selection of the same measurement normalized by the concentration ratio C_AA/F (see also Figure S4):

$$C_{\text{th}}=\frac{AA}{A^{\prime }}=\frac{F_{\text{Select}\_\text{DonAndAcc}}}{F_{\text{Select}\_\text{AccOnly}}}.C_{\text{AA}/\text{F}}$$ (12)

Please note that for the histogram based on acceptor-only bursts, the same beta factor must be used as determined for the histogram based on donor and acceptor bursts. Thus, for the histogram based on acceptor-only bursts, the FRET population must NOT be located at S = 0.5. Then, we obtain (with equation (8)):

$$AA=(F+A^{\prime })\cdot P_{\text{D}}.C_{\text{th}}=F\cdot C_{\text{th}}$$ (13)

Inserting equations (11) and (13) into equation (9) and then equation (9) into (8) we obtain:

$$P_{\text{D}}=\frac{F}{F+(A_{\text{app}}-F\cdot C_{\text{th}})/(1+2\cdot C_{\text{AA}/\text{F}})}$$ (14)

These measurements resulted in C_AA/F = 0.7 and C_th20 = 1.1 (for a threshold of 20) for the Hsp90+ATP measurements and in C_AA/F = 0.75 and C_th20 = 1.4 (for a threshold of 20) for the Hsp90 APO measurements (APO: without nucleotides).

Results and Discussion

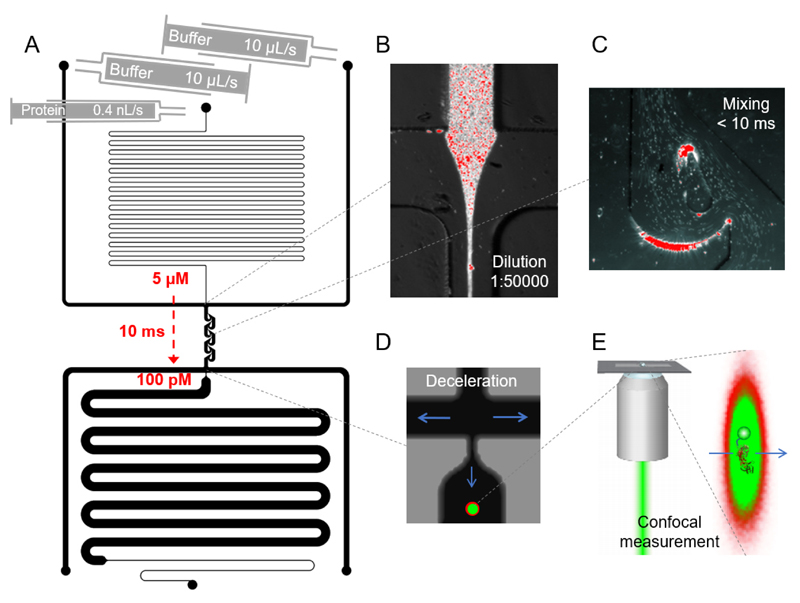
The microfluidic device is based on cost-efficient Polydimethylsiloxan (PDMS) stamping technology. In short, viscous PDMS and crosslinker are hardened on a structured surface to form microfluidic channels. This PDMS stamp is plasma-activated and covalently bound to an optical glass slide for optical measurements. The glass slide and the PDMS channels are passivated with PEG molecules after eliminating green fluorescing PDMS cross linker molecules. Figure 1 shows our microfluidic design, which can be divided into three sections: (i) dilution, (ii) mixing and (iii) deceleration. One aspect of our stably operating microfluidic device is using a constant flow rate at the inputs instead of constant pressure such as gravity flow. The constant flow rates for the buffer and protein chambers realized by step-motor driven syringes with different piston diameters enable a stable flow ratio between buffer and sample. In contrast to constant input pressures, constant input flow rates are not affected by temporarily increased hydrodynamic resistance due to impurities or bubbles. In addition, we adapted the hydrodynamic resistances of the input channels – by modifying channel widths and lengths, so that they are reciprocal to the flow rates. In this manner, we keep the input pressures constant and avoid recoil. To avoid concentration fluctuations in the measurement chamber, both a stable dilution and diffusion-independent mixing are important. The mixing is realized with specifically designed Tesla structures which generate local differences in flow rates to fold different parts of the flow into each other ²⁴. We found that already two pairs of those structures are sufficient to homogenize the concentration profile of a 50.000-fold dilution. This was additionally verified by observing the mixing of orange marker ink under a fluorescence microscope for different numbers of Tesla structures (see Figure S5). For an optimal mixing, it is important that the concentrated sample stream enters the very center of the mixing structures. Therefore, identical and constant flow rates in both buffer channels are necessary. This is guaranteed by two independent inputs enabling two independent constant flow rates that are not affected by local variations in hydrodynamic resistances. The deceleration in the measurement chamber is realized by bypassing the majority of the flow. This has the positive side effect that the remaining concentration profile gets flattened. The particle velocity in the measurement channel depends on the network of hydrodynamic resistances of measurement channel and bypass channels. This resistance network can be easily calculated analogous to an electrical resistor network. During measurement the local particle concentration is additionally verified via FCS (see Methods and Figure S2). The flow velocity is adjustable while 1 mm/s is a good compromise between fast time-resolution in the lower millisecond range and detecting sufficient photon counts. Further increasing the confocal volume would improve the photon statistics but would also decrease the necessary concentration for single-molecule detection and thereby also the dilution factor.

Figure 1.

Diffusion-independent microfluidic mixing combined with confocal fluorescence spectroscopy. (A) Design of a microfluidic device with two inlets for constant buffer flow and one inlet for concentrated protein sample with lower flow rate. After dilution by a factor of 50000 at the first T cross (B), the protein sample is mixed with the buffer via specifically designed mixing structures (C) enabling fast and homogenous diffusion-independent mixing with dead times of 10 ms and below. The bright white-red spots are fluorescently labelled microspheres measured in a wide-field fluorescence microscope. In the deceleration section (D) the two outer channels have a much lower hydrodynamic resistance than the measurement channel to slow down the flow rate in the measurement channel for collecting sufficient photons after confocal excitation (E).

With the presented design, we are able to fully dilute a concentrated protein sample within 10 ms from 5 μM down to 100 pM. The dead time can be further decreased down to the microsecond timescale by increasing the flow rates of buffer and protein. However, this would lead to an increased waste production rate of buffer and sample. Similarly, the dilution factor of 50.000 can be further increased by increasing the ratio of the flow rates and increasing the hydrodynamics resistance of the protein incubation channel.

For a set of measurements, the confocal foci of the red and the green laser are subsequently placed at different positions in the measurement chamber. These positions correspond to different times after dilution (Figure 2A). The final challenge is to quantitatively distinguish dissociated and associated species (here: Hsp90 monomers and Hsp90 dimers). Therefore, we label one half of the Hsp90 monomer concentration with green fluorophores (ATTO550) and the other half with red fluorophores (ATTO647N). Then the stoichiometry (S) histograms are calculated for all acceptor bursts, namely bursts with sufficient large fluorescence intensity in the red detection channel after red excitation. Within those histograms (Figure 2B), associated species (0.2 < S < 0.8) can be clearly distinguished from dissociated species (S < 0.2). The dimer fraction at each time point is calculated from those two populations by using equation (14) (see Methods section for the derivation). This equation corrects for the acceptor only population that is present already at time zero because of dimers that have two acceptors caused by the binomial distribution of exchanged dimers randomly formed from green and red labelled monomers.

Figure 2C shows the result of this analysis for starting concentrations of 1 μM Hsp90 in the nucleotide free APO state (black curve) and for 1 μM Hsp90 + 2 mM ATP (red curve). The dimer fraction plotted over logarithmic time after dilution reveals two exponential decays for HSP90 APO with dissociation rates of k_dis,APO,high=52 s^-1 with a fraction of about A_APO,high=32 % and k_dis,APO,low=0.025 s^-1 with a fraction of about A_APO,low=68 %. Interestingly, in presence of 2 mM ATP, three dissociation rates can be observed. The fast dissociation rate of ATP Hsp90, k_dis,ATP,high=51/s with A_ATP,high=28 %, is almost identical with the fast dissociation rate of APO Hsp90. At larger timescales, two dissociation rates can be fitted, namely k_dis,ATP,mid=0.09 s^-1 with A_ATP,mid=36 % and k_dis,ATP,low=0.006 s^-1 with A_ATP,low=36 %.

If the above analysis is performed at different sample concentrations in the incubation chamber, the equilibrium dissociation constant K_D can be determined. The K_D value for a certain dissociation rate can be found by measuring with different sample concentrations at the same time point. This time point should be in a range where this dissociation rate is dominant, ideally in a plateau regime at a time point that is about one order of magnitude shorter than the inverse dissociation rate. This plateau regime can be best found when plotting dimer fractions against the logarithm of the time. The K_D can then be found at a sample concentration that results in about 50 % of the original dimer fraction, which in turn is determined using concentrations much larger than the K_D. We have done this for the lower dissociation rate of APO Hsp90, k_dis,APO,low=0.025 s^-1,by measuring the dimer fraction at the dilution time of 1 s, which lies in the plateau region between the fast and the slow rate (see square marks in figure 2C). The found K_D of about 64 nM fits well to the literature value of 60 nM ¹⁵. The respective association rate is then obtained by dividing the dissociation rate by the K_D value.

The broad distribution of dissociation rates found for APO and ATP Hsp90 can be caused by an ensemble of associated dimer states with slightly different affinities similar to as observed with a dynamic multi-pair FRET approach ².

However, the dissociation constant, K_D,APO,high, for the fast rate, k_dis,APO,high=52 s^-1, should not differ more than an order of magnitude from the dissociation constant of K_D,APO,low=64 nM found for the slow rate, k_dis,APO,low=0.025 s^-1. This is because K_D,APO,high cannot be much larger than 1 μM – the starting concentration of Hsp90 before dilution – as K_D,APO,high appears with a relative large amplitude of about 32 %. This upper limit for K_D,APO,high would result in a lower limit for the association rate of 5.2·10⁷ s^-1 M^-1. Interestingly, this rate is significantly larger than typical protein association rates of 10³ – 10⁶ s^-1 M^-1 that include alignment of reactive sites ²⁵. Therefore, this fast association has to be a conformation-independent transient interaction. This could be caused by a fast and transient interaction of the hydrophobic middle domains of the monomers that might then lead into the association process for the longer-living state with k_dis,APO,low. Future concentration-dependent dilution measurements will shine further light into the thermodynamic properties and possible kinetic model.

While the fast dissociation rate seems to occur independently of Hsp90’s nucleotide state, the dissociation rates found at larger timescales apparently depend on the Hsp90’s nucleotide state.

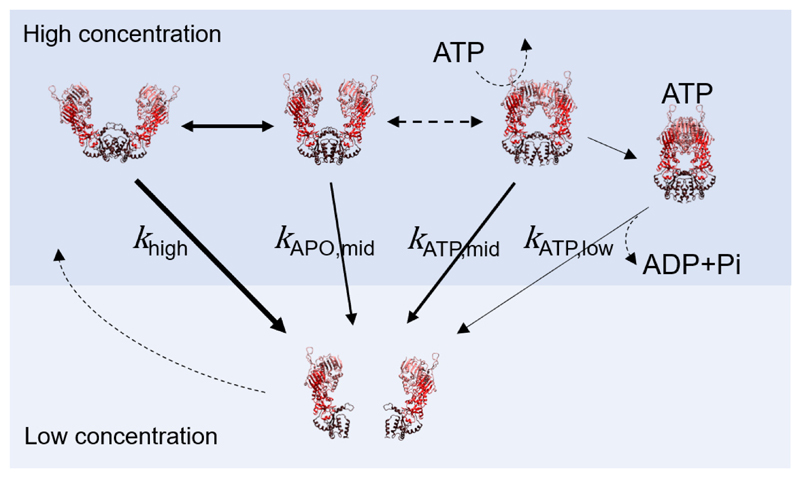
Interestingly, both APO Hsp90 dimer dissociation rates are faster than the lower dissociation rate for ATP Hsp90. This indicates that ATP binding might partially stabilize the dimer binding affinity of Hsp90. On the other hand, the APO Hsp90 dimer dissociation rates are faster than the ATP hydrolysis rate. Also, the association rate of APO Hsp90 is faster with at least 0.4 s^-1, considering typical concentrations of 1-100 μM for Hsp90 in the cell ^26,27. Only the lower dissociation rate, k_dis,ATP,low=0.006 s^-1, measured for ATP Hsp90 is comparable to the yeast hydrolysis rate of about 0.006 s^-1 at 30 °C ²⁸. This further indicates that hydrolysis might be directly coupled to dimer dissociation. See Figure 3 for a summary of the found dissociation rates and possible overall transitions.

Figure 3.

Dimer dissociation of Hsp90 depends on the initial state. The dimer dissociation of Hsp90 + 2 mM ATP is potentially coupled to ATP hydrolysis, while the dimer association in a stable closed dimer state is potentially coupled to ATP binding. The arrow thickness is about proportional to the logarithmic of the found dissociation rates.

Our single molecule microfluidic approach further reveals structural and mechanistic insights of transient protein states. For example, the protein state from which the dimer dissociation takes place can now be estimated by following FRET efficiency histograms over time. Here, we found ATP and APO Hsp90 to be mainly populated in the N-terminally open state for dilution times up to some seconds (see Figure 2B). At larger timescales (> 10 s) a slightly increased closed population can be observed indicating that the slowest dissociation rate, k_dis,ATP,low, (partially) occurs from a closed dimer state.

It might be possible that the Hsp90 dimer dissociation is necessary for re-association into different N-terminally open or closed conformations and also for reaching the ATP hydrolysis competent state. In other words, the Hsp90 homodimer might be describable with the morpheein model of allosteric regulation. Thus, Hsp90 might interchange between different states via transient dissociation.

Conclusion

The microfluidic device demonstrates a novel way for measuring the affinities and transient structural properties of low-affinity protein complexes. In contrast to standard approaches such as stopped-flow experiments, we were able to observe very fast dissociation rates, extract a quantitative dissociation model and analyse time-resolved structural properties from the single-molecule fluorescence parameters.

We have shown that for a complex multi-domain protein like Hsp90, a broad distribution of dissociation rates can be determined in a nucleotide- and conformation-dependent manner. We found so far unknown dissociation rates for both APO Hsp90 and ATP Hsp90. The results give credence to the hypothesis that hydrolysis is coupled to dimer dissociation and indicates that ATP binding stabilizes Hsp90 dimerization. The presented approach provides the basis for future studies of transient binding in the Hsp90 system and other multi-protein complexes.

Supplementary Material

The supporting information contains one table, five figures and one note.