Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 May 1;10(10):2578–2584. doi: 10.1021/acs.jpclett.9b00862

Environmentally Controlled Charge Carrier Injection Mechanisms of Metal/WS2 Junctions

Rik van Bremen †,*, Kevin Vonk †, Harold J W Zandvliet †, Pantelis Bampoulis ‡,†,*
PMCID: PMC6526467  PMID: 31041866

Abstract

graphic file with name jz-2019-008622_0005.jpg

Here we report on a novel, noninvasive route for operando tailoring of the charge transport properties of metal/WS2 contacts without the negative impacts to two-dimensional materials arising from conventional doping methods. The doping level of thin WS2 flakes supported on insulating mica is susceptible to local charge variations induced by the presence of a hydration layer between mica and WS2. We demonstrate, via the use of several complementary scanning probe techniques, that the direct control of the state and thickness of this intercalated water film controls the charge injection properties of Pt/WS2 nanocontacts. A switch from unipolar to ambipolar transport was achieved by environmentally controlling the thickness of the intercalated water. We show that the effect persists even for multilayer flakes and that it is completely reversible, opening a new route toward the realization of novel electronics with environmentally controllable functionalities.

A major challenge when incorporating two-dimensional (2D) materials in devices is the control of the contact properties of the metallic leads1−6 and the influence of atmospheric conditions on these contact properties.7−11 For 2D semiconductors, the transport behavior of devices is often determined by the metal–semiconductor junction. In the Schottky–Mott model, the barrier height for charge carrier injection in such a junction is determined by the difference between the Fermi level of the metal and the electron affinity of the semiconductor. However, Fermi level pinning and metalization of the semiconductor often make it difficult to control the barrier height via the metal contact.12−14 It has been shown that Fermi level pinning can be alleviated by using transferred atomically flat metal contacts15 or by the use of 2D buffer layers.16−18 Vacuum deposition of Au contacts19 and annealing in vacuum20 have also resulted in lower contact resistances. Another promising method to control the contact properties is the adjustment of the Fermi level of the 2D semiconductor.21 Unfortunately, shifting the Fermi level by incorporating dopants in an atomically thin layer is not as successful as it is in bulk semiconductors as the embedding of dopants with traditional techniques induces damage to the 2D semiconductor.22

WS2 is one of the members of the transition-metal dichalcogenide (TMDC) family with semiconducting properties. As a bulk crystal it has an indirect band gap of 1.3 eV, while single-layer WS2 has a direct band gap of 2.1 eV.23 A transistor of a single layer of WS2 shows mobilities up to 50 cm2/(V s) and a current on/off ratio of 106.24 The electric properties of WS2 transistors manufactured on standard Si/SiO2 are strongly affected by charge puddles and ripples induced by the substrate.25,26 An alternative substrate is muscovite mica. Muscovite mica is atomically flat and therefore does not lead to rippling of the adlayer.27 This makes mica an ideal candidate for maintaining high carrier mobilities and high switching speeds of the adlayer.28 As we will show, another advantage of mica is its hydrophilicity, which promotes water adsorption at ambient conditions.29 These water films are still present between the mica and a supported 2D material.30 The thickness of the water film depends on the relative humidity (RH) and temperature of the environment.31,32 This way the water thickness can be varied from 1 to 3 layers.33−35

In this Letter we will show that the properties of a Pt/WS2 contact can be controlled not only by the thickness of the WS2 flake36 but also by the hydration state of the underlying supporting substrate. Static water doping of the WS2 layer is induced by charge transfer from the underlying substrate and further controlled by the exact thickness of the water film.37 We demonstrate that the charge carrier injection mechanism in Pt/WS2 nanocontacts is directly controlled by the thickness of the intercalated water film. In ambient conditions, thermionic emission (TE) is identified to be the dominant injection mechanism in thicker WS2 flakes. At lower RH, water doping leads to a substantial enhancement of Fowler–Nordheim (F–N) tunneling, increasing the reverse bias current. The contact properties of thinner WS2 flakes are well-described by a combination of F–N and direct tunneling (DT). In particular, we show a shift from unipolar to ambipolar transport when reducing the thickness of the intercalated water (between thin WS2 and mica) from two layers to one layer. We show that water doping can reduce the contact resistance and eliminate the unipolar properties of the contact. This method of controlling the local charge transfer from the supporting substrate is a nonintrusive doping approach, which retains the intrinsic physical properties of the 2D semiconductor. Furthermore, we demonstrate that this approach provides a novel pathway for the realization of environmentally controlled 2D TMDC-based devices with in situ tunability.

Figure 1a shows the optical micrograph of a thin WS2 flake on mica. To study the system with conductive-atomic force microscopy (c-AFM), we have made an electrical connection to the AFM tip by placing a graphite flake on the WS2, as shown in Figure 1b. A metallic lead is then connected to the graphite flake. AFM topography reveals that the flake consists of regions of single-layer (SL), bilayer (BL), and few-layer (FL) WS2, where the FL part is 10 layers thick. The determination of the WS2 flake thickness is described in detail in the Supporting Information, Figure S1. An AFM topography image of the regions containing SL and BL WS2 is shown in Figure 1c. During the sample preparation, a water film is trapped between the mica and the 2D material.30 The water film is difficult to detect by AFM at ambient conditions because of its uniform thickness. Upon reduction of the relative humidity (RH) to <1% (hereby referred to as low RH), fractal-shaped depressions become visible because of partial evaporation of the water layer through defects such as wrinkles and step-edges as seen in Figure 1d.32,38 Similar fractals trapped between mica and graphene were previously found to be due to a monolayer of ordered ice (termed 1L-H2O) surrounded by thicker regions of less ordered bilayer of water (termed 2L-H2O).38 We emphasize that the notations 1L-H2O and 2L-H2O refer to one layer and two layers of water trapped between WS2 and mica. While the exact nature of these fractal structures is still under debate,31,32,38 the influence of these two different regions to the 2D cover is remarkable, as we will show shortly.

Figure 1.

Figure 1

Open in a new tab

(a) Optical microscopy image of a thin WS2 flake placed on mica. The indicated SL and BL areas were identified by AFM. (b) Schematic representation of the experimental setup. (c) Contact mode AFM topography image of the SL and BL areas at ambient conditions. (d) The same area after reducing the relative humidity of the chamber. The intercalated water film evaporated partially, resulting in 1L-H2O ice fractals. (e) Current map, recorded simultaneously with the topography map of panel d. The measured current is higher at the fractal regions as compared to its surrounding 2L-H2O regions. (f) Contact potential difference map. The simultaneously recorded topography is shown in the inset.

Earlier studies using graphene as the cover layer demonstrated that the fractal-shaped depressions lead to p-type doping of the graphene.37 This doping was previously attributed to charge transfer from the underlying negatively charged substrate, due to either the mica39 or the presence of an ordered intercalated water film.38 To determine the influence of the underlying water layer on the metal/WS2 contact, we measured the conductivity of the tip/sample contact with the AFM probe. This is done by applying a bias voltage between the AFM tip and sample and measuring the resulting current during scanning. The measured conductivity is dominated by the tip/sample contact as the resistances of the channel and the graphite/WS2 contact are both negligible.40 This way the c-AFM map of Figure 1e has been obtained simultaneously with the topography map of Figure 1d. The c-AFM map reveals indeed a difference between WS2 placed on 1L-H2O and WS2 placed on 2L-H2O, with the 1L-H2O regions being more conductive than the 2L-H2O regions. The reason for this change in conductivity is due to the state of the intercalated water layer and will be explored in the remainder of this Letter. In the c-AFM image it can also be seen that the thickness of the WS2 flake has a profound influence on the measured conductivity, where the conductivity is higher for the BL flake compared to the SL flake. This trend is continued for thicker flakes, as shown in the Supporting Information. Still, it should be noted that for different flake thicknesses the qualitative influence of the intercalated water layer is the same: the conductivity on 1L-H2O regions is higher than on 2L-H2O regions. A particular interesting detail in the c-AFM map is that there is a conductivity difference between the BL flake in the bottom right part of the map compared to the BL flake of the same thickness in the top left part of the map. This difference can be explained by the fact that the top layer of the BL part in the top left corner is partially isolated from the rest of the flake, as shown by the optical microscopy image in Figure 1b. This means that charge carriers cannot be transported laterally through the top layer and experience two contacts in series: one contact from the tip to the WS2 and a second contact from the top layer to the bottom layer. Because the BL region is relatively small, this second contact has a substantial contribution to the contact resistance, resulting in a lower conductivity.36

In order to determine why the contact properties differ between 2L-H2O and 1L-H2O regions, we have investigated the local work function variations over the sample (Φ) by Kelvin probe force microscopy (KPFM). Φ is calibrated on a thick WS2 flake to the known work function of bulk WS2 (as is described in more detail in the Supporting Information).41 As shown in Figure 1f, Φ is higher at the WS2/1L-H2O regions than at the WS2/2L-H2O regions. The work function difference between WS2/1L-H2O and WS2/2L-H2O is 0.11 eV. The work function of the mica is 0.03 eV higher than that of the WS2/2L-H2O region and 0.08 eV lower than that of the WS2/1L-H2O region. A detailed description of how these average values are obtained from the measurement can be found in the Supporting Information, Figure S3. This shift in work function indicates p-type doping of WS2, similar to the findings for graphene.38,39 Previous work has shown that the thickness of the intercalated water film influences the capacitance of the total system.42 Here, the water layers are below the WS2 flake; thus, they do not (directly) influence the capacitance of the system. Another notable feature in Figure 1f is that Φ varies spatially within the fractals, increasing toward the center of the fractals. This nonuniform Φ can be attributed either to horizontal charge screening or to artifacts due to tip-convolution. It should be noted that the Φ decreases with increasing thickness of the WS2 flake, as shown in the KPFM map in Figure S2.

To study the topographic and electronic transition from the 1L-H2O to the 2L-H2O regions, we have performed scanning tunneling microscopy (STM) and scanning tunneling spectroscopy (STS) measurements. In Figure 2a, a topographic STM image of a FL WS2 flake on mica is shown. Part of a large 1L-H2O fractal is captured within the recorded image. A small-scale STM image of WS2 of a border between a 1L-H2O region and a 2L-H2O region is shown in Figure 2b. The cross section of the transition reveals that the lattice periodicity of WS2 spans over both regions, unambiguously demonstrating that the fractal structure is located underneath the WS2 cover. Atomically resolved images of WS2 on the 1L-H2O regions, e.g., Figure 2c, reveal an almost perfect lattice with only a few sulfur defects (S-defects). The Fourier transform in the inset reveals the hexagonal periodicity of WS2. Figure 2d shows dI(V)/dV curves that are obtained from I(V) traces recorded on WS2 on the 1L-H2O and 2L-H2O regions. By tracking the small peak in the density of states between −0.1 V and −0.3 V, it is revealed that the valence band maximum (VBM) of the WS2 on the 1L-H2O is shifted to the right by about 0.1 eV as compared to the VBM of WS2 on 2L-H2O. This shift brings the Fermi level of the WS2/1L-H2O closer to the VBM, confirming p-type doping of the WS2, in line with the KPFM results. The full bias range of the dI(V)/dV curves are shown in Figure S4. The measured dI(V)/dV curves undergo a continuous transition from one region to the other, as can be seen by the dI(V)/dV cross section to the bottom of the panel. The individual traces of the cross section are recorded over a transition region, as shown in detail in Figure S4.

Figure 2.

Figure 2

Open in a new tab

(a) STM topography image of an area with fractal shaped 1L-H2O regions surrounded by 2L-H2O regions (V = −1.5 V; I = 500 pA). (b) A smaller-scale topography map of the transition from a 2L-H2O region to a 1L-H2O region. The cross section is indicated by the red arrow (V = −1.0 V; I = 400 pA). (c) Atomically resolved image from within a 1L-H2O area (V = −1.0 V; I = 400 pA). The Fourier transform of the lattice is shown in the inset, and the hexagonal symmetry of WS2 is indicated by the green circles. (d) dI(V)/dV curves recorded on WS2/2L-H2O and WS2/1L-H2O regions. The shift of 0.1 V of a peak in the LDOS is indicated. At the bottom, a dI(V)/dV cross section recorded across a transition region is shown. The black dashed line is a guide to the eye.

The direct control of the doping level of the WS2 cover by manipulation of the underlying water structure is of particular interest in controlling the metal–semiconductor contact characteristics. First, we note that similar to the graphene–mica system,32 wetting and dewetting of the interface are reversible and can be controlled by the RH of the environment as shown in Figure 3a–d. The scans are obtained at the same location as Figure 1c. By repeated changing of the environment from ambient conditions to low RH, the water film will completely fill (Figure 3a), partly evaporate (Figure 3b), refill (Figure 3c), and evaporate again (Figure 3d). It should be noted that the shape of the fractals at low RH can differ in every cycle. Nevertheless they provide regions where the charge carriers experience lower resistances, as is evident from the higher currents recorded at these sites. Controlling the charge doping and contact properties of future devices by intercalation of water (or molecules with different dipole strengths)43 could provide a novel route to environmentally gate the 2D material.7,8 In the following, we will experimentally investigate the influence of the intercalated water on the charge carrier injection mechanism at the Pt/WS2 contacts.

Figure 3.

Figure 3

Open in a new tab

Four panels showing a current map of the same region. A bias voltage of 2.0 V was applied between the tip and sample. Through repeated decrease and increase of the RH, water evaporates from and recondensates between the mica and WS2. (a) At ambient conditions, no fractals are visible in the current map. (b) After the RH is reduced, fractals start to grow where 2L-H2O reduces to 1L-H2O, resulting in a local increase in current. (c) Exposing the system to ambient conditions restores the complete water film. (d) This process is completely reversible, and the fractals regrow upon another reduction of the RH.

With c-AFM, the I(V) characteristics of the Pt/WS2 contact can be determined locally by placing the metallic tip on the WS2 and subsequently ramping the bias voltage. Because TE, F–N, and DT each have their own typical I(V) characteristics, the recorded I(V) curves can be linked to the dominant charge injection mechanism. In Figure 4a, I(V) curves are shown for contact locations on WS2 of different thicknesses: SL, BL, FL, and multilayer (ML) as schematically shown in Figure 4b. For each thickness, I(V) curves are recorded both on a 2L-H2O region as well as on a 1L-H2O region. The details of the acquirement of the I(V) curves is presented in Figure S6. The conductivity of the recorded I(V) curves depends on the layer thickness; the conductivity is lowest for SL-WS2, while it becomes higher for thicker WS2 flakes. This is in agreement with the c-AFM maps recorded in Figure 1e, where higher currents are obtained for thicker flakes. This thickness-dependent conductivity can be associated with either the thickness-dependent Schottky barrier height (SBH) or a possible thickness-dependent change of the charge injection mechanism.36,44

Figure 4.

Figure 4

Open in a new tab

(a) Averaged I(V) curves recorded by c-AFM on regions of different thickness from SL to BL, FL, and ML on 1L-H2O and 2L-H2O. The lower panel shows the same data in a linear scale. (b) A side-view of the schematic setup used to obtain the data in panel a. (c) Schematic representation of the three injection mechanisms considered: TE, DT, and F–N. (d–g) The same data as in panel a for the ML and SL areas is plotted in logarithmic-linear (d and f, respectively) and F–N scales (e and g, respectively). The dashed lines are linear (TE, F–N) and logarithmic (DT) relations fitted to the data.

Moreover, it is noted that the conductivity on the 1L-H2O regions is higher at both positive and negative sample biases compared to the lower conductivity on the 2L-H2O regions. However, the difference in conductivity is larger at positive sample bias than at negative sample bias. Strikingly, the functional shape of the curves in Figure 4a differs too. This indicates different injection mechanisms across the different contacts.1−3 The three main injection mechanisms that we consider here are TE, F–N, and DT.22 TE is expected when electrons are thermally excited to overcome the Schottky barrier. For DT, electrons tunnel through an additional interfacial barrier which was found to be formed between van der Waals material and metal lead.1 DT becomes more prominent at lower temperatures and for thinner barriers. F–N typically occurs at higher bias voltages. For F–N, electrons tunnel through part of a triangular barrier.1 The three injection mechanisms are schematically described in Figure 4c.

TE is described by22,45

graphic file with name jz-2019-008622_m001.jpg 1

with I0 the saturation current for TE equal to

graphic file with name jz-2019-008622_m002.jpg 2

where V is the bias voltage, T the temperature, kB the Boltzmann constant, q the elementary charge, n the ideality factor, A the electrical contact area, A* the Richardson constant, and ΦB the Schottky barrier height.

DT is described by22,46

graphic file with name jz-2019-008622_m003.jpg 3

where m* is the effective mass of an electron (0.31 m0,47 with m0 the rest mass), d the barrier width, and h the Planck constant.

F–N is described by22,46

graphic file with name jz-2019-008622_m004.jpg 4

A careful investigation of the characteristic shape of the I(V) traces can provide qualitative information on which of these injection mechanisms is dominant. TE results in a linear line when plotting ln(I) as a function of V and in the bias range where qV ≫ 3kBT.45 From the slope of the linear part that equals q/nkBT, the ideality factor can be extracted (eq 1), giving a measure of the applicability of the model to describe the current transport by pure TE. F–N and DT can be distinguished when plotting ln(I/V2) as a function of 1/V (F–N plot). For F–N tunneling, the curve will decrease linearly, whereas for DT, it should increase logarithmically.48,49 DT shows a linear behavior when plotted in a ln(I/V2) versus ln(|1/V|) scale. F–N is generally expected for higher applied bias voltages, while DT is expected for thin and small barriers. 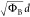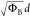The two regimes are separated by an inflection point.48,49 For F–N and DT, it is possible to determine the barrier parameters ΦB3/2d and Inline graphic, respectively. The details of acquiring the parameters ΦB and n for TE, ΦB3/2d for F–N, and Inline graphic for DT are described in the Supporting Information.

To identify which injection mechanism dominates in different contacts, we have plotted the data acquired on SL-WS2 and ML-WS2 in two different ways: ln(I) versus V and ln(I/V2) versus 1/V in Figure 4d–g. The data plotted in a ln(I/V2) versus ln(|1/V|) scale is shown in Figure S7. We first focus on the contact properties of ML-WS2. As shown in Figure 4d, the I(V) curves are unipolar for both ML-WS2 on 1L-H2O as well as for ML-WS2 on 2L-H2O. In the forward bias regime (negative sample bias) and at low bias voltage, the data can be fitted well with the TE model, as shown in Figure 4d (−0.3 V to −0.05 V). From TE we extract barrier heights of 1.1 eV (both 1L-H2O and 2L-H2O) and ideality factors equal to 5.5 (both 1L-H2O and 2L-H2O). The injection mechanisms at higher forward biases and at reverse biases are dominated by F–N and DT, as can be seen in Figure 4e. At high forward bias (< −1.2 V), both the 1L-H2O and 2L-H2O regions can be described by F–N with barrier parameters of 0.60 eV3/2 nm (1L-H2O) and 0.49 eV3/2 nm (2L-H2O). In the reverse bias regime, the dominating injection mechanism depends on the hydration state of the substrate. In a 1L-H2O region, the F–N plot reveals a clear inflection point with a linear decreasing behavior at high voltages (F–N) and a logarithmic increasing behavior at lower voltages (DT).48 The barrier parameter of the DT regime is 0.34 eV1/2 nm, while in the F–N regime the barrier parameter is 3.27 eV3/2 nm. In the 2L-H2O region, on the other hand, the injection mechanism is DT over the full reverse bias range with a barrier parameter of 0.37 eV1/2 nm.

On SL-WS2, we see a much different behavior. While the Pt/SL-WS2/2L-H2O contact is unipolar, the Pt/SL-WS2/1L-H2O contact shows an ambipolar behavior. This change in contact properties can be explained by the different injection mechanisms that are dominant at SL-WS2, as can be seen in Figures 4f,g. In Figure 4f, no linear trend is found at low bias voltages, indicating that the curves can not be described properly by TE. Meanwhile, in Figure 4g it is shown that at lower voltages the I(V) traces are well described by DT with barrier parameters of 0.48 eV1/2 nm (1L-H2O, forward bias), 0.45 eV1/2 nm (1L-H2O, reverse bias), 0.62 eV1/2 nm (2L-H2O, forward bias), and 1.06 eV1/2 nm (2L-H2O, reverse bias). At higher bias voltages in the reverse bias regime (V > 5 V) at 2L-H2O, a clear F–N contribution can be distinguished with a barrier parameter of 3.28 eV3/2 nm. Comparing 1L-H2O to 2L-H2O, the current at the reverse bias regime is substantially increased, changing the behavior of the device from unipolar to ambipolar. The BL and FL results show that the dominant charge injection mechanisms are the same as for the case of SL WS2 as is shown in Figure S7. Still, the measured barrier parameters change for thicker parts of the flake. The barrier parameters for DT decrease overall for increasing flake thickness, as can be seen in Table 1, which explains the increase in conductivity.

Table 1. Barrier Parameters for Thin WS2.

  SL BL FL
F–N, 2L-H2O reverse (eV3/2 nm) 3.28 3.04 5.23
DT, 2L-H2O forward (eV1/2 nm) 0.62 0.54 0.39
DT, 2L-H2O reverse (eV1/2 nm) 1.06 0.93 0.87
DT, 1L-H2O forward (eV1/2 nm) 0.48 0.45 0.28
DT, 1L-H2O reverse (eV1/2 nm) 0.45 0.47 0.35
Open in a new tab

The results obtained here are also of interest for larger macroscopic contacts to WS2 on mica (or any 2D semiconductor on a hydrophilic substrate). At low RH, the charge carrier injection through the contact will occur at the 1L-H2O regions, as the resistance is the lowest in these regions. Exposing the system to ambient RH leads to filling of the fractals and the completion of the second H2O layer. The contact properties will now be determined by the injection mechanism on 2L-H2O. Switching between injection mechanisms and switching between unipolar and ambipolar transport by controlling the RH is therefore also possible for macroscopic contacts.

In conclusion, we have demonstrated that by controlling the hydration state of the underlying supporting substrate it is possible to modify the charge carrier injection mechanism in WS2–metal nanocontacts. This environmentally controlled process is the consequence of doping due to charge transfer from the underlying water layer. In addition, the charge injection mechanism strongly depends on the thickness of the WS2 flake. TE was observed only on ML WS2, whereas for SL, BL, and FL WS2, a switch from unipolar to ambipolar behavior was observed when decreasing the thickness of the intercalated water from 2L to 1L. The reversibility of the dewetting process along with its noninvasive character provides a viable alternative for fabricating devices with in situ control of the metal–semiconductor junction characteristics.

Acknowledgments

R.v.B., H.J.W.Z., and P.B. thank the Dutch organization for scientific research NWO for financial support (FV157 14TWDO07). P.B. thanks the Alexander von Humboldt foundation for financial support.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.9b00862.

  • Methods section and details on the acquirement of the c-AFM I(V) curves, thickness-dependent work function, KPFM analysis, acquirement of the STM data, and the carrier injection mechanisms. (PDF)

The authors declare no competing financial interest.

Supplementary Material

jz9b00862_si_001.pdf (4.6MB, pdf)

References

  1. Ahmed F.; Choi M. S.; Liu X.; Yoo W. J. Carrier Transport at the Metal–MoS2 Interface. Nanoscale 2015, 7, 9222–9228. 10.1039/C5NR01044F. [DOI] [PubMed] [Google Scholar]
  2. Liu H.; Si M.; Deng Y.; Neal A. T.; Du Y.; Najmaei S.; Ajayan P. M.; Lou J.; Ye P. D. Switching Mechanism in Single-Layer Molybdenum Disulfide Transistors: An Insight into Current Flow across Schottky Barriers. ACS Nano 2014, 8, 1031–1038. 10.1021/nn405916t. [DOI] [PubMed] [Google Scholar]
  3. Allain A.; Kang J.; Banerjee K.; Kis A. Electrical Contacts to Two-Dimensional Semiconductors. Nat. Mater. 2015, 14, 1195–1205. 10.1038/nmat4452. [DOI] [PubMed] [Google Scholar]
  4. Schulman D. S.; Arnold A. J.; Das S. Contact Engineering for 2D Materials and Devices. Chem. Soc. Rev. 2018, 47, 3037–3058. 10.1039/C7CS00828G. [DOI] [PubMed] [Google Scholar]
  5. Schultz B. J.; Jaye C.; Lysaght P. S.; Fischer D. A.; Prendergast D.; Banerjee S. On Chemical Bonding and Electronic Structure of Graphene–Metal Contacts. Chemical Science 2013, 4, 494–502. 10.1039/C2SC21018E. [DOI] [Google Scholar]
  6. Wang Y.; Kim J. C.; Wu R. J.; Martinez J.; Song X.; Yang J.; Zhao F.; Mkhoyan A.; Jeong H. Y.; Chhowalla M. Van Der Waals Contacts between Three-Dimensional Metals and Two-Dimensional Semiconductors. Nature 2019, 568, 70. 10.1038/s41586-019-1052-3. [DOI] [PubMed] [Google Scholar]
  7. Lee S. Y.; Kim U. J.; Chung J.; Nam H.; Jeong H. Y.; Han G. H.; Kim H.; Oh H. M.; Lee H.; Kim H.; et al. Large Work Function Modulation of Monolayer MoS2 by Ambient Gases. ACS Nano 2016, 10, 6100–6107. 10.1021/acsnano.6b01742. [DOI] [PubMed] [Google Scholar]
  8. Tongay S.; Zhou J.; Ataca C.; Liu J.; Kang J. S.; Matthews T. S.; You L.; Li J.; Grossman J. C.; Wu J. Broad-Range Modulation of Light Emission in Two-Dimensional Semiconductors by Molecular Physisorption Gating. Nano Lett. 2013, 13, 2831–2836. 10.1021/nl4011172. [DOI] [PubMed] [Google Scholar]
  9. Politano A.; Chiarello G.; Samnakay R.; Liu G.; Gürbulak B.; Duman S.; Balandin A. A.; Boukhvalov D. W. The Influence of Chemical Reactivity of Surface Defects on Ambient-Stable InSe-Based Nanodevices. Nanoscale 2016, 8, 8474–8479. 10.1039/C6NR01262K. [DOI] [PubMed] [Google Scholar]
  10. Viti L.; Politano A.; Vitiello M. S. Black Phosphorus Nanodevices at Terahertz Frequencies: Photodetectors and Future Challenges. APL Mater. 2017, 5, 035602. 10.1063/1.4979090. [DOI] [Google Scholar]
  11. Politano A.; Chiarello G. Unravelling Suitable Graphene–Metal Contacts for Graphene-Based Plasmonic Devices. Nanoscale 2013, 5, 8215–8220. 10.1039/c3nr02027d. [DOI] [PubMed] [Google Scholar]
  12. Kim C.; Moon I.; Lee D.; Choi M. S.; Ahmed F.; Nam S.; Cho Y.; Shin H.-J.; Park S.; Yoo W. J. Fermi Level Pinning at Electrical Metal Contacts of Monolayer Molybdenum Dichalcogenides. ACS Nano 2017, 11, 1588–1596. 10.1021/acsnano.6b07159. [DOI] [PubMed] [Google Scholar]
  13. Sotthewes K.; van Bremen R.; Dollekamp E.; Boulogne T.; Nowakowski K.; Kas D.; Zandvliet H. J. W.; Bampoulis P. Universal Fermi-Level Pinning in Transition-Metal Dichalcogenides. J. Phys. Chem. C 2019, 123, 5411–5420. 10.1021/acs.jpcc.8b10971. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Das S.; Chen H.-Y.; Penumatcha A. V.; Appenzeller J. High Performance Multilayer MoS2 Transistors with Scandium Contacts. Nano Lett. 2013, 13, 100–105. 10.1021/nl303583v. [DOI] [PubMed] [Google Scholar]
  15. Liu Y.; Guo J.; Zhu E.; Liao L.; Lee S.-J.; Ding M.; Shakir I.; Gambin V.; Huang Y.; Duan X. Approaching the Schottky–Mott Limit in van Der Waals Metal–Semiconductor Junctions. Nature 2018, 557, 696. 10.1038/s41586-018-0129-8. [DOI] [PubMed] [Google Scholar]
  16. Liu Y.; Wu H.; Cheng H.-C.; Yang S.; Zhu E.; He Q.; Ding M.; Li D.; Guo J.; Weiss N. O.; et al. Toward Barrier Free Contact to Molybdenum Disulfide Using Graphene Electrodes. Nano Lett. 2015, 15, 3030–3034. 10.1021/nl504957p. [DOI] [PubMed] [Google Scholar]
  17. Cui X.; Shih E.-M.; Jauregui L. A.; Chae S. H.; Kim Y. D.; Li B.; Seo D.; Pistunova K.; Yin J.; Park J.-H.; et al. Low-Temperature Ohmic Contact to Monolayer MoS2 by van Der Waals Bonded Co/h-BN Electrodes. Nano Lett. 2017, 17, 4781–4786. 10.1021/acs.nanolett.7b01536. [DOI] [PubMed] [Google Scholar]
  18. Nowakowski K.; van Bremen R.; Zandvliet H. J. W.; Bampoulis P. Control of the Metal/WS2 Contact Properties Using 2-Dimensional Buffer Layers. Nanoscale 2019, 11, 5548–5556. 10.1039/C9NR00574A. [DOI] [PubMed] [Google Scholar]
  19. English C. D.; Shine G.; Dorgan V. E.; Saraswat K. C.; Pop E. Improved Contacts to MoS2 Transistors by Ultra-High Vacuum Metal Deposition. Nano Lett. 2016, 16, 3824–3830. 10.1021/acs.nanolett.6b01309. [DOI] [PubMed] [Google Scholar]
  20. Baugher B. W. H.; Churchill H. O. H.; Yang Y.; Jarillo-Herrero P. Intrinsic Electronic Transport Properties of High-Quality Monolayer and Bilayer MoS2. Nano Lett. 2013, 13, 4212–4216. 10.1021/nl401916s. [DOI] [PubMed] [Google Scholar]
  21. Khalil H. M. W.; Khan M. F.; Eom J.; Noh H. Highly Stable and Tunable Chemical Doping of Multilayer WS2 Field Effect Transistor: Reduction in Contact Resistance. ACS Appl. Mater. Interfaces 2015, 7, 23589–23596. 10.1021/acsami.5b06825. [DOI] [PubMed] [Google Scholar]
  22. Durán Retamal J. R.; Periyanagounder D.; Ke J.-J.; Tsai M.-L.; He J.-H. Charge Carrier Injection and Transport Engineering in Two-Dimensional Transition Metal Dichalcogenides. Chemical Science 2018, 9, 7727–7745. 10.1039/C8SC02609B. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Kuc A.; Zibouche N.; Heine T. Influence of Quantum Confinement on the Electronic Structure of the Transition Metal Sulfide TS2. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 83, 245213. 10.1103/PhysRevB.83.245213. [DOI] [Google Scholar]
  24. Ovchinnikov D.; Allain A.; Huang Y.-S.; Dumcenco D.; Kis A. Electrical Transport Properties of Single-Layer WS2. ACS Nano 2014, 8, 8174–8181. 10.1021/nn502362b. [DOI] [PubMed] [Google Scholar]
  25. Withers F.; Bointon T. H.; Hudson D. C.; Craciun M. F.; Russo S. Electron Transport of WS2 Transistors in a Hexagonal Boron Nitride Dielectric Environment. Sci. Rep. 2015, 4, 4967. 10.1038/srep04967. [DOI] [Google Scholar]
  26. Samaddar S.; Yudhistira I.; Adam S.; Courtois H.; Winkelmann C. B. Charge Puddles in Graphene near the Dirac Point. Phys. Rev. Lett. 2016, 116, 126804. 10.1103/PhysRevLett.116.126804. [DOI] [PubMed] [Google Scholar]
  27. Lui C. H.; Liu L.; Mak K. F.; Flynn G. W.; Heinz T. F. Ultraflat Graphene. Nature 2009, 462, 339–341. 10.1038/nature08569. [DOI] [PubMed] [Google Scholar]
  28. Low C. G.; Zhang Q.; Hao Y.; Ruoff R. S. Graphene Field Effect Transistors with Mica as Gate Dielectric Layers. Small 2014, 10, 4213–4218. 10.1002/smll.201303929. [DOI] [PubMed] [Google Scholar]
  29. Verdaguer A.; Sacha G. M.; Bluhm H.; Salmeron M. Molecular Structure of Water at Interfaces: Wetting at the Nanometer Scale. Chem. Rev. 2006, 106, 1478–1510. 10.1021/cr040376l. [DOI] [PubMed] [Google Scholar]
  30. Bampoulis P.; Sotthewes K.; Dollekamp E.; Poelsema B. Water Confined in Two-Dimensions: Fundamentals and Applications. Surf. Sci. Rep. 2018, 73, 233–264. 10.1016/j.surfrep.2018.09.001. [DOI] [Google Scholar]
  31. Xu K.; Cao P.; Heath J. R. Graphene Visualizes the First Water Adlayers on Mica at Ambient Conditions. Science 2010, 329, 1188–1191. 10.1126/science.1192907. [DOI] [PubMed] [Google Scholar]
  32. Severin N.; Lange P.; Sokolov I. M.; Rabe J. P. Reversible Dewetting of a Molecularly Thin Fluid Water Film in a Soft Graphene–Mica Slit Pore. Nano Lett. 2012, 12, 774–779. 10.1021/nl2037358. [DOI] [PubMed] [Google Scholar]
  33. He K. T.; Wood J. D.; Doidge G. P.; Pop E.; Lyding J. W. Scanning Tunneling Microscopy Study and Nanomanipulation of Graphene-Coated Water on Mica. Nano Lett. 2012, 12, 2665–2672. 10.1021/nl202613t. [DOI] [PubMed] [Google Scholar]
  34. Song J.; Li Q.; Wang X.; Li J.; Zhang S.; Kjems J.; Besenbacher F.; Dong M. Evidence of Stranski–Krastanov Growth at the Initial Stage of Atmospheric Water Condensation. Nat. Commun. 2014, 5, 4837. 10.1038/ncomms5837. [DOI] [PubMed] [Google Scholar]
  35. Dollekamp E.; Bampoulis P.; Faasen D. P.; Zandvliet H. J. W.; Kooij E. S. Charge Induced Dynamics of Water in a Graphene-Mica Slit Pore. Langmuir 2017, 33, 11977–11985. 10.1021/acs.langmuir.7b02759. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Pam M. E.; Li Z.; Ang Y. S.; Shi Y.; Geng D.; Huang S.; Zhao X.; Pennycook S. J.; Yao H.; Gong X.; et al. Thermal-Assisted Vertical Electron Injections in Few-Layer Pyramidal-Structured MoS2 Crystals. J. Phys. Chem. Lett. 2019, 10, 1292–1299. 10.1021/acs.jpclett.9b00274. [DOI] [PubMed] [Google Scholar]
  37. Goncher S. J.; Zhao L.; Pasupathy A. N.; Flynn G. W. Substrate Level Control of the Local Doping in Graphene. Nano Lett. 2013, 13, 1386–1392. 10.1021/nl3039508. [DOI] [PubMed] [Google Scholar]
  38. Bampoulis P.; Siekman M. H.; Kooij E. S.; Lohse D.; Zandvliet H. J. W.; Poelsema B. Latent Heat Induced Rotation Limited Aggregation in 2D Ice Nanocrystals. J. Chem. Phys. 2015, 143, 034702. 10.1063/1.4926467. [DOI] [PubMed] [Google Scholar]
  39. Shim J.; Lui C. H.; Ko T. Y.; Yu Y.-J.; Kim P.; Heinz T. F.; Ryu S. Water-Gated Charge Doping of Graphene Induced by Mica Substrates. Nano Lett. 2012, 12, 648–654. 10.1021/nl2034317. [DOI] [PubMed] [Google Scholar]
  40. Bampoulis P.; van Bremen R.; Yao Q.; Poelsema B.; Zandvliet H. J. W.; Sotthewes K. Defect Dominated Charge Transport and Fermi Level Pinning in MoS2/Metal Contacts. ACS Appl. Mater. Interfaces 2017, 9, 19278–19286. 10.1021/acsami.7b02739. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Britnell L.; Ribeiro R. M.; Eckmann A.; Jalil R.; Belle B. D.; Mishchenko A.; Kim Y.-J.; Gorbachev R. V.; Georgiou T.; Morozov S. V.; et al. Strong Light-Matter Interactions in Heterostructures of Atomically Thin Films. Science 2013, 340, 1311–1314. 10.1126/science.1235547. [DOI] [PubMed] [Google Scholar]
  42. Olson E. J.; Ma R.; Sun T.; Ebrish M. A.; Haratipour N.; Min K.; Aluru N. R.; Koester S. J. Capacitive Sensing of Intercalated H2O Molecules Using Graphene. ACS Appl. Mater. Interfaces 2015, 7, 25804–25812. 10.1021/acsami.5b07731. [DOI] [PubMed] [Google Scholar]
  43. Kim H. H.; Yang J. W.; Jo S. B.; Kang B.; Lee S. K.; Bong H.; Lee G.; Kim K. S.; Cho K. Substrate-Induced Solvent Intercalation for Stable Graphene Doping. ACS Nano 2013, 7, 1155–1162. 10.1021/nn306012p. [DOI] [PubMed] [Google Scholar]
  44. Li H.-M.; Lee D.; Qu D.; Liu X.; Ryu J.; Seabaugh A.; Yoo W. J. Ultimate Thin Vertical p–n Junction Composed of Two-Dimensional Layered Molybdenum Disulfide. Nat. Commun. 2015, 6, 6564. 10.1038/ncomms7564. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Rhoderick E. H. Metal-Semiconductor Contacts. IEE Proc., Part I: Solid-State Electron Devices 1982, 129, 1–14. 10.1049/ip-i-1.1982.0001. [DOI] [Google Scholar]
  46. Das S.; Prakash A.; Salazar R.; Appenzeller J. Toward Low-Power Electronics: Tunneling Phenomena in Transition Metal Dichalcogenides. ACS Nano 2014, 8, 1681–1689. 10.1021/nn406603h. [DOI] [PubMed] [Google Scholar]
  47. Jin Z.; Li X.; Mullen J. T.; Kim K. W. Intrinsic Transport Properties of Electrons and Holes in Monolayer Transition-Metal Dichalcogenides. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 90, 045422. 10.1103/PhysRevB.90.045422. [DOI] [Google Scholar]
  48. Beebe J. M.; Kim B.; Gadzuk J. W.; Daniel Frisbie C.; Kushmerick J. G. Transition from Direct Tunneling to Field Emission in Metal-Molecule-Metal Junctions. Phys. Rev. Lett. 2006, 97, 026801. 10.1103/PhysRevLett.97.026801. [DOI] [PubMed] [Google Scholar]
  49. Ikuno T.; Okamoto H.; Sugiyama Y.; Nakano H.; Yamada F.; Kamiya I. Electron Transport Properties of Si Nanosheets: Transition from Direct Tunneling to Fowler-Nordheim Tunneling. Appl. Phys. Lett. 2011, 99, 023107. 10.1063/1.3610486. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz9b00862_si_001.pdf (4.6MB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES