Skip to main content
PMC home page
NIST Author Manuscripts logoLink to NIST Author Manuscripts
. Author manuscript; available in PMC: 2019 May 20.
Published in final edited form as: Phys Rev Lett. 2018 Dec 14;121(24):246801. doi: 10.1103/PhysRevLett.121.246801

Spin-Mechanical Coupling of an InAs Quantum Dot Embedded in a Mechanical Resonator

S G Carter 1,*, A S Bracker 1, G W Bryant 2, M Kim 3, C S Kim 1, M K Zalalutdinov 1, M K Yakes 1, C Czarnocki 4, J Casara 4, M Scheibner 4, D Gammon 1
PMCID: PMC6527321  NIHMSID: NIHMS1526080  PMID: 30608739

Abstract

We demonstrate strain-induced coupling between a hole spin in a quantum dot and mechanical motion of a cantilever. The optical transitions of quantum dots integrated into GaAs mechanical resonators are measured synchronously with the motion of the driven resonators. In a Voigt magnetic field, both electron and hole spin splittings are measured, showing negligible change for the electron spin but a large change for the hole spin of up to 36%. This large effect is attributed to the stronger spin orbit interaction of holes compared to electrons.

Coupling a quantum system to a mechanical resonator is of strong practical and fundamental interest. The coherent quantum states can be very sensitive to mechanical motion, making it possible to sense motion down to the quantum limit. Conversely, mechanical motion may then be sensitive to the quantum states. By manipulating the quantum state, motion can be induced, suppressed, or even put in non-classical states [1–3]. This hybrid system can then be used for quantum sensing [4], for coupling multiple quantum systems [5,6], or to investigate motion at the quantum limit [7].

Producing a large coupling between the quantum system and mechanical resonator is of great importance to achieving these goals [8,9]. In solid state systems, an elegant approach is to embed the quantum system into the mechanical resonator, with coupling through strain [9–17]. Semiconductor quantum dots (QDs) are strongly affected by strain, with a number of reports demonstrating that their optical properties can be fine-tuned through strain, primarily with static strain applied with piezoelectric actuators [18–24]. Coupling QDs to dynamic strain in a mechanical resonator opens up many new opportunities. Several recent demonstrations have focused on coupling mechanical resonators to the optical transitions of QDs [14–17], which have coherence times less than 1 ns, limiting their use as a quantum system. Resident electron or hole spins can have much longer coherence times of over 1 μs, but there is almost no experimental work to determine the coupling strength of spin to strain. In one study, the effects of static strain on the spin of an electron-hole pair (exciton) were measured [24], but because that study was done in the Faraday geometry, the electron and hole contributions could not be experimentally separated.

In this Letter, we perform measurements of spin-mechanical coupling in semiconductor quantum dots. These InGaAs quantum dots are integrated into GaAs cantilever structures with charge injection, and a magnetic field is applied perpendicular to the growth axis (Voigt geometry). In this geometry, the Zeeman splitting of both the electron and hole can be measured separately. As the mechanical resonance is optically driven, high resolution photoluminescence (PL) is measured synchronously with the mechanical drive, determining the strain-induced changes in the Zeeman splittings as a function of time. We find negligible effect on the electron spin splittings but a rather large effect on the hole spin splittings. These results are consistent with our atomistic calculations of spin-strain couplings. The larger spin-orbit coupling of holes tends to orient the spin along the strongly confined growth direction of the QD, resulting in a small Zeeman splitting for Voigt fields [25] that is quite sensitive to the geometry, composition, and alloy configuration of the QD. Strain changes the degree to which the hole spin is locked to the growth direction and results in large relative changes in the Zeeman splitting. This large coupling, combined with the longer coherence time of hole spins [26–29], make it a promising hybrid spin-mechanical system.

The InGaAs QDs are grown by molecular beam epitaxy on a GaAs substrate, with a 950 nm sacrificial layer of Al0.7Ga0.3As grown first, followed by 60 nm of GaAs, a layer of InGaAs QDs, and 120 nm of GaAs. Contacted doped layers above and below the QDs allow electrical control of the charge state, as displayed in Fig. 1(d) [30–32].

FIG. 1.

FIG. 1.

Open in a new tab

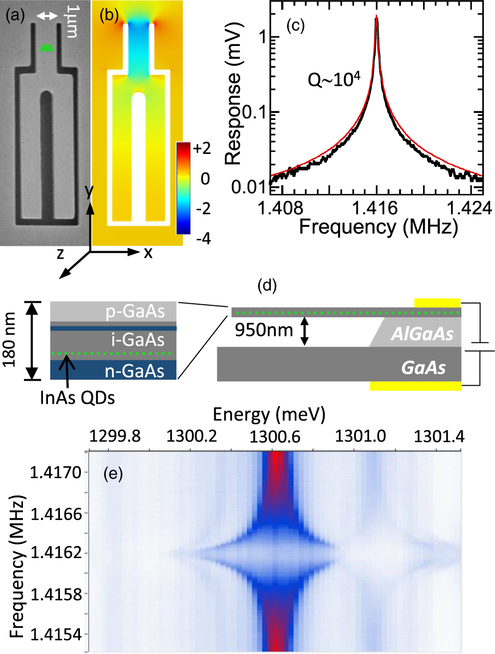
(a) Scanning electron micrograph of a tuning fork cantilever, with a green trapezoid indicating the estimated position of the QDs studied. (b) Finite element model of strain ϵyy within the cantilever at the QD depth for a displacement at the end of 160 nm. The color scale labels are in 10−4 fractional change in length. (c) Reflectivity response of a cantilever vs drive frequency, with a fit (red line) to the square root of a Lorentzian.(d) Schematic of the suspended sample structure with n-i-n-i-p diode. (e) Time-integrated PL color map as a function of emission energy and drive frequency at zero magnetic field for a negatively charged exciton.

Mechanical resonators are defined using electron beam lithography and an inductively coupled plasma etch. These structures are undercut with hydrofluoric acid that etches away the Al0.7Ga0.3As layer, leaving suspended mechanical resonators, as shown in Fig. 1(a). Tuning forks are fabricated, but here we only make use of the lowest cantilever mode in which the entire tuning fork flexes up and down along the growth axis. For this reason we refer to these structures as cantilevers. The total length of the cantilevers is 8 μm, the width is either 1 or 1.5 μm, and the thickness is 180 nm. The lowest mechanical resonance is at 1.35 MHz (1 μm width) or 1.4 MHz (1.5 μm width). Figure 1(b) displays a map of the strain ϵyy at the depth of the QDs in a 1 μm wide cantilever, calculated using a finite element model. The calculated resonance frequency is 1.2 MHz, and the strain is clearly concentrated near the clamping point. The strain is zero within the middle plane, so the QDs are grown 30 nm below the center.

In our experiments the mechanical resonances are measured by optically driving the suspended structure with an amplitude modulated laser at ~920 nm, focused near the clamped end, while measuring the displacement using the reflectance of a 2nd laser at 940 or 950 nm, focused near the free end [17]. The drive laser generates a local, optically induced strain that results in vibration of the cantilever when the modulation frequency matches the mechanical resonance. The vibrations modulate the probe laser reflectivity by changing the degree of interference between reflections from the cantilever and substrate [32]. Figure 1(c) displays the reflected probe laser signal as a function of the modulation frequency for a 1 μm width cantilever driven with 0.5 μW, showing a resonance at 1.416 MHz and a Q of 10 800. From a model of the cantilever reflectivity [32], we estimate ±160 nm displacement at the end of the cantilever for 30–40 μW drive power. Based on the finite element model, this corresponds to in-plane strain amplitude ϵyy of 2.1 × 10−4 at the QD depth near the clamped end.

The effect of the mechanical vibrations on QDs is measured through low temperature (4–5 K) PL, with a PL laser at 923.5 nm replacing the reflectivity probe laser. The sample bias is set to charge the QD with a single electron. At zero magnetic field, where the spin states are degenerate, only one transition is present, and the effect of mechanical vibrations on the optical transition is measured. In Fig. 1(e) the PL spectrum of a QD near the clamped end of the resonator is measured as a function of modulation frequency for an average drive laser power of 30 μW. At the mechanical resonance the emission line is strongly broadened as it shifts back and forth by more than ±300 μeV.

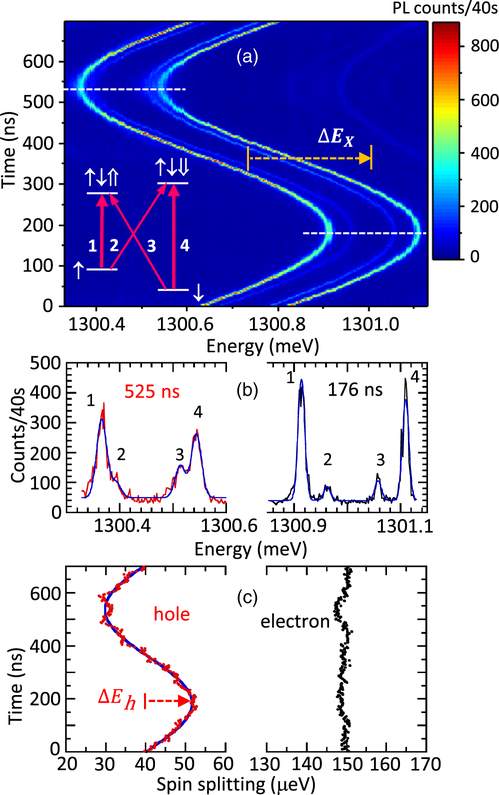
The effect of the vibration-induced strain on the spin properties of the QD is measured by applying a magnetic field and performing time-resolved PL synchronized to the drive laser. The energy levels of a QD charged with a single electron are shown in the inset of Fig. 2(a). The two ground states are split by the electron Zeeman energy, Ee. In the optically excited charged exciton (X−) states, with an additional electron and a heavy hole, the two electrons are in a singlet state, so the energy separation is determined by the heavy hole Zeeman energy, Eh. In a magnetic field applied perpendicular to the growth axis, all four optical transitions are allowed, with diagonal and vertical transitions having opposite linear polarizations. Figure 2(a) shows the variation in QD emission energies vs time with By = 6 T (Voigt field) when resonantly driving the cantilever with 30 μW average power and exciting PL with 5 μW. The data are obtained by sending PL through a scanning Fabry-Perot interferometer (FPI) with 1.5 μeV resolution, followed by a 750 mm grating spectrometer, before being detected by a silicon single photon counting module (SPCM). Time-correlated photon counting is performed at each emission energy, using the drive laser modulation as a reference. All four lines are visibly shifting with an average of ΔEX = 281 μeV, with the outer transitions much brighter than the inner. The difference in brightness is due to polarization selection rules and the fact that the cantilever couples out light polarized along y more efficiently at this position.

FIG. 2.

FIG. 2.

Open in a new tab

(a) Emission from X− in a 6 T Voigt magnetic field under resonant driving of the cantilever at 1.4162 MHz with 30 μW power at 923.5 nm. The emission is measured as a function of time, synchronized to the mechanical drive frequency. The inset shows a level diagram of X−, indicating the four possible transitions. The horizontal, dashed lines indicate the times of maximum and minimum energy, for which spectra are displayed in (b). (c) Hole and electron spin splittings as a function of time. The hole data are fit to a sine function (solid curve).

Figure 2(b) displays the emission spectra at the times of maximum and minimum energies in the oscillation cycle. The energy differences between emission lines and the linewidths change significantly during the motion of the cantilever. The change in linewidth and emission intensity is attributed to changes in the stability of the charge state, which is affected by strain-induced shifts in the electron and hole confinement energies [20]. The changes in energy differences are due to strain-induced changes of Zeeman energies. The electron Zeeman energy |Ee| is obtained from the energy difference between lines 1 and 3 or 2 and 4, and the hole Zeeman energy |Eh| is obtained from the energy difference between lines 1 and 2 or 3 and 4. (The signs of Ee and Eh are not determined.) These energies are obtained from fits to the data at each time in Fig. 2(a) and averaged with two other data sets taken under the same conditions. The results are plotted for electrons and holes in Fig. 2(c), showing a strong change in the hole Zeeman energy, ΔEh of ±10.9 μeV out of 40 μeV and no discernable change in the electron Zeeman energy, ΔEe. With an estimated strain amplitude of 2.1 × 10−4, the coupling of the optical transitions to strain is 1.34 eV=strain (324 THz=strain), and the coupling of the hole spin to strain in this QD is 52 meV=strain (12.5 THz=strain). These measurements have been performed for a series of magnetic fields from 2 T to 6.75 T, which show a linear dependence of ΔEh on the magnetic field (not shown). Measurements on a different QD-cantilever system for drive laser powers from 20 to 40 μW are consistent with ΔEh having a linear dependence on strain [32]. The sign of the coupling is not clear from the measurements, due to difficulties in determining the sign of the displacement.

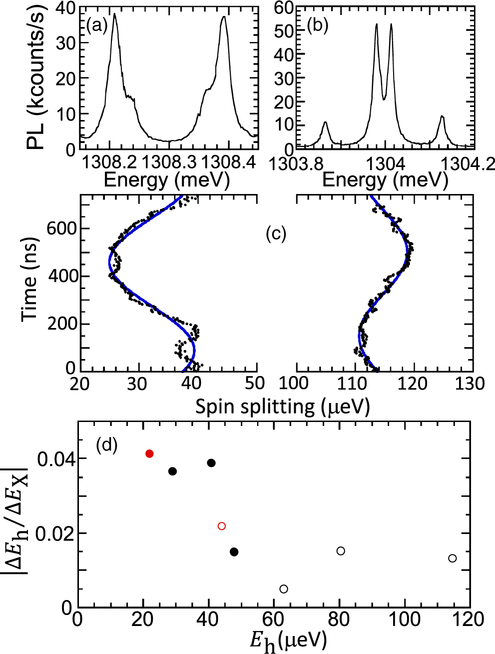
The response of spin states to the motion-induced strain has been measured for 8 QDs, embedded in cantilevers at similar positions. The static value of |Ee| is quite similar for all QDs with an average of 152 μeV, but |Eh| Varies from 22–115 μeV. This large variation of the hole Zeeman splitting for an in-plane field has been measured previously [35] and can be attributed to a strong sensitivity to the size, shape, composition, and strain of the QD [25,36–39]. The emission spectra of two particular QDs in different cantilevers are displayed in Figs. 3(a) and 3(b), which have quite different values of |Eh|, 29 μeV, and 115 μeV. The emission intensity of the inner and outer transitions are reversed between these QDs, either due to different polarization axes for the QDs or a change in the sign of Eh. Figure 3(c) displays |Eh| for both QDs as a function of time while driving the mechanical resonances. The oscillations of |Eh| are roughly 180° out of phase, and the QD with higher |Eh| has about half the amplitude. No clear oscillations in |Ee| were detected for either QD.

FIG. 3.

FIG. 3.

Open in a new tab

(a),(b) PL spectra of X− in a 6 T magnetic field for two other QDs, showing the variation in hole ɡ factor and polarization. The Fabry-Perot resolution is 9 μeV for these measurements. (c) Hole spin splitting (solid circles) as a function of time under mechanical driving for these two QD-cantilever systems, with sine function fits. The average drive power is 20 μW. (d) Change in the hole Zeeman energy divided by the change in the optical transition energy for 8 different QDs. For red circles, only one set of lines could be measured (inner or outer), so ΔEe is assumed to be negligible to find ΔEh. Closed (open) circles indicate the hole and optical transition shifts are in phase (out of phase). The average drive power varies from 20–40 μW for different QDs, and the PL laser power is 5 μW for all QDs.

The amplitude of the shifts in the transition energies ΔEX vary from 192 to 327 μeV for the 8 QDs, which we attribute to different lateral positions of QDs, different vibration amplitudes, and differences in QD strain coupling. The QDs measured are all near the cantilever clamping point but the exact position can vary within 1–2 μm. There are also differences in the cantilever sizes and in the exact position of the drive laser on the cantilever that modify the vibration amplitude. In order to compare the amplitude of ΔEh for different QDs, we divide ΔEh by ΔEX and plot this value as a function of |Eh| for each QD in Fig. 3(d). There appears to be a decrease in the amplitude with higher |Eh| that indicates that the hole spin strain coupling is somewhat weaker with higher Zeeman energies.

Another interesting observation is that for some QDs ΔEh and ΔEX are in phase (closed circles) and for other QDs they are out of phase (open circles). For example, ΔEh and ΔEX shift in phase for the QDs in Figs. 2(a) and 3(a) but shift out of phase for the QD in Fig. 3(b). Assuming that the sign of the strain coupling for ΔEX is the same for all QDs, this means that the hole spin strain coupling has opposite signs for different QDs. The four QDs that shift in phase (out of phase) have stronger emission from the outer (inner) transitions.

We use an atomistic tight binding theory to calculate the electron and hole spin properties and their coupling to strain. The tight binding theory includes nearest-neighbor hopping, strain from lattice mismatch in a valence force-field model, piezoelectric effects, and atomic spin-orbit interaction [18]. The effects of alloy randomness are determined by considering different randomly chosen configurations of In and Ga atoms in the QD. We obtain strain couplings for the hole spins that are the same order of magnitude as those obtained experimentally, with significant variation from one QD to another for different alloy configurations, including changes in the sign of the coupling. Moreover, strain coupling of the electron spins is significantly lower than that of holes, by roughly a factor of 3–4, which is sometimes below experimental limits. Because of strong spin-orbit coupling, the hole spin tends to be locked to the orbital angular momentum which, because of the large hole-effective mass and the resulting strong confinement, is locked to the QD geometry and local variations due to the alloy configuration. The hole spin prefers to be locked to the QD growth axis (vertical). In a Voigt field, the hole spin at each lattice site is close to vertically aligned, but variations from site to site cancel the vertical component, giving a total spin oriented closer to the in-plane magnetic field. The applied strain can increase or decrease hole spin locking by changing the balance of these competing effects. This changes the degree of alignment with the magnetic field, which changes the Zeeman splitting. This strain coupling is particularly sensitive to the spatial distribution of In and Ga atoms and the size and shape of the QD, as is the hole Zeeman energy. In any QD sample there will be significant variations in these properties from one QD to another, so this result is consistent with the experimental variations in strain-induced shifts. For Faraday fields, the strain coupling is similar, but the hole spin is already well aligned to the magnetic field, and the large Zeeman splitting means the fractional strain-induced change is smaller. This is consistent with recent experiments on QDs [24], which inferred a hole spin coupling of ~10 THz=strain for a Faraday field and a small (~1%) fractional change in the Zeeman splitting. The electron spin is already well aligned to the magnetic field for Voigt and Faraday fields because of its weak spin-orbit coupling, so the applied strain has little effect on electron spin alignment.

While the coupling of the hole spin to strain is stronger than for the electron spin, it is still much weaker (1%–4%) than that of the optical transitions. However, the hole spin coherence time can be up to about 1 μs [26,28,29] compared to an optical coherence time of less than 1 ns. This means that the hole spin can be much more sensitive to strain than the optical transitions. These current experiments using optically excited holes do not take advantage of the longer spin coherence time. With a resident hole, we can use Raman spin flip spectroscopy [40–42], in which the emission line can be as sharp as the spin transition, or Ramsey fringe techniques [26,27,43], to measure much smaller changes in the spin splitting.

The coupling of the hole spin to a single quantum of mechanical motion, g0, is about 2 kHz in this cantilever [32]. While this value is small, it compares well to other quantum systems using strain-based coupling to spin, such as defects, which have spin-strain couplings that are orders of magnitude weaker [9,44,45]. While the hole spin g0 is much less than the decoherence rate of the hole spin, scaling down the dimensions of the mechanical resonator will increase the strain of a single quantum of motion [9,12,46]. Reducing the length and width of cantilevers by a factor of 10 should increase g0 by a factor of 100, approaching single phonon sensitivity. The results presented here indicate that hybrid spin mechanical systems based on hole spins combine strong spin-strain coupling with long coherence times, making it a promising system for quantum sensing [47,48], for coupling multiple quantum systems [5,6], and for accessing the quantum limits of motion.

Acknowledgments

This work was supported by the U.S. Office of Naval Research, the Defense Threat Reduction Agency (Grant No. HDTRA1-15-1-0011), and the OSD Quantum Sciences and Engineering Program.

References

  • [1].Schwab KC and Roukes ML, Phys. Today 58, No. 7, 36 (2005). [Google Scholar]
  • [2].Ramos T, Sudhir V, Stannigel K, Zoller P, and Kippenberg TJ, Phys. Rev. Lett 110, 193602 (2013). [DOI] [PubMed] [Google Scholar]
  • [3].Wilson-Rae I, Zoller P, and Imamoḡlu A, Phys. Rev. Lett 92, 075507 (2004). [DOI] [PubMed] [Google Scholar]
  • [4].Bennett SD, Kolkowitz S, Unterreithmeier QP, Rabl P,Jayich ACB, Harris JGE, and Lukin MD, New J. Phys 14, 125004 (2012). [Google Scholar]
  • [5].Rabl P, Kolkowitz SJ, Koppens FHL, Harris JGE, Zoller P, and Lukin MD, Nat. Phys 6, 602 (2010). [Google Scholar]
  • [6].Bennett SD, Yao NY, Otterbach J, Zoller P, Rabl P, and Lukin MD, Phys. Rev. Lett 110, 156402 (2013). [DOI] [PubMed] [Google Scholar]
  • [7].O’Connell AD, Hofheinz M, Ansmann M, Bialczak RC, Lenander M, Lucero E, Neeley M, Sank D, Wang H, Weides M, Wenner J, Martinis JM, and Cleland AN, Nature (London) 464, 697 (2010). [DOI] [PubMed] [Google Scholar]
  • [8].Treutlein P, Genes C, Hammerer K, Poggio M, and Rabl P, in Cavity Optomechanics, edited by Aspelmeyer M, Kippenberg TJ, and Marquardt F (Springer, Heidelberg, Berlin, 2014), pp. 327–351. [Google Scholar]
  • [9].Lee D, Lee KW, Cady JV, Ovartchaiyapong P, and Jayich ACB, J. Opt 19, 033001 (2017). [Google Scholar]
  • [10].MacQuarrie ER, Gosavi TA, Jungwirth NR, Bhave SA, and Fuchs GD, Phys. Rev. Lett 111, 227602 (2013). [DOI] [PubMed] [Google Scholar]
  • [11].Teissier J, Barfuss A, Appel P, Neu E, and Maletinsky P, Phys. Rev. Lett 113, 020503 (2014). [DOI] [PubMed] [Google Scholar]
  • [12].Ovartchaiyapong P, Lee KW, Myers BA, and Jayich ACB, Nat. Commun 5, 4429 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [13].Lee KW, Lee D, Ovartchaiyapong P, Minguzzi J, Maze JR, and Jayich ACB, Phys. Rev. Applied 6, 034005 (2016). [Google Scholar]
  • [14].Yeo I, de Assis P-L, Gloppe A, Dupont-Ferrier E, Verlot P, Malik NS, Dupuy E, Claudon J, Gérard J-M,Auffeves A, Nogues G, Seidelin S, Poizat J, Arcizet O, and Richard M, Nat. Nanotechnol 9, 106 (2014). [DOI] [PubMed] [Google Scholar]
  • [15].Montinaro M, Wüst G, Munsch M, Fontana Y, Russo-Averchi E, Heiss M, i Morral AF, Warburton RJ, and Poggio M, Nano Lett 14, 4454 (2014). [DOI] [PubMed] [Google Scholar]
  • [16].Munsch M, Kuhlmann AV, Cadeddu D, Gérard J-M, Claudon J, Poggio M, and Warburton RJ, Nat. Commun 8, 76 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [17].Carter SG, Bracker AS, Yakes MK, Zalalutdinov MK, Kim M, Kim CS, Czarnocki C, Scheibner M, and Gammon D, Appl. Phys. Lett 111, 183101 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [18].Bryant GW, Zieliński M, Malkova N, Sims J, Jaskólski W, and Aizpurua J, Phys. Rev. Lett 105, 067404 (2010). [DOI] [PubMed] [Google Scholar]
  • [19].Ding F, Singh R, Plumhof JD, Zander T, Křápek V, Chen YH, Benyoucef M, Zwiller V, Dörr K, Bester G, Rastelli A, and Schmidt OG, Phys. Rev. Lett 104, 067405 (2010). [DOI] [PubMed] [Google Scholar]
  • [20].Kuklewicz CE, Malein RNE, Petroff PM, and Gerardot BD, Nano Lett 12, 3761 (2012). [DOI] [PubMed] [Google Scholar]
  • [21].Trotta R, Zallo E, Ortix C, Atkinson P, Plumhof JD, van den Brink J, Rastelli A, and Schmidt OG, Phys. Rev. Lett 109, 147401 (2012). [DOI] [PubMed] [Google Scholar]
  • [22].Sun S, Kim H, Solomon GS, and Waks E, Appl. Phys. Lett 103, 151102 (2013). [Google Scholar]
  • [23].Zallo E, Trotta R, Křápek V, Huo YH, Atkinson P, Ding F, Šikola T, Rastelli A, and Schmidt OG, Phys. Rev. B 89, 241303(R) (2014). [Google Scholar]
  • [24].Tholen HMGA, Wildmann JS, Rastelli A, Trotta R, Pryor CE, Zallo E, Schmidt OG, Koenraad PM, and Silov AY, Phys. Rev. B 94, 245301 (2016). [Google Scholar]
  • [25].Winkler R, Spin Orbit Coupling Effects in Two-Dimensional Electron and Hole Systems (Springer-Verlag, Berlin, Heidelberg, 2003). [Google Scholar]
  • [26].De Greve K, McMahon PL, Press D, Ladd TD, Bisping D, Schneider C, Kamp M, Worschech L, Höfling S, Forchel A, and Yamamoto Y, Nat. Phys 7, 872 (2011). [Google Scholar]
  • [27].Greilich A, Carter SG, Kim D, Bracker AS, and Gammon D, Nat. Photonics 5, 702 (2011). [Google Scholar]
  • [28].Carter SG, Economou SE, Greilich A, Barnes E, Sweeney T, Bracker AS, and Gammon D, Phys. Rev. B 89, 075316 (2014). [Google Scholar]
  • [29].Prechtel JH, Kuhlmann AV, Houel J, Ludwig A, Valentin SR, Wieck AD, and Warburton RJ, Nat. Mater 15, 981 (2016). [DOI] [PubMed] [Google Scholar]
  • [30].Carter SG, Sweeney TM, Kim M, Kim CS, Solenov D, Economou SE, Reinecke TL, Yang L, Bracker AS, and Gammon D, Nat. Photonics 7, 329 (2013). [Google Scholar]
  • [31].Vora PM, Bracker AS, Carter SG, Sweeney TM, Kim M, Kim CS, Yang L, Brereton PG, Economou SE, and Gammon D, Nat. Commun 6, 7665 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  • [32].See Supplemental Material at http://link.aps.org/supplemental/10.1103/PhysRevLett.121.246801 for details on the sample structure, cantilever displacement calibration, dependence on drive laser power, measurement techniques, and single phonon coupling strength, which includes Refs. [33,34].
  • [33].Novotny L and Hecht B, in Principles of Nano-Optics (Cambridge University Press, Cambridge, England, 2012), pp. 45–63. [Google Scholar]
  • [34].Aspelmeyer M, Kippenberg TJ, and Marquardt F, Rev. Mod. Phys 86, 1391 (2014). [Google Scholar]
  • [35].Crooker SA, Brandt J, Sandfort C, Greilich A, Yakovlev DR, Reuter D, Wieck AD, and Bayer M, Phys. Rev. Lett 104, 036601 (2010). [DOI] [PubMed] [Google Scholar]
  • [36].Koudinov AV, Akimov IA, Kusrayev YG, and Henneberger F, Phys. Rev. B 70, 241305 (2004). [Google Scholar]
  • [37].Pryor CE and Flatte ME, Phys. Rev. Lett 96, 026804 (2006). [DOI] [PubMed] [Google Scholar]
  • [38].Léger Y, Besombes L, Maingault L, and Mariette H, Phys. Rev. B 76, 045331 (2007). [Google Scholar]
  • [39].Testelin C, Bernardot F, Eble B, and Chamarro M, Phys. Rev. B 79, 195440 (2009). [DOI] [PubMed] [Google Scholar]
  • [40].Sweeney TM, Carter SG, Bracker AS, Kim M, Kim CS, Yang L, Vora PM, Brereton PG, Cleveland ER, and Gammon D, Nat. Photonics 8, 442 (2014). [Google Scholar]
  • [41].He Y, He Y-M, Wei Y-J, Jiang X, Chen M-C, Xiong F-L, Zhao Y, Schneider C, Kamp M, Höfling S, Lu C-Y, and Pan J-W, Phys. Rev. Lett 111, 237403 (2013). [DOI] [PubMed] [Google Scholar]
  • [42].Fernandez G, Volz T, Desbuquois R, Badolato A, and Imamoglu A, Phys. Rev. Lett 103, 087406 (2009). [DOI] [PubMed] [Google Scholar]
  • [43].Kim D, Carter SG, Greilich A, Bracker AS, and Gammon D, Nat. Phys 7, 223 (2011). [Google Scholar]
  • [44].Falk AL, Klimov PV, Buckley BB, Ivády V, Abrikosov IA, Calusine G, Koehl WF, Gali Á, and Awschalom DD, Phys. Rev. Lett 112, 187601 (2014). [DOI] [PubMed] [Google Scholar]
  • [45].Soykal ÖO and Reinecke TL, Phys. Rev. B 95, 081405 (2017). [Google Scholar]
  • [46].Balram KC, Davanco M, Lim JY, Song JD, and Srinivasan K, Optica 1, 414 (2014). [Google Scholar]
  • [47].Krause AG, Winger M, Blasius TD, Lin Q, and Painter O, Nat. Photonics 6, 768 (2012). [Google Scholar]
  • [48].Barson MSJ, Peddibhotla P, Ovartchaiyapong P, Ganesan K, Taylor RL, Gebert M, Mielens Z, Koslowski B, Simpson DA, McGuinness LP, McCallum J, Prawer S,Onoda S, Ohshima T, Jayich ACB, Jelezko F, Manson NB, and Doherty MW, Nano Lett 17, 1496 (2017). [DOI] [PubMed] [Google Scholar]

RESOURCES