A deep learning approach for real-time detection of sleep spindles

Abstract

Objective.

Sleep spindles have been implicated in memory consolidation and synaptic plasticity during NREM sleep. Detection accuracy and latency in automatic spindle detection are critical for real-time applications.

Approach.

Here we propose a novel deep learning strategy (SpindleNet) to detect sleep spindles based on a single EEG channel. While the majority of spindle detection methods are used for off-line applications, our method is well suited for online applications.

Main results.

Compared with other spindle detection methods, SpindleNet achieves superior detection accuracy and speed, as demonstrated in two publicly available expert-validated EEG sleep spindle datasets. Our real-time detection of spindle onset achieves detection latencies of 150-350 ms (~2-3 spindle cycles) and retains excellent performance under low EEG sampling frequencies and low signal-to-noise ratios. SpindleNet has good generalization across different sleep datasets from various subject groups of different ages and species.

Significance.

SpindleNet is ultra-fast and scalable to multichannel EEG recordings, with an accuracy level comparable to human experts, making it appealing for long-term sleep monitoring and closed-loop neuroscience experiments.

1. Introduction

Sleep spindles are brief bursts of neural oscillations (9-16 or 11-16 Hz, 0.5-3 sec) generated by the interplay of the thalamic reticular nucleus and other thalamic nuclei during NREM sleep (N2 and N3 stages) (Gennaro and Ferrara 2003). Spindles can be observed in a wide range of thalamic and neocortical structures, and are temporally coupled with neocortical slow oscillations (SOs, 0.5-1 Hz) and hippocampal sharp-wave ripples (SWRs, 150-250 Hz) during NREM sleep (Mölle et al. 2011; Mölle et al. 2002; Staresina et al. 2015). Spindles and SOs might have differential roles in memory consolidation at different sleep stages, or for consolidation of different types of memory traces (Born and Wilhelm 2012; Wei et al. 2018). In addition, spindles are thought to contribute to a number of neural processes, such as somatosensory development, thalamocortical sensory gating, and synaptic plasticity (Johnson et al. 2012; Cox, Hofman, and Talamini 2012; Mednick et al. 2013; Astori, Wimmer, and Lüthi 2013). Spindles have also been implicated in integrating new memories with existing knowledge (Tamminen et al. 2011). Online monitoring and entrainment of sleep spindles can provide additional benefits, as experimental evidence has suggested that spindle density predicts the effect of prior knowledge on memory consolidation (Hennies et al. 2016). Sleep disorders or disturbances are important symptoms in many neurological or neuropsychiatric disorders. Characterization of sleep spindles (e.g., oscillatory frequency, spindle density, duration) can be used as an important biomarker related to brain health, for early detection of neurodegenerative disorders such as mild cognitive impairment (MCI) and Alzheimer’s disease (Astori, Wimmer, and Lüthi 2013; Hennies et al. 2016; Gorgoni et al. 2016; Mander et al. 2014; Kam et al. 2016), for assessment of children’s cognitive development (Chatburn et al. 2013), and for prediction of stress and schizophrenia (Dang-Vu et al. 2015; Castelnovo et al. 2018; D’Agostino et al. 2018).

Spindles provide an important signature for N2-stage sleep. In human sleep labs, spindle detection requires manual annotation by sleep experts, a resource-intensive task that is time consuming and subject to inter-rater variability (Campbell, Kumar, and Hofman 1980; Warby et al. 2014; Zhao et al. 2017). In animal sleep research, there are no publicly available datasets with expert-annotated spindles. Additionally, there may be great variability in spindle characteristics across different brain areas (e.g., hippocampus, thalamus, and neocortex) and recording tools (e.g., surface or intracortical EEG). Therefore, detection of sleep spindles has been an active area of research in human and animal sleep studies for decades. To date, the majority of work on automatic spindle detection is geared towards off-line applications for specific cohorts, which may rely on various unsupervised or supervised techniques, including constant or adaptive thresholds, matching pursuit, time-frequency transform, decision tree and low-rank optimization (Schönwald et al. 2006; Huupponen et al. 2007; Duman et al. 2009; Devuyst et al. 2011; Nonclercq et al. 2013; Babadi et al. 2012; Warby et al. 2014; O’Reilly and Nielsen 2015; Parekh et al. 2017; Parekh et al. 2015; Lajnef 2016; LaRocco et al. 2018). Although a few spindle detection algorithms have been adapted for online applications, their detection latencies have not been fully investigated. Therefore, their flexibility and detection latency for real-time brain-machine interface (BMI) applications requiring spindle-triggered closed-loop auditory or electrical stimulation (Lustenberger et al. 2017; Latchoumane et al. 2017) remains untested. For instance, in order to enhance memory processing during sleep, targeted memory reactivation (TMR) is aimed to expose the sleeping brain with an olfactory or auditory cue that is used in the context of learning or task behavior during the pre-sleep wakeful period (Schouten et al. 2017). The latency consideration is critical because the timing of closed-loop stimulation affects TMR, in that acoustic stimulation has been shown to be most efficient when delivered at the descending phase of SO down state (Batterink, Creery, and Paller 2016) or during the transition from cortical down states to up states (Ngo et al. 2013). Furthermore, since fast (13-16 Hz) or slow (9-13 Hz) spindles may occur during different phases of SO (half cycle: 0.5-1 s) or cortical (up vs. down) state (Mölle et al. 2011) and they may have differential roles in memory consolidation. If sleep spindles are detected too late (>350 ms), the phase of SO will not be properly selected; as a consequence, stimulation won’t be properly applied.

To date, although numerous methods or algorithms have been developed for detecting sleep spindles, most of them are not suitable for online detection or real-time applications. To accommodate real-time processing, the spindle detection method needs to process the neural data on the fly, with a computational speed faster or comparable to the data streaming speed. Many available spindle detection algorithms cannot be used directly in online applications, either because they don’t process data in a sequential manner, or because they do not meet the speed requirement.

Machine learning has recently emerged as a powerful tool in big data analysis. Deep learning algorithms, powered by scalable computational resources and large datasets, have shown superior performances in a wide range of tasks, including playing the game of Go (Silver et al. 2016), large-scale image and speech recognition (Russakovsky et al. 2017; LeCun, Bengio, and Hinton 2015), sleep staging (Supratak et al. 2017; Biswal et al. 2017; Mikkelsen and de Vos 2018), EEG-based prediction (Antoniades et al. 2017; Van Putten, Olbrich, and Arns 2018), clinical monitoring (Lee et al. 2018), and medical image analysis (Esteva et al. 2017). However, deep learning has not been fully investigated in the context of automatic spindle detection (Dakun et al. 2015; Chambon et al. 2018). To improve detection latency and accuracy of sleep spindles, we have developed a deep neural network (DNN) approach, termed as SpindleNet, to learn the complex nonlinear features and spectrotemporal structures of sleep spindles. Based on two public annotated sleep spindle datasets, we construct a large number (order of millions) of labeled examples and train the DNN using advanced machine-learning techniques. Since annotated spindles are rare, we propose a transfer learning method in combination with synthetic spindles through computer simulations, to extend spindle detection to a wide variety of datasets (patient populations, noninvasive and invasive EEG, human and animal). Transfer learning allows us to store knowledge gained from solving one problem with sufficient existing labeled data in one domain, and apply it to a different but related problem in another domain (Pan and Yang 2010). We validate the robustness of our transfer learning method on cross-subject, cross-age/health group, and cross-species scenarios.

2. Methods

2.1. Experimental data.

We tested our deep learning approach on four publicly available human sleep datasets, one non-public human sleep spindle data set, and one non-public rat sleep dataset. All studies were approved by the New York University School of Medicine (NYUSOM) Institutional Review Board (IRB) and Institutional Animal Care and Use Committee (IACUC).

The first human sleep spindle dataset was derived from the Montreal archive of sleep studies (MASS)---an open-access and collaborative database of laboratory-based polysomnography (PSG) recordings (O’Reilly et al. 2014). MASS is composed of several cohorts divided into subsets. Cohort one has five subsets and comprises of 200 complete night PSG recordings of 97 men and 103 women of age varying between 18 and 76 years (mean±SD: 38.3±18.9 years), stored in European data format (EDF). The subset #2 within cohort one (19 healthy subjects) was annotated for N2 stage spindles (start-time and duration) by two human experts based on the C3 channel (linked-ear reference). A total of fifteen subjects were annotated by two human experts, whereas the remaining four subjects were annotated by only one expert. The EEG signals were originally sampled at 256 Hz and resampled to 200 Hz for standardization. For each subject’s sleep recording, we observed consistent variability between the annotations of the two experts in terms of start-time, duration and total number of spindles (figure 1). In our study, we used the union of annotations from the two experts as our ground-truth in training the neural network. We also evaluated the performance using an intersection of the annotations from the two experts, which resulted in lower performance. We used the MASS dataset for the 5-fold cross-validation analysis, and tested the performance of the algorithm on the other independently acquired datasets.

Figure 1. Statistics of MASS dataset.

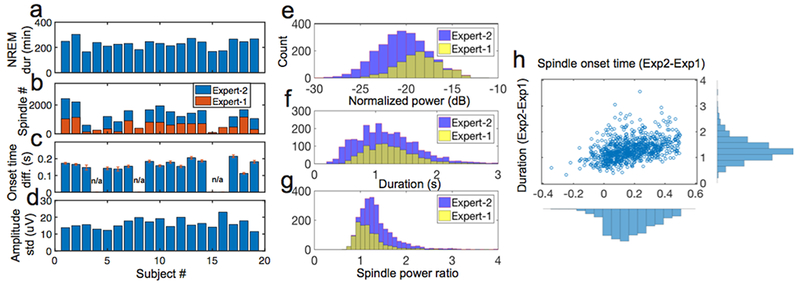
a, Statistics of NREM duration (min) on 19 human subjects. b-d, Statistics of annotated spindle number (b), onset time difference between two experts (c) and amplitude standard deviation (d). In panel c, n/a represents the condition only one expert’s annotation was available; the onset time difference among 15 subjects were 0.167 ± 0.007 s (mean±SEM). e-h, In subject #1, statistics discrepancy between two experts on the commonly annotated sleep spindles’ normalized power (e), duration (f), power ratio (g) and difference between two experts (Expert 2-Expert 1) on the spindle onset and duration (h).

The second human sleep spindle dataset was derived from the DREAMS database from the University of MONS-TCTS Laboratory and Universite Libre de Bruxelles--CHU de Charleroi Sleep Laboratory under terms of the Attribution-NonCommerical-NoDerivs 3.0 Unported (CC BY-NC-ND 3.0) License (Devuyst et al. 2006). The DREAMS dataset consists of 30 minute PSG excerpts from eight subjects (4 males and 4 females, age: 45.88 ± 7.87 years) with various sleep pathologies (dysomnia, restless syndrome, insomnia and apnea/hypopnea syndrome. The excerpts contain three EEG channels (FP1-A1, C3-A1, O1-A1), two EOG channels and one EMG channel. They were scored independently by two sleep experts based on the C3 channel. The original EEG recordings had varying sampling frequency of 50-200 Hz, and then were uniformly resampled to 200 Hz for standardization. Since not all EEG recordings were annotated by two experts (six only by one expert), and there were consistent differences in their annotations (for e.g. expert two only annotated the start-time while expert one annotated both start-time and duration of the spindles), we used the union of their annotations (‘OR’ criterion) as the ground-truth to assess the performance of the sleep spindle detection.

The third and fourth human sleep datasets were derived from the national sleep research resource (NSRR) repository (Zhang et al. 2018). The third dataset consisted of overnight PSG recordings from elderly men (65 years or older), collected as a part of a multi-center study of osteoporotic fractures (MrOS) (Blank et al. 2005). The fourth dataset consisted of overnight PSG date from children (ages 5 to 9.9 years) collected as a part of a multi-center childhood adenotonsillectomy (CHAT) study (Redline et al. 2011). Both datasets consisted of EEG recordings for channels C3 and C4 with expert-annotated sleep-stages. Original sampling rates varied from 200 Hz to 512 Hz, and were uniformly resampled to 200 Hz. We randomly selected five subjects from each dataset and tested SpindleNet on stage-2 NREM sleep data from channel C3.

The fifth human sleep spindle dataset consisted of intracranial EEG (iEEG) recordings (on average 120 electrodes per subject) from a study of 18 epileptic patients who underwent surgery for invasive monitoring (Lafon et al. 2017). The original signal was sampled at 512 Hz and resampled to 200 Hz. We selected three subjects who had entrained sleep spindles following randomly applied acoustic stimuli.

Finally, for rat sleep recordings, multichannel local field potential (LFP) signals were acquired from the rat primary somatosensory cortex (coordinate: AP −1.5 mm, ML +3.0, and DV −1.5) across four sessions (1-2 hours duration) from three animals (male Sprague-Dawley rats). Rats were kept with controlled humidity, temperature, and 12-hour (6:30 AM to 6:30 PM) light-dark cycle. Food and water were available ad libitum. Rats were anesthetized with isoflurane (1.5-2%) and implanted with silicon probes (NeuroNexus) mounted on custom-built microdrives. One or two probes were implanted in the right hemisphere. Rats were allowed to recover for about one week after surgery. Rats were allowed to habituate in the recording room and remained in their home cage with food and water available during the daytime for 5-7 days. Lights were on in the recording room during the recording. Raw neural signals were recorded with 64-channel digital headstage (RHD2132, Intan Technologies) and acquisition board (Open Ephys) at a sample rate of 1 kHz (resampled to 200 Hz). To obtain LFPs, we further filtered the raw signal by a bandpass filter between 0.3 and 300 Hz.

2.2. Training setup for SpindleNet.

The SpindleNet is comprised of two deep learning modules: convolutional neural network (CNN) and recurrent neural network (RNN), which are integrated in a sequential structure (figure 2a, ‘network 1’ and ‘network 2’). The CNN consists of 5 convolution layers (figure 2b) of 40 one-dimensional (1D) temporal filters (vectors) of size 1×7 in each layer, followed by exponential linear units (ELUs). Input to ‘network 1’ consists of 1 × 50 (0.25 s × 200 Hz) vector of raw EEG time series. Input to ‘network 2’ consists of the envelope of the band-pass filtered (9-16 Hz) signals of the same length. Finally, EEG power features are combined along with the outputs of ‘network 1’ and ‘network 2’ and the concatenated vector is processed through a fully connected layer.

Figure 2. SpindleNet: deep neural network (DNN) architecture used for spindle detection.

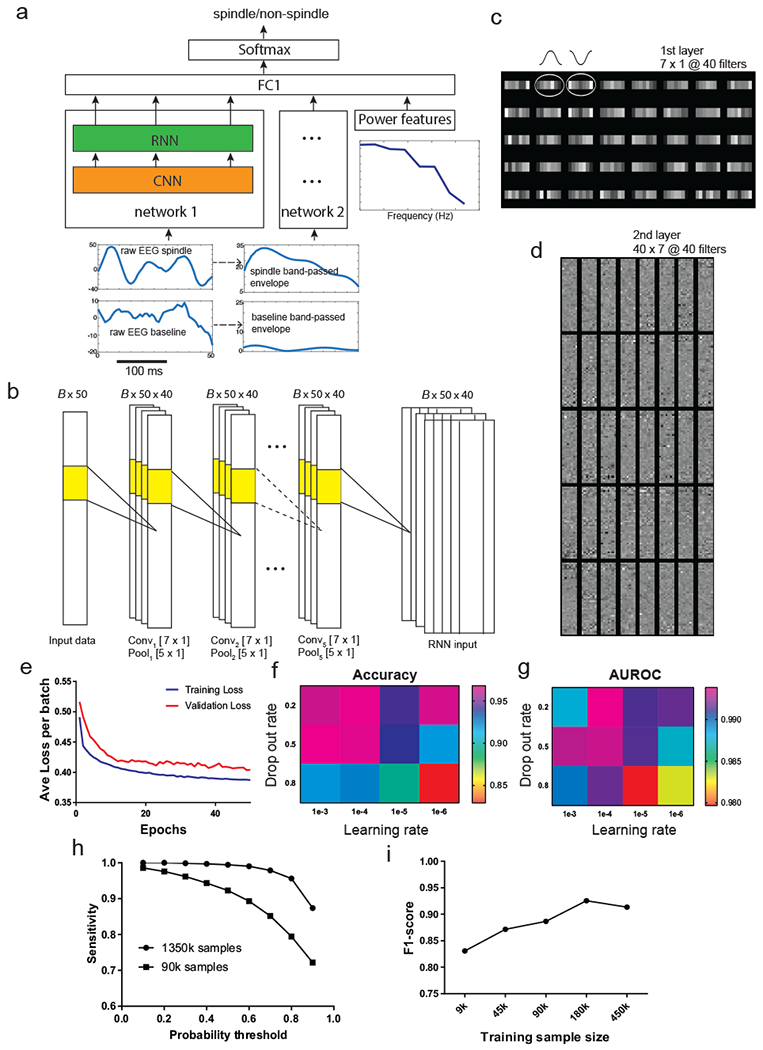
a, Overall architecture of the network. The input to subnetwork 1 and 2 consists of raw EEG signal and the envelope of bandpass filtered (9-16 Hz) EEG signal, respectively. The power features that are directly input to the fully connected layer consist of the ratio of the average power of spindle-band frequencies (9-16 Hz) to that of lower frequencies (2-8 Hz) and the instantaneous power of all frequencies from (2-16 Hz). The convolutional neural network (CNN) acts as a temporal feature extractor. The features learned by the CNN are further passed to a recurrent neural network (RNN) that is intendent to discover temporal patterns within the CNN features. The RNN implementation consists of a single-layer long short-term memory (LSTM). The output of the RNN (from 50 time steps) of subnetwork 1 is combined with the output of RNN from the subnetwork 2 and the power features using a fully connected layer. Output of this layer (of length 50) is further processed by a softmax activation function that produces a probability output (spindle vs non-spindle). b, Detailed architecture of the 5-layer CNN. The input is processed by a total of 5 layers. Every layer consists of 40 1D filters of size 7×1, followed by max-pooling with kernel size 5×1. For 250-ms EEG with 200 Hz sampling frequency, the size of input is 50. Batch size is set to B=20. c, A set of 7×1 learned receptive fields (RFs) from the first-layer CNN filters upon completion of training. The 1D filters share a resemblance to the shape of half cycle of spindle oscillation. d, A set of 40×40×7 learned RFs from the second-layer CNN filters. e, The learning convergence curve on training and validation data. f, The change of detection accuracy with respect to two learning hyperparameters: learning rate and drop-out rate. g, The change of AUROC statistic with respect to the learning rate and drop-out rate. h, The sensitivity of spindle detection improved with increasing training sample size (both tested on the same test data). i, The F1-score of detection gradually increased with increasing training sample size.

We used a large receptive field in the first layer inspired by some of the early work in ImageNet classification (Krizhevsky, Stuskefer, and Hinton 2012), and decided to maintain the size of the receptive fields across the layers based on the network design suggestions by VGG Net (Simonyan and Zisserman 2014). However, we found that changing the number of layers or receptive field size did not significantly affect our outcome. We used the exponential activation function for all the CNN units due to its demonstrated faster learning time and higher accuracy compared to other types of nonlinearity (Clevert, Unterthiner, and Hochreiter 2015). Every layer was followed by max-pooling using a filter size of five samples and stride equal to one. The CNN with ELUs has been previously tested in EEG data analyses (Schirrmeister et al. 2017). The RNN consists of 100 long short-term memory (LSTM) cells, followed by one fully connected layer and one output layer with a softmax activation function.

The dropout strategy has been shown to outperform other regularization methods (Hinton 2014), which randomly sets a specified percentage of input units in every layer (except the first layer) to zero. In all experiments, we empirically set the dropout rate equal to 0.5.

The temporal input for online spindle prediction consisted of single-channel EEG (or LFP) signal with a moving window of length 250 ms, approximately one quarter of the average spindle size. The parameters of SpindleNet were updated using the Adam optimizer (Kingma and Ba 2014). We used the following default learning hyperparameters: an initial learning rate of 0.0001 and mini-batch size of 500 (with a balanced size of examples from two classes).

Within each fold of 5-fold cross validation, we used 70% of all balanced augmented samples as the training set, and 30% for validation. At each fold, we used 30% data for validation of independent data samples and for early stopping (to avoid overfitting). We tested SpindleNet on the test subjects’ complete recordings by using a moving window with a stride of one. For each training sample, we preprocessed the sample by detrending, demeaning, and scale normalization for calibration.

The SpindleNet was developed on the basis of the TensorFlow (https://www.tensorflow.org), an open source platform for deep learning and neural network development. Our custom code was written and implemented on a Linux Computer (OS Ubuntu, 4-core Intel Core i7-7700K; 32GB RAM and NVIDIA GTX-Ti 1080 GPU card with 11GB). On average, the online execution time of SpindleNet (including computation of EEG features) was approximately 6 ms.

2.3. Data calibration.

In practice, EEG signals have different amplitude or variance statistics depending on the sleep stage, electrode conductance, and recording depth. Therefore, we applied scale normalization for data calibration. For the benchmark experimental testing, the scale was chosen as the average standard deviation of the expert-annotated spindles). For other datasets, we scaled the signals (EEG, iEEG or rodent LFP) with the standard deviation statistic of the raw time series of a randomly selected subject from the dataset. This was based on the assumption that the ratio of spindle amplitude relative to EEG amplitude in NREM sleep was similar or stable.

2.4. Data augmentation.

The occurrence of spindles was distributed throughout stage-2 or stage-3 NREM (N2, N3) sleep with a density that varied by subject and pathology. This resulted in an imbalanced dataset with few samples from the positive class (spindles) compared to the negative class (non-spindles). To generate a balanced training sample size, we augmented the positive and negative class until they were balanced. This was done by selecting a fixed time interval before and after the center of the spindle and generating samples using a moving window of size T_w with a stride of one (Figure 3a). A positive label was generated for every window of length T_w if more than 50% samples within that window overlapped with the expert-annotated spindles; otherwise a negative label was used.

Figure 3. Spindle data augmentation and generation of synthetic spindles.

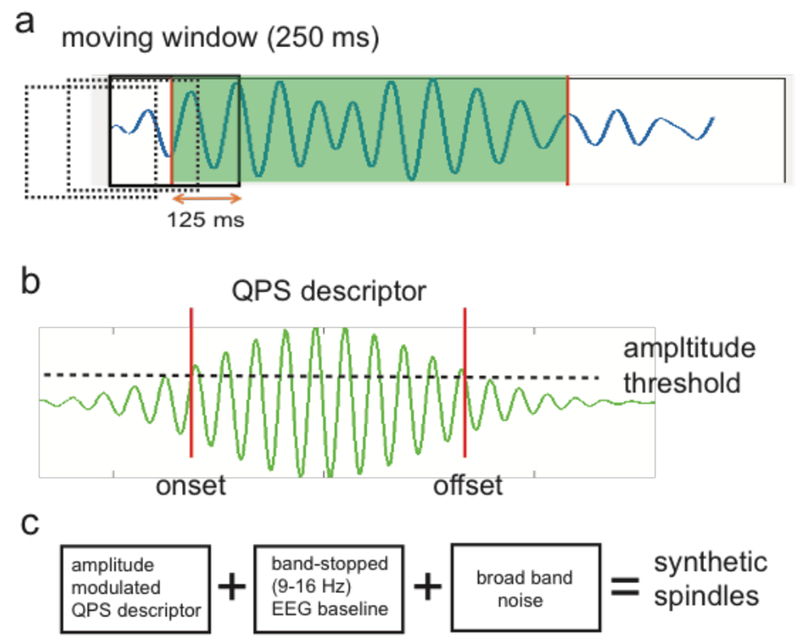
a, We used a 250-ms overlapping moving window (dashed and solid boxes) to construct positive and negative samples. Any EEG traces with ≥50% duration (i.e., 125 ms) coverage of the annotated spindle event (shaded period) was treated as a spindle (positive) example; everything else was a non-spindle (negative) example. b, An amplitude-modulated, quadratic parameter sinusoid (QPS) descriptor for spindles. The two vertical lines mark the onset and offset of spindles, which pass the threshold of 20% of peak amplitude. c, Schematic diagram of generating synthetized sleep spindles.

2.5. Feature selection and fusion.

Spindles are characterized by a localized high power in the spindle band (9-16 Hz) of spectrogram. To accommodate additional spectral features, we computed the multi-taper spectrum using a time window of 500 ms and step size of 5 ms (i.e., 1/sampling frequency). The power features were computed after data spindle (9-16 Hz)band preprocessing. In addition, we computed the spectral power ratio $\frac{\text{spindle}(9–16\mathrm{Hz})\text{band}}{\text{delta}+\text{theta}(2–8\mathrm{Hz})\text{bands}}$ as one of the features. The power features were appended to the output of the RNN in two subnetworks (figure 2a).

2.6. Online vs. offline detection of sleep spindles.

Depending on specific application, we employed different criteria to define sleep spindles. In online spindle detection, the latency is the most important factor. Detection latency is not an issue for offline spindle detection applications, therefore we used a stricter duration criterion to eliminate the detected events shorter than a specified length (e.g., 400 ms).

….. We set two detection criteria (softmax probability and minimum spindle duration) to determine the confidence of online detection. Introducing a minimum spindle duration would inevitably introduce a detection latency. In contrast, there would be no duration criterion in off-line detection.

2.7. Assessment of performance.

We used the following performance metrics:

$$\text{Sensitivity}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}},\text{Specificity}=\frac{\mathrm{TN}}{\mathrm{TN}+\mathrm{FP}},\text{Precision}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}},$$

$$\text{Accuracy}=\frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{TP}+\mathrm{FP}+\mathrm{TN}+\mathrm{FN}},\mathrm{F}1-\text{score}=\frac{2\times \mathrm{TP}}{2\times \mathrm{TP}+\mathrm{FP}+\mathrm{FN}}$$

$$\text{False positive rate}(\mathrm{FPR})=\frac{\mathrm{FP}}{\mathrm{FP}+\mathrm{TN}},\text{False discovery rate}(\mathrm{FDR})=\frac{\mathrm{FP}}{\mathrm{FP}+\mathrm{TP}}$$

where TP (true positive) denotes agreement between the algorithm and ground truth. FN (false negative) denotes a true spindle was missed by the algorithm but marked by experts. FP (false positive) denotes a spindle was detected by algorithm but not marked by the experts. TN (true negative) was defined as in (Devuyst et al. 2011): TN=signal duration in seconds–FP–TP–FN. We assess a true positive when the absolute difference between the estimated spindle onset by the algorithm and the onset of ground truth is less than 0.25 s. We used the same assessment metrics for comparing other sleep detection methods with SpindleNet.

We also computed the false event rate and true event rate (per minute). Specifically, we used a non-overlapping 1min moving window to calculate the statistics of spindle events (regardless of the duration). In addition, we computed the detection latency by comparing the spindle onset detected by SpindleNet to that of the experts’ annotation.

2.8. Synthetic spindle generation.

We used a quadratic parameter sinusoid (QPS) model (figure 3b) to characterize sleep spindles (Palliyali, Ahmed, and Ahmed 2015).

$$s(t)=e^{(a+bt+c{t}^2)}\cos (d+et+f{t}^2)$$

where a, b, c, d, e and f are the free parameters of the quadratic functions. We set a=0 (such that the peak amplitude is 1, or s_max(t)=1) and set b, c, d, e, f as random variables with normal distributions derived from the annotated spindle statistics. In the case of MASS dataset, based on the results published in (Palliyali, Ahmed, and Ahmed 2015), we used the following parameters (mean, standard deviation): c = (−10, 3.87), d = (0, 4.69), e = (84.5, 3.86), and f = (−0.9, 4.96). For the DREAMS dataset, we fitted the QPS model to expert-annotated sleep spindles to compute the simulation parameters for each subject separately (Table 1) which were then used to generate synthetic spindles.

Table 1.

Synthetic spindle parameters (mean, standard deviation) for the DREAMS dataset (n=8 subjects).

DREAMS subject #	c	d	e	f
1	−9.34 (9.6)	−0.7 (4.77)	82.09 (5.45)	−0.77 (9.45)
2	−8.5 (9.66)	0.16 (4.23)	81.32 (4.69)	−1.84 (8.25)
3	−5.38 (4.98)	−0.62 (4.08)	86.56 (4.12)	0.14 (6.81)
4	−8.49 (8.19)	0.36 (4.6)	79.85 (8.34)	−2.21 (14.17)
5	−10.86 (8.72)	−0.01 (4.33)	83.76 (3.59)	−4.12 (10.41)
6	−12.76 (14.63)	−0.19 (4.51)	85.2 (4.09)	−5.52 (13.31)
7	−9.01 (8.13)	1.73 (3.94)	84.17 (7.14)	1.86 (7.9)
8	−13.26 (14.8)	−0.44 (4.8)	86.13 (5.26)	−2.58 (17.83)

To mimic the rich spectrotemporal components of raw EEG data, we merged the synthetic spindles with experimental EEG signals. The peak of a simulated spindle was centered at 0. To define the onset/offset of simulated spindle, we defined the threshold to be at 0.4 (i.e., 40% of the peak amplitude of s(t)). We used a Butterworth ‘bandstop’ filter to obtain a clean baseline EEG by removing 9-16 Hz frequency components. Adding these two components together with (optional) broadband noise yielded synthetic spindles (figure 3c).

2.9. Other sleep spindle detection methods.

There are numerous automatic sleep spindle algorithms in the literature, but the majority of them are not suitable for online applications because they rely on multiple spindles to determine the best thresholds and compute signal decompositions that are not performed in real time. In addition, some algorithms require prior knowledge or parameter fitting, therefore it is nearly impossible to have a completely fair comparison between methods.

For the purpose of comparison, here we selected two recently published spindle detection algorithms. The first one is known as McSleep (Parekh et al. 2017) (https://github.com/aparek/mcsleep.git), which has been shown to outperform seven other spindle detection methods (Warby et al. 2014) in the MASS and DREAMS datasets. The McSleep algorithm is a nonlinear subspace detection method, which decomposes the input EEG signal into the sum of a transient and an oscillatory component. The envelope of oscillatory activity is further detected by a Teager operator, followed by spindle threshold detection. The second spindle detection algorithm is known as Spindler (LaRocco et al. 2018) (https://github.com/VisLab/EEG-Spindles). Spindler performs matching pursuit using Gabor atoms for estimating spindle locations, which is then thresholded to further identify the spindles. The open-source software of these two tested algorithms are not suitable for the online application.

2.10. Assessment of agreement between detection results.

Cohen’s kappa and other kappa variants are commonly used for assessing inter-rater reliability (IRR) for nominal (i.e., categorical) variables (Cohen 1960). Kappa statistics measure the observed level of agreement between two raters or classifiers for a set of nominal ratings and corrects for agreement that would be expected by chance. Specifically, we computed kappa based on the equation

$$\kappa =\frac{P(a)-P(e)}{1-P(e)}$$

where P(a) denotes the observed percentage of agreement, and P(e) denotes the probability of expected agreement at a chance level (for a two-class classification problem, P(e) =0.5). κ =1 denotes a perfect agreement.

3. Results

3.1. Overview

Two of the most widely used types of deep learning architectures are convolutional neural networks (CNNs) and recurrent neural networks (RNNs). We developed a DNN architecture that integrates a CNN with a RNN in a sequential structure (figure 2a). The CNN consists of 5 convolution layers (figure 2b). The input consists of i) a 1 × 50 (0.25 s × 200 Hz) vector of EEG time series; ii) the envelope of the band-pass filtered (9-16 Hz) signals of the same length; and iii) EEG power features. The convolution operation consists of 40 one-dimensional (1D) temporal filters (vectors) of size 1×7, followed by exponential linear activation. The RNN consists of 100 long short-term memory (LSTM) cells, followed by one fully connected layer and one output layer with a softmax activation function.

We constructed independent training and validation samples for sleep spindles from annotated human EEG recordings. Using discriminative supervised learning, we trained SpindleNet using a stochastic optimization algorithm (Methods). For each subject’s recording, SpindleNet was trained on approximately 1-2 million experimental EEG traces in the time domain. Upon completion of training, we examined the receptive field (RF) representation of the learned convolution filters. The first-layer filters behaved as matched filters that showed temporal structure characterizing spindle oscillations (figure 2c). The second and higher-layer filters represented complex and hard-to-interpret higher-order spectrotemporal features (figure 2d). During training, we monitored the convergence process based on training and validation loss functions to avoid overfitting (figure 2e), and the network size and hyperparameters were optimized using grid search method. However, the detection performance was robust to the exact choice of hyperparameters (figure 2f,g). Detection performance of deep learning depended on the size of training samples. Adding training samples gradually improved the accuracy of testing data until ultimately reaching the performance plateau (figure 2h,i), indicating the importance of large-scale data in deep learning.

Among all annotated spindle events, there was inevitably an unknown level of label noise where two experts disagreed. As a result, the histograms of duration, power and power ratio statistics of annotated spindles varied between two human raters (figure 1). Differences in these statistics suggested subjective biases in human annotation.

3.2. Results on two annotated human sleep datasets

We tested two public annotated sleep spindle datasets (Methods), which contained nocturnal sleep EEG recordings from healthy subjects (MASS) and from subjects with sleep pathologies (DREAMS). The training data were constructed from a subset of 19 healthy adult subjects from the MASS dataset. The NREM sleep duration and spindle statistics varied across subjects (figure 1a–d). In addition, there was a large variability in annotated spindle statistics between two human experts (figure 1e–h). We used an “OR” criterion from two experts to construct putative true positives (TPs) for spindles. In addition, there were unlabeled spindle examples from two experts, which could nevertheless be detected by our method (see an example marked by arrows in figure 4a,b). Although sleep spindles were only annotated during N2 sleep in the MASS dataset, we were able to identify sleep spindles during N3-stage sleep, which are often temporally coupled with slow oscillations (figure 4d). Due to the lack of expert-identified spindles to provide ground truth, N3-stage spindle statistics were not used in the result assessment.

Figure 4. Results on online sleep spindle detection.

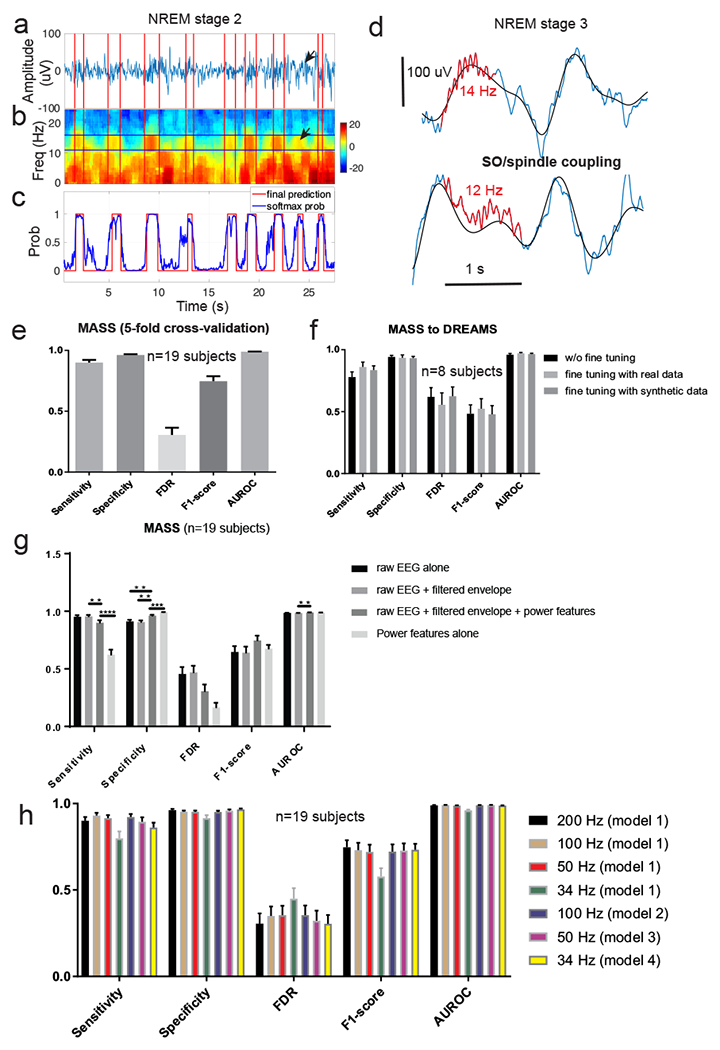
a, A representative snapshot of EEG trace (during stage-2 NREM sleep) with human marked sleep spindles (in red). b, Associated EEG multi-taper spectrogram (1 s moving window, 5 ms step size). Arrows in panels a and b denote a potentially unlabeled spindle by two experts, which was detected by SpindleNet. c, Softmax probability output (blue) and the final hard decision (red, probability threshold 0.9) for online spindle detection. d, Representative EEG traces (blue) during stage-3 NREM sleep that demonstrate coupling between slow wave (0.5-4 Hz, black trace) and spindles (marked in red). In these two examples, fast (13-16 Hz) sleep spindles tend to occur in the ascending phase of SO cycle (or be coordinated with depolarizing cortical up state), whereas slow (9-12 Hz) spindles tend to occur in the descending phase of SO cycle, or during the transition from cortical down to up states. Note that a large latency in spindle detection may switch from the up ascending phase to the down descending phase of the SO. e, Summarized results (from 5-fold cross validation) of sensitivity, specificity, false discovery rate (FDR), F1-score and AUROC statistics in the MASS dataset (n=19 subjects). Error bar represents SEM. f, Summarized results of sensitivity, specificity, FDR, F1-score and AUROC statistics in the DREAM dataset (n=8 subjects), using SpindleNet trained from the MASS dataset without further fine tuning as well as with fine-tuning using real and simulated spindles. Fine-tuning with real and simulated data further improved the performance. Error bar represents SEM. g, Performance comparison (5-fold cross-validated results) of DNN using different input features: raw EEG signal, filtered EEG envelope within the spindle frequency band (9-16 Hz), and the power feature. h, Results on spindle detection from the MASS dataset (n=19 subjects, error bar represents SEM) under various EEG sampling frequencies. Model 1: standard model trained with EEG signal with 200 Hz sampling rate; Models 2-4: models trained on down-sampled EEG signals at frequencies 100 Hz, 50 Hz, 34 Hz, respectively. In testing EEG signals with <200 Hz sampling frequency, we either up-sampled the signal and applied the standard model (Model 1), or applied the respective model for the sampling frequency. SpindleNet demonstrated robust performance across various sampling frequencies.

We first assessed the spindle detection performance based on the MASS dataset. We trained SpindleNet with the N2-stage sleep recordings using a 5-fold cross-validation scheme and computed sensitivity, specificity, false discovery rate (FDR), and F1-score (Methods, figure 4e). Among the subsets of 25,453 putative spindles (n=19 subjects), our method achieved sensitivity of 90.07± 2.16%, specificity of 96.19 ± 0.71%, FDR of 30.36 ± 5.88%, F1-score of 0.75 ± 0.05 and AUROC of 98.97 ± 0.13% (mean±SEM). We also compared the statistics of false positive (FP) detections with that of the spindle TPs (ground truth) for duration and power, and found that these two sets were nearly inseparable in the overlapping feature space, indicating the possibility that SpindleNet detected spindles that might be missed by experts. Among those putative spindles, we further computed their Fourier spectra and categorized them into fast (13-16 Hz) and slow (9-12 Hz) spindles. During N2 sleep, the occurrence distribution of fast and slow spindles varied.

Next, we tested SpindleNet trained from the MASS dataset on the unseen DREAMS dataset. Despite the differences in spindle statistics between the two datasets, SpindleNet achieved good generalization (sensitivity, 77.85 ± 4.28%; specificity, 94.2 ± 1.26%; FDR, 61.96 ± 7.39%; F1-score, 0.48 ± 0.07; and AUROC, 95.97 ± 0.96%) while testing on the DREAMS dataset (figure 4f, w/o fine tuning; referred to as baseline). To further improve the baseline performance, we fine-tuned SpindleNet using annotated spindles from the DREAMS dataset. As a result, the detection accuracy showed an improved trend for a small sample size (figure 4f, signed rank test: FDR, p=0.0547; F1-score, p=0.0547, sensitivity, p=0.25; n=8). Alternatively, we fine-tuned SpindleNet using simulated spindle samples; and the detection results were also similar or slightly improved compared to the baseline.

In addition, we evaluated the performance gain achieved by the various input components of SpindleNet (figure 4g). We found that although the network with all three inputs had lower sensitivity, using additional inputs (envelope and power features) helped improve the performance of SpindleNet on all other metrics (specificity, FDR, F1-score and AUROC). Finally, for the purpose of comparison, we also ran the non-DNN component of SpindleNet by using the power features alone. We found that the deep learning components (using raw EEG and envelope features) achieved significantly higher sensitivity and higher F1-score compared to the shallow network component based upon the power features. This suggests that the deep learning component of SpindleNet played a more significant role in the overall performance, which was further improved when additional power features were used in conjunction with raw EEG and envelope features. Overall, SpindleNet have demonstrated excellent generalization ability between human EEG sleep datasets, with varying health conditions and/or spindle statistics.

Furthermore, we investigated the robustness of SpindleNet with respect to the sampling frequency of EEG signals. We resampled EEG signals from the MASS dataset with lower sampling frequencies (100 Hz, 50 Hz and 34 Hz). As a result of down sampling, spindle detection may suffer from the loss of fidelity of EEG signals (figure 5). By default, the standard model trained with a sampling frequency of 200 Hz was termed as Model 1. By keeping the input duration (250 ms) unchanged, we retrained different network models under different EEG sampling frequencies (Models 2-4 for sampling frequencies of 100 Hz, 50 Hz, and 34 Hz, respectively) but with the same training sample size. During the testing phase, the EEG signals with lower sampling frequency were either first up-sampled to 200 Hz and then tested by Model 1 (ad hoc option 1), or directly tested by their respective reduced models (Models 2-4; option 2). Compared to the ad hoc option, option 2 produced comparable or slightly better performance (figure 5g). The difference between these two options was most pronounced in the lowest sampling frequency, where the sensitivity, FDR and F1-score statistics were significantly better in option 2 than in option 1 (signed rank test, sensitivity, p=0.0158; FDR, p<0.001; F1-score, p<0.001; n=19). This result suggested that SpindleNet was robust with respect to a wide range of sampling frequencies, and even performed well up to the Nyquist limit (twofold of the maximum spindle frequency of 16 Hz).

Figure 5. Illustration of EEG traces and spectrograms with annotated (between two red vertical lines) and detected (marked by green vertical lines) sleep spindles at four different sampling frequencies.

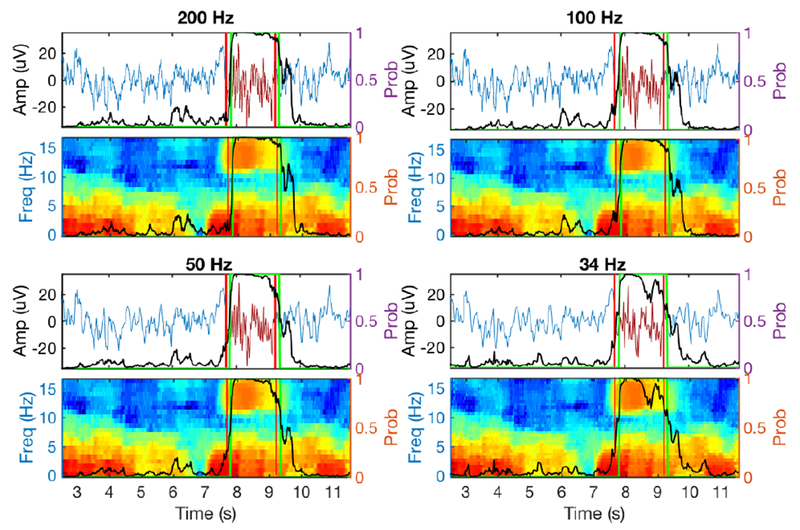
Black trace denotes the softmax probability output from SpindleNet. Despite the lower sampling rate and loss of fidelity in EEG spindles, SpindleNet detected the spindle onset reliably.

3.3. Comparison with state-of-the-art spindle detection methods

We compared SpindleNet with two recently published open-source spindle detection methods: McSleep (Parekh et al. 2017) and Spindler (LaRocco et al. 2018). We chose these two algorithms because they have been tested on the MASS and/or DREAMS datasets, and have been compared against a wide range of spindle detection methods (see Parekh et al. 2017) for details).

First, we selected the sleep spindle recordings with annotations from two human experts in both datasets (n=15 subjects for MASS and n=6 subjects for DREAMS, which contained annotations from two experts). We ran these detection methods and compared various performance indices (figure 6b–d). On the MASS dataset (n=15 subjects,), SpindleNet achieved specificity of 97.06±0.67% (McSleep: 94.49±0.77%, p=0.0183; Spindler: 98.37±0.37%, p=0.1003); FDR of 19.03± 3.18% (McSleep: 35.71±4.6%, p=0.0061; Spindler: 14.42±2.6%, p=0.2747); F1 score of 0.83±0.02 (McSleep: 0.72±0.04, p=0.0124; Spindler: 0.75±0.02, p=0.0196); accuracy of 96.08±0.44% (McSleep: 93.75±0.57%, p=0.003; Spindler: 95.37±0.36%, p=0.2222); and false event rate of 1.57±0.36 spindles/min (McSleep: 2.97±0.43 spindles/min, p=0.0177; Spindler: 0.87±0.2 spindles/min). All comparisons are done with unpaired t-tests. Notably, our false event rate was significantly lower (nearly half) compared to that derived from the McSleep algorithm. A representative FP example that was misidentified by the McSleep algorithm but correctly identified by SpindleNet is shown in figure 6a. In comparison with SpindleNet, Spindler achieved better specificity, FDR and false event rate but its sensitivity, F1-score and true event rate were worse, suggesting the trade-off between sensitivity and specificity in spindle detection. In assessing the consistency between detected spindles and annotated ground truth, we also obtained a higher Cohen’s kappa value of 0.71 ±0.014 (McSIeep: 0.45±0.035, p<0.0001), indicating a high degree of agreement between our detected spindle results and annotated ground truth (figure 6d). On the DREAMS dataset, although SpindleNet performed better on some metrics, the performances of these tested detection methods were not significantly different (figure 6e,f), possibly due to a shorter sleep recording duration (30 min) or small sample size (n=6).

Figure 6. Performance comparison between SpindleNet and two other spindle detection algorithms (McSIeep and Spindler).

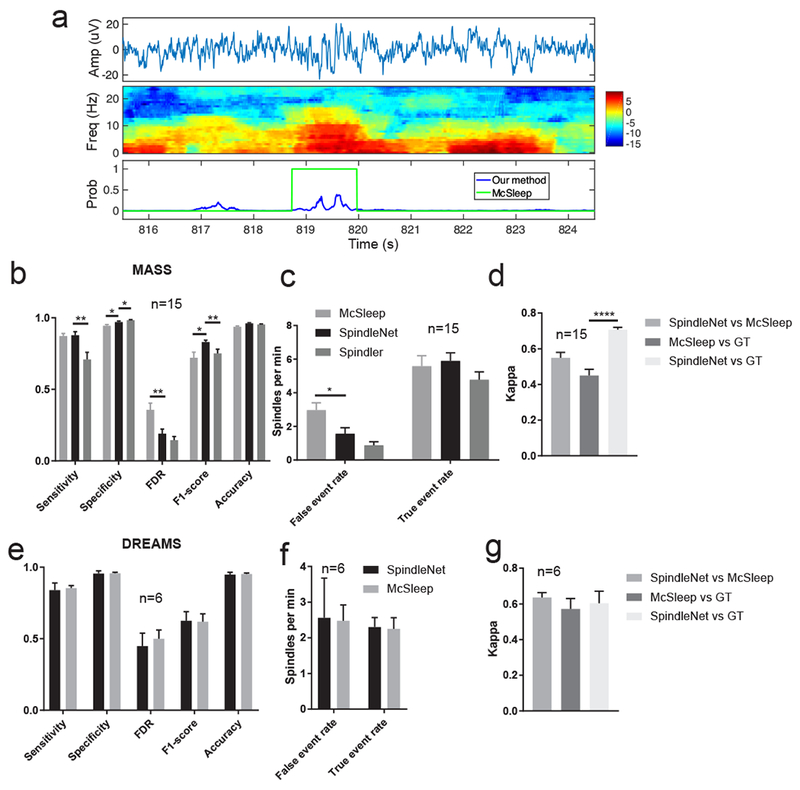
a, Examples of sleep spindle detection where the McSIeep algorithm detected a false event in the MASS dataset, whereas the softmax probability output (blue trace) from SpindleNet was below the detection threshold. b,c, Summarized comparative performance on the reduced MASS dataset (n=15 subjects, with annotations from two experts). *, p<0.05; **, p<0.01, unpaired t-test. d, Comparison of the kappa statistic between SpindleNet and McSleep, as well as between them and ground truth (GT). e-g, Similar to panels b-d, except for the reduced DREAMS dataset (n=6 subjects, with annotations from two experts).

Next, we generated 30-minute EEG recordings containing synthetic spindles (density: 10 spindles per minute) with varying spindle durations (0.3-1.2 s). Unlike human-labeled spindles that contain expert variability, the ground truth of synthetic spindles (onset and duration) is predetermined. We varied the SNR of EEG signals during testing and compared the detection performance of our method and the McSleep algorithm. At the level of infinity (noiseless) or 5 dB SNR, the performances of these two methods were similar. However, when the SNR was reduced to 0 dB or below, SpindleNet showed superior performance in all detection performance categories (i.e., sensitivity, specificity, FDR and F1-score; figure 7a–d). In the noiseless condition, SpindleNet achieved a mean detection latency of 150 ms during online spindle detection (figure 7e), and the mean detection latency degraded gradually with a decreasing SNR (figure 7f). When the detection latency is not a concern, the off-line detection performance could be slightly improved in comparison with on-line detection (figure 7h).

Figure 7. Performance comparison between our method (SpindleNet) and McSleep on simulated sleep spindle data with varying levels of signal-to-noise ratio (SNR).

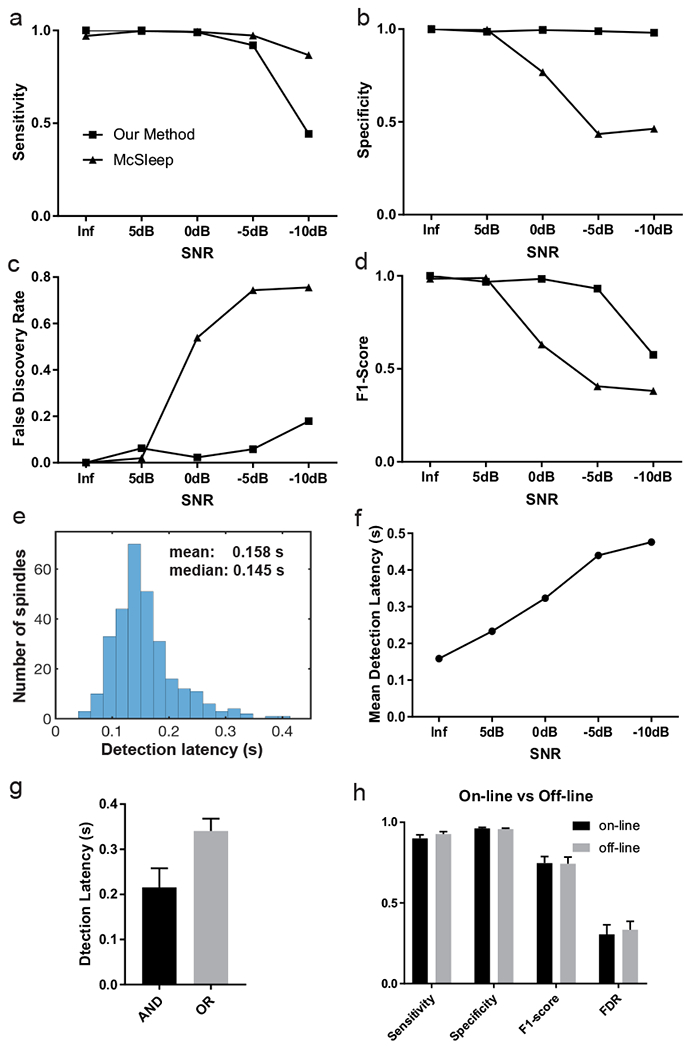
a, Sensitivity. b, Specificity. c, False discovery rate. d, F1-score. The Inf SNR denotes the noiseless condition. e, Histogram of detection latency in the noiseless condition. f, Mean detection latency of our proposed method with respect to the SNR. g, Spindle detection latency based on the AND and OR criteria. Error bar represents SEM (n=19 subjects). h, Performance comparison of on-line vs off-line detection in SpindleNet. Error bar represents SEM (n=19 subjects, MASS dataset).

On the MASS dataset (n=19 subjects), SpindleNet achieved a mean detection latency of ~340 ms based on from the OR criteria (choosing the earliest onset) and ~205 ms based on the AND criterion (conservative onset, figure 7g)---these statistics are reasonable considering the uncertainty in expert labeling of spindle onset, figure 1c). In contrast, the McSleep algorithm is not suitable for online processing, thereby yielding no latency comparison. A detailed result summary is shown in Table 2 and Table 3.

Table 2.

Summarized spindle detection performance of SpindleNet on the MASS dataset (n=19 subjects).

MASS subject #	Cross validation fold #	Median latency (ms)	Sensitivity	Specificity	FDR	F1-score	AUROC	False event rate (spindles/min)	True event rate (spindles/min)
1	1	250.85	0.8739	0.9888	0.0566	0.9072	0.9944	0.5517	9.1818
2		250.16	0.927	0.9829	0.1088	0.9087	0.9951	0.8892	7.2782
3		286.44	0.7142	0.9971	0.0572	0.8127	0.9954	0.1633	2.6917
4		215.09	0.9353	0.9633	0.2682	0.8211	0.99	3.5114	1.0182
5	2	269.76	0.7153	0.9919	0.1418	0.7802	0.9902	1.9859	5.4174
6		262.96	0.89	0.9672	0.1904	0.8479	0.9864	0.4571	2.765
7		355.86	0.7882	0.9926	0.0601	0.8574	0.9906	1.7033	7.2412
8		342.94	0.7355	0.9987	0.0096	0.8441	0.9953	6.3961	2.11
9	3	238.9	0.954	0.9597	0.2215	0.8574	0.9923	0.3857	6.0288
10		273.01	0.8854	0.9805	0.1681	0.8579	0.9912	0.0647	6.6039
11		227.11	0.9711	0.9414	0.3486	0.7798	0.9909	2.1067	7.4065
12		179.2	0.9774	0.9018	0.4145	0.7323	0.9807	1.0538	5.2166
13	4	333.87	0.9087	0.9829	0.1761	0.8642	0.9944	3.1616	5.9087
14		207.54	0.9444	0.9491	0.2721	0.8222	0.9888	5.1579	7.2868
15		223.6	0.9604	0.9609	0.3601	0.768	0.9927	2.4406	0.5715
16		47.91	0.9605	0.9404	0.7752	0.3643	0.976	4.0902	2.5528
17	5	58.425	0.9974	0.8895	0.7519	0.4977	0.9808	0.9449	4.4194
18		118.88	0.9897	0.9589	0.8102	0.3184	0.9938	2.6696	7.1434
19		114.9	0.9845	0.9288	0.6157	0.5528	0.9858	2.1905	3.8921

Table 3.

Performance comparison of SpindleNet and other two sleep spindle methods on the MASS dataset (n=19 subjects).

MASS subject #	Sensitivity		Specificity		FDR		F1-score
	McSleep	Spindler	McSleep	Spindler	McSleep	Spindler	McSleep	Spindler
1	0.8145	0.5481	0.9809	0.5481	0.0996	0.0232	0.8553	0.7022
2	0.9472	0.8289	0.9440	0.8289	0.2818	0.0491	0.8169	0.8857
3	0.7929	0.6067	0.9705	0.6067	0.3568	0.0847	0.7103	0.7297
4	0.9842	0.9328	0.8874	0.9328	0.8642	0.8158	0.2387	0.3077
5	0.9034	0.7381	0.9317	0.7381	0.4143	0.1656	0.7107	0.7833
6	0.7773	0.3031	0.9545	0.3031	0.4593	0.1511	0.6378	0.4467
7	0.9575	0.7311	0.8832	0.7311	0.4374	0.0965	0.7088	0.8082
8	0.9740	0.9481	0.8849	0.9481	0.7639	0.5913	0.3801	0.5712
9	0.8578	0.9034	0.9691	0.9034	0.1980	0.1710	0.8289	0.8646
10	0.8872	0.6303	0.9557	0.6303	0.2209	0.0331	0.8296	0.7632
11	0.7929	0.9188	0.9705	0.9188	0.3568	0.1605	0.7103	0.8774
12	0.9842	0.8226	0.8874	0.8226	0.8642	0.2260	0.2387	0.7976
13	0.9034	0.9204	0.9317	0.9204	0.4143	0.2950	0.7107	0.7984
14	0.7773	0.5028	0.9545	0.5028	0.4593	0.0797	0.6378	0.6503
15	0.9575	0.9485	0.8832	0.9485	0.4374	0.7229	0.7088	0.4289
16	0.9740	0.8673	0.8849	0.8673	0.7639	0.6198	0.3801	0.5287
17	0.8578	0.4667	0.9690	0.4667	0.1980	0.1000	0.8289	0.6147
18	0.8872	0.7447	0.9557	0.7447	0.2209	0.1233	0.8296	0.8054
19	0.9509	0.9641	0.9153	0.9641	0.3748	0.4038	0.7544	0.7368

Furthermore, we investigated the robustness of SpindleNet to the label noise (Frénay and Verleysen 2014). In the annotated spindles, there were inevitably uncertainties of spindle onset/offset that contributed to the label noise. From the training samples of the MASS dataset, we randomly switched the spindle/non-spindle labels with 5% and 10%, retrained the SpindleNet and retested the noiseless testing samples. On these noisy-label datasets, SpindleNet achieved a performance comparable with the noise-free training performance (sensitivity: 97.77±0.6% and F1-score: 98.83±0.6% across all noise scales). This further confirms the robustness of deep learning algorithm despite the label noise---which is inevitable in the case of human spindle annotation.

3.4. Application of other datasets and transfer learning

Sleep spindle characteristics (e.g., power, duration, and frequency) are known to vary with age, health condition, and species (Purcell et al. 2017). However, it is costly to annotate large amount of sleep spindles from EEG recordings from all groups. Therefore we explored transfer learning to understand how knowledge can learned from one domain (such as sleep spindles in healthy young adults) can be transferred to other domains.

Between different sleep recordings, the amplitude/duration/frequency statistics of EEG or spindle features might vary significantly. We first tested SpindleNet on un-annotated human EEG sleep recordings from three distinct age groups, first from young children (n=5 randomly selected subjects, ages 5-9.9 years), second from elderly subjects (n=6 randomly selected subjects, ages 65-89 years), and third from epilepsy patients (n=3 randomly selected subjects, ages 17-26 years). Figure 8a–c shows representative examples our spindle detections in these sleep datasets. Notably, the tested EEG sleep recordings had different amplitude range, and we performed a data calibration before testing (Section 2.3). However, the spindle detection accuracy was robust to the calibration scale (figure 9).

Figure 8. Representative examples of sleep spindle detection from various sleep datasets.

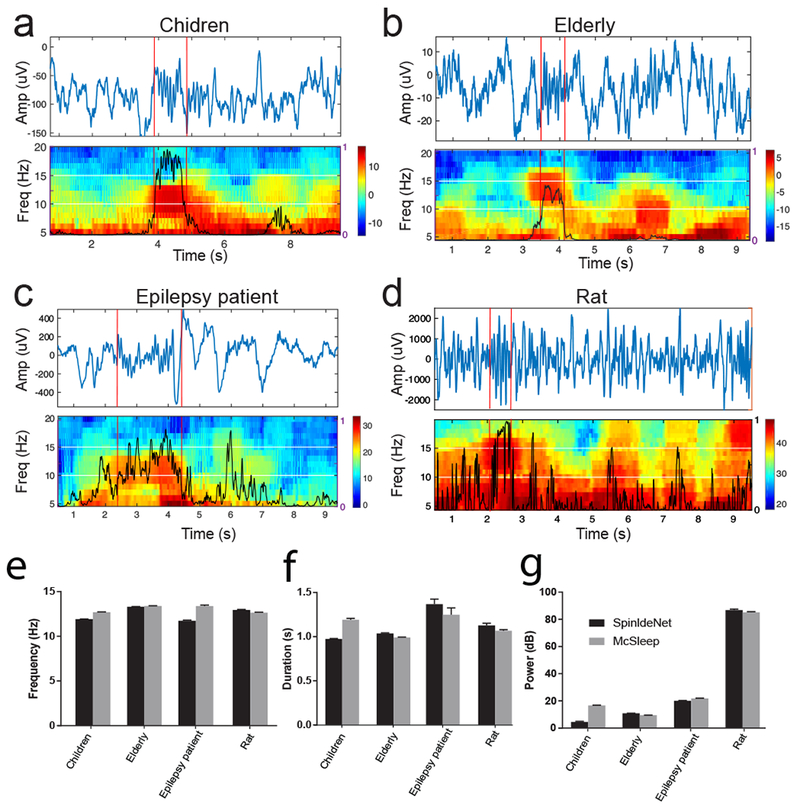
a, Children (CHAT). b, Elderly (MrOS). c, Epilepsy patient. d, Rat. e-g, Comparison of detected sleep spindle characteristics (frequency, duration and power) between SpindleNet and the McSleep algorithm.

Figure 9. Sleep spindle detection performance with respect to different normalization factors.

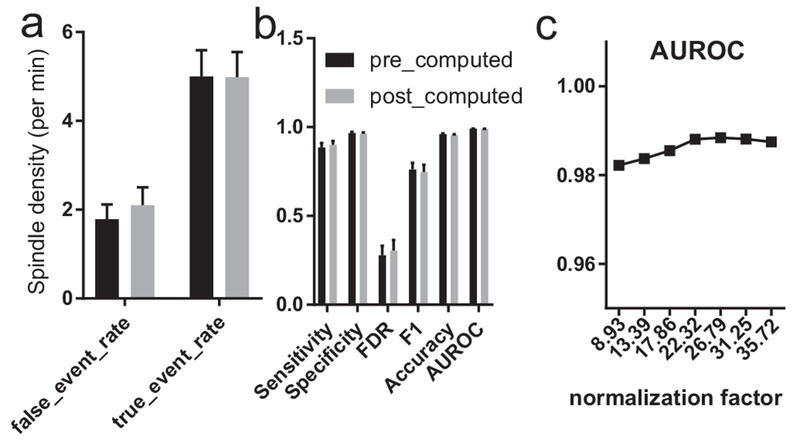
a, False event rate and true event rate for pre- and post-computed normalization on the MASS dataset (n=19). b, Sensitivity, specificity, FDR, F1-score, accuracy and AUROC for pre- and post-computed normalization on the MASS dataset (n=19). Pre-computed normalization is the average spindle standard deviation from the training set, whereas post-computed normalization is the average standard deviation from the testing set. c, Testing on the MASS subject #18 with various normalization factors in sleep EEG calibration.

To date, an outstanding question remains for defining sleep spindles in animal sleep studies. To our knowledge, there was no consensus or annotated ground truth on rodent sleep spindles among published sleep datasets. Next, we investigated whether the knowledge of human sleep spindles can be transferred to animal sleep research, a significantly more challenging task. Due to the lack of annotated sleep spindles in rats, it is difficult to directly train a DNN based on rat LFP recordings. To remove slow oscillations and potential low-frequency artifacts, we applied bandpass (2-50 Hz) filtering to LFP signals before feeding them to SpindleNet. Rats have a different distribution than humans of sleep EEG power at various frequency bands, so we did not use power features for rat sleep spindle prediction and used only the raw signal input. Although we only used the temporal features, SpindleNet was still able to identify spindles in rat LFP recordings (figure 8d). Due to the lack of ground truth, we could not quantify the TP and FP rates. Instead, we compared the spindle characteristics derived from SpindleNet with those from the McSleep algorithm (figure 8e–g). Results show that SpindleNet generated spindle statistics comparable with the McSleep algorithm.

….. It is worth pointing out that transfer learning would often involve learning on a new dataset with partial labeled ground truth, which was used for fine tuning based on the pre-trained network (Yosinski et al., 2014); however, generating ground truth annotations for the new human and animal datasets we used here is beyond the scope of the current study. Furthermore, to the best of our knowledge, there is no established consensus on annotating sleep spindles in animals. Therefore, we decided to use transfer learning primarily to demonstrate the generalizability of our approach on independently acquired datasets with human subjects in different age groups as well as adult rats. With further addition of ground truth on these datasets, we expect to obtain improved performance by retraining parts of SpindleNet. As part of demonstration of our method, we have used SpindleNet trained from the MASS dataset and tested on the DREAMS dataset, and compared the performance with and without transfer learning (figure 4f).

4. Discussion

We have proposed a deep learning approach (SpindleNet) for real-time sleep spindle detection. In the context of learning single-channel EEG patterns, the CNN is aimed at extracting or detecting scale-invariant oscillatory features of EEG signal (such as spindle oscillations), whereas the RNN is aimed at modeling the temporal structure of those features. In contrast to imaging processing, CNNs or CNN+RNN architectures are been used sparingly in EEG processing (Bashivan et al. 2015; Antoniades et al. 2017). By constructing a large number of labeled samples (from either annotated EEG traces or synthetic examples), our DNN approach is capable of detecting spindles with high accuracy (figure 4e,f) and short detection latency (figure 7e), as confirmed by multiple independent spindle datasets and synthetic spindle simulations. We also found that the deep learning components of our network (based on raw EEG and envelope features) have overall higher F1-score and significantly higher sensitivity compared to non-deep learning component (based on power features alone) (figure 4g). We further validated that the learned knowledge of SpindleNet from human sleep can be directly transferred to identify rat sleep spindles, despite the between-species difference in spindle statistics. This will impact animal sleep research, as it is time-consuming to annotate sleep recordings under irregular sleep conditions during the course of murine experiments, and there is lack of labeled data given relatively shorter sleep recordings. SpindleNet is also insensitive to the sampling frequency of EEG recordings (figure 4h) and robust to noise (figure 7). This suggests that it might be directly applied to wireless EEG-based sleep recordings with low sampling rate transmission for preservation of bandwidth or battery power (Wu and Wen 2009; Mckenzie et al. 2017).

SpindleNet is capable of extracting complex features from large amounts of time-series data, and is also conceptually different from previous applications of DNN in EEG data classification (Bashivan et al. 2015; Nir et al. 2012; Schirrmeister et al. 2017). While the previous research has primarily relied on applying CNNs or RNNs to EEG data in a single domain, here we process the EEG data in the time-domain using a combination of CNN and RNN, in addition to power features. Our solution is inspired by applications of DNN for video classification problems (Ng and Hausknecht 2015). SpindleNet has several key benefits over state-of-the-art spindle detection methods (Devuyst et al. 2006; Ferrarelli 2007; Martin et al. 2013; Mölle et al. 2002; Parekh et al. 2017; Wamsley et al. 2012; Wendt et al. 2012). Most spindle detection methods rely on offline processing of filtered EEG data followed by various thresholding schemes. The online spindle detection method proposed in (Lustenberger et al. 2016) employed an open-source system (rtxi.org) and adaptive threshold-based detection method; but no detection latency was reported. However, threshold-based detection methods are often sensitive to selection of globally optimal thresholds, and the threshold adaption is purely heuristic. SpindleNet bypasses these limitations by learning the higher-order spectrotemporal filters and temporal structures. In addition, previous methods have limited scalability across subjects, diseases, and species since they require hand-tuned features and parameters. In contrast, our method is able to generalize across datasets and learn the common spectrotemporal features. Finally, since SpindleNet is able to learn spindle characteristics that are most discriminative for spindle detection, it performs consistently better on multiple performance metrics compared to other detection methods (figure 6). In our investigations, we have also compared SpindleNet with the McSleep and Spindler algorithms for sleep spindle detection. As these three methods are used rather differently (in terms of training, sample size requirement, channel requirement, online vs. offline), a fair comparison might not be completely possible. Nevertheless, the robust detection performance derived from SpindleNet highlights the strength of data-driven deep learning. However, a comprehensive comparison between different sleep spindle methods would require one or multiple independent, large annotated spindle datasets.

Our SpindleNet (rooted in deep learning) outperforms other state-of-the-art spindle detection methods. In the presence of large number of labeled samples, deep learning can provide several advantages over traditional methods for sleep spindle detection. First, the deep learning method is purely data driven (“let the data speak for themselves”), and is very effective to learn discriminative features directly from temporal data. Therefore, it can potentially achieve better generalization, whereas traditional methods may be limited by specific parametric or statistical assumptions. Second, deep learning can greatly benefit from the use of synthetic or simulated samples. Third, deep learning can potentially incorporate multiple network structures (e.g., CNN, RNN, or generative adversarial network) and capture complex and high-order features of the data. Since each building block may be modular, deep learning is more flexible than the other methods.

Real-time detection of sleep spindles has potential applications in closed-loop neuroscience experiments, where the onset of sleep spindle can be used as a neurofeedback of BMIs to trigger an optogenetic intervention (Mckenzie et al. 2017), auditory stimulation (Antony and Paller 2017; Leminen et al. 2017), or transcranial current stimulation (Lustenberger et al. 2017; Lafon et al. 2017). For instance, the theory of TMR is built upon the assumption that pairing memory cues with brain oscillations at certain phase may mediate effective memory consolidation (Tambini, Berners-Lee, and Davachi 2017; Cairney et al. 2016; Schouten et al. 2017; Shimizu et al. 2018). Therefore, ultrafast detection with the shortest detection latency would be desirable, as the strength or effectiveness of memory enhancement depends on the timing of acoustic or electrical stimulation. SpindleNet can be easily extended to multi-channel EEG recordings for identifying spatiotemporal patterns of propagating spindle waves (De Souza et al. 2016). Same analysis is also applicable to MEG or ECoG recordings, which might have higher sensitivity for spindle detection (Dehghani, Cash, and Halgren 2011). In addition, SpindleNet is suitable for sleep monitoring, since an accurate characterization of dysfunctional spindle activity, in combination with other metrics, can help diagnose a thalamic dysfunction or neurodevelopmental disorders (Mckenzie et al. 2017).

Our proposed deep learning strategy is limited to labeled data and supervised learning. However, obtaining labeled data samples is time consuming and costly in practice, and there are often a much larger number of unlabeled samples. Incorporating unsupervised deep learning strategies for feature selection may overcome the sample size issue of labeled data, and further improve the detection performance on sleep spindles.

Finally, future research may determine whether our deep learning strategy can be generalized to detect other EEG oscillations during distinct neural states. This is particularly interesting for EEG oscillations with overlapping frequency as sleep spindles, such as the alpha and mu rhythms. For instance, detection of pre-stimulus alpha waves (9-15 Hz) may be useful in predicting mistake or lapse-of-attention (Mazaheri et al. 2009). The alpha oscillatory wave may also emerge during the so-called “alpha-delta sleep”, an abnormal intrusion of alpha activity into the delta wave during NREM sleep (Roizenblatt et al. 2001). On the other hand, human EEG mu-rhythms have been widely adopted in the motor imagery BMI (Pfurtscheller et al. 2006), as well as the assessment of child development (e.g., infant’s ability to imitate) and autism (Bernier, Dawson, and Webb, 2007).

5. Conclusion

In conclusion, we have proposed a novel deep learning approach for single-channel sleep spindle detection and tested the algorithm on a wide range of human and rodent sleep EEG datasets. Our approach is driven by deep learning---a powerful data-driven machine learning approach to extract spatiotemporal features among the EEG signals during training. In the testing mode, our algorithm is ultrafast, appealing for real-time or closed-loop experiments. In testing two public annotated sleep spindle datasets, our method produces better or similar predictive performance compared to the state-of-the-art sleep spindle detection methods. Moreover, our algorithm is robust to the noise and EEG sampling frequency.