Biases in self-reported height and weight measurements and their effects on modeling health outcomes

Abstract

Self-reported anthropometrics are often used as proxies for measured anthropometrics, but research has shown that heights and weights are often misreported. Using the Study on global AGEing and adult health, I analyze misreporting patterns of height, weight, and BMI in China, India, Russia, and South Africa. Adjustments of self-reported heights and weights using demographic, social, and anthropometric characteristics are evaluated and found to be useful in studying the distribution of anthropometrics within a population. Measured, self-reported, and adjusted BMI are then compared in logistic regression models on the reporting of health outcomes, as well as the resulting accuracy of individual prediction. When BMI is used as a continuous variable in models of health outcomes, measured, self-reported, and adjusted BMI produce similar coefficient estimates, and so self-reported data would be a natural choice because of its accessibility and convenience. In other applications, such as models using categorical BMI and individual prediction using either continuous or categorical BMI, self-reported data in lieu of measured data might not be accurate enough, but adjustments could serve as a potential compromise.

Highlights

• •There is heterogeneity in height and weight reporting patterns.
• •Adjustments can be useful in studying population-level distributions.
• •Variants of continuous BMI produce similar results in models of health outcomes.
• •Variants of categorical BMI should not be used in lieu of measured data.
• •Measured BMI is better for individual prediction of health outcomes.

1. Introduction

Self-reported measures are often solicited in questionnaires, with the expectation that responses are reasonably accurate. However, it has been found that self-reported data are often not reliable, perhaps due to lack of recall or a desire to conform to aspired norms. Regardless of the reason, misreporting could be detrimental, as it could render the results derived therefrom unreliable. Height and weight are components in the determination of body mass index (BMI), an important metric associated with overall health. A low BMI would suggest under-nourishment, which is associated with, among other ailments, infectious diseases. On the other end, a high BMI would suggest over-nourishment, which is associated with chronic diseases, including diabetes, cardiovascular disease, and cancer (World Health Organization, 2017).

BMI is defined as the ratio of weight (kg) to height squared (m²). While misreporting of both height and weight in the same direction could reduce the error in BMI, misreporting in opposite directions, such as over-estimating height and under-estimating weight, would magnify the error. Is the BMI derived from self-reported height and weight a reliable proxy?1 Furthermore, BMI classification is conventionally based on strict cut-points. Thus even if the numerical discrepancy in BMI is not too blatant, it could cause a person to be classified into another BMI category. It has been found in two different surveys that despite the high and positive correlation between measured and self-reported BMI, there is disagreement in BMI categorization between the two measures for about 20% of the samples (Preston et al., 2015; Spencer et al., 2001).

With such discrepancy, it is important to determine whether there are significant differences between measured and self-reported anthropometric measures, and if so, where these biases are most prevalent. In higher-income countries, height is generally over-estimated and weight under-estimated, leading to an overall under-estimation of BMI, but there are substantial differences across demographic, socioeconomic, and anthropometric sub-groups (Dahl et al., 2010; Jalkanen et al., 1987; Krul et al., 2010; Kuczmarski, Kuczmarski, & Najjar, 2001; Niedhammer et al., 2000).

It has also been observed that self-reported values ending in zero and five appear more than what a uniform distribution of last digits would suggest. While it is not surprising that numbers are rounded to convenient digits, the rounding across individuals does not cancel out, and there is a noticeable direction in which it occurs – upward for height and downward for weight (Niedhammer et al., 2000). Heaping is found in many other studies, in anthropometric measures (Heineck, 2006; Palloni, Soldo, & Wong, 2004) as well as in age and cigarette consumption (A’Hearn, Baten, & Crayen, 2009; Wang et al., 2012).

These referenced studies give some indication as to the directions and magnitudes of height and weight reporting biases. However, they are in high-income contexts, and only a few studies on this have been in other economic and development settings (Avila-Funes, Gutiérrez-Robledo, & Ponce De Leon Rosales, 2004; Gildner et al., 2015; Palloni et al., 2004; Thomas, Silva, & Costa, 2013; Zhou et al., 2010). These latter studies reveal that patterns in high-income countries might not be generalizable to low- and middle-income countries, and that there is heterogeneity among developing countries as well.

While understanding reporting biases is useful, what might be more important is understanding how these biases might affect anthropometric applications. Regressions in the health literature are commonly run with self-reported measures (Jeffery et al., 2006; Kristensen et al., 2005; Narayan et al. 2007). Slight misreporting might not be problematic if substantive results thence derived are not severely distorted. If so, it would make sense to use self-reported data, as they are not as administratively onerous or costly to collect. Otherwise, actual measures might be needed. Preston et al. found that hazard ratios for risk of mortality are similar when measured or self-reported BMI is used as a continuous variable, but not so when BMI is used as a categorical variable (Preston et al., 2015).

A compromise would be to devise an adjustment methodology to convert self-reported information into reasonably reliable data. Attempts have been made to adjust self-reported measures by using such measures and other characteristics on a training sample and predicting height and weight values on a testing sample (Dutton and McLaren, 2014; Spencer et al., 2001). Spencer et al. were able to decrease BMI misclassification by making adjustments to self-reports (Spencer et al., 2001). Dutton and McLaren concluded that while adjustments are useful for modeling BMI distributions and estimating obesity prevalence, adjusted BMI does not fix the biases of self-reported BMI in models on health outcomes; in fact, self-reported data are sometimes even better (Dutton and McLaren, 2014). Both papers on adjustment study high-income countries and present the results from just one random split of the dataset into training and testing datasets.

With the availability of both self-reported and measured data from the World Health Organization's Study on global AGEing and adult health (SAGE), I examine the biases in self-reported heights, weights, and BMIs in China, India, Russia, and South Africa. Adjustments are explored to make self-reported measures to, on average, better approximate actual measures. These measured, self-reported, and adjusted BMIs are then used as independent variables in models of chronic health outcomes that are commonly associated with high BMI to ascertain to what extent self-reported data or adjusted data could replace measured data in a two-pronged investigation. First, even if BMI is misreported, might such misreporting still result in insignificant differences in the associations between the BMI metric and the reporting of certain health outcomes? Second, might the use of different BMI metrics give noticeably different prediction accuracy rates? In this paper, proposed models are subject to multiple validations to check their reliability.

This study could have implications for many of the analyses in the health arena that rely on self-reported anthropometric measurements. The conclusions from these analyses are important, as policies are often recommended and decided based on them.

2. Data and methods

For my analyses, I use the first wave of SAGE, implemented between 2007 and 2010. SAGE is an ongoing longitudinal study of health and well-being that focuses mostly on people aged 50 years or over in China, Ghana, India, Mexico, Russia, and South Africa, though data from later waves have yet to be released (World Health Organization (WHO) & Health statistics and information systems, 2017). Even though there are smaller samples of younger adults, I focus on those 50 + years of age since they are more susceptible to chronic diseases.

In each country, interviewers asked respondents to report their heights and weights and then took the respondents' physical measurements. There was a standardized protocol for height and weight measurements, including the use of a stadiometer for height, a scale for weight, and guidelines for preparing respondents for measurement. As a result, measured height and weight are mostly available and expected to be fairly accurate and consistent across study samples. However, self-reported values range from under 10% missing in China and Russia to over 60% missing in the other four countries. Nevertheless, the distributions of sociodemographic characteristics are generally somewhat similar between those with and those without self-reported anthropometric measurements, and thus it is reasonable to expect that those with missing information are similar to the rest. To ensure good-sized samples for statistical reliability, I restrict my analyses to only China, India, Russia, and South Africa. Sample sizes are 9122, 1487, 3396, and 645, respectively, after excluding observations with missing data by listwise deletion.2

This information allows investigation of whether measured height, weight, and BMI are significantly different from their self-reported counterparts, whether biases are systematic across different population segments within a country, and whether the directions of biases are similar to those in the countries previously studied.

The availability of both measured and self-reported anthropometrics for these countries provides an opportunity to model measured height/weight based on self-reported height/weight, along with other variables previously observed to be associated with measured height and weight in other contexts, as follows:

$$\begin{array}{l}Measuredheight={\alpha }_0+{\alpha }_1\ast sex+{\alpha }_2\ast placeofresidence+{\alpha }_3\ast educationalattainment+{\alpha }_4\ast maritalstatus+{\alpha }_5\ast age\\ +{\alpha }_6\ast 0/5digitindicatorforself-reportedheight\\ +{\alpha }_7\ast self-reportedweight\\ +{\alpha }_8\ast self-reportedheight+error\end{array}$$ (1)

$$\begin{array}{l}Measuredweight={\beta }_0+{\beta }_1\ast sex+{\beta }_2\ast placeofresidence+{\beta }_3\ast educationalattainment+{\beta }_4\ast maritalstatus+{\beta }_5\ast age\\ +{\beta }_6\ast 0/5digitindicatorforself-reportedweight\\ +{\beta }_7\ast self-reportedheight\\ +{\beta }_8\ast self-reportedweight+error\end{array}$$ (2)

For the categorical variables, the reference groups are male for sex, urban for place of residence, less than high school for educational attainment, never married for marital status, and not 0/5 for the digit indicator. The rest of the variables are continuous. Interactions have also been tested, but the models with interactions are not significantly distinguishable from the models without interactions, as determined by Vuong tests for model comparison.

I validate the models using repeated holdout cross-validation. For each country sample, I partition it into a training set with 60% of the data and a testing set with its complement, as illustrated in Fig. 1. Adult underweight is defined as having a BMI under 18.5 kg/m², overweight as having a BMI of 25 kg/m² or above, and the normal range falls in between (World Health Organization, 2006). Partitions are stratified by self-reported BMI categorization to ensure that each self-reported BMI category is properly represented in sub-datasets.

Fig. 1.

Dataset splitting.

With coefficient estimates from the regression models using data in the training set, adjusted height and weight, and consequently BMI, can be calculated for each observation in the testing set. Each of them thus has measured, self-reported, and adjusted BMI values. This partition and modeling process is repeated 100 times. Two-sided paired t-tests are performed between measured and self-reported height/weight/BMI, and between measured and adjusted height/weight/BMI, in each of the 100 runs. A reasonable hypothesis is that, if the models are any good, the latter tests are less likely to be significant than the former.

Subjects were asked whether they had ever been diagnosed with stroke, diabetes, and hypertension. I run logistic regression models to study the log odds of reporting such diagnoses. The main covariate of interest is BMI, but the demographic and socioeconomic characteristics in the previous height/weight models are also included here.

$$\log \left(\frac{P\left(reportinghealthoutcome\right)}{1-P\left(reportinghealthoutcome\right)}\right)={\delta }_0+{\delta }_1\ast sex+{\delta }_2\ast placeofresidence+{\delta }_3\ast educationalattainment+{\delta }_4\ast maritalstatus+{\delta }_5\ast age+{\delta }_6\ast BMI+error$$ (3)

As described above, the height and weight models estimated from each training set are used to adjust self-reported height and weight in the complementary testing set. This testing dataset is then used to estimate the health-outcome logistic models, with measured, self-reported, or adjusted BMI as covariates. Some logistic regression runs encounter quasi-complete separation, which tends to occur with small samples or with “extreme splits on the frequency distribution of either the dependent or independent variables” (Allison, 2008). For example, since strokes are not that common, it is not unthinkable that at least one level of an independent categorical variable would have few observations with a diagnosis in at least one run. To resolve the problem of possible non-existence of maximum likelihood estimates, median bias reduction is used (Pagui, Salvan, & Sartori, 2017). The median of the coefficient estimates for each independent variable is taken over the 100 runs and significance at the five-percent level is determined using the 2.5% and 97.5% quantiles of the empirical distribution of the coefficient estimates. The reported McFadden R² values are the median over the 100 runs.

Moving from the aggregate to the individual level, I investigate how the rate of correct individual prediction depends on which BMI metric is used. The median coefficient estimates from the health-outcome models discussed above are used to calculate the predicted probabilities of reporting the health outcomes among observations in the 100 testing sets. A threshold for each testing set, based on Youden's J statistic to maximize the sum of sensitivity (true positive rate) and specificity (true negative rate) (Lalkhen & McCluskey, 2008; Youden, 1950), is determined to evaluate the accuracy of the resulting predictions in the testing set. A predicted probability above this threshold is classified as reporting the condition and a predicted probability below is classified as not. Choosing such a threshold is an attempt to better predict the reporting of a health condition than an arbitrary constant such as 0.5. The accuracy rates are averaged over 100 runs.

Finally, these analyses are re-run, but with BMI as a categorical variable. Categorical BMI is split into two levels, overweight and not overweight (i.e., normal and underweight combined), since only overweight is a risk factor for chronic conditions. Since a switch in the binary BMI categorization could be considered more drastic than a unit change in the continuous BMI, might using a categorical BMI render differences in coefficient estimates and prediction accuracy more noticeable than using a continuous BMI?

All analyses are run using the statistical software R (version 3.4.1) (Core Team. (2017)). The R package brglm2 is used for median bias reduction in generalized linear models (Kosmidis, 2017). When discussing results, the term “significant” means significant at the level of five percent.

3. Results

3.1. Self-reported vs. measured anthropometrics

To determine whether mean self-reported and measured anthropometrics are significantly different in each of the four countries, two-sided paired t-tests are used. Table 1, Table 2, Table 3 below show these results, both overall and by various population sub-groups. In the tables, each cell shows the mean difference (self-reported heights/weights/BMIs – measured heights/weights/BMIs), and whether the difference is significantly non-zero.

Table 1.

Mean differences between self-reported height and measured height (cm).

	China	India	Russia	South Africa
Overall	0.93 ***	−5.88 ***	0.42 ***	−3.24 ***
Male	0.79 ***	−5.73 ***	0.30 ***	−4.33 ***
Female	1.09 ***	−6.42 ***	0.49 ***	−2.42 ***
Urban	1.24 ***	−4.42 ***	0.46 ***	−3.18 ***
Rural	0.56 ***	−6.61 ***	0.32 *	−3.62 *
Less than high school	0.91 ***	−6.63 ***	0.57 ***	−3.72 ***
Completed high school	1.02 ***	−4.62 ***	0.44 ***	−0.29
Completed college	1.04 ***	−3.82 ***	0.16	−3.55 *
Never married	1.81 **	−9.84 *	0.98 ***	−2.59
Cohabiting or currently married	0.89 ***	−5.80 ***	0.31 ***	−3.51 ***
Previously married	1.22 ***	−6.01 ***	0.56 ***	−3.09 ***
Age [50, 65)	0.72 ***	−6.06 ***	0.15	−3.85 ***
Age [65, 80)	1.19 ***	−5.55 ***	0.63 ***	−2.19 **
Age [80, maximum]	2.99 ***	−4.93 *	1.16 ***	−2.26

* denotes significance at the 0.05 level, ** at the 0.01 level, and *** at the 0.001 level.

Table 2.

Mean differences between self-reported weight and measured weight (kg).

	China	India	Russia	South Africa
Overall	0.72 ***	−0.50	−0.63 ***	−1.42 *
Male	0.66 ***	−0.50	−0.51 ***	−1.22 *
Female	0.78 ***	−0.52	−0.69 ***	−1.56
Urban	1.35 ***	−1.08 *	−0.63 ***	−1.41 *
Rural	−0.05	−0.21	−0.63 ***	−1.47
Less than high school	0.64 ***	−0.07	−0.46 *	−1.52 *
Completed high school	1.03 **	−1.03	−0.67 ***	−0.78
Completed college	0.92	−1.97 *	−0.76 ***	−1.45
Never married	3.07	−3.97 *	−0.56	−0.28
Cohabiting or currently married	0.56 ***	−0.41	−0.68 ***	−2.04 **
Previously married	1.80 **	−0.73	−0.56 ***	−0.92
Age [50, 65)	0.23	−0.74 *	−0.92 ***	−2.96 ***
Age [65, 80)	1.09 ***	0.01	−0.33 **	1.43
Age [80, maximum]	7.56 ***	0.17	−0.22	−0.66

* denotes significance at the 0.05 level, ** at the 0.01 level, and *** at the 0.001 level.

Table 3.

Mean differences between self-reported BMI and measured BMI (kg/m²).

	China	India	Russia	South Africa
Overall	−0.05	2.33 ***	−0.37 ***	1.69 **
Male	−0.02	2.05 ***	−0.26 ***	2.10 **
Female	−0.08	3.30 ***	−0.43***	1.38 *
Urban	0.02	1.33 **	−0.39 ***	1.43 **
Rural	−0.13 *	2.83 ***	−0.30 **	3.19
Less than high school	−0.07	2.91 ***	−0.35 **	2.04 **
Completed high school	0.03	1.41 ***	−0.39 ***	−0.20
Completed college	0.01	0.70	−0.34 ***	1.58
Never married	0.25	2.09	−0.53 **	2.81
Cohabiting or currently married	−0.09	2.31 ***	−0.33 ***	1.47 *
Previously married	0.25	2.54 **	−0.42 ***	1.55 *
Age [50, 65)	−0.12 *	2.43 ***	−0.36 ***	1.37 *
Age [65, 80)	−0.03	2.18 ***	−0.35 ***	2.39 *
Age [80, maximum]	1.41 **	1.46	−0.48 *	0.91

* denotes significance at the 0.05 level, ** at the 0.01 level, and *** at the 0.001 level.

For the overall population, the mean height differences are significantly non-zero for all countries. Individuals in China and Russia, on average, report being taller than they actually are. Individuals in India and South Africa, on average, report being shorter than they actually are. The mean weight differences are significantly non-zero for China, Russia, and South Africa. On average, individuals in China report being heavier than they actually are, while individuals in Russia and South Africa report being lighter than they actually are.

From the reported height and weight biases, it is clear that BMI would be significantly over-reported in India and significantly under-reported in Russia. In China and South Africa overall, the signs are the same for height and weight differences. In China, the effects of misreported height and weight might have canceled each other to make the measured and self-reported BMIs about the same, but the case of South Africa does not exhibit this cancellation effect and the mean BMI difference is significantly non-zero and positive.

The paired t-tests are run again by various population sub-groups. In each country, sub-group height and weight misreporting is usually in the same direction as the country's overall sample. The more educated and not married sub-groups have fewer instances of significant misreporting. An exception to this is the case of weight in India, since the same sub-groups that tend not to misreport in other contexts misreport their weights here, even when an overall pattern of weight misreporting is not observed.

Table 4 shows how self-reported BMI and measured categorizations compare. The agreement proportion is the sum along the main diagonal.

Table 4.

Agreement on self-reported and measured BMI categorization.

China	Measured
Self-reported		Underweight	Normal	Overweight
	Underweight	0.025	0.019	0.001
	Normal	0.012	0.572	0.075
	Overweight	0.001	0.031	0.264
Agreement proportion = 0.861.

India	Measured
Self-reported		Underweight	Normal	Overweight
	Underweight	0.122	0.063	0.006
	Normal	0.110	0.397	0.042
	Overweight	0.026	0.111	0.123
Agreement proportion = 0.642.

Russia	Measured
Self-reported		Underweight	Normal	Overweight
	Underweight	0.006	0.003	0.000
	Normal	0.003	0.207	0.042
	Overweight	0.001	0.020	0.719
Agreement proportion = 0.932.

South Africa	Measured
Self-reported		Underweight	Normal	Overweight
	Underweight	0.019	0.008	0.005
	Normal	0.012	0.135	0.084
	Overweight	0.005	0.062	0.671
Agreement proportion = 0.825.

The agreement is highest for Russia, followed by China, South Africa, and India. The agreement in India is noticeably worse than that in the other three countries. In India, almost half of the people who are underweight when using measured BMI actually report being in the normal category and about 20% of the people who are normal weight using measured BMI actually report being in the overweight category, revealing a tendency in India to over-report BMI category.

3.2. Adjustments to self-reported height and weight

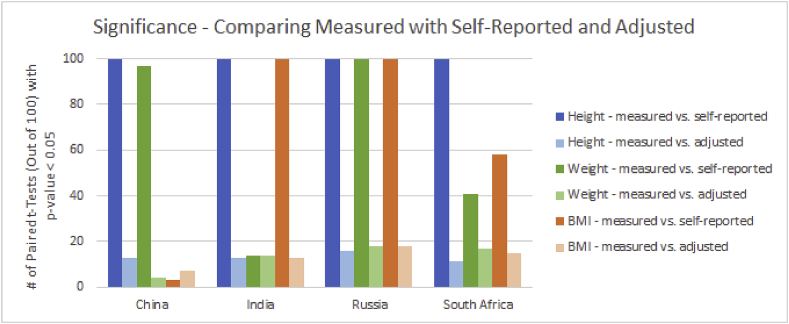
Models of measured height and weight are run on a 60% training set 100 times. Over 100 runs, the measured height model has average adjusted R² values of 0.74, 0.57, 0.85, and 0.48 while the measured weight model has average adjusted R² values of 0.41, 0.46, 0.88, and 0.59 for China, India, Russia, and South Africa, respectively. The resulting models are then used to adjust heights and weights for the observations in the testing set. To analyze how well these adjustments perform, I use two-sided paired t-tests to determine, among 100 holdout validations, how often the measured and self-reported means are significantly different, and how often the measured and adjusted means are significantly different. These results are shown in Fig. 2.

Fig. 2.

Frequency of significance when comparing measured with self-reported and with adjusted values.

From Fig. 2, it is evident that, when there is significant misreporting in height or weight (i.e., all cases, except for weight in India), the frequency of significance in the holdout validations decreases drastically from measured versus self-reported height/weight to measured versus adjusted height/weight. That is, measured values tend to be closer to adjusted than to self-reported. What does this mean for BMI? Although the height and weight adjustments do appear to be beneficial for China, the misreporting in height and misreporting in weight seem to have canceled out in the calculation of BMI, rendering BMI adjustment to be not useful. Nevertheless, BMI is not significantly misreported in China anyway. In the other three countries, there is a drop in the frequency of significant results when going from measured versus self-reported to measured versus adjusted BMI, and so adjustment appears to be beneficial.

3.3. Using measured, self-reported, and adjusted BMI as continuous covariates

Logistic regressions are run on the reporting of three health outcomes (stroke, diabetes, and hypertension) for each of the four countries. Table 5 shows the models for the log odds, using measured, self-reported, and adjusted BMI. For each health outcome and country, median coefficient estimates from 100 runs on the testing sets and whether zero falls outside the empirical 95% confidence interval (i.e., significance at five percent) are shown.

Table 5.

Logistic regressions of reporting health outcomes on continuous BMI (measured, self-reported, and adjusted) and other demographic and socioeconomic covariates.

China	Stroke			Diabetes			Hypertension
	Measured	Self–reported	Adjusted	Measured	Self–reported	Adjusted	Measured	Self–reported	Adjusted
Intercept	−9.75 ∼	−9.50 ∼	−10.01 ∼	−6.94 ∼	−6.21 ∼	−7.41 ∼	−6.77 ∼	−5.62 ∼	−7.45 ∼
Female	−0.26	−0.26	−0.27	0.17	0.17	0.13	0.14 ∼	0.18 ∼	0.13 ∼
Rural	−0.43 ∼	−0.44 ∼	−0.42 ∼	−1.11 ∼	−1.14 ∼	−1.10 ∼	−0.51 ∼	−0.54 ∼	−0.49 ∼
Completed high school	0.22	0.21	0.21	0.01	0.00	0.01	0.09	0.08	0.10
Completed college	0.16	0.15	0.15	0.01	0.01	0.00	0.18	0.19	0.17
Cohabiting/currently married	1.48	1.49	1.45	0.57	0.64	0.59	0.07	0.14	0.05
Previously married	1.27	1.25	1.21	0.32	0.36	0.35	−0.01	−0.00	−0.05
Age	0.07 ∼	0.07 ∼	0.07 ∼	0.04 ∼	0.04 ∼	0.04 ∼	0.06 ∼	0.05 ∼	0.06 ∼
BMI	0.04 ∼	0.02 ∼	0.05 ∼	0.05 ∼	0.03 ∼	0.08 ∼	0.10 ∼	0.05 ∼	0.13 ∼
McFadden R2	0.069	0.070	0.066	0.070	0.068	0.066	0.081	0.071	0.070
India	Stroke			Diabetes			Hypertension
	Measured	Self–reported	Adjusted	Measured	Self–reported	Adjusted	Measured	Self–reported	Adjusted
Intercept	−5.43 ∼	−5.78 ∼	−5.70 ∼	−6.68 ∼	−5.16 ∼	−7.83 ∼	−6.41 ∼	−4.95 ∼	−7.01 ∼
Female	−0.37	−0.41	−0.41	0.22	0.30	0.14	0.78 ∼	0.84 ∼	0.76 ∼
Rural	−0.35	−0.34	−0.28	−0.79 ∼	−0.86 ∼	−0.68 ∼	−0.14	−0.23	−0.14
Completed high school	0.17	0.17	0.13	0.16	0.22	0.07	0.41	0.47	0.38
Completed college	0.73	0.69	0.71	0.48	0.70 ∼	0.35	0.60 ∼	0.75 ∼	0.51
Cohabiting/currently married	0.17	0.17	0.15	1.68 ∼	1.52 ∼	1.62 ∼	0.01	−0.01	−0.03
Previously married	0.70	0.74	0.75	1.63 ∼	1.50 ∼	1.53 ∼	−0.05	−0.13	−0.08
Age	0.04 ∼	0.04 ∼	0.04 ∼	0.03 ∼	0.03	0.03 ∼	0.05 ∼	0.05 ∼	0.05 ∼
BMI	0.00	0.01	0.01	0.07 ∼	0.01	0.13 ∼	0.07 ∼	0.01 ∼	0.10 ∼
McFadden R2	0.016	0.028	−0.016	0.063	0.059	0.041	0.079	0.067	0.068
Russia	Stroke			Diabetes			Hypertension
	Measured	Self–reported	Adjusted	Measured	Self–reported	Adjusted	Measured	Self–reported	Adjusted
Intercept	−7.83 ∼	−7.69 ∼	−7.78 ∼	−6.19 ∼	−6.23 ∼	−6.55 ∼	−6.36 ∼	−6.32 ∼	−6.53 ∼
Female	−0.21	−0.21	−0.22	0.50 ∼	0.50 ∼	0.46 ∼	0.68 ∼	0.70 ∼	0.66 ∼
Rural	0.03	0.04	0.04	−0.39 ∼	−0.39 ∼	−0.41 ∼	−0.21	−0.20	−0.20
Completed high school	0.04	0.04	0.03	−0.11	−0.11	−0.12	−0.04	−0.03	−0.03
Completed college	0.09	0.08	0.08	0.03	0.04	0.03	−0.15	−0.14	−0.13
Cohabiting/currently married	0.40	0.41	0.41	0.37	0.35	0.34	−0.06	−0.08	−0.08
Previously married	0.34	0.35	0.35	0.36	0.35	0.36	−0.09	−0.12	−0.11
Age	0.06 ∼	0.06 ∼	0.06 ∼	0.02 ∼	0.02 ∼	0.02 ∼	0.06 ∼	0.06 ∼	0.06 ∼
BMI	0.02	0.02	0.03	0.06 ∼	0.06 ∼	0.07 ∼	0.09 ∼	0.09 ∼	0.10 ∼
McFadden R2	0.040	0.039	0.039	0.049	0.048	0.051	0.115	0.112	0.113
South Africa	Stroke			Diabetes			Hypertension
	Measured	Self–reported	Adjusted	Measured	Self–reported	Adjusted	Measured	Self–reported	Adjusted
Intercept	−1.47	−2.24	−1.91	−3.43 ∼	−2.97 ∼	−4.07 ∼	−2.07 ∼	−1.51	−1.50
Female	0.37	0.41	0.37	0.22	0.27	0.14	0.35	0.41	0.43
Rural	0.28	0.21	0.24	−0.22	−0.22	−0.29	−0.20	−0.13	−0.14
Completed high school	0.25	0.22	0.23	−0.25	−0.22	−0.26	−0.18	−0.15	−0.15
Completed college	−1.73 ∼	−1.80 ∼	−1.80 ∼	−0.17	−0.16	−0.19	−0.70	−0.70	−0.70
Cohabiting/currently married	0.37	0.31	0.33	−0.14	−0.14	−0.10	−0.07	−0.08	−0.08
Previously married	0.90	0.81	0.87	0.28	0.30	0.30	−0.06	−0.04	−0.05
Age	−0.03	−0.03	−0.03	0.02	0.01	0.02	0.02	0.01	0.01
BMI	−0.01	0.01	0.00	0.02	0.01	0.04 ∼	0.02	−0.00	−0.00
McFadden R2	0.083	0.088	0.084	0.044	0.039	0.050	0.036	0.034	0.034

∼ denotes a case when zero falls outside the 95% empirical confidence interval.

First, I look at the overarching results from Table 5 – how is BMI associated with reporting stroke/diabetes/hypertension? In South Africa, BMI is never significant in any of these models, regardless of which BMI metric is used, with one exception – the adjusted BMI model for diabetes. Among the four countries, South Africa has the smallest sample size, which might explain the lack of significance. Besides the case of South Africa, BMI is generally a significant covariate in models of diabetes and hypertension. However, BMI is significant for stroke only in China.

I then compare the models using measured and self-reported BMI. For the same country and health outcome, the coefficient estimate for measured BMI is usually greater than that of self-reported BMI, meaning that measured BMI predicts a higher probability of reporting the health outcome than self-reported BMI does. Since self-reported BMI has reporting errors, that its coefficient estimates tend to bias downward toward zero is not unexpected. Of special note is the variable BMI in the diabetes model for India. Measured BMI is a significant variable for diabetes, but self-reported BMI is not. Not only might the BMI variable itself change in significance, but the choice of metric might also affect the significance of other variables in the model. The results show that substantive conclusions might change depending on whether measured or self-reported BMI is used as a covariate. However, discrepancies between significance and non-significance occur infrequently.

When a variable is significant using adjusted BMI, the coefficient estimate matches up pretty closely with the corresponding coefficient estimates from the measured and self-reported models. While the coefficient estimate for self-reported BMI is typically lower than that of measured BMI, the coefficient estimate for adjusted BMI is typically greater than that of measured BMI. If the assumption is that the model with measured BMI is the correct model, the adjustment overcorrects the association of BMI with these health outcomes. This is potentially due to certain variables being used as covariates in the measured height/weight models and again in the health-outcome models. There is only one discrepancy between the significance of BMI in models using measured BMI and models using adjusted BMI (diabetes for South Africa). But again, this case is an exception rather than the norm. Generally, the measured, self-reported, and adjusted models actually perform quite similarly.

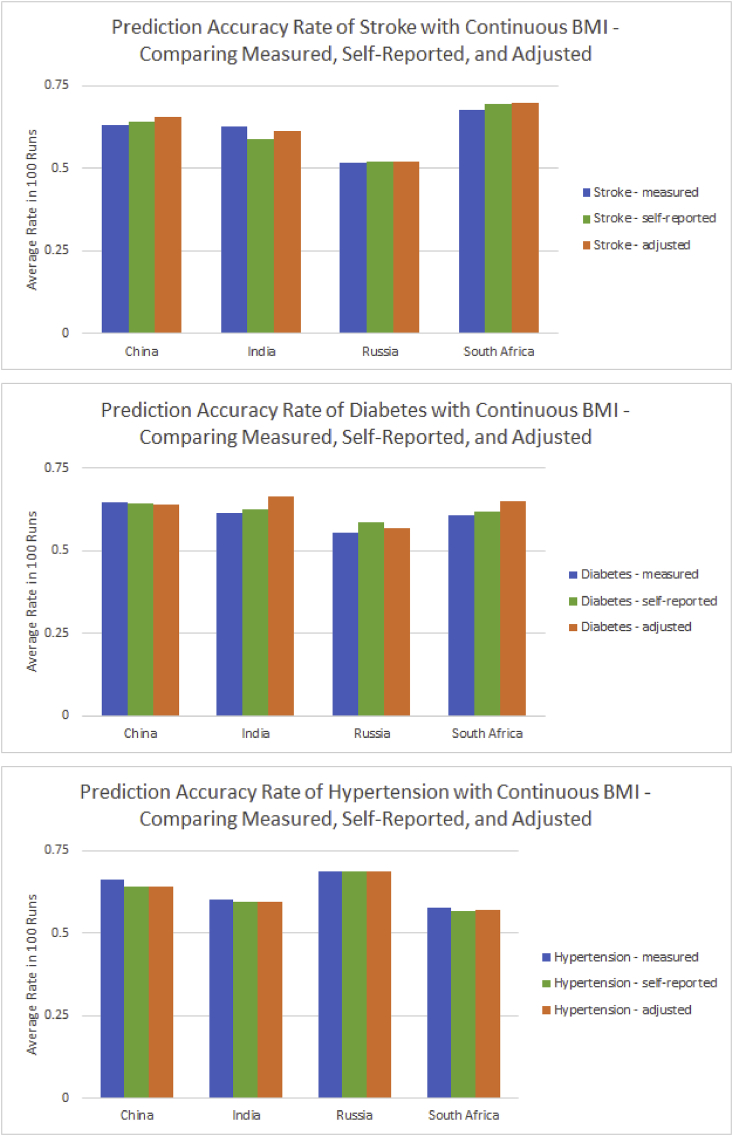
How well could measured/self-reported/adjusted BMI help predict a person's reporting of stroke/diabetes/hypertension? Using the median model coefficient estimates, I estimate a prediction accuracy rate for each of the 100 testing sets. Fig. 3 compares the average prediction accuracy rate over 100 runs for each health outcome, country, and BMI metric combination.

Fig. 3.

Comparison of prediction accuracy rates using measured, self-reported, and adjusted continuous BMI in China, India, Russia, and South Africa.

The prediction accuracy rates in these health outcome, country, and BMI metric combinations range from about 0.5 to 0.7. Measured BMI produces the highest average prediction accuracy rate among six health outcome and country combinations, followed by adjusted BMI with five, and self-reported BMI with one. Interestingly, measured BMI is best for hypertension in all four countries, and adjusted BMI is best for stroke in all countries except India. However, self-reported BMI generally does not perform best.

3.4. Using continuous versus categorical BMI

The above analyses were repeated, replacing the continuous variable BMI with a dichotomous variable, overweight and not overweight, with not overweight as the reference category. The results are exhibited in Table 6.

Table 6.

Logistic regressions of reporting health outcomes on categorical BMI (measured, self-reported, and adjusted) and other demographic and socioeconomic covariates.

China	Stroke			Diabetes			Hypertension
	Measured	Self–reported	Adjusted	Measured	Self–reported	Adjusted	Measured	Self–reported	Adjusted
Intercept	−8.97 ∼	−9.00 ∼	−9.06 ∼	−5.63 ∼	−5.57 ∼	−5.62 ∼	−4.55 ∼	−4.50 ∼	−4.56 ∼
Female	−0.26	−0.25	−0.29	0.15	0.16	0.11	0.14 ∼	0.17 ∼	0.11
Rural	−0.46 ∼	−0.43 ∼	−0.42 ∼	−1.14 ∼	−1.13 ∼	−1.11 ∼	−0.55 ∼	−0.54 ∼	−0.50 ∼
Completed high school	0.21	0.21	0.21	0.01	0.02	0.04	0.08	0.07	0.11
Completed college	0.15	0.14	0.15	−0.02	−0.01	−0.00	0.16	0.17	0.18
Cohabiting/currently married	1.51	1.50	1.47	0.57	0.58	0.59	0.09	0.09	0.08
Previously married	1.28	1.24	1.24	0.33	0.33	0.32	−0.01	−0.03	−0.03
Age	0.07 ∼	0.07 ∼	0.07 ∼	0.04 ∼	0.04 ∼	0.04 ∼	0.05 ∼	0.05 ∼	0.06 ∼
Overweight	0.30	0.45 ∼	0.42	0.61 ∼	0.63 ∼	0.55 ∼	0.79 ∼	0.75 ∼	0.72 ∼
McFadden R2	0.069	0.072	0.070	0.072	0.072	0.069	0.080	0.076	0.071
India	Stroke			Diabetes			Hypertension
	Measured	Self–reported	Adjusted	Measured	Self–reported	Adjusted	Measured	Self–reported	Adjusted
Intercept	−5.50 ∼	−5.69 ∼	−5.60 ∼	−5.13 ∼	−4.91 ∼	−5.03 ∼	−4.86 ∼	−4.82 ∼	−4.68 ∼
Female	−0.32	−0.45	−0.34	0.23	0.24	0.21	0.80 ∼	0.79 ∼	0.83 ∼
Rural	−0.34	−0.32	−0.34	−0.81 ∼	−0.84 ∼	−0.82 ∼	−0.18	−0.21	−0.22
Completed high school	0.17	0.14	0.18	0.18	0.22	0.16	0.45	0.47	0.46
Completed college	0.78	0.70	0.77	0.63	0.70 ∼	0.55	0.69 ∼	0.73 ∼	0.72 ∼
Cohabiting/currently married	0.17	0.17	0.21	1.57 ∼	1.53 ∼	1.62 ∼	0.01	0.00	0.00
Previously married	0.75	0.75	0.70	1.51 ∼	1.46 ∼	1.59 ∼	−0.08	−0.15	−0.12
Age	0.04	0.04	0.04	0.03	0.03	0.03	0.05 ∼	0.05 ∼	0.05 ∼
Overweight	−0.23	0.39	−0.18	0.62 ∼	0.42	0.60	0.57 ∼	0.67 ∼	0.27
McFadden R2	0.017	0.022	0.020	0.062	0.061	0.058	0.071	0.078	0.066
Russia	Stroke			Diabetes			Hypertension
	Measured	Self–reported	Adjusted	Measured	Self–reported	Adjusted	Measured	Self–reported	Adjusted
Intercept	−7.47 ∼	−7.41 ∼	−7.46 ∼	−5.08 ∼	−4.93 ∼	−4.97 ∼	−4.21 ∼	−4.21 ∼	−4.20 ∼
Female	−0.19	−0.18	−0.20	0.61 ∼	0.61 ∼	0.60 ∼	0.83 ∼	0.82 ∼	0.80 ∼
Rural	0.05	0.05	0.05	−0.33 ∼	−0.33 ∼	−0.33	−0.12	−0.13	−0.12
Completed high school	0.03	0.03	0.02	−0.13	−0.14	−0.14	−0.04	−0.05	−0.05
Completed college	0.08	0.08	0.08	−0.03	−0.03	−0.03	−0.18	−0.19	−0.18
Cohabiting/currently married	0.41	0.40	0.39	0.33	0.35	0.40	−0.02	−0.03	0.01
Previously married	0.34	0.35	0.36	0.33	0.36	0.42	−0.07	−0.07	−0.04
Age	0.06 ∼	0.06 ∼	0.06 ∼	0.02 ∼	0.02 ∼	0.02 ∼	0.06 ∼	0.05 ∼	0.05 ∼
Overweight	0.34	0.28	0.37	0.95 ∼	0.85 ∼	0.82 ∼	0.77 ∼	0.78 ∼	0.76 ∼
McFadden R2	0.042	0.042	0.042	0.044	0.041	0.038	0.096	0.098	0.094
South Africa	Stroke			Diabetes			Hypertension
	Measured	Self–reported	Adjusted	Measured	Self–reported	Adjusted	Measured	Self–reported	Adjusted
Intercept	−1.49	−2.12	−1.23	−3.18 ∼	−2.90 ∼	−3.56 ∼	−2.04 ∼	−1.59	−1.43
Female	0.43	0.33	0.45	0.22	0.27	0.22	0.36	0.40	0.41
Rural	0.32	0.22	0.22	−0.21	−0.19	−0.20	−0.17	−0.17	−0.15
Completed high school	0.29	0.22	0.30	−0.25	−0.23	−0.26	−0.17	−0.14	−0.14
Completed college	−1.72 ∼	−1.79 ∼	−1.67 ∼	−0.19	−0.16	−0.22	−0.68	−0.69	−0.69
Cohabiting/currently married	0.38	0.37	0.36	−0.17	−0.14	−0.13	−0.09	−0.07	−0.06
Previously married	0.85	0.80	0.90	0.25	0.29	0.25	−0.06	−0.04	−0.02
Age	−0.03	−0.03	−0.03	0.02	0.01	0.02	0.02	0.01	0.01
Overweight	−0.65	0.04	−0.69	0.53	0.26	0.82	0.47 ∼	0.02	0.03
McFadden R2	0.072	0.057	0.054	0.048	0.040	0.043	0.040	0.033	0.034

∼ denotes a case when zero falls outside the 95% empirical confidence interval.

When overweight is significant, its median coefficient estimate is always positive. That is, those who are overweight are more likely to report these health outcomes compared to those who are not overweight, which is expected as overweight is a known risk factor for chronic conditions. As in Table 5, the health-outcome models for South Africa and stroke have the fewest significant relationships.

There appear to be more discrepancies between models when BMI is categorical instead of continuous. These discrepancies are most apparent in the overweight variable. There are three changes in significance in the overweight variable between measured and self-reported categorical BMI – overweight is significant for diabetes in India and hypertension in South Africa only when classified by measured BMI, while overweight is significant for stroke in China only when classified by self-reported BMI. When comparing measured and adjusted, there are three changes in significance in the overweight variable – overweight is significant for diabetes and hypertension in India, and hypertension in South Africa only when classified by measured BMI. The argument for not using measured BMI appears weaker with a categorical specification.

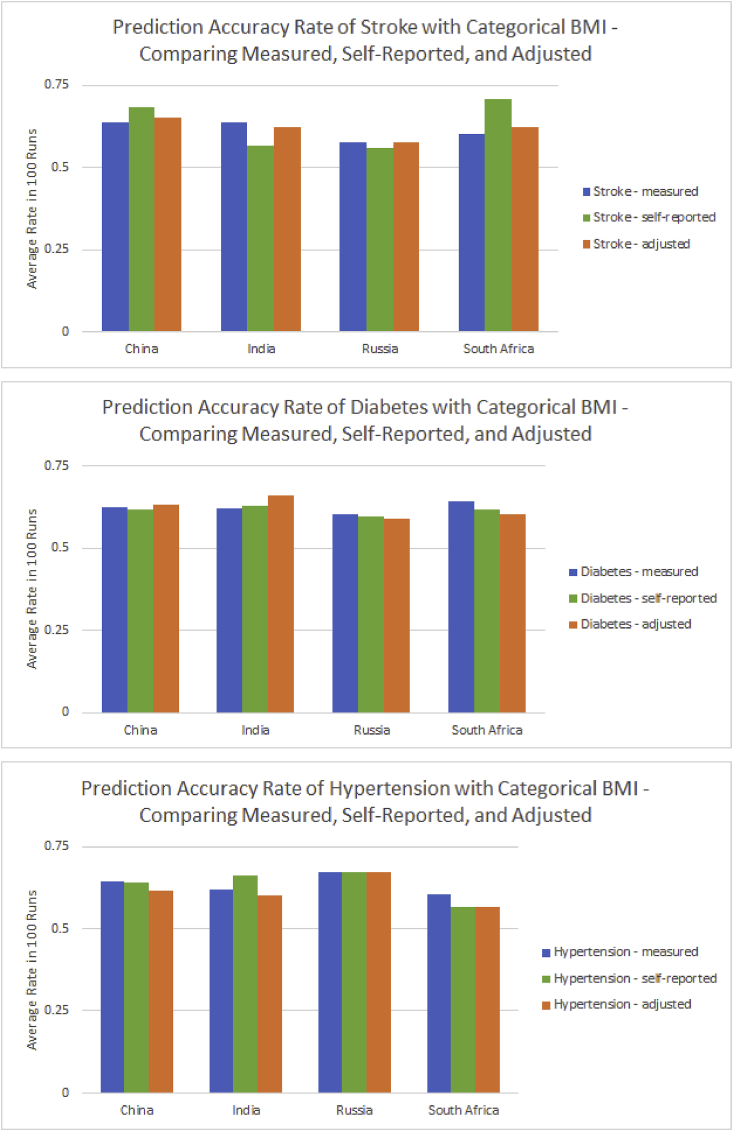
I then look at prediction accuracy using categorical BMI (Fig. 4).

Fig. 4.

Comparison of prediction accuracy rates using measured, self-reported, and adjusted categorical BMI in China, India, Russia, and South Africa.

The range in average prediction accuracy rates using categorical BMI is similar to that using continuous BMI. Here, the average prediction accuracy rate is highest for measured in seven of the health outcome and country combinations, followed by self-reported with three, and adjusted with two. Measured BMI appears to be the best choice when using BMI with a categorical specification, but the higher average for self-reported in the case of stroke for South Africa is quite distinct, again highlighting differences in specific contexts.

4. Discussion

Most research in high-income countries has shown that, typically, height is over-reported and weight is under-reported. While there are significant differences between measured and self-reported height and weight in this study, the directions vary by country and sociodemographic sub-group within a country. The reporting patterns in Russia are closest to those of higher-income countries. Interestingly, in terms of the Human Development Index, Russia is ranked the highest, followed by China, South Africa, and India (United Nations Development Programme (UNDP), 2016). The different patterns of anthropometric misreporting among these four countries indicate the heterogeneity among them, and suggest that there might be a relationship between reporting patterns and level of development. Perhaps height and weight aspirations shift as countries develop, leading to misreporting in different directions for countries at different stages of development.

In addition to development, cross-cultural differences have been found to impact how anthropometrics are reported (Gorbor et al., 2007; Howard et al., 2008; Gil & Mora, 2011), though much of such research has been done in higher-income countries. There might be a tendency to misreport anthropometrics based on the cultural ideals of height and weight, as “body ideals are culturally bound” (Yam, 2013). For example, in Table 3, it appears that BMI is over-reported in India. Could it be that being overweight, like beauty or wealth, is something that people in India tend to aspire to? Research has shown that there is a desire to be thin among Indian adolescent girls (Dixit et al., 2011; Zimik, 2016), but perhaps this difference could be attributed to their having grown up in periods belonging to different stages of development in India. In Table 2, all the significant differences in China indicate over-reported weights. In a sample of Chinese adolescent boys, a higher body weight is favored by both these boys as well as their parents (Shi et al., 2007).

Measured data are often difficult to acquire. To avoid collecting measured data, researchers could adjust self-reported height and weight based on height and weight models. If the goal is to study anthropometric distributions, adjusting self-reported measures could be beneficial. These adjusted data could then be used in other applications, if appropriate. Is it advisable to use the data in a population or a subset thereof to estimate a model, and then use it in adjustments in a similar population or another subset of the same population? Researchers are strongly cautioned that the models for one population should not be indiscriminately used for another population, given the heterogeneous patterns observed in this study. Further research is warranted to see whether coefficients in one setting can be safely applied to another context.

BMI is often used as a covariate in models to analyze various health outcomes, since it is a major risk factor for chronic diseases. While there are some minor differences among models using continuous measured, self-reported, and adjusted BMI, they are actually quite similar. When using categorical BMI, there are more discrepancies in the magnitude of coefficient estimates and even in their significance when different BMI metrics are used, results consistent with previous research on the United States (Preston et al., 2015). It appears that, with a couple of exceptions, choice of BMI metric is not too important when using BMI as a continuous variable for understanding associations, and so the simplest option of using self-reported data is acceptable. However, its tendency to understate the relationship should be kept in mind. Collecting measured data would be more crucial when using BMI as a categorical variable. However, one could not have BMI categories without having numerical BMI values, and so the safest alternative might be self-reported BMI without any categorization or adjustment.

If the goal is to predict individuals' reporting of health outcomes, self-reported BMI rarely performs best among the continuous BMI metrics, with either measured or adjusted BMI usually producing the best average prediction accuracy for most of the health outcome and country combinations. With a categorical specification, measured BMI has the highest average prediction accuracy in more health outcome and country combinations than the other two metrics combined. From this, it appears that measured BMI is still superior for prediction accuracy in most cases, though adjustments could be useful in some contexts.

While researchers are cautioned against using or not using self-reported data in health-outcome models for other populations without further investigation, this study does appear promising. China, India, Russia, and South Africa are diverse contexts with varying degrees of misreporting and BMI classification agreement. Despite these differences, the general substantive conclusions are similar – self-reported data could be sufficient for certain purposes. If deemed necessary, adjustments could be made to self-reported data to improve the reliability of conclusions derived therefrom. However, there are applications for which measured data are still superior, and if resources are available, it would be preferable to have the most accurate data at the researcher's disposal.

In this study, only older adults are included, and selection bias could distort true associations between BMI and health outcomes. To the extent that overweight is associated with a certain outcome of interest, a subset of the overweight population might have already died from the outcome, thus biasing associations downward in the selected sample. However, the comparisons here are among the associations resulting from different BMI metrics. There is no reason to believe that the choice of sample would bias the associations in different ways for different BMI metrics.

There are also two points of note on the diagnoses of health outcomes. First, such diagnoses are self-reported in SAGE. It should be borne in mind that reporting a certain health condition is not necessarily the same as having the health condition. Second, under-diagnosis of health conditions is common in many contexts (Banjerjee et al., 2012; Enright et al., 1999; Halter, 2000; Ravikumar et al., 2011; Strauss et al., 2010). It is not clear whether under-diagnosis is similar across countries or across sub-groups – another reason why a model for a country should not be indiscriminately used for a sub-group of this country or for another country.

While I randomly split my data into training and testing sets 100 times to confirm validity, “final” models on the whole samples for all combinations of countries, health outcomes, and BMI metrics have been run and are very similar to the median results presented in Table 5, Table 6. Further testing of these models with additional data, such as future waves of SAGE, would be a good next step.

5. Conclusion

There is often significant height and weight misreporting, which in turn lead to significant differences between measured and self-reported BMI. The use of misreported heights, weights, or resulting BMI might or might not have dire consequences for specific applications. The implication here is that measured data on anthropometrics are not always absolutely needed, depending on what the research question at hand is. For some questions, measuring and using actual BMI is important. For others, self-reported data might be sufficient. There is a trade-off between accuracy and resource constraints, and data that are often considered unreliable for one purpose might be “good enough” for another.

Ethics approval and consent to participate

Not applicable.

Consent for publication

Not applicable.

Availability of data and material

The data used can be found here: http://www.who.int/healthinfo/sage/en/.

Conflicts of interest

The author declares that she has no competing interests.

Funding

The author received support from the Population Research Training grant (NIH T32 HD007242) from the Eunice Kennedy Shriver National Institute of Child Health and Human Development (NICHD).

Authors' contribution

CN is the sole author of this paper.