Abstract
Coronary artery bypass grafts used to treat coronary artery disease (CAD) often fail due to compliance mismatch. In this study, we have developed an experimental/computational approach to fabricate an acellular biomimetic hybrid tissue engineered vascular graft (TEVG) composed of alternating layers of electrospun porcine gelatin/polycaprolactone (PCL) and human tropoelastin/PCL blends with the goal of compliance-matching to rat abdominal aorta, while maintaining specific geometrical constraints. Polymeric blends at three different gelatin:PCL (G:PCL) and tropoelastin:PCL (T:PCL) ratios (80:20, 50:50, and 20:80) were mechanically characterized. The stress–strain data were used to develop predictive models, which were used as part of an optimization scheme that was implemented to determine the ratios of G:PCL and T:PCL and the thickness of the individual layers within a TEVG that would compliance match a target compliance value. The hypocompliant, isocompliant, and hypercompliant grafts had target compliance values of 0.000256, 0.000568, and 0.000880 mmHg−1, respectively. Experimental validation of the optimization demonstrated that the hypercompliant and isocompliant grafts were not statistically significant from their respective target compliance values (p-value = 0.37 and 0.89, respectively). The experimental compliance values of the hypocompliant graft were statistically significant than their target compliance value (p-value = 0.047). We have successfully demonstrated a design optimization scheme that can be used to fabricate multilayered and biomimetic vascular grafts with targeted geometry and compliance.
1. Introduction
Cardiovascular disease (CVD) continues to be the largest cause of death in the U.S. According to the American Heart Association, as of 2014, 92.1 million American adults (more than 1 in 3) have one or more type of CVD, which is also listed as the leading underlying cause of 800,000 American deaths (1 out of every 3 deaths) [1]. The highest percentage of CVD-related deaths was attributed to coronary artery disease (CAD). Approximately every 40 s, an American will have a myocardial infarction as part of CAD [1]. It is estimated that 150,000 coronary artery bypass graft procedures are performed in the U.S. annually [1]. As such, there is an ongoing need for a suitable bypass graft for treatment of CAD. Autologous grafts like the bilateral mammary artery, radial artery, and the saphenous vein have been considered to be the gold standard in obtaining total arterial myocardial revascularization [2]. However, the 10-year patency in small-diameter autologous grafts like the saphenous vein was shown to be 55% [3]. Autologous graft failure factors include poor graft quality [4], graft unavailability, lack of durability [5], and graft compliance mismatch to the native vessel [6,7]. One alternative to autologous grafts are tissue engineered vascular grafts (TEVGs), which can be engineered to have specific geometric and mechanical specifications to compliance-match native tissue. TEVGs can also be biocompatible, nonthrombogenic, and produced with good durability and deliverability.
Synthetic materials like Dacron and polytetrafluoroethylene (PTFE) have been clinically used as bypass graft materials in peripheral vascular surgery [8] and aortic root or ascending aorta replacement [9]. However, small-diameter synthetic grafts have shown poor patency rates due to acute thrombogenicity and anastomotic intimal hyperplasia [6,10–12]. Some researchers have attempted to make synthetic TEVGs less thrombogenic by modifying the synthetic material [13,14], by adding growth factors and proteins intraluminally to encourage endothelialization in situ [15,16], or by growing an endothelial cell monolayer on the luminal surface of the small-diameter grafts in vitro before implantation [17–19]. However, TEVGs created from nonbiological synthetic materials tend to be stiffer and have shown compliance mismatch to native arteries [20,21], which can lead to anastomotic intimal hyperplasia and subsequent graft failure [22].
Artery walls are comprised of three layers: the intimal layer consisting of a monolayer of endothelial cells on an elastic basal lamina, the medial layer, and the adventitial layer made up of additional matrix and fibroblasts. The medial layer has an extracellular matrix (ECM) largely composed of concentric layers composed of elastin fibers and smooth muscle cells (SMCs) [23]. These lamellar units are separated by type III collagen, microfibrils, proteoglycans, and glycoproteins [23–25]. The ECM fibers are predominately circumferentially aligned to regulate and facilitate vasoactivity, while also contributing to appropriate mechanical anisotropy [26]. The medial layer ECM is the primary determinant of biomechanical properties of the vessel and plays a critical role in biological function, including their ability to bind multiple interacting partners such as growth factors and cell signal receptors [27]. Vascular ECM can also serve as a sequestration and storage site for growth factors and cytokines that regulate cell behavior and fiber deposition [26,28]. ECM-embedded proteins provide instructional signals that induce, define, and stabilize vascular cell phenotypes [25]. Therefore, mimicking the microstructure of native vascular is an important consideration in fabricating vascular grafts.
Researchers have attempted to mimic ECM microstructure using different fiber-like structure fabrication methods like thermally induced phase separation [29–31] and electrospinning [32–34]. Electrospinning is a fabrication method that involves creating nonwoven polymer fibers, which, when deposited on a cylindrical target, can create hollow cylindrical constructs. The process of electrospinning is an attractive fabrication method, as it allows control over dimensions and alignment of fibers, porosity, and overall microstructure of the scaffold [35]. This allows researchers to create structures similar to the vascular ECM, which would provide the necessary capacity for cell proliferation and healthy remodeling [7,36]. It also offers the ability to modulate the mechanical properties of scaffolds by changing different electrospinning parameters [37]. Some research groups have used electrospinning to fabricate TEVGs from nonbiological synthetic polymers like poly(ester urethane) urea [38,39] and polyurethane [40]. Drawing from the composition of native tissue, one option to create TEVGs is to use biological nonsynthetic polymers native to the body. These biopolymers may have the potential to be more biocompatible, biodegradable, and to encourage in situ cell migration, proliferation, and remodeling. There are several studies that have investigated creating grafts by electrospinning biopolymers including collagen [41–43] and collagen/elastin mixtures [44–47].
Collagen and elastin are fundamental components of vascular ECM, which provide strength and elasticity to vascular tissue while playing important roles in cell signaling. Some researchers have questioned the efficacy of electrospinning collagen, arguing that electrospinning collagen out of solvents may effectively denature this biopolymer, resulting in the production of electrospun gelatin [48]. Gelatin is a derivative of collagen, which has been found to be a cost-effective readily available biodegradable biopolymer, which our laboratory group has used to create electrospun and computationally optimized cylindrical constructs [49,50]. The soluble monomer of elastin is tropoelastin, which is composed of alternating hydrophobic and hydrophilic domain structures crucial for the process of crosslinking and overall mechanical behavior [51]. Tropoelastin is also a main functional component in wound healing through chemotactic activity [52]. Obtaining the tropoelastin monomer from various tissues has historically been highly inefficient as it requires the perturbation of the fast natural crosslinking process of tropoelastin into elastin [53]. However, the availability of large quantities of highly purified human tropoelastin has only recently become available through recombinant bacterial system expression [54]. Researchers have successfully electrospun tropoelastin fibers [55–57], while some have demonstrated that crosslinked electrospun fibers retain the monomer's conformation, biological activity [58], and low thrombogenicity of elastin [51]. Tropoelastin and elastin have been described as one of the most elastic biosolid materials [51], and our laboratory group has previously observed that adding tropoelastin to gelatin constructs resulted in an increased in elasticity and compliance.
It should be noted that noncrosslinked electrospun natural polymers do not provide the necessary mechanical integrity for TEVG applications and that these materials are not stable in aqueous solutions as they can dissolve easily [48,59]. Some researchers have resorted to using crosslinking agents that strengthen these biopolymers and provide stability while retaining the elastic properties intrinsic to these materials [60]. Synthetic chemical crosslinking agents like glutaraldehyde have been widely used to crosslink electrospun biopolymers [45,50]. However, these biomaterials have been shown to promote cytotoxicity [61] and in vivo calcification [62–64]. While one study has investigated different methods of detoxifying glutaraldehyde-crosslinked materials [65], others have searched for alternative crosslinking agents. One such agent is genipin, a natural crosslinking agent that has been used to crosslink different biomaterials. Similar to the crosslinking mechanism of glutaraldehyde [66], research has shown that genipin reacts with free amino groups of amino acids like lysine, hydroxylysine, or arginine within biological tissues [67]. This can result in forming intramolecular and intermolecular crosslinks within protein fibers [68], which forms a crosslinked biomaterial that exhibits less cytotoxicity [69] and reduced calcification in vivo [65].
Studies investigating the mechanical properties of biopolymers have shown that crosslinked natural materials lack the necessary mechanical integrity when compared to native tissue [70–72]. Our research group previously demonstrated that glutaraldehyde-crosslinked gelatin/fibrinogen constructs lacked the necessary physiological axial/circumferential deformability and mechanical strength, even though they successfully compliance matched to porcine coronary artery [50]. One solution to overcoming this mechanical limitation of biopolymer TEVGs is to add biocompatible synthetic polymer to the composition of the construct. For example, some researchers have created hybrid constructs by mixing collagen with different synthetic polymers [73–75]. Polycaprolactone is a common biocompatible biodegradable synthetic polymer, which has been mixed with collagen [76,77], elastin [78,79], collagen\elastin mixtures [80], gelatin [81], and tropoelastin [72]. These hybrid scaffolds demonstrated additional mechanical strength and stability, while retaining some of the elastic and biochemical properties of the biopolymers they contain.
Compliance mismatch between vascular graft and vascular tissue has been shown to be detrimental to graft performance and patency [82]. Researchers have determined a relationship between compliance mismatch and the development of intimal hyperplasia [21], possibly due to flow disturbances and disruption of chemical transport in the fluid at the distal anastomosis [83,84]. Some researchers have utilized finite element methods to analyze arterial anastomoses to study the effects of graft compliance mismatch [85], while other researchers have used computational fluid dynamics analysis to understand the effect of graft diameter mismatch [84,86]. Computational methods can be effective tools in determining the appropriate geometry and material properties for compliance matching grafts while saving time and resources. Our research group has previously developed a computational/experimental optimization scheme for compliance matching native tissue by predicting the thickness and glutaraldehyde crosslinking duration time of electrospun gelatin/fibrinogen cylindrical constructs [50]. This program performed finite element simulations using predicted mechanical properties by interpolating between characterized properties of three crosslinking time points for single-layered construct. However, native arteries have concentrically arranged matrix of alternating layers of elastin and collagen. In an effort to match this geometry, this study aims to create biomimetic multilayered TEVGs with alternating electrospun layers of porcine gelatin and human tropoelastin, which are meant to be analogous to collagen and elastin, respectively. PCL was chosen as a synthetic polymer to be added to our electrospun gelatin constructs as a means of varying the stiffness of the individual layers while providing mechanical support. Due to concerns regarding the toxicity of the previously used glutaraldehyde, we opted to use genipin as a crosslinking agent. We aimed to add tropoelastin to the graft compositions for the purpose of increasing the elasticity of our biomimetic TEVGs for better mechanical optimization and deliverability. The overall purpose of this study was to use our previously validated computational/experimental scheme to predict the individual thicknesses and biopolymer/PCL ratios of alternating gelatin/tropoelastin layers to create a hybrid (synthetic and nonsynthetic) biomimetic TEVG that is compliance matched to rat abdominal aorta.
2. Materials and Methods
2.1. Rat Abdominal Aorta Tissue Acquisition and Preparation.
All tissue acquisitions were performed in accordance with approved protocols with the University of Pittsburgh Institutional Animal Care and Use Committee. Male Sprague-Dawley rats (n = 13, 175–235 g) were ordered and sacrificed. Within 1 h postmortem, each rat was dissected and the infrarenal abdominal aorta was extracted. All connective tissues were removed and the sample was placed in 1× phosphate-buffered saline (PBS) pH 7.4 (Thermo Fisher Scientific, Waltham, MA) with 1% (v/v) Gibco Penicillin–Streptomycin 10,000 U/mL (Thermo Fisher) and 1% (v/v) Gibco Amphotericin B (Thermo Fisher) for 24–48 h postmortem at 4 °C before mechanical testing.
2.2. Electrospun Materials.
Gelatin extracted from porcine skin (Sigma-Aldrich, St. Louis, MO) and polycaprolactone with a molecular weight ∼80,000 (Sigma-Aldrich) were dissolved in 1,1,1,3,3,3-hexafluoro-2-propanol (HFP) (Sigma-Aldrich) at ratios of 80:20, 50:50, and 20:80 (referred to henceforth as 80G:20PCL, 50G:50PCL, and 20G:80PCL, respectively) to create 10% (w/v) solutions. Human recombinant tropoelastin was acquired from Protein Genomics (Sedona, AZ), which was produced by fermentation of recombinant Escherichia coli containing pET21a and expression induced by the addition of isopropyl β-d-1-thiogalactopyranoside. Tropoelastin was solubilized from the lysed cells and purified resulting in approximately 95% purity determined by sodium dodecyl sulfate polyacrylamide gel electrophoresis. The final product was tropoelastin lyophilized with polyethylene glycol (PEG) into a cake with an end concentration of 0.48 mg tropoelastin/1 mg of cake (referred to henceforth as tropoelastin). Tropoelastin and PCL with a molecular weight ∼80,000 (Sigma-Aldrich) were dissolved in HFP at ratios of 80:20, 50:50, and 20:80 (referred to henceforth as 80T:20PCL, 50T:50PCL, and 20T:80PCL, respectively) to create 10% (w/v) solutions.
2.3. Fabricating Electrospun Constructs for Material Characterization.
A commercial electrospinning device (IME Technologies, Waalre, The Netherlands) was used to create all electrospun constructs in this study. All solutions were loaded into 5 ml syringes (BD, Franklin Lakes, NJ), which were attached to computer-controlled syringe pumps. The syringes were connected to transparent PTFE tubing with a 1 mm inner diameter (ID) and 2 mm outer diameter (OD), which fed the solutions into the ventilated insulated electrospinning chamber. For the G:PCL solutions and T:PCL solutions, the feeding PTFE tubing was fed through a positively charged translating stage on the same horizontal level as the target and above the target, respectively. All feeding PTFE tubes were connected to a 0.6 mm ID hollow stainless steel dispensing tips, which were all at a distance of 10 cm away from the target. The two dispensing tips alternatingly translated back and forth at a speed of 300 mm/s along a total axial distance of 10 cm. The G:PCL and T:PCL solutions were dispensed at a rate of 100 and 30 μL/min, respectively. The electrospinning system included a gas shield module (IME Technologies), which was utilized to prevent the accumulation of biopolymer at both nozzles and stabilize the electrospinning streams for increased reproducibility. Additionally, an anti-static module (IME Technologies, Waalre, The Netherlands) was used to electrically neutralize any electric charge accumulated inside the electrospinning chamber, which played a role in minimizing nonspecific fiber binding and increasing throughput yield and quality. A voltage difference of 15 kV was generated between both dispensing tips and a grounded rotating stainless steel rod with a 1.55 mm OD rotating at a speed of 300 rpm. The electrospinning chamber's temperature and relative humidity were controlled to be 25±3 °C and 30 ± 2%, respectively. Polymeric solutions were dispensed to create electrospun cylindrical constructs for each protein:PCL ratio for both gelatin and tropoelastin (n = 3 for each ratio, 18 total). All constructs were removed and placed in 0.5% (m/v) concentration of genipin (Wako Chemicals USA, Inc., Richmond, VA) in 200 proof ethanol for 24 h at 37 °C for crosslinking. The concentration of the genipin solution was chosen as a result of preliminary experimentation that took into account information from existing literature as well as the mechanical integrity and measured stiffness of preliminary constructs. After crosslinking, the constructs were rinsed with ethanol to remove the crosslinking agent and hydrated in 1× PBS. The electrospinning setup is shown in Fig. 1.
Fig. 1.
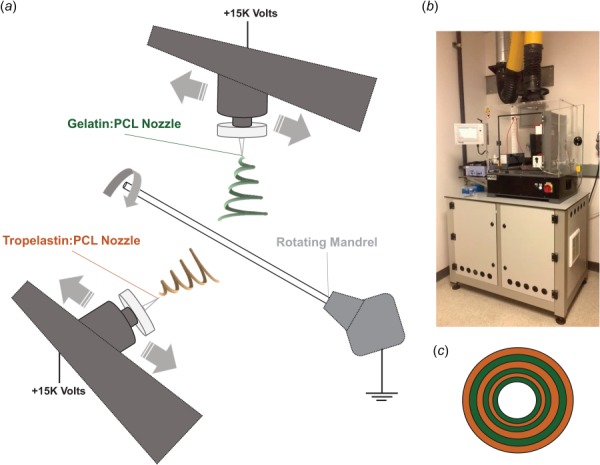
(a) Representation of the electrospinning setup with two translating positively charged dispensing nozzles and a rotating grounded mandrel, (b) IME Technologies commercial electrospinning chamber, and (c) graphical representation of construct cross section showing the alternating G:PCL and T:PCL layers
2.4. Sample Imaging and Thickness Measurements.
Representative 0.5 cm long samples were taken from each of the fabricated constructs and rat aorta samples and placed in plastic molds filled with Fisher HealthcareTissue-Plus O.C.T. Compound (Thermo Fisher Scientific). The molds were kept in a freezer at −20 °C until frozen. Each sample was mounted in a Microm HM550 cryostat microtom (Thermo Fisher Scientific) and cryosectioned at a thickness of 40 μm and mounted onto glass slides. The glass slides were imaged using a Nikon 90i Eclipse fluorescence microscope (Nikon Inc., Melville, NY). The autofluorescence signal of the fabricated constructs was collected through a Cy3 filter cube (excitation at 545 nm; emission at 610 nm), while the autofluorescence signal of the rat aorta media layer was collected using a FITC filter cube (excitation at 494 nm; emission at 518 nm). All samples were imaged using both a Nikon Plan APO 4×/0.2 [infinity]/- WD 12.7 objective (Nikon) and a Nikon Plan Apo 20×/0.75 DIC N2 WD 1.0 objective (Nikon). The nis-elements imaging software (Nikon) was used to determine an average thickness measurement for each sample.
2.5. Tubular Biaxial Mechanical Testing.
Mechanical testing of the fabricated characterization constructs and the rat aorta samples were performed using an in-house custom-made microbiaxial optomechanical device (MOD), which has been used extensively by our laboratory group to mechanically characterize tubular and planar biomaterials [49,87–92]. Briefly, both ends of each sample were cannulated to 1 mm OD glass capillaries using suture and super glue gel (Loctite). The cannulated sample was mounted into the MOD bath filled with 1× PBS, which was kept at 37 °C, and preconditioned axially (1 to 1.2 axial stretch) and circumferentially (0 to 120 mmHg intraluminal pressure) seven times. For mechanical testing, the constructs were axially stretched to 1.2 at 0.05 mm/s in 0.05 increments. At each axial stretch increment, the intraluminal pressure was slowly increased from 0 to 120 mmHg at an approximate rate of 4 mmHg/s using the hydrostatic pressure from a refillable fluid saline bag filled with 1× PBS. During these tests, the axial load was measured by the MOD system using 1000 g load cells. The real-time construct axial stretch and OD were determined by tracking small cyanoacrylate/ceramic powder markers placed on the constructs, which were digitally tracked using a camera and image processing software integrated into the MOD system. Each mechanical test generated raw data including axial stretch, axial load, OD, and intraluminal pressure.
2.6. Constitutive Modeling and Stress–Strain Surface Averaging.
The raw data generated by the MOD system and thickness data measured by fluorescence imaging were used to calculate strain and stress values for each sample in both axial and circumferential directions. The equations used to calculate the second Piola Kirchhoff stresses and Green strains are detailed in our previous publication [49]. Briefly, Eq. (1) was used to calculate the circumferential Green strain
| (1) |
where and are the circumferential Green strain and the circumferential stretch ratio (unitless), respectively. Equation (2) was used to calculate the axial Green strain
| (2) |
where is the axial Green strain and is the axial stretch (unitless). The circumferential and axial second Piola Kirchhoff stresses (Pa) ( and , respectively) were calculated using Eqs. (3) and (4), respectively,
| (3) |
| (4) |
where and are axial and circumferential Cauchy stresses, respectively (Pa). The stress–strain data were fit to the following modified Fung strain-energy constitutive equation [93]:
| (5) |
where , is the strain energy density (Pa), and (Pa), , , and are material constants. The axial and circumferential second Piola Kirchhoff stresses can be derived from the strain energy density using the differentiations shown by Eqs. (6) and (7), respectively [93]
| (6) |
| (7) |
For each mechanically tested replicate within each group, the stress–strain data were fit to Eqs. (6) and individually using the matlab multivariable minimization function, fmincon. Coefficient of determination (R2) values and visual assessment were used to evaluate the accuracy of these individual fits. This resulted in stress–strain response surfaces of axial and circumferential second Piola Kirchhoff stresses as a function of axial and circumferential Green strains for each replicate. Both axial and circumferential stress–strain response surfaces within each group were averaged over the appropriate overlapping strains ranges. Upper limit and lower limit response surfaces for each group were generated by adding and subtracting one standard deviation from the average responses surface, respectively. Finally, the average, upper limit and lower limit stress–strain datasets were fit to Eqs. (6) and (7) simultaneously to generate one set of constants for each response surface for each group. The Fung constitutive model constants with corresponding R2 values for all three response surfaces for each group are shown in Table 1. Compliance values at zero axial strain were calculated using the below equation [94]:
| (8) |
Table 1.
Fung strain energy equation material constants, / values, and R2 values for the average, upper, and lower limit dataset for the G:PCL characterization constructs (80G:20PCL, 50G:50PCL, and 20G:80PCL) and the T:PCL characterization constructs (80T:20PCL, 50T:50PCL, and 20T:80PCL). R2 values compare the Fung equation surface plots to the averaged surface data for all three replicates for the respective experimental group. These material constants are determined based on a multivariable error minimization function and as such are covariant for each dataset. In other words, the relative values of parameter c and the other material constants may independently increase or decrease to achieve an adequate fit to the data. Therefore, the values of the c parameter may not necessarily be consistent with the trend of the labels: upper limit, average, and lower limit.
| Group | Dataset | c (MPa) | 1 | 2 | 3 | 2/1 | R2 |
|---|---|---|---|---|---|---|---|
| 20G:80PCL | Upper limit | 77.9 | 0.051 | 0.26 | 0.044 | 5.2 | 0.99 |
| Average | 146.9 | 0.020 | 0.12 | 0.016 | 6.1 | 0.99 | |
| Lower limit | 14.1 | 0.122 | 1.01 | 0.088 | 8.3 | 0.99 | |
| 50G:50PCL | Upper limit | 93.7 | 0.012 | 0.065 | 0.009 | 5.6 | 0.98 |
| Average | 21.6 | 0.044 | 0.22 | 0.034 | 4.9 | 0.98 | |
| Lower limit | 72.5 | 0.011 | 0.045 | 0.009 | 4.0 | 0.96 | |
| 80G:20PCL | Upper limit | 70.9 | 0.003 | 0.027 | 0.001 | 9.5 | 0.98 |
| Average | 1.3 | 0.119 | 1.063 | 0.057 | 9.0 | 0.98 | |
| Lower limit | 0.2 | 0.502 | 3.95 | 0.23 | 8.0 | 0.97 | |
| 20T:80PCL | Upper limit | 302.2 | 0.024 | 0.063 | 0.015 | 2.6 | 0.81 |
| Average | 3.3 | 1.621 | 4.79 | 1.034 | 3.0 | 0.81 | |
| Lower limit | 0.3 | 9.208 | 29.434 | 5.723 | 3.2 | 0.92 | |
| 50T:50PCL | Upper limit | 57.2 | 0.073 | 0.260 | 0.047 | 3.6 | 0.80 |
| Average | 4.5 | 0.834 | 2.834 | 0.545 | 3.4 | 0.80 | |
| Lower limit | 0.8 | 3.982 | 11.744 | 2.589 | 3.0 | 0.87 | |
| 80T:20PCL | Upper limit | 319.7 | 0.004 | 0.021 | 0.002 | 5.1 | 0.99 |
| Average | 13.2 | 0.092 | 0.461 | 0.052 | 5.0 | 0.99 | |
| Lower limit | 272.2 | 0.004 | 0.021 | 0.002 | 5.0 | 0.99 |
where is the diameter of the vessel at 120 mmHg intraluminal pressure (m) and is the diameter of the vessel at 70 mmHg intraluminal pressure (m).
2.7. Stress–Strain Predictive Model.
To develop an optimization scheme that would determine suitable fabrication parameters to produce a construct with desired mechanical properties, it was necessary to develop a predictive model that could produce stress–strain data for any protein:PCL ratio for both gelatin and tropoelastin between the ratios already mechanically characterized. The averaged axial and circumferential response surface data for all previously mentioned protein:PCL ratios (80:20, 50:50, and 20:80) for both gelatin and tropoelastin were used as part of a weighted sum interpolation method. Specifically, Lagrange interpolating polynomials [95] were used to interpolate between stress–strain response data such that the actual characterized experimental data are recovered if protein percentage equals 20, 50, or 80 for both gelatin and tropoelastin. The interpolating second order polynomials expressions for the three datasets are shown in the below equation:
| (9) |
| (10) |
where is the protein percentage between 20 and 80, , and are the circumferential and axial predicted stress–strain surface data for any protein percentage between 20 and 80, respectively, , , and are the circumferential stress–strain surface data for the 80:20, 50:50, and 20:80 protein:PCL ratios, respectively, , , and are the axial stress–strain surface data for the 80:20, 50:50, and 20:80 protein:PCL, respectively, and , , and are Lagrangian interpolating polynomials defined by the following equations:
| (11) |
| (12) |
| (13) |
For any value of between 20 and 80, the Lagrangian interpolating polynomials are used to calculate the appropriate weighted contribution of stress–strain data at 80:20, 50:50, and 20:80 for either protein. These equations were applied to both the G:PCL and T:PCL datasets to calculate axial and circumferential stress–strain datasets for each protein:PCL material separately. These predicted datasets were fit simultaneously to Eqs. (6) and (7) to produce one set of Fung constitutive model constants for G:PCL and T:PCL at a specific biopolymer percentage for each that were used in the optimization scheme.
2.8. Optimization Routine.
Our research group previously developed a finite element optimization scheme that predicted the thickness and crosslinking time of glutaraldehyde electrospun single-layered gelatin/fibrinogen constructs that were compliance-matched to porcine coronary arteries [50]. This optimization routine was adapted to predict the thickness and protein:PCL ratios of alternatingly layered constructs to match the geometry and compliance of rat aorta. Briefly, matlab (MathWorks, Inc.) code was used to generate abaqus FEA (Dassault Systemes Simulia, Johnston, RI) input files for a four-noded, reduced-integration, axisymmetric element model using a hybrid formulation. The mesh geometry consisted of a user-defined number of alternating G:PCL and T:PCL layers. The element regions associated with the G:PCL layers and the T:PCL layers were assigned appropriate material constants generated by the previously mentioned predictive model. abaqus then simulated the intraluminal pressurization from 0 to 120 mmHg and the OD measurement was extracted at 70 and 120 mmHg, which was used to calculate the simulated compliance value per Eq. (8). The open fit design parameters in the optimization scheme included the thicknesses and the protein:PCL ratios for each of the G:PCL and T:PCL layers. The fixed parameters included the total number of layers, construct ID, and total thickness. The rat aorta ID and media layer thickness values were averaged and used as the target ID and thickness values for the optimized grafts, respectively. Additionally, the average observed number of layers of elastin in rat aorta was chosen as the fixed number of alternating layers for all optimized compliance values. A construct total thickness computational tolerance of 20% was deemed acceptable to allow for flexibility in the optimization scheme. The matlab bounded optimization function (fminsearchbnd) iterated while changing the open design parameters until the difference between the predicted compliance value from the finite element simulation and the target compliance value fell within less than 1% of the target compliance. A summary of the optimization scheme is shown in Fig. 2.
Fig. 2.
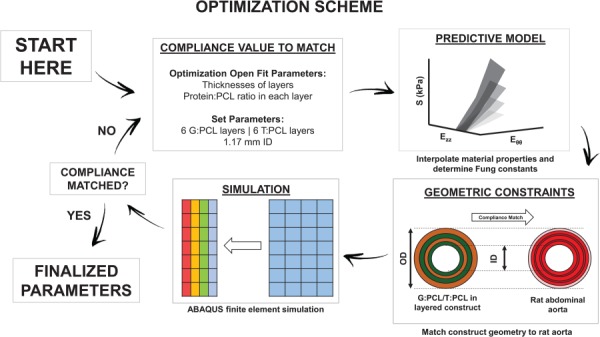
A diagram illustrating the optimization scheme used in this study
2.9. Compliance Matching and Optimization Model Validation.
Multiple compliance targets were chosen to demonstrate the flexibility of our model to compliance match to a wide range of values. The optimized grafts targeted to compliance match the average, the upper limit (one standard deviation added to the average), and lower limit (one standard deviation subtracted from the average) measured compliance values were referred to as isocompliant, hypercompliant, and hypocompliant optimized grafts, respectively. The optimization scheme was run to determine the design parameters necessary to create multilayered constructs that compliance matched all three targets. The optimization results were used to fabricate optimized grafts for all experimental groups. To match the target layer thicknesses, the thickness data from the characterization constructs were used to estimate the appropriate volumetric flow rate that would result in the appropriate G:PCL and T:PCL layer thicknesses. To evaluate the accuracy of experimental individual layer thicknesses, cross section of the fabricated grafts were imaged to determine the individual thickness of each G:PCL and T:PCL layer. The relative error of individual layer thicknesses according to the below equation:
| (14) |
The individual rat aorta thicknesses were subtracted from the OD values extracted from the MOD experiments. Compliance values and Fung constitutive model constants were determined for all optimized grafts, for which stress–strain response surfaces were generated.
2.10. Statistical Analysis.
All values are presented as the average ± standard deviation unless otherwise specified. Two-sample two-tailed t-tests were conducted comparing the IDs and total thickness of optimized grafts to those of rat aorta. One sample two-tailed t-tests were conducted comparing the compliance of optimized grafts to their respective target compliance values. A Bonferroni correction was applied to the p-values of comparative statistical tests to account for familywise error. For all statistical tests, a critical p-value of 0.05 was used to determine significance.
3. Results
3.1. Material Characterization.
The G:PCL characterization constructs (80G:20PCL, 50G:50PCL, and 20G:80PCL) and the T:PCL characterization constructs (80T:20PCL, 50T:50PCL, and 20T:80PCL) were mechanically characterized and the Fung constitutive model constants, 2/1 (measure of anisotropy) and R2 values are shown in Table 1.
3.2. Stress–Strain Predictive Model.
For both gelatin and tropoelastin, the developed predictive model was used to interpolate circumferential and axial stress–strain data for any ratio between 80:20 and 20:80. Predicted circumferential and axial stress–strain response surfaces for the G:PCL and T:PCL ratios are shown in Figs. 3 and 4, respectively.
Fig. 3.
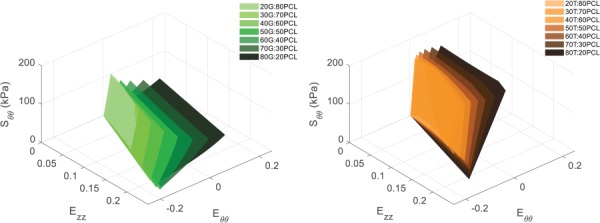
Predicted circumferential stress–strain response surfaces for (left) G:PCL ratios and (right) T:PCL ratios of 80:20, 70:30, 60:40, 50:50, 40:60, 30:70, and 20:80
Fig. 4.
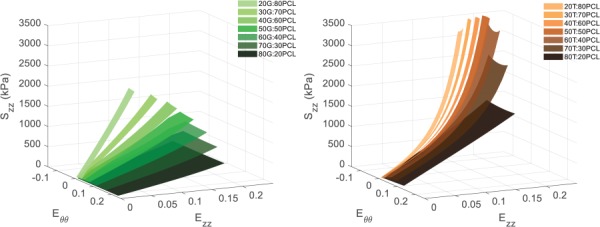
Predicted axial stress–strain response surfaces for (left) G:PCL ratios and (right) T:PCL ratios of 80:20, 70:30, 60:40, 50:50, 40:60, 30:70, and 20:80
3.3. Rat Aorta and Optimized Graft Characterization.
The average ODs of the rat aortas (n = 13) were determined to be 1.28±0.11 mm. The average rat aorta media layer thickness was determined to be 55±7 μm. The individual rat aorta thicknesses were subtracted from the OD values and the average ID was determined to be 1.17±0.15 mm. To match the ID of the optimized grafts to the ID of rat aorta, the electrospinning mandrel target was chosen to have an OD of about 1.17 mm. To qualitatively match the number of elastin/collagen layers of rat aorta, the total number of G:PCL and T:PCL layers was set at 12 layers (6 each). Using the MOD system, the average compliance value of the rat aorta was determined to be 0.000568±0.000318 mmHg−1. Based on this compliance range, the target compliance values for the hypocompliant, isocompliant, and hypercompliant optimized grafts were set at 0.000256, 0.000568, and 0.000880 mmHg−1, respectively. The optimization scheme was utilized and the resulting G:PCL ratios, T:PCL ratios, and individual layer thicknesses for all optimized experimental groups are shown in Table 2, which were used to fabricate all optimized grafts.
Table 2.
Optimization scheme predicted results for G:PCL and T:PCL layer ratios and thicknesses for individual layers for all optimized graft groups
| Predicted individual layer thickness (μm) | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Optimized experimental group | Predicted G:PCL layer ratio | Predicted T:PCL layer ratio | G1 | T1 | G2 | T2 | G3 | T3 | G4 | T4 | G5 | T5 | G6 | T6 | Total |
| Hypercompliant | 75:25 | 68:32 | 7 | 5 | 7 | 5 | 8 | 5 | 8 | 5 | 7 | 5 | 7 | 5 | 74 |
| Isocompliant | 71:29 | 48:52 | 6 | 5 | 5 | 5 | 6 | 5 | 7 | 5 | 6 | 5 | 7 | 5 | 67 |
| Hypocompliant | 35:65 | 28:72 | 5 | 5 | 9 | 5 | 9 | 5 | 9 | 5 | 8 | 5 | 9 | 5 | 79 |
Fluorescence images of the cross section of fabricated optimized grafts were used to determine the actual thickness values, which were compared to the optimized target values. The average G:PCL layer thickness relative error (%) for the hypocompliant (n = 3), isocompliant (n = 3), and hypercompliant (n = 3) were 30.0±7.3%, 12.7±8.7%, and 27.15±8.7%, respectively. The average T:PCL layer thickness relative error (%) for the hypocompliant, isocompliant, and hypercompliant was 16.0±8.8%, 15.6±8.5%, and 33.2±5.7%, respectively. The average ID values for the hypocompliant, isocompliant, and hypercompliant grafts were 1.04±0.01 mm, 0.86±0.07 mm, 0.92±0.05 mm, respectively. The IDs of the isocompliant and hypercompliant grafts were significantly lower than that of rat aorta (p-value = 0.002 and 0.001, respectively), whereas the ID values of the hypocompliant grafts were not statistically different than that of rat aorta (p-value = 0.25). The average wall thickness values for the hypocompliant grafts, isocompliant grafts, hypercompliant grafts were 57±4 μm, 59±8 μm, and 56±6 μm, respectively. The total wall thickness of the hypocompliant, isocompliant, and hypercompliant grafts were not statistically different than that of rat aorta (p-value > 0.99 for all). Fluorescence images of cross section of the optimized grafts and graphs demonstrating the ID values and thickness values of the optimized grafts are shown compared to rat aorta in Fig. 5.
Fig. 5.
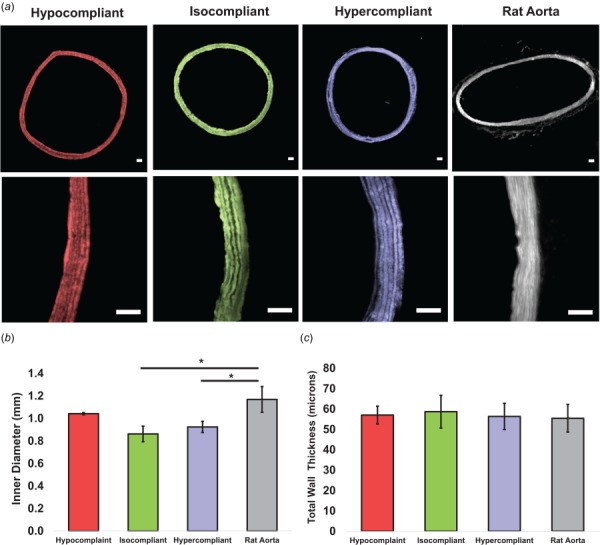
(a) 4× and 20× fluorescence images of representative samples of the hypocompliant, isocompliant, and hypercompliant optimized grafts and rat aorta. Scale bar indicates 50 μm for all images. (b) Inner diameter and (c) total thickness of the hypocompliant, isocompliant, and hypercompliant optimized grafts compared to rat aorta. Error bars indicate one standard deviation. Asterisk indicates statistical significance of difference compared to rat aorta using two-sample two-tailed t-test (p-value < 0.05).
3.4. Optimized Compliance and Mechanical Characterization.
The compliance values of the hypercompliant optimized grafts (0.0010±0.00020 mmHg−1) and isocompliant optimized grafts (0.00056±0.000051 mmHg−1) were not statistically different than their respective target compliances (p-value = 0.37 and 0.89, respectively). The compliance values of the hypocompliant optimized grafts (0.00017±0.000055 mmHg−1) were statistically different than their respective target compliance value (p-value = 0.047). The average compliance values are shown in Fig. 6. The Fung equation constants, R2 values and / values for the upper limit, average, and lower limit dataset for each of these groups are shown in Table 3. The average circumferential and axial stress–strain Fung-fit responses surfaces for the hypocompliant, isocompliant, and hypercompliant optimized grafts (n = 3 for each) and rat aorta (n = 8) are shown in Figs. 7 and 8, respectively.
Fig. 6.
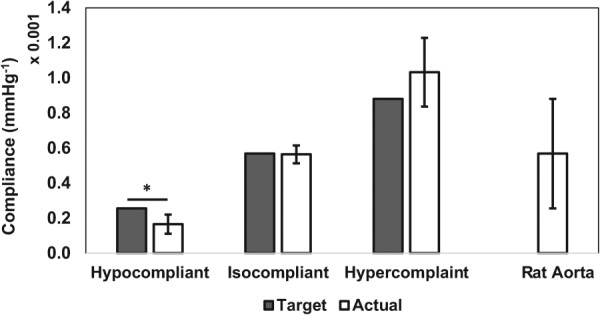
Target and actual compliance values of the hypocompliant, isocompliant, and hypercompliant optimized grafts compared to rat aorta compliance values. Error bars indicate one standard deviation. Asterisk indicates significant difference to target compliance value using one sample two-tailed t-test.
Table 3.
Fung strain energy equation constants, / values, and R2 values for the average, upper, and lower limit dataset for the hypocompliant, isocompliant, and hypercompliant optimized grafts and rat aorta. R2 values compare the Fung equation surface plots to the averaged surface data for all three replicates for the respective experimental group. These material constants are determined based on a multivariable error minimization function and as such are covariant for each dataset. In other words, the relative values of parameter c and the other material constants may independently increase or decrease to achieve an adequate fit to the data. Therefore, the values of the c parameter may not necessarily be consistent with the trend of the labels: upper limit, average, and lower limit.
| Group | Dataset | c (MPa) | 1 | 2 | 3 | 2/1 | R2 |
|---|---|---|---|---|---|---|---|
| Hypocompliant | Upper limit | 188.21 | 0.046 | 0.17 | 0.029 | 3.7 | 0.99 |
| Average | 149.40 | 0.048 | 0.19 | 0.029 | 4.0 | 0.99 | |
| Lower limit | 122.98 | 0.047 | 0.21 | 0.027 | 4.5 | 0.99 | |
| Isocompliant | Upper limit | 1.35 | 1.033 | 9.62 | 0.487 | 9.3 | 0.97 |
| Average | 1.55 | 0.865 | 7.92 | 0.399 | 9.2 | 0.96 | |
| Lower limit | 2.23 | 0.587 | 5.31 | 0.264 | 9.1 | 0.92 | |
| Hypercompliant | Upper limit | 154.93 | 0.011 | 0.062 | 0.006 | 6.0 | 0.86 |
| Average | 64.34 | 0.024 | 0.14 | 0.014 | 5.8 | 0.85 | |
| Lower limit | 74.92 | 0.020 | 0.12 | 0.011 | 5.9 | 0.83 | |
| Rat aorta | Upper limit | 136.08 | 0.011 | 0.038 | 0.005 | 3.4 | 0.98 |
| Average | 1.10 | 0.850 | 2.66 | 0.371 | 3.1 | 0.98 | |
| Lower limit | 0.005 | 31.805 | 50.11 | 9.433 | 1.6 | 0.90 |
Fig. 7.
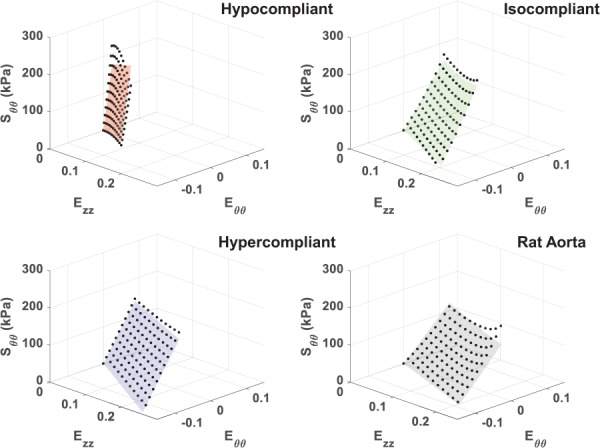
Average circumferential stress–strain Fung-fitted response surface plots for the hypocompliant, isocompliant, and hypercompliant optimized grafts as well as for rat aorta. Averaged data points from all replicates are displayed for fit evaluation and visualization.
Fig. 8.
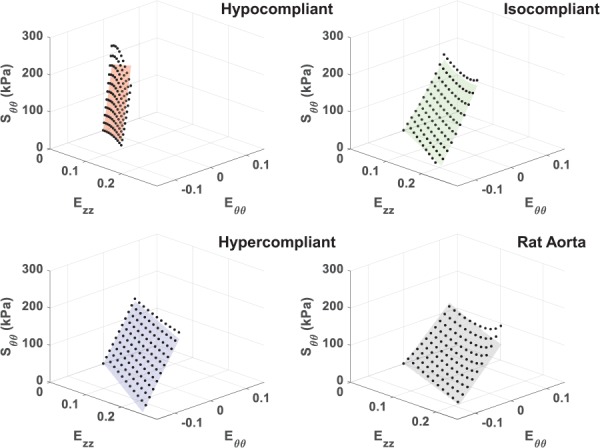
Average axial stress–strain Fung-fitted response surface plots for the hypocompliant, isocompliant, and hypercompliant optimized grafts as well as for rat aorta. Averaged data points from all replicates are displayed for fit evaluation and visualization.
4. Discussion
Electrospun cylindrical hybrid constructs comprised of various G:PCL and T:PCL ratios were mechanically characterized. The mechanical data were used to develop a stress–strain predictive model, which could predict the mechanical properties of any ratio G:PCL and T:PCL between 80:20 and 20:80 using Lagrangian polynomial interpolation. The predictive model was used as part of an optimization scheme to determine the appropriate protein:PCL ratios and thicknesses, which were then used to fabricate G:PCL/T:PCL alternatingly layered constructs that could compliance match to rat aorta. The alternating two-nozzle electrospinning method produced optimized grafts with distinct G:PCL and T:PCL layers for all three target compliances (Fig. 5). These optimized grafts had G:PCL and T:PCL layers with thickness percentage relative errors averages of less than 30.0% and 33.2%, respectively. Mechanical characterization of the optimized grafts showed that the optimization scheme was successful at compliance-matching grafts with higher gelatin and tropoelastin content. Specifically, the optimization model successfully determined the appropriate protein:PCL ratios and layer thickness configurations to properly match the compliance of hypercompliant (75G:25PCL and 68T:32PCL) and isocompliant (71G:29PCL and 48T:52PCL) grafts. However, the experimental results showed that the optimization scheme overestimated the compliance of the hypocompliant grafts, which had lower gelatin and tropoelastin content (35G:65PCL and 28T:72PCL).
As expected, the mechanical data generated from the pure G:PCL and T:PCL characterization constructs, and consequently the predictive model, showed that as the gelatin and tropoelastin content increases the material became less stiff and exhibited higher deformability (Figs. 3 and 4). Our laboratory group had previously demonstrated in preliminary experiments (data not shown) that electrospinning cylindrical constructs composed of a blend of tropoelastin and gelatin crosslinked with glutaraldehyde allowed for greater elasticity, deformability, and compliance compared to that made of exclusively gelatin. We had expected that any T:PCL ratio would be less stiff than G:PCL with the same protein:PCL ratio, and hence, that tropoelastin would be used to help tune the optimized grafts to become more compliant. However, T:PCL materials were stiffer than G:PCL of the same protein:PCL ratio in both circumferential and axial directions (Figs. 3 and 4). Additionally, the T:PCL materials were the only ones to strain-stiffen in the axial direction compared to their respective G:PCL equivalent (Fig. 4). This may be due to a difference in crosslinking mechanism between glutaraldehyde and genipin. Whereas our previous crosslinking method consisted of exposing constructs to glutaraldehyde vapor phase, our genipin crosslinking procedure involved submerging our electrospun constructs in a 0.5% genipin solution in ethanol (m/v). Since a portion of the tropoelastin cake is comprised of PEG, it may be possible that the electrospun PEG fibers dissolved in the ethanol. This may have resulted in a higher degree of crosslinking on T:PCL materials, due to an increase in crosslinking site availability, compared to the G:PCL materials, which did not contain PEG. Another explanation of this behavioral discrepancy may be due to how differently genipin interacts with gelatin compared to tropoelastin. It may be necessary to investigate other crosslinking nontoxic methods that could better utilize the elastic nature of tropoelastin. It is important to note that for both gelatin and tropoelastin, as protein content increased so did the anisotropic behavior as indicated by / values for both the G:PCL and T:PCL materials. This could be due to a higher diversity of fiber diameters in materials with higher protein content. The results also show that the IDs of the optimized grafts with higher protein content were lower compared to those with lower protein content. Although all optimized grafts were electrospun on the same mandrel with a fixed OD to match rat aorta ID, only the hypocompliant optimized graft had an ID not statistically different than that of rat aorta. The decrease in ID of the hypercompliant and isocompliant could be attributed to a compressive effect of the genipin crosslinking, which only affected the protein component of the graft. Mandrels with larger ODs may be necessary in order to match IDs of rat aorta for optimized grafts with higher percentages of protein to account for the crosslinking shrinking effect. Another solution to this problem could be crosslinking the graft while it is still on the mandrel so as to keep the graft ID equal to the OD of the mandrel.
In previous work, we fabricated and characterized glutaraldehyde-crosslinked gelatin/fibrinogen constructs, which were limited in deformability and mechanical integrity [49]. Our current study added PCL to the graft composition, allowing axial strains beyond the 0.17 limit exhibited by some gelatin/fibrinogen grafts previously fabricated [49]. This was achieved while still compliance matching to the different compliance range values of rat aorta. It should also be noted that most values of the anisotropy indicator /for the protein:PCL grafts in our current study increased compared to that of the previous study. Few researchers have reported fabricated layered constructs compared to a biological native sample. Huang et al. created a triple-layered vascular graft composed of two synthetic polymers (PCL and PEG) using a combination of E-Jet 3D printing and electrospinning [96]. The authors found that their layered grafts, which had thicknesses on the order of 700 microns, had higher burst strength and tensile strength to abdominal aortas from Sprague Dawley rats. While the study by Huang et al. did not report on compliance measures, it is unlikely that their grafts compliance matched rat aorta, because of the observed higher thicknesses and synthetic polymer composition. Yu et al. developed a biomimetic hybrid small-diameter vascular graft at different ratios of polyurethane and fibroin [97]. Similar to our study, they demonstrated that the mechanical properties (Young's modulus and ultimate strength) could be changed by varying the ratio of the synthetic polymer to the natural polymer. The focus of this study was mainly on the suitability of the graft for endothelialization and did not compare the mechanical properties of the graft to native tissue. In contrast, the thicknesses of our optimized grafts in this study were not statistically different from that of our target biological sample, and we have demonstrated that at least two of our optimized graft experimental groups compliance matched their target compliance value. Nonetheless, future studies are necessary to determine the suitability of the graft for endothelialization and cell culture.
Few researchers have attempted to compliance match vascular grafts to native tissue. Nezarati et al. fabricated electrospun different poly(carbonate urethanes) and evaluated the effect of changing thickness and microstructure on the compliance of the constructs with IDs and thicknesses on the order of 5 mm and 400 μm, respectively [98]. This study attempted to tune the compliance of their synthetic constructs (0.0006±0.00006 mmHg−1) to exceed that of human saphenous vein (0.00044±0.00008 mmHg−1) mechanically characterized in other literature [99]. Soletti et al. fabricated a bilayered vascular graft using both electrospinning and thermally induced phase separation and were compared mechanically to native human saphenous veins (hSV) and porcine internal mammary arteries (IMAs) [100]. The compliance values of the grafts were measured to be 0.00046±0.00005 mmHg−1 and were considered similar to both hSV and porcine IMAs without matching geometric dimensions of native tissue. These compliance values were similar to those of the isocompliant optimized grafts in our study, which measured at 0.00056 ±0.000051 mmHg−1. However, the geometrical dimensions of the grafts in the study by Soletti et al. (4.7 mm ID with 490 μm thickness) were larger than the small diameter rat aorta, as they were meant for the larger dimensions of hSV and porcine IMAs. In another study, Soletti et al. fabricated electrospun synthetic grafts with IDs and thicknesses similar to that of Lewis rat abdominal aorta [101]. However, in this case, the compliance values of their synthetic grafts were significantly lower than that of measured Lewis rat aorta. This mismatch shown in the literature between native tissue and grafts, in regards to geometry and compliance, highlights the importance and significance of having strategy to tune compliance by adding natural polymers while also controlling geometrical parameters. As mentioned, this was successfully demonstrated by our optimization scheme as presented in this study.
There are few studies that have also electrospun recombinant human tropoelastin [45,58,72]. In one study, Wise et al. fabricated an electrospun bilayered construct by sequentially delivering tropoelastin and T:PCL [72]. Similar to our study, Wise et al. added tropoelastin to PCL to fabricate cylindrical constructs and determined mechanical properties like compliance, burst pressure, and elastic modulus. Their constructs had two layers, with only one outer hybrid layer of tropoelastin:PCL at one ratio of 80:20 with a thickness and ID on the order of 300 μm and 3 mm, respectively. The compliance value of their construct was on the order 0.0008 mmHg−1, which they demonstrated was not statistically different than that of human IMAs but was different from that of human saphenous vein. Their study did not show how changing the T:PCL ratio can tune the compliance of their constructs to match different compliance ranges nor did they perform biaxial mechanical characterization and constitutive modeling. They were, however, able to show that these layered tropoelastin/T:PCL grafts had the mechanical integrity and biocompatibility to be successfully implanted in an animal model for one month. Although these grafts were crosslinked with glutaraldehyde instead of genipin, these results exhibit the suitability of our materials to be used for a functional vascular graft in future studies.
Some studies in the literature have utilized computational methods to characterize vascular constructs. A study by Jankowska et al. used constitutive modeling to characterize the mechanical behavior of human coronary artery using a Holzapfel constitutive model at different stages of atherosclerosis [102], which could prove useful in developing finite element models for vascular grafts with the goal of targeting suitable mechanical properties. There are few examples in the literature of studies that utilize computational methods to predict vascular graft compliance. Szafron et al. developed and performed a parametric computational study of different parameters, like thickness and shear modulus, on the compliance of a bilayered cylindrical construct [103]. This study did not present experimental validation of their findings. However, it did provide a wide range of insights into the parameters important to vascular graft design. A study by Castillo-Cruz et al. investigated the suitability of an analytical expression to determine the compliance of a cylindrical construct made of Tecoflex (polyurethane). Their analytical solution was successful at compliance prediction based solely on the elastic modulus and Poisson's ratio of the polymer material, which was determined through uniaxial tensile and compressive tests of the materials [104]. Castillo-Cruz et al. used finite element analysis to predict compliance using a four-noded axisymmetric model, similar to the finite element technique presented in this study [104]. Although the material was modeled using a simple isotropic linear elastic model, the finite element model was validated by predicting the compliance values measured experimentally. The scope of their study was limited to the prediction of the behavior of one isotropic nonfibrous synthetic material. Our approach adds to the current state of the art by combining a computational predictive model with finite element-based optimization, anisotropic constitutive modeling, and the prediction and validation of a multilayered construct composed of biomimetic materials.
There are a number of limitations to this study. All finite element simulations were performed at zero axial load. This was done as our vascular grafts will initially be implanted into the aorta of rats at near zero axial stretch. Therefore, our optimization scheme did not take into account the axial mechanical properties of the graft, which resulted in none of the optimized grafts having axial stress–strain response surfaces qualitatively similar to rat aorta. All optimized grafts exhibited noticeably stiffer behavior in the axial strain range presented (Fig. 8). This axial behavior mismatch was expected as the optimization scheme was focused on compliance matching, which would most directly impact the stress–strain behavior in the circumferential direction. Future studies will investigate compliance matching grafts while also taking into account the axial behavior so as to match all mechanical properties of rat aorta. One important factor in determining the mechanical behavior of our fibrous constructs is fiber orientation, which was not investigated in this study. Based on existing literature [105–107], we believe that the rotational speed of the target and the translational speed of the nozzles were both not high enough to create aligned fibers. Instead, we assume that our constructs were composed of random, nonwoven and nonaligned fibers. Future studies should measure fiber orientation and diameter distribution in an effort to explain the anisotropic behavior exhibited by our constructs. We would also like to note that although the optimization scheme did not take into account the axial stiffness of our graft, our research group has successfully implanted several optimized constructs interpositionally in rats at zero axial stretch and have thus far shown adequate axial stability and patency. Future studies should also study the interfaces and interactions between the different G:PCL and T:PCL layers, which could shed light on graft transluminal stability and potential for layer delamination. The consideration of both fiber orientation and the interactions between the layers of our graft will further drive the microstructure and mechanical properties of our grafts toward that of native tissue. One additional limitation to this study is the low resolution in creating the relatively low layer thicknesses that are required to match the number of elastin layers of a rat aorta, as thicknesses on the order of 5 μm are difficult to fabricate in a controlled manner with our current electrospinning setup. This may explain the overestimated compliance for hypocompliant grafts, which had the highest percentage relative error for the G:PCL and T:PCL materials (27.15±8.7% and 33.2±5.7%, respectively). Additionally, the predictive model used to fabricate the hypocompliant grafts used mechanical data of materials that exhibited low strain ranges due to the high synthetic polymer content. Finite element simulations may result in strains beyond what is captured by the mechanical data and may therefore be less accurate at predicting mechanical behavior. The accuracy of the predictive model is heavily dependent on the captured mechanical data and strain ranges of the characterization constructs. Therefore, it is important in future studies to conduct mechanical tests that capture a broader range of strains and characterize other different types of synthetic and biological polymers blends that would increase our capacity to simulate different strain and compliance ranges. The circumferential stress–strain data were limited by the arbitrary intraluminal pressure limit of 120 mmHg, which resulted in circumferential maximum stress values significantly smaller than that of the axial stresses. Future studies should expand the availability of circumferential stress data by pressurizing all constructs beyond 120 mmHg to reach circumferential stresses on the same order of magnitude as the axial stresses. Finally, additional studies are necessary to evaluate important mechanical and biological properties of our optimized grafts such as permeability, burst pressure, and cell and blood biocompatibility.
Our study is one of the first research efforts to use a computational/experimental optimization scheme to fabricate a multilayered biomimetic vascular graft using protein analog to elastin and collagen. We have demonstrated that these grafts can be designed to compliance match to a wide range of compliance values. In this study, we have replaced the use of glutaraldehyde with genipin in an effort to reduce cytotoxicity. Our laboratory group is currently investigating the biodegradability and biocompatibility of our materials using vascular SMCs. We are also evaluating the effect of the degradation of crosslinked proteins on the release profiles of growth factors, which could be loaded into the optimized grafts and influence the interaction of SMCs with the material. Furthermore, preliminary results have indicated that implanting optimized layered grafts into the abdominal aorta of rats have resulted in good patency. Overall, we have shown that we can tune the mechanical properties of our hybrid grafts by varying the ratio of protein to synthetic polymer using an optimization scheme that can be used to target a specific compliance value while considering geometry. These methods are a stepping-stone toward the design of a functional and clinically translatable tissue-engineered vascular graft.
Acknowledgment
This research was funded by the NIH, grant 1R56HL136517-01 to JPVG. Additional support for E.A. Tamimi was also provided by the National Institute of Biomedical Imaging and Bioengineering under award number EB003392. We would also like to acknowledge Scott Harrison for his important contributions to the optimization scheme used in this work.
Contributor Information
Ehab A. Tamimi, Department of Bioengineering, , University of Pittsburgh, , Pittsburgh, PA 15213 , e-mail: ehab.t@pitt.edu
Diana Catalina Ardila, Department of Bioengineering, , University of Pittsburgh, , Pittsburgh, PA 15213 , e-mail: cata.ardila28@pitt.edu.
Burt D. Ensley, Protein Genomics, Inc, , Sedona, AZ 86336 , e-mail: burt@burtensley.com
Robert S. Kellar, Center for Bioengineering Innovation, , Northern Arizona University, , Flagstaff, AZ 86011; , Department of Mechanical Engineering, , Northern Arizona University, , Flagstaff, AZ 86011; , Department of Biological Sciences, , Northern Arizona University, , Flagstaff, AZ 86011 , e-mail: robert.kellar@nau.edu
Jonathan P. Vande Geest, Mem. ASME , Department of Bioengineering, , University of Pittsburgh, , Pittsburgh, PA 15213; , McGowan Institute for Regenerative Medicine, , 300 Technology Drive, , Pittsburgh, PA 15219 , e-mail: jpv20@pitt.edu.
Funding Data
National Institute of Biomedical Imaging and Bioengineering (Grant No. EB003392; Funder ID: 10.13039/100000070).
National Institutes of Health (Grant No. 1R56HL136517-01; Funder ID: 10.13039/100000002).
References
- [1]. Benjamin, E. J. , Blaha, M. J. , Chiuve, S. E. , Cushman, M. , Das, S. R. , Deo, R. D. , Ferranti, S. D. , Floyd, J. , Fornage, M. , Gillespie, C. , Isasi, C. R. , Jiménez, M. C. , Jordan, L. C. , Judd, S. E. , Lackland, D. , Lichtman, J. H. , Lisabeth, L. , Liu, S. , Longenecker, C. T. , Mackey, R. H. , Matsushita, K. , Mozaffarian, D. , Mussolino, M. E. , Nasir, K. , Neumar, R. W. , Palaniappan, L. , Pandey, D. K. , Thiagarajan, R. R. , Reeves, M. J. , Ritchey, M. , Rodriguez, C. J. , Roth, G. A. , Rosamond, W. D. , Sasson, C. , Towfighi, A. , Tsao, C. W. , Turner, M. B. , Virani, S. S. , Voeks, J. H. , Willey, J. Z. , Wilkins, J. T. , Wu, J. H. , Alger, H. M. , Wong, S. S. , and Muntner, P. , 2017, “ Heart Disease and Stroke Statistics—2017 Update: A Report From the American Heart Association,” Circulation, 135(10), pp. e146–e603. 10.1161/CIR.0000000000000485 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2]. Ferrari, E. R. , and von Segesser, L. K. , 2006, “ Arterial Grafting for Myocardial Revascularization: How Better Is It?,” Curr. Opin. Cardiol., 21(6), pp. 584–588.https://www.ncbi.nlm.nih.gov/pubmed/17053408 [DOI] [PubMed] [Google Scholar]
- [3]. Goldman, S. , Zadina, K. , Moritz, T. , Ovitt, T. , Sethi, G. , Copeland, J. G. , Thottapurathu, L. , Krasnicka, B. , Ellis, N. , Anderson, R. J. , and Henderson, W. , 2004, “ Long-Term Patency of Saphenous Vein and Left Internal Mammary Artery Grafts After Coronary Artery Bypass Surgery: Results From a Department of Veterans Affairs Cooperative Study,” J. Am. Coll. Cardiol., 44(11), pp. 2149–2156. 10.1016/j.jacc.2004.08.064 [DOI] [PubMed] [Google Scholar]
- [4]. Hess, C. N. , Lopes, R. D. , Gibson, C. M. , Hager, R. , Wojdyla, D. M. , Englum, B. R. , Mack, M. , Califf, R. , Kouchoukos, N. T. , Peterson, E. D. , and Alexander, J. H. , 2014, “ Saphenous Vein Graft Failure After Coronary Artery Bypass Surgery: Insights From PREVENT IV,” Circulation, 130(17), pp, 1445–1451. 10.1161/CIRCULATIONAHA.113.008193 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5]. Kurobe, H. , Maxfield, M. W. , Breuer, C. K. , and Shinoka, T. , 2012, “ Concise Review: Tissue-Engineered Vascular Grafts for Cardiac Surgery: Past, Present, and Future,” Stem Cells Transl. Med., 1(7), pp. 566–571. 10.5966/sctm.2012-0044 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6]. Kannan, R. Y. , Salacinski, H. J. , Butler, P. E. , Hamilton, G. , and Seifalian, A. M. , 2005, “ Current Status of Prosthetic Bypass Grafts: A Review,” J. Biomed. Mater. Res., Part B, 74(1), pp. 570–581. 10.1002/jbm.b.30247 [DOI] [PubMed] [Google Scholar]
- [7]. Rocco, K. A. , Maxfield, M. W. , Best, C. A. , Dean, E. W. , and Breuer, C. K. , 2014, “ In Vivo Applications of Electrospun Tissue-Engineered Vascular Grafts: A Review,” Tissue Eng. Part B, 20(6), pp. 628–640. 10.1089/ten.teb.2014.0123 [DOI] [PubMed] [Google Scholar]
- [8]. Roll, S. , Müller-Nordhorn, J. , Keil, T. , Scholz, H. , Eidt, D. , Greiner, W. , and Willich, S. N. , 2008, “ Dacron® vs. PTFE as Bypass Materials in Peripheral Vascular Surgery—Systematic Review and Meta-Analysis,” BMC Surg., 8, p. 22. 10.1186/1471-2482-8-22 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9]. Spadaccio, C. , Nappi, F. , Al-Attar, N. , Sutherland, F. W. , Acar, C. , Nenna, A. , Trombetta, M. , Chello, M. , and Rainer, A. , 2016, “ Old Myths, New Concerns: The Long-Term Effects of Ascending Aorta Replacement With Dacron Grafts. Not All That Glitters Is Gold,” J. Cardiovasc. Transl. Res., 9(4), pp. 334–342. 10.1007/s12265-016-9699-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10]. Catto, V. , Farè, S. , Freddi, G. , and Tanzi, M. C. , 2014, “ Vascular Tissue Engineering: Recent Advances in Small Diameter Blood Vessel Regeneration,” ISRN Vasc. Med., 2014, p. 27. [Google Scholar]
- [11]. Nemeno-Guanzon, J. G. , Lee, S. , Berg, J. R. , Jo, Y. H. , Yeo, J. E. , Nam, B. M. , Koh, Y.-G. , and Lee, J. I. , 2012, “ Trends in Tissue Engineering for Blood Vessels,” J. Biomed. Biotechnol., 2012, p. 956345. 10.1155/2012/956345 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12]. Wang, X. , Lin, P. , Yao, Q. , and Chen, C. , 2007, “ Development of Small-Diameter Vascular Grafts,” World J. Surg., 31(4), pp. 682–689. 10.1007/s00268-006-0731-z [DOI] [PubMed] [Google Scholar]
- [13]. Wang, S. , Mo, X. M. , Jiang, B. J. , Gao, C. J. , Wang, H. S. , Zhuang, Y. G. , and Qiu, L. J. , 2013, “ Fabrication of Small-Diameter Vascular Scaffolds by Heparin-Bonded P(LLA-CL) Composite Nanofibers to Improve Graft Patency,” Int. J. Nanomed., 8, pp. 2131–2139. 10.2147/IJN.S44956 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14]. Hashi, C. K. , Derugin, N. , Janairo, R. R. R. , Lee, R. , Schultz, D. , Lotz, J. , and Li, S. , 2010, “ Anti-Thrombogenic Modification of Small-Diameter Microfibrous Vascular Grafts,” Arterioscler., Thromb., Vasc. Biol., 30(8), pp. 1621–1627. 10.1161/ATVBAHA.110.208348 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15]. Guo, H.-F. , Dai, W.-W. , Qian, D.-H. , Qin, Z.-X. , Lei, Y. , Hou, X.-Y. , and Wen, C. , 2017, “ A Simply Prepared Small-Diameter Artificial Blood Vessel That Promotes In Situ Endothelialization,” Acta Biomater., 54, pp. 107–116. 10.1016/j.actbio.2017.02.038 [DOI] [PubMed] [Google Scholar]
- [16]. Williams, S. K. , Kleinert, L. B. , and Patula-Steinbrenner, V. , 2011, “ Accelerated Neovascularization and Endothelialization of Vascular Grafts Promoted by Covalently-Bound Laminin Type 1,” J. Biomed. Mater. Res., Part A, 99(1), pp. 67–73. 10.1002/jbm.a.33138 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17]. Heath, D. E. , Kobe, C. , Jones, D. , Moldovan, N. I. , and Cooper, S. L. , 2013, “ In Vitro Endothelialization of Electrospun Terpolymer Scaffolds: Evaluation of Scaffold Type and Cell Source,” Tissue Eng. Part A, 19(1–2), pp. 79–90. 10.1089/ten.tea.2011.0655 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18]. Melchiorri, A. J. , Bracaglia, L. G. , Kimerer, L. K. , Hibino, N. , and Fisher, J. P. , 2016, “ In Vitro Endothelialization of Biodegradable Vascular Grafts Via Endothelial Progenitor Cell Seeding and Maturation in a Tubular Perfusion System Bioreactor,” Tissue Eng. Part C, 22(7), pp. 663–670. 10.1089/ten.tec.2015.0562 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19]. Rupnick, M. A. , Hubbard, F. A. , Pratt, K. , Jarrell, B. E. , and Williams, S. K. , 1989, “ Endothelialization of Vascular Prosthetic Surfaces After Seeding or Sodding With Human Microvascular Endothelial Cells,” J. Vasc. Surg., 9(6), pp. 788–795. 10.1016/0741-5214(89)90086-4 [DOI] [PubMed] [Google Scholar]
- [20]. Trubel, W. , Moritz, A. , Schima, H. , Raderer, F. , Scherer, R. , Ullrich, R. , Losert, U. , and Polterauer, P. , 1994, “ Compliance and Formation of Distal Anastomotic Intimal Hyperplasia in Dacron Mesh Tube Constricted Veins Used as Arterial Bypass Grafts,” ASAIO J., 40(3), pp. M273–M278. 10.1097/00002480-199407000-00007 [DOI] [PubMed] [Google Scholar]
- [21]. Trubel, W. , Schima, H. , Moritz, A. , Raderer, F. , Windisch, A. , Ullrich, R. , Windberger, U. , Losert, U. , and Polterauer, P. , 1995, “ Compliance Mismatch and Formation of Distal Anastomotic Intimal Hyperplasia in Externally Stiffened and Lumen-Adapted Venous Grafts,” Eur. J. Vasc. Endovascular Surg., 10(4), pp. 415–423. 10.1016/S1078-5884(05)80163-7 [DOI] [PubMed] [Google Scholar]
- [22]. Ballyk, P. D. , Walsh, C. , Butany, J. , and Ojha, M. , 1997, “ Compliance Mismatch May Promote Graft-Artery Intimal Hyperplasia by Altering Suture-Line Stresses,” J. Biomech., 31(3), pp. 229–237. 10.1016/S0197-3975(97)00111-5 [DOI] [PubMed] [Google Scholar]
- [23]. Xu, J. , and Shi, G.-P. , 2014, “ Vascular Wall Extracellular Matrix Proteins and Vascular Diseases,” Biochim. Biophys. Acta, 1842(11), pp. 2106–2119. 10.1016/j.bbadis.2014.07.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24]. Aydin, S. , Aydin, S. , Eren, M. N. , Sahin, İ. , Yilmaz, M. , Kalayci, M. , and Gungor, O. , 2013, “ The Cardiovascular System and the Biochemistry of Grafts Used in Heart Surgery,” SpringerPlus, 2(1), p. 612. 10.1186/2193-1801-2-612 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25]. Wagenseil, J. E. , and Mecham, R. P. , 2009, “ Vascular Extracellular Matrix and Arterial Mechanics,” Physiol. Rev., 89(3), pp. 957–989. 10.1152/physrev.00041.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26]. Xing, Q. , Qian, Z. , Tahtinen, M. , Yap, A. H. , Yates, K. , and Zhao, F. , 2017, “ Aligned Nanofibrous Cell-Derived Extracellular Matrix for Anisotropic Vascular Graft Construction,” Adv. Healthcare Mater., 6(10), (epub). 10.1002/adhm.201601333 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27]. Kim, S. H. , Turnbull, J. , and Guimond, S. , 2011, “ Extracellular Matrix and Cell Signalling: The Dynamic Cooperation of Integrin, Proteoglycan and Growth Factor Receptor,” J. Endocrinol., 209(2), pp. 139–151. 10.1530/JOE-10-0377 [DOI] [PubMed] [Google Scholar]
- [28]. Schultz, G. S. , and Wysocki, A. , 2009, “ Interactions Between Extracellular Matrix and Growth Factors in Wound Healing,” Wound Repair Regener., 17(2), pp. 153–162. 10.1111/j.1524-475X.2009.00466.x [DOI] [PubMed] [Google Scholar]
- [29]. Ma, H. , Hu, J. , and Ma, P. X. , 2010, “ Polymer Scaffolds for Small-Diameter Vascular Tissue Engineering,” Adv. Funct. Mater., 20(17), pp. 2833–2841. 10.1002/adfm.201000922 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30]. Nieponice, A. , Soletti, L. , Guan, J. , Hong, Y. , Gharaibeh, B. , Maul, T. M. , Huard, J. , Wagner, W. R. , and Vorp, D. A. , 2010, “ In Vivo Assessment of a Tissue-Engineered Vascular Graft Combining a Biodegradable Elastomeric Scaffold and Muscle-Derived Stem Cells in a Rat Model,” Tissue Eng. Part A, 16(4), pp. 1215–1223. 10.1089/ten.tea.2009.0427 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31]. Wang, W. , Hu, J. , He, C. , Nie, W. , Feng, W. , Qiu, K. , Zhou, X. , Gao, Y. , and Wang, G. , 2015, “ Heparinized PLLA/PLCL Nanofibrous Scaffold for Potential Engineering of Small-Diameter Blood Vessel: Tunable Elasticity and Anticoagulation Property,” J. Biomed. Mater. Res., Part A, 103(5), pp. 1784–1797. 10.1002/jbm.a.35315 [DOI] [PubMed] [Google Scholar]
- [32]. Jing, X. , Mi, H. Y. , Salick, M. R. , Cordie, T. M. , Peng, X. F. , and Turng, L. S. , 2015, “ Electrospinning Thermoplastic Polyurethane/Graphene Oxide Scaffolds for Small Diameter Vascular Graft Applications,” Mater. Sci. Eng., C, 49, pp. 40–50. 10.1016/j.msec.2014.12.060 [DOI] [PubMed] [Google Scholar]
- [33]. Tan, Z. , Wang, H. , Gao, X. , Liu, T. , and Tan, Y. , 2016, “ Composite Vascular Grafts With High Cell Infiltration by Co-Electrospinning,” Mater. Sci. Eng., C, 67, pp. 369–377. 10.1016/j.msec.2016.05.067 [DOI] [PubMed] [Google Scholar]
- [34]. Woods, I. , and Flanagan, T. C. , 2014, “ Electrospinning of Biomimetic Scaffolds for Tissue-Engineered Vascular Grafts: Threading The Path,” Expert Rev. Cardiovasc. Ther., 12(7), pp. 815–832. 10.1586/14779072.2014.925397 [DOI] [PubMed] [Google Scholar]
- [35]. Li, Z. , and Wang, C. , 2013, “ Effects of Working Parameters on Electrospinning,” One-Dimensional Nanostructures: Electrospinning Technique and Unique Nanofibers, Li Z., and Wang C., eds., Springer, Berlin, pp. 15–28. [Google Scholar]
- [36]. Hasan, A. , Memic, A. , Annabi, N. , Hossain, M. , Paul, A. , Dokmeci, M. R. , Dehghani, F. , and Khademhosseini, A. , 2014, “ Electrospun Scaffolds for Tissue Engineering of Vascular Grafts,” Acta Biomater., 10(1), pp. 11–25. 10.1016/j.actbio.2013.08.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37]. Yao, J. , Bastiaansen, C. , and Peijs, T. , 2014, “ High Strength and High Modulus Electrospun Nanofibers,” Fibers, 2(2), pp. 158–186. 10.3390/fib2020158 [DOI] [Google Scholar]
- [38]. Hong, Y. , Ye, S.-H. , Nieponice, A. , Soletti, L. , Vorp, D. A. , and Wagner, W. R. , 2009, “ A Small Diameter, Fibrous Vascular Conduit Generated From a Poly(Ester Urethane)Urea and Phospholipid Polymer Blend,” Biomaterials, 30(13), pp. 2457–2467. 10.1016/j.biomaterials.2009.01.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39]. Awad, N. K. , Niu, H. , Ali, U. , Morsi, Y. S. , and Lin, T. , 2018, “ Electrospun Fibrous Scaffolds for Small-Diameter Blood Vessels: A Review,” Membranes, 8(1), p. E15 10.3390/membranes8010015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40]. Punnakitikashem, P. , Truong, D. , Menon, J. U. , Nguyen, K. T. , and Hong, Y. , 2014, “ Electrospun Biodegradable Elastic Polyurethane Scaffolds With Dipyridamole Release for Small Diameter Vascular Grafts,” Acta Biomater., 10(11), pp. 4618–4628. 10.1016/j.actbio.2014.07.031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41]. Jha, B. S. , Ayres, C. E. , Bowman, J. R. , Telemeco, T. A. , Sell, S. A. , Bowlin, G. L. , and Simpson, D. G. , 2011, “ Electrospun Collagen: A Tissue Engineering Scaffold With Unique Functional Properties in a Wide Variety of Applications,” J. Nanomater., 2011, p. 15. 10.1155/2011/348268 [DOI] [Google Scholar]
- [42]. Matthews, J. A. , Wnek, G. E. , Simpson, D. G. , and Bowlin, G. L. , 2002, “ Electrospinning of Collagen Nanofibers,” Biomacromolecules, 3(2), pp. 232–238. 10.1021/bm015533u [DOI] [PubMed] [Google Scholar]
- [43]. Le Corre-Bordes, D. , Hofman, K. , and Hall, B. , 2018, “ Guide to Electrospinning Denatured Whole Chain Collagen From Hoki Fish Using Benign Solvents,” Int. J. Biol. Macromol., 112, pp. 1289–1299. 10.1016/j.ijbiomac.2018.02.088 [DOI] [PubMed] [Google Scholar]
- [44]. Buttafoco, L. , Kolkman, N. G. , Engbers-Buijtenhuijs, P. , Poot, A. A. , Dijkstra, P. J. , Vermes, I. , and Feijen, J. , 2006, “ Electrospinning of Collagen and Elastin for Tissue Engineering Applications,” Biomaterials, 27(5), pp. 724–734. 10.1016/j.biomaterials.2005.06.024 [DOI] [PubMed] [Google Scholar]
- [45]. Rnjak-Kovacina, J. , Wise, S. G. , Li, Z. , Maitz, P. K. M. , Young, C. J. , Wang, Y. , and Weiss, A. S. , 2012, “ Electrospun Synthetic Human Elastin:Collagen Composite Scaffolds for Dermal Tissue Engineering,” Acta Biomater., 8(10), pp. 3714–3722. 10.1016/j.actbio.2012.06.032 [DOI] [PubMed] [Google Scholar]
- [46]. Boland, E. D. , Matthews, J. A. , Pawlowski, K. J. , Simpson, D. G. , Wnek, G. E. , and Bowlin, G. L. , 2004, “ Electrospinning Collagen and Elastin: Preliminary Vascular Tissue Engineering,” Front Biosci., 9(2), pp. 1422–1432https://www.researchgate.net/publication/5242291_Electrospinning_collagen_and_elastin_Preliminary_vascular_tissue_engineering. [DOI] [PubMed] [Google Scholar]
- [47]. Boland, E. D. , Matthews, J. A. , Pawlowski, K. J. , Simpson, D. G. , Wnek, G. E. , and Bowlin, G. L. , 2004, “ Electrospinning Collagen and Elastin: Preliminary Vascular Tissue Engineering,” Front. Biosci., 9(1–3), pp. 1422–1432. 10.2741/1313 [DOI] [PubMed] [Google Scholar]
- [48]. Zeugolis, D. I. , Khew, S. T. , Yew, E. S. , Ekaputra, A. K. , Tong, Y. W. , Yung, L. Y. , Hutmacher, D. W. , Sheppard, C. , and Raghunath, M. , 2008, “ Electro-Spinning of Pure Collagen Nano-Fibres—Just an Expensive Way to Make Gelatin?,” Biomaterials, 29(15), pp. 2293–2305. 10.1016/j.biomaterials.2008.02.009 [DOI] [PubMed] [Google Scholar]
- [49]. Tamimi, E. , Ardila, D. C. , Haskett, D. G. , Doetschman, T. , Slepian, M. J. , Kellar, R. S. , and Vande Geest, J. P. , 2015, “ Biomechanical Comparison of Glutaraldehyde-Crosslinked Gelatin Fibrinogen Electrospun Scaffolds to Porcine Coronary Arteries,” ASME J. Biomech. Eng., 138(1), p. 011001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50]. Harrison, S. , Tamimi, E. , Uhlorn, J. , Leach, T. , and Vande Geest, J. P. , 2016, “ Computationally Optimizing the Compliance of a Biopolymer Based Tissue Engineered Vascular Graft,” ASME J. Biomech. Eng., 138(1), p. 014505. 10.1115/1.4032060 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51]. Wise, S. G. , Yeo, G. C. , Hiob, M. A. , Rnjak-Kovacina, J. , Kaplan, D. L. , Ng, M. K. C. , and Weiss, A. S. , 2014, “ Tropoelastin: A Versatile, Bioactive Assembly Module,” Acta Biomater., 10(4), pp. 1532–1541. 10.1016/j.actbio.2013.08.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52]. Senior, R. M. , Griffin, G. L. , and Mecham, R. P. , 1980, “ Chemotactic Activity of Elastin-Derived Peptides,” J. Clin. Invest., 66(4), pp. 859–862. 10.1172/JCI109926 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53]. Wise, S. G. , and Weiss, A. S. , 2009, “ Tropoelastin,” Int. J. Biochem. Cell Biol., 41(3), pp. 494–497. 10.1016/j.biocel.2008.03.017 [DOI] [PubMed] [Google Scholar]
- [54]. Indik, Z. , Abrams, W. R. , Kucich, U. , Gibson, C. W. , Mecham, R. P. , and Rosenbloom, J. , 1990, “ Production of Recombinant Human Tropoelastin: Characterization and Demonstration of Immunologic and Chemotactic Activity,” Arch. Biochem. Biophys., 280(1), pp. 80–86. 10.1016/0003-9861(90)90521-Y [DOI] [PubMed] [Google Scholar]
- [55]. Machula, H. , Ensley, B. , and Kellar, R. , 2014, “ Electrospun Tropoelastin for Delivery of Therapeutic Adipose-Derived Stem Cells to Full-Thickness Dermal Wounds,” Adv. Wound Care, 3(5), pp. 367–375. 10.1089/wound.2013.0513 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56]. McKenna, K. A. , Gregory, K. W. , Sarao, R. C. , Maslen, C. L. , Glanville, R. W. , and Hinds, M. T. , 2012, “ Structural and Cellular Characterization of Electrospun Recombinant Human Tropoelastin Biomaterials,” J. Biomater. Appl., 27(2), pp. 219–230. 10.1177/0885328211399480 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57]. McKenna, K. A. , Hinds, M. T. , Sarao, R. C. , Wu, P.-C. , Maslen, C. L. , Glanville, R. W. , Babcock, D. , and Gregory, K. W. , 2012, “ Mechanical Property Characterization of Electrospun Recombinant Human Tropoelastin for Vascular Graft Biomaterials,” Acta Biomater., 8(1), pp. 225–233. 10.1016/j.actbio.2011.08.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58]. Nivison-Smith, L. , Rnjak, J. , and Weiss, A. S. , 2010, “ Synthetic Human Elastin Microfibers: Stable Cross-Linked Tropoelastin and Cell Interactive Constructs for Tissue Engineering Applications,” Acta Biomater., 6(2), pp. 354–359. 10.1016/j.actbio.2009.08.011 [DOI] [PubMed] [Google Scholar]
- [59]. Sell, S. A. , Francis, M. P. , Garg, K. , McClure, M. J. , Simpson, D. G. , and Bowlin, G. L. , 2008, “ Cross-Linking Methods of Electrospun Fibrinogen Scaffolds for Tissue Engineering Applications,” Biomed. Mater., 3(4), p. 045001. 10.1088/1748-6041/3/4/045001 [DOI] [PubMed] [Google Scholar]
- [60]. Luo, X. , Guo, Z. , He, P. , Chen, T. , Li, L. , Ding, S. , and Li, H. , 2018, “ Study on Structure, Mechanical Property and Cell Cytocompatibility of Electrospun Collagen Nanofibers Crosslinked by Common Agents,” Int. J. Biol. Macromol., 113, pp. 476–486. 10.1016/j.ijbiomac.2018.01.179 [DOI] [PubMed] [Google Scholar]
- [61]. Gough, J. E. , Scotchford, C. A. , and Downes, S. , 2002, “ Cytotoxicity of Glutaraldehyde Crosslinked Collagen/Poly(Vinyl Alcohol) Films Is by the Mechanism of Apoptosis,” J. Biomed. Mater. Res., 61(1), pp. 121–130. 10.1002/jbm.10145 [DOI] [PubMed] [Google Scholar]
- [62]. Kim, K. M. , Herrera, G. A. , and Battarbee, H. D. , 1999, “ Role of Glutaraldehyde in Calcification of Porcine Aortic Valve Fibroblasts,” Am. J. Pathol., 154(3), pp. 843–852. 10.1016/S0002-9440(10)65331-X [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63]. Chanda, J. , Kondoh, K. , Ijima, K. , Matsukawa, M. , and Kuribayashi, R. , 1998, “ In Vitro and In Vivo Calcification of Vascular Bioprostheses,” Biomaterials, 19(18), pp. 1651–1656. 10.1016/S0142-9612(98)00038-6 [DOI] [PubMed] [Google Scholar]
- [64]. Golomb, G. , Schoen, F. J. , Smith, M. S. , Linden, J. , Dixon, M. , and Levy, R. J. , 1987, “ The Role of Glutaraldehyde-Induced Cross-Links in Calcification of Bovine Pericardium Used in Cardiac Valve Bioprostheses,” Am. J. Pathol., 127(1), pp. 122–130. [PMC free article] [PubMed] [Google Scholar]
- [65]. Lim, H. G. , Kim, S. H. , Choi, S. Y. , and Kim, Y. J. , 2012, “ Anticalcification Effects of Decellularization, Solvent, and Detoxification Treatment for Genipin and Glutaraldehyde Fixation of Bovine Pericardium,” Eur. J. Cardio-Thorac. Surg., 41(2), pp. 383–390. 10.1016/j.ejcts.2011.05.016 [DOI] [PubMed] [Google Scholar]
- [66]. Kawahara, J-I. , Ishikawa, K. , Uchimaru, T. , and Takaya, H. , 1997, “ Chemical Cross-Linking by Glutaraldehyde Between Amino Groups: Its Mechanism and Effects,” Polymer Modification, Swift G., Carraher C. E., and Bowman C. N., eds., Springer, Boston, MA, pp. 119–131. [Google Scholar]
- [67]. Sung, H.-W. , Huang, R.-N. , Huang, L. L. H. , Tsai, C.-C. , and Chiu, C.-T. , 1998, “ Feasibility Study of a Natural Crosslinking Reagent for Biological Tissue Fixation,” J. Biomed. Mater. Res., 42(4), pp. 560–567. [DOI] [PubMed] [Google Scholar]
- [68]. Chang, Y. , Tsai, C. C. , Liang, H. C. , and Sung, H. W. , 2001, “ Reconstruction of the Right Ventricular Outflow Tract With a Bovine Jugular Vein Graft Fixed With a Naturally Occurring Crosslinking Agent (Genipin) in a Canine Model,” J. Thorac. Cardiovasc. Surg., 122(6), pp. 1208–1218. 10.1067/mtc.2001.117624 [DOI] [PubMed] [Google Scholar]
- [69]. Sisson, K. , Zhang, C. , Farach-Carson, M. C. , Chase, D. B. , and Rabolt, J. F. , 2009, “ Evaluation of Cross-Linking Methods for Electrospun Gelatin on Cell Growth and Viability,” Biomacromolecules, 10(7), pp. 1675–1680. 10.1021/bm900036s [DOI] [PubMed] [Google Scholar]
- [70]. Balasubramanian, P. , Prabhakaran, M. P. , Kai, D. , and Ramakrishna, S. , 2013, “ Human Cardiomyocyte Interaction With Electrospun Fibrinogen/Gelatin Nanofibers for Myocardial Regeneration,” J. Biomater. Sci. Polym. Ed., 24(14), pp. 1660–1675. 10.1080/09205063.2013.789958 [DOI] [PubMed] [Google Scholar]
- [71]. Kumar, V. A. , Caves, J. M. , Haller, C. A. , Dai, E. , Liu, L. , Grainger, S. , and Chaikof, E. L. , 2013, “ Acellular Vascular Grafts Generated From Collagen and Elastin Analogs,” Acta Biomater., 9(9), pp. 8067–8074. 10.1016/j.actbio.2013.05.024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [72]. Wise, S. G. , Byrom, M. J. , Waterhouse, A. , Bannon, P. G. , Ng, M. K. C. , and Weiss, A. S. , 2011, “ A Multilayered Synthetic Human Elastin/Polycaprolactone Hybrid Vascular Graft With Tailored Mechanical Properties,” Acta Biomater., 7(1), pp. 295–303. 10.1016/j.actbio.2010.07.022 [DOI] [PubMed] [Google Scholar]
- [73]. Brown, J. H. , Das, P. , DiVito, M. D. , Ivancic, D. , Poh Tan, L. , and Wertheim, J. A. , 2018, “ Nanofibrous PLGA Electrospun Scaffolds Modified With Type I Collagen Influence Hepatocyte Function and Support Viability In Vivo,” Acta Biomater., 73, pp. 217–227. 10.1016/j.actbio.2018.02.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [74]. Yao, Q. , Zhang, W. , Hu, Y. , Chen, J. , Shao, C. , Fan, X. , and Fu, Y. , 2017, “ Electrospun Collagen/Poly(L-Lactic Acid-Co-Epsilon-Caprolactone) Scaffolds for Conjunctival Tissue Engineering,” Exp. Ther. Med., 14(5), pp. 4141–4147. 10.3892/etm.2017.5073 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [75]. Han, J. , Lazarovici, P. , Pomerantz, C. , Chen, X. , Wei, Y. , and Lelkes, P. I. , 2011, “ Co-Electrospun Blends of PLGA, Gelatin, and Elastin as Potential Nonthrombogenic Scaffolds for Vascular Tissue Engineering,” Biomacromolecules, 12(2), pp. 399–408. 10.1021/bm101149r [DOI] [PubMed] [Google Scholar]
- [76]. Zhang, Q. , Lv, S. , Lu, J. , Jiang, S. , and Lin, L. , 2015, “ Characterization of Polycaprolactone/Collagen Fibrous Scaffolds by Electrospinning and Their Bioactivity,” Int. J. Biol. Macromol., 76, pp. 94–101. 10.1016/j.ijbiomac.2015.01.063 [DOI] [PubMed] [Google Scholar]
- [77]. Hackett, J. M. , Dang, T. T. , Tsai, E. C. , and Cao, X. , 2010, “ Electrospun Biocomposite Polycaprolactone/Collagen Tubes as Scaffolds for Neural Stem Cell Differentiation,” Materials, 3(6), pp. 3714–3728. 10.3390/ma3063714 [DOI] [Google Scholar]
- [78]. Swindle-Reilly, K. E. , Paranjape, C. S. , and Miller, C. A. , 2014, “ Electrospun Poly(Caprolactone)-Elastin Scaffolds for Peripheral Nerve Regeneration,” Prog. Biomater., 3, p. 20. 10.1007/s40204-014-0020-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [79]. Annabi, N. , Fathi, A. , Mithieux, S. M. , Martens, P. , Weiss, A. S. , and Dehghani, F. , 2011, “ The Effect of Elastin on Chondrocyte Adhesion and Proliferation on Poly (ɛ-Caprolactone)/Elastin Composites,” Biomaterials, 32(6), pp. 1517–1525. 10.1016/j.biomaterials.2010.10.024 [DOI] [PubMed] [Google Scholar]
- [80]. Liu, Y. , Xu, Y. , Wang, Z. , Wen, D. , Zhang, W. , Schmull, S. , Li, H. , Chen, Y. , and Xue, S. , 2016, “ Electrospun Nanofibrous Sheets of Collagen/Elastin/Polycaprolactone Improve Cardiac Repair After Myocardial Infarction,” Am. J. Transl. Res., 8(4), pp. 1678–1694. [PMC free article] [PubMed] [Google Scholar]
- [81]. Yang, G. , Lin, H. , Rothrauff, B. B. , Yu, S. , and Tuan, R. S. , 2016, “ Multilayered Polycaprolactone/Gelatin Fiber-Hydrogel Composite for Tendon Tissue Engineering,” Acta Biomater., 35, pp. 68–76. 10.1016/j.actbio.2016.03.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [82]. Abbott, W. M. , Megerman, J. , Hasson, J. E. , L'Italien, G. , and Warnock, D. F. , 1987, “ Effect of Compliance Mismatch on Vascular Graft Patency,” J. Vasc. Surg., 5(2), pp. 376–382. 10.1016/0741-5214(87)90148-0 [DOI] [PubMed] [Google Scholar]
- [83]. Matsumoto, T. , Naiki, T. , and Hayashi, K. , 1992, “ Flow Visualization Analysis in a Model of Artery-Graft Anastomosis,” Bio-Med. Mater. Eng., 2(4), pp. 171–183. [PubMed] [Google Scholar]
- [84]. Stewart, S. F. C. , and Lyman, D. J. , 2004, “ Effects of an Artery/Vascular Graft Compliance Mismatch on Protein Transport: A Numerical Study,” Ann. Biomed. Eng., 32(7), pp. 991–1006. 10.1023/B:ABME.0000032462.56207.65 [DOI] [PubMed] [Google Scholar]
- [85]. Chandran, K. B. , Gao, D. , Han, G. , Baraniewski, H. , and Corson, J. D. , 1992, “ Finite-Element Analysis of Arterial Anastomoses With Vein, Dacron and PTFE Grafts,” Med. Biol. Eng. Comput., 30(4), pp. 413–418. 10.1007/BF02446179 [DOI] [PubMed] [Google Scholar]
- [86]. Rickard, R. F. , Meyer, C. , and Hudson, D. A. , 2009, “ Computational Modeling of Microarterial Anastomoses With Size Discrepancy (Small-to-Large),” J. Surg. Res., 153(1), pp. 1–11. 10.1016/j.jss.2008.02.038 [DOI] [PubMed] [Google Scholar]
- [87]. Haskett, D. , Speicher, E. , Fouts, M. , Larson, D. , Azhar, M. , Utzinger, U. , and Vande Geest, J. , 2012, “ The Effects of Angiotensin II on the Coupled Microstructural and Biomechanical Response of C57BL/6 Mouse Aorta,” J. Mech., 45(2), pp. 722–729. 10.1016/j.jbiomech.2011.11.017 [DOI] [PubMed] [Google Scholar]
- [88]. Haskett, D. , Azhar, M. , Utzinger, U. , and Vande Geest, J. , 2013, “ Progressive Alterations in Microstructural Organization and Biomechanical Response in the ApoE Mouse Model of Aneurysm,” Biomatter, 3(3), p. e24648. 10.4161/biom.24648 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [89]. Haskett, D. , Doyle, J. J. , Gard, C. , Chen, H. , Ball, C. , Estabrook, M. A. , Encinas, A. C. , Dietz, H. C. , Utzinger, U. , Vande Geest, J. P. , and Azhar, M. , 2012, “ Altered Tissue Behavior of Non-Aneurysmal Descending Thoracic Aorta in the Mouse Model of Marfan Syndrome,” Cell Tissue Res., 347(1), pp. 267–277. 10.1007/s00441-011-1270-y [DOI] [PubMed] [Google Scholar]
- [90]. Keyes, J. T. , Borowicz, S. M. , Rader, J. H. , Utzinger, U. , Azhar, M. , and Vande Geest, J. P. , “ Design and Demonstration of a Microbiaxial Optomechanical Device for Multiscale Characterization of Soft Biological Tissues With Two-Photon Microscopy,” Microsc. Microanal., 17(2), pp. 167–175. 10.1017/S1431927610094341 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [91]. Keyes, J. T. , Lockwood, D. R. , Utzinger, U. , Montilla, L. G. , Witte, R. S. , and Vande Geest, J. , 2013, “ Comparisons of Planar and Tubular Biaxial Tensile Testing Protocols of the Same Porcine Coronary Arteries,” Ann. Biomed. Eng., 41(7), pp. 1579–1591. 10.1007/s10439-012-0679-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [92]. Keyes, J. T. , Haskett, D. G. , Utzinger, U. , Azhar, M. , and Vande Geest, J. P. , 2011, “ Adaptation of a Two-Photon-Microscope-Interfacing Planar Biaxial Testing Device for the Microstructural and Macroscopic Characterization of Small Tubular Tissue Specimens,” ASME J. Biomech. Eng., 133(7), p. 075001. 10.1115/1.4004495 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [93]. Fung, Y. C. ,1982, Biomechanics Mechanical Properties of Living Tissues, Springer-Verlag, New York. [Google Scholar]
- [94]. Tai, N. R. , Salacinski, H. J. , Edwards, A. , Hamilton, G. , and Seifalian, A. M. , 2000, “ Compliance Properties of Conduits Used in Vascular Reconstruction,” Br. J. Surg., 87(11), pp. 1516–1524. 10.1046/j.1365-2168.2000.01566.x [DOI] [PubMed] [Google Scholar]
- [95]. Al-Jarrah, R. , 1984, “ On the Lagrange Interpolation Polynomials of Entire Functions,” J. Approximation Theory, 41(2), pp. 170–178. 10.1016/0021-9045(84)90110-2 [DOI] [Google Scholar]
- [96]. Huang, R. , Gao, X. , Wang, J. , Chen, H. , Tong, C. , Tan, Y. , and Tan, Z. , 2018, “ Triple-Layer Vascular Grafts Fabricated by Combined E-Jet 3D Printing and Electrospinning,” Ann. Biomed. Eng., 46(9), pp. 1254–1266. 10.1007/s10439-018-2065-z [DOI] [PubMed] [Google Scholar]
- [97]. Yu, E. , Mi, H. Y. , Zhang, J. , Thomson, J. A. , and Turng, L. S. , 2018, “ Development of Biomimetic Thermoplastic Polyurethane/Fibroin Small-Diameter Vascular Grafts Via a Novel Electrospinning Approach,” J Biomed Mater Res A., 106(4), pp. 985–996. 10.1002/jbm.a.36297 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [98]. Nezarati, R. M. , Eifert, M. B. , Dempsey, D. K. , and Cosgriff-Hernandez, E. , 2015, “ Electrospun Vascular Grafts With Improved Compliance Matching to Native Vessels,” J. Biomed. Mater. Res., Part B, 103(2), pp. 313–323. 10.1002/jbm.b.33201 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [99]. Salacinski, H. J. , Goldner, S. , Giudiceandrea, A. , Hamilton, G. , Seifalian, A. M. , Edwards, A. , and Carson, R. J. , 2001, “ The Mechanical Behavior of Vascular Grafts: A Review,” J. Biomater. Appl., 15(3), pp. 241–278. 10.1106/NA5T-J57A-JTDD-FD04 [DOI] [PubMed] [Google Scholar]
- [100]. Soletti, L. , Hong, Y. , Guan, J. , Stankus, J. J. , El-Kurdi, M. S. , Wagner, W. R. , and Vorp, D. A. , 2010, “ A Bilayered Elastomeric Scaffold for Tissue Engineering of Small Diameter Vascular Grafts,” Acta Biomater., 6(1), pp. 110–122. 10.1016/j.actbio.2009.06.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [101]. Soletti, L. , Nieponice, A. , Hong, Y. , Ye, S.-H. , Stankus, J. J. , Wagner, W. R. , and Vorp, D. A. , 2011, “ In Vivo Performance of a Phospholipid-Coated Bioerodable Elastomeric Graft for Small-Diameter Vascular Applications,” J. Biomed. Mater. Res., Part A, 96(2), pp. 436–448. 10.1002/jbm.a.32997 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [102]. Jankowska, M. A. , Bartkowiak-Jowsa, M. , and Bedzinski, R. , 2015, “ Experimental and Constitutive Modeling Approaches for a Study of Biomechanical Properties of Human Coronary Arteries,” J. Mech. Behav. Biomed. Mater., 50, pp. 1–12. 10.1016/j.jmbbm.2015.05.021 [DOI] [PubMed] [Google Scholar]
- [103]. Szafron, J. M. , Breuer, C. K. , Wang, Y. , and Humphrey, J. D. , 2017, “ Stress Analysis-Driven Design of Bilayered Scaffolds for Tissue-Engineered Vascular Grafts,” J. Biomech. Eng., 139(12), (epub). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [104]. Castillo-Cruz, O. , Pérez-Aranda, C. , Gamboa, F. , Cauich-Rodríguez, J. V. , Mantovani, D. , and Avilés, F. , 2018, “ Prediction of Circumferential Compliance and Burst Strength of Polymeric Vascular Grafts,” J. Mech. Behav. Biomed. Mater., 79, pp. 332–340. 10.1016/j.jmbbm.2017.12.031 [DOI] [PubMed] [Google Scholar]
- [105]. Qasim, S. B. , Najeeb, S. , Delaine-Smith, R. M. , Rawlinson, A. , and Ur Rehman, I. , 2017, “ Potential of Electrospun Chitosan Fibers as a Surface Layer in Functionally Graded GTR Membrane for Periodontal Regeneration,” Dental Mater., 33(1), pp. 71–83. 10.1016/j.dental.2016.10.003 [DOI] [PubMed] [Google Scholar]
- [106]. Gnavi, S. , Fornasari, B. E. , Tonda-Turo, C. , Laurano, R. , Zanetti, M. , Ciardelli, G. , and Geuna, S. , 2015, “ The Effect of Electrospun Gelatin Fibers Alignment on Schwann Cell and Axon Behavior and Organization in the Perspective of Artificial Nerve Design,” Int. J. Mol. Sci., 16(6), pp. 12925–12942. 10.3390/ijms160612925 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [107]. Ayres, C. , Bowlin, G. L. , Henderson, S. C. , Taylor, L. , Shultz, J. , Alexander, J. , Telemeco, T. A. , and Simpson, D. G. , 2006, “ Modulation of Anisotropy in Electrospun Tissue-Engineering Scaffolds: Analysis of Fiber Alignment by the Fast Fourier Transform,” Biomaterials, 27(32), pp. 5524–5534. 10.1016/j.biomaterials.2006.06.014 [DOI] [PMC free article] [PubMed] [Google Scholar]


