Abstract
Although tremor is the most common movement disorder, there are few noninvasive treatment options. Creating effective tremor suppression devices requires a knowledge of where tremor originates mechanically (which muscles) and how it propagates through the limb (to which degrees-of-freedom (DOF)). To simulate tremor propagation, we created a simple model of the upper limb, with tremorogenic activity in the 15 major superficial muscles as inputs and tremulous joint displacement in the seven major DOF as outputs. The model approximated the muscle excitation–contraction dynamics, musculoskeletal geometry, and mechanical impedance of the limb. From our simulations, we determined fundamental principles for tremor propagation: (1) The distribution of tremor depends strongly on musculoskeletal dynamics. (2) The spreading of tremor is due to inertial coupling (primarily) and musculoskeletal geometry (secondarily). (3) Tremorogenic activity in a given muscle causes significant tremor in only a small subset of DOF, though these affected DOF may be distant from the muscle. (4) Assuming uniform distribution of tremorogenic activity among muscles, tremor increases proximal-distally, and the contribution from muscles increases proximal-distally. (5) Although adding inertia (e.g., with weighted utensils) is often used to suppress tremor, it is possible to increase tremor by adding inertia to the wrong DOF. (6) Similarly, adding viscoelasticity to the wrong DOF can increase tremor. Based solely on the musculoskeletal system, these principles indicate that tremor treatments targeting muscles should focus first on the distal muscles, and devices targeting DOF should focus first on the distal DOF.
Keywords: tremor characterization, tremor distribution, degrees of freedom, biomechanics, physiological systems, essential tremor, Parkinson's disease
1. Introduction
Tremor, defined as “an involuntary, rhythmic, oscillatory movement of a body part” [1], is the most common movement disorder [2–4]. Essential tremor (ET) alone is estimated to affect 7 × 106 people in the U.S. [5,6]. Tremor most commonly manifests in the upper limb and makes activities of daily living (eating, clothing, writing, etc.) difficult or impossible [7,8].
Although tremor is widespread, current treatment options are unsatisfactory. A survey of ET patients found that only one in ten was satisfied with their medical care [9]. The two main treatment options for ET are medication and neurosurgery. The most common medications are only effective in 50% of patients, and in these patients, they are only 50% effective on average [10,11]; consequently, many ET patients stop taking their prescribed medications [12,13]. Surgical treatments such as deep brain stimulation (DBS) have proven more effective (about 90% tremor reduction [14]) and are effective for a higher percentage of patients [10,15]. However, they are highly invasive and usually reserved for patients with severe tremor. In addition, DBS can cause significant side effects [15–20] and lose effectiveness over time [21], requiring surgical revisions in more than 25% of cases [19,22,23]. For these and other reasons, less than 3% of patients with ET and Parkinson's Disease undergo DBS surgery [24].
A recent survey of ET patients found that one of the things most lacking in their treatment was an effective, alternative treatment option—something other than medication or surgery [9]. Peripheral tremor suppression devices could provide such an option. However, one of the obstacles to developing effective peripheral tremor suppression devices is that we do not currently know where to intervene (which muscles or degrees-of-freedom (DOF)) because we do not know where in the upper limb the tremor originates mechanically (which muscles), how it propagates (i.e., spreads) throughout the upper limb, and where it manifests the most (which DOF).
In a recent simulation study, we investigated a portion of this tremor propagation problem, focusing on propagation from tremorogenic joint torque to tremulous joint displacement [25]. Our multi-input-multi-output (MIMO) model included torque inputs in the seven main DOFs of the upper limb (excluding fingers), and displacement outputs in those same DOF. Approximating tremorogenic joint torque as a sinusoidal input, we used the model to establish the following fundamental principles describing how input parameters (torque location and frequency) and joint impedance (inertia, damping, and stiffness) affected tremor propagation: (1) Tremor amplitude is significantly affected by limb mechanics; because the DOFs are mechanically coupled, tremor in a given DOF depends not only on the amount of tremorogenic torque in that DOF but also on the amount of tremorogenic torque in other DOF—thus the limb mechanics cause tremor to propagate throughout the upper limb. (2) Tremor propagates mostly because of inertial coupling; although DOFs are also coupled by joint stiffness and damping, this coupling contributes little to how tremor propagates. (3) Tremor spreads narrowly, whereas tremorogenic torque in a DOF could cause tremulous displacement in many DOF, in reality it significantly affects only a small number of DOF (though the affected DOF may be far from the DOF with the tremorogenic torque). (4) Given equal amounts of input torque, the distal DOFs have the greatest tremor magnitude; the largest tremor was always found in one of the three distal DOFs (wrist flexion–extension (WFE), wrist radial-ulnar deviation (WRUD), or forearm pronation–supination (FPS)), even when the tremorogenic torque was in a proximal DOF. (5) Increasing inertia can decrease or increase tremor; although adding inertia (e.g., with weighted utensils) is often used to suppress tremor, it is possible to increase tremor by adding inertia to the wrong DOF. (6) Increasing viscoelasticity can decrease or increase tremor; similar to principle 5, it is possible to increase tremor by adding viscoelasticity to the wrong DOF.
These principles describe tremor propagation from tremorogenic joint torques to tremulous joint displacements. However, mechanically, tremor originates in muscles, not joints; tremorogenic muscle activity creates tremorogenic muscle force, which produces tremorogenic joint torque, which results in tremulous joint displacements. Thus, to more fully understand tremor in the upper limb, we need an expanded model of tremor propagation all the way from tremorogenic muscle activity to tremulous joint displacement. Such an expanded model would enable us to establish principles of tremor propagation all the way from the mechanical origin of tremor (muscle activity) to its end manifestation (tremulous joint displacement). Unlike the model from joint torque to joint displacement, in the expanded model, both inputs (muscle activity) and outputs (joint displacement) can be measured experimentally, allowing for future experimental validation of the principles of tremor propagation. Ultimately, such an expanded model could enable one to determine which muscles to target (e.g., through injection of Botulinum toxin type A [26,27] or electrical stimulation [28–31]) to suppress tremor in an optimal manner.
Here, we present an expanded MIMO model of tremor propagation all the way from neural inputs in the 15 main superficial muscles of the upper limb to displacement outputs in the seven main DOFs of the upper limb (excluding fingers). Using this model, we focused on the following questions: (1) To what extent do musculoskeletal dynamics affect tremor? (2) Which aspects of the system are most responsible for spreading the tremor? (3) Does tremor spread broadly from a given muscle to most DOF, or does it spread narrowly, affecting only a small subset of DOF? (4) To which DOF does the input (tremorogenic muscle activity) spread the most? With the answers to these questions, we revised the previously established principles to reflect tremor propagation all the way from muscle activity to joint displacement.
2. Methods
2.1. Model Structure.
As this is the first simulation of tremor propagation from muscle activity to joint displacement of which we are aware, we deliberately chose a simple model to capture first the most fundamental effects. This model consists of three submodels that successively transform muscle activity into muscle force, muscle force into joint torque, and joint torque into joint displacement (Fig. 1). As postural tremor consists of relatively small displacements about an equilibrium posture, we used a linear, time-invariant model.
Fig. 1.

Model of upper limb neuromusculoskeletal dynamics used to simulate tremor propagation. The excitation-contraction dynamics of muscle low-pass filters muscle activity into muscle force; the musculoskeletal geometry of the limb mixes force from various muscles into joint torques; and the mechanical impedance filters and mixes joint torques, resulting in joint displacement. and are time constants representing the dynamics of muscle excitation and contraction, respectively; is the gain between muscle activity and muscle force; is a matrix of moment arms; , , and are matrices representing the coupled joint inertia, damping, and stiffness, respectively.
The inputs to the model are the neural drives to the 15 major superficial muscles (Table 1) that actuate the seven main DOFs from the shoulder to the wrist. We focused on superficial muscles to allow future comparison of our simulations against measurements of surface electromyography (sEMG)—the effect of including only a portion of upper-limb muscles is explained in the Discussion. Although not the same as neural drive, sEMG measurements provide “a valid signal to represent the average motor unit activity of most superficial muscles” [32]. In this paper, we refer to both the input (neural drive to muscle) and sEMG loosely as “muscle activity.”
Table 1.
| # | Muscle | Abbrev. | Peak force (N) | Scaled peak force |
|---|---|---|---|---|
| 1 | Anterior deltoid | DELT1 | 1218.9 | 1.00 |
| 2 | Lateral deltoid | DELT2 | 1103.5 | 0.91 |
| 3 | Posterior deltoid | DELT3 | 201.6 | 0.17 |
| 4 | Pectoralis major | PECM2 | 658.3 | 0.54 |
| 5 | Long head biceps brachii | BIClong | 525.1 | 0.43 |
| 6 | Short head biceps brachii | BICshort | 316.8 | 0.26 |
| 7 | Long head of triceps brachii | TRIlong | 771.8 | 0.63 |
| 8 | Lateral head of triceps brachii | TRIlat | 717.5 | 0.59 |
| 9 | Brachialis | BRA | 1177.4 | 0.97 |
| 10 | Brachioradialis | BRD | 276 | 0.23 |
| 11 | Pronator teres | PT | 557.2 | 0.46 |
| 12 | Flexor carpi radialis | FCR | 407.9 | 0.33 |
| 13 | Flexor carpi ulnaris | FCU | 479.8 | 0.39 |
| 14 | Extensor carpi radials (brevis and longus together) | ECRB/ECRL | 589.8 | 0.48 |
| 15 | Extensor carpi ulnaris | ECU | 192.9 | 0.16 |
The first submodel, which represents the excitation–contraction coupling dynamics of muscle, transforms muscle activity into muscle force. The excitation–contraction coupling dynamics are approximated by a linear, second-order submodel that has been shown to provide a good prediction of the relationship between sEMG and muscle force [32] and has been used successfully to model the control of upper limb movements [33,34]. This submodel is defined by time constants representing the dynamics of muscle excitation () and contraction ()
where is the 15-element vector of activity in each of the 15 muscles, is the 15-element vector of force produced by each muscle, t1 and t2 are 15-by-15 diagonal matrices containing the muscle time constants, and C is the 15-by-15 diagonal gain matrix between and .
The middle submodel transforms muscle force into joint torques
where is the 7 × 15 matrix of moment arms (equal to the transpose of the Jacobian from muscle to joint space) and is the seven-element vector of joint torques in the major degrees-of-freedom from the shoulder to the wrist (positive directions listed first): 1—shoulder flexion–extension (SFE), 2—shoulder adduction–abduction (SAA), 3—shoulder internal–external rotation (SIER), 4—elbow flexion–extension (EFE), 5— FPS, 6—WFE, and 7— WRUD.
The third submodel transforms joint torques into joint displacements
where q is the seven-element vector of joint displacements corresponding to , and , , and are 7 × 7 matrices representing the coupled joint inertia, damping, and stiffness in these 7DOFs.
Thus, the entire model transforms the tremorogenic muscle activity in the 15 major superficial muscles from the shoulder to the wrist into tremulous joint displacement in the seven major DOFs actuated by those muscles. It expands the previous investigation of tremor propagation [25], which focused only on the propagation from joint torques to joint displacements (the third submodel).
2.2. Model Parameters.
We took great care to identify physiologically plausible model parameters, as described next. Nevertheless, since we performed an extensive sensitivity analysis (Secs. 2.7 and 3.3), the exact model parameter values are not critical to the conclusions drawn from the simulations.
2.2.1. Muscle Excitation–Contraction Dynamics.
The time constants representing the dynamics of excitation (t1) and contraction (t2) depend on the muscle, person, and experimental technique used to measure them [32]. Nevertheless, the two time constants are known to be close to each other and have been measured in both proximal and distal muscles of the upper limb (biceps, triceps, and dorsal interossei) to be on the order of 20–75 ms [32]. Following Ref. [34], we chose default values for t1 and t2 as 30 ms and 40 ms, respectively (same for all muscles). With these default values, this submodel acts as an overdamped low-pass filter (cut-off frequency 2.9 Hz) with impulse response (representing a muscle twitch) shown in Fig. 2(c).
Fig. 2.
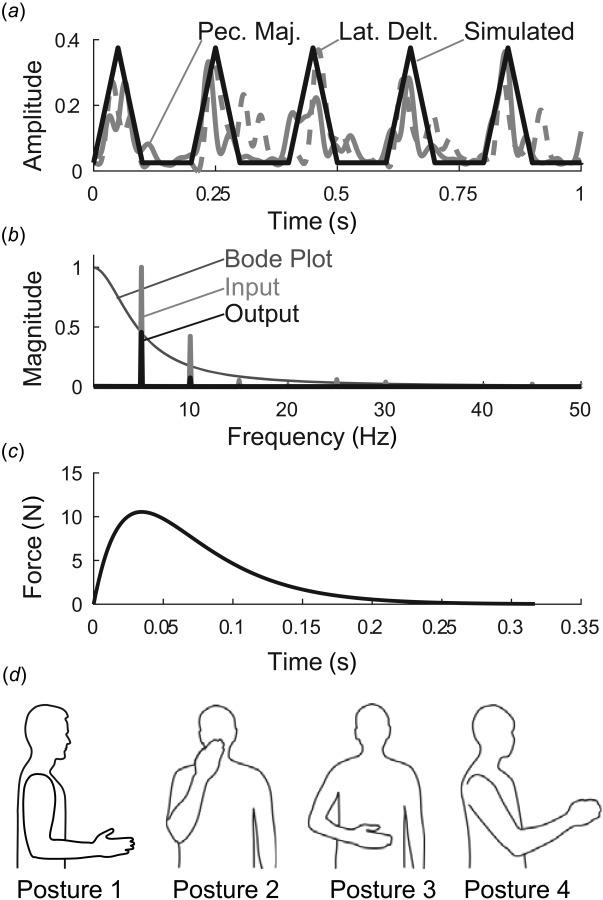
Methodological details. (a) input muscle activity was approximated by triangular waves, based on experimentally observed sEMG in tremor patients. Shown are detrended, rectified, and low-pass filtered sEMG signals from pectoralis major (solid gray) and lateral deltoid (dashed gray) muscles from a subject with severe tremor, compared to triangular waves (black), (b) Magnitude ratio of first submodel (excitation–contraction dynamics, with default values and ), along with the Fourier transforms of the input signal, (5 Hz triangle wave of width 110 ms), and the output, , (c) The dynamics of the first submodel (muscle excitation–contraction dynamics) are illustrated by the submodel's impulse response, which represents a muscle twitch (simulated using default values and ), (d) Postures included in our simulation. Posture 1 is the default posture. Postures 2–4 were used in the sensitivity analysis. Posture 2: hand in front of mouth, representing feeding and grooming activities; Posture 3: hand in workspace in front of abdomen, representing many activities of daily living; and Posture 4: arm somewhat outstretched, representing reaching. Joint angles for each posture are given in Ref. [25].
Matrix C represents the conversion from steady-state muscle activity to muscle force. In addition, it scales the input in each muscle according to the maximum force of that muscle (Table 1). Maximum force values were taken from Refs. [35–37]. Muscle 14 combines extensor carpi radialis brevis and longus (Table 1), so the peak force in muscle 14 was taken as the sum of the peak forces in each individual muscle.
Because t1, t2, and C are diagonal, this submodel does not propagate (i.e., mix or spread) tremor between muscles but simply transforms muscle activity into force within each muscle. Since the default values for t1 and t2 are the same for all muscles, but the diagonal values of C depend on the maximum force of each muscle, the impulse responses of different muscles are simply scaled versions of each other (and of the response shown in Fig. 2(c)).
2.2.2. Musculoskeletal Geometry.
The moment-arm matrix, M (Table 2), was determined from opensim [38] using a dynamic model of the upper limb “designed to represent the anthropometry and muscle force-generating characteristics of a 50th percentile adult male” [35]. For muscle 14, Extensor Carpi Radialis (brevis and longus together), we used the average of the moment arms for extensor carpi radialis longus and extensor carpi radialis brevis. The moment arms are configuration-dependent, so we calculated a different M for different postures; we first simulated tremor propagation with the upper limb in a default posture (posture 1 in Fig. 2(d)) but then repeated the simulations in three additional postures (postures 2–4 in Fig. 2(d)) in the sensitivity analysis (Secs. 2.7 and 3.3). Since postural tremor involves relatively small displacements from the reference posture, we left M constant in a given posture.
Table 2.
Default moment-arm matrix for posture 1 (in mm)
| DELT1 | DELT2 | DELT3 | PECM2 | BIClong | BICshort | TRIlong | TRIlat | BRA | BRD | PT | FCR | FCU | ECRB/ECRL | ECU | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SFE | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| SAA | −15.5* | 34.1* | 17.9* | −56.5* | 5.33† | −30.7* | −6.93 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| SIER | 5.08* | 1.88* | −8.58* | 9.61† | 5.84 | 4.19* | −4.88 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| EFE | 0 | 0 | 0 | 0 | 45.8† | 45.8† | −19.6† | −19.6† | 22.7† | 78.6† | 14.5† | 13.0† | 13.6† | 13.1† | −2.66† |
| FPS | 0 | 0 | 0 | 0 | −12.8† | −12.8† | 0 | 0 | 0 | 5.09† | 9.95† | 1.97† | 1.17† | −0.22‡ | −0.69† |
| WFE | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 14.9* | 14.9* | −11.5* | −6.30† |
| WRUD | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | −7.47* | 21.8* | −17.3* | 25.1* |
Note: Each element represents the moment arm of a given muscle (column) in a given DOF (row). Shaded values indicate the largest moment arm of a given muscle; only these values were retained for simulations without moment arm coupling. Using an arm model representing a 10th or 90th percentile male (by height) instead of the default model (50th percentile male) changed moment arms by different amounts; changes of 1–5%, 8–11%, and 23–36% are indicated by *, †, and ‡, respectively. Muscle abbreviations are given in Table 1. DOF abbreviations are defined as follows (positive direction listed first): SFE, SAA, and SIER represent SFE, adduction–abduction, and internal–external rotation, respectively; EFE and FPS represent EFE and forearm pronation–supination, respectively; and WFE and WRUD represent wrist flexion–extension and ulnar-radial deviation, respectively. Negative moment-arm values indicate resultant torques in the negative direction for that DOF. An explanation of the top row of zeros is given in the Appendix and discussed in the Limitations section of the Discussion.
Note that opensim follows the ISB convention for joint angles [39], which specifies a YXY Euler angle sequence [35] for the shoulder. Unfortunately, this sequence places the default posture in gimbal lock, so we used a ZXY angle sequence at the shoulder instead and transformed M from YXY to ZXY (see Appendix). Nevertheless, in the default posture (but not the other postures), the top row of the transformed is zero (see Table 2). This limitation is caused by the gimbal lock of the YXY angle sequence in the default posture (see detailed explanation in Appendix) and is discussed in the Limitations section of the Discussion.
2.2.3. Mechanical Impedance.
Matrices I, D, and K are 7 × 7 impedance matrices representing inertia, damping, and stiffness, respectively. The default values of I, D, and K were obtained from the literature [40–43] and are described in detail in Ref. [25]. Summarizing, I was calculated from the inertia values of individual limb segments for an average young adult male [43] using the robotics, vision and control toolbox in matlab [44]. As for M, we calculated the I matrix for each posture but left it constant in a given posture since tremulous displacements about that posture are relatively small. The default values for D and K represented average joint damping and stiffness of the passive limb (i.e., in the absence of muscle contraction), but we included in the sensitivity analysis simulations of active damping and stiffness as well. The diagonal elements of the impedance matrices represent the relationship between torque applied in a DOF and the resulting displacement in that DOF, whereas the off-diagonal elements represent mechanical coupling, i.e., the relationship between torque applied in a DOF and the resulting displacement in other DOF.
2.3. Input–Output Relationships.
Our full model has 15 inputs (muscle activity in each of the 15 muscles) and 7 outputs (displacement in each of the 7DOF). Since the model is linear, the relationship between each input and each output is fully described by the transfer function associated with that input and output. For our model, this means the response of the whole system can be described by a 7 × 15 matrix of transfer functions, derived as follows. In the Laplace domain, the three submodels can be expressed as , , and , where , , , and are the Laplace transforms of , , , and , respectively, and , , and . Variable is the Laplace variable and is the 15 × 15 identity matrix. Combining these submodels yields , where is the 7 × 15 matrix of transfer functions relating each input in to each output in . Therefore, the output in DOF due to an input in muscle is , where is the transfer function in row and column of . The total output in DOF is the linear combination of the inputs in all 15 muscles, the weights of the linear combination being the transfer functions associated with that DOF (row of ): .
2.4. Input.
The input, u, was based on past studies [45,46] and unpublished data from our lab. According to these sources, the envelope of (detrended and rectified) tremorogenic muscle activity can be approximated as a train of triangular pulses separated by periods of no activity (Fig. 2(a)). The duration between pulses is the period of the tremor and thus depends on the tremor frequency, but the mean width of the triangular pulses was 110–120 ms (range 70–160 ms) [46], which is within the 50–200 ms “EMG burst duration” range in Ref. [47] (see also Refs. [48] and [49]). We simulated tremor frequencies in the 4–12 Hz tremor band where tremor usually resides [1,4] and chose the default width of the triangular pulses to be 110 ms. That said, the sensitivity analysis revealed tremor propagation to be quite insensitive not only to the width of the triangular pulses but even to the shape of the pulses.
2.5. Output.
The response of a stable, linear system to a periodic input is composed of the transient response, which decays and disappears with time, and the steady-state response, which remains while the input is applied [50]. We used matlab functions impulse and stepinfo to characterize the transient response of the system (for all 105 transfer functions). Most of our investigation, however, focused on the steady-state response, which we analyzed as follows. The steady-state response of a linear system to a periodic input is characterized by the frequency response of the system at the frequencies of the input [25,50]. The input, approximated as a train of triangular pulses, contains power at the frequency at which the pulses repeat (i.e., the fundamental frequency of the tremor) and at higher harmonics. However, because the full model is a low-pass filter, the harmonics are strongly suppressed, resulting in an output that is practically indistinguishable from a pure sinusoid at the fundamental tremor frequency (Fig. 2(b)). Therefore, for practical purposes, the frequency response of the system is characterized by the frequency response of the system at the fundamental frequency; there is no need to include the frequency response at harmonic frequencies, allowing us to focus on the frequency response in the 4–12 Hz tremor band.
2.6. Simulation Protocol.
As mentioned in the introduction, in a previous study that focused only on the propagation from joint torque to joint displacement (the third submodel in Fig. 1), we established six principles of tremor propagation [25]. The main goal of the current study was to determine equivalent principles for the propagation of tremor from muscle activity to joint displacement (the full model in Fig. 1). To this end, we determined the extent to which the original principles (established for the third submodel) held true for the full model. More specifically, we investigated the following questions:
(1) To what extent do musculoskeletal dynamics affect tremor? Musculoskeletal dynamics have the potential to affect tremor in two ways by (1) shaping the input through low-pass filtering and (2) mixing the input into a variety of outputs. The first submodel low-pass filters muscle activity into force in the same muscle but does not mix between muscles; the second submodel does not filter but mixes force from multiple muscles into torque in a given DOF; and the third submodel both low-pass filters and mixes torque from multiple DOF into displacement in a given DOF. To investigate the amount of low-pass filtering and mixing in each input–output relationship, we used Matlab's bode function to calculate the magnitude ratio and phase shift of all 105 input–output relationships in the 4–12 Hz tremor band.
(2) Which aspects of the system are most responsible for spreading the tremor? As explained earlier, only the second and third submodels are capable of spreading tremor from a given muscle to multiple DOFs. In our previous investigation of spreading that focused only on the third submodel, we determined that most of the spreading was due to I, and that D and K contributed very little [25]. Therefore, we focused here on the relative contributions of M versus I in spreading tremor. To determine how much of the spreading came from M versus I, we compared the output from the default model to the output from two partially uncoupled models. In the first model, was altered so it transformed muscle force to joint torque in only 1DOF (the DOF with the largest moment arm), reducing to a “quasi-diagonal” matrix with only one nonzero value per column (Table 2). In the second model, I was diagonalized to remove all coupling terms. Comparing the difference between the outputs of the default model and each adjusted model allowed us to determine the contribution of M versus I.
(3) Does tremor spread broadly from a given muscle to most DOF, or does it spread narrowly, affecting only a small subset of DOF? To answer this question, we used phasor plots to compare the magnitudes of the outputs from a given muscle and determine if outputs in one or two DOF dominated over the outputs in the other DOF.
(4) To which DOF does the input (tremorogenic muscle activity) spread the most? Assuming equal input into all muscles (which, because of the matrix, results in equal proportion of the maximum force in each muscle), we compared the magnitude of the output tremor between DOFs.
The final two principles (listed as principles 5 and 6 in the introduction) address the effect of adding inertia and viscoelasticity to submodel 3. These principles are unchanged by the addition of submodels 1 and 2, so we did not re-investigate them in this study.
2.7. Sensitivity Analysis.
We performed a sensitivity analysis to evaluate the effect of inaccuracies in our model parameters and simulate differences between subjects. Our main goal was to assess if the principles of tremor propagation were robust to changes in input and model parameters. To this end, we varied the input, each of the model parameters (t1, t2, C, M, I, D, and K), and the posture of the limb and determined the sensitivity of the principles to these changes.
2.7.1. Input.
As mentioned earlier, we approximated tremorogenic muscle activity as a train of triangular pulses. In the sensitivity analysis, we varied the width of the triangular pulse from 50 to 200 ms. This range is the range of “EMG burst duration” measured in Ref. [47] and is larger than the range of triangular pulse widths (70–160 ms) observed in Ref. [46]. Furthermore, we assessed the effect of input shape by repeating our simulations with the following input shapes: a train of narrow (20 ms wide) rectangles to approximate impulses, a squared sine wave following [51], and the sum of two squared sine waves (the second wave having a frequency three times larger than the first) to determine the effect of power at multiple frequencies. For each shape, the fundamental frequency was varied throughout the tremor band.
2.7.2. Model Parameters.
Submodel 1: Time constants t1 and t2 represent the dynamics of muscle excitation and contraction, respectively. To simulate a generous range of variability between subjects, we halved and doubled the default values (30 and 40 ms), resulting in four simulations: with t1 at 15 and 30 ms (with t2 kept at 40 ms) and with t2 at 80 ms (with t1 at 15 and 30 ms). Varying the time constants over this range varied the low-pass filter cut-off frequency of submodel 1 between 1.8 and 3.5 Hz. As mentioned earlier, varying individual diagonal elements of simply scales the magnitude of the response in the DOF associated with that element.
Submodel 2: To test the effect of different moment-arm values, we repeated our simulations with a moment-arm matrix () of a 10th percentile male and of a 90th percentile male based on height (the moment-arm values in the opensim model were independent of subject weight). We obtained these moment-arm matrices by scaling the height of the opensim model to reflect a 10th percentile male and a 90th percentile male, using heights of 1671 and 1843 mm for the 10th and 90th percentile male, respectively [52]. We were unable to find published measurements of moment-arm values for the female upper limb.
Submodel 3: We previously performed a detailed analysis of the sensitivity of the tremor propagation principles on I, D, and K [25]. To summarize, we tested a large variety of physiologically plausible variations, including halving and doubling entire matrices (by factors from 0.5 to 2), scaling individual matrix elements, replacing elements initially set to zero (no coupling) to nonzero values (coupling), targeting the most sensitive matrix elements, and increasing stiffness and damping at different rates to mimic co-contraction. Because the sensitivity of the full model to the impedance matrices is the same as the sensitivity of the third submodel to these matrices,2 we did not repeat the sensitivity analysis of I, D, and K here but instead relied on the one performed in Ref. [25].
2.7.3. Postures.
Both the inertia matrix and the moment-arm matrix depend on the configuration of the upper limb (see Model Parameters). To determine if the principles were robust to changes in posture, we repeated our simulations in three additional postures (Fig. 2(d)): with the hand in front of the mouth, representing feeding and grooming activities (posture 2); with the hand in the workspace in front of the abdomen, representing many activities of daily living requiring fine manipulation (posture 3); and with the arm somewhat outstretched, representing reaching (posture 4). Joint angles for each posture are given in Ref. [25].
3. Results
3.1. Transient Response.
The full model transformed the muscle activity into muscle force, joint torque, and finally joint displacement (Fig. 3). Both the transient and steady-state responses are clearly observable in the output. Since the system acts as a low-pass filter, higher harmonics are attenuated, and the signal becomes progressively more sinusoidal as it passes from the input (train of triangular pulses) to the output, the steady-state portion of which is practically indistinguishable from a pure sinusoid.
Fig. 3.
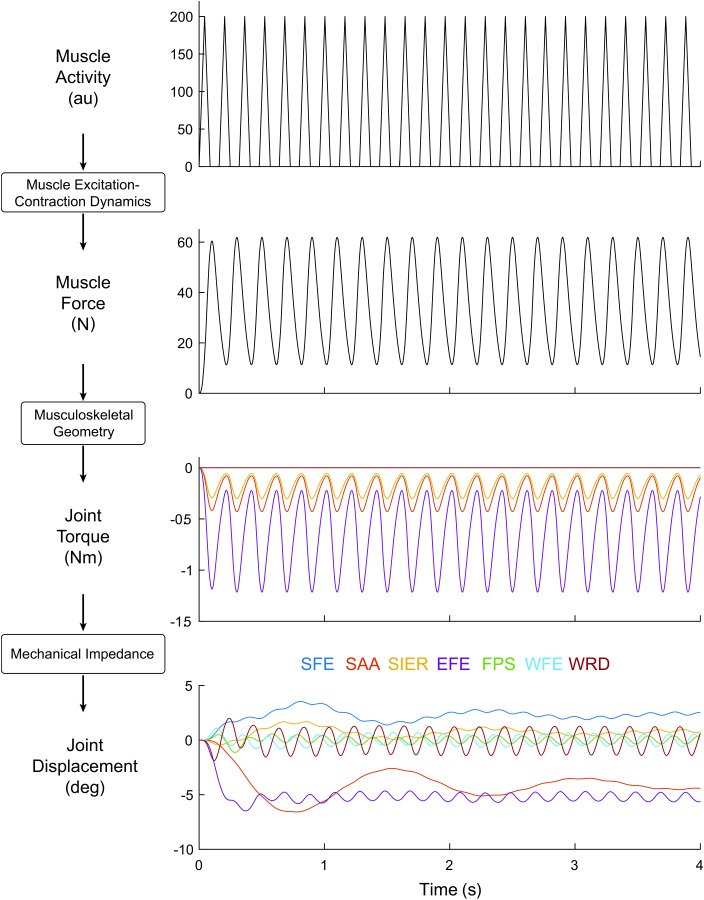
Progression through the model, from input in a single muscle (triceps longus; 5 Hz triangle wave with of width 110 ms) to muscle force in that same muscle, joint torque in the DOF crossed by that muscle, and joint displacement in all DOFs (DOF colors indicated at the bottom of the figure). Both the transient and steady-state responses are visible.
The transient responses of the 105 input–output relationships are characterized by their impulse responses (Fig. 4). There is considerable variation in the frequency and decay rate of the impulse responses. In particular, the settling times decrease proximal-distally, becoming smallest for responses from distal muscles to distal DOF (Fig. 5).
Fig. 4.
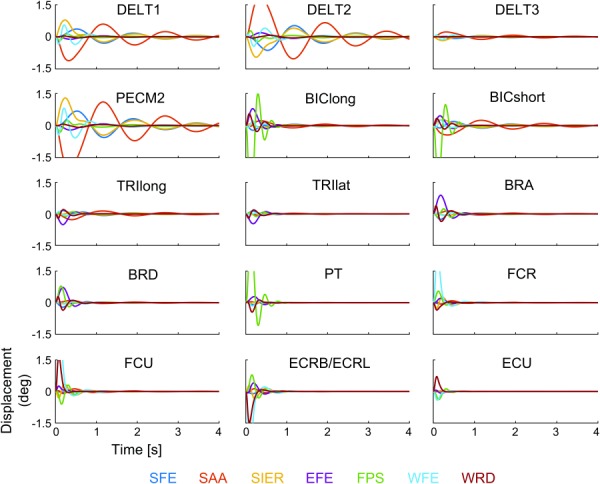
Impulse responses of all 105 input–output relationships, organized into subplots by input muscle (listed in each subplot) and color-coded by output DOF (color code listed below figure)
Fig. 5.
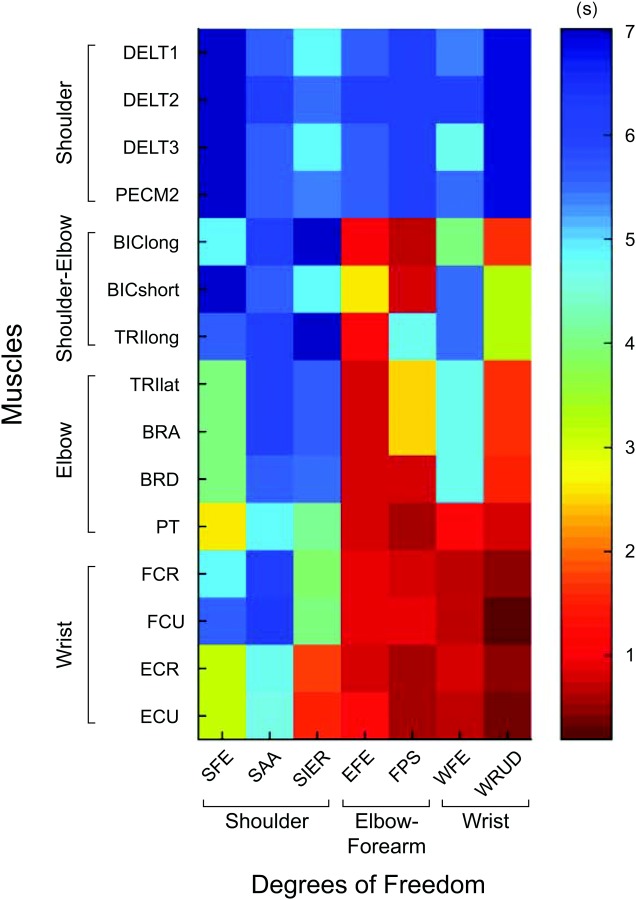
Settling times of the impulse responses of the 105 input–output relationships shown in Fig. 4, showing the trend that settling times decrease proximal-distally for both inputs (muscles) and outputs (DOF). The settling time was defined as the time required for the impulse response to remain within 2% of its steady-state value.
3.2. Steady-State Response.
The magnitude ratios exhibited resonance below the tremor band (resonance frequencies ranged from 0.02 to 3.2 Hz, mean 1.2 Hz; not shown), but the vast majority of magnitude ratio curves (about 95%) decreased within the tremor band (Fig. 6). Although individual magnitude ratios changed significantly in the tremor band, the order of the magnitude ratios (which DOF had the largest magnitude ratio, second-largest magnitude ratio, and so on) was mostly constant throughout the tremor band; the slopes of various magnitude ratio lines changed together, resulting in relatively few crossings, most of which were at the low end of the tremor band (4–6 Hz). Therefore, tremor propagation patterns (how tremor distributes from input in a given muscle to output in multiple DOF) were quite independent of tremor frequency. Importantly, all 15 muscles produced the greatest tremor in one of the three most distal DOFs (FPS, WFE, or WRD). This was true for the entire tremor band (Fig. 6). For most of the tremor band, most of the muscles produced the greatest tremor in WFE (7 or 6 muscles, depending on frequency), followed closely by RUD (5 or 6 muscles) and then FPS (3 muscles). To determine which muscles contribute most to tremor in a given DOF, we investigated the output tremor by DOF, plotting the contribution from each muscle as a phasor (Fig. 7). For most frequencies in the tremor band, the greatest contributor in DOFs 1–7 was BRA, PECM2, FCU, FCU, BIClong, FCU, and FCU, respectively. Thus, FCU was the greatest contributor to tremor in 4 of the 7DOFs.
Fig. 6.
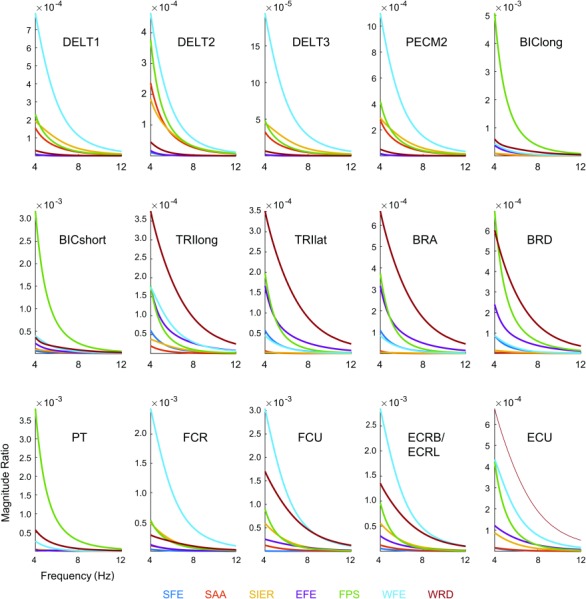
Magnitude ratios of all 105 input–output relationships in the tremor band (4–12 Hz), organized by input muscle (listed in each subplot) and color coded by output DOF (color code listed below figure). The units of the magnitude ratio are the units of the output displacement (rad) divided by the units of the input muscle activity (arbitrary units).
Fig. 7.
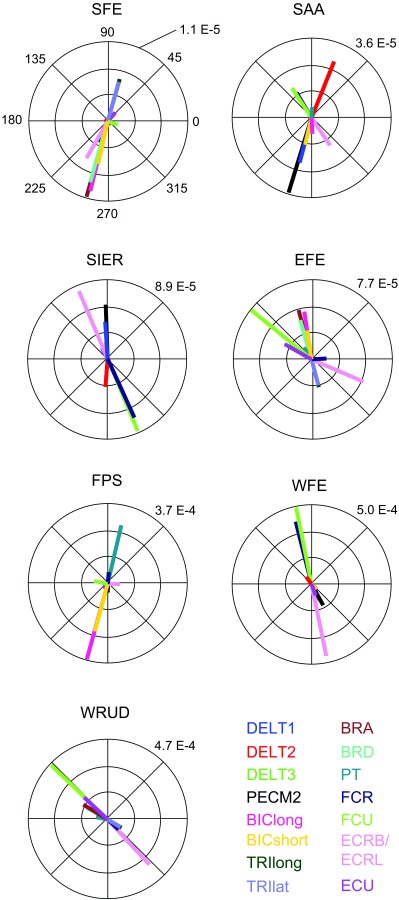
Phasor plot of the frequency response at 8 Hz (middle of the tremor band), grouped by output DOF (listed above each subplot) and color coded by input muscle. The numeric value on each subplot indicates the radius of the outer circle (in rad/a.u.; see caption of Fig. 6).
The pattern of spreading is summarized in Fig. 8, which illustrates that (assuming equal inputs in all muscles, which results in equal proportion of the maximum force in each muscle): (1) tremor increases proximal-distally and (2) the importance of muscles (to tremor) increases proximal-distally. In particular, most of the tremor appears in the three most distal DOFs (FPS, WFE, and WRUD), and most of this tremor comes from BIC and PT (FPS); FCR, FCU, and ECR (WFE); and FCU, ECR, and ECU (WRUD).
Fig. 8.
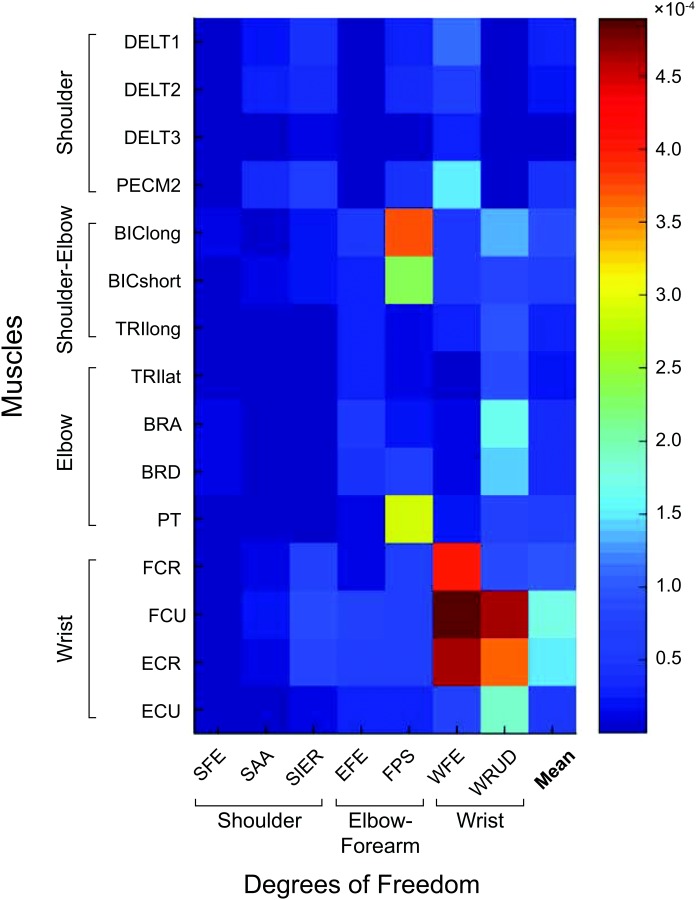
Magnitude ratios for all 105 input–output relationships at 8 Hz (middle of tremor band), showing that the distal DOFs exhibit the most tremor, and that most of this tremor comes from the distal muscles (and, for FPS, from the biceps muscles). This trend was largely consistent throughout the tremor band. The last column shows the mean magnitude ratio for each row. The units of the magnitude ratio are rad/a.u. (see caption of Fig. 6).
To determine how much of the spreading was due to the moment-arm matrix () versus inertia (), we compared the output from the model with default parameter values to a model in which only contributed to spreading ( was diagonalized to remove coupling terms) and a model in which only contributed to spreading ( was pseudo-diagonalized—see Methods). For the vast majority of input–output cases (about 80%), inertia contributed more to spreading than the moment-arm matrix (Fig. 9; by median, the difference between the full model and the model in which only M contributed to spreading was about 5× larger than the difference between the full model and the model in which only I contributed to spreading). This trend was observed throughout the tremor band.
Fig. 9.
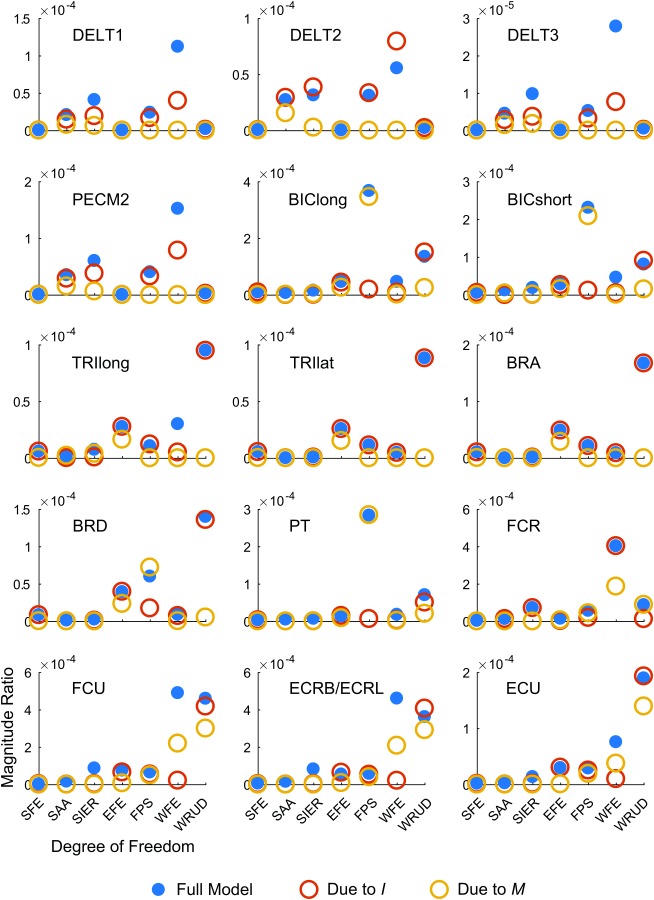
Coupling analysis. Each subplot shows the magnitude ratio at 8 Hz (middle of tremor band) for a given input muscle (listed in each subplot), listed by output DOF (horizontal axis) for the default model (solid blue circles), a model with coupling due to inertia but not moment arms (, empty red circles), and a model with coupling due to moment arms but not inertia (, empty yellow circles). For the majority of input–output cases, spreading due to inertia only (red) is more similar to the full model than spreading due to moment arms only (yellow), indicating that inertia spreads tremor more than musculoskeletal geometry (i.e., moment arms). The units of the magnitude ratio are rad/a.u. (see caption of Fig. 6).
3.3. Sensitivity Analysis.
As discussed earlier, we altered parameters within physiological ranges to explore the effects of inaccuracies and intersubject variability in our model parameters. The goal of the analysis was to determine the robustness of our findings.
3.3.1. Input.
The output displacement was quite insensitive to the width of the triangular pulses of the input, even over a large range of widths (50–200 ms); the output was essentially sinusoidal, independent of pulse width. Decreasing the pulse width increased the relative magnitude of the harmonics but, as mentioned earlier, the harmonics were greatly attenuated by the low-pass filtering properties of the model (Fig. 6). By comparison, the magnitude at the fundamental frequency, which was given by the frequency at which the pulses repeated, was relatively unaffected by low-pass filtering.
We also tested different input shapes (a train of narrow rectangular pulses representing impulses, a squared sine wave, and a squared sine wave with multiple frequencies) to test the effect of input shape on the results. The output displacement was found to be quite insensitive to the shape of the input; independent of input shape, the output resembled a pure sinusoid at the fundamental frequency of the input. The low-pass filtering properties of the model attenuated the higher frequency components that distinguish the shapes. Therefore, our conclusions were virtually unaffected by the shape of the input.
3.3.2. Model Parameters.
Submodel 1: Increasing the time constants of an overdamped low-pass filter decreases its cut-off frequency, decreasing the magnitude ratio in the tremor band. Therefore, halving and doubling the time constants (default 30 and 40 ms) simply increased and decreased the magnitude ratio, respectively (Fig. 10(a)). As mentioned earlier, scaling the value of C associated with a given muscle simply scaled the magnitude ratio of all outputs due to that muscle.
Fig. 10.
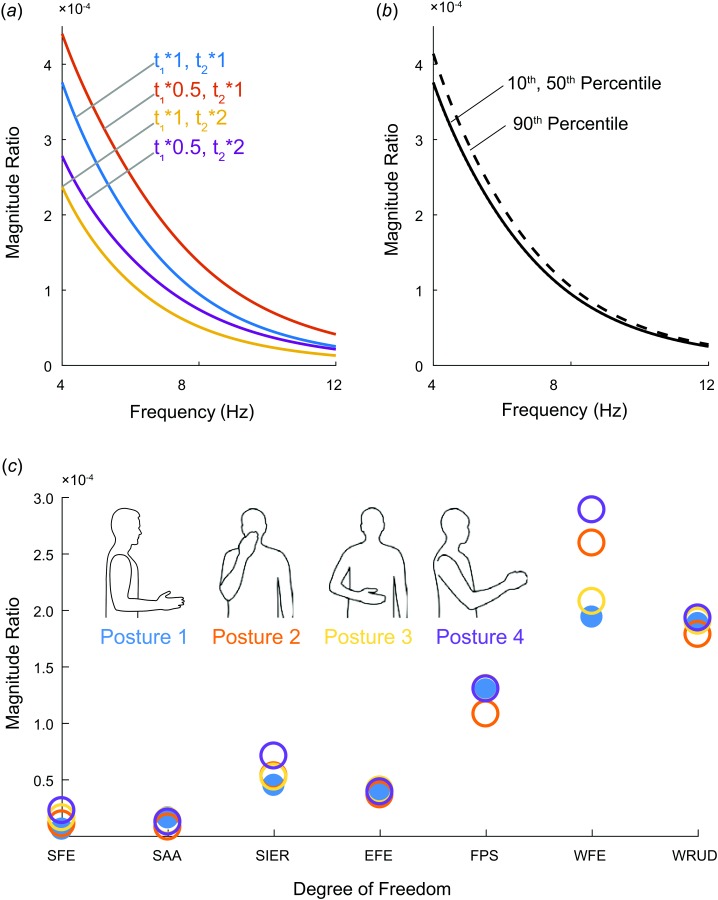
Results of sensitivity analysis: (a) Effect of varying muscle time constants t1 and t2, (b) effect of changing moment arms from default model (50th percentile male) to 10th or 90th percentile male. The line of the 10th percentile male is nearly indistinguishable from the 50th percentile male. (c) Changes to total summed magnitude ratio at 8 Hz for each DOF for different postures. The units of the magnitude ratio are rad/a.u. (see caption of Fig. 6).
Submodel 2: Changing the opensim model from 50th percentile male (default) to 10th and 90th percentile male did not have a large effect on the values of the moment-arm matrix, M (Table 2). As expected, default values that were zero did not change, and the vast majority of the other default values decreased for the 10th percentile male and increased for the 90th percentile male. Nevertheless, the effect on the magnitude ratio was small (Fig. 10(b)).
Submodel 3: In a previous sensitivity analysis of the impedance matrices, we found that although physiologically reasonable variations in these matrices can have a significant effect on individual magnitude ratios, “the pattern of propagation remains relatively unchanged” [25]. In summary, Davidson and Charles found the following: increasing D was the only change that always decreased tremor magnitude, increasing stiffness and damping with no change in the damping ratio (similar to co-contraction) usually decreased tremor, and increasing I can decrease or increase tremor [25]. Most importantly, changing the matrices (either by scaling the whole matrix or by scaling individual elements) did not significantly change the patterns of propagation.
3.3.3. Postures.
To determine the effect of changing the posture of the upper limb, we compared the summed magnitude ratios in four different postures (see Methods). Changing the posture only changed the I and M matrices, and the effect on the summed magnitude ratios was not large (Fig. 10). The most noticeable change occurred in WFE, but the relative magnitudes of tremor in the DOF remained the same; throughout the tremor band, the three most distal DOFs still had the greatest tremor amplitude. The magnitude ratios of different postures (results not shown) revealed the same trends in terms of tremor spreading to the DOF. For the most part (13 of the 15 muscles), a single dominant magnitude ratio was present through the tremor band. The only exception was posture 4 (the most out-stretched position—see Fig. 2(d)), which had significant magnitude ratios in two or more DOFs in approximately half of the muscles, though only in the 10–12 Hz range.
4. Discussion
4.1. Fundamental Principles.
The goal of this work was to identify principles governing the propagation of tremor from muscle activity to joint displacement. To this end, we (1) determined the extent to which the original tremor propagation principles [25] established for propagation from joint torque to joint displacement (submodel 3 in Fig. 1) held true for propagation from muscle activity to joint displacement (full model in Fig. 1), and (2) modified the original principles where necessary to reflect propagation from muscle activity to joint displacement. Thus, the following revised principles govern simulated tremor propagation from muscle activity to joint displacement:
Principle 1: The distribution of tremor depends strongly on musculoskeletal dynamics. In other words, which DOF has the greatest tremor (output) depends not only on which muscle has the most tremorogenic activity (input) but also on how the musculoskeletal system transforms the input into the output (the dynamics of the system). This transformation from tremorogenic muscle activity in multiple muscles to tremulous joint displacement in multiple DOF should be viewed as a multi-input/multi-output process that is not dynamically transparent (i.e., the system does not simply pass inputs straight through to outputs). Rather, the system both low-pass filters and mixes the inputs. More specifically, the muscle excitation–contraction dynamics (submodel 1) filter, the musculoskeletal geometry (submodel 2) mixes, and the mechanical impedance (submodel 3) filters and mixes.
Principle 2: The spreading of tremor is due to inertial coupling (primarily) and musculoskeletal geometry (secondarily). By comparison, coupling due to joint damping and stiffness played a smaller role [25], and muscle excitation–contraction dynamics played no role. Note that the spreading resulting from inertial coupling not only exceeded the spreading due to musculoskeletal geometry, but was also farther-reaching. To clarify, the moment-arm matrix is only capable of spreading tremor from a given muscle to the DOF the muscle crosses, limiting the extent to which the moment-arm matrix can spread tremor (e.g., proximal muscles cannot spread to distal DOF, or vice versa). In contrast, the inertia matrix can spread distantly, from torque in proximal DOF to displacement in distal DOF, and vice versa.
Principle 3: Tremor spreads narrowly. Tremorogenic activity in a muscle does not spread significantly to many DOF; instead, most of the tremor caused by a muscle occurs in a small number of DOF. According to our simulations, the frequency response of most muscles was dominated by a single DOF or two DOFs (Fig. 6). Averaged across the tremor band, the largest magnitude ratio was approximately three times larger than the second-largest ratio. In muscles with two dominant magnitude ratios, these two ratios were approximately three times larger than the third-largest ratio. Note that narrow spreading does not imply local spreading; the dominant magnitude ratio was frequently in a DOF that was far from the muscle (e.g., from deltoid muscles to WFE, see Fig. 6).
Principle 4: Assuming uniform distribution of tremorogenic activity among upper-limb muscles (i.e., an equal proportion of the maximum force in each muscle), tremor increases proximal-distally, and the contribution from muscles increases proximal-distally. In other words, unless proximal muscles receive significantly more tremorogenic muscle activity than distal muscles, most of the tremor will occur in distal DOF, and most of this tremor will come from distal muscles (Fig. 8). The proximal-distal increase in tremor was remarkably consistent: throughout the entire tremor band, all 15 muscles produced the greatest tremor in one of the three most distal DOFs. This increase was not due to muscle excitation–contraction dynamics: muscle time constants were assumed equal for all muscles, and peak force (represented in the gain matrix ) roughly decreases from proximal to distal (Table 1), which would produce the opposite effect. Nor does the proximal-distal increase in tremor come from musculoskeletal geometry, which lacks any clear proximal-distal trend in moment arms (Table 2). Instead, the proximal-distal increase in tremor is “caused by proximal–distal differences in impedance. Going from proximal to distal, inertia decreases more rapidly than stiffness… This creates a proximal–distal increase in the natural frequency, which pushes the resonance band to higher frequencies, elevating the magnitude ratios in the tremor band” [25].
The original tremor propagation principles [25] included two additional principles that depend only on submodel 3. These principles are unchanged by the addition of submodels 1 and 2 (see Sec. 2.7.2), and we repeat them here for completeness: Increasing inertia can decrease or increase tremor (principle 5) and increasing viscoelasticity can decrease or increase tremor (principle 6).
4.2. Robustness of Principles.
Here, we discuss the results of the sensitivity analyses in the context of the fundamental principles. Generally, the principles were quite robust to changes to the input, model parameters, and posture within physiologically plausible ranges.
4.2.1. Input.
Because the full system is a low-pass filter with low cut-off frequency (Fig. 6), harmonics are strongly attenuated, and the final output of the system is almost identical to a pure sine at the fundamental frequency of the input pulse train, no matter the shape of the pulses. The fundamental frequency of the input pulse train lies in the 4–12 Hz tremor band. Consequently, the steady-state output of the system is fully characterized (except for a scaling factor) by the frequency response of the system in the tremor band. Since the magnitude of the input to individual muscles is unknown (and likely varies by subject), we formulated the tremor propagation principles in terms of the magnitude ratio (output divided by input), which in a linear model is independent of the magnitude of the input. Therefore, with the exception of principle 4, for which we assumed uniform distribution of tremorogenic activity among muscles (see limitations), the tremor propagation principles are robust to changes in the shape or magnitude of the tremorogenic muscle activity.
In addition to tremorogenic activity, real muscle activity would likely also include significant voluntary activity, for example, to oppose gravity or stabilize a joint through co-contraction. Such voluntary muscle activation is known to fall below the tremor band. In a linear model such as the one used here, inputs at a given frequency produce outputs at the same frequency. Therefore, voluntary muscle activity creates joint displacement below the tremor band and does not directly affect tremor propagation. Furthermore, increased muscle activity is known to increase joint viscoelasticity, which could theoretically affect propagation patterns secondarily, but tremor propagation was shown to be relatively insensitive to changes in viscoelasticity (principle 2). In summary, the tremor propagation principles are robust to muscle activity outside of the tremor band.
4.2.2. Model Parameters.
As mentioned earlier, submodel 1 (representing muscle excitation–contraction dynamics) low-pass filters the input but does not mix inputs. The cut-off frequency of submodel 1 is given by the muscle time constants. In the model with default parameters, the cut-off frequency was below the tremor band (around 3 Hz). Although the principles are based on the fact that the harmonics are filtered out (see above), the exact value of the cut-off frequency is not important for two reasons: (1) as long as the cut-off frequency is below the frequency of the first harmonic (8–24 Hz, depending on the fundamental frequency), the harmonics are attenuated relative to the fundamental frequency, and (2) since submodel 3 also low-pass filters with a low cut-off frequency (range of 1–6 Hz, mean 3 Hz), the harmonics would be attenuated even if the cut-off frequency of submodel 1 were much higher.
Likewise, the exact values of the gain matrix (representing peak force in each muscle) were not critical to the principles. Scaling uniformly has no impact whatsoever on the principles. Scaling nonuniformly would change the contribution of each muscle to the total output (essentially scaling all phasors of the same color in Fig. 7 by the same amount), but the principles are quite robust to physiologically reasonable scaling; Principle 1 is not directly influenced by , and although it may be possible to construct a that would invalidate principle 2, it would require just the right set of values in , which would be highly unlikely. No scaling of will invalidate principle 3 because the outputs of a given muscle are always scaled the same.
The first part of principle 4 (tremor increases proximal-distally) is somewhat robust to nonuniform scaling. Some muscles have a proximal DOF in their top three DOFs, and increasing the values of for these muscles (and not the others) will increase tremor in the proximal DOF relative to the distal DOF. For example, if the peak forces of muscles 1–4 were scaled by a factor of 10, one of the proximal DOFs would enter the top three. However, for every muscle, the top DOF is a distal one, so the most tremor will always be in a distal DOF, no matter what values are used for . The second part of principle 4 (the contribution from muscles increases proximal-distally) does depend on . Increasing the proximal values of would increase the contribution of the proximal muscles to tremor. However, one would have to increase the proximal values of by approximately 2× before the proximal muscles would provide the same contribution to tremor as the distal muscles.3
Changing the moment-arm matrix over a large range (10th–90th percentile male) did not affect the principles. No moment-arm values that were zero became nonzero, or vice versa, so basic coupling patterns remained unchanged. In addition, the observed change in moment-arm values was only on the order of 10% and scaled more or less in unison. Consequently, tremor propagation patterns were minimally affected, including which DOF exhibited the greatest tremor: the three distal DOFs dominated throughout the tremor band in all three models (10th, 50th, and 90th percentile).
As discussed earlier, Davidson and Charles thoroughly explored the effects of changing the I, D, and K matrices [25]. In summary, they found that the principles were quite insensitive to physiologically reasonable changes in the impedance matrices; although changes sometimes produced large changes in the frequency response of the system, the pattern of propagation remained relatively unchanged (see Ref. [25] for details).
4.2.3. Postures.
Changing posture did not have a large effect on the magnitude ratio (Fig. 10), so it is clear that principle 1 was unaffected. Repeating the analysis shown in Fig. 9 for the three additional postures (results not shown) confirmed that principle 2 was not affected by changes in posture. Principle 3 was robust to posture changes in most cases: averaged across all postures, 13 of the 15 muscles exhibited a single dominant magnitude ratio. If a muscle had a second magnitude ratio similar to the largest one, the others were comparatively small. Finally, the three distal DOFs dominated throughout the tremor band (principle 4) in all four postures.
4.2.4. Gravity.
Although gravity likely affects the amount of tremorogenic activity in various muscles, we do not expect it to significantly affect tremor propagation. In fact, in a linear time-invariant system such as the one presented in this paper, gravity has no direct effect on tremor propagation. To clarify, because postural tremor usually consists of relatively small displacements around an equilibrium position, gravitational torque can be approximated as constant. In a linear system, a constant input torque simply adds a constant output displacement, which has no effect on tremulous (i.e., nonconstant) displacement.
Opposing gravity clearly requires increased voluntary muscle activity and may elicit increased tremorogenic muscle activity (as evidenced by the difference between rest and postural tremor in ET), but this reflects a change in the input, not the system. Furthermore, increases in torque such as those required to hold the arm against gravity are known to increase joint viscoelasticity, which is a system property and could therefore theoretically alter propagation patterns, but these patterns were shown to be relatively insensitive to changes in viscoelasticity (principle 2).
4.2.5. Phase.
Since tremor from different muscles can add constructively or destructively, the total tremor in a DOF depends on the relative phases of the tremor from different muscles. For example, it is theoretically possible that the phasors in WFE could cancel each other out, resulting in little total tremor even though the individual tremor components are large. Unfortunately, our knowledge of the phase shift between outputs is limited. To clarify, the phases of the outputs are the sum of (1) the phase shifts between inputs and outputs induced by the system and (2) the phases of the inputs. We will briefly discuss each in turn.
Using the model, we estimated the phase shifts induced by the system and found that, because antagonist muscles often had moment-arm values of similar magnitude but opposite sign, the phase shifts induced in antagonist muscles were usually close to 180 deg out of phase (Fig. 7). Thus, if the inputs to antagonist muscles were in phase with each other, the outputs would add destructively, potentially leading to very little total tremor despite large contributions from individual muscles. However, even in this case, vector summing (not shown) confirmed that the greatest tremor still occurred in one of the three distal DOFs (principle 4).
The phases of the inputs are the sum of the phase shifts due to transmission delay (between the spinal cord and the neuromuscular junction) and the phase of the signal exiting the spinal cord. A conservative estimate indicated that the relative phase shift induced by differences in transmission delay (e.g., between a proximal muscle and a distal muscle) could be up to approximately 30 deg. Rotating distal phasors by 30 deg relative to proximal phasors are not enough to change the sum from constructive to destructive (or even to orthogonal), and therefore, not enough to drastically alter the total tremor. Furthermore, only phasors from muscles that are significantly removed from each other may have significant transmission delay relative to each other, but the output in most DOFs was dominated by phasors from muscles located close to each other (Fig. 7); for these reasons, we expect the effect of phase shift due to transmission delay to be negligible. In contrast, the phase shift between tremorogenic signals exiting the spinal cord is almost completely unknown, even for antagonist muscles [53].
Because the phase shift between tremorogenic signals leaving the spinal cord is virtually unknown, the phase shift between outputs is unknown even though much is known about the phase shift induced by the system and the phase shift due to differences in transmission delay. Consequently, although it is possible to simulate the magnitude of individual tremor components, it is not currently possible to predict the total tremor in a DOF. Therefore, we based our conclusions (including the principles of tremor propagation) on the magnitudes of individual tremor components in each DOF and not on the total magnitude.
4.3. Limitations
4.3.1. Linear Time-Invariant Model of Steady-State Effects.
As this is the first investigation of tremor propagation from muscle activity to joint displacement throughout the upper limb, we deliberately used a simple (linear, time-invariant) model to focus on first-order, steady-state effects. Consequently, our results largely ignored transient responses and higher-order effects, including nonlinear dynamics and time-varying impedance parameters. That said, postural tremor involves relatively small displacements from an equilibrium position, so nonlinear dynamics and time-varying changes in moment-arms and inertia are expected to be small. Furthermore, there is no reason to expect systematic variations in muscle time constants or joint viscoelasticity while holding a posture for a 30 s period. We therefore expect the principles established above to be robust to nonlinear dynamics and time-varying changes in impedance parameters associated with postural tremor. Nevertheless, our conclusions cannot be extrapolated to tremor during voluntary movement (kinetic tremor) or even tremor in a postural task requiring modulation of joint torque or co-contraction (e.g., in response to perturbations, such as during tool use).
4.3.2. Inclusion of Only a Subset of Upper-Limb Muscles.
Our model included the major superficial muscles from the shoulder to the wrist. We focused on superficial muscles to allow for future experimental validation using inputs measured by sEMG. Consequently, our model does not include the following muscles: supraspinatus and infraspinatus; subscapularis; teres major and minor; pectoralis major clavicular and ribs (the sternal head was included); latissimus dorsi thoracic, lumbar, and iliac; coracobrachialis; triceps medial (long and lateral heads were included); anconeus; supinator; and palmaris longus. Also, the extrinsic hand muscles have a moment arm about the wrist joint but were not included in our model. Comparing the maximum torque of these excluded muscles to those of the muscles included in our model, we calculated the percentage of the total maximum torque included in our model to be 0%, 57%, 27%, 87%, 69%, 41%, and 72% in SFE, SAA, SIER, EFE, FPS, WFE, and WRUD, respectively (an explanation of the 0% contribution in SFE is given in the Appendix and discussed in Sec. 4.3.4). Fortunately, most of the principles are remarkably robust to the exclusion of many muscles from our model. To clarify, including only these percentages of the total maximum torque in our model has exactly the same effect as multiplying the diagonal values of the gain matrix by these percentages. As explained earlier, uniform scaling of (e.g., by including only half of the muscles in all DOF) has no effect whatsoever on the principles, but nonuniform scaling of (e.g., by including the percentages of muscles listed above in each DOF) could potentially affect principle 4. To test for this possibility, we repeated the relevant simulations, but included all 50 upper-limb muscles instead of only 15. The input from each muscle was scaled according to its maximum force. We found that tremor still increased proximal-distally (13% in the proximal 3DOF versus 82% in the distal 3 DOFs), and most of the tremor still came from distal muscles (20% from torque in the proximal 3 DOFs versus 67% from torque in the distal 3 DOFs). The proportions were similar for all four postures tested. We conclude that the six tremor propagation principles presented here would hold for a model that included all 50 upper-limb muscles.
4.3.3. Simplified Muscle Activity.
The distribution of tremorogenic muscle activity among the muscles of the upper limb is currently unknown. For this reason, we investigated tremor propagation in terms of magnitude ratios (output divided by input), which in a linear model are independent of the input (muscle activity). Nevertheless, one of the principles (principle 4) assumed uniform distribution of tremorogenic muscle activity among all muscles, i.e., an equal proportion of the maximum force in each muscle. That all muscles would receive the same amount of tremorogenic activity is admittedly unlikely, but as explained earlier, principle 4 is somewhat robust to deviations from this assumption.
Similarly, the phase shifts of tremorogenic activity between muscles are currently unknown [53]. As mentioned earlier, it is therefore not currently possible to predict the total tremor in a DOF, and we therefore based our conclusions and the tremor propagation principles on the magnitudes of individual tremor components. However, we have recently recorded sEMG in the 15 muscles (included in our current model) in 23 patients with ET and plan to use these data to characterize the phase shift in tremorogenic activity between these muscles. Such a characterization will allow us in the future to predict the total tremor in a DOF, not just the magnitudes of the individual components.
Numerous studies have suggested that afferent feedback could play a significant role in tremor (e.g., Refs. [54–56]). Such feedback could cause tremor to spread to other DOF through “neural coupling” even if they are not mechanically coupled. Here, we have focused on propagation through mechanical coupling and have excluded neural coupling for the sake of tractability, but future work should include the effect of neural coupling on tremor propagation.
4.3.4. No Input Torque in Shoulder Flexion–Extension in Default Posture.
In the default posture (posture 1 in Fig. 2), the top row of the moment-arm matrix is zero (Table 2), so the torque in SFE will always be zero, no matter how much force is applied about the SFE axis. Consequently, in our simulations in the default posture, the tremor seen in SFE is entirely due to propagation from torque in other DOF, and none of the tremor in other DOF is due to torque in SFE. This limitation stems from the original (untransformed) moment-arm matrix from opensim, which does not contain any moment-arm information for SFE in the default posture (see detailed explanation in Appendix). Fortunately, two insights provide evidence that this limitation is negligible. First, this limitation vanishes in almost all other postures, including all the other postures tested in our simulations (postures 2–4 in Fig. 2). Our finding that the pattern of tremor propagation in posture 1 was similar to the patterns in the other postures (Fig. 10) indicates that the torque in SFE is not a significant contributor to the pattern. Second, in prior simulations of tremor propagation from tremorogenic joint torques to tremulous joint displacements, we input equal torque into all DOFs (including SFE) and likewise found that the torque in SFE was not a significant contributor to the pattern of tremor propagation [25].
4.3.5. Simulation Without Validation.
Finally, these principles were based entirely on simulation results and were not validated by experiments. We have recently recorded both the inputs (sEMG in the 15 muscles in our model) and outputs (joint displacement in the 7DOFs in our model) in 23 patients with ET. We plan to combine these data with our model to experimentally validate (and revise where necessary) the principles derived from simulated tremor propagation.
4.4. Conclusion.
The aim of this research was to establish principles governing the propagation of tremor all the way from tremorogenic muscle activity to tremulous joint displacement. As discussed in Davidson and Charles [25], tremor propagation through the upper limb should be viewed as the result of a MIMO system whose dynamics include both filtering and mixing. Using a MIMO model that approximated the excitation-contraction dynamics of muscle and the geometry and impedance of the musculoskeletal system of the upper limb, we evaluated and revised the tremor propagation principles previously established for musculoskeletal impedance alone [25], resulting in the following, partially revised principles: (1) the distribution of tremor depends strongly on musculoskeletal dynamics; (2) the spreading of tremor is due to inertial coupling (primarily) and musculoskeletal geometry (secondarily); (3) tremor spreads narrowly; (4) assuming uniform distribution of tremorogenic activity among upper-limb muscles (i.e., an equal proportion of the maximum force in each muscle), tremor increases proximal-distally, and the contribution from muscles increases proximal-distally; (5) increasing inertia can decrease or increase tremor; and (6) increasing viscoelasticity can decrease or increase tremor.
As mentioned in the introduction, one of the obstacles to developing effective peripheral tremor suppression devices is that we do not currently know where to intervene, in part because we do not know where in the upper limb the tremor originates mechanically, how it propagates, and where it manifests the most. Based solely on the system (and not the input), the principles listed above indicate that tremor treatments targeting muscles (e.g., electrical stimulation [28] or botox injections [26]) should focus first on the distal muscles, and devices targeting DOF (e.g., passive orthoses [57] or active exoskeletons [58]) should focus first on the distal DOF. For example, assuming 8 Hz tremorogenic activity uniformly distributed across all muscles (Fig. 8), our model estimates that the six distal-most muscles (BRD-ECU), whose bellies are close to each other in the forearm, cause 63% of the magnitude of the tremor components caused by all muscles, and the three distal-most DOFs (FPS, WFE, and WRUD), which roughly intersect at the wrist joint, exhibit 83% of the magnitude of the tremor components observed in all DOFs.
Of course, tremor also depends on the input (i.e., the strength of tremorogenic activity in each muscle), and future research is needed to characterize the distribution of tremorogenic activity among the muscles of the upper limb in tremor patients. Combining such measurements with simulations of tremor propagation could allow one to determine which muscles are most responsible for an individual patient's tremor, and where to intervene to suppress tremor in an optimal manner.
Acknowledgment
SK Charles and TH Corie received financial support from the National Institute of Neurological Disorders and Stroke through NIH Grant R15NS087447, Quantitative Characterization of Essential Tremor for Future Tremor Suppression.
Appendix: Moment Arm Conversion
A.1 General Derivation.
The values in the moment-arm matrix () were taken from OpenSim, which expresses shoulder rotations using a Euler-angle sequence. However, in our model, we used a sequence for the shoulder. Therefore, we transformed the 3 × 15 submatrix of associated with the shoulder (the top three rows of the moment-arm matrix in Table 2) from to as follows:
Muscle force () can be transformed into torque expressed in terms of a sequence () or a sequence ()
| (A1) |
| (A2) |
where and are the top three rows of the moment-arm matrix (i.e., 3 × 15 matrices) expressed in and , respectively.
To find the relationship between and , one can express these two torque vectors in the universal frame (), where they are the same. If (i.e., , , and are the elements of projected along the , , and axes), then
| (A3) |
where , , and are the Euler/Cardan angles associated with rotations about , , and , respectively, and , , and are the corresponding rotation matrices (the third rotation axis, angle, and matrix do not contribute to the transformation). Likewise, if , then
| (A4) |
where , , and are the Euler/Cardan angles associated with rotations about , , and , respectively, and , , and are the corresponding rotation matrices. Here we made use of the rotation convention used in Robotics [44] as opposed to the convention used in Dynamics [59]. Incidentally, this is the same relationship that links the angular velocities expressed as and sequences: .
Solving Eqs. (A3) and (A4) for and , respectively, inserting into Eqs. (A1) and (A2), and solving each resulting equation for yields
| (A5) |
| (A6) |
Comparing Eqs. (A5) and (A6) gives
Therefore
| (A7) |
Calculating the and matrices in Eq. (A7) required a knowledge of Euler/Cardan angles in the frame ( and ) and in the frame ( and ), but typically only one set of Euler/Cardan angles was known. To calculate the other set, we noted that the rotation matrices of the two sets must be equal
| (A8) |
where and represent sine and cosine, respectively. Therefore, we inserted the known set of angles into Eq. (A8) and solved for the other set, calculated and using Eqs. (A3) and (A4), and finally determined using Eq. (A7).
A.2 Default Posture.
In the default posture (posture 1 in Fig. 2), all angles in both sets are zero. Inserting these values into Eqs. (A3) and (A4) to calculate and , and then inserting and into Eq. (A7) yields
We note the following two insights:
-
(1)
The third row of is the sum of the first and third rows of . As mentioned earlier, in the default posture, the angle sequence is in gimbal lock: and are aligned, and there are infinitely many ways to divide the total torque about the axis among the - and -axes. Consequently, there are infinitely many ways to divide the moment arms among the first and third rows of . For example, assigning all of the moment arms to the first row and zeros to the third row, or assigning all of the moment arms to the third row and zeros to the first row, or assigning half of each moment arm to the first and third rows are all acceptable options (incidentally, opensim follows the second example). The important thing is that no matter how the moment arms are divided among the - and -axes of the frame, the sum of the moment arms is appropriately assigned to the axis of the frame.
-
(2)
No matter how the moment arms are divided among the first and third rows of , the top row of will always be zero even though some muscles have nonzero moment arms about the-axis. Consequently, the torque about the -direction (shoulder flexion–extension) will always be zero, no matter how much force is applied about this axis. This is obviously a limitation, which is also caused by the gimbal lock of the system in the default posture: since is aligned with , and is aligned with , the frame has no component in the -direction. Consequently, does not contain any information about moment arms about the -axis, and no transformation can yield this information. In other words, the moment-arm matrix from opensim, or any transformation of this moment-arm matrix (including in our model), cannot provide information about torques produced about the -direction. Fortunately, when the limb is moved away from the default posture, and are no longer aligned, the frame has a nonzero component in the -direction, and this limitation vanishes (see Limitations section in Discussion).
Footnotes
To clarify, because the transfer function of the full system is simply the product of the transfer functions of the individual sub-models (see Input-Output Relationships), the magnitude ratio of the full system is simply the product of the magnitude ratios of the individual sub-models: , where the magnitude ratio of the full model () and of the sub-models (, , and ) were expressed as the magnitude of the associated transfer function [50]. Since and are not functions of , , and , changes in the impedance matrices affect but not or . Therefore, changes in caused by changes in the impedance matrices are the same as changes in caused by changes in the impedance matrices.
Calculated as the ratio of the average tremor magnitude in the three distal DOFs due to the proximal muscles (DELT1-TRIlat) to the average tremor magnitude in the three distal DOFs due to the distal muscles (BRA-ECU).
Contributor Information
Thomas H. Corie, Mechanical Engineering, , 350 EB, , Provo, UT 84602
Steven K. Charles, Mechanical Engineering and Neuroscience, , Brigham Young University, , 350 EB, , Provo, UT 84602 , e-mail: skcharles@byu.edu.
Funding Data
National Institute of Neurological Disorders and Stroke (Funder ID: 10.13039/100000065).
References
- [1]. Bhatia, K. P. , Bain, P. , Bajaj, N. , Elble, R. J. , Hallett, M. , Louis, E. D. , Raethjen, J. , Stamelou, M. , Testa, C. M. , and Deuschl, G. , 2018, “ Consensus Statement on the Classification of Tremors. From the Task Force on Tremor of the International Parkinson and Movement Disorder Society,” Mov. Disord., 33(1), pp. 75–87. 10.1002/mds.27121 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2]. Anouti, A. , and Koller, W. C. , 1995, “ Tremor Disorders. Diagnosis and Management,” West. J. Med., 162(6), pp. 510–513.https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1022828/ [PMC free article] [PubMed] [Google Scholar]
- [3]. Gallego, J. Á. , Rocon, E. , Belda-Lois, J. M. , and Pons, J. L. , 2013, “ A Neuroprosthesis for Tremor Management Through the Control of Muscle Co-Contraction,” J. NeuroEng. Rehabil., 10(1), p. 36. 10.1186/1743-0003-10-36 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4]. Deuschl, G. , Bain, P. , and Brin, M. , 2008, “ Consensus Statement of the Movement Disorder Society on Tremor,” Mov. Disord., 13(S3), pp. 2–23. 10.1002/mds.870131303 [DOI] [PubMed] [Google Scholar]
- [5]. Louis, E. D. , and Ferreira, J. J. , 2010, “ How Common Is the Most Common Adult Movement Disorder? Update on the Worldwide Prevalence of Essential Tremor,” Mov. Disord., 25(5), pp. 534–541. 10.1002/mds.22838 [DOI] [PubMed] [Google Scholar]
- [6]. Louis, E. D. , and Ottman, R. , 2014, “ How Many People in the USA Have Essential Tremor?, Deriving a Population Estimate Based Epidemiological Data,” Tremor Other Hyperkinetic Mov., 4, p. 259. 10.7916/D8TT4P4B [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7]. Koller, W. , Biary, N. , and Cone, S. , 1986, “ Disability in Essential Tremor: Effect of Treatment,“ (in Eng),” Neurology, 36(7), pp. 1001–1004. 10.1212/WNL.36.7.1001 [DOI] [PubMed] [Google Scholar]
- [8]. Tröster, A. I. , Pahwa, R. , Fields, J. A. , Tanner, C. M. , and Lyons, K. E. , 2005, “ Quality of Life in Essential Tremor Questionnaire (QUEST): Development and Initial Validation,” Parkinsonism Relat. Disord., 11(6), pp. 367–373. 10.1016/j.parkreldis.2005.05.009 [DOI] [PubMed] [Google Scholar]
- [9]. Louis, E. D. , Rohl, B. , and Rice, C. , 2015, “ Defining the Treatment Gap: What Essential Tremor Patients Want That They Are Not Getting,” Tremor Other Hyperkinetic Mov., 5, p. 331. 10.7916/D87080M9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10]. Zesiewicz, T. A. , Elble, R. , Louis, E. D. , Hauser, R. A. , Sullivan, K. L. , Dewey, R. B. , Ondo, W. G. , Gronseth, G. S. , and Weiner, W. J. , and., 2005, “ Practice Parameter: Therapies for Essential Tremor,” Neurology, 64(12), pp. 2008–2020. 10.1212/01.WNL.0000163769.28552.CD [DOI] [PubMed] [Google Scholar]
- [11]. Deuschl, G. , Raethjen, J. , Hellriegel, H. , and Elble, R. , 2011, “ Treatment of Patients With Essential Tremor,” Lancet Neurol., 10(2), pp. 148–161. 10.1016/S1474-4422(10)70322-7 [DOI] [PubMed] [Google Scholar]
- [12]. Louis, E. D. , Rios, E. , and Henchcliffe, C. , 2010, “ How Are We Doing With the Treatment of Essential Tremor (ET)?, Persistence ET Patients Medication: Data From 528 Patients Three Settings,” Eur. J. Neurol., 17(6), pp. 882–884. 10.1111/j.1468-1331.2009.02926.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13]. Diaz, N. L. , and Louis, E. D. , 2010, “ Survey of Medication Usage Patterns Among Essential Tremor Patients: Movement Disorder Specialists vs. general Neurologists,” Parkinsonism Relat. Disord., 16(9), pp. 604–607. 10.1016/j.parkreldis.2010.07.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14]. Schneider, S. A. , and Deuschl, G. , 2014, “ The Treatment of Tremor,” Neurotherapeutics, 11(1), pp. 128–138. 10.1007/s13311-013-0230-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15]. Flora, E. D. , Perera, C. L. , Cameron, A. L. , and Maddern, G. J. , 2010, “ Deep Brain Stimulation for Essential Tremor: A Systematic Review,” Mov. Disord., 25(11), pp. 1550–1559. 10.1002/mds.23195 [DOI] [PubMed] [Google Scholar]
- [16]. Wharen, R. E. , Okun, M. S. , Guthrie, B. L. , Uitti, R. J. , Larson, P. , Foote, K. , Walker, H. , Marshall, F. J. , Schwalb, J. , Ford, B. , Jankovic, J. , Simpson, R. , Dashtipour, K. , Phibbs, F. , Neimat, J. S. , Stewart, R. M. , Peichel, D. , Pahwa, R. , Ostrem, J. L. , and SJM DBS ET Study Group, 2017, “ Thalamic DBS With a Constant-Current Device in Essential Tremor: A Controlled Clinical Trial,” Parkinsonism Relat. Disord., 40, pp. 18–26.https://www.ncbi.nlm.nih.gov/pubmed/28400200 [DOI] [PubMed] [Google Scholar]
- [17]. Dembek, T. A. , Barbe, M. T. , Åström, M. , Hoevels, M. , Visser-Vandewalle, V. , Fink, G. R. , and Timmermann, L. , 2017, “ Probabilistic Mapping of Deep Brain Stimulation Effects in Essential Tremor,” NeuroImage: Clin., 13, pp. 164–173. 10.1016/j.nicl.2016.11.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18]. Pahwa, R. , Lyons, K. E. , Wilkinson, S. B. , Simpson, R. K. , Ondo, W. G. , Tarsy, D. , Norregaard, T. , Hubble, J. P. , Smith, D. A. , Hauser, R. A. , and Jankovic, J. , 2006, “ Long-Term Evaluation of Deep Brain Stimulation of the Thalamus,” J. Neurosurg., 104(4), pp. 506–512. 10.3171/jns.2006.104.4.506 [DOI] [PubMed] [Google Scholar]
- [19]. Ramirez-Zamora, A. , Boggs, H. , and Pilitsis, J. G. , 2016, “ Reduction in DBS Frequency Improves Balance Difficulties After Thalamic DBS for Essential Tremor,” J. Neurol. Sci., 367, pp. 122–127. 10.1016/j.jns.2016.06.001 [DOI] [PubMed] [Google Scholar]
- [20]. Blomstedt, P. , and Hariz, M. I. , 2006, “ Are Complications Less Common in Deep Brain Stimulation Than in Ablative Procedures for Movement Disorders?,” Stereotactic Funct. Neurosurg., 84(2–3), pp. 72–81. 10.1159/000094035 [DOI] [PubMed] [Google Scholar]
- [21]. Shih, L. C. , LaFaver, K. , Lim, C. , Papavassiliou, E. , and Tarsy, D. , 2013, “ Loss of Benefit in VIM Thalamic Deep Brain Stimulation (DBS) for Essential Tremor (ET): How Prevalent Is It?,” Parkinsonism Relat. Disord., 19(7), pp. 676–679. 10.1016/j.parkreldis.2013.03.006 [DOI] [PubMed] [Google Scholar]
- [22]. Sydow, O. , Thobois, S. , Alesch, F. , and Speelman, J. D. , 2003, “ Multicentre European Study of Thalamic Stimulation in Essential Tremor: A Six Year Follow Up,” J. Neurol., Neurosurg., Psychiatry, 74(10), pp. 1387–1391. 10.1136/jnnp.74.10.1387 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23]. Baizabal-Carvallo, J. F. , Kagnoff, M. N. , Jimenez-Shahed, J. , Fekete, R. , and Jankovic, J. , 2014, “ The Safety and Efficacy of Thalamic Deep Brain Stimulation in Essential Tremor: 10 Years and Beyond,” J. Neurol., Neurosurg. Psychiatry, 85(5), pp. 567–572. 10.1136/jnnp-2013-304943 [DOI] [PubMed] [Google Scholar]
- [24]. Kestenbaum, M. , Ford, B. , and Louis, E. D. , 2015, “ Estimating the Proportion of Essential Tremor and Parkinson's Disease Patients Undergoing Deep Brain Stimulation Surgery: Five‐Year Data From Columbia University Medical Center (2009–2014),” Mov. Disord. Clin. Pract., 2(4), pp. 384–387. 10.1002/mdc3.12185 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25]. Davidson, A. D. , and Charles, S. K. , 2017, “ Fundamental Principles of Tremor Propagation in the Upper Limb,” Ann. Biomed. Eng., 45(4), pp. 1133–1147. 10.1007/s10439-016-1765-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26]. Samotus, O. , Rahimi, F. , Lee, J. , and Jog, M. , 2016, “ Functional Ability Improved in Essential Tremor by IncobotulinumtoxinA Injections Using Kinematically Determined Biomechanical Patterns—A New Future,” PLoS One, 11(4), p. e0153739. 10.1371/journal.pone.0153739 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27]. Samotus, O. , Lee, J. , and Jog, M. , 2017, “ Long-Term Tremor Therapy for Parkinson and Essential Tremor With Sensor-Guided Botulinum Toxin Type a Injections,” PLoS One, 12(6), p. e0178670. 10.1371/journal.pone.0178670 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28]. Dosen, S. , Muceli, S. , Dideriksen, J. L. , Romero, J. P. , Rocon, E. , Pons, J. , and Farina, D. , 2015, “ Online Tremor Suppression Using Electromyography and Low-Level Electrical Stimulation,” IEEE Trans. Neural Syst. Rehabil. Eng., 23(3), pp. 385–395. 10.1109/TNSRE.2014.2328296 [DOI] [PubMed] [Google Scholar]
- [29]. Freeman, C. T. , Sampson, P. , Burridge, J. H. , and Hughes, A. M. , 2015, “ Repetitive Control of Functional Electrical Stimulation for Induced Tremor Suppression,” Mechatronics, 32, pp. 79–87 (in English). 10.1016/j.mechatronics.2015.10.008 [DOI] [Google Scholar]
- [30]. Manesk, L. P. , Jorgovanović, N. , Ilić, V. , Došen, S. , Keller, T. , and Popović, M. B. , 2011, “ Electrical Stimulation for the Suppression of Pathological Tremor,” Medical Biol. Eng. Comput., 49(10), pp. 1187–1193 (in English). 10.1007/s11517-011-0803-6 [DOI] [PubMed] [Google Scholar]
- [31]. Prochazka, A. , Elek, J. , and Javidan, M. , 1992, “ Attenuation of Pathological Tremors by Functional Electrical-Stimulation—1: Method,” Ann. Biomed. Eng., 20(2), pp. 205–224. 10.1007/BF02368521 [DOI] [PubMed] [Google Scholar]
- [32]. Winter, D. A. , 2009, Biomechanics and Motor Control of Human Movement, Wiley, Hoboken, NJ. [Google Scholar]
- [33]. Burdet, E. , 2013, Human Robotics, The MIT Press, Cambridge, MA. [Google Scholar]
- [34]. Haruno, M. , and Wolpert, D. M. , 2005, “ Optimal Control of Redundant Muscles in Step-Tracking Wrist Movements,” J. Neurophysiol., 94(6), pp. 4244–4255. 10.1152/jn.00404.2005 [DOI] [PubMed] [Google Scholar]
- [35]. Saul, K. R. , Hu, X. , Goehler, C. M. , Vidt, M. E. , Daly, M. , Velisar, A. , and Murray, W. M. , 2015, “ Benchmarking of Dynamic Simulation Predictions in Two Software Platforms Using an Upper Limb Musculoskeletal Model,” Comput. Methods Biomech. Biomed. Eng., 18(13), pp. 1445–1458. 10.1080/10255842.2014.916698 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36]. Holzbaur, K. R. S. , Murray, W. M. , Gold, G. E. , and Delp, S. L. , 2007, “ Upper Limb Muscle Volumes in Adult Subjects,” J. Biomech., 40(4), pp. 742–749. 10.1016/j.jbiomech.2006.11.011 [DOI] [PubMed] [Google Scholar]
- [37]. Holzbaur, K. R. , Delp, S. L. , Gold, G. E. , and Murray, W. M. , 2007, “ Moment-Generating Capacity of Upper Limb Muscles in Healthy Adults,” J. Biomech., 40(11), pp. 2442–2449. 10.1016/j.jbiomech.2006.11.013 [DOI] [PubMed] [Google Scholar]
- [38]. Holzbaur, K. R. S. , Murray, W. M. , and Delp, S. L. , 2005, “ A Model of the Upper Extremity for Simulating Musculoskeletal Surgery and Analyzing Neuromuscular Control,” Ann. Biomed. Eng., 33(6), pp. 829–840. 10.1007/s10439-005-3320-7 [DOI] [PubMed] [Google Scholar]
- [39]. Wu, G. , van der Helm, F. C. T. , (DirkJan) Veeger, H. E. J. , Makhsous, M. , Van Roy, P. , Anglin, C. , Nagels, J. , Karduna, A. R. , McQuade, K. , Wang, X. , Werner, F. W. , and Buchholz, B. , 2005, “ ISB Recommendation on Definitions of Joint Coordinate Systems of Various Joints for the Reporting of Human Joint Motion—Part II: Shoulder, Elbow, Wrist and Hand,” J. Biomech., 38(5), pp. 981–992. 10.1016/j.jbiomech.2004.05.042 [DOI] [PubMed] [Google Scholar]
- [40]. Formica, D. , Charles, S. K. , Zollo, L. , Guglielmelli, E. , Hogan, N. , and Krebs, H. I. , 2012, “ The Passive Stiffness of the Wrist and Forearm,” J. Neurophysiol., 108(4), pp. 1158–1166. 10.1152/jn.01014.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41]. Drake, W. B. , and Charles, S. K. , 2014, “ Passive Stiffness of Coupled Wrist and Forearm Rotations,” Ann. Biomed. Eng., 42(9), pp. 1853–1866. 10.1007/s10439-014-1054-0 [DOI] [PubMed] [Google Scholar]
- [42]. Pando, A. L. , Lee, H. , Drake, W. B. , Hogan, N. , and Charles, S. K. , 2014, “ Position-Dependent Characterization of Passive Wrist Stiffness,” IEEE Trans. Bio-Med. Eng., 61(8), pp. 2235–2244 (in English). 10.1109/TBME.2014.2313532 [DOI] [PubMed] [Google Scholar]
- [43]. de Leva, P. , 1996, “ Adjustments to Zatsiorsky-Seluyanov's Segment Inertia Parameters,” J. Biomech., 29(9), pp. 1223–1230. 10.1016/0021-9290(95)00178-6 [DOI] [PubMed] [Google Scholar]
- [44]. Corke, P. , 2017, Robotics, Vision and Control: Fundamental Algorithms in MATLAB® Second, Completely Revised, Extended and Updated Edition, Springer International Publishing, Berlin. [Google Scholar]
- [45]. Matsumoto, Y. , Seki, M. , Ando, T. , Kobayashi, Y. , Iijima, H. , Nagaoka, M. , and Fujie, G. M. , 2012, “ Analysis of EMG Signals of Patients With Essential Tremor Focusing on the Change of Tremor Frequency,” Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), San Diego, CA, Aug. 28–Sept. 1, pp. 2244–2250. 10.1109/EMBC.2012.6346409 [DOI] [PubMed]
- [46]. He, F. , Sarrigiannis, P. G. , Billings, S. A. , Wei, H. , Rowe, J. , Romanowski, C. , Hoggard, N. , Hadjivassilliou, M. , Rao, D. G. , Grünewald, R. , Khan, A. , and Yianni, J. , 2016, “ Nonlinear Interactions in the Thalamocortical Loop in Essential Tremor: A Model-Based Frequency Domain Analysis,” Neuroscience, 324, pp. 377–389. 10.1016/j.neuroscience.2016.03.028 [DOI] [PubMed] [Google Scholar]
- [47]. Grimaldi, G. , and Manto, M. , 2008, “ Tremor: From Pathogenesis to Treatment,” Synth. Lectures Biomed. Eng., 3(1), pp. 1–212. 10.2200/S00129ED1V01Y200807BME020 [DOI] [Google Scholar]
- [48]. Nisticò, R. , Pirritano, D. , Salsone, M. , Novellino, F. , Del Giudice, F. , Morelli, M. , Trotta, M. , Bilotti, M. , Condino, F. , Cherubini, A. , Valentino, P. , and Quattrone, A. , 2011, “ Synchronous Pattern Distinguishes Resting Tremor Associated With Essential Tremor From Rest Tremor of Parkinson's Disease,” Parkinsonism Relat. Disord., 17(1), pp. 30–33. 10.1016/j.parkreldis.2010.10.006 [DOI] [PubMed] [Google Scholar]
- [49]. Milanov, I. , 2001, “ Electromyographic Differentiation of Tremors,” Clin. Neurophysiol., 112(9), pp. 1626–1632. 10.1016/S1388-2457(01)00629-0 [DOI] [PubMed] [Google Scholar]
- [50]. Palm, W. J. , 2014, System Dynamics, 3rd ed., McGraw-Hill, New York. [Google Scholar]
- [51]. Matsumoto, Y. , Seki, M. , Nakashima, Y. , Ando, T. , Kobayashi, Y. , Iijima, H. , Nagaoka, M. , and Masakatsu, G. , 2017, “ Algorithm to Demodulate an Electromyogram Signal Modulated by Essential Tremor,” Robomech J., 4(1), p. 15. 10.1186/s40648-017-0082-6 [DOI] [Google Scholar]
- [52]. Parkinson, M. , 2014, “ Anthropometric Data Explorer,” Penn State University Open Design Lab, State College, PA, accessed Feb. 18, 2014, http://tools.openlab.psu.edu/tools/explorer.php
- [53]. Gallego, J. A. , Dideriksen, J. L. , Holobar, A. , Ibanez, J. , Glaser, V. , Romero, J. P. , Benito-Leon, J. , Pons, J. L. , Rocon, E. , and Farina, D. , 2015, “ The Phase Difference Between Neural Drives to Antagonist Muscles in Essential Tremor Is Associated With the Relative Strength of Supraspinal and Afferent Input,” J. Neurosci., 35(23), pp. 8925–8937. 10.1523/JNEUROSCI.0106-15.2015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54]. Britton, T. C. , Thompson, P. D. , Day, B. L. , Rothwell, J. C. , Findley, L. J. , and Marsden, C. D. , 1994, “ Rapid Wrist Movements in Patients With Essential Tremor. The Critical Role of the Second Agonist Burst,” Brain: J. Neurol., 117(1), pp. 39–47. 10.1093/brain/117.1.39 [DOI] [PubMed] [Google Scholar]
- [55]. Pedrosa, D. J. , Quatuor, E.-L. , Reck, C. , Pauls, K. A. M. , Huber, C. A. , Visser-Vandewalle, V. , and Timmermann, L. , 2014, “ Thalamomuscular Coherence in Essential Tremor: Hen or Egg in the Emergence of Tremor?,” J. Neurosci., 34(43), p. 14475. 10.1523/JNEUROSCI.0087-14.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56]. Dideriksen, J. L. , Enoka, R. M. , and Farina, D. , 2011, “ A Model of the Surface Electromyogram in Pathological Tremor,” IEEE Trans. Biomed. Eng., 58(8), pp. 2178–2185. 10.1109/TBME.2011.2118756 [DOI] [PubMed] [Google Scholar]
- [57]. Belda-Lois, J. M. , Martinez-Reyero, A. I. , Castillo, A. , Rocon, E. , Pons, J. L. , Loureiro, R. , Manto, M. , Normie, L. , and Soede, M. , 2007, “ Controllable Mechanical Tremor Reduction.Assessment of Two Orthoses,” Technol. Disability, 19(4), pp. 169–178.https://content.iospress.com/articles/technology-and-disability/tad00238 [Google Scholar]
- [58]. Rocon, E. , Belda-Lois, J. M. , Ruiz, A. F. , Manto, M. , Moreno, J. C. , and Pons, J. L. , 2007, “ Design and Validation of a Rehabilitation Robotic Exoskeleton for Tremor Assessment and Suppression,” IEEE Trans. Neural Syst. Rehabil. Eng., 15(3), pp. 367–378. 10.1109/TNSRE.2007.903917 [DOI] [PubMed] [Google Scholar]
- [59]. Baruh, H. , 2014, Applied Dynamics, CRC Press, Boca Raton, FL. [Google Scholar]


