Abstract
Non-contrast perfusion ultrasound imaging remains challenging due to spectral broadening of the tissue clutter signal caused by patient and sonographer hand motion. To address this problem, we previously introduced an adaptive demodulation scheme to suppress the bandwidth of tissue prior to high-pass filtering. Our initial implementation used single plane wave power Doppler imaging and a conventional tissue filter. Recent advancements in beamforming and tissue filtering have been proposed for improved slow-flow imaging, including coherent flow power Doppler (CFPD) imaging and singular value decomposition (SVD) filtering. Here, we aim to evaluate adaptive demodulation in conjunction with improvements in beamforming and filtering using simulations, single vessel phantoms, and an in vivo liver tumor embolization study. We show that simulated blood-to-background contrast-to-noise ratios are highest when using adaptive demodulation with CFPD and a 100ms ensemble, which resulted in a 13.6dB average increase in contrast-to-noise ratio compared to basic IIR filtering alone. We also show that combining adaptive demodulation with SVD and with CFPD+SVD results in 9.3dB and 19dB increases in contrast-to-noise ratios compared to IIR filtering alone at 700ms and 500ms ensembles for phantom data with 1mm/s and 5mm/s average flows, respectively. In general, combining techniques resulted in higher signal-to-noise, contrast-to-noise, and generalized contrast-to-noise ratios in both simulations and phantoms. Finally, adaptive demodulation with SVD resulted in the largest qualitative and quantitative change in tumor-to-background contrast post-embolization.
Index Terms—: perfusion, adaptive demodulation, blood flow, power Doppler, clutter filter, ultrasound, SVD, CFPD
I. Introduction
CHANGES in perfusion level blood flow can indicate several clinically relevant events, such as tumor viability and treatment response. Compared to other modalities, non-contrast ultrasound is an attractive tool for measuring these changes because it is affordable, noninvasive, can provide real-time information, and is not dependent on time and dose of contrast agents in the bloodstream. However, measuring these changes with non-contrast ultrasound remains challenging, mainly due to tissue clutter interference with blood [1], [2].
Without contrast, blood signal is weak compared to tissue [1], [3], [4]. Because of this, tissue needs to be filtered to reveal blood signal. This is trivial with high pass filters if tissue is stationary. However, realistically tissue is not stationary and is moving primarily because of patient physiological or sonographer hand motion [1], [4]. This motion results in spectral broadening of the tissue signal causing it to overlap with the signal from lower velocity blood flow, making it difficult to filter tissue without also removing slow blood flow signal [1], [2], [4].
To address this, we previously introduced an adaptive phase and amplitude demodulation scheme to reduce the bandwidth of the tissue clutter signal prior to high pass filtering [5]. We developed and implemented an initial realization of the method using single plane wave power Doppler imaging with conventional high pass filtering on experimental phantom and in vivo data. We demonstrated that adaptive demodulation can solve the tissue clutter spectral broadening problem and potentially allow for lower blood velocities (<1mm/s) to be detected without contrast [5]. However, our results were mainly proof-of-concept, and we have yet to fully explore the boundaries and limitations of the method. Additionally, apart from the spectral broadening problem, there are several other factors that can limit perfusion visualization.
In our initial implementation of adaptive demodulation, we overcame other limitations associated with slow blood flow imaging, like beam-to-flow angle dependence and short ensemble lengths, by using power Doppler and plane wave imaging. Power Doppler is less angle-dependent and more sensitive to smaller vessels since it measures the amount of blood rather than the true velocity [3], [6]. Therefore, because we are focusing on perfusion, or the slowest, most randomly-oriented flow, we use power Doppler. Additionally, we use plane wave imaging to eliminate the trade-off between frame rate and ensemble length, allowing for high frame rate imaging while also maintaining sufficient sampling for tissue filtering [7], [8]. However, limitations still exist with single plane wave imaging and conventional tissue filtering, and recent advancements in both beamforming and tissue clutter removal have been proposed to help solve these additional problems [6], [9]–[12].
Plane wave synthetic focusing and coherent flow power Doppler (CFPD) applied to plane wave synthetic focused data are alternative beamforming methods that can help overcome single plane wave imaging limitations. Single plane wave images suffer from low signal-to-noise ratio and reduced lateral resolution because it only uses a single unfocused transmit event per image. Plane wave synthetic focusing involves transmitting and coherently summing multiple angled plane waves to increase signal-to-noise ratio and synthesize transmit focusing at all locations in the image [13]. Because plane wave synthetic focusing only needs a few angles to regain the resolution of a focused transmit, it maintains the frame rate and ensemble length benefits of single plane wave imaging [6]. CFPD applied to plane wave synthetic focused data intends to further improve signal-to-noise ratio by suppressing non-stationary diffuse reverberation clutter in addition to thermal noise [9], [10]. Although plane wave synthetic focusing and CFPD can improve sensitivity to slow flow, they still rely on effective tissue filtering.
Conventional Doppler tissue filtering, which typically uses infinite or finite impulse response or polynomial regression filters, has been extensively studied and optimized [4], [8], [14]. Two of the main limitations with conventional filters are that they rely on clear temporal spectral separation of tissue and blood, and they are applied only in the slow-time dimension [12]. Adaptive demodulation helps overcome the former. Singular value decomposition (SVD) methods have been proposed to help overcome both of these limitations, assuming long slow-time ensembles are used [12], [15]. These SVD methods incorporate both temporal and spatial information to better separate tissue from blood, presumably decreasing the reliance on clear temporal spectral separation [12], [15]. However, it has been shown that the frequency content of temporal eigenvectors is still important to consider when using these filters [15], [16].
Here we aim to improve upon our initial implementation of adaptive demodulation by using controlled simple simulation experiments to assess the limitations and boundaries of the method. We also evaluate beamforming and tissue filter improvements with and without adaptive demodulation. Additionally, because adaptive demodulation is a pre-filtering method, CFPD is a beamforming technique, and SVD is a filter, we are able to assess each of these proclaimed slow-flow techniques separately as well as in combination. We test our simulation findings using phantom and in vivo data.
II. Methods
A. Principles of Adaptive Demodulation
Here we present a brief description of the theory and implementation of adaptive demodulation, which is explained in more detail in previous work [5]. To describe the fundamentals of adaptive demodulation, we first start with a simple idealistic signal model of stationary tissue, blood, and noise,
| (1) |
where and are the sums of the complex amplitudes of the tissue (Am) and blood (An) scatterers, respectively, at slow-time t and at a single axial and lateral location. Axial blood motion is indicated by the angular frequency term, ωn(t), while lateral and elevational blood motion is accounted for by the time dependence on the blood scatterer amplitude term, An. No time dependence or angular frequency terms are included in the tissue signal equation because we are assuming tissue is stationary in this simplified model. Tissue filtering is trivial with (1) because tissue and blood have completely distinct spectral content.
Realistically, we know tissue moves, and we expect that motion to result in both a phase and amplitude modulation of the signal [1]. Phase modulation can be described as an exponential term that incorporates motion due to patient physiological, sonographer hand, and other sources of axial motion. This exponential term is applied to both tissue and blood signals since we assume the blood traveling through the small vessels of interest moves with the tissue. Amplitude modulation will manifest as a time dependence on the tissue amplitude term and indicates any residual lateral or elevational tissue motion. The resulting phase and amplitude modulated signal is shown in (2),
| (2) |
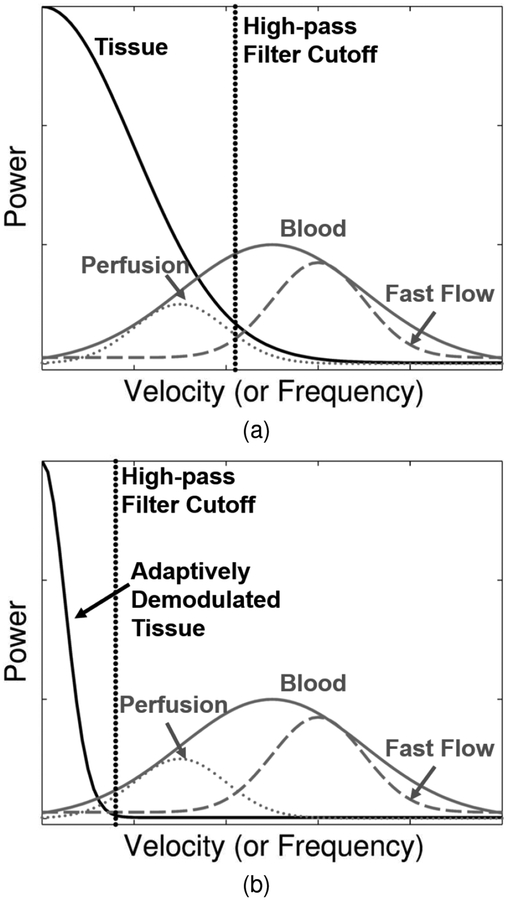
Where ωphysio+sono is the angular frequency caused by patient and sonographer motion. This modulation causes a spectral broadening of the tissue signal causing it to overlap with the signal from blood, as depicted in Figure 1a.
Fig. 1.
(a) Patient and sonographer motion causes spectral broadening of tissue clutter signal (black) causing it to overlap with low velocity blood flow or perfusion signal (dotted gray). Conventional high-pass tissue clutter filters (dotted black) preserve only high velocity blood signal (dashed gray). The full blood distribution is depicted as the solid gray curve. (b) Adaptive demodulation suppresses the tissue clutter bandwidth, allowing for perfusion signal to pass through the tissue clutter filter.
Adaptive demodulation works by adaptively phase and amplitude demodulating the signal. For the phase demodulation, we use an in-phase quadrature-based 2D autocorrelation axial displacement estimator [17] followed by a least squares reconstruction—similar to phase aberration estimation methods [18], [19]—to estimate the total axial displacement through slow-time for each depth and lateral location. We can then interpolate the signals through depth from the estimated displacement to zero displacement. In doing so, we adaptively phase demodulate the signal, as shown in (3),
| (3) |
where is an estimate of the angular frequency caused by patient and sonographer motion and n′(t) is the demodulated noise term. We assume the error induced by the demodulated noise is insignificant.
After phase demodulation, we are ideally left with only tissue amplitude modulation contributing to the spectral broadening of the tissue signal. To demodulate the amplitude, we normalize the RF data by the amplitude of the analytic signal, which is computed by taking the absolute value of the Hilbert transformed RF data. To preserve power, we multiply by the power of the signal. To avoid blood amplitude demodulation, we apply a median filter to the normalization function, assuming tissue coherence is longer than blood. This normalization function is described in (4),
| (4) |
where L is the total number of slow-time points, and R{x, k} represents the median filter operation on signal x of size k samples.
Finally, by multiplying (3) by (4), we are ideally left with (1), which, again, makes tissue filtering trivial, as depicted in Figure 1b. In practice, we multiply the real part of (3) by (4). Also, despite our simple narrow-band model description, our time-domain implementation is wide-band. A narrow-band model is used here to describe the theory for mathematical simplicity. The time-domain implementation is used to simultaneously account for amplitude and phase modulation.
B. Simulations
To evaluate the limitations and boundaries of adaptive demodulation as well as improvements in beamforming and tissue filtering, we use a single small vessel simulation experiment. Using Field II [20], we simulated plane wave channel data of a 0.5mm diameter vessel of blood scatterers angled 30° to the beam and centered at a depth of 2cm within a 0.6cm by 1cm area of tissue scatterers (Figure 2a). In the following subsections, we describe how tissue motion was implemented and how each adaptive demodulation, beamforming, and tissue filtering parameter was adjusted and evaluated.
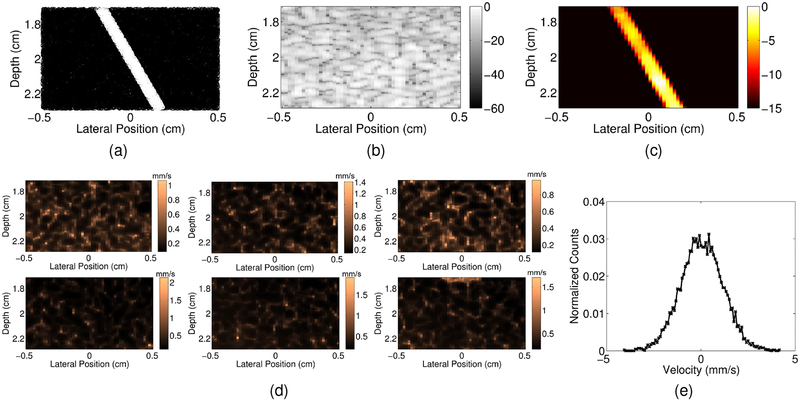
Fig. 2.
(a) Example realization of tissue (black) and blood (white) scatterers used for simulations. (b) Example simulated plane wave synthetic focused B-mode image. (c) Example simulated power Doppler image with no tissue motion. (d) Root mean square of hand motion velocities (mm/s) for each tissue clutter realization. (e) Histogram of velocities for an example pixel from an example tissue clutter realization.
1). Tissue Motion:
To simulate realistic tissue motion, we used displacements estimated from sonographer hand motion phantom data to displace both the tissue and blood scatterers. Six volunteers acquired 0° plane wave channel data of a stationary quality assurance phantom (CIRS Model 040GSE, Norfolk, VA) using a 7.8125MHz center frequency at a pulse repetition frequency of 9kHz for 3s using a Verasonics Vantage System (Verasonics, Inc., Kirkland, WA) and L12–5 probe. A Hann apodization and aperture growth to achieve an F/# of 2 were implemented during receive beamforming. Beamformed data were band-pass filtered and up-sampled by a factor of 2 to achieve a sampling frequency of 62.5MHz. Total displacements over the first second of data were computed using the same method described in Section II-A using an axial kernel size of 1.25λ and a lag of 1ms for the relative displacement estimator. Total displacements were interpolated according to the location of the tissue and blood scatterers and used to generate 6 realistic tissue clutter realizations. Root mean square of hand motion velocities through slow-time are shown for each realization in Figure 2d. Velocities were computed on the hand motion data sets using a slow-time lag of 8ms and a kernel size of 1.25λ. Figure 2e shows a histogram of velocities for an example pixel from an example realization.
2). Parameter Study:
For each realization, we simulated 1s of channel data using 9 transmit angles evenly spaced between −8° and 8° at a pulse repetition frequency of 9kHz using a 1 cycle pulse. We simulated tissue and blood channel data separately. We varied transmit frequency, blood-to-noise channel signal ratio, tissue-to-blood channel signal ratio, peak blood scatterer velocity, beamforming methods, tissue filter methods, and also displacement estimation parameters used for adaptive demodulation. The adaptive demodulation displacement estimation parameters are axial kernel size and slow-time lag. The kernel size defines the window size used for axial averaging in the 2D autocorrelation relative displacement estimator. For a given kernel, relative displacements are computed between slow-time samples that are up to a maximum lag apart. A summary of all parameters is shown in Table I. We used a fixed sampling frequency of 31.25MHz. We band-pass filtered and up-sampled all data to 62.5MHz after beamforming. We band-pass filtered all data again after applying adaptive demodulation.
TABLE I.
Simulation Experiment Parameter Summary. Baseline parameters are in bold font. AD, SPW, PWSF, and IIR stand for adaptive demodulation, single plane wave, plane wave synthetic focusing, and infinite impulse response, respectively.
| Parameter | Values/Methods |
|---|---|
| AD Kernel Size (wavelengths) | 1.25, 2.5, 5, 10, 15 |
| AD Lag (ms) | 1, 3, 5, 7 |
| Blood-to-Noise Ratio (dB) | −30, −20, −10, 0, 10, 20 |
| Tissue-to-Blood Ratio (dB) | 10, 20, 30, 40, 50, 60 |
| Peak Blood Velocity (mm/s) | 0.5, 1, 2, 5, 10 |
| Imaging Frequency (MHz) | 2, 4, 6, 7.8125, 10 |
| Beamforming Method | SPW, PWSF, CFPD |
| Tissue Filtering Method | IIR, SVD |
3). Baseline Parameters:
When varying each parameter, we used the same baseline values for all other parameters. Our baseline case used a 7.8125MHz transmit frequency and the full ensemble (1s). We scaled the blood channel data to be 40dB lower than tissue and added noise 0dB relative to the blood. Blood scatterers moved laminarly with a peak velocity of 1mm/s. We beamformed the data using the plane wave synthetic focusing method (resulting in a frame rate of 1kHz and 1s ensemble) and filtered tissue using a conventional 1Hz (≈0.1mm/s) high-pass infinite impulse response (IIR) filter.
We performed adaptive demodulation using a kernel size of 10λ for our axial displacement estimator. However, when varying imaging frequencies, we adjusted the kernel size to ensure the same number of samples was used for each case. We used a single 1ms lag to compute total displacements, which is equivalent to performing a cumulative sum of the relative displacements through slow-time. For all simulations, we did not incorporate any amplitude demodulation because we controlled the experiment to only have axial tissue motion. Baseline parameter values are bold font in Table I.
4). Beamforming and Tissue Filtering:
We used the same channel data for all three beamforming methods. For the single plane wave case, we used only the 0° plane wave channel data and parallel receive beamforming [7]. For the plane wave synthetic focusing case, we used all 9 angles and summed consecutive angled beamformed plane wave data [13]. For the CFPD case, we applied short-lag spatial coherence (SLSC) beamforming to filtered plane wave synthetic focused data using a max aperture lag of 20 and a kernel size of 1.5λ, as in Li et. al. [10]. For all cases, we used a Hann apodization and aperture growth to achieve an F/# of 2 during receive beamforming. For the CFPD case, we up-sampled and bandpass filtered the delayed channel data.
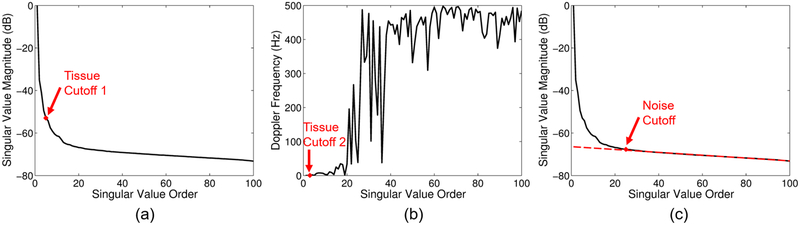
We used two different tissue filtering methods for this study: a conventional IIR filter and an SVD filter [12], [15]. A conventional 6th order type 1 Chebyshev IIR high-pass filter with a 1Hz cutoff was used. The cutoff was adjusted only for the peak blood scatterer velocity study. For all peak velocities, ranges of cutoffs were tested on the full 1s ensemble for a single realization, and an optimal cutoff was chosen based on the highest blood-to-background signal-to-noise ratio (see (6)). A 1Hz cutoff was used for the 0.5mm/s and 1mm/s normal and adaptively demodulated cases. A 10Hz cutoff was used for the 2mm/s normal and adaptively demodulated cases. 30Hz and 20Hz cutoffs were used for the 5mm/s normal and adaptively demodulated cases, respectively. 55Hz and 50Hz cutoffs were used for the 10mm/s normal and adaptively demodulated cases, respectively. For the SVD filter, tissue and noise eigenvalue cutoffs were chosen adaptively, as in Song et al. [15]. This process is summarized in Figure 3 and involves thresholding the singular value magnitude and temporal eigenvector mean Doppler frequency curves to select tissue and noise cutoffs. Thresholds were tested and chosen separately for data with and without adaptive demodulation based on which produced the closest to optimal SNR (see (6)). For tissue cutoff selection, two pre-cutoffs are chosen [15], as depicted in Figures 3a and 3b. In the method by Song et al., the maximum of these two cutoffs is used as the final tissue cutoff [15]. We looked at both the maximum and minimum and, based on highest blood-to-background SNR (see (6)), used the minimum for data with adaptive demodulation. For CFPD data, tissue filtering was performed on delayed channel data and all channels were included as spatial information for the SVD filter. Thresholds for choosing tissue cutoff 1, tissue cutoff 2, and the noise cutoff are respectively based on the slope of the singular value magnitude curve, mean Doppler frequency, and deviation of a linear fit to the singular value magnitude curve at the highest singular value orders. For all data without adaptive demodulation, thresholds of 5, 1Hz, and 0.05 were used for selecting tissue cutoff 1, tissue cutoff 2, and the noise cutoff, respectively. For all data with adaptive demodulation, thresholds of 1.5, 0.5Hz, and 0.05 were used for selecting tissue cutoff 1, tissue cutoff 2, and the noise cutoff, respectively.
Fig. 3.
Example tissue and noise eigenvalue cutoff selection. (a) Tissue cutoff 1 is selected by finding when the slope of the singular value magnitude curve goes below a certain threshold (e.g., 5). (b) Tissue cutoff 2 is selected by finding the first temporal eigenvector mean Doppler frequency to go above a certain threshold (e.g., 1Hz). (c) The noise cutoff is selected by fitting a line to the singular value magnitude curve and finding when the curve starts to deviate from the line by more than a certain threshold (e.g. 0.05).
For the beamforming and filtering parameter studies, we also varied the ensemble size that we use for high-pass filtering and power Doppler estimation. For these studies, we looked at ensemble sizes of 20ms-1s (20–1000 samples).
Additionally, for both filtering techniques, we performed a more extensive tissue cutoff analysis on the 1mm/s peak velocity baseline and adaptively demodulated data. For the IIR filter, we tested a range of cutoffs between 0.5 and 25Hz (spaced by 1Hz from 1 up to 10Hz then spaced by 5Hz up to 25Hz) for ensemble sizes between 20ms and 1s for each realization. For the SVD filter, we tested tissue eigenvalue cutoffs between 1 and 20 for ensemble sizes between 20ms and 1s for each realization. For the SVD cutoff analysis, we did not incorporate any noise filtering.
5). Qualitative and Quantitative Metrics:
The power Doppler signal was computed using
| (5) |
where s(x, z, t) is the filtered SLSC signal for the CFPD cases and the magnitude of the filtered analytic signal for all other cases, x, z, t are the spatial, axial, and temporal dimensions, and T is the total number of slow-time samples or ensemble size. A 1mm by 1mm spatial median filter was applied to each power Doppler image. To quantify differences between different parameter values and techniques, we used blood-to-background signal-to-noise ratio (SNR), contrast-to-noise ratio (CNR), and generalized contrast-to-noise ratio (GCNR) metrics from Li et al. [10], Baranger et al. [21], and Molares et al. [22], respectively,
| (6) |
| (7) |
| (8) |
where N and M are the total number of pixels in the vessel and background, respectively, PDsig and PDbkgd are the power Doppler values in the vessel and background, respectively, STD stands for the standard deviation, and OV L represents the overlap between histograms of the background and vessel pixels. The vessel mask was interpolated as necessary for the varying center frequency study to account for changes in resolution. Power Doppler images were made by log compressing (5) (I = 10log10PD(x, z)). Images were scaled to individual maximums and dynamic ranges were chosen separately for each beamformer and filter combination by computing the average power value of the background pixels of the adaptively demodulated data for that beamformer and filter. This value was used as the minimum value in the image for both data with and without adaptive demodulation. Example B-mode and power Doppler images are shown in Figures 2b and 2c, respectively, for a case with no tissue motion.
C. Phantom Experiment
Polyvinyl alcohol (PVA) and graphite phantoms with a single small diameter vessel were used to further evaluate improvements in beamforming and tissue filtering with and without adaptive demodulation. Phantoms were made by placing 0.60–0.64mm diameter wire through the short ends of 2 by 3cm molds. A PVA and graphite mixture [23] was then poured into the molds, and then the molds were placed in the freezer for several days.
After thawing for a few hours and removing the molds and wire, a syringe pump was used to flow blood-mimicking fluid (CIRS Model 046, Norfolk, VA) through the vessel of each phantom at flow rates of 95μl/min (90 for 0.60mm diameter vessel) and 17μl/min, which equates to average velocities of about 5 and 1mm/s. For each flow speed, 6 different phantoms were used to ensure 6 different speckle realizations. For each phantom, a volunteer sonographer acquired 1s of plane wave channel data using the same Verasonics L12–5 probe used for the sonographer hand motion realizations described in Section II-B. Channel data were acquired using a 7.8125MHz center frequency, 9 transmit angles evenly spaced between −8° and 8°, a pulse repetition frequency of 9kHz and a 1 cycle pulse length.
Channel data were beamformed using both the plane wave synthetic focusing and CFPD methods with the same receive beamforming parameters described in Section II-B. Beamformed data were band-pass filtered and up-sampled to a sampling frequency of 62.5MHz. Adaptive demodulation was performed using the same baseline settings as in Section II-B. Although lateral motion was likely present in this experiment, amplitude demodulation was not used in order to maintain consistency with the simulations. Data were band-pass filtered again after adaptive demodulation. The same IIR and adaptive SVD filters were used as described in Section II-B, except that a 25Hz cutoff was used for the IIR filter for the faster flow case, and the thresholds were adjusted for the adaptive SVD filter for both cases. For the faster flow case, for data without adaptive demodulation, tissue cutoffs 1, 2, and the noise cutoff were selected using thresholds of 2, 8Hz, and 0.01, respectively. For data with adaptive demodulation, tissue cutoffs 1, 2, and the noise cutoff were selected using thresholds of 0.5, 10Hz, and 0.01, respectively. For the slower flow case, for data without adaptive demodulation, tissue cutoffs 1, 2, and the noise cutoff were selected using thresholds of 2, 1Hz, and 0.01, respectively. For data with adaptive demodulation, tissue cutoffs 1, 2, and the noise cutoff were selected using thresholds of 2.5, 1.5Hz, and 0.01, respectively. Similar to the simulation experiment, the maximum tissue cutoff was used for data without adaptive demodulation, while the minimum was used for data with adaptive demodulation.
For this experiment, we considered our baseline case to be the plane wave synthetic focusing beamforming method with the conventional IIR filter and without adaptive demodulation. Adaptive demodulation, SVD, and CFPD were then evaluated separately as well as in combination. Power Doppler was computed and images were formed the same way as in Section II-B. As was done for simulations, dynamic ranges were computed adaptively for each beamformer and filter combination by using the average power of the background of the adaptively demodulated data as the minimum value in the images with and without adaptive demodulation. Blood-to-background SNR, CNR, and GCNR were computed for ensemble sizes between 20ms and 1s, as was done for the simulations.
D. In Vivo Experiment
To demonstrate in vivo feasibility, we tested all combinations of adaptive demodulation, CFPD, and SVD on data acquired from a patient receiving trans-arterial chemoembolization (TACE). TACE is a minimally invasive treatment for intermediate stage liver lesions that do not qualify for curative resection or transplant [24]. TACE works by delivering high doses of chemotherapy as well as embolizing agents to simultaneously treat a tumor and occlude its arterial supply [25]. Therefore, because these tumors are highly vascularized compared to the surrounding healthy liver tissue, we expect to see increased power or perfusion in a tumor before TACE and suppressed or no power in a tumor after TACE.
The patient gave informed written consent in accordance with Vanderbilt’s Institutional Review Board prior to the start of the study. Using a Verasonics C5–2 probe, we acquired 2s of angled plane wave channel data (9 angles spaced evenly between −8° and 8°) immediately before and after TACE. The channel data were acquired using a 1 cycle pulse at a pulse repetition frequency of 5.4kHz (600Hz frame rate after beamforming) and an imaging frequency of 4.2MHz. Channel data were acquired at a sampling frequency of 16.7MHz, and all beamformed data were up-sampled by a factor of 3 to achieve a sampling frequency of 50MHz. For anatomical reference, immediately prior to the acquisition of each plane wave scan, a conventional focused scan was acquired at 6cm. SLSC beamforming was performed using a maximum lag of 10 and a kernel size of 1.5 wavelengths [26].
Using the same plane wave synthetic focusing and CFPD methods and the same receive beamforming parameters described in Section II-B, 0.5s ensembles of channel data before and after TACE were beamformed. Adaptive demodulation was performed using the same baseline settings as in Section II-B. The same IIR filter described in Section II-B was used except with a 30Hz cutoff. SVD was applied using the same adaptive SVD approach with adjusted thresholds that was used for the simulation and phantom experiments. Thresholds of 0.25, 10Hz, and 0.0005 were used for selecting tissue cutoffs 1 and 2 and the noise cutoff, respectively. The same thresholds were used for data with and without adaptive demodulation.
Power Doppler was computed and images were formed the same way as in Section II-B, except that a 2mm by 2mm spatial median filter was applied to each image (instead of 1mm by 1mm). Displayed images were scaled to individual maximums. Dynamic ranges were chosen to achieve qualitatively similar noise floors. To quantify differences between techniques and time points, a tumor-to-background contrast metric was computed as follows,
| (9) |
where N and M are the total number of pixels in the tumor and background, respectively, and PDtumor and PDbkgd are the power Doppler values in the tumor and background, respectively. GCNR was also computed as in Equation (8), where OV L represents the overlap between histograms of the power Doppler values in the tumor and background.
Gold-standard contrast-enhanced computed tomography (CT) was also acquired before and 2 months after TACE. Before TACE, we expect to see tumor enhancement. After TACE, assuming successful treatment, we expect to see lipiodol uptake with no enhancement. Lipiodol is a carrier substance for the chemotherapy that is selectively retained in tumors and enhances CT images separate from the contrast agents used for enhancing blood flow in follow-up imaging [27]. Therefore, bright lipiodol enhancement in the tumor in follow-up imaging indicates successful retention of the chemotherapy [28].
III. Results
A. Simulations
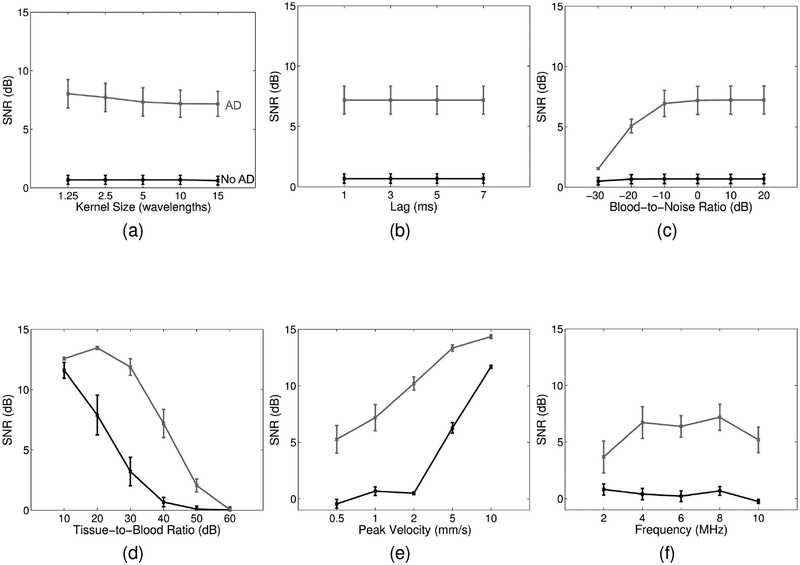
Figure 4 shows blood-to-background SNR for the parameters listed in Table I (except for beamforming and tissue filtering). The kernel size of the relative displacement estimator and the lag used for computing total displacements have minimal effect on SNR (Figures 4a and 4b). The blood-to-noise ratio result shown in Figure 4c suggests that adaptive demodulation becomes less effective if blood is more than 20dB lower than noise (i.e., overall SNR is less than 20dB). Figure 4d shows that adaptive demodulation is most effective when the tissue-to-blood ratio is between 20 and 50dB. Adaptive demodulation is most effective and necessary for velocities below 5mm/s, as shown in Figure 4e. Finally, Figure 4f shows that with adaptive demodulation, SNRs increase slightly with increasing imaging frequency. Without adaptive demodulation, SNRs remain fairly constant with increasing imaging frequencies.
Fig. 4.
Simulated blood-to-background SNR (± standard error) for (a) varying adaptive demodulation (AD) kernel sizes, (b) AD slow-time lag, (c) blood-to-noise ratio, (d) tissue-to-blood ratio, (e) peak blood velocity, and (f) imaging frequency. SNRs with and without AD are shown in gray and black, respectively. Plane wave synthetic focusing and IIR filtering were used for each case.
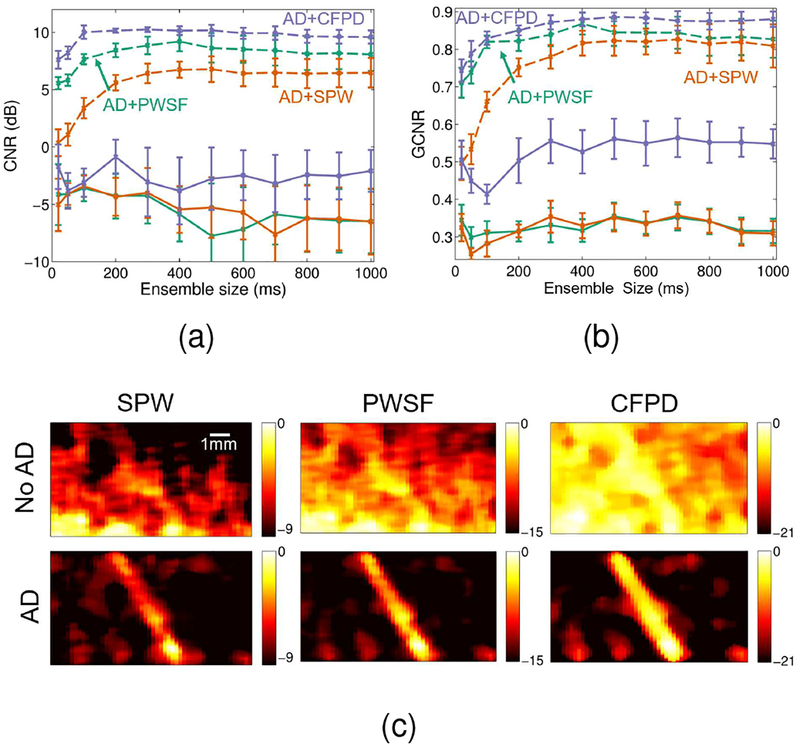
Figure 5 compares single plane wave, plane wave synthetic focusing, and CFPD beamforming methods with and without adaptive demodulation. A 1Hz IIR cutoff was used for tissue filtering. Figures 5a and 5b show that CNR and GCNR increase with adaptive demodulation for all ensembles for all three methods. Adaptive demodulation with CFPD produces the highest CNRs for all ensembles and shows a peak between 100 and 200ms ensembles. Without adaptive demodulation, CFPD produces the highest CNRs and GCNRs compared to plane wave synthetic focusing and single plane wave beam-forming. Figure 5c supports these results qualitatively and shows power Doppler images for an example tissue motion realization for the 400ms ensemble for each beamforming method with and without adaptive demodulation. For the cases without adaptive demodulation, the images are primarily dominated by tissue clutter, but the vessel can be seen in the CFPD case. With adaptive demodulation, the vessel can be seen in all three cases, but the tissue clutter and noise are suppressed the best with the combination of adaptive demodulation and CFPD.
Fig. 5.
Simulated (a) CNR and (b) GCNR (± standard error) vs. ensemble size are plotted for single plane wave (SPW) (orange), plane wave synthetic focusing (PWSF) (teal), and CFPD (purple) beamforming methods with adaptive demodulation (AD) (dotted) and without (solid). (c) Simulated power Doppler images for an example tissue motion realization are shown for SPW (left), PWSF (middle), and CFPD (right) beamforming methods with AD (bottom) and without (top) for the 400ms ensemble. Images are on a dB scale.
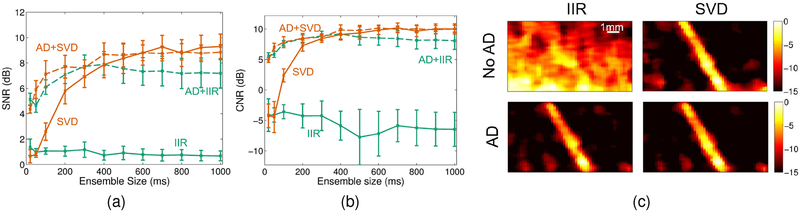
Figure 6 compares conventional IIR (with a 1Hz cutoff) and adaptive SVD filtering methods with and without adaptive demodulation. Figures 6a and 6b show that adaptive demodulation increases blood-to-background SNR and CNR for all ensembles for the IIR filter. With SVD filtering, adaptive demodulation improves SNR and CNR for ensembles below 500ms. For ensembles below 500ms, adaptive demodulation with SVD produces the highest SNRs. Figure 6c supports these results qualitatively and shows power Doppler images for an example tissue motion realization for the 400ms ensemble for each filtering method with and without adaptive demodulation. Without adaptive demodulation, the IIR image is dominated by tissue clutter, but the vessel is seen clearly with SVD by itself. With adaptive demodulation, the vessel can be seen in both cases, but the background noise and tissue clutter are suppressed the best in the image with adaptive demodulation and SVD.
Fig. 6.
Simulated blood-to-background (a) SNR and (b) CNR (± standard error) vs. ensemble size is plotted for IIR (teal) and SVD (orange) filtering methods with adaptive demodulation (AD) (dotted) and without (solid). (c) Simulated power Doppler images for an example tissue motion realization are shown for IIR (left) and SVD (right) filtering methods with AD (bottom) and without (top) for the 400ms ensemble. Images are on a dB scale.
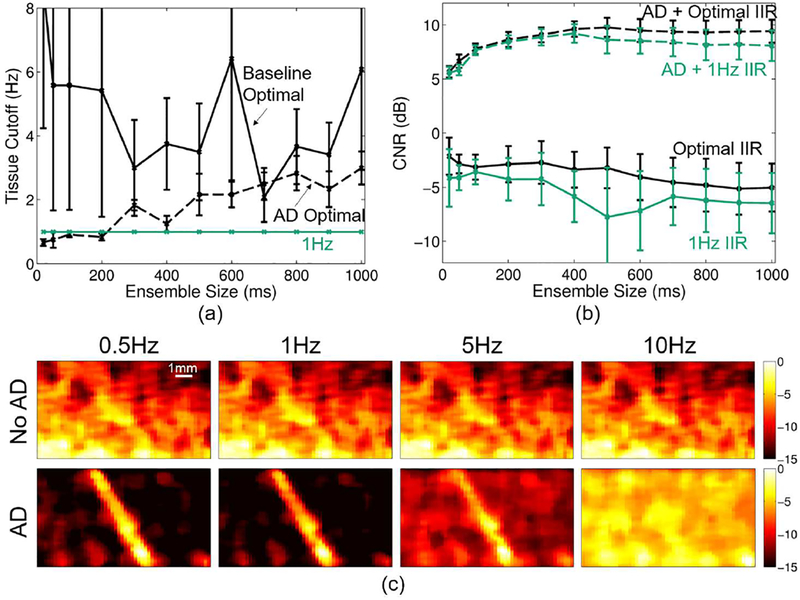
Figure 7 summarizes the IIR filter cutoff selection analysis. Figure 7a shows the average (across realizations) optimal cutoff to produce maximum CNR for each ensemble size for baseline and adaptively demodulated data. Based on this plot, a 1Hz cutoff is not the exact optimal cutoff on average for baseline or adaptively demodulated data for most ensemble sizes. However, the optimal cutoff for all cases is below 5Hz. Figure 7b shows how using a 1Hz cutoff for all realizations and ensemble sizes produces fairly similar CNR to the optimized cases. These observations are supported qualitatively in Figure 7c, which shows power Doppler images for an example realization using a 400ms ensemble for different cutoffs for baseline and adaptively demodulated data. Regardless of cutoff, the vessel cannot be seen in the baseline case. A 1Hz cutoff suppresses background noise better than a 0.5 or 5Hz cutoff for the adaptively demodulated case. Also, as expected with a peak velocity of 1mm/s (10Hz), flow cannot be seen when using a 10Hz cutoff in either case.
Fig. 7.
(a) Average optimal IIR cutoff (± standard error) (black) vs. ensemble size for baseline (solid) and adaptively demodulated (AD) data (dashed). 1Hz cutoff is shown in teal. (b) Average CNR (± standard error) obtained with optimal cutoff (black) and with a 1Hz cutoff (teal) vs. ensemble size for baseline (solid) and AD (dashed). (c) Baseline (top) and AD (bottom) power Doppler images for a single realization made using a 400ms ensemble size and conventional high-pass IIR filter with the following cutoffs (imaged from left to right): 0.5, 1, 5, and 10Hz. Images are on a dB scale.
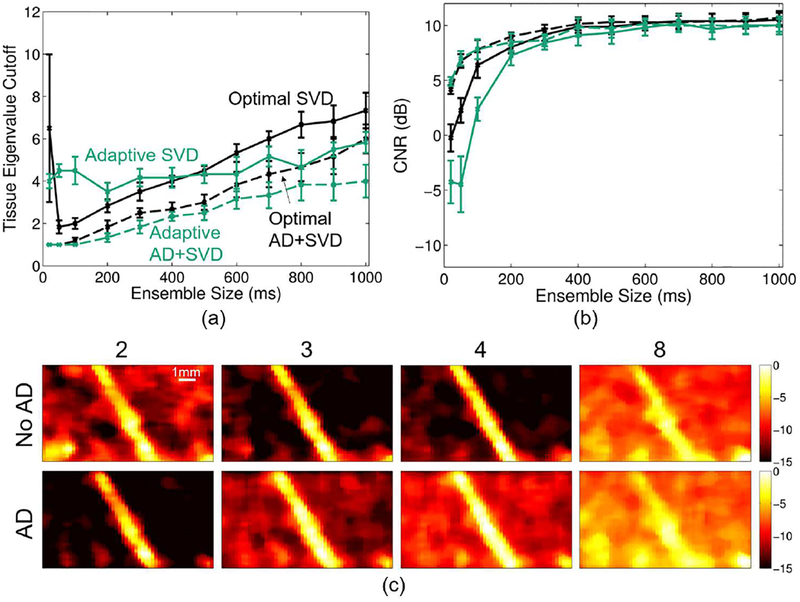
Figure 8 summarizes the SVD tissue filter cutoff selection analysis. Figure 8a shows the average (across realizations) optimal tissue cutoff to produce maximum CNR for each ensemble size for baseline and adaptively demodulated data. Based on this plot, we are not able to reproduce the exact optimal average tissue cutoff for baseline or adaptively demodulated data using the adaptive cutoff selection technique. Figure 8b shows how using the adaptive method for all realizations and ensemble sizes produces very similar CNR to the optimized cases and preserves the overall trends of the optimal curves. These findings are supported qualitatively in Figure 8c, which shows power Doppler images for a range of tissue eigenvalue cutoffs for an example realization using a 400ms ensemble. For this example, the optimal tissue eigenvalue cutoffs are 3 and 2 for the baseline and adaptively demodulated data, respectively. The adaptively chosen cutoffs are 4 and 2. Although the adaptive cutoff selection is an eigenvalue off for the baseline case, the resulting power Doppler images are fairly comparable. Also, the optimal adaptively demodulated case suppresses background noise better than the optimal baseline case. For both cases, the vessel is clearly seen within 1–2 eigenvalues away from the optimal cutoff, but tissue clutter and noise strongly interfere when a larger eigenvalue of 8 is used.
Fig. 8.
(a) Optimal (black) and adaptive (teal) SVD average tissue cutoff (± standard error) vs. ensemble size for baseline (solid) and adaptively demodulated (AD) data (dashed). (b) Average CNR (± standard error) obtained with optimal (black) and adaptively selected (teal) cutoffs vs. ensemble size for baseline (solid) and AD data (dashed). (c) Baseline (top) and AD (bottom) power Doppler images for a single realization made using a 400ms ensemble size and SVD filter (without noise filtering) with the following tissue eigenvalue cutoffs (imaged from left to right): 2, 3, 4, and 8. Images are on a dB scale.
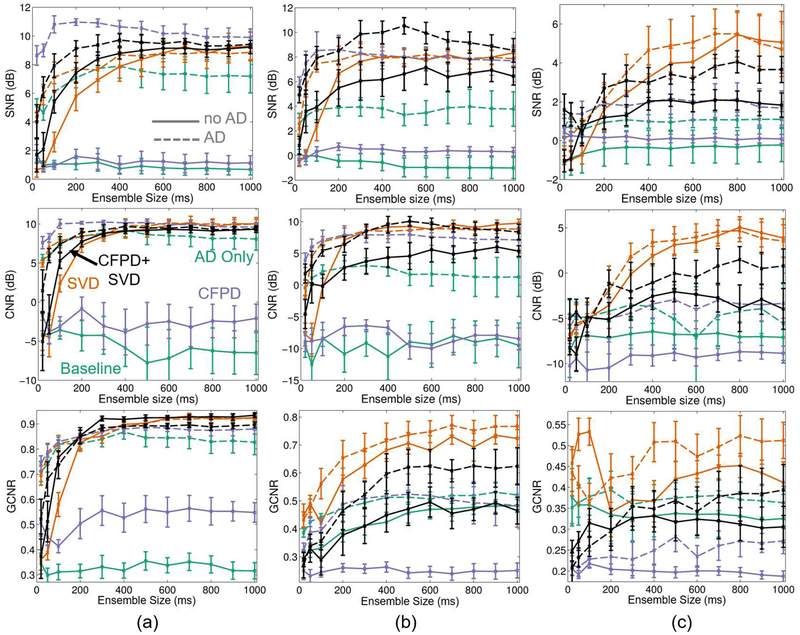
Adaptive demodulation, CFPD, and SVD have all been proposed as potential methods for improving slow blood flow imaging with ultrasound [5], [9], [12]. Because adaptive de modulation is a pre-filtering method, CFPD is a beamforming method, and SVD is a filtering method, they can be used separately or in combination. Figure 9a compares blood-to-background SNR and CNR for varying ensemble sizes for each proclaimed slow flow method separately as well as for each combination of the methods (adaptive demodulation with CFPD, adaptive demodulation with SVD, CFPD+SVD, adaptive demodulation with CFPD+SVD). Adaptive demodulation in combination with CFPD with a 100ms ensemble produced the highest SNR and CNR overall while CFPD+SVD produced the highest GCNR overall. For smaller ensemble sizes (below 200ms), combinations with adaptive demodulation produced the highest SNRs, CNRs, and GCNRs, while combinations with SVD perform similarly to those with adaptive demodulation for larger ensembles.
Fig. 9.
Blood-to-background SNR (top), CNR (middle), and GCNR (bottom) (± standard error) vs. ensemble size is plotted for baseline (teal), SVD (orange), CFPD (purple), and CFPD+SVD (black) with adaptive demodulation (AD) (dotted) and without (solid) for (a) 1mm/s simulations (b) 5mm/s phantom and (c) 1mm/s phantom. Baseline is plane wave synthetic focusing beamforming with a conventional IIR filter and no AD. AD was applied for all cases using a 10λ kernel size and 1ms slow-time lag. Simulated data had a blood-to-noise ratio of 0dB and a tissue-to-blood ratio of 40dB. For both simulations and phantoms, a 7.8125MHz transmit frequency was used.
B. Phantom
Figure 9b shows the same information as Figure 9a for the 5mm/s average velocity single vessel phantom data. The overall SNR and CNR trends and values match fairly well to those observed in simulations. Similar to simulations, adaptive demodulation with CFPD results in a peak SNR and CNR around 100ms. However, the highest overall SNR and CNR was produced using adaptive demodulation with CFPD+SVD.
For the smallest ensemble sizes (below 200ms), combinations with adaptive demodulation produced the highest SNRs and CNRs, while SVD by itself performs similarly to methods with adaptive demodulation for larger ensembles. GCNR shows different trends than SNR and CNR. SVD with and without adaptive demodulation produces the most separation between blood and background, while CFPD by itself produces the most overlap.
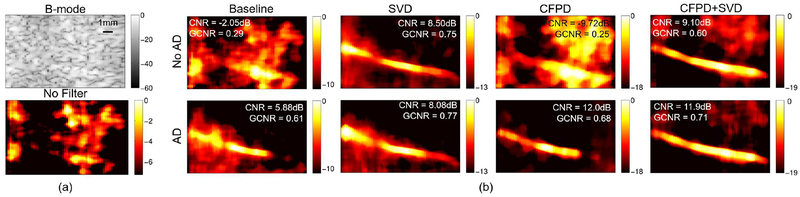
Figure 10 supports the results in Figure 9b qualitatively and shows power Doppler images for an example case for the 400ms ensemble for all combinations of adaptive demodulation, CFPD, and SVD. Figure 10a shows the B-mode and no filter power Doppler images for reference. Adaptive demodulation with CFPD suppresses the background noise the best and resulted in the highest CNR, but adaptive demodulation with CFPD and SVD shows the most uniform flow through the vessel. However, adaptive demodulation with SVD resulted in the highest GCNR.
Fig. 10.
(a) B-mode and power Doppler images made without filtering of the single vessel phantom with 5mm/s average blood velocity. (b) Power Doppler images made with adaptive demodulation (AD) (bottom) and without (top) for baseline, SVD, CFPD, and CFPD+SVD. A 400ms ensemble was used for all power Doppler images. CNR and GCNR values are displayed on each image for reference. Images are on a dB scale.
The quantitative results for the 1mm/s average velocity single vessel phantom data are shown in Figure 9c. For this case, SNR and CNR are low for all methods at the smallest ensembles (below 200ms), indicating poor vessel visibility. However, SNR and CNR improve with ensembles above 200ms, especially when using adaptive demodulation with SVD. Adaptive demodulation with SVD also resulted in the highest GCNR for ensemble sizes above 200ms, but SVD by itself produces the least amount of overlap for ensembles below 200ms. Generally, adaptive demodulation improved SNR, CNR, and GCNR for each method.
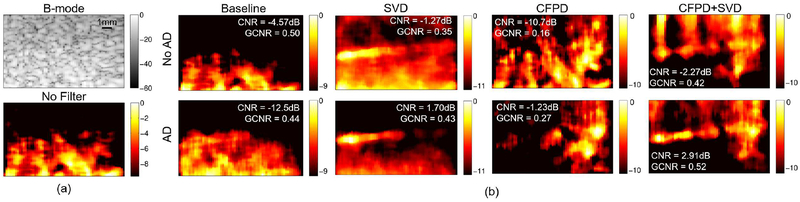
Figure 11 shows power Doppler images for an example case for the 400ms ensemble for all combinations of adaptive demodulation, CFPD, and SVD for the 1mm/s average flow phantom data. Figure 11a shows the B-mode and no filter power Doppler images for reference. Adaptive demodulation with SVD appears to suppress the background noise the best, but, similar to the faster flow phantom data, adaptive demodulation with CFPD+SVD shows the most uniform flow through the vessel and resulted in both the highest CNR and GCNR.
Fig. 11.
(a) B-mode and power Doppler images made without filtering of the single vessel phantom with 1mm/s average blood velocity. (b) Power Doppler images made with adaptive demodulation (AD) (bottom) and without (top) for baseline, SVD, CFPD, and CFPD+SVD. A 400ms ensemble was used for all power Doppler images. CNR and GCNR values are displayed on each image for reference. Images are on a dB scale.
C. In Vivo
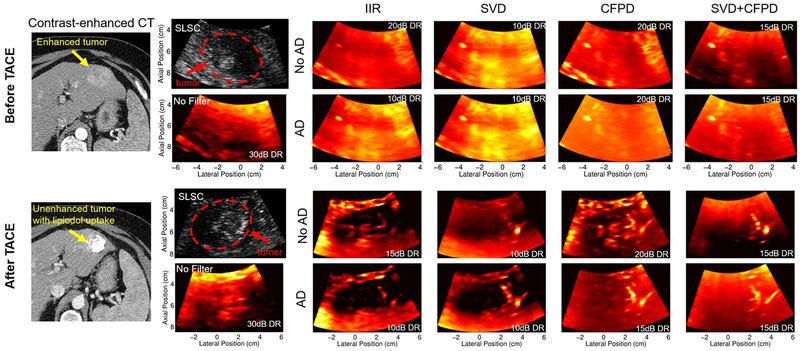
Figure 12 shows anatomical SLSC images with corresponding power Doppler images before and after TACE. Before TACE, SVD and adaptive demodulation with SVD show the most heightened power in the tumor compared to the surrounding healthy liver tissue. After TACE, adaptive demodulation by itself and adaptive demodulation with SVD show the clearest suppression of power in the tumor compared to the surrounding tissue. There is an apparent vessel to the right of the tumor after TACE that is most clearly seen with CFPD combined with adaptive demodulation and CFPD combined with adaptive demodulation and SVD.
Fig. 12.
Gold-standard contrast-enhanced CT, anatomical SLSC and power Doppler images before (top) and after (bottom) TACE. Post-treatment CT and ultrasound were acquired 2 months and immediately after TACE, respectively. Power Doppler images are shown for each combination of adaptive demodulation (AD), SVD, and CFPD as well as for baseline IIR filtering and no tissue filtering. Dynamic ranges (DR) are displayed on each power Doppler image and were chosen to ensure qualitatively similar noise floors.
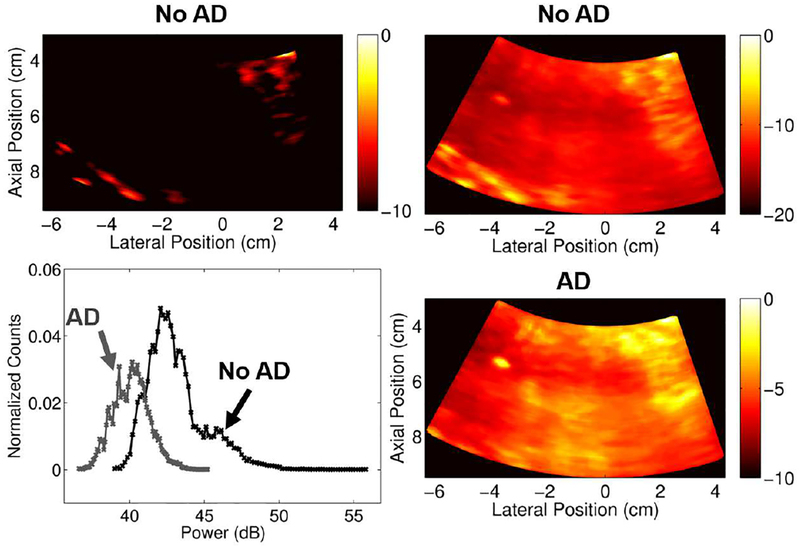
Figure 13 demonstrates the potential need for different dynamic ranges for data with and without adaptive demodulation. Based on the example in Figure 13, a 10dB dynamic range includes the majority of the signal for the image with adaptive demodulation. However, if a 10dB dynamic range is used for the data without adaptive demodulation, the majority of the signal is excluded. This is likely because more tissue passed through the conventional IIR filter when adaptive demodulation was not used. Therefore, a 20dB dynamic range was chosen for the data without adaptive demodulation to obtain qualitatively similar overall intensities.
Fig. 13.
In vivo dynamic range evaluation. Power Doppler images are on a dB scale and are shown for the data before TACE made with conventional IIR filtering. Images without adaptive demodulation (AD) are shown in the top row with dynamic ranges of 10dB (left) and 20dB (right). The image with AD is shown in the bottom right and is made with a dynamic range of 10dB. The plot in the bottom left shows the histograms of the data (after log compression but before scaling to the maximums) with AD (gray) and without AD (black).
The quantitative tumor-to-background contrast results are displayed in Table II. SVD by itself resulted in the highest contrast and GCNR before TACE, while adaptive demodulation with IIR filtering resulted in the lowest contrast after TACE (i.e., largest suppression of power in the tumor compared to surrounding tissue). Adaptive demodulation with SVD resulted in the largest temporal change in power (6.9dB).
TABLE II.
Tumor-to-background contrast (dB) before and after TACE computed on power Doppler images with no filtering and with all possible combinations of IIR, SVD, CFPD, and adaptive demodulation (AD). GCNR values are indicated in parentheses. Change in contrast = Cbefore − Cafter.
| Method | Before TACE |
After TACE |
Change |
|---|---|---|---|
| No Filter | 2.4 (0.19) | 7.4 (0.64) | −5.0 |
| IIR | 2.2 (0.88) | −3.3 (0.91) | 5.5 |
| AD+IIR | 1.8 (0.90) | −5.0 (1.00) | 6.8 |
| SVD | 2.4 s(0.97) | −3.7 (1.00) | 6.0 |
| AD+SVD | 2.3 (0.96) | −4.6 (1.00) | 6.9 |
| CFPD | 0.1 (0.33) | 2.2 (0.58) | −2.1 |
| AD+CFPD | −0.7 (0.62) | 0.1 (0.07) | −0.7 |
| CFPD+SVD | 0.4 (0.29) | 3.7 (0.93) | −3.3 |
| AD+CFPD+SVD | −0.4 (0.49) | 2.6 (1.00) | −3.1 |
The gold-standard contrast-enhanced CT images support the ultrasound results. The pre-treatment CT image confirms that the tumor had greater cumulative vasculature compared to the surrounding healthy liver tissue. The 2 month follow-up CT image after TACE confirms that the treatment successfully stopped blood flow to the tumor and that lipiodol was retained, indicating tumor necrosis [28].
IV. Discussion
The simulated parameter study resulted in expected trends for the blood-to-noise ratio, tissue-to-blood ratio, and peak velocity experiments. We anticipated that adaptive demodulation would become less effective in noisy environments because, regardless of tissue bandwidth suppression, blood would be overpowered by noise, which is what we saw for blood-to-noise ratios below −20dB. Also, because adaptive demodulation relies on tissue to be sufficiently stronger than blood so as not to estimate and demodulate blood motion, we expected to see a decrease in blood-to-background SNR at low tissue-to-blood ratios, which is what we observed for tissue-to-blood ratios less than 20dB. Finally, we expected to see increased blood-to-background SNR as peak blood velocity increased because this would lead to better spectral separation between blood and tissue, which is what we saw for all velocities tested.
The parameter study also resulted in a few unexpected trends. We expected to see an increase in blood-to-background SNR with larger kernel sizes, longer lags, and higher imaging frequencies, but we saw minimal changes when varying these parameters. We expected that increasing the kernel size would improve the accuracy of the tissue displacement estimator and thereby improve the adaptive demodulation of the tissue clutter [29], but we actually observed a slight decrease with larger kernels. It is possible that small tissue displacements were averaged out with the larger kernels [29], preventing full demodulation of the tissue clutter. We also expected tissue displacement estimation accuracy, and therefore adaptive tissue clutter demodulation, to improve with larger lags [19], and although we did see a very slight increase in SNR for lags above 1 slow-time sample, the small improvement does not warrant the trade off for longer processing times. For the realizations used in this experiment, it is possible that a lag of 1 slow-time sample produces estimates that are sufficiently close to the true displacement which is why we do not see much improvement with larger lags. Larger kernel sizes and lags can also suffer from decorrelation effects which could also explain the observed trends [30]. Finally, we expected to see a consistent increase in SNR with increasing imaging frequencies, which would support the findings by Heimdal and Torp [1]. However, without adaptive demodulation, SNRs are relatively constant, and with adaptive demodulation, SNR does increase slightly, but decreases for the 10MHz case. These discrepancies could be because we used different kernel sizes for different center frequencies to maintain similar axial fields of view. Also, it is possible that we would see a steadier increase if we looked at more frequencies above 10MHz.
Although precisely optimal tissue cutoffs were not used for IIR and SVD filtering, Figures 7 and 8 demonstrate that the observed optimal trends are still generally achieved with a fixed IIR cutoff and an adaptive SVD approach. Optimal cutoff selection is impossible clinically with unknown structures in the field of view. Therefore, for realistic clinical scenarios, cutoffs are chosen based on the application, which we have reproduced here to showcase the feasibility of these methods.
The simulation results were mostly validated with the single vessel phantom data with 5mm/s average blood flow. The phantom blood-to-background SNRs, CNR, and GCNRs for this case have similar trends and values to the simulated SNRs, CNRs, and GCNRs. However, unlike simulations, the highest SNR is achieved when combining all three methods together. Apart from this discrepancy, the 5mm/s velocity phantom trends generally agree with the simulation trends, which supports the reproducibility of our simulations. The slower flow phantom data (1mm/s average flow) produced lower metric values overall and the trends were not as well matched to the simulation and faster flow phantom data. For this case, SVD with and without adaptive demodulation produced the highest SNR, CNR, and GCNR. For ensembles below 500ms, adaptive demodulation with SVD improves SNR and CNR compared to SVD by itself. Although this phantom case produced different trends than the simulations and 5mm/s phantom case, it still demonstrates the value of adaptive demodulation for each method (i.e., the dotted AD curves are all generally higher than the solid no AD curves). Furthermore, the example realization shown in Figure 11 shows how these techniques have the potential to resolve predominately lateral flow.
For both the simulations and 5mm/s average flow phantom data, the SNRs, CNRs, and GCNRs for all cases appear to either peak at smaller ensembles and then converge at larger ensembles or slowly plateau. This is less apparent for the 1mm/s average flow phantom, but still generally true. It is possible that the metrics converge due to signal decorrelation at long ensembles and that averaging over shorter ensembles would produce higher image quality metrics. Another hypothesis is that the demodulated noise becomes a more significant source of error for longer ensembles. Future work will aim to investigate correlation changes through slow-time as well as the effects of the demodulated noise term. Additionally, longer than 1s ensembles should be evaluated to see if SNR, CNR, and GCNR truly converge or if they ultimately continue to increase or decrease.
The in vivo TACE study provides a unique setting for testing slow flow techniques because it involves both spatial and temporal changes in perfusion. Before TACE we expect to see heightened power in the tumor because we know liver tumors are highly vascularized compared to the surrounding healthy liver tissue. Gold-standard pre-treatment CT imaging confirms this, and 2-month follow-up CT imaging confirms that the treatment was successful. Therefore, after TACE we expect to see suppressed power Doppler in the tumor compared to surrounding tissue. For the example case included in this work, adaptive demodulation combined with IIR and adaptive demodulation combined with SVD resulted in the largest changes in tumor contrast, suggesting that there is a potential benefit of using adaptive demodulation for detecting both temporal and spatial changes in tumor perfusion before and after TACE. Although other factors could contribute to the increase in power in the tumor before TACE, it is reasonable to believe that most of the enhanced power is due to increased flow because we know this happens physiologically. Also, because we are using a 30Hz (5.5mm/s) IIR cutoff, we do not expect power in the images to be directly correlated to perfusion, but we do expect to be visualizing flow in vessels that directly feed into and drain out of capillaries, such as arterioles and venules. In the power Doppler images after TACE, a vessel to the right of the tumor is clearly resolved. This residual flow could potentially be from the pressure head of the feeding artery reaching but not perfusing the tumor branches, indicating successful arterial occlusion.
GCNR is a newly proposed metric that should be robust to dynamic range alterations caused by adaptive beamformers [22]. By computing the probability of detection, GCNR avoids the inherent issue with scaling SNR, CNR, and contrast for different beamformers that alter the signal in some way. We have implemented it in this work to account for comparisons between the different beamformers used in simulations, phantoms, and in vivo data, namely plane wave synthetic focusing and SLSC used in CFPD. In our initial implementation, GCNR generally agrees with the SNR, CNR, and contrast metrics. However, we also observed that GCNR can result in discrepancies between what is observed qualitatively. For example, in Figure 11, the GCNR value for conventional IIR filtering by itself (i.e., baseline) is 0.5, suggesting that there is a 50% chance of detecting flow in the vessel, which is not seen in the image. However, for adaptive demodulation and SVD, the GCNR value is only 0.43, even though the vessel is clearly seen in the image. The GCNR values make sense because the vessel signal is clearly much lower compared to background in the baseline image, while the vessel and background have more overlapping pixels in the adaptive demodulation and SVD image. However, the vessel is visually detected in the adaptive demodulation with SVD image despite the GCNR metric. Therefore, GCNR along with CNR, SNR, and contrast should be used carefully for flow detection comparisons.
The single vessel model used for the simulation and phantom experiment is useful for comparing techniques. However, it is not fully representative of realistic in vivo settings in which many small vessels will be in the field of view and within a given resolution cell. The simulation and phantom vessel diameters used in this work are relatively small, but they are not on the order of capillary or other small vessel diameters, which are smaller than the achievable lateral resolution. Therefore, we do not expect to resolve flow in individual capillaries or other small vessels, especially with lower transmit frequencies and at deeper depths, as was used in our in vivo study, but we do expect to be sensitive to flow from the collection of small vessels within a given resolution cell. Based on this assumption, we hypothesize that heightened power within a single pixel in the tumor in our in vivo images before TACE in Figure 12 potentially results from increased flow in several small vessels within that pixel.
Apart from resolution limitations, depth-dependent SNR limitations will also affect perfusion imaging techniques at deeper depths. The simulation and phantom experiments in this work focus on shallower depths for testing different techniques, but realistic in vivo imaging will require sensitivity at deeper depths, as we observe in our in vivo example. We demonstrate that these techniques, especially adaptive demodulation and SVD, can work in realistic settings at depths down to 9.5cm and produce results that are consistent with expected physiological treatment effects. However, we show in Figure 4c that adaptive demodulation performs best at blood-to-noise SNRs above 20dB. This suggests that adaptive demodulation will suffer as SNR decreases. Similarly, the global SVD approach that we have applied relies on similar noise statistics throughout the field of view. This is less attainable in vivo with larger, deeper fields of view [15]. Song et al. addresses this with a block-wise approach with noise equalization [15]. Also, CFPD intends to improve depth-dependent SNR limitations by reducing near field reverberation clutter and thermal noise [10]. Therefore, implementing and optimizing some of these techniques could further improve imaging of slow flow at deeper depths.
It is worth noting that the CFPD signal has not yet been shown to be linearly correlated to blood volume as is the case with conventional power Doppler. Also, conventional power Doppler signal will become less correlated to blood volume in low SNR environments. Because capillaries and other small vessels often cannot be qualitatively resolved, blood volume quantification is crucial. Therefore, the value of CFPD may be most relevant for resolvable structures, and, assuming reasonable SNR, conventional power Doppler with adaptive demodulation and SVD would be the best option for sub-resolution structures.
V. Conclusion
Perfusion ultrasound imaging is difficult, mainly because of spectral broadening of tissue clutter signal caused by patient and sonographer hand motion, but other issues like SNR are also challenging. We previously introduced adaptive demodulation as a solution for suppressing tissue clutter bandwidths. We implemented the method using single plane wave imaging and conventional IIR filtering. Here, we showed that we can improve this technique with better beamforming (plane wave synthetic focusing and CFPD) and tissue filtering (SVD). Simulated blood-to-background CNRs were highest when using adaptive demodulation with CFPD with smaller ensembles. Phantom CNRs were highest when combining adaptive demodulation, CFPD and SVD for the 5mm/s flow speed and when combining adaptive demodulation and SVD for the 1mm/s flow speed. Finally, we showed clinical feasibility and potential benefit for combining adaptive demodulation and SVD in our in vivo liver tumor embolization study. Combining these proclaimed slow-flow techniques has the potential to make perfusion ultrasound imaging possible.
Acknowledgment
The authors would like to thank the staff of the Vanderbilt University ACCRE computing resource. This work was supported in part by NIH grants 1R35HL135790–01 and S10OD016216–01.
Contributor Information
Jaime Tierney, Department of Biomedical Engineering, Vanderbilt University, Nashville, TN, USA.
Kristy Walsh, Department of Biomedical Engineering, Vanderbilt University, Nashville, TN, USA.
Helen Griffith, Department of Biomedical Engineering, Vanderbilt University, Nashville, TN, USA.
Jennifer Baker, Department of Radiology, Vanderbilt University Medical Center, Nashville, TN, USA.
Daniel Brown, Department of Radiology, Vanderbilt University Medical Center, Nashville, TN, USA.
Brett Byram, Department of Biomedical Engineering, Vanderbilt University, Nashville, TN, USA.
References
- [1].Heimdal A and Torp H, “Ultrasound doppler measurements of low velocity blood flow: limitations due to clutter signals from vibrating muscles,” IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, vol. 44, pp. 873–881, 1997. [Google Scholar]
- [2].Tremblay-Darveau C, Williams R, Milot L, Bruce M, and Burns PN, “Combined perfusion and doppler imaging using plane-wave nonlinear detection and microbubble contrast agents,” IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, vol. 61, pp. 1988–2000, 2014. [DOI] [PubMed] [Google Scholar]
- [3].Jensen JA, Estimation of Blood Velocities Using Ultrasound: A Signal Processing Approach. Cambridge: Cambridge UP, 1996. [Google Scholar]
- [4].Bjaerum S, Torp H, and Kristoffersen K, “Clutter filters adapted to tissue motion in ultrasound color flow imaging,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 49, pp. 693–704, 2002. [DOI] [PubMed] [Google Scholar]
- [5].Tierney J, Coolbaugh C, Towse T, and Byram B, “Adaptive clutter demodulation for non-contrast ultrasound perfusion imaging,” IEEE Transactions on Medical Imaging, vol. 36, pp. 1979–1991, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Mace E, Montaldo G, Osmanski BF, Cohen I, Fink M, and Tanter M, “Functional ultrasound imaging of the brain: theory and basic principles,” IEEE transactions on ultrasonics, ferroelectrics, and frequency control, vol. 60, pp. 492–506, 2013. [DOI] [PubMed] [Google Scholar]
- [7].Udesen J, Gran F, Hansen KL, Jensen JA, Thomsen C, and Nielsen MB, “High frame-rate blood vector velocity imaging using plane waves: Simulations and preliminary experiments,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 55, pp. 1729–1743, 2008. [DOI] [PubMed] [Google Scholar]
- [8].Bjaerum S, Torp H, and Kristoffersen K, “Clutter filter design for ultrasound color flow imaging,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 49, pp. 204–216, 2002. [DOI] [PubMed] [Google Scholar]
- [9].Li YL and Dahl JJ, “Coherent flow power doppler (cfpd): Flow detection using spatial coherence beamforming,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 62, pp. 1022–1035, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Li YL, Hyun D, Abou-Elkacem L, Willmann JK, and Dahl J, “Visualization of small-diameter vessels by reduction of incoherent reverberation with coherent flow power doppler,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 63, pp. 1878–1889, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Gallippi C and Trahey G, “Adaptive clutter filtering via blind source separation for two-dimensional ultrasonic blood velocity measurement,” Ultrasonic Imaging, vol. 24, pp. 193–214, 2002. [DOI] [PubMed] [Google Scholar]
- [12].Demene C, Deffieux T, Pernot M, Osmanski BF., Biran V, Franqui S, and Tanter M, “Spatiotemporal clutter filtering of ultrafast ultrasound data highly increases doppler and fultrasound sensitivity,” IEEE Transactions on Medical Imaging, vol. 34, pp. 2271–2285, 2015. [DOI] [PubMed] [Google Scholar]
- [13].Montaldo G, Tanter M, Bercoff J, Benech N, and Fink M, “Coherent plane-wave compounding for very high frame rate ultrasonography and transient elastography,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 56, pp. 489–506, 2009. [DOI] [PubMed] [Google Scholar]
- [14].Fadnes S, Bjaerum S, Torp H, and Lovstakken L, “Clutter filtering influence on blood velocity estimation using speckle tracking,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 62, pp. 2079–2091, 2015. [DOI] [PubMed] [Google Scholar]
- [15].Song P, Manduca A, Trzasko JD, and Chen S, “Ultrasound small vessel imaging with block-wise adaptive local clutter filtering,” IEEE Transactions on Medical Imaging, vol. 36, pp. 251–262, 2017. [DOI] [PubMed] [Google Scholar]
- [16].Yu ACH and Lovstakken L, “Eigen-based clutter filter design for ultrasound color flow imaging: a review,” IEEE transactions on ultrasonics, ferroelectrics, and frequency control, vol. 57, pp. 1096–1111, 2010. [DOI] [PubMed] [Google Scholar]
- [17].Loupas T, Powers JT, and Gill RW, “An axial velocity estimator for ultrasound blood flow imaging, based on a full evaluation of the doppler equation by means of a two-dimensional autocorrelation approach,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 42, pp. 672–688, 1995. [Google Scholar]
- [18].Dahl JJ, McAleavey SA, Pinton GF, Soo MS, and Trahey GE, “Adaptive imaging on a diagnostic ultrasound scanner at quasi real-time rates,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 53, pp. 1832–1843, 2006. [DOI] [PubMed] [Google Scholar]
- [19].Guass RC, Trahey GE, and Soo MS, “Wavefront estimation in the human breast,” in Medical Imaging 2001. International Society for Optics and Photonics, May 2001, pp. 172–181. [Google Scholar]
- [20].Jensen JA, “Field: A program for simulating ultrasound systems,” Med. Biol. Eng. Comput, vol. 34, pp. 351–353, 1996.8945858 [Google Scholar]
- [21].Baranger J, Arnal B, Perren F, Baud O, Tanter M, and Demene C, “Adaptive spatiotemporal svd clutter filtering for ultrafast doppler imaging using similarity of spatial singular vectors,” IEEE Transactions on Medical Imaging, 2018. [DOI] [PubMed] [Google Scholar]
- [22].Molares, “The generalized contrast-to-noise ratio,” in Proceedings of the IEEE International Ultrasonics Symposium, Kobe, Japan, October 2018. [Google Scholar]
- [23].Dumont D, Dahl J, Miller E, Allen J, Fahey B, and Trahey G, “Lower-limb vascular imaging with acoustic radiation force elastography: demonstration of in vivo feasibility,” IEEE transactions on ultrasonics, ferroelectrics, and frequency control, vol. 56, pp. 931–944, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Lammer J, Malagari K, Vogl T, Pilleul F, Denys A, Watkinson A, Pitton M, Sergent G, Pfammatter T, Terraz S, Benhamou Y, Avajon Y, Gruenberger T, Pomoni M, Langenberger H, Schuchmann M, Dumortier J, Mueller C, Chevallier P, and Lencioni R, “Prospective randomized study of doxorubicin-eluting-bead embolization in the treatment of hepatocellular carcinoma: Results of the precision v study,” Cardiovascular and Interventional Radiology Society of Europe, vol. 33, pp. 41–52, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Gaba RC, Lewandowski RJ, Hickey RH, Baerlocher MO, Cohen EI, Dariushnia SR, d’Othee BJ, Padia SA, Salem R, Wang DS, Nikolic B, and Brown DB, “Transcatheter therapy for hepatic malignancy: Standardization of terminology and reporting criteria,” Journal of Vascular Interventional Radiology, vol. 27, pp. 457–473, 2016. [DOI] [PubMed] [Google Scholar]
- [26].Lediju MA, Trahey GE, Byram BC, and Dahl JJ, “Shortlag spatial coherence of backscattered echoes: Imaging characteristics,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 58, pp. 1377–1388, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Vogl TJ, Naguib N, Nour-Eldin A, Rao P, Emami AH, Zangos S, Nabil M, and Abdelkader A, “Review on transarterial chemoembolization in hepatocellular carcinoma: palliative, combined, neoadjuvant, briding, and symptomatic indications,” European Journal of Radiology, vol. 72, pp. 505–516, 2009. [DOI] [PubMed] [Google Scholar]
- [28].Brown DB, Nikolic B, Covey AM, Nutting CW, Saad WE, Salem R, Sofocleous CT, and Sze DY, “Quality improvement guidelines for transhepatic arterial chemoembolization, embolization, and chemotherapeutic infusion for hepatic malignancy,” Journal of Vascular and Interventional Radiology, vol. 23, pp. 287–294, 2012. [DOI] [PubMed] [Google Scholar]
- [29].Pinton GF, Dahl JJ, and Trahey GE, “Rapid tracking of small displacements with ultrasound,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 53, pp. 1103–1117, 2006. [DOI] [PubMed] [Google Scholar]
- [30].Walker WF and Trahey GE, “A fundamental limit on delay estimation using partially correlated speckle signals,” IEEE transactions on ultrasonics, ferroelectrics, and frequency control, vol. 42, pp. 301–308, 1995. [Google Scholar]