Empirical Bayes Estimation and Prediction Using Summary-Level Information From External Big Data Sources Adjusting for Violations of Transportability

Abstract

Large external data sources may be available to augment studies that collect data to address a specific research objective. In this article we consider the problem of building regression models for prediction based on individual-level data from an “internal” study while incorporating summary information from an “external” big data source. We extend the work of Chatterjee et al (2016a) by introducing an adaptive empirical Bayes shrinkage estimator that uses the external summary-level information and the internal data to trade bias with variance for protection against departures in the conditional probability distribution of the outcome given a set of covariates between the two populations. We use simulation studies and a real data application using external summary information from the Prostate Cancer Prevention Trial to assess the performance of the proposed methods in contrast to maximum likelihood estimation and the constrained maximum likelihood (CML) method developed by Chatterjee et al (2016a). Our simulation studies show that the CML method can be biased and inefficient when the assumption of a transportable covariate distribution between the external and internal populations is violated, and our empirical Bayes estimator provides protection against bias and loss of efficiency.

1. Introduction

Large external data sources, e.g. health care and claims databases, registries and various consortia of individual studies, are becoming available to investigators for research purposes. These data sources are appealing due to their large sample sizes; however, they often do not contain the same detailed information as an individual-level study carefully designed to address a specific research aim of interest. Combining information from large external studies with information from a smaller but more detailed study can improve efficiency in estimation and prediction. Methods that only require summary-level information from the external data source are appealing in that they do not require sharing of the external data and may be publicly available. In this article we consider the problem of building regression models based on individual-level data from an “internal” study while incorporating summary-level information from an “external” big data source. Improving efficiency of model parameter estimates and prediction are the main goals of this article.

There is substantial literature describing methods to combine external and internal information when external individual-level data are available. For example, many authors (Deville and Sarndal (1992); Robins et al (1994); Wu and Sitter (2001); Wu (2003); Lumley et al (2011)) use optimal calibration equations to improve efficiency of parameter estimates within various classes of unbiased estimators. In special cases where it can be assumed that the covariate information in the external data source can be summarized into discrete strata, a number of researchers have proposed semi-parametric maximum likelihood methods (Breslow and Holubkov (1997); Scott and Wild (1997); Lawless et al (1999)). However, as noted in Chatterjee et al (2016a), the external data set may often include combinations of many variables and summarizing this information into strata can be subjective and inefficient.

Chatterjee et al (2016a) addressed these issues by developing a semi- parametric maximum likelihood estimation method that assumes the external information is summarized by a finite set of parameters rather than a discrete set of strata defined by the study variables. Their framework allows arbitrary types of covariates and arbitrary types of regression models. In addition, they showed via simulation studies that their constrained maximum likelihood (CML) method can achieve major efficiency gains over generalized regression (GR) calibration estimators such as those proposed in Chen and Chen (2000). However, as indicated in Chatterjee et al (2016b); Patel and Dominici (2016); Han and Lawless (2016); Louis and Keiding (2016); Haneuse and Rivera (2016); Mefford et al (2016), many estimators considered in the existing literature of survey sampling, two-phase sampling, empirical likelihood methodology and their proposed CML method assumes that the entire probability distribution (outcome and covariates) is transportable between the two populations, i.e., the joint probability distributions are the same in both populations. Ignoring differences in the covariate distributions in the internal and external populations can yield substantially biased parameter estimates and a loss of efficiency. To address this issue, Chatterjee et al (2016a) introduce synthetic maximum likelihood, which requires that an external reference sample is available for unbiased estimation of the covariate distribution for the external population. When such a reference is not available, which is likely to be the case in practice, we propose an Empirical Bayes estimation procedure that shrinks the parameter estimates of the full model fitted to the internal data via maximum likelihood towards the CML estimates, which borrows information from the external data source, using weights, that in a sense, quantify available evidence against the assumption of a transportable conditional probability distribution of the outcome given a set of covariates.

More recently, Grill et al (2017) compared different approaches for incorporating new information into existing risk prediction models. Methods considered included the CML and various updating methods based on Bayes’ Theorem and likelihood ratio approaches whose performance depends on restrictions such as rare disease prevalence and/or independence between risk predictors and newly collected markers. Based on their studies, they recommended the use of CML or a likelihood ratio joint estimation method for prediction model updating, but note the appeal of CML because it does not require specification of the conditional distribution of the new marker given the risk predictors. Thus, we focus on maximum likelihood and CML as comparators to our proposed EB methods.

Our paper is organized as follows. We introduce empirical Bayes (EB) estimators in Section 2.2, and carry out simulation studies in Section 3. In Section 4, we present a motivating data application involving external summary-level information obtained from an online risk prediction calculator resulting from the Prostate Cancer Prevention Trial Thompson et al (2006), an internal data set including novel biomarkers and a validation data set obtained from men scheduled for a diagnostic prostate biopsy at community clinics throughout the United States as described in Tomlins et al (2016). We compare the performance of our EB estimators with maximum likelihood and CML when significant differences exist in the covariate distributions between the two data sources. Concluding remarks are made in Section 4.

2. Methods

2.1. Model Definition

Let Y be an outcome variable of interest and X be a set of covariates. We assume a model $g_{\theta }(y|x)$ has been built from an “external” big data set and the individual-level data from the external data set are not available. Data on Y, X, and a new set of covariates Z are available from an “internal” study to build a model of the form $f_{\beta }(y|x,z).$ Henceforth, $f_{\beta }(y|x,z)\text{and}{g}_{\theta }(y|x)$ will be referred to as the “full” and “reduced” models respectively. We assume $f_{\beta }(y|x,z)$ is correctly specified, but the external model $g_{\theta }(y|x)$ need not be.

2.2. Empirical Bayes Shrinkage Estimator of Model Parameters

Let $\left\{\left(Y_i,X_i,Z_i\right):i=1,\dots ,N\right\}$ denote a random sample of subjects from an internal population, and let F(X, Z) denote the joint distribution function of (X, Z). The CML estimation method introduced in Chatterjee et al (2016a) gives $\widehat{\beta }$ that maximizes

$$\log \left(L_{\beta ,F}\right)+{\text{λ}}^{\text{T}}\int {\mu }_{\beta }(X,Z;\theta )dF(X,Z)$$ (1)

with respect to $(\beta ,\text{λ},F)$ where $L_{\beta ,F}={\prod }_{i=1}^N{f}_{\beta }\left(Y_i|X_i,Z_i\right)dF\left(X_i,Z_i\right),{\mu }_{\beta }(X,Z;\theta )={\int }_{Y}U(Y|X,\theta )f_{\beta }(Y|X,Z)dY,U(Y|X,\theta )=\partial \log \left\{g_{\theta }(Y|X)\right\}/\partial \theta$ is the score function associated with the reduced model, and λ is a vector of Lagrange multipliers with the same dimension as θ. The value of θ is given to us externally, and is fixed at this value in ${\mu }_{\beta }(X,Z;\theta ).$ Thus, the proposed method can be thought of as a function $\psi :{ℝ}^p\to {ℝ}^{p+K}$ that takes an input $\widehat{\theta }$ and outputs an estimate $\widehat{\beta }\equiv \psi (\widehat{\theta })$ of β where p is the number of parameters in the reduced model and p + K is the number of parameters in the full model. Under various conditions noted in Chatterjee et al (2016a), the CML estimator is asymptotically more efficient than the maximum likelihood estimator based only on the internal data.

An implicit assumption of the CML method is that the entire probability distribution pr(y, x, z) is transportable between the internal and external populations. Since Z is only observed in the internal study, this assumption cannot be checked directly via the external summary-level information and the internal study data. However, evidence against the transportability of pr(y, x) provides evidence against the transportability of pr(y, x, z). Let ${\theta }_I\text{and}{\theta }_E$ denote the limiting parameter values of the reduced model in the internal and external populations respectively. When pr(y, x) is transportable so is $\text{pr}(y|x),$ and we expect the difference between ${\widehat{\theta }}_I\text{and}{\widehat{\theta }}_E$ to be small for sufficiently large internal sample size n where ${\widehat{\theta }}_I\text{and}{\widehat{\theta }}_E$ are the maximum likelihood estimates of ${\theta }_I\text{and}{\theta }_E$. Similar to Mukherjee and Chatterjee (2008), when one is not certain about the assumption of transportability, one may posit a stochastic framework for the underlying true parameter $\theta ~N\left({\theta }_0,\mathbf{A}\right)$ for some covariance matrix A. A first order Taylor’s expansion of $\psi (\theta )$ about ${\theta }_0$ gives

$$\psi (\theta )\approx \psi \left({\theta }_0\right)+{\nabla }^{\text{T}}\left(\theta -{\theta }_0\right)$$ (2)

where ${\nabla }^{\text{T}}$ is the gradient matrix of $\psi (\theta )$ with dimension $(p+K)\times p$ evaluated at $\theta ={\theta }_0$ yielding a prior distribution $N\left\{\psi \left({\theta }_0\right),{\nabla }^{\text{T}}\mathbf{A}\nabla \right\}\text{on}\psi (\theta ).$ Let ${\mathit{\Sigma }}_I$ be the asymptotic variance of $\psi \left({\widehat{\theta }}_I\right).$ Then an approximation to the Bayes estimate of $\psi (\theta )$ for a fixed A is given by

$${\nabla }^{\text{T}}\mathbf{A}\nabla {\left\{{\mathit{\Sigma }}_I+{\nabla }^{\text{T}}\mathbf{A}\nabla \right\}}^{-1}\psi \left({\widehat{\theta }}_I\right)+{\mathit{\Sigma }}_I{\left\{{\mathit{\Sigma }}_I+{\nabla }^{\text{T}}\mathbf{A}\nabla \right\}}^{-1}\psi \left({\theta }_0\right).$$ (3)

The components in (3) are estimated as follows. Under the assumption that the external population is representative of the target population of interest, θ₀ is estimated via ${\widehat{\theta }}_E.$ From Result 1 below, $\psi \left({\widehat{\theta }}_I\right)$ is equal to ${\widehat{\beta }}_I,$ the maximum likelihood estimate of the parameters in the full model fitted to the internal data which has an asymptotic normal distribution $N\left({\beta }_0,{\mathit{\Sigma }}_I\right).$ We estimate ${\mathit{\Sigma }}_I$ via its maximum likelihood estimate ${\widehat{\mathit{\Sigma }}}_I,\mathbf{A}$ is estimated via $\left({\widehat{\theta }}_I-{\widehat{\theta }}_E\right)({\widehat{\theta }}_I-{\widehat{\theta }}_E{)}^{\text{T}}$ and the columns of ${\nabla }^{\text{T}}$ are estimated numerically via $h^{-1}\{\psi \left({\widehat{\theta }}_E+{\Delta }_l\right)-\psi \left({\widehat{\theta }}_E\right)\}\text{where}h={10}^{-6},{\Delta }_l$ is a vector with h in the lth component and zero otherwise, and $l=1,\dots ,p.$ Thus, our EB shrinkage estimator of the full model parameters, denoted ${\widehat{\beta }}_{EB},$ is given as

$${\widehat{\beta }}_{EB}={\widehat{\nabla }}^{\text{T}}\widehat{\mathbf{A}}\widehat{\nabla }{\left\{{\widehat{\mathit{\Sigma }}}_I+{\widehat{\nabla }}^{\text{T}}\widehat{\mathbf{A}}\widehat{\nabla }\right\}}^{-1}\psi \left({\widehat{\theta }}_I\right)+{\widehat{\mathit{\Sigma }}}_I{\left\{{\widehat{\mathit{\Sigma }}}_I+{\widehat{\nabla }}^{\text{T}}\widehat{\mathbf{A}}\widehat{\nabla }\right\}}^{-1}\psi \left({\widehat{\theta }}_E\right).$$ (4)

Result 1 Let ${\widehat{\theta }}_I$ denote the maximum likelihood estimate of θ using the internal data. Then $\psi \left({\widehat{\theta }}_I\right)=\widehat{\beta },$ the maximum likelihood estimate of β.

Proof. The semi-parametric likelihood $L_{\beta ,F}={\prod }_{i=1}^N{f}_{\beta }\left(Y_i|X_i,Z_i\right)dF\left(X_i,Z_i\right)$ is to be maximized under the constraint $\int {\mu }_{\beta }(X,Z;\theta )dF(X,Z)=0$ where ${\mu }_{\beta }(X,Z;\theta )={\int }_{Y}U(Y|X,\theta )f_{\beta }(Y|X,Z)dY.$ By definition, ${\widehat{\theta }}_I$ is the value of θ that maximizes $L(\theta )={\prod }_{i=1}^N{f}_{\theta }\left(Y_i|X_i\right).$ Then $U\left(Y|X,{\widehat{\theta }}_I\right)=0\mathit{\text{and}}{\mu }_{\beta }\left(X,Z;{\widehat{\theta }}_I\right)=0$ forcing the constraint to be satisfied for any value β that maximizes $L_{\beta ,F}.$

2.3. Empirical Bayes Shrinkage of Model Predictions

In Section 2.2 we proposed an empirical Bayes shrinkage estimator for the full model parameters. We now propose three different shrinkage approaches for prediction in sections 2.3.1, 2.3.2 and 2.3.3. We assume the full and reduced models are generalized linear models (GLMs) defined by

$$g\left\{E\left(Y_i|X_i,Z_i\right)\right\}=X_i^{\text{T}}{\beta }_X+Z_i^{\text{T}}{\beta }_Z$$ (5)

and

$$g\left\{E\left(Y_i|X_i\right)\right\}=X_i^{\text{T}}{\theta }_X$$ (6)

where g is some link function. Let W^T denote a newly collected subject-specific covariate row vector with observed data on variables X and Z.

2.3.1. Predictions via Direct Use of EB Model Parameter Estimates

The EB full model parameter estimates defined by (4) can be used to construct predictions for the newly observed subject covariate vector e.g. ${\widehat{Y}}_{EB}=g^{-1}\left(W^{\text{T}}{\widehat{\beta }}_{EB}\right).$A quick inspection of this definition will show that ${\widehat{Y}}_{EB}$ (or simply EB) is the inverse-link function of

$$W^{\text{T}}{\widehat{\nabla }}^{\text{T}}\widehat{\mathbf{A}}\widehat{\nabla }{\left\{{\widehat{\mathit{\Sigma }}}_I+{\widehat{\nabla }}^{\text{T}}\widehat{\mathbf{A}}\widehat{\nabla }\right\}}^{-1}\psi \left({\widehat{\theta }}_I\right)+W^{\text{T}}{\widehat{\mathit{\Sigma }}}_I{\left\{{\widehat{\mathit{\Sigma }}}_I+{\widehat{\nabla }}^{\text{T}}\widehat{\mathbf{A}}\widehat{\nabla }\right\}}^{-1}\psi \left({\widehat{\theta }}_E\right)$$ (7)

which modifies the weights of $\psi \left({\widehat{\theta }}_I\right)\text{and}\psi \left({\widehat{\theta }}_E\right)$ in (4) by left-multiplication of the row vector W^T. An alternative approach is to sandwich the components of the weights in (4) by W^TW as presented in Section 2.3.3.

2.3.2. Empirical Bayes Shrinkage Estimator of Model Predictions

Rather than shrink estimates of the full model parameters, one can shrink estimates of the linear predictor of the full model fitted to the two data sources via

$${\widehat{\varphi }}^2{\left[W^{\text{T}}{\widehat{\mathit{\Sigma }}}_{I}W+{\widehat{\varphi }}^2\right]}^{-1}{W}^{\text{T}}\psi \left({\widehat{\theta }}_I\right)+W^{\text{T}}{\widehat{\mathit{\Sigma }}}_{I}W{\left\{W^{\text{T}}{\widehat{\mathit{\Sigma }}}_{I}W+{\widehat{\varphi }}^2\right\}}^{-1}{W}^{\text{T}}\psi \left({\widehat{\theta }}_E\right)$$ (8)

where $\widehat{\varphi }=W^{\text{T}}\psi \left({\widehat{\theta }}_I\right)-W^{\text{T}}\psi \left({\widehat{\theta }}_E\right).$ We note that when the link function g is the identity function, (8) is identical to shrinking the predictions ${\widehat{Y}}_I=W^{\text{T}}\psi \left({\widehat{\theta }}_I\right)\text{and}{\widehat{Y}}_E=W^{\text{T}}\psi \left({\widehat{\theta }}_E\right).$ Thus, (8) may be useful when the reduced model parameter estimates resulting from the external data are unavailable and predicted outcomes are available. The inverse-link of (8) defines our empirical Bayes shrinkage estimator ${\widehat{Y}}_{EBP1}$ (or simply EBP1) and is motivated by assuming a prior distribution $N\left\{W^{\text{T}}\psi \left({\theta }_0\right),v\right\}\text{on}{W}^{\text{T}}\psi (\theta )$ where v is a scalar. The Bayes estimate of $W^{\text{T}}\psi (\theta )$ for a fixed value v, estimated via ${\widehat{\varphi }}^2,$ is given by

$$v{\left\{{\sigma }_I^2+v\right\}}^{-1}{W}^{\text{T}}\psi (\theta )+{\sigma }_I^2{\left\{{\sigma }_I^2+v\right\}}^{-1}{W}^{\text{T}}\psi \left({\theta }_0\right)$$ (9)

where ${\sigma }_I^2$ is the asymptotic variance of $W^{\text{T}}\psi \left({\widehat{\theta }}_I\right).$

2.3.3. Alternate Empirical Bayes Shrinkage Estimator of Model Predictions

From the Taylor’s expansion in (2), we approximate $W^{\text{T}}\psi (\theta )$ via

$$W^{\text{T}}\psi (\theta )\approx W^{\text{T}}\psi \left({\theta }_0\right)+W^{\text{T}}{\nabla }^{\text{T}}\left(\theta -{\theta }_0\right)$$ (10)

yielding a prior distribution $N\left\{W^{\text{T}}\psi \left({\theta }_0\right),W^{\text{T}}{\nabla }^{\text{T}}\mathbf{A}\nabla W\right\}\text{on}{W}^{\text{T}}\psi (\theta ).$ Then an approximation to the Bayes estimate of $W^{\text{T}}\psi (\theta )$ is given by

$$W^{\text{T}}{\nabla }^{\text{T}}\mathbf{A}\nabla W{\left\{W^{\text{T}}\mathit{\Gamma }W\right\}}^{-1}{W}^{\text{T}}\psi \left({\theta }_I\right)+W^{\text{T}}{\mathit{\Sigma }}_{I}W{\left\{W^{\text{T}}\mathit{\Gamma }W\right\}}^{-1}{W}^{\text{T}}\psi \left({\theta }_0\right)$$

yielding a shrinkage prediction estimate as the inverse-link of

$$W^{\text{T}}{\widehat{\nabla }}^{\text{T}}\widehat{\mathbf{A}}\widehat{\nabla }W{\left\{W^{\text{T}}\widehat{\mathit{\Gamma }}W\right\}}^{-1}{W}^{\text{T}}\psi \left({\widehat{\theta }}_I\right)+W^{\text{T}}{\widehat{\mathit{\Sigma }}}_{I}W{\left\{W^{\text{T}}\widehat{\mathit{\Gamma }}W\right\}}^{-1}{W}^{\text{T}}\psi \left({\widehat{\theta }}_E\right),$$ (11)

denoted by ${\widehat{Y}}_{EBP2}$ (or simply EBP2), where $\mathit{\Gamma }={\mathit{\Sigma }}_I+{\nabla }^{\text{T}}\text{A}\nabla \text{and}\widehat{\mathit{\Gamma }}={\widehat{\mathit{\Sigma }}}_I+{\widehat{\nabla }}^{\text{T}}\widehat{\text{A}}\widehat{\nabla }.$

2.3.4. Comments Regarding the Empirical Bayes Estimators

Starting with the identity ${\widehat{\nabla }}^{\text{T}}\widehat{\mathbf{A}}\widehat{\nabla }+{\widehat{\mathit{\Sigma }}}_I={\widehat{\nabla }}^{\text{T}}\widehat{\mathbf{A}}\widehat{\nabla }+{\widehat{\mathit{\Sigma }}}_I$ and multiplying on the right by ${\left\{{\widehat{\mathit{\Sigma }}}_I+{\widehat{\nabla }}^T\widehat{\mathbf{A}}\widehat{\nabla }\right\}}^{-1},$ we get the equation ${\widehat{\nabla }}^{\text{T}}\widehat{\mathbf{A}}\widehat{\nabla }{\left\{{\widehat{\mathit{\Sigma }}}_I+{\widehat{\nabla }}^{\text{T}}\widehat{\mathbf{A}}\widehat{\nabla }\right\}}^{-1}+{\widehat{\mathit{\Sigma }}}_I{\left\{{\widehat{\mathit{\Sigma }}}_I+{\widehat{\nabla }}^{\text{T}}\widehat{\mathbf{A}}\widehat{\nabla }\right\}}^{-1}=I$ where I is the identity matrix. Thus, the matrix weights in expression (4) sum to the identity matrix and so can be thought of as a matrix generalization of a weighted scalar sum. For sufficiently large sample sizes, when pr(y, x, z) is transportable, ${\widehat{\theta }}_I-{\widehat{\theta }}_E$ will approximately equal the zero vector, and hence $\widehat{\mathbf{A}}$ will approximately equal the zero matrix. This is a motivation behind our estimators because as seen in (4), when $\widehat{\mathbf{A}}$ equals the zero matrix, the weight in front of the maximum likelihood estimator is the zero matrix, and the weight in front of the CML estimator is the identity matrix. When the transportability of pr(y, x) is violated, we would expect ${\widehat{\theta }}_I-{\widehat{\theta }}_E$ to be away from zero inflating the matrix weight associated with the maximum likelihood estimator. Thus, our empirical Bayes estimator (4) can be thought of as an estimator that tends to shrink towards the maximum like-lihood estimator when transportability is violated and tends to shrink towards the CML estimator when transportability is not violated. Similar observations can be made with the other empirical Bayes estimators.

3. Simulation Study

We carry out simulation studies in the standard linear and logistic regression settings to study operating characteristics of our proposed EB estimators in contrast to maximum likelihood and the CML estimator proposed in Chatterjee et al (2016a). In both regression settings, we consider four different specifications of the joint distributions of (X, Z)^T directly or indirectly through the conditional distribution of $X|Z$ and the marginal distribution of X in the external and internal populations. The motivation behind these settings (I, II, III and IV) is to assume the model $f_{\beta }(y|x,z)$ is correctly specified in both the internal and external populations, but the covariate distributions of (X, Z) need not be the same in both populations. Details of the different settings are explicitly summarized in Table 1. The full models of interest are

$$g\left\{E\left(Y_i|X_i,Z_i\right)\right\}={\beta }_0+{\beta }_1{X}_i+{\beta }_2{Z}_i$$ (12)

and

$$g\left\{E\left(Y_i|X_i,Z_i\right)\right\}={\beta }_0+{\beta }_1{X}_i+{\beta }_2{Z}_i+{\beta }_3{X}_i{Z}_i$$ (13)

where g is the identity link function in the normal linear regression setting and the logit-link function in the logistic regression setting. The reduced model of interest has the form

$$g\left\{E\left(Y_i|X_i\right)\right\}={\theta }_0+{\theta }_1{X}_i.$$ (14)

Table 1.

Distributions specified in our simulation settings.

Linear Regression
Setting	Population	Distribution
I	External Internal	(X,Z) ~ N{(0, 0), [1, .3; .3, 1]} (X,Z) ~ N{(0, 0), [1, .3; .3, 1]}
II	External Internal	(X,Z) ~ N{(0, .25), [1, .3; .3, 1]} (X,Z) ~ N{(0, 0), [1, .3; .3, 1]}
III	External Internal	X ~ N(.25, 1), Z | X ~ N(−1 + .5X, 1) X ~ N(0,1), Z | X ~ N(−1 + .5X, 1)
IV	External Internal	X ~ N(0,1), Z | X ~ N(−1 + .5X, 1) X ~ N(0,1), Z | X ~ N(−1 + .25X, 1)
Logistic Regression
Setting	Population	Distribution
I	External Internal	(X, Z) ~ N{(0, 0), [1, .3; .3, 1]} (X,Z) ~ N{(0, 0), [1, .3; .3, 1]}
II	External Internal	(X, Z) ~ N{(0, .5), [1, .3; .3, 1]} (X,Z) ~ N{(0, 0), [1, .3; .3, 1]}
III	External Internal	X ~ N(.5,1), Z | X ~ N(−1+ X, 1) X ~ N(0,1), Z | X ~ N(−1+ X, 1)
IV	External Internal	X ~ N(0,1), Z | X ~ N(−1+ X, 1) X ~ N(0,1), Z | X ~ N(−1 + .5X, 1)

These models are motivated by the scenario when a new predictor Z (and possibly an interaction) is included in the full model of the internal study. In our simulation studies, the sample sizes of the internal studies are 1000, and the sample sizes of the large external studies are 100000.

In each setting, we generate data under full models (12) and (13) given a set of parameters and then obtain the values of external parameters by fitting the reduced model (14) to a very large dataset. In the normal linear regression settings, we define (β₀, β₁, β₂) = (6, 4, 4) in (12) and (β₀, β₁, β₂, β₃) = (6, 4, 4, 2) in (13). In the logistic regression settings, (β₀, β₁, β₂) = (−1, −.5, .5) in (12) and (β₀, β₁, β₂, β₃) = (−1, −.5, .5, .25) in (13). The operating characteristics of interest are estimated bias, standard deviation and mean squared error defined by $R^{-1}{\sum }_{r=1}^R\left({\widehat{\gamma }}_r-{\gamma }_0\right),{\left\{{(R-1)}^{-1}{{\sum }_{r=1}^R\left({\widehat{\gamma }}_r-\overline{\gamma }\right)}^2\right\}}^{1/2}\text{and}{R}^{-1}{{\sum }_{r=1}^R\left({\widehat{\gamma }}_r-{\gamma }_0\right)}^2,$ respectively, where R = 1000 is the number of simulation runs, $\overline{\gamma }={\sum }_{r=1}^R{\widehat{\gamma }}_r,$ and $\widehat{\gamma }$ is an estimate of the true value ${\gamma }_0.$ In this context, ${\gamma }_0$ is a placeholder for β₀,β₁, β₂, or β₃ and $\overline{\gamma }$ is a placeholder for the estimate of ${\gamma }_0.$ resulting from either maximum likelihood, our empirical Bayes estimator defined in (4), or the CML estimator.

To evaluate estimation accuracy of the conditional mean of Y given (X, Z) via maximum likelihood, our empirical Bayes estimators, and the CML estimator, we randomly drew a covariate vector from both the external and internal populations, denoted by W_E and W_I respectively (includes 1 for the intercept), and calculate the average squared deviation from the estimated and true conditional means. In the cases of maximum likelihood and constrained maximum likelihood, the estimated conditional mean is obtained via the inverse link of the product of the covariate row vectors (W_E and W_I) and the parameter estimates (maximum likelihood or constrained maximum likelihood). With respect to our empirical Bayes estimators, we use ${\widehat{Y}}_{EB},{\widehat{Y}}_{EBP1}\text{and}{\widehat{Y}}_{EBP2}$ as defined in Section 2.3 to estimate the conditional mean. More specifically, the quantities used for estimation accuracy were defined by $R^{-1}{\sum }_{r=1}^R{\left\{{\widehat{M}}_{E,r}-g^{-1}\left(W_{E,r}^{\text{T}}\beta \right)\right\}}^2$ and $R^{-1}{\sum }_{r=1}^n{\left\{{\widehat{M}}_{I,r}-g^{-1}\left(W_{I,r}^{\text{T}}\beta \right)\right\}}^2$ over R = 1000 simulation runs where ${\widehat{M}}_{E,r}\text{and}{\widehat{M}}_{I,r}$ denote estimates of the condition mean of Y given (X, Z) in the external and internal populations respectively resulting from maximum likelihood, our empirical Bayes estimators, and the CML estimator in the rth simulation run.

3.1. Simulation Results

The results of our simulation settings with full model (12) and reduced model (14) are summarized in Table 2 and Table 3 of the main text, which will be the main focus in our commentary below. Across all simulation settings, the CML estimator results in substantial reduction in standard deviation of the estimates of (β₀, β₁) in comparison to the maximum likelihood estimates and EB estimates. For example, the standard deviations of the maximum likelihood, EB and CML estimates of (β₀, β₁) in linear regression setting I are (.192, .199), (.154, .161) and (.104, .115) respectively. In logistic regression setting I, the standard deviations of the maximum likelihood, EB and CML estimates of (β₀, β₁) are (.074, .081), (.056, .064) and (.021, .032) respectively. Consequently, the CML estimator results in substantial reduction in mean squared error (MSE) of (β₀, β₁) in comparison to the maximum likelihood estimates and EB estimates. The mean squared error of the maximum likelihood, EB and CML estimates of (β₀, β₁) in linear regression setting I are (.037, .039), (.024, .026) and (.011, .013) respectively. In logistic regression setting I, the mean squared error of the maximum likelihood, EB and CML estimates of (β₀, β₁) are (.005, .007), (.003, .004) and (.001, .001) respectively. Thus, when the covariate distribution of (X, Z) is transportable between the external and internal populations (Setting I), we see efficiency gains in the EB and CML estimates of (β₀, β₁) (EB: ~ 36% and 34% reduction in MSE, CML: ~ 70% and 66% reduction in MSE) with respect to the maximum likelihood estimates in linear regression framework. In logistic regression setting I, we found efficiency gains of approximately 41% and 37% for the EB estimators and 87% and 78% for the CML estimators. As expected, the EB and CML estimators did not acheive efficiency gains in estimation of β₂ with respect to maximum likelihood; however, as noted in our simulations studies, bias can be induced in β₂ particularly in Settings II and IV.

Table 2.

Simulation results. Estimated bias, standard deviation (SD) and mean squared error (MSE) of parameter estimates in linear regression settings I, II, III and IV specified in Table 1 with full model (12) and reduced model (14) based on 1000 simulation runs. LR denotes the maximum likelihood estimates of (12) fitted to the internal data, EB denotes our empirical Bayes estimator defined in (4) and CML denotes the constrained maximum likelihood estimator proposed in Chatterjee at al. (2016).

		BIAS			SD			MSE
Setting	Method	${\widehat{\beta }}_0$	${\widehat{\beta }}_1$	${\widehat{\beta }}_2$	${\widehat{\beta }}_0$	${\widehat{\beta }}_1$	${\widehat{\beta }}_2$	${\widehat{\beta }}_0$	${\widehat{\beta }}_1$	${\widehat{\beta }}_2$
	LR	.002	.001	.006	.192	.199	.198	.037	.039	.039
I	EB	.001	.005	.004	.154	.161	.198	.024	.026	.039
	CML	.000	.007	.012	.104	.115	.198	.011	.013	.039
	LR	−.001	.005	.003	.192	.194	.195	.037	.038	.038
II	EB	.054	.018	−.049	.195	.184	.197	.041	.034	.041
	CML	.700	−.036	.064	.106	.119	.196	.501	.015	.043
	LR	−.015	−.011	.012	.267	.209	.191	.072	.044	.037
III	EB	−.016	−.009	.010	.242	.176	.191	.059	.031	.037
	CML	−.027	−.009	.017	.222	.142	.191	.050	.020	.037
	LR	−.013	.007	.003	.273	.197	.195	.075	.039	.038
IV	EB	.041	.079	−.050	.267	.193	.197	.073	.043	.041
	CML	−.064	.681	.062	.229	.127	.198	.056	.480	.043

Table 3.

Simulation results. Estimated bias, standard deviation (SD) and mean squared error (MSE) of parameter estimates in the logistic regression settings I, II, III and IV specified in Table 1 with full model (12) and reduced model (14) based on 1000 simulation runs. LR denotes the maximum likelihood estimates of (12) fitted to the internal data, EB denotes our empirical Bayes estimator defined in (4) and CML denotes the constrained maximum likelihood estimator proposed in Chatterjee at al. (2016).

		BIAS			SD			MSE
Setting	Method	${\widehat{\beta }}_0$	${\widehat{\beta }}_1$	${\widehat{\beta }}_2$	${\widehat{\beta }}_0$	${\widehat{\beta }}_1$	${\widehat{\beta }}_2$	${\widehat{\beta }}_0$	${\widehat{\beta }}_1$	${\widehat{\beta }}_2$
	LR	−.001	−.002	.007	.074	.081	.080	.005	.007	.006
I	EB	−.005	−.006	.007	.056	.064	.080	.003	.004	.006
	CML	−.017	−.019	.007	.021	.032	.080	.001	.001	.006
	LR	−.004	−.004	−.002	.075	.079	.079	.006	.006	.006
II	EB	.016	−.003	−.002	.078	.074	.079	.006	.005	.006
	CML	.236	.009	−.002	.021	.032	.079	.056	.001	.006
	LR	.001	−.004	.006	.104	.116	.085	.011	.013	.007
III	EB	.002	−.003	.006	.089	.103	.085	.008	.011	.007
	CML	.002	−.002	.006	.064	.085	.085	.004	.007	.007
	LR	.003	−.012	.007	.101	.094	.083	.010	.009	.007
IV	EB	.002	.011	.007	.096	.097	.083	.009	.010	.007
	CML	−.009	.235	.008	.062	.049	.083	.004	.057	.007

Although the CML estimator can result in substantial efficiency gains, the CML estimator can result in severe loss of efficiency when the assumption of a transportable covariate distribution is violated as seen in Settings II and IV. In our simulation studies, we find that our EB estimators provide protection against severe loss of efficiency. For example, in the linear regression settings, the mean squared error of the CML estimates of β₀ and β₁ in settings II and IV respectively are approximately 13.6 and 12.3 times higher than the corresponding MSEs reported for the maximum likelihood estimates. However, the MSEs of the corresponding EB estimates were approximately 1.1 and 1.1 times the MSEs for the maximum likelihood estimates of β₀ and β₁ respectively (Tables 2 and 3).

Substantial bias in estimation can be problematic for prediction. Let F_I(X, Z) and F_E (X, Z) denote the covariate distribution functions of (X, Z) in the internal and external populations respectively, and let $\left(X_{I,r},Z_{I,r}\right)~F_I(X,Z)\text{and}\left(X_{E,r},Z_{E,r}\right)~F_E(X,Z)\text{for}r=1,\dots ,R\text{and}R=1000.$ Random covariate row vectors from the internal and external populations are defined by $W_{I,i}=\left(1,X_{I,i},Z_{I,i}\right)\text{and}{W}_{E,i}=\left(1,X_{E,i},Z_{E,i}\right)$ respectively. We consider absolute estimation error defined by $\left|{\widehat{M}}_{E,r}-g^{-1}\left(W_{E,r}^{\text{T}}\beta \right)\right|\text{and}|{\widehat{M}}_{I,r}-g^{-1}\left(W_{I,r}^{\text{T}}\beta \right)|\text{where}{\widehat{M}}_{E,r}\text{and}{\widehat{M}}_{I,r}$ denote estimates of the condition mean of Y given (X, Z) in the external and internal populations respectively resulting from maximum likelihood, our empirical Bayes estimators, and the CML estimator in the rth simulation run.. Box plots of absolute estimation errors are displayed in Figure 1 (linear regression) and Figure 2 (logistic regression). Figure 1 is comprised of Setting I (a), Setting II (b) and (c), Setting III (d) and (e) and Setting IV (f) and (g). Figures (a), (b), (d) and (f) corresponds to $\left(X_{E,r},Z_{E,r}\right)~F_E(X,Z)$ and (c), (e) and (g) correspond to $\left(X_{I,r},Z_{I,r}\right)~F_I(X,Z).$

Fig. 1.

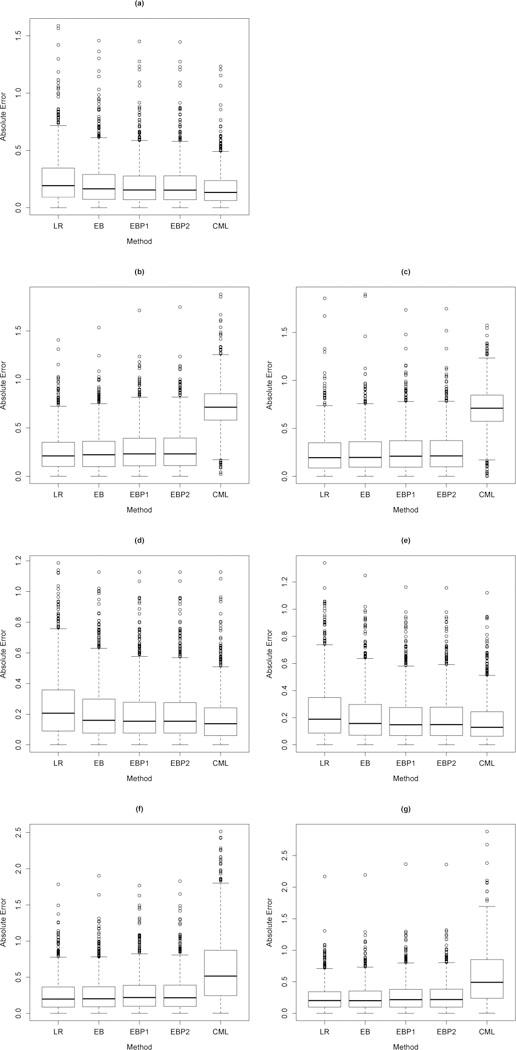
Box plots of absolute estimation error defined by (a),(b),(d),(f) $|{\widehat{M}}_{E,r}-W_{E,r}^{\text{T}}\beta |$ and (a),(c),(e),(g) $\left|{\widehat{M}}_{I,r}-W_{I,r}^{\text{T}}\beta \right|$ based on r = 1,...,1000 simulation runs in the standard linear regression settings I (a), II (b and c), III (d and e), IV (f and g) specified in Table 1 with full model (12) and reduced model (14) where $W_{E,r}^{\text{T}}$ is a covariate vector drawn from the external population, $W_{I,r}^{\text{T}}$ is drawn from the internal population, ${\widehat{M}}_{E,r}\text{and}{\widehat{M}}_{I,r}$are estimates of the conditional mean of Y given (X, Z) in the external and internal populations respectively resulting from maximum likelihood (LR), our empirical Bayes estimators EB, EBP1, and EBP2 or the constrained maximum likelihood estimator CML.

Fig. 2.

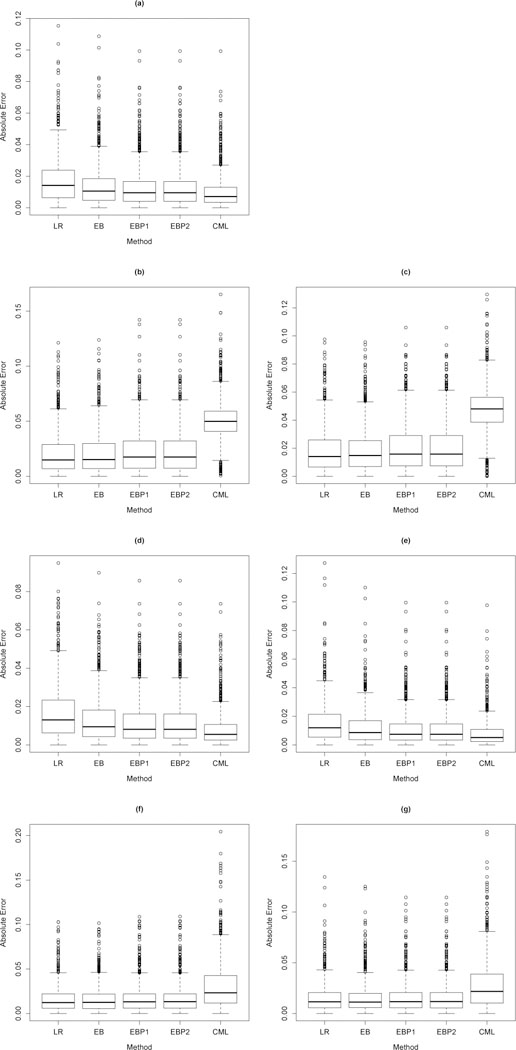
Box plots of absolute estimation error defined by (a),(b),(d),(f) $\left|{\widehat{M}}_{E,r}-g^{-1}\left(W_{E,r}^{\text{T}}\beta \right)\right|$ and (a),(c),(e),(g) $\left|{\widehat{M}}_{I,r}-g^{-1}\left(W_{I,r}^{\text{T}}\beta \right)\right|$ based on r = 1,...,1000 simulation runs in the standard logistic regression settings I (a), II (b and c), III (d and e), IV (f and g) specified in Table 1 with full model (12) and reduced model (14) where $W_{E,r}^{\text{T}}$ is a covariate vector drawn from the external population, $W_{I,r}^{\text{T}}$ is drawn from the internal population, ${\widehat{M}}_{E,r}\text{and}{\widehat{M}}_{I,r}$ are estimates of the conditional mean of Y given (X, Z) in the external and internal populations respectively resulting from maximum likelihood (LR), our empirical Bayes estimators EB, EBP1, and EBP2 or the constrained maximum likelihood estimator CML.

The quartiles of absolute estimation errors in Figure 1 (a) corresponding to EB, EBP1, EBP2 and CML indicate that absolute estimation error is reduced (with respect to maximum likelihood) using EB, EBP1, EBP2 or CML estimators when the covariate distributions are the same in the internal and external populations, i.e. $F_I(X,Z)=F_E(X,Z).$ However, the largest reduction in absolute estimation error is achieved in this setting with CML. We note similar findings in Figures 1 (d) and (e) corresponding to Setting III in which the covariate distributions of (X, Z) differ between the internal and external populations only through the marginal distribution of X. When the covariate distributions of (X, Z) differ between the internal and external populations through the marginal distribution of Z (Figures 1 (b) and (c)) or the conditional distribution $Z|X$ (Figures 1 (f) and (g)) absolute estimation error is substantially increased using CML, but mildly increased using our EB estimators indicating protection against heterogeneity in the population distributions. Figure 2 displays the quartiles of absolute estimation errors resulting from Settings I, II, III, and IV in the logistic regression framework. Results noted above in the normal linear regression framework are also observed in the logistic regression framework.

In Web Table 5, we tabulate proportions of the 1,000 simulation runs for which absolute estimation error resulting from CML or EB was less than absolute estimation error resulting from maximum likelihood or CML in each of the regression settings I, II, III and IV. For example, in Setting I, we found that EB resulted in smaller absolute estimation error in 71% and 75% of our simulation runs relative to maximum likelihood in the standard linear and standard logistic regression frameworks respectively. In settings II and IV, our EB estimator results in smaller absolute estimation error in 93% and 79% of the simulation runs relative to CML in the linear regression framework and roughly 91% and 74% in the logistic regression framework respectively.

To evaluate the impact of a newly collected covariate Z and the inclusion of an interaction term XZ in the full model, we carried out our simulation studies again using the full model (13) and the reduced model (14). We summarize the results in Web Table 1 and Web Table 2. Although our findings are similar to our findings above, we found that the CML estimator is seriously biased in Settings II, III and IV. These results suggest that the inclusion of the interaction term XZ plays a role in the bias induced in our simulation settings.

4. Data Application

The Prostate Cancer Prevention Trial (PCPT) Risk Calculator 1.0 (PCPTrc 1.0) was developed based upon 5519 men in the placebo group of the PCPT Thompson et al (2006) for individualized risk assessment of prostate cancer (PCa) using race (african american, caucasian, hispanic, other), age, PSA level (ng/ml), family history of PCa (yes, no), DRE (abnormal, normal, not performed), and prior prostate biopsy (never, past negative, past positive) as predictors. In 2016, Tomlins et al (2016) demonstrated improved prediction of high-grade PCa using the additional PCa specific biomarkers TMPRSS2:ERG and PCA3 as additional predictors. Since individual-level patient data from the 5519 were not available, Tomlins et al (2016) incorporated summary-level information into their models by using scaled PCPTrc 1.0 scores as predictors e.g.

$$g\left\{E\left[Y_i|T_i\right]\right\}={\gamma }_0+{\gamma }_1*{\text{score}}_i+{\gamma }_2*{\text{lpcs3}}_i+{\gamma }_4*{\text{lt2erg}}_i$$ (15)

where score_i denotes 100 times the PCPTrc 1.0 score, lPCS3_i denotes the base 2 logarithm of one plus the PCA3 score, lt2erg_i denotes the base 2 logarithm of one plus the TMPRSS2:ERG score, Y_i denotes the binary indicator of high risk PCa defined by a Gleason score greater than 6 for subject i and T_i is the design row vector (score_i, lpcs3_i, lt2erg_i). Their conclusions were based on comparisons of area under the curve (AUC) statistics calculated from (15) fitted to a validation set of 1225 men schedule for a diagnostic prostate biopsy at community clinics throughout the United States. In their analysis, they used a training cohort of 711 patients scheduled for a diagnostic prostate biopsy and prospectively collected post-digital rectal exam (DRE) urine for the assessment of TMPRSS2:ERG and PCA3.

Alternatively, one can incorporate external information from the PCPTrc 1.0 using the empirical Bayes estimators proposed in Section 2.2. The implementation is done as follows. The reduced model used in the calculation of PCPTrc is

$$g\left\{E\left[Y_i|X_i\right]\right\}={\theta }_0+{\theta }_1*{\text{lpsa}}_i+{\theta }_2*{\text{age}}_i+{\theta }_3*{\text{dre}}_i+{\theta }_4*{\text{priorbiop}}_i+{\theta }_5*{\text{aa}}_i$$ (16)

where lpsa_i denotes the natural logarithm of PSA, age_i denotes subject age, dre_i is a binary indicator of a digital rectal exam, priorbiop_i is a binary indicator of prior negative biopsy, aa_i is a binary indicator of african american race and X_i is the design row vector (lpsa_i, age_i, dre_i, priorbiop_i, aa_i) for subject i. The external parameter estimates of ${\theta }_E={\left({\theta }_0,\dots ,{\theta }_5\right)}^{\text{T}}$ in Thompson et al (2006) are ${\widehat{\theta }}_E=(-6.2461,1.2927,0.0306,1.0008,-0.3634,0.9604)$ The full model fitted to the training data is given as

$$\begin{gathered} g\left\{E\left[Y_i|X_i,Z_i\right]\right\}={\beta }_0+{\beta }_1*{\text{lpsa}}_i+{\beta }_2*{\text{age}}_i+{\beta }_3*{\text{dre}}_i+{\beta }_4*{\text{priorbiop}}_i+ \\ {\beta }_5*{\text{aa}}_i+{\beta }_6*{\text{1t2erg}}_i+{\beta }_7*{\text{lpca3}}_i \end{gathered}$$ (17)

where Z_i is the covariate row vector (lt2erg_i, lpca3_i). Model (17) is fitted to the training data set via maximum likelihood (LR), the CML estimate is obtained via $\psi \left({\widehat{\theta }}_E\right),$ the empirical Bayes estimates (EB, EBP1 and EBP2) are calculated as defined in (4), (7) and (11) and Model (15) is fitted to the training data set to obtain estimates (TOM) proposed in Tomlins et al (2016).

We compared predicted outcomes from the internal, validation and combined (internal + validation) data sets resulting from the six proposed methods (LR, EB, EBP1, EBP2, CML, TOM) and the PCPTrc. Sum of squared errors (SSE) and area under the receiver-operator curves (AUC) are used to quantify accuracy of prediction and classification respectively. Results are displayed in Table 4. SSE of the CML estimates were 6.1% less (157.211 vs. 167.436) than the SSE of the maximum likelihood estimates in the validation set; however, we found a 14.9% increase (119.828 vs. 104.326) in SSE calculated from the internal data set and a 1.9% increase (277.039 vs. 271.762) in SSE calculated from the combined data sets in comparison to maximum likelihood. An explaining factor of these observations are the notable differences in the covariate distributions among the external, internal and validation data sets (Web Table 3) i.e. the covariate distributions are not transportable between populations. Specifically, all individuals in the external data set were 55 years of age or older in contrast to 74% and 78% in the internal and validation data sets respectively. Additionally, 95.6% of individuals in the external data set were white compared to 80% and 41.8% in the internal and validation data sets respectively. Finally, rates of high grade PCa (outcome variable) were 4.7%, 27.0% and 18.3% in the external, internal and validation sets respectively.

Table 4.

Sum of squared errors (SSE) and area under the receiver-operator curve (AUC) in the internal, validation and both data sets using standard logistic regression (LR), empirical Bayes estimates EB, EBP1 and EBP2 defined in Section 2.3, constrained maximum likelihood (CML), the prediction model proposed in Tomlins et al. (2016) (TOM) and the Prostate Cancer Prevention Trial Risk Calculator (PCPTrc).

	Internal		Validation		Int+ Val
Method	SSE	AUC	SSE	AUC	SSE	AUC
LR	104.326	0.799	167.436	0.786	271.762	0.787
EB	104.333	0.799	167.063	0.786	271.396	0.787
EBP1	104.850	0.797	164.405	0.786	269.256	0.787
EBP2	104.769	0.797	164.803	0.785	269.571	0.786
CML	119.828	0.783	157.211	0.782	277.039	0.781
TOM	108.737	0.780	165.865	0.776	274.603	0.775
PCPTrc	133.545	0.687	170.040	0.707	303.586	0.698

Although there are notable differences among the covariate distributions, our empirical Bayes estimates EB, EBP1, and EBP2 offers protection against increasing prediction error with respect to maximum likelihood. For example, Table 4 indicates that SSE for the EB estimates ranged from 104.333 to 104.850 in the internal data set, 164.405 to 167.063 in the validation data set and 269.256 to 271.396 in the combined data sets compared to 104.326, 167.436 and 271.762 resulting from maximum likelihood respectively. In other words, our EB estimates offer a mild reduction in SSE in the validation and combined data set with respect to maximum likelihood even though the covariate distributions are very different among the three data sets. In contrast, the CML estimates results in a substantial increase (14.9%) in SSE in the internal data set, a moderate decrease (6.1%) in SSE in the validation data set and a mild increase in SSE (1.0%) in the combined data set relative to maximum likelihood.

Table 4 displays calculated AUC statistics resulting from the six different prediction models. In all three data sets, AUC resulting from maximum likelihood and our EB estimates were nearly identical, but very mild reductions occurred in AUC resulting from CML when compared to maximum likelihood in all three data sets. Web Figure 3 displays receiver-operator curves resulting from the six different procedures applied to the internal, validation and combined data sets. In the internal and combined data sets, we see some deviations between the receiver-operator curves corresponding to CML and TOM, and the alternative methods, near the center of the curves indicating slight changes in classification (sensitivity and specificity). While there does not appear to be notable differences among the AUC statistics, there are notable differences in prediction at the individual-level which is lost in the AUC statistics.

Web Table 4 displays the full and reduced model parameter estimates resulting from maximum likelihood as well as the prediction model parameter estimates resulting from EB and CML. The reduced model parameter estimates resulting from maximum likelihood fitted to the internal data and the external data are (−4.740, 0.958, 0.034, 1.139, −1.154, 0.460) and (−6.2461, 1.2927, 0.0306, 1.0008, −0.3634, 0.9604) respectively. Notably, the intercept estimates are very different. A contributing explanatory factor is the proportion of high grade PCa in the external and internal data sets which are observed to be 4.7% and 27.0% respectively (Web Table 3). Thus, the EB estimator will adapt by shrinking towards the maximum likelihood estimates whereas the CML estimator will move towards the external estimates. Consequently, the CML parameter estimates generally result in predicted outcomes closer to 0 relative to LR. For example, 52% and 54% of the predicted outcome values in the internal and validation data sets respectively are predicted below .10 when using CML compared to 25% and 26% when using LR. Thus, CML will require a much lower value c used in a decision rule to classify predicted outcomes as indications of disease than LR e.g. when c = .3, a predicted outcome of .35 will be classified as an indication of disease since .35 > .3. In fact, the classification value c that minimizes the Euclidean distance between the point (0,1) and the ROC curves resulting from CML and LR applied to the validation data set are .1108 and .3457 respectively. Web Figures 4 (internal data set) and 5 (validation data set) displays scatterplot matrices of predicted outcomes resulting from EB, CML, TOM and PCPTrc. Notable deviations from a diagonal line are seen in each of the plots indicating that predicted outcomes at the individual-level are very different in both the internal and validation data sources.

5. Discussion

In this paper, we extended the constrained maximum likelihood estimator proposed in Chatterjee et al (2016a) to an adaptive estimator that shrinks towards the maximum likelihood estimate when the external summary-level information and internal data provides evidence against the assumption of transportability, and shrinks towards the CML estimate otherwise. Furthermore, this paper is the first to do a comparative study of methods shrinking prediction directly using summary-level information. Our simulation studies indicates that our empirical Bayes estimators can yield efficiency gains when the covariate distributions are the same in both the internal and external populations as well as provides protection against bias and loss of efficiency when the external summary-level information and internal data gives evidence of differences in the covariate distributions. A bootstrap procedure can be easily implemented to approximate the standard errors of our EB estimator, since computationally, all estimators are quickly obtained via a simple Newton-Raphson procedure. In Web Table 6, we show that the bootstrap standard errors approximate the Monte Carlo standard deviations in both the linear and logistic regression setting. Although the transportability of (Y, X, Z) is not directly testable since information on Z in the external population is not available, our method uses available evidence against the assumption of a transportable covariate distribution by focusing on the conditional distribution of Y given X in both the internal and external populations.

It is important when borrowing information from external data sources that the researcher carefully evaluates the target population of interest, and whether or not there is evidence supporting heterogeneity in the distributions of covariates between populations which can make establishing a well defined and valid population of interest challenging. We suspect it will often be the case in practice (as seen in our data application) that internal and external data sources may exhibit heterogeneity, in which case, the researcher will need to carefully decide whether or not the external population, internal population or a broader population encapsulating both the internal and external populations is the target population of interest.

In our data application, we found that incorporating external information using CML reduced prediction error in the validation data but largely increased prediction error in the internal data set and modestly increased prediction error in the combined data sources. However, our EB estimators provided protection against increasing prediction error. Our simulation studies suggest that EBP1 and EBP2 achieves slight gains in estimation error over EB when the assumption of transportability holds, but at the cost of protection when the assumption does not hold. We therefore recommend, in the case that the external information is viewed to be completely auxiliary, and the internal data is a random sample from the target population, to use our EB estimator. In the event that only predicted outcomes from the external data source are available along with some measure of uncertainty, then EBP1 and EBP2 would be the candidates of choice since it would not be possible to use the EB estimator in this case. Our simulation studies suggest that EBP2 achieves slight gains in estimation error over EBP1 when the assumption of transportability holds, but at the cost of protection when the assumption does not hold. We therefore recommend EBP1 over EBP2.