The effect of articular geometry features identified using statistical shape modelling on knee biomechanics

Abstract

Articular geometry in the knee varies widely among people which has implications for risk of injury and pathology. The goals of this work were to develop a framework to systematically vary geometry in a multibody knee model and to use this framework to investigate the effect of morphological features on dynamic knee kinematics and contact mechanics. A statistical shape model of the tibiofemoral and patellofemoral joints was created from magnetic resonance images of 14 asymptomatic knees. The shape model was then used to generate 37 unique multibody knee models based on −3 to +3 standard deviations of the scores for the first six principal components identified. Each multibody model was then incorporated into a lower extremity musculoskeletal model and the Concurrent Optimization of Muscle Activations and Kinematics (COMAK) routine was used to simulate knee mechanics for overground walking. Changes in articular geometry affected knee function, resulting in differences up to 17° in orientation, 8 mm in translation, 0.7 BW in contact force, and 2.0 MPa in mean cartilage contact pressure. Understanding the relationship between shape and function in a joint could provide insight into the mechanisms behind injury and pathology and the variability in response to treatment.

Introduction

Bone and cartilage geometry varies widely among people and these morphological differences have important implications for risk of injury and pathology. In the knee, geometrical features have been associated with anterior cruciate ligament (ACL) injury [1], patellofemoral pain and instability [2,3], and knee osteoarthritis [4–6]. Increased posterior tibial plateau slope has been associated with ACL injury [7] and decreased lateral inclination of the trochlea is common in those with patellofemoral pain and instability [8]. While most studies have searched for correlations between geometry and existing pathology, Neogi, et al. [4] were able to predict the onset of tibiofemoral osteoarthritis based on three-dimensional geometric features, including wider, flatter femoral condyles, tibial plateau, and patella facet. However, inferring the causal factors behind these relationships is challenging and, at times, misleading.

Investigations into how morphology affects joint function can provide insight into why certain geometrical features may put a person at risk for injury or pathology. In the knee, correlations between morphology and tibiofemoral and patellofemoral kinematics have been studied using magnetic resonance imaging [9–11], biplanar videoradiography [12,13], and cadaveric specimens [14,15]. There have been few studies that have examined effects of geometry on contact mechanics [15,16]. Yet, cartilage loading has a critical role in the development of pathologies such as osteoarthritis [17,18] and patellofemoral pain [19,20]. Furthermore, since morphology cannot be modified non-invasively in vivo and not all aspects of geometry can be readily modified in vitro, most existing studies have been observational, examining correlations between geometry and function.

Using computational models, specific geometric features can be systematically modified. This allows the effect of geometry to be isolated from the influence of confounding factors such as differences in muscle or soft tissue properties, strength, or body weight. Musculoskeletal models with simplified knee joint models have been used to examine the influence of parameters such as joint alignment and contact point locations on knee biomechanics [21,22]. However, more sophisticated representations of geometry are possible using models that include full six degree-of-freedom joints constrained by ligament, muscle, and cartilage contact forces [23,24].

Few computational modelling studies have involved direct modification of articular geometry to examine the effect on joint function [25]. This is likely due in part to the difficulty of modifying the articular geometry in a systematic manner that ensures other relevant structures, such as ligament and muscle attachments and wrapping surfaces, remain consistent with the new morphology. Statistical shape modelling provides an objective way to quantify complex three-dimensional morphology by characterizing the variability in a population of shapes using principal component analysis. By parameterizing the geometric variability in a low-dimensional space, the statistical shape model can be used to systematically generate new geometries that are representative of the morphological differences in the population [26,27].

A better understanding of the shape-function relationship in the knee can provide insight into injury and pathology risk and help to tailor treatments to specific patients. Therefore, our overarching research goal is to determine how features of joint geometry affect functional joint biomechanics. Here, we aim to contribute to development of this understanding through two main objectives. The first objective of this work was to develop a method to systematically vary the bone and cartilage geometry in a multibody knee model using statistical shape modelling. The second objective was to use this technique to determine the effect of prominent shape features on knee kinematics, contact mechanics, and ligament loading during gait.

Methods

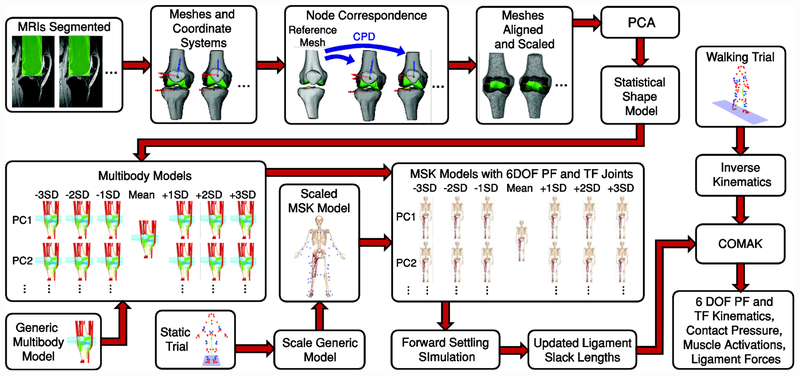
A statistical shape model was generated based on the knees of fourteen asymptomatic participants. The statistical shape model was used to generate multibody models with geometry that varied according to the features identified. These were integrated into a musculoskeletal model and the same overground walking trial was simulated using each model (Figure 1).

Figure 1:

MRIs from 14 asymptomatic knees were segmented to create surface meshes. Node correspondence was established between these using Coherent Point Drift (CPD). Principal Component Analysis (PCA) was applied to create a whole joint statistical shape model. This was used to generate multibody models ranging from −3 to +3 standard deviations (SD) of the first six principal components (PCs). These were incorporated into a musculoskeletal model to create models with 6 degree of freedom (DOF) patellofemoral (PF) and tibiofemoral (TF) joints. Ligament slack lengths were updated for each model using a forward settling procedure. An overground walking trial from one participant was simulated using the Concurrent Optimization of Muscle Activations and Kinematics (COMAK) with each model to assess the effects of geometry on knee kinematics, cartilage contact, and ligament forces.

Statistical Shape Model

A statistical shape model of the femur, tibia, and patella bone and cartilage geometry was created using the right knees of fourteen healthy participants who had no history of knee injury, pathology, surgery, or chronic pain (6F, 24.1±4.4 years, 74.8±10.6 kg). Participants provided informed consent according to a protocol approved by the University of Wisconsin’s Health Sciences Institutional Review Board. High resolution magnetic resonance images (MRIs) were obtained using a 3D IDEAL SPGR sequence for bone (in-plane resolution, 0.37×0.37; slice thickness, 0.9 mm; matrix, 512×512×304; repetition time, 10 ms; echo times, 4.5/5.5/6.1 ms; flip angle, 14°) and 3D FSE Cube sequence for cartilage (in-plane resolution, 0.39×0.39; slice thickness, 1.0 mm; matrix, 384×384×96; repetition time, 2066.7 ms; echo time, 19.8 ms; flip angle, 90°) in a clinical 3.0T scanner (MR750, General Electric Healthcare, Waukesha, WI). These images were manually segmented (Mimics, Materialise, Leuven, Belgium) to create surface meshes of the distal femur, proximal tibia, and patella bone and cartilage. Anatomical coordinate systems were generated automatically for each bone [28,29] and each bone and cartilage mesh was registered to its anatomical coordinate system.

Node correspondence was established using the Coherent Point Drift algorithm [30] with the mesh with surface area closest to the mean selected as the reference mesh. The reference geometry was meshed to have average edge lengths of 1.8 and 0.8 mm for the bone and cartilage, respectively. The resulting bone meshes contained 7313, 5880, and 1510 nodes for the femur, tibia, and patella, respectively, and the cartilage meshes contained 10931, 4109, and 2624 nodes for the femur, tibia, and patella, respectively. Participant femur, tibia, and patella meshes were separately isometrically scaled and aligned using a Procrustes analysis in MATLAB (MathWorks, Natick, MA) which minimized the sum of squared distances between the mesh nodes. This ensured scaling and alignment would not be included in the statistical shape model. Principal component (PC) analysis was then applied to the whole joint with the meshes registered to their anatomical coordinate systems. The resulting statistical shape model quantified variations in geometry for the femur, tibia, and patella simultaneously and was independent of alignment and isometric scaling.

Multibody Knee Model

The statistical shape model was used to generate new bone and cartilage geometries for a multibody knee model that included six degrees-of-freedom in each of the tibiofemoral and patellofemoral joints [31]. The joints were constrained by muscle, ligament, and cartilage contact forces. Fourteen ligaments were modelled as bundles of nonlinear elastic springs and cartilage contact was modelled with a nonlinear elastic foundation formulation [32]. Briefly, cartilage contact pressure was calculated based on the overlap between cartilage surfaces [33]. The combined cartilage thickness for the tibiofemoral and patellofemoral joints was set to be uniform at 6 and 7 mm, respectively, based on mean measured cartilage thickness. Ellipsoid and cylinder wrap objects were included to model ligament paths and prevent penetration of the bony geometry by ligaments.

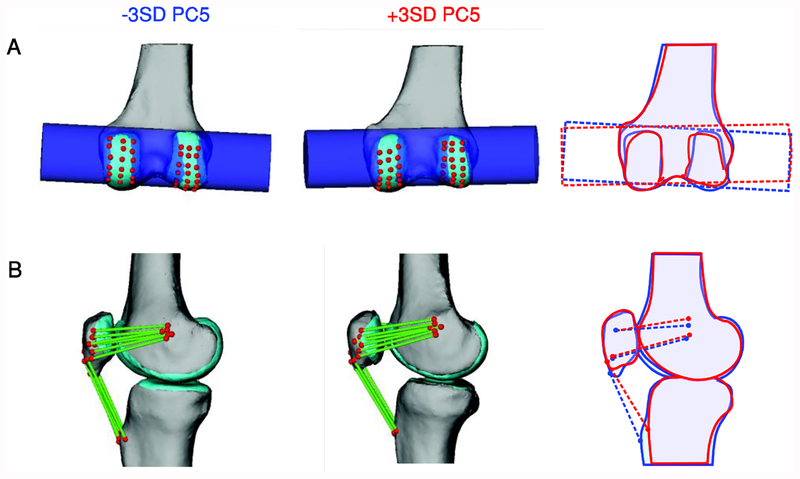
For the first six PCs, new knee geometries were created by adding ± 1, 2, or 3 standard deviations of the PC score multiplied by the loading vector for that PC to the mean mesh. This range was selected to generate the largest realistic variation in shape across these PCs. These geometries were then used to create new multibody knee models. Ligament and muscle attachment points and wrap objects were morphed with the geometry using the corresponding nodes of the surface meshes (Figure 2). The attachments were identified in magnetic resonance images for one participant [24] and the nodes in the shape model corresponding to these locations were then used to place ligaments and muscles in the generated models. Wrap objects were generated based on measurements using specific nodes in the model.

Figure 2:

Wrapping surfaces and ligament and muscle attachments were morphed with the geometry. An example wrapping surface and ligaments are shown for two deformed models. The third panel shows an outline of the two models to highlight the differences. A) Wrapping surface dimensions were defined based on nodes in the shape model. The cylindrical wrapping surface for the posterior capsule was generated based on a least-squares cylinder fit to nodes on the posterior femoral condyles (red points). B) Ligament and muscle attachments were fixed to nodes in the shape model (red points). The fibres for the medial patellofemoral ligament and the patellar tendon are shown. Only the central fibre of the patellar tendon and the more inferior and superior fibres of the medial patellofemoral ligament are shown in the outlined image for clarity.

Musculoskeletal Model and Gait Simulation

The 37 generated multibody knee models were integrated into a previously validated lower extremity musculoskeletal model that included 44 muscle-tendon units [24,34]. The anatomical coordinate systems of the distal femur and proximal tibia models were registered to the coordinate systems of the thigh and shank, respectively, in the musculoskeletal model. The musculoskeletal model was scaled based on the anatomical dimensions of the participant for whom the nominal model was generated [24]. Ligament slack lengths were calculated using reference strains from the nominal multibody model [24] and a reference pose with the knee in full extension. The reference pose was determined by performing two iterations of a forward settling simulation. The tibiofemoral flexion angle was fixed at 0° with no external forces applied, muscles were assumed to be relaxed (1% activation), and the remaining tibiofemoral and patellofemoral degrees-of-freedom were allowed to settle into an equilibrium orientation. After two iterations, the secondary kinematics of the reference pose converged and the resting lengths of the ligaments were calculated based on this posture and the defined reference strains.

The participant for whom the nominal model was constructed (23 year old female) walked overground at her preferred speed of 1.3 m/s while whole body kinematics and ground reaction forces were recorded. Pelvis kinematics and hip flexion, adduction, and rotation, knee flexion, and ankle plantarflexion angles were computed using a global optimization inverse kinematics procedure [35]. The inverse kinematics solution using the mean geometry was used for all subsequent walking simulations.

The muscle activations, cartilage contact pressure, and knee kinematics were simulated for the walking trial using the Concurrent Optimization of Muscle Activations and Kinematics (COMAK) routine [31]. At each frame in the gait cycle, pelvis kinematics, hip, tibiofemoral flexion, and ankle plantarflexion angles, and ground reaction forces were set to measured values. The ground reaction force was applied in the calcaneus reference frame so that the centre of pressure on the foot would be the same for all models. COMAK was then used to simultaneously solve for the muscle activations and secondary knee kinematics (i.e. patellofemoral and tibiofemoral degrees of freedom, excluding tibiofemoral flexion) that minimized an objective function while whole-body and joint-level movement dynamic constraints were satisfied. The objective function was the volume-weighted sum of muscle activations plus net cartilage contact elastic energy [36]. The movement constraints ensured the hip, tibiofemoral flexion, and ankle generalized accelerations calculated in the inverse kinematics procedure were produced in the final results. In this way, the tibiofemoral flexion angle was set based on the inverse kinematics solution while the patellofemoral and remaining tibiofemoral degrees of freedom were allowed to evolve in response to cartilage contact, muscle, and ligament forces.

The resulting knee kinematics and contact mechanics from the different models were compared throughout the gait cycle to assess the influence of articular geometry on functional knee mechanics. The instant of peak tibiofemoral contact force was selected for closer examination of cartilage contact pressure patterns as both tibiofemoral and patellofemoral contact forces were greatest at this point in early stance.

Comparison to Experimental Measures

The effects of articular geometry on knee mechanics determined using this simulation framework were compared with experimental correlations to assess the predictive capability of the model and the causality of the observed relationships. The participants used to develop the statistical shape model all performed an active knee flexion-extension task with resistance provided by an inertial load [37]. A dynamic, volumetric MRI sequence was used to track tibiofemoral and patellofemoral degrees of freedom during this task (for details, refer to [38,39]). PC scores were computed for each participant’s segmented bone and cartilage geometry. The active flexion-extension task was simulated for a similar range of flexion using each of the 37 models generated using the statistical shape model. Tibiofemoral and patellofemoral kinematics at 20° of knee flexion were plotted against participant PC scores and compared to the changes in kinematics at 20° flexion induced by modifying the geometry across the PC. 20° was selected as it was in the midrange of flexion angles covered by all participants.

Results

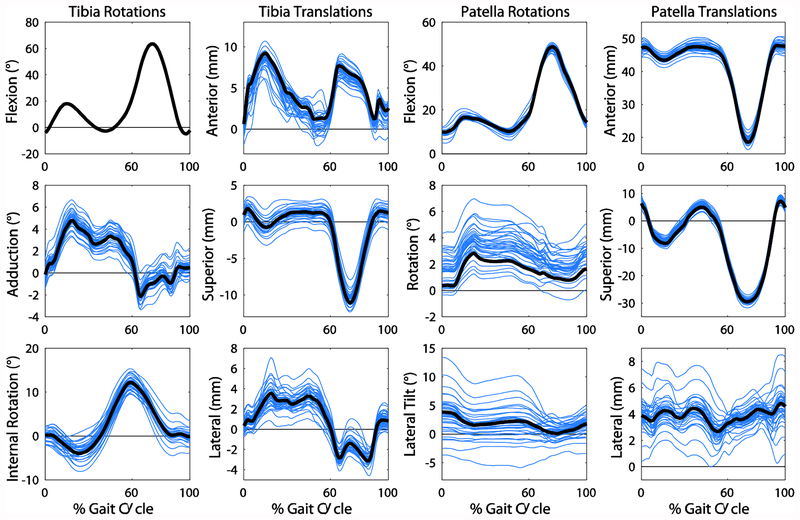
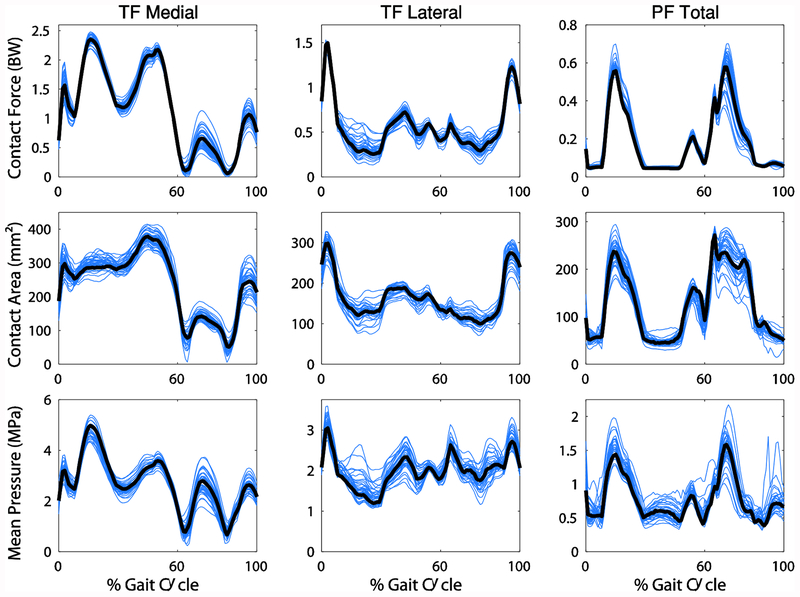
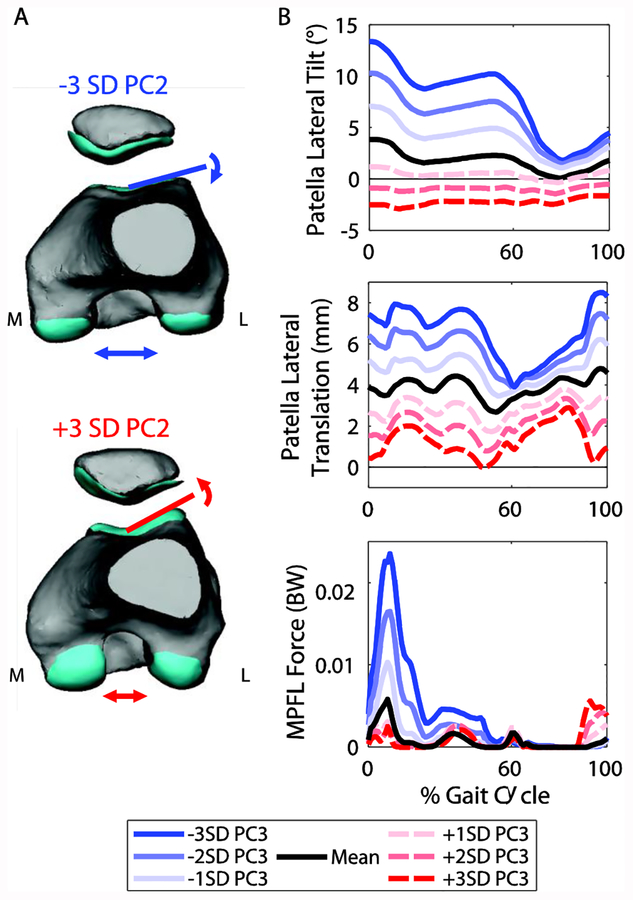
The first six PCs captured 70% of the variance in knee joint geometry. All degrees of freedom were affected by changes in geometry, with differences in angles up to 17° and translations up to 8 mm (Figure 3). Contact force and area and the mean contact pressure were affected by geometry as well with maximum differences in contact force, area, and mean pressure of 0.7 BW, 148 mm², and 2.0 MPa, respectively (Figure 4). PCs 2 and 3 were chosen for closer examination based on the relevance of the shape features and their effect on mechanics to pathology.

Figure 3:

The tibia and patella rotations and translations with respect to the femur resulting from all knee geometries. The waveforms for the mean geometry are shown in black. Note that the tibia flexion angle is equivalent for all geometries since this is set in the simulation.

Figure 4:

Cartilage contact mechanics for the tibiofemoral (TF) and patellofemoral (PF) joints resulting from all knee geometries. The waveforms for the mean geometry are shown in black.

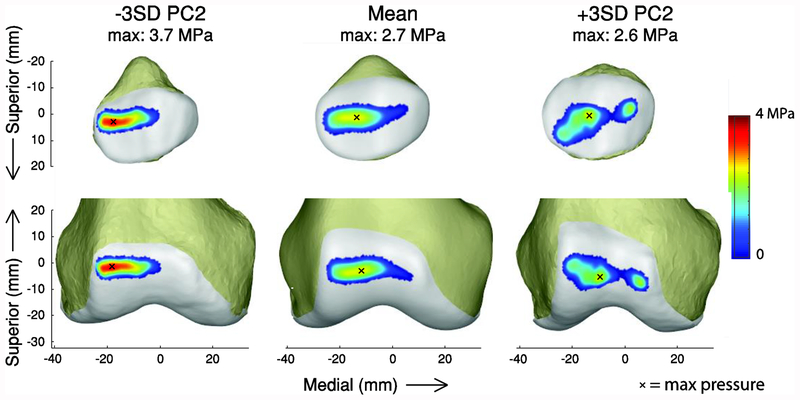
PC2 captured variation in the lateral trochlear inclination angle and intercondylar notch width of the femur (Figure 5A; Table 1). This PC was of particular interest because of the association between lateral trochlear inclination and patellofemoral pain and instability [8,10]. A smaller lateral inclination angle caused increased lateral shift and lateral tilt of the patella throughout the gait cycle, but particularly in stance (Figure 5B). A smaller lateral inclination angle also resulted in increased force in the medial patellofemoral ligament (MPFL) during stance. From −3 to +3 standard deviations of PC2, the maximum change in patella tilt was 15.9°, patella lateral translation was −8.2 mm, and MPFL force was −0.022 BW (−13.2 N). The trochlear groove geometry also affected the cartilage contact pressure distribution at the instant of the first peak in the tibiofemoral contact force during stance (Figure 7). The pressure was greater and more concentrated on the lateral side for smaller lateral inclination angles.

Figure 5:

A. Changes in geometry from −3 to +3 standard deviations (SD) of PC2. PC2 captured variations in the lateral trochlear inclination and intercondylar notch width. B. Selected patellofemoral kinematics and medial patellofemoral ligament (MPFL) force for the seven models representing −3 to +3 SD of PC2. A smaller lateral inclination angle caused increased lateral shift and tilt of the patella and increased MPFL force.

Table 1:

Anatomical measurements for ±3 standard deviations (SD) of PCs 2 and 3 to aid in interpretation of the geometrical features captured by these PCs. The medial plateau sagittal plane radius was determined by fitting a circle to a sagittal plane section of the tibial cartilage at the midpoint of the medial tibial plateau. The remaining measures are described in [8,51,52].

Femur measurement	−3SD PC2	+3SD PC2	Tibia measurement	−3SD PC3	+3SD PC3
Lateral Trochlear Inclination	16.1°	28.0°	Medial plateau sagittal plane radius	120 mm convex	60 mm concave
Sulcus Angle	152.1°	138.1°	AP Depth Medial	50.1 mm	41.5 mm
Intercondylar Notch Width	29.5 mm	19.7 mm	Anatomical medial proximal tibial angle	88.2°	83.7°

Figure 7:

Effect of PC2 on patellofemoral contact pressure in early stance. Contact patterns are shown at the first peak tibiofemoral contact force during stance. An x indicates the location of the maximum pressure.

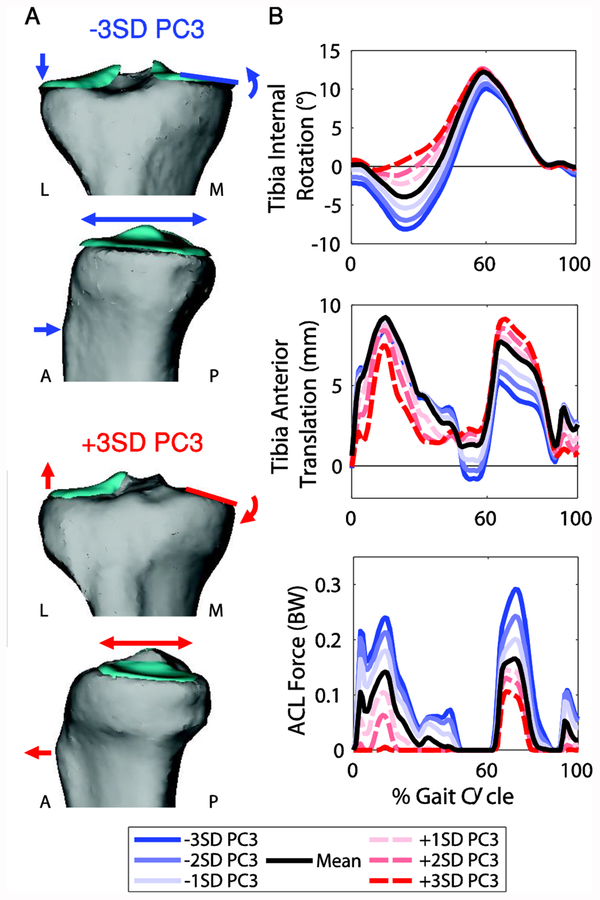
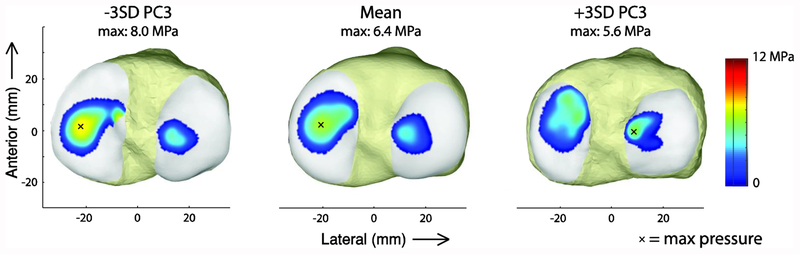
PC3 represented changes in the frontal plane slope, anterior-posterior depth, and concavity of the medial tibial plateau (Figure 6A; Table 1). This was of particular interest because of its effects on tibiofemoral kinematics and cartilage contact pressure. A smaller, more concave medial tibial plateau with a larger frontal plane slope caused decreased external rotation and anterior translation of the tibia relative to the femur during stance. Additionally, the ACL force decreased (Figure 6B). From −3 to +3 standard deviations of PC3, the maximum change in the knee internal rotation angle was 9.3°, tibia anterior translation was 4.2 mm, and ACL force was −0.23 BW (−137.6 N). This feature also caused a decrease in medial tibial cartilage contact pressure in late stance (Figure 8). In the model with a small, concave medial tibial plateau (−3SD of PC3), the contact patch was shifted anteriorly and the mean contact pressure was reduced by 2.4 MPa compared to the model with the large, flat medial tibial plateau (+3SD of PC3).

Figure 6:

A. Changes in geometry from −3 to +3 SD of PC3. PC3 captured variation in frontal plane slope, anterior-posterior depth, and concavity of the medial tibial plateau. B. Selected tibiofemoral kinematics and anterior cruciate ligament (ACL) force for the seven models representing −3 to +3 SD of PC3. A large, flat medial tibial plateau with a shallow frontal plane slope caused increased external rotation and anterior translation of the tibia relative to the femur and increased the ACL force.

Figure 8:

Effect of PC3 on tibial cartilage contact pressure at the second peak in the medial tibiofemoral contact force during stance. An x indicates the location of the maximum pressure.

A summary of the geometrical features explained by the remaining PCs and the effects on knee biomechanics at the instant of first peak tibiofemoral contact force during stance are included in the supplementary material.

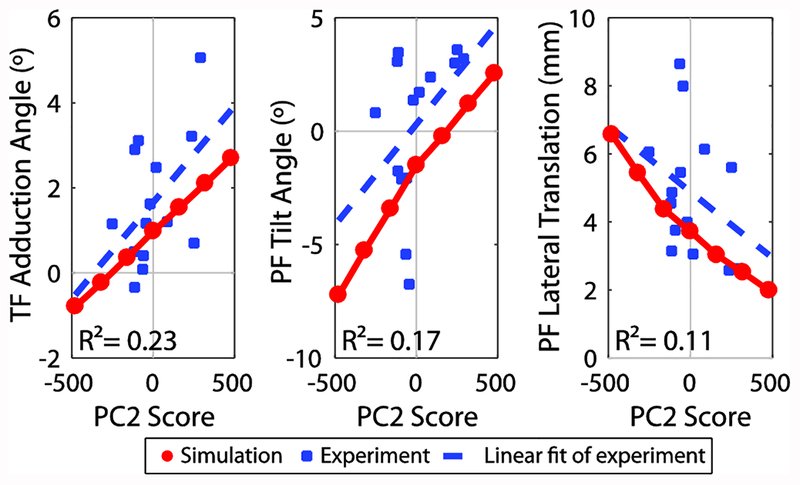
The dependence of secondary tibiofemoral and patellofemoral kinematics on PC2 was similar for both the simulated and experimental knee flexion-extension tasks. Notably, tibiofemoral adduction and patellofemoral tilt increased with PC2 score (lateral inclination angle), while lateral patella translation decreased (Figure 9). A complete comparison of the measured and simulated tibiofemoral and patellofemoral kinematics is included in the supplementary material.

Figure 9:

Comparison of correlation between PC2 score and experimental kinematics with effect of PC2 from simulation. Tibiofemoral (TF) adduction angle, patellofemoral (PF) tilt, and PF lateral translation at 20° of flexion during the extension phase of the active flexion-extension task as measured using dynamic, volumetric MRI tracking is plotted against PC2 score, which represents lateral trochlear inclination (blue squares). Coefficient of determination, R², for the linear fit to the experimental data is shown. Kinematics at 20° of flexion for simulated flexion-extension task are shown for the generated knee models ranging from −3 to +3 SD of PC2 (red circles).

Discussion

A statistical shape modelling approach was used to systematically vary articular geometry in a multibody knee model according to prominent features identified in a set of asymptomatic knees. The shape model was used in conjunction with musculoskeletal simulation to isolate the effect of typical variations in articular geometry on tibiofemoral and patellofemoral kinematics, contact mechanics, and ligament loading during gait. Changes in morphology affected knee mechanics in ways that have relevance to joint pathologies, injuries, and treatments. The developed framework provides a complement to in vivo and in vitro studies of shape and function. When correlations are observed between geometry and pathology or function, this method can be used to directly explore the isolated influence of the geometric feature on joint biomechanics to better understand the mechanism involved and to inform designs of future experiments.

Femoral trochlear dysplasia, a geometric abnormality where the trochlear groove is extremely shallow, has been associated with patellofemoral pain and instability [3,8,10]. As a result, the effect of trochlear dysplasia on patellofemoral biomechanics has been relatively well studied. Dysplastic, shallow trochlear grooves have been found to result in increased lateral tilt and translation of the patella, increased contact pressure, and decreased contact area [9,10,16,40]. Though in this study, the trochlear groove did not reach levels of dysplasia (lateral trochlear inclination < 11° [41]), the relationship between trochlear groove depth and patellofemoral mechanics was confirmed during gait. The MPFL force was also increased with the shallow trochlear groove, indicating that this ligament may be playing a larger role in stabilization of the patella in these geometries. In addition, the contact pressure was increased and concentrated on the lateral border of the patella for the shallow trochlear groove. Those who experience patellofemoral pain often have elevated cartilage contact stresses [19] and it is thought that increased cartilage stress may be transferred to pain receptors in the subchondral bone [42]. To further examine the cause and effect relationship between these shape features and patellofemoral disorders, future work should extend the approach used here to the study of patient populations. This would make it possible to identify prevalent features in a pathological population and investigate the effect of these features on function to understand the role of geometry in the pathology.

In the tibiofemoral joint, we found that a larger flatter medial tibial condyle caused increased external rotation, ACL force, and anterior translation during walking. A flatter tibial plateau decreases the articular constraint of the joint, thus increasing anterior translation and ACL force as the soft tissues become more important to maintaining joint stability. It has been found that those who have sustained an ACL injury tend to have a shallower, less concave medial tibial plateau compared to asymptomatic controls [43]. The direct effect of medial tibial concavity on ACL force and anterior translation shown here could provide a mechanism for this observed correlation. Similarly, Neogi et al. [4] found that a wider, flatter medial tibial plateau was associated with initiation of osteoarthritis in an examination of data from the Osteoarthritis Initiative. In the current study, a larger, flatter medial tibial plateau resulted in increased cartilage contact pressure throughout stance, particularly in late stance (Figure 8). It is possible that this elevated loading could contribute to the increased risk of knee osteoarthritis associated with this geometry. However, further work is required to ensure the same geometric feature was captured in both studies and to better understand detrimental cartilage loading conditions.

Our simulations provide a measure of the uncertainty in secondary kinematics and contact loads that could be expected when using generic articular geometry to simulate knee mechanics during gait. The medial tibiofemoral contact force, an important measure in the study of knee osteoarthritis, changed by a maximum 0.29 BW at the first peak over all of the geometries considered, which is 12% of the medial contact force for the mean model. Furthermore, contact pressure patterns were affected by geometry (Figures 7 and 8), with the pressure changing in magnitude and location. The relevance of this variability depends on the application. The variation observed in medial contact force is within the range of decrease that can be achieved using interventions such as valgus unloader braces [46,47], for example. The statistical shape model was created based on the knees of asymptomatic controls and the change in frontal plane alignment was relatively small (maximum of 3° over all generated models). If pathological geometries were included, greater changes in frontal plane alignment may occur which would lead to an increase in the variability in medial/lateral distribution of tibiofemoral contact force [48]. Our results point to the importance of considering patient-specific geometry to better understand biomechanical factors associated with pathologies such as osteoarthritis.

An important outcome of this work is the introduction of a framework for rapid generation of model geometries used to perform simulations that are representative of a population. This framework also has the potential to enable development of patient-specific models through deformation of the statistical shape model. By fixing ligaments and wrapping surfaces to specific nodes in the statistical shape model, we were able to morph these with the bone and cartilage geometry. Statistical shape modelling is beginning to be used in segmentation of 3D images [49] and generation of cartilage meshes from bony geometry [50]. Therefore, this type of morphable model based on a statistical shape model may enable an automated process to generate multibody knee models from 3D medical images in the future.

The effects of trochlear groove geometry (PC2) seen in the simulations were similar to correlations in the experimental data for the active knee flexion-extension task. This indicates that the associations between kinematics and geometry observed experimentally are causal in nature. While correlations did exist, they were somewhat weak, with R² ranging from 0.11–0.23. However, there are many additional sources of variability in the in vivo data that may affect kinematics including concurrent geometrical differences, overall body dimensions, strength, tissue properties, and neuromuscular control strategies. An advantage of the simulation method is the ability to control these factors. Using the methods introduced in this study, the interactions between such factors and knee geometry could be systematically investigated in future simulations.

The result of this work should be interpreted in the context of a few limitations. First, the statistical shape model in this study was generated based on fourteen asymptomatic controls. Because of this sample size, the features may not be representative of the population in general and likely do not represent geometries that may be found in pathological knees. However, the statistical shape model provides a means to systematically modify geometry based on objectively quantified shape features. Furthermore, the geometrical variation in this small asymptomatic group produced substantial changes in knee biomechanics. A logical next step would be to extend this approach to a pathological population to identify and assess the impact of geometrical features associated with the pathology on knee mechanics. Second, while this model has the advantage of containing cartilage and ligament structures, other soft tissue structures are not represented; for example, variations in meniscus geometry would undoubtedly affect tibiofemoral biomechanics [25]. Third, it is also possible that morphological differences are associated with muscle properties and neuromuscular control strategies. However, our aim was to isolate the effect of geometry from this type of confounding factor so that the effect of geometry alone could be examined. Fourth, the ground reaction force was applied in the calcaneus reference frame. Thus the position and orientation of the ground reaction force vector with respect to the whole body centre of mass could be different between models if the secondary knee kinematics changed. We evaluated this assumption by performing a second set of simulations with the ground reaction force fixed in global coordinates. Similar trends and interpretations were obtained in this case.

Our study demonstrates how a statistical shape modelling approach can automate the generation of knee models suitable for simulating knee mechanics during gait. We found that variations in articular geometry can substantially alter secondary tibiofemoral and patellofemoral kinematics, articular cartilage loading, and ligament loading during gait. Understanding the relationship between shape and function can provide insight into the mechanisms behind joint pathologies that may lead to improved prevention and treatment options.

Highlights.

• Knee joint geometry characterized using statistical shape modelling

• Multibody knee models spanning identified geometrical features generated

• Effect of geometry on joint biomechanics assessed using musculoskeletal simulation

• Articular geometry affected kinematics, contact mechanics, and ligament loading