Local and global influences of visual spatial selection and locomotion in mouse primary visual cortex

SUMMARY:

Sensory selection and movement locally and globally modulate neural responses in seemingly similar ways. For example, locomotion enhances visual responses in mouse primary visual cortex (V1), resembling the effects of spatial attention on primate visual cortical activity. However, interactions between these local and global mechanisms and the resulting effects on perceptual behavior remain largely unknown. Here we describe a novel mouse visual spatial selection task in which animals either monitor one of two locations for a contrast change (“selective mice”) or monitor both (“non-selective mice”) and can run at will. Selective mice perform well only when their selected stimulus changes, giving rise to local electrophysiological changes in the corresponding hemisphere of V1 including decreased noise correlations and increased visual information. Non-selective mice perform well when either stimulus changes, giving rise to global changes across both hemispheres of V1. During locomotion, selective mice have worse behavioral performance, increased noise correlations in V1, and decreased visual information, while non-selective mice have decreased noise correlations in V1 but no change in performance or visual information. Our findings demonstrate that mice can locally or globally enhance visual information, but the interaction of the global effect of locomotion with local selection impairs behavioral performance. Moving forward, this mouse model will facilitate future studies of local and global sensory modulatory mechanisms and their effects on behavior.

eTOC Blurb:

The effects of locomotion on mouse visual cortical activity are often compared to those of primate spatial attention. Here, McBride et al. show that behavioral and neural effects of locomotion differ depending on the trained visual task. Locally selective mice are impaired by global locomotion effects, while non-selective mice are unaffected.

INTRODUCTION:

Accurate perception is supported by a combination of local and global neural mechanisms, such as selective attention and arousal. These local and global effects are most often studied in isolation and in different species, so we know little about how they interact to affect neural responses and behavior.

In rodent studies, global arousal and its correlates are strongly associated with movement, including locomotion and active whisking. Global neural effects of locomotion in mouse resemble local effects of spatial attention in primates [1–3]. Similar neural effects include reduced spike count correlations [4–7], reduced low-frequency (<10Hz) and changes in gamma (30–80Hz) local field potential (LFP) power [7–11], increased stimulus-evoked firing rates [6,7,11–16], and reduced trial-to-trial spiking variability [6,17]. The combination of reduced spike count correlations (r_sc) and reduced low-frequency LFP power amounts to a desynchronized brain state [1], which is often associated with improved perceptual behavior. Reduced r_sc in particular may increase the information coding capacity of a neural population, though it depends on task specifics and the particular correlation structure [18–21].

While the behavioral effects of attention are well-established [12,13,22], behavioral effects of locomotion in the mouse remain largely untested, with the exception of one study in which locomotion improved the behavioral performance of mice [23]. Locomotion was also shown to improve visual information in neural responses outside the context of a task [24,25]. More recent studies have shown that a great deal of cortical activity in awake mice can be explained solely by the animals’ movements [26,27], and that movement-related activity dominates task-related activity [27]. Effects of this broad movement-related activity on behavioral performance have not been directly examined, though one study found that a global desynchronized state was more related to task engagement than task performance [28].

We sought to develop a mouse model for spatial selection and to use it to investigate interactions between local and global mechanisms of sensory modulation, the effects of locomotion on task performance and sensory representations in primary visual cortex (V1), and whether and how local and global mechanisms affect neural representations of visual information in V1. We show that selecting a single location in space locally modulates neural responses, while monitoring two spatial locations symmetrically modulates neural responses. Locomotion has a global effect on neural responses in both groups, and impairs the behavioral performance of selective mice, while not significantly affecting the behavior of non-selective mice. Consistently, visual information in V1 population activity improved on correct trials in the selected hemisphere and decreased during locomotion for selective mice. In non-selective mice, visual information in V1 was lower compared to selective mice and was not modulated by locomotion.

Our results show that on a trial-to-trial basis mice can enhance cortical representations of visual information in V1 in a spatially-selective manner. Contrary to previous proposed models, locomotion does not generally enhance visual information processing and behavior. Instead, the effect of locomotion depends on behavioral context, and its largest effect is to impair spatially selective behavior.

RESULTS:

A mouse spatial selection task

We developed a spatial selection task for mice in which one group selectively monitored one of two locations for a contrast change (80–20 mice), and a separate group monitored both locations for a contrast change (50–50 mice). Water-restricted mice were head-fixed and able to run freely on a wheel, with a computer monitor centered in each visual hemifield (Figure 1A). At the start of each trial, screens were gray, and then randomly-oriented drifting square wave gratings appeared simultaneously on both sides (see Methods for detailed grating parameters). After a 2 second initial delay, the contrast of one of the two gratings changed after a random additional time governed by a flat hazard function, to ensure a constant change probability and attentional demand [29], and prevent mice from using timing strategies to perform the task. To receive a sucrose water reward, the mice were required to withhold licking prior to the contrast change and then lick within a short duration after the change. This was classified as a correct trial (Figure 1B). Early licks prevented water delivery and initiated a timeout by increasing the inter-trial interval. Trials during which the mouse did not lick were classified as miss trials and were neither rewarded nor punished.

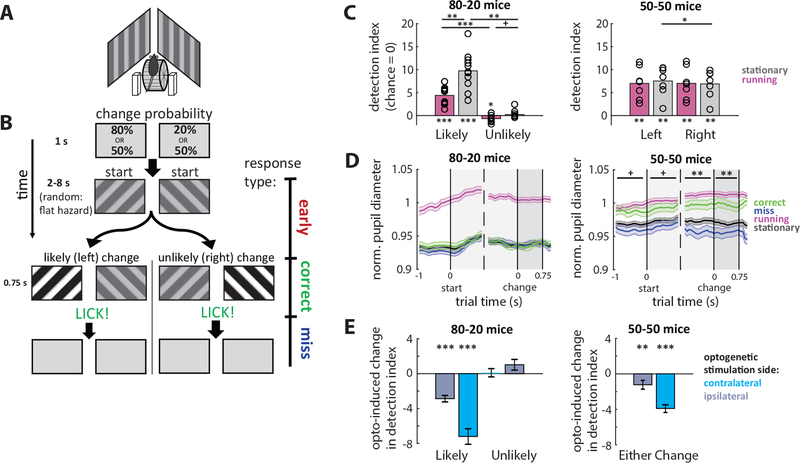
Figure 1: Spatial selection task and behavioral performance.

(A) Schematic of behavioral rig. Mice were head-fixed on a wheel and allowed to walk or run at will. Computer monitors for displaying visual stimuli were angled to the left and right sides of the mouse, centered in each hemifield and avoiding the binocular zone.

(B) Spatial selection task. Mice were water restricted, and to receive a water reward they had to lick in response to a contrast change in an oriented drifting grating stimulus that could occur on either the right or left side (correct trial). If mice licked prior to (early) or after the change (miss) or failed to respond (miss) they did not receive water on that trial. We trained two groups of mice with different change probabilities for the left and right sides: asymmetric (80%−20%) or symmetric (50%−50%). This simple difference in change probabilities produced differences in behavior between the two groups.

(C) Differences in behavior between groups. 80–20 trained mice performed well above chance only when the change occurred on the more likely side. Performance was at chance levels when the unlikely change occurred. (Detection index represents the number of standard deviations away from chance performance. For further explanation of detection index, see main text or methods.) In addition, 80–20 mice performed much worse while running than while stationary. 50–50 mice performed well when either change occurred, and performance was unaffected by running. Some 50–50 mice performed slightly better on one side; when aligned to this bias, there was a significant difference in performance between different side change trials. 80–20: N=11 mice; 50–50: N=7 mice. Error bars SEM. Asterisks above individual bars indicate statistical tests relative to zero.

(D) Changes in pupil diameter. Running reliably increased pupil diameter in both groups, so we normalized to the average diameter during running (magenta line). We also report pupil diameters during stationary trials (black line) and further separate stationary trials into correct (green line) and miss (blue line) trials. Data are aligned to trial time points and averaged across trial types. Pupil diameter in 80–20 mice was not different between correct and miss trials, while pupil diameter in 50–50 mice was larger on correct than miss trials across all time points. Comparisons between correct and miss trial pupil diameters using rank-sum test. 80–20: N= 3249 trials, 4 mice; 50–50: N=2752 trials, 4 mice. Error bars SEM.

(E) Optogenetic inactivation of V1 impairs performance. To determine the necessity of V1 to the task, we expressed ChR2 in PV+ inhibitory neurons in both hemispheres of V1 allowing optogenetic V1 silencing (see Methods and Main text). Optogenetic silencing in the hemisphere contralateral to the change significantly impaired behavior in both groups of mice. Ipsilateral silencing also impaired behavior, though this could be due to light spread across hemispheres. 80–20: N=45 sessions, 2 mice; 50–50: N=34 sessions, 2 mice. Error bars SEM. Statistical test relative to zero.

(All plots: *p<0.05, **p<0.01, ***p<0.001; +p<0.05 before Bonferroni adjustment. Unless otherwise noted, we performed a Shapiro-Wilk test for a normal distribution. If the null hypothesis of a normal distribution held, we used a one-sample or paired t-test. Otherwise, if the sample was not normal, we used a non-parametric Wilcoxon sign-rank or rank-sum test. We then performed a Bonferroni adjustment for multiple comparisons. All adjustments in this plot used n=4.) See also Figures S1, S7.

The only difference between the training regimens of the two groups of mice was the probability of the contrast change occurring in each hemifield (for more details see Methods). Selective (80–20) mice were trained with asymmetric change probabilities, 80% and 20% so that one side was always more likely to change. Non-selective (50–50) mice were trained with symmetric change probabilities so that each side changed 50% of the time. Importantly, both groups of mice were rewarded when correctly responding to a contrast change on either side. As we will show, this simple difference in the probability of target appearance was enough to produce dramatic differences in behavior and neural activity. A similar paradigm for macaque monkeys demonstrated that animal performance was best when a cue indicated the location of a high probability orientation change (80% of trials), worst when the uncued location changed (20% of trials), and intermediate in blocks when both locations were simultaneously cued and equally likely to occur (50% of trials each) [30]. In our case, the cue is the animal’s experience of learning the change probabilities, and the neutral and cued conditions are trained with separate groups of mice.

Due to individual variability and the structure of the task not conforming to typical signal detection theory analysis, we developed a measure of performance called detection index that compares each animal’s performance each day to its chance performance (see methods and Figure S1 for details).

80–20 and 50–50 mice performed differently

We began by comparing behavioral performance between the two target locations and between running and stationary conditions. When stationary, 80–20 mice performed well above chance on trials when the more likely change occurred (9.74 standard deviations above chance (detection index), p<0.0001, Figure 1C), and performed no better than chance when the unlikely change occurred (0.22, p=1.0, Figure 1C), due to a difference in z(correct) but not z(early) (Figure S1). In contrast, 50–50 mice performed well when the change occurred on either side (detection index of 7.52 and 6.89, p<0.01 relative to chance, Figure 1C). Performance of 50–50 mice was aligned to their best side, and there was a slight but significant difference in performance between the two sides on stationary trials (p=0.023, Figure 1C). Additionally, 80–20 mice were more likely to respond to likely changes than unlikely changes (attributable to differences in z(correct)), while 50–50 mice were likely to respond to either change (Figure S1). Mean reaction times were not significantly different between the two groups (80–20: 475±39ms; 50–50: 435±81ms; standard deviation, p=0.479, rank-sum test; Figure S1).

We also found that behavior was dependent on the magnitude of the contrast change. 80–20 mice performed better on likely change trials than 50–50 mice did when either side changed, particularly at larger contrast changes, but did not perform above chance when the unlikely stimulus changed, even with large contrast changes (Figure S1). 80–20 mice were either completely ignoring the unlikely change or failed to learn to respond to them. In either case, the behavioral differences between 80–20 and 50–50 mice are robust, and that 50–50 mice were outperformed suggests that dividing perceptual resources limits their maximum performance.

We then examined locomotion trials, during which the mouse moved >0.5 cm/sec in the one second prior to the contrast change. Interestingly, 80–20 mice performed much worse during locomotion (detection index of 4.39 versus 9.74, p=0.0011, Figure 1C), which was due to both a decrease in correct trials and an increase in early lick trials (Figure S1). In contrast, locomotion did not significantly affect the detection index of 50–50 mice (Figure 1C). Both groups responded less often while running versus while stationary (Figure S1). Higher speeds were less common and associated with increasingly worse performance by 80–20 mice, but no change in performance by 50–50 mice (Figure S1). Neural mechanisms of locomotion-induced modulation are well established and not lateralized, which we later show to be true in both groups of mice. Therefore, this difference in the effect of locomotion suggests that 80–20 and 50–50 mice support their behavioral states with different configurations of neural activity, or brain states.

Pupil diameter increases on correct trials for 50–50 but not 80–20 mice

Pupil diameter and global arousal are closely linked. In mice, pupil diameter increases dramatically with locomotion, though it has been correlated with arousal and task performance separately from locomotion [7,31–33]. We measured pupil diameter and found that, consistent with previous studies, pupil diameter increased reliably with locomotion in both groups. (Figure 1D). By examining stationary trials separately, we found a curious difference between the two groups. 50–50 mice had larger pupil diameter on correct trials than on miss trials both before and after the initial stimulus onset (p<0.05 before Bonferroni adjustment) and the contrast change (p<0.01 after Bonferroni adjustment, Figure 1D), consistent with studies linking larger pupil diameter to task engagement and arousal. However, in 80–20 mice there was no difference in pupil diameter between correct and miss conditions on likely or unlikely change trials (Figure 1D). This suggests that 50–50 mice were aided by recruiting global arousal mechanisms to perform the task, while 80–20 mice refrained from recruiting global arousal, perhaps because it, like locomotion related effects, disrupts the neural activity required to perform the task.

Optogenetic inactivation of V1 impairs performance

To test the involvement of V1 in the task, we expressed ChR2 in V1 parvalbumin-positive (PV) inhibitory neurons and optogenetically activated them to silence V1. Previous studies have demonstrated the effectiveness of this strategy for inactivating cortex [34]. We injected Cre-dependent AAV1-DIO-ChR2 bilaterally into V1 of PV-Cre mice. Expression of the ChR2 protein selectively in PV+ neurons was confirmed either electrophysiologically or histologically. We found that optogenetic activation of PV neurons effectively silenced V1 and impaired detection of the contralateral contrast change in both groups of mice (80–20: detection index decrease of 7.21, p<1e-5, 45 sessions; 50–50: decrease of 3.90, p<1e-9, 34 sessions; Figure 1E). This shows that V1 is necessary for optimal performance of the task. The change in performance was due to both a decrease of correct trials and an increase in early licks (Figure S1). In 80–20 mice, silencing the likely hemisphere caused an increase in early licks in general and a relative increase in response tendency on unlikely change trials. Interestingly, inactivation of V1 also somewhat impaired detection of the ipsilateral contrast change (80–20: decrease of 2.87; 50–50: decrease of 1.23, Figure 1E), which could be explained by light leakage across hemispheres but may also suggest a role for the ipsilateral hemisphere in task performance, or simply a broad effect of the strong and artificial optogenetic manipulation.

Local and global effects of spatial selection and locomotion on spike count correlations

To investigate how neural activity relates to the behavior of these animals, we performed simultaneous bilateral recordings in the monocular region of V1 using high density silicon laminar microprobes. We recorded simultaneously from up to 70 isolated single units in each hemisphere and identified cortical layers using current source density analysis. We compared neural activity between recordings from the two hemispheres, likely and unlikely, which represent the locations of likely and unlikely changes (Figure 2A) at distinct time points during the trial (Figure 2B). We also compared activity within-unit on correct versus miss trials and running versus stationary trials. With this strategy we can compare how neural activity changes due to behavioral state in each hemisphere, and whether those changes were symmetric or asymmetric. Unless otherwise noted, we show analyses of only likely change trials due to very few unlikely change correct trials.

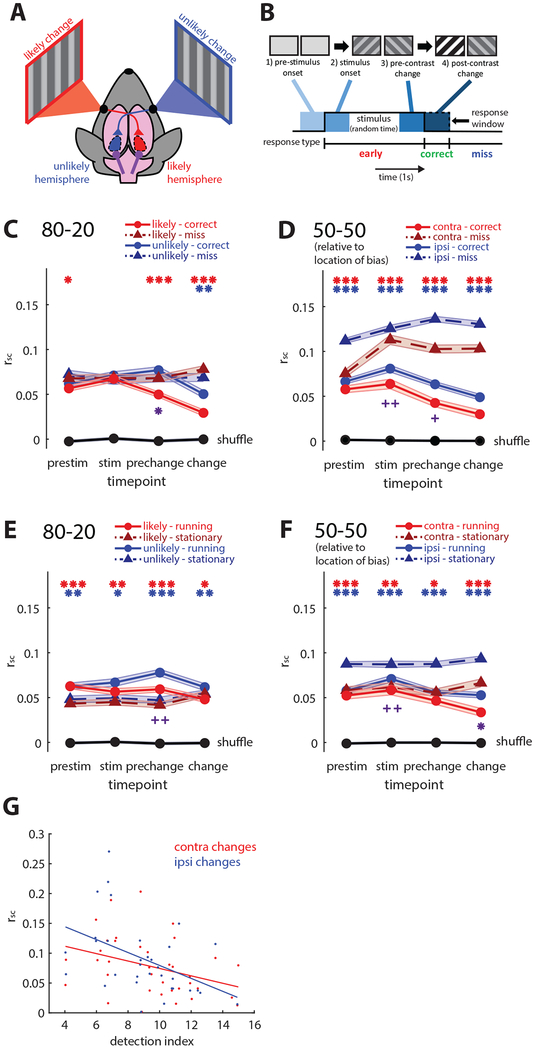
Figure 2: Local and global modulation of correlated variability.

(A) Schematic of hemisphere comparisons and terminology. In 80–20 mice, the likely hemisphere represents the more likely contrast change, and the unlikely hemisphere represents the less likely change. In 50–50 mice, we examined activity in both hemispheres, aligning the sides to their behavioral bias if they had one.

(B) Illustration of examined time points: pre-stimulus onset, just after stimulus onset, just prior to the contrast change, and just after the contrast change.

(C) Local reduction of spike count correlations (r_sc) in 80–20 mice. Prior to the contrast change, r_sc in the likely hemisphere decreases selectively on correct trials (solid red line) relative to miss trials (dotted red line), while pre-change r_sc in the unlikely hemisphere slightly increases (blue lines). Black line shows r_sc calculated with shuffled trials. Likely hemisphere, N=4786 pairs; unlikely, N=3187 pairs.

(D) Global reduction of r_sc in 50–50 mice. Across all time points and in both hemispheres, r_sc is decreased on correct (solid lines) relative to miss trials (dotted lines). When aligned to the slight behavioral biases of these 50–50 mice, the hemisphere corresponding to higher performance had lower r_sc (p<0.05, rank-sum test). Hemisphere contra to bias, N=2891 pairs; ipsi, N=7412 pairs.

(E) Locomotion globally increases r_sc in 80–20 mice. Across both hemispheres, locomotion (“running” solid lines) increased r_sc in 80–20 mice relative to stationary trials (dotted lines).

(F) Locomotion globally decreases r_sc in 50–50 mice. Across both hemispheres, locomotion (solid lines) decreases r_sc relative to stationary trials (dotted lines).

(G) Variations in overall r_sc (not separated by trial) across sessions are correlated with variations in detection index across sessions. Data combined between both 80–20 and 50–50 groups of mice. Red, r_sc versus contralateral behavioral performance, N=36 sessions. Blue, r_sc versus ipsilateral behavioral performance, N=33 sessions. 80–20 unlikely trials excluded because of low performance.

(plots C-F: *p<1e-2, **p<1e-4, ***p<1e-8, sign-rank test. Error bars SEM. Red * reflect comparisons in the likely hemisphere in 80–20 mice, and in the contra hemisphere of 50–50 mice. Blue * reflect comparisons in the unlikely hemisphere of 80–20 mice, and in the ipsi hemisphere of 50–50 mice. Cross-hemisphere comparisons on correct or running trials denoted with purple * below plots, computed with rank-sum test. Bonferroni adjustment performed with N=4. +p<0.05, ++p<0.01 before Bonferroni adjustment) See also Figures S2, S7.

Decreased pairwise spike count correlations (r_sc) are often associated with increased behavioral performance [4,5]. We calculated Pearson’s correlations for each pair of simultaneously recorded single units at each time point across trial types, using spike counts from 400ms time windows. Performance-related differences were not affected by the time window used to calculate r_sc (Figure S4). We found that in 80–20 mice, r_sc decreased selectively on correct versus miss trials in the hemisphere representing the likely change just prior to the time the change occurred (r_correct=0.050, r_miss=0.068, p<1e-8, sign-rank test; Figure 2C). This change occurred in pairs of lower-layer neurons, but not in pairs of upper-layer neurons, perhaps in part because we recorded relatively few simultaneous upper layer pairs in 80–20 mice (Figure S2). In the unlikely hemisphere, r_sc did not differ between correct and miss trials prior to the contrast change (r_correct=0.077, r_miss=0.068, p=0.378, sign-rank test; Figure 2C). However, when we separately examined pairs of upper- and lower-layer neurons, r_sc in lower layers of the unlikely hemisphere was slightly but significantly higher on correct versus miss trials (Figure S2). Importantly, r_sc was significantly lower in the likely versus unlikely hemisphere on correct trials just prior to the change (r_likely=0.050, r_unlikely=0.077, p=0.0011, rank-sum test; Figure 2C), but r_sc did not significantly differ between the two hemispheres on miss trials. The spatially and temporally selective changes in r_sc in 80–20 mice are consistent with their selective behavior and suggest a local brain state that follows the task structure.

In contrast to the asymmetry between hemispheres in 80–20 mice, the 50–50 mice had reduced r_sc on correct versus miss trials in both hemispheres and at all time points (p<1e-33, sign-rank test; Figure 2D), and across upper and lower layers (Figure S2), consistent with their non-selective behavior. When aligned to their behavioral bias, r_sc was lower in the contralateral hemisphere (pre-change: contra: r_correct=0.043, r_miss=0.103; ipsi: r_correct=0.063, r_miss=0.136; contra versus ipsi correct p<0.02, miss p<1e-5; rank-sum test; Figure 2D), again consistent with the association of higher behavioral performance and lower correlations. Despite the slight bias, the largely non-spatially and non-temporally selective modulation in 50–50 mice is consistent with our finding that pupil diameter in these animals is larger across all time points on correct trials (Figure 1D), suggesting they use a global mechanism to improve sensory representations.

We then examined the effect of locomotion on r_sc. Previous studies have shown that locomotion decreases correlations in V1 [6,7]. Our data from 50–50 mice were consistent with the literature, as locomotion decreases correlations (contra: r_running=0.047, r_stationary=0.056, p<2e-3; ipsi: r_running=0.056, r_stationary=0.088, p<1e-70; sign-rank test, Figure 2F), except in lower layer pairs in the hemisphere contralateral to the slight behavioral bias (Figure S2). In contrast, we found that in 80–20 mice, locomotion globally increases correlations prior to the contrast change (likely: r_running=0.059, r_stationary=0.042, p<1e-10; unlikely: r_running=0.078, r_stationary=0.047, p<1e-17; sign-rank test; Figure 2C), across both upper and lower layers (Figure S2), which is consistent with their impaired performance during locomotion. The effect of locomotion, though different across groups of mice, was present in both hemispheres and therefore global in 80–20 and 50–50 mice. This shows that while selection and locomotion alone each decrease r_sc, these effects do not simply combine in 80–20 mice; instead they interfere with each other.

Even among well-trained mice, performance was variable from day to day. We tested whether these global changes in performance were associated with r_sc by plotting behavioral performance for each session versus r_sc among simultaneously recorded neurons across all trials from that session. A similar association has been shown over the course of learning in primates [35]. We found a significant negative correlation between r_sc and performance in both the hemispheres contralateral and ipsilateral to the contrast change, when collapsed across all recordings in both groups of mice, indicating that globally decreased pairwise correlations are associated with improved performance in general, not just at a particular location (contra: r=0.360, p<0.05; ipsi r=0.463, p<0.01; contra vs. ipsi p=0.6599, Fisher z-transformation; Figure 2G).

Local and global effects of selection and locomotion on firing rates

Studies of attention, arousal, and locomotion have all reported associated changes in firing rates. To investigate changes in firing rates in our data, we first z-scored the firing rates of each recorded single unit across 50ms bins to its baseline firing rate during a gray screen. We then compared correct versus miss and running versus stationary trials by subtraction to capture changes associated with each condition (Figure 3A, S3). For statistical comparisons we pooled neurons from layer 4 and above (superficial and granular) versus neurons below layer 4 (deep).

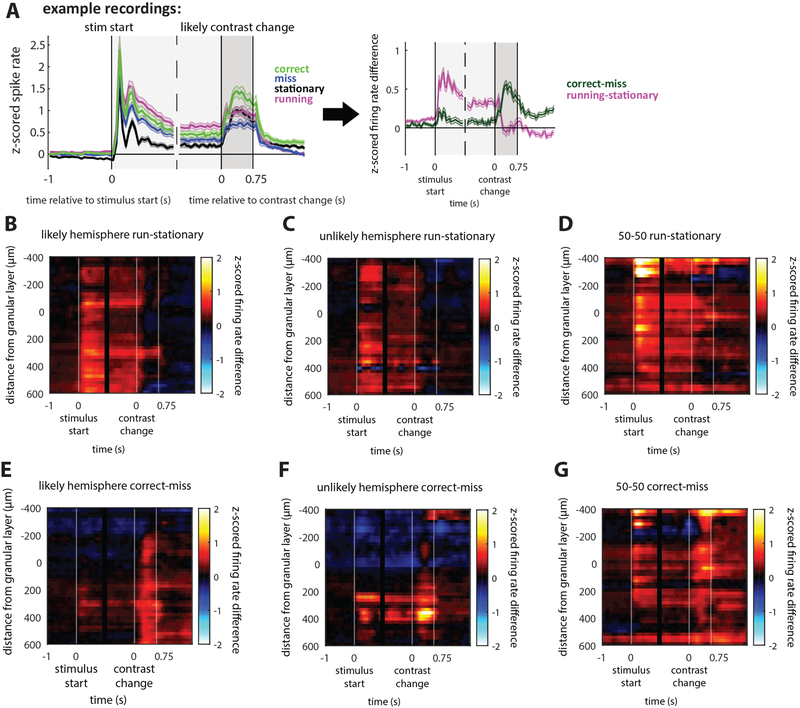
Figure 3: Changes in firing rate across conditions.

(A) Example z-scored firing rates averaged from deep-layer (infragranular, below layer 4) neurons in the likely hemisphere of 80–20 mice. Different trial conditions are shown and aligned to stimulus start and contrast change: correct (green line), miss (blue line), running (magenta line), and stationary (black line) trials. To compare conditions, we subtracted correct minus miss (correct-miss) and running minus stationary (running-stationary) z-scored firing rates. Example corresponds to average of deep layer units (panels B and E). Significant differences shown in Figure S5.

(B-D) Effect of locomotion on stimulus-aligned z-scored firing rates versus recording depth. Color indicates magnitude of firing rate difference. Locomotion increases stimulus-evoked firing rates relative to stationary trials across layers in both 80–20 and 50–50 mice, which is sustained until the contrast change, but the increase is not sustained after the contrast change.

(E-F) Selection affects firing rates differently to locomotion. On correct versus miss trials in 80–20 mice, stimulus-evoked firing rates increase slightly in deep layers and decrease in superficial layers. The response to the contrast change is selectively enhanced on correct trials versus miss trials.

(G) In 50–50 mice on correct trials, both stimulus-evoked and change-evoked activity are increased across layers in 50–50.

80–20 likely hemisphere N=643 neurons; unlikely N=403 neurons; 50–50 N=658 neurons. See also Figures S3, S7.

In both 80–20 and 50–50 groups, locomotion globally increased the stimulus-evoked response across all layers (p<1e-5, sign-rank test, Figure 3B–D, S3). The difference peaked at z-scored firing rates of 0.5 for 80–20 mice and 1 for 50–50 mice. This is consistent with previous findings that locomotion increases stimulus-evoked firing rates in V1 [6,7,11,36]. Baseline firing rates also increased with locomotion across layers in 50–50 mice and in deep layers in 80–20 mice (Figure 3B–D, S3).

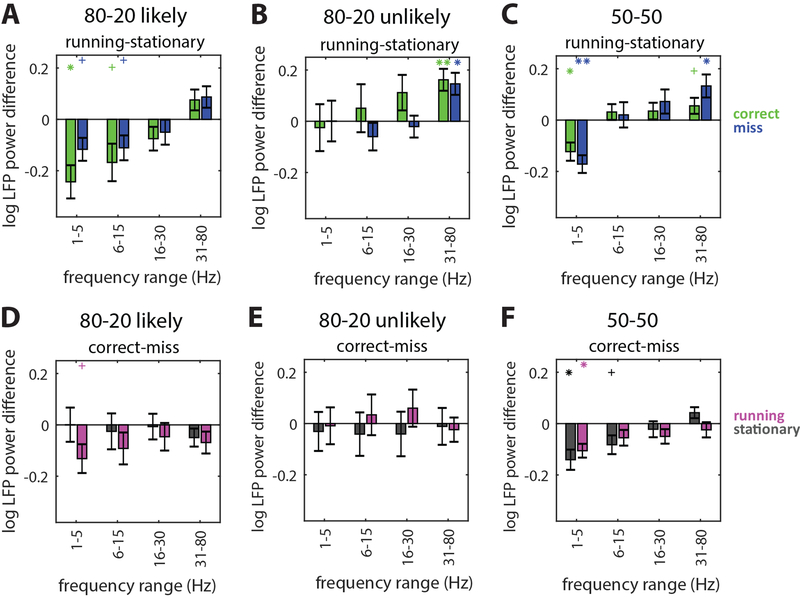
Figure 6: Local field potential power changes consistently with locomotion.

(A) LFP power differences in different frequency bands between running and stationary trials in the likely hemisphere of 80–20 mice. Data from pre-change time point, a time window of 1000ms was used. Running versus stationary differences were separately calculated on correct (green bars) and miss trials (blue bars). Running reduces low frequency (1–5Hz and 6–15Hz) LFP on both correct and miss trials. N=15 included recordings. Error bars SEM. Statistical comparison relative to zero indicated directly above each bar in the matching color. *p<0.05, **p<0.01, **p<0.001, sign-rank test. Bonferroni correction performed with N=4; +p<0.05 before Bonferroni correction.

(B) Same as (A) but for the 80–20 unlikely hemisphere. Running increases high frequency (31–80Hz) LFP. N=14 included recordings.

(C) Same as (A) but for 50–50 mice. Running reduces low frequency (1–5Hz) and increases high frequency (31–80Hz) LFP. N=19 total recordings (both hemispheres, contralateral changes).

(D) LFP power differences in different frequency bands between correct and miss trials in 80–20 mice. Differences between correct and miss LFP power were separately calculated on running (magenta bars) and stationary trials (gray bars).

(E) Same as (D) but for the 80–20 unlikely hemisphere.

(F) Same as (D) but for 50–50 mice.

See also Figure S5.

We next examined how firing rates changed with task performance by comparing correct and miss trials. Contrast change responses were larger on correct versus miss trials in deep layers of 80–20 mice and across all layers of 50–50 mice, with differences peaking at z-scored firing rates of approximately 0.5 (p<1e-11, sign-rank test, Figure 3E–G, S3). This increase in firing rate largely preceded licks (Figure S3), and could represent a detection signal the mouse uses to perform the task. Interestingly, in both groups of mice this signal is present even in the hemisphere not directly representing the location of the change: in 80–20 mice, the unlikely hemisphere (Figure 3F), and in 50–50 mice, the ipsilateral hemisphere (Figure S3). Even though these neurons do not directly represent the contrast change, they may perform a role in the task, consistent with our finding that optogenetically inactivating the unlikely hemisphere in 80–20 or the ipsilateral hemisphere in 50–50 mice impairs task performance (Figure 1E).

In contrast, stimulus onset responses differed between the two groups of mice. While in 50–50 mice the onset responses were enhanced across all layers on correct versus miss trials (p<1e- 5, sign-rank test, Figure 3G, S3), in 80–20 mice the onset responses were only enhanced slightly in deep layers of cortex (p<0.03, sign-rank test, Figure 3E, S3). Furthermore, in the unlikely hemisphere of 80–20 mice, both baseline activity and responses to the onset of the stimulus in superficial and granular layers were decreased on correct versus miss trials (stimulus onset mean value −0.21; p<1e-6, sign-rank test, Figure 3F, S3), reflecting a suppression of the representation of the unlikely-change stimulus. Stimulus onset responses in superficial and granular layers of the likely hemisphere were also somewhat suppressed (p<0.02, sign-rank test, Figure 3E, S3), perhaps reflecting a broad suppression of the behaviorally irrelevant stimulus onset. However, correct versus miss suppression was significantly stronger in the unlikely than the likely hemisphere at the prechange time point (unlikely mean: −0.211, likely mean: −0.106, p=0.023, rank-sum test), further demonstrating asymmetric task-related neural activity changes in 80–20 mice. In contrast, in 50–50 mice correct versus miss firing rates on contralateral versus ipsilateral change trials were not significantly different, consistent with global task-related neural activity changes.

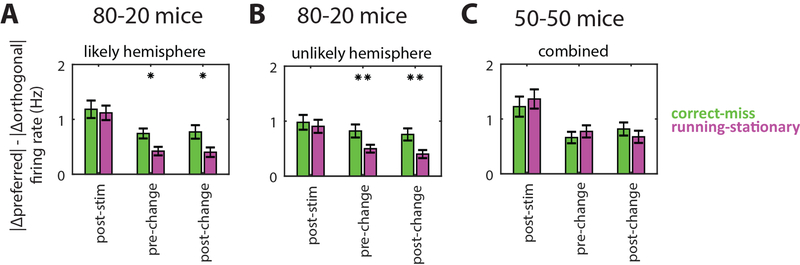
We then compared effects of locomotion and selection on changes in neural responses to preferred versus non-preferred orientations. By subtracting |Δpreferred|-|Δorthogonal| we found that in both hemispheres of 80–20 mice, the gain due to selection is larger than that of locomotion (Figure 4A,B). In contrast, gain in 50–50 mice was not different between selection and locomotion (Figure 4C). This indicates that in 80–20 mice, the effect of selection is more specific to neurons’ preferred stimuli, while the effect of locomotion is less specific, suggesting selection and locomotion may employ different gain mechanisms in these mice. On the other hand, in 50–50 mice locomotion and task performance are not significantly different, consistent with these mice recruiting similar global mechanisms to perform the task.

Figure 4: Specific effects on responses to preferred stimuli.

Average difference across neurons between absolute change in firing rate in response to preferred versus orthogonal orientation.

(A-B) In 80–20 mice at pre-change and post-change time points and in both hemispheres, the change in response to the preferred versus orthogonal stimulus is larger for correct versus miss trials (green) than for running versus stationary trials (magenta) (likely N=303; unlikely N=217 significantly tuned neurons).

(C) In 50–50 mice, effects of selection (correct versus miss trials) and locomotion (running versus stationary) were not significantly different (N=177 significantly tuned neurons). *p<0.05, **p<0.01, sign-rank test between (correct-miss) and (running-stationary).

These results show that 80–20 and 50–50 mice modulate V1 firing rates in different ways. 80–20 mice selectively and asymmetrically modulate firing rates while 50–50 mice globally increase stimulus-evoked firing rates, similar to the broad effect of locomotion and consistent with a recruitment of global arousal mechanisms.

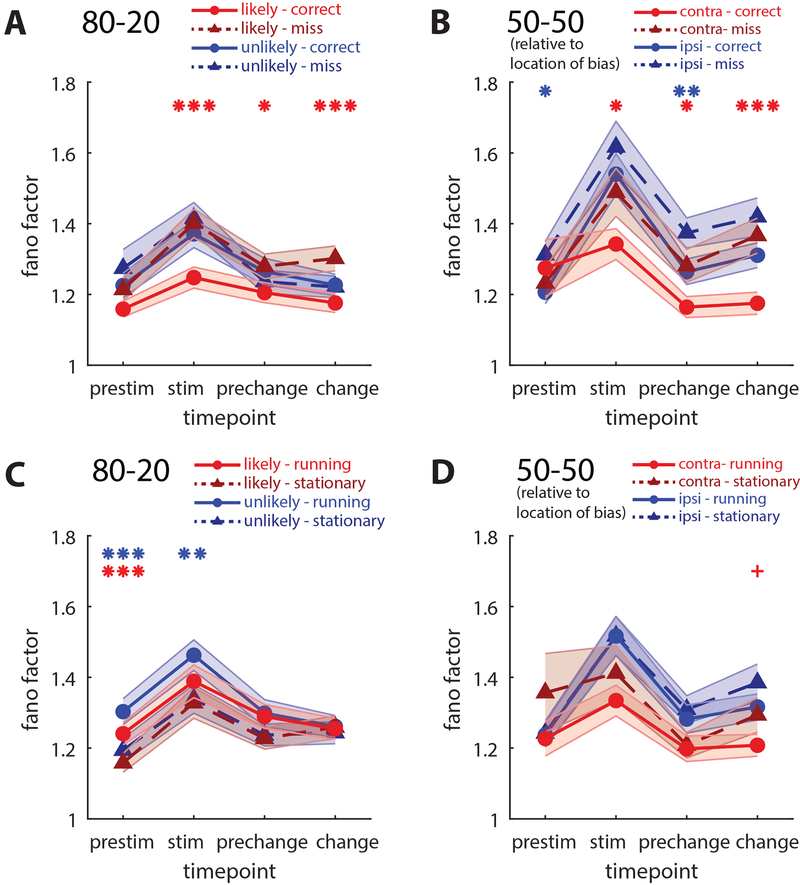
Task performance is associated with decreased trial-to-trial variability

Another reported effect of both spatial attention in monkeys and locomotion in mice is a decrease in trial-to-trial variability [6,17]. For each unit across different trial types, we calculated Fano factor, the variability across trials divided by the mean, in 100ms time bins, then averaged across 400ms time windows. In 80–20 mice, Fano factor decreased selectively in the likely hemisphere on correct versus miss trials (pre change: fano_correct=1.205, fano_miss=1.280, p<0.05, sign-rank test, Figure 5A), and this effect was restricted to lower layer neurons (Figure S4). In 50–50 mice, the Fano factor decreased in both hemispheres on correct versus miss trials (prechange, p<0.02, sign-rank test; Figure 5B), though when separately examining layers there was no change in lower layer neurons in the hemisphere contralateral to the contrast change (Figure S4). Locomotion slightly increased Fano factor in the likely hemisphere of 80–20 mice at the stimulus onset time point but not at the contrast change (Figure 5C), and locomotion slightly decreased Fano factor in 50–50 mice after the contrast change (Figure 5D), but overall effects of locomotion on Fano factor were not nearly as striking as its effects on other measures, in contrast to a previous study that showed locomotion decreased Fano factor [6]. These results provide further evidence that 80–20 mice produce a spatially selective brain state.

Figure 5: Local and global decreases in individual variability.

(A) Comparison of mean Fano factor (variability/mean) across time points on correct (solid lines) versus miss (dotted lines) trials in likely (red) and unlikely (blue) hemispheres of 80–20 mice. Fano factor in the likely hemisphere on correct trials is selectively decreased relative to other conditions. Likely hemisphere, N=303 neurons; unlikely, N=217 neurons.

(B) Correct versus miss Fano factor in 50–50 mice. Fano factor decreases in both hemispheres on correct versus miss trials. Hemisphere contra to bias, N=91 neurons; ipsi, N=121 neurons.

(C-D) Locomotion has inconsistent effects on Fano factor.

(All plots, *p<0.05, **p<0.01, ***p<0.001, sign-rank test. Error bars SEM. Red * reflect comparisons in the likely hemisphere in 80–20 mice, and in the contra hemisphere of 50–50 mice. Blue * reflect comparisons in the unlikely hemisphere of 80–20 mice, and in the ipsi hemisphere of 50–50 mice. Bonferroni adjustment performed with N=4. +p<0.05 before Bonferroni adjustment) See also Figure S4.

Locomotion and selection reduce low-frequency LFP power in both groups

Previous studies report decreases in low-frequency and changes in high-frequency local field potential (LFP) power with both attention in primates and locomotion in rodents [7–9,11]. We found consistent decreased delta (1–5Hz) and alpha band (6–15Hz) power with locomotion selectively in the 80–20 likely hemisphere (Figure 6A), increased gamma band (30–80Hz) power in the 80–20 unlikely hemisphere (Figure 6B), while both delta decreases and gamma increases were present in 50–50 mice (Figure 6C). Interestingly, changes in LFP power with locomotion were different across hemispheres in 80–20 mice, perhaps a result of their asymmetric modulation of V1 to perform the task (Figure 6A–B).

Task-related changes in LFP power were restricted to low frequencies (Figures 6D–F). On correct versus miss trials, delta-band LFP power decreased significantly in 50–50 mice (p<0.05, sign-rank test, Figure 6F), and decreased in the likely hemisphere of 80–20 mice but only when mice were also running (p<0.05 before Bonferroni correction, sign-rank test, Figure 6D), while no task-related changes were observed in the unlikely hemisphere (Figure 6E). That the effects of running and task performance on LFP power in 50–50 mice are similar suggests similar global mechanisms. An unexpected finding is that, while locomotion decreases low-frequency LFP power in 80–20 mice, it also increases r_sc and is associated with poorer performance. Low-frequency LFP power and r_sc usually tend to change in the same direction, but our findings suggest that these effects are not always linked. Furthermore, under our experimental conditions, r_sc reflects behavioral performance better than low-frequency LFP does.

Selection improves and locomotion impairs visual information in 80–20 mice

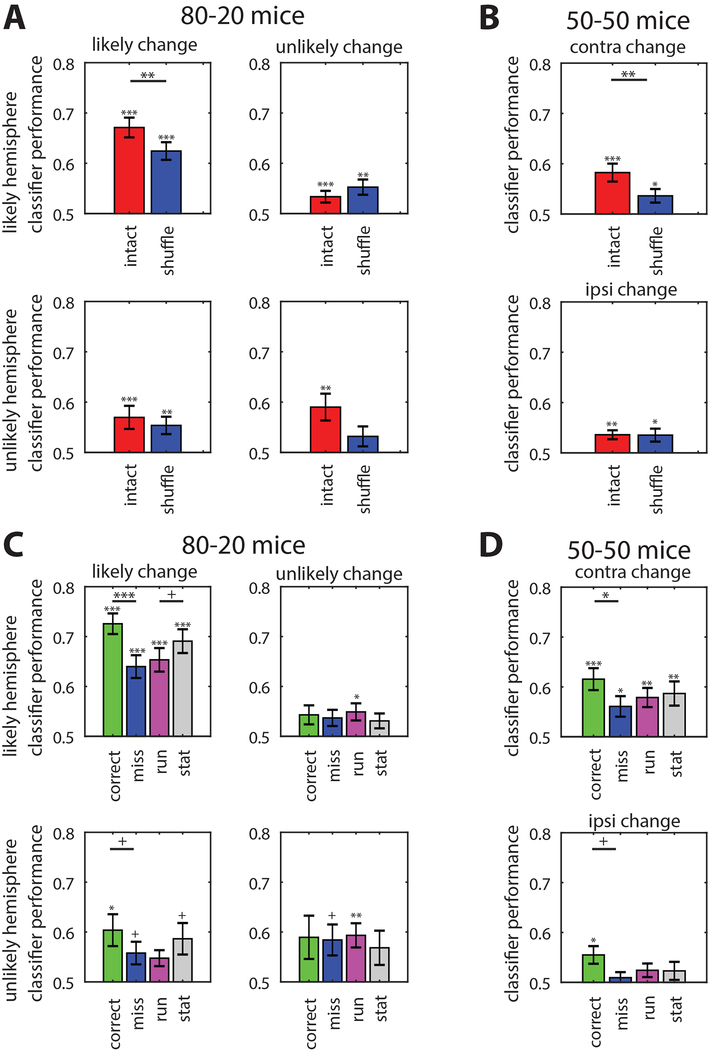
To assess how changes in neural responses affected task-relevant information in the brain, we trained a linear classifier to distinguish between V1 population activity 400ms before and after the contrast change for each recording in each hemisphere (for other time windows see Figure S6). We also independently trial-shuffled neural activity within each neuron to remove the correlation structure but maintain the relationship between pre- and post-change firing rates on average. By training the classifier on these shuffled data we could compare performance to the unaltered dataset to assess the contribution of trial-to-trial correlated variability. Since we classified between just two time points, pre- and post-change, chance performance was 50%. A similar approach has been used previously to decode visual stimuli from neural activity in both primates and mice [25,37–39].

Not surprisingly, the classifier performed best at distinguishing pre-change versus post-change activity on likely trials when using the full population activity from the likely hemisphere of 80–20 mice (67.2% accuracy, Figure 7A). It performed significantly worse when using the shuffled activity (62.4%; p<0.002 relative to intact), but still above chance (Figure 7A). The classifier generated from activity in the unlikely hemisphere performed worse overall with likely changes, but still above chance (full: 57.0%, p<0.001 relative to chance; p<0.001 relative to likely hemisphere; Figure 7A), while shuffling did not affect classifier performance (shuffled: 55.4%, p=0.161 relative to intact). However, shuffling did affect the performance of a classifier trained on unlikely hemisphere data for unlikely changes (intact: 59.0%, p=0.009 relative to chance; shuffled: 53.2%, p=0.167 relative to chance).

Figure 7. Local and global effects on linear classifier performance.

Linear classifier performance decoding pre- versus post-change population activity.

(A) Classifier performance when using raw spike counts (red bars) and trial-shuffled spike counts (blue bars) in 80–20 mice. The classifier performed best using raw spike counts from the 80–20 likely hemisphere on likely change trials. Trial shuffling decreased performance in the 80–20 likely hemisphere on likely change trials, and in the unlikely hemisphere on unlikely change trials. Error bars SEM. 80–20 likely N=18 recordings; 80–20 unlikely N=15 recordings.

(B) Same as (A) but using data from 50–50 mice. Trial shuffling reduced classifier performance only on contralateral change trials. N=19 recordings (both hemispheres’ responses to contralateral change trials combined).

(C) Linear classifier performance using spike counts from 80–20 mice on different subsets of trials: correct (green), miss (blue), running (magenta), and stationary (gray). Performance differed across different trial conditions in the likely, but not unlikely hemisphere of 80–20 mice. Error bars SEM. 80–20 likely N=18 recordings; 80–20 unlikely N=15 recordings.

(D) Same as (C) but using data from 50–50 mice. Performance differed between correct and miss trials when either contralateral or ipsilateral changes occurred. N=19 recordings (both hemispheres’ responses to contralateral change trials combined). Statistical comparisons between correct and miss or running and stationary trials.

(Comparisons to chance shown directly above each bar. Comparisons across conditions shown above a horizontal line corresponding to the conditions compared.

*p<0.05, **p<0.01, ***p<0.001; +p<0.05 before Bonferroni adjustment. Unless otherwise noted, we performed a Shapiro-Wilk test for a normal distribution. If the null hypothesis of a normal distribution held, we used a one-sample or paired t-test. Otherwise, if the sample was not normal, we used a non-parametric Wilcoxon sign-rank or rank-sum test. We then performed a Bonferroni adjustment for multiple comparisons. Adjustments for A,B used n=2; C,D used n=4.) See also Figure S6.

With activity recorded from 50–50 mice, trial shuffling also significantly reduced classifier performance using the contralateral hemisphere (full: 58.2%, shuffled: 53.6%; p<0.005; Figure 7B). However, shuffling did not affect classifier performance using ipsilateral hemisphere data (full: 53.6%, shuffled: 53.5%). This shows that in both groups, the correlated variability of the task-relevant neural population activity contributes information about the visual stimulus, but only in the neural population that directly represents the visual stimulus. In addition, classifier performance was worse using 50–50 activity versus 80–20 likely hemisphere activity (p<0.005, Figure 7A), suggesting that dividing perceptual resources between the two locations limits visual information.

To determine whether information encoded in the neural activity changed along with the behavioral state, we assessed the performance of each classifier on the different trial types (correct, miss, running, and stationary) and averaged across recordings. We found that the classifier trained with 80–20 likely hemisphere data performed far better on correct trials than miss trials (72.6% versus 64.0%, p<0.001) and worse on locomotion trials than stationary trials (65.4% versus 69.1%, p<0.05 before Bonferroni correction), consistent with behavior. (Figure 7C). The classifier trained with unlikely hemisphere data on likely change trials performed better on correct versus miss trials (60.4% versus 55.8%, p<0.05 before Bonferroni correction) though did not differ between running and stationary trials, and performance on correct trials was significantly worse compared to the likely hemisphere (p<0.001). This is consistent with our finding of increased firing rates in the unlikely hemisphere following a likely change on correct versus miss trials. However, the classifier trained with unlikely hemisphere data on unlikely change trials did not perform differently between trial types, as would be expected if that activity was not task-relevant (Figure 7C). In 50–50 mice, the classifier trained on either contralateral or ipsilateral hemisphere data also performed best on correct trials, but it did not perform significantly differently between running and stationary trials (Figure 7D). Thus, in both groups of mice, the neural activity in the hemisphere ipsilateral to the behaviorally relevant change encodes task-relevant information, consistent with our finding that optogenetic silencing of the ipsilateral hemisphere impairs performance.

To summarize, on correct trials, the 80–20 mice selectively enhance visual information in V1 about the likely change location, but locomotion decreases that information, while the visual information in the unlikely hemisphere about the unlikely change location is not altered from trial to trial. The 50–50 mice also enhance visual information to perform the task, but locomotion does not affect overall visual information. Shuffling affects only the neural population information about a directly represented stimulus, suggesting that correlated variability is tied to improving direct stimulus representation. In contrast, on correct trials, information is improved about behaviorally relevant stimuli, whether they are represented or not, consistent with our observed changes in firing rate. These changes in information are consistent with changes in behavior, suggesting that the classifier performance reflects changes in neural population information in V1 that are important for the perception and behavioral performance of these animals.

Performance-matched sessions from 80–20 and 50–50 mice recapitulate results

As described above, task performance on stationary trials was better (for likely change trials) for 80–20 mice than for 50–50 mice (Figure S1). While these differences are consistent with selective versus distributed attention [30], they raise the possibility that differences in electrophysiological measures in 80–20 versus 50–50 mice might reflect differences in task difficulty rather than local versus global effects related to spatial selection and/or locomotion. To address this possibility, we analyzed the changes in r_sc and firing rates for a subset of recording sessions where 80–20 and 50–50 mice performed equally well. Performance of 80–20 mice was better on average, but more variable than 50–50 mice, with at least 2 sessions where an 80–20 mouse performed worse than any 50–50 mouse (Figure S7). This allowed us to select a subset of behavior-matched recording sessions from 80–20 and 50–50 mice, with a detection index range of 8–13 (n=8 sessions for both groups, Figure S7). 50–50 mice were only included if they performed within this range in response to changes in both locations. Analyzing this subset of data recapitulated our results that in order to perform the task (correct versus miss comparisons), 80–20 mice selectively and asymmetrically modulate neural activity while 50–50 mice symmetrically modulate neural activity (See Figure S7 for details). Furthermore, the opposite effects of locomotion on r_sc for 80–20 versus 50–50 mice persist for this subset of recording sessions. This shows that differences observed between 80–20 and 50–50 groups are not simply due to the level of performance of the mice or the task difficulty.

DISCUSSION:

Our results reveal novel interactions between local and global modulatory mechanisms in mouse V1 and their differential modulation by locomotion. Despite the many similarities, locomotion in mice is not the same as attention. We show that the effects of locomotion on behavior and visual information representation vary with the task. Importantly we find a consistent relationship between correlated neural variability, behavioral performance, and visual information encoded in V1. Our mouse model of spatial selection will facilitate future studies into the roles of different cell types in the neural circuitry supporting both selective and non-selective brain states and the extent to which they differ.

How the spatial selection task relates to attention tasks

A simple difference in contrast change probability at different locations was enough to produce striking differences in behavior and brain states between 80–20 and 50–50 mice. Interpreting our results requires examining how this spatial selection task relates to previously described attention tasks. We demonstrated a spatially specific behavior in the 80–20 mice, though unexpectedly, the 80–20 mice did not perform above chance on unlikely change trials, even with very large contrast changes (Figure S1). In a typical attention task, one would expect detection of the unattended stimulus to be decreased, but not to fall to chance. This asymmetric behavior of the 80–20 group of mice could potentially be explained by asymmetric learning, perhaps not representing spatial attention in the traditional, dynamic sense. These two possibilities would be difficult to distinguish, given evidence that learning and attention cause similar electrophysiological changes [35].

Despite this possibility, our data do demonstrate spatially-selective trial-to-trial dynamic changes at the behavioral and electrophysiological levels. Previous studies have used similar 80–20, 100–0, or 50–50 attention tasks in primates and found similar behavioral and electrophysiological results [30,40]. Broadly, those studies show that with a neutral or non-cued paradigm (50–50), behavioral performance and electrophysiological correlates of attention are intermediate compared to a cued paradigm (80–20), which is consistent with our results even though our different tasks were performed by separate animals. The 80–20 brain state may not be a perfect analogue of spatial attention, but our findings demonstrate that it selectively enhances representations of one hemifield and actively suppresses the other, while 50–50 mice enhance representations of both hemifields, but cannot match the behavioral performance of 80–20 mice.

Correlated variability and behavioral performance

Our findings are consistent with recent studies of correlated variability and offer some new insights. Decreases in spike count correlations (r_sc) were associated with improved performance (except for locomotion-induced decreases in 50–50 mice), and increases in r_sc were associated with impaired performance. Importantly, in 80–20 mice task-related decreases were selective to the target, occurring in the likely hemisphere, while locomotion-related increases occurred in both hemispheres, showing how this form of selection has a local effect while locomotion has a global effect (at least in V1). Furthermore, we observed slight increases in r_sc in the unlikely hemisphere where the mouse did not detect changes. While consistent with previous studies linking r_sc and behavioral performance, our results demonstrate that different mechanisms that alone decrease r_sc – selection and locomotion – do not necessarily combine additively. Rather, these interactions are complex and task-dependent.

As further evidence of complex interactions, we show both global and local components of r_sc associated with behavioral performance. On a session-to-session basis, mean spike count correlations were negatively correlated with performance, even in the hemisphere of V1 that did not represent those changes (Figure 2G). This suggests that a component of the r_sc decrease is attributable to changes in global arousal from session to session, consistent with a recent study [35]. However, there is also clearly a local, trial-to-trial component of correlations, as evidenced by the local decrease in 80–20 mice (Figure 2C). Further complexity is evidenced by the surprising observation that locomotion decreases low frequency LFP activity in the likely hemisphere of 80–20 mice but increases r_sc (discussed further below).

Neural population information

Previous studies have shown that changes in r_sc do not necessarily affect population information [18–21]. To address this, we more directly assessed changes in population information by using a linear classifier to decode pre- versus post-change population activity. Our finding that the classifier performed best on 80–20 likely hemisphere correct trials, but worse on running trials, shows that those mice can dynamically improve information in V1 about the behaviorally relevant stimulus, and that locomotion decreases that information.

To determine the contribution of different aspects of neural activity to population information, we also trained the classifier on trial-shuffled population activity, which removes correlated variability. Trial-shuffled activity did not perform as well as the full population activity, demonstrating that in this task and experimental setup, spike count correlations contribute to information encoding in mouse V1. However, the shuffle only impacted classifier performance when the neural activity directly represented the contrast change. In contrast, on correct trials information about the behaviorally relevant stimulus was improved regardless of whether the neural population directly represented the stimulus, likely in part due to increased firing rates in both hemispheres following a contrast change. This suggests that correlated variability is important for directly encoding sensory information but firing rates could be sufficient for change detection in this task.

Most neurons in V1 increase their firing rates in response to changes in contrast, so simply summing or averaging across the firing rates of many neurons could be an effective coding strategy for this change detection task. This may be why the effect of locomotion has such a negative effect on behavioral performance of 80–20 mice in this task – the firing rate increase due to locomotion could be conflated with an actual stimulus-related increase. This is consistent with our observation of a higher rate of early lick trials when 80–20 mice run. However, the lack of increased early licks in 50–50 mice with running suggests that they may use a different decoding strategy to detect contrast changes.

Locomotion reliably influences local field potential

Reduced r_sc is typically associated with specific changes in the local field potential (LFP), but we found these LFP changes to be more reliably associated with locomotion. Task performance, particularly in attention tasks, is often linked with decreases in low-frequency LFP and sometimes increases in high-frequency or gamma LFP [8,9]. In 80–20 mice, we found a significant decrease in delta-band LFP power between correct and miss trials, but only when the mouse was also running (Figure 6D). This was surprising; since 80–20 mice perform better on stationary trials, we would have expected a larger difference in LFP on those trials. In 50–50 mice, delta band LFP power decreased on correct trials whether or not the mouse was running, consistent with their ability to perform the task well when running or stationary.

Nevertheless, the most reliable driver of changes in LFP power was locomotion. It decreased both delta and alpha band LFP in the likely hemisphere of 80–20 mice, and decreased delta band LFP and increased gamma band LFP in 50–50 mice, and increased gamma LFP in the unlikely hemisphere of 80–20 mice. The difference in the effect of locomotion on LFP power in the two hemispheres of 80–20 mice may reflect that the two hemispheres have asymmetric brain states for task performance. Locomotion-induced changes in LFP appear to be larger and more reliable than task-related changes. Perhaps locomotion is simply a more reliable driver of synchronization; locomotion causes increased firing rates in all interneuron subtypes [41,42], which are thought to be major drivers of oscillatory activity in cortex [43].

Furthermore, in 80–20 mice, locomotion decreases low-frequency LFP power yet increases spike count correlations, contrary to previous findings. This shows that low frequency power and correlated variability are not necessarily linked and can change independently.

Movement-related activity

Our results are also consistent with recent studies showing that animal movement accounts for a great deal of cortical activity [26,27], and demonstrate the importance of recording multiple movement variables in any experiment with an awake animal. This raises the possibility that some effects on recorded electrophysiological activity could be due to movement or at least some combination of movement and task related neural activity. During training sessions, we only recorded locomotion, pupil diameter, and licking, but occasionally the mice performed several other distinct behaviors such as grooming. Our task design did not incorporate a delay period, making it difficult to fully separate detection from response, but we did reliably see increases in activity prior to the typical reaction times of approximately 450ms (Figure S1, S3). We largely confined our analyses of post-change activity to time windows before the mice responded, so the act of licking was not primarily responsible for the increases in response to the contrast change on correct trials. Future studies should record more movement variables to disentangle movement-related from task-related activity.

Conclusion

To a coffee or tea drinker, these complex and task-dependent local and global interactions should be familiar. One cup of coffee may provide the optimal state for writing a scientific paper, while two cups may impair writing, but enhance a less cognitively demanding task such as checking spelling or grammar. In this way, each task or category of tasks has its own optimal state to produce optimal behavior. Our results shed light on why this extra dimension affects behavior. Local selection mechanisms, generally associated with more difficult behaviors, are more specific and likely more vulnerable to perturbation. Too much global arousal may disrupt the local optimal state by injecting noise into the system, such as an overall increase in firing rate with locomotion in our experiments. In other circumstances, these same global perturbations could improve behavior, but it depends a great deal on the task specifics.

Many questions remain. What are the neural circuits and cell types that facilitate and control these local and global modulations of visual information? Which brain areas participate in this modulation and how, including extrastriate visual areas, thalamus, and superior colliculus? Do the local and global effects use the same or different modulatory mechanisms? Moving forward, this mouse spatial selection task will enable the use of available genetic tools to investigate these questions and elucidate the neural circuit mechanisms of local and global sensory modulation.

STAR METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Edward Callaway (callaway@salk.edu)

EXPERIMENTAL MODEL AND SUBJECT DETAILS

All animal procedures followed institutional and national guidelines and were approved by the Salk Institute IACUC. 13 C57/Bl6 mice (Jackson Laboratory stock # 000664) and 5 PV-Cre mice (Jackson Laboratory stock # 008069) were used, comprised of both male and females. Due to length of training, mice aged 4–14 months were used. Mice were group housed with littermates when possible and given wheels in their cages. Littermates were randomly assigned to the different training paradigms.

METHOD DETAILS

Surgery

Before behavioral training, all mice were implanted with a metal head post for head fixation during training. Briefly, animals were anesthetized with 2% isoflurane in oxygen and were placed on a heating pad in order to maintain their body temperature. A small patch of skull was exposed and the head post was attached with dental cement (C&B-Metabond, Parkell Inc.) posterior to the known location of V1, with the remaining exposed skull covered by additional dental cement. The location of bregma was marked with a small piece of plastic embedded in the cement for future reference. Carprofen (5mg/kg) and ibuprofen (0.11mg/mL in ad-lib water) were given for postoperative analgesia for all procedures, and for craniotomies dexamethasone (2mg/kg) was also delivered.

For virus injections, at least one week after mice recovered from headframe surgery, we again anesthetized the mice and made small crainiotomies over the center of V1 using coordinates from bregma (3mm posterior, 2.5mm lateral), and pressure-injected 100nl of AAV1.EF1a.DIO.hChR2(H134R).EYFP.wPRE.HGH (AAV1-DIO-ChR2; Addgene 20298; from UPenn vector core) at depths of both 300um and 600um. Following injections, the craniotomy was first sealed with a clear silicone elastomer (Kwik-Sil, World Precision Instruments) or gel (3–4680, Dow Corning), then the site was covered with clear dental cement (C&B-Metabond, Parkell Inc.) and a 3mm coverslip was placed over the injection site to create a window through which light for optogenetics could be directed. Finally, we built small wells with dental cement around these windows and painted the cement with black nail polish to minimize the spread of optogenetic light (though we could not completely rule out the possibility that light from one brain hemisphere could reach the other, particularly with higher light levels).

To prepare for subsequent electrophysiological recordings, we anesthetized mice and made 1–2mm diameter craniotomies over the center of V1 to provide space for up to 5 consecutive recordings. Dura was left intact. Recordings were performed on awake animals on the day of the craniotomy and up to 4 additional consecutive days. Before the craniotomy and before each subsequent day of recording, mice were given carprofen as an analgesic and dexamethasone to limit brain swelling. After each recording session, the craniotomies were covered first with non-bioreactive silicone elastomer (Kwik-cast, World Precision Instruments), then a thin layer of dental cement to ensure the silicone stayed in place and the mouse could not inadvertently remove it.

Behavior rigs and visual stimuli

Mice were trained on custom behavior rigs, which used custom MATLAB software to present visual stimuli with Psychtoolbox based on visual stimulus software described previously [44,45], with extensive modifications to record behavioral variables and deliver rewards using Arduinos. The rigs consisted of a running wheel attached to a base plate, with clamps to hold the headframe above the wheel. A rotation encoder was attached to the wheel to record locomotion, and an infrared sensor was used to record licking, while a metal tube was positioned just behind the sensor to deliver rewards. Two monitors controlled by a dedicated visual stimulus computer were positioned in the center of the mouse’s hemifield and were calibrated to ensure linear gamma response. The electrophysiology recording rig had monitors placed 17cm away from each eye of the mouse. A second, master computer controlled the stimulus computer and the Arduinos by sending relevant parameters and saving behavioral data during each trial. All components were synchronized by a digital pulse generated by the stimulus computer once the graphics card built and started to play the stimulus for that trial (the rate-limiting step). Visual stimuli were full-field square-wave drifting gratings with 8 possible different directions, a temporal frequency of 1.5Hz, and a spatial frequency of 0.05 cycles/degree. For all but one mouse, stimulus onset contrast was 25% of the maximum contrast (the other began at 50%). Mice experienced a variety of contrast changes during training, but for recording sessions, all experienced a 20% change, and all but one were shown an increment. All reported contrasts are relative to the maximum of 100%, in which white corresponded to a 255 value and black a 0 value in Psychtoolbox. Random stimulus time was determined by a hazard function. After a consistent 2 second delay, every 25ms the stimulus had a 1% chance of changing in contrast. On trial times greater than 10 seconds, the mouse was automatically delivered a reward if it refrained from licking, to encourage waiting. These trials comprised less than 5% of total trials and were excluded from analysis, along with any other trials in which an automatic reward was delivered.

Behavioral task and training

In order to motivate mice to perform the task, we restricted their water intake. Water restrictions began after mice fully healed from head-post implant surgery (~1 week). Each mouse received ~1 mL water per day until 15% ad libitum weight was lost (1–2 weeks). During training days, mice received all water during training (0.5–2 mL), but excess water was given after training if the animal did not drink enough to sustain health (at least 0.5mL). On break days, we gave enough water to maintain health and thirst, which depended on weight (minimum 0.5 mL).

We acclimated mice to being handled by hand-delivering water during initial days of water restriction, and habituated mice to the behavior rig by placing their cages between the two monitors and playing stimuli for 0.5–1 hour. During the first 1–2 sessions, mice were briefly anesthetized with isoflurane prior to head fixation. Once water-restricted mice had lost at least 15% of their body weight, and after 1–2 days of habituation, mice were trained in four main phases. In the first phase, rewards were associated with a large contrast change (increase of 40–50%). During this phase, rewards were automatically delivered at the same time as the contrast change, with no punishment for early licks. Rewards dispensed approximately 4μL of 10% sucrose water. We also gradually increased the duration of training sessions from approximately 0.5 to 2 hours. Once mice began to anticipate the reward by licking, we moved to the next phase. In the second phase, mice had to lick within the correct window to receive the reward, but were still not penalized for early licks. At this point, some mice began to restrict their licks to the response window, others licked throughout the trial, and a few never learned to lick on their own (these last ones usually did not move on to the next phase). Once mice reliably licked to receive rewards on their own, we moved them to the third phase. In the third phase, an early lick would prevent a reward on that trial, even if the mice subsequently licked in the correct window. In addition, on those early lick trials the mice would be punished with a timeout, which would elongate the inter-trial-interval by 5–15 seconds. This was often the hardest part for mice to learn. Some mice performed above chance within 30 sessions but only gradually reduced early licks over the next 30–60 sessions. Once mice were able to withhold licking to the initial stimulus onset and then lick in response to the contrast change, they were moved to the final phase. In the final phase of training, the magnitude of the contrast change and the length of the response window were gradually decreased until the mouse performed well with the target contrast change of 20% and response window of 750ms.

In most cases we used additional parameters to aid in training. We observed that most mice would lick at the initial stimulus onset, so we implemented a one second forgiveness period after the stimulus onset so that these licks would not trigger an early response and a timeout. In addition, we delayed the response window by at least 100ms to ensure that the mouse could not lick and receive a reward before the visual information could have possibly been perceived. We also observed a great deal of variability between mice in terms of tendency to lick and rate of licking, so we varied the definition of a “response” depending on the mouse’s licking tendency. A single lick in the response window was counted as a correct response, but only if no licks occurred before the contrast change. If the mouse did lick prior to the contrast change, it only counted as an early response if the mouse licked twice within a certain time window, usually 300ms. However, if the mouse did lick just once prior to the change on a trial, the mouse could still earn a reward with a double lick in the response window. In this way, what counted as a “response” could dynamically adjust to individual tendencies of the mice, even varying between days.

Optogenetic stimulation

For optogenetics experiments, we used two Thorlabs LED drivers (LEDD1B) with 470nm LED modules (M470F3), positioned with micromanipulators (17011702, Märzhäuser Wetzlar GmbH & Co). LEDs were controlled through the same Arduino used to record behavioral variables and deliver reward, using digital-to-analog converters to enable precise light stimulation at different intensities. Light intensities used ranged from 20mW to 40mW, measured at the tip of the optic fiber with a handheld power meter (1098293, Coherent LaserCheck). In behavioral only experiments, optic fibers were positioned above each implanted chronic window. In combined electrophysiology and optogenetics experiments for confirmation of ChR2 expression, both electrodes and optic fibers were positioned near the craniotomies (see below for electrophysiology methods). Optic fibers were positioned such that the light cone covered as much of the craniotomy as possible, and always covered the recording site. This was sufficient since with the skull removed, much less light power (<10mW) was required to activate ChR2.

Electrophysiology

For electrophysiological recordings, we used the Intan system and software with 64-channel laminar silicon probes from Sotiris Masmanidis at UCLA (64D configuration)[46,47]. Before craniotomies were performed, wells were built using dental cement and silver epoxy (8331–14G, MG Chemicals) was applied to the headframe and to surrounding surfaces near the future recording sites to provide a ground. Once craniotomies were performed (as described above), the mouse was placed on the wheel and clamped into the headframe holder, then electrodes were positioned with micromanipulators (1760–61, David Kopf Instruments) above sites both clear of blood vessels and stereotactically determined to be within V1. Electrodes were advanced to the brain surface, then agarose (A6138, Sigma-Aldrich) in ACSF was applied to the craniotomy wells to provide both stability and electrical grounding. Once the agarose solidified, a thin layer of transparent silicone gel (3–4680, Dow Corning) was added to the surface of the agarose to prevent drying. (In some cases, drying agarose moved electrodes). Once the silicone was set, we slowly advanced each electrode approximately 1mm while watching and listening for spikes. Once both electrodes were at 1mm, we determined the receptive field of neurons to make sure it was in the relative center of the screens. We then performed a current course density (CSD) analysis (see below) to determine if the electrodes were advanced far enough and also to confirm that this location looked like V1. If we could not distinguish layer 4 in the CSD, we tried removing and re-placing the electrode, but if the recording on the other hemisphere was good, we limited ourselves to only 1–2 additional tries because each retry risked a bump that could ruin the quality of the other recording. 15/66 electrode penetrations were ultimately excluded because we could not distinguish layer 4.

QUANTIFICATION AND STATISTICAL ANALYSIS

Behavior analysis

This behavior was difficult for mice to learn, taking between 30–90 days (Figure S1). 5/23 mice did not learn the task, likely due to a failure to lick frequently enough to receive reinforcement. Even once mice reached proficiency, there was still a great deal of variability in performance between individuals, thus we developed a detection index to normalize animals’ performance to chance in order to better assess their performance. Since this task is neither a Go-NoGo nor a two-alternative forced choice task, the assumptions underlying typical calculation of d-prime were inaccurate (namely, that chance = 50%). Thus, we bootstrapped percent chance by shuffling lick responses relative to stimulus time within each training session for each mouse, and averaging over 1000 shuffles (chance = ~15%). We also separately shuffled running and stationary trials to compare performance under those conditions to what would be expected by chance. We chose 0.5 cm/sec as the running threshold to ensure adequate running trials for analysis, since 80–20 mice ran on fewer trials than 50–50 mice (80–20: 30.8% of trials, 50–50: 45.3% of trials; p=0.0346, rank-sum test, Figure S1). We then computed a z-score by comparing the actual proportion correct z-scored to the shuffled proportion correct for each training session, and did the same for early lick trials.

$$\text{z}\left(\text{correct}\right)=\left(\text{correct\hspace{0.17em}}-\hspace{0.17em}\text{correc}{\text{t}}_{\text{shuff}}\right)/\text{\hspace{0.17em}std}\left(\text{correc}{\text{t}}_{\text{shuff}}\right)$$

Our detection index is the z-scored proportion of correct trials with the z-scored proportion of early lick trials subtracted. Detection index roughly corresponds to the number of standard deviations away from chance performance (Figure S1).

$$\text{detection\hspace{0.17em}index\hspace{0.17em}}=\text{\hspace{0.17em}z}\left(\text{correct}\right)-\text{z}\left(\text{early}\right)$$

We also computed the tendency of a mouse to respond, whether correct or not, by adding the z-scored proportions of correct and early trials.

$$\text{responce\hspace{0.17em}tendency\hspace{0.17em}}=\text{\hspace{0.17em}z}\left(\text{correct}\right)+\text{z}\left(\text{early}\right)$$

Subsequent behavior analyses used detection index under different conditions. For contrast change sensitivity, we computed detection index for subsets of trials each day corresponding to different magnitudes of contrast change. For effects of optogenetic stimulation on behavior, we computed changes in detection index in light-on versus light-off conditions in each hemisphere.

Pupil recording and analysis

Pupil videos were recorded using an infrared USB camera (DMK 21BU04.H, The Imaging Source) with infrared illumination and the MATLAB image acquisition toolbox. Acquisition occurred at 7.5Hz or 15Hz and was triggered using the synchronization signal sent by the stimulus computer. Before analysis, images were rotated so that the horizontal axis of the eye was horizontal in the image. Pupil diameter was determined by using custom MATLAB software (generously shared by Dr. Céline Matéo in Dr. David Kleinfeld’s lab and modified to fit our requirements). Briefly, videos were cropped to include only the eye, then manually thresholded to segregate the pupil from the rest of the eye. Then the MATLAB image processing toolbox was used to connect areas of the pupil that were occasionally separated by an out-of-focus eyelash. Finally, the horizontal and vertical diameters were extracted by summing in either the vertical or horizontal directions, then plotting these sums across time, and cropping out any confounding dark areas, such as shadows in the corner of the eye. Diameters were manually verified by viewing every other frame of the video at 10x speed with the diameters superimposed on the eye. Horizontal diameter was most reliable, because sometimes the eyelid would occlude part of the vertical extent of the pupil. In cases of eyelid closure or other obstruction of the pupil, those frames were excluded from analysis. Due to individual differences in eye size and slight differences in camera angle and zoom, we normalized pupil diameter to the average pupil diameter observed during >1 second bouts of locomotion within the same session because locomotion pupil diameter was reliably large. If there were no bouts of locomotion long enough, we excluded those sessions from analysis.

Field potential data processing and analysis

Analyses were performed on both the low-frequency (LFPs, CSDs) and high-frequency (spikes) components of the signal recorded from electrodes. For 80–20 mice we examined only likely change trials unless otherwise noted, because the small number of correct trials on unlikely change trials prevented useful analyses. Thus, we largely compared activity in the likely and unlikely hemispheres on likely trials in 80–20 mice. For 50–50 mice, we combined data from the two hemispheres in one of two ways. We either combined the neurons from both hemispheres in response to the contralateral change to examine changes in the stimulus response (spike rate analyses, local field potential analyses, linear classifier analyses), or kept hemispheres separate and combined responses on both contralateral and ipsilateral change trials to examine whether and how responses in the two hemispheres differed (spike count correlations, Fano factor).

As mentioned above, for each recording in each hemisphere, we performed a current source density (CSD) analysis to determine the laminar position of the electrode contacts. CSD was performed using CSDPlotter [48], and involves taking the second spatial derivative of the low-pass-filtered (<1000Hz) local field potential across all channels during transitions from black to white and white to black on the screen [49]. This allowed identification of supragranular, granular, and infragranular layers, which we used to identify effects in these different layers. If we could not discern layer 4 in the CSD, we excluded that recording from analysis (15/66 were excluded).

To analyze the local field potentials, we first downsampled raw voltage traces to 1000 Hz and low-pass filtered at 1000Hz. We then used a multitaper method included in an open-source package for MATLAB (Chronux, http://chronux.org, [50]) to compute LFP power spectra between 2 and 80Hz. To examine changes in spectral power in different trial conditions, we separately computed spectra with subsets of LFP trials corresponding to when the mice correctly responded, missed the change, or were running or stationary. We restricted analyses to the one second time window prior to the contrast change on each trial, and excluded spectral peaks corresponding to 60Hz line noise from further analyses. To avoid inclusion of trials with either movement or electrical artifacts, we removed trials where the LFP amplitude deviated more than one standard deviation of the average LFP voltage deviation for all trials. Group analyses were performed on the average spectra from each recording in each condition, using either a sign-rank or rank-sum test.

Spike data processing and analysis

To extract spike times from raw voltage traces, we used the open source automated spike sorting package Kilosort [51] and manual curation with phy [52]. Subsequent analyses were performed with custom MATLAB software. We only included units that had clear refractory periods and neuronal-like waveforms. For most analyses, spike times were binned into either 50ms bins for peri-stimulus time histograms (PSTHs) or larger bins for spike count correlations, Fano factor, or linear classifier analyses. Spikes were aligned to three events: initial stimulus onset, contrast change, and time of the first lick. For all analyses, we only included units with significantly altered spiking relative to the baseline firing rate following either the initial stimulus onset or the contrast change (Wilcoxon sign-rank test, p<0.01), 1709 of 2218 total units or 77.05%. We also occasionally observed drift in our recordings, and on a few occasions a neuron would either drop out or appear. For these units we only analyzed the subset of trials when the unit was present.

To compute the pairwise correlated variability, we used spike counts from 400ms time windows. We then z-scored spike counts across orientations to remove the effect of different orientations on spike count variability. We then found the Pearson’s correlation between the z-scored firing rates of every pair of simultaneously recorded single units across different conditions (subsets of trials). Effects of different window sizes are shown in Figure S2. For population measures, we averaged these correlation values across all pairs from all recording sessions. To examine how the correlated variability changed across sessions, we averaged the Pearson’s correlation computed in 800ms time windows between pairs of simultaneously recorded neurons across all trials during each session, and correlated those values with the behavior of the recorded mice the corresponding sessions.

We compared how different conditions affected firing rates by first binning spike rates into 50ms bins, then z-scoring each unit’s firing rate relative to its baseline firing rate, then subtracting averages between correct and miss and running and stationary trials to compare the relative impact of each condition. To visualize these changes across layers, we averaged z-scored firing rates of units that were recorded at the same depth relative to the base of layer 4, and concatenated the layer-delineated activity aligned to the initial stimulus onset and the contrast change. Heatmap values were smoothed with a Gaussian kernel. We performed statistical comparisons on average firing rate differences in upper layer versus lower layer units by pooling according to whether the units were in layers 2–4 or 5–6 (Figure S3). Comparisons were relative to zero and were performed over a 750ms time window for the post-contrast change time point, and a 1000ms time window for all other time points.

To examine how responses to preferred stimuli changed relative to responses to non-preferred stimuli, we first determined which units had a significant orientation preference by performing Hotelling’s T-squared test for equality of means across firing rate responses to differently oriented stimuli. We included units with p<0.05 for further orientation-tuning related analyses (697 of 1709 single units). We then compared changes in responses (in 500ms windows) to the preferred orientation, which triggered the maximum average firing rate, to changes in responses to the adjacent orthogonal orientations, across correct versus miss and running versus stationary conditions. If responses to the preferred orientation changed more than responses to the orthogonal orientation, the neuron experienced a more multiplicative gain, whereas if the changes were equal, the neuron experienced an additive gain. Thus, we calculated |Δpreferred|-|Δorthogonal| for correct-miss and running-stationary changes in the different groups and hemispheres.

We also examined within-unit variability with Fano factor, the ratio of variance of spike counts across trials to the mean spike count. To calculate the Fano factor, we binned spike rates into 100ms bins and divided the variability and mean spike counts in those bins for each unit in response to its preferred orientation. Only units that were significantly tuned, as described above, were included in Fano factor analysis. We then computed the average Fano factor in different conditions across 400ms time windows (or 4 bins), and directly compared either correct versus miss trials or running versus stationary trials.

For the linear classifier, we binned pre- and post-change spike counts within differently sized windows for each recording. We trained a linear classifier to decode pre- versus post-change counts from the population activity with custom MATLAB code using a regularized support vector machine with leave-one-out cross validation. We then averaged classifier performance across recordings, either including all trials or a subset such as correct trials to determine if classifier performance changed in different conditions. We also trained the linear classifier on trial-shuffled activity, where we individually shuffled spike counts within each neuron to remove correlated variability structure while keeping intact the pre-post change firing rate relationship. This allowed us to compare performance to the classifier trained on unaltered population activity and determine the contribution of correlated neural variability to classifier performance and neural population information.

For performance-matched sessions, we selected the recording sessions where mice performed at a detection index between 8–13. For 80–20 mice, they had to perform at this level only in response to likely changes, while 50–50 mice had to perform at this level for both changes. We then ran the same analyses as described above on that subset of recordings.

Highlights:

• Mice were trained in a spatially selective or non-selective visual task.

• Selective mice locally modulate V1, while non-selective mice globally modulate V1.

• Locomotion’s effect on behavior and neural activity depends on behavioral context.

• Locomotion impairs behavior and visual information in local, but not global mice.