Abstract
RNA molecules in solution tend to undergo structural fluctuations of relatively large amplitude and to populate a range of different conformations some of which with low populations. It is still very challenging, however, to characterise the structures of these low populated states and to understand their functional roles. In the present study, we address this problem by using NMR residual dipolar couplings (RDCs) as structural restraints in replica-averaged metadynamics (RAM) simulations. By applying this approach to a 14-mer RNA hairpin containing the prototypical UUCG tetraloop motif, we show that it is possible to construct the free energy landscape of this RNA molecule. This free energy landscapes reveals the surprisingly rich dynamics of the UUCG tetraloop and identifies the multiple substates that exist in equilibrium owing to thermal fluctuations. The approach that we present is general and can be applied to the study of the free energy landscapes of other RNA or RNA-protein systems.
Introduction
Experimental studies of the conformational properties of RNA are challenging as these molecules are structurally heterogeneous.1–8 These conformational properties, however, are highly important, since the dynamics of RNA molecules are often associated with their cellular functions.1–3 From a theoretical perspective, the free energy landscape framework enables one to represent the structural and dynamical properties of macromolecules in an effective and concise manner.2,9–12 The conformational space of a protein13,14 or a nucleic acid15 molecule typically comprises a highly-populated native conformation and one or more low populated (or ‘excited’) states. Particularly for RNA, the existence of low populated states has long been recognised, but we have just started to understand the structures and functional roles of these states.15–19
Although it is generally difficult to characterise the structures of low populated states, recent advances in NMR techniques have made this possible to do so both in proteins13,14 and in nucleic acids.16 Evidence for low populated state structures appears in NMR relaxation dispersion experiments on RNA16 due to extensive conformational changes that are accessible to non-canonical (i.e. non Watson–Crick base-paired) regions such as bulges and loops. To characterise the structurally and functionally relevant classes of RNA excited states, different types of RNA systems were recently analysed, including HIV TAR apical loop,15 the ribosomal A-site internal loop,15 the HIV-1 stem-loop 1,15 and U6 spliceosomal RNA.20 A consistent feature appearing from these studies is that low populated states of RNA arise due to localised secondary structural rearrangements. For example, flipped bases in the ground state tend to become increasingly stacked in excited states, and base-paired residues in the ground state tend to lose stacking in higher energy conformers.15,16 Such conformational changes lead to sequestering or exposure of certain residues in the low populated states that can promote or inhibit RNA function depending upon the location and direction of local motion of the residue. Thus, such studies point out that RNA is inherently prone to complex structural dynamics at several hierarchical tiers4,15,16,18,21 and it is a challenging task to isolate and characterise the sparsely populated states that are relevant to cellular function.
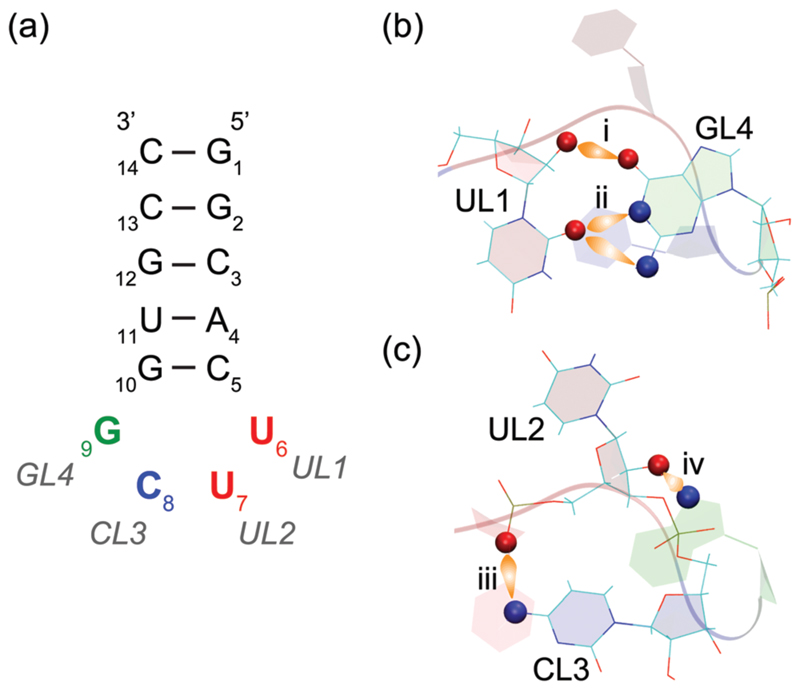
In this study, we address this challenge by exploiting the information about the dynamics of RNA provided by NMR residual dipolar couplings (RDCs), showing that this information makes it possible to obtain low populated structures in a prototypical RNA system – the UUCG tetraloop motif (Fig. 1). UUCG tetraloops, which belong to the UNCG family of RNA tetraloops, are thermodynamically stable,22,23 and are frequently observed to cap RNA hairpins24,25 and to provide nucleation sites for RNA folding,26 although they have not been implicated yet in RNA–RNA or RNA-protein interactions.27 Since its initial report in 1988,22 the UUCG structure has been characterized in great detail using high-resolution X-ray crystallography, and NMR structures are available for this tetraloop in the context of different RNA hairpins, where all its structural features are characterised in detail.27–37 The network of hydrogen bonds between the tetraloop residues confers high thermodynamic stability to this structural motif (Fig. 1b and c), which has also been investigated in detail using molecular dynamics simulations, probing the structural basis for its exceptional thermostability.38–40 Although studies on dynamics of the tetraloop have been mainly focused on the nanosecond timescale using in particular 13C NMR relaxation methods,41,42 it is also important to study its dynamics on longer timescales because of the importance of this tetraloop in functioning as a ‘molecular staple’ that is involved in the initiation and stabilization of RNA folding.
Fig. 1.
Schematic representation of the 14-nucleotide RNA hairpin containing the UUCG tetraloop that we studied in this work. (a) The nucleobases of the tetraloop are referred to as UL1, UL2, CL3 and GL4. (b and c) Signature hydrogen bond interactions and residue orientations in the UUCG tetraloop. (b) UL1 and GL4 are base-paired via (i) UL1 (O2′)…GL4(O6) and (ii) UL1(O2)…GL4(N1 and/or N2). (c) Additionally, base-backbone interactions appear via (iii) CL3(N4)…UL2(phosphate) and (iv) GL4(N7)…UL2(O2′). This network of hydrogen bonds between the tetraloop residues confers high thermodynamic stability to this structural motif. The GL4 base is in the syn conformation (i.e. with −90° < χ < 90°, where the dihedral angle χ defines the rotation around the ribose-nucleobase glycosidic bond). CL3 stacks under UL1, while UL2 remains unpaired, non-stacked and exposed to the solvent. Both UL2 and CL3 are in a C2′ -endo conformation of the sugar pucker that facilitates the bending of the RNA backbone at the tetraloop.
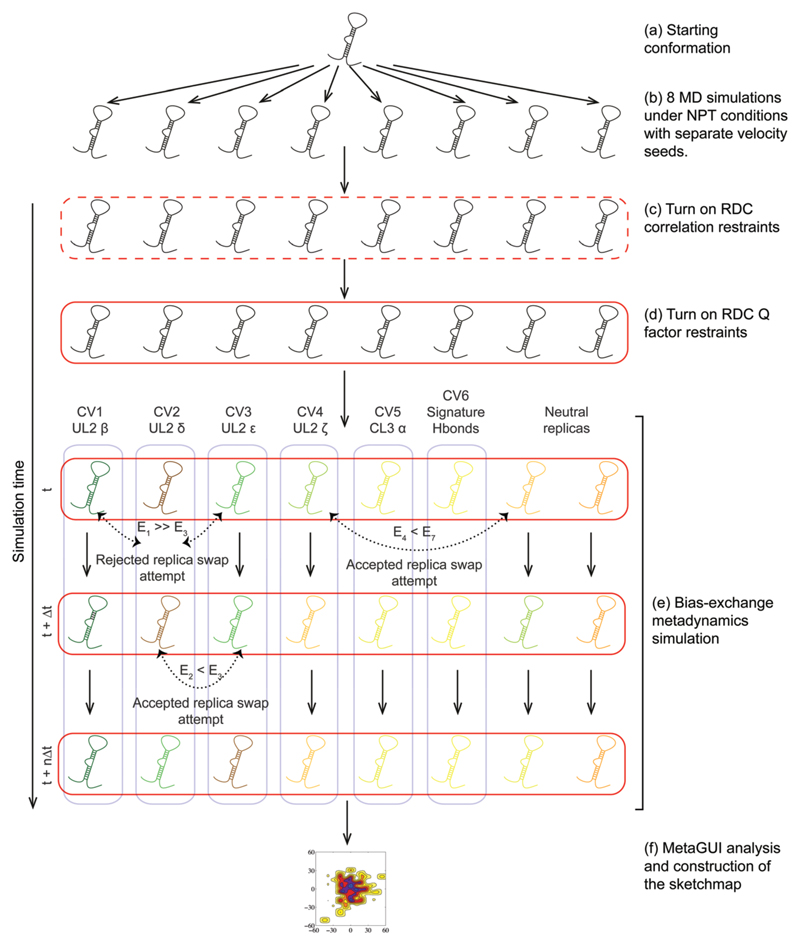
Using a high-resolution NMR structure of the UUCG tetraloop in a 14-nucleotide RNA hairpin (PDB 2KOC30) as the initial model, we generated a conformational ensemble representing the dynamics of this molecule by incorporating NMR residual dipolar couplings43,44 as structural restraints in RAM simulations45,46 (Fig. 2). By analysing a free energy landscape corresponding to this conformational ensemble, we then characterised the structures of the UUCG tetraloop associated with the multiple minima in the landscape. Our method does not bias the analysis towards any particular low populated state conformation and aims to represent the range of millisecond timescale structural fluctuations experienced by this RNA molecule in solution. Our results reveal a level of conformational heterogeneity that has not been previously detected for this system, which has been so far considered to be rather rigid on the basis of experimental measurements reporting on nanosecond timescale motions. Our results illustrate instead a fairly rugged free energy landscape for this RNA tetraloop where several substates exist in equilibrium, consistently with a recent study on a related tetraloop.31
Fig. 2.
Step-by-step schematic illustration of the RAM simulations implemented in this work. (a) For the starting conformation we used a recent high-resolution NMR structure of the UUCG tetraloop in a 14-nucleotide RNA hairpin (PDB 2KOC30), which was solvated in water, neutralized with counter ions and 100 mM MgCl2. (b) This structure was replicated 8 times to obtain the starting 8 replicas. The use of different velocity seeds leads to independently evolving replicas in the molecular dynamics (MD) simulations, which were carried out under isothermal-isobaric (NPT) conditions; the independence is tested by computing the average correlation between the pairwise RMSD of the trajectories (eqn (S1), ESI†). (c) In the first phase of the simulations (broken red rectangle), the correlation between the Dexp and Dcalc is restrained to reach values close to 1 (eqn (S3), ESI†) to obtain an estimate of the scaling factor. (d) This scaling factor is then used in the second phase (solid red rectangle) to restrain the Q factor (see ESI†) to be close to 0 (eqn (S4), ESI†). In (c) and (d), we used the recently introduced tensor-free ϑ method71 to calculate Dcalc. (e) RAM simulations were then carried out using metadynamics simulations in the bias-exchange mode72 to enhance the conformational sampling of the system along the chosen collective variable (blue rectangles). In the bias-exchange mode, the evolution of the trajectory is changed stochastically with time according to rules of the replica-exchange method (broken double-headed arrows). (f) After the simulations are converged, the free energy landscape of the system is reconstructed using the Sketch-map approach73 within the MetaGUI interface.74
Results and discussion
Replica-averaged metadynamics simulations
There are two major challenges in characterizing the structure and dynamics of the UUCG tetraloop, as well as more generally those of RNA molecules, via in situ experiments. The first is the ‘timescale problem’, which concerns the length of the simulations. To obtain an accurate sampling of the heterogeneous conformational space of this type of molecule it is necessary to identify the major structures that are populated, together with their corresponding populations, which at equilibrium are given by the statistical weights defined by the Boltzmann distribution.11,47 This is a challenging task, since the molecular dynamics simulations should be long enough to sample this distribution, or in other words, to converge to equilibrium. As standard molecular dynamics simulations, even for a system as simple as a RNA tetraloop, require trajectories well above the millisecond timescale, the ‘timescale problem’ can be more readily addressed by adopting enhanced sampling methods, which enable an efficient exploration of the conformational space by circumventing the requirement of generating realistic trajectories, thus enabling longer timescales to be accessed.48–52 In this work we used the metadynamics approach,53,54 where, in order to enhance the conformational sampling, molecular dynamics simulations are biased by a history-dependent potential constructed as a sum of Gaussian functions deposited along the trajectory for suitably chosen collective variables.53,54 This bias enables the system to readily overcome energy barriers by discouraging the return to regions of the conformational space that have already been visited.
The second major challenge is the ‘force field problem’, which concerns the accuracy of the force field used during the sampling. This problem is distinct from the first, as using a force field that does not reproduce accurately the interatomic interactions that determine the motion of RNA molecules will result in a precise, but not necessarily accurate, free energy landscape, even if the sampling has fully reached convergence. In this case, the statistical weights obtained from the simulations will reproduce closely those corresponding to the force field used, but not necessarily those of the actual system under study. Given the importance of this challenge, substantial work has been carried out over many years to improve the accuracy of the force fields for nucleic acids.36,55–57 Here, rather than aiming at generating a ‘transferable’ force field by modifying its parameters to enable the simulations of any RNA system, we implement a ‘system-dependent’ strategy in which experimental data for a specific system are incorporated in the simulations as structural restraints.58–60 Alternatively, the simulated trajectories could be ‘filtered’ a posteriori by requiring experimental measurements to match the values back-calculated by selected conformations.61,62 In this work, we use the recently proposed replica-averaged metadynamics (RAM) approach,45,46 which enables the generation of ensembles of conformations consistent with the maximum entropy principle.63–66 We choose this strategy because it results in a structural ensemble that is the most probable one, given the force field and the experimental data used as restraints. Thus, by combining the advantages of enhanced sampling and of the experimental restraints, the RAM approach enables us to address both the timescale and the force field problems.
RAM simulations of the 14-nucleotide RNA hairpin
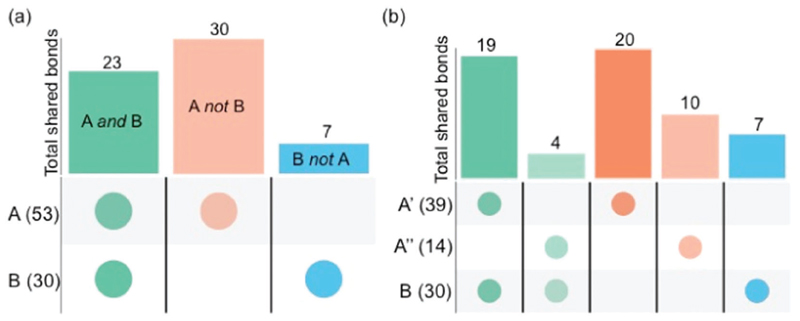
In order to characterize the conformational fluctuations of the 14-nucleotide RNA hairpin containing the UUCG tetraloop, we measured RDCs for 53 CH bonds in Pf1 phage alignment (see ESI,† Table S1 and Fig. 3a, set A). We used 39 (Fig. 3b, set A′) of these RDCs as restraints in RAM simulations, which at convergence (Fig. S1, ESI†) generated the RAM ensemble (see ESI†). The remaining 14 RDCs (Fig. 3b, set A″) from set A were used to validate the results of the RAM simulations. The initial conformation for the RAM simulations (see ESI†) was taken from a high-resolution NMR structure of the RNA hairpin, which was determined using an independent set of 30 RDCs30 (Fig. 3a, set B, and Table S2, ESI†). We note that both the RAM and the 2KOC30 structures were generated using RDCs as restraints, with the difference that the RAM structures are aimed at characterizing the conformational fluctuations of the RNA hairpin, while the 2KOC structures provide a representation of its high-resolution average conformation. The 23 bonds in common between the A and B sets of RDCs (Fig. 3a, green) are correlated (Fig. S2, ESI†) since they were measured under similar experimental conditions except for the concentration of the Pf1 phage used for alignment.
Fig. 3.
Summary of the RDC sets used as restraints in the molecular dynamics simulations and in the validation of the UUCG structural ensembles described in this work. The bars denote the intersection (total number of common bonds) or negation (number of unique bonds) and the circles below them denote the sets from which these are derived. For example, 23 bonds are common between the RDC sets A and B (green bar in panel a). Intersections are shown in green, and unique bonds in sets A and B are shown in orange and blue, respectively. (a) The set A of 53 measured RDCs comprises a set A′ of 39 RDCs, which are used as restraints to generate the RAM ensemble, and a set A″ of 14 RDCs, which are used for validation. A previously reported30 set B of 30 RDCs is also used for validation; from the set B, a subset ‘B not A’ of 7 RDCs is extracted by considering RDC measurements for bonds not included in the set A. (b) From the set A, a subset ‘A not B’ of 30 RDCs is extracted by considering RDC measurements for bonds not included in set B.
For validation, in addition to the set A″ of 14 RDCs mentioned above, we selected the subset ‘A not B’ (Fig. 3a, orange) of 30 RDCs for the 2KOC ensemble, and the subset ‘B not A’ (Fig. 3a, blue), of 7 RDCs for the RAM ensemble. We thus back-calculated the RDCs in five sets (A′, ‘A not B’, A″, B and ‘B not A’) for the 2KOC, RAM and MD ensembles, and compared them using three different metrics (Table S3, ESI†): the RMSD (in Hz), the Q factor and the Pearson’s coefficient of correlation (R). As expected, a consistent feature from the comparison between the experimental and calculated RDCs (Table 1 and Table S3, ESI†) is that the use of restraints led to an improvement in the agreement for the restrained bonds in the different ensembles. These results are closely resembling those obtained by a similar approach in the case of proteins.45,67 Both set B RDCs back-calculated over the 2KOC structures and set A′ RDCs back calculated over the RAM ensemble resulted in low RMSD values (2.20 Hz and 1.17 Hz, respectively). However, while the value for set A′ is within the average experimental error (1.36 Hz) for RDCs measured here, the value for set B is larger. For the bonds that were not used as restraints for the 2KOC structure determination (set ‘A not B’), the RMSD (4.68 Hz, Table 1) is comparable to those back-calculated over the MD ensemble (4.57 Hz, Table 1). Conversely, the set A″ back-calculated over the RAM shows a RMSD (3.12 Hz) approximately consistent with the experimental error (2.2 Hz) and lower than that back-calculated over the 2KOC (4.17 Hz) or the MD (4.13 Hz) ensembles. Thus, the RAM ensemble consists of structures in good agreement with the relative orientations of both the restrained and unrestrained bonds as monitored by the experimental RDC values. These results indicate that the RAM ensemble describes rather accurately the motions of the 14-nucleotide RNA hairpin.
Table 1.
Assessment of the quality of the 2KOC, RAM and MD ensembles. Root mean square distance (RMSD, in Hz) between experimental and calculated RDCs. The results are shown for the three conformational ensembles (rows) and five RDC sets (columns) analysed in this study (see Fig. 3). RMSD values in italics denote the quality check of the restrained bonds and those in bold denote the validation of the unrestrained bonds in the 2KOC and RAM ensembles. All RMSD values for RAM and MD ensembles are calculated as weighted-averages of the RDCs obtained by fitting a single alignment tensor to each substate in the ensembles. Experimental errors for the 53 measured RDCs span about a 1–5 Hz range, as the measurements were performed at natural 13C abundance. The majority of these RDCs had, however, an experimental error of about 1 Hz, and most of such RDCs were included in set A′, which was used for generating the RAM ensemble. More precisely, the experimental errors for the RDCs sets are about 1.4 Hz (set A′), 1.8 Hz (set ‘A not B’), and 2.2 Hz (set A″). All RDCs in set B have been reported to have an experimental error of about 1 Hz30
| Set A′ | Set A″ | Set ‘B not A’ | Set B | Set ‘A not B’ | |
|---|---|---|---|---|---|
| 2KOC | 3.58 | 4.17 | 1.13 | 2.20 | 4.68 |
| RAM | 1.17 | 3.12 | 1.17 | 2.46 | 2.62 |
| MD | 4.44 | 4.13 | 1.35 | 3.78 | 4.57 |
| Exp. error | 1.4 | 2.2 | 1.0 | 1.0 | 1.8 |
RAM ensemble validation with data not used as restraints
To assess the quality of the RAM ensemble, which was generated using RDCs as structural restraints, we used independent NMR measurements. In the present case, the use of NMR S2 order parameters is problematic because the presence of multiple substates of the RNA tetraloop (see below) complicates the structural interpretation of the experimental measurements, as these parameters measure the amplitude of motion around a given axis, which here may be different in the different substates. Thus, we used other available NMR parameters, including the nuclear Overhauser enhancement (NOE)-derived distances30 (Fig. S3, ESI†) and dihedral angles derived form J-couplings30 (Fig. S4, ESI†). The dihedral angles in Fig. S4 (ESI†) were calculated as an average from the Cartesian coordinates of the conformations in the RAM and MD ensembles. In this way, the fluctuations between rotameric states were also averaged without taking into account rotameric population distributions. The experimental dihedral angles values used for the validation of these calculated averages were sourced from ref. 30, where these values were calculated from 3J homo- and heteronuclear coupling constants and cross correlation rates.
The RAM and MD ensembles had only four NOE violations >1 Å (Fig. S3, ESI†). Two NOE violations are between the sugar 1H5′ and the base H8 atoms in G2 and A4. As there can be spin diffusion between the 1H5′ and 2H5′ nuclei that are right next to each other, these NOE violations are not surprising. The other two violations arise in the C5:G10 and A4:U11 base pairs immediately adjoining the UUCG tetraloop. Also the ensemble-averaged dihedral angles calculated from the RAM and MD ensembles conform mostly to the values determined from the experimental J-couplings, except for a few notable cases where the dihedral angles exhibit a high standard deviation from their calculated ensemble-averaged values and thus seem to deviate significantly from the experimental restraints (Fig. S4, ESI†). These results are indicative of conformational dynamics at individual residues of the RNA hairpin. For example α and ζ dihedral angles exhibit highest conformational flexibility in RNA,68 particularly in the non-helical regions and this is reflected in the ζ values for UL2 and GL4 in the simulations. These angles show bimodal populations at gauche− (major) and gauche+ (and trans too for UL2) values and thus seem to, on average, deviate away from the gauche− restraints. In the recent NMR 2KOC structure,30 although the β and ε dihedral angles for the tetraloop residues fit better to a conformational distribution30, a higher number of NOE restraints has resulted in a higher precision of the loop structure and thus it is likely that the 2KOC structure underestimates the conformational dynamics of the tetraloop, in particular for UL2.
Free energy landscape of the UUCG tetraloop
In order to characterise the conformational ensembles of the UUCG tetraloop, we constructed the free energy landscape of the RAM ensemble as a function of its sketch-map CVs (see ESI†) and compared it with the corresponding free energy landscape of the MD ensemble. The advantage of using the sketch-map CVs is that the construction of the free energy landscape is not biased towards the CVs used in the RAM simulations; instead it is a two-dimensional projection of the multi-dimensional parameter hyperspace used to classify the RAM structures. In this study, we wanted to characterise the UUCG dynamics and thus we used the six backbone (α, β, γ, δ, ε and ζ) and the glycosidic (χ) torsion angles of the six residues (CL − 1, UL1, UL2, CL3, GL4 and GL + 1) that include the UUCG tetraloop residues and its closing base pair (CL − 1 and GL + 1). The sketch-map CVs are thus a two-dimensional projection of the 42-dimensional cUUCGg torsion angle hyperspace.
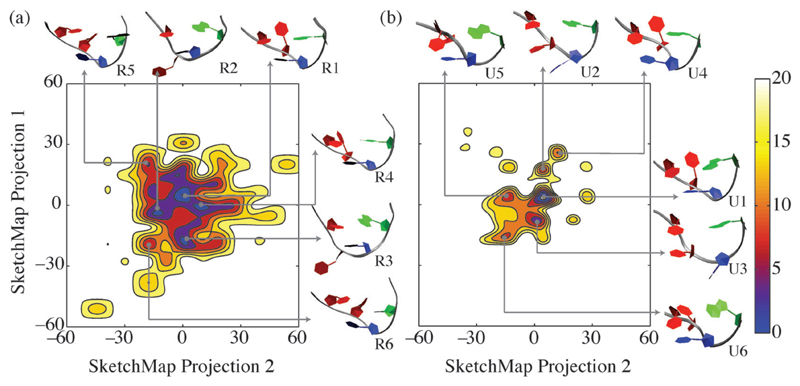
The free energy landscape of the RAM ensemble (Fig. 4a) is more extended than that of the MD ensemble (Fig. 4b). For example, apart from the native conformations (R1 in Fig. 4a and U1 in Fig. 4b), we found other native-like conformations (R4 in Fig. 4b and U4, U5 and U6 in Fig. 4b) that only differ in the relative orientations of the UL2 χ angle, as well as other non-canonical conformations (R2, R3, R5 and R6 in Fig. 4a and U2 and U3 in Fig. 4b) involving significantly larger rearrangements of the tetraloop residues. A comparison between the 2KOC structure of the UUCG tetraloop and the native and native-like conformations obtained in the RAM and MD ensembles is shown in Fig. S6 (ESI†). Although in Fig. 4 representative conformations might look similar, they have distinct sets of the 42 torsion angles used to calculate the sketch-map (Fig. S5, ESI†). Thus, different combinations of the torsion angles in RNA can result in apparently similar arrangement of the individual residues in the molecule.
Fig. 4.
Comparison of the free energy landscapes (in kJ mol−1) of the UUCG tetraloop corresponding to the RAM (a) and MD (b) ensembles. We also show representative conformations for the six lowest free energy minima (R1-R6 for the RAM ensemble and U1-U6 for the MD ensemble), which are within 7 kBT from the ground state. Their populations and RMSD values from the 2KOC structure are reported in Table S4 (ESI†) and indicate that the R1 and R4 structures in the RAM ensemble and the U1 and U4 structures in the MD ensemble are the closest (within 1 Å) to the 2KOC structure. UL1, UL2, CL3 and GL4 are coloured grey, red, blue and green respectively. Isolines are depicted at 2.5 kJ mol−1 intervals.
Validation of the non-canonical UUCG conformations
Since multiple substates are present in both the RAM and MD ensembles, it is important to consider whether the structures of the substates in the MD ensemble are as accurate as those in the RAM ensemble. To test this possibility, we back-calculated (Table 2) the sets A′ and A″ of RDCs (Fig. 3) individually on the R1–R6 substates in the RAM ensemble (Fig. 4a), and on the U1–U6 substates in the MD ensemble (Fig. 4b). An important and consistent feature that we found is that the RMSD of the weighted-averages of the RDCs back-calculated over all the substates in the RAM and MD ensembles is better than that of any individual substate in the ensembles. This result illustrates the importance of taking into account conformational averaging for systems that populate different substates, rather than an individual free energy minimum. However, only for the RAM ensemble this average value is approximately consistent with the experimental error for the restrained (set A′, 1.4 Hz) and unrestrained (set A″, 2.2 Hz) bonds. This analysis suggests that the conformational heterogeneity present in the RAM ensemble represents better the extent of the structural fluctuations occurring in the UUCG tetraloop in solution.
Table 2.
Validation of the RAM and MD ensembles. Root mean square distance (RMSD, in Hz) between experimental and calculated RDCs for the RAM and MD ensembles, and for the individual substates R1-R6 in RAM (Fig. 4a) and U1–U6 in MD (Fig. 4b). The RMSD values indicate that for the RAM ensemble, the weighted average of the back-calculated RDCs for both the restrained (set A′) and unrestrained (set A″) bonds is significantly better for the complete RAM ensemble with both canonical and non-canonical structures than any of the individual substates within the ensemble. For comparison, the MD ensemble is in worse agreement with the RDC measurements
| Set A′ | Set A″ | ||
|---|---|---|---|
| RAM | 1.17 | 3.12 | |
| R1 | 6.97 | 8.22 | |
| R2 | 5.53 | 5.12 | |
| R3 | 2.62 | 3.75 | |
| R4 | 2.07 | 4.45 | |
| R5 | 5.87 | 4.57 | |
| R6 | 9.67 | 8.22 | |
| MD | 4.44 | 4.13 | |
| U1 | 5.66 | 5.27 | |
| U2 | 6.12 | 6.65 | |
| U3 | 7.53 | 7.34 | |
| U4 | 8.43 | 5.65 | |
| U5 | 7.47 | 7.29 | |
| U6 | 4.50 | 4.69 |
Non-canonical UUCG conformations in structural databases
Conformational ensembles derived from structural databases may provide a representative sample of the structural fluctuations of nucleic acids under native conditions.69 As observed previously in the case of protein dynamics, this analysis is based on the fluctuation-dissipation theorem, according to which the equilibrium structural fluctuations are equivalent to the changes caused by small perturbations.69 One can consider each structure in the conformational ensemble derived from structural databases as subject to a slightly different perturbation, such as a bound ligand, a mutation, or the effect of crystal packing, which favours a particular minimum on the native state energy surface. If a sufficiently large number of conformations are collected they will reflect the statistical weights of the various minima in the free energy landscape of the unperturbed system.
In case of the UUCG structural database ensemble, a wide range of conformations occurring in the context of diverse full-length parent RNA molecules are available. In many of these cases, the UUCG is a component of the biological sequence of the RNA studied, and in others it is added to cap the truncated portions of some larger systems. We thus used these conformations to better understand the possible biological function of non-canonical UUCG states. In this analysis, we found several examples of non-canonical conformations, in ligand bound forms (PDB IDs 1EKZ, 1RAW, 1TLR and 3AMI) and ribosome structures arrested in translocation (PDB IDs 1FKA, 2GY9, 2GYB and 3IZF). These results are consistent with the view that RNA conformational transitions occur through complex, often multilayer RNA dynamics consisting of internal motions and externally induced rearrangements.70 Thus, the dynamics of individual tetraloops seem to be relevant in the biological function of the whole parent molecule.31
Conclusions
In this work we have addressed the problem of characterizing accurately the extent of conformational heterogeneity present in RNA in solution. By using molecular dynamics simulations with replica-averaged RDC restraints, we have described the conformational fluctuations of the UUCG tetraloop, detecting the presence of multiple interchanging minima. We have thus gained an understanding about why this motif exhibits high thermodynamic stability and yet is present in databases in alternative structures. More generally, our results illustrate the features of the free energy landscapes of RNA where several low populated states may exist in the vicinity of the most populated conformation.
Supplementary Material
† Electronic supplementary information (ESI) available: 4 tables and 6 figures. See DOI: 10.1039/c6cp08313g
Notes and references
- 1.Zhang Q, Sun X, Watt ED, Al-Hashimi HM. Resolving the motional modes that code for RNA adaptation. Science. 2006;311:653–656. doi: 10.1126/science.1119488. [DOI] [PubMed] [Google Scholar]
- 2.Cruz JA, Westhof E. The dynamic landscapes of RNA architecture. Cell. 2009;136:604–609. doi: 10.1016/j.cell.2009.02.003. [DOI] [PubMed] [Google Scholar]
- 3.Lee M-K, Gal M, Frydman L, Varani G. Real-time multidimensional NMR follows RNA folding with second resolution. Proc Natl Acad Sci U S A. 2010;107:9192–9197. doi: 10.1073/pnas.1001195107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Mustoe AM, Brooks CL, III, Al-Hashimi HM. Hierarchy of RNA Functional Dynamics. Annu Rev Bio-chem. 2014;83:441–466. doi: 10.1146/annurev-biochem-060713-035524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zhao B, Zhang Q. Characterizing excited conformational states of RNA by NMR spectroscopy. Curr Opin Struct Biol. 2015;30:134–146. doi: 10.1016/j.sbi.2015.02.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Herschlag D, Allred BE, Gowrishankar S. From static to dynamic: the need for structural ensembles and a predictive model of RNA folding and function. Curr Opin Struct Biol. 2015;30:125–133. doi: 10.1016/j.sbi.2015.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Furtig B, Nozinovic S, Reining A, Schwalbe H. Multiple conformational states of riboswitches fine-tune gene regulation. Curr Opin Struct Biol. 2015;30:112–124. doi: 10.1016/j.sbi.2015.02.007. [DOI] [PubMed] [Google Scholar]
- 8.Puglisi JD. RNA dances to center stage. RNA. 2015;21:712–713. doi: 10.1261/rna.051078.115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Frauenfelder H, Sligar SG, Wolynes PG. The energy landscapes and motions of proteins. Science. 1991;254:1598–1603. doi: 10.1126/science.1749933. [DOI] [PubMed] [Google Scholar]
- 10.Salmon L, Bascom G, Andricioaei I, Al-Hashimi HM. A general method for constructing atomic-resolution RNA ensembles using NMR residual dipolar couplings: the basis for interhelical motions revealed. J Am Chem Soc. 2013;135:5457–5466. doi: 10.1021/ja400920w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Vendruscolo M. Determination of conformationally heterogeneous states of proteins. Curr Opin Struct Biol. 2007;17:15–20. doi: 10.1016/j.sbi.2007.01.002. [DOI] [PubMed] [Google Scholar]
- 12.Vendruscolo M, Dobson CM. Towards complete descriptions of the free–energy landscapes of proteins. Philos Trans R, Soc A. 2005;363:433–452. doi: 10.1098/rsta.2004.1501. [DOI] [PubMed] [Google Scholar]
- 13.Baldwin AJ, Kay LE. NMR spectroscopy brings invisible protein states into focus. Nat Chem Biol. 2009;5:808–814. doi: 10.1038/nchembio.238. [DOI] [PubMed] [Google Scholar]
- 14.Neudecker P, et al. Structure of an intermediate state in protein folding and aggregation. Science. 2012;336:362–366. doi: 10.1126/science.1214203. [DOI] [PubMed] [Google Scholar]
- 15.Dethoff EA, Petzold K, Chugh J, Casiano-Negroni A, Al-Hashimi HM. Visualizing transient low-populated structures of RNA. Nature. 2012;491:724–728. doi: 10.1038/nature11498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Al-Hashimi HM. NMR studies of nucleic acid dynamics. J Magn Reson. 2013;237:191–204. doi: 10.1016/j.jmr.2013.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Blad H, Reiter NJ, Abildgaard F, Markley JL, Butcher SE. Dynamics and metal ion binding in the U6 RNA intramolecular stem–loop as analyzed by NMR. J Mol Biol. 2005;353:540–555. doi: 10.1016/j.jmb.2005.08.030. [DOI] [PubMed] [Google Scholar]
- 18.Borkar AN, Bardaro MF, Camilloni C, Aprile FA, Varani G, Vendruscolo M. Structure of a low-population binding intermediate in protein-RNA recognition. Proc Natl Acad Sci U S A. 2016;113:7171–7176. doi: 10.1073/pnas.1521349113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zeng X, Chugh J, Casiano-Negroni A, Al-Hashimi HM, Brooks CL. Flipping of the ribosomal A-site adenines provides a basis for tRNA selection. J Mol Biol. 2014;426:3201–3213. doi: 10.1016/j.jmb.2014.04.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Reiter NJ, Blad H, Abildgaard F, Butcher SE. Dynamics in the U6 RNA intramolecular stem-loop: a base flipping conformational change. Biochemistry. 2004;43:13739–13747. doi: 10.1021/bi048815y. [DOI] [PubMed] [Google Scholar]
- 21.Dethoff EA, Chugh J, Mustoe AM, Al-Hashimi HM. Functional complexity and regulation through RNA dynamics. Nature. 2012;482:322–330. doi: 10.1038/nature10885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Tuerk C, et al. CUUCGG hairpins: extraordinarily stable RNA secondary structures associated with various biochemical processes. Proc Natl Acad Sci U S A. 1988;85:1364–1368. doi: 10.1073/pnas.85.5.1364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Molinaro M, Tinoco I. Use of ultra stable UNCG tetraloop hairpins to fold RNA structures: thermodynamic and spectroscopic applications. Nucleic Acids Res. 1995;23:3056–3063. doi: 10.1093/nar/23.15.3056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Woese C, Winker S, Gutell R. Architecture of ribosomal, RNA: constraints on the sequence of “tetra-loops”. Proc Natl Acad Sci U S A. 1990;87:8467–8471. doi: 10.1073/pnas.87.21.8467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wolters J. The nature of preferred hairpin structures in 16S-like rRNA variable regions. Nucleic Acids Res. 1992;20:1843–1850. doi: 10.1093/nar/20.8.1843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Cheong C, Varani G, Tinoco I. Solution structure of an unusually stable RNA hairpin, 5GGAC (UUCG) GUCC. Nature. 1990;346:680–682. doi: 10.1038/346680a0. [DOI] [PubMed] [Google Scholar]
- 27.Williams DJ, Hall KB. Experimental and computational studies of the G [UUCG] C RNA tetraloop. J Mol Biol. 2000;297:1045–1061. doi: 10.1006/jmbi.2000.3623. [DOI] [PubMed] [Google Scholar]
- 28.Allain FH-T, Varani G. Structure of the P1 helix from group I self-splicing introns. J Mol Biol. 1995;250:333–353. doi: 10.1006/jmbi.1995.0381. [DOI] [PubMed] [Google Scholar]
- 29.Ennifar E, et al. The crystal structure of UUCG tetraloop. J Mol Biol. 2000;304:35–42. doi: 10.1006/jmbi.2000.4204. [DOI] [PubMed] [Google Scholar]
- 30.Nozinovic S, Fürtig B, Jonker HR, Richter C, Schwalbe H. High-resolution NMR structure of an RNA model system: the 14-mer cUUCGg tetraloop hairpin RNA. Nucleic Acids Res. 2010;38:683–694. doi: 10.1093/nar/gkp956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Miner JC, Chen AA, García AE. Free-energy landscape of a hyperstable RNA tetraloop. Proc Natl Acad Sci U S A. 2016;113:6665–6670. doi: 10.1073/pnas.1603154113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Williams DJ, Boots JL, Hall KB. Thermodynamics of 20-ribose substitutions in UUCG tetraloops. RNA. 2001;7:44–53. doi: 10.1017/s1355838201001558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zirbel CL, Šponer JE, Šponer J, Stombaugh J, Leontis NB. Classification and energetics of the base-phosphate interactions in RNA. Nucleic Acids Res. 2009;37:4898–4918. doi: 10.1093/nar/gkp468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Salmon L, et al. Modulating RNA Alignment Using Directional Dynamic Kinks: Application in Determining an Atomic-Resolution Ensemble for a Hairpin using NMR Residual Dipolar Couplings. J Am Chem Soc. 2015;137:12954–12965. doi: 10.1021/jacs.5b07229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Giambasu GM, York DM, Case DA. Structural fidelity and NMR relaxation analysis in a prototype RNA hairpin. RNA. 2015;21:963–974. doi: 10.1261/rna.047357.114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Bergonzo C, Henriksen NM, Roe DR, Cheatham TE. Highly sampled tetranucleotide and tetraloop motifs enable evaluation of common RNA force fields. RNA. 2015;21:1578–1590. doi: 10.1261/rna.051102.115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Sripakdeevong P, et al. Structure determination of non-canonical RNA motifs guided by 1H NMR chemical shifts. Nat Methods. 2014;11:413–416. doi: 10.1038/nmeth.2876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Banas P, et al. Performance of molecular mechanics force fields for RNA simulations: Stability of UUCG and GNRA hairpins. J Chem Theory Comput. 2010;6:3836–3849. doi: 10.1021/ct100481h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Miller JL, Kollman PA. Theoretical studies of an exceptionally stable RNA tetraloop: observation of convergence from an incorrect NMR structure to the correct one using unrestrained molecular dynamics. J Mol Biol. 1997;270:436–450. doi: 10.1006/jmbi.1997.1113. [DOI] [PubMed] [Google Scholar]
- 40.Villa A, Widjajakusuma E, Stock G. Molecular dynamics simulation of the structure, dynamics, and thermostability of the RNA hairpins uCACGg and cUUCGg. J Phys Chem B. 2008;112:134–142. doi: 10.1021/jp0764337. [DOI] [PubMed] [Google Scholar]
- 41.Duchardt E, Schwalbe H. Residue specific ribose and nucleobase dynamics of the cUUCGg RNA tetraloop motif by MNMR 13C relaxation. J Biomol NMR. 2005;32:295–308. doi: 10.1007/s10858-005-0659-x. [DOI] [PubMed] [Google Scholar]
- 42.Ferner J, et al. NMR and MD studies of the temperature-dependent dynamics of RNA YNMG-tetraloops. Nucleic Acids Res. 2008;36:1928–1940. doi: 10.1093/nar/gkm1183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Tjandra N, Bax A. Direct measurement of distances and angles in biomolecules by NMR in a dilute liquid crystalline medium. Science. 1997;278:1111–1114. doi: 10.1126/science.278.5340.1111. [DOI] [PubMed] [Google Scholar]
- 44.Tolman J, Flanagan J, Kennedy M, Prestegard J. NMR evidence for slow collective motions in cyanometmyoglobin. Nat Struct Mol Biol. 1997;4:292–297. doi: 10.1038/nsb0497-292. [DOI] [PubMed] [Google Scholar]
- 45.Camilloni C, Cavalli A, Vendruscolo M. Replica-averaged metadynamics. J Chem Theory Comput. 2013;9:5610–5617. doi: 10.1021/ct4006272. [DOI] [PubMed] [Google Scholar]
- 46.Camilloni C, Vendruscolo M. Statistical mechanics of the denatured state of a protein using replica-averaged metadynamics. J Am Chem Soc. 2014;136:8982–8991. doi: 10.1021/ja5027584. [DOI] [PubMed] [Google Scholar]
- 47.Bussi G, Donadio D, Parrinello M. Canonical sampling through velocity rescaling. J Chem Phys. 2007;126:014101. doi: 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- 48.Sugita Y, Okamoto Y. Replica-exchange molecular dynamics method for protein folding. Chem Phys Lett. 1999;314:141–151. [Google Scholar]
- 49.Hansmann UH. Parallel tempering algorithm for conformational studies of biological molecules. Chem Phys Lett. 1997;281:140–150. [Google Scholar]
- 50.Voter AF. Hyperdynamics: Accelerated molecular dynamics of infrequent events. Phys Rev Lett. 1997;78:3908. [Google Scholar]
- 51.Markwick PR, Bouvignies G, Blackledge M. Exploring multiple timescale motions in protein GB3 using accelerated molecular dynamics and NMR spectroscopy. J Am Chem Soc. 2007;129:4724–4730. doi: 10.1021/ja0687668. [DOI] [PubMed] [Google Scholar]
- 52.Adcock SA, McCammon JA. Molecular dynamics: survey of methods for simulating the activity of proteins. Chem Rev. 2006;106:1589–1615. doi: 10.1021/cr040426m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Laio A, Parrinello M. Escaping free-energy minima. Proc Natl Acad Sci U S A. 2002;99:12562–12566. doi: 10.1073/pnas.202427399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Laio A, Gervasio FL. Metadynamics: a method to simulate rare events and reconstruct the free energy in biophysics, chemistry and material science. Rep Prog Phys. 2008;71 126601. [Google Scholar]
- 55.Cornell WD, et al. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J Am Chem Soc. 1995;117:5179–5197. [Google Scholar]
- 56.Case DA, et al. The Amber biomolecular simulation programs. J Comput Chem. 2005;26:1668–1688. doi: 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Chen AA, García AE. High-resolution reversible folding of hyperstable RNA tetraloops using molecular dynamics simulations. Proc Natl Acad Sci U S A. 2013;110:16820–16825. doi: 10.1073/pnas.1309392110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Clore GM, Schwieters CD. How much backbone motion in ubiquitin is required to account for dipolar coupling data measured in multiple alignment media as assessed by independent cross-validation? J Am Chem Soc. 2004;126:2923–2938. doi: 10.1021/ja0386804. [DOI] [PubMed] [Google Scholar]
- 59.Lindorff-Larsen K, Best RB, DePristo MA, Dobson CM, Vendruscolo M. Simultaneous determination of protein structure and dynamics. Nature. 2005;433:128–132. doi: 10.1038/nature03199. [DOI] [PubMed] [Google Scholar]
- 60.Best RB, Vendruscolo M. Determination of protein structures consistent with NMR order parameters. J Am Chem Soc. 2004;126:8090–8091. doi: 10.1021/ja0396955. [DOI] [PubMed] [Google Scholar]
- 61.Mittag T, Forman-Kay JD. Atomic-level characterization of disordered protein ensembles. Curr Opin Struct Biol. 2007;17:3–14. doi: 10.1016/j.sbi.2007.01.009. [DOI] [PubMed] [Google Scholar]
- 62.Jensen MR, Zweckstetter M, Huang J-R, Blackledge M. Exploring free-energy landscapes of intrinsically disordered proteins at atomic resolution using NMR spectroscopy. Chem Rev. 2014;114:6632–6660. doi: 10.1021/cr400688u. [DOI] [PubMed] [Google Scholar]
- 63.Pitera JW, Chodera JD. On the use of experimental observations to bias simulated ensembles. J Chem Theory Comput. 2012;8:3445–3451. doi: 10.1021/ct300112v. [DOI] [PubMed] [Google Scholar]
- 64.Cavalli A, Camilloni C, Vendruscolo M. Molecular dynamics simulations with replica-averaged structural restraints generate structural ensembles according to the maximum entropy principle. J Chem Phys. 2013;138:094112. doi: 10.1063/1.4793625. [DOI] [PubMed] [Google Scholar]
- 65.Boomsma W, Ferkinghoff-Borg J, Lindorff-Larsen K. Combining experiments and simulations using the maximum entropy principle. PLoS Comput Biol. 2014;10:e1003406. doi: 10.1371/journal.pcbi.1003406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Roux B, Weare J. On the statistical equivalence of restrained-ensemble simulations with the maximum entropy method. J Chem Phys. 2013;138:084107. doi: 10.1063/1.4792208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.De Simone A, Richter B, Salvatella X, Vendruscolo M. Toward an accurate determination of free energy landscapes in solution states of proteins. J Am Chem Soc. 2009;131:3810–3811. doi: 10.1021/ja8087295. [DOI] [PubMed] [Google Scholar]
- 68.Schneider B, Morávek Z, Berman HM. RNA conformational classes. Nucleic Acids Res. 2004;32:1666–1677. doi: 10.1093/nar/gkh333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Best RB, Lindorff-Larsen K, DePristo MA, Vendruscolo M. Relation between native ensembles and experimental structures of proteins. Proc Natl Acad Sci U S A. 2006;103:10901–10906. doi: 10.1073/pnas.0511156103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Al-Hashimi HM, Walter NG. RNA dynamics: it is about time. Curr Opin Struct Biol. 2008;18:321–329. doi: 10.1016/j.sbi.2008.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Camilloni C, Vendruscolo M. A Tensor-Free Method for the Structural and Dynamical Refinement of Proteins using Residual Dipolar Couplings. J Phys Chem B. 2015;119:653–661. doi: 10.1021/jp5021824. [DOI] [PubMed] [Google Scholar]
- 72.Piana S, Laio A. A bias-exchange approach to protein folding. J Phys Chem B. 2007;111:4553–4559. doi: 10.1021/jp067873l. [DOI] [PubMed] [Google Scholar]
- 73.Ceriotti M, Tribello GA, Parrinello M. Simplifying the representation of complex free-energy landscapes using sketch-map. Proc Natl Acad Sci U S A. 2011;108:13023–13028. doi: 10.1073/pnas.1108486108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Biarnés X, Pietrucci F, Marinelli F, Laio A. METAGUI. A VMD interface for analyzing metadynamics and molecular dynamics simulations. Comput Phys Commun. 2012;183:203–211. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.