Abstract.
Predicting infarct volume from magnetic resonance perfusion-weighted imaging can provide helpful information to clinicians in deciding how aggressively to treat acute stroke patients. Models have been developed to predict tissue fate, yet these models are mostly built using hand-crafted features (e.g., time-to-maximum) derived from perfusion images, which are sensitive to deconvolution methods. We demonstrate the application of deep convolution neural networks (CNNs) on predicting final stroke infarct volume using only the source perfusion images. We propose a deep CNN architecture that improves feature learning and achieves an area under the curve of , outperforming existing tissue fate models. We further validate the proposed deep CNN with existing 2-D and 3-D deep CNNs for images/video classification, showing the importance of the proposed architecture. Our work leverages deep learning techniques in stroke tissue outcome prediction, advancing magnetic resonance imaging perfusion analysis one step closer to an operational decision support tool for stroke treatment guidance.
Keywords: deep learning, convolutional neural network, stroke, perfusion imaging, tissue fate prediction
1. Introduction
Stroke is the primary cause of long-term disability1 and the fifth leading cause of death in the United States, with Americans experiencing a new or recurrent stroke each year;2 only one-fourth of surviving adults recover to normal health status.3 Imaging is an integral part of the work-up of acute stroke patients. Magnetic resonance (MR) images are often obtained, including diffusion-weighted images (DWIs), apparent diffusion coefficient (ADC) maps, perfusion-weighted images (PWIs), and gradient recalled echo images. Typical features to examine from pretreatment magnetic resonance imaging (MRI) studies are volume of DWI positive ischemic tissue, volume of PWI positive perfusion defect, volume of the salvageable tissue (penumbra),4 presence/absence of hemorrhage,5 and location of vessel occlusion. Another potential feature is the final infarct volume, which researchers have attempted to predict using machine learning techniques.6–18
Although these techniques have proven to be useful, most of them rely on estimated model-based perfusion parameters [e.g., cerebral blood flow (CBF)] to predict tissue infarction. Recently, concerns have been raised about the use of these parameters,19,20 due to drawbacks (e.g., parameter inconsistency) that have been discussed in several studies.21–24 One such drawback is the sensitivity of PWI to vascular delays and dispersion effects caused by physiologic changes such as heart rate and cardiac output that can substantially change the perfusion image parameters.21 Another drawback is the fact that choosing the appropriate arterial input function (AIF), which describes the contrast input to the vasculature over time, from PWIs is a challenging and generally subjective task due to the need to account for the partial volume effect. This can lead to variability in blood flow measurements caused by varying delays and/or dispersion based on different AIF choices.22 Although deconvolution by singular value decomposition (SVD) can address this problem, studies have found that the deconvolution process can introduce distortions that influence the measurement of perfusion parameters23 and the decoupling of delay may negatively impact infarct prediction.24 All of these factors have contributed to the imperfect prediction of tissue outcome by current methods.
Recent work has shown that deep learning techniques25 outperform many state-of-the-art algorithms in classification tasks. One example is the ImageNet competition,26 in which participating teams are ranked based on the performance of their classifiers on classifying 1000 different image categories. The applications of deep learning techniques are not limited to static images but also include video classification.27–30 Spatio-temporal filters are learned during the training of deep learning algorithms, which are used to extract meaningful patterns from input videos for classification.
Medical image researchers have recognized the tremendous ability of deep learning techniques and have begun to apply these techniques in medical image challenges. In segmentation tasks, Davy et al.31 developed a multiscale CNN approach in a cascade architecture that exploits both local features as well as more global contextual features to perform brain tumor segmentation. Ronneberger et al.32 alternatively proposed a new CNN architecture, U-Net, that favors precise localization using symmetric expanding paths to improve cell segmentation. This architecture has been adapted in many applications, including high-resolution histological segmentation.33 Recently, Li et al.34 developed a region-based convolution neural network (CNN) that utilizes an R-CNN35 to achieve an epithelial cell segmentation with an accuracy of 99.1%. In medical prediction and classification tasks, Shin et al.36 tested the application of unsupervised deep autoencoders on organ (e.g., liver, kidney, and spleen) identification on MR images. Roth et al.37 proposed a classification method that exploits random aggregation of deep CNN outputs from rotated image patches to predict bone lesions. Ertosun and Rubin38 trained a deep CNN for automated classification of gliomas grading using digital pathology images. All of these proposed deep learning models have shown superior performance over existing methods.
In this work, we investigated the use of the source four-dimensional () pretreatment PWIs (pre-PWIs) to predict final infarct volume, instead of the derived model-based perfusion parameters (e.g., CBF). We have developed an approach to use deep CNNs to predict voxel-wise tissue death (infarct versus noninfarct). The results show that the proposed deep CNN can generate new features that significantly improve the prediction of tissue death as compared to standard deep CNNs for image/video classification. We compared our approach to the published tissue fate models, and the results show that the proposed model achieved better performance.
In summary, the main contributions of this work are:
-
1.
We propose to train the deep CNN with information from the source perfusion images (the patches of interest and their contralateral patches) to improve tissue outcome prediction.
-
2.
We design a deep CNN architecture to learn pairs of unit voxel-wise temporal filters that favor the learning of features from the modified training data.
-
3.
We compare our proposed deep CNN with previous models and show that it outperforms the existing tissue fate models.
One significant contribution of this work is the application of the proposed CNN architecture in automatic feature learning that are more predictive than hand-crafted features (e.g., CBF) for tissue outcome prediction using only the source perfusion images. The results show that the proposed deep CNNs are a robust tool for tissue outcome prediction when confounding patient imaging variables present (e.g., different AIFs), requiring neither AIF identification nor deconvolutions. This work represents a step toward an operational decision support tool for guiding stroke treatment.
2. Related Work
2.1. Tissue Outcome Prediction
Models have been developed to predict tissue outcome and estimate the growth of infarcts in order to provide more information for clinicians to make treatment decisions.6–11 One of the earliest models is the MR tissue signature model developed by Welch et al.,12 which utilized the ADC and images to identify reversible and irreversible volumes in the ischemic brain regions. Another early model is the generalized linear model (GLM) developed by Wu et al.6 This model used patients’ DWIs and estimated perfusion parameters (e.g., CBF) to predict voxel outcome; the result showed that using both PWIs and DWIs provided better performance in prediction compared to using DWIs alone. Later, Wu et al.7 applied this model to animal data to investigate the effectiveness of tissue plasminogen activator (tPA). Nguyen et al.8 further improved the basic GLM by introducing a correlation term that integrated spatial correlation information of voxels.
In addition to linear classifiers, nonlinear classifiers have been explored. Bagher-Ebadian et al.9 developed a four-layer artificial neural network (ANN) to predict the final extent of the three-month poststroke -lesion in stroke patients using -weighted, -weighted, diffusion-weighted, and proton density-weighted images. Huang et al.10 attempted to use an ANN to predict tissue outcome of rats with induced stroke by incorporating more information into the model. A spatial infarction incidence map and nearest-neighborhood information (8 neighboring voxels for a 2-D patch; 26 neighboring voxels for a 3-D patch) were used in the model. Scalzo et al.11 exploited spectral regression kernel discriminant analysis (SR-KDA)39 to predict voxel infarction using individual voxel time-to-maximum () and ADC value. SR-KDA is an effective algorithm to project high-dimensional nonlinear distributed data into a low-dimensional space, enabling efficient nonlinear dimension reduction. The result showed that learning nonlinear functions of the neighboring relationships of a patch is important for classification.
2.2. Deep Learning on Classification
Deep learning techniques have widely been adopted on 2-D classification tasks, such as multicategory image classification,26,40,41 pedestrian detection,42 and human pose identification.43 Variations of these techniques have been proposed to deal with higher dimensional data (e.g., video). Le et al.27 proposed an unsupervised deep learning algorithm, called independent subspace analysis, to learn spatio-temporal features from unlabeled video data. Simonyan and Zisserman30 implemented a two-stream CNN that performs separate convolution and pooling on the target video patch and the corresponding multiframe dense optical flow patch (temporal data), and then learns the joined features at the fully connected layers. Their results showed that this model can achieve very good performance with limited training data. Karpathy and Leung29 took a different deep learning approach to video data analysis. Instead of using all of the frames given in the input, they created a fusion model that slowly fuses a subset of frames throughout the network such that higher layers get access to progressively more global information. This model displayed significant improvement over feature-based baseline models. Tran et al.28 implemented a CNN to learn feature filters for 3-D convolution on video. The proposed network generated generic features for video object recognition, scene classification, and action similarity.
In this work, we propose a deep CNN to predict tissue outcome from perfusion data. We compare the proposed deep CNN model with several baseline models, including GLM, SR-KDA, support vector machine (SVM), and two baseline deep CNNs.27–30 The implementation details of the baseline deep CNNs are described in Sec 4.
3. Materials and Image Processing
3.1. Patient Cohort and Imaging Data
Under institutional review board (UCLA IRB#11-000728) approval, a total of 444 patient MR images were retrieved and examined from the University of California-Los Angeles picture archiving and communication system between December 2005 and December 2015. The inclusion criteria were: (1) acute ischemic stroke due to middle cerebral artery (MCA) occlusion; (2) MRI performed both before and after (3 to 7 days) treatment (e.g., clot retrieval and tPA); and (3) absence of hemorrhage. A total of 48 patients satisfied these inclusion criteria and were used in this study. Final infarct volumes were semiautomatically determined and measured on the posttreatment (post-FLAIR) images44 by an expert neuroradiologist (Dr. S. El-Saden) using Medical Image Processing, Analysis, and Visualization software.45 Pretreatment (pre-FLAIR) images were used to identify preexistent lesions that were not related to the current stroke, and these lesions were not labeled as part of the final infarct volumes. The patient characteristics are summarized in Table 1.
Table 1.
Ischemic stroke patient cohort characteristics.
| Patients () | |
|---|---|
| Demographics | |
| Age | |
| Gender | 20 males |
| Clinical presentation | |
| Time since stroke | |
| NIHSSa | |
| Atrial fibrillation | 15 |
| Hypertension | 32 |
| Treatments (received)b | |
| IV-tPA | 24 |
| IA-tPA | 6 |
| Clot-retrieval devices (e.g., Solitaire™) | 29 |
| Treatment evaluation | |
| TICI scorec | 0 (4), 1 (0), 2a (13), 2b (8), 3 (1), N/A (22) |
| AOL scored | 0 (3), 1(0), 2(4), 3(16), N/A (25) |
| Outcome | |
| Discharge mRSe | |
| Discharge lesion size | |
NIHSS, NIH Stroke Scale International; scale: 0 (no stroke symptoms) − 42 (severe stroke).
A patient could receive more than one treatment in a visit. IV-tPA, intravenous tissue plasminogen activator; IA-tPA, intraarterial tissue plasminogen activator.
TICI, thrombolysis in cerebral infarction; scale: 0 (no reperfusion), 1, 2a, 2b, 3 (full reperfusion), N/A (missing). Available only for patients with clot-retrieval devices.
AOL, arterial occlusive lesion; scale: 0 (complete occlusion) − 3 (complete recanalization), N/A (missing). Available only for patients with clot-retrieval devices.
Discharge mRS, discharge modified Rankin scale; scale: 0 (no stroke symptoms) − 6 (dead).
All patients underwent MRI using a 1.5- or 3-Tesla echo planar MRI scanner (Siemens Medical Systems); scanning was performed with 12-channel head coils. The PWIs were acquired using a repetition time (TR) range of 1490 to 2890 ms and an echo time (TE) range of 23 to 50 ms. The pixel dimension of the PWIs varied from to . The pre-FLAIR images were acquired using a TR range of 8000 to 10000 ms and a TE range of 82 to 123 ms. The pixel dimension of the pre-FLAIR images varied from to . The post-FLAIR images were acquired using a TR range of 8000 to 10000 ms and a TE range of 82 to 134 ms. The pixel dimension of the post-FLAIR images varied from to . The perfusion parameter maps of , CBF, time-to-peak (TTP), cerebral blood volume (CBV), and mean transit time (MTT) were calculated using block-circulant singular value decomposition as provided by the sparse perfusion deconvolution toolbox.46 We note that in MRI, each brain voxel has three spatial dimensions for three axes (, , and ). We ignore the -dimension in data generation (i.e., patch creation) due to slice thickness. Thus our notation is simplified as we may denote the size of a “voxel” as only.
3.2. Image Preprocessing
First, intrapatient registration of axial pre-PWIs, pre-/post-FLAIR images, and post-FLAIR images was performed with a six-degree-of-freedom rigid transformation using FLIRT.47 Through the registration, each voxel in pre-PWIs and post-FLAIR was made to correspond to the same anatomical location in pre-FLAIR. Then all pre-PWIs were interpolated so that each had the same unit increment in the time dimension. The multiatlas skull-stripping algorithm48 was used to remove the skulls. Brain ventricle voxels were excluded in training. All brain images were aligned to their central lines in the axial plane using MATLAB image processing toolbox (version 9.4.0 Mathworks, Inc., Natick, Massachusetts). Each source signal of pre-PWIs was then converted to a tissue concentration time curve based on the baseline signal TE and :49
| (1) |
where is the average of the first five values of the signal curve, and is a scaling factor provided by Mouridsen et al.,49 with a value of 2000. All CTCs were standardized to zero-mean and unit-variance globally on a voxel-by-voxel basis.50
4. Methods
This section is divided into three parts: Sec. 4.1 describes the prediction task and the training patch generation; Sec. 4.2 describes the existing deep CNN models and the proposed architecture; Sec. 4.3 describes the configurations and implementation details of the deep CNNs, the baseline models, and the evaluation metrics.
4.1. Patch Sampling and Ground Truth
The task is to predict the final outcome of every brain voxel (i.e., infarcted or noninfarcted) given its CTC. The ground truth binary mask is derived from the post-FLAIR images (acquired 3 to 7 days posttreatment), where the positive class is infarcted and the negative class is noninfarcted. The deconvolution of a CTC with its AIF generates a residue curve, from which perfusion parameters are derived using a curve-fitting-based approach.22 While baseline tissue fate models6,7,11–14 used these derived perfusion parameters (e.g., ) to predict a voxel outcome, the deep CNNs learn features directly from the CTC to predict outcomes and, therefore, do not depend on the AIF.
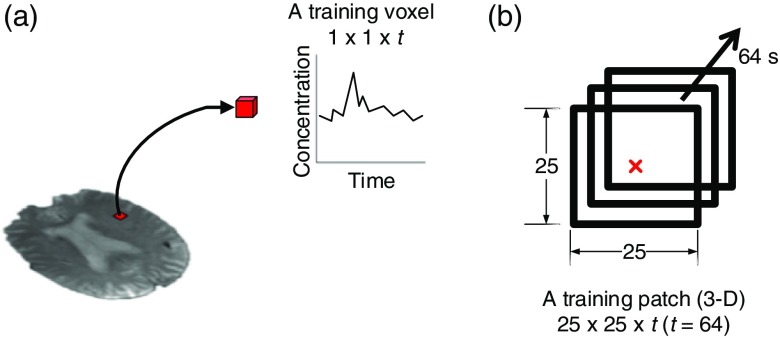
To generate training data from a perfusion signal associated with a given voxel, one straightforward approach is to only use each voxel’s time signal information (concentration change along time) [Fig. 1(a)]. For example, a single training sample has a dimension of , in which is the total time length of the study (equivalent to the total number of brain volumes in the pre-PWI). However, this approach is sensitive to noise (e.g., small motion artifacts can cause apparent concentration changes in a voxel) and it incorrectly assumes voxels are independent. Recent work14 revealed that incorporating neighboring voxel information improved classification performance. Therefore, training data were sampled as a 3-D “patch” sequence instead of a single sequence; each training example had a size of , where is the width/height of the patch and the center of the patch is the voxel of interest [Fig. 1(b)]. Deep CNNs then learn filters to extract spatio-temporal features from the patch to predict the outcome of the central voxel. We experimented with different values of in the 2-D CNN architecture and determined the optimal training patch size is ( and ) in the 10-fold cross validation. We used this patch size for all the deep CNN model training and testing.
Fig. 1.
Training data generation: (a) a training voxel with a dimension of , containing the concentration change along time and (b) a training patch with a dimension of , where . The center of the patch (red) is the voxel of interest. A patch is associated with the outcome value (0 or 1) of the voxel of interest.
4.2. Deep CNN Architecture
4.2.1. Baseline deep CNN framework
Typical deep CNNs consist of multiple convolutional, pooling, nonlinear, fully connected layers and a softmax classifier. The convolutional layers produce feature maps (usually ) from the input through automatically learned feature filters (weight matrices). These feature filters detect local characteristics of regions given the input; each of these local regions is connected to a location of the output (feature map). The pooling layers employ max-operators that pool values in a local region together (i.e., given a small region, only the maximum value is returned), which makes the network more translation invariant. The nonlinear layers contain rectified linear units51 (ReLU) that introduce nonlinearity, enabling the network to learn nonlinear features. After multiple stacking of convolutional-ReLU-pooling layers, fully connected layers (inputs are fully connected to each previous layer’s output) are added to generate summarized features, which are the inputs to the softmax classifier for classification. Given a deep CNN with layers and data samples (), the parameters () of a softmax classifier in binary form (i.e., logistic classifier) are obtained by minimizing the cost function:
| (2) |
| (3) |
where is a parameter for controlling the weight decay term , is the sigmoid function, and is the output of the fully connected layer before the softmax classifier. The weights in a deep CNN layer [] are updated via gradient descent, namely
| (4) |
where is the learning rate. The gradient is obtained through backpropagating the loss from the softmax classifier and chain rule. There are two basic approaches to train deep CNNs with the 3-D training data. In the first approach, we treat the time channel of the training data as if it was a color channel; this allows us to use standard 2-D deep CNN architectures that are typically applied to images.52 The filter learning of a convolutional layer in a 2-D deep CNN is two-dimensional. In the second approach, we can employ a 3-D deep CNN architecture,28 which is composed of 3-D filters in convolutional layers. Complex spatio-temporal features are learned progressively along the network, and they are more descriptive for small changes in both the spatial and temporal dimensions.
4.2.2. Baseline CNN limitations and the proposed architecture
The motivation for using deep CNNs is their strong ability to learn data-driven filters to obtain complex features that are predictive of infarction. With the baseline 2-D or 3-D deep CNN architecture, spatio-temporal filters can be learned to extract features from input patches that predict tissue fate. However, when we trained these architectures using the perfusion image training patches, we implicitly assumed that every training patch was sampled from a distribution generated by the same global AIF (as obtained from the MCA), an assumption that does not hold across patients due to a variety of factors, such as a patient’s unique cerebrovascular architecture. (Note: We can also define a lot of local AIFs22 in which each is based on the closest artery to the voxel of interest. This approach is difficult to use with low-resolution PWIs due to the challenge of finding suitable arterial voxels throughout the brain. In the context of this paper, we refer to the global AIF obtained from MCA as the “AIF.”)
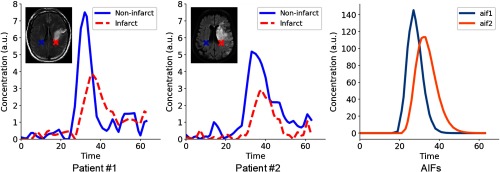
Figure 2 illustrates an example of the tissue CTCs of a noninfarcted voxel and infarcted voxel in two different patients with different AIFs. Within the curves of a particular patient, the noninfarcted voxel has a CTC with an earlier and higher peak (solid line) relative to the CTC of the infarcted voxel (dotted line). However, when we compare curves across patients, the CTC of the noninfarcted voxel of patient #2 is delayed and lower than the CTC of the noninfarcted voxel of patient #1. These differences are due to their unique AIFs (Fig. 2), which describe the unique pattern of flow of the contrast agent traveling within the cerebrovasculature and which also reflects the effects of both of the administration method as well as the cardiac function and vasculature between the intravenous administration site and the brain.22 This information is not incorporated into the training of the baseline 2-D or 3-D deep CNN architecture, and this makes the learning of representative features difficult. The learned feature filters from these 2-D and 3-D deep CNN architectures are limited to only detect features within a patch signal (e.g., peak maximum value) and do not account for the difference in patient AIFs.
Fig. 2.
Illustration of tissue CTCs of a noninfarcted voxel and infarcted voxel in two different patients, and the patient AIFs.
To overcome this limitation, the network must be capable of learning features that are independent of confounding patient-specific variables, such as AIFs, and that are predictive of tissue outcome. Thus we propose a deep CNN model (Fig. 3) to improve feature learning, including a new form of input patches (patches of interest paired with contralateral patches), a new architecture for the convolutional layer, and explicit learning of unit temporal filters, i.e., a set of filters that have size of , where is the time dimension. The use of a contralateral patch as a matched control (reference) has also been used in the simple thresholding approach for lesion delineation.53
Fig. 3.
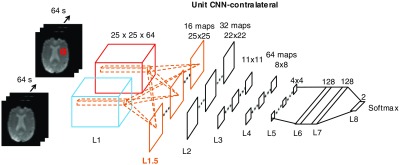
The proposed eight-layer deep CNN (unit CNN-contralateral) with the new architecture of the convolutional layer and unit temporal filter learning (orange) for tissue outcome prediction (only the interconnections within first layer are shown). An input consists of a pair of patches (the patch of interest, red, and its contralateral patch, blue). Pairs of unit temporal filters (L1) are learned simultaneously, which feed into the first convolutional layer (L1.5); 2-D operations (convolution, L2 and L4, and pooling, L3 and L5) are then performed to generate features for the fully connected layers (L6 and L7) and softmax classifier (L8). See Sec. 8.1 (Fig. 6) for a more detailed configuration of this proposed deep CNN for tissue outcome prediction.
Matched controls for input patches
The features learned on an input patch of interest are implicitly affected by the AIF. In contrast, features that are derived from the comparisons between the input patch of interest and a matched control might be independent of the confounding variables. We exploited the natural symmetry of the brain to create a matched control for each patch, which is the patch contralateral to the patch of interest (we refer to it as the “contralateral patch”). Each original training patch is paired with its contralateral patch, and it is then used to train the CNN. To improve the feature learning with the new form of training data, we proposed a new architecture that involves paired convolutions in the standard convolutional layer.
Proposed architecture for learning paired unit temporal filters
To learn feature filters that extract relationships between a pair of input patches (i.e., the patch of interest and its contralateral patch), we proposed a new architecture for the convolutional layer where pairs of 3-D convolutional filters are learned simultaneously. Each “filter” in the new convolutional layer consists of two 3-D filters (, ), each of which has a size of for the dimension, dimension, and time dimension. Each “filter” convolves local regions on the patch of interest and the contralateral patch, respectively. An output location () on a feature map produced from the new convolution layer is defined to be the sum of the convolved values of the same local regions on the patch of interest () and the contralateral patch ():
| (5) |
The advantage of this formulation is that all pairs of filters (, ) are learned simultaneously, without modification to our loss backpropagation and weight updating methodology. Since the resolution of perfusion images is low, the spatial filters may not be easily learned to capture fine-grained features to distinguish between positive and negative labels. Therefore, we hypothesize that the CNN architecture should be designed to favor the learning of temporal features between patches. To optimize learning filters that detect these temporal features, we first made the network “explicitly” learn paired unit voxel-wise temporal filters in the new convolutional layer. More specifically, each filter in a pair had a size of for the dimension, dimension, and time dimension; these filters capture the local voxel-wise temporal characteristics. We then performed normal 2-D convolution and pooling (similar to a 2-D deep CNN) to derive the final compressed features in the fully connected layer, which was then fed into a softmax classifier to predict tissue outcome. The new feature map formulation and the explicit learning of temporal filters lead to the proposed eight-layer deep CNN (Fig. 3). It is incorporated with the new convolutional layer and unit temporal filter learning (L1.5) for tissue outcome prediction. We denote the new proposed deep CNN as “unit CNN-contralateral.”
4.3. Experimental Setup
4.3.1. CNN configurations and implementation details
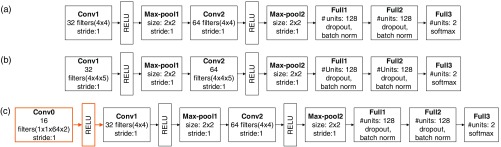
To compare to the unit CNN-contralateral, we trained two baseline deep CNNs based on the 2-D and 3-D approach. The architecture details of all three deep CNNs are shown in Sec. 8.1 (Fig. 6). In summary, each of these two baseline deep CNNs consists of two sequences of convolutional (conv)-nonlinear (ReLU)-pooling (max-pool) layers, followed by two fully connected layers. The two fully connected layers are incorporated with dropout54 and batch normalization41 to reduce overfitting of the data and address the issue of internal covariate shift. With this multilayer deep CNN architecture, 128 features are generated in the last fully connected layer, which are the inputs to a softmax classifier for voxel outcome prediction. The unit CNN-contralateral has an additional first layer (the new convolutional layer) that learns paired unit temporal filters. This layer (orange boxes) is inserted into the 2-D deep CNN architecture; 128 features were generated for tissue outcome prediction. For these deep CNNs, the number of filter maps and the parameters (e.g., stride) of the filters and the use of max-pooling layers are based on published architectures.28,52 Briefly, a small filter size (i.e., ) was used and the number of filter maps was a factor or a multiple of 2 (i.e., 16, 32, 64, or 128).
Fig. 6.
The deep CNNs for predicting voxel-wise tissue outcome: (a) 2-D deep CNN, (b) 3-D deep CNN, and (c) the proposed deep CNN (denoted as “unit CNN-contralateral”); the first layer is the new convolutional layer that learns paired unit temporal filters for comparing the patch of interest and its contralateral patch, which is followed by a nonlinear layer (ReLU) and then the standard 2-D deep CNN. These deep CNNs learn feature filters to generate 128 complex hierarchical features in the last fully connected layer, which are then used by the softmax classifier to predict outcome. Abbreviations: conv, convolutional layer; max-pool, max-pooling layer; full, fully connected layer; softmax, softmax classifier, batch norm (batch normalization).
The deep CNNs were trained with batch gradient descent (batch size: 50) and backpropagation. A momentum of 0.9 and a learning rate of 0.05 were used. A heuristic was applied to improve the learning of weights,52 where the learning rate was divided by 10 when the validation error rate stopped improving with the current learning rate. This heuristic was repeated three times. An early stopping strategy was applied to improve the learning of deep CNNs weights and prevent overfitting. In this strategy, the training was terminated if the performance failed to improve in five consecutive epochs (maximum number of training epochs: 40). The CNNs were implemented in Torch7,55 and the training was done on two NVIDIA Titan X GPUs and an NVIDIA Tesla K40 GPU.
4.3.2. Baseline model comparison
In addition to the baseline 2-D and 3-D deep CNN models, we compared the proposed deep CNN with published tissue fate models (GLM6 and SR-KDA14) and an SVM designed for large-scale classification56 using the same perfusion parameters as the GLM. The details of the baseline model training are described in Sec. 8.2. To investigate the importance of using contralateral patches, we compared the performance of the deep CNNs (with the new convolutional layer) trained with contralateral patches (unit CNN-contralateral), random patches (unit CNN-random), and duplicate patches (unit CNN-duplicate). All the comparisons were performed using 10-fold patient-based cross validation, with a nested validation in each cross-validation fold for performance evaluation, i.e., identifying the optimal cutoff point that optimizes the Youden Index57 for receiver operating characteristic (ROC) curve. For each of the 48 patients in the dataset, 1000 patches were randomly selected without replacement from the set of infarcted voxels and the set of noninfarcted voxels, respectively, generating a randomized, stratified, and balanced training dataset with a total of 96,000 patches to avoid biased training.58
4.3.3. Evaluation metrics
We computed the area under the ROC curve (AUC), which is a classifier’s probability of predicting an outcome better than chance. The accuracy and overlap coefficient were also calculated.59 Accuracy measured the percentage of voxels that were given the correct label. Overlap coefficient measured the similarity between the prediction and ground truth masks; it is defined as the size of the intersection divided by the smaller size of the two sets. A value of 0 indicates no overlap, a value of 1 indicates perfect similarity. All the evaluation metrics were computed for the whole brain data set, in which the held-out validation set belonged in the 10-fold cross validation.
To determine if the performance of the models significantly differed, we used Hanley and McNeil significant test60 to compare the model AUCs and used two-tailed Wilcoxon signed-rank test61 to compare the overlap coefficient and the accuracy of the models.
5. Results
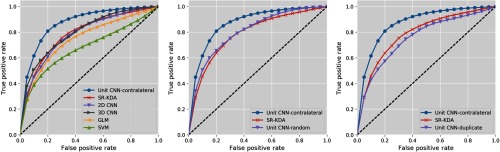
5.1. Baseline Versus Unit CNN-Contralateral
Figure 4 shows the ROC curves of the deep CNNs and the baseline tissue outcome models (GLM, SR-KDA, and standard SVM) on predicting tissue outcome, and Table 2 shows the average accuracy, overlap coefficient, and AUC of each classifier calculated from the 10-fold cross validation. The precision and recall of each classifier calculated from the 10-fold cross validation are shown in Sec. 8.3 (Table 3). In each step of the 10-fold patient-based cross validation, we applied the trained model to the held-out whole brain dataset (including all voxels in the brains) to calculate the evaluation metrics. The total training time for the CNNs was 124.5 h (about 5 days).
Fig. 4.
10-fold cross-validation ROC curves for unit CNN-contralateral, unit CNN-random, unit CNN-duplicate, and baseline models.
Table 2.
Average performance on held-out whole brain data in 10-fold cross validation.
| Accuracy | Overlap | AUC | |
|---|---|---|---|
| 2-D CNN | 0.746 | 0.728* | * |
| 3-D CNN | 0.790 | 0.717* | * |
| Unit CNN-random | 0.780 | 0.753* | * |
| Unit CNN-duplicate | 0.770 | 0.698* | * |
| Unit CNN-contralateral |
0.818 |
0.811 |
|
| GLM | 0.751* | 0.628* | * |
| SVM | 0.724* | 0.633* | * |
| SR-KDA | 0.784 | 0.679* | * |
Note: Bold values indicate the highest values within each group of models (CNNs and baselines).
Indicated statistically significant results () against the unit CNN-contralateral model.
Table 3.
Average precision and recall on held-out whole brain data in ten-fold cross-validation.
| Precision | Recall | ||
|---|---|---|---|
| 2-D CNN | 0.211 | 0.700 | 0.324 |
| 3-D CNN | 0.220 | 0.693 | 0.334 |
| Unit CNN-random | 0.221 | 0.716 | 0.338 |
| Unit CNN-duplicate | 0.208 | 0.670 | 0.317 |
| Unit CNN-contralateral |
0.222 |
0.799 |
0.347 |
| GLM | 0.627 | 0.139 | 0.228 |
| SVM | 0.624 | 0.151 | 0.243 |
| SR-KDA | 0.671 | 0.171 | 0.273 |
Note: Bold values indicate the highest values within each group of models (CNNs and baselines).
Among all the baseline tissue outcome models, SR-KDA achieved the best AUC and overlap coefficient. We speculate this could be due to SR-KDA’s patch-based approach, which predicts voxel outcomes using neighboring voxels’ features, whereas SVM/GLM only used the features of the voxel of interest. Compared to the best baseline results (SR-KDA), deep CNNs achieve better performance. The 3-D deep CNN is slightly better than 2-D deep CNN, likely due to the greater learning capability as a result of the higher number of model parameters. However, these two deep CNNs did not offer significant performance improvement of AUC compared to SR-KDA. Among all deep CNNs, the proposed deep CNN trained with contralateral patches (unit CNN-contralateral) achieved the best performance in all evaluation metrics. It achieved the highest AUC and overlap coefficient of 0.871 and 0.811, respectively. The significance test results show that the proposed deep CNN achieved significantly better AUC than all other deep CNN classifiers. Overall, the AUC and overlap coefficient indicates that the proposed deep CNN performed significantly better than SR-KDA, 0.871 versus 0.788 () and 0.811 versus 0.679 (). These results indicate that the proposed deep CNN is the best model for predicting tissue outcome.
5.2. Unit CNN with Different Types of Patches
To investigate the significance of using the contralateral patch as part of the input, we performed additional experiments to verify whether using the contralateral patch in our proposed network provides better results than using other potential patch selections. We used the same proposed deep CNN architectures to build models with two types of training data: (1) the patch of interest with a patch randomly selected from the brain and (2) the patch of interest with a copy of itself. The results are shown in Table 2 and Fig. 4. The performance of the deep CNNs significantly dropped when trained with random or duplicate paired patches instead of contralateral patches. The unit CNN trained with duplicate patches performed worse than other deep CNNs. The unit CNN trained with random patches achieved only slightly higher performance than a 3-D deep CNN, but falls short of the performance of the deep CNN trained with contralateral patches, indicating the value of having the contralateral patch as part of the input. This suggests that using the contralateral patch provides additional information that allows the deep CNN to learn useful comparison filters rather than merely signal filters to extract features for tissue outcome prediction. One interesting observation is that the deep CNN trained with random patches has higher AUC () than the deep CNN trained with duplicate patches. This illustrates that additional random information can boost model performance. However, this boosting is not as good as using contralateral patches. The visualization of the CNN first layer filters trained with different types of patches is shown in Sec. 8.4, Fig. 7.
Fig. 7.
Seven of the sixteen pairs of 3-D filters learned in the first layer of the proposed unit CNNs trained with contralateral patches, random patches, and duplicate patches, respectively. Each 3-D filter is composed of 64 unit filters (along time) with a size of ; therefore, each 3-D filter has a size of ().
5.3. Examples of Prediction
Figure 5 shows the tissue outcome predictions of the unit CNN-contralateral, SR-KDA, and 3-D deep CNN models. For large infarcts (patient #1), unit CNN-contralateral and SR-KDA predicted well on visual inspection, whereas 3-D deep CNN predicted high probability (red color) only in certain parts of the final infarct regions. For patient #2, all models predicted the correct locations of the final infarct regions. Unit CNN-contralateral and the 3-D deep CNN both predicted larger final infarct volumes with high probabilities than SR-KDA. The volume of prediction with the highest probability () of unit CNN-contralateral matches well with the ground truth. For patient #3, SR-KDA and unit CNN-contralateral predicted larger final infarct volume with high probabilities, whereas 3-D deep CNN predicted only partial volume. For patient #4, the region of high probability of unit CNN-contralateral matched well with the ground truth. However, the regions with high probability of SR-KDA and 3-D deep CNN were larger and smaller, respectively.
Fig. 5.
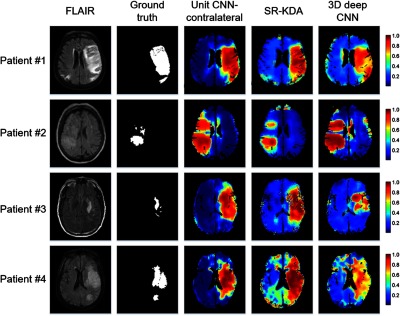
Tissue outcome prediction of unit CNN-contralateral, SR-KDA, and 3-D deep CNN.
6. Discussion
Predicting ischemic tissue outcome is a challenging and important task for better stroke evaluation and treatment planning. Knowing the potential tissue outcome before the use of an intervention has the potential to provide important information to clinicians about the relative value of interventions. For example, if the volume of predicted infarct tissue despite treatment is large, a clinician may reconsider the utility of a treatment such as thrombolysis or clot retrieval, either of which can increase the chance of hemorrhage and potentially worsen the clinical outcome. In addition, predicting stroke tissue outcome helps to generate new knowledge that may be useful in patient selection for clinical trials.62 In this work, we demonstrated the use of deep CNNs in ischemic tissue outcome prediction (infarcted versus noninfarcted) and proposed a deep CNN that outperformed the existing models.
There are two major advantages of using deep learning in predicting tissue outcome. First, the proposed algorithm can automatically learn hierarchical imaging features from only source pretreatment perfusion images. It eliminates the use of deconvolution and still achieves better performance than the baseline models that utilize perfusion parameters. The superior performance of the deep learning algorithm reinforces the findings of Christensen et al.24 and Willats et al.63 that summary parameters calculated without an AIF from source perfusion images contain enough information to determine tissue outcome. The feature generation of the proposed deep CNN is fully data driven and automatic. The learned features represent more complicated characteristics than just the summary perfusion parameters (e.g., TTP) and are shown to be more predictive of tissue outcome. Second, the deep learning algorithm can better capture nonlinear relationships than other models. Such nonlinear relationships cannot be captured by linear models, such as GLMs, and have been shown to be important for tissue outcome prediction.14 Compared to models such as SR-KDA and SVM, deep CNNs automatically learn spatio-temporal features from the source perfusion images that are more complex and predictive than perfusion parameters (e.g., ). Such nonlinear feature learning is made possible by the stacked layer architecture, which is a distinctive feature of deep learning algorithms. The greater learning capability of the deep CNNs was validated by the improved performance of the 2-D deep CNN and 3-D deep CNN compared to other baseline models.
In this work, we proposed a new architecture for the convolutional layer, which learned pairs of unit temporal filters simultaneously from the patch of interest and its contralateral patch. This new layer was inserted as the first layer to the standard 2-D deep CNN and allowed the deep CNN to derive paired filters to obtain useful correlations between inputs in the first layers such that the learned filters in the subsequent convolutional layers no longer detected the spatio-temporal features of a single input. Instead, these filters were learned to detect spatial features of the differences between two input patches (i.e., the patch of interest and its contralateral patch).
Such differences were further expanded and stacked through multiple layers in the deep CNN and finally became the 128 features that were used to train a softmax classifier. The incorporation of the new convolutional layer changed the nature of the learned features of the deep CNN, which ultimately led to features that achieved the best performance among all the models.
Our study has several limitations. First, we did not consider treatment information in our predictions, which has a direct impact on outcome. Also changes in MR image acquisition parameters (e.g., field strength) or clinical variables (e.g., age) may impact the classifier performance.64 We did not perform subgroup analysis based on image acquisition parameters or clinical variables because of a relatively small dataset (). Future studies will include larger patient cohorts with imaging and pre-/posttreatment information, which will allow subgroup analysis to evaluate how well the proposed method would generalize across different imaging protocols and patient characteristics. Second, we note that the proposed deep CNN has high recall and low precision (Sec. 8.3, Table 3), which is likely due to the imbalance of our classes.65 Future work could explore different methodologies, including sampling strategies,66 to improve model precision while maintaining recall with our imbalanced dataset. Finally, our proposed model only used perfusion images to achieve better performance than baseline models, which also used DWIs. We plan to further expand the deep CNNs in order to incorporate these images and generate better composite feature representations.
7. Conclusion
In this work, we proposed a deep CNN to learn pairs of unit temporal filters for outcome prediction in ischemic tissue using only the source perfusion images. We compared it with baseline models including two deep CNNs, SVM, GLM, and SR-KDA and showed that it achieved the best performance. Our work demonstrates the potential use of deep learning techniques in stroke MR perfusion imaging analysis. This temporal feature learning approach may also benefit the weight initialization of the deep learning models via transfer learning67 for body parts other than the brain when MR perfusion images are available. More improvements are possible, including the incorporation of clinical variables into the network and exploring the use of composite features generated from different MR image types. The deep CNN model proposed here provides a foundation to utilize deep learning techniques in perfusion image analysis, which could ultimately provide useful information for clinicians when deciding upon a treatment intervention.
8. Appendix A
8.1. Architecture Details of the Baseline 2-D and 3-D Deep CNNs, and the Unit CNN-Contralateral
Figure 6 shows the deep CNNs for predicting voxel-wise tissue outcome. The 2-D and 3-deep CNN have the same architecture, except that the convolutional layers are 2-D and 3-D, respectively. The proposed deep CNN has a new convolutional layer in the first layer, which learns paired unit temporal filters for comparing the patch of interest and its contralateral patch.
8.2. Baseline Models (SR-KDA, GLM, and SVM) Construction
We implemented three baseline models for tissue outcome prediction following the corresponding paper implementations: SR-KDA,14 GLM,6 and SVM.56 Briefly, SR-KDA is a patch-based model for which patches (with a size of )14 were generated for model training. GLM is a single-voxel-based model, in which several image parameters (ADC, pre-FLAIR, CBF, CBV, and MTT) are the inputs used by the model. SVMs were trained using the same features as the GLM. The optimal hyperparameters for SR-KDA (alpha) and SVM ( and epsilon) were determined using nested validation in the 10-fold cross validation. The range of tested alpha value for SR-KDA was (0.001, 100). The range of tested and epsilon values for SVM were (0.00001, 16) and (0.0001, 10), respectively.
8.3. Precision and Recall on Held-Out Whole Brain Data in 10-Fold Cross-Validation
The precision and recall of each classifier calculated from a fixed specificity (specificity = 0.830)6 are shown in Table 3. We note that both the proposed and the baseline classification approaches have low precision, low score, and high recall. The low precision value may limit the real-world application of the proposed model in clinical practice. However, the high recall value of the model shows the possibility of using the model as a first-pass screening method to prescreen stroke patients who may have high risk of large infarcted regions. In addition to the possible clinical utility, the results show that the proposed Unit CNN approach achieved the best performance compared to other CNN and baseline models. The proposed model also achieved higher sensitivity (0.819 versus 0.660) than the previously published model6 while maintaining the same specificity. This provides evidence that the proposed approach has the best performance in stroke tissue outcome prediction.
8.4. Visualization of Feature Filters Learned in the First Layer of the Proposed Unit CNNs Trained with Contralateral Patches, Random Patches, and Duplicate Patches, Respectively
Seven of the sixteen learned pairing filters of the proposed deep CNNs (trained with contralateral patches, random patches, and duplicate patches, respectively) are shown in Fig. 7. Each pair of filters consists of two () 3-D filters. Instead of capturing spatial features (e.g., edges) as typical 2-D filters do, these pairs of 3-D filters capture the relationships between two input signals in the time dimension. When looking at the pairing filters of the deep CNN trained with duplicate patches, one may observe that filters are similar within a pairing filter. In contrast, the variability of the pairing filters of the deep CNN trained with contralateral patches is higher: some pairing filters appear to be the “opposite” of each other, whereas others appear to be similar. For example, in filter pair number 7, the first filter (top) can detect later signals (indicated as black first and then white along time), whereas the second filter detects early signals (indicated as white first and then black along time). Compared to these pairing filters, those paired filters trained by the deep CNN with random patches were inconsistent and more random in appearance; those paired filters trained by the deep CNN with duplicate patches looked similar. This result shows that training with contralateral patches results in a distinct class of filters that are associated with better model performance.
Acknowledgments
The authors would like to thank Samantha Ma of the Keck School of Medicine, University of Southern California, for helpful discussions and feedback. This research was supported by the National Institutes of Health (NIH) Grant Nos. R01 NS076534 and R01 NS100806, Computational Integrated Diagnostics Program under the UCLA Departments of Radiological Sciences and Pathology and Laboratory Medicine, UCLA Radiology Department Exploratory Research Grant (No. 16-0003), an NVIDIA Academic Hardware Grant, an AMA Foundation Seed Grant, NIH NCI (No. F30CA210329), NIH NIGMS (No. GM08042), and the UCLA-Caltech Medical Scientist Training Program.
Biographies
King Chung Ho received his BS degree in bioengineering from the University of California, Berkeley, in 2011, and his MS and PhD degrees in biomedical engineering from the University of California, Los Angeles, in 2013 and 2019, respectively. He was a graduate student at the University of California, Los Angeles. His current research interests include deep learning, machine learning, and medical imaging informatics.
Biographies of the other authors are not available.
Disclosures
No conflicts of interest, financial or otherwise, are declared by the authors.
References
- 1.Centers for Disease Control and Prevention, “Prevalence of disabilities and associated health conditions among adults—United States, 1999,” Morb. Mortal. Wkly. Rep. 50(7), 120 (2001). [PubMed] [Google Scholar]
- 2.Mozaffarian D., et al. , “Executive summary: heart disease and stroke statistics-2016 update: a report from the American Heart Association,” Circulation 133(4), 447–454 (2016). 10.1161/CIR.0000000000000366 [DOI] [PubMed] [Google Scholar]
- 3.Dobkin B. H., “Rehabilitation after stroke,” N. Engl. J. Med. 108, 600–606 (2005). 10.1056/NEJMcp043511 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Olivot J. M., et al. , “Geography, structure, and evolution of diffusion and perfusion lesions in diffusion and perfusion imaging evaluation for understanding stroke evolution (DEFUSE),” Stroke 40(10), 3245–3251 (2009). 10.1161/STROKEAHA.109.558635 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Heiss W. D., “Ischemic penumbra: evidence from functional imaging in man,” J. Cereb. Blood Flow Metab. 20(9), 1276–1293 (2000). 10.1097/00004647-200009000-00002 [DOI] [PubMed] [Google Scholar]
- 6.Wu O., et al. , “Predicting tissue outcome in acute human cerebral ischemia using combined diffusion- and perfusion-weighted MR imaging,” Stroke 32, 933–942 (2001). 10.1161/01.STR.32.4.933 [DOI] [PubMed] [Google Scholar]
- 7.Wu O., et al. , “Infarct prediction and treatment assessment with MRI-based algorithms in experimental stroke models,” J. Cereb. Blood Flow Metab. 27(1), 196–204 (2007). 10.1038/sj.jcbfm.9600328 [DOI] [PubMed] [Google Scholar]
- 8.Nguyen V., Pien H., Menenzes N., “Stroke tissue outcome prediction using a spatially-correlated model,” in Pan Pacific Imaging Conf., vol. 3, pp. 238–241 (2008). [Google Scholar]
- 9.Bagher-Ebadian H., et al. , “Predicting final extent of ischemic infarction using artificial neural network analysis of multi-parametric MRI in patients with stroke,” PLoS One 6(8), e22626 (2011). 10.1371/journal.pone.0022626 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Huang S., Shen Q., Duong T. Q., “Artificial neural network prediction of ischemic tissue fate in acute stroke imaging,” J. Cereb. Blood Flow Metab. 30(9), 1661–1670 (2010). 10.1038/jcbfm.2010.56 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Scalzo F., et al. , “Regional prediction of tissue fate in acute ischemic stroke,” Ann. Biomed. Eng. 40(10), 2177–2187 (2012). 10.1007/s10439-012-0591-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Welch K. M. A., et al. , “A model to predict the histopathology of human stroke using diffusion and T2-weighted magnetic resonance imaging,” Stroke 26(11), 1983–1989 (1995). 10.1161/01.STR.26.11.1983 [DOI] [PubMed] [Google Scholar]
- 13.Jacobs M. A., et al. , “Multiparametric MRI tissue characterization in clinical stroke with correlation to clinical outcome,” Stroke 32(4), 950–957 (2001). 10.1161/01.STR.32.4.950 [DOI] [PubMed] [Google Scholar]
- 14.Mitsias P. D., et al. , “Multiparametric iterative self-organizing MR imaging data analysis technique for assessment of tissue viability in acute cerebral ischemia,” Am. J. Neuroradiol. 25(9), 1499–1508 (2004). [PMC free article] [PubMed] [Google Scholar]
- 15.Soltanian-Zadeh H., et al. , “Multiparametric iterative self-organizing data analysis of ischemic lesions using pre-or post-Gd T1 MRI,” Cerebrovasc. Dis. 23(2–3), 91–102 (2007). 10.1159/000097044 [DOI] [PubMed] [Google Scholar]
- 16.Zavaljevski A., et al. , “Multi-level adaptive segmentation of multi-parameter MR brain images,” Comput. Med. Imaging Graphics 24(2), 87–98 (2000). 10.1016/S0895-6111(99)00042-7 [DOI] [PubMed] [Google Scholar]
- 17.Bernarding J., et al. , “Histogram-based characterization of healthy and ischemic brain tissues using multiparametric MR imaging including apparent diffusion coefficient maps and relaxometry,” Magn. Reson. Med. 43(1), 52–61 (2000). 10.1002/(ISSN)1522-2594 [DOI] [PubMed] [Google Scholar]
- 18.Parekh V. S., Jacobs J. R., Jacobs M. A., “Unsupervised nonlinear dimensionality reduction machine learning methods applied to multiparametric MRI in cerebral ischemia: preliminary results,” Proc. SPIE 9034, 90342O (2014). 10.1117/12.2044001 [DOI] [Google Scholar]
- 19.Menon B. K., et al. , “Role of imaging in current acute ischemic stroke workflow for endovascular therapy,” Stroke 46(6), 1453–1461 (2015). 10.1161/STROKEAHA.115.009160 [DOI] [PubMed] [Google Scholar]
- 20.Goyal M., Menon B. K., Derdeyn C. P., “Perfusion imaging in acute ischemic stroke: let us improve the science before changing clinical practice,” Radiology 266(1), 16–21 (2013). 10.1148/radiol.12112134 [DOI] [PubMed] [Google Scholar]
- 21.Lai V., “Application of diffusion-and perfusion-weighted imaging in acute ischemic stroke,” in Advanced Brain Neuroimaging Topics in Health and Disease-Methods and Applications, Papageorgiou T. D., Christopoulos G. I., Smirnakis S. M., Eds., IntechOpen, London: (2014). [Google Scholar]
- 22.Calamante F., “Arterial input function in perfusion MRI: a comprehensive review,” Prog. Nucl. Magn. Reson. Spectrosc. 74, 1–32 (2013). 10.1016/j.pnmrs.2013.04.002 [DOI] [PubMed] [Google Scholar]
- 23.Calamante F., et al. , “The physiological significance of the time-to-maximum (Tmax) parameter in perfusion MRI,” Stroke 41(6), 1169–1174 (2010). 10.1161/STROKEAHA.110.580670 [DOI] [PubMed] [Google Scholar]
- 24.Christensen S., et al. , “Comparison of 10 perfusion MRI parameters in 97 sub-6-hour stroke patients using voxel-based receiver operating characteristics analysis,” Stroke 40(6), 2055–2061 (2009). 10.1161/STROKEAHA.108.546069 [DOI] [PubMed] [Google Scholar]
- 25.LeCun Y. A., Bengio Y., Hinton G. E., “Deep learning,” Nature 521(7553), 436–444 (2015). 10.1038/nature14539 [DOI] [PubMed] [Google Scholar]
- 26.Russakovsky O., et al. , “ImageNet large scale visual recognition challenge,” Int. J. Comput. Vision 115(3), 211–252 (2015). 10.1007/s11263-015-0816-y [DOI] [Google Scholar]
- 27.Le Q. V., et al. , “Learning hierarchical invariant spatio-temporal features for action recognition with independent subspace analysis,” in Proc. IEEE Comput. Soc. Conf. Comput. Vision Pattern Recognit., pp. 3361–3368 (2011). 10.1109/CVPR.2011.5995496 [DOI] [Google Scholar]
- 28.Tran D., et al. , “Learning spatiotemporal features with 3d convolutional networks,” in Proc. IEEE Int. Conf. Comput. Vision, pp. 4489–4497 (2015). 10.1109/ICCV.2015.510 [DOI] [Google Scholar]
- 29.Karpathy A., Leung T., “Large-scale video classification with convolutional neural networks,” in Proc. 2014 IEEE Conf. Comput. Vision Pattern Recognit., pp. 1725–1732 (2014). 10.1109/CVPR.2014.223 [DOI] [Google Scholar]
- 30.Simonyan K., Zisserman A., “Two-stream convolutional networks for action recognition in videos,” in Adv. Neural Inf. Process. Syst., pp. 568–576 (2014). [Google Scholar]
- 31.Davy A., et al. , “Brain tumor segmentation with deep neural networks,” Med. Image Anal. 35, 1–17 (2017). 10.1016/j.media.2016.05.005 [DOI] [PubMed] [Google Scholar]
- 32.Ronneberger O., Fischer P., Brox T., “U-net: convolutional networks for biomedical image segmentation,” in Int. Conf. Med. Image Comput. Comput.-Assist. Interv., pp. 234–241 (2015). [Google Scholar]
- 33.Li J., et al. , “An EM-based semi-supervised deep learning approach for semantic segmentation of histopathological images from radical prostatectomies,” Comput. Med. Imaging Graphics 69, 125–133 (2018). 10.1016/j.compmedimag.2018.08.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Li W., et al. , “Path R-CNN for prostate cancer diagnosis and Gleason grading of histological images,” IEEE Trans. Med. Imaging 38(4), 945–954 (2019). 10.1109/TMI.2018.2875868 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ren S., et al. , “Faster R-CNN: towards real-time object detection with region proposal networks,” in Adv. Neural Inf. Process. Syst., pp. 91–99 (2015). [DOI] [PubMed] [Google Scholar]
- 36.Shin H. C., et al. , “Stacked autoencoders for unsupervised feature learning and multiple organ detection in a pilot study using 4D patient data,” IEEE Trans. Pattern Anal. Mach. Intell. 35(8), 1930–1943 (2013). 10.1109/TPAMI.2012.277 [DOI] [PubMed] [Google Scholar]
- 37.Roth H. R., et al. , “Detection of sclerotic spine metastases via random aggregation of deep convolutional neural network classifications,” in Recent Adv. Comput. Methods Clin. Appl. Spine Imaging, pp. 3–12 (2015). [Google Scholar]
- 38.Ertosun M. G., Rubin D. L., “Automated grading of gliomas using deep learning in digital pathology images: a modular approach with ensemble of convolutional neural networks,” in AMIA Annu. Symp. Proc. (2015). [PMC free article] [PubMed] [Google Scholar]
- 39.Cai D., He X., Han J., “Speed up kernel discriminant analysis,” VLDB J. 20(1), 21–33 (2011). 10.1007/s00778-010-0189-3 [DOI] [Google Scholar]
- 40.He K., et al. , “Delving deep into rectifiers: surpassing human-level performance on imagenet classification,” in Proc. IEEE Int. Conf. Comput. Vision, pp. 1026–1034 (2015). 10.1109/ICCV.2015.123 [DOI] [Google Scholar]
- 41.Ioffe S., Szegedy C., “Batch normalization: accelerating deep network training by reducing internal covariate shift,” in ICML'15 Proc. 32nd Int. Conf. Machine Learning, Vol. 37, pp. 448–456 (2015). [Google Scholar]
- 42.Sermanet P., et al. , “Pedestrian detection with unsupervised multi-stage feature learning,” in Proc. IEEE Comput. Soc. Conf. Comput. Vision Pattern Recognit., pp. 3626–3633 (2013). 10.1109/CVPR.2013.465 [DOI] [Google Scholar]
- 43.Chen X., Yuille A. L., “Articulated pose estimation by a graphical model with image dependent pairwise relations,” in Adv. Neural Inf. Process. Syst., pp. 1736–1744 (2014). [Google Scholar]
- 44.Tourdias T., et al. , “Final cerebral infarct volume is predictable by MR imaging at 1 week,” Am. J. Neuroradiol. 32(2), 352–358 (2011). 10.3174/ajnr.A2271 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.McAuliffe M. J., et al. , “Medical image processing, analysis and visualization in clinical research,” in Proc. 14th IEEE Symp. Comput.-Based Med. Syst. (CBMS 2001), pp. 381–386 (2001). 10.1109/CBMS.2001.941749 [DOI] [Google Scholar]
- 46.Fang R., Chen T., Sanelli P. C., “Towards robust deconvolution of low-dose perfusion CT: sparse perfusion deconvolution using online dictionary learning,” Med. Image Anal. 17(4), 417–428 (2013). 10.1016/j.media.2013.02.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Smith S. M., et al. , “Advances in functional and structural MR image analysis and implementation as FSL,” Neuroimage 23(1), S208–S219 (2004). 10.1016/j.neuroimage.2004.07.051 [DOI] [PubMed] [Google Scholar]
- 48.Doshi J., et al. , “Multi-Atlas skull-stripping,” Acad. Radiol. 20(12), 1566–1576 (2013). 10.1016/j.acra.2013.09.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Mouridsen K., et al. , “Automatic selection of arterial input function using cluster analysis,” Magn. Reson. Med. 55(3), 524–531 (2006). 10.1002/(ISSN)1522-2594 [DOI] [PubMed] [Google Scholar]
- 50.LeCun Y. A., et al. , “Efficient backprop,” in Neural Networks: Tricks of the Trade, Springer, Berlin, Heidelberg, pp. 9–48 (2012). [Google Scholar]
- 51.Nair V., Hinton G. E., “Rectified linear units improve restricted Boltzmann machines,” in Proc. 27th Int. Conf. Mach. Learn., vol. 3, pp. 807–814 (2010). [Google Scholar]
- 52.Krizhevsky A., Sutskever I., Hinton G. E., “ImageNet classification with deep convolutional neural networks,” in Adv. Neural Inf. Process. Syst., pp. 1–9 (2012). [Google Scholar]
- 53.Campbell B. C. V., et al. , “Cerebral blood flow is the optimal CT perfusion parameter for assessing infarct core,” Stroke 42(12), 3435–3440 (2011). 10.1161/STROKEAHA.111.618355 [DOI] [PubMed] [Google Scholar]
- 54.Srivastava N., et al. , “Dropout: a simple way to prevent neural networks from overfitting,” J. Mach. Learn. Res. 15, 1929–1958 (2014). [Google Scholar]
- 55.Collobert R., Kavukcuoglu K., Farabet C., “Torch7: a Matlab-like environment for machine learning,” in BigLearn, NIPS Work, pp. 1–6 (2011). [Google Scholar]
- 56.Fan R. E., et al. , “LIBLINEAR: a library for large linear classification,” J. Mach. Learn. Res. 9(Aug), 1871–1874 (2008). 10.1145/1390681.1442794 [DOI] [Google Scholar]
- 57.Fluss R., Faraggi D., Reiser B., “Estimation of the Youden Index and its associated cutoff point,” Biometrical J. 47(4), 458–472 (2005). 10.1002/(ISSN)1521-4036 [DOI] [PubMed] [Google Scholar]
- 58.Ho K. C., et al. , “Predicting discharge mortality after acute ischemic stroke using balanced data,” in AMIA Annu. Symp. Proc., vol. 2014, p. 1787 (2014). [PMC free article] [PubMed] [Google Scholar]
- 59.Manning C. D., Schütze H., Foundations of Statistical Natural Language Processing, vol. 999, MIT Press, Massachusetts, London: (1999). [Google Scholar]
- 60.Hanley J. A., McNeil B. J., “A method of comparing the areas under receiver operating characteristic curves derived from the same cases,” Radiology 148(3), 839–843 (1983). 10.1148/radiology.148.3.6878708 [DOI] [PubMed] [Google Scholar]
- 61.Gibbons J. D., Chakraborti S., Nonparametric Statistical Inference, Springer, Berlin, Heidelberg: (2011). [Google Scholar]
- 62.Furlan A. J., “Endovascular therapy for stroke—it’s about time,” N. Engl. J. Med. 372(24), 2347–2349 (2015). 10.1056/NEJMe1503217 [DOI] [PubMed] [Google Scholar]
- 63.Willats L., et al. , “The role of bolus delay and dispersion in predictor models for stroke,” Stroke 43(4), 1025–1031 (2012). 10.1161/STROKEAHA.111.635888 [DOI] [PubMed] [Google Scholar]
- 64.Mayerhoefer M. E., et al. , “Effects of MRI acquisition parameter variations and protocol heterogeneity on the results of texture analysis and pattern discrimination: an application-oriented study,” Med. Phys. 36(4), 1236–1243 (2009). 10.1118/1.3081408 [DOI] [PubMed] [Google Scholar]
- 65.Wei Q., Dunbrack R. L., “The role of balanced training and testing data sets for binary classifiers in bioinformatics,” PLoS One 8(7), e67863 (2013). 10.1371/journal.pone.0067863 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Weiss G. M., Provost F., “The effect of class distribution on classifier learning: an empirical study,” Technical Report ML-TR-43, Deptartment of Computer Science, Rutgers University, Piscataway, New Jersey: (2001). [Google Scholar]
- 67.Shin H.-C., et al. , “Deep convolutional neural networks for computer-aided detection: CNN architectures, dataset characteristics and transfer learning,” IEEE Trans. Med. Imaging 35(5), 1285–1298 (2016). 10.1109/TMI.2016.2528162 [DOI] [PMC free article] [PubMed] [Google Scholar]