Mechanically Coupled Reaction-Diffusion Model to Predict Glioma Growth: Methodological Details

Abstract

Biophysical models designed to predict the growth and response of tumors to treatment have the potential to become a valuable tool for clinicians in care of cancer patients. Specifically, individualized tumor forecasts could be used to predict response or resistance early in the course of treatment, thereby providing an opportunity for treatment selection or adaption. This chapter discusses an experimental and modeling framework in which noninvasive imaging data is used to initialize and parameterize a subject-specific model of tumor growth. This modeling approach is applied to an analysis of murine models of glioma growth.

1. Introduction

Biophysical models of tumor growth and treatment response have the potential to fundamentally change the clinical care for cancer patients by providing clinicians with accurate and precise patient-specific predictive models. Through the use of noninvasive imaging data, these biophysical models can be parameterized by the unique characteristics of an individual’s tumor to provide a “forecast” of future tumor growth and treatment response [1]. We [2–6] and others [7–11] have begun investigating the development of patient-specific mathematical models of cancer. In this work, we provide a detailed guide to the implementation of a mechanically coupled reaction-diffusion model [4, 6, 12] applied to glioma growth in rats.

The standard reaction-diffusion equation, Eq. 1, is commonly used to model glioma growth [5, 7] and describes the spatial-temporal evolution of tumor cell number due to the random movement of tumor cells (diffusion, first term on the right-hand side) and the proliferation of cells (reaction, second term on the right-hand side):

$$\frac{\partial N(x,y,z,t)}{\partial t}=\nabla \cdot (D(x,y,z)\nabla N(x,y,z,t))+k(x,y,z)N(x,y,z,t)\left(1-\frac{N(x,y,z,t)}{\theta }\right),$$ (1)

where N(x, y, z, t) is the number of tumor cells at the three­dimensional position (x, y, z) and time t, D(x, y, z) is the tumor cell diffusion coefficient, k(x, y, z) is the net tumor cell proliferation, and θ is the tumor cell carrying capacity. One important limitation of the standard reaction-diffusion equation is that tumor growth is only restricted by the boundaries of the simulation domain (i.e., the skull for gliomas). In reality, as the tumor expands it interacts with the healthy brain tissue causing increased mechanical stress and the displacement of surrounding tissue, a phenomena termed the “mass effect” [13] and observed in several types of brain tumors [14]. The increased stress experienced by the tumor can impede further growth as demonstrated in the seminal work by Helmlinger et al. [15]. In Helmlinger et al.’s [15] contribution multi-cellular spheroids were grown in agar gel concentrations ranging from 0% to 1%. Increasing the agar concentration resulted in inhibited expansion of the spheroid as the substrate stiffness increased. More specifically, similar spheroid interactions with the surrounding environment would require increased force at elevated levels of stiffness. This phenomenon can also result in the preferential growth of tumors in areas of increasing mechanical compliance. To incorporate this effect, we first describe the mechanical equilibrium, Eq. 2:

$$\nabla \cdot \sigma -{\lambda }_{\text{f}}\cdot \nabla N=0,$$ (2)

where σ is the stress tensor and λ_f is tumor cell-force coupling constant. For implementation, Eq. 2 is rewritten in terms of the tissue displacement $(\stackrel{\rightharpoonup }{u})$ under a linear elastic isotropic material assumption in Eq. 3:

$$\nabla \cdot G\nabla \stackrel{\rightharpoonup }{u}+\nabla \frac{G}{1-2\nu }\cdot (\nabla \cdot \stackrel{\rightharpoonup }{u})-{\lambda }_{\text{f}}\nabla N=0,$$ (3)

where G is the shear modulus (a material property that represents the constant of proportionality between shear stress to shear strain) and ν is Poisson’s ratio (a material property that is a ratio relating lateral to longitudinal strain). The first two terms on the left-hand side in Eq. 3 represent the linear-elastic description of tissue displacement, while the third term represents a local body force generated by the invading tumor. $(\stackrel{\rightharpoonup }{u})$ is then used to calculate the local normal (ε_xx, ε_yy, ε_zz) and shear strains (ε_xy, ε_xz, ε_yz). For small deformations, strain ε_i,j is defined as the total deformation in the direction i divided by the original length in direction j and is calculated using Eq. 4:

$$\left[\begin{array}{c}{\epsilon }_{xx}\\ {\epsilon }_{yy}\\ {\epsilon }_{zz}\\ {\epsilon }_{xy}\\ {\epsilon }_{xz}\\ {\epsilon }_{yz}\end{array}\right]=\left[\begin{array}{c}\partial u/\partial x\\ \partial v/\partial y\\ \partial w/\partial z\\ \partial u/\partial y\\ \partial u/\partial z\\ \partial v/\partial z\end{array}\right]\text{'}$$ (4)

where u, v, and w represent the deformation in the x-, y-, and z-directions, respectively. The normal and shear strains are then used to calculate the normal and shear stresses using Hooke’s law, Eq. 5:

$$\left[\begin{array}{l}{\sigma }_{xx}\hfill \\ {\sigma }_{yy}\hfill \\ {\sigma }_{zz}\hfill \\ {\sigma }_{xy}\hfill \\ {\sigma }_{xz}\hfill \\ {\sigma }_{yz}\hfill \end{array}\right]=\frac{2G}{1-2\nu }\left[\begin{array}{cccccc}1-\nu & \nu & \nu & 0& 0& 0\\ \nu & 1-\nu & \nu & 0& 0& 0\\ \nu & \nu & 1-\nu & 0& 0& 0\\ 0& 0& 0& (1-2\nu )& 0& 0\\ 0& 0& 0& 0& (1-2\nu )& 0\\ 0& 0& 0& 0& 0& (1-2\nu )\end{array}\right]\left[\begin{array}{c}{\epsilon }_{xx}\\ {\epsilon }_{yy}\\ {\epsilon }_{zz}\\ {\epsilon }_{xy}\\ {\epsilon }_{xz}\\ {\epsilon }_{yz}\end{array}\right].$$ (5)

The normal and shear stresses for a given voxel are then incorporated into a single term called the Von Mises stress, σ_vm(x, y, z, t), in Eq. 6:

$${\sigma }_{\text{vm}}(x,y,z,t)={\left[\frac{1}{2}\left(\begin{array}{c}{\left({\sigma }_{xx}(x,y,z,t)-{\sigma }_{yy}(x,y,z,t)\right)}^2+{\left({\sigma }_{xx}(x,y,z,t)-{\sigma }_{zz}(x,y,z,t)\right)}^2\\ +{\left({\sigma }_{zz}(x,y,z,t)-{\sigma }_{yy}(x,y,z,t)\right)}^2\\ +6\left({\sigma }_{xy}{(x,y,z,t)}^2+{\sigma }_{xz}{(x,y,z,t)}^2+{\sigma }_{yz}{(x,y,z,t)}^2\right)\end{array}\right)\right]}^{1/2}.$$ (6)

The Von Mises stress is a term that reflects the total experienced stress for a given section of tissue, and is often used within failure criterion strategies in materials. We use the Von Mises stress to reflect the interaction between the growing tumor and its environment, that is, in our approach we use the Von Mises stress to spatially and temporally restrict tumor cell diffusion [4, 6, 12] using Eq. 7:

$$D(x,y,z,t)=D_0{\text{e}}^{-{\lambda }_{\text{D}}\cdot {\sigma }_{\text{vm}}(x,y,z,t)},$$ (7)

where D₀ represents the diffusion coefficient of tumor cells in the absence of mechanical restrictions and λ_D is a stress-tumor cell diffusion coupling constant.

In this chapter, we will discuss how to implement this model system using the finite difference method as well as how to individualize this model using an individual patient’s imaging data. Noninvasive imaging measurements from diffusion-weighted magnetic resonance imaging (DW-MRI [16]) and contrast enhanced MRI (CE-MRI, [17]) are used to estimate the spatial distribution of tumor cell number in a murine model of glioma at several experimental time points. The in vivo estimated cell number then provides the initial tumor cell distribution and is also used to solve an inverse problem to return estimates of the model parameters. The estimated model parameters can then be used to simulate future tumor growth.

2. Materials

2.1. Dataset

The numerical methods presented in this chapter use an in vivo dataset acquired in rats with intracranially inoculated glioma cells [5, 18, 19]. Alternatively, an in silico dataset can also be used [5]. For both approaches the dataset should contain:

1. Three-dimensional estimates of the distribution of tumor cells at several time points.

2. Three-dimensional map of k (or initial guess).

3. Single value for D₀ (or initial guess).

4. Values for G, ν, λ_D, λ_f, and θ (based on literature, calculation, or assignment, see Note 1).

For use in Matlab this dataset should be saved as a “.mat” file consisting of a 4D array of tissue cellularity, a 3D array of k values, and one-element arrays of D₀, G, ν, λ_D, λ_f, and θ all with double precision.

2.2. Software/Hardware Requirements

The forward evaluation and parameter optimization of the mechanically coupled model was ran on a Dell PowerEdge R820 server consisting of four Intel Xenon E5–4610 2.3 GHz processors with a total of 256 GB of memory using Matlab 2015b. The forward evaluation is relatively less computationally intensive and takes less than 16 s for a 10 day simulation on a laptop with 8 GB of memory and an Intel i5–2550 M 2.5 GHz processor. The parameter optimization computation time, however, depends on both the number of parameters being estimated and the number of iterations of the optimization algorithm until stopping criteria are met. Parallelization of the parameter perturbation code can reduce computation time by a factor approximately equal to the number of parallel threads. (For example parameter perturbation for 100 parameters takes 13.1 min with 1 thread, 3.1 min with 4 threads, 1.7 min with 8 threads, 0.9 min with 16 threads, and 0.7 min with 32 threads.)

3. Methods

3.1. Animal Experiments

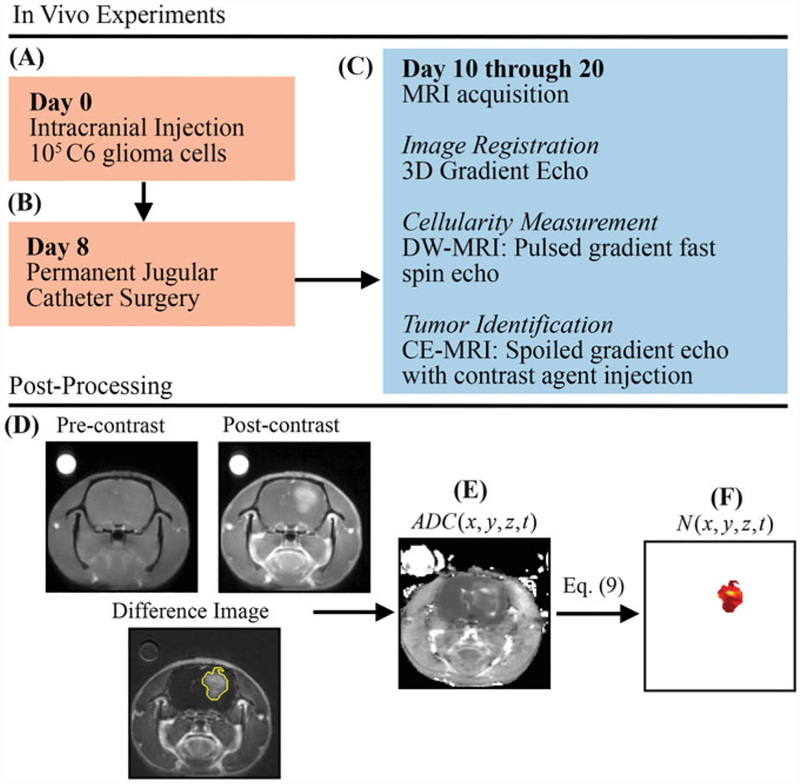
While details are presented in [5], we here discuss the salient features of the experimental procedure (see Fig. 1). The in vivo dataset described in this section was acquired in female Wistar rats inoculated intracranially with C6 Glioma cells (1 × 10⁵) via stereo­taxic injection on day 0 (Fig. 1a). On day 8, permanent jugular catheters were placed in each rat (Fig. 1b). Beginning on day 10, rats are imaged (Fig. 1c), with a 3D gradient echo, DW-MRI and CE-MRI (see Note 2 for remarks on the experiment timeline and measurement frequency). The 3D gradient echo data was collected with a larger field of view (45 mm × 45 mm × 45 mm) and larger sampling matrix (256 × 256 × 128) for image registration purposes. The DW-MRI and CE-MRI data was acquired with a 32 mm × 32 mm × 16 mm field of view and a 128 × 128 × 16 sampling matrix. During the CE-MRI acquisition, a 200 μL bolus (0.05 mmol/kg) of gadolinium-diethylenetriamine pentaacetic acid, an MRI contrast agent, is injected to identify tumor regions (Fig. 1d). Areas of signal enhancement in the post-contrast CE-MRI data were used to identify tumor regions of interest (ROI). Tumor cellularity (N(x, y, z, t)) was estimated from DW-MRI. Briefly, DW-MRI is an imaging method that is sensitive to the diffusion of water within tissue, and several groups have observed an inverse relationship between the apparent diffusion coefficient (ADC) and cellularity [20–24]. The ADC is estimated voxel-wise from DW-MRI (Fig. 1e) data acquired at several b-values by fitting Eq. 8 to the acquired signal at each b-value:

$$S(x,y,z,b)=S_0(x,y,z)\cdot {\text{e}}^{-b\cdot \text{ADC}(x,y,z)},$$ (8)

where S(x, y, z, b) is the acquired signal at three-dimensional position (x, y, z) and b-value b, S₀(x, y, z) is the intrinsic signal, and ADC (x, y, z) is the apparent diffusion coefficient. The tumor ROI identified from CE-MRI is then applied as a mask to ADC(x, y, z) (Fig. 1f), to estimate cellularity only within the tumor using Eq. 9:

$$N(x,y,z)=\theta \left(\frac{{\text{ADC}}_{\text{w}}-\text{ADC}(x,y,z)}{{\text{ADC}}_{\text{w}}-{\text{ADC}}_{\text{min}}}\right),$$ (9)

where θ is the maximum tumor cell carrying capacity, ADC_w is the ADC of waterat37 °C(2.5 × 10⁻³ mm²/s) [25],ADC(x, y, z)is the ADC value at position (x, y, z), and ADC_min is the minimum ADC value which corresponds to the voxel with the largest number of cells [2]. θ can be calculated using the imaging voxel dimensions (0.25 mm × 0.25 mm × 1.00 mm), and assuming spherical tumor cells with a packing density of 0.7405 [26] and an average cell volume of 908 μm3 [27] (see Note 3 for further remarks on packing density and cell volume).

Fig.1.

Experimental timeline and estimation of in vivo cell number from DW-MRI data. (a) On day 0, rats are injected intracranially with 10⁵ C6 glioma cells. (b) Jugular catheters are then inserted on day 8. (c) On days 10 through 20, rats are imaged with MRI with 3D gradient echo, DW-MRI, and CE-MRI. (d) CE-MRI is used to identify tumor tissue by subtracting pre-contrast image from the post-contrast image. (e) ADG(x, y, z, t) is then estimated from DW-MRI data. Finally, N(x, y, z, t) is estimated (f) within the tumor tissue using Eq. 9 and ADC(x, y, z, t)

A voxel-wise k and a global D₀ are estimated from serial measurements of N(x, y, z, t) in a parameter optimization procedure [5]. G is assigned from literature values to anatomical regions identified in imaging data (e.g., cortex, corpus callosum, hippo­campus, thalamus, putamen) [28, 29], while ν is set to 0.45 (as we assume that tissue is nearly incompressible). λ_D can be assigned or a range of values can be evaluated to apply different degrees of mechanical coupling, while λ_f is set to 1.

3.2. Modeling

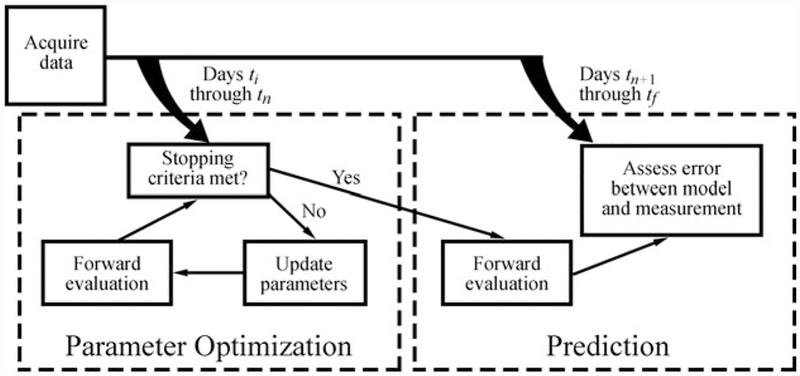
We now discuss the details of the finite difference simulation for Eqs. 1 and 2, the forward evaluation of the model system, and the parameter optimization and the tumor growth prediction approach. Figure 2 shows an overview of the data collection, parameter optimization, and prediction approach. Briefly, data is acquired from t_i to t_f. A subset of the total data (days t_i to t_n, where t_n is less than t_f) are first used to determine the optimal model parameters. Once the stopping criteria are met for the parameter optimization approach, the optimized model parameters are then used in a forward evaluation of the model to simulate future tumor growth. The measured data is then compared to the model predicted growth on days t_n+₁ to t_f. With respect to the clinical context, t_n would represent the time point at which early-course of therapy data could be collected, and calibrated to the patient. Once complete, assessments on efficacy of therapy would be forecasted in silico for future time point t_f and perhaps lead to changes to therapy regimen or alternate therapies.

Fig. 2.

Tumor growth modeling and prediction flow chart. DW-MRI and CE-MRI data is first acquired in rats at days t_i to t_f. A subset of the total data (t_i to t_n is used to first estimate model parameters using an iterative optimization algorithm. The optimized model parameters are then used in a forward evaluation of the model system to predict tumor growth at the remaining data points (t_{n + 1} to t_f). The error is then assessed between the model and measured values of N(x, y, z, t)

3.2.1. Finite Difference Simulation Setup

As an illustrative example for clarity, we show the derivation of the finite difference model for a 1D implementation, followed by extending the model to the full 3D implementation. A Taylor series expansion is used to derive the finite difference approximation of the tumor cell model (Eq. 1) as shown for the 1D implementation in Eq. 10:

$$\frac{N\left(x,t+h_{\text{t}}\right)-N(x,t)}{h_{\text{t}}}=\left(\frac{\delta N(x,t)}{2h_x}\cdot \frac{\delta D(x)}{2h_x}\right)+D(x)\cdot \left(\frac{{\delta }^{2}N(x,t)}{h_x^2}\right)+k(x)\cdot N(x,t)\cdot \left(1-\frac{N(x,t)}{\theta }\right),$$ (10)

where h_t is the time step, and h_x is the grid spacing in the x-direction, and δ represents the central difference operator, defined below in Eqs. 11 and 12. Finite difference approximations are derived using a full grid approach to take advantage of the natural, voxelized gridding from the experimental imaging data measurements. The central difference approximation of the first derivative in (for example) the x-direction is shown in Eq. 11:

$$\frac{\partial N(x,t)}{\partial x}\approx \frac{\delta N(x,t)}{2h_x}=\frac{N\left(x+h_x,t\right)-N\left(x-h_x,t\right)}{2h_x}.$$ (11)

Similarly, the central difference approximation of the second derivative in (for example) the x-direction is shown in Eq. 12:

$$\frac{{\partial }^{2}N(x,t)}{\partial x^2}\approx \frac{{\delta }^{2}N(x,t)}{h_x^2}=\frac{N\left(x+h_x,t\right)-2\cdot N(x,t)+N\left(x-h_x,t\right)}{h_x^2}.$$ (12)

In the case of a mesh boundary, where the node at either (x + 1) or (x −−1) does not exist, the zero flux boundary condition (∂N/∂x = 0) can be used to relate N(x + h_x, t) to N(x − h_x, t) (or vice versa) as shown in Eq. 13:

$$\frac{N\left(x+h_x,t\right)-N\left(x-h_x,t\right)}{2h_x}=0\Rightarrow N\left(x+h_x,t\right)=N\left(x-h_x,t\right).$$ (13)

The 3D implementation of Eq. 1 is shown below in Eq. 14:

$$\frac{N\left(x,y,z,t+h_t\right)-N(x,y,z,t)}{h_{\text{t}}}=\left(\frac{\delta N(x,y,z,t)}{2h_x}\cdot \frac{\delta D(x,y,z)}{2h_x}\right)+D(x,y,z)\cdot \left(\frac{{\delta }^{2}N(x,y,z,t)}{h_x^2}\right)+\left(\frac{\delta N(x,y,z,t)}{2h_y}\cdot \frac{\delta D(x,y,z)}{2h_y}\right)+D(x,y,z)\cdot \left(\frac{{\delta }^{2}N(x,y,z,t)}{h_y^2}\right)+\left(\frac{\delta N(x,y,z,t)}{2h_z}\cdot \frac{\delta D(x,y,z)}{2h_z}\right)+D(x,y,z)\cdot \left(\frac{{\delta }^{2}N(x,y,z,t)}{h_z^2}\right)+k(x,y,z)\cdot N(x,y,z,t)\cdot \left(1-\frac{N(x,y,z,t)}{\theta }\right).$$ (14)

The derivation of the finite difference approximation of Eq. 2 is shown for the 1D implementation in Eqs. 15–17. Equation 2 is first rewritten in terms of the 1D stress in the x-direction (σ_x) in Eq. 15:

$$\nabla \cdot {\sigma }_x(x)-{\lambda }_{\text{f}}\nabla N(x,t)=0.$$ (15)

σ_x is then replaced with Hooke’s law for a linear elastic isotropic material (σ_x = E ε_x) in Eq. 16:

$$\nabla \cdot \left(E{\epsilon }_x(x)\right)={\lambda }_{\text{f}}\nabla N(x,t),$$ (16)

where E is Young’s Modulus, and ε_x is equal to ∂u/∂x. The divergence is then evaluated and the finite difference approximations are applied in Eq. 17:

$$\left(\frac{\delta E(x)}{2h_x}\frac{\delta u(x)}{2h_x}+E(x)\frac{{\delta }^{2}u(x)}{h_x^2}\right)={\lambda }_{\text{f}}\frac{\delta N(x,t)}{2h_x}.$$ (17)

A similar approach as shown in Eqs. 15–17 can be followed to obtain the full 3D implementation of Eq. 2. Equations 18–20 show the finite difference approximation for the 3D implementation of Eq. 2. Equation 18 shows the x-direction component of Eq. 2:

$$\left(\frac{2(1-v)}{1-2v}\right)\left(\frac{\delta G}{2h_x}\frac{\delta u}{2h_x}+G\frac{{\delta }^{2}u}{h_x^2}\right)+\left(\frac{2v}{1-2v}\right)\left(\frac{\delta G}{2h_x}\frac{\delta v}{2h_y}+G\frac{\delta }{2h_x}\left(\frac{\delta v}{2h_y}\right)\right)+\left(\frac{2v}{1-2v}\right)\left(\frac{\delta G}{2h_x}\frac{\delta w}{2h_z}+G\frac{\delta }{2h_x}\left(\frac{\delta w}{2h_z}\right)\right)+2\left(\frac{\delta G}{2h_x}\frac{\delta u}{2h_y}+G\frac{\delta }{2h_x}\left(\frac{\delta u}{2h_y}\right)\right)+2\left(\frac{\delta G}{2h_x}\frac{\delta u}{2h_z}+G\frac{\delta }{2h_x}\left(\frac{\delta u}{2h_z}\right)\right)={\lambda }_f\left(\frac{\delta N}{2h_x}\right),$$ (18)

where u, v, and w represent tissue displacement in the x-, y-, and z-directions, respectively. Eq. 19 shows the y-direction component of Eq. 2:

$$\left(\frac{2(1-v)}{1-2v}\right)\left(\frac{\delta G}{2h_y}\frac{\delta v}{2h_y}+G\frac{{\delta }^{2}v}{h_y^2}\right)+\left(\frac{2v}{1-2v}\right)\left(\frac{\delta G}{2h_y}\frac{\delta u}{2h_x}+G\frac{\delta }{2h_y}\left(\frac{\delta u}{2h_x}\right)\right)+\left(\frac{2v}{1-2v}\right)\left(\frac{\delta G}{2h_y}\frac{\delta w}{2h_z}+G\frac{\delta }{2h_y}\left(\frac{\delta w}{2h_z}\right)\right)+2\left(\frac{\delta G}{2h_y}\frac{\delta v}{2h_x}+G\frac{\delta }{2h_y}\left(\frac{\delta v}{2h_x}\right)\right)+2\left(\frac{\delta G}{2h_y}\frac{\delta v}{2h_z}+G\frac{\delta }{2h_y}\left(\frac{\delta v}{2h_z}\right)\right)={\lambda }_f\left(\frac{\delta N}{2h_y}\right).$$ (19)

Equation 20 shows the z-direction component of Eq. 2:

$$\left(\frac{2(1-v)}{1-2v}\right)\left(\frac{\delta G}{2h_z}\frac{\delta w}{2h_z}+G\frac{{\delta }^{2}w}{h_z^2}\right)+\left(\frac{2v}{1-2v}\right)\left(\frac{\delta G}{2h_z}\frac{\delta u}{2h_x}+G\frac{\delta }{2h_z}\left(\frac{\delta u}{2h_x}\right)\right)+\left(\frac{2v}{1-2v}\right)\left(\frac{\delta G}{2h_z}\frac{\delta v}{2h_y}+G\frac{\delta }{2h_z}\left(\frac{\delta v}{2h_y}\right)\right)+2\left(\frac{\delta G}{2h_z}\frac{\delta w}{2h_x}+G\frac{\delta }{2h_z}\left(\frac{\delta w}{2h_x}\right)\right)+2\left(\frac{\delta G}{2h_z}\frac{\delta w}{2h_y}+G\frac{\delta }{2h_z}\left(\frac{\delta w}{2h_y}\right)\right)={\lambda }_f\left(\frac{\delta N}{2h_z}\right).$$ (20)

The unknown tissue displacements u, v, and w are solved by rewriting Eqs. 18–20 into a matrix system shown in Eq. 21:

$$[M]\left\{U\right\}={\lambda }_{\text{f}}\{\nabla N\},$$ (21)

where [M] is a square 3n × 3n matrix of the finite difference coefficients, {U} is equal to {u₁, ⋯·u_n, v₁, ⋯·v_n, w₁, ⋯w_n}^T, where u_i, v_i, and w_i represent the displacement at the ith node in the x-, y-, and z-direction, respectively. {∇N} is equal to {∂N₁/∂x, ⋯·∂N_n/∂x, ∂N₁/∂y, ⋯ ∂N_n/∂y, ∂N₁/∂z, ⋯·∂N_n/∂z}^T, where ∂N_i/∂x, ∂N_i/∂y, and ∂N_i/∂z represent the gradient at the ith node in the x-, y-, and z-direction, respectively. Rows 1 through n of [M]represent coefficients for Eq. 18, rows n + 1 through 2n of [M]represent the coefficients for Eq. 19, and 2n + 1 through 3n of [M]represent the coefficients for Eq. 20. Rows 1 through n of {U} and {∇N} represent the x-direction components (u and ∂N/∂x, respectively), rows n + 1 through 2n of {U} and {∇N} represent the y-direction components (v and ∂N/∂y, respectively), and rows 2n + 1 through 3n of {U} and {∇N} represent the z-direction components (w and ∂N/∂z, respectively). [M] is built only once and can be factorized into lower and upper triangular matrices (refer to Note 4 for further details on the construction and solving of Eq. 21). Equations 1 and 2 are solved using a three dimension in space (grid spacing: 250 × 250 × 1000 μm), fully explicit in time (for Eq. 1, time step = 0.01 days) finite difference simulation. (Refer to Note 5 for details on selecting an appropriate time step.) Equation 1 has no diffusive flux at the brain tissue boundaries (Neumann boundary condition [30]). Equation 2 has no tissue displacement in the Cartesian direction of the boundary (Dirichlet boundary condition), while displacement in the other Cartesian directions is unknown (slip condition [31]).

3.2.2. Forward Evaluation

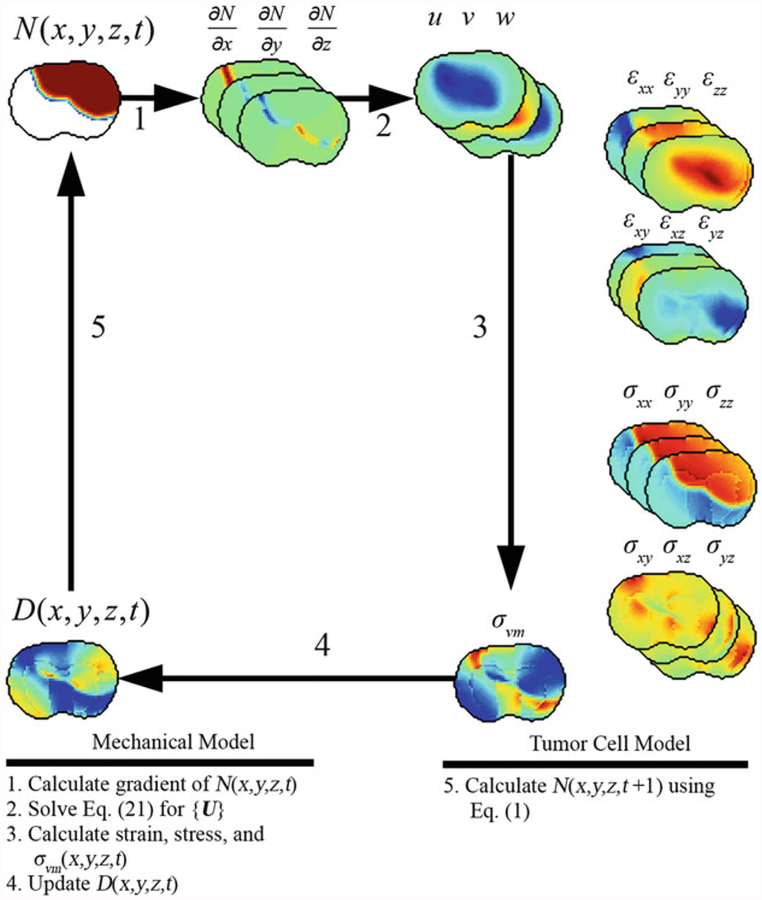
A summary and example of the forward evaluation algorithm is presented in Fig. 3. The forward evaluation begins with solving the mechanical model (steps 1 through 4 in Fig. 3). At the beginning of each iteration, the gradient of the current distribution of tumor cells, ∇N(x, y, z, t), is calculated and is assigned to {∇N} (step 1 in Fig. 3). {U} is then solved for in Eq. 21 (step 2 in Fig. 3). The strains (Eq. 4) and stresses (Eqs. 5 and 6) are calculated (step 3 in Fig. 3). σ_vm(x, y, z, t) is then used to update D(x, y, z, t) (Eq. 7, step 4 in Fig. 3). Finally, D(x, y, z, t) is used in the evaluation of Eq. 1 to determine N(x, y, z, t + 1) (step 5 in Fig. 3). The forward evaluation of the model system is then repeated at each simulation time step.

Fig. 3.

Algorithm and example forward evaluation of mechanical and tumor cell model. The mechanical model is first solved to calculate the tissue displacement vector {U} due to N(x, y, z, t), Eq. 21. {U} is then used to calculate strain, stress, and σ(x, y, z, t). The new value of D(x, y, z, t)is calculated using Eq. 2 and σ_vm(x, y, z, t). Finally, D(x, y, z, t) is used in Eq. 6 to calculate the value of N(x, y, z, t + 1)

3.3. Parameter Optimization and Tumor Growth Prediction

The optimal model parameters are determined using an iterative Levenberg-Marquardt [32, 33] weighted least squares optimization:

$$\left[J^{T}WJ+\alpha \cdot D_{J^{T}WJ}\right]\cdot \left\{\mathrm{\Delta }\beta \right\}=J^{T}W\left\{N_{\text{meas}}-N_{\text{model}}(\beta )\right\},$$ (22)

where J is the Jacobian matrix, W is a diagonal weighting matrix, α is a damping parameter, $D_{J^{T}WJ}$ is a diagonal matrix consisting of the diagonal elements of J^TWJ, {Δβ}is as vector of updates to model parameters, {N_meas} is a vector of the measured cell number, and {N_model(β)} is a vector of the model described cell number using the current best set of parameters β. J is a (n (number of voxels) × nt (number of time points)) by p (the number of model parameters) matrix, W is a (n × nt) × (n × nt) matrix, has p components, and {N_meas} has (n × nt) components. J can be estimated using numerical differentiation (refer to Note 6 for further comments on J). For example, the J element at row i and column j, Eq. 23, represents the partial derivative of the model cell number at node i with respect to the jth model parameter and is calculated by individually perturbing model parameters as described below:

$$J_{i,j}=\frac{\partial N_i}{\partial {\beta }_j}=\frac{N_{\text{ model }}\left(i,{\beta }_{\text{ alt }}\right)-N_{\text{ model }}(i,\beta )}{{\beta }_{\text{ alt },j}-{\beta }_j},$$ (23)

where N_model(i, β_alt) is the model cell number at the ith index of {N_model} using parameters β_alt, N_model(i, β) is the model cell number at the ith index of {N_model} using parameters β. β_alt is equal to β at all indices except for the jth index which is perturbed by a factor f (i.e., β_alt,j = f × β_j).(Note f should be a number close to but not equal to 1. Inthiswork, weassign f = 1.001.) W is as quare matrix with n × nt rows and columns. W weights the elements of J by the reciprocal of the total number of cells at each time point. This weighting is included to balance the influence of later time points to the earlier time points (which often have much fewer nonzero voxel measurements compared to the later time points). For nt = 2, W_i,i is calculated using Eq. 24:

$$W_{i,i}=\{\begin{array}{cc}i\le n& {\left(\sum _{j=1}^{j=n}\left(N_{\text{ meas }}(j,t=1)\right)\right)}^{-1}\\ i>n\text{ and }i\le 2n& {\left(\sum _{j=1}^{j=n}\left(N_{\text{ meas }}(j,t=2)\right)\right)}^{-1}\end{array}.$$ (24)

Figure 4 summarizes the parameter optimization approach used to estimate model parameters k(x, y, z) and D₀. The model is initially evaluated with a guess of the model parameters (step 1 in Fig. 4). A guess of β is used to evaluate the objective function described in Eq. 25 (step 2 in Fig. 4):

$$\text{Error}=\sum _{t=t_1}^{t_n}\left({\left(\sum _{i=1}^{i=n}\left(N_{\text{ meas }}(i,t)\right)\right)}^{-1}\cdot \left(\sum _{i=1}^{i=n}{\left(N_{\text{ model }}(i,t,\beta )-N_{\text{ meas }}(i,t)\right)}^2\right)\right).$$ (25)

Fig. 4.

Iterative parameter optimization approach. A schematic is shown above for the iterative parameter optimization algorithm using the Levenberg-Marquardt method [32, 33]. The model is first evaluated with an initial guess of model parameters, line 1. The objective function is then evaluated with the current set of model parameters, line 2. The optimal model parameters are then determined in an iterative “while-loop” which ceases when stopping criteria are met. At the beginning of each iteration, the Jacobian is built, line 3, and is used to solve for the new guess of model parameters, line 4. The model is then re-evaluated with the new model parameters, line 5, and the objective function is calculated, line 6. Finally, the error is compared to the previously observed lowest error to determine if the new parameter values are acceptable. The optimization ceases when the stopping criteria are met

The initial evaluation of Eq. 25 sets the current minimum error or Error(β). J, W, and $D_{J^{T}WJ}$ are then built (step 3 in Fig. 4). The parameter update vector {Δβ} is then calculated using Eq. 22 and then added to {β} for the current guess of model parameters {β_test} (step 4 in Fig. 4). The forward evaluation of the model is performed using model parameters {β_test} (step 5 in Fig. 4). Equation 25 is then re-calculated using {β_test} (step 6 in Fig. 4). The error evaluated using {β_test} or Error(β_test) is compared to Error(β). If Error(β_test) is less than Error(β), {β_test} is accepted (i.e., {β} = {β_test}) and α decreased by a factor of 12. If Error(β_test) is greater than Error(β), {β_test} is rejected and α increased by a factor of 3. (Note, the factors that α is increased or decreased by (3 and 12 in this work) are often problem-specific and need to be empirically determined to improve convergence.) At this point, the stopping criteria are also evaluated. The stopping criterion can be a maximum number of iterations, a minimal threshold of error, or a minimal relative change in model error between successful iterations, or a minimal relative change in model [34] between successful iterations. In general, error will never reach zero for this type of system so selecting a stopping criteria that is sensitive to the relative change in error or parameter values will indicate convergence. The parameter optimization process continues by returning to step 3 until the stopping criteria are met.

At the conclusion of the parameter optimization process, the optimized model parameters are used in a final forward evaluation of the model from t_i to t_f. The error between N_model(x, y, z, t) and N_meas(x, y, z, t)is assessed at the time points not used in the parameter optimization t_n + ₁ to t_f.

3.4. Summary and Outlook

In this chapter, a modeling and experimental framework was described which can be used to individualize a predictive biophysical model from an individual patient’s imaging data. Clinically available imaging measurements from CE-MRI and DW-MRI were used to provide serial estimates of tumor cell number that were then used in an inverse problem to optimize model parameters for the measured tumor. These individually optimized model parameters could then be used to predict future growth or response. For example, acquiring data early in the course of a patient’s therapy could be used to calibrate a patient-specific model that could then be used to predict the efficacy of the current treatment weeks or months before response is identifiable through standard criteria (e.g., the Response Evaluation Criteria in Solid Tumors [34]). For predicted non-responders, the calibrated model could potentially be used to evaluate other treatment regimens to adapt clinical care to improve the outcome on an individual patient basis. While this is a promising avenue for the future of clinical cancer care, further development of predictive biophysical models is needed to characterize patient response to a variety of available patient treatments [35].

4. Notes

1. When collecting a new dataset or evaluating this model in a different disease setting, model parameters should be measured or estimated on an individual basis. When this is not the case, however, model parameters should be assigned (or calculated) from literature values (e.g., G, ν, θ) obtained from experiments that most closely match the tumor or tumor location that is currently under investigation. For model parameters that cannot be measured experimentally or assigned from literature (e.g., λ_D, λ_f) can be assigned empirically based on results observed in a cohort. Sensitivity analysis (e.g., [36]) of the model system can also be used to help determine which model parameters require assignment on an individual basis and which model parameters may be assigned for the cohort.

2. The experimental time line may change depending on the particular cancer under investigation, its growth rate, and the initial size of the tumor. We selected day 10 to start our imaging experiments, as the tumors are approximately 20–40 mm³ and typically extend over multiple imaging slices.

3. To calculate the physical carrying capacity (i.e., the maximum number of cells a space can contain) assumptions will need to be made about the overall tissue structure and cellular shape which can be verified through histological observations of the tissue. For the C6 line, we assumed that the tumor cell tissue was predominately composed of spherical tumor cells with a packing density and an average cell volume obtained from the literature [26, 27]. When comparing between the DW-MRI estimate of cellularity and the model predicted cellularity the precise values for packing density and average cell volume are not critical as long as the same carrying capacity is used in both the model and the ADC to cellularity calculation. However, when comparing to histological data, more care is required to match the average size, shape, and packing density of the tumor cells to what is observed in vivo. Packing density can be calculated from Hematoxylin and Eosin (H&E) stained tissue sections by calculating the fraction of the H&E stained area over the total tumor ROI. The average cell area can then be calculated as the total occupied area (packing density multiplied by total ROI area) divided by the number of positive stained Hematoxylin cells. The average cell area can then be used to calculate an average cell radius and volume. In H&E stained sections obtained in one rat we calculated an average packing density of 0.764 ± 0.054% (mean ± 95% confidence interval) and an average volume of 982 ± 247 μm³.

4. The coefficient matrix [M]is a sparse and potentially very large (3n × 3n) matrix. To conserve memory and accelerate computational time, [M] can be represented by a sparse matrix [M_compact] which is an nz × 3 matrix, where nz is the number of nonzero elements of [M], and the three columns represent the matrix nonzero entry, the entry’s matrix row, and entry’s matrix column entry, respectively. While many sparse matrix data formats exist, in this realization we used the format native to MATLAB. With respect to solution methods associated with sparse matrices, standardly some form of iterative approach would be adopted with an accompanying matrix precondition method to increase speed of calculation. In this realization, we employed one of the available MATLAB methods, namely, the bi-conjugate gradient stabilized method with an incomplete LU factorization as a preconditioner.

5. The simulation time step, h_t, is selected to maintain numerical stability for a range of diffusion coefficients for the parameter optimization process. To be stable, the product $D\cdot h_t\left(1/h_x^2+1/h_y^2+1/h_z^2\right)$ must be less than 1/2, or for iso­tropic dimensions the product $D\cdot h_t/h^2$ must be less than 1/6. To be monotonic and stable, the product $D\cdot h_t\left(1/h_x^2+1/h_y^2+1/h_z^2\right)$ must be less than 1/4, or for iso­tropic dimensions the product $D\cdot h_t/h^2$ must be less than 1/12.

6. Building or updating the Jacobian matrix, J, can be time intensive as the number of model parameters increases as Eq. 23 (and thus a full model evaluation) needs to be evaluated for each model parameter perturbation. Parallelized code can be used to simultaneously build several columns of J at a time, dramatically decreasing the computation time. For example, non-parallelized code takes approximately 13.1 min per 100 parameters, while parallelized code divided among 32 threads takes 0.7 min per 100 parameters. Alternatively, approaches such as Broyden’s method [37] can be used to update J at each iteration while only building the full J matrix in the first iteration. Briefly, Broyden’s method is a secant method update that estimates J at the nth iteration based on the previous J, the difference between the model evaluation at the (n − 1) and (n −−2) iterations, and the difference between model parameters at the (n − 1) and (n − 2) iterations.