“Time Traveling Is Just Too Dangerous” But Some Methods Are Worth Revisiting: The Advantages of Expected Loss Curves Over Cost-Effectiveness Acceptability Curves and Frontier

Abstract

Objective.

Cost-effectiveness acceptability curves (CEACs) and frontier (CEAF) are the recommended graphical representations of uncertainty in a cost-effectiveness analysis (CEA). However, many limitations of the CEAC/CEAF have been recognized by others. Expected loss curves (ELCs) overcome these limitations by displaying the expected foregone benefits of choosing one strategy over others, the optimal strategy in expectation and the value of potential future research all in a single figure. Our aim is to revisit ELCs, illustrate their benefits using a case study and promote their adoption by providing open-source code.

Study Design.

A probabilistic sensitivity analysis (PSA) of a CEA comparing six cerebrospinal fluid biomarker test-and-treat strategies in patients with mild cognitive impairment

Methods.

We show how to calculate ELCs for a set of decision alternatives. We use the case study PSA to illustrate the limitations of currently recommended methods for communicating uncertainty. We then demonstrate how ELCs can address these issues.

Results.

ELCs combine the probability that each strategy is not cost-effective based on current information and the expected foregone benefit resulting from choosing that strategy (i.e., how much is lost if we recommended a strategy with a higher expected loss). ELCs display how the optimal strategy switches across willingness-to-pay thresholds and enables comparison between different strategies in terms of the expected loss.

Conclusions.

ELCs provide a more comprehensive representation of uncertainty and overcome current limitations of CEACs and the CEAF. Communication of uncertainty in CEA would benefit from greater adoption of ELCs as a complementary method to CEACs, CEAF and the EVPI.

Précis:

The expected loss curves (ELCs) display the expected foregone benefits of choosing a suboptimal, the optimal strategy and the value of potential future research.

Introduction

Cost-effectiveness analyses (CEAs) are generally conducted with some degree of parameter uncertainty. This parameter uncertainty is often accounted for in a probabilistic sensitivity analysis (PSA), which translates parameter uncertainty into decision uncertainty, namely the probability that a given strategy is cost-effective.[1] In a typical CEA, the decision maker is assumed to be risk neutral, with the optimal decision defined as the strategy maximizing the expected net benefit regardless of the level of decision uncertainty. Therefore, the primary purpose of the quantification of decision uncertainty is simply to provide confidence in the chosen strategy.[2] Nevertheless, parameter uncertainty plays a crucial role in determining the potential consequences of a decision, which are used to quantify the value of potential future research.[1–3]

PSA has become widely adopted and is now required by many journals, guidelines, and funding agencies [1,4–9] and is even considered “essential to high-quality cost-effectiveness analysis (CEA)”[4]. In a typical analysis, the PSA is used to construct a cost-effectiveness acceptability curve (CEAC) for each strategy and the cost-effectiveness acceptability frontier (CEAF). A CEAC illustrates the proportion of PSA samples in which a given strategy is cost-effective (i.e., with the highest net benefit) as a function of the willingness-to-pay (WTP) threshold.[10–13] This proportion is interpreted as the probability that a strategy is cost-effective, given the level of parameter uncertainty present in the analysis. The CEAC plot displays the CEAC of each of the strategies and is used to allow comparison of multiple strategies in the presence of uncertainty.[11] The CEAF can be overlaid on top of the CEAC plot, showing the probability that the optimal strategy (i.e., the strategy with the highest expected net benefit) is cost-effective as a function of WTP.[11,14] Notably, the CEAF in combination with the CEAC sometimes reveals that the best strategy in expectation is not always the strategy that is most likely to be cost-effective at a given WTP [3] (see Appendix A for a more detailed description on the differences between the strategy with the highest probability of being cost-effective and the most-cost effective strategy). The inclusion of the CEAF alongside the CEAC is important, as the strategy that is most likely to be cost-effective should not be conflated with the strategy that is optimal in expectation in the decision-making process.[1]

Despite their widespread use [15], it is unclear if CEACs and the CEAF have much influence on policy recommendations. Ultimately, a risk-neutral decision-maker will choose the strategy with the highest net benefit in expectation, regardless of the level of uncertainty about whether this strategy is cost-effective. In situations where the CEACs and CEAF reveal that the optimal strategy has a qualitatively low probability of being cost-effective and is not the strategy that is most likely to be cost-effective at a decision-maker’s WTP, the decision-maker may feel a certain level of discomfort in their decision. However, the extent to which their level of decision uncertainty is truly a cause of concern is not among the information provided by the CEAC/CEAF plot.

In particular, the CEAC/CEAF do not capture the magnitude of the net benefit lost in the proportion of PSA samples when chosen strategy is not cost-effective [3]; and yet it is the expected loss in net benefits that is truly the concern of the decision-maker because this represents the foregone benefits resulting from having chosen a given strategy. For example, consider a situation where the optimal strategy in expectation is cost-effective for only 30% of PSA samples at a given WTP. If among the remaining 70% of PSA samples the difference in net benefit between the optimal strategy and the strategy that achieves the maximal net benefit for that sample is generally small, this may not be of great concern to a decision-maker. However, if there are even just a few PSA samples for which the optimal strategy results in a large amount of foregone benefits, the low level of decision uncertainty should be of greater concern. Furthermore, the CEACs and the CEAF do not communicate the ordinal information in the ranking of the strategies by their expected benefits, which could be useful when implementing the optimal strategy is not feasible.

Value of information (VOI) is the quantification of the value of potential future research to better inform a decision in the presence of parameter uncertainty. In general, VOI measures the foregone benefit from choosing a strategy given imperfect information.[16,17] The most commonly used VOI metric is the expected value of perfect information (EVPI), which represents the value of eliminating parameter uncertainty of CEA.[18–20] Formally, EVPI is the difference between the expected net benefit given current information and the expected net benefit given perfect information (i.e., no uncertainty in model parameters). EVPI also represents the maximum value provided by potential future research [17] that could help inform decisions on research prioritization, which is something not provided by CEACs or CEAF.

These limitations of the CEAC and the CEAF in communicating the extent to which decision uncertainty matters have been recognized by others [21] and can be addressed by using expected loss curves (ELCs). ELCs have been proposed by others [22–25] and present a quantification of the consequences of choosing a suboptimal strategy in terms of expected foregone benefits, plotted as a function of WTP. In addition to showing the extent to which decision uncertainty results in a loss in benefits, ELCs also display the optimal strategy for a risk-neutral decision maker (like the CEAF), the value of eliminating the current level of decision uncertainty through additional research (like the EVPI) [22], and the ranking of strategies in terms of expected losses. That is, ELCs are a practical way to convey information about what is optimal given current information, the consequences of decision uncertainty, and the value of potential future research in a single graphical representation. ELCs are arguably a more useful representation of uncertainty than the information contained in CEACs, CEAF and EVPI alone; yet, the use of ELCs has been limited in the field of medical decision making to a handful conceptual and methodological papers.

The aim of this manuscript is to revisit the ELCs and promote their use as a complementary approach to CEACs, the CEAF and EVPI to represent the results of uncertainty analysis in CEA. We start with the mathematical definitions of the CEAC, the CEAF, and the ELCs and provide open-source code to compute these methods from a typical PSA dataset. We then illustrate the issues with CEACs and the CEAF for communicating results of uncertainty analysis in CEA using a published study of cerebrospinal fluid (CSF) biomarker testing in patients with mild cognitive impairment (MCI) and show how ELCs can address these issues. We show that ELCs not only highlight the optimal strategy in the presence of parameter uncertainty, but also the quantification of the value of potential future research to address this uncertainty. We conclude by arguing that ELCs provide additional information to a decision-maker not revealed by CEACs and the CEAF.

Methods

To compute the CEACs, the CEAF and ELCs, we need to compute the net benefit for each strategy. Consider a CEA that compares D strategies in terms of their effectiveness, E, and costs, C. The net benefit of a given strategy is often considered in monetary terms and referred to as net monetary benefit (NMB). The NMB for strategy d, B_d, is defined as E_dλ − C_d, where E_d and C_d are its effectiveness and costs, respectively, and λ is the WTP for one unit of effectiveness.[26]

The cost-effectiveness acceptability curves

The probability that strategy d is cost effective, Pr(CE)_d, is computed as:

$$\text{Pr}{(\text{CE})}_d=\frac{N_d}{N},$$ (1)

where N_d is the number of simulations in which strategy d has the maximum net benefit and N is the total number of PSA samples. The CEAC plot is the representation of Pr(CE)_d for all strategies being compared in the CEA as a function of WTP.

The cost-effectiveness acceptability frontier

Let B_i,d be the net benefit for the i-th simulation of the PSA dataset for a strategy d, and $\overline{B}=\left[{\overline{B}}_1{\overline{B}}_2\cdots {\overline{B}}_d\cdots {\overline{B}}_D\right]$ be the expected net benefits of all D strategies averaged across all N simulations of a PSA, where the expected net benefit for strategy d, ${\overline{B}}_d$, is defined as ${\overline{B}}_d=\frac{1}{N}{\sum }_{i=1}^N{B}_{i,d}\forall d\in [1,\dots ,D]$. Then, the optimal strategy based on the highest expected net benefit, $d_B^{*}$, is defined as:

$$d_B^{*}=\text{argma}{\text{x}}_{d\in \{1,2,\cdots ,D\}}\left\{{\overline{B}}_d\right\}.$$ (2)

The CEAF is the representation of the optimal strategy, $d_B^{*}$, as a function of WTP.

Definition and mathematical notation of expected losses

The expected loss is the quantification of the foregone benefit when choosing a suboptimal strategy given current evidence. Formally, the expected loss of strategy d, ${\overline{L}}_D$, averaged across all N simulations of a PSA, is computed as

$${\overline{L}}_d=\frac{1}{N}\sum _{i=1}^N\left[B_{i,d_i^{*}}-B_{i,d}\right],$$ (3)

$${\overline{L}}_d=\frac{1}{N}\sum _{i=1}^N{B}_{i,d_i^{*}}-\frac{1}{N}\sum _{i=1}^N{B}_{i,d};\forall d\in [1,\dots ,D],$$ (4)

where $B_{i,d_i^{*}}=ma{x}_d(B_{i,d})$ is the net benefit of the optimal strategy for the i-th PSA sample, denoted $d_i^{*}$.

For a risk-neutral decision maker, the optimal strategy is the strategy with the highest expected benefit, which is equivalent to the strategy with the lowest expected loss. Furthermore, the expected loss of the optimal strategy equals the EVPI in the decision problem.[23] (see Appendix B for a step-by-step derivation of these statements). Thus, once the expected loss is calculated for all D strategies, it is possible to determine both the optimal strategy and the EVPI.

The expected loss curves

ELCs are a representation of the expected loss of all D strategies, $L=\left[{\overline{L}}_1{\overline{L}}_2\cdots {\overline{L}}_d\cdots {\overline{L}}_D\right]$, as a function of WTP. The ELCs reveals the optimal strategy defined as the strategy with the lowest expected loss at a given WTP. The lower envelope of the ELCs is the expected loss of the optimal strategy and also the EVPI of the decision problem at that WTP. The ELCs also reveals by how much the optimal strategy is better than each of the other alternatives in terms of expected foregone benefits, which could be relevant when determining how resources should be spent.[27] Furthermore, ELCs could be used to rank the strategies based on their expected loss, which could be useful in cases where implementing the optimal strategy is not feasible (e.g. a technology not available in a local setting).

The ELCs show the expected loss (y-axis) of all strategies as a function of the WTP threshold (x-axis). If the differences in expected loss among strategies are small, these differences could be visually magnified by log-transforming the y-axis. R code to compute the CEACs, the CEAF, ELCs and EVPI from a typical PSA dataset is provided in the Appendix C. Readers could also have access to these methods through the R package dampack hosted on GitHub available at: https://github.com/DARTH-git/dampack.

Case study: CEA of CSF Biomarker Testing in Patients with MCI

Here, we summarize a previously published model for assessing the cost-effectiveness of 6 CSF biomarker test-and-treat strategies in patients with MCI. For full model details, see Michaud et al.[28] All analyses were conducted in R version 3.5.0.[29]

The CEA of CSF biomarker testing and targeted treatment compared 6 test-and-treat strategies in patients with MCI where the treatment decision was based on patients’ risk level (low, intermediate, high) of progression to Alzheimer’s disease (AD). The analysis used a Markov model of MCI and AD to project lifetime quality-adjusted life-years (QALYs) and costs for a cohort of 65-year-old MCI patients from a US societal perspective. The six strategies were:

1. Test-and-treat low risk. Test MCI patients and treat those with a low-risk result until AD conversion; no treatment for high- and intermediate-risk patients until they convert to AD and stop treatment when they progress to the severe stage.

2. Test-and-treat low or intermediate risk. Test MCI patients and treat those with a low- or intermediate-risk result until AD conversion; no treatment for high-risk.

3. No testing and no MCI treatment. Treat only when MCI patients convert to AD and stop treatment when they progress to the severe stage.

4. Test-and-treat high risk. Test MCI patients and only treat those with a high-risk result until AD conversion; no treatment for low- and intermediate-risk patients until they convert to AD and stop treatment when they progress to the severe stage.

5. Test-and-treat high or intermediate risk. Test MCI patients and treat those with a high- or intermediate-risk result until AD conversion; no treatment for low-risk patients until they convert to AD and stop treatment when they progress to the severe stage.

6. No testing and treat all MCI patients. Treat all MCI patients and stop treatment when patients convert to AD.

For MCI patients who received treatment, the authors assumed they would not be eligible for treatment once they converted to AD and stopped treatment when they progressed to the severe stage of AD. The PSA of the CEA of CSF biomarker testing included uncertainty in parameters describing disease progression, treatment effectiveness and harm, health utilities, and costs of disease, treatment and CSF biomarker testing. The PSA dataset was conducted with 10,000 samples.

Results

Results of the probabilistic sensitivity analysis of the case study

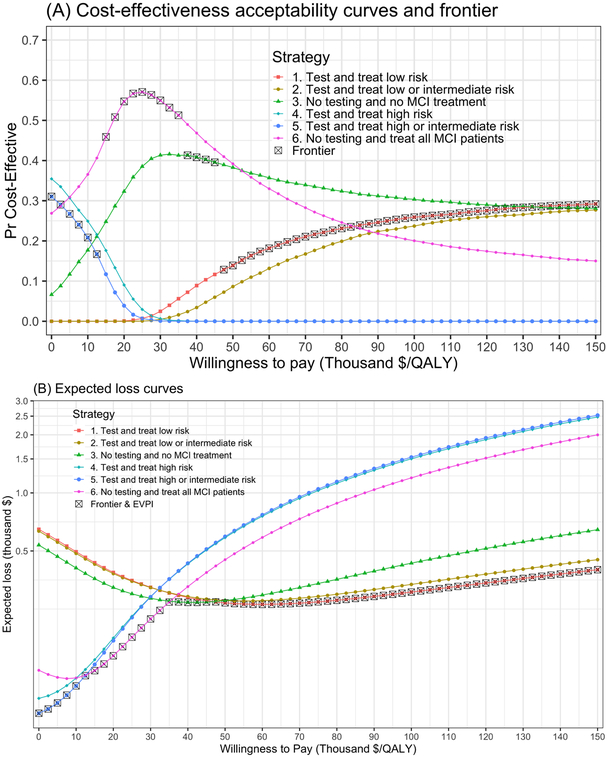
Figure 1A shows the CEACs and CEAF generated from the PSA of the CEA of CSF biomarker test-and-treat strategies in patients with MCI. For a WTP threshold lower than $15,000/QALY, testing and treating MCI patients at high or intermediate risk has the highest expected net benefit but has a lower probability of being cost-effective compared with some of the other strategies. For WTP thresholds between $15,000 and $35,000/QALY, no-testing and treating all MCI patients is the strategy with the highest expected net benefit and also the strategy with the highest probability of being cost-effective. No-testing and no-treating MCI patients has the highest expected net benefit for WTP thresholds greater or equal than $37,500 and lower than $47,500/QALY and is the strategy with the second highest probability of being cost-effective.

Figure 1.

(A) Cost-effectiveness acceptability curves (CEAC) displaying the probability of each strategy being cost-effective across all simulations of the PSA and cost-effectiveness acceptability frontier (CEAF) displaying the probability of the optimal strategy (in a gray square) being cost-effective across a range of WTP thresholds. (B) Expected loss curves (ELC) displaying across a range of WTP thresholds: (1) the expected loss in thousand USD for each of the strategies of the CEA of CSF biomarker testing, (2) the optimal strategy inside the gray square, which is the strategy with the lowest expected loss and (3) the expected value of perfect information (EVPI) which is the expected loss corresponding to the optimal strategy inside the gray square. The scale of the y-axis is logarithmic.

The strategy of testing and treating MCI patients at low risk has the highest expected net benefit for WTP thresholds greater than $45,000/QALY.

Limitations of CEACs and CEAF in the case study

As shown above, by combining CEACs and the CEAF in Figure 1A, it is possible to determine the optimal strategy and its probability of being cost-effective. However, this graph neither shows by how much the optimal strategy is better than the rest nor what the second or third best strategies are in terms of expected net benefit. Furthermore, there could be cases were the optimal strategy is only better than the second best by a small margin in terms of expected net benefits but their differences in the probability of being cost-effective are high. In addition, to display the value of conducting additional research, an additional graphical representation is required.

ELCs of the case study

The previous limitations could be overcome with ELCs in Figure 1B that displays the expected loss of each of the strategies from the PSA of the CEA of CSF biomarker testing. In this figure, it is possible to better observe how the optimal strategy switches across WTP thresholds and by how much the optimal strategy is better compared to the rest of the strategies based on their expected loss. For example, at a WTP threshold of $50,000/QALY in Table 1 and Figure 1B, the optimal strategy is testing and treating only low risk patients (strategy 1), which is the third strategy in terms of probability of being cost-effective with only 14% and an expected loss of $2,690 (Table 1 and Figure 1B). Then, the second-best strategy (from Figure 1B) is no testing and no treatment for any patient (strategy 3) with an expected loss of $2,766, which is also the second in terms of probability of being cost-effective with 38% (Table 1). The difference of 24 percentage points in the probability of being cost-effective between these two strategies might seem high but when looking at the difference in expected losses (and also visually in Figure 1B), there is only a $76 difference (Table 1). This contrast gets magnified when comparing strategy 3 with the third best strategy (strategy 2) that has 9% chance of being cost-effective with an expected loss of $2,767, where the difference in probability of being cost effective is 29% points but only $1 in expected losses (Table 1). In terms of expected losses, strategy 2 is practically indistinguishable from strategy 3 but looks extremely different in the CEAC on Figure 1A. Furthermore, with neither CEACs nor CEAF it is possible to determine which are the second or third best strategies in terms of their expected loss. That is, the relative order on the probability of being cost-effective is not related to the actual ranking based on expected loss. This information may be useful to decision makers in cases where not all strategies are viable alternatives in their setting.

Table 1.

Probability (Pr.) of being cost-effective and expected loss at different willingness-to-pay thresholds (WTP) of the cost-effectiveness analysis of 6 cerebrospinal (CSF) biomarker test-and-treat strategies in patients with mild cognitive impairment (MCI).

	WTP = $50,000/QALY		WTP = $100,000/QALY		WTP = $150,000/QALY
Strategy	Pr. cost- effective	Expected loss ($)	Pr. cost- effective	Expected loss ($)	Pr. cost- effective	Expected loss ($)
1. Test-and-treat low risk*	14%	2,690	26%	3,061	29%	3,997
2. Test-and-treat low or intermediate risk	9%	2,767	24%	3,354	28%	4,506
3. No testing and no MCI treatment	38%	2,766	30%	4,323	28%	6,445
4. Test-and-treat high risk	0%	5,863	0%	15,021	0%	24,744
5. Test-and-treat high or intermediate risk	0%	5,939	0%	15,313	0%	25,253
6. No testing and treat all MCI patients	39%	4,505	20%	11,963	15%	19,986

^*Optimal strategy at the three willingness-to-pay thresholds of this table given by the lowest expected loss assuming a risk-neutral decision maker. QALY, quality-adjusted life year.

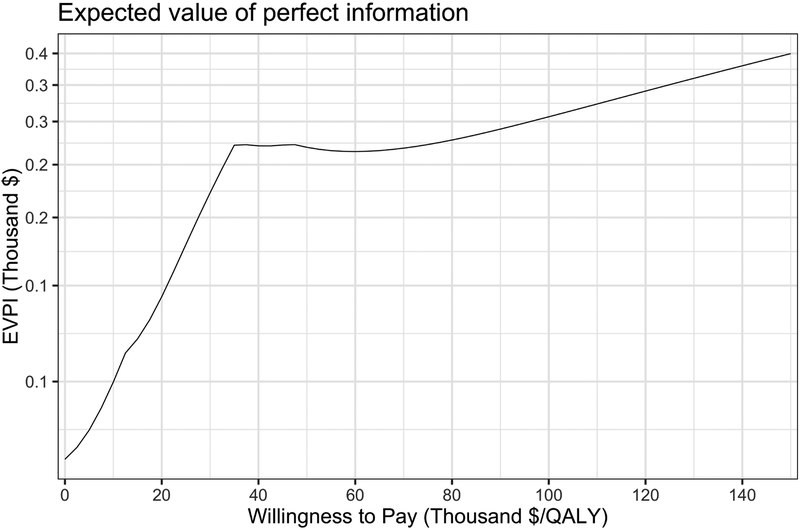
As mentioned above, the lower frontier of the ELCs in Figure 1B is the expected loss of the optimal strategy, which corresponds to the same values on the EVPI graph in Figure 2.[22] For example, at a WTP threshold of $100,000/QALY, testing and treating MCI patients at low risk is the optimal strategy with an expected loss and per-person EVPI of $3,061, followed by testing and treating MCI patients at low or intermediate risk with an expected loss of $3,353 (Table 1). In Figure 1B it is now evident that the kinks on the per-person EVPI graph in Figure 2 correspond to the WTP thresholds at which the optimal strategy switches.

Figure 2.

Expected value of perfect information (EVPI) per patient in USD across a range of WTP thresholds. The scale of the y-axis is logarithmic.

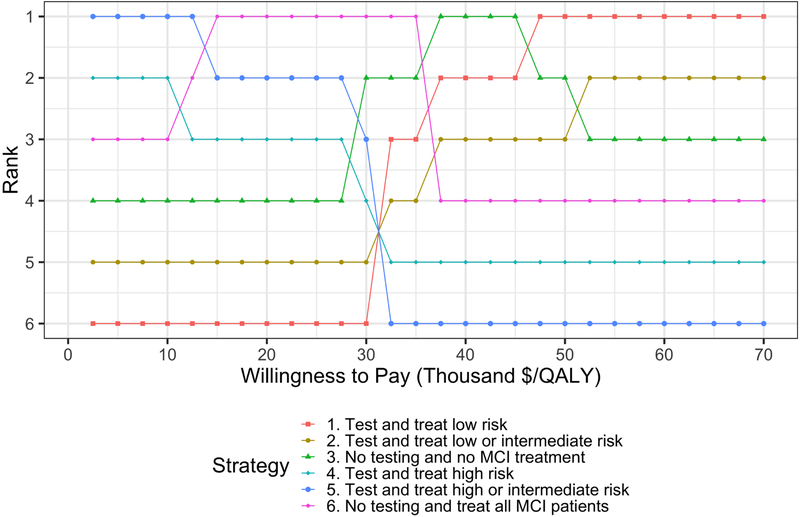
From the ELCs it is also possible to rank the strategies based on their expected loss. To facilitate determining the ranking of the strategies of the case study, we ordered them in Figure 3 based on their expected loss across a range of WTP thresholds. Figure 3 shows the change on the relative ranking of the strategies as the WTP threshold varies where the first row represents the optimal strategy across WTP thresholds. For example, testing and treating MCI patients with high or intermediate risk goes from being the highest ranked (i.e., optimal) strategy for WTP thresholds lower than $15,000/QALY to the lowest ranked strategy for WTP thresholds greater than $30,000/QALY. The opposite behavior is shown by testing and treating MCI patients with low risk, where this strategy goes from the lowest rank for WTP thresholds lower or equal than $30,000/QALY to the highest rank for WTP thresholds greater than $45,000/QALY.

Figure 3.

Ranking of the strategies based on expected loss across a range of WTP thresholds. The top strategy is the optimal strategy with the lowest expected loss and the bottom strategy is the worst strategy with the highest expected loss.

Discussion

In this manuscript, we revisited the ELCs, showed its advantages over currently recommended methods for communicating parameter uncertainty by providing additional information that could be useful for decision making, and illustrated its use on a published CEA of biomarker testing in patients with MCI. We show that with the ELCs it is possible to display not only the expected loss for all the strategies in a CEA, but also the optimal strategy and the EVPI all combined in one graphical representation.

While the CEAC represents the probability of a strategy being cost-effective alone, the ELC combines the probability that each strategy is not cost-effective based on current information with gravity of the loss at each PSA sample (i.e., how much is lost if we recommended a strategy with a higher loss than the loss of the cost-effective strategy). Information on which strategy is optimal is also displayed by the CEAF, but with ELCs, it is possible to determine the value of eliminating all parameter uncertainty from the CEA by comparing different strategies in terms of the expected loss.

Using CEACs in isolation for decision making could be misleading, particularly when the differences among strategies in the probability of being cost-effective are high when the optimal strategy is only better than the second best by a small margin in terms of expected net benefits. ELCs are a summary statistic that shows how the optimal strategy ranks and compares relative to the rest of the strategies and provides an estimate of the EVPI as a function of WTP. That is, the ELCs is a practical approach that conveys both information on what is optimal given current information and value of future research representation in one single graphical representation and addresses many of the limitations of the current practice of presenting PSA results.

Although the use of ELCs is not widespread, EVPI is increasingly being reported. By complementing EVPI with ELCs, decision makers will not only be presented with the foregone benefit associated with the optimal strategy but also the foregone benefit of the competing strategies, enabling the ranking of the strategies. Information on how large the expected loss of the other options compares to the optimal strategy and to each other could be useful to decision makers. Thus, we argue for the use of ELCs in addition to EVPI to complement what is presented by CEACs and the CEAF.

The use of expected losses and ELCs to guide decision making in the presence of uncertainty based on current information and to quantify the value of potential further research was proposed more than a decade ago followed by subsequent publications promoting its use [22–25]. Despite their advantages over more commonly used methods, the use of ELC in the field has been limited. In this manuscript, we illustrate the benefits of such existing method, its advantages over CEACs and the CEAF and aim to promote its wide adoption.

A similar approach to expected losses for decision making has been recently proposed by Grimm et al. in the context of managed entry agreement schemes.[30] In this approach, the authors define the concept of Payer Strategy and Uncertainty Burden (P-SUB) as a measure of overall risk in decision making in the presence of uncertainty, which is equivalent to the expected losses described in this manuscript. In that paper, the P-SUB is calculated for one WTP threshold, while ELCs are calculated over a range of WTP thresholds. Both the P-SUB and the ELCs argue for a better representation of results of decision problems in the presence of uncertainty than currently adopted methods.

ELCs do have some limitations in that they only represent the average loss and do not reflect worst/best case scenarios. Some decision-makers may find large losses concerning, even if they are relatively rare across PSA samples; other decision-makers may explicitly wish to minimize the worst-case scenario (i.e., the largest loss) rather than in expectation. For these decision makers, ELCs are insufficient because a small number of large losses could be averaged out by a larger number of smaller losses. To overcome this limitation, loss curves could be constructed that reflect a weighted average of both foregone benefit (i.e., expected losses) and worse case scenarios (i.e., maximum losses), weighted according to preferences of the decision-maker. This, however, is a topic for further research.

A strength of this work is that it makes explicit the advantages of ELCs over CEACs and the CEAF and illustrates these with a published case study. ELCs could be calculated directly from a traditional PSA dataset. To even further facilitate their use and increase their adoption, we provide open-source code in the supplementary material that can be applied with slight or no modifications to the output of a PSA that could be obtained from currently used software.

Current guidelines recommend the use of CEACs and the CEAF to provide decision makers with enough information to make a decision based on current information and present EVPI analysis to quantify the value of potential future research over a relevant range of WTP thresholds.[1,9] However, these methods only provide a partial insight into the impact of parameter uncertainty. The ELCs is a more comprehensive approach that provides decision makers with all the required information necessary to make decisions based on current information, quantify the value of eliminating parameter uncertainty, determine the value of potential future research to better inform the decision and provide the ordinal ranking of strategies.

Conclusion

By adopting ELCs as a complementary method to CEACs, the CEAF and EVPI to report results of uncertainty analysis in CEA, decision makers are presented with the probability that each strategy is cost-effective, the optimal strategy, the foregone benefits of the optimal and the rest of the strategies, a ranking of the strategies and the value of conducting potential further research. We hope that this contribution can aid in the adoption of ELCs in future CEAs.

Highlights.

• Cost-effectiveness acceptability curves (CEACs) and frontier (CEAF) are the currently recommended approaches to represent results of uncertainty analyses in cost-effectiveness analysis (CEA) but they do not reflect the consequences of choosing a suboptimal strategy and could be misleading.

• The expected loss curves (ELCs) is a comprehensive graphical representation of uncertainty results that displays the foregone benefit of choosing a suboptimal strategy, shows the optimal strategy and the value of potential future research, and allows the ranking of strategies in the presence of uncertainty.

• ELCs provide a more comprehensive representation of uncertainty and overcome current limitations of CEACs and CEAF. Communication of uncertainty in CEA would benefit from greater adoption of ELCs as a complementary method to CEACs, CEAF and EVPI.