Computational design of structured loops for new protein functions

Abstract

The ability to engineer the precise geometries, fine-tuned energetics, and subtle dynamics that are characteristic of functional proteins is a major unsolved challenge in the field of computational protein design. In natural proteins, functional sites exhibiting these properties often feature structured loops. However, unlike the elements of secondary structure that comprise idealized protein folds, structured loops have been difficult to design computationally. Addressing this shortcoming in a general way is a necessary first step towards the routine design of protein function. In this perspective, we will describe the progress that has been made on this problem and discuss how recent advances in the field of loop structure prediction can be harnessed and applied to the inverse problem of computational loop design.

Introduction: Why focus on computational design of structured protein loops

The routine engineering of functional proteins has been a longstanding goal in the field of computational protein design. However, while the computational engineering of new protein structures has advanced rapidly (Huang et al., 2016), the computational engineering of new functions has been more difficult (Fleishman et al., 2012).

One important reason for this discrepancy is that protein structures are largely built from secondary structural elements (e.g. α-helices, β-sheets, and canonical turns) with well-understood and predictable patterns of backbone torsion angles and hydrogen bonds, while functional sites (e.g. active sites and binding interfaces) are often built from structured loops with less regular conformations, shaped by the complex and competing requirements of protein function. Early efforts in protein design focused on secondary structure, defining the rules for α-helix formation (Errington et al., 2006) and creating simple β-sheet elements (Lacroix et al., 1999). Exploring the principles of protein secondary structure and their topological arrangements ultimately led to the development of methods — based on the assembly of protein structures from peptide fragments, together with high-resolution sampling methods and all-atom energy functions — that have been highly successful in combining helical and sheet elements to create a variety of new, idealized protein folds (Koga et al., 2012).

Now, attention is shifting to the design of protein function. Computational protein design, sometimes in conjunction with directed evolution, has been applied to place catalytic groups (Bolon et al., 2001; Jiang et al., 2008; Privett et al., 2012; Rothlisberger et al., 2008; Siegel et al., 2010), engineer shape-complementary binding interfaces (Chevalier et al., 2002; Fleishman et al., 2011; Kapp et al., 2012; Karanicolas et al., 2011; Kortemme et al., 2004), and switch between different conformational states (Ambroggio et al., 2006; Davey et al., 2017). In natural proteins, these functions are more often performed by structured loops than by α-helices or β-sheets, presumably because loops can access a broader range of conformations with greater variation in flexibility or rigidity. For this reason, it seems inevitable that the design of complex protein functions will require the ability to design structured loops with high accuracy. But the same conformational and dynamical breadth that make structured loops functionally useful also makes them challenging to design: the number of possible conformations is vast, and even single mutations can have important long-range effects on loop structure and flexibility. Despite these challenges, a few examples of successful loop design have been reported. There have also been significant advances made in the field of loop structure prediction (Li, 2013), making it timely to discuss how these advances might be harnessed for to computationally design structured loops with greater control than is currently possible.

In this perspective, we will begin by discussing examples of functional loops found in nature, to illustrate different applications that loop design aims to enable. We will then continue by reviewing the progress that has been made to date towards the design of structured loops, before concluding by discussing several promising ways for the field to continue moving forward.

Functional loops in nature

Many examples of functional loops can be found in enzymes. In fact, loops are much more common in enzyme active sites (50% of residues) than they are in general (30% of residues) (Bartlett et al., 2002). One way loops can contribute to catalysis is by positioning functional groups in the active site (Figure 1A). A good example is ketosteroid isomerase, where the positioning of a general base (Asp38) by a structured loop is estimated to have a 1700-fold effect on k_cat(Schwans et al., 2014).

Figure 1. Important applications of loops design:

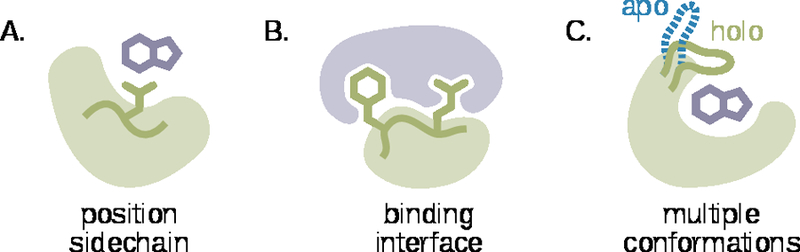
(A) accurately positioning a functional sidechain to interact with a ligand (light green: protein, dark green: loop with functional sidechain, purple: ligand), (B) creating a binding interface (light purple: binding partner), and (C) adopting different functional conformation in response to environmental stimuli, e.g. ligand binding (blue, dashed: loop conformation in the absence of ligand, dark green: loop conformation in the presence of ligand).

Loops can also contribute to catalysis by acting as a lid for the active site (Figure 1C) and changing the reaction environment. For example, upon substrate binding to triose phosphate isomerase (TIM), an active site loop moves more than 7Å to surround the substrate and hydrogen-bond with the substrate’s phosphate group. This substantial conformational change excludes solvent from the active site and prevents the release of reaction intermediates (Pompliano et al., 1990). However, the closed “lid” also limits the rate of product release, highlighting a carefully balanced trade-off between creating a protected active site environment and exchanging product for substrate. The active site loop structure in TIM is mostly preorganized, moving primarily around a hinge, suggesting that the loop might be optimized to reduce the entropy penalty of closing (Lolis et al., 1990). Rationally designing similar systems will require exquisite finesse.

Structured loops also play an important role in protein-protein interactions (Figure 1B). Perhaps the most prominent examples in this category are antibodies, which use six structured loops — called complementarity determining regions (CDRs) — to bind an astonishing breadth of targets with high affinity and specificity. As antibody CDRs mature, their shape complementarity to their antigen increases (Kuroda et al., 2016; Li et al., 2003). Moreover, mature CDRs often adopt conformations that are pre-organized for binding (i.e. conformations that resemble the bound structure, even in the absence of antigen) to minimize the loss of conformational entropy upon antigen binding (Davenport et al., 2016; Thorpe et al., 2007; Wong et al., 2011). However, pre-organization is not a universal feature of high-affinity antibodies (Jeliazkov et al., 2018). Antibodies with less organized CDRs may benefit from the ability to change their conformation to maximize complementarity, or to bind their antigen in multiple modes (James et al., 2003; Wang et al., 2013). The challenge for rational design will be to create loops that can similarly present the complementary surfaces necessary for tight and specific recognition.

Another class of functional loops can be found in proteins that react to their environment. One example is the bacterial outer membrane protein G (OmpG) that forms a pH-gated pore in the membrane. The gating is mediated by an extracellular strand-loop-strand motif containing two histidine residues (Yildiz et al., 2006; Zhuang et al., 2013). At basic pH, the histidines are neutral and positioned on adjacent strands of the β-barrel that forms the pore. At acidic pH, protonation of the histidines results in charge repulsion that causes the strands to unfold, lengthening the loop and allowing it to adopt a conformation that covers the pore. Another prominent example is the activation loop present in protein kinases. When phosphorylated, this loop forms contacts that stabilize the active site and contributes to catalysis (Steichen et al., 2012). These examples illustrate the utility of being able to design and balance multiple functional loop conformations.

What is loop design?

Here we define loop design as the problem of predicting sequences that will allow a loop to satisfy certain structural and functional requirements (Figure 2A), such as positioning one or more sidechain groups, adopting a particular binding conformation, or changing conformation in the presence of a ligand (Figure 1). We define a loop as a contiguous stretch of protein backbone anchored within a larger scaffold and typically — although not necessarily — lacking secondary structure. For the purpose of this review, we will consider loop design distinct from the field of loop grafting, which aims to present a fragment of one protein on the scaffold of another, with important applications in vaccine design (Azoitei et al., 2011; Correia et al., 2014; Jardine et al., 2013). Both loop grafting and loop design aim to create loops in particular conformations. However, for loop grafting the sequence and structure of the loops is known in advance while for loop design determining the sequence and structure of the loops is the key challenge.

Figure 2. Schematic of a generic loop design protocol.

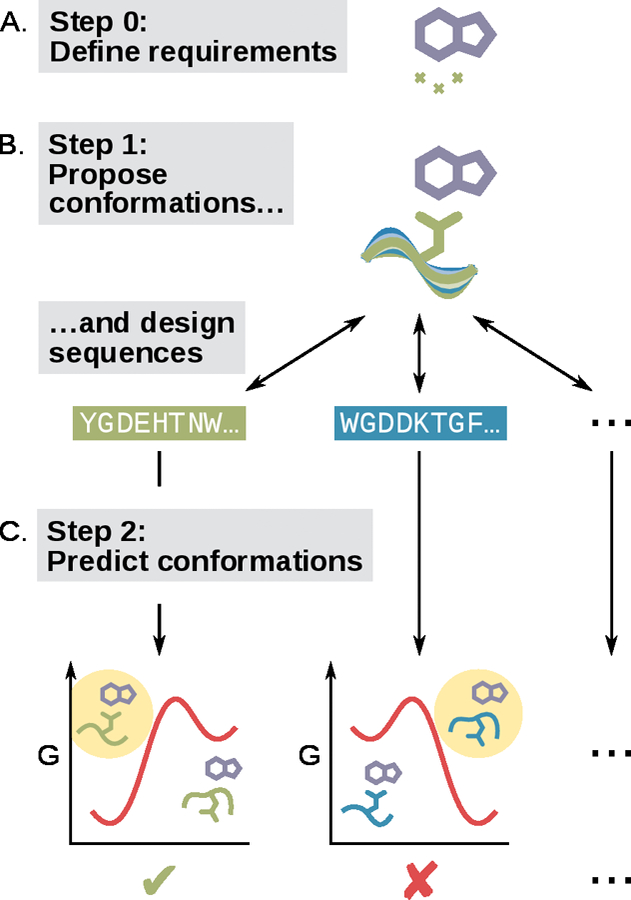
(A) A loop design problem is defined by one or more target interactions (functional requirements). (B) The first step of a generic loop design protocol is to generate design models that satisfy the design goal (shades of blue and green: different design models with different conformations and sequences). (C) The second step of a generic loop design protocol is to identify which models will satisfy the design goal in their minimum free energy conformations. The free energy diagrams each illustrate two hypothetical states, one that satisfies the design goal (left) and one that does not (right). The green checkmark indicates a design that should be experimentally tested, while the red cross indicates a design predicted to be non-functional.

It is instructive to consider how a loop design algorithm might operate given a perfect score function and infinite computing resources. In such a hypothetical situation, the first step would be to exhaustively propose design models (combining both sequence and structure) that satisfy the structural requirements without introducing any breaks in the backbone (Figure 2B). The second step would be to subject these designs to intense simulation for the purpose of locating their free energy minima (Figure 2C). Any design that still satisfies the structural requirements in its free energy minimum would be an excellent candidate for experimental validation. In reality, of course, both steps of this algorithm are prohibitively expensive. However, the growing body of literature on loop design (which we will review below) has found various ways to approximate the ideal scenario, for example by copying fragments of structure from existing proteins, using sophisticated macromolecular structure prediction algorithms, and even incorporating human intuition into the design process.

Loop design: The state of the art

In spite of the numerous applications, there are not many examples of loop design using computational prediction and design methods. An early example is the effort to improve a monomeric variant of TIM by restabilizing an 8-residue active site loop (Figure 3A) that, in wildtype TIM, participated in the dimer interface (Thanki et al., 1997). In four iterations, computational models of the loop were predicted using Monte Carlo simulations, then mutations were proposed by visual inspection to correct various defects in the models. The final result was a 7-residue loop that improved the activity of monomeric TIM. Furthermore, a crystal structure of the designed protein agreed well with the predicted loop conformation (0.5Å root mean squared deviation (RMSD) of the backbone heavy atoms C/Cα/N/O in the loop). This report established early on that loop design is both achievable and useful.

Figure 3. Successful applications of loop design.

Each panel shows crystal structures of a protein with redesigned loops (red and dark grey) and the starting structure (termed scaffold, blue and light grey). The redesigned loops are shown in red and the loops in the starting scaffolds are shown in blue. Ligands (if any are present) are shown in green. PDB IDs for the relevant structures are given in the top-right corner of each panel. Note that the design models are not shown, so these images do not illustrate how accurate the designs were, only how different they were from their starting scaffolds. (A) The stabilized active site loop of MonoTIM (Thanki et al., 1997). The catalytic Lys supported by this loop is shown. The dashed backbone in the scaffold indicates a lack of electron density. (B) The active site of a computationally designed Diels-Alderase (Eiben et al., 2012). (C) An exogenous loop grafted onto the FN3 scaffold (Hu et al., 2007). (D) A de novo loop inserted into a de novo five-residue-repeat scaffold (MacDonald et al., 2016). (E) The substrate binding loop in the active site of hGDA (Murphy et al., 2009). The Cβ of the Asn intended to bind ammelide is shown, but the remainder of the sidechain was not resolved. (F) The engineered CDR loops (bold labels) of an insulin-binding antibody (Lapidoth et al., 2015). Note that the crystal structure does not include the antigen (insulin).

Another example of loop design via computational prediction and visual inspection was reported more recently. In this case, players of FoldIt (Cooper et al., 2010) — a gamified version of the Rosetta structure prediction and design program (Kaufmann et al., 2010; Leaver-Fay et al., 2011) — were asked to improve a computationally designed Diels-Alderase (Siegel et al., 2010) by designing an active site loop that would better desolvate the substrate (Eiben et al., 2012). In the first round of design, the players were allowed to make 5-residue insertions into any of the four active site loops. The authors experimentally tested the 4 best designs (as judged by the score of the Rosetta energy function and by visual inspection) and over 500 variants of these designs. In the second round of design, the players were instructed to stabilize the best first-round design through the creation of a helix-turn-helix motif (Figure 3B). This time, the authors tested the 2 best designs and over 400 variants. The end result was a variant with a 13-residue insertion that improved catalysis by 150-fold. A model of the final variant created by the players was similar to the crystal structure, except for a rotation in one of the helices (3.1Å C/Cα/N/O RMSD). Although the design process required experimentally testing hundreds of variants, it demonstrated that human intuition can guide the design of long and functional loops.

An early example of automated computational loop design was an effort to build new loops into the fibronectin type III (FN3) domain (Hu et al., 2007) (Figure 3C). This domain had already been established as a non-antibody scaffold for evolving loop-based binding interfaces, and like an immunoglobulin domain, it has a β-sandwich fold from which it presents three mutation-tolerant loops. The authors redesigned one of these loops by searching for 12-residue fragments in the protein data bank (PDB) with similar take-off and landing points to the loops in question (within 3Å), grafting each of those fragments onto the FN3 scaffold, repairing the resulting (small) discontinuities in the backbone and finally optimizing the sequence of the inserted residues while allowing slight backbone movement (≈0.3Å C/Cα/N/O RMSD). Three designs were purified and two were successfully crystallized. One design had the intended loop conformation (0.46Å RMSD), which was similar to the original native loop (0.77Å RMSD). The conformation of the loop in the other design could not be determined due to missing electron density for the loop, which suggests the lack of a single defined conformation. The significance of this work is that it demonstrated that a structured loop could be computationally designed, by borrowing a loop backbone conformation from a naturally existing structure and redesigning the sequence to match the new environment. However, the work did not address the problem of designing function.

A more recent report addressed the design of de novo loops, which were built into a de novo scaffold assembled from 24 repeats of a 5-residue motif (MacDonald et al., 2016) (Figure 3D). The loops were designed by inserting 8 residues in the middle of the scaffold, sampling conformations with a coarse-grained and sequence-independent algorithm, then reconstructing the insertion in full-atom detail and performing fixed-backbone sequence optimization. This protocol produced 4000 loop designs. The conformations represented by these designs (which remained sequence-independent) were assumed to approximate the ensemble of states accessible to an 8-residue loop, allowing the authors to estimate the probability that each design would fold into its intended conformation by threading the design sequence onto each backbone and comparing the resulting Boltzmann-weighted scores. The 10 designs with the highest predicted probabilities of folding correctly were tested. Of these, 5 could be purified and 4 could be crystallized. The crystal structures were relatively low-resolution (>3.5Å), but two were consistent with their design models, one was inconsistent with its model, and one had missing density for the loop. This report showed that it is possible to create loops with de novo conformations, but these conformations emerged during the design process (rather than being defined a priori) and were not intended to be functional.

Computational loop design was used to alter protein function in an effort to change the substrate specificity of the enzyme human guanine deaminase (hGDA) from guanine to ammelide (Murphy et al., 2009) (Figure 3E). The ultimate goal was to change the substrate specificity of hGDA from guanine to cytosine, but ammelide was chosen as an intermediate step because it resembles guanine on one face and cytosine on the other. The design approach was to remodel the loop in hGDA that positions an arginine (Arg) to recognize guanine to instead position either asparagine (Asn) or glutamine (Gln) with the right geometry to bind the cytosine-resembling face of ammelide. (Interestingly, in natural cytosine deaminases the corresponding Asn/Gln is positioned by a different active site loop, so this project is in essence attempting to build a novel active site architecture). The loop was remodeled by (i) positioning the amide groups of the Asn and Gln sidechains ideally with respect to ammelide, (ii) rotating the sidechain χ angles to generate backbone conformations capable of supporting that ideal positioning, (iii) superimposing segments from the scaffold on those backbones, (iv) randomly adding or removing residues from either end of those segments, and (v) repairing the backbone with peptide fragment insertions (Simons et al., 1997), cyclic coordinate descent (CCD) (Canutescu et al., 2003) and minimization of backbone torsions using Rosetta (Kaufmann et al., 2010). This loop remodeling protocol was then followed by fixed-backbone sequence design on the lowest-scoring backbone model (which featured Asn and two deletions) to create designs. A single design (with Gly-Asn-Gly-Val as the loop sequence) was chosen for experimental characterization, based on visual inspection and the results of an unrestrained loop modeling simulation predicting that the design would fold into the desired conformation. The chosen design yielded a 100-fold increase in ammelide deaminase activity, along with a 25,000-fold decrease in guanine deaminase activity. A crystal structure revealed that the loop was close to the computational design model (1.0Å Cα RMSD), but that the designed Asn was not visible in the electron density. This report is significant because it showed that loops can be designed for function. But there is still room for improvement. The designed loop was relatively short (4 residues) and its conformation only differed slightly from that of the starting wildtype structure. For more ambitious design goals, we must learn how to design larger loops and more dramatic conformational changes.

Loop design has also been applied to the problem of computationally designing antibody CDRs to bind particular targets of interest. This is an especially challenging problem for a number of reasons: (i) there are 6 CDRs, which interact with each other to form a large binding interface, (ii) some of the CDRs, most notably the 3^rd CDR on the antibody heavy chain (termed H3), can be long (typically between 3 and 20 residues (Regep et al., 2017)), and (iii) the position and conformation of the antigen must be predicted in concert with the CDRs. However, there is also an exceptional amount of sequence and structural data available for antibodies. These data were recently leveraged to rationally design antibody binding interfaces for human insulin and Mycobacterium tuberculosis acyl-carrier protein 2 (Baran et al., 2017; Lapidoth et al., 2015). The design protocol was premised on the long-standing concept that each CDR except H3 can be assigned to a small number of conformational clusters (Chothia et al., 1987). By combining CDRs from each cluster, 4500 models were created. The epitope was docked against each model, and the antibody sequence was designed to stabilize both the binding interface and the interactions between the CDRs, subject to sequence restraints derived from the natural sequence profiles for each cluster. Each CDR was then optimized by iteratively installing different backbone conformations from the same cluster and re-sampling the sidechains (Lapidoth et al., 2015). With the benefit of manual design and directed evolution, this protocol produced antibodies with mid-nanomolar binding affinities. The anti-insulin antibody was crystallized in its unbound form (Figure 3F) and showed atomic-level accuracy in of 4 of the 6 CDRs (backbone and sidechain), with the only errors being in H1 and the notoriously difficult H3 (Baran et al., 2017). This method shows that it is possible to design structured loops in binding interfaces, even while also optimizing other degrees of freedom (e.g. epitope docking). The drawback to this method is that it depends on the vast amount of information available for the antibody scaffold. Other common scaffolds, e.g. TIM-barrels, might also be amenable to this type of design, but there remains a need for methods that can be applied more generally to any existing scaffold or to new protein folds designed entirely de novo.

What can we learn from loop modeling?

With the current state of computational loop design in mind, it is interesting and worthwhile to consider how the field might progress in the near future. To do so, it is instructive to examine the related — but much more mature — field of loop modeling. Loop modeling is the problem of predicting the structure of a loop given its sequence. This is the inverse of the loop design problem, which can be framed as predicting sequences that will adopt a particular loop structure. By considering the similarities and differences between these two related problems in the following sections, we will highlight how previous advances in loop modeling can illuminate the way forward in loop design.

The basic structure of a loop modeling algorithm is as follows: The inputs are (i) the sequences of one or more loops and (ii) the atomic coordinates for the remainder of the protein, which might be taken from homology models or experimental structures with missing atoms. The outputs are the atomic coordinates for loops in question. To produce these coordinates, a loop modeling algorithm has four components: (i) a suitable representation of the system, (ii) an algorithm to sample new loop conformations, (iii) an algorithm to ensure that the protein backbone stays closed, and (iv) an energy function to score different loop conformations. We will discuss each of these components, and how they might be repurposed for loop design, below.

Representation

There are two main classes of representations employed in loop modeling algorithms: full-atom and coarse-grained. Full-atom representations include all protein backbone and sidechain atoms, although most still exclude solvent atoms. Coarse-grained representations strip away some atomic detail in the interest of simplicity. This could mean replacing the sidechain atoms with a single large sphere, removing the sidechain atoms altogether, or retaining only the protein α-carbons. One advantage of coarse-grained representations is that they typically have smoother energy landscapes, which can be more thoroughly explored. In contrast, full-atom representations have the potential to be more accurate since details of physical interactions, such as the precise geometries of hydrogen bonds in functional sites, can be modeled. To combine the potential advantages of both classes of representations, many loop modeling methods begin by searching for reasonable loop conformations in a coarse-grained representation, then switch to a full-atom representation to winnow and refine those conformations (de Bakker et al., 2003; Fiser et al., 2000; Jacobson et al., 2004; Lee et al., 2010; Mandell et al., 2009; Wang et al., 2007). An interesting exception are algorithms that use only a full-atom representation (Das, 2013; Wong et al., 2017). These methods are based on the premise that loops can be sampled stepwise, so these algorithms build loops by sampling each residue in full-atom detail, one-at-a-time, until the whole loop has been assembled.

The sequential approach of many loop modeling algorithms — coarse-grained exploration followed by full-atom refinement — may not generally be appropriate for loop design. As defined above, loop design is fundamentally a search for sequences adopting desired conformations subject to functional requirements (Figure 2). Coarse-grained versions of this search could in principle include a representation that encodes sequence. One such representation is the Rosetta “centroid-mode”, which represents different sidechain types as spheres with different sizes and charge properties (Simons et al., 1997; Simons et al., 1999). However, it is unclear whether sequence-aware coarse-grained representations can encode the functional requirements of a design problem in sufficient detail. A prototypical example is a design goal where functional groups of specific side chains need to be accurately positioned within an active site. In this case, design solutions will need to take into account the specific size and geometry of these sidechains, even during coarse-grained remodeling of the surrounding backbone environment. To address this problem, it will be desirable to develop hybrid representations — perhaps specific to the loop design problem — with tunable levels of detail. For example, one could imagine an algorithm where functional side chain groups are placed using all atom detail while the rest of the loop (i.e. the backbone and any peripheral sidechains) is built in lower resolution. Plausible models could then be subjected to full-atom sequence design and structural refinement.

Sampling

Loop modeling algorithms differ in their approaches to sampling different conformations. These approaches are traditionally categorized as either “template-based” or “template-free/de novo” (Fiser, 2017; Li, 2013; Shehu et al., 2012), where the former query databases of known structures to sample loop conformations, and the latter do not. However, most recent sampling algorithms lie on a continuum between the two. On one side of this continuum are the algorithms that do not borrow three-dimensional coordinates from any existing “template” protein structure. For example, some algorithms randomly place atoms in a “cloud” around the loop and subsequently refine them to satisfy certain physical or experimental restraints (Fiser et al., 2000; Heo et al., 2017; Liu et al., 2009). Other algorithms begin with a physically plausible backbone conformation and perturb it via Monte Carlo (Collura et al., 1993; Macdonald et al., 2013) or molecular dynamics (MD) (Hornak et al., 2003; Olson et al., 2011; Rapp et al., 1999) simulations. A small step along the continuum is to sample backbone torsions from a Ramachandran distribution derived from the frequencies of the φ and ψ backbone torsions in high-resolution protein structures (Adhikari et al., 2012; DePristo et al., 2003; Galaktionov et al., 2001; Jacobson et al., 2004; Liang et al., 2014; Mandell et al., 2009; Spassov et al., 2008; Tang et al., 2014; Xiang et al., 2002). This approach has also been extended to two-residue (Stein et al., 2013) and three-residue (Rata et al., 2010) φ and ψ distributions. A further step along the continuum are algorithms that sample new loop conformations by stitching together larger fragments (usually 3–9 residues) from known structures (Lee et al., 2010; Rohl et al., 2004; Wang et al., 2007). This fragment-based approach is based on the assumption that all relevant local conformations are present in the PDB (Perskie et al., 2008; Simons et al., 1997), and is widely recognized for its successful application to the ab initio prediction of protein tertiary structures (Bradley et al., 2005). Finally, on the far side of the continuum are fully template-based algorithms. These algorithms query structural databases for loops of the right length that approximately match the takeoff and landing points of the loop in the input structure (Choi et al., 2010; Deane et al., 2001; Fernandez-Fuentes et al., 2006; Holtby et al., 2013; Marks et al., 2017; Messih et al., 2015; Michalsky et al., 2003; Nguyen et al., 2017; Peng et al., 2007). Matching loops are usually ranked by how well they fit the gap and align with the input sequence, and can be subsequently relaxed using a full-atom score function. Template-based algorithms can be very fast, a fact that was recently leveraged to create an interactive program for loop modeling and design (Hooper et al., 2018).

In terms of sampling, the clearest difference between loop modeling and loop design is that the former only needs to sample conformation-space, while the latter needs to simultaneously sample conformation- and sequence-space. This poses a challenge called the “designability” problem (Helling et al., 2001): given a desired conformation, is it possible for some sequence (in some environmental context) to adopt that conformation?

For loop design, one might hypothesize that the template- and fragment-based algorithms (Bonet et al., 2014; Lapidoth et al., 2015; Murphy et al., 2009) might be more successful than de novo methods since the former address the designability problem: if conformations are sampled from a structural database, there is at least one known sequence for each conformation. However, there are still significant challenges in applying template-based algorithms to the problem of loop design. The most significant challenge is ensuring that the loop will still adopt its conformation in the new structural context of the design. Moreover, template-based methods would need to be modified to account for the additional structural requirements imposed on the loop by the design goal. For example, to design a loop that places the functional group of an active site residue in a defined geometry, a database query would have to find loops that not only start and stop in the right place, but are also capable of positioning the residue in question, limiting the number of potential results. This problem is amplified as more residues are included in the design, for example in large binding sites and protein-protein interfaces. That said, loop design also makes finding suitable loops easier because the algorithm can pick its takeoff and landing points, and the loop can be of any length or sequence. Some design problems can also take advantage of scaffolds belonging to large families with many homologs of known structure, like antibodies or TIM-barrels, for which template-based algorithms are especially likely to be successful. Taken together, it is not clear a priori how difficult it will be to apply template-based algorithms to loop design. However, fragment-based sampling algorithms might be more generally applicable. They offer analogous advantages to the template-based algorithms in terms of designability, but since the backbone can be built by combination of different shorter fragments rather than one large segment, it might be easier to find solutions that accommodate functional requirements imposed by the design goal (which could be expressed using spatial restraints, for example).

Another aspect of sampling in structure prediction is the difficulty of traversing large barriers in the energy landscape, leading to simulations that get trapped in local minima and fail to produce native conformations. A common strategy for addressing this problem is simulated annealing, whereby the temperature of the simulation is gradually increased (to traverse barriers) and decreased over the course of the simulation (Adhikari et al., 2012; Collura et al., 1993; Fiser et al., 2000; Liang et al., 2014; Macdonald et al., 2013; Mandell et al., 2009; Rapp et al., 1999; Rohl et al., 2004; Wang et al., 2007). A related alternative is parallel tempering, whereby simulations at different temperatures are run simultaneously and occasionally swap coordinates (Olson et al., 2011; Olson et al., 2008). Unlike simulated annealing, parallel tempering produces ensembles with defined temperatures. Although such ensembles may be helpful for estimating entropies, few loop modeling applications have applied this strategy as of yet. Genetic algorithms have also been used to enhance sampling (Heo et al., 2017; Li et al., 2011; Park et al., 2014). While genetic algorithms can traverse barriers efficiently, they have to confront the fact that crossover operations involving backbone torsions are likely to produce large clashes (Unger, 2004). Lastly, a handful of methods have attempted to exhaustively sample conformational space, subject to some binning and pruning (Das, 2013; Jacobson et al., 2004; Spassov et al., 2008; Wong et al., 2017).

At least in principle, any of these barrier traversal strategies could be applied to loop design, especially to the step where proposed designs are simulated to assess which will in fact adopt the desired conformation (Figure 2C). This computational “validation” step (more specifically a consistency check) is similar to a loop modeling simulation, but with a subtle difference: a design fails the validation and the simulation can stop as soon as it finds a robust number of alternative conformations with lower predicted energies than the design being validated. This difference could allow the validation problem to be recast as a comparison between a small number of plausible off-target states, rather than as a large-scale search of conformational space for the energy minimum. In turn, this comparison could be addressed using enhanced sampling techniques that estimate the free energy difference between small numbers of known states (Comer et al., 2015; Kastner, 2011).

Closure

A specific feature of loop sampling algorithms is that they must be able sample new loop conformations without creating chain breaks in the protein backbone. This problem is referred to as loop closure. A conceptually simple (although combinatorially complex) solution is to allow the sampling algorithm to build the loop from both ends, and to keep the fraction of models that meet in the middle (Das, 2013; DePristo et al., 2003; Jacobson et al., 2004). This approach is common for sampling algorithms that are enumerative. Another solution is to define a score term that favors a closed backbone (e.g. a harmonic restraint across the break) and to let the sampling algorithm (or a gradient minimizer) find conformations that satisfy that term (Adhikari et al., 2012; Collura et al., 1993; Fernandez-Fuentes et al., 2006; Fiser et al., 2000; Heo et al., 2017; Liu et al., 2009; Macdonald et al., 2013; Rohl et al., 2004; Spassov et al., 2008; Tang et al., 2014). However, this solution may require spending a significant amount of time sampling conformations that are not closed, which is inefficient. An alternative is to use inverse kinematics algorithms borrowed from the field of robotics that calculate the accessible conformations of objects subject to constraints, such as determining the possible positions of the interior joints of a robot arm given fixed positions for the shoulder and fingertips. In the context of loop modeling, such algorithms can be used after sampling to adjust the backbone torsions in the loop such that the loop remains closed. Iterative inverse kinematics algorithms such as cyclic coordinate descent (CCD) (Canutescu et al., 2003) converge on a closed backbone over a series of steps and have been applied in many protocols (Li et al., 2011; Liang et al., 2014; Marks et al., 2017; Minary et al., 2010; Shenkin et al., 1987; Wang et al., 2007; Xiang et al., 2002). Analytical inverse kinematics algorithms such as kinematic closure (KIC) (Coutsias et al., 2004) calculate exact solutions to the closure problem using 6 degrees of freedom (such as backbone torsions) to achieve closure, allowing any other degrees of freedom to be sampled freely. These algorithms have also been used in many protocols (Coutsias et al., 2004; Lee et al., 2010; Mandell et al., 2009; Park et al., 2014; Wedemeyer et al., 1999; Wong et al., 2017). Loop design will require efficient sampling in sequence- and conformation-space, so the efficiency of the inverse kinematics methods makes them good choices for maintaining closure. KIC in particular can simultaneously satisfy multiple geometric restraints (such as ring closure (Coutsias et al., 2016), disulfide bonding (Bhardwaj et al., 2016) and catalytic group placement), which may be particularly valuable for loop design.

Scoring

The final component of a loop modeling algorithm is the score function used to evaluate which conformations are the most realistic. Loop modeling algorithms lie on a continuum based on the score function they employ. On one side of the continuum are the algorithms that use physical score functions like AMBER (Rapp et al., 1999), CHARMM (Olson et al., 2011; Olson et al., 2008; Spassov et al., 2008), and OPLS (Jacobson et al., 2004). Some algorithms also use a “colony” score term that tries to capture the effects of entropy by favoring the models with the most conformationally similar neighbors (Fogolari et al., 2005; Xiang et al., 2002). On the other side of the continuum are algorithms that use statistical score functions derived from distributions of atoms and residues observed in high-resolution structures, such as DFIRE (Holtby et al., 2013; Lee et al., 2010; Wong et al., 2017; Yang et al., 2008), DOPE (Adhikari et al., 2012), SOAP-Loop (Marks et al., 2017), GOAP (Zhou et al., 2011) and others (Galaktionov et al., 2001; Macdonald et al., 2013). However, many loop modeling algorithms use hybrid score functions which include both physical and statistical terms (de Bakker et al., 2003; Fiser et al., 2000; Heo et al., 2017; Li et al., 2011; Liang et al., 2014; Mandell et al., 2009; Park et al., 2014; Rohl et al., 2004; Wang et al., 2007). Some methods use a statistical score function for coarse-grained sampling and a physical score function in the full-atom sampling stage.

What considerations are relevant to loop design? Hybrid score functions have been shown to be successful in many applications of computational protein design using Rosetta (Huang et al., 2016). Although there are clear examples of shortcomings (Das, 2011; Dou et al., 2017; Mandell et al., 2009), all of the computational loop design methods reviewed above used the Rosetta score function (Alford et al., 2017; Kuhlman et al., 2003). While other score functions could also be applied to loop design, one consideration is the need for a score term that allows for the comparison of models with different sequences. For example, arginine might be more likely to score better than alanine simply because the former has more atoms, and thus more opportunities to make favorable contacts. Design score functions must use an additional score term (called a “reference energy” in Rosetta) to counteract this bias.

Another consideration for loop design is the solvent model. While many loop modeling methods use an implicit solvent model for computational efficiency, it may be possible to apply explicit solvent models in the context of loop design. As mentioned in the section on barrier traversal, the computational validation step of a loop design protocol (Figure 2C) may be able to devote more time towards a small number of structures, allowing the use of more resource-intensive techniques. As loops are typically solvent exposed, an explicit treatment of the solvent may yield worthwhile improvements in accuracy.

What problems are unique to loop design?

Having discussed loop design in the context of loop modeling, let us now focus on aspects that are specific to loop design. The first of these aspects is a technical consideration: how many residues should be in the designed loop? The loop must be long enough to address the design goal (e.g. if the goal is to position a residue, the loop must be able to reach said residue), but ideally as short as possible. Not only are shorter loops less likely to be conformationally heterogeneous, they are also easier to model accurately. The most naive approach to designing loop length is to simply try several different lengths, but this is inefficient. Loop design already has to grapple with the enormous task of sampling both sequence- and conformation-space. Two more thoughtful approaches have already been explored. Murphy et al. randomly added and removed residues from the loop during design, and validated their approach with a loop length recovery benchmark (Murphy et al., 2009). Lapidoth et al. sampled loop sequences and conformations from a database, which included loops of different lengths (Lapidoth et al., 2015). However, neither of these approaches modified their score function to compare loops of different lengths. Just as score functions will prefer large amino acids over short ones (as described above), so too will they prefer long loops over short ones. While this bias did not prevent either group from creating successful designs, it could be addressed using the worm-like chain model to create a reference state for loop lengths. Specialized algorithms are also needed to make length-independent structural comparisons (e.g. for clustering) (Nowak et al., 2016).

The second, more fundamental problem that loop design must confront is: how can the flexibility or rigidity of a loop be accounted for during the design process? For example, one may wish to ensure that a designed loop is adequately rigid, or conversely, to create a loop with defined functional flexibility. Although it is well known that protein native states are best thought of as occupying an ensemble of conformations, only a handful of loop modeling methods have tried to account for the possibility that a loop might not have a single defined conformation (Marks et al., 2018; Nilmeier et al., 2011; Shehu et al., 2006). This consideration may be less important for loop modeling, where the sequence segments being predicted come from natural proteins and are often well-structured, but it is of immediate importance to loop design, where the sequences being predicted were created computationally and disorder could be a common mode of failure. There are many methods for predicting protein flexibility, and while a recent report has begun addressing the issue of designing flexibility by engineering exchange between different sidechain conformations at equilibrium (Davey et al., 2017), to our knowledge these approaches have not yet been applied to the design of loop flexibility. There are two main approaches for predicting flexibility. The first is to generate an ensemble of possible conformations and then to calculate Boltzmann-averaged quantities (like RMSD) over that ensemble (Benson et al., 2008; Hilser et al., 1996; Nilmeier et al., 2011; Shehu et al., 2006; Shehu et al., 2007). The challenge with this approach is the expense of computing the ensembles and the impossibility of knowing whether all of the relevant states have been sampled. The ensembles must also be generated by a method that obeys detailed balance, which adds complexity. The second approach is to represent the protein as a graph and to infer rigidity from the connectivity of that graph (Bramer et al., 2018; Dobbins et al., 2008; Jacobs et al., 2001; Pandey et al., 2005; Sarkar, 2017). Usually the nodes represent atoms or residues, and the edges represent the covalent and non-covalent interactions between those nodes. The challenge with this approach is that it abstracts the details of protein structure and is often more focused on motions at the domain level than at the individual residue level. It is an open question which of these approaches will work best for loop design.

Closing remarks

In conclusion, we have reviewed the current state of the loop design field and highlighted several promising avenues for progress in the near future: (i) hybrid representations of functional and structural requirements, (ii) template- or fragment-based sampling, (iii) inverse kinematic closure methods, (iv) hybrid score functions that account for sequence- and length-biases and accurately balance polar interactions and solvation, (v) enhanced sampling methods for evaluating competing conformations, and (vi) methods that incorporate loop flexibility and rigidity into the design process. The field has had success designing small loops and antibodies, and is poised to continue making progress by repurposing and improving existing loop modeling algorithms. Questions such as how to sample loop lengths and how to make a loop either rigid or flexible still need to be grappled with. That said, we believe that many of the technologies enabling the next steps forward are largely in place. Our hope is these steps will lead to methods capable of routinely and accurately designing structured loops. As loops are an integral feature of many functional proteins — including enzymes, binders, and switches — such methods will be a boon to the broader and ongoing effort to design functional proteins using computational methods.