Classification of cocaine-dependent participants with dynamic functional connectivity from functional magnetic resonance imaging data

Abstract

Static functional connectivity (FC) analyses based on functional magnetic resonance imaging (fMRI) data have been extensively explored for studying various psychiatric conditions in the brain, including cocaine addiction. A recently emerging, more powerful technique, dynamic functional connectivity (DFC), studies how the FC dynamics change during the course of the fMRI experiments. The aim in this paper was to develop a computational approach, using a machine learning framework, to determine if DFC features were more successful than FC features in the classification of cocaine-dependent patients and healthy controls. fMRI data were obtained from of 25 healthy and 58 cocaine-dependent participants while performing a motor response inhibition task, stop signal task. Group independent component analysis was carried out on all participant data to compute spatially independent components (ICs). Eight ICs were selected manually as relevant brain networks, which were used to classify healthy versus cocaine-dependent participants. FC and DFC measures of the chosen IC pairs were used as features for the classification algorithm. Support Vector Machines were used for both feature selection/reduction and participant classification. Based on DFC with only seven IC pairs, participants were successfully classified with 95% accuracy (and with 90% accuracy with three IC pairs), whereas static FC yielded only 81% accuracy. Visual, sensorimotor, default mode, and executive control networks, amygdala, and insula played the most significant role in the DFC-based classification. These findings support the use of DFC-based classification of fMRI data as a potential biomarker for the identification of cocaine dependence.

1 ∣. INTRODUCTION

Functional neuroimaging methods, functional magnetic resonance imaging (fMRI) in particular, have provided unparalleled possibilities to explore brain mechanisms in vivo in human participants. Although findings based on neuroimaging methods have advanced our understanding of neural mechanisms of brain diseases, including substance use disorders, the diagnostic utility of neuroimaging methods has not yet been fully realized (Adinoff & Stein, 2011). For example, the methodology of functional connectivity (FC) (Sinha, 2001) was first applied in the addiction field only about a decade ago (Hong et al., 2009), relatively recently, given its first use in 1995 (Sinha, 2001). Exploring a new analytic methodology to advance our understanding and diagnosis of cocaine dependence based on neuroimaging, our study applies a novel and powerful analytic method to fMRI datasets of cocaine-dependent (CD) and non-cocaine-abusing, healthy control (HC) participants.

The task used in this work was a Stop Signal Task (SST), which assesses motor response inhibition (impulse control). Motor response inhibition is a function that has been closely associated with impulsiveness (Bari & Robbins, 2013) and has been consistently found to be impaired in patients with addiction, including cocaine addiction (Elton et al., 2014; Wang et al., 2018). SST assesses the countermanding of a prepotent motor response to go signals, when the go signals are unexpectedly followed by stop signals. The task response is a modified version of the classic go/no-go task (Littman & Takács, 2017). SST has a higher load on inhibitory control than the go/no-go task, which requires selective attention and selective response inhibition to some trials and not others. As a result, the SST, which measures “controlled inhibition,” is a more difficult motor inhibition task than go/no-go task, which measures “automatic inhibition” (Logan, 2015; Verbruggen & Logan, 2008a,2008b,2008c). Furthermore, the tracking SST is particularly challenging since it is titrated to the inhibitory performance of the participant. Nonetheless, since response inhibition is highly relevant in substance abuse and addiction, both tasks are widely used in neuroimaging of substance abuse and addiction (Ahmadi et al., 2013; Wang et al., 2018; Zhang, Zhang, et al., 2018) since they assess how well a participant can inhibit his/her response and functional neuroimaging methods such as fMRI during the performance of these tasks can capture brain regions’ responses that mediate inhibitory control, such as inferior frontal cortex, sensorimotor area, subthalamic nucleus, more consistently than the go/no-go task (Rubia, Smith, Brammer, & Taylor, 2003; Zhang & Li, 2012). Combining dynamic functional connectivity (DFC) with a task that is more closely aligned with the phenotypic cognitive deficit of impulse control is also more meaningful than using resting-state data. The goal of this study was hence to examine differentiations of brain functional connectivity (FC) in cocaine-dependent participants relative to healthy controls using DFC applied to fMRI data during a task which is highly relevant to addiction, i.e., during inhibition performance (that is indicative of impulse control) in an SST.

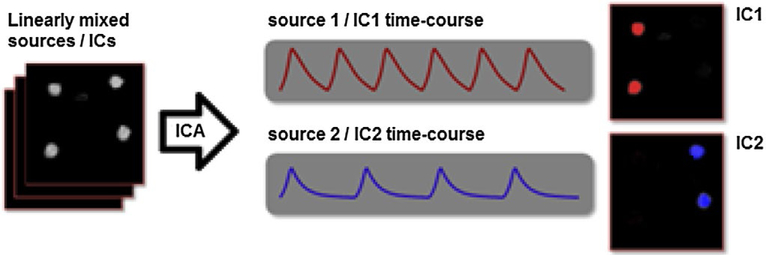
In this study, fMRI data collected from cocaine-dependent individuals and healthy controls during the SST experiments were utilized to develop a statistical model to separate healthy controls from cocaine-dependent participants based on only the fMRI data. A data-driven entropy-based algorithm, independent component analysis (ICA), was used to extract spatially independent brain regions (independent components, ICs) in cocaine-dependent and control participants. Since these regions play significant roles in recognition of being addicted or healthy, a machine learning/pattern classification method was trained and applied to separate control participants from the cocaine-dependent participants. ICA is one of the most widely used methods to analyze the functional organization of the brain in terms of two complementary principles, localization (segregation) and connectionism (integration) (Phillips, Zeki, & Barlow, 1984). ICA decomposes data into statistically independent components by assuming that observations are linear mixtures of independent sources. ICA then utilizes higher order statistics to decompose data iteratively, and the output of ICA are components with maximal mutual independence. In fMRI applications of ICA, data are viewed as a two-dimensional (2D) spatio-temporal matrix obtained by flattening the four-dimensional (4D) fMRI data. A 2D spatio-temporal matrix can be separated into either spatially or temporally independent components. Specifically, the application of spatial ICA to fMRI data has been used in order to identify spatially independent and temporally coherent components of brain activity. Figure 1 explains the spatial ICA with a toy example (Calhoun, Liu, Liu, & Adali, 2009; McKeown et al., 1998).

FIGURE 1.

A cartoon illustration of independent component analysis (ICA) on fMRI time courses, which are assumed to be comprised of linearly mixed sources. Spatial extent of statistically independent components (such as IC1 and IC2 in this example) which represent two sources (which can represent spatially independent brain networks), and their representative time courses for each source, can be extracted with ICA from a (linear) mix of the sources, the overall spatial extent of which is shown on the left (Calhoun, Liu, et al., 2009). Note that, as in this example, the sources do not have to be spatially clustered for ICA to extract them

ICA has gained particular attention for functional connectivity analysis since it is a blind or data-driven algorithm, i.e., it is not model-driven like the general linear model, and the only assumptions it has are having linear mixture of independent sources/components and an additive Gaussian noise (Calhoun, Liu, et al., 2009). ICA, in the form of group spatial ICA, has also been used in many group studies revealing functional connectivity among different brain networks in the group level (Calhoun et al., 2006; Calhoun, Adali, Pearlson, & Pekar, 2001; Calhoun, Eichele, & Pearlson, 2009). Recently, ICA has been used in studying cocaine dependence. For example, Zhang, Zhang, et al. (2018) studied dynamics of functional connectivity to address differences between cocaine-dependent and non-drug-using individuals using a graph theoretical framework. There are also earlier ICA studies using SST in healthy participants (Zhang & Li, 2012; Zhang et al., 2015) and more recent ICA studies of the SST in cocaine-dependent people (Wang et al., 2018). In particular, Elton et al. (2014) studied the classification of cocaine-dependent males from nondrug-abusing males using ICA and SST; Worhunsky et al. (2013) investigated networks of functional connectivity underlying cognitive control in cocaine dependence and examined the relationship of the networks to the disorder and its treatment using ICA and Stroop task; Kilts et al. (2014) explored the role of discrete neural processing networks in the representation of individual differences in cocaine dependence using ICA and Stroop task.

In this study, we applied ICA to fMRI data recorded during an SST to calculate both static and dynamic functional connectivity (FC and DFC), which are then used as features by a machine learning algorithm to classify participants. Investigation of the dynamics of FC, henceforth referred to as DFC, is a relatively new field of neuroimaging research (Sakoglu & Calhoun, 2009; Sakoğlu & Calhoun, 2009; Sakoglu et al., 2010) and shows great potential to enhance and complement the findings of FC analyses, which are static. When applied to task data, DFC analyses can also reveal how a particular task enhances or affects (inhibits) functional connections between pairs of brain networks (Sakoglu & Bohra, 2013; Sakoglu & Calhoun, 2009; Sakoglu et al., 2010). By comparing FC and DFC measures from both groups, our goal was to find brain networks in relation to inhibitory control which are the most discriminative in classifying cocaine-dependent patients versus healthy controls.

As for substance use disorders, alcohol intoxication effects have been studied with ICA of fMRI (Calhoun, Carvalho, Astur, & Pearlson, 2005). Alcohol-dose effects on brain activation were explored using ICA to isolate systematically nonoverlapping networks and their time courses (Calhoun, Pekar, & Pearlson, 2004). ICA and DFC analyses have been recently used to study alcohol, nicotine, and marijuana dependence (Vergara, Weiland, Hutchison, & Calhoun, 2018). Networks found with ICA have been further used to study DFC characteristics in schizophrenia patients both with task (auditory oddball task) (Sakoglu & Calhoun, 2009; Sakoglu et al., 2010) and at rest (Sakoğlu & Calhoun, 2009; Sakoğlu, Michael, & Calhoun, 2009). To our knowledge, there is currently only one other published study using DFC analysis of fMRI datasets in cocaine dependence; Zhang, Zhang, et al. (2018) recently studied network dysfunction in cocaine dependence using graph theoretical analysis. There have been many static functional connectivity analyses of cocaine dependence. For example, Li et al. (2000) explored static FC in seven cocaine users. More recently, several groups reported functional connectivity alterations in cocaine dependence in the reward and executive control networks (Hobkirk, Bell, Utevsky, Huettel, & Meade, 2019), between lateral and medial hypothalamus and dorsolateral prefrontal cortex and ventral precuneus (Zhang, Wang, Zhornitsky, & Li, 2018), and between ventral striatum and hippocampus and prefrontal cortex (Zhang & Li, 2018), using fMRI.

In this study, once significantly discriminative clusters of brain voxels were found, a machine learning/ pattern classification algorithm, the support vector machine (SVM) algorithm, was used to automatically map a participant into one of the two groups, cocaine-addicted or healthy control. An SVM-based classification algorithm was trained with FC and DFC features for each participant. The proposed DFC-based participant classification was compared with the FC-based classification using the same ICA generated regions for all participants. Through a feature selection framework, the classification was repeated to find a subset of brain regions (same brain regions for all participants), maximizing the accuracy of the classification. SVM-based techniques using MRI or fMRI data have also been used in classification of various brain disorders, including nicotine addiction (Pariyadath, Stein, & Ross, 2014; Vergara, Mayer, Damaraju, Hutchison, & Calhoun, 2017), and mild traumatic brain injury (Vergara, Mayer, Damaraju, & Calhoun, 2017; Vergara, Mayer, Damaraju, Hutchison, et al., 2017). SVM has also been used in combination with the SST in another disorder of impulse control, Attention Deficit Hyperactivity disorder (ADHD) for classification (Hart et al., 2014). More recently, in a large analysis study which involves over 3,000 subjects, an SVM-based classification of regional brain volumes from MRI data successfully classified individuals with substance dependence to nondependent control subjects (Mackey et al., 2019).

In summary, in this work, we investigated ICA-based DFC in cocaine-dependent and control participants’ fMRI data collected while they are performing a controlled response inhibition task (SST), and we performed classification of the two groups using a state-of-the-art machine learning technique, SVM. By focusing on the most discriminative brain regions, the developed methodology can be validated in larger studies, potentially offering a useful clinical diagnostic tool. We describe our methods in the next section, which is followed by the results section, and we present our discussions and conclusions in the last section.

2 ∣. METHODS AND MATERIALS

2.1 ∣. Participants

Research participants were 58 cocaine-dependent individuals and 25 age-matched healthy controls. Cocaine-dependent participants were recruited from three residential treatment programs in Dallas, Texas: the VA North Texas Health Care System, Homeward Bound, Inc., and Nexus Recovery Center, Inc. Participants were financially compensated for their participation. The criteria for cocaine dependence was the Structured Clinical Interview for DSM-IV-TR Axis I Disorders; all cocaine-dependent participants endorsed cocaine as their primary drug of choice. Cocaine-dependent participants were administered a comprehensive medical history and physical examination, a general laboratory panel, urine drug screen, and a guided interview of lifetime substance use history during the first and second week of inpatient treatment. Participants were excluded if they had any history of major illness, had an estimated IQ below 70 (per the Wechsler Test of Adult Reading), met criteria for any neurological or active Axis I disorder (other than substance use disorders), or were on any central nervous system active medications (including all psychotropics). Other drug use among cocaine-dependent individuals was not a criterion for exclusion, as long as cocaine dependence was the primary diagnosis. 15 of the CD participants also had history of alcohol, whereas none of the CD participants had alcohol abuse history. Cocaine-dependent participants were recruited following admission to one of three residential cocaine dependence treatment programs in Dallas, Texas, and were admitted as soon as possible after their last reported use of cocaine. All three programs utilized the Minnesota Model psychosocial treatment approach. Urine drug screens were conducted throughout residential treatment to verify abstinence. The time in treatment varied between 2 and 4 weeks. This time frame allowed the resolution of cocaine intoxication, cocaine withdrawal symptoms, and reasonable stability of other mood symptoms while remaining in a monitored residential setting. It was anticipated that variability with this small window of abstinence in a substance-free, residential treatment program would be minimal. All participants admitted into the three treatment programs over a 4-year period were screened. Informed consent was obtained on 180 participants (46 female, 134 male). Ninety seven were excluded from the analyses of this paper due to not meeting inclusion criteria, early discharge from program, or withdrawal of consent or technical problems with fMRI data.

Healthy control participants had no lifetime history of substance use disorder. Other psychiatric, medical, and cognitive exclusion criteria were similar to that of the cocaine-dependent participants. All aspects of the research protocol were reviewed and approved by the Institutional Review Boards of the University of Texas Southwestern Medical Center at Dallas and the Veterans Administration North Texas Health Care System. Participants signed an informed consent before study participation and were compensated for their participation. Relevant demographic and clinical characteristics of the participants are provided in Table 1.

TABLE 1.

Demographic and clinical characteristics of control and cocaine-dependent (CD) participants (means ± SD)

	Control (n = 25)	CD (n = 58)
Age (years)**	42.2 ± 8.9	44.5 ± 6.6
Sex*
Male	16 (64.0%)	52 (89.7%)
Female	9 (36.0%)	6 (10.3%)
Race*
African-American	12 (48.0%)	43 (74.1%)
Caucasian	11 (44.0%)	10 (17.2%)
Hispanic	1 (4.0%)	5 (8.7%)
Other	1 (4.0%)	0 (0%)
Education (years)*	13.8 ± 1.0	12.2 ± 1.7
Estimated FSIQ*	97.9 ± 10.7	87.8 ± 8.8
Nicotine Use
Packs/day*	0.05 ± 0.2	1.0 ± 0.9
% smokers*	5	67
Time from admission to MRI scan (days)		21.3 ± 4.4
InDUC
Recent*	1.2 ±2.9	80.3 ± 19.9
Lifetime*	5.2 ± 6.9	39.3 ± 4.7
Craving
CCQ-brief	–	2.4 ± 0.9
OCCS	–	24.5 ± 7.7
Stop signal test (SST)
MRT (ms)**	748.9 ± 237.8	711.7 ± 180.6
SSD (ms)**	198.6 ± 86.3	190.5 ± 71.5
SSRT (ms)**	411.8 ± 310.6	364.0 ± 283.9
Omission (%)**	12.1 ± 3.1	11.8 ± 3.1
Inhibition (%)**	52.2 ± 5.2	51.0 ± 4.1

Note. Comparisons between groups were done by t test two-sample t-test with unequal variance.

Abbreviations: CCQ-Brief: Cocaine Craving Questionnaire-Brief; FSIQ: full-scale IQ; InDUC: Inventory of Drug Use Consequences; OCCS: Obsessive-Compulsive Cocaine Scale; SSRT: stop signal response time; MRT: mean response time to go trials. SSD: stop signal delay.

^*Difference between groups, p < 0.05, (n₁ = 25, n₂ = 58).

^**No statistically significant difference between groups, p > 0.05, (n₁ = 25, n₂ = 58).

2.2 ∣. MRI data acquisition

Cocaine-dependent individuals completed scans during their final week of a 2- to 4-week residential treatment program. Participants completed fMRI scans during which they were instructed to lie as still as possible with their eyes open. Two control participants were excluded from all imaging analysis due to a technical error during acquisition of the resting data. Functional MRI acquisition was performed on a Philips 3T magnetic resonance scanner (Philips Medical Systems, Best, The Netherlands). BOLD fMRI data during the SST experiment were acquired using a single-shot echo-planar imaging sequence with 3.25 χ 3.25 mm² in-plane resolution, 36 slices (thickness/gap = 3/0 mm), field-of-view (FOV) 208 × 208 × 108 mm, matrix size 64 × 64 × 36, repetition time/echo time = 1,700/25 milliseconds, gradient-echo echo-planar imaging (EPI) with flip angle 70°, and 384 volumes over the duration of about 653 s. For spatial normalization purposes, high-resolution T1-weighted images were acquired with a spatial resolution of 1 × 1 × 1 mm³.

2.3 ∣. Stop signal task

The task has previously been proposed and described by Rubia et al. (2003) and been used to classify ADHD from healthy controls with almost 80% classification accuracy (Hart et al., 2014). Goggles were used for stimulus presentation. A rapid mixed-trial event-related fMRI design was used. Horizontal white arrows (“Go” stimulus) on a black background pointing either left or right appeared for 500 ms with a mean inter-stimulus interval (ISI) of 1.8 s (1.6, 1.8, 2.0 s). The three ISIs were randomly presented to optimize statistical efficiency. Participants were instructed to make a button response to Go signals with their left or right thumb corresponding to the arrow direction as soon as possible. In the unpredictable, infrequent Stop trials (74 Stop trials, approximately 20% of the trials), horizontal arrows were followed (after a variable 250–900 ms delay), by vertical arrows pointing upward (“Stop” stimulus). Participants were instructed to inhibit their response to the preceding Go stimulus when a Stop arrow was presented after the Go stimulus. The delay between Go and Stop stimuli was titrated, according to each participant’s performance. The tracking algorithm was designed to assure the task was equally challenging for each individual, providing 50% successful (StopSuccess) and 50% unsuccessful (StopFail) inhibition trials. Seventy-four Stop trials (evenly distributed between right and left Go arrows) were pseudo-randomly interspersed with 288 Go trials. Successive Stop trials were separated by at least three Go trials to allow better separation of the hemodynamic response. Stop and Go trials were equally distributed between right and left arrows. The number of Stop and Go trials, 74 and 288, respectively, were the same for each participant. Performance on the SST was calculated for each participant. The Stop Signal Response Time (SSRT) is the time required for a participant to cancel their movement after seeing the stop signal, where longer SSRTs indicate poorer response inhibition. SSRT was calculated by subtracting the average stop signal delay at which participants achieve 50% of inhibition from the average reaction time to go signals (Rubia et al., 2003). The mean and standard deviation of the SSRT for each of the two groups, as well as other task performance measures such as mean response time to Go trials (MRT), stop signal delay (SSD), omission percentage to Go trials, and inhibition percentage, are presented in Table 1.

2.4 ∣. Data processing and analysis

The fMRI time series data were realigned (motion-corrected) using MCFLIRT (Jenkinson, Bannister, Brady, & Smith, 2002), slice time corrected, resampled, and normalized into standard 2 mm × 2 mm × 2 mm MNI space (91 × 109 × 91 matrix) for all of the volumes, using FSL (http://fsl.fmrib.ox.ac.uk). Spatial smoothing with a Gaussian kernel of 5-mm full-width at half-maximum (FWHM) was also performed. A 2 mm MNI T1 brain mask was applied for the brain extraction. Spatial group ICA was done on normalized data using the Group ICA of fMRI (GIFT) Toolbox (http://mialab.mrn.org/ software/gift). The number of independent components was set to 20 to keep the number or ICs manageable. Static FC and DFC analyses were done using a MATLAB-based graphical user interface software (Esquivel, Mete, & Sakoglu, 2013,2014) which was developed in-house and was based on an earlier work by Sakoglu and Calhoun (2009), Sakoğlu and Calhoun (2009), Sakoglu et al. (2010).

Procedurally the Group ICA begins by reducing the ICs to be evaluated by ICA by first using principal component analysis (PCA) in two stages. Each participant file contains 384 fMRI time points. The first stage reduced each of the 83 participants with 384 BOLD fMRI time points to 83 participants, each with 20 ICs. The second stage of PCA reduced this group to a single group of 20 ICs for the participants grouped together. This final group is evaluated with InfoMax ICA. InfoMax ICA was setup with bias and sphering on. Block size, stop, Irate, max step, anneal, and anneal angle were set to default values of 275, 1 × 10⁶, 0.0050071, 512, 0.9, and 60 degrees, respectively. The results are then back reconstructed for each of the 83 participants, each with 20 ICs and an accompanying time course for each IC. After detailed visual inspection, 12 of the 20 ICs were found to be artifactual or nonrelevant components; therefore, the number of relevant ICs were reduced to 8, which constitute the relevant brain networks for our analysis.

Static FC between any two ICs was measured by calculating the 2D correlation between the time courses of the two ICs. The result is a single cross-correlation coefficient (cc), which reveals how strong the connection is between the two ICs. A matrix of cc values is generated by calculating the 2D correlation for all IC and participant combinations. Therefore, with 83 participants, 8 ICs and 28 IC-pair combinations, a matrix with 83 rows and 28 columns is generated. Column labels were added to the data to identify the IC combinations the data belonged to. Row labels were added to identify which group (control or CD) each participant belonged to. This static FC matrix is then used for classification between control and CD.

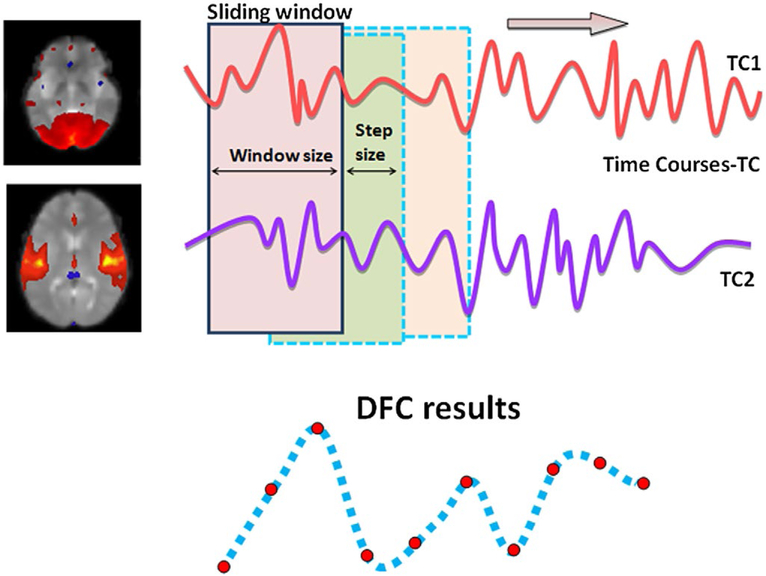
The method used to calculate DFC was by sweeping a time window across a time course (Figure 2). All points from each time course that are inside the sliding window rectangle are used in the 2D correlation to produce a single cross-correlation coefficient (cc). For each participant, pair-wise regions are determined and their fMRI time courses are recorded in two single-dimensional arrays. Two parameters were required: window size and window step size. Correlation coefficients of the resulting DFC, which is also a dynamic time series data, are calculated for each of the windowed time courses of each IC pair, at every window step. Each IC for each of the participants has a corresponding time course, and thereby the time coursers were extracted from the ICA’s computations, for the IC’s of interest (the ones that are deemed to represent meaningful brain networks, not artifacts). Throughout this paper, the calculation of DFC correlation coefficients from two time courses is considered the smallest calculation unit of the DFC analyses. In general, once the time courses are extracted (via ICA or otherwise, such as ROI-based average time course extraction), DFC analyses investigate interactions among brain networks or regions using sliding window correlation. The outcome of DFC analysis between two networks or brain regions is also another time course that summarizes dynamics between the regions of interest. At the end, this method identified pairs of brain areas that are interacting together and the dynamics of the interaction. The DFC between two brain networks or regions is summarized in Figure 2. In our case, we determined the brain networks via ICA. More details on the methodology of the DFC can be found in Sakoglu et al. (2010).

FIGURE 2.

Visualization of Dynamic Functional Connectivity (DFC) analysis on two brain regions (or two ICs, if ICA is employed). The two brain regions (ICs), each with their own fMRI time course, constitute a “pair”. For each pair, and for each time window, one DFC time point is obtained. By sliding the time window, the DFC time course for the pair is obtained

In our study, the size of the sliding window is 32 time points. With a TR = 1.7 s, the time window is 54.4 s wide. Each time the window steps across the TCs, 8 time points are jumped over (window step size of 8), which corresponds to a 13.6 s. We chose the size of 32 for the sliding window since one needs n > 30 data points in order to obtain a reliable correlation coefficient statistically (for n > 30 samples, the t-distribution and the Normal distribution are very similar). Choice of 8 for the window step size was somewhat arbitrary; we wanted to keep a balance between having too short of a step size (which would probably not capture any real DFC changes but probably mostly noise) and too long (which could miss any real DFC changes). We discuss the effects of our window size and the window step size more in the Discussion section. In our case, since there are 384 total time points, as a result, the DFC analysis results in 45 cc values. There are 28 pairing combinations between 8 ICs. Therefore, with 83 participants, 8 ICs, 28 IC pairs, and 45 cc values per IC combination, a matrix with 83 rows and 1,260 columns was generated. Column labels were added to the data to identify the IC combination that the data belonged to as well as the order number of the cc. Row labels were added to identify which group (controls or CD) each participant belonged to. This DFC cc matrix was then used for classification between controls and CD.

2.5 ∣. Anatomical identification of the independent components

Anatomical identification of the ICs was performed using the Harvard-Oxford brain atlas (Desikan et al., 2006; Peng, Long, & Ding, 2005) in order to determine which anatomical brain regions that had the most coverage by each IC. The procedure which is used to score the coverage of each atlas region by an IC network is described in the pseudocode shown in Table 2. In this process, we calculate regionCoverage, which is the percent coverage of the region by the IC. Only ICA voxels for which the absolute value Z-score is greater than 1.7 qualify as region covering voxels. The value of 1.7 indicates that the voxel is beyond 99% of the Z-score distribution. For the Harvard-Oxford atlas, the values outside the region have a value zero, but the values inside the region are between the values 0 and 1. The Harvard-Oxford atlas is a probability map so the voxel values inside a region increase as the likelihood of being in the region increases. Therefore, the regionCoverage for the Harvard-Oxford atlas is percent likelihood of being a specific region as opposed to being a flat coverage or overlap of the region.

TABLE 2.

Pseudocode showing the process for anatomical region (AR) identification of the independent components (ICs)

regionSum = regionTotal = 0

for each xyz in DimSize

regionTotal = regionTotal + AR3D[xyz]

if abs( IC3D[xyz]) > 3.5

regionSum = regionSum + AR3D[xyz]

regionCoverage = regionSum/regionTotal

IC3D: 3D spatial ICA map which has a Z-score value at each IC-voxel.

AR3D: 3D spatial atlas which has a value K at each AR-voxel.

IC3D and AR3D have the same 3D [xyz] dimensions which we name DimSize.

2.6 ∣. Feature selection and classification

Classification was performed using Weka (Frank, Hall, Trigg, Holmes, & Witten, 2004), a widely used data mining and classification software written with a Java platform. The FC and DFC matrices were converted from MATLAB into Weka’s.arff data format to be compatible with the Weka software. All features, which are cross-correlation coefficients, are normalized between [−1, 1]; however, no standardization (zero-mean, unit-standard deviation) was applied to the dataset. Each column (28 columns in FC, 1,232 columns in DFC) in the two matrices was initially considered a feature to be used in the classification. The SVM classification algorithm from LIBSVM (Chang & Lin, 2011), a popular open source machine learning library, was used. During classification, the least significant IC pairs were iteratively reduced one at a time, in order to determine how the classification accuracy changed after removal of the pair. Having a high number of features does not simply yield the highest classification accuracy for nonlinear classification algorithms such as SVM, and in general when the number of samples are not high (curse of dimensionality). Therefore, the number of features were reduced. This process constitutes the first step in feature reduction in which the minimal set of ICs yielding the best classification accuracy was found.

The process of iterative removal of IC pairs started with the set of all 28 pairs, including all initial feature sets used in SVM classification. In the case of DFC-based classification, the features associated with an IC pair were removed all together as a group, i.e., removal of an IC pair required removal of all 45 DFC measures computed for the IC pair. This group removal process was only specific to DFC since each pair in FC involves only one FC measure, not a group of 45 features as in DFC. In the beginning of DFC experiments, the number of features was 28 × 45, whereas FC experiments started with only 28 features (one for each IC pair).

In both experiments (DFC, FC), the pair to be removed in each iteration were selected utilizing a weight vector $\mathit{w}\in \{\mathbb{R}{\}}^n$ (where n = 28 for FC and n = 28 × 45 for DFC) in SVM. Since each entry of w corresponds to a feature in the classification problem, Guyon, Weston, Barnhill, and Vapnik (2002) showed that the larger ∣w_j∣ ,j ≤ n, the more the contribution to the classification decision. In this notation, n is the number of features in the classification problem, and n-element w vector is the weight vector, which, after iterations of the classification algorithm, becomes the solution of the classification problem. W_j is the jth element of w. Following Guyon et al. (2002), linear SVM classifiers were run iteratively, removing the least significant pair from the current set at every iteration. The stopping condition was satisfied once all but one pair was removed. In each iteration, participants were classified using the leave-one-out (LOO) model validation method. The LOO scheme is the exhaustive version of k-fold cross-validation with k = N = 83 and avoids the combination-driven calculation problem of k-fold cross-validation. In an LOO scheme, one test participant, S, is excluded from the overall group of N = 83, and it is classified to be control or CD using the model built based on the remaining N – S = 82 participants, which is the training group. S is also called the validation participant. This classification process is repeated N = 83 times, once for each of the participants. The accuracy of model is reported in each case. Note that SVM classification models obtained for each training dataset result in different but similar classification models (a hyperline in multidimensional space) even if the SVM is trained with exactly the same parameters and constraints. In general, a dataset with significant informative features would be more robust to removal of a particular S, assuming that the other participants who are of the same class as S will cover the missing information excluded by the removal of S.

Because of the nature of SVM’s heavy dependence to parameter selection, in each iteration, training and classification were done using various parameters and kernels. The list of parameters and kernels is provided in Table 3. The parameters used for DFC-based results, which provide the best classification with 7 IC pairs, are provided in bold font.

TABLE 3.

Parameters and their ranges tested with support vector machine (SVM) algorithm on the dataset. Parameters in bold font are the ones that provided the highest classification accuracy

Kernels	linear, radial basis function, polynomial, sigmoid
SVM type	C – SVM, ν – SVM
Degree of polynomial function	3, 4, 5, 6, 7
C	2, 4, 10, 12, 16, 20 (N/A in ν–SVM)
Gamma (γ)	0.001, 0.003, 0.01, 0.03, 0.05, 0.1
Coefficient	0.01, 0.1, 1, 5, 10, 15, 20
Nu (ν)	0.2, 0.3, 0.4, 0.5
Normalization	Normalized and not normalized training set

3 ∣. RESULTS

Control and CD participants did not differ in age, but differed in race. Controls had significantly less male participant percentage, higher education, and less nicotine use than the CD participants (Table 1). Unexpectedly, the SSRT, and any of the other task-related behavioral measures, mean response time to Go trials (MRT), stop signal delay (SSD), omission percentage to Go trials, and inhibition percentage did not differ significantly between the two groups either (Table 1).

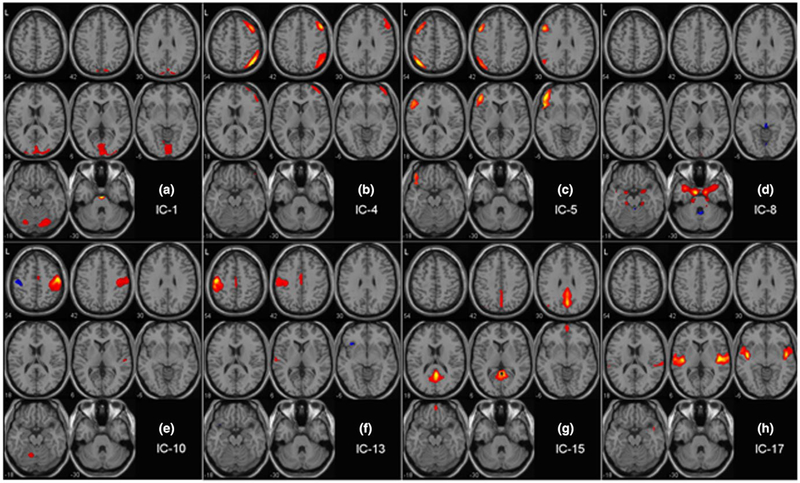
All 20 ICs are shown in the supplementary Figure S1. Number of the ICs were reduced to 8 after detailed visual inspection by eliminating 12 presumed artifactual ICs. ICs 2, 6, 7, 9, 11, 12, 16, and 20 included ventricular, orbital, cerebellar, or cerebrospinal fluid-related artifacts. ICs 3, 6, 14, and 20 have heavy motion-related artifacts. IC 18 includes mostly the brainstem. The remaining eight ICs, used in the subsequent analyses, were IC1: Primary Visual Cortex (PVC); IC4: Right Executive Control Network (R ECN); IC5: Left Executive Control Network (L ECN); IC8: Amygdala + Med. Temporal Lobe (MTL); IC10: Right Motor and Sensorimotor Cortex (R MSMC); IC13: Left Motor and Sensorimotor Cortex (L MSMC); IC15: Ventral Default Mode Network (VDMN); and IC17: Insula (Figure 3). The Z-score significance threshold used in this figure was 3.5, which was also used for identification of the networks. The selected ICs primarily consisted of: The DFC-based classification algorithm started with all 28 IC pairs for a total of 28 × 45 = 1260 initial features (Figure 4). In the FC analysis, the classification framework started with 28 features since each IC pair was represented by only one FC measure. Further details of the anatomical coverage of each of the ICs are listed in Table 4.

FIGURE 3.

Axial view of the eight relevant independent components (ICs, or “networks”, out of the 20 ICs found by the ICA) with Z-score cutoff of 3.5. IC1: Primary Visual Cortex (PVC); IC4: Right Executive Control Network (R ECN); IC5: Left Executive Control Network (L ECN); IC8: Amygdala + Med. Temporal Lobe (MTL); IC10: Right Motor and Sensorimotor Cortex (R MSMC); IC13: Left Motor and Sensorimotor Cortex (L MSMC); IC15: Ventral Default Mode Network (VDMN); IC17: Insula

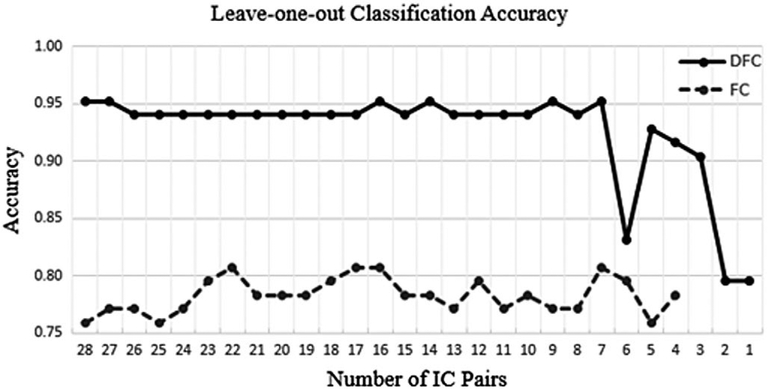
FIGURE 4.

Classification accuracy versus number of independent component (IC) pairs used. Solid line: DFC results. Dashed line: Static FC results

TABLE 4.

Anatomical regions with the most coverage by each independent component (IC) using the AAL atlas

IC 1		IC 4		IC 5		IC 8
Region name	% Overlap	Region name	% Overlap	Region name	% Overlap	Region name	% Overlap
Inf Occip R	90.6	Angular R	94.0	Angular L	92.9	Vermis	84.9
Lingual R	76.0	Inf Parietal R	80.8	Inf Front Tri L	89.2	Temp Mid Pole L	76.5
Lingual L	72.8	Inf Front Tri R	76.7	Inf Front Oper L	79.6	ParaHippo L	75.1
Cuneus R	67.5	Mid Front Orb R	76.5	Inf Front Orb L	62.4	Amygdala L	74.1
Calcarine L	65.5	Mid Front R	75.7	Sup Temp Pole L	57.8	ParaHippo R	68.7
Cuneus L	64.8	Inf Front Oper R	59.8	Mid Front Orb L	50.2	Amygdala R	67.3
IC 10		IC 13		IC 15		IC 17
Region Name	% Overlap	Region Name	% Overlap	Region Name	% Overlap	Region Name	% Overlap
Heschl R	73.4	Postcentral L	83.1	Post Cing L	80.3	Heschl R	100.0
Postcentral R	69.6	Heschl L	73.3	Post Cing R	69.6	Heschl L	98.7
Precentral R	55.2	Paracentral Lob L	55.1	Med Front Orb L	59.5	Sup Temp L	95.1
Cerebellum 3 L	32.9	Precentral L	42.3	Precuneus L	48.8	Sup Temp R	83.6
Sup Parietal R	32.9	Sup Temp L	39.6	Cuneus L	47.1	Rolandic Oper R	64.0
Supp Motor R	31.9	Mid Cing L	37.2	Precuneus R	45.0	Rolandic Oper L	56.8

The accuracy axis in Figure 4 shows the LOO value obtained with the DFW and FC datasets. Classification based on DFC features outperformed the FC approach. The DFC-based classification results showed a stable performance of over 94% until the number of IC pairs were decreased to 6. The FC classification fluctuated significantly between 76% and 81%, utilizing any number of IC pairs between 28 and 4. Since a polynomial kernel of up to degree 7 was utilized, we stopped at 4 IC pairs (hence, 4 features) for FC, due to the computational complexity of fitting data with a large degree kernel to small number of features. One of best classification accuracies using DFC-based features (95%) was obtained with seven IC pairs (308 features); this dropped sharply to 83.0% with six IC pairs, increased to 93% with five IC pairs, and then decreased to 79% with a single IC pair (45 features). DFC-based classification still attained over 90% accuracy with only three IC pairs. The top seven IC pairs attained over 95% LOO accuracy. These seven IC pairs involved primary visual cortex, the executive control network, motor and sensorimotor cortex, ventral default mode network, and insula. The top three IC pairs are also noteworthy since they attained over 90% classification accuracy. These top three pairs involved primary visual cortex, left motor and sensorimotor cortex, ventral default mode network, and insula. The top three and top seven IC pairs are listed in Figure 5.

FIGURE 5.

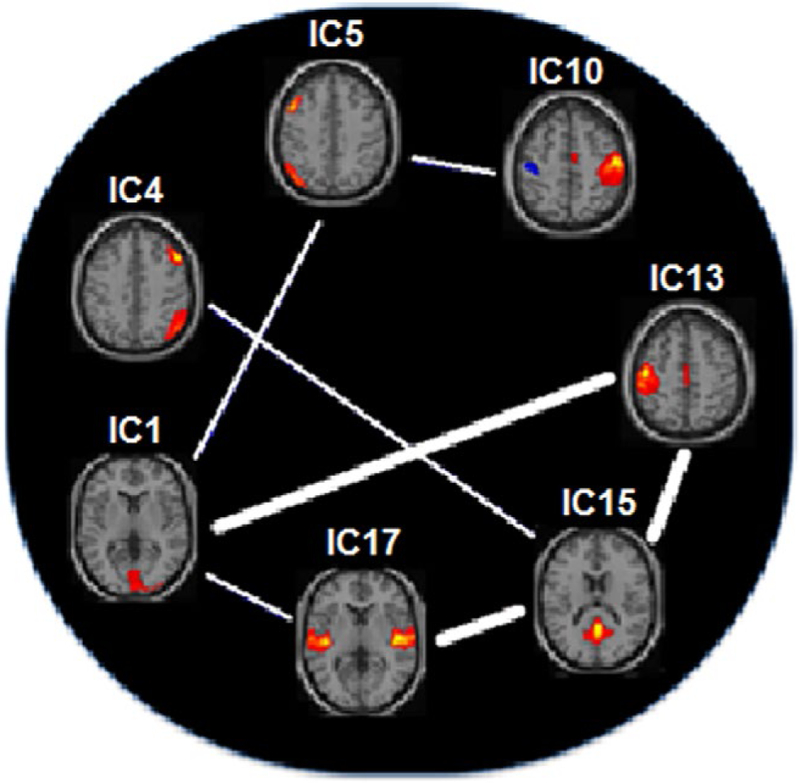
The most significant top seven independent component (IC) pairs which provide the best classification accuracies when their DFC measures are used as features. The top three pairs are shown with the thick lines in between. The IC pairs resulting in the most significant contribution to classification, from the most significant to less, are: (1) IC13 – IC15, (2) IC1 – IC13, (3) IC15 – IC17, (4) IC1 – IC5, (5) IC4 – IC15, (6) IC1 – IC17, and (7) IC5 – IC10. IC1: Primary Visual Cortex (PVC); IC4: Right Executive Control Network (R ECN); IC5: Left Executive Control Network (L ECN); IC10: Right Motor and Sensorimotor Cortex (R MSMC); IC13: Left Motor and Sensorimotor Cortex (L MSMC); IC15: Ventral Default Mode Network (VDMN); IC17: Insula

4 ∣. DISCUSSION AND CONCLUSION

In classification algorithms, successful classification between any two groups based on the selected features points to systematic differences between the two groups in terms of the selected features. The key finding in this study is the superior utility of DFC when compared with static FC. DFC among insula, visual, sensorimotor, executive control, and ventral default-mode networks resulted in high (95%) classification accuracy and appear to be the most informative features to classify cocaine-dependent patients from healthy controls. This result points to consistent differences between the two groups in the temporal dynamics of the functional connectivity among these networks, which may further suggest that these interactions may be altered or impaired. Involvement, alteration and possible impairment, in cocaine dependence, of temporal and visual regions as well as regions involved in executive control networks such as the prefrontal cortex, is in line with existing literature (Prisciandaro, Joseph, et al., 2014; Prisciandaro, McRae-Clark, Myrick, Henderson, & Brady, 2014; Prisciandaro, Myrick, Henderson, McRae-Clark, & Brady, 2013; Prisciandaro, Myrick, Henderson, McRae-Clark, Santa Ana, et al., 2013). ECN and DMN, and their functional coupling in particular, were also shown to be involved and possibly impaired in cocaine addiction (Geng et al., 2017; McHugh, Gu, Yang, Adinoff, & Stein, 2016) and also in other types of addiction, such as nicotine addiction (Lerman et al., 2014). More recent functional connectivity studies found disruptions or differences in the brain networks which include default mode network, salience network, prefrontal cortex, insula, and medial prefrontal cortex in cocaine-dependent participants (Geng et al., 2017; Liang et al., 2015; Wang et al., 2018; Zhang & Li, 2018; Zhang, Zhang, et al., 2018; Zhang, Zhang, et al., 2018). The top discriminating network pairs we found in this study, which included brain regions of insula, default mode network, sensorimotor, and executive control networks, are in line with the networks which have been reported to be disrupted in cocaine dependence.

The choice of window size and window step size are important in DFC analyses; however, there is not an established or optimal choice, and they are still subject to exploration and experimentation. In general, it is advised that the window size be long enough to have enough number of samples such that the computed correlation values carry a significance (Sakoglu et al., 2010) and not too short to have any spurious fluctuations (Preti, Bolton, & Van De Ville, 2017). Statistically speaking, one needs at least n > 30 samples (time points) in the window in order to have the correlation coefficients to have a statistically significant meaning (stems from the fact that the t-distribution and the Normal distribution values are almost the same for n > 30) (Walpole, Myers, Myers, & Ye, 2012). On the other hand, the window should not be too long, i.e., it should be short enough to capture any real, genuine dynamics of FC, otherwise the dynamics would be averaged out (Allen et al., 2014; Hutchison et al., 2013; Preti et al., 2017; Sakoglu et al., 2010). In our study, we set the window size to 32 (54.4 s), which is within the generally suggested range of window length (Allen et al., 2014; Hutchison et al., 2013; Preti et al., 2017; Sakoglu et al., 2010). A recent study indicated that artifacts might occur if the time courses are not filtered to remove frequencies lower than 1/window length (Leonardi & Van De Ville, 2015). According to these findings, since our window length is 54.4 s, time course frequencies below 1/54.4 = 0.018 Hz might generate spurious fluctuations. However, our fMRI data is not at resting state, but we have an SST task, the frequencies related to the task signals (with ISI 1.6 s, 1.8 s, 2.0 s) which correspond to a frequency range of 0.5–0.625 Hz are much stronger than those of any artifacts or noise (low frequency artifactual signals are also mostly filtered out during the preprocessing stage). A spectral density analysis showed that, for the eight ICs that we used in our DFC analyses, the frequencies between 0 and 0.018 Hz have only 4.7% of the total spectral power on the average, and this percentage did not differ significantly between the groups. Choice of eight steps (13.6 s) for the window step size was somewhat arbitrary; too short of a step size (e.g., 1 or 2) would mean too much overlap (>90%) of the windows and also too many dynamic (DFC) data points. Our choice of step size results in 75% overlapping windows, which allows capturing the dynamics of transitions in DFC between the windows. In summary, we also wanted to keep a balance between having too short or too long windows size and step size. The choice of a fixed window size limits the analysis to the fluctuations in the frequency range below the window size, independently of the true frequency content of dynamics of FC (Preti et al., 2017). The “optimal” choice of window length and step size in sliding window DFC analysis of fMRI is still under debate and subject to ongoing research (Allen et al., 2014; Hutchison et al., 2013; Preti et al., 2017). Doing an exploratory analysis of how the DFC changes while varying the window size and the step size within certain limits can be the subject of future study.

Sliding window DFC analyses are simpler and easy to interpret when compared to other dynamic analysis techniques such as dynamic causal modeling, structural equation modeling, and time℃frequency analysis; however, it has its limitations. The window length is fixed, hence it is not adaptive to the frequency content of the inherent fluctuations, therefore any fluctuations that are greater or smaller than the window size allows may be missed. Using a rectangular window is another limitation, albeit small, since it can increase the sensitivity to outliers and noise; using smooth/tapered windows (such as a raised cosine window, or a Hamming window) can help overcome this limitation (Betzel, Fukushima, He, Zuo, & Sporns, 2016; Lindquist, Xu, Nebel, & Caffo, 2014; Preti et al., 2017).

In this study, using 28 (all) IC pairs’ DFC as features achieved the most classification accuracy (95%, Figure 4). The classification accuracy changed very little, it was almost constant (94%−95%), when the number of IC pairs that was used decreased to seven, and these seven IC pairs involved primary visual cortex, the executive control network, motor and sensorimotor cortex, ventral default mode network, and insula. The brain is a highly interconnected organ, many different brain regions constantly communicate and interact, and the dynamics of the interactions as captured with fMRI and DFC in some or all of these brain regions can be systematically different for different brain conditions versus the “normal healthy” brain. Isolating these changes in DFC to a few interactions between a few brain regions is of particular interest for focusing diagnosis and treatment strategies to a small number of regions, and isolating the few brain regions which still provide the maximum classification of brain condition can provide clues about what the extent of these brain networks can be. Therefore, in this work, we wanted to find the smallest number of brain networks and IC pairs which provide the maximum classification accuracy via DFC. The classification accuracy decreased to 83% for six pairs and decreased to 90%−93% for five, four, and three pairs, which shows that the seven found IC pairs, and the networks which constitute these pairs (as listed above), are all important for classification of cocaine dependence. A more bruteforce and more detailed analysis of which network pairs provide how much classification accuracy would require studying each of the 2²⁸ IC pair combinations and their classification accuracies, which would be computationally challenging.

Rates of nicotine use were very high in the cocaine-dependent group (67% of participants smoked an average of one pack of cigarettes daily) whereas use of cigarettes was negligible in the controls. The near absence of cigarette use in the control group did not allow nicotine use to be considered as a covariate. As cocaine and nicotine are highly comorbid in the cocaine-dependent population, the distinct (or combined) contribution of each drug to the findings is extremely difficult to determine and not particularly meaningful from a clinical perspective. A recent study found that heavy nicotine users were characterized by an increment of connectivity between dorsal striatum and sensorimotor areas (Vergara et al., 2018); therefore, the nicotine use of the CD participants may have an influence in our results since our top three classifying networks include left motor and sensorimotor areas.

The small and skewed number of female participants (only 6/58 of the CD group and 9/25 of the HC group) was not sufficient to explore sex differences between groups. A visual inspection of the ICA networks did not reveal any meaningful differences between the two sexes. Nonetheless, sex could be a potential covariate and therefore it is a limitation of our study.

In summary, the goal of this study was to classify cocaine-dependent patients versus healthy controls using DFC of their fMRI data collected while they are responding to a SST. A well-established group ICA identified active and independent brain networks common to all participants, which were then used for evaluating static and dynamic FC. The networks identified included visual, sensorimotor, executive control networks, and the DMN. The SVM classification model based on the DFC successfully classified cocaine-dependent versus healthy control participants, with more accuracy than the static FC. These findings support the use of ICA- and DFC-based SVM classification of fMRI data as an additional, complementary tool for searching for potential biomarkers of cocaine dependence, and potentially other substance use disorders. It also reinforces that visual, sensorimotor, executive control networks, and the DMN are among the networks which are potentially most involved and possibly altered or impaired in cocaine-addiction.

Our study does not address why the interactions between the networks identified are different or how these brain networks are altered, which should be part of future investigations. What our study confirms is that when the dynamics of the interactions between different brain functional networks are taken into account as features in classification analysis, the classification accuracy of cocaine-dependent individuals versus healthy controls is improved, when compared to using only static brain network interaction features. Our results may suggest focusing on these identified brain networks and the interactions between these networks in future investigations of cocaine addiction. It can be concluded that fMRI data, DFC analysis of the fMRI data in particular, can be a very useful in detecting underlying brain network abnormalities in cocaine addiction.

Supplementary Material

supp info

Figure S1. A view of all of the independent components (ICs) of the group independent component analysis (ICA)

Significance.

This study identifies involvement of certain brain networks in discriminating cocaine-dependent patients from controls, using independent component analysis, dynamic functional connectivity, and multivariate pattern classification of fMRI data. The networks include visual, sensorimotor, executive control networks and the default mode network (DMN). These findings support the use of fMRI dynamic connectivity analyses as a tool for searching potential neuroimaging biomarkers of cocaine addiction. It also reinforces that visual, sensorimotor, executive control networks, and the DMN are among the networks which are potentially most involved, possibly altered or impaired, in cocaine addiction. Our results can help addiction researchers focus more attention on these networks.