Abstract
Two-pore PBPK models have been used for characterizing the PK of protein therapeutics since 1990s. However, widespread utilization of these models is hampered by the lack of a priori parameter values, which are typically estimated using the observed data. To overcome this hurdle, here we have presented the development of a two-pore PBPK model using de novo derived parameters. The PBPK model was validated using plasma PK data for different size proteins in mice. Using the “two pore theory” we were able to establish the relationship between protein size and key model parameters, such as: permeability-surface area product (PS), vascular reflection coefficient (σ), peclet number (Pe), and glomerular sieving coefficient (θ). The model accounted for size dependent changes in tissue extravasation and glomerular filtration. The model was able to a priori predict the PK of 8 different proteins: IgG (150 kDa), scFv-Fc (105 kDa), F(ab)2 (100 kDa, minibody (80 kDa), scFv2 (55 kDa), Fab (50 kDa), diabody (50 kDa), scFv (27 kDa), and nanobody (13 kDa). In addition, the model was able to provide unprecedented quantitative insight into the relative contribution of convective and diffusive pathway towards trans-capillary mass transportation of different size proteins. The two-pore PBPK model was also able to predict systemic clearance (CL) vs. Molecular Weight relationship for different size proteins reasonably well. As such, the PBPK model proposed here represents a bottom-up systems PK model for protein therapeutics, which can serve as a generalized platform for the development of truly translational PBPK model for protein therapeutics.
Keywords: Protein Therapeutics, Monoclonal Antibody (mAb), Antibody Fragments, Physiologically Based Pharmacokinetic (PBPK) Model, Two-Pore Theory, QSPKR, De Novo Parameter Derivation
Introduction
In the past few decades, great advances have been made in the development of physiologically based pharmacokinetic (PBPK) models for protein therapeutics, especially for monoclonal antibodies (mAbs) [1–5]. Compared to the traditional compartmental modeling approaches, PBPK models can be used to predict drug concentrations at tissue level, which better represents the concentration of drug at the site-of-action. Additionally, PBPK models can account for complex drug-target interactions and pathophysiological changes in the body, and can be easily translated from preclinical species to humans, which make them useful tool for facilitating bench-to-bedside translation of novel protein therapeutics.
However, to date, the application of PBPK modeling approaches for large molecules is still largely limited to mAbs. These PBPK models cannot be directly applied to other types of proteins, because the mechanisms of tissue extravasation and systemic elimination can be significantly different. Several quantitative structure-pharmacokinetic relationship (QSPKR) studies have tried to investigate the effect of various physicochemical properties (e.g. size, charge, glycosylation, etc.) on tissue distribution and systemic clearance of proteins [6–9]. Among these physicochemical properties, the effect of protein size on protein PK is studied most extensively. It is well known that glomerular filtration is a size dependent process, where molecules larger than ~70 kDa can hardly pass the glomerulus and molecules smaller than ~12 kDa can be freely filtered [10]. Using published PK studies for various size antibody fragments, our lab has previously shown that there is a sigmoidal relationship between protein size and systemic clearance, which is constant across several animal species and in part caused by size dependency in renal clearance [11]. Besides clearance, the extent of tissue distribution for proteins is also strongly correlated with molecular size. Our retrospective studies have shown that the extent of tissue distribution for various size antibody fragments, termed as the “biodistribution coefficient”, can be characterized as a function of protein size [12,13]. Consequently, we hypothesize that incorporating the effect of size on the distribution and elimination of protein therapeutics would an important first step towards building a generalized platform PBPK model for protein therapeutics.
In the late 1980s, Rippe and Haraldsson proposed the “two pore hypothesis” to quantitatively describe the trans-capillary transportation of macromolecules [14,15]. They assumed that the tissue vascular endothelium is “porous” and the pore radius between endothelial cells can be classified into two groups, small pores (~40 nm) and larges pores (~220 nm) [15]. Because of the two sets of pores with different sizes, the “two pore hypothesis” is able to explain the accumulation of macromolecules in the tissue interstitial space that was observed ex vivo, using a circular isogravimetric flow between large pores and small pores that is driven by the osmotic pressure. Therefore, the “two pore hypothesis” is considered to be advantageous over the “one pore hypothesis” because it better reflects the essential physiology of tissue vasculature. In fact, the two pore theory has been applied to PBPK models developed for antibodies and other protein therapeutics since the early 1990s. [2,3,16–20] However, the efforts to widely utilize the “two pore hypothesis” in the PBPK models have encountered difficulties. The biggest problem for this approach is the availability and identifiability of the system parameters. Some important parameters, including pore size, permeability-surface area product (PS), Peclet number (Pe), vascular reflection coefficient (σv), and isogravimetric flow (Jiso), are hard to measure. Further, the values of these parameters can be both drug specific and tissue specific, which adds more complexity for the use of this approach. Consequently, researchers have so far estimated the values of these parameters based on observed PK profiles. In addition, the approaches for the estimation of these parameters and the estimated values of these parameters differ greatly between different studies [3,16,20,17,19]. As a result, broad utilization and predictive ability of the two-pore PBPK model has been greatly compromised.
In 2015, Sepp et al. further derived the two pore theory related equations, and found out that two important parameters, Permeability-surface area product (PS) and isogravimetric flow (JISO), are directly correlated with tissue lymph flow [18]. They mathematically derived the values of PS, Pe, and Jiso for a 25.6 kDa domain antibody, with tissue lymph flow as the only independent variable in the two-pore model. We hypothesize that this approach can be expended to describe the trans-vascular transportation processes of proteins with other sizes, and thus can help us in incorporating protein size as an independent variable in the generalize platform PBPK model for protein therapeutics. Also, by assuming that glomerular filtration process dominates renal clearance of macromolecules, we hypothesize that it is possible to a priori develop a relationship between renal clearance and protein size using established glomerular sieving coefficient (θ) and protein size relationships [6,21]. As such, in this manuscript we have presented the development of a novel two-pore platform PBPK model, which utilizes all de novo derived parameters and predicts plasma PK of different size protein therapeutics in mice without estimating a single parameter.
Methods
PK dataset for model validation
Plasma PK of various-size proteins in mice were collected from the literature. These proteins included: IgG (150 kDa, n=1) PK in FcRn KO mice, scFv-Fc (105 kDa, n=2), F(ab)2 (100 kDa, n=6), minibody (80 kda, n=3), scFv2 (55 kDa, n=2), Fab (50 kDa, n=6), diabody (50 kDa, n=2), scFv (27 kda, n=13), and nanobody (13 kDa, n=2). A detailed list of the proteins included for model validation is provided in Supplementary Table-s1 and Supplementary Table-s2. All PK data was digitized using the software ‘Grab it! XP’.
PBPK model structure and equations
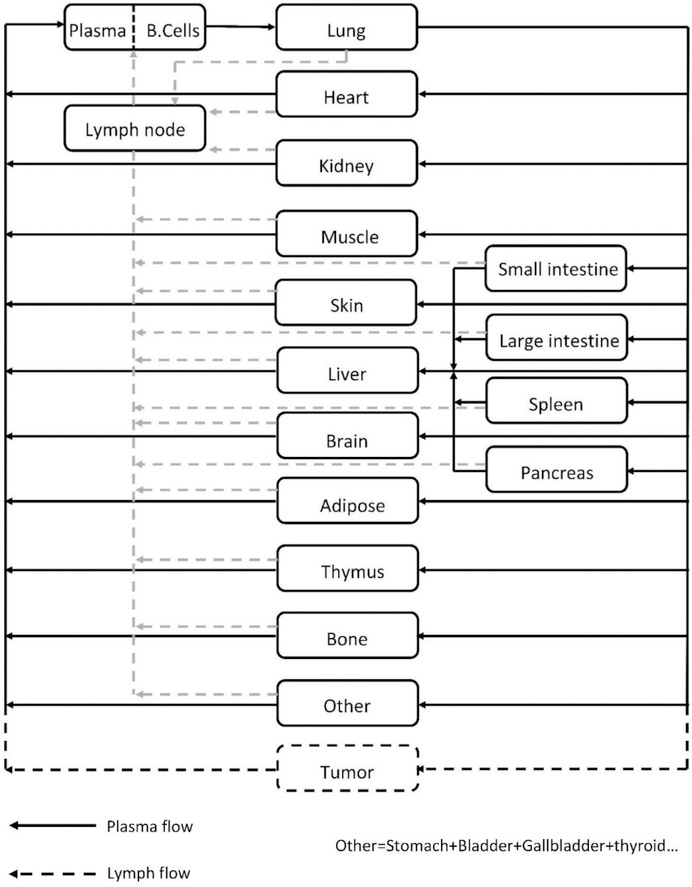
The overall structure of the PBPK model (Figure-1) is similar to the IgG PBPK model published by us before [5]. Briefly, 16 tissues are included in the model, which are blood, lung, heart, kidney, muscle, skin, liver, small intestine, large intestine, spleen, pancreas, adipose, bone, thymus, lymph node, and an “other” compartment that contains all other tissues that are not explicitly considered in the model. Protein molecules are assumed to enter each tissue via arterial plasma flow (Q), and exit through venous plasma flow (Q-J). Lymph flow (J) in each tissue is assumed to drive the fluid phase convection from vascular space to interstitial space, which is then assumed to recycle via the lymphatic circulation. The “lymph node” compartment in the model represents all lymph nodes in the body, which collects exiting lymph flow from each tissue, followed by draining it into the venous blood pool. The typical equations that describe mass balance of protein molecules in the plasma and lymph node compartment is shown in Equation 1 and 2 below.
Figure-1:
Structure of the whole-body platform PBPK model. All organs are represented by a rectangular compartment, and connected in an anatomical manner with blood flow (solid arrows) and lymphatic flow (dashed arrows). Arrows represent the direction of the flow. Each tissue within this model, except blood and lymph node, is divided into sub-compartments, as shown in Figure-2.
| Eq.1 |
| Eq.2 |
Tissue level protein disposition and degradation
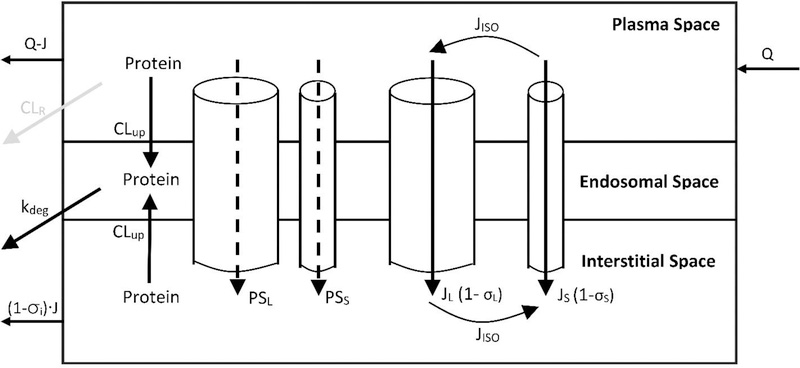
The tissue level protein disposition in the proposed PBPK model is characterized using the two pore hypothesis [14,15]. A detailed diagram of the tissue-level model is shown in Figure-2. The tissue microvascular endothelium is assumed to be “porous” and the pore radius between endothelial cells can be classified into two groups, small pores (~40 Å) and large pores (~220 Å) [15]. Protein molecules are assumed to passively transport from tissue vascular space to the interstitial space via both groups of pores, through either diffusion (PS) or fluid phase convection (J). The size-dependent restriction of large pores and small pores are represented as the vascular reflection coefficient (σL and σS). Isogravimetric flow (Jiso) is included to account for the circular flow across the endothelial cell layer, which is driven by osmotic pressure [15]. In the current model, it is assumed that the size of large pores and small pores, as well as the relative abundance of both pores (αL and αS), are the same in all tissues. Lymph flow of each tissue (Ji) is set as 0.2% of the plasma flow to that tissue. [3] The uptake clearance of protein molecules mediated by the trans-capillary exchange processes is represented as the “two-pore clearance” (CLtp). Interstitial protein molecules can recycle back to the systemic circulation via lymphatic flow (J). The level of resistance at the lymphatic openings is represented as the interstitial reflection coefficient (σIS), which is assumed to be the same for all the tissues.
Figure-2:
Structure of tissue level PBPK model. Each tissue is divided into endothelial, endosomal, and interstitial spaces. Solid arrows represent mass transport following plasma/lymph flow. Dashed arrows represent mass transport following diffusion. Gray arrow represents glomerular filtration in kidney. Detailed description of the tissue level model is presented in the Methods section.
In addition to trans-capillary exchange, proteins in the vascular space and interstitial space can also be taken up by the vascular endothelial cells via fluid phase pinocytosis (CLup). It is assumed that the cellular pinocytosis rate is the same for all the tissues. Protein molecules that enters the vascular endothelial cells end up in the endosomes, which eventually leads to protein degradation (kdeg). Typical equations that describe mass balance of protein molecules in the vascular, endosomal, and interstitial compartments of a tissue are provided in Equation 3, 4, and 5 below.
| eq.3 |
| eq.4 |
| eq.5 |
Renal clearance
In the kidney microvascular space, protein molecules can be removed from the systemic circulation via glomerular filtration. Large protein molecules, such as IgGs (~150 kDa), have negligible glomerular filtration. However, as the size of proteins decreases (< 70 kDa), the extent of filtration can become significant. In the current PBPK model, renal clearance (CLR) of protein molecules is assumed to be mainly through glomerular filtration in a size-dependent manner. The equations that describe renal clearance and protein concentrations in kidney vascular space are shown below:
| eq.6 |
| eq.7 |
In Equation 6, GFR represents glomerular filtration rate in mice, and θ represents the glomerular sieving coefficient for a protein molecule of a given size. Haraldsson and co-workers studied in detail the relationship between θ and several physicochemical properties of large molecules, including size and charge. [22] In the current PBPK model, the relationship between θ and protein size (in kDa) was described using an empirical equation, which was generated based on the data presented by Haraldsson et al. for slightly positively charged macromolecules of a wide size range [22]. The relationship is shown below in Equation 8.
| eq.8 |
Two pore theory related equations for various size proteins
The development of two-pore theory related equations for various-size proteins was based on the original publications from Rippe and Haraldsson, as well as further derivations by Sepp et al. [14,15,18]. Detailed derivation is presented in the supplementary material. Two-pore clearance (CLtp) for large pores and small pores can be expressed using the following equations:
| eq.9 |
| eq.10 |
In Equations 9 and 10, CLtp,L,i and CLtp,S,i are the “two-pore clearance” through large pores and small pores in a given tissue. PSL,i and PSS,i are the permeability-surface area products for large pores and small pores. JL,i and JS,i are the fractional tissue lymph flows through large and small pores. σL and σS are the vascular reflection coefficients. and are the Peclet number, which is defined as the ratio between convective flow rate and diffusive flow rate:
| eq.11 |
| eq.12 |
Tissue lymph flow through large and small pores (JL,i and JS,i) can be expressed as:
| eq.13 |
| eq.14 |
| eq.15 |
As demonstrated by Sepp et al., both permeability-surface area product (PSL,i and PSS,i) and isogravimetric flow (JL,iso,i and JS,iso,i) can be expressed as a dependent variable of tissue lymph flow (Ji). PS and Jiso can be expressed as:
| eq.16 |
| eq.17 |
| eq.18 |
In Equations 16 and 17, XP,L and XP,S are constants. The value of these two parameters is dependent on pore size, relative hydraulic conductance of large and small pores, and protein size. In Equation 18, XJ is a constant, which is only determined by relative pore abundance. Detailed derivation and calculation of these three constants is provided in the supplementary material.
Model parameters
The present PBPK model is built for mouse. All mouse physiological parameters that are used in the model were taken from the literature [2,5,23–25]. These parameters are summarized and presented in Table-1. Hydrodynamic radius of a protein is calculated based on the reported relationship by Venturoli and Rippe [21]:
| eq.19 |
Table-1.
Mouse (28 g) physiological parameters used to build the PBPK model.
| Total Volume (mL) | Plasma Volume (mL) | Interstitial Volume (mL) | Endosomal Volume (mL) | Plasma flow (mL/hr) | |
|---|---|---|---|---|---|
| Heart | 0.152 | 0.00585 | 0.0217 | 0.00076 | 36.5 |
| Lung | 0.204 | 0.0295 | 0.0384 | 0.00102 | 373 |
| Muscle | 11.3 | 0.249 | 1.47 | 0.0566 | 86.1 |
| Skin | 5.02 | 0.188 | 1.66 | 0.0251 | 27.8 |
| Adipose | 1.98 | 0.0218 | 0.337 | 0.00991 | 13.4 |
| Bone | 2.82 | 0.0621 | 0.525 | 0.0141 | 15.2 |
| Brain | 0.485 | 0.0107 | 0.0873 | 0.00243 | 11.8 |
| Kidney | 0.525 | 0.0289 | 0.0788 | 0.00263 | 68.5 |
| Liver | 1.93 | 0.164 | 0.385 | 0.00963 | 10.3 |
| S.Intestine | 0.728 | 0.0116 | 0.127 | 0.00364 | 58.1 |
| L.Intestine | 0.314 | 0.005 | 0.0545 | 0.00157 | 17.3 |
| Pancreas | 0.097 | 0.00534 | 0.0169 | 0.000485 | 6.24 |
| Thymus | 0.009 | 0.0005 | 0.00153 | 0.00005 | 1.19 |
| Spleen | 0.127 | 0.0154 | 0.0254 | 0.000635 | 8.18 |
| Ly. Node | 0.113 | – | – | – | 1.65 |
| Other | 0.465 | 0.0195 | 0.0797 | 0.00233 | 10.9 |
| Plasma | 0.944 | – | – | – | 373 |
The radius of large pores and small pores (rL and rS) are 22.85 nm and 4.44 nm, respectively, based on the reported values [14]. The relative conductivity of large pores and small pores (αL and αS) are 0.042 and 0.958, respectively, based on literature values [3,18]. Lymph flow of all tissues is assumed to be 0.2% of tissue plasma flow, and the lymphatic reflection coefficient (σi) in all tissues is set at 0.2, according to our previously published PBPK model [5]. Mouse glomerular filtration rate (GFR) is set at 0.278 mL/min [26]. Endothelial pinocytosis rate (CLup) and lysosome degradation rate (kdeg) for all proteins are set at 0.55 L/h/L and 32.2 h−1, based on our previously reported values [5]. A detailed summary of all model parameters is provided in Table-2.
Table-2.
PBPK model parameters that do not change based on protein size.
| Parameter | Description | value |
|---|---|---|
| rL (nm) | Large pore radius | 22.85 [14] |
| rS (nm) | Small pore radius | 4.44 [14] |
| αL | Fractional hydraulic conductance of large pores | 0.042 [3,18] |
| αS | Fractional hydraulic conductance of small pores | 0.958 [3,18] |
| Clup (L/hr/L) | Pinocytosis rate of vascular endothelial cells | 0.55 [5] |
| GFR (mL/min) | Glomerular filtration rate in mouse | 0.278 [26] |
| kdeg (1/hr) | First order lysosomal degradation rate | 32.2 [5] |
| σi | Lymphatic reflection coefficient | 0.2 [5] |
PBPK model predicted elimination pathway analysis for different size proteins
To better understand the elimination mechanism of different size proteins, relative contribution of renal filtration and lysosomal degradation towards systemic elimination of different size proteins was simulated using the pathway analysis of PBPK model. The following equations were used for this analysis:
| eq.20 |
| eq.21 |
Results
Evaluation of PBPK model simulated plasma PK profiles for various size proteins
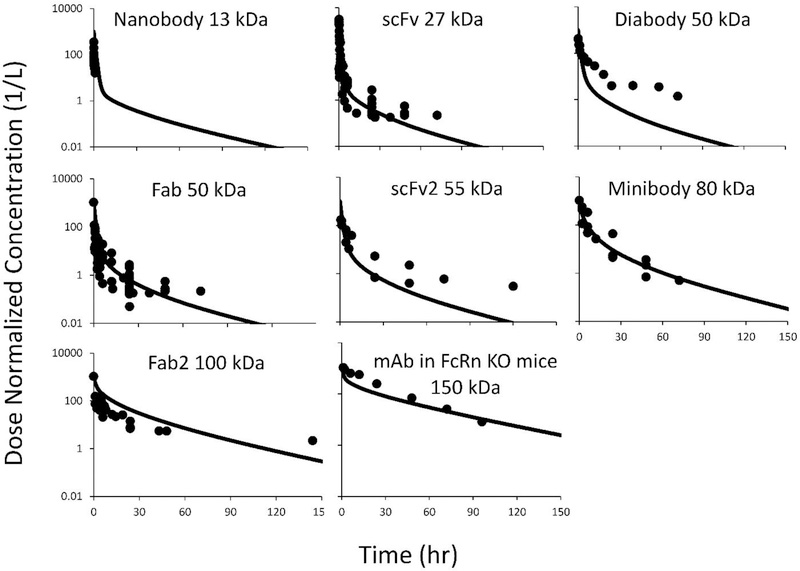
The PBPK model was used to predict plasma PK of proteins ranging in size from ~13 kDa (nanobody) to ~150 kDa (IgG). In order to eliminate the confounding effect of FcRn recycling, PK of IgG in FcRn knockout mice was used for validation. Simulated plasma PK profiles were compared with the literature reported PK profiles of similar size molecules, which were obtained from diverse sources. Detailed list of the studies included in the analysis is provided in supplementary Table-s1 and Table-s2. The comparison of model predicted and observed (i.e. reported) plasma PK profiles is shown in Figure-3. Overall, the model was able to predict plasma PK of most proteins reasonably well. For diabody (50 kDa) and scFv2 (55 kDa), the model showed underprediction of plasma PK at later time points. This could be due to smaller sample sizes for these two types of molecules (n=1 for diabody and n=2 for scFv2), or other physicochemical properties of these molecules that differ from 50 kDa Fab molecules, whose PK was predicted reasonably well by the model. Model simulation results were further validated by comparing the observed average AUC values for each group of molecules with the model predicted AUC values, using percentage prediction error (%PE). The calculated %PE value for each group of molecules are provided in Table-3. It was observed that model predicted exposure values were within 2.5-fold of the observed values for all the molecules evaluated.
Figure-3:
PBPK model predicted vs. observed plasma PK profiles of different-size proteins. The solid lines represent model predictions, and solid symbols represent pool observed data from one or more studies. The dataset include: nanobody (13 kDa, n=3), scFv (27 kDa, n=13), diabody (50kDa, n=2), Fab (50kDa, n=6), scFv2 (55 kDa, n=2), minibody (80 kDa, n=3), F(ab)2 (100 kDa, n=6), scFv-Fc (105 kDa, n=2), and IgG in FcRn KO mice (150 kDa, n=1).
Table-3.
Percentage prediction error (%PE) values for different size proteins.
| %PE based on AUC0-t | |
|---|---|
| Nanobody (13 kDa) | 22.7 |
| scFv (27 kDa) | 54.9 |
| Fab (50 kDa) | 130 |
| Diabody (50 kDa) | −21.9 |
| ScFv2 (55 kDa) | −9.06 |
| Minibody (80 kDa) | −15.9 |
| F(ab)2 (100 kDa) | 135 |
| IgG in FcRn KO mice (150 kDa) | −53.7 |
Effect of protein size on two-pore theory related parameters
Since the two-pore PBPK model presented here is truly a bottom-up systems PK model, it can be used to gain more insight into how the size of a protein affects different physiological parameters.
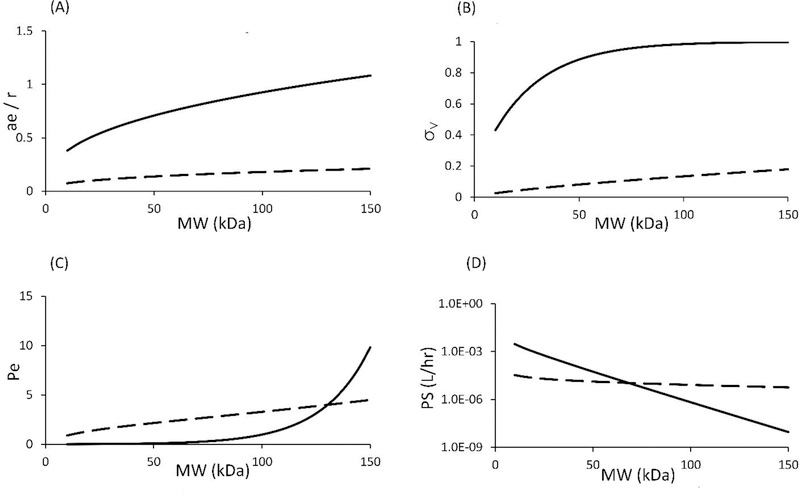
Size dependence of ae/r, σ, Pe and PS
As described in the Methods section, four important two-pore model related parameters can be a priori derived mathematically without fitting the model to any data. These parameters include: relative molecule to pore size ratio (ae/rL and ae/rS), vascular reflection coefficient (σL and σS), Peclet number (PeL and PeS), and permeability-surface area product (PSL and PSS). These parameters can be written as dependent variables of protein size. A summary of values for these parameters is presented in Table-4. In Figure-4, the relationship between these four parameters and molecular weight of protein therapeutics is illustrated. As shown in panel A, with increasing the molecular weight, the radius of protein molecule reaches that of the small pore, which hinders mass transportation of large proteins through the small pores. This effect can also be seen in the reflection coefficient vs. molecular weight plot, which is shown in the panel B. Peclet number reflects the fold difference between convective clearance and diffusive clearance. If the Peclet number is smaller than 1/3, then diffusion is considered predominant in the transvascular transportation processes. On the other hand, Peclet number larger than 3 indicates convection being predominant. In panel C, it is shown that as the molecular weight increases, convection becomes more and more important for both large and small pore. However, Peclet number for small pores (PeS) increases drastically for proteins larger than 100 kDa. The reason is that diffusive clearance through small pores decreases much faster than convective clearance in this high molecular weight range. Panel D shows the effect of protein size on diffusion through both large pores (PSL) and small pores (PSS). As evident, small pore is more sensitive to protein size than large pores, which is reflected by the faster decline in the PS values.
Table-4.
Calculated “two pore theory” related parameters for IgG (150 kDa), F(ab)2 (100 kDa), Minibody (80 kDa), scFv2(55 kDa), Fab and Diabody (50 kDa), scFv (27 kDa), and nanobody (13 kDa).
| Parameter | Description | Nanobody (13 kDa) | scFv (27 kDa) | Fab and Diabody (50 kDa) | scFv2 (55 kDa) | Minibody (80kDa) | F(ab)2 (100 kDa) | IgG (150 kDa) |
|---|---|---|---|---|---|---|---|---|
| ae (nm) | Stokes-Einstein radius | 1.87 | 2.48 | 3.15 | 3.26 | 3.77 | 4.11 | 4.81 |
| ae/rS | relative ratio between protein size and small pore size | 0.421 | 0.559 | 0.709 | 0.735 | 0.849 | 0.926 | 1.083 |
| ae/rL | relative ratio between protein size and large pore size | 0.0819 | 0.109 | 0.138 | 0.143 | 0.165 | 0.18 | 0.21 |
| σS | Small pore vascular reflection coefficient | 0.495 | 0.712 | 0.885 | 0.906 | 0.965 | 0.984 | 0.998 |
| σL | Large pore vascular reflection coefficient | 0.0312 | 0.0526 | 0.0819 | 0.0877 | 0.115 | 0.135 | 0.18 |
| A/A0S | Fractional accessible pore size of small pore | 8.08E-02 | 2.50E-02 | 3.72E-03 | 2.45E-03 | 3.09E-04 | 5.87E-05 | 9.28E-07 |
| A/A0L | Fractional accessible pore size of large pore | 0.693 | 0.599 | 0.533 | 0.522 | 0.469 | 0.431 | 0.349 |
| PsS_heart (L/hr) | Permeability-surface area product of small pore (heart as an example) | 2.02E-03 | 4.73E-04 | 5.53E-05 | 3.52E-05 | 3.83E-06 | 6.69E-07 | 9.04E-09 |
| PsL_heart (L/hr) | Permeability-surface area product of large pore (heart as an example) | 2.87E-05 | 1.87E-05 | 1.31E-05 | 1.24E-05 | 9.64E-06 | 8.13E-06 | 5.63E-06 |
| Jiso_heart (L/hr) | Circular isogravimetric flow (heart as an example) | 2.77E-05 | 2.77E-05 | 2.77E-05 | 2.77E-05 | 2.77E-05 | 2.77E-05 | 2.77E-05 |
| PeS | Peclet number of small pore | 0.0105 | 0.0257 | 0.0876 | 0.113 | 0.381 | 0.981 | 9.82 |
| PeL | Peclet number of large pore | 1.04 | 1.59 | 2.15 | 2.27 | 2.83 | 3.28 | 4.48 |
| θ | Glomerular sieving coefficient | 0.667 | 0.403 | 0.131 | 0.0986 | 0.022 | 0.00703 | 0.0011 |
Figure-4:
(A) ae / r vs. molecular weight, (B) vascular reflection coefficient vs. molecular weight, (C) peclet number vs. molecular weight, and (D) permeability-surface area product for a representative tissue (heart) vs. molecular weight relationships. Solid line represents small pore, and dashed line represents large pore.
Size dependence of transvascular transportation pathway
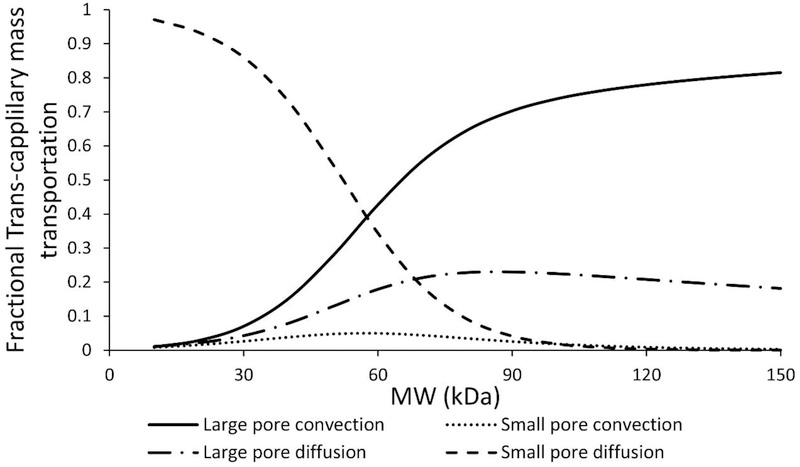
With the derivation of de novo relationships between protein size and two-pore model parameters, it is possible to analyze the relative importance of each trans-capillary pathway for different size proteins using the PBPK model. As shown in Figure-4C, the percentage of protein molecules that enters the tissue interstitial space via diffusion (PSs and PSL) or convection (PeS × PSS, and PeL × PSL) can be inferred using these relationships. For large proteins, such as IgGs (~150 kDa), most molecules extravasate through convection. However, for small proteins, such as scFv (~27 kDa), the majority of molecules transport through diffusion. Figure-5 provides further insight into the different pathways for transportation of various-size proteins through large and small pores. Contribution of convection and diffusion through either group of pores as a percentage of total mass transportation is presented in this figure. For large proteins (>100 kDa), mass transportation almost exclusively happens via larges pores. For small proteins (<25 kDa), mass transportation mostly takes place through diffusion via small pores.
Figure-5:
Pathway analysis of trans-capillary mass transportation through large and small pores for different size proteins. Solid line represents convection through large pores, dashed and dotted line represents diffusion through large pore, dotted line represents convection through small pores, and dashed line represents diffusion through small pores.
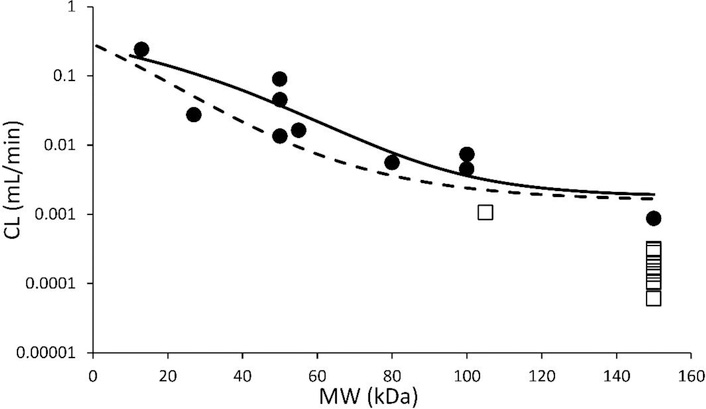
PBPK model predicted CL vs. protein size relationship
The PBPK model simulated systemic clearance (CL) vs. molecular weight relationship is shown in Figure-6 (solid line). This relationship is compared with a previously published similar relationship, which was derived from the published data using compartmental modeling approach [11]. Each data point in this figure represents an observed clearance value for a unique protein that was obtained from published mouse PK studies. Of note, open squares represent either scFv-Fc or IgG CL in normal mice. Because of the well-known salvage pathway mediated by FcRn-Fc interaction, these molecules are expected to have prolonged half-life and lower clearance when compared to other size matched proteins.
Figure-6:
Model simulated clearance (CL) vs. molecular weight relationship. Solid line represents the clearance values simulated using the PBPK model. Dashed line represents our previous reported CL vs. MW relationship based on compartmental modeling [11]. Each closed circle represents NCA calculated CL value for a given protein. Open squares represents NCA calculated CL values for scFv-Fc or IgG in normal mice.
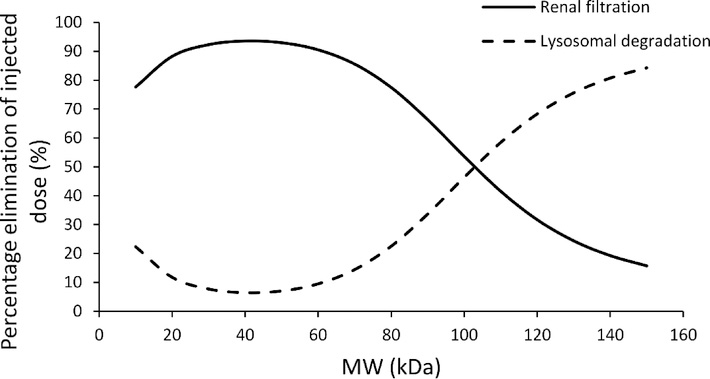
PBPK model predicted elimination pathway analysis for different size proteins
Results from the elimination pathway analysis are shown in Figure-7. It was found that large proteins (> 100 kDa) mostly eliminate via nonspecific degradation pathway (i.e. catabolized in the lysosomes of the tissue vascular endothelial cells), and small proteins (< 100 kDa) mostly eliminate via renal filtration. Interestingly, it was found that when proteins are smaller than ~40 kDa, the contribution of lysosomal degradation pathway increases again.
Figure-7:
Model simulated relationship for relative (percentage) contribution of renal filtration and lysosomal degradation pathways towards the elimination of different size proteins. Solid line represents renal filtration and dashed line represents lysosomal degradation.
Discussion
PBPK models have been developed for macromolecules since decades. These models represent the complex anatomy and physiology of preclinical species and humans as well, which allow them to better predict the PK of drug molecules in the plasma and at the site-of-action. So far, PBPK models for mAbs are relatively well developed and have been widely used in translational studies [4,27,28]. For example, our lab has previously published a platform PBPK model for mAbs, which can be used to a priori predict plasma and tissue PK of mAbs in several preclinical species and humans. [5] However, when it comes to other types of protein therapeutics, the application of PBPK models for drug development is still challenging. This stems from the complex and diverse structures and physicochemical properties of these molecules, and largely unknown ADME processes responsible for the disposition of these molecules. Current PBPK models for these protein therapeutics usually employ the “two pore theory” to characterize tissue extravasation of these molecules. However, this approach adds to more uncertainty towards the model, due to several unknown two-pore model parameters, which are estimated using the observed data. To overcome this challenge, in this manuscript we have presented the development of a two-pore PBPK model for different size protein therapeutics using de novo derived parameters. Since no model fitting is needed, we believe this model can serve as a generalized platform for the development of truly translational PBPK model for protein therapeutics.
As shown in Figure-3 and Table-3, the PBPK model was able to a priori predict plasma PK of various size proteins reasonably well (within 2.5 fold). The PK of nanobody, scFv, Fab, minibody, F(ab)2, and IgG (in FcRn KO mice) was precited very well. However, the PK of diabody and scFv2 was underpredicted (the exposure was still within 20% of observed value). We hypothesize this could be due to either smaller sample size of the PK profiles available for these two proteins (n=1 for diabody and n=2 for scFv2) or peculiar physiochemical properties inherent to these molecules. Careful comparison of observed and model predicted PK profiles reveal that the model predicted α-phase for all PK profiles agreed well with the observed data, which indicates that the distribution processes for different size proteins were successfully characterized by our two-pore model. In the current model, a protein molecule is cleared from the system via two main pathways. Either through non-specific degradation in the tissue vascular endothelial cells following pinocytosis or through renal clearance. For the non-specific degradation pathway, the rate of pinocytosis determines intracellular degradation rate, since for all the FcRn non-binding proteins evaluated here no transcytosis or recycling is assumed. Since there is no reported values for the relationship between the rate of pinocytosis and protein size, we assumed that the pinocytosis rate is consistent for proteins of all sizes in all the tissues. This rate was 0.55 L/h/L, which is based on the estimates from our previously published platform PBPK model for IgG [5]. However, when future evidence become available on any tissue or molecular property specific selectivity of the pinocytosis process, it can be readily incorporated in the model.
Another important assumption of our model is that the renal clearance is determined only by the glomerular filtration process, and no active secretion or passive reabsorption pathway is included. The renal clearance is represented as the product of glomerular filtration rate (GFR) and glomerular sieving coefficient (θ). Mouse GFR was taken from literature, which is 0.278 mL/min [26]. The relationship between θ and macromolecule size has been reported in several studies [6,21,22]. Haraldsson et al. used synthetic macromolecules with different charges to develop the relationship between θ and molecular size [22]. We have developed an empirical equation to characterize this relationship based on the data from Haraldsson et al. for slightly positively charged molecules, as most protein therapeutics are either neutral or slightly positively charged. However, for proteins with negative or strong positive charges, this relationship may not be accurate, and modification in the PBPK model may be required regarding the rate of renal clearance. Careful evaluation of all PK profiles (Figure-3) reveal that the slope of the β-phase gradually increases as the size of protein decreases, and it reaches plateau at lower molecular weight range (< 50 kDa). Since renal clearance is the only size dependent clearance pathway in the current model, this result indicates that the size selectivity in the glomerular filtration process is a dominant mechanism that determines different rate of clearance for different size proteins. As shown in Figure-6, the systemic clearance (CL) values for different-size proteins predicted by our PBPK model compares well with the observed (i.e. calculated based on NCA) values. While the CL vs. MW relationship agrees well with most data points, CL of molecules with Fc domain (i.e., scFv-Fc and IgG in normal mice) is over predicted. This is excepted, as these molecules are known to show lower clearance compared to size-matched proteins because of the well-known FcRn mediated salvage pathway. In addition, PBPK model predicted relationship also compares well with our previously reported CL vs. MW relationship derived based on compartmental modeling approach (Figure-6) [11]. While the PPBK model derived relationship predicts higher CL for proteins in the middle molecular weight range, it agrees well with the observed values. Using the proposed PBPK model it is also possible to simulate relative contribution of renal filtration and lysosomal degradation towards total elimination of different size proteins. The simulation results are shown in Figure-7. The model suggests that large molecules, such as IgG (150 kDa), are mainly removed from the body through nonspecific lysosomal degradation process (~83%), as the contribution of renal filtration pathway is insignificant at this molecular size. On the other hand, renal filtration pathway takes over the elimination process when protein molecular weight is smaller than ~100 kDa, and this contribution is maximum at ~40 kDa (~93%). Interestingly, model simulations suggest that when the protein is smaller than 40 kDa, the contribution of nonspecific degradation will increase again. This peculiar observation stems from enhanced extravasation of proteins in this size range (Figure-4B), which leads to higher interstitial concentrations and in turn higher endosomal uptake and degradation of proteins in this size range.
The most important feature of our PBPK model is the use of “two pore theory” published by Rippe and Haraldsson, and the derivation method introduced by Sepp et al., to calculate two-pore model related parameters de novo. All derivations and detailed equations can be found in the supplementary material. As shown in Figure-2, we were able to derive the relationship between protein molecular weight (in kDa) and several important system parameters for the first time. These parameters include: relative molecule to pore size ratio (ae/rL and ae/rS), vascular reflection coefficient (σL and σS), Peclet number (PeL and PeS), and permeability-surface area product (PSL and PSS). In the current model, the radius of large and small pores (rL and rS), and the fractional hydraulic conductance of large and small pores (αL and αS) is assumed to be similar throughout all tissues. Accurate measurements of these parameters for each tissue is still not available. Researchers have reported rough measurements of these values for continuous and fenestrated capillaries, however, large discrepancies exists for fenestrated capillaries [15,29]. Rippe and Haraldsson reported that in dog fenestrated capillaries, the fractional hydraulic conductance of large pores is about 2% [15]. However, from Taylor and Granger’s result, this value can be as large as 80% [29]. In some modeling approaches, researchers sometimes decided to manually adjust these values, based on their experiment results [17]. For simplicity, we adopted the values reported by Rippe and Haraldsson in the current model [15]. From our simulated plasma PK results, it is evident that the current parameter set is capable of capturing plasma PK of most molecules. In the future, however, these values can be changed to tissue specific values if more accurate measurements are reported. As shown in the Methods section, permeability-surface area product (PSL and PSS) and isogravimetric flow rate (JISO) are dependent on tissue lymph flow (Ji). Therefore, the value of net lymph flow in each tissue greatly influences protein concentrations in that tissue.
However, currently there is no accurate measurement of tissue lymph flow in preclinical species and humans. Many times researchers fit tissue lymph flow values to capture the observed tissue PK data, which actually results in estimated values that can vary more than an order of magnitude from one study to another [2,18,19]. In our current model, we assume that tissue lymph flow is 0.2% of tissue plasma flow. The same assumption was used in our previously published mAb PBPK model, and works well across several preclinical species and humans [5].
Permeability-surface area product (PS) determines the rate of transvascular diffusion processes. As shown in Equations 16 and 17, PS can be expressed as the product of a constant (XP,L or XP,S) and tissue lymph flow (Ji). The derivation of constant XP is shown in the supplementary material. This constant is determined by several physicochemical properties of tissue endothelial membrane and protein molecules, which are protein radius (ae), pore radius (rL or rS), the fractional hydraulic conductance (αL or αS), and fractional available cross-sectional pore area ( or ). As a result, for a given tissue, the effect of protein size on PS can be derived, as shown in Figure-4. The derived PS value is comparable to literature reported values. For example, heart PS values for a 25.8 kDa domain antibody estimated by Sepp et al. were 1.5E-4 and 7.4E-6 (L/hr) for small and large pores, respectively, which are in the ballpark of our derived values of 5.3E-4 and 1.9E-5 (L/hr) [18].
Vascular reflection coefficient (σV) represents the level of resistance for trans-capillary convective transportation through tissue vasculature. In the current model, the relationship between the vascular reflection coefficient for large pores and small pores (σV,L and σV,S) and protein molecular weight (MW) is derived based on the reported values from Rippe and Haraldsson [15]. In several IgG PBPK models, vascular reflection coefficient is represented as the weighted average value for the whole tissue endothelium [5,1,4]. The net reflection coefficient for IgG is usually reported to be around 95% (i.e. 0.95) in most tissues [4]. However, in the current model, σV,L and σV,S for IgG are calculated to be around 18.0% and 99.7%, respectively. The calculated net vascular reflection coefficient of IgG is then calculated to be 96.2%, which is close to the literature reported value. When it comes to smaller proteins, Baxter et al. reported that for Fab (~50 kDa), σV,L and σV,S are 10% and 95%, respectively [2], which are similar to our calculated values of 8.19% and 88.5%.
Using the PBPK model, we were also able to predict relative contribution of each trans-capillary mass transportation pathway for different size proteins. The Peclet number (Pe) represents the relative contribution of convective and diffusive transportation in the trans-capillary mass exchange. In the current model, Pe can be derived for a given protein based on the molecular weight (MW). As shown in Figure-4, with increasing molecular weight, Pe of a protein in both small pore and large pore increases. Calculated Pe for IgG is 4.9, which indicates that for large proteins, such as IgG (~150 kDa), more than 82% of tissue extravasation is through convection. In contrast, for small proteins, such as scFv (~27 kDa), more than 91% of tissue extravasation is through diffusion. To further investigate the relative contribution of convection and diffusion in large and small pores, we derived the percentage contribution of each pathway via each set of pores. As shown in Figure-5, for small proteins (MW < 30 kDa), small pore diffusion is the dominant pathway. For large proteins (MW > 100 kDa), large pore convection plays a major role, while large pore diffusion plays a minor role. For proteins with intermediate size (between 30 and 100 kDa), large pore convection, large pore diffusion, and small pore diffusion contribute to the majority of tissue extravasation. Interestingly, from the derived relationship, small pore convection has little contribution to the overall tissue extravasation throughout the whole molecular size range. These results are comparable to the reported values by Baxter et al [2]. However, since this is the first quantitative tissue extravasation pathway analysis for different-size proteins, more experimental data is needed to verify this relationship.
It should be noted that despite the effect of molecular size, other physiochemical factors may also affect the pharmacokinetics of macromolecules. The purpose of the PBPK model proposed here is to focus on establishing mathematical models to help understand the importance of protein size on its plasma PK. It is naïve to consider protein size as the only physiochemical parameter of importance. Several other physiochemical parameters are also known to be important. One example is protein charge/isoelectric point (pI). The pI values of most therapeutic antibodies fall in the range of 8–9. [8] It was shown that by increasing the pI value by one unit, antibodies bind more strongly with the negatively charged cell membrane and thereby increases plasma clearance. On the other hand, changing the pI value by one unit to the acidic side would increase the overall whole-body clearance. [30] Another key physiochemical factor is the glycosylation of the Fc region. Although the exact effect of glycosylation on the PK of antibodies is still under debate, several recent studies have shown that high-mannose glycans on the Fc region may lead to high clearance, possibly mediated through binding to the mannose receptors on macrophages. [31,32] As such, going forward we plan to evolve the 2-pore PBPK model proposed here to account for other important physicochemical parameters.
In summary, here we have presented the development of a two-pore PBPK model, using de novo derived parameters, to predict plasma PK of different-size proteins in mice. The model was able to a priori predict plasma PK of 8 different classes of proteins without estimating any model parameter. The proposed model represents a true bottom-up systems PK model for protein therapeutics, which takes into account size selectivity of tissue extravasation and glomerular filtration. Going forward, we plan to evaluate the ability of this model to a priori predict tissue PK of different size protein therapeutics. The two-pore PBPK model presented here can serve as a generalized platform for the development of truly translational PBPK model for protein therapeutics.
Supplementary Material
ACKNOWLEDGMENTS
This work was supported by National Institute of General Medical Sciences grant [GM114179]. D.K.S is also supported by and National Institute of Allergy and Infectious Diseases grant [AI138195].
References
- 1.Covell DG, Barbet J, Holton OD, Black CD, Parker R, Weinstein JN (1986) Pharmacokinetics of monoclonal immunoglobulin G1, F (ab′) 2, and Fab′ in mice. Cancer research 46 (8):3969–3978 [PubMed] [Google Scholar]
- 2.Baxter LT, Zhu H, Mackensen DG, Jain RK (1994) Physiologically based pharmacokinetic model for specific and nonspecific monoclonal antibodies and fragments in normal tissues and human tumor xenografts in nude mice. Cancer research 54 (6):1517–1528 [PubMed] [Google Scholar]
- 3.Ferl GZ, Wu AM, DiStefano JJ (2005) A predictive model of therapeutic monoclonal antibody dynamics and regulation by the neonatal Fc receptor (FcRn). Annals of biomedical engineering 33 (11):1640–1652 [DOI] [PubMed] [Google Scholar]
- 4.Garg A, Balthasar JP (2007) Physiologically-based pharmacokinetic (PBPK) model to predict IgG tissue kinetics in wild-type and FcRn-knockout mice. Journal of pharmacokinetics and pharmacodynamics 34 (5):687–709 [DOI] [PubMed] [Google Scholar]
- 5.Shah DK, Betts AM (2012) Towards a platform PBPK model to characterize the plasma and tissue disposition of monoclonal antibodies in preclinical species and human. Journal of pharmacokinetics and pharmacodynamics 39 (1):67–86 [DOI] [PubMed] [Google Scholar]
- 6.Norden AG, Lapsley M, Lee PJ, Pusey CD, Scheinman SJ, Tam FW, Thakker RV, Unwin RJ, Wrong O (2001) Glomerular protein sieving and implications for renal failure in Fanconi syndrome. Kidney international 60 (5):1885–1892 [DOI] [PubMed] [Google Scholar]
- 7.Zheng Y, Tesar DB, Benincosa L, Birnböck H, Boswell CA, Bumbaca D, Cowan KJ, Danilenko DM, Daugherty AL, Fielder PJ Minipig as a potential translatable model for monoclonal antibody pharmacokinetics after intravenous and subcutaneous administration In: MAbs, 2012. vol 2 Taylor & Francis, pp 243–255 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Boswell CA, Tesar DB, Mukhyala K, Theil F-P, Fielder PJ, Khawli LA (2010) Effects of charge on antibody tissue distribution and pharmacokinetics. Bioconjugate chemistry 21 (12):2153–2163 [DOI] [PubMed] [Google Scholar]
- 9.Newkirk M, Novick J, Stevenson M, FOURNIER MJ, Apostolakos P (1996) Differential clearance of glycoforms of IgG in normal and autoimmune‐prone mice. Clinical & Experimental Immunology 106 (2):259–264 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Vegt E, De Jong M, Wetzels JF, Masereeuw R, Melis M, Oyen WJ, Gotthardt M, Boerman OC (2010) Renal toxicity of radiolabeled peptides and antibody fragments: mechanisms, impact on radionuclide therapy, and strategies for prevention. Journal of nuclear medicine 51 (7):1049–1058 [DOI] [PubMed] [Google Scholar]
- 11.Li Z, Krippendorff B-F, Shah DK (2017) Influence of Molecular size on the clearance of antibody fragments. Pharmaceutical research 34 (10):2131–2141 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Shah DK, Betts AM (2013) Antibody biodistribution coefficients. Inferring tissue concentrations of monoclonal antibodies based on the plasma concentrations in several preclinical species and human, mAbs 5:297–305 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Li Z, Krippendorff B-F, Sharma S, Walz AC, Lavé T, Shah DK I nfluence of molecular size on tissue distribution of antibody fragmentsI In: MAbs, 2016. vol 1 Taylor & Francis, pp 113–119 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rippe B, Haraldsson B (1987) Fluid and protein fluxes across small and large pores in the microvasculature. Application of two‐pore equations. Acta physiologica 131 (3):411–428 [DOI] [PubMed] [Google Scholar]
- 15.Rippe B, Haraldsson B (1994) Transport of macromolecules across microvascular walls: the two-pore theory. Physiological reviews 74 (1):163–219 [DOI] [PubMed] [Google Scholar]
- 16.Davda JP, Jain M, Batra SK, Gwilt PR, Robinson DH (2008) A physiologically based pharmacokinetic (PBPK) model to characterize and predict the disposition of monoclonal antibody CC49 and its single chain Fv constructs. International immunopharmacology 8 (3):401–413 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gill KL, Gardner I, Li L, Jamei M (2016) A bottom-up whole-body physiologically based pharmacokinetic model to mechanistically predict tissue distribution and the rate of subcutaneous absorption of therapeutic proteins. The AAPS journal 18 (1):156–170 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Sepp A, Berges A, Sanderson A, Meno-Tetang G (2015) Development of a physiologically based pharmacokinetic model for a domain antibody in mice using the two-pore theory. Journal of pharmacokinetics and pharmacodynamics 42 (2):97–109 [DOI] [PubMed] [Google Scholar]
- 19.Niederalt C, Kuepfer L, Solodenko J, Eissing T, Siegmund H-U, Block M, Willmann S, Lippert J (2017) A generic whole body physiologically based pharmacokinetic model for therapeutic proteins in PK-Sim. Journal of pharmacokinetics and pharmacodynamics:1–23 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Baxter LT, Zhu H, Mackensen DG, Butler WF, Jain RK (1995) Biodistribution of monoclonal antibodies: scale-up from mouse to human using a physiologically based pharmacokinetic model. Cancer research 55 (20):4611–4622 [PubMed] [Google Scholar]
- 21.Venturoli D, Rippe B (2005) Ficoll and dextran vs. globular proteins as probes for testing glomerular permselectivity: effects of molecular size, shape, charge, and deformability. American Journal of Physiology-Renal Physiology 288 (4):F605–F613 [DOI] [PubMed] [Google Scholar]
- 22.Haraldsson B, Nyström J, Deen WM (2008) Properties of the glomerular barrier and mechanisms of proteinuria. Physiological reviews 88 (2):451–487 [DOI] [PubMed] [Google Scholar]
- 23.Urva SR, Yang VC, Balthasar JP (2010) Physiologically based pharmacokinetic model for T84. 66: A monoclonal anti‐CEA antibody. Journal of pharmaceutical sciences 99 (3):1582–1600 [DOI] [PubMed] [Google Scholar]
- 24.Brown RP, Delp MD, Lindstedt SL, Rhomberg LR, Beliles RP (1997) Physiological parameter values for physiologically based pharmacokinetic models. Toxicology and industrial health 13 (4):407–484 [DOI] [PubMed] [Google Scholar]
- 25.Davies B, Morris T (1993) Physiological parameters in laboratory animals and humans. Pharmaceutical research 10 (7):1093–1095 [DOI] [PubMed] [Google Scholar]
- 26.Bivona BJ, Park S, Harrison-Bernard LM (2010) Glomerular filtration rate determinations in conscious type II diabetic mice. American Journal of Physiology-Renal Physiology 300 (3):F618–F625 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Glassman PM, Balthasar JP (2016) Physiologically-based pharmacokinetic modeling to predict the clinical pharmacokinetics of monoclonal antibodies. Journal of pharmacokinetics and pharmacodynamics 43 (4):427–446 [DOI] [PubMed] [Google Scholar]
- 28.Glassman PM, Balthasar JP Physiologically-based modeling to predict the clinical behavior of monoclonal antibodies directed against lymphocyte antigens In: mAbs, 2017. vol 2 Taylor & Francis, pp 297–306 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Taylor AE, Granger DN (1984) Exchange of macromolecules across the microcirculation. Handbook of Physiology The Cardiovascular System Microcirculation 4 (pt 1):467–520 [Google Scholar]
- 30.Bumbaca D, Boswell CA, Fielder PJ, Khawli LA (2012) Physiochemical and biochemical factors influencing the pharmacokinetics of antibody therapeutics. The AAPS journal 14 (3):554–558 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Goetze AM, Liu YD, Zhang Z, Shah B, Lee E, Bondarenko PV, Flynn GC (2011) High-mannose glycans on the Fc region of therapeutic IgG antibodies increase serum clearance in humans. Glycobiology 21 (7):949–959 [DOI] [PubMed] [Google Scholar]
- 32.Alessandri L, Ouellette D, Acquah A, Rieser M, LeBlond D, Saltarelli M, Radziejewski C, Fujimori T, Correia I Increased serum clearance of oligomannose species present on a human IgG1 molecule In: MAbs, 2012. vol 4 Taylor & Francis, pp 509–520 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.