Quantifying the Impact of Partial Measurement Invariance in Diagnostic Research: An Application to Addiction Research

Abstract

Establishing measurement invariance, or that an instrument measures the same construct(s) in the same way across subgroups of respondents, is crucial in efforts to validate social and behavioral instruments. Although substantial previous research has focused on detecting the presence of noninvariance, less attention has been devoted to its practical significance and even less has been paid to its possible impact on diagnostic accuracy. In this article, we draw additional attention to the importance of measurement invariance and advance diagnostic research by introducing a novel approach for quantifying the impact of noninvariance with binary items (e.g., the presence or absence of symptoms). We illustrate this approach by testing measurement invariance and evaluating diagnostic accuracy across age groups using DSM alcohol use disorder items from a public national data set. By providing researchers with an easy-to-implement R program for examining diagnostic accuracy with binary items, this article sets the stage for future evaluations of the practical significance of partial invariance. Future work can extend our framework to include ordinal and categorical indicators, other measurement models in item response theory, settings with three or more groups, and via comparison to an external, “gold-standard” validator.

1. Overview

1.1. Measurement Invariance

Measurement is the foundation of science. Establishing measurement invariance, or that an instrument or a test measures the same construct(s) in the same way across subgroups of respondents, is crucial in efforts to validate social and behavioral instruments (Meredith, 1993; van de Vijver & Poortinga, 1997; Vandenberg, 2002). When the properties of an instrument vary across subgroups of participants with different characteristics (e.g., language spoken, age, gender, and other demographic characteristics), the observed scores in different groups will be on different metrics and cannot be directly compared—any observed group differences in means, regression coefficients, or prevalence rates of disorders will be confounded with the inconsistent properties of the instrument (e.g., Millsap, 2011). Thus, at least some degree of measurement invariance is needed for meaningful interpretations of research findings (Schmitt & Kuljanin, 2008).

With the advance of methodological research in evaluating measurement invariance (e.g., Millsap, 2011) and increased awareness from substantive researchers, measurement invariance evaluation has been applied to a growing array of instruments designed to measure social and behavior constructs (e.g., personality traits, Nye et al., 2008; prosocial behaviors, Carlo, Knight, McGinley, Zamboanga, & Jarvis, 2010). Measurement invariance has also been evaluated in research of psychopathologies such as depression (Borsboom, 2008; Crockett, Randall, Shen, Russell, & Driscoll, 2005) and substance use disorder (e.g., Aiken, Stein, & Bentler, 1994). Although evaluations of measurement invariance is becoming more common, researchers in many disciplines still frequently compare groups without establishing equivalence of measurement (Davidov, Meuleman, Cieciuch, Schmidt, & Billiet, 2014; Vandenberg & Lance, 2000).

1.2. Partial Invariance

Full measurement invariance holds when all the measurement parameters of all items are the same across all groups. This is rather difficult to achieve empirically. Often researchers find that measurement invariance holds for only a subset of items, a condition known as partial measurement invariance (also known as differential item functioning in item response theory; see Penfield & Lam, 2000). Whereas it is possible to make valid group comparisons (e.g., on means, path coefficients) using latent variable models when only some of the items are invariant (Byrne, Shavelson, & Muthén, 1989), group comparisons based on observed scores (e.g., scale or composite scores; Steinmetz, Schmidt, Tina-Booh, Wieczorek, & Schwartz, 2009) may yield misleading conclusions, as noninvariant items are not precluded from biasing comparisons of means (Schmitt & Kuljanin, 2008), path coefficients (Hsiao & Lai, 2018), and prevalence rates across groups.

1.3. Practical Significance of Partial Invariance

Although substantial previous research has focused on detecting the presence of partial invariance (e.g., Byrne, Shavelson, & Muthén, 1989; Stark, Chernyshenko, & Drasgow, 2006), discussion of the practical significance (e.g., Ferguson, 2009; Kirk, 1996) of partial invariance, that is, whether the degree of noninvariance is large enough in a practically meaningful way, has been scarce. Specifically, just as a statistically significant t test may indicate a negligible mean difference, or in other words a trivial effect size (e.g., Kirk, 1996), statistical indication of measurement invariance violations may or may not have substantial practical impact on research findings and the efficacy of the instrument. As Millsap and Kwok (2004) discussed, the practical significance of partial invariance should be interpreted “in relation to the purpose of the measure” (pp. 94–95).

1.4. Diagnostic Accuracy Analysis

Even less attention has been devoted to the practical impact of partial invariance on diagnostic accuracy based on observed scores (Millsap, 2011). Millsap and Kwok (2004; see also Lai, Kwok, Yoon, & Hsiao, 2017) first proposed to examine the practical significance of partial invariance by comparing the accuracy of selection (of individuals for, e.g., job promotion, or classification of drinking behaviors) based on a given partially invariant instrument to the accuracy of selection when full measurement invariance is assumed, and the framework can be extended to cover diagnostic accuracy of partially invariant instruments. If diagnostic accuracy in one or more groups changes a lot due to noninvariant items, then the partial invariance has a relatively large practical impact. Note that in this article we used the term diagnostic accuracy to mean the estimated performance of a test in the absence of an external validator (e.g., actual clinical diagnosis and “gold standard” measure; see Faraone & Tsuang, 1994).

1.5. Current Study

Above we have drawn additional attention to the importance of measurement invariance as well as identified a significant gap in the literature with respect to the impact of partial invariance on diagnostic accuracy. Next we advance diagnostic research by introducing a novel approach for quantifying the impact of noninvariance with binary items (e.g., the presence or absence of symptoms). We illustrate this approach by testing measurement invariance and then evaluating diagnostic accuracy across age groups using Diagnostic and Statistical Manual of Mental Disorders (DSM; American Psychiatric Association [APA], 1994) alcohol dependence items from a public national data set. The current application to addiction research is significant because (a) addiction researchers and clinicians often classify people into substance use disorder (SUD) categories by summing the SUD criteria and comparing the scores to cut-points (e.g., endorsing > 3 items), which requires measurement invariance to hold (Midanik, Greenfield, & Bond, 2007), and (b) although research suggests the DSM-IV criteria for alcohol, marijuana, and cocaine use disorders are measurement invariant between community and selected (i.e., clinical) samples (Derringer et al., 2013), evidence also suggests that SUD criteria (e.g., DSM-IV alcohol dependence tolerance and time spent) function differentially across age groups, gender, and race/ethnicity (e.g., Harford, Yi, Faden, & Chen, 2009; Martin, Chung, Kirisci, & Langenbucher, 2006; Saha, Chou, & Grant, 2006). The current study is also significant given recent calls in addiction research for analyses that examine item and measure performance across critical populations (e.g., Baker, Breslau, Covey, & Shiffman, 2012; Burlew, Feaster, Brecht, & Hubbard, 2009). Importantly, we are aware of no studies that have examined the impact of partial invariance on SUD diagnosis. If SUD is only partially invariant, diagnostic/classification estimates for subpopulations may not be comparable across groups. There is, therefore, a critical need for studies addressing this gap in the literature.

Application to Addiction Research

2.1. Definition and Model Notations

Formally, measurement invariance (Mellenbergh, 1989) holds when the conditional probability distribution of the observed item score variable, X, given the latent variable to be measured, ξ, does not depend on the group membership variable. In other words, for participants with the same score on the latent construct, their group membership plays no role in determining how they respond to an item.

In addiction research, items in a scale or an instrument, such as the diagnostic criteria for alcohol use disorder (AUD), are sometimes formulated with a binary response format with 0/1 = absence/presence of a symptom. Then a common choice of measurement model under the structural equation model (SEM) framework is to assume a continuous unobserved response variate, X_ij*, underlying the observed response for person i on the jth binary item X_ij, so that

$$\{\begin{array}{l}{X}_{ij}=1,\text{if}\hspace{0.17em}{X}_{ij}^{*}\hspace{0.17em}>{\tau }_j\\ X_{ij}=0,\text{if}\hspace{0.17em}{X}_{ij}^{*}\le \hspace{0.17em}{\tau }_j{}^{\prime }\end{array}$$

where τ_j is a threshold parameter of the unobserved variate over which the observed score will be 1; in other words, when the degree of symptom (X_ij*) is above the threshold, a participant will respond with a “1.” With the continuous X_ij*, one can then apply the common factor model with the form

$$X_{ij}^{*}={\lambda }_j{\xi }_i+{\epsilon }_{ij},$$

where ξ_i denotes the latent score (e.g., true degree of AUD) for person i; λ_j is the factor loading for item j, which is the regression slope of X_ij* on ξ_i; and ε_ij is the unique factor score that captures the influence of construct-irrelevant factors on the item response (e.g., machine error).¹ Here we assume that ξ_i and ε_ij for all items are jointly normal and independent to each other.² Measurement invariance thus would imply that the thresholds, factor loadings, and unique factor variances are all the same across groups.

2.2. Measurement Invariance With Binary Items

In many areas of diagnostic research, binary items that assess the presence or absence of a symptom are used. Importantly, there are substantial differences in the stages of measurement invariance under a factor model for binary items and for continuous items. With continuous items, researchers commonly distinguished between four stages of invariance (e.g., Vandenberg & Lance, 2000): configural, metric, scalar, and strict invariance. However, with binary and categorical items, these four stages may not be fully applicable because of (a) the addition of thresholds and (b) the observed scores having limited categories. As discussed in Wu and Estabrook (2016), with binary items only three stages of measurement invariance can be tested, and one way to organize the three stages would be to first establish configural invariance (having the same factor structure but no constraints on the measurement parameters), followed by scalar invariance (equal factor loadings and thresholds), and then finally strict invariance (scalar invariance + equal unique factor variances of the unobserved response variates). Unlike in the case of continuous items where scalar invariance is sufficient for valid mean comparisons, with binary items, only when strict invariance holds would respondents from two populations with the same level of the latent trait have equal probabilities of responding “1.” As far as we are aware, no studies have developed approaches for evaluating the impact of partial invariance on diagnostic accuracy in the context of binary items.

2.3. Diagnostic Accuracy Indices With Two Populations

Consider an example of a diagnostic test used to screen White and Asian participants in the United States for AUD. Following previous literature, we call the majority population (i.e., White) the reference population and the minority population (i.e., Asian) the focal population. For each population, one can conceptualize the relation between the observed score on the diagnostic test and the true latent AUD score on a graph, as shown in Figure 1. For each population, the relation between the latent score and the observed test score is represented with an ellipse. The horizontal and vertical lines, which denote the cutoffs for the observed diagnostic test and for the true latent AUD score, divide the total area into four quadrants. The area above the horizontal line (i.e., Quadrants A and B) represents those receiving a positive diagnosis whereas area on the right of the vertical line (i.e., Quadrants A and D) represents individuals who truly have AUD. Thus, Quadrant A represents true positives, and Quadrant C denotes the true negatives. Quadrant B represents the false positives—individuals who do not have AUD but are incorrectly diagnosed by the instrument as having AUD. Finally, Quadrant D denotes the false negatives—individuals who truly have AUD but are not diagnosed by the instrument. Conventional terminologies used in diagnostic testing (Altman & Bland, 1994a, 1994b) provide four indices (see Table 1) that summarize diagnostic accuracy: proportion selected (PS; or proportion diagnosed), success ratio (SR) or positive predictive value, sensitivity (SE), and specificity (SP).

Figure 1.

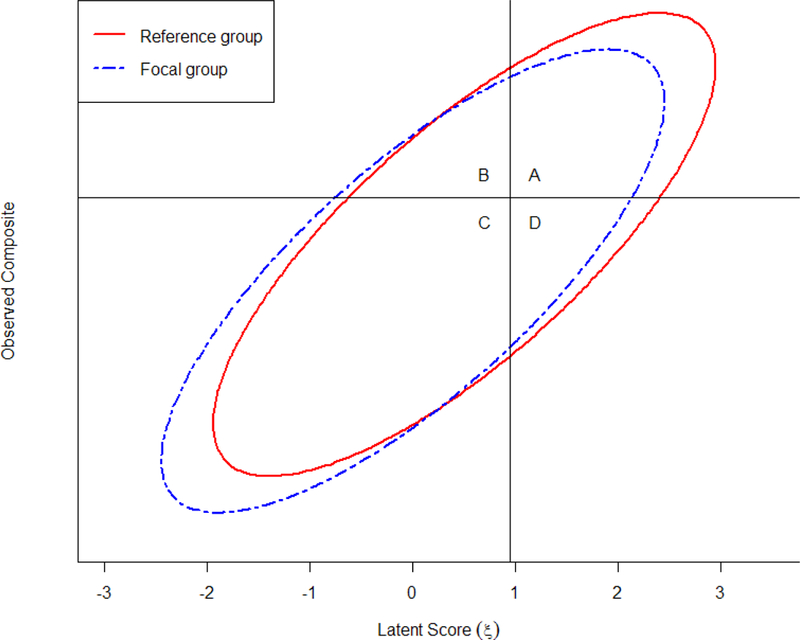
Recreation of Figure 2 from Millsap and Kwok (2004) showing the bivariate distribution of latent score and observed sum score with respect to two subpopulations. Note that the graph is used mainly for conceptual understanding; when the indicators were binary, the contour is not smooth and continuous.

Table 1.

Definition of the Diagnostic Accuracy Indices

	Mathematical Definition	Meaning
Proportion Selected (Diagnosed)	PSk = p(Ak) + p(Bk)	Proportion of individuals being Positively diagnosed; prevalence rates based on the criteria
Success Ratio	SRk = p(Ak) / [p(Ak) + p(Bk)]	Proportion of individuals who are truly positive among all individuals being positively diagnosed by the diagnostic criteria
Sensitivity	SEk = p(Ak) / [p(Ak) + p(Dk)]	Proportion of individuals who are correctly positively diagnosed by the diagnostic criteria among all individuals who truly are positive
Specificity	SPk = p(Ck) / [p(Ck) + p(Bk)]	Proportion of individuals who are correctly ruled out by the diagnostic criteria among all individuals who are negative

Note: A = true positive, B = false positive, C = true negative, D = false negative, and p(·) represents the probability of a particular possibility. The index k denotes the population, where k = r represents the reference population and k = f represents the focal population.

Proportion selected (A + B) in our example refers to the proportion of individuals being diagnosed as having AUD by the diagnostic criteria, which is the prevalence rate of AUD for each population. Success ratio (A / [A + B]) is the proportion of individuals who truly have AUD among all individuals being positively diagnosed by the diagnostic criteria; a low success ratio means that many individuals who do not have AUD are given the diagnosis, which may lead to potential stigmatization as well as wasted resources. Sensitivity (A / [A + D]) is the proportion of individuals who are correctly positively diagnosed among all individuals who truly have AUD; a low sensitivity indicates many individuals with AUD are undiagnosed, which means failure to provide help and resources to those who are truly in need. Finally, specificity (C / [B + C]) is the proportion of individuals who are correctly ruled out among all individuals who do not have AUD; a low specificity indicates that many individuals without AUD are being labelled as having such a problem, potentially leading to stigmatization and wasted resources.

2.4. Heuristic Example

Now consider an example of five AUD items tested across two groups (populations). Assume that the latent factor means are 0 and −0.5 for the reference and the focal groups. Assume that the factor variances are both 1.0, and the unique factor variances are all 1.0 for both groups. Also assume that the loadings (λ₁ to λ₅) are invariant and equal 1, 0.8, 1.2, 0.9, and 1.3, but only the first three indicators are scalar invariant across the two groups with thresholds (τ₁ to τ₃) of 1, 2, and 0.5. For the remaining two items, assume that the thresholds (τ₄ and τ₅) are 2.1 and 2.4 for the reference group and are 1.4 and 1.5 for the focal group. Thus, Asians would be more likely to endorse the forth and the fifth items than White people at the same latent AUD level (as illustrated in Figure 2). However, knowing that the test is partially invariant in that the thresholds are lower for the focal group by differences of 0.7 and 0.9 for items 4 and 5 does not help researchers understand the practical impact, and diagnostic accuracy analysis can provide such information in the context of screening or diagnostic tests with binary items.

Figure 2.

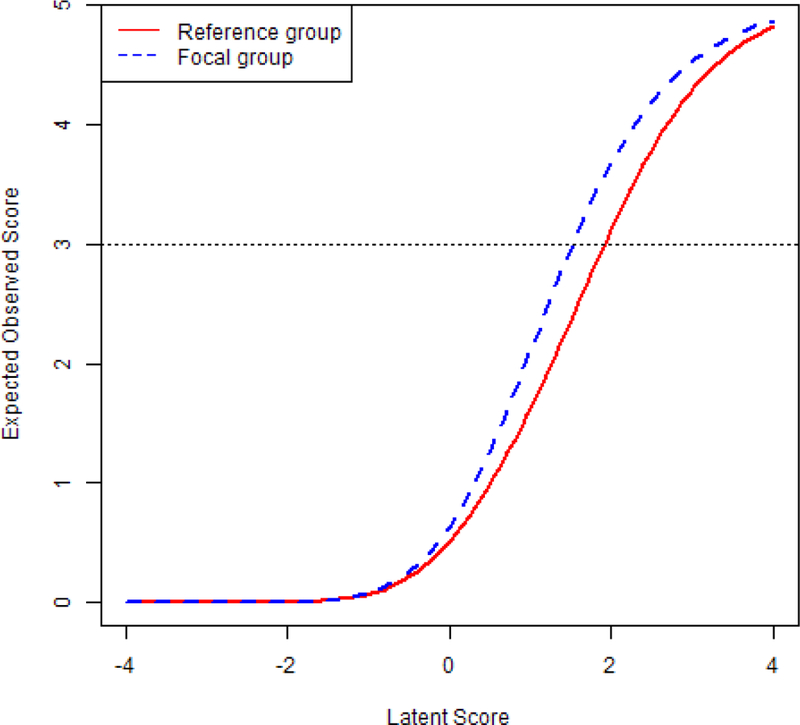
Expected number of endorsed items as a function of the latent factor score for the heuristic example.

Assume that the test would screen an individual endorsing three or more items. To perform diagnostic accuracy analysis, one needs to obtain the diagnostic accuracy indices for the partially invariant parameters as well as if the parameters were invariant.³ The PartInv_cat() R function in Supplemental material 1 automates this process by taking as input the parameter estimates from standard SEM output based on the partial invariance model. A tutorial on using the R script can be found in Supplemental material 2, with the resulting diagnostic indices shown in Table 2.

Table 2.

Diagnostic Accuracy Indices for the Heuristic Example

	Strict Invariance		Partial Scalar Invariance
	Reference	Focal	Reference	Focal
Proportion diagnosed	.107	.047	.081	.064
Success Ratio	.672	.562	.715	.460
Sensitivity	.648	.614	.551	.740
Specificity	.960	.979	.974	.964

For this example, if the test were fully invariant, 10.7% of the reference group and 4.7% of the focal group would have been diagnosed using the cutoff score of 3, compared to 8.1% and 6.4% for the actual partial invariant test. Therefore, the partial invariance has a substantial impact as it causes the test to positively classify fewer people in the reference group but more people in the focal group, mainly because the two noninvariant items are more likely to be endorsed by the focal group at the same level of the latent variable. Also, while the noninvariance did not have a strong influence on the specificity of the test (from .960 to .974 for the reference group and from .979 to .964 for the focal group), it has a relatively big impact on its sensitivity: it drops from .648 to .551 for the reference group while increases from .614 to .740 for the focal group.

Therefore, with the diagnostic accuracy analysis, one has more information regarding the impact of the partial invariance, which in this example seems matter most if one is interested in obtaining accurate prevalence rates for both groups and/or if one is concerned about identifying people who should be diagnosed based on their true latent scores (potentially for treatment and interventions) in the reference group (in which high sensitivity is needed).

3. Real Data Illustration

To further illustrate the diagnostic accuracy analysis, we used alcohol use data from the 2014 National Survey on Drug Use and Health (NSDUH), which is an annual nationally representative survey of substance use and health in the United States conducted by the Substance Abuse and Mental Health Services Administration (SAMHSA). We examined diagnostic accuracy across two age groups (12–25 vs. 26 and older) given evidence of differential item functioning between older and younger participants on some of the items (e.g., slope was lower among older compared to younger participants for tolerance and greater in the older group for activities given up; Saha, et al., 2006).

3.1. Sample

Participants were noninstitutionalized civilians aged 12 or older sampled across all 50 states and the District of Columbia. More details regarding NSDUH study design and survey procedures are available elsewhere (Center for Behavioral Health Statistics and Quality, 2015). There were 55,271 participants in the original data set; however, after excluding participants who had never used alcohol or had not used alcohol in the past 12 months, or had missing data on all AUD items (n = 293),⁴ the final sample of the real data illustration consisted of 28,629 participants (50.1% females), with 36.1% (n = 10,340) aged between 12 to 25 years and 63.9% (n = 18,289) aged 26 years or above. In the final sample, participants reported their race as White (66.3%), Hispanic (14.7%), Black/African American (10.7%), Asian (3.3%), Native American (1.5%), Native HI/Pacific Islanders (0.4%), mixed (3.1%).

3.2. Measure

Participants were asked about their alcohol use via the DSM-IV alcohol dependence criteria (APA, 1994). Following the NSDUH coding manual for substance dependence, we combined and recoded participants’ responses to 10 alcohol related items to form the seven binary DSM-IV alcohol dependence criteria, and participants were considered to have alcohol dependence if they met three of the seven dependence criteria.⁵

3.3. Tests of Measurement Invariance

As mentioned, we evaluated measurement invariance of the seven binary DSM-IV items for diagnosing alcohol dependence across two age groups. A configural invariance one-factor model was first fitted to the data using Mplus 7.4 with the robust weighted least square estimator (ESTIMATOR=WLSMV) and the THETA parameterization.⁶ The model fit was good, but an examination of the modification indices (MIs) showed that a large unmodeled unique factor covariance between Item 2 and Item 4, especially for the group with older age (MI = 383.38). Freeing this unique factor covariance in both groups resulted in substantially improved model fit, χ²(df = 26) = 170.18, Δχ²(df = 2) = 225.129, p < .001, RMSEA = .020, 90% CI [.017, .023], CFI = .995.

We then tested for scalar invariance by constraining the factor loadings and the thresholds to be equal across groups. The χ² difference test was statistically significant, with Δχ²(df = 5) = 56.50, p < .001, and MIs showed evidence for threshold noninvariance of item 3 (MI = 97.17). A partial scalar invariance model with unequal item 3 threshold across groups demonstrated good fit, with χ²(df = 30) = 165.56, RMSEA = .018, 90% CI [.015, .020], CFI = .996. For the remaining scalar invariant items, we found evidence of noninvariance for the unique factor variances with Δχ²(df = 6) = 138.33. Modification indices suggested noninvariance of the unique factor variance for item 4 (MI = 143.55), and further sequential investigation (Yoon & Millsap, 2007) suggested noninvariance for item 1, 2, and 5 (MIs = 18.19 to 33.19). In other words, only items 6 and 7 were considered invariant in the final partial strict invariance model.

The latent factor mean and variance were fixed to be 0 and 1.0 for the younger group and were estimated to be −1.29 and 3.16 for the older group, so the older group (aged 26+) had lower alcohol dependence tendency and was more heterogeneous. The model parameters were shown in Table 3, with the thresholds for item 3 estimated to be 0.76 for the younger group and 1.18 for the older group, and the unique factor variances for the noninvariant items were between 1.41 and 1.83. Thus, with the same degree of alcohol dependence, an older participant would be less likely to endorse item 3 than a younger participant.

Table 3.

Parameter Estimates of the Alcohol Use Disorder Items Based on the Partial Invariance Model

	Loadings	Thresholds		Unique Factor Variancesa Older
		Younger	Older
1. Great deal of time spent	1.00 (---)	1.01 (0.03)		1.70 (0.24)
2. Larger amounts than intended	0.84 (0.05)	2.19 (0.05)		1.41 (0.09)
3. Tolerance	0.74 (0.04)	0.76 (0.02)1.18 (0.06)		1.76 (0.22)
4. Unsuccessful attempts to cut down	0.66 (0.04)	2.24 (0.05)		1.83 (0.10)
5. Continued use despite problems	1.21 (0.08)	2.57 (0.09)		1.63 (0.14)
6. Reduced or given up important activities	1.02 (0.06)	2.39 (0.06)		1.00 (---)
7. Withdrawal	0.82 (0.05)	2.47 (0.06)		1.00 (---)

Note: The younger group aged between 12–25 years, and the older group aged 26 years or above. Robust weighted least squares estimator (ESTIMATOR=WLSMV) and THETA parameterization were used. Numbers shown in parentheses were the standard errors.

^aThe unique factor variances were fixed to be 1.0 for the younger group.

3.4. Diagnostic Accuracy Analysis

Despite the statistical evidence of noninvariance, it is not clear what practical impact is associated with the noninvariant threshold and unique factor variances, so we conducted a diagnostic accuracy analysis (see Supplemental material 3). As shown in Table 4, if the items were measurement invariant, 8.8% in the younger population and 5.4% in the older population would be identified as potentially having alcohol dependence. The statistically significant noninvariant items changed the rates to 8.6% and 5.5%, and most people would agree that a change of 0.2 percentage points is small unless very high precision is needed. If measurement invariance held, the sensitivity values were .645 and .716 for the younger and older populations, respectively, and the specificity values were .965 and .986. With the partial invariance found on the items, the sensitivity (.663 and .698) and specificity values (.968 and .983) were still quite comparable. Therefore, with the diagnostic accuracy analysis, one can see that the statistically significant noninvariance had a small impact on the efficacy of the items for diagnostic purpose.

Table 4.

Diagnostic Accuracy Indices for the Real Data Example

Age	Strict Invariance		Partial Strict Invariance
	12–25	26 or above	12–25	26 or above
Proportion diagnosed	.088	.054	.086	.055
Success Ratio	.636	.746	.660	.709
Sensitivity	.645	.716	.663	.698
Specificity	.965	.986	.968	.983

4. Discussion

4.1. Statistical and Practical Significance of Noninvariance

Measurement invariance is particularly crucial in ensuring inferences about cross-group differences are correct (e.g., gender, age, and culture; Milfont & Fischer, 2010; Widaman & Reise, 1997). Despite increasing awareness from methodologists and addiction researchers on the need for measurement invariance testing, there has been little methodological discussion regarding metrics that quantify the practical significance of violations of measurement invariance(Putnick & Bornstein, 2016; Vandenberg, 2002). In this article, we reviewed one approach to answer the practical significance question—selection/diagnostic accuracy analysis. This approach directly links noninvariance to the efficacy of the instrument for diagnostic, selection, or classification purposes. Whereas the original framework was developed for continuous and normally distributed indicators, we extended the framework to accommodate binary items and developed an R program to perform the analysis. Furthermore, through heuristic and real data examples, we illustrated how diagnostic accuracy analysis can provide more concrete information about how measurement noninvariance impacts the diagnostic results given by tests, and showed that statistically significant violations of measurement invariance may or may not be practically significant.

It should be emphasized that the interpretation of practical significance depends on the context and the constructs being measured. For example, a difference of one percentage points in proportion selected may be considered small for relatively low stake traits (e.g., attitudes), but this difference may be substantial in more high-stake contexts where instruments play a major role in diagnosis (e.g., SUD and other mental disorders), despite Millsap and Kwok’s (2004) suggestion that changes under five percentage points “are unlikely to be meaningful in most applications” (p. 111).⁷ The question of practical significance should also be answered differently depending on intended use of the test (Millsap & Kwok, 2004). Whereas diagnostic accuracy analysis would be highly suitable for instruments used for diagnosis and classifications, it may be less meaningful for instruments intended to score individuals on a continuum that does not involve a cutoff score, and researchers should consult alternative metrics for quantifying practical impact of invariance violations (e.g., Nye & Drasgow, 2011; Oberski, 2014; Stark, Chernyshenko, & Drasgow, 2004).

4.2. Conclusions

In the past few decades there has been a strong emphasis on effect size and practical significance for quantitative research in behavioral sciences (e.g., Ferguson, 2009; Henson, 2006; Lai & Kwok, 2016). Similarly, for measurement invariance, we urge addiction researchers to not only conduct invariance testing for psychological instruments, which is extremely important to ensure valid research findings, but to also evaluate and report the practical significance of any detected invariance violations as a function of the purposes of tests and the associated research contexts, in the same manner as interpreting effect size statistics. We hope that by (a) successfully raising researchers’ awareness on recent developments in the measurement invariance literature, (b) highlighting the importance of understanding and reporting the practical significance of the diagnostic accuracy indices to violations of invariance for diagnostic tools, and (c) providing researchers with an easy-to-implement R program to perform such analyses, this article helps to increase the extent to which future research evaluates and reports the practical significance of partial invariance. Finally, we expect future methodological work to extend the framework to include ordinal and categorical indicators, other measurement models in item response theory, settings with three or more groups, and via comparison to an external, “gold-standard” validator.

Highlights.

• Noninvariant measurement can bias prevalence rate estimates in subgroups

• Diagnostic accuracy analysis quantifies practical significance of partial invariance

• Noninvariant alcohol dependence items across age did not affect diagnostic accuracy

• The diagnostic accuracy analysis can be easily implemented with the R program