Transmission of Mechanical Information by Purinergic Signaling

Abstract

The skeleton constantly interacts and adapts to the physical world. We have previously reported that physiologically relevant mechanical forces lead to small repairable membrane injuries in bone-forming osteoblasts, resulting in release of ATP and stimulation of purinergic (P2) calcium responses in neighboring cells. The goal of this study was to develop a theoretical model describing injury-related ATP and ADP release, their extracellular diffusion and degradation, and purinergic responses in neighboring cells. After validation using experimental data for intracellular free calcium elevations, ATP, and vesicular release after mechanical stimulation of a single osteoblast, the model was scaled to a tissue-level injury to investigate how purinergic signaling communicates information about injuries with varying geometries. We found that total ATP released, peak extracellular ATP concentration, and the ADP-mediated signaling component contributed complementary information regarding the mechanical stimulation event. The total amount of ATP released governed spatial factors, such as the maximal distance from the injury at which purinergic responses were stimulated. The peak ATP concentration reflected the severity of an individual cell injury, allowing to discriminate between minor and severe injuries that released similar amounts of ATP because of differences in injury repair, and determined temporal aspects of the response, such as signal propagation velocity. ADP-mediated signaling became relevant only in larger tissue-level injuries, conveying information about the distance to the injury site and its geometry. Thus, we identified specific features of extracellular ATP and ADP spatiotemporal signals that depend on tissue mechanoresilience and encode the severity, scope, and proximity of the mechanical stimulus.

Introduction

The human skeleton is constantly interacting and adapting to the physical world, as seen by the loss of bone in astronauts experiencing microgravity (1) or gain of bone in athletes engaged in intense activities (2). The magnitude, frequency, and duration of mechanical loading are known determinants of the mechanoadaptive response of bone at the tissue level (3, 4, 5) and at the cellular level, as observed with intracellular free calcium ([Ca²⁺]_i) elevations in osteocytes during in vivo mechanical loading (6).

We have recently reported that physiologically relevant mechanical loading routinely injured bone cells in vitro and in vivo, resulting in release of ATP through plasma membrane disruptions and stimulation of calcium responses in the neighboring cells (7). These membrane disruptions in bone cells are counteracted by rapid vesicle-mediated membrane repair (7, 8), which limits ATP spillage. Thus, contrary to previous generalizations that ATP is released as a bolus proportional to mechanical stimulus (9), our data suggest that mechanically stimulated ATP release contains dynamic information about both the extent of the injury and the rate of repair.

ATP stimulates autocrine and paracrine [Ca²⁺]_i signaling through the purinergic (P2) receptor network, which consists of seven ionotropic P2X receptors and eight G-protein-coupled P2Y receptors (10, 11, 12). Several P2 receptors have been implicated in the mechanoadaptive response in bone (13, 14, 15); however, it is uncertain why so many receptors are required and how they integrate mechanical information. Although individual P2 receptors are sensitive to ATP concentrations over 2–3 orders of magnitude, the entire P2 receptor network covers over a millionfold range of ATP concentrations (16, 17). In addition, many P2Y receptors are differentially sensitive to ADP and ATP. Thus, it is possible that unique subsets of P2 receptors are activated in neighboring bone cells depending on the position and severity of the mechanical stimulus.

We hypothesized that the dynamics of mechanically stimulated ATP release reflect the balance between cell membrane injury and repair, and that ATP and ADP released from the injury site generate unique spatiotemporal signatures that convey information to nonstimulated neighboring cells, such as injury severity and distance to stimulus, as well as the state of tissue mechanoresilience. We developed a mathematical model to account for injury-related ATP and ADP release and their extracellular diffusion and degradation, as well as paracrine purinergic responsiveness of neighboring cells. The experimentally validated model was scaled to a tissue-level mechanical stimulus to investigate how a cellular population responds to mechanical stimuli with position- and severity-appropriate responses.

Materials and Methods

Solutions

The solutions used were as follows: phosphate-buffered saline (140 mM NaCl, 3 mM KCl, 10 mM Na₂HPO₄, 2 mM KH₂PO₄ (pH 7.4)), autoclaved; physiological solution (PS; 130 mM NaCl, 5 mM KCl, 1 mM MgCl₂, 1 mM CaCl₂, 10 mM glucose, 20 mM HEPES (pH 7.6)), filtered through 0.2 μm; bioluminescence reaction buffer (0.1 M dithiothreitol, 25 mM tricine, 5 mM MgSO₄, 0.1 mM EDTA, 0.1 mM NaN₃ (pH 7.8)), filtered through 0.2 μm.

Reagents

The reagents used were as follows: minimum essential medium (MEM) α (12000-022; Gibco, Gaithersburg, MD); Fura2-AM (F1221; Invitrogen, Carlsbad, CA); D-luciferin (L2916; Invitrogen); collagenase P from Clostridium histolyticum (11213857001; Roche, Basel, Switzerland); adenosine 5′-triphosphate (A9187; Sigma-Aldrich, St. Louis, MO); adenosine 5′-diphosphate (A2754; Sigma-Aldrich); adenosine 5′-monophosphate (01930; Sigma-Aldrich); adenosine (A4036; Sigma-Aldrich); hexokinase from Saccharomyces cerevisiae (H6380; Sigma-Aldrich); L-ascorbic acid (A8960; Sigma-Aldrich); luciferase from Photinus pyralis (L9420; Sigma-Aldrich); phosphoenolpyruvic acid (860077; Sigma-Aldrich); pyruvate kinase from rabbit muscle (P9136; Sigma-Aldrich); quinacrine (Q3251; Sigma-Aldrich); Venor GeM Mycoplasma PCR-based detection kit (MP0025; Sigma-Aldrich); ARL 67156 (1283; Tocris Bioscience, Bristol, UK); suramin (1472; Tocris Bioscience); Dulbecco’s modified Eagle’s medium (319-020 CL; Wisent Bio Products, Saint-Jean-Baptiste, QB, Canada); fetal bovine serum (FBS) (080152; Wisent Bio Products); penicillin streptomycin (450-201-EL; Wisent Bio Products); pyruvate (600-110-UL; Wisent Bio Products); collagenase type II (LS004176; Worthington Biochemical).

Cell culture

All procedures were approved by McGill University’s Animal Care Committee and complied with the ethical guidelines of the Canadian Council on Animal Care. For compact bone-derived osteoblasts (CB-OB), 4- to 6-week-old C57BL/6 mice (Charles River Laboratories, Wilmington, MA) femurs and tibia bone fragments were enzymatically digested and cultured for 3–5 days in αMEM (with 10% FBS, 1% pyruvate, 1% penicillin streptomycin) as described previously (7). Cells were trypsinized, filtered, plated at 10⁴ cells/cm² in osteoblast differentiation medium (+50 μg/mL ascorbic acid), and cultured for 2–3 days before experiments. The C2C12 cell line (CRL-1772; ATCC, Manassas, VA), stably transfected with BMP-2 (C2-OB, courtesy of Dr. M. Murshed, McGill University) was plated at 10⁴ cells/cm² in DMEM (with 10% FBS, 1% pyruvate, 1% penicillin streptomycin) and cultured for 2–3 days before experiments. Absence of mycoplasma contamination was verified in cryo-preserved stocks of C2-OB cells using PCR-based detection kit.

Intracellular calcium recordings and analysis

Cells plated in glass-bottomed 35 mm dishes or 48-well plates (MatTek, Ashland, MA) were loaded with Fura2-AM for 30 min, bathed in PS, acclimatized for 10 min on the stage of an inverted fluorescence microscope (T2000; Nikon, Tokyo, Japan), and imaged as described previously (18). The data were analyzed using a previously developed MATLAB (The MathWorks, Natick, MA) algorithm (19).

Generating homogenous solutions of ATP and ADP

ADP present in ATP solutions was converted to ATP by 0.1 U/mL pyruvate kinase in the presence of excess (100 μM) phosphoenolpyruvate (PEP). ATP present in ADP solutions was converted to ADP by 0.1 U/mL hexokinase. On the day of experiment, enzymatic reactions were carried out in PS at 37°C for 30 min, then heat inactivated at 95°C for 2 min.

ATP and ADP dose-dependencies

Fura2-loaded C2-OB cells in a 48-well plate were bathed in 270 μL PS, and 30 μL of ATP or ADP solution at 10× of the desired final concentration was added (e.g., 30 μL of 10 μM ATP solution was added to cells to achieve 1 μM ATP stimulation). Application of PS alone evoked no discernable response. A solution containing desired concentrations of both ATP and ADP was obtained from homogenous solutions of ATP and ADP. Response probabilities P were measured as the proportion of cells in the field of view that evoked a discernable [Ca²⁺]_i response. Reaction times t_rxn were measured as the average time between the first discernable [Ca²⁺]_i response and subsequent cell responses.

Single-cell mechanical stimulation

A micropipette was positioned ∼10 μm from the cell membrane at a 45° angle from the horizontal plane and moved at a speed of 250 μm/s with a contact duration of 60 ms using a FemtoJet microinjector NI2 (Eppendorf, Hamburg, Germany).

Vesicle release kinetics

Cells were incubated with 10 μM quinacrine solution for 15 min at room temperature and washed with PS, and time-lapse recordings were acquired with a Nikon T2000 inverted fluorescence microscope at a sampling rate of 2 Hz. Vesicular release was identified as sudden loss of localized fluorescence using an ImageJ plugin, SparkSpotter (Babraham Bioinformatics, Cambridge, UK), applied to temporally reversed and contrast-enhanced image stacks (7).

ATP measurement

ATP content was measured in 100 μL of supernatant by bioluminescence luciferin-luciferase assay using FB 12 single-tube luminometer (Titertek-Berthold, Pforzheim, Germany).

Computational analysis

Data are representative images and traces or means ± SEM, with N indicating the number of independent trials. Statistical significance was assessed by analysis of variance (ANOVA), followed by a Bonferroni post hoc test and accepted as significant at p < 0.05. Numerical simulation of diffusion profiles was conducted in Mathematica 11.2 (Wolfram Research, Champaign, IL). Curve fitting and model-related analyses was conducted in MATLAB R2018a (The MathWorks). Logistic regression and receiver operating characteristic curves were generated in SPSS 24 (IBM, Armonk, NY).

The model parameter space that predicted expected outcomes θ_E (where θ = T, P) most consistent with experimental observations θ_O was identified by computing the bias between θ_E and θ_O as the root difference between mean-squared error ($MSE\left({\theta }_E,{\theta }_O\right)=\frac{1}{m}\sum _{i=1}^m{\left({\theta }_E-{\theta }_O\right)}^2$, m is the number of distances from primary cell at which observed secondary responses θ_O were compared to predicted outcomes θ_E) and sampling variance (Var),

$$Bias\left({\theta }_E,{\theta }_O\right)=\sqrt{MSE\left({\theta }_E,{\theta }_O\right)-Var\left({\theta }_O\right)}.$$

When two sets of outcome measurements were available (response time T, response probability P), the parameter space with minimal Bias_{T, P} was identified by combining Bias_T and Bias_P as

$$Bia{s}_{T,P}=\sqrt{Bia{s}_T^2+Bia{s}_P^2}.$$

Results

Mechanical stimulation of a single osteoblast leads to release of purinergic signals that convey position- and magnitude-related information to neighboring osteoblasts

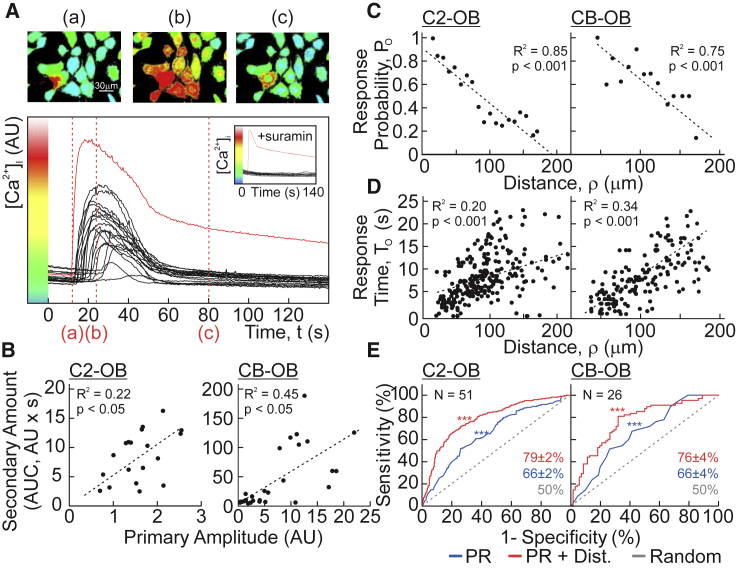
CB-OBs or C2-OBs were loaded with the calcium indicator Fura2, and a single osteoblast (primary cell) was mechanically stimulated with a glass micropipette, which we have shown to result in a repairable plasma membrane disruption, the severity of which correlates with the magnitude of [Ca²⁺]_i elevation in the stimulated cell (7). Now, we focus on [Ca²⁺]_i elevations in nonstimulated neighboring cells (secondary responses), which were inhibited by the purinergic antagonist suramin (Fig. 1 A). The magnitudes of the secondary responses were proportional to the amplitude of [Ca²⁺]_i elevation in the primary cell (Fig. 1 B). The responding fraction of cells (observed response probability, P_O) decreased with increasing distance from the primary cell (Fig. 1 C), whereas the delay between the primary and secondary responses (observed response time, T_O) increased (Fig. 1 D). Using a logistic regression model, we demonstrated that the parameters of the primary Ca²⁺ response and distance to the primary cell predicted the onset of secondary responses with 76–79% accuracy (p < 0.001, Fig. 1 E). These data suggest that purinergic signals convey information regarding the magnitude and proximity of the mechanical stimulus.

Figure 1.

Mechanically induced purinergic signaling conveys the magnitude and distance to stimulus. (A) A single Fura2-loaded C2-OB was mechanically stimulated by micropipette, and [Ca²⁺]_i was recorded. Top shows pseudocolored 340/380 Fura2 ratio images. Bottom shows [Ca²⁺]_i recording of mechanically stimulated (primary) cell (red) and neighboring (secondary) responders (black). Red dashed lines show time points in top panel. Inset shows experiment performed in presence of P2 receptor antagonist suramin (100 μM). (B) Correlation between the primary response amplitude and area under curve of secondary [Ca²⁺]_i elevations is shown for C2-OBs (left) and CB-OBs (right). (C and D) Correlation between distance from primary cell and observed response probability P_O of neighboring cells (C) and observed response time T_O after mechanical stimulation (D) is shown for C2-OBs (left) and CB-OBs (right). Black dashed lines show linear regressions. (E) Receiver operating characteristic curves demonstrate the performance of the logistic regression model in predicting incidence of secondary responses based on primary response parameters (blue), primary response parameters and distance (dist., red), or chance alone (gray) for C2-OBs (left) and CB-OBs (right). Accuracies of logistic models ± SEM are shown; N indicates number of trials. To see this figure in color, go online.

ATP release depends on the size and resealing kinetics of membrane repair after mechanical injury

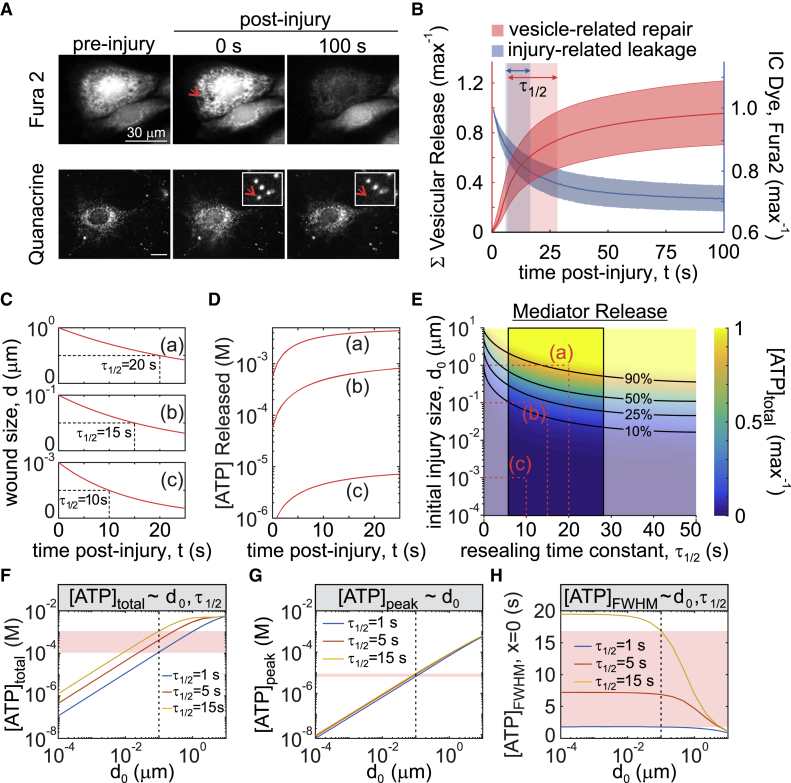
We have shown that micropipette stimulation generates nonlethal membrane injury, detectable by decrease in Fura2 fluorescence (dye leakage), through which intracellular ATP is released (7). Membrane injury is quickly repaired through protein kinase C-dependent vesicular exocytosis, thus limiting ATP release (7). The size of initial membrane injury, d₀, was estimated to be on the nanometer scale based on cell intake of membrane-impermeable dyes of variable size (7). To quantify the rate of membrane resealing, we determined the repair kinetics using two independent methods: plateau of dye leakage and cessation of vesicular release (20). Depletion of Fura2 fluorescence (340 ex/510 em) after C2-OB cell micropipette stimulation was monitored until a plateau was achieved, indicating membrane repair (Fig. 2 A, top). Alternatively, quinacrine-loaded C2-OB cells were micropipette stimulated and vesicular release was monitored as a proxy of the membrane repair process (Fig. 2 A, bottom). The repair time τ_1/2—calculated as the exponential half-life—was 11 s (95% confidence interval (CI): 6–16) for Fura2-leakage assay (Fig. 2 B, blue) and 18 s (95% CI: 7–28) for vesicular release imaging (Fig. 2 B, red). Despite using two surrogate measures of membrane repair, both methods provided similar estimates of τ_1/2, suggesting that the contribution of other processes is limited. Thus, nanometer-scale mechanically induced membrane injury reseals with an exponential half-time of 11–18 s.

Figure 2.

The size and resealing kinetics of the membrane injury determine the kinetics of ATP release. (A and B) A single Fura2- (A, top) or quinacrine- (A, bottom) loaded C2-OB was mechanically stimulated by a micropipette, and the time course of intracellular Fura2 decrease (B, blue, n = 51) and cumulative vesicular release (B, red, n = 15) was recorded. Data are means ± 95% confidence intervals (CIs). Shaded boxes show 95% CI of time to half max (τ_1/2) for Fura2 leakage (blue) or vesicular release (red). (C and D) Simulated temporal changes in injury size d(t) (C) and ATP release (D) are shown for indicated initial injury size d₀ and the characteristic membrane repair times τ_1/2. (E) Solution space for injury-related ATP release with respect to changes in initial injury size d₀ and the characteristic membrane repair time τ_1/2 are shown. Black lines show isoclines for parameter pairs that yield equal percentage of total ATP release. Red dashed lines show parameter pairs (a, b, c) used in (C) and (D). The outlined region shows experimentally measured τ_1/2. (F–H) Relationship between initial injury size d₀ and total ATP released [ATP]_total (F), peak extracellular ATP concentration [ATP]_peak (G), and full-width half maximum (FWHM) duration of extracellular ATP concentration [ATP]_FWHM at the source (H) are shown for τ_1/2 = 1, 5, 15 s. Red bands show sensitivity of ATP release parameters to changes in τ_1/2 for d₀ = 100 nm (dashed black line). To see this figure in color, go online.

Mediator release model

To describe the release of mediators, such as ATP, from a mechanically injured cell, we assumed that a circular injury (21, 22) with the diameter d(t) and an initial diameter d₀ is repaired with an exponential half-time τ_1/2 (Table 1):

$$d\left(t\right)=d_0{2}^{-t/{\tau }_{1/2}}$$ (1)

Table 1.

Model Parameters

Symbol	Description	Value(s)	Reference
${\text{c}}_{\text{in},0}^{\text{i}}$	initial intracellular concentration, i = ATP, ADP	5.0 mM ATP; 0.5 mM ADP	(56)
τ1/2	reseal half-time constant	0.1–20 s	estimated in study
d0	initial injury (diameter)	10−4 to 101μm	estimated in study
Rcell	osteoblast cell radius	8.3 μm	estimated for C2-OB cells
Vcell	osteoblast cell volume	2400 μm3	estimated for C2-OB cells
DATP	ATP diffusion coefficient	347 μm2 s−1	(24, 25, 26)
DADP	ADP diffusion coefficient	377 μm2 s−1	(24, 25, 26)
kATP	ATP degradation constant	0.05 min−1	estimated in study
kADP	ADP degradation constant	0.25kATP	approximated from (57)
PO	observed response probability	Table S1	estimated in study
trxn	reaction time	Table S1	estimated in study
TO	observe response time	Table S1	estimated in study
Symbol	Description		Value
ρ	distance from mechanically stimulated cell		NAa
t	time postinjury		NA
d(t)	diameter of cellular injury postinjury		Eq. 1
βi(t)	transport coefficient, i = ATP, ADP		Eq. 2
${\text{c}}_{\text{in}}^{\text{i}}\left(\text{t}\right)$	intracellular concentration, i = ATP, ADP		Eq. 3
${\text{c}}_{\text{source}}^{\text{i},\text{'}}$	rate of release at source, i = ATP, ADP		Eq. 4
${\text{c}}_{\text{ex}}^{\text{i}}\left(\rho ,\text{t}\right)$	extracellular concentration, i = ATP, ADP		Eqs. 5 and 6
pinst(ρ, t)	instantaneous response probability		Eq. 7
PE(ρ, t)	expected response probability		Eq. 7
λ(ρ, t)	instantaneous rate of response		Eq. 8
S1(ρ, t)	proportion of cells that will eventually respond		Eqs. 9 and 10
S0(ρ, t)	proportion of cells that will not respond		Eq. 10
R(ρ, t)	proportion of cells that have responded		Eq. 10
S∗(ρ, t)	conditional survival function		Eq. 11
TE(ρ)	expected response time		Eq. 12
f(ρ, t)	probability density function of S∗; spatiotemporal distribution of paracrine responses		Eq. 13
Symbol	Description
[ATP]total	total ATP released after cell injury
[ATP]peak	peak extracellular ATP concentration after cell injury
[ATP]FWHM	duration that extracellular [ATP] was sustained above half-maximal [ATP]
Rsignal	distance at which the expected response probability P declines below 5%
Vsignal	average speed at which the paracrine signal propagates

^aNA, not applicable.

Mediator release from the injured cell was modeled as described previously by Zarnitsyn and colleagues (23) as diffusion through the membrane opening, with the rate of intracellular mediator depletion $c_{in}^{i^{\text{'}}}\left(t\right)$ (i = ATP or ADP; ′ indicates the time derivative) proportional to the diffusion-dependent transport coefficient β_i, which in turn depends on the injury diameter d(t), cell volume V_cell, and intracellular $D_{cyto}^i$ and extracellular D_i diffusivity of ATP and ADP ($D_{cyto}^i\mathrm{≌}0.25D_i$ (23); i = ATP, ADP; Table 1):

$${\beta }_i={\left(\frac{1}{4D_{cyto}^i\times d\left(t\right)}+\frac{1}{4D_i\times d\left(t\right)}\right)}^{-1}{\left(V_{cell}\right)}^{-1}=\frac{4D_i}{5V_{cell}}d\left(t\right).$$ (2)

The rate of intracellular mediator depletion $c_{in}^{i^{\text{'}}}\left(t\right)$ is then expressed as

$$\{\begin{array}{cc}{c}_{in}^{i^{\text{'}}}\left(t\right)=-{\beta }_i{c}_{in}^i\left(t\right)& ,t>0\\ c_{in}^i\left(0\right)=c_{in,0}^i& ,t=0\end{array}.$$ (3)

Finally, the rate of mediator release at the site of the injured cell $c_{source}^{i^{\text{'}}}\left(t\right)$ is

$$c_{source}^{i^{\text{'}}}\left(t\right)=-c_{in}^{i^{\text{'}}}\left(t\right).$$ (4)

At varying d₀ and τ_1/2, the rate of ATP release is the highest immediately after membrane disruption and declines exponentially with time (Fig. 2, C and D). The total amount of ATP released ([ATP]_total) is proportional to the initial injury size d₀ and inversely proportional to the repair half-time τ_1/2 (Fig. 2, E and F). The peak of extracellular ATP ([ATP]_peak) is determined by the initial injury size (Fig. 2 G), whereas ATP persistence at the source ([ATP]_FWHM; time during which extracellular [ATP] was above half-maximal [ATP]) is governed by the rate of membrane resealing (Fig. 2 H). Thus, the severity and dynamics of membrane repair contribute differentially to the peak, total amount, and persistence of extracellular ATP.

Contribution of ADP to the mechanically stimulated purinergic signal

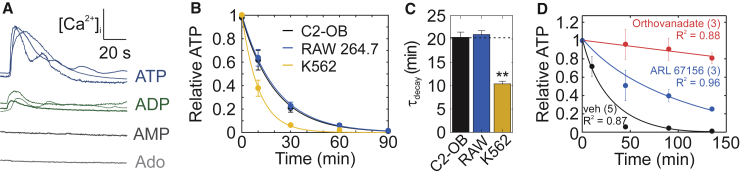
Mediator spillage through membrane injury is nonspecific, and therefore, purines present in the cytosol will be released from the cell in proportional amounts. We tested ATP, ADP, AMP, and adenosine for their ability to induce calcium responses. Only ATP and ADP evoked [Ca²⁺]_i elevations in C2-OB cells (Fig. 3 A). Extracellular ATP and ADP are degraded by ectonucleotidases present on cells resident to bone, including osteoblasts, osteoclasts, and bone marrow cells. Osteoblast (C2-OB) and osteoclast (Raw 264.7) precursor-like cells metabolized extracellular ATP with similar rate constants of 0.049 min⁻¹ (95% CI: 0.043–0.055) and 0.048 min⁻¹ (95% CI: 0.044–0.042), respectively, whereas erythroid K562 cells hydrolyzed ATP significantly faster, with a rate constant of 0.096 min⁻¹ (95% CI: 0.085–0.11) (Fig. 3, B and C; Tables 1 and S1). The degradation rate was independent of cell density (Fig. S1). In C2-OB cells, ATP degradation was partially inhibited by the ectonucleotidase inhibitor ARL 67156 (Fig. 3 D, blue) and potently inhibited by the alkaline-phosphatase inhibitor orthovanadate (Fig. 3 D, red). These data suggest that the mechanical signal is composed of ATP and ADP and is regulated by extracellular enzymatic degradation.

Figure 3.

Contribution of ADP to the mechanically stimulated purinergic signal. (A) Representative [Ca²⁺]_i elevations in Fura2-loaded C2-OBs stimulated by 1 μM ATP, 1 μM ADP, 10 μM AMP, or 10 μM adenosine (Ado) are shown. (B and C) 1 μM ATP was added to cultures of C2-OB osteoblasts, RAW 264.7 osteoclast precursors, and K562 erythrocyte-like cells; ATP degradation was measured (B); and decay time constants τ_decay were estimated (C), data are means ± SEM, n = 3 per time point per cell type. (D) Degradation of 1 μM ATP by C2-OBs in the presence of the ectonucleotidase inhibitor ARL 67156 (10 μM) or the alkaline-phosphatase inhibitor orthovanadate (10 μM) is shown, data are means ± SEM, the sample sizes are shown in parentheses. For (B)–(D), solid curves show fitted exponential functions (Table S1). To see this figure in color, go online.

Paracrine response probabilities and times are governed by ATP and ADP diffusion and purinergic reaction times

We next extended our mediator release model to describe the extracellular diffusion of ATP and ADP released by mechanical injury and subsequent cellular responsiveness to ATP and ADP, using experimental data to validate model predictions.

Diffusion model

We coupled ATP and ADP release and extracellular diffusion using the geometrical constraints imposed by our in vitro experiments. The mechanically stimulated primary cell was modeled as a finite sphere (defined by radius R_cell), from which ATP and ADP molecules were released uniformly within the cell volume at a rate $c_{source}^{i^{\text{'}}}\left(t\right)$ (i = ATP, ADP). Of note, the geometry of the primary cell minimally affected ATP and ADP diffusion profiles because of their rapid diffusion over the cell length scale $\left(\left(R_{cell}^2/6D_i\right)<0.04s;i=ATP,ADP\right)$. Diffusion of extracellular ATP and ADP ($c_{ex}^i\left(\rho ,t\right)$; i = ATP, ADP) with coefficients D_i was computed using the three-dimensional (3D) radial diffusion equation with spherical boundaries of radius R_bound, such that the radial variable satisfied 0 < ρ < R_bound. This spherical boundary has no physical significance and was chosen to be much larger than the other dimensions in our problem, i.e., $\sqrt{6D_{i}t}\ll R_{bound}$, where t is any time in the time range considered in this work. To account for extracellular degradation of ATP and ADP, we assumed the first-order degradation rate constant of ATP to ADP as k_ATP and the first-order degradation rate constant of ADP out of the system as k_ADP. To impose no-flux boundary (Neumann) conditions to emulate the culture dish bottom, we doubled the concentration in the upper hemisphere (i.e., polar angle limited to 0 < θ < π/2) while ignoring the solution in the lower hemisphere (i.e., π/2 < θ < π) after computation of the concentration in full 3D space. The equations that were solved (in full 3D space) for extracellular ATP (Eq. 5) and ADP (Eq. 6) were

$$\{\begin{array}{c}\frac{\partial }{\partial t}{c}_{ex}^{ATP}\left(\rho ,t\right)=D_{ATP}\left(\frac{{\partial }^2}{\partial {\rho }^2}+\frac{2}{\rho }\frac{\partial }{\partial \rho }\right)c_{ex}^{ATP}\left(\rho ,t\right)+I\left(\rho <R_{cell}\right)c_{source}^{AT{P}^{\text{'}}}\left(t\right)-k_{ATP}{c}_{ex}^{ATP}\left(\rho ,t\right),|\rho <R_{bound},t\ge 0\\ \frac{\partial }{\partial t}{c}_{ex}^{ATP}\left(\rho ,t\right)=0,|\rho =R_{bound},t\ge 0\end{array}$$ (5)

and

$$\{\begin{array}{c}\frac{\partial }{\partial t}{c}_{ex}^{ADP}\left(\rho ,t\right)=D_{ADP}\left(\frac{{\partial }^2}{\partial {\rho }^2}+\frac{2}{\rho }\frac{\partial }{\partial \rho }\right)c_{ex}^{ADP}\left(\rho ,t\right)+I\left(\rho <R_{cell}\right)c_{source}^{AD{P}^{\text{'}}}\left(t\right)+k_{ATP}{c}_{ex}^{ATP}\left(\rho ,t\right)-k_{ADP}{c}_{ex}^{ADP}\left(\rho ,t\right),|\rho <R_{bound},t\ge 0\\ \frac{\partial }{\partial t}{c}_{ex}^{ADP}\left(\rho ,t\right)=0|\rho =R_{bound},t\ge 0\end{array},$$ (6)

where I(.) denotes the indicator function (1 when true, otherwise 0). Eqs. 5 and 6 were solved using the NDSolve routine provided by Mathematica 11.2 (Fig. 4 A).

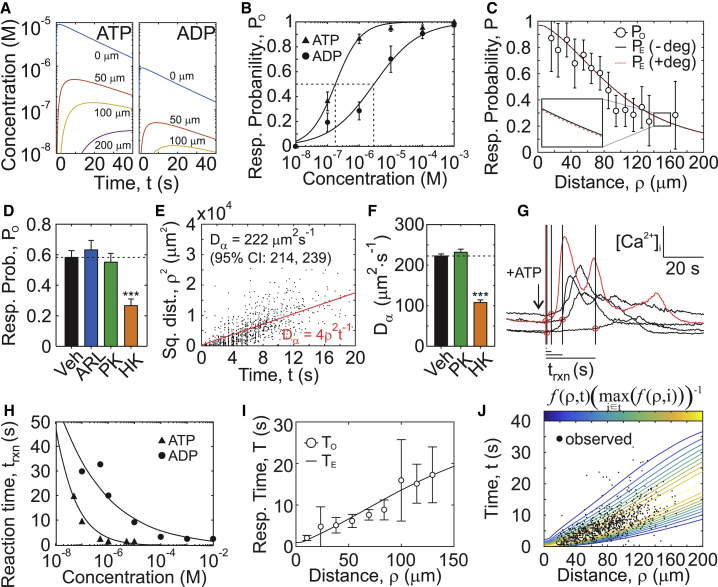
Figure 4.

Modeling diffusion and purinergic reaction times to predict the spatial and temporal distribution of secondary responses. (A) ATP and ADP release and diffusion were numerically simulated after mechanical injury of a single cell (d₀ = 100 nm, τ_1/2 = 15 s, k_ATP = 0, Eqs. 5 and 6). (B) Dose dependence of ATP and ADP response probabilities are shown. Means ± SEM, n = 6–8. Fitted curves show Hill functions (Table S1). (C) Expected response probabilities P_E after mechanical stimulation of a single cell in the presence (+deg; k_ATP = 0.05 min⁻¹) or absence (−deg; k_ATP = 0 min⁻¹) of extracellular ATP degradation compared to observed response probabilities P_O (means ± SEM, n = 51) are shown. (D) Observed response probabilities P_O after micropipette stimulation of C2-OB cell in the presence of vehicle 10 μM ARL 67156 (ARL), 0.1 U/mL pyruvate kinase + 100 μM PEP (PK), or 0.1 U/mL hexokinase (HK). Means ± SEM, ^∗∗∗p < 0.001 by ANOVA. (E) The relationship between observed secondary response times T_O and the squared distance from the source is shown. Red line shows the apparent diffusion coefficient D_α estimated by linear regression. (F) D_α in presence of vehicle, PK, or HK. Means ± SEM, n = 10–15, ^∗∗∗p < 0.001 assessed by ANOVA. (G) [Ca²⁺]_i traces demonstrating reaction times for ATP-stimulated responses (1 μM) are shown. The first discernable response is indicated in red; black lines/red circles: reaction times t_rxn. (H) ATP and ADP dose dependences for t_rxn are shown. Black lines show fitted exponential functions (Table S1). (I) A comparison of expected T_E and observed T_O (means ± SEM, n = 51) secondary response times is shown. (J) A spatiotemporal map of secondary responses represented as probability density function f (Eq. 13) overlaid with observed raw data is shown. To see this figure in color, go online.

Response probabilities

To examine whether the diffusion model can predict the secondary responses after stimulation of a single primary cell, we first characterized how the observed response probability P_O depends on ATP and ADP concentrations. ATP induced responses at lower concentrations compared to ADP (${\text{EC}}_{50}^{\text{ATP}}$ = 180 nM, ${\text{EC}}_{50}^{\text{ADP}}$ = 2.9 μM; Fig. 4 B; Table S1). When ATP and ADP were applied together, P_O was dictated by the nucleotide species with the highest P_O when applied alone (Fig. S2 A). Next, ATP and ADP spatiotemporal concentration profiles obtained by Eqs. 5 and 6 (Fig. 4 A) were mapped to the respective P_O values (Fig. 4 B; Fig. S2 A), generating a spatiotemporal map of instantaneous response probabilities denoted p_inst(ρ, t) (Fig. S2 B). The expected response probability P_E describing the proportion of cells expected to respond at distance ρ and time t was determined as the time-cumulative maxima of p_inst (Fig. S2 B):

$$P_E\left(\rho ,t\right)=\underset{j\mathit{\epsilon }t}{\max }\left(p_{inst}\left(\rho ,j\right)\right).$$ (7)

P_E(ρ, ∞) was computed for a range of injury-related parameters (d₀ = 10⁻⁴ to 10¹ μm, τ_1/2 = 1 to 20 s) and compared to P_O after single-cell micropipette stimulation. P_E values for τ_1/2 > 4 s, d₀ = 0.05–1 μm injuries were consistent with P_O (Fig. S3 A), with the best-fit parameter set being d₀ = 100 nm and τ_1/2 = 15 s (Fig. 4 C).

The model also predicted that extracellular nucleotide degradation (with k_ATP = 0.05 min⁻¹, k_ADP = 0.25k_ATP; Eqs. 5 and 6) has a negligible influence on the purinergic signal released by a single cell (Fig. 4 C). Experimentally, we confirmed that inhibition of ATP degradation or enzymatic conversion of ADP to ATP using pyruvate kinase and PEP did not affect P_O after single-cell micropipette stimulation, whereas hexokinase-mediated ATP-to-ADP conversion significantly reduced response radius and fraction (Fig. S4; Fig. 4 D).

Response times

We next examined whether ATP and ADP diffusion can predict the timing of secondary responses after single-cell micropipette stimulation. The apparent diffusion coefficient D_α (Fig. 4 E), estimated from the slope of the linear relationship between secondary response times and squared distances from the source as 222 μm² s⁻¹ (95% CI: 214–239), was significantly lower than diffusion coefficients reported for ATP (347 μm² s⁻¹) or ADP (377 μm² s⁻¹) (24, 25, 26). Enzymatic conversion of ADP to ATP using pyruvate kinase and PEP did not affect secondary response times, whereas hexokinase-mediated ATP-to-ADP conversion further reduced D_α (Fig. 4 F; Fig. S5), contrary to what would be expected based on the lower molecular weight of ADP compared to ATP. We hypothesized that the reaction times (t_rxn) of ATP- and ADP-mediated responses exhibit purine species-dependent differences. Applying ATP, ADP, or their combination to Fura2-loaded C2-OBs, we estimated the average time delay between purine application (approximated by the time of discernable response in the first cell) and subsequent responses (Fig. 4 G). Responses induced by ADP were slower compared to ATP, and reaction times were substantially slower at low nucleotide concentrations (Fig. 4 H; Table S1). When ATP and ADP were applied together, the nucleotide that evoked the fastest response governed the observed reaction time (Fig. S6 A). Thus, diffusion alone is insufficient to account for the observed response times and requires additional consideration of P2 reaction times.

Response time model

We next formulated a response time model to predict the expected response times T_E in neighboring cells (27). Spatiotemporal ATP and ADP concentrations after single-cell injury were numerically simulated (Fig. 4 A; Eqs. 5 and 6) and mapped to their corresponding observed reaction times (Fig. S6 A; Table S1) to obtain a spatiotemporal map of instantaneous reaction times t_rxn(ρ, t), from which the instantaneous rate of response λ(ρ, t) was obtained (Fig. S6 B):

$$\lambda \left(\rho ,t\right)=\frac{1}{t_{rxn}\left(\rho ,t\right)},$$ (8)

which then allowed us to derive the time-dependent proportion of responding cells $S_1\left(\rho ,t\right)$:

$$S_1\left(\rho ,t\right)=\exp \left\{-\underset{0}{\overset{t}{\int }}\lambda \left(\rho ,u\right)du\right\}.$$ (9)

To account for situations in which nucleotide concentrations are insufficient to induce response in all the cells, we partitioned the neighboring cells into three subpopulations: 1) cells that respond to the stimulus without delay R(ρ, t), 2) cells that have not yet responded but will respond eventually S₁(ρ, t), and 3) cells that will not respond to the stimulus S₀(ρ, t):

$$R\left(\rho ,t\right)+S_1\left(\rho ,t\right)+S_0\left(\rho ,t\right)=1.$$ (10)

These cellular subpopulations could further be expressed in terms of the expected response probability such that R(ρ, t) + S₁(ρ, t) = P_E(ρ, t) and S₀(ρ, t) = 1 − P_E(ρ, t) (Fig. S6 C). This partitioning of the neighboring cell population allows us to limit our focus to the subpopulation of responders (R(ρ, r) + S₁(ρ, t)) and define the conditional survival function S^∗(ρ, t), which describes the time-dependent proportion of responding cells:

$$S^{\ast }\left(\rho ,t\right)=\frac{S_1\left(\rho ,t\right)}{1-S_0\left(\rho ,\infty \right)}=\frac{\exp \left\{-{\int }_0^t\lambda \left(\rho ,u\right)du\right\}}{P_E\left(\rho ,\infty \right)}.$$ (11)

S^∗(ρ, t) was then integrated to obtain the expected response times T_E(ρ) at distance ρ:

$$T_E\left(\rho \right)=\underset{0}{\overset{\infty }{\int }}{S}^{\ast }\left(\rho ,u\right)du.$$ (12)

The values of T_E(ρ) derived for single-cell injuries where τ_1/2 > 4 s and d₀ = 100–500 nm were consistent with T_O (Fig. S3 B), with d₀ = 100 nm and τ_1/2 = 15 s remaining the best-fit parameter set (Fig. 4 I). Importantly, the observed spatial (P_O) and temporal (T_O) responses were best predicted by the same set of injury parameters (d₀ = 100 nm and τ_1/2 = 15 (Fig. S3 C)). The spatiotemporal distribution of observed secondary responses strongly correlated with predicted by the model using probability density function f(ρ, t) corresponding to the conditional survival function S^∗(ρ, t) (28) (Fig. 4 J):

$$f\left(\rho ,t\right)=\left(-\frac{d}{dt}\ln \left|S^{\ast }\left(\rho ,t\right)\right|\right)S^{\ast }\left(\rho ,t\right).$$ (13)

Thus, we have coupled ATP and ADP release, degradation, and diffusion to the secondary response and validated the expected response probabilities and times using experimental data. In addition, we have demonstrated that taking into account ATP and ADP reaction times is required to accurately describe the spatial and temporal aspects of secondary purinergic responses.

Injury severity and repair dynamics differentially affect the spatial and temporal recruitment of secondary purinergic responses

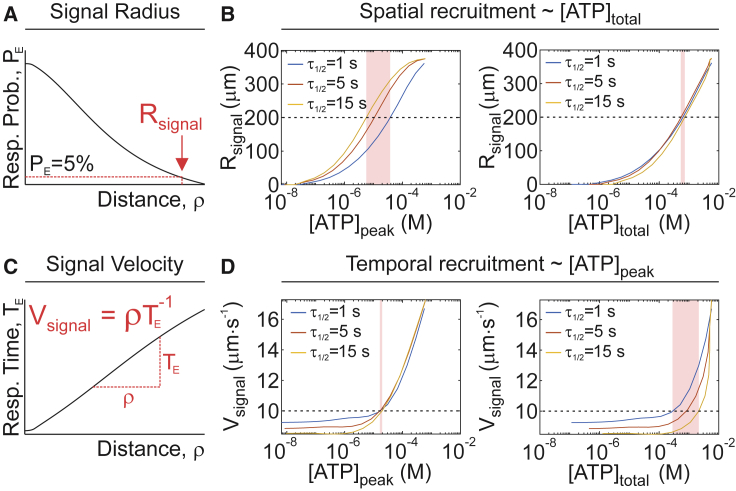
Using the validated model, we examined how the purinergic signal guides the spatial and temporal recruitment of secondary responses. The signal radius R_signal, the distance at which the expected response probability declines below 5% (Fig. 5 A), was governed by the total amount of ATP released, regardless of whether ATP was spilled from a severe injury or from a slowly repaired minor injury (Fig. 5 B). The signal velocity V_signal, the average speed at which the paracrine signal propagated (Fig. 5 C), was predominantly controlled by the peak concentration of ATP achieved after injury (Fig. 5 D). Thus, the total amount of ATP released, which depends on the overall damage to the stimulated cell, governs the degree of involvement of the neighboring population, whereas peak ATP concentration that only depends on the size of initial injury determines how fast the neighboring cells will respond.

Figure 5.

Relationship between ATP release and spatial and temporal recruitment of [Ca²⁺]_i responses. (A) Schematic of signaling radius (R_signal). (B) The relationship between ATP release parameters [ATP]_peak and [ATP]_total and spatial recruitment parameter R_signal is shown for τ_1/2 = 1, 5, 15 s. (C) A schematic of signal velocity (V_signal) is shown. (D) The relationship between ATP release parameters [ATP]_peak or [ATP]_total and temporal recruitment parameter V_signal is shown for τ_1/2 = 1, 5, 15 s. For (B) and (D), shaded bands show the sensitivity of ATP release parameters to changes in τ_1/2 for a given level of spatial (R_signal = 200 μm, B) or temporal (V_signal = 10 μm s⁻¹, D) recruitment. To see this figure in color, go online.

Propagation of purinergic signal resulting from a tissue-level injury

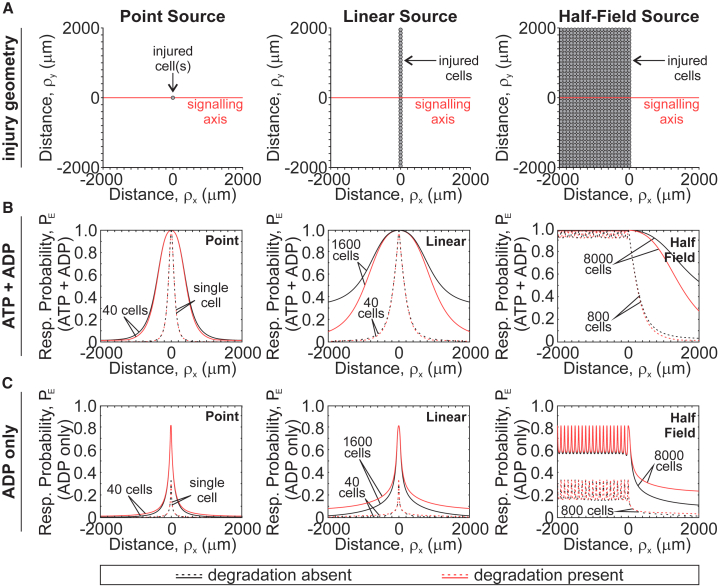
Physiologically, mechanical stimuli affect multiple cells occupying a tissue area of a certain size and geometry. This results in the release of purinergic mediators from numerous sources in the tissue, unlike the single-cell experimental setup that we have considered thus far. We extended the model to consider three injury geometries: 1) point source, consisting of one or 40 injured cells (Fig. 6 A, left); 2) linear source, consisting of 40 or 1600 injured cells evenly distributed along a 2000 μm linear plane (Fig. 6 A, middle); and 3) half-field source, consisting of 800 or 8000 cells evenly arranged as a series of point sources over a 2000 × 4000 μm² surface area (Fig. 6 A, right). For each of these geometries, we assumed simultaneous and identical cell-level injury (d₀ = 100 nm, τ_1/2 = 15 s) and assessed expected response probability along the signaling axis perpendicular to the injury front in the presence of extracellular nucleotide degradation (k_ATP = 0.05 min⁻¹, k_ADP = 0.25k_ATP) and in its absence (k_ATP = 0, k_ADP = 0) (Fig. 6 B). Because certain P2 receptors (e.g., P2Y1, P2Y12, and P2Y13) are predominantly sensitive to ADP (29), we also isolated the ADP-mediated response component (Fig. 6 C). The expected response probability was the highest at the site of injury and declined at increasing distances from the injury. For all geometries, the more cells were initially injured, the more neighboring cells exhibited P2 responses. The effect of extracellular nucleotide degradation became apparent for larger tissue-level injuries, especially when higher ATP levels (due to more injury) were sustained for longer (due to injury geometry). In these cases, ATP degradation attenuated total paracrine responsiveness while increasing the ADP-mediated signaling component (Fig. 6, B and C; red versus black curves). Importantly, the effects of extracellular nucleotide degradation were not observed at the site of injury but rather at increasing distances from the source. Thus, scaling a single-cell injury to a tissue-level injury with varying geometries revealed that ATP- and ADP-mediated components of the purinergic response reflect the extent of injury and differentially change with increasing distance from the injury site.

Figure 6.

Paracrine purinergic signaling after tissue-level injury. ATP and ADP release and diffusion from point (left), linear (middle), and half-field (right) source injuries (A) were numerically simulated, and contributions of ATP and ADP (B) or ADP alone (C) to expected response probabilities P_E were determined for varying number of injured cells in the presence (red) or absence (black) of extracellular ATP and ADP degradation. Simulation parameters: k_ATP = 0 (degradation absent) or 0.05 min⁻¹ (degradation present), k_ADP = 0.25k_ATP, d₀ = 100 nm, τ_1/2 = 15 s. To see this figure in color, go online.

Discussion

Overview

The goals of this study were 1) to determine how mechanically induced cell membrane injury and repair govern ATP and ADP release dynamics, 2) to characterize ATP and ADP spatiotemporal diffusion profiles, and 3) to understand the basic principles dictating the spatial and temporal recruitment of responses in neighboring (nonstimulated) cells to the presented levels of ATP and ADP. For each elementary step (ATP and ADP release, diffusion, and degradation and P2 responses in neighboring cells), we developed and experimentally validated mathematical descriptions. Using the combined model of ATP-driven mechanotransduction, we scaled a single-cell injury to a tissue-level injury with varying geometries and described how neighboring cells may detect the magnitude of injury and discern their proximity to the injury site. We were able to identify specific features of the ATP and ADP spatiotemporal signal that encode the severity of mechanical stimulus and distance to the stimulus, as well as the state of tissue mechanoresilience.

ATP release due to mechanical injury

Several groups have shown that mechanically induced membrane disruptions occur under physiological conditions in muscle fibers (30), the gastrointestinal tract (31), the heart (32), the aorta (33), and bone (7, 8). Despite these injuries, cell death is minimal because cells can rapidly repair their membranes (34). Membrane disruption results in nonspecific spillage of intracellular content, which includes growth factors (32, 35) as well as ATP (7, 36, 37). The extent of this spillage is determined by the size of membrane disruption (parameter d₀) and the rate of membrane repair (parameter τ_1/2). Importantly, both membrane integrity and repair rates are sensitive to pharmacological interventions along the Ca²⁺/phospholipase C/protein kinase C axis (7, 38) and are improved after exposure to mechanical stimulation (7, 39, 40). We demonstrated that injuries with an initial size of d₀ ∼ 100 nm that resealed exponentially with a half-time of τ_1/2 ∼ 15 s predicted ATP concentrations at the surface of the mechanically stimulated cell (∼10 μM) that were consistent with experimental measurements (0.05–80.5 μM) (7). Modeling ATP release using theoretical description developed for the transport of fluorescent dyes though membrane pores (23), we showed that the total amount of ATP released depended on both the severity of mechanical injury d₀ and rate of membrane repair τ_1/2, whereas the peak extracellular ATP was determined by the injury severity alone. The P2 receptor network consists of 15 receptor subtypes with ATP affinities covering over a millionfold range of ATP concentrations (16, 17). Therefore, peak ATP release will determine the degree of activation of low-affinity P2 receptors (e.g., P2X7; EC₅₀ = 1.9 mM (16)), whereas the total amount of ATP released will determine the area over which high-affinity P2 receptors are activated (e.g., P2Y2; EC₅₀ = 200 nM (16)). Thus, information about the extent of the injury and the rate of repair encoded in the dynamics of ATP release can be deciphered at the level of the P2 receptor network. Importantly, these mechanistic insights are applicable to any form of stimulus-related mediator release that can be described in terms of its magnitude and temporal dynamics, including conductive and vesicular ATP release.

Signal propagation through ATP diffusion and degradation and P2 responses in neighboring cells

After release into the extracellular space, ATP diffuses and is concurrently metabolized by ectonucleotidases (41), producing ADP, AMP, and adenosine, which may also stimulate cellular responses (14, 42, 43, 44). Moreover, because mediator spillage through a membrane injury is nonspecific, all purines present in the cytosol will be released in proportional amounts. Of the tested purine metabolites, ADP was capable of stimulating calcium responses in C2-OB, consistent with prior work (45, 46). ATP degradation half-time in the extracellular space was 20 min (95% CI: 17–25) for C2-OB cells, compared to ∼10 min for primary rat osteoblasts (47) and ∼5 min for primary murine osteoblasts (48). Osteoblastic ATP degradation was too slow to affect purinergic transmission initiated by a single cell, contrary to endothelial cells (49, 50) or keratinocytes (51), in which paracrine responses after single-cell stimulation were potentiated when ectonucleotidases were inhibited. Nevertheless, because most ectonucleotidases have a micromolar affinity for ATP (41), low hydrolysis rates were consistent with the amounts of ATP released by a single osteoblast. Spatiotemporal ATP and ADP concentration profiles after mechanical stimulation were computed by coupling injury-related ATP release to radial diffusion. We validated the model using [Ca²⁺]_i recordings of secondary responders after micropipette stimulation of a single osteoblast because direct ATP measurements were performed with limited sensitivity and spatial resolution (7). Surprisingly, we have found that the apparent diffusion coefficients derived from the [Ca²⁺]_i recordings were lower than previously reported (24, 25, 26). To account for this discrepancy, we used a response-time modeling framework to predict the probability and timing of secondary [Ca²⁺]_i elevations (27), which allowed us to explain the high degree of variability observed in [Ca²⁺]_i response times and to predict experimentally observed propagation velocities of ∼10 μm/s, consistent with previously reported velocities (52). Accounting for response times resolved the discrepancy between observed and expected ATP diffusion coefficients that was identified by us and others (53). Finite wave propagation was sufficient to explain observed [Ca²⁺]_i elevations in osteoblasts, without need for the regenerative propagation terms (e.g., ATP-mediated ATP release) that were proposed in airway epithelia (54) or astrocytes (55). Thus, ATP and ADP diffusion and degradation, as well P2 receptor response times, collectively explained the spatial and temporal recruitment of purinergic signaling events in osteoblasts.

Mechanical information encoding

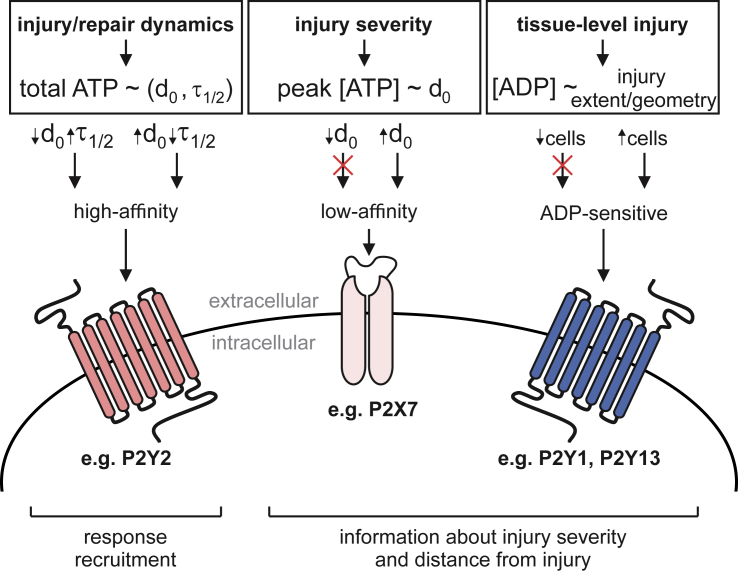
We identified three features of purinergic signal that communicate complimentary mechanically relevant information to neighboring cells: 1) the total amount of ATP released, 2) the peak extracellular [ATP], and 3) the ADP-mediated signaling component. The total amount of ATP released, regulated by the injury severity (d₀) and repair dynamics (τ_1/2), determined the P2 receptor signaling radius, thus governing the spatial recruitment of the neighboring population. The peak extracellular ATP concentration reflected the severity of the cell injury (d₀ only) and strongly influenced the temporal recruitment of the neighboring population. Peak [ATP] allowed cells to discriminate between severe (large d₀) and minor (small d₀) injuries that led to the release of similar total amounts of ATP because of differences in injury repair dynamics (e.g., fast repair for large injury, slow repair for small injury). This framework enables situations in which severe injuries—associated with higher peak ATP concentrations—can recruit low-affinity P2 receptors. The third signaling feature was ADP-mediated signaling, which manifested only when tissue-level injuries were considered. In the case of a single-cell injury, the amounts of ADP released and produced from ATP degradation were too low to induce paracrine responses. However, when the injury included multiple cells, ATP degradation resulted in overall dampening of paracrine responses, especially at further distances from the injury site, together with the proportional increase in ADP-mediated signaling. The observed injury-related increase in ADP-mediated signaling is supported by prior work in which ADP-sensitive P2Y1 (14) and P2Y13 (48) receptors were implicated in osteoblast mechanotransduction. Thus, our findings support a model in which mechanical information—encoded within ATP and ADP diffusion waves—is differentially decoded by low-affinity P2 receptors, high-affinity P2 receptors, and ADP-sensitive P2 receptors (Fig. 7). It is important to note that in this study, we focused on the population-level responses (i.e., spatial and temporal recruitment) and did not consider specific features of [Ca²⁺]_i responses in individual cells, such as amplitude, duration, and oscillatory behavior. Based on our insights at the population level, future efforts investigating how mechanical information is decoded at the cellular level are warranted.

Figure 7.

Proposed model of mechanical information decoding by the P2 receptor network. Left: single-cell membrane injury (d₀) and repair (τ_1/2) dynamics regulate the total amount of ATP released and the extent of recruitment of neighboring cells (i.e., spatial recruitment) through high-affinity P2 receptors. Middle: severity of injury (d₀) is conveyed to neighboring cells through peak extracellular ATP concentrations that influence the timing of responses (i.e., temporal recruitment) and low-affinity P2 receptor signaling. Right: extent and geometry of tissue-level injury determine the amount of ADP released and produced by ATP degradation and thus stimulation of ADP-sensitive P2 receptors. To see this figure in color, go online.

Conclusions

We developed and validated a theoretical model to investigate how extracellular ATP and ADP released by mechanical stimulation encode information about the position and severity of the mechanical stimulus and how this information can be subsequently decoded at the level of the paracrine responses. We demonstrate that purinergic signaling fields are tuned by the severity of injury and dynamics of repair, thereby enabling neighboring cells to evoke responses appropriate to the injury severity and the neighboring cell proximity to the event.

Author Contributions

Study conception and design, N.M. and S.V.K.; acquisition of experimental data, N.M.; modeling, N.M., S.S., P.W.W., and S.V.K.; analysis and interpretation of data, N.M. and S.V.K.; drafting of manuscript, N.M. and S.V.K. All authors contributed to the critical revision and approval of the final manuscript.

Editor: Arthur Sherman.