A totally data-driven whole-brain multimodal pipeline for the discrimination of Parkinson's disease, multiple system atrophy and healthy control

Abstract

Parkinson's Disease (PD) and Multiple System Atrophy (MSA) are two parkinsonian syndromes that share many symptoms, albeit having very different prognosis. Although previous studies have proposed multimodal MRI protocols combined with multivariate analysis to discriminate between these two populations and healthy controls, studies combining all MRI indexes relevant for these disorders (i.e. grey matter volume, fractional anisotropy, mean diffusivity, iron deposition, brain activity at rest and brain connectivity) with a completely data-driven voxelwise analysis for discrimination are still lacking. In this study, we used such a complete MRI protocol and adapted a fully-data driven analysis pipeline to discriminate between these populations and a healthy controls (HC) group. The pipeline combined several feature selection and reduction steps to obtain interpretable models with a low number of discriminant features that can shed light onto the brain pathology of PD and MSA. Using this pipeline, we could discriminate between PD and HC (best accuracy = 0.78), MSA and HC (best accuracy = 0.94) and PD and MSA (best accuracy = 0.88). Moreover, we showed that indexes derived from resting-state fMRI alone could discriminate between PD and HC, while mean diffusivity in the cerebellum and the putamen alone could discriminate between MSA and HC. On the other hand, a more diverse set of indexes derived by multiple modalities was needed to discriminate between the two disorders. We showed that our pipeline was able to discriminate between distinct pathological populations while delivering sparse model that could be used to better understand the neural underpinning of the pathologies.

Highlights

• •Structuro-functional MRI can discriminate between parkinsonian syndromes
• •Discriminant MRI modalities vary as a function of the discrimination task
• •fMRI is crucial in discriminating between Parkinson's disease patients and controls
• •Structural MRI discriminate between Multiple System Atrophy patients and controls

1. Introduction

Parkinson's Disease (PD) and Multiple System Atrophy (MSA) are two neurodegenerative diseases characterized at the neuropathological level by the accumulation of α-synuclein, either in neurons in PD or in oligodendrocytes in MSA (Halliday et al., 2011). The clinical diagnosis of MSA can be challenging as no specific symptom or biomarker allows a “definite” diagnosis in vivo. Currently, the “definite” diagnosis of MSA requires post-mortem confirmation, by means of a neuropathological examination. It is often challenging in clinical practice to differentiate MSA, especially its parkinsonian variant (MSA-p) as opposed to the cerebellar variant (MSA-c), from PD as both entities can share similar phenotypes, especially in early stages.

Brain modifications related to neurodegeneration due to aging as well as psychiatric or neurodegenerative diseases can be characterized using multimodal MRI protocols with sequences sensitive to different tissue characteristics (Barbagallo et al., 2016; Cherubini et al., 2016; Eustache et al., 2016; Lee et al., 2018; Nemmi et al., 2015; Péran et al., 2010, Péran et al., 2018; Spoletini et al., 2011). Previous multimodal MRI studies have mainly used structural markers: grey and white matter volume (calculated using T1-weighted imaging), microstructural integrity of the white and grey matter by using diffusion weighted imaging (DWI) related indexes (e.g. fractional anisotropy, FA, and mean diffusivity, MD) and iron deposition by using R2* imaging. Several studies have focused on characterizing the pathophysiological substrate of PD and MSA from a multimodal perspective. Our group showed that PD patients displayed higher iron deposition (as measured by R2* imaging) in the substantia nigra (SN), lower FA in the SN and thalamus, and higher MD in the thalamus compared to healthy controls (HC) (Péran et al., 2010). Moreover, a combination of indexes extracted from three clusters by using voxel-wise analysis (i.e. R2* in a cluster in the SN, MD in the putamen and FA in the SN) reached area under the curve in ROC analysis as high as 95% (Péran et al., 2010). More recently, we extended these methods to MSA patients, showing that they show microstructural changes in the putamen and the cerebellum, regardless of the subtype, relative to both HC and PD patients (Barbagallo et al., 2016; Péran et al., 2018). To our knowledge, no previous studies combined functional and structural MRI indexes to discriminate between PD and MSA patients.

Together with the development of multimodal MRI imaging, there has been an increasing use of multivariate assessments and machine learning for the analyses of MRI data (Haller et al., 2014). Multivariate methods are intrinsically well suited for the analysis of brain imaging; they use the global pattern of the data, rather than focusing on one voxel at a time as in massive univariate analyses, thus leveraging the information about the whole spatial pattern of brain modifications. When multivariate methods are coupled with multimodal imaging, one can make full use of the complementarity of the information acquired through the different MRI sequences. Several studies have used multivariate methods to discriminate PD patients from healthy controls, both using single modality (Adeli et al., 2016; Chen et al., 2015; Huppertz et al., 2016; Zhang et al., 2014) and multimodal MRI imaging (Bowman et al., 2016; Long et al., 2012), or different indexes extracted from the same modalities (Focke et al., 2011; Peng et al., 2017). Only two of these studies also included MSA patients (Focke et al., 2011; Huppertz et al., 2016), without using multimodal protocol. Although these studies could successfully discriminate between PD and controls (and MSA and controls) they have some limitations: some of them used non-independent features selection (Zhang et al., 2014), some used a-priori parcellation of the brain (Adeli et al., 2016; Bowman et al., 2016; Huppertz et al., 2016; Long et al., 2012; Peng et al., 2017), and some used a leave-one-out cross-validation scheme (Chen et al., 2015; Focke et al., 2011; Huppertz et al., 2016; Long et al., 2012; Zhang et al., 2014), which is known for introducing an optimistic bias in the evaluation of the performance of the classifier (Varoquaux et al., 2017). Most importantly, to our knowledge the most complete multimodal protocol was used by DuBois Bowman et al. (2016), including T1, rs-fMRI and DWI, but not another important biomarker for parkinsonian syndromes, as R2*.

In the light of the limitation of the previous studies, we performed a study with the following characteristics

• •A complete multimodal MRI protocol including T1, DWI, rs-fMRI and R2* sequences
• •A completely data-driven (i.e. voxel-wise rather than ROI based) pipeline
• •A pipeline striking a good balance between performance (i.e. accuracy) and interpretability of the model (i.e. final number of features included in the model)
• •A pipeline that could evaluate the relative importance of the different modalities
• •The use of 10-folds cross-validation, less prone to optimistic bias
• •A comparison of performance when discriminating between PD and HC, MSA and HC, and PD and MSA, using the same sequences.

To this aim we adapted a pipeline recently developed by Meng et al. (2017). As in the original pipeline, we used several feature reduction steps and further reduced feature dimensionality by clustering spatially close voxels before fitting the discriminative model. However, at variance with Meng and colleagues, we used what we call a “totally data driven” pipeline; we included a nested cross-validation step to select the most relevant modalities for each classification problem. This has the added benefit of identifying the minimum set of modalities needed to achieve the best discrimination between groups. Moreover, we tested several cluster extent thresholds in the clustering step.

2. Materials and methods

2.1. Patients

Twenty-nine MSA and 26 PD patients matched for age and sex were prospectively recruited at the outpatient clinic of the Toulouse PD Expert Center and the Toulouse site of the French Reference Center for MSA. Inclusion criteria were: (1) diagnosis of PD or MSA according to established international diagnostic criteria (Gilman et al., 2008; Hughes et al. 1992); (2) Hoehn and Yahr score (Zhang et al., 2014, Benarroch, 2003) < 4 on treatment; (3) negative history of neurological or psychiatric diseases other than PD or MSA; (4) lack of significant cognitive decline (Mini Mental State Examination score > 24); (5) no treatment with deep brain stimulation; and (6) no evidence of movement artefacts, vascular brain lesions, brain tumor, and/or marked cortical and/or subcortical atrophy on MRI scan (2 expert radiologists examined all MRIs to exclude potential brain abnormalities as apparent on conventional FLAIR, T2-weighted, and T1-weighted images). At the time of MRI data acquisition, 22 MSA patients were classified as “probable”, while 7 MSA patients were classified as “possible”. All “possible” MSA patients were subsequently reclassified as “probable” while followed-up for another 2 years at the French Reference Center for MSA. No PD patient had his/her diagnosis reclassified after 2 years of subsequent follow-up. All patients receiving antiparkinsonian treatments were tested on medication. A healthy control group of 26 right-handed subjects closely matched to patients for age, sex, and education was also included.

The study was conducted according to the Declaration of Helsinki and approved by the Toulouse Ethics Committee. Written informed consent was obtained from all participants.

2.2. Image acquisition

We used a multimodal MRI protocol including T1-weighted imaging, T2 relaxometry, DWI and resting state fMRI (rs-fMRI) (details in Supplemental data).

2.3. Images preprocessing

2.3.1. T1 images

T1 images were segmented in grey matter and white matter map using CAT12 (http://www.neuro.uni-jena.de/cat/) (Gaser and Dahnke 2016). This toolbox is an improvement over the VBM8 toolbox. Briefly, the tissue probability maps are only used in a first (affine) registration step, the actual segmentation is performed using an adaptive MAP approach with local adaptation of local intensity changes in order to deal with varying tissue contrast (Dahnke et al. 2012; Gaser and Dahnke 2016). The final normalization is performed using DARTEL (Ashburner, 2007). The grey and white matter tissue maps were not modulated, as it has been shown that unmodulated maps are best suited to detect atrophy (Radua et al., 2014). The grey matter volume images were smoothed with a Gaussian kernel of 8 mm FWHM (results obtained using non-smoothed images are reported in the supplementary materials).

CAT12 provide an automatic QA value for each segmented image; this normalized QA values take into account resolution, bias and noise present in the images. This unique value is then transformed in a note that ranges from A to E. Images with note lower than D are usually discarded from the analysis. None of our subjects had a QA note lower than D.

2.3.2. Resting state images

rs-fMRI data were analyzed using the conn toolbox (Whitfield-Gabrieli and Nieto-Castanon, 2012). Briefly, all images were time-slicing corrected, unwarped and realigned to the first volume, normalized using the standard normalization algorithm in SPM12 (Friston et al. 2007) and smoothed with a Gaussian kernel of 8 mm FWHM (results obtained using non-smoothed images are reported in the supplementary materials). We also used the art toolbox (http://nitrc.org/projects/artifact_detect/) to detect corrupted volumes, defined as volume with >2 mm movement in any direction or a root mean squared change in bold signal from volume to volume >9. Noise correction was performed using CompCor (Behzadi et al., 2007), that regresses out from the functional time-series the first two principal components of the time-series extracted from white matter and CSF. Moreover, six movement regressors calculated during realignment plus their time derivatives and their quadratic values were regressed out from the BOLD time-series. Volumes deemed corrupted were also regressed out. No subjects showed a mean framewise displacement >2 mm. Note that the CONN preprocessing pipeline output QA measurement that can be accounted for in statistical analyses and to compare groups. From these variables we retained the mean movement and the mean global signal change for each subject.

After preprocessing and denoising we calculated the fraction of amplitude of low frequency fluctuations (fALFF). fALFF measure the proportion of the power of each frequency at the low-frequency range (0.01–0.08 Hz) to that of the entire frequency range (0–0.25 Hz), thus providing a normalized quantity that it is thought to reflect local activity at rest (Zou et al., 2008). fALFF maps were smoothed with a Gaussian Kernel of 8 mm FWHM.

We also calculated two other indexes of voxel-wise connectivity: local correlation and global correlation. Local correlation is a measure of local coherence and measure the average correlation among each voxel and its neighbors. Local coherence has been shown to be reduced in PD patients (Borroni et al., 2015). On the other hand, global correlation is an index of a voxel network centrality; it measures the average correlation between each voxel and all the other voxels in the brain. It has been shown that the network centrality of several regions is modified in PD patients relative to controls (Gu et al., 2017; Wang et al., 2018).

All fMRI-derived indexes were calculated using the conn toolbox with the default parameters.

2.3.3. Diffusion weighted images

DWI were processed using fsl 5.0 (Jenkinson et al., 2012). In particular, DWI images were corrected for eddy current and realigned using eddy_correct, then a standard tensor model was fit to each image in order to calculate FA and MD (Behrens et al., 2003). FA images were non-linearly normalized onto the standard FA template provided with FSL using FLIRT (Jenkinson and Smith 2001) for the affine registration and FNIRT for the nonlinear registration (Anderson et al. 2010). FA and MD images were smoothed using a Gaussian kernel 8 mm FWHM (results obtained using non-smoothed images are reported in the supplementary materials). Both FA and MD have been shown to discriminate between PD and MSA patients, and to discriminate PD and MSA from healthy controls (Péran et al., 2010, Péran et al., 2018). While other DWI-derived indexes may have been calculated (e.g. radial or perpendicular diffusivity), we limited our choice to FA and MD because they differentiate the assessed groups and because they are the most used indexes in the literature.

2.3.4. R2* images

The six T2*-weighted volumes were averaged to generate a mean T2*-weighted volume. A full affine 3D alignment was calculated between each of the six T2*-weighted volumes and the mean T2*-weighted volume. For each subject, a voxel-by-voxel nonlinear least-squares fitting of the data was acquired at the six TEs to obtain a mono-exponential signal decay curve (S = S0e − t/T2*). This method combining data acquisition and data processing of T2* images demonstrated good reproducibility (Péran et al., 2007). To facilitate the analysis of the relaxation results, we considered the inverse of the relaxation times (i.e., relaxation rates R2* = 1/T2*) as previously described (Cherubini et al., 2009; Péran et al., 2007, Péran et al., 2009). The mean T2*-weighted volume was registered to the T1-weighted volume using a full affine alignment, T1-weighted volume was than non-linearly registered into the MNI space and the calculated deformation field applied to the R2* images. The normalized R2* images were smoothed with a Gaussian kernel of 8 mm FWHM (results obtained using non-smoothed images are reported in the supplementary materials).

2.4. Machine learning pipeline

The machine learning pipeline consisted of several feature selection and reduction steps detailed below.

2.4.1. Matrix reshaping and range normalization

Separately for each modality, images were reshaped from 3D matrix to 2D matrix with subject x voxel dimensions after being masked for the relevant mask (i.e. a liberal grey matter mask for grey matter and all rs-fMRI related indexes, white matter for FA and whole brain mask for MD and R2* maps). We chose to convert the images from 3D to 2D matrix for easiness of processing. These matrices were then normalized so that the values were comprised between 0 and 1. Note that the masking was performed to speed the computation, only limiting each modality to the brain regions meaningful for each modality (e.g. global connectivity of white matter would not be meaningful).

2.4.2. Variance thresholding

Similarly to (Meng et al., 2017) we reasoned that features with only minor variation among subjects would not be useful to separate the groups. For this reason, we adopted a simple variance feature reduction step in which, for each modality, we eliminated the 25% of features with the lowest variance. This step can be considered conceptually similar to the one described by (Wilhelm-Benartzi et al., 2013) and a more liberal version adapted to classification problem of the one proposed in (Meng et al., 2017).

2.4.3. Relieff based features selection

Relieff (Kira and Rendell, 1992; Kononenko et al., 1997) is a feature selection algorithm that is widely used in the machine learning literature. It estimates a weight for each feature by comparing, for each case, the distance of the closest intra and inter-class cases in that feature space and increasing the weight if the distance is greater for the inter-class than for the intra-class case. For each modality, we submitted the features surviving the variance threshold to the Relieff algorithm (as implemented in the CORElearn package for R (Robnik-Sikonja and Savicky 2017)). In order to select the most relevant features we used a screen test approach (Mori et al., 2000) as implemented in (Meng et al., 2017). We calculated the selection threshold as the first minimum of the second derivative of the sorted (in decreasing order) and smoothed (via a loess regression (Cleveland et al. 1992)) Relieff weights. This is equivalent to find the point at which the speed of the function approaches zero (i.e. the Relieff weight values drop dramatically). Only features with a weight exceeding the threshold were retained.

2.4.4. Spatial clustering of the features

Features from brain imaging are intrinsically non-independent; this is partially due to the smoothing applied to the images, but it is above all related to the fact that voxels that lie close usually belong to the same anatomical/functional region. In the light of this knowledge spatially cluster features (i.e. voxels) that are close to each other is an effective and meaningful way of reducing the number of features. For each modality, we submitted the features surviving the Relieff threshold to a recursive spatial clustering algorithm: at first adjacent voxels (i.e. <3 mm apart) were assigned the same cluster, all clusters smaller than a certain extent k (and isolated voxels) were then submitted to a second clustering step with a radius of 9 mm, again those clusters smaller than k and isolated voxels were submitted to a third and last clustering with a radius of 12 mm. After the third step all clusters smaller than k and isolated voxels were discarded (this step was performed using the spatstat package in R (Baddeley et al. 2015)). The rationale for this step was that voxels with supra-threshold Relieff weight but “isolated” could add noise in the model (i.e. due to the spatial dependency of voxels in the brain, isolated voxels have higher chance of not being physiologically relevant). Moreover, too many such voxels would increase the space of possible features subsets to evaluate (see below). We tried several k (i.e. 30, 50, 100, 200) in order to observe the effect that this parameter could have on the discrimination performance. Finally, we extract the average signal for each cluster, thus effectively reducing the number of features for each modality from hundreds to tens.

2.4.5. Merging of modalities and subset/modalities selection

In order to have a completely data-driven pipeline, one should empirically test the number and type of modalities that enter the discriminant model. Moreover, even after Relieff selection and spatial clustering, some clusters may be not very informative, and some clusters may convey redundant information (e.g. spatially overlapping low FA and high MD may actually capture similar characteristics of the white matter). For these reasons, we combined a cross-validated scheme to select the number and type of modalities to use for discrimination with subset selection based on correlation. The latter technique is aimed to found the subset of features (i.e. clusters in the case at hand) that maximize the predictive power relative to the outcome while minimizing redundancy among clusters (measured as collinearity) (Kohavi and John, 1997; Tripoliti et al., 2010). Using an inner 10-fold cross-validation scheme we tested all the possible combinations of modalities: for each combination we merged the modalities in one matrix (having dimensions [subjects] x [N of clusters from all modalities in the combination at hand]) and performed subset selection using the select.cfs function (Wang et al., 2005) of the Biocomb package (Novoselova et al. 2017). We chose a 10-folds cross validation to be consistent with the outer cross-validation loop. In the end, we obtained a cross-validated performance score for each combination (i.e. balanced accuracy). We selected the subset of cluster/modalities that maximized the performance score and used this subset to fit the discriminant model.

2.4.6. Fitting of the model

Finally, the model is fitted using the sequential minimal optimization (SMO) algorithm(Platt 1998; Schölkopf and Smola 2002) with polynomial kernel. The model was fitted using the RWeka package (Hornik et al., 2009), a wrapper of the java-based software Weka (Witten et al., 2011). The free parameters of the SMO algorithm are the order of the polynomial and the lambda (i.e. allowed error); we left these parameters to the default value of respectively 5 and 10.

2.4.7. Cross validation scheme

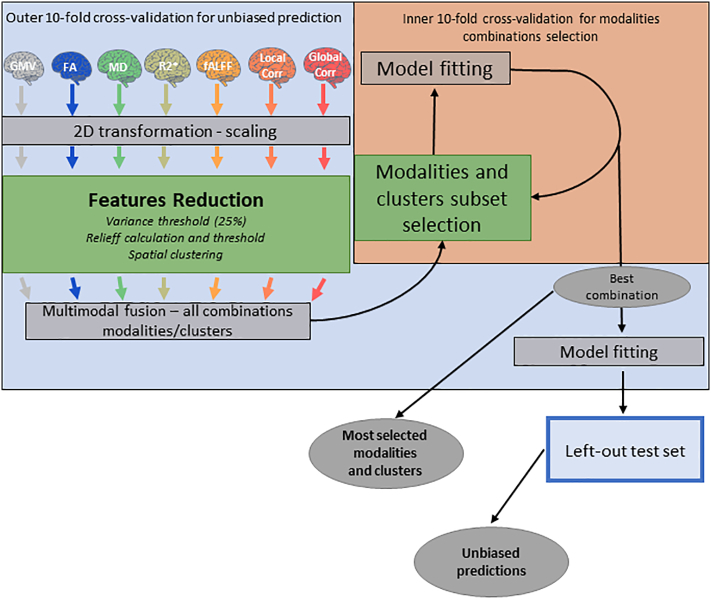
We adopted a 10-fold full cross-validation scheme. This means that each step in the machine learning pipeline (except for the images reshaping and range normalization) was performed within the cross-validation framework. At each iteration, we divided our sample in ten folds and used 9 of them as training set and 1 as testing set. The feature selection and reduction steps were carried out using the training sample, then we used the clusters found in the training sample as features in the test sample and evaluated the model using only the test sample. This procedure was repeated 10 times and then the predicted values for each fold were stacked in order to have a prediction for every and each subject in the sample. We then calculated accuracy, sensitivity and specificity for the stacked prediction (merged scores). Fig. 1 schematically represents the predictive pipeline. The code for the pipeline is released on github.

Fig. 1.

Predictive pipeline. Colored brains represent the different indexes used for prediction, brains of the same color represent indexes from the same MRI modality. The outer malva square represents the outer 10-folds CV scheme while the inner orange square represents the inner 10-folds CV set up to find the best combination of modalities. Green squares represent features selection and reduction steps while grey squares represent preprocessing, model fitting and prediction steps, grey ovals represent the intermediate and final outcome of the pipeline.

2.4.8. Model repetitions

Each discrimination (i.e. PD vs HC, MSA vs HC, PD vs MSA) and cluster extent (i.e. 30, 50, 100, 200) was repeated 10 times to have a better estimate of the performance of the model and a measure of its stability.

2.4.9. Modalities included

Considering the 10 repetitions of each 10-fold CV pipeline, we had a total of 100 folds for each discrimination and cluster extent. To gain insight about the relative importance of the different modalities we report the rate of occurrence of each modality in the 100 folds.

2.5. Statistical analysis

Sex distribution in the 3 groups was compared using a Fisher exact test. Age was normally distributed and was compared among groups using a one-way analysis of variance. The QA variables from structural, rs-fMRI and DWI acquisition were non-normally distributed and were compared among groups by means of a Kruskal-Wallis test.

Following (Combrisson and Jerbi, 2015) we used binomial cumulative distribution testing in order to assess the statistical significance of the classification pipelines. Briefly, classical binomial testing relies on the assumption that the theoretical chance level in a classification task is $\frac{1}{c}$ where c is the number of classis. However, this is only true when the number of observations is (or approach to) infinite. Whenever we are dealing with a sample of finite amount, the chance level depends on the sample size. One way of taking this into account is to assume that the classification error follows a binomial cumulative distribution and calculate the number of correctly classified observations that allows to say that the classification accuracy depart from chance with an α level of certitude. This can indeed be achieved using the binomial cumulative distribution function as follow Observation Correctly Classified(α) = binomial CDF (1 − α, n, chance level), where α is the desired statistical threshold, n is the sample size and chance level is the probability to correctly classify an observation at random. We used the qbinom function in R to calculate the binomial cumulative distribution function, testing several statistical thresholds. For two of the comparisons (i.e. MSA vs HC and MSA vs PD) we had an unbalanced sample, so instead of a chance level of 0.5 we used a chance level of $\frac{\mathit{most\; represented\; class}}{n}$ (i.e. 0.527). The reason to choose this chance level is that with unbalanced classes, the best expected random model is a model that simply classify all observations as member of the most represented class. On the other hand, for the comparison between PD and HC, we choose a chance level equal to 0.5. Combrisson and colleagues have shown that the binomial cumulative distribution function method yield similar results as permutations method, even if this latter is slightly more conservative for small sample.

Since we have 10 repetitions for each discrimination and cluster extent, we report the mean accuracy together with its [95% confidence interval], as well as the range of p values and the median p values for each combination of discrimination and cluster extent.

3. Results

3.1. Demographic and clinical variables

Table 1.

Demographic and clinical variables. The table reports frequency or mean ± sd of the relevant demographic and clinical variables. Comparisons between PD and MSA as a whole were performed using a Mann-Whitney U test while the comparisons among PD, MSA-p and MSA-c were performed using a Kruskal-Wallis one-way analysis of variance. The post-hoc comparisons for the variables leading to significant main effect of group among PD, MSA-cc and MSA-p are reported in Supplementary table 1.

	n	Sex, M/F	Age	Age at onset	Disease duration	MMSE	LEDD, mg/die	H&Y	UPDRS-III	UMSARS II-
Groups
PD	26	12/14	63.8 ± 6.3	56 ± 6.8	7.4 ± 4.5	29.1 ± 1.4	689 ± 367.2	2.3 ± 0.5	19.1 ± 10
MSA-tot	29	13/16	64 ± 7.5	58.3 ± 8.2	5.7 ± 2.3	27.9 ± 1.7	470 ± 500.5	2.4 ± 0.5		29.8 ± 8
MSA-p	16	7/9	66.1 ± 7.8	60.7 ± 7.9	5.4 ± 2.2	28.1 ± 1.5	700.1 ± 386.4	2.5 ± 0.5		31.1 ± 8.7
MSA-c	13	6/7	61.5 ± 6.5	55.2 ± 7.7	6.1 ± 2.5	27.7 ± 2	187.8 ± 490.8	2.2 ± 0.4		28.2 ± 7
Statistics
PD vs MSA-tot		0.92	0.899	0.227	0.317	<0.01	0.028	0.581	NA	NA
PD vs MSA-p vs MSA-c		0.99	0.277	0.147	0.527	<0.01	<0.01	0.278	NA	NA

Bold signifies p < .05.

3.2. PD patients versus control

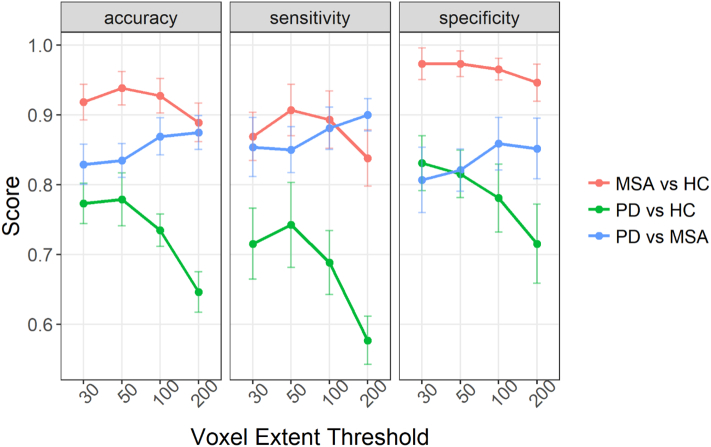
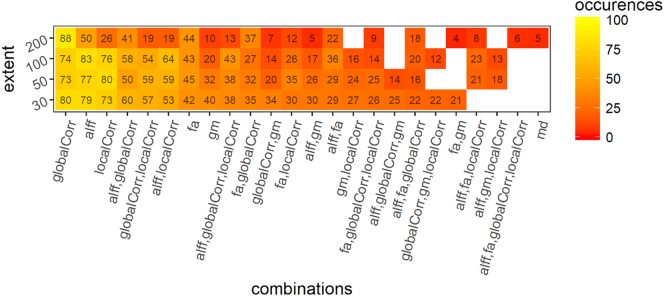
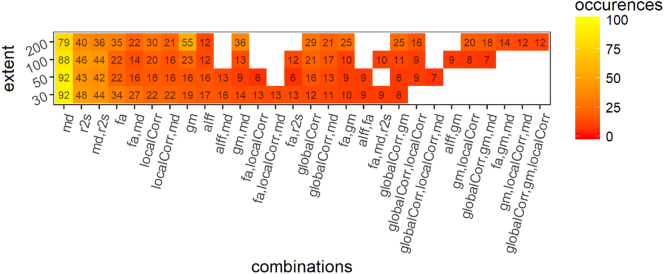
When training the model to discriminate between PD patients and HC we obtained the following results; for a cluster extent threshold (k) = 30 we obtained a mean accuracy of 0.76 [0.74–0.80] (range p = .00001–0.001, median p = .00005). For k = 50 a median accuracy of 0.78 [0.74–0.82] (range p = .00001–0.01, median p = .00001). For k = 100 we obtained an accuracy of 0.74 [0.71–0.76] (range p = .0001–0.01, median p = .0005). For k = 200 we obtained an accuracy of 0.65 [0.61–0.68] (range p = .001–0.2, median p = .01). Fig. 1 compares the performance of this discrimination in terms of accuracy, specificity and sensitivity to the other discriminations. Fig. 2 reports the frequency of occurrence of the different modalities (and combinations of modalities) for 100 folds.

Fig. 2.

Comparison of the performance of the different discrimination tasks and cluster extent.

For the anatomical localization of the clusters, Fig. 3 shows the results from the cluster extent pipeline with the highest accuracy (i.e. k = 50). The intensity of the images reflects the proportion of folds in which a certain voxel was selected (out of 100). The most frequently observed voxels for fALFF were in the left anterior parahippocampal gyrus/ temporal fusiform cortex (a contralateral cluster was observed less frequently) also covering part of the head of the hippocampus and the amygdala; a small cluster was observed in in the left VIIb lobule of the cerebellum. For the global correlation we found two clusters of frequently selected voxels in the right and left precentral/postcentral gyrus. A consistent cluster was found also spanning the cingulate gyrus and the precuneus. For the local correlation, a cluster of frequently observed voxels was observed in the left precentral gyrus, anterior to the cluster observed for the global correlation. A cluster with a similar frequency of observation was found in the left orbitofrontal cortex, extending into the subcallosal cortex.

Fig. 3.

Frequency of occurrence of the modalities and their combination in 100 folds (10 folds CV repeated 10 times) for the discrimination between PD and HC. globalCorr = global correlation; localCorr = local correlation; alff = fraction of alpha low frequency fluctuations, fa = fractional anisotropy, gm = grey matter volume, md = mean diffusivity.

3.3. MSA patients versus control

When training the model to discriminate between MSA patients and HC we obtained the following results; for a cluster extent threshold (k) = 30 we obtained a mean accuracy of 0.92 [0.89–0.94] (range p = .00001–0.00001, median p = .00001). For k = 50 a median accuracy of 0.94 [0.91–0.96] (range p = .00001–0.00001, median p = .00001). For k = 100 we obtained an accuracy of 0.93 [0.90–0.95] (range p = .00001–0.00001, median p = .00001). For k = 200 we obtained an accuracy of 0.89 [0.86–0.92] (range p = .00001–0.00001, median p = .00001). Fig. 4 report the frequency of occurrence of the different modalities (and combinations of modalities) for 100 folds.

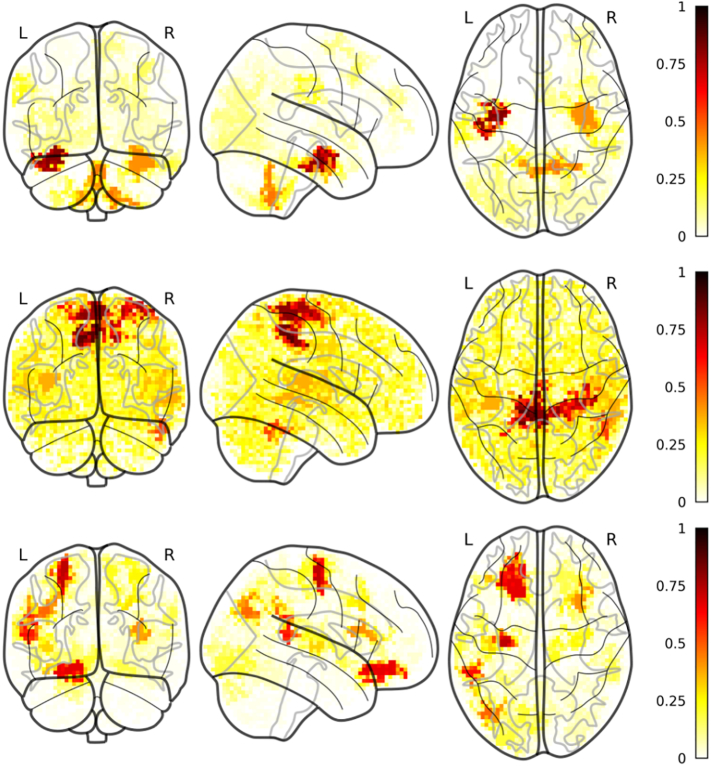
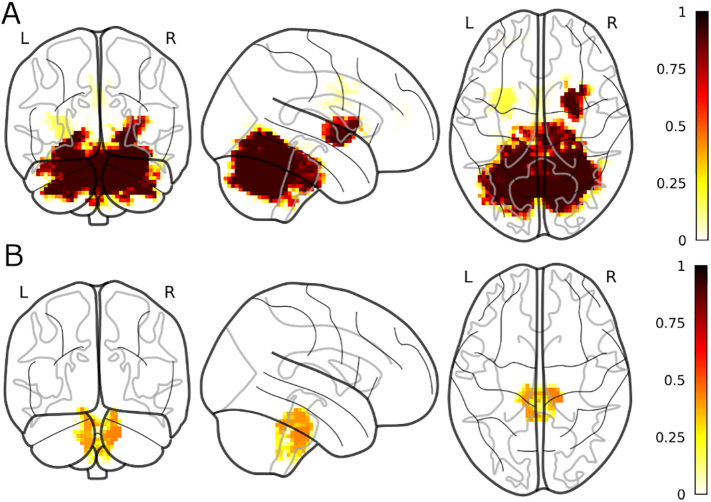
Fig. 4.

Most frequently selected voxels for the most frequently selected modalities (PD vs HC). A) fALFF; B) global correlation; C) local correlation.

For the spatial localization of the clusters, Fig. 5 shows the results from the cluster extent pipeline with the highest accuracy (i.e. k = 50).

Fig. 5.

Frequency of occurrence of the modalities and their combination in 100 folds (10 folds CV repeated 10 times) for the discrimination between MSA and HC. globalCorr = global correlation; localCorr = local correlation; alff = fraction of alpha low frequency fluctuations, fa = fractional anisotropy, gm = grey matter volume, md = mean diffusivity, r2s = R2*.

MD most observed voxels were in a cluster covering almost the entire cerebellum as well as part of the brainstem and the medial inferior occipital lobe. Of notice, in all the folds we observed MD voxels in the right putamen (and in a quarter of folds we observed a contralateral cluster in the left putamen). As for r2s, in half the folds we observed a cluster in the deep nuclei of the brainstem.

3.4. PD vs MSA patients

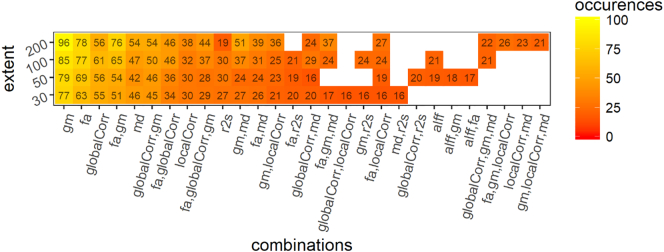
When training the model to discriminate between MSA patients and PD we obtained the following results; for a cluster extent (k) = 30 we obtained a mean accuracy of 0.83 [0.80–0.86] (range p = .00001–0.0001, median p = .00001). For k = 50 a median accuracy of 0.84 [0.81–0.86] (range p = .00001–0.0001, median p = .00001). For k = 100 we obtained an accuracy of 0.87 [0.84–0.90] (range p = .00001–0.00001, median p = .00001). For k = 200 we obtained an accuracy of 0.88 [0.85–0.90] (range p = .00001–0.00001, median p = .00001). Fig. 6 report the frequency of occurrence of the different modalities (and combinations of modalities) for 100 folds.

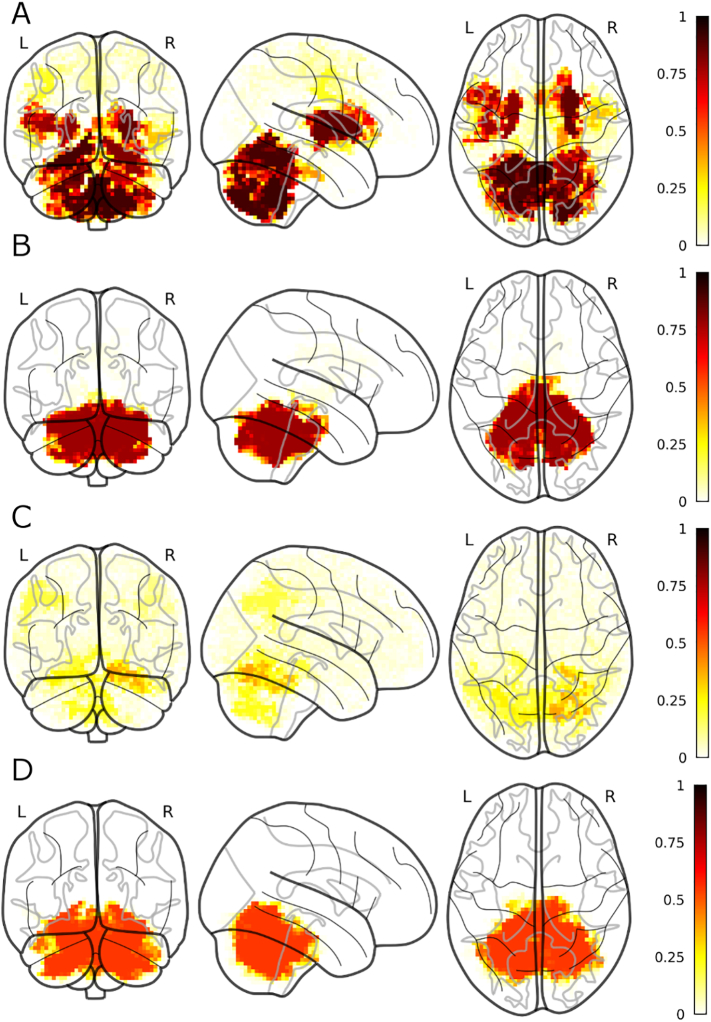
Fig. 6.

Most frequently selected voxels for the most frequently selected modalities (MSA vs HC). A) MD; B) r2s.

For the spatial localization of the clusters, in Fig. 7 shows the results from the cluster extent pipeline with the highest accuracy (i.e. k = 200).

Fig. 7.

Frequency of occurrence of the modalities and their combination in 100 folds (10 folds CV repeated 10 times) for the discrimination between PD and MSA. globalCorr = global correlation; localCorr = local correlation; alff = fraction of alpha low frequency fluctuations, fa = fractional anisotropy, gm = grey matter volume, md = mean diffusivity, r2s = R2*.

Discriminative grey matter volume voxels were consistently observed in the cerebellum, in particular in the vermis (expanding into the adjacent brainstem) and in the right and left crus II. Other consistent clusters were observed at the interface of the lingual gyrus and the VI lobule of the cerebellum bilaterally. Finally, bilateral clusters were observed in the whole putamen, extending into the adjacent insular cortex. For FA, a consistent discriminant cluster was observed covering almost the entirety of the cerebellum and the adjacent brainstem. This cluster closely resembled the one found for MD both when comparing PD and MSA patients (see below), and when comparing MSA patients and HC (see above). Global correlation was also consistently selected (56 out of 100 folds), however, its spatial distribution appeared less consistent, a small cluster observed in 30 folds comprised several sub regions of the right cerebellum (crus I, lobule V and VI). Finally, MD was observed almost as frequently as global correlation, but the spatial distribution of the discriminant clusters was much more consistent; in almost all the folds for which MD was selected, the relevant clusters covered the cerebellum and the brainstem, similarly to FA. For the sake of clarity, Fig. 8 summarizes the main findings.

Fig. 8.

Most frequently selected voxels for the most frequently selected modalities (PD vs MSA). A) gm; B) FA; C) global correlation; D) MD.

3.5. Non smoothed images and comparison between MSA-c vs MSA-p

We report the results of the discriminant analyses performed using non-smoothed data and the discriminant analysis between MSA-c and MSA-p in the supplementary materials.

4. Discussion

Using a data-driven whole brain discriminant approach based on both structural and functional MRI we could discriminate between PD and HC, MSA and HC, and PD and MSA. We showed that the most discriminative modalities were different according to the discriminant task at hand. In discriminating between PD and HC, resting state-related indexes were the only features consistently selected, MD in isolation (with some contribution by R2*) can discriminate with high accuracy between MSA and HC, and a combination of structural and functional indexes is needed to discriminate between PD and MSA. These results confirmed the complementarity and usefulness of using different MRI modalities and parameters to discriminate parkinsonian syndromes.

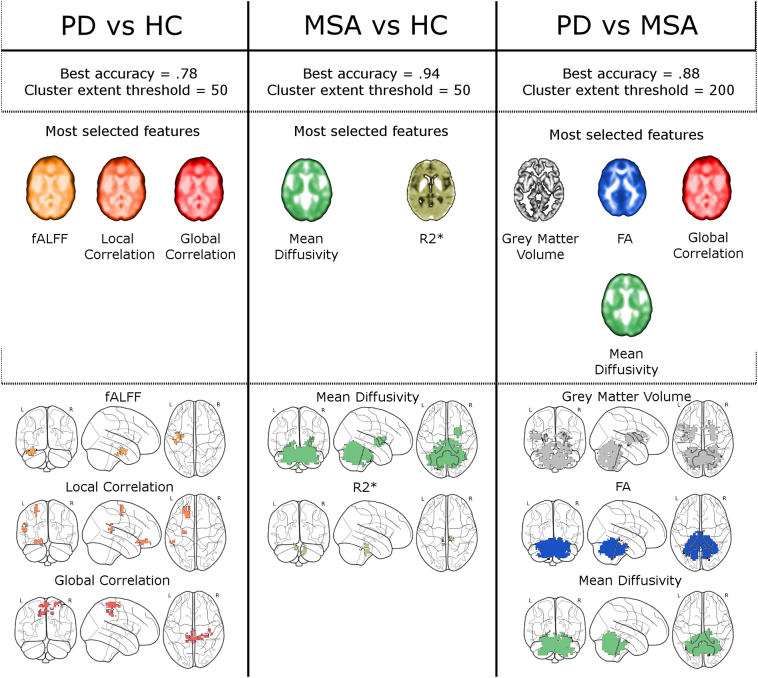
Relative to our previous studies, we have introduced several important novelties. First of all, for the first time we added rs-fMRI markers to structural ones to discriminate parkinsonian syndromes. Moreover, for the first time we combined a fully data-driven pipeline with a whole-brain approach. Perhaps more importantly, relative to our previous work (Barbagallo et al., 2016; Nemmi et al., 2015; Péran et al., 2010, Péran et al., 2018), for the first time we used cross-validation methods and independent feature selection steps that ensure generalizability. Another important aspect of this work is the competition between markers to discriminate patients determining the most effective markers. Studies that combine voxel-wise multimodal approaches with methods apt to select the most relevant modalities are uncommon in the literature (Fig. 9).

Fig. 9.

reports the performance of the best model together with its cluster extent for each discrimination task (upper panel). In the middle panel are reported the modalities most frequently selected for each discrimination task (the brain slices are from a representative subject and intensity coded). In the lower panel are reported the cluster most frequently observed (> 50 folds, excepts for R2* > 40 folds) for each of the most observed modalities. Spatial cluster for global correlation for the discrimination between PD and MSA are not shown as no voxel was observed in >25 folds.

4.1. PD vs HC

We obtained the best accuracy in discriminating between PD and HC when using a cluster extent of 50 voxels (0.78 [0.74–0.82]). This accuracy is higher than that reported in some previous studies (Focke et al., 2011; Huppertz et al., 2016), in line with the study of Adeli et al. (2016) and slightly lower than others (Chen et al., 2015; Long et al., 2012; Peng et al., 2017; Zhang et al., 2014). However, the comparison can be unfair, as all the studies reaching higher accuracy used LOO cross-validation, which is a biased estimator of the performance (Varoquaux et al., 2017). Moreover, Zhang et al. (2014) used non-independent feature selection (i.e. they performed the feature selection on the whole sample rather than within the cross-validation procedure).

As for the most discriminative modalities, only the rs-fMRI-related indexes were consistently chosen in the pipeline. This is in line with the study of Bowman and colleagues, that reported that the models with the best performance were those fitted using functional connectivity features (Bowman et al., 2016). This result suggest that even for non-de-novo PD patients, structural abnormalities can be very subtle and hard to detect, as confirmed by the contrasting results obtained using both VBM (Brenneis et al., 2003; Pan et al., 2013; Summerfield et al., 2005; Tessitore et al., 2012) and volumetry (Kosta et al., 2006; S. H. Lee et al., 2011; Messina et al., 2011; Péran et al., 2010; Pitcher et al., 2012). On the other hand, abnormalities in brain activity and connectivity may be detected before structural ones, and thus fMRI-related indexes are better suited to discriminate PD and HC. As for the spatial localization of the discriminative cluster, results for fALFF are partially in line with a recent metanalysis; indeed, Pan and colleagues (2017) found a reliable cluster of fALFF differences between PD and HC that was located in the parahippocampal gyrus/inferior temporal gyrus/hippocampus. The cluster found by Pan and colleagues was on the right, while the most consistent cluster we found was in the contralateral region. However, we also observed a less frequently selected cluster on the right. The fact that we did not observe any of the other clusters observed by Pan and colleagues can be related to the fact that our pipeline only selected the most discriminative clusters, eliminating redundant features (i.e. the other clusters found in Pan study (2017) discriminated between the two groups but were not necessary for discrimination). Although global correlation has not been widely used in the PD literature, it can be considered as conceptually similar to the graph-theory derived measure of degree connectivity; indeed, it has been shown that PD patients show higher average degree connectivity within the motor network (Göttlich et al., 2013), a result in line with our finding, as the discriminative clusters most frequently selected for global correlation were mainly located in the primary sensorimotor cortex. Finally, index of local connectivity as regional homogeneity (ReHo) and local efficiency have been repeatedly shown to be abnormal in PD patients (Choe et al., 2013; Kamagata et al., 2018; Li et al., 2016). Choe et al. (2013) found ReHo abnormalities in PD patients in motor and parietal regions close to the clusters we observed using local correlation.

The results of the discrimination between PD and HC are strikingly different from previous results obtained with a structural multimodal protocol. In a previous study, our group found that MD, FA and R2* in the subcortical structures (specifically, putamen and SN) were enough to discriminate between PD and HC with accuracy around 95% (Péran et al., 2010). However, several methodological differences can account for this difference: first, Peran et al. (2010) did not include any resting state imaging in their protocol, so that a direct comparison of the relevance of rs-fMRI relative to structural and microstructural MRI related indexes was not possible in their study. Moreover, the study by Peran and colleagues used a region of interest approach hypothesis driven, as even their voxel-wise analyses were limited by a mask only comprising the subcortical nuclei and the brain-stem. Moreover, they did not downsample nor smooth their images, allowing for difference in more spatially defined region to be observed, relative to our approach, which used downsampling and smoothing as a mean of feature reduction. The downsampling coupled with the smoothing (and the extent threshold we imposed on the clusters) can lead the pipeline not to pick up indexes in small and well-defined anatomical regions (e.g. SN) that are indeed markers of the pathology. Images in native resolution could be used and/or the cluster extent threshold could be avoided, however, this would probably lead to a lack of generalization from the training to the test set (i.e. spurious small cluster that are found to discriminate between the group in the training set but not in the testing set). Moreover, the subset selection step tests all the possible combinations of clusters, this means that the computational time increases exponentially with the increasing number of clusters. A more effective way of including imaging markers from regions that are well known to be useful in discriminating between the groups would be to include them directly before fitting the model or give them a fair chance of being selected by including them just before the subset selection step.

Finally, the feature selection approach used by Peran and colleagues (2010) was not independent: feature selection was performed using the whole set. On the other hand, the feature selection steps in our pipeline were performed within the cross-validation loop, thus ensuring independence and hence generalizability, to a certain extent.

4.2. MSA and HC

The most striking finding for the discrimination between MSA and HC was that MD almost in isolation was able to discriminate between the two groups with a high accuracy (0.94). This accuracy is higher than those obtained by Focke et al. (2011) using either grey or white matter volume and those in discriminating MSA-p from PD and MSA-c from PD in (Huppertz et al., 2016).

The most observed clusters for MD fell in the cerebellum and the putamen, whose atrophy and microstructural abnormalities are among the core features of MSA neuropathology (Barbagallo et al., 2016; Berg et al., 2011; Péran et al., 2018; Seppi et al., 2006a, Seppi et al., 2006b; Shin et al., 2007). Interestingly, diffusion related indexes in the cerebellum and the putamen have been shown to differ between MSA and HC and between MSA and PD (Nicoletti et al. 2006; Seppi et al., 2006a, Seppi et al., 2006b).

The second most selected modality was R2*, an index related to iron accumulation in the brain (Ordidge et al. 1994; Péran et al., 2007, Péran et al., 2009). The discriminant cluster for this modality was found in the brainstem. The involvement of the brainstem in MSA pathology is well-known (Benarroch 2003, 2007; Baddeley et al., 2015) and microstructural abnormalities have been observed in the brainstem of MSA-c patients using apparent diffusion coefficient (ADC) (Kanazawa et al., 2004). However, to our knowledge, this is the first time that iron accumulation has been found in the brainstem of MSA patients, at least relative to HC. Cluster of increased iron deposition in the brainstem have already been found for MSA patients relative to PD (Péran et al., 2018).

It is important to highlight that the fact that we did not found discriminant clusters for other modalities (e.g. GM or FA) does not mean that MSA and HC do not differ in these modalities. It is possible that univariate voxel-wise analyses would have found significant differences between the two groups, but MD abnormalities in the cerebellum and the putamen can be considered the signature of MSA in this sample.

4.3. PD and MSA

Not surprisingly, the accuracy for the discriminant model between PD and MSA (0.88) was lower than the accuracy for MSA vs HC but higher than the accuracy for PD vs HC. This accuracy is higher than those obtained by Focke et al. (2011) when discriminating between PD and MSA-p, and in line with the accuracy obtained by Huppertz et al. (2016) (0.90 and 0.94 for MSA-p and MSA-c respectively). However, one should bear in mind that the accuracy in Huppertz et al. (2016) was calculated using LOO cross-validation, which can introduce an optimistic bias in the performance (Varoquaux et al., 2017).

The comparison between MSA and PD led to the richest model, with 4 modalities that were selected in more than half the folds. Three of these four modalities covered almost the entire cerebellum. This result is not surprising, given the extensive differences in this region found by Peran and colleagues (2018) in the same sample for GM, MD and FA. Similarly, the fact that GM clusters were also found in the bilateral putamen is well in line with the known neuropathology of MSA (Berg et al., 2011; Seppi et al., 2006a, Seppi et al., 2006b; Shin et al., 2007). What is interesting about this result is that, at variance with the discrimination between MSA and HC, three separate indexes of microstructural integrity in the cerebellum were selected. This suggests that the differences in cerebellar microstructural integrity between MSA and PD are subtler than those between MSA and HC and thus a more complete “description” of the abnormality is needed in order to discriminate between the two groups.

As for global correlation, this modality has been choses quite often, but not in a stable spatial location. Indeed, the most frequently observed cluster, extending between cerebellum and occipital cortex, has only been observed in 38 out of 100 folds. One of the reasons for this lack of spatial consistency can be a lack of generalization for this modality between the training and the testing set: a cluster of global correlation could be discriminant within the training set but this discriminative power would not generalize to the testing set. Anyhow, this lack of spatial consistency suggests skepticism about the utility of global correlation in discriminating between the two groups.

4.4. General discussion

When comparing the results of the three different discrimination tasks there is a striking difference between the modalities selected to discriminate PD patients from HC, and those selected to discriminate MSA from PD and HC. Our results suggest that a single resting state fMRI acquisition, from which several parameters can be extracted, could be enough to successfully discriminate PD from HC. Combined with a T1 acquisition, necessary for the processing of the resting state data, this would mean an MRI sequence no longer than 15 min, much more feasible for any patient than a longer complete multimodal sequence. Of course, features studied should focus on rs-fMRI alone, trying to improve the overall performance of the model. There are several ways of doing so; one could avoid the resampling of the data to 3 mm isotropic voxels, thus gaining spatial specificity, derive more specific indexes related to the whole connectome (i.e. graph theory-related indexes), chose to use a-priori knowledge of PD pathology and only focus on selected resting state networks or functional connectivity of selected seed regions. On the other hand, when discriminating MSA patients from the other two groups, structural modality both related to macro (i.e. GM) and micro structure (i.e. MD) have been chosen. This is not to say that fMRI related indexes do not discriminate between MSA and the other groups, rather than structural pathology is more discriminant and the real hallmark of MSA pathology. Thus, our results suggest that to discriminate between MSA and other pathologies, an MRI protocol comprising a T1 and a DWI acquisition can be the best choice if one needs to strike a balance between accuracy and patients' comfort.

When focusing on the modalities chosen for each discriminant task it is important to consider the systematic effect that local atrophy might exert on diffusion, R2* and functional-derived indexes during spatial normalization. Although we have not corrected for this (possible) effect the correlation-based feature selection step accounted for it. Specifically, since the CFS step select the cluster subset that minimizes redundancy, if a non T1-related cluster is chosen together with or instead of a T1-related one, this means that the former brings independent information over and beyond the latter, and that this is over and beyond the atrophy effect. Note also that focusing on the discriminant clusters between PD and MSA, it is remarkable that even if there is a fair degree of overlap, each modality contributes with some degree of spatial specificity (supplementary fig. 10). It is also noteworthy that this approach (i.e. avoid correction for atrophy-related effect) was the one chosen in the original paper by Meng and colleagues (Meng et al., 2017) and the one used in a previous paper comparing PD, MSA-c and MSA-p (Péran et al., 2018).

Another interesting result is the influence the cluster extent threshold had on the different discrimination task: as Fig. 1 illustrates, while the discrimination between PD and HC as well as between MSA and HC benefitted more from small cluster extent (best accuracies for 30 and 50 voxels), the performance was higher for higher cluster extent threshold when discriminating between PD and MSA (best accuracies at 100 and 200 voxels). A tentative interpretation could be related to an information loss/generalizability trade off: when comparing patients (PD or MSA) with healthy controls, smaller cluster extents allow for a finer grained pattern of differences between the two groups, with these differences being mostly true positive, as one could expect real differences between patients and controls. On the other hand, when comparing two patient populations, larger cluster extent thresholds would lead to a loss of finer grained information but would ensure that only real (and thus generalizable) differences are retained, as smaller clusters may be due to noise. In any case, our results suggest that cluster extent is an important hyper parameter in our (and possibly others') pipeline and different cluster extent should be tested. Another approach could be to choose the cluster extent threshold in a nested cross-validation loop.

One advantage of our pipeline is that it can be easily extended by including different modalities: one example could be SPECT imaging (DATscan) or PET imaging acquired using marker of neuroinflammation (like 18 F-DPA-714, a TSPO radioligand (Arlicot et al., 2012)), which have been shown to be an important component of PD (Hirsch and Hunot, 2009) as well as MSA (Vieira et al., 2015). Moreover, we are planning to expand our pipeline to non-imaging modalities, as for example biological fluids (e.g. blood and cerebrospinal fluid) or cognitive testing. Of course, the clustering step of the pipeline should be adapted for non-imaging features, as spatial clustering would not be performable. However, there are several dimensionality reduction algorithms that could be used to this aim (e.g. PCA, multidimensional scaling).

The main limitation of our study is the small sample size; indeed, Varoquaux et al. (2017) cautioned about machine learning studies with small samples, drawing attention on the usual big confidence intervals for indexes of performance, especially when using LOO cross validation. We tried to partially avoid this problem using a 10-fold cross-validation, even if our samples were small relative to other studies. The choice of this cross-validation scheme naturally leads to a reduction in performance, as the training set gets smaller, but gives on the same time a less biased estimate of the performance. Moreover, it should be noted that this is a quite unique dataset; we have well characterized PD and MSA patients who underwent what is, to our knowledge, the most complete multimodal MRI protocol in the literature. We hope that in the future more centres specialized in movement disorders will acquire the same sequences we did, allowing to test our pipeline on a much bigger sample. Another limitation is related to the difficulty in the differential diagnosis between MSA-p and PD. However, the diagnosis for all patients have been confirmed at a 2-years follow up. A similar problem is present for the differential diagnosis between MSA (especially MSA-p) and progressive supranuclear palsy (O’Sullivan et al., 2008; Respondek et al., 2018; Wenning and Colosimo, 2010). Since only histological post-mortem analysis confirms the diagnosis, a misdiagnosis is always possible. However, the high positive predictive value of a clinical diagnosis of MSA should minimize this risk (Gilman et al., 2008; Osaki et al., 2009). Note also that we could indeed discriminate between MSA-c and MSA-p with our pipeline (supplementary results 1.4 MSA-c vs MSA-p), finding discriminant clusters in the brain regions with prominent neuropathological abnormalities in the two subtypes (bilateral putamen and cerebellum). However, these results should be interpreted with caution because of the small sample size. To conclude, we found that our fully data-driven multimodal voxel-wise pipeline could successfully discriminate between PD and HC, MSA and HC, and PD and MSA while informing us on the most useful MRI indexes and their localization to perform this discrimination. This pipeline could be easily applied to other degenerative conditions as well as neurological or psychiatric disorders.

Appendix A. Supplementary data

Supplementary material