Abstract
For over 20 years, genetically encoded Ca2+ indicators have illuminated dynamic Ca2+ signaling activity in living cells and, more recently, whole organisms. We are just now beginning to understand how they work. Various fluorescence colors of these indicators have been developed, including red. Red ones are promising because longer wavelengths of light scatter less in tissue, making it possible to image deeper. They are engineered from a red fluorescent protein that is circularly permuted and fused to a Ca2+-sensing domain. When Ca2+ binds, a conformational change in the sensing domain causes a change in fluorescence. Three factors can contribute to this fluorescence change: 1) a shift in the protonation equilibrium of the chromophore, 2) a change in fluorescence quantum yield, and 3) a change in the extinction coefficient or the two-photon cross section, depending on if it is excited with one or two photons. Here, we conduct a systematic study of the photophysical properties of a range of red Ca2+ indicators to determine which factors are the most important. In total, we analyzed nine indicators, including jRGECO1a, K-GECO1, jRCaMP1a, R-GECO1, R-GECO1.2, CAR-GECO1, O-GECO1, REX-GECO1, and a new variant termed jREX-GECO1. We find that these could be separated into three classes that each rely on a particular set of factors. Furthermore, in some cases, the magnitude of the change in fluorescence was larger with two-photon excitation compared to one-photon because of a change in the two-photon cross section, by up to a factor of two.
Introduction
The advent of fluorescent genetically encoded Ca2+ indicators (GECIs) has been revolutionary in understanding key aspects of biology, ranging from immunology (1, 2) to neuroscience (3, 4). These engineered proteins make it possible to visualize dynamic Ca2+ levels in genetically specific live cells and tissues under both one-photon or two-photon excitation. There are many different GECI designs (5, 6). The most popular one is based on a single fluorescent protein (FP) that is circularly permuted in the middle of its β-barrel and then fused to calmodulin (CaM) at the new C-terminus and a CaM-binding peptide at the new N-terminus. Initially, only green FP-based indicators of this type were made (7, 8, 9). Their continuous development through several generations to increase Ca2+ sensitivity resulted in the widely used GCaMP6 series (10). Later, protein engineers broadened the color palette to include blue and red (11). Red GECIs are especially desirable because red light penetrates deeper in living tissue than green or blue, enabling deeper imaging (12). In addition, red-shifted excitation wavelengths are associated with less autofluorescence and photodamage. Red GECIs also provide another spectral channel for multicolor imaging and optogenetic manipulation.
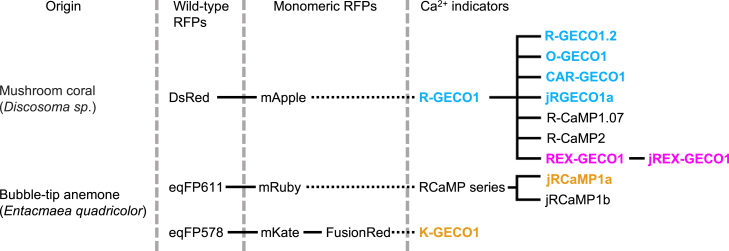
Current red GECIs originate from three different circularly permuted monomeric red FPs, which in turn come from three different wild-type FPs (Fig. 1). The first red GECI, R-GECO1 (11), was based on the directed evolution of circularly permuted mApple (13) fused to the same Ca2+-sensing domain as the green GECIs. From the R-GECO1 template, protein engineering efforts through random mutagenesis as well as site-specific mutations yielded the improved R-GECO1.2, a red-shifted variant CAR-GECO1, a long Stokes shift variant REX-GECO1, and a blue-shifted variant O-GECO1 (14, 15). Other R-GECO1 variants include R-CaMP1.07 and R-CaMP2 (16, 17). One of the latest is jRGECO1a (18), which was generated through directed evolution with a neuron screening platform to better detect Ca2+ transients produced by neuronal action potentials. Another line of red GECIs based on circularly permuted mRuby (19) was created and designated the RCaMPs (RCaMP1h was the most popular variant) (20). These were also further improved with the neuron screening platform, resulting in jRCaMP1a and jRCaMP1b (18). Most recently, K-GECO1 was developed from a third circularly permuted FP, mKate-derived FusionRed (21, 22), whose parent wild-type FP originates from the same organism as mRuby’s.
Figure 1.
Genealogy of red GECIs. The ones under study are in color. Adapted from (21).
In this wide range of red GECIs, Ca2+ binding causes an increase in fluorescence intensity. Three factors can contribute to a Ca2+-dependent fluorescence change on a molecular level. The first is a shift in the protonation equilibrium of the chromophore because the protonated and deprotonated forms behave quite differently. The second is a change in the fluorescence quantum yield. The third is a change in the molecular absorption coefficient at the excitation wavelength. For one-photon excitation, this is the extinction coefficient; for two-photon excitation, it is the two-photon cross section. This last factor could depend on shifts of the excitation spectrum, and how it changes could differ between one-photon and two-photon excitation.
In a detailed study of the popular green GECI GCaMP6m, Barnett et al. found that the main mechanism of its Ca2+-dependent fluorescence increase was a shift in the protonation-deprotonation equilibrium of the chromophore (23). When Ca2+ binds, the conformational change of the protein translates into a change in the electrostatic potential around the chromophore. A consequent shift in the chromophore pKa pushes the equilibrium from the protonated, neutral form toward the deprotonated, anionic form. For GCaMP6m, only the anionic form fluoresces when excited at the wavelengths used to detect Ca2+, so this results in an increase in fluorescence.
Although some of the red GECIs may depend on a similar mechanism, others appear to exhibit more of a change in the quantum yield (20, 21). How the molecular absorption coefficient plays a role is unclear. Additionally, any contrasts between the fluorescence change under one-photon and two-photon excitation have not been highlighted or explained. Our goal was to find the main factors responsible for the Ca2+-dependent change in fluorescence in a cohort of red GECIs.
Background and analytical considerations
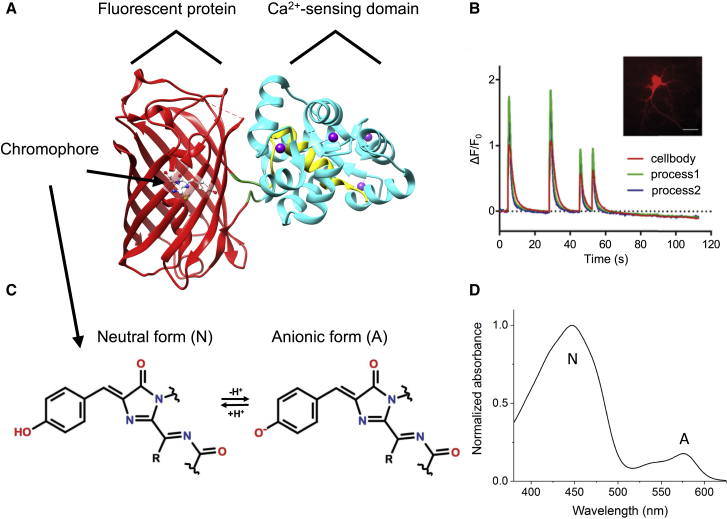
Fig. 2 A presents a typical red GECI design, using K-GECO1 in its Ca2+-saturated state as an example (21). It consists of a red FP that is circularly permuted so that the original N- and C-termini are linked together, and new ones are introduced into the seventh β-strand of the 11 β-strand barrel adjacent to the phenolic oxygen of the chromophore. The new termini are attached via short peptide linkers to a two-part Ca2+-sensing domain: CaM at the C-terminus and a CaM-binding peptide at the N-terminus. Depending on the red GECI, the N-terminus arm is either the rat CaM-dependent kinase peptide ckkap (as in K-GECO1 and R-CaMP2) or the chicken myosin light-chain kinase peptide RS20 (as in the other red GECIs mentioned). In the Ca2+-free state, CaM and its binding peptide are apart, and the FP is dim. In the Ca2+-saturated state, four Ca2+ ions bind to CaM, and it undergoes a conformational change to wrap around the CaM-binding peptide. This causes the FP to increase in fluorescence. Because the entire construct is genetically encoded, it is possible to follow Ca2+ dynamics by expressing it in living systems such as neurons and imaging fluorescence over time (Fig. 2 B).
Figure 2.
Red GECIs structure, function, and chromophore. (A) Crystal structure of K-GECO1 in the Ca2+-saturated state (PDB: 5UKG (21)) is shown. The FP is colored red, CaM is cyan, the CaM-binding peptide (ckkap in K-GECO1) is yellow, and the Ca2+ ions are purple. (B) (Adapted from (21)). Shown is the imaging of spontaneous Ca2+ oscillations in dissociated rat hippocampal neurons with K-GECO1. Graph shows the change in fluorescence normalized to baseline fluorescence over time in three different regions of interest. Inset: widefield image of K-GECO1 expression in neurons (Scale bars, 30 μm). (C) Shown is the molecular structure of the typical red FP chromophore in its neutral and anionic forms. (D) Absorption spectrum illustrates the presence of both forms of the chromophore in a red GECI. Shown is R-GECO1 in the Ca2+-free state.
How can binding Ca2+ modulate the fluorescence of the FP? As the chromophore is the molecule responsible for the fluorescence, we begin by examining its two possible protonation states, the protonated neutral form and the deprotonated anionic form (Fig. 2 C).
Nestled inside the FP β-barrel, the red FP chromophore exists in an equilibrium between its neutral and anionic forms that can shift in a Ca2+-dependent manner. The neutral (protonated) form maximally absorbs light at ∼450 nm, whereas the anionic (deprotonated) form absorbs at ∼570 nm (Fig. 2 D). Each form has a distinct fluorescence quantum yield (φ), maximal extinction coefficient (ε), and maximal two-photon cross section (σ2). These properties can depend on whether the protein is bound to Ca2+. Because of this, the neutral and anionic forms have their own Ca2+-dependent one-photon brightness (φ × ε) and two-photon brightness (φ × σ2). These, weighted by their relative fractions (ρ), combine to make the total brightness of a GECI in the Ca2+-saturated and Ca2+-free states. Equations 1 and 2 show the total one-photon brightness (F1) and two-photon brightness (F2) as a function of excitation wavelength (λ), where the subscripts A and N denote the anionic or neutral form, respectively. The relative fraction ρX is defined by the concentration of form X divided by the total concentration of chromophore.
| (1) |
| (2) |
The fluorescence ratio between the Ca2+-saturated and Ca2+-free states can be expressed as Fn,sat/Fn,free, where the subscript n is 1 or 2. Conveniently, at the excitation wavelengths that are relevant to sensing Ca2+ (that is, the Fn ratio is at or near its maximum), only one form of the chromophore per Ca2+ state has to be considered because the brightness of the other form is close to zero. Here, the fluorescence ratios simplify to Eqs. 3 and 4, where the subscript e denotes the “excitable” form of the chromophore: the form that yields appreciable fluorescence when excited at the wavelengths where the Fn ratio is maximal. We call it excitable because it dominates the excitation spectrum of the red fluorescence at these wavelengths. The excitable form could be neutral or anionic, and it could also be different depending on whether the protein is bound to Ca2+.
| (3) |
| (4) |
Because there are two forms of the chromophore, measuring the quantum yield, or φ, corresponding to just the excitable form can require a more involved approach. Specifically, this can occur when the excitable form of the chromophore is anionic, but the concentration of the neutral form is significant. In this case, the red tail of the neutral absorption band can overlap considerably with the blue tail of the anionic absorption band (as in Ca2+-free R-GECO1, see Fig. 2 D). Therefore, both forms could contribute to the optical density (OD) at a typical excitation wavelength (that does not overlap with emission) used to excite the anionic form and measure its full fluorescence spectrum. We developed a new method that accounts for this and produces the correct φ of the anionic form (see Materials and Methods).
Finding the extinction coefficient, ε, of the excitable form is also a more involved process because of the presence of two forms of the chromophore. With the alkaline denaturation method, both forms of the chromophore give rise to the denatured form with the known ε. Because of this, the extinction coefficients listed in the original red GECIs articles (11, 14, 15, 18, 20, 21) are effective values and technically equal to a product of εe and ρe. We measured the individual ε values for both the neutral and the anionic form of each protein in both Ca2+-free and -bound states (see Materials and Methods).
The first two factors, ρe and φe, are the same for both one-photon and two-photon excitation. However, the ratios εe,sat/εe,free and σ2,e,sat/σ2,e,free might not be equal since ε and σ2 can depend differently on the local environment of the chromophore (24, 25, 26). Therefore, the Ca2+-dependent change in fluorescence could depend on the mode of excitation.
Materials and Methods
Fluorescence quantum yields
Fluorescence quantum yields (φ) were measured with an integrating sphere fluorometer (Quantaurus-QY; Hamamatsu Photonics, Hamamatsu City, Japan). The solvent-only reference measurement was done in the same cuvette as the sample (1 cm pathlength quartz cuvette). The peak OD of the sample was less than 0.1. Values presented in Table 1 are from one independent measurement that includes averaging three to four reference measurements and 3–20 sample measurements from the same software acquisition file.
TABLE 1.
Photophysical Properties of the Nine Red GECIs
| Class | Protein | Ca2+ | ea | ρe ± 11%b | φe ± 5% | εA,max ± 5% mM−1cm−1 (λ nm) | εN,max ± 5% mM−1cm−1 (λ nm) | σ2,e,max ± 17% GM (λ nm) | F1,max ± 13% mM−1cm−1 (λ nm) | F2,max ± 21% GM (λ nm) | F1 max. ratio ± 9% (λRmax nm)c | F2 max. ratio ± 9% (2λRmax nm)c |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| I | R-GECO1 | − | A | 0.06 | 0.15 | 89 (577) | 33 (447) | 24 (1072) | 0.8 (577) | 0.21 (1072) | 23 (516) | 38 (1032) |
| + | A | 0.82 | 0.21 | 69 (563) | 30 (451) | 31 (1056) | 12 (563) | 5 (1056) | ||||
| R-GECO1.2 | − | A | 0.033 | 0.21 | 71 (573) | 27 (443) | 21 (1072) | 0.49 (573) | 0.14 (1072) | 45 (514) | 73 (1028) | |
| + | A | 0.8 | 0.31 | 56 (558) | 26 (445) | 31 (1044) | 14 (558) | 8 (1044) | ||||
| jRGECO1a | − | A | 0.054 | 0.18 | 88 (577) | 32 (447) | 18 (1076) | 0.8 (577) | 0.17 (1076) | 23 (514) | 44 (1028) | |
| + | A | 0.86 | 0.21 | 74 (563) | 39 (443) | 31 (1056) | 13 (563) | 5 (1056) | ||||
| O-GECO1 | − | A | 0.0076 | 0.22 | 80 (557) | 30 (433) | 19 (1044) | 0.14 (557) | 0.032 (1044) | 140 (502) | 220 (1004) | |
| + | A | 0.9 | 0.23 | 59 (544) | 23 (422) | 24 (1028) | 12 (544) | 5 (1028) | ||||
| CAR-GECO1 | − | A | 0.039 | 0.17 | 92 (575) | 38 (447) | 25 (1072) | 0.59 (575) | 0.16 (1072) | 42 (516) | 62 (1032) | |
| + | A | 0.9 | 0.26 | 71 (563) | 40 (425) | 36 (1060) | 17 (563) | 8 (1060) | ||||
| II | K-GECO1 | − | A | 0.25 | 0.19 | 75 (569) | 45 (451) | 16 (1068) | 3.6 (569) | 0.8 (1068) | 11 (530) | 13 (1060) |
| + | A | 0.75 | 0.48 | 84 (566) | 34 (440) | 23 (1068) | 30 (566) | 8 (1068) | ||||
| jRCaMP1a | − | A | 0.55 | 0.29 | 78 (573) | 37 (451) | 25 (1076) | 13 (573) | 4.0 (1076) | 3.4 (518) | 4.3 (1036) | |
| + | A | 0.8 | 0.54 | 77 (572) | 24 (450) | 23 (1076) | 34 (572) | 10 (1076) | ||||
| III | REX-GECO1 | − | A | 0.43 | 0.05 | 89 (583) | 34 (449) | 24 (1076) | 2.1 (583) | 0.6 (1076) | 32 (450) | 31 (900) |
| + | N | 1 | 0.21 | 83 (577) | 33 (489) | 35 (920) | 6.9 (489) | 7 (920) | ||||
| jREX-GECO1 | − | A | 0.37 | 0.06 | 86 (579) | 32 (447) | 30 (1080) | 1.9 (579) | 0.7 (1080) | 28 (450) | 26 (900) | |
| + | N | 1 | 0.21 | 78 (570) | 34 (488) | 39 (920) | 7.0 (488) | 8 (920) |
Excitable form of the chromophore, anionic (A) or neutral (N).
Estimated relative SD.
The Fn maximal ratios were measured directly by taking the ratio of total fluorescence signals normalized to the known relative protein concentration between the Ca2+-free and Ca2+-saturated samples.
It is trivial to measure the φ of a sample with only one chromophore. However, in these Ca2+ indicators, there are two forms of the red chromophore that maximally absorb at distinct wavelengths: the neutral form at ∼450 nm and the anionic form at ∼570 nm. We measured the φ of the excitable form of the chromophore: the form that dominates the fluorescence signal when excited at the wavelengths where the Ca2+-induced fluorescence change is largest. If the excitable form is anionic and the relative fraction of the neutral form is significant, then because of spectral overlap, both forms could contribute to the absorbance at a typical excitation wavelength used to excite the anionic form and measure its full fluorescence spectrum. We developed the following method to correct for this.
The method requires measurements at two different wavelengths. One is at the typical excitation wavelength to get the full emission spectrum of the anionic form, called λblue, where the neutral form still absorbs. The other is at the peak of the anionic form absorption, λred, where the neutral form absorption becomes insignificant in comparison. With information from these two measurements and the following equations, we can get the correct φ of the anionic form.
In an integrating sphere, the φ is calculated as the integral of the emission spectrum of the sample, P, divided by the difference of the integrals of the excitation light intensity transmitted by the reference (solvent only), R, and the sample, S: φ = P/(R − S). The integral P is proportional to the total number of photons emitted by the sample, and (R − S) is proportional to the number of photons absorbed. Each integral is written explicitly in Eqs. 5, 6, and 7, where λex is the excitation wavelength, Δλ is the excitation half-bandwidth (∼10 nm), f(λ) is the fluorescence spectrum, and R(λ) and S(λ) are the spectral distributions of excitation light intensity reaching the detector from the reference and sample, respectively.
| (5) |
| (6) |
| (7) |
When exciting the sample at λred, the absorbance (Rred − Sred) should belong solely to the anionic form. However, the measured effective φ can be underestimated or overestimated because of two counteracting factors. First, only part of the emission spectrum can be integrated because the excitation light overlaps with it. We define this “short” fluorescence integral as Hred (Eq. 8). Second, the part of the fluorescence resonant with the excitation light contributes to the integral of the excitation light intensity of the sample Sred, resulting in the underestimation of absorbed photons. We call this the “very short” fluorescence integral Ered, which is the sample emission integrated over the bandwidth of excitation (Eq. 9). The correct φ, denoted C, requires the “full” integral, or the integral of the full fluorescence spectrum, Fred. It is described by Eq. 10.
| (8) |
| (9) |
| (10) |
To find C, we make an additional measurement with the excitation wavelength λblue, which is out of the range of emission. With this measurement, we can get the relative values of the full, short, and very short fluorescence integrals as Fblue, Hblue, and Eblue, respectively. Now we can use the relations Fred/Hred = Fblue/Hblue and Ered/Hred = Eblue/Hblue to find C (Eq. 11).
| (11) |
This method can be applied to find the correct quantum yield of the redder chromophore in a mixture of two chromophores as long as the emission of the bluer chromophore is negligible within the range of emission of the redder chromophore when exciting at λblue. This method was checked with a mixture of 6.5 μM 3,3′-dioctadecyloxacarbocyanine perchlorate (absorption peak 487 nm) and 1.2 μM Cresyl violet (CV) (absorption peak 601 nm) in ethanol (Fig. S1 A). The mixture was measured with λblue = 520 nm (where the absorption of the two overlap) and λred = 600 nm. The correct quantum yield C of CV as calculated with Eq. 11 was identical (<1% difference) to the quantum yield obtained with an excitation wavelength in which 3,3′-dioctadecyloxacarbocyanine perchlorate does not absorb (565 nm). The short and very short fluorescence integrals of CV in this case are illustrated in Fig. S1 B.
We applied this method to measure the correct quantum yield C of the anionic form for the Ca2+-free states of jRGECO1a, K-GECO1, jRCaMP1a, CAR-GECO1, O-GECO1, R-GECO1, and R-GECO1.2 (values are displayed in Table 1). For the Ca2+-saturated states of all proteins, and the Ca2+-free states of REX-GECO1 and jREX-GECO1, no corrections were necessary. In these cases, the correct quantum yields in Table 1 were simply measured with λblue excitation.
Chromophore pKa values and extinction coefficients
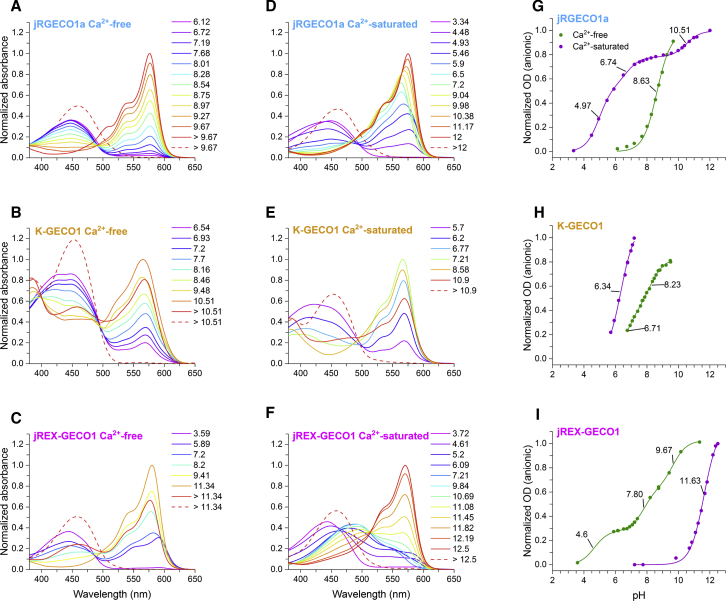
The Ca2+-free and Ca2+-saturated states of each protein were subjected to stepwise alkaline and acid titrations (Figs. 4, S7, and S8) by gradually adding 2–10 μL of 0.1–1 M NaOH or HCl, respectively, to a sample of 500–1200 μL. Absorption was measured at each step with a LAMBDA 950 Spectrophotometer (PerkinElmer, Waltham, MA), and pH was measured with an Orion PerpHecT ROSS combination pH microelectrode (Thermo Fisher Scientific, Waltham, MA). For the alkaline titrations of the Ca2+-saturated state, the protein was first diluted 1:100 into a pH 7.2 buffer with 30 mM 3-(N-morpholino)propane sulfonic acid (MOPS), 100 mM KCl, 50 μM CaCl2, and no EGTA because at a higher pH the Kd of EGTA for Ca2+ decreases dramatically (27). To determine the chromophore pKa values, the OD at the peak of the anionic absorbance (even if it shifted throughout the titration) was plotted versus pH in a range in which it was not denaturing, and the protein was not precipitating (which happened in some instances at the end of the acid titrations). The plot was fitted with 1, 2, or 3 pKa values using OriginPro 2017 (OriginLab, Northampton, MA) and Eq. 12 in which ODmaxn is the maximal OD of specie n for pKa,n (and was a free parameter):
| (12) |
Figure 4.
Absorbance pH titrations and shifts in pKa are starkly different between classes and between their Ca2+-free and Ca2+-saturated states. Titrations from neutral to acidic pH and neutral to alkaline pH were done separately and then combined. The figures are normalized to the observed maximal absorbance of the anionic form. (A–F) Representative spectra from absorbance pH titrations are shown, measured in either Ca2+-free or Ca2+-saturated buffer as noted. Each spectrum was measured at the pH value designated in the legends. The final spectrum (red dashed line) belongs to the denatured chromophore. (G–I) Apparent pKa curves are shown, showing the OD of the anionic form as a function of pH. The pKa values are indicated on the fitted curve. (H) Only part of the K-GECO1 titrations could be fitted because of protein precipitation at pH values below those displayed and early denaturation of the anionic form at higher pH values.
The anionic and neutral forms of the chromophore have distinct extinction coefficients (ε). To get the ε values of the anionic form for R-GECO1, R-GECO1.2, O-GECO1, jRGECO1a, REX-GECO1, and jREX-GECO1, we took the OD of the anionic peak at the pH in which it reached its maximum during the alkaline titration, divided it by the maximal OD of the alkaline denatured form with a known ε (44,100 M−1cm−1 (28)), and multiplied it by that known ε. The presence of the immature green chromophore was considered to be insignificant in these proteins. For R-GECO1, R-GECO1.2, O-GECO1, and jRGECO1a, in which the anionic peak shifted red at pH ≳ 8.5 in the Ca2+-saturated state, we took the maximal OD before the shift. The shift is probably due to a titration of residue(s) near the chromophore, and our method provided the ε of the chromophore in the environment corresponding to pH 7.2. To get the ε of the neutral form using the now-known ε of the anionic form, we plotted the anionic peak OD versus the neutral peak OD across the titration. Where the dependence was linear, we used the slope to calculate the neutral ε. The OD at the neutral and denatured peaks was corrected for any contribution of the blue tail of the anionic absorption, using the spectrum at the pH when the anionic form is maximal as a reference. This slope method is further detailed in (23).
For CAR-GECO1, K-GECO1, and jRCaMP1a, the slope method was used to find both the ε value of the anionic form and the neutral form because of the significant presence of the immature green chromophore in CAR-GECO1 and the appearance of a 380 nm peak in K-GECO1 and jRCaMP1a during denaturation. To obtain the anionic ε for these proteins, we plotted the OD of the anionic form versus the OD of the ∼450 nm denatured form and fit the slope at the end of the titration where it was linear and, in the case of K-GECO1 and jRCaMP1a, where the 380 nm peak had already reached its maximum. Linear plots with a fitted slope are displayed in Fig. S2 using CAR-GECO1 as an example. For special corrections to the pH titrations of jREX-GECO1 and REX-GECO1, see Supporting Materials and Methods.
Determination of the relative fraction of the excitable form of the chromophore
The relative fraction of the excitable form of the chromophore in the Ca2+-free and Ca2+-saturated states for each protein, ρe, was calculated with Eq. 13 using the absorption spectra collected at pH 7.2.
| (13) |
where ε is the extinction coefficient; the subscripts e and ne stand for the excitable and nonexcitable form, respectively. For special corrections to determining the relative fraction for K-GECO1 and CAR-GECO1, see Supporting Materials and Methods.
Two-photon characterization
To collect the two-photon absorption spectra, the tunable femtosecond laser InSight DeepSee (Spectra-Physics, Santa Clara, CA) was used to excite the fluorescence of the sample contained in a 3 mm glass cuvette (Starna Cells, Atascadero, CA) within a PC1 Spectrofluorimeter (ISS, Champaign, IL). The laser was automatically stepped to each wavelength over the spectral range with a custom LabVIEW program (National Instruments, Austin, TX), with at least 30 s at each wavelength to stabilize. We measured two samples per laser scan by using both the sample and reference holders and switching between them with the autoswitching mechanism on the PC1. The laser was focused on the sample through a 45-mm near-infrared achromatic lens with antireflection coating from 750–1550 nm (Edmund Optics, Barrington, NJ). Fluorescence was collected from the first 0.7 mm of the sample at 90° with the standard PC1 collection optics through a combination of either 680/SP, 633/SP, or 694/SP filters together with a 745/SP filter (Semrock) to remove all laser-scattered light and a 570/longpass filter (Edmund Optics) to remove the residual green fluorescence of the immature chromophore. To correct for wavelength-to-wavelength variations of laser parameters, we used LDS798 (Exciton, Lockbourne, OH) in 1:2 CHCl3:CDCl3 as a reference standard between 900 and 1240 nm (29) and Coumarin 540A (Exciton) in 1:10 dimethyl sulfoxide:deuterated dimethyl sulfoxide between 700 and 952 nm (30). Adding the deuterated solvents (MilliporeSigma, Darmstadt, Germany) was necessary to decrease near-infrared solvent absorption. The standards were measured at least twice a week in both the sample and the reference holder. All the dyes were magnetically stirred throughout the measurements. Quadratic power dependence of fluorescence in the proteins and standards was checked at several wavelengths across the spectrum.
For the two-photon cross sections, we measured each protein versus Rhodamine 6G in MeOH at 1052 nm (two-photon cross section, σ2 = 9.9 GM (31)). Rhodamine 6G was chosen because the value for σ2 at this wavelength agrees across the literature (30, 31). (Rhodamine B, which was the standard for previous two-photon measurements of some red GECIs, is pH-sensitive with variable σ2 values.) Power dependence of fluorescence intensity was recorded with the PC1 monochromator at a wavelength in which the OD was ≳ 0.05 and fitted to a parabola with the curvature coefficient proportional to σ2. These coefficients were normalized for the differential fluorescence quantum yield at the registration wavelength and the concentrations. The differential quantum yields of the standard and the sample were obtained using the data from the fluorescence quantum yield measurements and selecting an integral range from ∼5 nm to the left and right of the registration wavelength. Concentrations were determined by Beer’s Law. For Rhodamine 6G in MeOH, ε = 100,500 M−1cm−1 (31). For most of the proteins (except for the Ca2+-saturated state of REX-GECO1 and jREX-GECO1), the σ2 at 1052 nm corresponds to the anionic form of the chromophore, and the concentration was determined with the maximal OD of the anionic form and its ε. For the Ca2+-saturated state of REX-GECO1 and jREX-GECO1, the OD at the peak of the absorption spectrum and the ε of the neutral chromophore was used to find the concentration.
Direct measurements of Ca2+-saturated/free F1 and F2 ratios
We measured the Ca2+-saturated/free F1 and F2 ratios for each protein directly by comparing the Ca2+-saturated and Ca2+-free states with known concentrations of protein relative to each other. To make the samples, a portion of Ca2+-free protein was diluted 10 times to a total volume of 150 μL into a Ca2+-saturated buffer (30 mM MOPS, 100 mM KCl, and 10 mM CaCl2) and then the pH was adjusted back to 7.2 with 3–5 μL of 0.1 M NaOH. An equivalent volume of 18.2 MΩ water was added to the Ca2+-free sample to maintain a known concentration ratio between the two samples.
For the F2 ratio spectra, the shape was calculated by dividing the Ca2+-saturated two-photon excitation spectrum by the Ca2+-free two-photon excitation spectrum. Then, the ratio of the fluorescence signals was measured at three laser wavelengths around the maximal ratio. The setup from the two-photon characterization section was employed, and fluorescence was collected through 745/shortpass (SP) and 770/SP filters (Semrock, Rochester, NY). After applying the known concentration ratio, the F2 ratio spectrum was normalized to the three fluorescence signal ratios, and the results were averaged (Fig. S3).
For the F1 ratios, the samples were diluted further into 1 cm glass cuvettes for a total volume of 2 mL. The excitation spectrum for each sample was scanned with the LS 55 Fluorescence Spectrometer (PerkinElmer) with excitation slits set to 10 nm, and the entire fluorescence was collected by setting the emission grating to the 0-th diffraction order. The background fluorescence spectrum of water in a 1 cm glass cuvette was subtracted from each spectrum, scaled so that the fluorescence at 650 nm became approximately zero. The ratio between the Ca2+-saturated and Ca2+-free spectra was calculated and adjusted to account for the concentration difference between the two.
Results
The red GECIs studied here are highlighted in Fig. 1: R-GECO1, R-GECO1.2, CAR-GECO1, O-GECO1, REX-GECO1, jRGECO1a, jRCaMP1a, and K-GECO1. Although the chromophores in O-GECO1 and jRCaMP1a have slightly different structures than the typical red FP chromophore displayed in Fig. 2 C (Fig. S4), the same analysis still applies because they also undergo the protonation-deprotonation reaction. We additionally present a new red GECI, jREX-GECO1, which is derived from REX-GECO1 and incorporates mutations present in jRGECO1a. A protein sequence alignment of these nine GECIs can be found in Fig. S5.
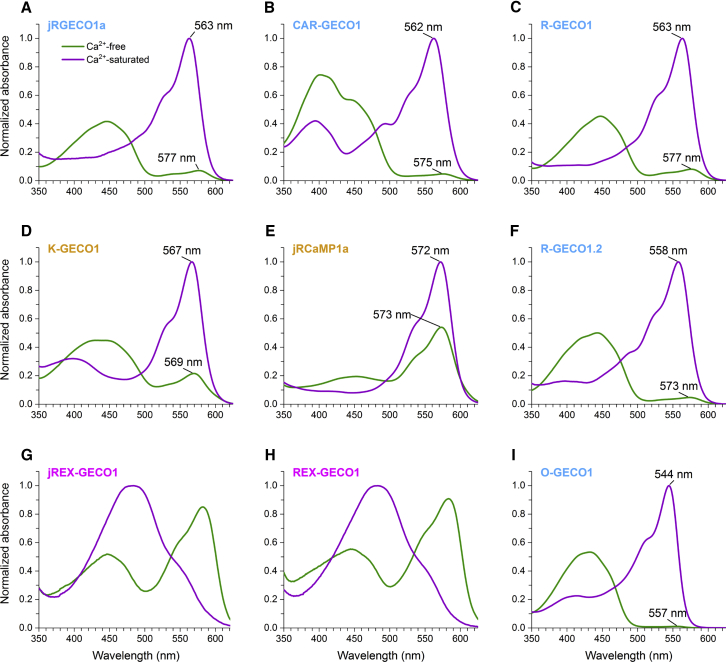
The first clue to the mechanism behind the Ca2+-dependent change in fluorescence comes from the one-photon absorption spectra of the Ca2+-free and saturated states (Fig. 3). Any changes in spectra between the two states could reveal changes in the neutral/anionic chromophore equilibrium and thus the relative fraction of the excitable form, ρe. In all but two of the indicators, the concentration of the anionic form appears to increase when Ca2+ binds. The two exceptions, jREX-GECO1 (Fig. 3 G) and REX-GECO1 (Fig. 3 H), display an opposite effect: the chromophore distribution shifts from predominantly anionic in the Ca2+-free state to neutral in the Ca2+-saturated state. Among the other seven, there is a consistent blue shift of the anionic form absorption peak upon Ca2+ binding. K-GECO1 (Fig. 3 D) and jRCaMP1a (Fig. 3 E) stand out as having both a smaller increase and a shorter blue shift of the anionic form compared to the other five (≤2 nm vs. ≥13 nm). The spectral shifts are also apparent in the one-photon excitation and emission spectra (Fig. S6). Based on these observations, these nine red GECIs can be separated into three classes: class I, which includes jRGECO1a, CAR-GECO1, R-GECO1, R-GECO1.2, and O-GECO1 (names colored blue in the figures); class II, which includes K-GECO1 and jRCaMP1a (names colored gold); and class III, which includes jREX-GECO1 and REX-GECO1 (names colored magenta).
Figure 3.
The red GECIs under study can be separated into three classes based on their one-photon absorption spectra. Plotted are the respective spectra of the nine indicators under study (A–I). In each plot, the Ca2+-free state (green) and Ca2+-saturated state (purple) are shown at the same protein concentration and normalized to the peak absorbance in the Ca2+-saturated state. The names are colored by class: blue for class I, gold for class II, and magenta for class III.
Again, the excitable form of the chromophore is the one that dominates the excitation spectrum at the wavelengths where the Ca2+-dependent fluorescence change is maximal. In classes I and II, we find that the excitable form of the chromophore is anionic regardless of the presence of Ca2+. In class III, the excitable form is anionic in the Ca2+-free state and neutral in the Ca2+-saturated state (Fig. S6). Quantitative values of ρe are displayed in Table 1.
We can gain insight into why ρe changes with Ca2+ binding by looking at the one-photon absorption spectra as a function of pH and finding the apparent pKa values for each Ca2+ state (Figs. 4, S7, and S8). Starting from Fig. 4, we chose to highlight jRGECO1a, K-GECO1, and jREX-GECO1 as examples of their respective classes. Figures for the other six red GECIs can be found in the Supporting Materials and Methods. The absorbance pH titrations generally show the neutral form titrating to the anionic form as the pH increases, and they display different behaviors depending on both the Ca2+ state and the class.
In class I, when no Ca2+ is present, the titration displays a clean isosbestic point between the neutral and anionic peaks belonging to the red chromophore and no spectral shifts (Figs. 4 A, S7, A–C, and S8 A). On the contrary, in the Ca2+-saturated state, the anionic form undergoes clear spectral shifts (Figs. 4 D, S7, D–F, and S8 D). The Ca2+-free state has one wave of titration and one apparent pKa, whereas the Ca2+-saturated state exhibits two to three waves of titration, each corresponding to a different pKa value (Figs. 4 G, S7, G–I, and S8 G). This is likely due to titratable residues near the chromophore in the Ca2+-saturated state that affect its pKa as well as the absorption of the anionic form (32, 33, 34). The titration of jRGECO1a exemplifies these observations. In the Ca2+-free titration (Fig. 4 A), there is just one pKa, and the peak position of the anionic form stays at 577 nm (Fig. 4 G). For Ca2+-saturated jRGECO1a, there are three apparent pKa values (Fig. 4 D), and the absorption peak of the anionic form shifts to three distinct wavelengths throughout the titration (Fig. 4 A): 577 nm at pH ≤ ∼5.5, 563 nm from pH ∼6.5–9, and 575 nm at pH ≥ ∼9.
The titrations in class II were best fit with a single pKa (Figs. 4 H and S8 H), except for K-GECO1 in the Ca2+-free state, which displayed a broad titration curve that could only be satisfactorily fit with two pKa values. There are subtle spectral shifts of the anionic peak in both Ca2+ states of class II; it shifts blue as it increases and shifts red right before it denatures (Figs. 4, B and E and S8, B and E). The pH titrations in class II are also characterized by a peak at ∼380 nm that irreversibly appears at alkaline pH, which may be due to the denatured form of the cleaved protein chromophore shown in Fig. S4 C (20, 22, 35, 36, 37).
Interestingly, in class III, when titrating the Ca2+-saturated state from neutral to acidic pH, the spectrum unexpectedly morphs from the broad ∼490 nm peak into two peaks that presumably belong to the neutral and anionic forms of the chromophore (Figs. 4 F and S8 F). This could be due to protonation of the Glu49 residue (numbered as in Fig. S5) near the phenolic oxygen of the chromophore that somewhat stabilizes the anionic form. The clean isosbestic point when titrating from neutral to alkaline pH between the 490 nm form and the 570 nm form suggests that the 490 nm form is singularly neutral. Assuming it is, the alkaline titration can be fit with one very high pKa (11.63 ± 0.02 for jREX-GECO1). The Ca2+-free titrations of class III are best fit with three pKa values (Figs. 4 I and S8 I), and spectral shifts of the anionic form are present.
For classes I and II in which the excitable form is always anionic, the Ca2+-induced changes in ρe qualitatively follow from the shifts in apparent pKa (Table S1). In class I, the Ca2+-saturated pKa with the largest amplitude change of the curve is always the first (most acidic) one (Figs. 4 G, S7, G–I, and S8 G). It is usually ∼3.5 pH units smaller than the Ca2+-free pKa. In class II, the pKa changes less between Ca2+ states. For K-GECO1, the shift is ∼0.4 pH units if we consider the first wave of titration in the Ca2+-free state, and jRCaMP1a has a shift of only 0.3 pH units. The Ca2+-saturated/free ρe ratios of class I and class II reflect their differences in pKa shifts. In class I, the ratio ranges between 14 and 121, whereas in class II, the ρe ratio is 3 for K-GECO1 and 1.5 for jRCaMP1a. In class III, there is a large pKa shift in the opposite direction when Ca2+ binds, showing how the neutral form is favored in the Ca2+-saturated state (Figs. 4 I and S8 I).
After investigating the change in ρe, the next clue is the fluorescence quantum yield of the excitable form, φe (Table 1). In class I, φe ranges from 0.15 to 0.31, and φe increases when Ca2+ is bound, from an insignificant change in O-GECO1 to 1.5 times in CAR-GECO1. In class II, the φe values in the Ca2+-saturated state are higher than in class I (0.48–0.54). Also, the Ca2+-dependent increase of φe is more prominent: 1.85 times for jRCaMP1a and 2.5 times for K-GECO1. Class III has the largest increases of φe (2.5–3.5 times) because whereas the Ca2+-saturated φ values of the neutral form equal 0.21, the φ values of the Ca2+-free anionic form are much lower (0.05–0.06). In every class the φe increases when Ca2+ binds, although the degree to which it does depends on the class.
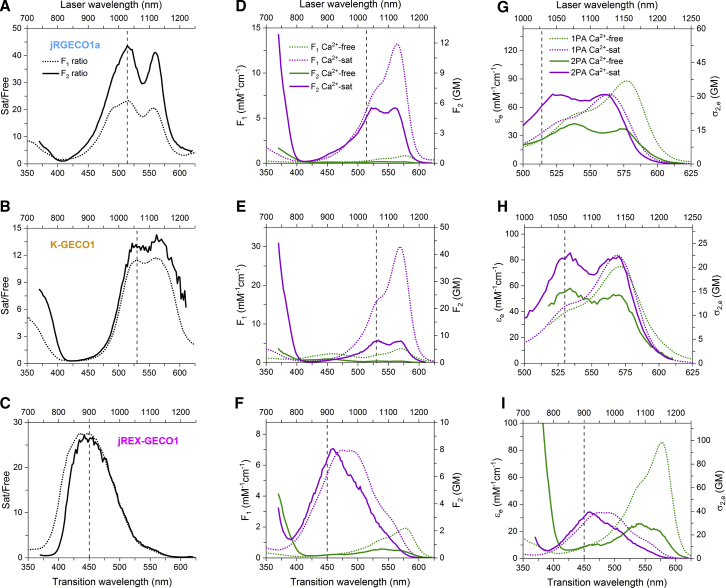
The final factor contributing to the Ca2+-saturated/free ratio of the fluorescence signal is the molecular absorption coefficient of the excitable form and how it changes because of Ca2+ at the excitation wavelength. This is the factor that can be quite different in one-photon versus two-photon excitation. Directly measuring the Ca2+-saturated/free F1 and F2 ratios as a function of excitation wavelength can reveal these differences. To do this, we took the ratio of the integrated fluorescence signal across the excitation spectrum for samples with and without Ca2+, normalized to known relative concentrations of protein. When the Ca2+-saturated/free F1 and F2 ratios are plotted together versus transition wavelength (corresponding to half the laser wavelength in the two-photon case), the shapes of the ratios look similar for both modes of excitation (Figs. 5, A–C, S9, A–C, and S10, A–C). However, the absolute values of the ratios are not always the same. This is especially apparent at the transition wavelength where the ratios are maximal, marked with a vertical dashed line, and called λRmax. In classes I and II, the ratio spectra have a double-humped nature because of the spectral shift of the anionic form between Ca2+ states, and we selected the shorter wavelength hump as λRmax for consistency. For all members of class I, the F2 ratio is significantly larger than the F1 ratio by 1.5–1.9 times as exemplified by jRGECO1a (Figs. 5 A, S9, A–C, and S10 A). For classes II and III, represented by K-GECO1 and jREX-GECO1, respectively, the F1 and F2 ratios are not significantly different (Figs. 5, B and C and S10, B and C).
Figure 5.
Spectral analysis of jRGECO1a (row 1), K-GECO1 (row 2), and jREX-GECO1 (row 3), representing classes I, II, and III of red GECIs, respectively. The vertical dashed line on each plot indicates the transition wavelength of excitation (λRmax) where the Ca2+-saturated/free F1 and F2 ratios are approximately maximal. (A–C) Ca2+-saturated/free (Sat/Free) F1 (dotted line) and F2 (solid line) ratios as a function of excitation wavelength were measured directly by taking the ratio of the integrated fluorescence signal normalized to the known relative protein concentration between the Ca2+-free and Ca2+-saturated samples. (D–F) Shown are the spectra of the one-photon brightness (F1, dotted lines, left and bottom axes) and two-photon brightness (F2, solid lines, right and top axes) of the Ca2+-free and Ca2+-saturated states. (G–I) Shown are the one-photon absorption (1PA) and two-photon absorption (2PA) spectra of the excitable form of the chromophore, shown in values of εe (left and bottom axes) and σ2,e (right and top axes), respectively, for the Ca2+-free and Ca2+-saturated states.
To get the molecular brightness spectra for the Ca2+-free and saturated states separately, we normalized their one- and two-photon absorption spectra to F1 and F2, respectively (Figs. 5, D–F, S9, D–F, S10, D–F, and S11). F1 and F2 values were calculated from the independently measured parameters ρe, φe, εe, and σ2,e. Next, to explain the differences between the directly measured F1 and F2 ratios for class I versus the other classes, we normalized the one- and two-photon absorption spectra of the excitable form to εe and σ2,e, respectively (Figs. 5, G–I, S9, G–I, and S10, G–I). At λRmax (again marked with a vertical dashed line), the σ2,e of jRGECO1a increases by 2.4 times in the Ca2+-saturated state. In comparison, the increase of εe at λRmax is much smaller (∼1.2 times) (Fig. 5 D). A similar phenomenon occurs for the rest of class I. Curiously, εe at λRmax only increases because of the spectral shift, whereas εe at the peak actually decreases slightly for class I when Ca2+ binds (Table 1). In class II, there is no significant change of σ2,e or εe (Figs. 5 H and S10 H). Although the σ2,e of K-GECO1 appears to increase, the uncertainty of the measurement is too large to consider it statistically significant (Table 1). Finally, class III, represented by jREX-GECO1, exhibits equivalent Ca2+-induced increases of εe and σ2,e (Figs. 5 I and S10 I). They both increase ∼3.6 times on average at λRmax. This is due to the switch of the excitable form from the anionic to the neutral, and the major shift between their absorption spectra under both one- and two-photon excitation.
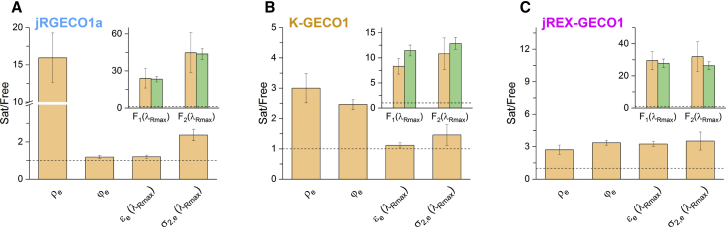
The final question remains: of the three different factors, which one matters the most for the Ca2+-saturated/free fluorescence ratios? We have found that the answer to this question depends on the indicator class. The Ca2+-saturated/free ratios for each parameter are visualized in Figs. 6 and S12. Representing class I, jRGECO1a (Fig. 6 A) has a ρe,sat/ρe,free ratio that far exceeds the other ratios. An increase in σ2,e increases the F2 ratio by two times. From class II, K-GECO1 (Fig. 6 B) has comparable contributions to the overall Fn ratios from changes in both ρe and φe. Last, in class III, all three factors play a significant role as illustrated by the example of jREX-GECO1 (Fig. 6 C).
Figure 6.
Each class depends on a different set of factors for the Ca2+-induced fluorescence change. Shown are Ca2+-saturated/free ratios (Sat/Free) of ρe, φe, εe(λRmax), and σ2,e(λRmax) of (A) jRGECO1a, (B) K-GECO1, and (C) jREX-GECO1. Insets: Ca2+-saturated/free F1 and F2 ratios were both calculated from the independent measurements of ρe, φe, εe, and σ2,e (tan) and measured directly (green) as described for Fig. 5. The horizontal dashed line marks a Ca2+-saturated/free (Sat/Free) ratio of 1 (no change) for each plot. Error bars represent estimated SDs.
Discussion
We set out to determine the main factors that contribute to the Ca2+-dependent fluorescence change in nine red GECIs under both one-photon and two-photon excitation. The key parameters that could change because of Ca2+ are the following: 1) the relative fraction of the chromophore in the excitable protonation state (ρe), 2) the quantum yield of the excitable state (φe), and 3) the extinction coefficient (εe) or two-photon cross section (σ2,e) of the excitable state at the excitation wavelength.
We found that the nine red Ca2+ indicators could be separated into three different classes, each of which relied on different factors. Class I consists of jRGECO1a, CAR-GECO1, R-GECO1, R-GECO1.2, and O-GECO1. Class II includes K-GECO1 and jRCaMP1a. In these two classes, the excitable form of the chromophore is anionic for both the Ca2+-free and saturated states. Class III contains jREX-GECO1 and REX-GECO1. It is unique because the excitable form switches from anionic in the Ca2+-free state to neutral in the Ca2+-saturated state. The fluorescence change in class I is mostly due to a dramatic increase in ρe because of a large Ca2+-dependent shift in pKa. This is much like GCaMP6m (23). Additionally, an increase in σ2,e when Ca2+ binds contributes to the F2 ratio by approximately twofold on average for class I. The indicators in class II depend on both a Ca2+-induced increase in ρe and φe. In class III, all the factors are comparably important to the change in fluorescence. Classes I and II were previously alluded to in (20), where the importance of the change in the chromophore pKa between Ca2+ states was highlighted for R-GECO1, and the change in φ was seen to be more important for the RCaMP series (which jRCaMP1a was based on).
The spectral shapes of the Ca2+-saturated/free fluorescence excitation ratios are very similar under one-photon excitation and two-photon excitation. Interestingly, for class I, the value of the fluorescence ratio is greater under two-photon excitation compared to one-photon excitation at λRmax. This is because the σ2 of the anionic form increases upon Ca2+ binding, whereas the ε of the anionic form changes little or not at all. The increase in σ2 for the anionic chromophore can be explained by its sensitivity to the local electric field created by the protein surrounding (24, 25, 26). This sensitivity is due to a factor describing the change of the permanent dipole moment of the chromophore upon excitation that enters the expression for σ2, and the electric field affects this factor through polarizability.
Notably, the increase in σ2 of the anionic chromophore is always paralleled by a shift of the one-photon absorption peak to a shorter wavelength. We previously developed a physical model (24, 25, 26) that predicts that both of these changes will happen if the electric field increases, directed from the center of the phenolate ring to the center of the imidazole ring. In red GECIs, the chromophore is oriented such that its phenolate oxygen points toward the site of circular permutation where the Ca2+-sensing domain is fused to the FP (as observed for RCaMP, Protein Data Bank (PDB): 3U0K (20); R-GECO1, PDB: 4I2Y (20); and K-GECO1, PDB: 5UKG (21); see Fig. 1 A). Because of this geometry, the conformational change of the protein when it binds to Ca2+ would likely modulate the electric field along the phenolate-imidazole axis of the chromophore. We propose that the increase in σ2 results from an increase in the electric field in this direction, in which positive charges move closer to the phenolate oxygen and/or negative charges move farther away.
With this in mind, we can compare potential Ca2+-induced electric field changes for both class I and class II because the excitable form of the chromophore is always anionic. The indicators in class I show the greatest increases in σ2 and the largest blue shifts (13–15 nm), whereas those in class II show insignificant increases in σ2 and small blue shifts (1–2 nm). These differences might be because of what is hydrogen bonded to the phenolate oxygen of the chromophore in the Ca2+-saturated state. In class I, it is a positive residue (Lys49, numbered according to Fig. S5), based on the crystal structure of R-GECO1 (20). In class II, only neutral residues (Asn32 and Thr278 for K-GECO1 and jRCaMP1a, respectively) and water molecules are bound to that oxygen (20, 21). If those hydrogen bonds are disrupted in the Ca2+-free state, then this could explain the largest changes in σ2 for class I and insignificant changes for class II. There is likely a Ca2+-induced increase in the electric field along the phenolate-imidazole axis that is much stronger for class I.
The changes in ρe for class I and class II qualitatively follow the same trend as the changes in σ2, which can be explained on similar electrostatics grounds. For class I, the major Ca2+-induced shift of the acid-base equilibrium of the chromophore toward its deprotonated, anionic form is probably a result of the positive charge on Lys49 coming closer to the phenolic oxygen. In class II, this pKa shift is not as prominent because there are no charges to redistribute.
In support of these observations, the indicators in class III were initially developed by mutating the positive Lys49 in R-GECO1 to the negative Glu49, stabilizing the protonated, neutral form in the Ca2+-saturated state (15). Importantly, the proximity of the Glu49 carboxylate in the Ca2+-saturated state also makes excited-state proton transfer possible for class III proteins (15, 38). The neutral form of the chromophore undergoes excited-state proton transfer upon excitation by giving its proton to Glu, and then it emits from the anionic state, resulting in the long Stokes shift. This pathway is disrupted in the Ca2+-free state because the Glu49 carboxylate is not in close proximity. This is why the excitable form is anionic in the Ca2+-free state and neutral in the Ca2+-saturated state, even though, technically, it is the anionic form of the chromophore which emits in both cases.
We also observe that the φ of the anionic form increases in the Ca2+-saturated state in all cases except O-GECO1 (where it did not change) and class III indicators (where no anionic form is present in the Ca2+-saturated state). This effect can also be explained by the Ca2+-induced changes in the electric field. Quantum chemistry calculations predict that in a vacuum, the nonradiative decay of the excited state proceeds through substantial twisting around the phenolate exocyclic C-C bond (39). This is coupled with electron density transfer from the phenolate to the imidazolinone and acylimine groups (39). If the field increases in the same direction of electron density transfer, the activation energy for the transfer will increase. As a result, the nonradiative decay rate will slow, and the fluorescence quantum yield will increase. The independence of quantum yield on conformational changes in GCaMP6m (23) and O-GECO1 (Table 1) may be due to no acylimine group in their chromophore structures. In fact, it was shown that the electronegativity of acylimine makes the described mechanism of nonradiative relaxation highly probable specifically for the red FP chromophore (39).
In summary, red GECIs can be divided into three classes, and the factors that mainly contribute to the Ca2+-dependent change in fluorescence vary based on the class. It is interesting to note that the three factors, ρe, φe, and σ2,e, synergistically increase in almost all the red GECIs because of a favorable geometric arrangement of the chromophore with respect to the fusion site and to the local electrostatic/hydrogen bonding interactions. In class I, the change under one-photon excitation was smaller than the change under two-photon excitation. We suggest that this should be carefully considered when further developing these red GECIs.
We characterized the Ca2+-free and Ca2+-saturated states for each red GECI. These measurements can only give us information about the protein in these limiting states. They do not tell us about the dynamics of the conformational change between these states or the indicators’ performance in live cells. Some of these aspects were recently reviewed for red GECIs in other work (40, 41). Our results do reveal that there is no single perfect red GECI. For maximal changes in fluorescence, the indicators in classes I and III appear to be the best. For fluorescence lifetime imaging, the proteins with the largest changes in quantum yield are promising (classes II and III). This follows from the fact that the fluorescence lifetime τ is proportional to the quantum yield: τ = τRφ, where τR is the radiative lifetime and can be considered virtually constant (24). For two-photon imaging simultaneously with a green FP-based probe, jREX-GECO1 is an excellent candidate because it shows the maximal change in fluorescence at ∼900 nm. This has been demonstrated with its predecessor REX-GECO1 (15). Finally, to inform the optimum optical setup for these red GECIs, it is important to consider the Ca2+-dependent spectral shifts in excitation (one-photon and two-photon) and emission.
The red fluorescent Ca2+ indicator is a man-made molecular machine found nowhere in nature. Just as understanding how microscopes work can lead to better microscopes and better imaging, so it is important to understand how these biological tools work, both to improve them and make the best use out of them.
Author Contributions
R.S.M. and M.D. designed and conducted research. J.W. and Y.Q. developed jREX-GECO1. Y.S. provided plasmids and critical advice along the way. R.S.M. analyzed data and wrote the manuscript. R.E.C., T.E.H., and M.D. supervised research. R.S.M., Y.Q., Y.S., R.E.C., T.E.H., and M.D. revised the manuscript.
Acknowledgments
We thank Alexey Drobizhev for the custom LabVIEW program, Phidlynn Augustin for technical help, and Merrilee Thomas and Edward Johnson for proofreading the manuscript. We are also grateful to the anonymous reviewers for their helpful and critical feedback.
This work was supported by grants from National Institutes of Health (U01 NS094246, U24 NS109107, and U01 NS090565), Natural Sciences and Engineering Research Council of Canada (RGPIN 288338-2010), Canadian Institutes of Health Research (FS 154310), and Brain Canada. R.S.M. is supported by the National Institute of Neurological Disorders and Stroke of the National Institutes of Health Ruth L. Kirschstein National Research Service Award under award number F31NS108593. R.S.M. is particularly indebted to National Institute of Neurological Disorders and Stroke program staff Ned Talley and Steve Korn for their encouragement and support.
Editor: Amy Palmer.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2019.04.007.
Supporting Material
References
- 1.Mues M., Bartholomäus I., Krishnamoorthy G. Real-time in vivo analysis of T cell activation in the central nervous system using a genetically encoded calcium indicator. Nat. Med. 2013;19:778–783. doi: 10.1038/nm.3180. [DOI] [PubMed] [Google Scholar]
- 2.Dong T.X., Othy S., Cahalan M.D. T-cell calcium dynamics visualized in a ratiometric tdTomato-GCaMP6f transgenic reporter mouse. eLife. 2017;6:e32417. doi: 10.7554/eLife.32417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Grienberger C., Konnerth A. Imaging calcium in neurons. Neuron. 2012;73:862–885. doi: 10.1016/j.neuron.2012.02.011. [DOI] [PubMed] [Google Scholar]
- 4.Lin M.Z., Schnitzer M.J. Genetically encoded indicators of neuronal activity. Nat. Neurosci. 2016;19:1142–1153. doi: 10.1038/nn.4359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Mank M., Griesbeck O. Genetically encoded calcium indicators. Chem. Rev. 2008;108:1550–1564. doi: 10.1021/cr078213v. [DOI] [PubMed] [Google Scholar]
- 6.Chen Z., Truong T.M., Ai H.W. Illuminating brain activities with fluorescent protein-based biosensors. Chemosensors (Basel) 2017;5:32. doi: 10.3390/chemosensors5040032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Nagai T., Sawano A., Miyawaki A. Circularly permuted green fluorescent proteins engineered to sense Ca2+ Proc. Natl. Acad. Sci. USA. 2001;98:3197–3202. doi: 10.1073/pnas.051636098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Nakai J., Ohkura M., Imoto K. A high signal-to-noise Ca(2+) probe composed of a single green fluorescent protein. Nat. Biotechnol. 2001;19:137–141. doi: 10.1038/84397. [DOI] [PubMed] [Google Scholar]
- 9.Tian L., Hires S.A., Looger L.L. Imaging neural activity in worms, flies and mice with improved GCaMP calcium indicators. Nat. Methods. 2009;6:875–881. doi: 10.1038/nmeth.1398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chen T.W., Wardill T.J., Kim D.S. Ultrasensitive fluorescent proteins for imaging neuronal activity. Nature. 2013;499:295–300. doi: 10.1038/nature12354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zhao Y., Araki S., Campbell R.E. An expanded palette of genetically encoded Ca2+ indicators. Science. 2011;333:1888–1891. doi: 10.1126/science.1208592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Deliolanis N.C., Kasmieh R., Ntziachristos V. Performance of the red-shifted fluorescent proteins in deep-tissue molecular imaging applications. J. Biomed. Opt. 2008;13:044008. doi: 10.1117/1.2967184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Shaner N.C., Campbell R.E., Tsien R.Y. Improved monomeric red, orange and yellow fluorescent proteins derived from Discosoma sp. red fluorescent protein. Nat. Biotechnol. 2004;22:1567–1572. doi: 10.1038/nbt1037. [DOI] [PubMed] [Google Scholar]
- 14.Wu J., Liu L., Campbell R.E. Improved orange and red Ca2± indicators and photophysical considerations for optogenetic applications. ACS Chem. Neurosci. 2013;4:963–972. doi: 10.1021/cn400012b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Wu J., Abdelfattah A.S., Campbell R.E. A long Stokes shift red fluorescent Ca2+ indicator protein for two-photon and ratiometric imaging. Nat. Commun. 2014;5:5262. doi: 10.1038/ncomms6262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ohkura M., Sasaki T., Nakai J. An improved genetically encoded red fluorescent Ca2+ indicator for detecting optically evoked action potentials. PLoS One. 2012;7:e39933. doi: 10.1371/journal.pone.0039933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Inoue M., Takeuchi A., Bito H. Rational design of a high-affinity, fast, red calcium indicator R-CaMP2. Nat. Methods. 2015;12:64–70. doi: 10.1038/nmeth.3185. [DOI] [PubMed] [Google Scholar]
- 18.Dana H., Mohar B., Kim D.S. Sensitive red protein calcium indicators for imaging neural activity. eLife. 2016;5:e12727. doi: 10.7554/eLife.12727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kredel S., Oswald F., Wiedenmann J. mRuby, a bright monomeric red fluorescent protein for labeling of subcellular structures. PLoS One. 2009;4:e4391. doi: 10.1371/journal.pone.0004391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Akerboom J., Carreras Calderón N., Looger L.L. Genetically encoded calcium indicators for multi-color neural activity imaging and combination with optogenetics. Front. Mol. Neurosci. 2013;6:2. doi: 10.3389/fnmol.2013.00002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Shen Y., Dana H., Campbell R.E. A genetically encoded Ca2+ indicator based on circularly permutated sea anemone red fluorescent protein eqFP578. BMC Biol. 2018;16:9. doi: 10.1186/s12915-018-0480-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Shemiakina I.I., Ermakova G.V., Shcherbo D. A monomeric red fluorescent protein with low cytotoxicity. Nat. Commun. 2012;3:1204. doi: 10.1038/ncomms2208. [DOI] [PubMed] [Google Scholar]
- 23.Barnett L.M., Hughes T.E., Drobizhev M. Deciphering the molecular mechanism responsible for GCaMP6m’s Ca2+-dependent change in fluorescence. PLoS One. 2017;12:e0170934. doi: 10.1371/journal.pone.0170934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Drobizhev M., Tillo S., Rebane A. Color hues in red fluorescent proteins are due to internal quadratic Stark effect. J. Phys. Chem. B. 2009;113:12860–12864. doi: 10.1021/jp907085p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Drobizhev M., Callis P.R., Rebane A. Long- and short-range electrostatic fields in GFP mutants: implications for spectral tuning. Sci. Rep. 2015;5:13223. doi: 10.1038/srep13223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Molina R.S., Tran T.M., Drobizhev M. Blue-shifted green fluorescent protein homologues are brighter than enhanced green fluorescent protein under two-photon excitation. J. Phys. Chem. Lett. 2017;8:2548–2554. doi: 10.1021/acs.jpclett.7b00960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Tsien R., Pozzan T. Measurement of cytosolic free Ca2+ with quin2. Methods Enzymol. 1989;172:230–262. doi: 10.1016/s0076-6879(89)72017-6. [DOI] [PubMed] [Google Scholar]
- 28.Ward W.W. Green Fluorescent Protein. John Wiley & Sons, Inc; 2005. Biochemical and physical properties of green fluorescent protein; pp. 39–65. [PubMed] [Google Scholar]
- 29.Makarov N.S., Campo J., Perry J.W. Rapid, broadband two-photon-excited fluorescence spectroscopy and its application to red-emitting secondary reference compounds. Opt. Mater. Express. 2011;1:551–563. [Google Scholar]
- 30.de Reguardati S., Pahapill J., Rebane A. High-accuracy reference standards for two-photon absorption in the 680-1050 nm wavelength range. Opt. Express. 2016;24:9053–9066. doi: 10.1364/OE.24.009053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Makarov N.S., Drobizhev M., Rebane A. Two-photon absorption standards in the 550-1600 nm excitation wavelength range. Opt. Express. 2008;16:4029–4047. doi: 10.1364/oe.16.004029. [DOI] [PubMed] [Google Scholar]
- 32.Oltrogge L.M., Wang Q., Boxer S.G. Ground-state proton transfer kinetics in green fluorescent protein. Biochemistry. 2014;53:5947–5957. doi: 10.1021/bi500147n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Bizzarri R., Nifosì R., Beltram F. Green fluorescent protein ground states: the influence of a second protonation site near the chromophore. Biochemistry. 2007;46:5494–5504. doi: 10.1021/bi602646r. [DOI] [PubMed] [Google Scholar]
- 34.Shu X., Shaner N.C., Remington S.J. Novel chromophores and buried charges control color in mFruits. Biochemistry. 2006;45:9639–9647. doi: 10.1021/bi060773l. [DOI] [PubMed] [Google Scholar]
- 35.Quillin M.L., Anstrom D.M., Remington S.J. Kindling fluorescent protein from Anemonia sulcata: dark-state structure at 1.38 A resolution. Biochemistry. 2005;44:5774–5787. doi: 10.1021/bi047644u. [DOI] [PubMed] [Google Scholar]
- 36.Yampolsky I.V., Remington S.J., Lukyanov K.A. Synthesis and properties of the chromophore of the asFP595 chromoprotein from Anemonia sulcata. Biochemistry. 2005;44:5788–5793. doi: 10.1021/bi0476432. [DOI] [PubMed] [Google Scholar]
- 37.Tretyakova Y.A., Pakhomov A.A., Martynov V.I. Chromophore structure of the kindling fluorescent protein asFP595 from Anemonia sulcata. J. Am. Chem. Soc. 2007;129:7748–7749. doi: 10.1021/ja071992c. [DOI] [PubMed] [Google Scholar]
- 38.Piatkevich K.D., Malashkevich V.N., Verkhusha V.V. Engineering ESPT pathways based on structural analysis of LSSmKate red fluorescent proteins with large Stokes shift. J. Am. Chem. Soc. 2010;132:10762–10770. doi: 10.1021/ja101974k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Olsen S., Smith S.C. Radiationless decay of red fluorescent protein chromophore models via twisted intramolecular charge-transfer states. J. Am. Chem. Soc. 2007;129:2054–2065. doi: 10.1021/ja066430s. [DOI] [PubMed] [Google Scholar]
- 40.Podor B., Hu Y.L., Fine A. Comparison of genetically encoded calcium indicators for monitoring action potentials in mammalian brain by two-photon excitation fluorescence microscopy. Neurophotonics. 2015;2:021014. doi: 10.1117/1.NPh.2.2.021014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kerruth S., Coates C., Török K. The kinetic mechanisms of fast-decay red-fluorescent genetically encoded calcium indicators. J. Biol. Chem. 2019;294:3934–3946. doi: 10.1074/jbc.RA118.004543. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.