Abstract
Endovascular treatment of Peripheral Arterial Disease (PAD) is notorious for high failure rates, and interaction between the arterial wall and the repair devices plays a significant role. Computational modeling can help improve clinical outcomes of these interventions, but it requires accurate inputs of elastic and damage characteristics of the femoropopliteal artery (FPA) which are currently not available. Fresh human FPAs from n=104 tissue donors 14–80 years old were tested using planar biaxial extension to capture elastic and damage characteristics. Damage initiation stretches and stresses were determined for both longitudinal and circumferential directions, and their correlations with age and risk factors were assessed. Two and four-fiber-family invariant-based constitutive models augmented with damage functions were used to describe stress softening with accumulating damage. In FPAs younger than 50 years, damage began accumulating after 1.51±0.13 and 1.49±0.11 stretch, or 196±110 kPa and 239±79 kPa Cauchy stress in the longitudinal and circumferential directions, respectively. In FPAs older than 50 years, damage initiation stretches and stresses decreased to 1.27±0.09 (106±52 kPa) and 1.26±0.09 (104±59 kPa), respectively. Damage manifested primarily as tears at the internal and external elastic laminae and within the tunica media layer. Higher body mass index and presence of diabetes were associated with lower damage initiation stretches and higher stresses. The selected constitutive models were able to accurately portray the FPA behavior in both elastic and inelastic domains, and properties were derived for six age groups. Presented data can help improve fidelity of computational models simulating endovascular PAD repairs that involve arterial damage.
Keywords: femoropopliteal artery, damage, inelastic deformations, mechanical testing, constitutive modeling, aging
Graphical Abstract
1. INTRODUCTION
Peripheral Arterial Disease (PAD) primarily refers to an atherosclerotic narrowing of the femoropopliteal artery (FPA) lumen obstructing blood flow to the lower limbs[1]. It is associated with high morbidity, mortality, and impairment in quality of life[2]. Late stages of PAD can progress to ischemic ulcers and gangrene and frequently require operations or interventions[3]. Endovascular treatment of PAD has surpassed surgical bypass to become the first-line therapy for most patients at many institutions, and it continues to gain in popularity due to its minimally invasive nature and significantly shorter recovery times. During endovascular repair, the lesion is typically accessed through the common femoral, or less frequently through the brachial or pedal artery, and a balloon angioplasty is performed to damage the plaque and dilate the lumen. Shorter lesions may be treated with angioplasty alone, but in cases involving complex plaques and flow-limiting arterial dissections, a permanent metal mesh tube, called a stent, can be deployed to help maintain arterial lumen patency[4].
Despite the popularity of endovascular PAD repairs, their clinical outcomes continue to disappoint. Patency of stent-based therapy ranges 43–90% at 12 months[5–7] despite recent advances in stent design[4]. These poor clinical outcomes, combined with expensive reinterventions in third to half of the patients[5,8], significantly drive up the cost of repairs[9]. High failure rates of PAD treatment are frequently attributed to the adverse interaction between the artery and the repair devices[10], and significant effort is put into developing better stents to treat PAD[4]. Computational modeling can help improve clinical outcomes of endovascular PAD repairs, but it requires accurate inputs of elastic and damage characteristics of the artery to realistically simulate angioplasty and stenting procedures.
Damage of soft tissues has been explored experimentally in carotid[11,12], coronary[13], and cerebral arteries[14], aortas[15–20], tendons[14], ligaments[13], skin[21], veins[22,23], and vaginal tissue[21,23]. Despite differences in the type of biological specimens, vast majority of these studies used uniaxial extension tests and reported stress softening effects for each advancing level of stretch in the inelastic domain. Studies that used cyclic loading further reported stress softening for the same stretch maximum, with curves eventually saturating to the repeatable response until the stretch limit was further increased. Most studies also reported the presence of a permanent set – a lengthening of the specimen after removal of the load. Though quantitatively damage initiation and progression characteristics differed among species and the types of tissues, the characteristic features of soft fibrous biomaterial behavior in the inelastic domain were surprisingly consistent and were primarily attributed to the intramural collagen fiber compositions.
Constitutive models to describe stress softening, damage saturation, and permanent set have been developed by multiple research teams, and have advanced tremendously from the isotropic softening at large strains due to Mullins effect[24,25] to models that incorporate discontinuous damage[26], unloading hysteresis[27], remnant strains[28], and damage saturation[28,29]. Additionally, models that include statistical distributions of microstructural characteristics, such as constituent volume fractions[21], fiber alignment, and proteoglycan ultimate stretch[30,31] are currently available.
But despite recent advances in both experimental and constitutive modeling efforts, damage characteristics of human FPAs in different age groups remain unexplored. The goal of the current study was to characterize accumulation of damage in human FPAs of different ages using a continuum mechanics framework, and provide damage characteristics that can be readily used for computational modeling. These characteristics can help improve the fidelity of computational models that involve angioplasty and device-artery interactions.
2. MATERIALS AND METHODS
2.1. Materials
Fresh FPAs from 104 human subjects 14–80 years old (average age 54±15 years) were obtained from the Nebraska Organ Recovery System (NORS) within 24 hours of death after receiving consent from next of kin. Subjects were predominantly male (72%), half (49%) had hypertension (HTN), 17% had diabetes mellitus (DM), 33% had dyslipidemia, 21% had coronary artery disease (CAD), and 57% were current or former tobacco users (average pack-year history 18±24). Detailed demographics for each age group are presented in Table 1.
Table 1.
Subject demographics across all age groups. Here n represents the number of specimens in each group. BMI = Body Mass Index, HTN = Hypertension, DM = Diabetes Mellitus, CAD = Coronary Artery Disease.
| Age group | n | Male Sex | BMI | HTN | DM | Dyslipidemia | CAD | Smoking (pack years) |
|---|---|---|---|---|---|---|---|---|
| 11–30 | 11 | 73% | 25.5±5.4 | 0% | 0% | 0% | 0% | 1±2 |
| 31–40 | 9 | 67% | 32.3±7.0 | 22% | 11% | 0% | 22% | 5±5 |
| 41–50 | 8 | 88% | 33.8±10.0 | 50% | 38% | 50% | 25% | 13±14 |
| 51–60 | 36 | 53% | 31.6±6.5 | 53% | 14% | 39% | 22% | 18±24 |
| 61–70 | 32 | 81% | 31.4±5.2 | 59% | 22% | 47% | 25% | 26±26 |
| 71–80 | 8 | 100% | 31.0±4.0 | 88% | 25% | 13% | 38% | 29±25 |
2.2. Mechanical and structural assessment of damage
All FPAs were radially cut, and a segment of 13×13 mm (when permitted by diameter) was mounted on a CellScale Biotester equipped with 5N loadcells. Samples were submerged into a bath of Phosphate-Buffered Saline (PBS) kept at 37C to ensure constant pH and tissue hydration during testing. All samples were first evaluated in the elastic domain using 20 equibiaxial cycles of preconditioning within the physiologic range of loads, followed by 19 multi-ratio loading protocols as described previously[32]. During the assessment of elastic characteristics, several equibiaxial protocols were executed to ensure that specimens did not accumulate damage. After testing in the elastic domain, the equibiaxial damage protocol was executed. Since large supraphysiologic stretches damaged the tissue, it was not possible to run multi-ratio damage tests, and all data were obtained from an equibiaxially-loaded protocol conducted at 0.01 s−1 strain rate.
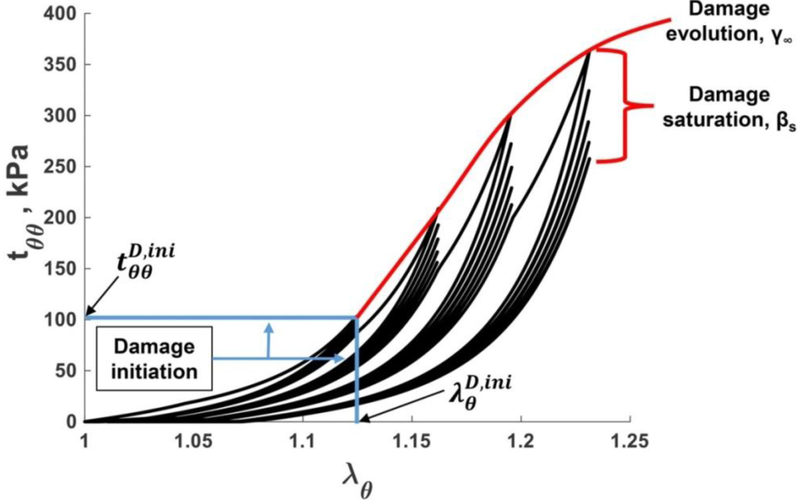
In the elastic domain, repeated loading and unloading of the pre-conditioned tissue results in repeatable non-linear stress-stretch curves. Non-linearity stems from the interplay of stiff undulated collagen fibers and straight compliant elastic fibers that contribute to the overall stress-stretch response differently depending on the applied load. When tissue accumulates damage, it demonstrates two distinct features[28], as demonstrated in Fig. 1. First, for each advancing stretch, the stress-stretch curves follow a new trajectory, typically repeating the unloading part of the previous cycle, but generating a softer response after reaching the stretch maximum. This stress softening response observed for increasing stretches is termed “damage evolution” since it is assumed to result from microscopic tissue damage. The second characteristic feature can be appreciated if instead of increasing the maximum stretch, the specimen is loaded to the same supraphysiologic stretch limit, but the loading is done repeatedly over several cycles. In this case the specimen also demonstrates stress-softening, but eventually the hysteresis reduces, and the stress-stretch curves saturate and become repeatable. This stress softening response observed for the fixed stretch limit during repeated loading is termed “damage saturation”.
Fig. 1.
Typical mechanical response of the FPA under supraphysiologic loading demonstrating damage evolution and damage saturation characteristics. Damage initiation stretches and stresses are marked with blue lines. Please note remnant stretches of 1.075 in the specimen after the last damage protocol.
To capture both effects, the damage protocol included an incremental 0.025–0.05 increase in the equibiaxial stretch with most specimens undergoing 5 cycles of repeated loading for each of the stretch limits. The test was terminated when the maximum force reached the 5N limit in either of the test directions. In-plane principal stretches were measured in the longitudinal (λz) and circumferential (λθ) directions and related to the respective loads on each axis (Pz and Pθ). Assuming incompressibility, the through-thickness average experimental Cauchy stresses (kPa) were then calculated as follows:
| (1) |
where H is the undeformed FPA thickness (μm) measured optically prior to the experiment, and Li are the undeformed specimen lengths (μm) over which the respective loads Pi (mN) act (i = θ, z).
The stress-stretch curves for both longitudinal and circumferential directions allowed to determine stretches and stresses at which damage initiated. These damage initiation stretches and stresses were defined as those at which the pre-conditioned FPA stopped demonstrating the repeatable elastic response and started exhibiting inelastic stress softening effects. This typically occurred at a stress drop of ~15 kPa between subsequent loading protocols. Structural changes associated with damage were studied using methacarn-fixed and Verhoeff-Van Gieson (VVG)-stained transverse and longitudinal sections of the FPAs. Undamaged specimens were obtained immediately adjacent to the biaxially tested samples, and were used to grade the disease stage in each specimen according to the previously published scale that ranges from 1 (healthy) to 6 (heavily diseased)[33]. Longitudinal sections were particularly enlightening because they allowed proper visualization of longitudinal elastic fibers in the external elastic lamina (EEL).
2.3. Modeling damage progression
Damage saturation for a fixed stretch limit and damage evolution for increasing stretches were modeled by augmenting the two and four-fiber-family invariant-based models with damage functions[28]. Though both are phenomenological, the four-fiber-family model is based on the intramural FPA structure with isotropic ground substance, longitudinal elastin, circumferential smooth muscle cells (SMCs), and two helical collagen families[2,32–34] oriented at an angle φ to the longitudinal axis of the artery. It has previously been shown to accurately portray the elastic behavior of the FPA[2,32–35], but given large number of parameters, this model requires many experimental protocols to ensure their uniqueness[2,36]. Since assessment of damage is a destructive process, the experimental data are limited to a single equibiaxial loading protocol. Usually this is not enough to ensure constitutive parameter uniqueness, and therefore models with smaller number of parameters are preferred. A simpler version of the four-fiber-family model is a classic two-fiber Holzapfel-Gasser-Ogden (HGO) formulation that considers only the contributions of the ground substance and the two collagen fiber families.
The strain energy function for the material with N = 2,4 fiber families can be written in the form:
| (2) |
In case of four-fiber families, Eq. (2) can be expanded to
| (3) |
and the two-fiber formulation contains only the first three terms of Eq. (3). In Eq. (3) Wgr constitutes the isotropic contribution, and account for the transversely isotropic energy of the two collagen families, describes longitudinal elastin, and represents passive contribution of circumferential SMCs. Right Cauchy-Green tensor C is a function of principal stretches λZ, λθ. Further, Mi are second-order structural tensors characterizing non-orthogonal material symmetry:
| (4) |
where Ai define fiber orientations, and N = 2,4 the number of fiber families.
The elastic strain energies for ground substance, collagen, elastin, and SMCs were taken in the forms:
| (5) |
| (6) |
| (7) |
| (8) |
Here Cgr, , , , , , , φ are material parameters that describe elastic mechanical properties of the FPA, and Macaulay brackets are used to filter out positive values, i.e. . The invariants of the right Cauchy-Green tensor C for the planar biaxial test are (accounting for incompressibility):
| (9) |
| (10) |
| (11) |
In order to model damage, transversely isotropic parts of the strain energy from Eq. 2 were modified as follows[28,37]:
| (12) |
with
| (13) |
and thus,
| (14) |
Here, Pi are internal energy functions, and Di are scalar damage functions for each fiber family used to capture remnant strains and the stress-softening effects. Please note that this specific form of incorporating the (1 − Di) term and multiplying it directly with inside the strain energy function allows capturing remnant strains in the fibers due to shifting of the stress-free reference configuration via the damage functions Di, and permits significant damage hysteresis even for curves that are highly nonlinear in nature. Further, D was taken in the form:
| (15) |
where Ds ∈ [0,1), rs ∈ [0,1), βs > 0 is the value of the internal variable β that describes damage saturation behavior for a fixed stretch limit reached at rs = 0.99 fraction of the maximum damage value Ds. Higher values of βs indicate that the tissue can tolerate more cycles of repetitive loading to the same stretch maximum before it reaches a saturated response. In order to activate damage during loading and unloading, the internal variable β that evolves depending on the loading and damage history, is defined as:
| (16) |
with
| (17) |
defines the damage initiation threshold set equal to the value when the supra-physiologic loading realm is reached, t defines the current loading situation, and İ4 is the first time derivative of the 4th invariant I4 fiber family. The maximum damage value Ds is defined as:
| (18) |
where D∞ ∈ [0,1), r∞ ∈ [0,1), and γ∞ > 0 is the value of the internal variable γ that describes damage evolution behavior at increasing stretches reached at the fraction r∞ = 0.99 of the convergence limit D∞ = 0.99. Please note that similar to β, variable γ also evolves depending on loading and damage history. Higher values of γ∞ indicate that tissue can tolerate more damage with increasing stretch limits. In order to ensure that Ds remains unchanged during cyclic loading under a fixed stretch maximum, the internal variable γ is taken in the form:
| (19) |
which can be interpreted as the maximum value over time of the effective fictitiously undamaged function in the current state, and I4,ini is the value of the fourth invariant at which damage is first initiated. This expression gives way to a damage progression criterion:
| (20) |
An algorithm used to calculate stresses and strain energy is summarized in Table A1 of the Appendix.
2.4. Constitutive parameter determination
The damage saturation and evolution parameters βs and γ∞ were determined from the experimental data, along with the 4 material parameters for the two-fiber-family (Cgr, , , φ), and 8 material parameters for the four-fiber-family (Cgr, , , , , , , φ) models that describe elastic behavior in the physiologic domain. While theoretically possible to first determine the elastic parameters by using the 19 multi-ratio tests, and then determine the inelastic parameters from the experimental damage protocol while keeping the elastic parameters fixed, in practice such fits were inferior to those obtained when all constitutive parameters were determined at the same time. Therefore, the set of 4 and 8 elastic parameters determined from multi-ratio tests was used to prescribe initial values (Cgr, , , , , , , φ), but both the elastic and the damage parameters were allowed to change when fitting the damage protocols. The initial values for damage parameters were assigned βs = 10 and γ∞ = 10 kPa for older specimens (>50 years old), while βs = 30 and γ∞ = 30 kPa were assigned for younger (≤50 years old) specimens, and both were bound at [0.001, ∞). Elastic parameters were bound at [0,∞) with collagen fiber angle φ bound at [0,π/2).
Fitting was done using a least squares approach with the MATLAB’s (MathWorks, Natick, Massachusetts, USA) lsqnonlin function. An error function was used to minimize the sum of the differences between the experimental Cauchy stresses and and the theoretical Cauchy stresses and multiplied by the weighting factors Vz and Vθ and in both the longitudinal and circumferential directions:
| (21) |
Here n is the total number of experimental data points, are the initial values for the elastic and damage parameters, and λz and λθ are the stretches in the longitudinal and circumferential directions, respectively. The weighting functions λz,θ were used to compensate for the variation in stress magnitude between the low and high stretch cycles that resulted in high-stretch protocols dominating the fit because they generated highest stresses. These weighting functions were constructed by assigning a scale of 1 for the lowest stretch limits in each direction, and then gradually reducing this value for each subsequent stretch limit depending on the observed maximum stress.
Quality of constitutive model fits to the experimental data was evaluated by calculating a traditional coefficient of determination R2:
| (22) |
where SST is the total sum of squares, SSR is the regression sum of squares, and represents the average of the entire set of experimental data. Values of R2 were computed for both directions of stretch and then averaged, and values closer to 1 generally represented better fits. In addition to calculating the R2, fit quality was also assessed using the normalized average error, which was also calculated in each direction of stretch and averaged:
| (23) |
Here n is the total number of experimental data points, and values of ERR closer to 0 represent better fits.
2.5. Constitutive parameters for age groups
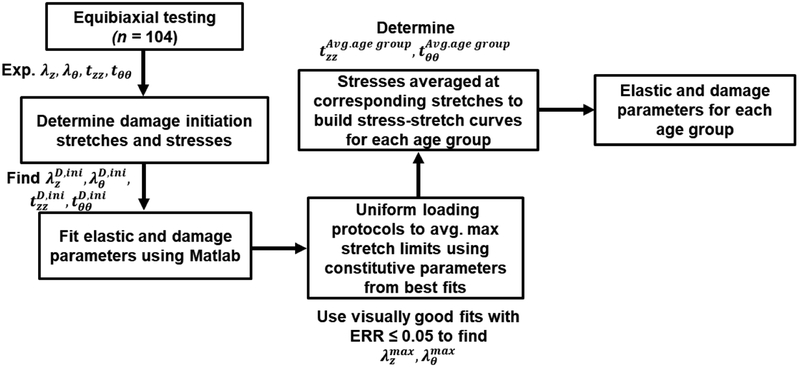
Due to the interrelated nature of constitutive parameters, they cannot be simply averaged to obtain average stress-stretch response. Aggregated fit that uses experimental curves from all specimens to derive the average constitutive parameters is also challenging in the inelastic domain because of the individual damage history and testing conditions of each specimen. Instead, these constitutive parameters can be obtained by first deriving the stress-stretch curves that are representative of a given group, and then obtaining constitutive parameters for these curves[2]. This procedure however is also not trivial and needs to account for the individual stretch limits and the loading history of each specimen.
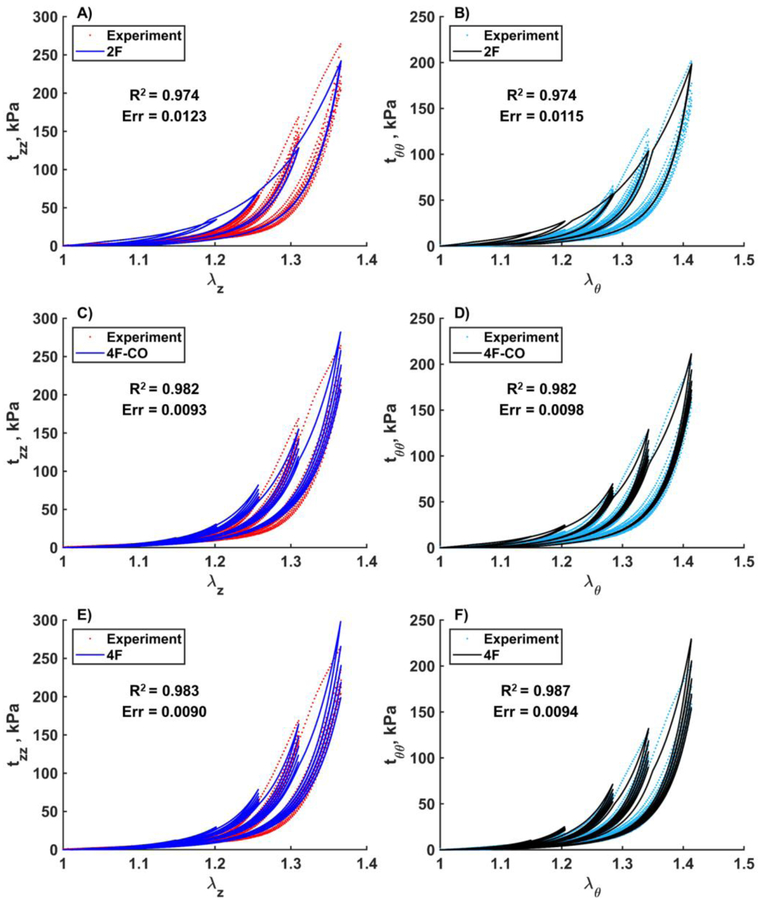
The process of deriving average damage characteristics for each age group is illustrated in Fig. 2. First, the experimental data for each specimen were used to determine damage initiation stresses and stretches, and the three constitutive models were fit to determine material parameters. These models included the two-fiber-family formulation allowing damage in the collagen fibers[18] (2F), the four-fiber-family model also allowing damage accumulation only in the collagen fibers (4F-CO), and the four-fiber-family model allowing damage accumulation across all four phenomenological fiber families (4F). These fits were then compared, and if all three produced an ERR > 0.05 or demonstrated visually poor portrayal of the experimental data, the specimen was excluded from further analysis. If however visually good fits were obtained with one or more of the three models, the model with the least number of parameters and the lowest ERR was selected.
Fig. 2.
Schematic demonstration of the process for obtaining age group-specific elastic and damage constitutive parameters.
Constitutive parameters for these selected specimens were then used to generate stress-stretch responses for each individual age group by first generating stretch-controlled tests, and then averaging interspecimen stresses for each stretch level. Importantly, this ensured that all specimens were loaded with exactly the same stretches which permitted averaging of the stresses. The resulting averaged stress-stretch curves were then used to fit the three constitutive models, producing parameters representative of the ≤30, 31–40, 41–50, 51–60, 61–70, and 71–80 age groups. Stress-stretch curves and the corresponding constitutive parameters representing specimens in 25th and 75th percentiles in each age group were found similarly[32].
2.6. Statistical analysis
Group comparisons were made using two-tailed independent sample t-tests with a significance set at p<0.05. For continuous variables, such as age and body mass index (BMI), correlations were assessed by calculating the Pearson’s correlation coefficient r, with values closer to ±1 indicating stronger relation. Statistical significance of correlation was assessed by testing the hypothesis of no correlation against the alternative that there is a nonzero correlation assuming statistical significance at p<0.05.
Since age was a likely confounding variable, a hierarchical multiple linear regression analysis was performed to account for its influence. Age was entered into the model as a first block, while gender and risk factors (BMI, HTN, DM, dyslipidemia, CAD, and tobacco use) were entered as a second block. The analysis was performed in SPSS v22 (IBM, Armonk, New York), and both unstandardized and standardized beta coefficients were determined for each model along with R2 to assess model quality.
3. RESULTS
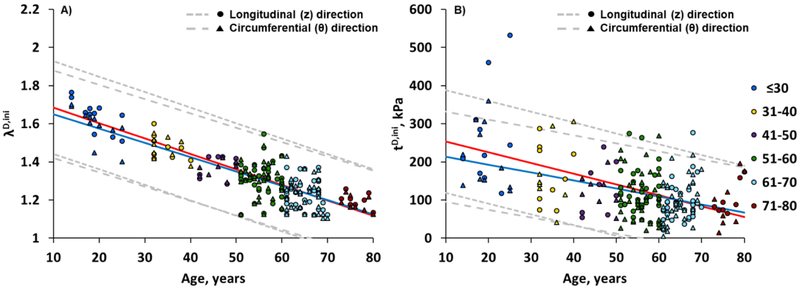
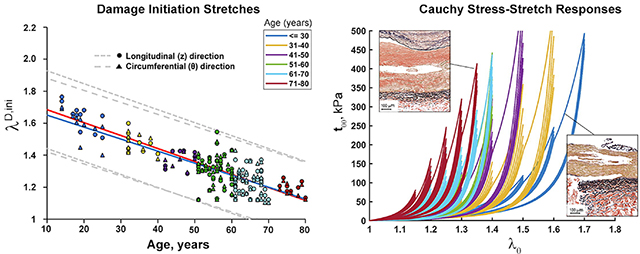
Age had a strong effect on damage initiation stretches in both longitudinal and circumferential directions, with older FPAs (>50 years old) beginning to accumulate damage at lower stretches (p<0.01) (Fig. 3A). On average, in specimens ≤50 years old damage occurred after 1.51±0.13 stretch longitudinally, and 1.49±0.11 stretch circumferentially. In FPAs >50 years old, damage accumulated after 1.27±0.09 longitudinal and 1.26±0.09 circumferential stretch. In subjects younger than 50 years, longitudinal damage initiation stretches were somewhat higher than circumferential, but the difference decreased with age.
Fig. 3.
Change in longitudinal (z, red line) and circumferential (θ, blue line) damage initiation stretches (A) and Cauchy stresses (B) with age. The dashed gray lines represent the 5th and 95th percentiles for each direction. Damage initiation stretches can be described by linear functions −0.0081*age+1.7656 (R2 =0.73, longitudinal) and −0.0075*age+1.7253 (R2 =0.71, circumferential). Damage initiation stresses can be described by linear functions −2.82*age+282 (R2 =0.29, longitudinal) and −2.09*age+235 (R2 =0.21, circumferential).
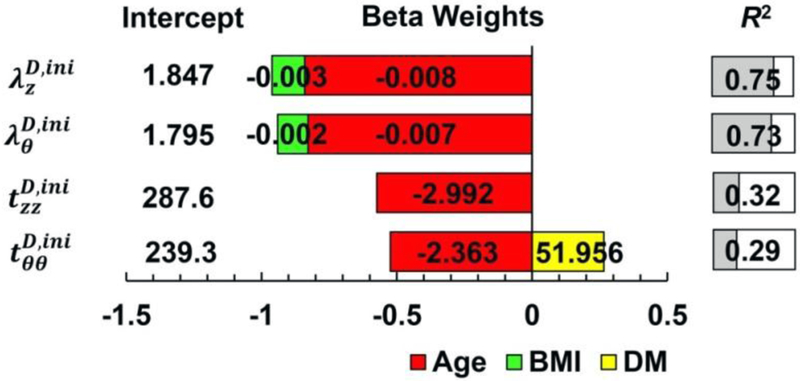
In addition to age, BMI demonstrated statistically significant effect on damage initiation stretches, with damage occurring at lower stretches in subjects with higher BMI as demonstrated by hierarchical multiple regression (Fig. 4). Though the effect of BMI was not as strong as the effect of age, together they were able to explain 75% and 73% of variation in longitudinal and circumferential damage initiation stretches, respectively.
Fig. 4.
Damage initiation stretches (λ) and Cauchy stresses (t) described by the hierarchical multiple linear regression that included age and risk factors. Unstandardized beta weights are provided within each bar, while the length of the bar corresponds to the standardized beta weights, representing the influence of each parameter on the damage characteristics. The R2 value demonstrates the quality of the model, i.e. how much variability in the damage characteristics is described by demographics and risk factors. For example, damage initiation stretch in the longitudinal direction can be found as = 1.847 – 0.003∙BMI – 0.008∙Age (years), and the model explains 75% of variation in the damage initiation stretch . BMI = Body Mass Index and DM = Diabetes Mellitus.
Change in longitudinal and circumferential damage initiating Cauchy stresses with age is demonstrated in Fig. 3B. As with stretches, stresses reduced with age indicating lower stress threshold for damage in older FPAs (p<0.01). FPAs ≤50 years old began accumulating damage at 196±110 kPa longitudinal and 239±79 kPa circumferential stress, while FPAs >50 years old were damaged at 106±52 kPa longitudinal and 104±59 kPa circumferential stress. For subjects younger than 60 years, longitudinal stresses were somewhat higher than circumferential, but the difference decreased and even reversed after the age of 65 years.
Apart from age, DM demonstrated statistically significant effect on circumferential damage initiation stresses, with diabetic FPAs requiring higher stress to induce damage (Fig. 4). Similarly to stretches, the effect of DM was not as strong as that of age, but together they were able to explain 29% of variation in circumferential damage initiation Cauchy stress.
FPAs with worse disease started accumulating damage at lower stretches and stresses (r=−0.70 and r=−0.29, p<0.01, respectively); however after controlling for age, only correlation with the damage initiation stretch remained statistically significant (r=−0.50, p<0.01).
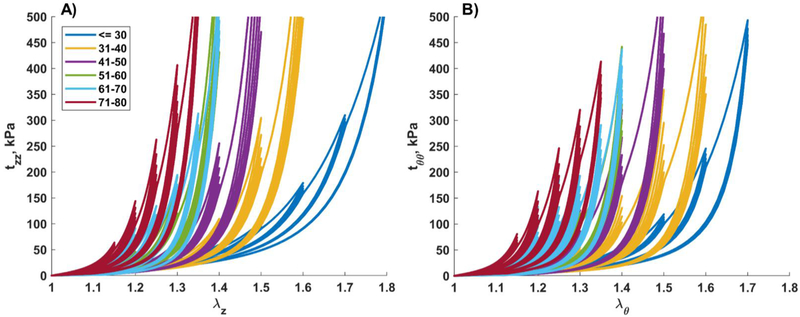
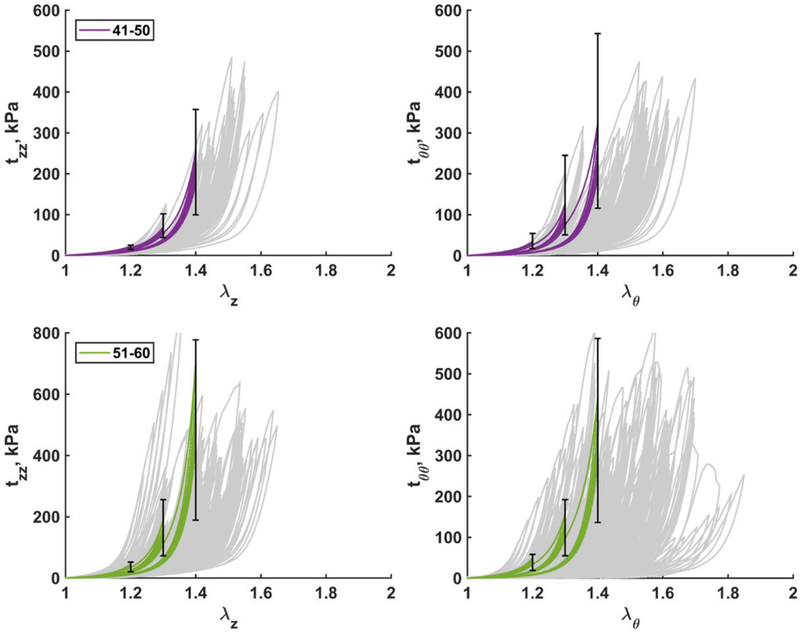
Mean stress-stretch curves representative of six age groups in both longitudinal (A) and circumferential (B) directions are demonstrated in Fig. 5, while error bars representing 25th and 75th percentiles are provided in Fig. 6 – Fig. 8 along with the appropriate constitutive parameters (see Appendix Table A2 and Table A3). The mean curves illustrate typical stress softening with increasing stretch, and the overall increase in stiffness in both directions with age. In the circumferential direction specimens generally demonstrated wider hysteresis and longer toe region with increasing stretch limits. Drop in stress for the fixed level of stretch on repeat loading was more pronounced in older FPAs. Stress-stretch curves were statistically different (p<0.01) among all age groups and both directions, with the exception of 51–60 and 61–70 year-old FPAs that had practically overlapping circumferential stress-stretch curves.
Fig. 5.
Mean age group-specific Cauchy stress-stretch responses in the A) longitudinal and B) circumferential directions. The legend shows age groups. Stress-stretch curves are statistically different (p<0.01) among all age groups and both directions, with the exception of 51–60 and 61–70 year-old FPAs in the circumferential direction.
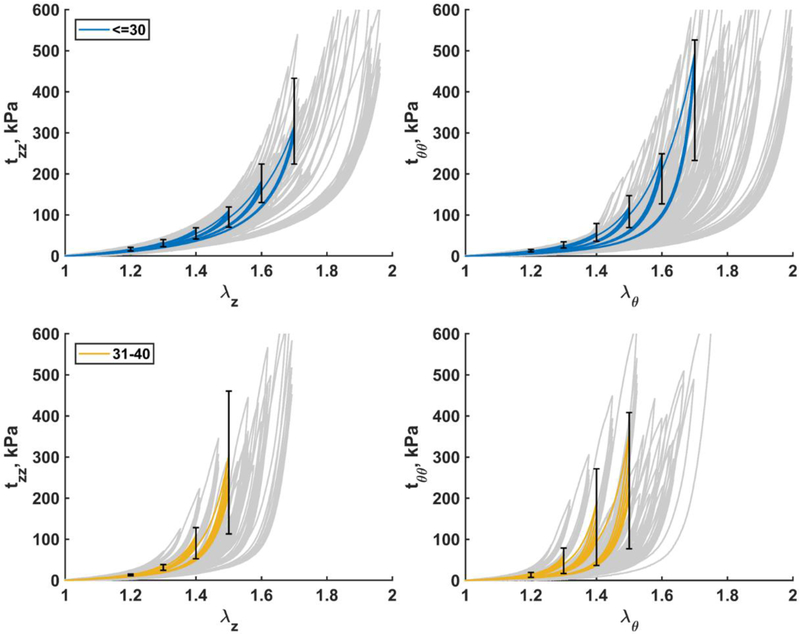
Fig. 6.
Mean Cauchy stress-stretch responses in the longitudinal (left) and circumferential (right) directions for the two youngest age groups (≤30 and 31–40 years old). Error bars correspond to the 25th and 75th percentiles when using the same stretch protocol. Grey curves in the background are experimental data.
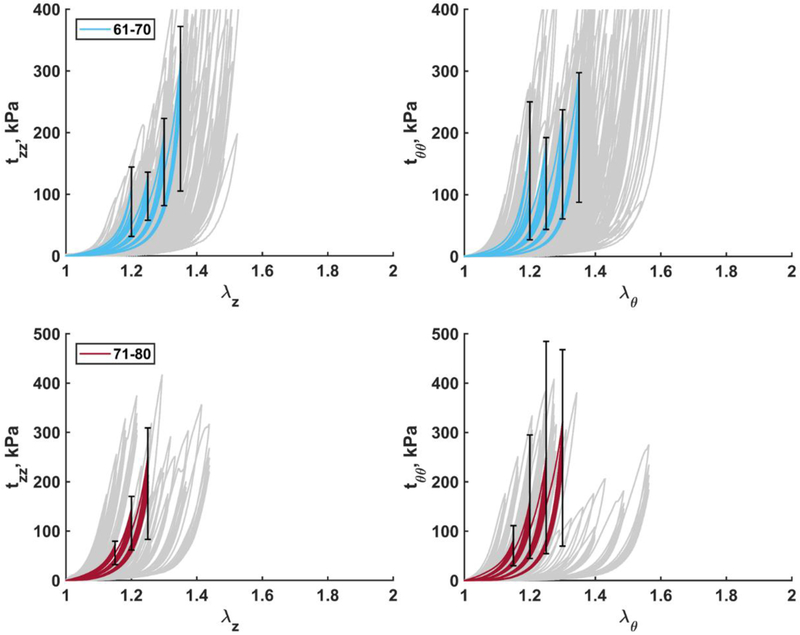
Fig. 8.
Mean Cauchy stress-stretch responses in the longitudinal (left) and circumferential (right) directions for the two eldest age groups (61–70 and 71–80 years old). Error bars correspond to the 25th and 75th percentiles. Grey curves in the background are experimental data.
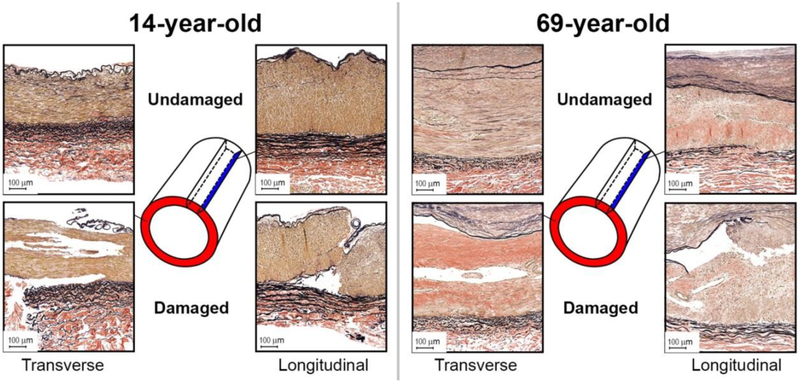
Representative transverse and longitudinal histological sections of young and old FPAs before and after accumulation of damage are presented in Fig. 9. Damage appeared as tears primarily along the internal (IEL) and external (EEL) elastic laminae from the side of the tunica media, and within the medial layer. In older FPAs that often contained intimal thickening, medial calcification, lipid deposits, and groups of inflammatory cells, damage was more diffuse, and often resulted in partial delamination of the intimal layer, often with the IEL detached from the tunica media but still attached to the thickened intima.
Fig. 9.
Verhoeff-Van Gieson (VVG)-stained transverse and longitudinal sections of the representative young (14-year-old, left), and old (69-year-old, right) FPAs before (top) and after (bottom) accumulation of damage. Note tears along the internal and external elastic laminae from the tunica media side, and tears within the medial layer. Also note significantly more degraded and fragmented longitudinal elastic fibers in the external elastic lamina of the old FPA compared with young.
Constitutive elastic and damage parameters for each of the six age groups are summarized in Table 2. Parameters are presented for three constitutive models: the two-fiber family model with damage in the collagen fibers (2F), the four-fiber-family model allowing damage accumulation only in the collagen fibers (4F-CO), and the four-fiber-family model allowing damage accumulation across all four fiber families (4F). Model fits for the 2F and 4F-CO typically produced high conventional R2 values, especially for older, stiffer tissues, but the fits were often noticeably worse than for the 4F, generally favoring the high stretch domain and saturating to a single stress-stretch response with small hysteresis (Fig. 10). Even ERR ≤ 0.05 was not a guarantee of a visually good fit, although as illustrated in Fig. 10, 2F and 4F-CO models with saturated stress-stretch responses did demonstrate notably higher ERR values. Of the n=104 FPAs, 94 specimens (90%) produced an ERR ≤ 0.05 and visually good fits when using the 4F. Only 85 specimens (82%) had the same quality fits when using the 4F-CO, and 81 specimens (78%) when using the 2F.
Table 2.
Elastic and damage constitutive parameters representing mean FPA specimens in each of the six age groups. Data are provided for three constitutive models: the two-fiber-family model with damage in the collagen fibers (2F), the four-fiber-family model also with damage only in the collagen fiber families (4F-CO), and the four-fiber-family model with damage accumulation across all four phenomenological fiber families (4F).
| Age group, years | ≤30 | 31–40 | 41–50 | 51–60 | 61–70 | 71–80 | |
|---|---|---|---|---|---|---|---|
| Samples per group | 11 | 9 | 8 | 36 | 32 | 8 | |
| Fits with ERR ≤ 0.05 | 2F | 5 | 8 | 7 | 28 | 26 | 7 |
| 4F-CO | 9 | 9 | 7 | 26 | 27 | 7 | |
| 4F | 10 | 8 | 7 | 31 | 30 | 8 | |
| Fits with R2 ≥ 0.9 | 2F | 11 | 9 | 8 | 33 | 30 | 8 |
| 4F-CO | 11 | 9 | 8 | 35 | 30 | 8 | |
| 4F | 11 | 8 | 8 | 31 | 31 | 8 | |
| Mean age, years | 18.8 | 35.0 | 46.0 | 55.4 | 65.0 | 76.3 | |
| Elastic Parameters | |||||||
| cgr (kPa) | 2F | 15.36 | 9.64 | 7.14 | 9.06 | 3.77 | 0.77 |
| 4F-CO | 9.85 | 9.79 | 6.02 | 6.17 | 1.25 | 16.53 | |
| 4F | 5.25 | 9.13 | 7.78 | 7.05 | 3.68 | 10.99 | |
| (kPa) | 4F-CO | 6.36 | 3.08 | 1.50 | 0.53 | 6.54 | 3.72 |
| 4F | 3.21 | 4.93 | 4.62 | 13.72 | 24.81 | 29.71 | |
| 4F-CO | 0.38 | 1.33 | 2.57 | 5.15 | 3.42 | 5.64 | |
| 4F | 2.40 | 2.30 | 4.82 | 5.19 | 9.29 | 11.43 | |
| (kPa) | 4F-CO | 0.67 | 0.21 | 1.76 | 0.62 | 3.15 | 5.93 |
| 4F | 4.86 | 9.01 | 6.33 | 14.39 | 27.96 | 41.72 | |
| 4F-CO | 1.11 | 1.53 | 1.13 | 2.15 | 0.12 | 3.97 | |
| 4F | 4.73 | 10.42 | 5.13 | 6.76 | 10.90 | 13.37 | |
| (kPa) | 2F | 2.50 | 3.59 | 4.84 | 7.07 | 12.91 | 28.72 |
| 4F-CO | 5.62 | 4.90 | 9.52 | 16.58 | 21.59 | 33.51 | |
| 4F | 11.93 | 3.93 | 5.33 | 3.52 | 1.66 | 10.74 | |
| 2F | 2.70 | 3.39 | 4.56 | 7.01 | 11.47 | 10.20 | |
| 4F-CO | 2.49 | 4.78 | 6.28 | 6.78 | 12.47 | 13.03 | |
| 4F | 0.21 | 4.41 | 4.28 | 7.33 | 9.19 | 10.83 | |
| φ (°) | 2F | 48.38 | 41.58 | 41.75 | 39.07 | 45.48 | 42.89 |
| 4F-CO | 51.60 | 50.30 | 46.49 | 41.44 | 50.60 | 42.12 | |
| 4F | 35.40 | 49.53 | 49.05 | 33.44 | 43.74 | 34.20 | |
| Damage Parameters | |||||||
| γ∞ (kPa) | 2F | 25.85 | 25.32 | 24.38 | 21.66 | 15.08 | 15.31 |
| 4F-CO | 22.21 | 18.61 | 18.06 | 19.41 | 14.11 | 14.06 | |
| (kPa) | 4F | 99.61 | 19.84 | 23.63 | 22.09 | 21.35 | 8.77 |
| (kPa) | 25.43 | 40.92 | 24.13 | 23.09 | 15.85 | 16.97 | |
| (kPa) | 19.35 | 11.40 | 20.10 | 18.76 | 13.09 | 13.25 | |
| βs | 2F | 35.15 | 39.26 | 32.75 | 19.15 | 14.30 | 17.91 |
| 4F-C0 | 46.51 | 43.61 | 28.30 | 21.12 | 14.96 | 18.23 | |
| 4F | 4.27 | 48.06 | 34.53 | 27.23 | 43.41 | 48.45 | |
| 39.25 | 0.88 | 42.53 | 22.64 | 14.98 | 16.45 | ||
| 14.89 | 1.69 | 25.61 | 15.75 | 18.04 | 15.41 | ||
Fig. 10.
Representative experimental results and model fits for a 59-year-old male FPA in the longitudinal (A,C,E) and circumferential (B,D,F) directions. Data are presented for the three constitutive models: the two-fiber-family model (A,B), the four-fiber-family model allowing damage only in the two collagen fiber families (C,D), and the four-fiber-family model allowing damage accumulation in all four phenomenological fiber families (E,F). Note the saturated response for the two-fiber-family model despite high R2 and low ERR.
While constitutive models used in this study are phenomenological, material parameters summarized in Table 2 appear to reflect typical intramural changes occurring with age. Specifically, for the 2F model age was associated with a decrease in isotropic Cgr and the two damage parameters γ∞ and βs (p<0.01, p=0.01, and p=0.03), and an increase in and (p=0.03, p=0.01) which may be associated with stiffening due to the accumulation of intramural collagen. Fiber angle φ did not change with age (p=0.46) and fluctuated around 43±3°. Parameters of the 4F model changed with age more sporadically, suggesting a local rather than a global minimum of the least-square functional, although , , , also increased with age (p<0.02), while fiber angle φ remained relatively constant at 41±8°.
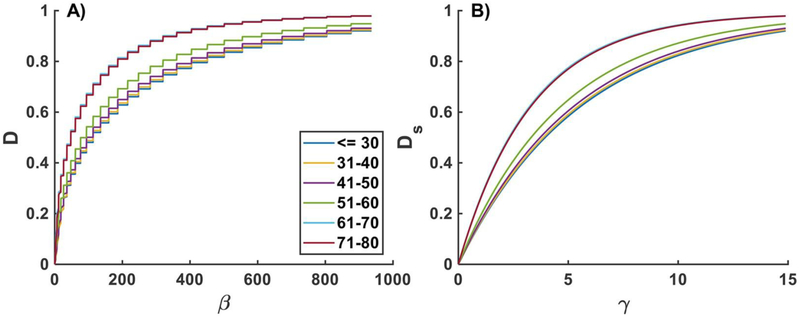
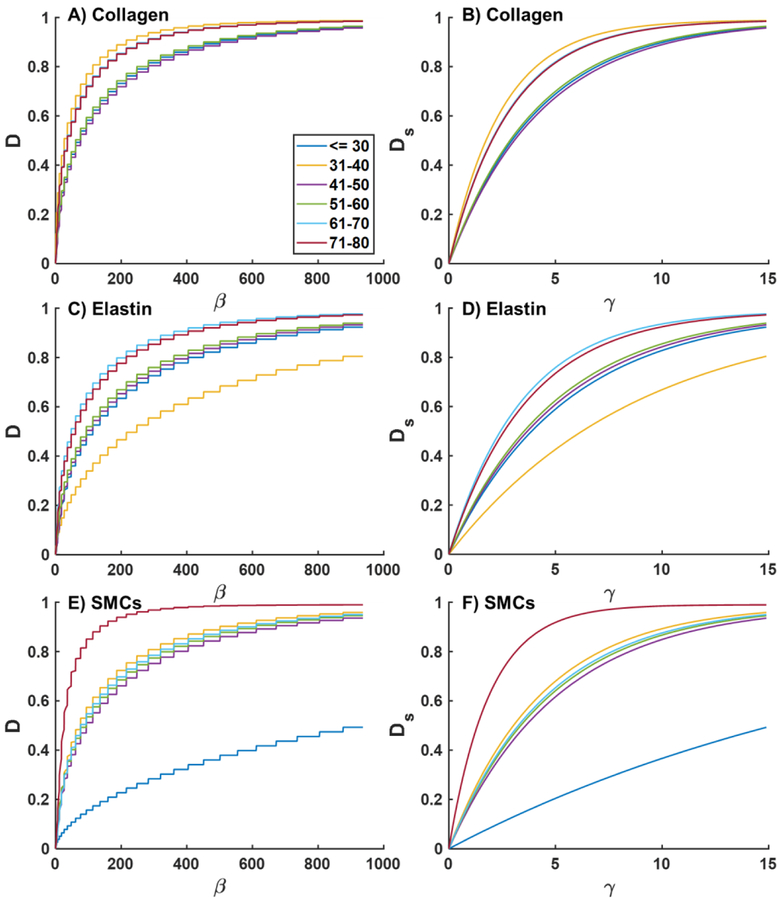
Damage functions D(β) and Ds(γ) for each of the phenomenological fiber families under equibiaxial loading for FPAs in different age groups are plotted in Figs. A1 (2F) and A2 (4F). Graphs for the 4F-CO were very similar to 2F and are not included. Younger FPAs demonstrate higher resilience to damage, while older FPAs damage at lower β and γ, with significant changes occurring after the age of 50 years (Fig A1). Damage in the phenomenological collagen fibers appears to be more pronounced than damage in longitudinally-oriented elastic fibers, and circumferential SMCs appear to be resistant to damage in the youngest age group, but appear to be easily damaged in 71–80 year-old FPAs (Fig A2).
4. DISCUSSION
Computational modeling can help improve clinical outcomes of endovascular PAD treatments by optimizing device-artery interactions, but it requires accurate inputs on FPA mechanical properties. Recent studies reported elastic mechanical characteristics of human FPAs in multiple age groups and across some risk factors[2,32,35,38], but damage properties essential for the simulations of balloon angioplasty remained largely unknown. The current study performed mechanical characterization of damage in human FPAs, and found significant dependence of its characteristics on age, BMI, and presence of DM. Specifically, both damage initiation stretches and stresses reduced with age, arteries from subjects with higher BMI started accumulating damage at lower stretches in both longitudinal and circumferential directions, and diabetic FPAs required higher circumferential stresses to start accumulating damage.
Age is one of the dominant factors that affect arterial intramural structure and mechanical properties. Structural changes occurring with age include degradation and fragmentation of elastin, its replacement by collagen and proteoglycans, altered turnover and crosslinking of collagen, and increased production of advanced glycation end products (AGEs), all of which contribute to the increased arterial stiffness[39–43]. Stiffening of the FPA wall with age is accompanied by a reduction of physiologic longitudinal and circumferential stresses and stretches, and a decrease in elastic strain energy[2], corroborating results of lower damage initiation stresses and stretches in older FPAs observed here. Furthermore, degradation and fragmentation of longitudinally-oriented elastic fibers in the EEL appeared to contribute to faster reduction of physiologic longitudinal stress and stretch with age compared with the circumferential direction[2], and that same result was also reported here for the damage-initiating stresses and stretches.
The mechanism of FPA damage accumulation was primarily delamination of the arterial wall at the IEL and EEL interfaces from the side of the tunica media, and tears within the medial layer. IEL and EEL are composed of elastic sheets and longitudinally-oriented elastic fibers that bound SMC-rich media. SMCs are attached to the elastic laminae with thin radially-oriented elastin protrusions and oxytalan fibers containing fibrillin, fibronectin, and type VI collagen that facilitate mechanotransduction[44,45]. Degradation and fragmentation of these fibers and their cross-linking with age may contribute to weaker interfacial links at the cell-elastic laminae interfaces and therefore may facilitate easier delamination of older FPAs. In addition, accumulation of proteoglycans and glycosaminoglycans with age can contribute to the increase of swelling pressure which may also contribute to delamination[45]. Finally, circumferential alignment of SMCs[2,33,46] may reinforce the circumferential direction in young healthy arteries, but medial degeneration and SMC loss with age may weaken the arterial wall[47], and result in lower damage initiation stresses in older FPAs.
Despite the overall reduction in damage threshold with age, presence of DM and higher BMI contributed to higher damage initiation stresses and lower stretches. Since DM and BMI were correlated (r=0.27, p<0.01), both factors may represent the same phenomena, and therefore should be considered together. A recent study investigating prevalence of calcification in FPAs and its association with risk factors[46], demonstrated a significant correlation between presence of DM and medial calcification. Furthermore, calcification was primarily circumferentially-oriented, aligning with the direction of the SMCs, and contributing to the significant circumferential stiffness of diabetic FPAs[32]. It was hypothesized that SMC-rich tunica media can contain a subpopulation of SMCs that in the setting of elevated glucose levels, diminished inhibitors, or increased stimulators of calcification, are capable of losing their ability to express SMC-specific markers and express more osteogenic or chondrogenic markers[48,49], effectively transforming parts of the media layer to rings of bone tissue. These rings of calcification in diabetic FPAs may require higher circumferential stress to induce damage, which is anecdotally supported by the empirical clinical evidence demonstrating the need for higher angioplasty balloon pressures to break heavily calcified PAD plaques.
From the quantitative standpoint, comparison of current results with prior work is somewhat complicated because experimental studies of human arteries under supra-physiologic loading conditions are rare and seldom report age and damage initiation thresholds. Nevertheless, some do provide experimental graphs that can be used to determine these characteristics. Thus, in their investigation of a human carotid artery tunica media, Balzani et al[28] included an experimental graph that suggests damage initiation at circumferential and longitudinal stretches of >1.11 and >1.34, respectively, observed at ~150 kPa Cauchy stress. Maher et al[29] conducted damage experiments on human carotid artery and aortic specimens. Their data suggest that damage started accumulating at >1.4 stretch (~50 kPa Cauchy stress) in the aortas, and at >1.3 stretch (~100 kPa Cauchy stress) in the carotid arteries. Gultova et al[50] investigated stress softening of human thoracic aortas using uniaxial testing. In their study damage started accumulating at >1.2 stretch (~100 kPa Cauchy stress). In tests performed by Weisbecker et al[20], a 45 year-old thoracic aortic media appeared to start accumulating damage at >1.2 circumferential and >1.28 longitudinal stretches, but both occurred around 70–100 kPa Cauchy stress. Similar results, and also for the thoracic aorta, were reported by Horny et al[16] who observed stress softening after 1.2 circumferential and 1.1 longitudinal stretch, both occurring at 100–120 kPa. In a 47-year-old abdominal aortic media test reported by Schriefl et al[18], damage in circumferential and longitudinal directions appeared to have initiated at 1.3 and 1.4 stretch, respectively, yet both were again observed at around a 100 kPa Cauchy stress.
To put these numbers in perspective, our results for >50-year-old FPAs demonstrated damage accumulation at 1.26±0.09 circumferential and 1.27±0.09 longitudinal stretches, but more interestingly, damage initiation Cauchy stresses in both directions also appeared to be at the 100–110 kPa threshold. This is surprising given previously reported differences in damage characteristics of elastic and muscular arteries in swine[51]. Another interesting similarity with previous studies is the behavior of elastase-treated aortic samples investigated by Weisbecker et al[20] and Schriefl et al[18]. Graphs presented by these authors suggest that chemical elastic fiber removal produced a significant reduction in circumferential damage initiating stretch, which aligns well with present findings describing similar trends in older FPAs with degraded and fragmented elastin due to aging. This also agrees with the findings of Maher et al[51] who reported lower damage thresholds, i.e. easier damage accumulation, in arteries with higher collagen to elastin ratio.
While multiple deterministic and probabilistic constitutive models have been proposed to describe damage accumulation in soft tissues[52], the invariant-based 4-fiber-family formulation that has previously been shown to adequately portray the elastic behavior of human FPAs in various age and risk factor groups[2,32–35], was also able to adequately capture multiaxial damage effects in most FPAs when augmented with the appropriate damage model[28]. Despite being phenomenological, the 4-fiber-family formulation is based on intramural structure of the FPA with longitudinal elastic fibers, circumferential SMCs, and two families of collagen fibers oriented at an angle to the longitudinal axis. In an attempt to minimize the number of constitutive parameters that describe damage, we have also considered two additional constitutive formulations: the two-fiber-family model with damage in the collagen fibers, the four-fiber-family model also with damage only in the collagen fibers. Inclusion of damage in the isotropic matrix did not appear to influence the results, which corroborated experimental findings of Schriefl et al[18], albeit latter study was performed on the aortic tissue in which isotropic matrix includes sheets of elastic lamellae that spread in both longitudinal and circumferential directions[53] – a structure that is different from that of the FPA. The simpler two-fiber-family formulation was able to adequately capture the mechanical response of mainly older FPAs that were less anisotropic[2,32], while the four-fiber-family formulations performed better in younger specimens. In some cases the four-fiber-family model with damage accumulation limited to collagen fibers was sufficient to capture multiaxial FPA behavior, but many samples demonstrated a “saturated” response and required a more complex model. For completeness, all three sets of material parameters are included in the manuscript, although it is important to remember that large number of parameters raises concerns regarding their uniqueness, particularly given the limited number of experimental protocols that can be performed on the tissue under damage conditions. In fact, the uniqueness of parameters even for the two-fiber-family model is not guaranteed, because 6 parameters are still determined from a single damage assessment protocol. We would also like to caution against physical interpretation of damage based on constitutive model parameters, as both non-uniqueness and phenomenological and interrelated nature of these parameters prevent one from making meaningful conclusions.
Finally, arterial wall contains three distinct layers that likely accumulate damage differently, yet this was not investigated in the current study. Layer separation and their individual testing are challenging (if at all possible) in young healthy FPAs, and separation by itself dramatically changes the state of the arterial wall and represents one of the damage accumulation mechanisms. Particularly in the setting of vascular disease, arterial tissues become highly inhomogeneous, even within the borders of one layer, which requires complex multiaxial assessments of individual tissue components. Such experiments are non-trivial, but future studies can perhaps use a combination of mechanical assessment and computational modeling to discern these different properties. While better tissue characterization approaches are being explored, we hope that presented damage characteristics of human FPAs in six age groups can be instrumental in improving fidelity of computational models investigating balloon angioplasty, bypass graft and stent-artery interactions, or in other studies of surgical and endovascular manipulations that apply supra-physiologic loads to arterial tissues[15].
Fig. 7.
Mean Cauchy stress-stretch responses in the longitudinal (left) and circumferential (right) directions for the two middle age groups (41–50 and 51–60 years old). Error bars correspond to the 25th and 75th percentiles. Grey curves in the background are experimental data.
ACKNOWLEDGEMENTS
Research reported in this publication was supported in part by the National Heart, Lung, And Blood Institute of the National Institutes of Health under Award Number R01 HL125736. The authors also wish to acknowledge Live On Nebraska for their help and support, and thank tissue donors and their families for making this study possible. The author Daniel Balzani appreciates financial support from the German Science Foundation (Deutsche Forschungsgemeinschaft DFG), project no BA2823/5–3.
APPENDIX
Table A1.
Algorithm for the computation of stress and strain energy. Here n is the iteration number, and N is the number of fiber families. Initially, n = 0 and .
| (I) Do for i = 1..N |
| (i) Compute , I1 using eqs. 9–11 |
| (ii) Check initial damage state |
| if λ < λD,ini, then go to (vi) |
| else |
| (a) Read history , , , |
| (b) Compute |
| (c) if first time in damage protocol, then |
| set , |
| else set from history , |
| (iii) Read history nγt and compute maximal damage saturation value |
| (a) Trial criterion |
| (b) Check algorithmic saturation criterion |
| if , then set |
| else set from history γi = nγi |
| (c) Compute damage saturation value |
| (iv) Compute internal variable |
| (v) Compute damage function |
| (vi) Compute transversely isotropic stress tensor |
| (a) Compute effective stress tensor |
| if λ > λD,ini, then |
| else where |
| (b) Compute the anisotropic Cauchy stress tensor |
| (vii) Compute the anisotropic strain energy |
| (II) Calculate isotropic Cauchy stress tensor |
| (III) Compute isotropic strain energy |
| (IV) Compute total strain energy |
| (V) Compute total Cauchy stress |
Table A2.
Constitutive elastic and damage parameters that correspond to the stress-stretch responses at the 25th percentile range in six age groups. Data are provided for the three constitutive models: the two-fiber-family model allowing damage in the collagen fibers (2F), the four-fiber-family model also allowing damage accumulation only in the collagen fibers (4F-CO), and the four-fiber-family model allowing damage accumulation across all four phenomenological fiber families (4F).
| Age group, years | ≤30 | 31–40 | 41–50 | 51–60 | 61–70 | 71–80 | |
|---|---|---|---|---|---|---|---|
| Samples per group | 11 | 9 | 8 | 36 | 32 | 8 | |
| Mean age, years | 18.8 | 35.0 | 46.0 | 55.4 | 65.0 | 76.3 | |
| Elastic Parameters | |||||||
| Cgr (kPa) | 2F | 7.50 | 6.48 | 6.57 | 2.07 | 0.17 | 0.85 |
| 4F-C0 | 9.14 | 4.53 | 4.35 | 0.61 | 0.05 | 0.61 | |
| 4F | 7.15 | 5.26 | 1.32 | 2.79 | 1.33 | 4.48 | |
| (kPa) | 4F-C0 | 2.36 | 4.35 | 2.43 | 3.67 | 1.59 | 2.92 |
| 4F | 13.32 | 1.86 | 6.36 | 16.69 | 0.04 | 0.94 | |
| 4F-C0 | 0.45 | 0.65 | 2.06 | 0.40 | 3.25 | 4.28 | |
| 4F | 0.60 | 1.85 | 3.88 | 3.27 | 5.26 | 7.12 | |
| (kPa) | 4F-C0 | 0.24 | 0.51 | 0.82 | 2.33 | 2.28 | 1.74E-03 |
| 4F | 5.70 | 2.72 | 9.59 | 14.99 | 2.64 | 3.65 | |
| 4F-C0 | 0.92 | 0.67 | 0.42 | 2.79E-07 | 2.82 | 0.43 | |
| 4F | 1.61 | 1.95 | 5.58 | 4.66 | 4.30 | 4.13 | |
| (kPa) | 2F | 4.12 | 4.54 | 3.49 | 6.69 | 8.57 | 14.21 |
| 4F-C0 | 5.41 | 5.03 | 9.59 | 11.83 | 14.77 | 28.50 | |
| 4F | 0.15 | 6.07 | 7.00 | 3.04 | 13.41 | 20.60 | |
| 2F | 1.43 | 2.24 | 3.26 | 4.33 | 5.78 | 8.62 | |
| 4F-C0 | 1.70 | 1.88 | 5.00 | 4.64 | 6.30 | 9.36 | |
| 4F | 4.09 | 1.50 | 1.67 | 6.55 | 5.59 | 10.59 | |
| φ (°) | 2F | 41.31 | 37.36 | 39.93 | 41.09 | 41.94 | 37.96 |
| 4F-C0 | 44.65 | 43.77 | 50.66 | 41.74 | 40.61 | 40.87 | |
| 4F | 40.03 | 25.36 | 41.45 | 39.84 | 38.93 | 36.12 | |
| Damage Parameters | |||||||
| γ∞ (kPa) | 2F | 29.20 | 27.24 | 31.07 | 19.58 | 17.97 | 14.77 |
| 4F-C0 | 25.37 | 29.86 | 18.86 | 19.11 | 15.13 | 13.31 | |
| (kPa) | 4F | 22.20 | 38.10 | 18.98 | 9.57 | 18.38 | 13.76 |
| (kPa) | 43.92 | 15.77 | 31.19 | 22.50 | 30.81 | 21.16 | |
| (kPa) | 26.45 | 16.93 | 18.01 | 17.34 | 26.95 | 19.41 | |
| βs | 2F | 38.60 | 16.31 | 31.00 | 26.45 | 23.03 | 14.71 |
| 4F-C0 | 50.93 | 53.14 | 16.83 | 25.86 | 26.06 | 14.03 | |
| 4F | 56.58 | 4.44 | 51.75 | 61.05 | 28.72 | 15.59 | |
| 4.49 | 39.95 | 7.61 | 0.81 | 21.36 | 30.93 | ||
| 51.41 | 151.32 | 14.07 | 0.89 | 20.21 | 14.26 | ||
Table A3.
Constitutive elastic and damage parameters that correspond to the stress-stretch responses at the 75th percentile range in six age groups. Data are provided for the three constitutive models: the two-fiber-family model allowing damage in the collagen fibers (2F), the four-fiber-family model also allowing damage accumulation only in the collagen fibers (4F-CO), and the four-fiber-family model allowing damage accumulation across all four phenomenological fiber families (4F).
| Age group, years | ≤30 | 31–40 | 41–50 | 51–60 | 61–70 | 71–80 | |
|---|---|---|---|---|---|---|---|
| Samples per group | 11 | 9 | 8 | 36 | 32 | 8 | |
| Mean age, years | 18.8 | 35.0 | 46.0 | 55.4 | 65.0 | 76.3 | |
| Elastic Parameters | |||||||
| Cgr (kPa) | 2F | 10.28 | 10.93 | 14.90 | 2.61 | 6.22 | 1.31 |
| 4F-CO | 21.28 | 7.62 | 11.79 | 4.07 | 3.52 | 28.62 | |
| 4F | 20.80 | 10.82 | 6.38 | 5.12 | 4.86 | 8.97 | |
| (kPa) | 4F-CO | 2.67 | 1.32 | 1.87 | 3.59 | 7.25 | 2.27 |
| 4F | 4.31 | 5.60 | 3.28 | 24.00 | 35.88 | 3.44 | |
| 4F-CO | 0.84 | 1.46 | 2.84 | 3.54 | 4.12 | 7.62 | |
| 4F | 1.95 | 2.98 | 5.54 | 5.84 | 9.61 | 8.96 | |
| (kPa) | 4F-CO | 0.82 | 1.28 | 1.49 | 2.14 | 3.87 | 9.74 |
| 4F | 3.16 | 3.07 | 4.15 | 19.05 | 8.99 | 13.96 | |
| 4F-CO | 1.14 | 1.19 | 2.45 | 3.87 | 1.12 | 3.03 | |
| 4F | 2.89 | 3.95 | 7.69 | 6.49 | 8.45 | 15.74 | |
| (kPa) | 2F | 7.60 | 2.57 | 4.36 | 11.68 | 15.74 | 24.94 |
| 4F-CO | 5.07 | 3.47 | 5.79 | 18.48 | 25.12 | 25.20 | |
| 4F | 3.59 | 0.74 | 23.04 | 0.64 | 13.40 | 35.81 | |
| 2F | 1.30 | 3.23 | 5.40 | 6.01 | 10.78 | 9.58 | |
| 4F-CO | 2.50 | 3.88 | 6.21 | 6.69 | 13.19 | 10.00 | |
| 4F | 2.15 | 4.46 | 3.84 | 6.89 | 15.77 | 13.69 | |
| φ (°) | 2F | 42.53 | 37.52 | 42.71 | 41.77 | 43.12 | 44.29 |
| 4F-CO | 45.33 | 37.87 | 45.99 | 41.93 | 50.40 | 41.34 | |
| 4F | 23.78 | 33.32 | 51.32 | 69.50 | 83.93 | 45.45 | |
| Damage Parameters | |||||||
| γ∞ (kPa) | 2F | 34.04 | 28.07 | 21.01 | 21.13 | 15.95 | 14.46 |
| 4F-CO | 16.14 | 25.31 | 14.63 | 15.99 | 13.64 | 25.71 | |
| (kPa) | 4F | 26.53 | 23.71 | 15.60 | 20.02 | 11.56 | 16.50 |
| (kPa) | 28.83 | 30.77 | 17.04 | 20.98 | 17.42 | 33.09 | |
| (kPa) | 24.95 | 23.88 | 16.76 | 21.20 | 16.09 | 12.15 | |
| βs | 2F | 28.93 | 64.81 | 44.57 | 23.10 | 11.39 | 44.66 |
| 4F-CO | 86.28 | 57.80 | 62.38 | 29.06 | 12.43 | 23.48 | |
| 4F | 29.70 | 37.45 | 18.85 | 29.19 | 8.36 | 17.72 | |
| 22.87 | 67.13 | 92.54 | 26.75 | 9.62 | 59.26 | ||
| 50.79 | 58.34 | 41.57 | 18.16 | 36.65 | 1.46 | ||
Fig. A1.
Damage functions D(β) (A) and Ds(γ) (B) plotted for the equibiaxial loading protocol for FPAs in different age groups. Results are presented for the two-fiber family model (2F). Please note that the “stair-like” appearance of D(β) comes from the increase in Ds(γ) due to change in γ.
Fig. A2.
Damage functions D(β) (A, C, E) and Ds(γ) (B, D, F) plotted for the equibiaxial loading protocol for FPAs in different age groups. Results are presented for the four-fiber family model (4F). Graphs in panels A and B phenomenologically describe damage in the collagen fibers, C,D represent damage in longitudinally-oriented elastic fibers, and E, F depict damage in circumferentially-oriented smooth muscle cells (SMCs).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
REFERENCES
- [1].Fowkes FGR, Rudan D, Rudan I, Aboyans V, Denenberg JO, McDermott MM, Norman PE, Williams UKASLJ, Mensah GA, Criqui MH, Comparison of global estimates of prevalence and risk factors for peripheral artery disease in 2000 and 2010: a systematic review and analysis., Lancet. 6736 (2013) 1–12. doi: 10.1016/S0140-6736(13)61249-0. [DOI] [PubMed] [Google Scholar]
- [2].Kamenskiy A, Seas A, Deegan P, Poulson W, Anttila E, Sim S, Desyatova A, MacTaggart J, Constitutive description of human femoropopliteal artery aging, Biomech. Model. Mechanobiol 16 (2017) 681–692. doi: 10.1007/s10237-016-0845-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Ouriel K, Peripheral arterial disease, Lancet. 358 (2001) 1257–1264. [DOI] [PubMed] [Google Scholar]
- [4].Maleckis K, Anttila E, Aylward P, Poulson W, Desyatova A, MacTaggart J, Kamenskiy A, Nitinol Stents in the Femoropopliteal Artery: A Mechanical Perspective on Material, Design, and Performance., Ann. Biomed. Eng (2018). doi: 10.1007/s10439-018-1990-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Stavroulakis K, Torsello G, Manal A, Schwindt A, Hericks C, Stachmann A, Schönefeld E, Bisdas T, Results of primary stent therapy for femoropopliteal peripheral arterial disease at 7 years, J. Vasc. Surg 64 (2016) 1696–1702. doi: 10.1016/j.jvs.2016.05.073. [DOI] [PubMed] [Google Scholar]
- [6].Laird JR, Yeo KK, The Treatment of Femoropopliteal In-Stent Restenosis Back to the Future*, (2012). doi: 10.1016/j.jacc.2011.09.037. [DOI] [PubMed] [Google Scholar]
- [7].Qato K, Conway AM, Mondry L, Giangola G, Carroccio A, Management of isolated femoropopliteal in-stent restenosis, J. Vasc. Surg 68 (2018) 807–810. doi: 10.1016/j.jvs.2018.01.030. [DOI] [PubMed] [Google Scholar]
- [8].Schillinger M, Sabeti S, Dick P, Amighi J, Mlekusch W, Schlager O, Loewe C, Cejna M, Lammer J, Minar E, Sustained benefit at 2 years of primary femoropopliteal stenting compared with balloon angioplasty with optional stenting., Circulation. 115 (2007) 2745–9. doi: 10.1161/CIRCULATIONAHA.107.688341. [DOI] [PubMed] [Google Scholar]
- [9].Scully RE, Arnaoutakis DJ, DeBord Smith A, Semel M, Nguyen LL, Estimated annual health care expenditures in individuals with peripheral arterial disease, J. Vasc. Surg 67 (2018) 558–567. doi: 10.1016/J.JVS.2017.06.102. [DOI] [PubMed] [Google Scholar]
- [10].MacTaggart J, Poulson W, Seas A, Deegan P, Lomneth C, Desyatova A, Maleckis K, Kamenskiy A, Stent Design Affects Femoropopliteal Artery Deformation., Ann. Surg (2018) 1. doi: 10.1097/SLA.0000000000002747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].García A, Martínez MA, Peña E, Determination and Modeling of the Inelasticity Over the Length of the Porcine Carotid Artery, J. Biomech. Eng 135 (2013) 031004. doi: 10.1115/1.4023371. [DOI] [PubMed] [Google Scholar]
- [12].Ghasemi M, Nolan DR, Lally C, An investigation into the role of different constituents in damage accumulation in arterial tissue and constitutive model development, Biomech. Model. Mechanobiol 17 (2018) 1757–1769. doi: 10.1007/s10237-018-1054-3. [DOI] [PubMed] [Google Scholar]
- [13].Calvo B, Peña E, Martinez MA, Doblaré M, An uncoupled directional damage model for fibred biological soft tissues. Formulation and computational aspects, Int. J. Numer. Methods Eng. 69 (2007) 2036–2057. doi: 10.1002/nme.1825. [DOI] [Google Scholar]
- [14].Converse MI, Walther RG, Ingram JT, Li Y, Yu SM, Monson KL, Detection and characterization of molecular-level collagen damage in overstretched cerebral arteries, Acta Biomater. 67 (2018) 307–318. doi: 10.1016/j.actbio.2017.11.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Fereidoonnezhad B, Naghdabadi R, Holzapfel GA, Stress softening and permanent deformation in human aortas: Continuum and computational modeling with application to arterial clamping, J. Mech. Behav. Biomed. Mater 61 (2016) 600–616. doi: 10.1016/j.jmbbm.2016.03.026. [DOI] [PubMed] [Google Scholar]
- [16].Horny L, Gultova E, Chlup H, Sedlacek R, Kronek J, Vesely J, Zitny R, Mullins effect in human aorta described with limiting extensibility evolution, in: IFMBE Proc, 2010: pp. 768–771. doi: 10.1007/978-3-642-13039-7_194. [DOI] [Google Scholar]
- [17].Pierce DM, Maier F, Weisbecker H, Viertler C, Verbrugghe P, Famaey N, Fourneau I, Herijgers P, Holzapfel GA, Human thoracic and abdominal aortic aneurysmal tissues: Damage experiments, statistical analysis and constitutive modeling, J. Mech. Behav. Biomed. Mater 41 (2015) 92–107. doi: 10.1016/j.jmbbm.2014.10.003. [DOI] [PubMed] [Google Scholar]
- [18].Schriefl AJ, Schmidt T, Balzani D, Sommer G, Holzapfel G. a., Selective enzymatic removal of elastin and collagen from human abdominal aortas: Uniaxial mechanical response and constitutive modeling, Acta Biomater. 17 (2015) 125–136. doi: 10.1016/j.actbio.2015.01.003. [DOI] [PubMed] [Google Scholar]
- [19].Peña E, Peña JA, Doblaré M, On the Mullins effect and hysteresis of fibered biological materials: A comparison between continuous and discontinuous damage models, Int. J. Solids Struct. 46 (2009) 1727–1735. doi: 10.1016/j.ijsolstr.2008.12.015. [DOI] [Google Scholar]
- [20].Weisbecker H, Viertler C, Pierce DM, Holzapfel GA, The role of elastin and collagen in the softening behavior of the human thoracic aortic media, J. Biomech 46 (2013) 1859–1865. doi: 10.1016/j.jbiomech.2013.04.025. [DOI] [PubMed] [Google Scholar]
- [21].Elías-Zúñiga A, Baylón K, Ferrer I, Serenó L, Garcia-Romeu ML, Bagudanch I, Grabalosa J, Pérez-Recio T, Martinez-Romero O, Ortega-Lara W, Elizalde LE, On the rule of mixtures for predicting stress-softening and residual strain effects in biological tissues and biocompatible materials, Materials (Basel). 7 (2014) 441–456. doi: 10.3390/ma7010441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Alastrué V, Peña E, Martínez MA, Doblaré M, Experimental study and constitutive modelling of the passive mechanical properties of the ovine infrarenal vena cava tissue, J. Biomech 41 (2008) 3038–3045. doi: 10.1016/j.jbiomech.2008.07.008. [DOI] [PubMed] [Google Scholar]
- [23].Peña E, Doblaré M, An anisotropic pseudo-elastic approach for modelling Mullins effect in fibrous biological materials, Mech. Res. Commun 36 (2009) 784–790. doi: 10.1016/j.mechrescom.2009.05.006. [DOI] [Google Scholar]
- [24].Simo J, On a fully three-dimensional finite-strain viscoelastic damage model: formulation and computational aspects, Comput. Methods Appl. Mech. Eng 60 (1987) 153–173. [Google Scholar]
- [25].Ogden RW, Roxburgh DG, Pseudo-Elastic Model for the Mullins Effect in Filled Rubber, Proc. R. Soc. Lond. A 455 (1999) 2861–2877. [Google Scholar]
- [26].Miehe C, Keck J, Superimposed Finite elastic-viscoelastic-plastoelastic stress response with damage in filled rubbery polymers. Experiments, modelling and algorithmic implementation, 2000. [Google Scholar]
- [27].Dorfmann A, Ogden RW, A pseudo-elastic model for loading, partial unloading and reloading of particle-reinforced rubber, (n.d.). doi: 10.1016/S0020-7683(03)00089-1. [DOI] [Google Scholar]
- [28].Balzani D, Brinkhues S, Holzapfel G. a., Constitutive framework for the modeling of damage in collagenous soft tissues with application to arterial walls, Comput. Methods Appl. Mech. Eng 213–216 (2012) 139–151. doi: 10.1016/j.cma.2011.11.015. [DOI] [Google Scholar]
- [29].Maher E, Creane A, Lally C, Kelly DJ, An anisotropic inelastic constitutive model to describe stress softening and permanent deformation in arterial tissue, J. Mech. Behav. Biomed. Mater 12 (2012) 9–19. doi: 10.1016/j.jmbbm.2012.03.001. [DOI] [PubMed] [Google Scholar]
- [30].Schmidt T, Balzani D, Holzapfel GA, Statistical approach for a continuum description of damage evolution in soft collagenous tissues, Comput. Methods Appl. Mech. Eng 278 (2014) 41–61. doi: 10.1016/j.cma.2014.04.011. [DOI] [Google Scholar]
- [31].Blanco S, Polindara A, Goicolea JM, A regularised continuum damage model based on the mesoscopic scale for soft tissue, Int. J. Solids Struct. 58 (2015) 20–33. doi: 10.1016/j.ijsolstr.2014.12.013. [DOI] [Google Scholar]
- [32].Desyatova A, MacTaggart J, Kamenskiy A, Constitutive modeling of human femoropopliteal artery biaxial stiffening due to aging and diabetes., Acta Biomater. 64 (2017) 50–58. doi: 10.1016/j.actbio.2017.09.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Kamenskiy A, Seas A, Bowen G, Deegan P, Desyatova A, Bohlim N, Poulson W, Mactaggart J, In situ longitudinal pre-stretch in the human femoropopliteal artery, Acta Biomater. 32 (2016) 231–237. doi: 10.1016/j.actbio.2016.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Kamenskiy A, Pipinos I, Dzenis Y, Lomneth C, Kazmi S. a J., Phillips N, MacTaggart J, Passive biaxial mechanical properties and in vivo axial pre-stretch of the diseased human femoropopliteal and tibial arteries., Acta Biomater. 10 (2014) 1301–1313. doi: 10.1016/j.actbio.2013.12.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].V Kamenskiy A, Pipinos II, Dzenis YA, Phillips NY, Desyatova AS, Kitson J, Bowen R, MacTaggart JN, Effects of age on the physiological and mechanical characteristics of human femoropopliteal arteries., Acta Biomater. 11 (2015) 304–13. doi: 10.1016/j.actbio.2014.09.050. [DOI] [PubMed] [Google Scholar]
- [36].Ferruzzi J, Vorp DA, Humphrey JD, On constitutive descriptors of the biaxial mechanical behaviour of human abdominal aorta and aneurysms., J R Soc Interface. 8 (2011) 435–450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Holzapfel GA, Nonlinear solid mechanics: a continuum approach for engineering, John Wiley & Sons Ltd. , 2000. [Google Scholar]
- [38].Cunnane EM, Mulvihill JJE, Barrett HE, Healy DA, Kavanagh EG, Walsh SR, Walsh MT, Mechanical, biological and structural characterization of human atherosclerotic femoral plaque tissue, Acta Biomater. 11 (2015) 295–303. doi: 10.1016/J.ACTBIO.2014.09.024. [DOI] [PubMed] [Google Scholar]
- [39].Sell DR, Monnier VM, Molecular basis of arterial stiffening: role of glycation - a mini-review., Gerontology. 58 (2012) 227–37. doi: 10.1159/000334668. [DOI] [PubMed] [Google Scholar]
- [40].Lee S-J, Park S-H, Arterial ageing., Korean Circ. J 43 (2013) 73–9. doi: 10.4070/kcj.2013.43.2.73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Kohn JC, Age-related vascular stiffening: causes and consequences, Front. Genet 6 (2015) 1–17. doi: 10.3389/fgene.2015.00112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Sims TJ, Rasmussen LM, Article in Diabetologia, (1996). doi: 10.1007/BF00403914. [DOI] [PubMed]
- [43].Schleicher ED, Wagner E, Nerlich AG, Increased accumulation of the glycoxidation product N(epsilon)-(carboxymethyl)lysine in human tissues in diabetes and aging., J. Clin. Invest 99 (1997) 457–468. doi: 10.1172/JCI119180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Dingemans KP, Teeling P, Lagendijk JH, Becker AE, Extracellular matrix of the human aortic media: an ultrastructural histochemical and immunohistochemical study of the adult aortic media., Anat. Rec 258 (2000) 1–14. [DOI] [PubMed] [Google Scholar]
- [45].Humphrey JD, Possible mechanical roles of glycosaminoglycans in thoracic aortic dissection and associations with dysregulated transforming growth factor-β, J. Vasc. Res 50 (2012) 1–10. doi: 10.1159/000342436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Kamenskiy A, Poulson W, Sim S, Reilly A, Luo J, Mactaggart J, Prevalence of Calcification in Human Femoropopliteal Arteries and its Association with Demographics, Risk Factors, and Arterial Stiffness., Arterioscler. Thromb. Vasc. Biol 38 (2018) ATVBAHA.117.310490. doi: 10.1161/ATVBAHA.117.310490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Wu D, Shen YH, Russell L, Coselli JS, Lemaire SA, Molecular mechanisms of thoracic aortic dissection, J. Surg. Res 184 (2013) 907–924. doi: 10.1016/j.jss.2013.06.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Tintut Y, Parhami F, Boström K, Jackson SM, Demer LL, cAMP stimulates osteoblast-like differentiation of calcifying vascular cells. Potential signaling pathway for vascular calcification, J. Biol. Chem 273 (1998) 7547–7553. doi: 10.1074/jbc.273.13.7547. [DOI] [PubMed] [Google Scholar]
- [49].Tyson KL, Reynolds JL, McNair R, Zhang Q, Weissberg PL, Shanahan CM, Osteo/chondrocytic transcription factors and their target genes exhibit distinct patterns of expression in human arterial calcification, Arterioscler. Thromb. Vasc. Biol 23 (2003) 489–494. doi: 10.1161/01.ATV.0000059406.92165.31. [DOI] [PubMed] [Google Scholar]
- [50].Gultova E, Horny L, Chlup H, A comparison between the exponential and limiting fiber extensibility pseudo-elastic model for the Mullins effect in arterial tissue, J. Theor. Appl. Mech Vol. 49 nr (2011) 1203–1216. [Google Scholar]
- [51].Maher E, Early M, Creane A, Lally C, Kelly DJ, Site specific inelasticity of arterial tissue, J. Biomech 45 (2012) 1393–1399. doi: 10.1016/j.jbiomech.2012.02.026. [DOI] [PubMed] [Google Scholar]
- [52].Li W, Damage Models for Soft Tissues: A Survey, Springer Berlin Heidelberg, 2016. doi: 10.1007/s40846-016-0132-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Kamenskiy AVA, Dzenis YYA, Kazmi SAJSAJ, Pemberton MMA, Pipinos III, Phillips NNY, Herber K, Woodford T, Bowen RRE, Lomneth CSC, MacTaggart JNJ, Biaxial Mechanical Properties of the Human Thoracic and Abdominal Aorta, Common Carotid, Subclavian, Renal and Common Iliac Arteries, Biomech. Model. Mechanobiol 13 (2014) 1341–59. doi: 10.1007/s10237-014-0576-6. [DOI] [PubMed] [Google Scholar]