NS-kNN: A modified k-nearest neighbors approach for imputing metabolomics data

Abstract

Introduction

A common problem in metabolomics data analysis is the existence of a substantial number of missing values, which can complicate, bias, or even prevent certain downstream analyses. One of the most widely-used solutions to this problem is imputation of missing values using a k-nearest neighbors (kNN) algorithm to estimate missing metabolite abundances. kNN implicitly assumes that missing values are uniformly distributed at random in the dataset, but this is typically not true in metabolomics, where many values are missing because they are below the limit of detection (LOD) of the analytical instrumentation.

Objectives

Here, we explore the impact of nonuniformly distributed missing values (missing not at random, or MNAR) on imputation performance. We present a new model for generating synthetic missing data and a new algorithm, No-Skip kNN (NS-kNN), that accounts for MNAR values to provide more accurate imputations.

Methods

We compare the imputation errors of the original kNN algorithm using two distance metrics, NS-kNN, and a recently developed algorithm KNN-TN, when applied to multiple experimental datasets with different types and levels of missing data.

Results

Our results show that NS-kNN typically outperforms kNN when at least 20-30% of missing values in a dataset are MNAR. NS-kNN also has lower imputation errors than KNN-TN on realistic datasets when at least 50% of missing values are MNAR.

Conclusion

Accounting for the nonuniform distribution of missing values in metabolomics data can significantly improve the results of imputation algorithms. The NS-kNN method imputes missing metabolomics data more accurately than existing kNN-based approaches when used on realistic datasets.

1. Introduction

Compared to a number of other -omics fields, metabolomics is a relatively new area of research with still-evolving best practices and data analysis tools. A problem that seems to be pervasive across the field is that typically 10-20% (sometimes more) of all values in metabolomics datasets are missing (Gromski et al., 2014). These missing values are most commonly attributed either to instrument processing error or to low metabolite abundances that are below the limit of detection (LOD) of the instrument (Armitage et al., 2015). Missing values caused by processing errors are often referred to as “missing completely at random”, or MCAR, because they are uniformly distributed across the dataset and are not missing directly due to any property of the metabolite or measurement itself. Values missing due to being below an instrument’s LOD are often referred to as “missing not at random”, or MNAR, as they occur disproportionately in specific metabolites rather than uniformly across all metabolites (though there is usually still some randomness to their occurrence in those metabolites).

When metabolomics datasets are complete, they have been shown to be a valuable asset in many applications (Dromms and Styczynski, 2012). However, missing values in metabolomics datasets are problematic because they can induce bias in downstream analyses or even completely prevent the use of some analysis methods (Barnard and Meng, 1999). If a significant number of missing values are due to abundances being below the instrument’s LOD, the distribution of the remaining data will be heavily skewed toward metabolites with higher abundances. Removing samples or metabolites that contain missing values is not a viable strategy, as up to 80% of all metabolites may typically have at least one missing value (Hrydziuszko and Viant, 2011). To deal with the issue of data missingness, many metabolomics software packages impute estimates of missing values, using a variety of methods. The simplest approaches replace missing values with zeros, the mean or median of a metabolite, or the minimum or half-minimum value of a metabolite. While these methods are easy to implement, they can be particularly destructive to downstream analyses and have been shown to be inferior to other approaches, such as k-nearest neighbors (kNN) and random forest, that use information from similar samples and metabolites to impute missing values (Gromski et al., 2014).

Although there have been a few studies in the literature examining the differences between imputation methods on metabolomics data (Armitage et al., 2015; Di Guida et al., 2016; Gromski et al., 2014; Wei et al., 2018b), the creation of realistic datasets for use in such studies has gone relatively unexplored. This is a critical step because the ideal assessment of imputations would be a comparison to the actual missing data, but these data are (by definition) not available for real experimental datasets. To allow direct assessment of imputation accuracy, putatively complete real datasets must have some values synthetically removed from them in order to know the “correct” answers to which imputations can be compared. Hrydziuszko and Viant found that most missing values in mass spectrometry datasets do not occur completely randomly, but are distributed in a way dependent on their peak abundances and m/z values (Hrydziuszko and Viant, 2011). A later study did not reproduce those results due to differences in pre-processing approaches (specifically, filtering out any metabolites with missingness greater than 20%), but still acknowledged that missing values may be due to peak areas being below the instrument’s LOD (Di Guida et al., 2016). Based on this literature evidence and our general experience with metabolomics data, we expect typical metabolomics datasets to contain more MNAR than MCAR values. However, several recent studies of missing value imputation use only datasets with uniformly distributed synthetic missing values (Armitage et al., 2015; Di Guida et al., 2016), which precludes a representative quantitative assessment of imputation performance. Recently, Shah et. al. acknowledged this issue and examined datasets with a mixture of MCAR and MNAR missing values, which has been done previously in the field of proteomics, but not in metabolomics (Lazar et al., 2016; Shah et al., 2017).

While kNN and random forest methods have been previously shown to perform better than simplistic replacement methods, these algorithms inherently assume data to be MCAR (Wei et al., 2018b). Because we expect more realistic metabolomics data to contain both types of missing data, and often a majority that are MNAR, it is critical that imputation algorithms account for MNAR values in order to reduce imputation errors. Nonetheless, the majority of imputation methods in statistics literature do not consider MNAR values (Lazar et al., 2016). To fill this void in the context of metabolomics imputation, Shah et. al. devised kNN truncation (KNN-TN) as an extension of kNN that estimates the true means and standard deviations of each metabolite to account for both MNAR and MCAR values and uses this information in standardization of raw data (Shah et al., 2017).

In this work, we take a different approach to improve kNN by modifying the underlying algorithm rather than the preprocessing steps before imputation (as is done, for example, in KNN-TN). We focus on GC-MS metabolomics datasets as a test case based on the prevalence of both types of missingness due to the nature of upstream GC-MS data processing, but also show that our method can be generalized to other analytical approaches, including liquid chromatography-mass spectrometry (LC-MS). We examine how missing values in nearest neighbor samples can be used as information to improve imputation accuracy. We assess this approach on datasets representing multiple models of missingness, and show that it can outperform three other kNN-based approaches (the original kNN method using either Euclidean distance or Pearson correlation as distance metrics, and KNN-TN) when tested on various real metabolomics datasets under experimentally realistic conditions.

2. Methods

2.1. Metabolomics datasets

Three publicly available and complete (i.e., with no missing values) GC-MS datasets were used for the majority of analyses and were selected to provide diversity in dataset sizes, sample organisms of origin, and sample matrices. Several other datasets, including LC-MS datasets, were used to test robustness and can be found in the Supplementary Information. All datasets can be accessed via the Metabolomics Workbench, www.metabolomicsworkbench.org.

2.1.1. YjgF/YER057c/UK114 (Rid) protein family data (Bacteria)

This dataset came from an experiment to examine the differences in intracellular metabolite concentrations between wild-type and knockout strains of E. coli and S. enterica to analyze the metabolic functions of the Rid protein family. The study consisted of five groups of six replicates, with one sample missing (29 samples total), with 249 metabolites measured by Gas Chromatography-Mass Spectrometry (GC-MS). This dataset, and details regarding its experimental acquisition, can be found under Study ID ST000118 (Niehaus et al., 2015).

2.1.2. Asthma/obesity correlation study (Mouse)

The experiment from which this dataset came studied how three different diets affected the arginine metabolism pathway in mouse lungs. This experiment contained 80 mouse lung tissue samples with 612 metabolites measured by GC-MS. The different experimental groups had varying numbers of replicates. This dataset, and details regarding its experimental acquisition, can be found under Study ID ST000419.

2.1.3. Metabolic profiles in non-diabetic and Type 2 diabetic obese African-American women (Human)

This dataset came from a study investigating differences in metabolite abundances between non-diabetic and Type 2 diabetic obese African-American women. Plasma samples came from 12 non-diabetic patients and 44 diabetic patients, half of whom had a specific single nucleotide polymorphism. 360 total metabolites were measured by GC-MS and were all reported in this dataset. This dataset, and details regarding its experimental acquisition, can be found under Study ID ST000383 (Fiehn et al., 2010).

2.1.4. Additional metabolomics datasets used

The three datasets described above were used for most of the analyses presented in this work. To test the generalizability of our algorithm and our conclusions, we used six additional datasets obtained from the Metabolomics Workbench, spanning source organisms from microbes to humans, for additional assessment of the different imputation algorithms using our improved model of synthetic missingness. These additional datasets also included data acquired using liquid chromatography-mass spectrometry (LC-MS), to support the generalizability of the algorithm and our conclusions beyond the initial three GC-MS datasets used throughout this work. Details on these additional datasets can be found in the Supplementary Information.

2.2. Missing value generation

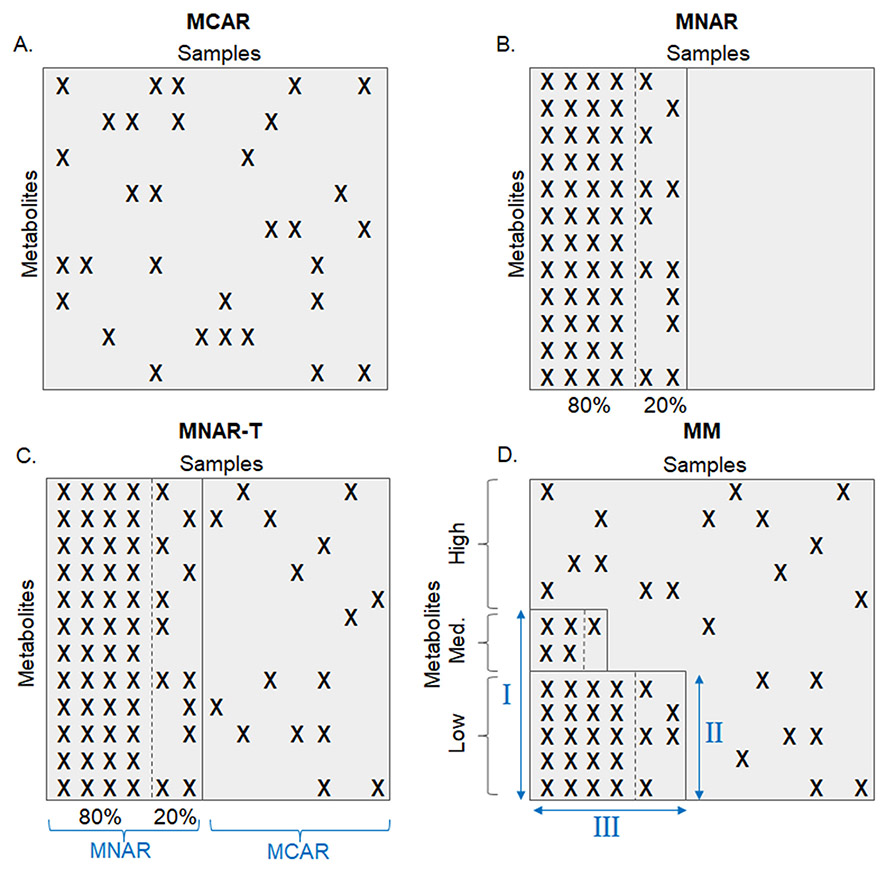
Four different methods for generating missing values were used in this study, to allow for comparison to previous literature assessments of imputation as well as more reasonable representations of the missingness observed in real datasets. Schematics for each of the four scenarios are shown in Figure 1. For each dataset, 100 different datasets with missing values based on each of the following methods were generated.

Fig. 1.

Schematics of the four different missing value generation methods used in this work. a Missing Completely at Random (MCAR); b Missing Not at Random (MNAR); c MNAR with MCAR values titrated in (MNAR-T); d Mixed Missingness (MM). Roman numerals in MM schematic represent adjustable percentage thresholds described in the main text. The solid line in b and c is also an adjustable parameter, used to control total missingness in b and the fraction of MNAR in c

2.2.1. Missing completely at random (MCAR)

As has been done in multiple previous imputation studies, a random number generator with a uniform distribution was used to select values to remove from the dataset (Armitage et al., 2015; Di Guida et al., 2016). This method approximates processing errors that are not dependent on the type or abundance of metabolite being measured.

2.2.2. Missing not at random (MNAR)

To simulate measurements missing due to instrument limits of detection, a percentage of the lowest abundance values for each metabolite were identified for potential removal, similar to cutoffs used in previous studies (Shah et al., 2017; Wei et al., 2018b). Of the values identified, the lowest 80% abundance values were removed (representing values below a hypothetical limit of detection). Of the remaining 20%, half were randomly selected for removal (to model values that are close to an instrument’s LOD). Various other percentage thresholds were also examined and observed to produce similar trends in our results (Figure S1).

2.2.3. MNAR with MCAR values titrated in (MNAR-T)

MNAR-T adds MCAR values to the MNAR method. First, a total percentage of missingness is set. Next, a percentage of the total missing values is chosen to be MNAR and values are removed based on the MNAR removal process described above. Finally, MCAR values are titrated into the rest of the dataset by randomly removing values above the threshold used to generate MNAR values, until the selected total percentage of missingness is reached.

2.2.4. Mixed missingness (MM)

MM is meant to be a more realistic representation of the distribution of missing values in a metabolomics dataset. Whereas MNAR and MNAR-T assume that all metabolites have equal missingness for their lower-abundance measurements, MM models vary levels of missingness across different metabolites, as it is more likely that metabolites with a lower average abundance will have more MNAR values, while some highly abundant metabolites may have no MNAR values at all. First, a total percentage of missingness is set. The metabolites are then ordered from lowest to highest average (arithmetic mean) abundance. A threshold percentage (I) is set to separate the highest average abundance metabolites from the rest; these will have no MNAR values. Metabolites below this threshold are further split by another threshold percentage (II) that separates low and medium (100% - II) abundance groups. In the low abundance group, a certain percentage (III) of values in each low abundance metabolite is removed based on the MNAR process described above. Half of this percentage (0.5 × III) is used to remove values in the medium abundance group using the MNAR process described above. From the remaining values across all groups not considered to be removed during the MNAR process, values are randomly selected to be removed (MCAR) until the defined total missingness percentage is reached.

2.3. Missing value imputation

2.3.1. Data filtering

Before imputation on synthetic missing datasets, any samples or metabolites containing >70% missing values are removed; removal of mostly-missing data is a common step in metabolomics data processing.

2.3.2. Data pre-processing and post-processing

To prevent metabolites with large abundances from dominating the distance calculations in the kNN algorithm, the data were autoscaled before imputation by subtracting the mean and dividing by the standard deviation of the non-missing values on a per-metabolite basis. After missing values were imputed, the values were post-processed to their original scale by multiplying by the original standard deviation and adding the original mean.

2.3.3. k-nearest neighbor (kNN)

kNN is an algorithm commonly used in machine learning for classification or regression. The basis of kNN is the assumption that biologically similar samples will have similar measured values across most of their metabolites (Troyanskaya et al., 2001). To impute a missing value for one target sample, the k most similar samples are found based on a defined distance metric calculated using the values of metabolites that are present in both the target sample and a candidate neighbor sample (Hu et al., 2016; Kim et al., 2005). Here we test kNN with Euclidean distance in-depth for all methods of missing value generation and also examine kNN with Pearson correlation when comparing NS-kNN to KNN-TN using the more realistic MM approach. Importantly, a sample can be a neighbor only if it has a measured value for the metabolite missing in the target sample. (Alternatively, nearest neighbor metabolites can be found instead of samples (Armitage et al., 2015; Gromski et al., 2014; Wei et al., 2018b)). A weighted combination of the corresponding values for the missing metabolite in the nearest neighbors is used as the imputed value. Additional details are available in the Supplementary Information.

2.3.4. kNN Truncation (KNN-TN)

KNN-TN is a recent imputation approach that uses maximum likelihood estimators to estimate the true means and standard deviations of each metabolite, which are then used to standardize the data before using kNN for imputation (Shah et al., 2017). This new standardization process was created to account for differences in distributions of metabolites with or without MNAR values. KNN-TN has shown promising results in terms of imputation error when compared to the standard kNN method with either Euclidean distance or the Pearson correlation as a distance metric.

2.3.5. No Skip-kNN (NS-kNN)

The motivation for creating a revised kNN algorithm lies in the observation that datasets typically contain both MCAR and MNAR values, and it is not uncommon for the majority of missing values to be MNAR. The weighted average of neighbors used in the original kNN algorithm performs well on MCAR datasets. However, if there are data MNAR, such that the missing values for a metabolite are among the lowest abundances across all samples, the imputed value will always be an overestimate because the available nearest neighbor abundances for imputation are all greater than the missing value. This phenomenon can cause high imputation errors in datasets that contain many MNAR values.

In creating a revised version of kNN, we conjectured that nearest neighbors with missing values for the same metabolite as the missing value being imputed contain useful information. Using kNN’s assumption that nearest neighbors should have similar values across all metabolites, if two nearest neighbors are missing a value for the same metabolite, it suggests that these missing values may not be completely at random and are more likely to be due to them both being below the LOD of the instrument. While the original kNN algorithm skips such neighbors and uses the next nearest neighbor with a value present for the metabolite abundance being imputed, our version of kNN instead retains those neighbors and replaces the missing values that would be used in the imputation calculation with the minimum measured value of the metabolite being imputed. We call this approach No Skip-kNN (NS-kNN). By replacing missing values in nearest neighbors with the minimum abundance of a given metabolite across all samples, NS-kNN will impute a value lower than the kNN imputation but still above the LOD. This has the advantage of more accurate imputation for MNAR values while minimizing impact on the few occurrences where a MCAR value’s nearest neighbor randomly also has a missing value for the same metabolite. Using the half-minimum value or zero instead of the minimum value worked similarly but generally gave slightly worse results in terms of the fraction of MNAR values required for them to perform better than kNN and the magnitude of performance loss at low MNAR fractions, though at high MNAR fractions the half-minimum or zero approach would even further improve performance (Figure S2). For this work, we used k = 6 as a reasonable default value based on preliminary testing on a variety of data sets (for example, Figure S3), though we found that between k = 5 and 10 the trends of our results were the same. We note that while KNN-TN focuses on the scaling of data before imputation, NS-kNN takes a different approach by directly modifying the underlying algorithm of kNN.

2.4. Imputation error calculation and comparison

To quantify imputation error, a normalized root mean square error (NRMSE) calculation was used to compare the imputed data after post-processing with the true values:

$$\sqrt{\frac{{\sum }_{i=1}^n{\sum }_{j=1}^m{\left(\frac{I_{ij}-R_{ij}}{{\overline{R}}_i}\right)}^2}{M}}$$ (1)

Here, I_ij and R_ij are the values in the imputed and original raw datasets (with dimensions n×m), respectively, corresponding to the ith metabolite and jth sample. ${\overline{R}}_i$ is the mean of metabolite i from the raw data (used to prevent high-abundance metabolites from being unduly weighted in the error metric), and M is the number of missing values imputed across the entire dataset. All statistical tests used to compare error between imputation algorithms (N = 100) were Mann-Whitney U tests (α = 0.05) to account for non-normal error distributions (Table S2).

3. Results and Discussion

3.1. kNN outperforms NS-kNN for values missing completely at random

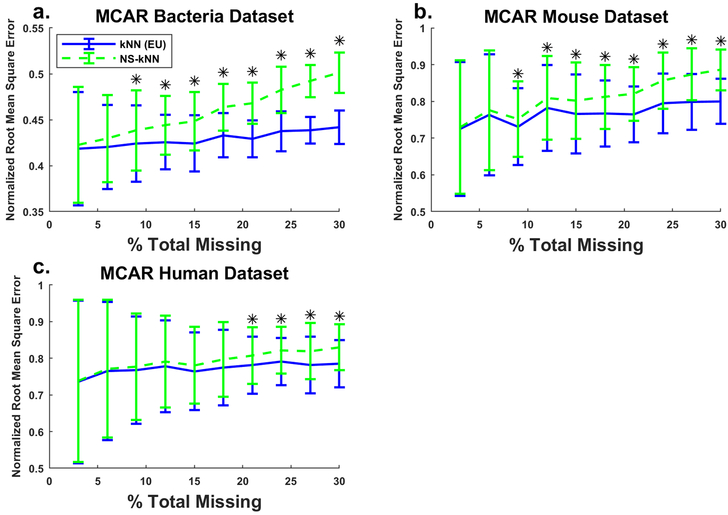
Comparison of kNN and NS-kNN imputation performance on datasets with only MCAR data recapitulated previous and expected results. Previous studies using MCAR values to compare imputation methods on metabolomics data have shown kNN to be one of the more robust approaches (Armitage et al., 2015; Di Guida et al., 2016). Figure 2 shows NS-kNN and kNN performance on the bacteria, mouse, and human datasets with only MCAR values, at varying levels of missingness. In all three cases, we observe that the NRMSE of kNN is lower than that of NS-kNN (though often not in a statistically significant fashion at low percentages of missingness). As total missingness increases, NS-kNN gradually performs worse, while the error of kNN increases at a slower rate, leading to an expanding gap between the two methods’ performances. This is perhaps unsurprising, as NS-kNN assumes the presence of MNAR values and forcibly imputes lower values in target samples with neighbors that contain the same missing metabolite, while KNN still treats those coinciding missing values as completely at random. As the percentage of missingness increases, neighbors have a higher chance of containing missing values for the same metabolite despite there only being MCAR data, and thus degrading NS-kNN performance.

Fig. 2.

Imputation error for kNN with Euclidean distance (EU) and NS-kNN on three different datasets with varying degrees of MCAR missingness. Curves represent the mean NRMSE for 100 randomly generated missingness datasets from the a bacteria, b mouse, and c human datasets. Error bars represent one standard deviation. Asterisks indicate statistical significance (p < 0.05)

We note that the NRMSE mean and standard deviations for the mouse and human datasets are greater than those for the bacteria data when imputing on MCAR values. Samples from the mouse and human datasets are more likely to be biologically diverse within each study condition, which could cause neighbors to be more phenotypically different and thus degrade the performance of neighbor-based methods. Throughout these experiments, we observed that the run time of NS-kNN was only marginally longer than the original method (milliseconds longer out of a total computation time of a few seconds).

3.2. NS-kNN performs better for values missing not at random

Although MCAR datasets are often employed for imputation comparison studies, there has been little justification for why they are used when a large portion of missing values are likely to be MNAR due to low metabolite abundances and instrument LOD. Here, we use MNAR datasets created from the bacteria, mouse, and human data to compare NS-kNN and kNN under these arguably more realistic conditions.

Figure 3 shows that for all three datasets, NS-kNN produces lower imputation errors than kNN. Again, this is perhaps unsurprising, as the data missingness tracks more closely with the assumptions of NS-kNN than those of kNN. Similar to the MCAR results (Figure 2), as the total percentage of missingness increases, the gap between the performance of the two methods widens. However, the difference in NRMSE is much greater and much more significant for the MNAR datasets than for the MCAR datasets. It is also noteworthy that while kNN increases in error as the percentage of total missingness increases for MNAR data, NS-kNN actually decreases in error, likely due to more missing values in neighbors yielding lower imputations that are more accurate for MNAR data.

Fig. 3.

Imputation error for kNN and NS-kNN on three different datasets with varying degrees of MNAR missingness. Curves represent the mean NRMSE for 100 randomly generated missingness datasets from the a bacteria, b mouse, and c human datasets. Error bars represent one standard deviation. Asterisks indicate statistical significance (p < 0.05)

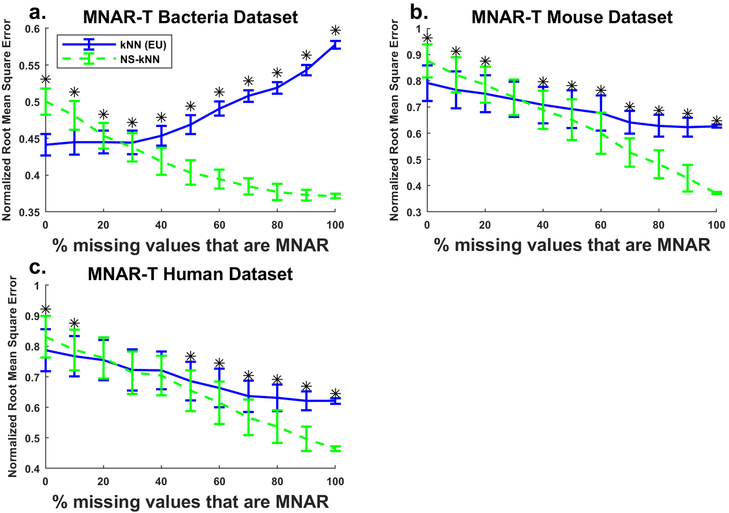
3.3. Titrating MNAR values into MCAR shows a crossover point between kNN and NS-kNN performance

While the results above show how both methods perform on different types of missing values, real experimental datasets will most likely have a combination of both types. We used the MNAR-T method to generate datasets with both MCAR and MNAR values at different ratios to assess algorithm performance for more realistic data. Figure 4 compares the NRMSE of NS-kNN and kNN when used on MNAR-T datasets with 30% total missingness and varying fractions of MNAR. Only at low fractions of MNAR values (almost all MCAR) does kNN outperform NS-kNN. Thus, once the missing values are less than approximately 75% MCAR, NS-kNN performs better. Figure S4 shows NS-kNN overtakes kNN at similar or even lower MNAR fractions for 10% total missingness, though there are changes in when the differences are statistically significant. Based on the quantitatively greater benefit of NS-kNN on MNAR over that of kNN on MCAR, the advantage of using NS-kNN on datasets with an experimentally likely fraction of MNAR values (approximately 30% or more) outweighs the disadvantage of its performance on MCAR values.

Fig. 4.

Imputation error for kNN and NS-kNN on three different datasets with 30% MNAR-T missingness and varying fractions of MNAR of the total missingness. Curves represent the mean NRMSE for 100 randomly generated missingness datasets from the a bacteria, b mouse, and c human datasets. Error bars represent one standard deviation. Asterisks indicate statistical significance (p < 0.05). The increasing behavior of kNN in a is discussed in the Supplementary Information

3.4. Mixed missingness also demonstrates generally superior performance for NS-kNN

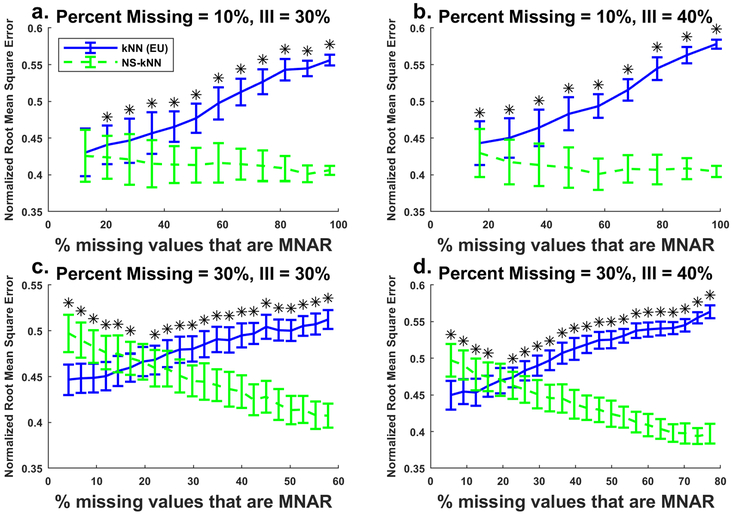
While the MNAR-T approach allows for a mixture of MCAR and MNAR values, it still may not model actual metabolomics data well, as it assumes all metabolites to have MNAR values. In real datasets, we expect there to be some metabolites whose levels never approach the LOD and would thus only have MCAR values. The MM approach of missing value generation attempts to model more realistic datasets where different metabolites can have different ratios of MCAR and MNAR values. Figure 5 shows four different scenarios for MM removal on the bacteria dataset with different percentages of total missingness and different percentages of values for each metabolite being removed in an MNAR fashion in the low (parameter III) and medium (0.5 × III) metabolite abundance groups. Different percentages of MNAR values across the dataset (the x-axis) are in this case generated by changing the percentage of metabolites that contain MNAR values (non-high abundance metabolites), represented as I in Figure 1d. In all four cases, NS-kNN outperformed kNN if the percentage of MNAR values was at least 19.6%.

Fig. 5.

Imputation error for kNN and NS-kNN on different versions of MM for the bacterial dataset. Curves represent the mean NRMSE for 100 randomly generated missingness datasets. The percentage of non-high abundance metabolites (I) for all plots ranged from 5 to 70%, as long as the total missingness percentage was not exceeded. II = 70% for all plots. Subpanels show results for a 10% total missingness with III = 30%; b 10% total missingness with III = 40%; c 30% total missingness with III = 30%; and d 30% total missingness with III = 40%. Error bars represent one standard deviation. Asterisks indicate statistical significance (p < 0.05)

When using the MM missing value generation method on the mouse and human data, the same general trends are observed (Figure S5 and Figure S6). NS-kNN was able to overtake kNN when the percentage of MNAR values was at least 36.1% for the mouse data and 21.7% for the human data. When looking at the distribution of abundances for each dataset, we found varying distribution shapes (Figure S7), which could be a cause for the different percentages of MNAR values where NS-kNN overtakes kNN. Overall, these results are consistent with those from the MNAR-T model.

3.5. Comparison to KNN-TN, kNN with Euclidean distance, and kNN with Pearson correlation

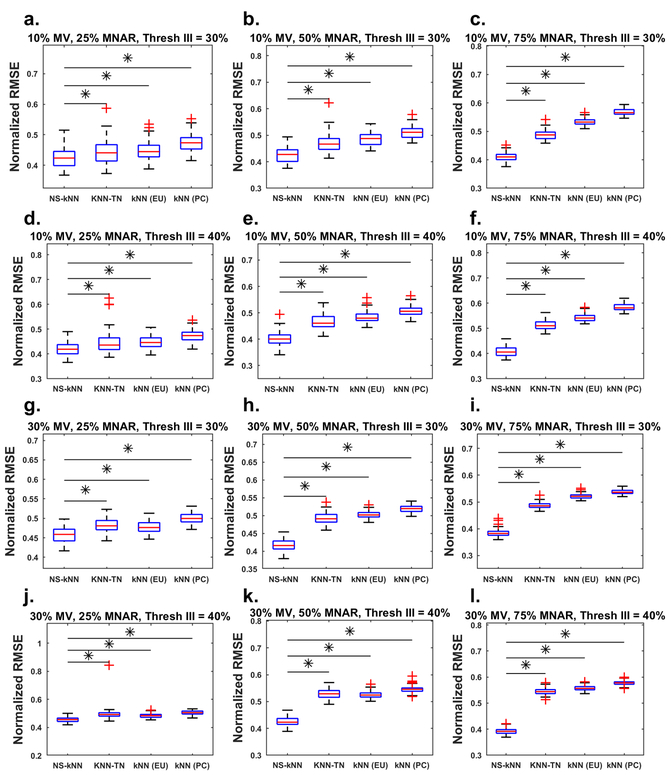
In the KNN-TN study, Shah et. al. used a missing value generation approach similar to MNAR-T. Because the assumptions of the Mixed Missingness (MM) model are more consistent with many phenomena observed in real metabolomics datasets (e.g. high abundance metabolites often have fewer missing values and likely no MNAR values), we compared NS-kNN to KNN-TN using MM datasets generated from several different sets of conditions selected from those tested in Figure 5. Additionally, we tested kNN with Euclidean distance and kNN with Pearson correlation as a distance metric based on results also shown in the Shah et al. work. A k value of 10 was used for KNN-TN, consistent with the optimal value found in the Shah paper when calculating distances between metabolites (Shah et al., 2017), and a k value of 6 was used for the three other kNN methods, as per our Methods. The only portion of the KNN-TN code that was edited was the error calculation to be consistent with the NRMSE equation described in the Methods section of this paper, and the missing value datasets were log-transformed before imputation, which is a necessary step before KNN-TN can impute on real datasets according to Shah et. al.

Figures 6, S8, and S9 show the results of the analysis for the bacteria, mouse, and human datasets, respectively. NS-kNN consistently outperforms KNN-TN, kNN with Euclidean distance, and kNN with Pearson correlation for all MNAR fractions in the bacteria dataset and in the mouse dataset when the MNAR fraction is at least 50%. The human dataset (Figure S9), on the other hand, yielded more conditions where NS-kNN is not significantly different or is statistically significantly worse than KNN-TN.

Fig. 6.

Boxplots comparing the NRMSE of NS-kNN, KNN-TN, kNN with Euclidean distance (EU), and kNN with Pearson correlation (PC) on the bacteria data with missing values generated using the MM approach. Results are shown for a-f 10% missingness; g-l 30% missingness; a-c, g-i III = 30%; d-f, j-l III = 40%; a, d, g, j 25% of missing values are MNAR; b, e, h, k 50% of missing values are MNAR; c, f, i, l 75% of missing values are MNAR. Threshold II = 70% for all plots and Threshold I varied based on the percentage of MNAR values being tested. Asterisks indicate statistical significance (p < 0.05) and are only shown for comparisons of NS-kNN to the other methods. The center line of the box is the median, the bottom and top edges of the box are the 25^th and 75^th percentiles, respectively, the whiskers are the most extreme non-outlier data points, and the plus symbols are outliers

Because realistic datasets are likely to have different distributions of MNAR values in each metabolite, which MM tries to model, low abundance metabolites will likely have a high number of missing values. We believe that KNN-TN decreases in performance, and eventually performs significantly worse than NS-kNN, as the percentage of MNAR values increases because KNN-TN has difficulty estimating means and standard deviations when a large amount of data is missing in these low abundance metabolites. This problem of estimating means and standard deviations when there is a high percentage of missing values is noted by the authors of KNN-TN.

Given these dataset-dependent differences in performance, we next analyzed more datasets to attempt to get a more representative sampling and to test hypotheses about the reasons for the differences in performance. We first suspected that the differences in performance may be due to the inherent high variability across “biological replicates” in human data that is not as prevalent in microbial or animal studies. While non-human data are obtained from subjects that are typically less diverse and where experimental conditions can be much more easily controlled, human data are naturally more heterogeneous given the varied genetic and environmental backgrounds of each patient, and this heterogeneity could have a different impact for NS-kNN due to the change in assumptions underlying the algorithm. We further tested the four imputation approaches on two other human (Figure S10 and S11) and two other non-human (Figure S12 and S13) datasets to test this hypothesis. In the non-human datasets, there were more cases where NS-kNN significantly outperformed KNN-TN than when using the human datasets. In particular, for the microbial datasets NS-kNN was quantitatively much more superior than in the human datasets, while in the additional mouse dataset it was generally superior but to a lesser magnitude, which taken together supports our hypothesis. We also note, though, that NS-kNN was still able to outperform KNN-TN on the additional human datasets in most cases where the percentage of MNAR values was high (>75%), suggesting that the performance in Figure S9 is a worst-case scenario, if not an outlier. We also tested the four methods on two non-human LC-MS datasets (Figure S14 and S15) and found similar results where NS-kNN is significantly better or not significantly worse than the other four methods when there is a sufficient amount of missing values that are MNAR (>50%). A comprehensive list of median errors and standard deviations for the four imputation methods on all of the datasets tested can be found in Table S1. We note that kNN with Euclidean distance consistently outperforms kNN with Pearson correlation (significance not shown in figures), which contradicts the findings of Shah et. al.; we believe this is due to our autoscaling of the data before imputing with kNN with Euclidean distance, which is not performed in the Shah study.

3.6. Sensitivity analysis on mixed missingness

To assess the sensitivity of NS-kNN and its superior performance compared to kNN with Euclidean distance, we used the MM dataset, which is arguably closest to experimental reality and has the most adjustable parameters. In 5% intervals, we perturbed the I and II parameters from 5% to 70%, and the III parameter from 5% to 40%, and assessed the relative performance of NS-kNN and kNN on the bacteria, mouse, and human datasets (Figure S16 – S18). Each parameter combination was then translated to a corresponding fraction of MNAR values, and the performance difference between kNN and NS-kNN was then assessed as a function of that fraction. Seeking to identify the worst-case scenario for NS-kNN performance as dataset parameters were perturbed, we found it to be for a specific case of the mouse dataset, when it only started outperforming kNN when 40.3% of the missing values were MNAR (Figure S17f). For the bacteria and human datasets, the worst-case performance of NS-kNN still saw it overtake kNN at 27.5% of values as MNAR (Figure S16f and Figure S18f). Generally, the performance of NS-kNN was quite insensitive to perturbations in parameters used to generate datasets with missing values; consistent with our other results, it was instead dependent upon the fraction of MNAR values.

4. Conclusion

In this study, we have formulated a new algorithm based on kNN that can reduce imputation errors on metabolomics datasets compared to the original kNN method and the recently developed KNN-TN. To assess its performance on different types of missing values, we used datasets with exclusively either MCAR or MNAR values, or a basic combination of both types. We further developed a new model of missingness that integrates more of the phenomena observed in experimental metabolomics datasets. Unlike many approaches that do not attempt to account for MNAR values, NS-kNN incorporates assumptions that lead to more reasonable imputations for metabolites that are at or below the limit of detection of the instrument. We showed using three real datasets that NS-kNN typically began to outperform kNN when the percentage of MNAR values was 20-30%, and always outperformed kNN when the percentage of MNAR values was at least 40.3% for these datasets. We further used six additional test datasets to assess the robustness of our algorithm and results, identifying that while NS-kNN does generally perform better than the approaches tested here under the improved model of missingness, that advantage is most evident when most values are MNAR, and tends to be more evident when variability across biological replicates is expected to be lower.

It is difficult to know for certain what fraction of missing values are due to random processing errors versus instrument detection limits, but most metabolomics datasets have many metabolites with no missing values and some metabolites with significant missingness. It thus seems likely that MNAR values constitute a substantial fraction of missing values, and probably the majority, meaning that for any real mass spectrometry metabolomics dataset, NS-kNN is likely to be a significant improvement over kNN and related methods.

We have applied NS-kNN to GC-MS and LC-MS datasets in this work, and it is likely to lower imputation errors on data generated from many other common types of instruments that are also likely to have fewer MCAR values than MNAR. Additional assessment of NS-kNN’s effect on downstream analysis tools, such as PCA or PLS-DA, will help to further characterize the impact of improved imputations. kNN has been shown to be robust in terms of post-imputation analysis, so we expect NS-kNN to perform similarly, if not better (Gromski et al., 2014). Finally, while other methods for imputation are undoubtedly under development, or have been developed in other fields (Boeckel et al., 2015; Chen et al., 2011; Lee et al., 2018; Liu and Brown, 2014; Wei et al., 2018a), we have chosen to focus on comparing NS-kNN to similar kNN-based methods, which includes the most widely-used imputation method, that each have a reasonable computational burden even for large cohorts or datasets. Taken together, this suggests NS-kNN is a simple but effective and significant improvement over commonly-used methods for missing value imputation.