Abstract
Objective
To evaluate the diagnostic performance of several biochemical predictors of insulin resistance (IR).
Design
A total of 90 nondiabetic subjects were tested with both the pancreatic suppression test (PST) and the oral glucose tolerance test (OGTT). Of them, 53 were non–insulin-resistant (NIR) subjects and the remaining 37 were insulin resistant subjects.
Results
All glucose and insulin values from the OGTT were positively correlated with the steady-state plasma glucose (SSPG) value of the PST. Among the OGTT values, basal insulin (I0) displayed a stronger correlation with SSPG (r = 0.604). Receiver operating characteristic analysis of the OGTT data demonstrated that I0 exhibited the highest area under the receiver operating characteristic curve (AUROC), compared with the rest of the OGTT data. However, the reduced sensitivity of this predictor precluded its clinical use.
We then tested six potential predictors of IR derived from the OGTT values. Of them, the I0*G60 had a correlation coefficient of 0.697 with the SSPG and an AUROC of 0.867, surpassing the respective values of the traditional biochemical predictors of IR. Its cutoff predicting IR was >1110 mg/dL*μΙU/mL (>428 nM*pM), its sensitivity was 0.865, and its global accuracy was 0.822. We then selected the six best biochemical predictors of IR according to their posttest probability ratio. The order was as follows: I0*G60, ISI composite, AUC-Gl*In/′, quantitative insulin sensitivity check index, homeostatic model assessment 1 (HOMA1), and HOMA2.
Conclusion
We conclude that the I0*G60 is a promising, inexpensive, and easily calculable predictor of IR that outperforms the predictive power of the traditional predictors of IR, including the insulin sensitivity index composite.
Keywords: insulin resistance, biochemical predictors, pancreatic suppression test, oral glucose tolerance test
The diagnosis of insulin resistance (IR) in the clinical arena is riddled with uncertainties because of the prevalent reluctance to measure it. Indeed, the hyperinsulinemic euglycemic clamp (HEC), the gold standard of insulin sensitivity measurement, is clearly beyond the resources and capabilities of most clinical facilities [1]. However, because many clinicians need to diagnose and estimate the degree of IR in a large number of patients on a daily basis, they resort to the so-called predictors of IR. These predictors are either biochemical measurements or simple clinical assessments to diagnose the so-called metabolic syndrome, a clinical surrogate of the IR syndrome. The biggest problem with these predictors of IR is their low sensitivity, associated with high specificity. In other words, they underdiagnose IR. For instance, Cheal et al. [2] reported in 2004 that the criteria of the Adult Treatment Panel III for the diagnosis of metabolic syndrome, a clinical surrogate of IR, had a sensitivity of 46% as a predictor of IR in 443 healthy volunteers, producing a false negative rate of 54%. In addition, as reported by McLaughlin et al. [3], in 260 normotensive overweight subjects the same Adult Treatment Panel III criteria had a sensitivity of just 52% as a predictor of IR. Therefore, a high sensitivity is one of the most appreciated assets of a predictor of disease to avoid underdiagnosing the condition sought.
The very existence of IR was initially suspected when insulin began to be used to treat diabetic patients. Wilhelm Falta of Vienna in 1931 [4] and Harold Himsworth of London in 1936 [5] established unequivocally the existence of two types of diabetes mellitus: insulin insensitive (or insulin resistant) and insulin sensitive. In 1880 Lancereaux [6] had described the two opposing clinical phenotypes in diabetic patients: fat diabetes and lean diabetes. Himsworth [5] concluded that insulin-sensitive patients with diabetes were insulin deficient, whereas insulin-insensitive patients with diabetes lacked some unknown insulin-sensitizing factor.
However, the IR phenomenon is by no means restricted to diabetic patients; it also affects an important proportion of the adult nondiabetic population (probably from one in four to one in three people, especially aggravated by aging, sedentarism, and obesity), as was described by Gerald Reaven in 1988 [7].
Although the HEC is not applicable to clinical work, there is an excellent, clinically applicable alternative to measure insulin sensitivity in selected clinical cases. In fact, most of the work developed by Gerald Reaven and associates in the field of IR was done not with the HEC but with the older (1970 vs 1979) pancreatic suppression test (PST) [8], which is much simpler to perform than the former, with the added advantages of being much less expensive and not requiring the measurement of serum insulin. It just requires the measurement of nine serum glucose levels. Greenfield et al. [9] claimed that it has a correlation of 0.93 with the clamp results. During the test, glucose and crystalline insulin are continuously infused, according to the body surface area. On the other hand, the continuously infused octreotide suppresses both endogenous insulin and glucagon secretions. Finally, the infused crystalline insulin raises steady-state serum insulin to ∼50 μIU/mL, thus promoting muscular uptake of glucose while suppressing glucose production by the liver. Under these conditions, steady-state plasma glucose (SSPG) becomes directly proportional to muscle IR. It is not necessary to measure steady-state serum insulin given the fact that serum insulin values are raised uniformly among subjects [9]. Knowles et al. [10] performed a direct comparison between the results of the octreotide-modified PST and the HEC in 15 nondiabetic subjects and demonstrated an excellent agreement between these two methods. They were also able to obtain accurate transformation equations between SSPG and HEC values.
In an excellent review focused on the measurement of IR, Ferrannini [11] stated that in his opinion, the somatostatin (currently replaced by octreotide)-modified PST is the best test, next to the HEC, to quantify insulin sensitivity: “it is easy and safe and it can be performed at the bedside with minimal training.” Our group has used the PST since 2003 in clinical practice in selected patients to overcome the diagnostic uncertainties surrounding the diagnosis of IR.
However, we cannot use the PST on every patient, given the work and cost involved, compared with the cost of several simple biochemical predictors of IR such as the homeostatic model assessment (HOMA) [12], the quantitative insulin sensitivity check index (QUICKI) [13], and the composite insulin sensitivity index (ISI) [14]. For that reason, we decided to compare the predictive power of several biochemical predictors of IR against the PST. Such comparison was made by using receiver operating characteristic (ROC) analysis, followed by a Bayesian calculation. In addition, we tried to find a simple, affordable, and improved biochemical predictor of IR by carefully looking into the glucose and insulin data provided by the oral glucose tolerance test (OGTT).
Also, we were able to compare the original HOMA (HOMA1) with the computer-calculated HOMA (HOMA2) [15] in terms of predictive power in the diagnosis of IR.
1. Materials and Methods
We had data from 715 PSTs done in subjects suspected of being insulin resistant. In 90 nondiabetic cases, we had both the PST results and the OGTT data. Sixty-nine patients were women, and 21 patients (23.3%) were men. Of them, 37 (41.1%), were categorized as insulin resistant (IR subjects) by the PST, and the remaining 53 patients (58.9%) were categorized as non–insulin resistant (NIR subjects). This research was approved by the Ethics Committee of the Reproductive Health Research Institute.
Their ages ranged from 16 to 61 years old (36 ± 1.1 years). Half of the subjects were overweight (body mass index ≥25 to <30 kg/m2) or obese (body mass index ≥30 kg/m2). Initially, we studied the predictive value of each glucose and insulin value obtained during the OGTT by performing both correlation and ROC analyses against the PST result. By using the OGTT data we selected, through correlation with the SSPG and ROC analysis, we found some potential predictors of IR: area under the curve of glucose values/min (AUC-Gl/′), area under the curve of insulin values/min (AUC-In/′), area under the curve of the product glucose values*insulin values/min (AUC-Gl*In/′), basal insulin*glucose 60 minutes (I0*G60), basal insulin*glucose 90 minutes (I0*G90), and basal insulin*average glucose 60-90 (I0*G60-90).
Bayesian calculation of the results from these potential predictors allowed us to select the I0*G60, the most efficient one in predicting IR. Finally, we compared the IR predictive power of the I0*G60 against those of several popular, already “traditional” biochemical predictors of IR: HOMA1, HOMA2, and QUICKI (reflecting hepatic IR), as well as the Matsuda-deFronzo ISI composite (reflecting both hepatic and muscular IR).
A. Pancreatic Suppression Test
Testing was done after 12-hour fasting. The PST involves the continuous infusion of glucose (267 mg/m2/min), crystalline insulin (32 mU/m2/min), and octreotide (0.27 μg/m2/min, to suppress endogenous insulin production) for 3 hours [16, 17]. Under such conditions, endogenous insulin production is suppressed by octreotide and the steady-state serum insulin is raised uniformly in the subjects to stimulate muscle uptake of glucose. The PST is the reverse of the euglycemic clamp: serum insulin levels are kept stable, while serum glucose is allowed to change, mainly as a function of muscle insulin sensitivity. The SSPG becomes an inverse function of insulin sensitivity. Blood glucose measurements were obtained at 0, 30, 60, 90, 120, 150, 160, 170, and 180 minutes. The averaged four final glucose values (150 to 180 minutes) constitute the SSPG. SSPG values <150 mg/dL indicate an NIR condition; values ≥150 mg/dL indicate an IR condition [18–20].
B. Oral Glucose Tolerance Test
After a 12-hour fast, subjects received 75 g of glucose. Blood was obtained at 0, 30, 60, 90, and 120 minutes for the measurement of glucose and insulin.
C. Measurements
Glucose was measured by the glucose-oxidase method. Insulin was measured with a chemiluminescent assay with Immulite 2000 and Siemens reagents [21].
D. Biochemical Predictors
We computed the following traditional biochemical predictors: HOMA1, HOMA2, QUICKI, and Matsuda-DeFronzo ISI composite. These predictors were calculated according to the formulas developed by their authors. ISI composite was computed with the modified algorithm offered online by Matsuda (http://mmatsuda.diabetes-smc.jp/english.html). We also compared the diagnostic performance of HOMA2 with that of HOMA1. HOMA2 was calculated online (www.dtu.ox.ac.uk/homacalculator/download.php).
E. Statistics
E-1. Correlation analysis
Pearson correlations between the SSPG result and the result of each potential and traditional biochemical predictor of IR were calculated.
E-2. ROC analysis
The ROC analysis for each predictor was computed with the help of the GraphPad Prism 7 package (www.graphpad.com/scientific-software/prism). A graph is constructed by the program plotting sensitivity (true positive rate, y-axis) against the false positive rate (1 − specificity, x-axis). The program provides the area under the receiver operating characteristic curve (AUROC), and this area is compared with the null hypothesis (AUROC not different from 0.5). A useless test has an AUROC of 0.5, whereas a perfect test has an AUROC of 1. The Youden index (sensitivity + specificity − 1) equals 1 with an AUROC of 1 (sensitivity = 1; specificity = 1) and zero with an AUROC of 0.5. In other words, in a perfect test, there are neither false positive (FP) nor false negative (FN) results, so both sensitivity and specificity are equal to 1 (100%), whereas the Youden index equals 1.
Usually, predictors are not perfect tests, so they yield both FP and FN results; for this reason, their AUROC, sensitivity, specificity, and Youden index are all <1. An AUROC = 1 indicates a perfect test; an AUROC ≥0.9 and <1.0 indicates outstanding discrimination; an AUROC ≥0.8 and <0.9 indicates excellent discrimination, and an AUROC ≥0.7 and <0.8 indicates acceptable discrimination [22]. An AUROC <0.7 indicates increasingly poor discrimination. When the AUROC reaches 0.5 the test is unable to discriminate at all.
The optimal cutoff value for the predictor found by ROC analysis is the one associated with the highest sum of sensitivity and specificity and therefore with the highest Youden value.
E-3. Bayesian calculation
Although an AUROC ≥0.8 and <0.9 indicates an excellent predicting power, this is not always accompanied by high sensitivity, a desirable characteristic in a predictor of disease. For that reason, it is necessary to perform a Bayesian calculation of the data. By using true positive (TP), false negative (FN), false positive (FP), and true negative (TN) numbers we computed the parameters seen in Table 1. The formulas for each parameter are indicated in the right column of the table.
Table 1.
Bayes-Derived Parameters and Their Formulas
| Parameter | Formula |
|---|---|
| Sensitivity (TP rate) | TP/(TP + FN) |
| Specificity (TN rate) | TN/(TN + FP) |
| PPV | TP/(TP + FP) |
| NPV | TN/(TN + FN) |
| PLR | Sensitivity/(1 − Specificity) |
| NLR | (1 − Sensitivity)/Specificity |
| Odds ratio | PLR/NLR |
| Prevalence | (TP + FN) / (TP + TN + FP + FN) |
| Youden index | Sensitivity + Specificity − 1 |
| Pretest odds | Prevalence / (1 − Prevalence) |
| Posttest odds | Pretest odds*PLR |
| PTPPR | Posttest odds / (1 + Posttest odds) |
| PTPNR | Prevalence*(1 − Sensitivity)/[Prevalence*(1 + Sensitivity)] |
| PTPR | PTPPR/PTPNR |
| Global accuracy | (TP + TN)/(TP + TN + FP + FN) |
The main parameters used in Bayes calculation are included, along with their formulas. The PTPR is the parameter most closely linked to the diagnostic power of a given predictor.
Abbreviations: NLR, negative likelihood ratio; NPV, negative predictive value; PLR, positive likelihood ratio; PPV, positive predictive value; PTPNR, posttest probability negative result; PTPPR, posttest probability positive result.
Of note, the higher the Youden index, the better the diagnostic performance of the predictor. The same is true for the global accuracy and the posttest probability ratio. At the simplest level, the performance of any given predictor is optimal when the sum of its sensitivity plus its specificity reaches a maximum level. In a perfect test (sensitivity and specificity both reach 1) this sum equals 2 and the Youden index equals 1 (sensitivity + specificity − 1). In nonperfect tests (those with both FN and FP results), the near-ideal situation is seen when a good Youden index is accompanied by a high sensitivity to reduce the probability of missing the condition sought. Indeed, an apparently good Youden index can result from an insufficient sensitivity accompanied by a very high specificity, in which case the predictor’s predictive power is diminished. In summary, the best predictor has the highest AUROC, the highest Youden index, and the highest sensitivity. Of note, the best single indicator of the usefulness of a given predictor of disease is the posttest probability ratio (posttest probability of a positive result/posttest probability of a negative result; see Table 1).
E-4. Areas under the curve of glucose and insulin
These areas were calculated by the trapezoid rule: time interval*average height of two adjacent measurements (i.e., 30 min*[(80 + 130)/2] = 30*105 = 3150 for such an interval). The calculated areas are expressed per minute.
E-5. Correlation coefficients and Student t test
Correlation between variables was calculated with Pearson correlations. Comparison between groups was done with the Student t test, as appropriate.
2. Results
The SSPG of the NIR subjects was 90.8 ± 4.2 mg/dL (39 to 149 mg/dL), whereas the corresponding value of the IR subjects was 229.4 ± 9.3 mg/dL (151 to 375 mg/dL, P < 0.0001). The lowest SSPG of the third tertile of these 90 values was ≥177 mg/d. However, the selected cutoff to label a subject as IR was ≥150 mg/dL (percentile 59, as explained later in this article).
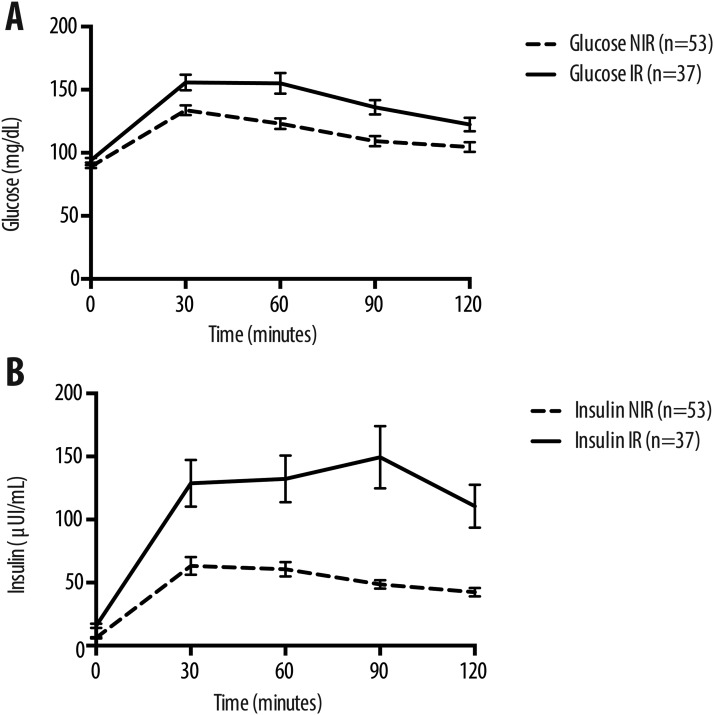
Table 1 shows Bayes-derived parameters and their formulas. Figure 1 and Table 2 show the serum glucose and insulin values at 0, 30, 60, 90, and 120 minutes from both the IR and the NIR subjects. At all times glucose and insulin values were statistically higher in IR compared with NIR subjects (P <0.05 to <0.0001). The highest mean serum insulin value was observed at 30 minutes in NIR subjects, whereas in IR subjects the maximal mean insulin value was observed at 90 minutes.
Figure 1.
Graphical representation of Table 2. Every mean ± SEM glucose or insulin value of the OGTT curve was higher in IR subjects than in NIR subjects. The differences in glucose curves between the two groups were amplified in the insulin curves.
Table 2.
Serum Glucose and Insulin Values During the OGTT
| G0 (mg/dL) | G30 (mg/dL) | G60 (mg/dL) | G90 (mg/dL) | G120 (mg/dL) | |
|---|---|---|---|---|---|
| NIR, n = 53 | 89.1 ± 1.2 | 133.7 ± 3.9 | 123.0 ± 4.3 | 109.3 ± 4.0 | 104.6 ± 3.8 |
| IR, n = 37 | 94.1 ± 1.9 | 155.7 ± 6.2 | 155.1 ± 8.2 | 136.0 ± 5.7 | 122.4 ± 5.3 |
| P | <0.05 | <0.005 | <0.0001 | <0.005 | <0.01 |
| I0 μIU/mL | I30 μIU/mL | I60 μIU/mL | I90 μIU/mL | I120 μIU/mL | |
|---|---|---|---|---|---|
| NIR, n = 53 | 6.3 ± 0.5 | 63.2 ± 7.1 | 60.6 ± 5.7 | 48.6 ± 3.4 | 42.4 ± 3.4 |
| IR, n = 37 | 15.8 ± 1.8 | 128.4 ± 18.6 | 132.3 ± 18.6 | 149.4 ± 24.6 | 110.5 ± 17.0 |
| P | <0.0001 | <0.0005 | <0.0005 | <0.0005 | <0.0005 |
At all times glucose and insulin values of the IR subjects were statistically higher than the corresponding values of the NIR subjects.
In Table 3 the Pearson correlation and the AUROC value of potential (n = 16) and traditional predictors of IR are shown. Both the correlation coefficient of the I0*G60 with the SSPG and its AUROC were higher than the respective values of the traditional predictors.
Table 3.
Pearson Correlation Coefficients and AUROCs of Potential (n = 16) and Traditional (n = 4) Predictors of Insulin Resistance
| Predictor | r | AUROC | Predictor | r | AUROC |
|---|---|---|---|---|---|
| G0 | 0.292 | 0.642 | AUC-Gl/′ | 0.516 | 0.760 |
| G30 | 0.438 | 0.632 | AUC-In/′ | 0.537 | 0.765 |
| G60 | 0.472 | 0.722 | AUC-Gl*In/′ | 0.586 | 0.805 |
| G90 | 0.392 | 0.736 | I0*G60 | 0.697 | 0.867 |
| G120 | 0.364 | 0.673 | I0*G90 | 0.607 | 0.863 |
| I0 | 0.604 | 0.822 | I0*G60-90 | 0.665 | 0.868 |
| I30 | 0.418 | 0.721 | HOMA1 | 0.629 | 0.829 |
| I60 | 0.484 | 0.712 | HOMA2 | 0.616 | 0.826 |
| I90 | 0.474 | 0.784 | QUICKI | −0.589 | 0.829 |
| I120 | 0.548 | 0.763 | ISI composite | −0.547 | 0.835 |
The highest correlation with the SSPG value was exhibited by the I0*G60, surpassing the respective coefficients of the traditional predictors. The two highest AUROCs were exhibited by the I0*G60-90 and by the I0*G60, both surpassing the respective AUROCs of the traditional predictors.
As shown in Table 4 all OGTT glucose and insulin values were predictive of IR (P = 0.0224 to P < 0.0001). The least predictive serum glucose value was observed at 30 minutes (AUROC 0.632, P = 0.013), whereas the most predictive one was at 90 minutes (AUROC 0.736, P = 0.001). The least predictive serum insulin value was observed at 60 minutes (AUROC 0.712, P = 0.0007), whereas the most predictive one was registered at time 0 (basal condition, AUROC 0.822, P < 0.0001).
Table 4.
ROC and Bayes Analyses of the OGTT Data
| G0 | G30 | G60 | G90 | G120 | |
|---|---|---|---|---|---|
| AUROC | 0.642 | 0.632 | 0.722 | 0.736 | 0.672 |
| Cutoff | >94 | >160.5 | >133.5 | >114.7 | >98.5 |
| P | 0.0224 | 0.013 | 0.0004 | 0.0001 | 0.0054 |
| Youden | 0.273 | 0.246 | 0.373 | 0.390 | 0.285 |
| Se-Sp-PPV | 0.407-0.868-0.682 | 0.378-0.868-0.667 | 0.656-0.698-0.610 | 0.730-0.660-0.600 | 0.811-0.472-0.522 |
| FN rate-PTPR-GA | 0.682-2.11-0.678 | 0.622-2.00-0.667 | 0.324-2.49-0.689 | 0.270-2.70-0.689 | 0.189-2.36-0.611 |
| I0 | I30 | I60 | I90 | I120 | |
|---|---|---|---|---|---|
| AUROC | 0.822 | 0.721 | 0.712 | 0.784 | 0.763 |
| Cutoff | >13.2 | >51.9 | >112.4 | >75.9 | >52.7 |
| P | <0.0001 | 0.0005 | 0.0007 | <0.001 | <0.0001 |
| Youden | 0.548 | 0.414 | 0.357 | 0.527 | 0.439 |
| Se-Sp-PPV | 0.568-0.981-0.955 | 0.811-0.604-0.588 | 0.432-0.925-0.800 | 0.751-0.660-0.609 | 0.703-0.736-0.650 |
| FN rate-PTPR-GA | 0.432-4.06-0.811 | 0.189-3.28-0.689 | 0.568-2.67-0.722 | 0.249-2.98-0.700 | 0.297-2.95-0.722 |
All 10 glucose and insulin values of the OGTT were predictive of IR. The highest AUROC was exhibited by I0 (0.822, P < 0.0001) and the lowest by G30 (0.632, P = 0.013). An I0 >13.2 μIU/mL and a G60 >133.5 mg/dL both predicted IR with low sensitivity.
Abbreviations: GA, global accuracy; PPV, positive predictive value; Se, sensitivity; Sp, specificity.
Table 5 also shows the Bayesian calculation results of the 10 OGTT values. The most promising potential predictor of IR, the basal insulin value, despite its high AUROC, displayed a low sensitivity (0.568), thus limiting its predictive power to diagnose IR.
Table 5.
ROC and Bayes Analyses of Six Potential Predictors of IR
| Predictors and Parameters | AUC-Gl/′ | AUC-In/′ | AUC-Gl*In/′ | I0*G60 | I0*G90 | I0*G60-90 |
|---|---|---|---|---|---|---|
| AUROC | 0.760 | 0.765 | 0.805 | 0.867 | 0.863 | 0.868 |
| Cutoff | >129.1 | >115 | >5816 | >1110 | >1203 | >1257 |
| P | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
| Youden | 0.514 | 0.441 | 0.488 | 0.657 | 0.681 | 0.699 |
| Se-Sp-PPV | 0.703-0.811-0.722 | 0.460-0.981-0.944 | 0.865-0.623-0.615 | 0.865-0.793-0.744 | 0.757-0.925-0.875 | 0.784-0.906-0.853 |
| FN rate-PTPR-GA | 0.297-3.55-0.767 | 0.540-3.40-0.767 | 0.135-4.68-0.722 | 0.135-7.00-0.822 | 0.243-5.64-0.856 | 0.216-5.97-0.856 |
The highest AUROC was exhibited by the I0*G60-90 (0.868), followed by the I0*G60 (0.863). Similarly, the highest Youden index was displayed by the I0*G60-90 (0.699), followed by the I0*G60 (0.681). In contrast, the highest sensitivity (0.865) and the lowest FN rate (0.135) were exhibited by the I0*G60. Moreover, the highest PTPR (7.0) was also displayed by the I0*G60.
Abbreviations: GA, global accuracy; PPV, positive predictive value; Se, sensitivity; Sp, specificity.
With these data, we explored the usefulness of six potential predictors of IR derived from the OGTT: AUC-Gl/′, AUC-In/′, AUC-Gl*In/′, I0*G60, I0*G90, and I0*G60-90.
Table 5 shows the AUROC, the cutoff value, the P value, and the Youden index for each of these six potential predictors. The two most promising potential predictors were the I0*G60 and the I0*G60-90, according to their AUROCs.
Table 5 also shows the Bayesian calculation results of these potential predictors: sensitivity (TP rate), specificity (TN rate), positive predictive value, posttest probability ratio (PTPR), and global accuracy. Despite the fact that I0*G60 had a Youden index below those of the I0*G90 and the I0*G60-90, it exhibited the highest PTPR value (7.0), the highest sensitivity (0.865), and consequently the lowest FN rate (0.135).
Table 6 shows the Bayes parameters of the I0*G60 compared with those of the I0 and the G60. It is clear that the I0*G60 exhibited much higher sensitivity (0.865 vs 0.568 and 0.676, respectively) and consequently a much lower FN rate (0.135 vs 0.432 and 0.334, respectively). Furthermore, the PTPR of the I0*G60 was higher than those of the I0 and the G60 (7.0 vs 4.06 and 2.49, respectively). The same happened with global accuracy (0.822 vs 0.811 and 0.689, respectively). When I0 and G60 are multiplied to produce the I0*G60, a remarkable improvement in predictive power takes place: AUROC rises to 0.867, and sensitivity reaches 0.865 (Tables 6 and 7).
Table 6.
Bayes Parameters of the I0*G60 Compared With I0 and G60
| Predictors With Cutoffs | Sensitivity | Specificity | PPV | FN Rate | PTPR | Global Accuracy |
|---|---|---|---|---|---|---|
| I0*G60 >1110 (>428 SI units) | 0.865 | 0.793 | 0.744 | 0.135 | 7.00 | 0.822 |
| I0 >13.2 | 0.568 | 0.981 | 0.955 | 0.432 | 4.06 | 0.811 |
| G60 >133.5 | 0.676 | 0.698 | 0.610 | 0.324 | 2.49 | 0.689 |
The sensitivity achieved by the I0*G60 (0.865) amply surpassed those of the I0 (0.568) and the G60 (0.676). The FN rate of the I0*G60 (0.135) was much lower than those of the I0 (0.432) and the G60 (0.324). Global accuracy of the I0*G60 (0.822) was higher than the corresponding values of the I0 (0.811) and the G60 (0.689).
Table 7.
ROC and Bayes Analyses of Traditional Predictors of IR Compared With the I0*G60
| Predictors With Cutoffs and Parameters | HOMA1 > 2.09 | HOMA2 > 1.24 | QUICKI < 0.341 | ISI Composite < 4.45 | I0*G60 > 1110 |
|---|---|---|---|---|---|
| AUROC | 0.829 | 0.826 | 0.829 | 0.835 | 0.867 |
| P | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 |
| Youden | 0.568 | 0.541 | 0.568 | 0.585 | 0.657 |
| Se-Sp-PPV | 0.757-0.811-0.737 | 0.730-0.811-0.730 | 0.757-0.811-0.737 | 0.811-0.774-0.714 | 0.865-0.793-0.744 |
| FN rate-PTPR-GA | 0.243-4.26-0.789 | 0.270-3.87-0.778 | 0.243-4.26-0.789 | 0.189-4.90-0.789 | 0.135-7.00-0.822 |
The I0*G60 exhibited the best AUROC, the best sensitivity, the lowest FN rate, and the highest PTPR, compared with the respective values of HOMA1, HOMA2, QUICKI, and ISI composite. Second in performance was the ISI composite. HOMA1 and QUICKI had similar performances (slightly better for QUICKI). HOMA2 displayed a weaker performance than HOMA1.
Abbreviations: GA, global accuracy; PPV, positive predictive value; Se, sensitivity; Sp, specificity.
Both I0 (>13.2 μIU/mL) and G60 (>133.5 mg/dL) predicted IR (AUROC 0.822 and 0.722, respectively) and correlated positively with SSPG (Pearson correlation of 0.623 and 0.499, respectively). In contrast, whereas I0 correlated positively with hepatic IR (r = 0.753), G60 did not (r = 0.071, NS). On the contrary, I0*G60 strongly correlated with hepatic IR (r = 0.746). Similarly, although I0 correlated positively with muscle IR (r = 0.262, P 0.017), G60 did not (r = −0.04, NS). Instead, I0*G60 correlated positively with muscle IR (r = 0.220, P 0.046). Both hepatic and muscle IR were calculated as shown by Abdul-Ghani et al. [23], and they were significantly lower in NIR subjects, compared with IR subjects (hepatic IR, 9352 ± 1415 vs 4017 ± 464, P < 0.001; muscle IR, 0.519 ± 0.03 vs 0.845 ± 0.08, P < 0.005).
Table 7 shows that the I0*G60 also exhibited better ROC analysis and Bayes parameters compared with those of the traditional biochemical predictors of IR. The ROC analysis–selected cutoff for this predictor was >1110 mg/dL*μIU/mL [equivalent to >428 nM*pM (1110*6.945/18)]. The I0*G60 performance clearly surpassed that of the ISI composite (the best performing of the traditional predictors of IR) in AUROC (0.867 vs 0.835), Youden index (0.657 vs 0.585), sensitivity (0.865 vs 0.811), FN rate (0.135 vs 0.189), and global accuracy rate (0.822 vs 0.789). Behind the ISI composite’s performance, HOMA1 and QUICKI displayed almost identical performances. Although HOMA1 and HOMA2 were highly correlated (r = 0.99), and their specificities were identical (0.811), and the sensitivity, positive predictive value, PTPR, and global accuracy of the older HOMA1 were slightly higher than the respective values of the newer, less accessible (computer-solved) HOMA2. On top of that, the FN rate of the HOMA2 was slightly higher than the respective value of the HOMA1.
Finally, the six best biochemical predictors of IR (SSPG ≥150 mg/dL) are arranged in Table 8 according to their PTPRs, the most effective indicator of the usefulness of a given predictor. The PTPR values of these predictors ranged from 7.0 (I0*G60) to 3.69 (HOMA2). Coincidentally, the best AUROC, the best sensitivity, the best Youden index, and the best global accuracy were displayed by the I0*G60. The second performance was that of the Matsuda-DeFronzo ISI composite, followed by AUC-Gli*In/′, QUICKI, HOMA1, and HOMA2.
Table 8.
Best 6 Predictors of Insulin Resistance (Cutoffs ≥150 and ≥177 mg/dL) Arranged According to Their PTPRs
| Predictors With Cutoffs | Cutoff | PTPR | AUROC | Sensitivity | Specificity | Positive Predictive Value | FN Rate | Youden Index | Global Accuracy |
|---|---|---|---|---|---|---|---|---|---|
| I0*G60 >1110 (>428 SI units) | ≥150 | 7.00 | 0.867 | 0.865 | 0.793 | 0.744 | 0.135 | 0.657 | 0.822 |
| ≥177 | 9.84 | 0.868 | 0.900 | 0.733 | 0.628 | 0.100 | 0.633 | 0.789 | |
| ISI composite <4.45 | ≥150 | 4.90 | 0.835 | 0.811 | 0.774 | 0.714 | 0.189 | 0.584 | 0.789 |
| ≥177 | 7.43 | 0.843 | 0.868 | 0.733 | 0.619 | 0.133 | 0.600 | 0.778 | |
| AUC-Gl*In/′ >5816 | ≥150 | 4.68 | 0.805 | 0.865 | 0.623 | 0.615 | 0.135 | 0.487 | 0.722 |
| ≥177 | 6.58 | 0.817 | 0.900 | 0.583 | 0.519 | 0.100 | 0.483 | 0.689 | |
| QUICKI <0.341 | ≥150 | 4.26 | 0.829 | 0.757 | 0.811 | 0.737 | 0.243 | 0.568 | 0.789 |
| ≥177 | 5.47 | 0.835 | 0.800 | 0.767 | 0.632 | 0.200 | 0.567 | 0.778 | |
| HOMA1 >2.09 | ≥150 | 3.87 | 0.826 | 0.793 | 0.811 | 0.730 | 0.207 | 0.541 | 0.778 |
| ≥177 | 5.47 | 0.836 | 0.800 | 0.767 | 0.632 | 0.200 | 0.567 | 0.778 | |
| HOMA2 >1.24 | ≥150 | 3.69 | 0.829 | 0.649 | 0.887 | 0.800 | 0.351 | 0.535 | 0.789 |
| ≥177 | 4.71 | 0.829 | 0.767 | 0.767 | 0.800 | 0.233 | 0.533 | 0.767 |
The highest PTPR, the best sensitivity, the best Youden index, and the best global accuracy were exhibited by the I0*G60, along with the lowest FN rate. The second performance was that of the ISI composite, followed by AUC-Gli*In/′, QUICKI, HOMA1, and HOMA2. Had we chosen the lowest value of the third tertile of the SSPG values (≥177 mg/dL) as the diagnostic cutoff to define IR (instead of ≥150 mg/dL) the ROC-defined cutoffs of the six best predictors would have remained unchanged, and the I0*G60 would have remained the best predictor. Exempting HOMA2, their AUROCs would have experienced a slight improvement. The sensitivities of the predictors would have improved, and their FN rates would have been reduced. However, the specificities would have been reduced, and the global accuracies would have fallen slightly (with the exemption of HOMA1). These changes would have occurred at the expense of labeling 18.9% of the IR subjects as NIR subjects.
As also shown in Table 8, had we chosen the lower limit of the third tertile of the SSPG values (≥177 mg/dL) as the cutoff value to diagnose IR, the ROC-determined cutoffs of the six best predictors would have remained unchanged, and the I0*G60 would have retained its place as the best predictor. Regarding their AUROCs, the respective figures, with the exception of HOMA2 (no change), experienced a slight improvement. Regarding sensitivities, all of them would have experienced an improvement, along with a concomitant reduction in FN rates. Specificities for all predictors would have declined, paralleling the increment in sensitivity. Of note, with the single exception of HOMA1 (no change), the global accuracy of these predictors would have fallen slightly. All these changes would have occurred at the expense of labeling 7 of 37 IR subjects (18.9%, those with an SSPG value between 150 and 177 mg/dL) as NIR subjects.
3. Discussion
Defining an SSPG cutoff value diagnostic of IR is crucial to appropriately calculate the predictive power of any biochemical predictor of IR. Reaven’s group followed two strategies to define this cutoff. One strategy was simply choosing the lower SSPG observed in the third tertile of IR of a healthy, nondiabetic population [24, 25] as the diagnostic cutoff for IR. The other strategy was to select a single figure, an SSPG ≥150 mg/dL [18], as the diagnostic cutoff. The first strategy yielded variable cutoffs, depending on the overall IR of the studied population. In fact, Abbasi et al. [24, 25] published two studies in 2018 with 454 and 535 apparently healthy subjects; the SSPG cutoff values defining IR were, respectively, ≥182 and ≥198 mg/dL (lower limit of the SSPG values for the third tertiles). For comparison, in our subjects, the lower limit of the SSPG values of the third tertile was ≥177 mg/dL, whereas the chosen cutoff to define the presence of IR was ≥150 mg/dL, equivalent to the percentile 59 of the SSPG values.
As mentioned, we opted to define the presence of IR with an SSPG of ≥150 mg/dL [19, 20]. The reasoning for this decision is as follows: as shown by Reaven’s group [26], insulin sensitivity in the population at large is distributed continuously and, consequently, SSPG values in the population vary widely (from a little less than 50 mg/dL to ∼350 mg/dL). Reaven’s group performed the PST in different groups of subjects, both including and excluding obese subjects, who are at high risk of being insulin resistant. When obese subjects were included in these studies, the lowest value of the third tertile of SSPG (the most IR subgroup) ranged between 182 to 198 mg/dL [24, 25]. However, when obese subjects were excluded from these studies, the lowest values of the third tertiles were reported to be substantially lower, ≥142.4 and ≥140.4 mg/dL [27, 28]. Nonobese subjects in the third tertile of the SSPG distribution have been followed prospectively and shown to be prone to cardiovascular [27] and age-related diseases [28]. In 2006 Reaven’s group [29], using the octreotide-modified protocol for the PST, labeled as insulin resistant those with an SSPG ≥145 mg/dL. In 2015, the same group labeled as insulin resistant subjects with an SSPG ≥150 mg/dL [18]. A single SSPG value defining IR is clinically advantageous over the opposing situation of variable diagnostic cutoffs, depending on the overall insulin sensitivity of the studied populations. In this regard, the chosen SSPG cutoff (≥150 mg/dL) is reasonable given the fact that, over time, subjects surpassing this cutoff have been shown to be prone to cardiovascular and age-related diseases [27, 28].
We were able to compare the IR predictive power of several traditional biochemical predictors of IR. Matsuda-DeFronzo’s ISI composite, reflecting both hepatic and muscle IR, was more efficient at diagnosing IR compared with predictors taken under fasting conditions (homeostatic predictors, reflecting hepatic IR only): HOMA1, HOMA2, and QUICKI.
QUICKI and HOMA1 were very similar in diagnostic efficiency, although QUICKI displayed slightly better numbers. The older HOMA1 turned out to be slightly more efficient than the newer HOMA2, which has the added inconvenience that its calculation requires software.
The 1 measurements of the OGTT were all positively correlated with the SSPG. The highest correlation with SSPG was exhibited by basal insulin (I0, r = 0.604). In addition, the highest AUROC was also displayed by basal insulin (I0, AUROC = 0.822). However, Bayesian calculation disclosed that the sensitivity of this simple parameter was to low (0.568) to serve as a useful predictor of IR. However, I0 had a very high positive predictive value (0.955, Table 4), which means that an I0 >13.2 μIU/mL is highly suggestive of IR. Unfortunately, an I0 below this figure does not rule out the presence of IR (low sensitivity). It is important to recall that I0 reflects islet secretion, insulin distribution, and insulin clearance, so an IR subject will not always have an elevated I0, and in fact, 43.2% of our IR subjects had an I0 <13.2 μΙU/mL (Table 4).
It is important to recall that Yeni-Komshian et al. [26] reported that in 490 healthy, nondiabetic subjects, the SSPG decile means varied widely between 47 (first decile) and 295 mg/dL (10th decile); in contrast, basal insulin means varied much less, from 7 (first decile) to 22 μIU/mL (10th decile). In other words, although both SSPG and I0 values rose from the first to the 10th decile, the SSPG increment was twice as steep as the insulin increment, and the respective curves were not parallel.
On the other hand, the OGTT glucose value most highly correlated with SSPG (r = 0.472) was observed at 60 minutes (G60). Again, the sensitivity of G60 was too low (0.656) to serve as a useful predictor of IR. Although a G60 >133.5 mg/dL predicts IR with low sensitivity (0.656), a G60 >155 mg/dL has been shown by Abdul-Ghani et al. [30] to predict the future development of type 2 diabetes with a sensitivity of 0.75 and a specificity of 0.79. In contrast, a G120 >140 mg/dL predicted the future diagnosis of diabetes less efficiently, with a sensitivity of just 0.51 and a specificity of 0.91. Thus, crucial information is provided by the G60 concerning the risk of actual IR and the risk of future diabetes.
These reflections on the information present in both I0 and G60 may partially explain the unexpected excellent performance of the I0*G60 in predicting the presence of IR.
We tested six potential predictors of IR by using two or more values of the OGTT: AUC-Gl/′, AUC-In/′, AUC-Gl*In/′, I0*G60, I0*G90, and I0*G60-90. Of those six potential predictors, only two (I0*G60 and AUC-Gl*In/′) finally ranked among the six best biochemical predictors of IR, joining HOMA1, HOMA2, QUICKI, and Matsuda-DeFronzo ISI composite. Although the performance of the AUC-Gl*In/′ was better than the respective performances of QUICKI, HOMA1, and HOMA2, it was inferior to the Matsuda-DeFronzo ISI composite’s performance, at the same cost.
As already discussed, the I0*G60, despite its simplicity, turned out to be the most powerful predictor of IR in our cohort of 90 nondiabetic subjects. A simple OGTT with three glucose measurements (0, 60, and 120 minutes) and a single basal insulin measurement would allow categorizing a patient both in terms of glucose tolerance and insulin sensitivity. The cost of the I0*G60 is modest, and it can be calculated manually.
The performance of the I0*G60 is promising, but its real value will be defined over time, provided that other investigators and clinicians working in various settings and different locations are willing to explore its usefulness. If a given patient, strongly suspected of being insulin resistant, exhibits an I0*G60 value below its ROC-defined cutoff, it would be advisable to perform a PST to establish clearly his or her insulin sensitivity status. If a PST is not possible to perform, we would treat such a patient as an IR subject. After all, weight loss, exercise, and a metformin prescription will probably produce much more benefit than eventual harm. The whole idea is to avoid depriving IR patients of adequate treatment.
Setting up a PST is feasible for most clinical facilities. Compared with the HEC, the PST is simpler to perform and much less expensive. Although it takes 3 hours of work, the greatest expense of the procedure is the octreotide ampoule. Side effects of the PST rare, and, when present (mainly gastrointestinal discomfort or a headache), they are usually mild. An added advantage of having the PST as a backup for the diagnosis of IR is the possibility of keeping a continuous and rigorous evaluation of the predictors of IR. Without doubt, the HEC remains the gold standard to measure insulin sensitivity directly; however, few groups are able to perform it on a regular basis given its expense and technical complexity. In contrast, the PST is within the reach of many research groups around the world. The direct measurement of insulin sensitivity by PST is feasible for most research groups.
Acknowledgments
Financial Support: Reproductive Health Research Institute research grant A2018 to P.H.C.
Disclosure Summary: The authors have nothing to disclose.
Glossary
Abbreviations:
- AUC
area under the curve
- AUROC
area under the receiver operating characteristic curve
- FN
false negative
- FP
false positive
- Gl
glucose value
- HEC
hyperinsulinemic euglycemic clamp
- HOMA
homeostatic model assessment
- I0
basal insulin
- In
insulin value
- IR
insulin resistance
- ISI
insulin sensitivity index
- NIR
non–insulin-resistant
- OGTT
oral glucose tolerance test
- PST
pancreatic suppression test
- PTPR
posttest probability ratio
- QUICKI
quantitative insulin sensitivity check index
- ROC
receiver operating characteristic
- SSPG
steady-state plasma glucose
- TN
true negative
- TP
true positive
References and Notes
- 1. DeFronzo RA, Tobin JD, Andres R. Glucose clamp technique: a method for quantifying insulin secretion and resistance. Am J Physiol. 1979;237(3):E214–E223. [DOI] [PubMed] [Google Scholar]
- 2. Cheal KL, Abbasi F, Lamendola C, McLaughlin T, Reaven GM, Ford ES. Relationship to insulin resistance of the adult treatment panel III diagnostic criteria for identification of the metabolic syndrome. Diabetes. 2004;53(5):1195–1200. [DOI] [PubMed] [Google Scholar]
- 3. McLaughlin T, Abbasi F, Cheal K, Chu J, Lamendola C, Reaven G. Use of metabolic markers to identify overweight individuals who are insulin resistant. Ann Intern Med. 2003;139(10):802–809. [DOI] [PubMed] [Google Scholar]
- 4. Falta W, Boller R. Insularer und insulinresistenter diabetes. Klin Wochenschr. 1931;10(10):438–443. [Google Scholar]
- 5. Himsworth HP. Diabetes mellitus: its differentiation into insulin-sensitive and insulin-insensitive types. Lancet. 1936;227(5864):127–130. [Google Scholar]
- 6. Lancereaux E. Le diabète maigre: ses symptômes, son évolution, son pronostic et son traitement; ses rapports avec les alterations du pancréas. Union Med (Paris). 1880;29:161–168. [Google Scholar]
- 7. Reaven GM. Banting lecture 1988. Role of insulin resistance in human disease. Diabetes. 1988;37(12):1595–1607. [DOI] [PubMed] [Google Scholar]
- 8. Shen S-W, Reaven GM, Farquhar JW. Comparison of impedance to insulin-mediated glucose uptake in normal subjects and in subjects with latent diabetes. J Clin Invest. 1970;49(12):2151–2160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Greenfield MS, Doberne L, Kraemer F, Tobey T, Reaven G. Assessment of insulin resistance with the insulin suppression test and the euglycemic clamp. Diabetes. 1981;30(5):387–392. [DOI] [PubMed] [Google Scholar]
- 10. Knowles JW, Assimes TL, Tsao PS, Natali A, Mari A, Quertermous T, Reaven GM, Abbasi F. Measurement of insulin-mediated glucose uptake: direct comparison of the modified insulin suppression test and the euglycemic, hyperinsulinemic clamp. Metabolism. 2013;62(4):548–553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Ferrannini E, Mari A. How to measure insulin sensitivity. J Hypertens. 1998;16(7):895–906. [DOI] [PubMed] [Google Scholar]
- 12. Mathews DR, Hosker JP, Rudenski AS, Naylor BA, Treacher DF, Turner RC. Homeostasis model assessment: insulin resistance and β-cell function from fasting glucose and insulin in man. Diabetologia. 1985;28(7):412–419. [DOI] [PubMed] [Google Scholar]
- 13. Katz A, Nambi SS, Mather K, Baron AD, Follmann DA, Sullivan G, Quon MJ. Quantitative insulin sensitivity check index: a simple, accurate method for assessing insulin sensitivity in humans. J Clin Endocrinol Metab. 2000;85(7):2402–2410. [DOI] [PubMed] [Google Scholar]
- 14. Matsuda M, DeFronzo RA. Insulin sensitivity indices obtained from oral glucose tolerance testing: comparison with the euglycemic insulin clamp. Diabetes Care. 1999;22(9):1462–1470. [DOI] [PubMed] [Google Scholar]
- 15. Levy JC, Matthews DR, Hermans MP. Correct homeostasis model assessment (HOMA) evaluation uses the computer program. Diabetes Care. 1998;21(12):2191–2192. [DOI] [PubMed] [Google Scholar]
- 16. Harano Y, Ohgaku S, Hidaka H, Haneda K, Kikkawa R, Shigeta Y, Abe H. Glucose, insulin and somatostatin infusions for the determination of insulin sensitivity. J Clin Endocrinol Metab. 1977;45(5):1124–1127. [DOI] [PubMed] [Google Scholar]
- 17. Pei D, Jones CNO, Bhargava R, Chen YDI, Reaven GM. Evaluation of octreotide to assess insulin-mediated glucose disposal by the insulin suppression test. Diabetologia. 1994;37(8):843–845. [DOI] [PubMed] [Google Scholar]
- 18. Kim MK, Reaven GM, Chen YD, Kim E, Kim SH. Hyperinsulinemia in individuals with obesity: role of insulin clearance. Obesity (Silver Spring). 2015;23(12):2430–2434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Vigil P, Contreras P, Alvarado JL, Godoy A, Salgado AM, Cortés ME. Evidence of subpopulations with different levels of insulin resistance in women with polycystic ovary syndrome. Hum Reprod. 2007;22(11):2974–2980. [DOI] [PubMed] [Google Scholar]
- 20. Contreras PH, Serrano FG, Salgado AM, Vigil P. Insulin sensitivity and testicular function in a cohort of adult males suspected of being insulin-resistant. Front Med (Lausanne). 2018;5:190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.RRID:AB_2750939, http://antibodyregistry.org/search.php?q=AB_2750939.
- 22. Hosmer DW, Lemeshow S. Applied Logistic Regression. 2nd edHoboken, NJ: John Wiley & Sons; 2000:154–164. [Google Scholar]
- 23. Abdul-Ghani MA, Matsuda M, Balas B, DeFronzo RA. Muscle and liver insulin resistance indexes derived from the oral glucose tolerance test. Diabetes Care. 2007;30(1):89–94. [DOI] [PubMed] [Google Scholar]
- 24. Abbasi F, Silvers A, Viren J, Reaven GM. Relationship between several surrogate estimates of insulin resistance and a direct measure of insulin-mediated glucose disposal: comparison of fasting versus post-glucose load measurements. Diabetes Res Clin Pract. 2018;136:108–115. [DOI] [PubMed] [Google Scholar]
- 25. Abbasi F, Shiffman D, Tong CH, Devlin JJ, McPhaul MJ. Insulin resistance probability scores for apparently healthy individuals. J Endocr Soc. 2018;2(9):1050–1057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Yeni-Komshian H, Carantoni M, Abbasi F, Reaven GM. Relationship between several surrogate estimates of insulin resistance and quantification of insulin-mediated glucose disposal in 490 healthy nondiabetic volunteers. Diabetes Care. 2000;23(2):171–175. [DOI] [PubMed] [Google Scholar]
- 27. Yip J, Facchini FS, Reaven GM. Resistance to insulin-mediated glucose disposal as a predictor of cardiovascular disease. J Clin Endocrinol Metab. 1998;83(8):2773–2776. [DOI] [PubMed] [Google Scholar]
- 28. Facchini FS, Hua N, Abbasi F, Reaven GM. Insulin resistance as a predictor of age-related diseases. J Clin Endocrinol Metab. 2001;86(8):3574–3578. [DOI] [PubMed] [Google Scholar]
- 29. Abbasi F, Farin HMF, Lamendola C, McLaughlin T, Schwartz EA, Reaven GM, Reaven PD. The relationship between plasma adiponectin concentration and insulin resistance is altered in smokers. J Clin Endocrinol Metab. 2006;91(12):5002–5007. [DOI] [PubMed] [Google Scholar]
- 30. Abdul-Ghani MA, Williams K, DeFronzo RA, Stern M. What is the best predictor of future type 2 diabetes? Diabetes Care. 2007;30(6):1544–1548. [DOI] [PubMed] [Google Scholar]