A theory of reactant-stationary kinetics for a mechanism of zymogen activation

Abstract

A theoretical analysis is performed on the nonlinear ordinary differential equations that govern the dynamics of a reaction mechanism of zymogen activation. The reaction consists of a primary non-observable zymogen activation reaction that it is coupled to an indicator (observable) reaction. The product of the first reaction is the enzyme of the indicator reaction, and both reactions are governed by the Michaelis–Menten reaction mechanism. Using singular perturbation methods, we derive asymptotic solutions that are valid under the quasi-steady-state and reactant-stationary assumptions. In particular, we obtain closed form solutions that are analogous to the Schnell–Mendoza equation for Michaelis–Menten type reactions. These closed-form solutions approximate the evolution of the observable reaction and provide the mathematical link necessary to measure the enzyme activity of the non-observable reaction. Conditions for the validity of the asymptotic solutions are also derived, and we demonstrate that these asymptotic expressions are applicable under reactant-stationary kinetics.

Graphical Abstract

1. Introduction

Many enzyme catalyzed reactions that occur in physiological processes require an activation step in which a precursor of a zymogen (inactive enzyme precursor or pro-enzyme) is converted to an active enzyme. This process, known generally as zymogen activation [1], is typically the first step in a cascade of coupled enzyme catalyzed reactions [2]. The activation step of the zymogen is itself an enzyme catalyzed reaction, and the inactive enzyme precursor is activated by a functional enzyme. The active enzyme can be generated by enzyme-catalyzed proteolosis or enzyme activation by phosphorylation [3]. For example, the digestive enzyme trypsin, which is the activate form of trypsinogen, is activated by the enzyme enterokinase; trypsin can then bind with trypsinogen to convert remaining trypsinogen into trypsin [2]. Likewise, plasminogen is activated by streptokinase to form plasmin (an enzyme), which then degrades fibrin (a substrate) to break down clots in blood coagulation [4]. Denoting the active enzyme, zymogen, activated enzyme, and intermediate complex of the activation reaction as E₁, $E_2^i$, E₂, and C₁ respectively, the preliminary zymogen activation step coupled with its secondary enzyme-catalyzed reaction can be expressed with the following reaction mechanism:

$$E_1+E_2^i\underset{{}_{k_{-1}}}{\overset{{}^{k_1}}{\rightleftharpoons }}{C}_1\stackrel{{}^{{}^{k_2}}}{\to }{E}_1+E_2.$$ (1)

Regardless of the reactants, the zymogen activation step simply produces E₂. The secondary reaction occurs when E₂ and substrate S bind to synthesize the final product P:

$$E_2+S\underset{{}_{k_{-3}}}{\overset{{}^{k_3}}{\rightleftharpoons }}{C}_2\stackrel{{}^{{}^{k_4}}}{\to }P+E_2.$$ (2)

In the above chemical pathways, k₁, k₋₁, k₃, k₋₃ are rate constants, and k₂, k₄ are catalytic constants.

As mentioned previously, the reaction mechanism of zymogen activation (1)–(2) occurs naturally in coagulation cascades [5]. As a distinct example, the activation of protein C (PC) by thrombin (T) follows a reaction consistent with (1):

$$T+PC\underset{{}_{{}_{k_{-1}}}}{\overset{{}^{{}^{k_1}}}{\rightleftharpoons }}TPC\stackrel{{}^{{}^{{}^{k_2}}}}{\to }T+APC$$ (3)

where “APC” denotes the activated form of PC. Assuming S is specific to APC and does not bind with T, the secondary observable reaction follows the form of (2):

$$APC+S\underset{{}_{{}_{k_{-3}}}}{\overset{{}^{{}^{k_3}}}{\rightleftharpoons }}SAPC\stackrel{{}^{{}^{{}^{k_4}}}}{\to }APC+P.$$ (4)

Another interesting aspect of coupled enzyme catalyzed reactions with a zymogen activation step (1)–(2) is the quantification of the catalytic conversion of zymogen in vitro. Formally, the quantification of enzyme activity through measurements obtained from an in vitro assay is mathematically known as an inverse problem. If the activation step (1) is not detectable experimentally (i.e., non-observable), then the secondary reaction step (2) is selected to be an easily observable reaction. This is done with the goal of measuring the enzyme activity of the non-observable reaction through analysis of progress curves generated by the observable reaction. In this case, the secondary reaction step (2) is known as the indicator reaction. Traditionally, coupled enzyme assays are designed so that the product of the non-observable reaction is a substrate for the secondary enzyme in the indicator reaction (see [6] for specific applications). While this type of assay is well-studied [7, 8, 9, 10], in vitro assays that consist of a zymogen activation step have not been analyzed with the same degree of interest.

The kinetics of the non-observable zymogen activation step is measured by decoupling the analysis of progress curves by adding excessive concentrations E₁. The assumption is then made that the first reaction (the activation step) is pseudo-first order (PFO) [5]. However, it has been demonstrated that an excessive concentration of E₁ is not sufficient to guarantee the validity of PFO model. Instead, it is necessary that initial concentration of zymogen for (1) be much less than the Michaelis constant of the primary reaction [11]. Thus, from an experimental point of view, it is difficult to ensure the validity of the PFO model when the Michaelis constant is unknown.

Since PFO models are difficult to validate when the Michaelis constant is unknown, it is more convenient to rely on the quasi-steady-state (QSS) models when quantifying enzyme activity in vitro. If appropriate experimental conditions are employed, then the MM reaction mechanism (5),

$$E+S\underset{{}_{{}_{k_{-}}}}{\overset{{}^{{}^k}}{\rightleftharpoons }}C\stackrel{{}^{{}^{{}^{k_{\text{cat}}}}}}{\to }P+E,$$ (5)

will obey QSS kinetics, and the rate of substrate depletion for the reaction is described by the MM equation

$$\stackrel{.}{s}=-\frac{V}{K_M+s}s,$$ (6)

where s is the concentration of S, K_M ≡ (k₋ + k_cat)/k is the Michaelis constant, and V ≡ k_cate₀ is the limiting rate of the reaction (5). Note that the zymogen activation step in (1)–(2) is a single-enzyme, single-substrate reaction. Once the QSS model is established, the inverse problem is carried out in two stages. First, experimental data is produced in the form of a progress curve for either s or p (we have used lower case letters to denote the concentrations of S and P respectively). Second, the experimental data is then used to estimate both K_M and V by optimally fitting the model (6) through the utilization of either a deterministic (i.e., such as Levenburg-Marquardt) or a stochastic (Markov Chain Monte Carlo) algorithm. In general, one seeks to estimate kinetic constants with an expression that contains the fewest number of parameters: this is why the MM equation is more attractive than the complete set of mass action equations. The MM equation is known as a reduced model; it is reduced in the sense that it contains fewer variables (s versus s and c) and fewer parameters (K_M and V versus k, k₋ and k_cat).

The inverse problem presents a unique challenge for both experimentalists and theorists in coupled enzyme assays like (1)-(2). First, the parameters that govern the enzyme activity of the non-observable reaction must somehow be determined from the indicator reaction, since progress curves from a typical in vitro laboratory experiment can only be generated for the indicator reaction. Second, a reduced model for the model mechanism of zymogen activation (1)–(2) must be developed. The reduced model should: (1) decrease the number of variables, and (2) lessen the number of parameters needed to describe the time course of the reaction mechanism (1)–(2).

1.1. Goals of this paper

The primary goal of this paper is the derivation of a reduced model that can be utilized to quantify the enzyme activity for an experimental assay of the model mechanism of zymogen activation (1)–(2). Central to the derivation will be the application of slow manifold projection. This is challenging for coupled reactions, since the time to completion of the indicator reaction can occur before, after, or at approximately the same time as the non-observable reaction. Furthermore, it is unlikely that the relative speeds and completion time of the non-observable reaction will be known. Thus, there is a need derive a reduced model that is general enough so that its validity is certain regardless of which reaction is faster. Finally, we will seek a model that admits a closed form solution. This will eliminate the need to generate explicit progress curves for substrate depletion of the primary reaction since the time course of substrate (i.e., $E_2^i$) is unknown in coupled enzyme assays.

1.2. Structure of this paper

As mentioned previously, the theoretical reduction analysis of zymogen activation reactions has been limited to PFO models [12, 1, 13, 4, 2]. Such models have limited validity in time course experiments [11], and the aim of this work is first and foremost to take a necessary “first step” in the nonlinear analysis of such reactions. First, we will introduce proper scaling techniques that can be employed in a general methodology to more complicated reactions. In Section 3 we will show how to estimate timescales based on these scaling methods, and we will formulate a reduced model from the analysis of these timescales (Section 4). The reduced model admits closed-form solutions in the form of a Schnell–Mendoza equation [14], and conditions for the validity of the model will be established. In addition, we will exploit the geometry of the mathematical structure [15, 16] in extreme situations when the speeds of the reactions are significantly disparate. This will allow us to “simplify” the reduced model and obtain asymptotic solutions that are essentially less complicated (in form) than both the general reduced model and the system of mass action equations. Finally, in Section 7, we conclude with a brief discussion of the results and their relevance in possible future work involving the inverse problem.

2. Derivation of the governing equations for the reaction mechanism of zymogen activation (1)–(2)

We first consider the mass action formulation of the zymogen activation reaction mechanism (1)–(2). In reaction (1), the zymogen $E_2^i$ is effectively a substrate. To distinguish mathematically between substrates and enzymes in (1)–(2), we will change notation by replacing $E_2^i$ with S₁ in (1), and S with S₂ in (2). Applying the law of mass action yields seven rate equations

$${\stackrel{.}{e}}_1=-k_1{e}_1{s}_1+(k_{-1}+k_2)c_1,$$ (7a)

$${\stackrel{.}{s}}_1=-k_1{e}_1{s}_1+k_{-1}{c}_1,$$ (7b)

$${\stackrel{.}{c}}_1=k_1{e}_1{s}_1-(k_{-1}+k_2)c_1,$$ (7c)

$${\stackrel{.}{e}}_2=k_2{c}_1-k_3{e}_2{s}_2+(k_{-3}+k_4)c_2,$$ (7d)

$${\stackrel{.}{s}}_2=-k_3{e}_2{s}_2+k_{-3}{c}_2,$$ (7e)

$${\stackrel{.}{c}}_2=k_3{e}_2{s}_2-(k_{-3}+k_4)c_2,$$ (7f)

$$\stackrel{.}{p}=k_4{c}_2,$$ (7g)

where lowercase letters represent concentrations of the corresponding uppercase species. Typically, laboratory enzyme assays present the following initial conditions

$$(e_1,s_1,c_1,e_2,s_2,c_2,p){\mid }_{t=0}=(e_1^0,s_1^0,0,0,s_2^0,0,0).$$ (8)

We will subsequently refer to (8) as experimental initial conditions. By examining the system of rate equations (7), the reaction mechanism of zymogen activation (1)–(2) obeys three conservation laws:

$$e_1(t)+c_1(t)=e_1^0,$$ (9a)

$$s_1(t)+c_1(t)+c_2(t)+e_2(t)=s_1^0,$$ (9b)

$$s_2(t)+c_2(t)+p(t)=s_2^0.$$ (9c)

The solution trajectory to (7) must lie on the intersection of the hyperplanes defined in (9). This implies the presence of conserved quantities which can be used to reduce the dimension of the problem. Using (9a) and (9b) to decouple the enzyme concentrations, the redundancies in the system (7) are eliminated to yield

$${\stackrel{.}{s}}_1=-k_1(e_1^0-c_1)s_1+k_{-1}{c}_1,$$ (10a)

$${\stackrel{.}{c}}_1=k_1(e_1^0-c_1)s_1-(k_{-1}+k_2)c_1,$$ (10b)

$${\stackrel{.}{s}}_2=-k_3(s_1^0-s_1-c_1-c_2)s_2+k_{-3}{c}_2,$$ (10c)

$${\stackrel{.}{c}}_2=k_3(s_1^0-s_1-c_1-c_2)s_2-(k_{-3}+k_4)c_2,,$$ (10d)

where e₁(t), e₂(t) and p(t) are readily calculated once s₁(t), c₁(t), s₂(t) and c₂(t) are known.

3. Rate expressions for the non-observable enzyme catalyzed reaction

The rate equations (10a)–(10b) are uncoupled from (10c)–(10d), and have the same structure to those of the single-substrate, single-enzyme reaction that follows the MM mechanism. Therefore, it is possible to derive rate equations to model the reaction mechanism of zymogen activation (1)–(2), and estimate its kinetic parameters using the general theory of the reactant-stationary assumption (RSA, [17]).

3.1. Review of the single substrate, single enzyme MM reaction

It has long been established from the analysis of single-enzyme, single-substrate reactions that there there can be a rapid buildup of c₁ during an initial fast transient of the non-observable reaction. After the rapid buildup, c₁ is assumed to be in a QSS, and the rate of depletion of c₁ approximately equals its rate of formation:

$${\stackrel{.}{c}}_1\approx 0\text{for}t>t_{c_1}.$$ (11)

The timescale t_c1 is the time associated with the initial transient buildup of c₁, and is independent of the initial concentration of E₁:

$$t_{c_1}=\frac{1}{k_1(K_{M_1}+s_1^0)}.$$ (12)

In the above equation, K_M1 = (k₋₁ + k₂)/k₁ is the Michaelis constant for the zymogen activation step (1). The quasi-steady-state assumption (QSSA, 11), in combination with (10a)–(10b), leads to the derivation of the well-known rate expressions

$$c_1=\frac{e_1^0}{K_{M_1}+s_1}{s}_1$$ (13a)

$${\stackrel{.}{s}}_1=-\frac{V_1}{K_{M_1}+s_1}{s}_1.$$ (13b)

In (13b), $V_1\equiv k_2{e}_1^0$ is the limiting rate of the zymogen reaction. Note that the mass action equations (10a)–(10b) are reduced to a differential-algebraic equation systems with a single differential equation for s₁ in (13a)–(13b).

Since equations (13a) and (13b) are only valid after the initial fast transient, t_c1, it is necessary to define a boundary condition for s₁ at t = t_c1. We will assume that there is a negligible decrease in s₁ during the initial buildup of c₁. This is equivalent to the initial experimental condition for the initial rate or time course experiments. The assumption that the depletion of s₁ is negligible over the fast transient is known as the RSA. Formally, the RSA is

$$s_1(t<t_{c_1})\approx s_1^0.$$ (14)

The RSA provides an initial condition for (10a) under the variable transformation $\widehat{t}\mapsto t-t_{c_1}$. The mathematical expression (13b) is the MM equation, and the system (13a)–(13b) governs the dynamics of the substrate s₁ and complex c₁ of the non-observable reaction under the QSS and RSA. The explicit closed-form solution of (13b), with the initial condition (14), is known as the Schnell–Mendoza equation [14], and is written in terms of the Lambert-W function:

$$\frac{s_1(\widehat{t})}{K_{M_1}}=W[{\sigma }_1\text{exp}({\sigma }_1-{\eta }_1\widehat{t})],{\sigma }_1=\frac{s_1^0}{K_{M_1}},{\eta }_1=\frac{V_1}{K_{M_1}}.$$ (15)

Asymptotically, Schnell and Mendoza [14] have provided a piecewise solution for the MM reaction in terms of a fast transient solution for s₁ (16a) and a QSS solution for s₁ (16b):

$$s_1\simeq s_1^0,t\le t_{c_1}$$ (16a)

$$s_1\simeq K_{M_1}W[{\sigma }_1\text{exp}({\sigma }_1-{\eta }_1\widehat{t})],t>t_{c_1}.$$ (16b)

In addition, from the earlier work of Segel [18], we have the corresponding approximation for c₁:

$$c_1\simeq {\stackrel{‒}{c}}_1[1-\text{exp}(-t∕t_{c_1})]\text{with}{\stackrel{‒}{c}}_1=\frac{e_1^0}{K_{M_1}+s_1^0}{s}_1^0,t>t_{c_1},$$ (17a)

$$c_1\simeq \frac{e_1^0}{K_{M_1}+s_1}{s}_1,t\ge t_{c_1}.$$ (17b)

Collectively, equations (16a)–(17b) constitute an asymptotic solution that serves as an accurate approximation to the full time course of (10) when the appropriate qualifiers (i.e, the RSA and the QSSA) are obeyed.

The time it takes for the majority of the substrate s₁ to deplete is given by t_s1. Although there are several methods for estimating the significant timescales of chemical reactions [19], we employ the heuristic method proposed by Segel [18], and approximate the depletion time to be effectively the total depletion of s₁ (the total depletion is $s_1^0$) divided by the maximum rate of substrate of depletion after t_c1:

$$t_{s_1}=\frac{\Delta s_1}{\underset{0\le t}{\max }\mid {\stackrel{.}{s}}_1\mid }=\frac{K_{M_1}+s_1^0}{V_1}.$$ (18)

Generally speaking, t_s1 is a reasonable measure of how long it takes for a significant amount of s₁ to deplete, although its precise interpretation depends on the magnitude of σ₁.

3.2. Geometrical picture of the enzyme catalyzed reaction, and conditions for the validity of asymptotic solutions of the rate equations

While the asymptotic solutions are useful in that they can be employed to make certain predictions about the behavior of the reaction, asymptotic theory fails to yield a visual or geometric understanding of the dynamical behavior of the zymogen activation reaction mechanism (1)–(2). To paint a complete picture of the mathematical structure behind the reaction mechanism, we turn to dynamical systems theory, and analyze this problem from phase space. From this perspective, after the initial buildup of c₁, the phase space trajectory of the non-observable reaction (10a)–(10b) hugs a slow manifold, ${\mathcal{M}}_{\epsilon }$, and is asymptotic to ${\mathcal{M}}_{\epsilon }$ in the approach to equilibrium. The time it takes for the trajectory to reach the slow manifold is approximately t_c1, and the time it takes for the trajectory to equilibrium is approximately t_s1. The condition for the validity of the asymptotic solution resides in how well the c₁-nullcline approximates the slow manifold, and also how straight the phase space trajectory is in its approach to the slow manifold during the initial fast transient. The former of these conditions is known as the QSSA, and the latter is of course the geometrical interpretation of the RSA. We note that if the trajectory is close to ${\mathcal{M}}_{\epsilon }$, then the complex C₁ is assumed to be in a QSS and the difference between the rate of C₂ depletion is approximately equal to the rate C₂ formation.

It was originally proposed that (16a)–(16b) was valid if t_c1 ≪ t_s1. However, although timescale separation is necessary, the validity of (16a)–(16b) is actually determined by the validity of the RSA. To determine the criteria for the validity of the RSA, Segel [20] proposed that if one assumes little change in s₁ during the approach to the slow manifold (an almost straight phase space trajectory towards the slow manifold), then it should hold that

$$\underset{t\ge 0}{\max }\mid {\stackrel{.}{s}}_1\mid \cdot t_{c_1}\ll s_1^0.$$ (19)

Since $\mid {\stackrel{.}{s}}_1\mid \le k_1{s}_1^0{e}_1^0$, the strict inequality given in (19) translates to

$$\frac{e_1^0}{K_{M_1}+s_1^0}\equiv \epsilon \ll 1.$$ (20)

Through scaling analysis, Segel [18] went on to show that the RSA determines single-handedly the validity of the asymptotic solutions² (16) and (17). Introducing the dimensionless variables ${\widehat{s}}_1=s_1∕s_1^0$ and ${\widehat{c}}_1=c_1∕{\stackrel{‒}{c}}_1$, Segel and Slemrod [20] demonstrated that, with respect to the dimensionless timescale τ = t/t_c1, equations (10a)–(10a) scale as

$$\frac{d{\widehat{s}}_1}{d\tau }=\epsilon \left[-{\widehat{s}}_1+\frac{{\sigma }_1}{{\sigma }_1+1}{\widehat{c}}_1{\widehat{s}}_1+\frac{{\kappa }_1(1+{\kappa }_1{)}^{-1}}{{\sigma }_1+1}{\widehat{c}}_1\right],$$ (21a)

$$\frac{d{\widehat{c}}_1}{d\tau }={\widehat{s}}_1-\frac{{\sigma }_1}{{\sigma }_1+1}{\widehat{c}}_1{\widehat{s}}_1-\frac{1}{{\sigma }_1+1}{\widehat{c}}_1,$$ (21b)

where κ₁ = k₋₁/k₂. Moreover, (10a)-(10a) become

$$\frac{d{\widehat{s}}_1}{dT}=({\kappa }_1+1)({\sigma }_1+1)\left[-{\widehat{s}}_1+\frac{{\sigma }_1}{{\sigma }_1+1}{\widehat{c}}_1{\widehat{s}}_1+\frac{{\kappa }_1(1+{\kappa }_1{)}^{-1}}{{\sigma }_1+1}{\widehat{c}}_1\right],$$ (22a)

$$\epsilon \frac{d{\widehat{c}}_1}{dT}=({\kappa }_1+1)({\sigma }_1+1)\left[{\widehat{s}}_1-\frac{{\sigma }_1}{{\sigma }_1+1}{\widehat{c}}_1{\widehat{s}}_1-\frac{1}{{\sigma }_1+1}{\widehat{c}}_1\right],$$ (22b)

when the time is scaled with respect to the depletion timescale T = t/t_s1. Thus, it is apparent from the dimensionless equations (21a)-(22b) that if ε ≪ 1, then not only will the RSA hold, but the QSSA also holds. In fact the RSA (i.e., ε ≪ 1) is more restrictive than separation of timescales. After some algebraic calculations, the separation of timescales (t_c1/t_s1 ≪ 1) is equivalently expressed as

$$\frac{e_1^0}{K_{M_1}+s_1^0}\ll \left(1+\frac{K_{S_1}}{K_1}\right)\left(1+\frac{s_1^0}{K_{M_1}}\right),$$ (23)

where K_S1 = k₋₁/k₁, and K₁ = k₂/k₁. For the RSA to be valid, the condition

$$\frac{e_1^0}{K_{M_1}}\ll \left(1+\frac{s_1^0}{K_{M_1}}\right),$$ (24)

must be satisfied; this is more stringent than condition (23), and hence dictates the conditions under which equation (13b) or (15) can be applied. For this reason, the MM expressions are considered valid under the RSA (see Figures 1a and 1b) rather than the QSSA [21].

Figure 1:

Geometrical picture of the single-substrate, single-enzyme non-observable reaction (1) representing the zymogen activation step. (a) Phase space dynamics with $e_1^0=10$, k₁ = 1, k₂ = 1 and k₋₁ = 1. (b) Phase space dynamics with $e_1^0=1$, $s_1^0=78$, k₁ = 1, k₂ = 5 and k₋₁ = 1. As ε → 0, the accumulation of c₁ is more rapid, and the c₁-nullcline (dashed red curve) becomes a better approximation to the slow manifold, ${\mathcal{M}}_{\epsilon }$, which is the thick black curve. The slow manifold curve is a graphical representation of the steady-state kinetic rate equation. The thin black curves are trajectories (numerical solutions of the mass action equations (10)) starting from different initial conditions, and represent the fast-transient kinetics of the reaction.

3.3. Scaling analysis of the indicator reaction

The scaling analysis of the indicator reaction requires knowledge of fast and slow timescales as well as knowledge of reasonable upper and lower bounds of s₂ and c₂. We will start by trying to estimate a depletion timescale for the indicator reaction. An accurate depletion timescale should give us a reasonable estimation of the completion time for the indicator reaction. In the case of the reaction mechanism of zymogen activation (1)–(2), the completion of the indicator reaction can be faster, as fast, or slower than the non-observable reaction. For the non-observable reaction, the depletion timescale is expressed in terms of $s_1^0$, $e_1^0$, and K_M1:

$$t_{s_1}=\frac{K_{M_1}+s_1^0}{V_1}.$$ (25)

The quantity $e_1^0$ is the total amount of available enzyme for the non-observable reaction. The construction of a homologous depletion timescale for the indicator reaction is problematic since the total amount of available enzyme $e_2^A$,

$$e_2^A(t)=s_1^0-s_1-c_1,$$ (26)

is a time-dependent quantity. If we start by assuming the QSSA is valid, then the mass action equations reduce to

$$c_2\simeq \frac{e_2^A(t)}{K_{M_2}+s_2}{s}_2,$$ (27a)

$$s_2\simeq -\frac{V_2(t)}{K_{M_2}+s_2}{s}_2,$$ (27b)

where $V_2(t)\equiv k_4{e}_2^A(t)$. The general solution to (27b) is given in terms of a Lambert-W function:

$$s_2=K_{M_2}W[{\sigma }_2{e}^{{}^{{\sigma }_2-{\int }_0^t{V}_2(s)ds∕K_{M_2}}}].$$ (28)

The term “s” in (28) has been employed as a dummy variable, and ${\sigma }_2\equiv s_2^0∕K_{M_2}$. We will employ a mean-field approach to derive a depletion timescale for the indicator reaction. Let us first assume that we know the depletion timescale for the indicator reaction; we will denote this timescale as T_s2. The mean available enzyme over the time course of the indicator reaction is given by

$$\langle e_2^A\rangle =\frac{1}{T_{s_2}}{\int }_0^{T_{s_2}}{e}_2^A(t)\mathrm{d}t.$$ (29)

If the completion of the indicator reaction occurs long before the completion of the non-observable reaction, then we expect $\langle e_2^A\rangle \ll s_1^0$. In contrast, if the completion of the indicator reaction occurs long after the completion of the non-observable reaction, then we expect $\langle e_2^A\rangle \approx s_1^0$. In any case, we can define the depletion timescale as

$$T_{s_2}=\frac{K_{M_2}+s_2^0}{k_4\langle e_2^A\rangle },$$ (30)

which should yield a reasonable estimate for the slow timescale if the depletion of s₂ is influenced by a slow manifold. Note that K_M2 ≡ (k₋₃ + k₄)/k₃ is the Michaelis constant of the indicator reaction.

Next, we want to scale the mass action equations that model the indicator reaction with respect to the quantities $\mathbb{T}=t∕\widehat{t}$, $s_2^0$ and max($e_2^A$), where max($e_2^A$) is the maximum amount of $e_2^A$ over the course of the indicator reaction:

$$\max (e_2^A)\equiv \underset{t\le T_{s_2}}{\max }(s_1^0-s_1-c_1).$$ (31)

Utilizing max($e_2^A$) as an upper bound on the available enzyme dictates a natural scaling of c₂:

$$c_2\le \frac{\max (e_2^A)}{K_{M_2}+s_2^0}{s}_2^0\equiv {\widehat{c}}_2.$$ (32)

The remaining upper bounds provide us with the following ensemble of dimensionless variables,

$${\stackrel{‒}{s}}_2{s}_2^0=s_2,{\stackrel{‒}{c}}_2{\widehat{c}}_2=c_2,{\stackrel{‒}{e}}_2^A\max (e_2^A)=e_2^A,\mathbb{T}\widehat{t}=t,$$ (33)

where $\widehat{t}$ denotes an arbitrary timescale. Substitution of (33) into the mass action equation yields

$$\frac{d{\stackrel{‒}{s}}_2}{d\mathbb{T}}=\frac{\max (e_2^A)}{\langle e_2^A\rangle }\frac{\widehat{t}}{T_{s_2}}(1+{\kappa }_2)(1+{\sigma }_2)\left[\left(\frac{{\sigma }_2}{1+{\sigma }_2}{\stackrel{‒}{c}}_2-{\stackrel{‒}{e}}_2^A\right){\stackrel{‒}{s}}_2+\frac{\alpha }{1+{\sigma }_2}{\stackrel{‒}{c}}_2\right],$$ (34a)

$$\lambda \frac{d{\stackrel{‒}{c}}_2}{d\mathbb{T}}=\frac{\max (e_2^A)}{\langle e_2^A\rangle }\frac{\widehat{t}}{T_{s_2}}(1+{\kappa }_2)(1+{\sigma }_2)\left[\left({\stackrel{‒}{e}}_2^A-\frac{{\sigma }_2}{1+{\sigma }_2}{\stackrel{‒}{c}}_2\right){\stackrel{‒}{s}}_2-\frac{1}{1+{\sigma }_2}{\stackrel{‒}{c}}_2\right].$$ (34b)

In the above expressions, the dimensionless quantities σ₂, κ₂ and α are:

$${\sigma }_2\equiv s_2^0∕K_{M_2},{\kappa }_2\equiv k_{-3}∕k_4,\alpha \equiv {\kappa }_2∕(1+{\kappa }_2).$$ (35)

The parameter λ is defined as

$$\lambda \equiv \frac{\max (e_2^A)}{K_{M_2}+s_2^0},$$ (36)

and is unique in that if it is sufficiently small, then it mathematically characterizes the indicator reaction as a singularly perturbed differential equation for which model reduction is possible through means of projecting onto the slow manifold.

4. Asymptotic analysis of the reaction mechanism (1)–(2)

Now that we have a good idea as to how the mass action equations of the indicator reaction scale, we want to try and find closed-form asymptotic solutions to the mass action equations or, at the very least, try and reduce the dimension of the mass action differential equations. The exact form of the scaled mass action equations will depend on the slow timescales of both the observable and non-observable indicator reactions. Thus, given that the respective depletion timescales of the indicator and non-observable reactions are T_s2 and t_s1, we will analyze

$$\frac{d{\stackrel{‒}{s}}_2}{dT}=\frac{\max (e_2^A)}{\langle e_2^A\rangle }\frac{(1+{\kappa }_2)(1+{\sigma }_2)}{{\delta }_S}\left[\left(\frac{{\sigma }_2}{{\sigma }_2+1}{\stackrel{‒}{c}}_2-{\stackrel{‒}{e}}_2^A\right){\stackrel{‒}{s}}_2+\frac{\alpha }{{\sigma }_2+1}{\stackrel{‒}{c}}_2\right],$$ (37a)

$$\lambda \frac{d{\stackrel{‒}{c}}_2}{dT}=\frac{\max (e_2^A)}{\langle e_2^A\rangle }\frac{(1+{\kappa }_2)(1+{\sigma }_2)}{{\delta }_S}\left[\left({\stackrel{‒}{e}}_2^A-\frac{{\sigma }_2}{{\sigma }_2+1}{\stackrel{‒}{c}}_2\right){\stackrel{‒}{s}}_2-\frac{1}{{\sigma }_2+1}{\stackrel{‒}{c}}_2\right],$$ (37b)

where δ_S is the ratio of the substrate depletion timescales, δ_S ≡ T_s2/t_s1, and T = t/t_s1. Based on the scaling given in (37a) and (37b), we will derive an estimate for T_s2 as well as solutions for three particular cases: Case 1: the indicator reaction is faster than the non-observable reaction (δ_S ≪ 1). Case 2: the indicator reaction is roughly the same speed as the non-observable reaction (δ_S ≈ 1). Case 3: the indicator reaction is much slower than the non-observable reaction (δ_S ≫ 1).

4.1. Case 1: The indicator reaction is faster than the non-observable reaction (δ_S ≪ 1)

If the indicator reaction is fast, then the completion of the non-observable reaction will occur long after the completion of the indicator reaction, and the slow timescale is t_s1. To start the analysis, we will rescale the mass action equations that govern the non-observable reaction with respect to $\widehat{T}=t∕T_{s_2}$:

$$\frac{d{\widehat{s}}_1}{d\widehat{T}}={\delta }_S(1+{\kappa }_1)(1+{\sigma }_1)\left[-{\widehat{s}}_1+\frac{{\sigma }_1}{{\sigma }_1+1}{\widehat{c}}_1{\widehat{s}}_1+\frac{{\kappa }_1(1+{\kappa }_1{)}^{-1}}{{\sigma }_1+1}{\widehat{c}}_1\right],$$ (38a)

$$\epsilon \frac{d{\widehat{c}}_1}{d\widehat{T}}={\delta }_S(1+{\kappa }_1)(1+{\sigma }_1)\left[{\widehat{s}}_1-\frac{{\sigma }_1}{{\sigma }_1+1}{\widehat{c}}_1{\widehat{s}}_1-\frac{1}{{\sigma }_1+1}{\widehat{c}}_1\right].$$ (38b)

By inspection of (38a), if δ_S (1+κ₁) (1+σ₁) ≪ 1, then s₁ will be a slow variable over the T_s2 timescale, and thus we will expect s₁ to be essentially constant over the time course of the indicator reaction. In addition, let us assume that T_s2 ≫ t_c1, in which case c₁ will be on the order of its maximum value on the T_s2 timescale. Combining these observations leads to the approximation

$$s_1\simeq s_1^0,t\le T_{s_2}$$ (39a)

$$c_1\simeq \epsilon s_1^0,t\le T_{s_2}$$ (39b)

for the non-observable reaction over the timescale T_s2. Equations (39a) and (39b) suggest that $e_2^A\ll s_1^0$ over the T_s2 timescale. Furthermore, since the changes in s₁ and c₁ are comparatively minimal when t_c1 ≤ t ≤ T_s2, the production of $e_2^A$ is effectively constant over the T_s2 timescale:

$${\stackrel{.}{e}}_2^A\approx \epsilon k_2{s}_1^0\equiv \varpi .$$ (40)

Integration of (40) yields the following approximation of $e_2^A$ on the T_s2 timescale

$$e_2^A\approx {\int }_0^t\varpi \mathrm{d}u=\varpi t,$$ (41)

where “u” in (41) has been utilized to denote a dummy variable. The approximate average value $\langle e_2^A\rangle$ on T_s2 is easily obtained through straightforward integration

$$\langle e_2^A\rangle =\frac{\varpi }{T_{s_2}}{\int }_0^{T_{s_2}}t\mathrm{d}t=\frac{1}{2}{T}_{s_2}\varpi ,$$ (42)

and insertion of (42) into (30) yields an estimate for T_s2:

$$T_{s_2}=\sqrt{\frac{2(K_{M_2}+s_2^0)}{k_4\varpi }}\equiv T_{s_2}^{\ast }.$$ (43)

We can write (43) in a slightly more convenient form by defining the limiting depletion timescale $t_{s_2}^{\ast }$ as

$$t_{s_2}^{\ast }\equiv \frac{K_{M_2}+s_2^0}{V_2},$$ (44)

which allows us to express $T_{s_2}^{\star }$ as

$$T_{s_2}^{\ast }=\sqrt{2t_{s_1}{t}_{s_2}^{\ast }}.$$ (45)

Note that $V_2=k_4{s}_1^0$ is defined as the limiting rate of the indicator reaction.

$T_{s_2}^{\ast }$ should provide an accurate estimate for total completion time of the indicator reaction as long as the non-observable reaction is comparatively slow. For a generic (and linear) dynamical system of the form

$$\stackrel{.}{x}=-ax,x(0)=x_0,$$ (46)

the depletion or characteristic timescale is 1/a. Analogously, we will look for a timescale that is indicative of the time it takes for the initial quantity (i.e., x₀ in the context of (46)) to deplete to an amount that is less than or equal to x₀/e. Following suit from the linear theory, we will consider the timescale $T_{s_2}^{\ast }$ to be a sufficient depletion timescale as long as

$$s_2(T_{s_2}^{\ast })\le s_2^0∕e\approx 0.37s_2^0.$$ (47)

Numerical solutions of the mass action equations confirm the validity of the timescale $T_{s_2}^{\ast }$ when the indicator reaction is much faster than the non-observable reaction provided $t_{c_1}\ll T_{s_2}^{\ast }$ (see Figures 2a and 2b).

Figure 2:

The accuracy of the timescale $T_{s_2}^{\ast }$ when the indicator reaction (2) is fast (δ_S ≪ 1). The solid black curves are numerical solutions to the mass action equations of the complete reaction (10). The dashed line marks the timescale $T_{s_2}^{\ast }$ and the dotted line represents the quantity 1/e. (a) The constants (without units) used in the numerical simulation are: $e_1^0=1$, $s_1^0=100$, k₁ = 1, k₂ = 1 and k₋₁ = 1. $s_2^0=10$, k₃ = 10, k₄ = 100 and k₋₃ = 10. (b) The constants (without units) used in the numerical simulation are: $e_1^0=1$, $s_1^0=100$, k₁ = 1, k₂ = 1 and k₋₁ = 1. $s_2^0=100$, k₃ = 10, k₄ = 100 and k₋₃ = 10. In both cases, we see that the timescale $T_{s_2}^{\ast }$ yields an accurate approximation to the completion time of the indicator reaction. Time has been mapped to the t_∞ scale: t_∞(t) = 1 – 1/ ln(t + e).

Next, we develop an asymptotic solution to the mass action equations that will be valid when $T_{s_2}^{\ast }$ is an accurate depletion timescale, and the concentrations s₁ and c₁ remain on the order of their maximum values for the duration of the indicator reaction. To begin, let us assume that $s_2^0$ is large enough so that

$$\underset{t\le T_{s_2}^{\ast }}{\max }(e_2^A)\ll s_2^0,$$ (48)

in which case we can assume λ ≪ 1. Then, from Tikhonov’s theorem, we obtain

$$c_2\simeq \frac{e_2^A}{K_{M_2}+s_2}{s}_2$$ (49)

as a leading order approximation. Insertion of this approximation into the mass action equation for s₂ yields

$${\stackrel{.}{s}}_2\simeq -\frac{k_4{e}_2^A}{K_{M_2}+s_2}{s}_2.$$ (50)

Finally, substitution of $e_2^A\approx \varpi t$ into (50) gives us

$${\stackrel{.}{s}}_2\simeq -\frac{k_4\varpi t}{K_{M_2}+s_2}{s}_2$$ (51)

as our final asymptotic approximation to the differential equations governing the temporal depletion of s₂. Equation (51) has a closed-form solution in the form of the Schnell–Mendoza equation

$$s_2=K_{M_2}W\left[{\sigma }_2\text{exp}\left({\sigma }_2-\frac{k_4\varpi t^2}{2K_{M_2}}\right)\right],$$ (52)

and provides an accurate approximation to the mass action model (see Figures 3a and 3b).

Figure 3:

The leading order asymptotic solution (52) of the substrate concentration for the indicator reaction matches the numerical solution when the indicator reaction is faster than the non-observable reaction (δ_S ≪ 1). The solid black curves are numerical solutions to the mass action equations of the complete reaction (7) and the broken red curves are numerical solutions to the asymptotic differential equation (51). (a) The constants (without units) used in the numerical simulation are: $e_1^0=1$, $s_1^0=100$, k₁ = 1, k₂ = 1 and k₋₁ = 1. $s_2^0=10$, k₃ = 10, k₄ = 100 and k₋₃ = 10. (b) The constants (without units) used in the numerical simulation are: $e_1^0=1$, $s_1^0=100$, k₁ = 1, k₂ = 1 and k₋₁ = 1. $s_2^0=100$, k₃ = 10, k₄ = 100 and k₋₃ = 10. Time has been mapped to the t_∞ scale: t_∞(t) = 1 – 1/ ln(t + e).

4.2. Case 2: The indicator reaction is roughly the same speed as the non-observable reaction (δ ≈ 1)

If the non-observable reaction and the indicator reaction both complete at roughly the same time, then it is appropriate to use either t_s1 or T_s2 as the depletion timescale for the complete reaction. Of course, given our earlier definition of the timescale T_s2

$$T_{s_2}=\frac{K_{M_2}+s_2^0}{k_4\langle e_2^A\rangle },$$ (53)

we can formulate a nonlinear algebraic equation that will allow us to compute an estimate for the depletion timescale when the reactions are equivalent in speed. First,

$$\langle e_2^A\rangle =\frac{1}{T_{s_2}}{\int }_0^{T_{s_2}}(s_1^0-s_1-c_1)\mathrm{d}t,$$ (54)

and thus we see that T_s2 should satisfy

$${\int }_0^{T_{s_2}}(s_1^0-s_1-c_1)\mathrm{d}t=\frac{K_{M_2}+s_2^0}{k_4}.$$ (55)

Second, under the RSA, the concentration c₁ is expressible (algebraically) in terms of s₁. Therefore, the integrand given in (55) can be expressed as³

$${\int }_0^{T_{s_2}}(s_1^0-s_1-c_1)\mathrm{d}t\approx {\int }_0^{T_{s_2}}\frac{(K_{M_1}+s_1)\Delta s_1-e_1^0{s}_1}{K_{M_1}+s_1}\mathrm{d}t,$$ (56)

where $\Delta s_1=s_1^0-s_1$. Third, the definite integral on the right hand side of (56) is straightforward to compute analytically; evaluating it will yield a nonlinear equation in terms of the variable T_s2, and the solution to (55) can be approximated numerically. Using the average $\langle e_2^A\rangle$ provides an accurate estimate of the depletion timescale (see Figure 4).

Figure 4:

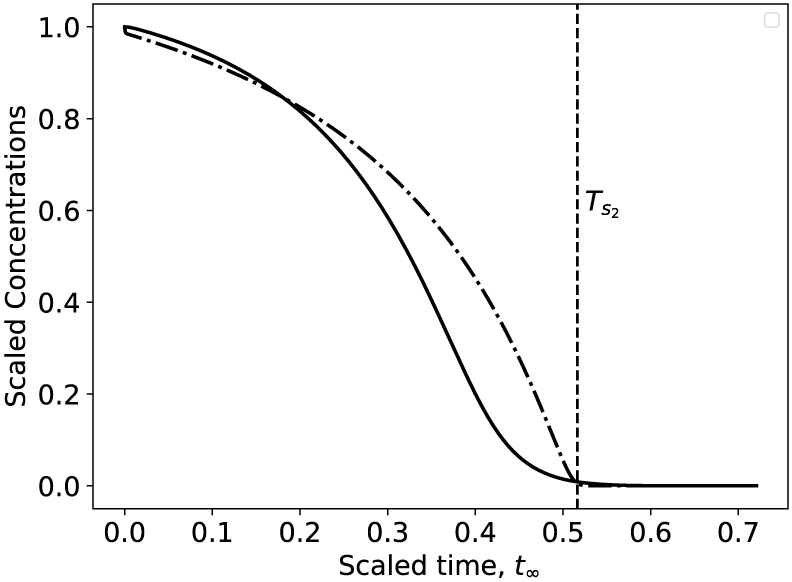
The averaging method for the estimation of the depletion timescale T_s2 for the indicator substrate is still valid when the non-observable and indicator reactions occur at roughly the same speed (δ_S ≈ 1). The solid black curve is the numerically-computed depletion curve of s₂ (10c) and the dotted/dashed black curve is the numerically-integrated depletion curve of s₁ (10a). In this numerical simulation k₃ = 1, k₄ = 1, k₋₃ = 10, $s_2^0=70$, and k₁ = 10, k₂ = 15, k₋₁ = 1, $e_1^0=1$ and $s_1^0=70$. Both substrates have been scaled as $s_2∕s_2^0$ and $s_1∕s_1^0$. Time has been mapped to the t_∞ scale: t_∞(t) = 1 – 1/ ln(t + e).

From a practical point of view, the utility in numerically estimating T_s2 is rather minimal. The objective here will be to construct a criteria from which a reduced model can be extracted from the mass action equations that will be valid without any a priori knowledge of the intrinsic timescales of the indicator reaction (or the non-observable reaction). To achieve this, let us first revisit the generic scaling introduced in the previous section:

$$\frac{d{\stackrel{‒}{s}}_2}{dT}=\frac{\max (e_2^A)}{\langle e_2^A\rangle }\frac{(1+{\kappa }_2)(1+{\sigma }_2)}{{\delta }_S}\left[\left(\frac{{\sigma }_2}{1+{\sigma }_2}{\stackrel{‒}{c}}_2-{\stackrel{‒}{e}}_2^A\right){\stackrel{‒}{s}}_2+\frac{\alpha }{1+{\sigma }_2}{\stackrel{‒}{c}}_2\right],$$ (57a)

$$\lambda \frac{d{\stackrel{‒}{c}}_2}{dT}=\frac{\max (e_2^A)}{\langle e_2^A\rangle }\frac{(1+{\kappa }_2)(1+{\sigma }_2)}{{\delta }_S}\left[\left({\stackrel{‒}{e}}_2^A-\frac{{\sigma }_2}{1+{\sigma }_2}{\stackrel{‒}{c}}_2\right){\stackrel{‒}{s}}_2-\frac{1}{1+{\sigma }_2}{\stackrel{‒}{c}}_2\right].$$ (57b)

Bearing in mind the assumption δ_S ≈ 1, it is sufficient (but not necessary) to bound λ in order to assemble a dynamical model that can be reduced (asymptotically) through slow manifold projection. The upper bound on λ, which we denote as λ^max, is given by

$$\lambda \le {\lambda }^{\max }\equiv \frac{s_1^0}{K_{M_2}+s_2^0}.$$ (58)

The parameter λ^max is the natural small parameter when the indicator is very slow. Furthermore, if the non-observable reaction completes very quickly relative to the non-observable reaction, and δ_S ≪ 1, then the average available enzyme should be on the order of $s_1^0$:

$$\langle e_2^A\rangle =\frac{1}{T_{s_2}}{\int }_0^{T_{s_2}}{e}_2^A\mathrm{d}t\approx s_1^0.$$ (59)

Thus, if $s_2^0\gg s_1^0$, then the approximation

$${\stackrel{.}{s}}_2\simeq \frac{k_4{e}_2^A}{K_{M_2}+s_2}{s}_2$$ (60)

will be valid if λ^max ≪ 1. Furthermore, (60) admits a closed-form solution using separation of variables that consists of composite Lambert-W functions (we do not present this expression here, although we remark that it is straightforward to obtain through careful integration). If the RSA is valid, then

$${\stackrel{.}{s}}_2\simeq -\left(\frac{(K_{M_1}+s_1)\Delta s_1-e_1^0{s}_1}{K_{M_1}+s_1}\right)\left(\frac{k_4}{K_{M_2}+s_2}\right)s_2$$ (61)

is the final form of our reduced differential equation for ${\stackrel{.}{s}}_2$ when the reactions are comparable in speed.

4.3. Case 3: The indicator reaction is much slower than the non-observable reaction (δ_S ≫ 1)

We now consider the case when δ_S ≫ 1. As mentioned in the previous subsection, a very slow indicator reaction suggests that s₂ will be slow over the timescale t_s1. Consequently, we can approximate s₂ as

$$s_2=s_2^0,t<t_{s_1}.$$ (62)

Furthermore, because the non-observable reaction has effectively completed when t = t_s1, we can approximate $\Delta s_1\approx s_1^0$ when t ≥ t_s1. This yields

$${\stackrel{.}{s}}_2\simeq -\frac{k_4{s}_1^0}{K_{M_2}+s_2}{s}_2,t\ge t_{s_1},$$ (63)

which should be valid if λ^max

$${\lambda }^{\max }\equiv \frac{s_1^0}{K_{M_2}+s_2^0}$$ (64)

is small. Equation (63) can be integrated directly to yield a Schnell–Mendoza equation for s₂:

$$s_2=K_{M_2}W[{\sigma }_2\text{exp}({\sigma }_2-{\eta }_2(t))],t\ge t_{s_1}.$$ (65)

The validity of the approximate solution (62) can be established by the mathematical formulation of the RSA for the indicator reaction. If $s_2\approx s_2^0$ over the interval [0, t_s1], then

$$\underset{t\le t_{s_1}}{\max }\mid {\stackrel{.}{s}}_2\mid \cdot t_{s_1}\ll s_2^0.$$ (66)

The inequality given in (66) translates to

$${\delta }_S\gg ({\sigma }_2+1)({\kappa }_2+1),$$ (67)

with max ${\stackrel{.}{s}}_2=k_3{s}_1^0{s}_2^0$. Thus, we have a RSA that is applicable to slow indicator reactions:

$$\frac{V_1}{V_2}\gg \frac{K_{M_1}}{K_{M_2}}(1+{\sigma }_1)(1+{\kappa }_2).$$ (68)

Equation (68) establishes a region of validity for the solution to the mass action equations during the initial build-up of c₂ when t ≤ t_s1 . Interestingly, (68) is analogous to the term used to measure the strength of fully competitive enzyme reactions with alternative substrates [22, 23]. Numerical simulations (see Figure 5) confirm the validity of $t_{s_2}^{\ast }$ and (63).

Figure 5:

Validity of the timescale $t_{s_2}^{\ast }$ and the reduced ordinary differential equation given by (63) for the substrate depletion of the indicator reaction when the indicator reaction is much slower than the non-observable reaction (δ_S ≫ 1). The solid black curve is the numerical solution to the mass action equations (7) and the solid red curve corresponds to the numerical solution to (63) extended to t ≥ 0. In this numerical simulation k₃ = 0.1, k₄ = 1, k₋₃ = 10, $s_2^0=10000$, and k₁ = 25, k₂ = 100, k₋₁ = 1, $e_1^0=1$ and $s_1^0=100$. The respective values of λ^max and δ_S are ≈ 0.009 and ≈ 0.01. Time has been mapped to the t_∞ scale: t_∞ (t) = 1 – 1/ ln(t + e).

5. Applicability of the QSSA for slow indicator reactions

In the context of coupled reactions, timescales are categorized as fast if they are short in comparison to the depletion timescale (t_s1) of the primary reaction. The QSSA is not necessarily valid with respect to the t_s1 timescale, and it is possible to derive a timescale that must be short in comparison to both t_s1 and T_s2 in order to apply QSSA over the time course of the non-observable reaction when the indicator reaction is substantially slower. Carefully rescaling the mass action equation for c₂ with respect to T = t/t_s1 yields

$$\lambda \frac{d{\stackrel{‒}{c}}_2}{dT}=\frac{\max (e_2^A)}{\langle e_2^A\rangle }\frac{(1+{\kappa }_2)(1+{\sigma }_2)}{{\delta }_S}\left[\left({\stackrel{‒}{e}}_2^A-\frac{{\sigma }_2}{1+{\sigma }_2}{\stackrel{‒}{c}}_2\right){\stackrel{‒}{s}}_2-\frac{1}{1+{\sigma }_2}{\stackrel{‒}{c}}_2\right].$$ (69)

If the indicator reaction is slow, and δ_S ≫ 1, then it is necessary that the inequality

$$\lambda \cdot \frac{\langle e_2^A\rangle }{\max (e_2^A)}\cdot \frac{1}{(1+{\kappa }_2)(1+{\sigma }_2)}\cdot {\delta }_S=\frac{t_{c_2}}{t_{s_1}}\ll 1,t_{c_2}\equiv \frac{1}{k_3(K_{M_2}+s_2^0)}$$ (70)

holds in order to impose the QSSA on the t_s1 timescale. The timescale t_c2 has no obvious physical interpretation in the context of experimental initial conditions: it simply arises naturally as a result of the scaling analysis.

To gain an understanding of the behavior of the indicator reaction over t_c2 , we rescale time with respect to T* = t/t_c2:

$$\frac{d{\stackrel{‒}{s}}_2}{d{T}^{\ast }}=\lambda \left[\left(\frac{{\sigma }_2}{1+{\sigma }_2}{\stackrel{‒}{c}}_2-{\stackrel{‒}{e}}_2^A\right){\stackrel{‒}{s}}_2+\frac{\alpha }{1+{\sigma }_2}{\stackrel{‒}{c}}_2\right],$$ (71a)

$$\frac{d{\stackrel{‒}{c}}_2}{d{T}^{\ast }}=\left({\stackrel{‒}{e}}_2^A-\frac{{\sigma }_2}{1+{\sigma }_2}{\stackrel{‒}{c}}_2\right){\stackrel{‒}{s}}_2-\frac{1}{1+{\sigma }_2}{\stackrel{‒}{c}}_2.$$ (71b)

We see from the scaled equations (71) that t_c2 defines a stagnation timescale when experimental initial conditions are prescribed and λ ≪ 1. If the timescale t_c2 is short, then the indicator reaction is essentially stationary over t_c2. This is because s₂ scales as a slow variable over t_c2, and the phase space trajectory should stay near the c₂-nullcline over short timescales. Thus, if t_c2 is small (i.e., t_c2 ≪ min{t_s2, t_s1}), then this timescale translates to a scale over which the indicator reaction exhibits a “slow response”. In fact, any timescale “t*” that satisfies t* ≪ min{t_s1 , T_s2} qualifies as a stagnation timescale.

In addition to the exposition of t_c2 as a stagnation timescale (when λ ≪ 1), the separation of t_c2 and t_s1 also retains a biophysical interpretation. After the initial fast transient of the non-observable reaction, the production rate of $e_2^A$ is roughly

$${\stackrel{.}{e}}_2^A\simeq \frac{V_1}{K_{M_1}+s_1^0}{s}_1^0\equiv \max ({\stackrel{.}{e}}_2^A).$$ (72)

If we demand that the total production of available enzyme be negligible over t_c2, then it is sufficient to require

$$\max ({\stackrel{.}{e}}_2^A)\cdot t_{c_2}\ll s_1^0.$$ (73)

The inequality, (73), is equivalent to t_c2/t_s1 ≪ 1, and we see that the QSSA can be imposed when production of $e_2^A$ is asymptotically negligible over t_c2. Moreover, the relationship between λ, t_c2 and T_s2 is now evident:

$$\frac{t_{c_2}}{T_{s_2}}<\lambda .$$ (74)

The strict inequality in (74) follows from the fact that

$$\frac{t_{c_2}}{T_{s_2}}=\frac{\stackrel{‒}{\lambda }}{(1+{\sigma }_2)(1+{\kappa }_2)},$$ (75)

where $\stackrel{‒}{\lambda }$ is given by

$$\stackrel{‒}{\lambda }\equiv \frac{\langle e_2^A\rangle }{K_{M_2}+s_2^0}.$$ (76)

Furthermore, since $\langle e_2^A\rangle \le \max (e_2^A)$, we see that

$$\stackrel{‒}{\lambda }\le \lambda ,$$ (77)

from which (74) follows. We note that the parameter λ^max is easily derived using Segel’s heuristic approach [18]:

$$\max \mid {\stackrel{.}{s}}_2\mid \cdot t_{c_2}\ll s_2^0\to {\lambda }^{\max }\ll 1.$$ (78)

Since it is clear that

$$\stackrel{‒}{\lambda }\le \lambda \le {\lambda }^{\max },$$ (79)

it follows that the RSA (i.e., λ^max ≪ 1) ensures separation of relevant timescales. Consequently, the RSA for the indicator reaction is a universal qualifier for the validity of the reduced model with respect to the timescale T_s2.

6. Estimation of lag times

Under the QSSA, enzyme catalyzed reactions usually express a lag time. The lag time is normally defined as the time is takes for the rate of product generation to reach its maximum (steady-state) value. This coincides with the time it takes for c₂ to reach its maximum value; it is straightforward to calculate under the limiting circumstances.

6.1. Estimation of the lag time for fast indicator reactions

Let us start by considering the case when the indicator reaction is very fast; we will assume s₂ is given by

$$s_2=K_{M_2}W[{\sigma }_2{e}^{{\sigma }_2-\nu t^2∕2K_{M_2}}].$$ (80)

If σ₂ ≪ 1, then (80) is approximately

$$s_2\simeq s_2^0{e}^{{\sigma }_2-\nu t^2∕2K_{M_2}}.$$ (81)

Next, notice that under the QSSA we have

$$c_2\simeq -\frac{1}{k_4}\frac{d{s}_2}{dt},t\ge 0.$$ (82)

Differentiating both sides of (82), we see that ${\stackrel{.}{c}}_2$ vanishes when ${\ddot{s}}_2$ vanishes:

$$\frac{d{c}_2}{dt}\simeq -\frac{1}{k_4}\frac{d^2{s}_2}{d{t}^2}.$$ (83)

Inserting (81) into the right hand side of (83), and setting the left hand side to zero yields

$$t=\sqrt{\frac{K_{M_2}}{V_2}\cdot t_{s_1}}\equiv t_{c_2}^{\ast }.$$ (84)

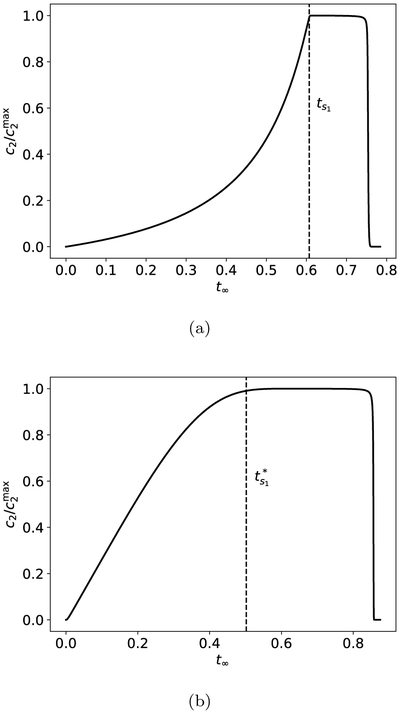
For the case of the fast indicator reaction, the timescale $t_{c_2}^{\ast }$ is identically the lag time when σ₂ ≪ 1 (see Figure 6).

Figure 6:

Validity of the timescale $t_{c_2}^{\ast }$. The curve represents the numerical solution to the mass action equations (10) (thick black line) with $s_1^0=100$, $e_1^0=1$, k₁ = 1, k₂ = 1, k₋₁ = 1, $s_2^0=1$, k₃ = 1, k₋₃ = 1 and k₄ = 100. The dashed line corresponds to $t_{c_2}^{\ast }$ and is the time it takes for c₂ to reach its maximum value. The total concentration c₂ has been scaled by $c_2∕c_2^{\max }$.

6.2. Estimation of the lag time for slow indicator reaction

For slow indicator reactions will can employ the RSA

$$\underset{t\le t_{s_1}}{\max }\mid {\stackrel{.}{s}}_2\mid \cdot t_{s_1}\ll s_2^0,$$ (85)

which allows us to linearize the mass action equation for c₂:

$${\stackrel{.}{c}}_2=k_3(e_2^A-c_2)s_2^0-(k_{-3}+k_4)c_2,t\le t_{s_1}.$$ (86)

Furthermore we will assume that max(c₂) is ${\lambda }^{\max }{s}_2^0$ when the indicator reaction is slow. In this case, the timescale t_s1 will serve as a good approximation to the lag time when σ₁ very large. However, when σ₁ is small, the asymptotic solution to the MM equation reduces to

$$s_1=K_{M_1}W\left[{\sigma }_1{e}^{{\sigma }_1-{\eta }_{1}t}\right]\simeq s_1^0{e}^{{\sigma }_1-{\eta }_{1}t}.$$ (87)

It follows from (87) that the timescale t_s1 is characteristic when σ₁ is small; this means roughly 1/3 of $s_1^0$ still needs to be converted to product when t = t_s1. Consequently, we need an estimate for the time it takes for the non-observable reaction to complete when σ₁ is small. To do this we set

$$s_1^0{e}^{{\sigma }_1-{\eta }_{1}t}=ϵ,ϵ\equiv t_{c_1}∕t_{s_1},$$ (88)

and solve for t. This yields

$$t=-t_{s_1}\text{ln}ϵ\equiv t_{s_1}^{\ast },$$ (89)

and is a much better estimate of the lag time when σ₁ is small. A similar analysis can be carried out when σ₁ is of order unity, but we will not dive into the details of this calculation here. Numerical results confirm the accuracy of the lag time estimates t_s1 and $t_{s_1}^{\ast }$ when the indicator reaction is slow (see Figures 7a– 7b).

Figure 7:

The validity of t_s1 and $t_{s_1}^{\ast }$. The former is the approximate lag time when σ₁ is large (dashed line in panel (a)) and the latter is the lag time when σ₁ is small (dashed line of panel (b)). The solid black curves are the numerical solutions to the mass action equations (7)) of the complete reaction. (a) The constants (without units) used in the numerical simulation are: $e_1^0=1$, $s_1^0=100$, k₁ = 100, k₂ = 10 and k₋₁ = 1. $s_2^0=5000$, k₃ = 1, k₄ = 1 and k₋₃ = 10. (b) The constants (without units) used in the numerical simulation are: $e_1^0=1$, $s_1^0=1$, k₁ = 1, k₂ = 100 and k₋₁ = 1. $s_2^0=1000$, k₃ = 1, k₄ = 1 and k₋₃ = 10. Time has been mapped to the t_∞ scale: t_∞(t) = 1 – 1/ ln(t + e).

7. Discussion

The primary contributions of this paper are the estimation of scaling variables and timescale for a reaction mechanism of zymogen activation (1)–(2). The identification of specific parameters through scaling has yielded necessary and sufficient conditions for the QSSA and RSA, whereas previous nonlinear studies of the coagulation cascade with zymogen activation reactions have employed the QSSA without justification [24]. Moreover, previous analyses [12, 1, 13, 4, 2] have only employed PFO kinetic models, and do not provide insight as to how to properly estimate kinetic timescales via nonlinear methods, even though reaction mechanism of zymogen activation is inherently nonlinear. This work outlines a clear procedure for estimating depletion timescales, and serves as a template for the analysis of more complicated reactions. We give a brief summary of the results of the analysis in what follows.

Scaling analysis of the mass action equations that model the kinetics of a reaction mechanism of zymogen activation (1)–(2) has revealed two small parameters:

$${\lambda }^{\max }=\frac{s_1^0}{K_{M_2}+s_2^0}\ll 1,$$

$$\epsilon =\frac{e_1^0}{K_{M_1}+s_1^0}\ll 1.$$

The QSSA is valid over the respective depletion timescales of the indicator and non-observable reactions when both λ^max and ε are sufficiently small.

In addition, simple asymptotic solutions to the mass action equations were derived that are valid when the indicator reaction is very fast (or very slow) in comparison to the non-observable reaction. If the indicator reaction is fast, then the time course of the indicator substrate s₂ is accurately approximated

$$s_2=K_{M_2}W\left[{\sigma }_2\text{exp}\left({\sigma }_2-\frac{k_4\varpi t^2}{2K_{M_2}}\right)\right],$$

where W denotes the Lambert-W function. In contrast, if the indicator reaction is very slow, then the time course of s₂ can be approximated by

$$s_2=K_{M_2}W\left[{\sigma }_2\text{exp}\left({\sigma }_2-\frac{V_{2}t}{K_{M_2}}\right)\right].$$

Note that the above two expressions are analogous to the Schnell–Mendoza equation [14].

It should be pointed out that the condition λ^max ≪ 1, which can be ensured by requiring an excess of the initial amount of substrate s₂ (i.e., requiring that $s_2^0$ be large enough so that $s_1^0\ll s_2^0$), is sufficient but not necessary for the validity of the reduced model presented in (61). In general, it is desirable that $s_2^0$ be much larger than the maximum of amount of $e_2^A$ over the timescale of the indicator reaction. If the indicator reaction is fast, then the maximum amount of available enzyme will be small; thus, the requirement that $s_1^0\ll s_2^0$ is unnecessary if $\max (e_2^A)\ll K_{M_2}$ (see Figure 7). Of course, the integrity of the reduced model does not diminish if $s_1^0\ll s_2^0$.

Finally, three reduced models have been derived that can be utilized in the analysis of the inverse problem. Our analysis seems to suggest that a fast indicator reaction is the most favorable case for parameter estimation. If the indicator reaction has sufficient speed, then theoretically these two expressions,

$$s_2=K_{M_2}W\left[{\sigma }_2\text{exp}\left({\sigma }_2-\frac{V_2{V}_1{t}^2}{2K_{M_2}(s_1^0+K_{M_1})}\right)\right]$$

and

$${\stackrel{.}{s}}_2=-\left(\frac{(K_{M_1}+s_1)\Delta s_1-e_1^0{s}_1}{K_{M_1}+s_1}\right)\left(\frac{k_4}{K_{M_2}+s_2}{s}_2\right),$$

can be utilized simultaneously to estimate the four unknown parameters: V₁, V₂, K_M1, and K_M2. However, the complete understanding of the inverse problem is beyond the scope of this paper, and we hope to investigate the parameter estimation for the reaction mechanism of zymogen activation (1)–(2) in subsequent future work.

Figure 8:

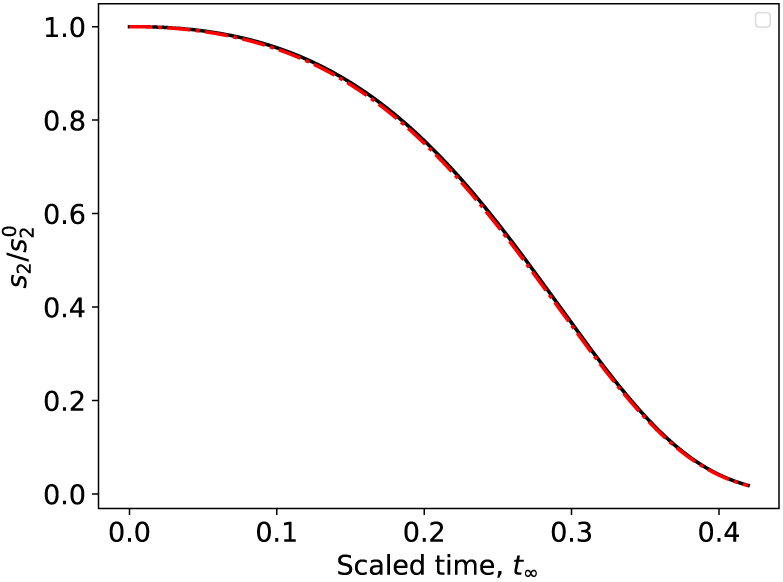
The condition that λ ≪ 1 is necessary for slow manifold projection, ${\mathcal{M}}_{\lambda }$, while the condition λ^max ≪ 1 is merely sufficient. The solid black curve is the numerical solution to the mass action equations (10) and the broken red curve is to the numerical solution to (61). In this simulation k₃ = 1, k₄ = 100, k₋₃ = 10, $s_2^0=1$, and k₁ = 1, k₂ = 1, k₋₁ = 1, $e_1^0=1$ and $s_1^0=100$. $s_1^0∕s_2^0=100$ and λ^max ≈ 1. However, max $e_2^A\approx 1.543$ and therefore λ ≈ 0.014 ≪ 1. Time has been mapped to the t_∞ scale: t_∞(t) = 1 – 1/ ln(t + e).

Highlights.

• A asymptotic analysis of zymogen activation coupled to its enzyme catalyzed reaction is conducted and kinetic rate expressions are formulated.

• The catalyzed reactions consist of a non-observable reaction as well as an indicator reaction.

• Timescale estimates for the completion of the indicator reaction are obtained.

• Conditions for the validity of the reduced equations are derived and interpreted both geometrically and biochemically.