Theta and alpha oscillations are traveling waves in the human neocortex

Summary

Human cognition requires the coordination of neural activity across widespread brain networks. Here we describe a new mechanism for large-scale coordination in the human brain: traveling waves of theta and alpha oscillations. Examining direct brain recordings from neurosurgical patients performing a memory task, we found contiguous clusters of cortex in individual patients with oscillations at specific frequencies within 2 to 15 Hz. These oscillatory clusters displayed spatial phase gradients, indicating that they formed traveling waves that propagated at ~0.25–0.75 m/s. Traveling waves were relevant behaviorally because their propagation correlated with task events and was more consistent when subjects performed the task well. Human traveling theta and alpha waves can be modeled by a network of coupled oscillators because the direction of wave propagation correlated with the spatial orientation of local frequency gradients. Our findings suggest that oscillations support brain connectivity by organizing neural processes across space and time.

Graphical Abstract

eTOC blurb

Zhang et al. use direct human brain recordings to show that neural oscillations are spatially propagating waves that move across the cortex. The results show that oscillations coordinate activity between brain regions rather than being a local phenomenon.

Introduction

Oscillations have a distinctive role in brain function because they coordinate neuronal activity on multiple scales. Brain oscillations are important at the microscale, because they modulate the timing of neuronal spiking (Bragin et al., 1995; Jacobs et al., 2007), and at the macroscale, where they synchronize distributed cortical networks that are communicating (Fries, 2005). Owing to oscillations’ ability to coordinate neural processes across multiple scales, characterizing their spatiotemporal properties may reveal how neurons across multiple regions are dynamically coordinated to support behavior (Kopell et al., 2014).

The human cortex displays oscillations at various frequencies during cognition (Buzsáki and Draguhn 2004). To understand how these patterns relate to behavior, researchers have generally examined the properties of oscillations at individual frequencies in local networks (Raghavachari et al., 2006; Jacobs et al., 2007) or in point-to-point links between distinct regions (Watrous et al., 2013). These approaches ignore a key feature of cortical oscillations that emerged from animal studies—that oscillations at multiple frequencies form spatially continuous neural patterns (Freeman and Schneider, 1982; Freeman et al., 2000; Agarwal et al., 2014).

One such pattern is a traveling wave, which consists of a spatially coherent oscillation that propagates progressively across the cortex, reiminscent of a wave moving across water. Traveling waves have been studied most extensively in animal models, where they were observed most often in fine-scale recordings and were shown to be functionally important to various behaviors, including visual perception (Zanos et al., 2015), spatial navigation (Lubenov and Siapas, 2009; Patel et al., 2012), and movement (Rubino et al., 2006). In conjunction with predictions of computational models, these findings suggest that traveling waves are a key mechanism for guiding the spatial propagation of neural activity and computational processes across the brain (Ermentrout and Kleinfeld, 2001; Muller et al., 2018).

There were some reports of traveling-wave-like patterns in humans, but these patterns were generally observed during sleep or rest (Massimini et al., 2004; Muller et al., 2016; Bahramisharif et al., 2013). Given the potential importance of spatially coordinated brain oscillations for distributed cortical processes, several studies tested for large-scale synchronized oscillations in the human cortex during cognition. However, this oscillatory synchrony was rare or present only on a small scale in humans (Bullock et al., 1995; Menon et al., 1996; Raghavachari et al., 2006). These results shed doubt on the possibility that large-scale spatially coordinated oscillations such as traveling waves figured prominently in human cortical processing.

We re-examined the potential role of cortical traveling waves in human cognition by analyzing electrocorticographic brain (ECoG) recordings from seventy-seven neurosurgical patients. We analyzed the data with a new technique that identifies traveling waves at the single-trial level across various frequencies and electrode configurations. As we describe below, we found traveling waves in 84% (65 of 77) of subjects (for subject details, see Table S1). Traveling waves were present across a wide frequency range (2 to 15 Hz) that included the theta and alpha bands, and were relevant behaviorally, as their propagation correlated with subject performance and events in a memory task. Our results indicate that human behavior is supported by traveling waves of theta- and alpha-band oscillations that propagate across the cortex.

Results

To identify traveling waves in the human cortex, we examined direct electrocorticographic (ECoG) brain recordings from neurosurgical patients performing a working-memory task (Sternberg, 1966). This task was shown previously to elicit large-amplitude oscillations related to memory at various frequencies (Raghavachari et al., 2001; Jacobs and Kahana, 2009). Here, we analyzed these data using a new analytical framework that can identify traveling waves by characterizing the spatiotemporal structure of the oscillations in each patient individually.

Human brain oscillations are spatially clustered.

One form of a traveling wave that could appear in ECoG signals from one patient is a phase wave, which is a neuronal oscillation that is visible simultaneously on multiple electrodes at the same frequency with a systematic timing (or phase) gradient across space. Owing to the spatial phase gradient, the oscillation appears to propagate across the cortex (Ermentrout and Kleinfeld, 2001). A requirement for this type of traveling wave is that the signals across multiple neighboring electrodes exhibit oscillations at the same frequency. Thus, our first step in identifying human cortical traveling waves was to find clusters of cortex where contiguous electrodes showed oscillations at the same frequency. To identify these patterns, we examined the recording from each electrode individually, identified sites that showed narrowband oscillations, and then measured their frequency. We distinguished these oscillations by using a peak-picking algorithm, which found narrowband oscillatory peaks that were elevated over the background 1/f ECoG power spectrum (Manning et al., 2009).

Using this technique, we identified electrodes with narrowband oscillations at various frequencies. Most patients had spatially contiguous clusters of electrodes that showed narrowband oscillations at the same or a similar frequency. We identified these electrode groups using a clustering algorithm (see Methods; Fig. S1A–F). We refer to a contiguous group of four or more electrodes with oscillations at similar frequencies as an oscillation cluster. Across 77 patients, we found a total of 208 oscillation clusters. Oscillation clusters were present at frequencies from 2 to 15 Hz, involved 59% of all electrodes (2401 of 4077), and were present in 74 (96%) of all patients.

The frequencies of oscillation clusters often differed across individuals even for electrodes in the same anatomical region (Fig. S2). This suggested to us that oscillation clusters could reflect distinctive cortical networks that were individualized for a given patient. To assess whether there were true intersubject differences in the frequencies of oscillation clusters, we tested for a spatial correlation in the frequencies of narrowband oscillations across electrodes in each subject using Moran’s I statistic (Moran, 1950). Here we computed I for each subject and compared the mean I with the values computed from a shuffling procedure that randomly interchanged electrodes between subjects. This analysis thus tested the hypothesis that the frequencies of oscillations were more correlated between nearby electrodes within a patient, compared to electrodes at similar anatomical locations in other patients. The mean within-subject frequency correlation that we observed(I=0.03) was entirely outside the range of values computed from the shuffled data (p <10⁻³; Fig. S1G). This result indicated that clusters of ECoG electrodes with narrowband oscillations at the same frequency reflected robust within-subject spatial frequency clustering.

The widespread presence of oscillation clusters indicates that neuronal oscillations at a single frequency were present across large regions of the human cortex. If the timing of these oscillations were synchronized, it could provide evidence for large-scale oscillatory networks (Kopell et al., 2014). Thus, we next characterized the timing of activity across each oscillation cluster to identify patterns of phase synchrony such as traveling waves (Prechtl et al., 1997; Rubino et al., 2006; Patel et al., 2012; Patten et al., 2012; Bahramisharif et al., 2013; Zhang and Jacobs, 2015).

Oscillation clusters contain traveling waves.

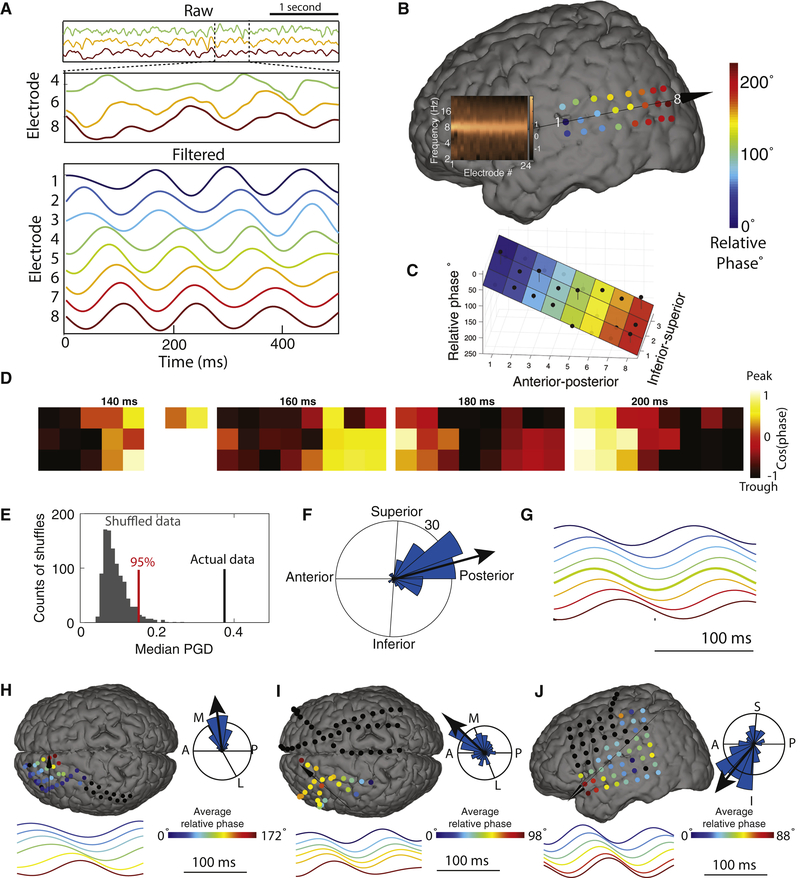
Visual inspection of the signals across many oscillation clusters indicated that the timing of individual oscillation cycles varied systematically with the electrode location, which is indicative of a traveling wave. As an example, Figure 1A–D shows the activity on one trial across an 8.3-Hz oscillation cluster in an electrode grid from Patient 1. While 8.3-Hz oscillations were visible on all channels in this grid, the relative timing of this signal varied systematically, such that the onset time of each oscillation cycle correlated with the electrode’s anterior–posterior position.

Figure 1: Example traveling waves in the human neocortex.

Panels A–G show data from an 8.3-Hz traveling wave in Patient 1. (A) Top panel, raw signals for 4 s of one trial from three selected electrodes. The selected electrodes are ordered from anterior (top) to posterior (bottom). Middle panel, a 500-ms zoomed version of the signals from the top panel. Bottom panel, signals filtered at 6–10 Hz. (B) Relative phase of this traveling wave on this trial across the 3×8 electrode grid. Color indicates the relative phase on each electrode. Arrow indicates direction of wave propagation. Inset shows the normalized power spectrum for each electrode, demonstrating that all the electrodes exhibit narrowband 8.3-Hz oscillations. (C) Illustration of the circular–linear model for quantifying single-trial spatial phase gradients and traveling waves. Black dots indicate the relative phase for each electrode in this cluster on this trial; colored surface indicates the fitted phase plane from the circular–linear model; black lines indicate residuals. (D) The topography of this traveling wave’s phase at four timepoints during this trial. (E) Illustration of the average traveling wave on this cluster across trials. Each electrode’s time-averaged waveform is computed as the average signal relative to oscillation troughs triggered from electrode 5. (F) Analysis of phase-gradient directionality (PGD) for the traveling waves on this cluster. Black line indicates the median PGD for this cluster, computed across trials. Gray bars indicate the distribution of median PGD values expected by chance for this cluster, estimated from shuffled data. (G) Histogram indicating the distribution across trials of propagation directions for the traveling waves on this cluster. (H) Example 5.9-Hz traveling wave from Patient 3.(I) Example 7.9-Hz traveling wave from Patient 63. (J) Example 8.8-Hz traveling wave from Patient 77.

We quantified this phenomenon by calculating the relative phase of the oscillation on each electrode and trial. On this trial, the electrodes in this cluster showed a continuous spatial phase shift across a range of ~240°(Fig. 1B). In this scheme, positive phase shifts correspond to oscillators that have been advancing for a longer period of time. Thus, because the phase was largest at posterior electrodes, it indicates that the electrode cluster showed an anterior-to-posterior traveling wave on this trial (see Supplemental Movie 1).

We used circular statistics (Fisher, 1993) to first identify human cortical traveling waves at the single-trial level and then to compare their properties at the group level. For each oscillation cluster, at each timepoint within a trial we used a circular–linear model to characterize the relation between electrode position and oscillation phase (Fig. 1C). This procedure models each cluster’s instantaneous phase distribution as a plane wave, finding the best fitting spatial phase gradient. The fitted phase gradient provides a quantitative estimate of the speed and direction of traveling wave propagation (Fig. S3). We compute the instantaneous robustness of the traveling wave on each electrode cluster by computing, for each trial, the proportion of phase variation that is explained by the circular–linear model, which we call the phase-gradient directionality (PGD).

We assessed whether each oscillation cluster exhibited a reliable traveling wave using a permutation procedure. Here we compared each electrode cluster’s median PGD value to the distribution of PGD values expected by chance (Fig. 1F). This analysis demonstrated that traveling waves on the cluster in

Figure 1A–D were statistically reliable on a single-trial basis (mean PGD = 0.35, p < 0.001). Furthermore, by assessing the distribution of propagation directions across trials for this cluster, we determined that these traveling waves consistently moved in an anterior-to-posterior direction($\overline{r}=0.94$, Rayleigh p < 0.001; Fig. 1G). The traveling wave on this cluster is also visible by using a simpler approach based on temporal averaging (Fig. 1E). Figure 1H–J shows example electrode clusters in other patients that also showed robust traveling waves.

We applied this methodology across our dataset and found that 140 (of 208; 67%) oscillation clusters had consistent traveling waves, as defined as showing both reliable plane waves at the single-trial level and having a consistent propagation direction (see Methods). 30 (14%) oscillation clusters showed reliable plane waves at the single-trial level but did not have a consistent propagation direction across trials; the remaining 38 (18%) clusters did not show reliable single-trial plane waves. Traveling waves involved 47% of all electrodes and were present in all lobes of the neocortex across both left and right hemispheres (Table S2). Thus, traveling waves are a broad phenomenon across the human brain.

Population analyses of traveling waves.

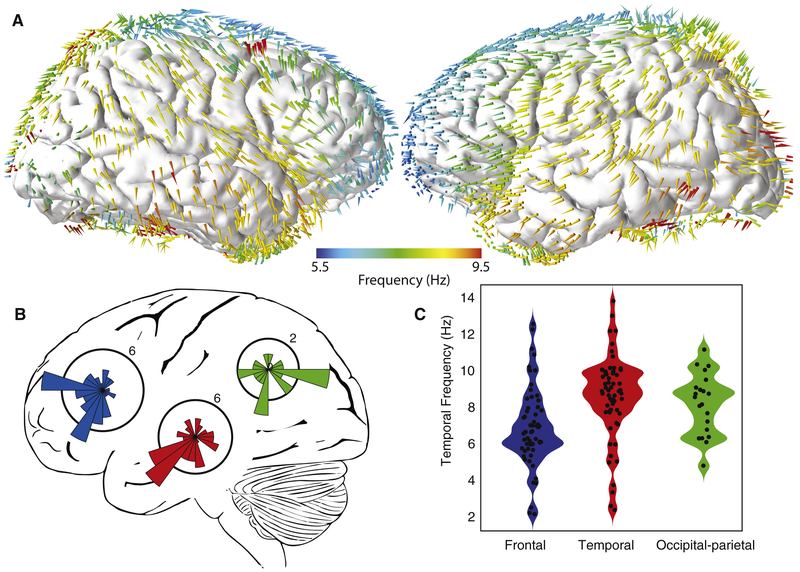
Having established that human cortical traveling waves were widespread, we next studied their properties in more detail at the population level. First, we compared the properties of traveling waves from oscillation clusters identified in different brain areas (Fig. 2A–B; Supplemental Movie 2). Traveling waves in the frontal and temporal lobes generally propagated in a posterior-to-anterior direction (p’s < 0.01, Rayleigh tests). In addition, frontal traveling waves had a tendency to propagate towards the midline. In the occipital and parietal lobes, the propagation direction of traveling waves varied and were not reliably clustered (p >0.05).

Figure 2: Population analysis of traveling wave direction and frequency.

(A) Spatial topography of mean traveling-wave direction and frequency. Colored arrows indicate the mean direction and frequency of traveling waves observed at an electrode within 1.5 cm. (B) Distribution of the mean direction of traveling waves from each lobe. The orientations of the polar histograms are projected to match the lateral brain view. (C) Distributions of temporal frequencies for traveling waves from different regions; shaded region indicates probability density. Black dots indicate the mean frequency from individual electrode clusters.

We also compared the temporal frequencies of the oscillation clusters that showed significant traveling waves (Fig. 2C). Traveling waves were present at frequencies from 2 to 15 Hz. Traveling waves in the frontal lobe had a slower mean temporal frequency in the “theta” range (6 Hz). In contrast, traveling waves in occipital and temporal regions had faster “alpha”-band frequencies (mean 9 Hz; ANOVA, F_(2,137) = 9.7, p < 0.01). It is notable that the frequencies of the traveling waves in these areas were similar to the frequencies of the oscillations that had been reported in these regions earlier (Klimesch, 1999; Canolty et al., 2006; Voytek et al., 2010; Groppe et al., 2013) because it suggests that many previously reported neural oscillations could in fact be traveling waves.

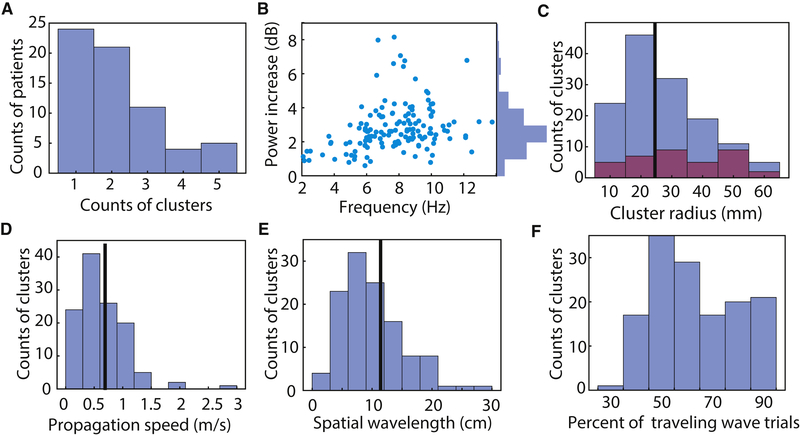
We computed additional properties of traveling waves at the group level. Although most subjects had only one or two electrode clusters with traveling waves, a small number of subjects showed up to five such clusters (Fig. 3A). In most cases (99% of electrodes), the multiple clusters in a subject did not overlap. Traveling waves with frequencies near ~8 Hz had the highest power (Fig. 3B). The electrode clusters with traveling waves ranged in size substantially (Fig. 3C), having a median radius of 2.5 cm (~20 cm²) up to a maximum of ~6 cm (~113 cm²). Traveling waves had a median propagation speed of 0.55 m/s and a median wavelength of 11.7 cm, but these values varied substantially across the population (Fig. 3D & E). Finally, we measured the prevalence of traveling waves at the single-trial level. Across the significant oscillation clusters, traveling waves were present on 61% of single trials (median), although some clusters showed traveling waves on 80–100% of trials (Fig. 3F).

Figure 3: Population summary statistics on traveling waves.

(A) Histogram showing the counts of electrode clusters per patient that showed significant traveling waves. (B) Distribution of the narrowband power (relative to 1/ f) of traveling waves. (C) Distributions of estimated spatial radius across traveling-wave clusters. Purple bars indicates data from grid electrodes; other bars come from strips. Black line indicates median. (D) Distributions of propagation speed across clusters. (E) Distribution of wavelength. (F) Distribution of the mean percentage of time when individual clusters showed reliable traveling waves at the single-trial level.

Traveling waves are behaviorally relevant.

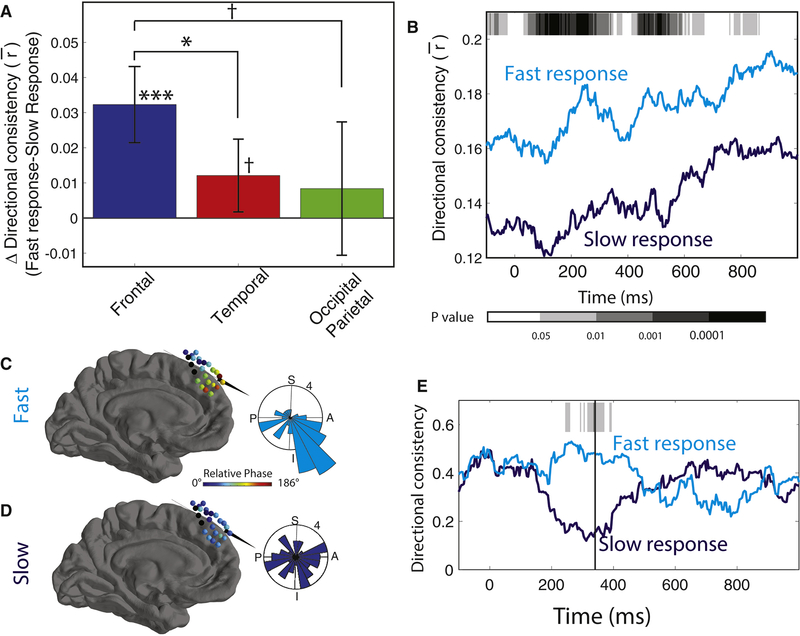
We hypothesized that the spatial propagation of traveling waves reflected the movement of neural activity across the cortex in a manner that was important for behavior. Although some previous studies had measured human cortical traveling waves during tasks, they did not show clear correlations to behavior (Massimini et al., 2004; Takahashi et al., 2011; Bahramisharif et al., 2013). We tested for a potential functional role for traveling waves by comparing their properties through the course of memory processing. In each trial of the memory task (Sternberg, 1966), patients learned a list of stimuli and then viewed a retrieval cue. By comparing traveling-wave properties during the task, we sought to identify functional properties of traveling waves and to test if they differ across brain regions.

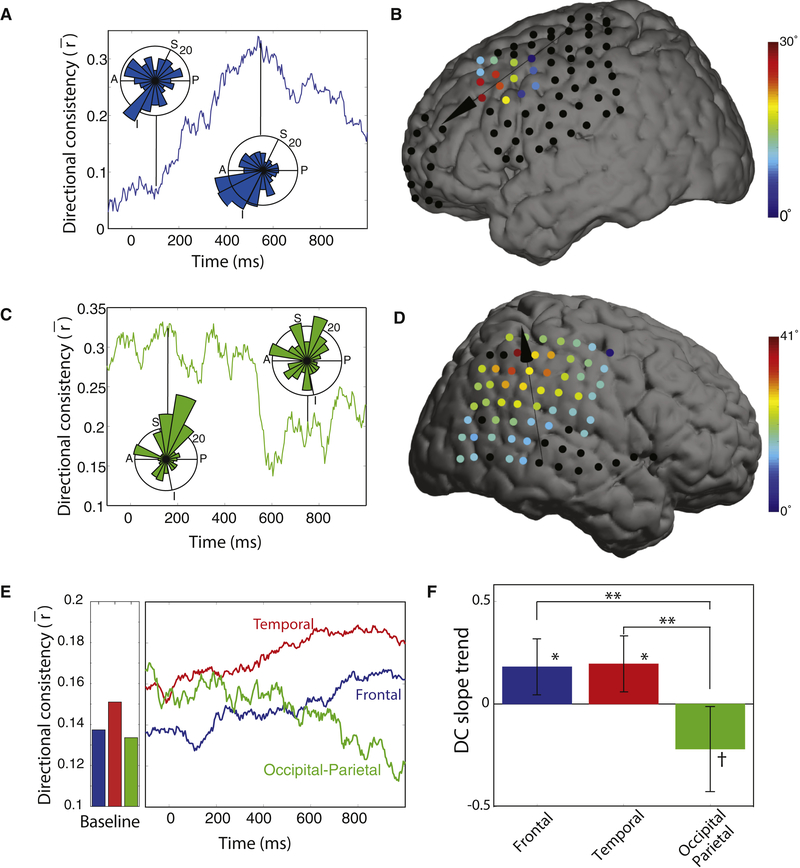
We computed each cluster’s directional consistency (DC), which measures the degree to which traveling waves on each cluster showed a consistent propagation direction at a particular timepoint within the task. DC, which is computed across trials, varies between 0 and 1, with 1 indicating that traveling waves always propagated in a single direction and 0 indicating that propagation directions were uniformly distributed. Figure 4A illustrates the timecourse of mean directional consistency (DC) during the cue response interval for the traveling waves in the frontal lobe of Patient 26. This plot indicates that the traveling waves on this cluster were not directionally organized at the moment of cue onset, but 500 ms later they reliably propagated anteriorly (DC=0.34). A different pattern was present for the traveling waves on an posterior electrode cluster in Patient 13 (Fig. 4C,D), whereby the directional organization was consistent at cue onset and subsequently decreased.

Figure 4: Temporal dynamics of traveling waves.

(A) Timecourse of directional consistency (DC) for a traveling wave at 12.5 Hz from Patient 26’s frontal lobe. Inset circular histograms indicate the distributions of propagation directions across trials at the labeled timepoints. (B) Brain plot showing the mean relative phase shift at each electrode at the timepoint of peak consistency for the same subject as Panel A. (C & D) Traveling 6.2-Hz parietoccipital wave from Patient 13, which showed a decrease in DC after cue onset. (E) Timecourse of traveling-wave DC. Bars indicate the mean DC for each region when patient is out of task. (F) Analysis of DC slope. Positive values indicate that DC increases following cue onset. Error bars denote 95% confidence intervals. Post-hoc test: ^** denotes p < 0.01; *, p < 0.05; ^†, p < 0.1

We confirmed that these patterns were reliable by measuring the timecourse of mean traveling wave DC at the group level. Following cue onset, traveling waves in the temporal and frontal lobes showed increases in DC above baseline levels (Fig. 4E). Inversely, traveling waves from occipitoparietal clusters showed decreased DC during this same period, which was significantly different from the DC increase in the frontal and temporal lobes (Fig. 4F; ANOVA, F_(2,137) = 5.4, p < 0.01). Because frontal and temporal regions specifically show increased DC following cue onset, it indicates that traveling waves in these areas move more consistently during memory retrieval.

After a person views a stimulus, the brain exhibits stimulus-locked neural patterns, including phase resets of ongoing brain oscillations and evoked activity (Rizzuto et al., 2003). Because these can have oscillatory components (Jacobs et al., 2006), we considered the possibility that stimulus-locked signals affected observations of traveling waves. We identified time- (evoked) and phase-locked signals on each electrode clusters and then compared the timing of these signals to the timecourse of the traveling waves on the same channels (Fig. S4). Evoked signals and phase resets were prominent ~200–400 ms post stimulus whereas traveling wave DC peaked later (~800 ms). There were no correlations between the timepoints of peak DC and of the strongest evoked or phase-reset activity (p’s > 0.1). These results suggest that the traveling waves we measured were not artifacts of previously known stimulus-locked signals.

Given that it can be challenging to measure an oscillation’s phase when amplitude is low (Canolty et al., 2006), it is theoretically possible that our ability to measure traveling waves was diminished due to decreases in oscillatory power. We examined this possibility by comparing the timecourses of power and DC between traveling waves from different areas (Fig. S5). In the frontal and temporal lobes, these timecourses diverged dramatically, indicating that the increases in DC that we observed in these areas were not artifacts of task-induced power changes.

We next examined whether traveling waves correlated with the efficiency of memory processing. We compared the DC of the traveling waves on each electrode cluster between trials where patients had fast versus slow reaction times (median split). Overall, DC positively correlated with performance, such that traveling waves moved more reliably in the preferred direction for each cluster on trials with fast reaction times (Fig. 5). This effect was significantly stronger for traveling waves in the frontal lobe (F_(2,137) = 4.5, p = 0.013; Fig. 5A). This result is consistent with the notion that frontal theta oscillations are implicated in working memory (Jensen and Tesche, 2002; Onton et al., 2005), although we have not ruled out the possibility that frontal traveling waves support a broader function, such as attention.

Figure 5: Traveling waves and behavior.

(A) Mean difference in DC between fast and slow trials for 1 s after cue onset, separately calculated for each region. (B) Timecourse of mean DC in the frontal lobe between fast and slow trials. Gray shading indicates significance (paired t tests). (C) Brain plot showing the mean relative phase distribution across an oscillation cluster in Patient 3. Inset plot shows distribution of propagation directions across trials 220 ms after probe onset. (D) Same as C, for trials where the patient responded slowly. (E) Time course of DC for data from Patient 3 that demonstrated elevated DC during trials where the patient responded rapidly. Shading indicates p values from a non-parametric circular direction comparison test (Fisher, 1993) between fast and slow response trials. Post-hoc test: ^*** denotes p < 0.001; *, p < 0.05; ^†, p < 0.1.

In addition to DC, we also examined how other properties of traveling waves correlated with performance (Table S3). On trials when patients had fast reaction times, traveling waves showed increased PGD (p = 0.003) and power (p < 0.001). Traveling waves did not show a reliable performance-related correlations with temporal frequency, spatial frequency, or propagation speed (p’s >0.5). Because the primary behavioral correlates of traveling waves are increased DC and PGD, it indicates that efficient cognitive processing is predicted by traveling waves maintaining their optimal propagation direction, as opposed to moving at a faster speed or oscillating at a different temporal frequency.

Mechanisms of traveling wave propagation.

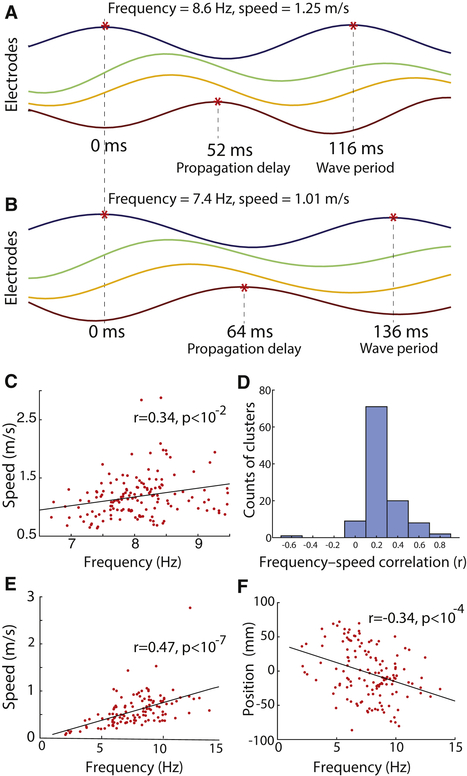
We next considered the neural mechanisms underlying traveling wave propagation. In animal model systems, identifying the mechanisms of traveling-wave propagation is an area of active research (Ermentrout and Kleinfeld, 2001; Sato et al., 2012). At first blush, examining this issue in humans might be even more challenging than in animals, because human brain oscillations are rather variable across time and frequency (Watrous et al., 2013) and because oscillations at neighboring frequencies in humans like alpha and theta are often considered to have different physiological roles (Roux and Uhlhaas, 2014). Nonetheless, we considered the possibility that a single physiological mechanism could support traveling waves at multiple frequencies (Lisman and Jensen, 2013). We would be confident in identifying such a mechanism if it could predict the properties of wave propagation across the range of traveling waves we observed, including signals that varied in frequency and speed across trials (e.g., Fig. 6A & B).

Figure 6: Characteristics of traveling-wave propagation.

(A) A traveling wave on one trial for four electrodes in an oscillation cluster (see Fig. 1B). (B) A traveling wave for these electrodes from a different trial when there was a slower temporal frequency. Same format as Panel A. (C) Across-trial analysis of the relation between traveling-wave propagation speed and frequency, for the electrode cluster whose signals are shown in Panel A & B. Each point indicates one trial. Black line is a least-squares fit. (D) Histogram of within-cluster correlations between propagation speed and frequency. Each correlation coefficent is computed separately for each cluster. (E) Across-cluster analysis of the relation between traveling-wave propagation speed and frequency. Each point indicates the mean frequency and mean propagation speed of the traveling waves from a given oscillation cluster. (F) Population analysis of the relation between traveling-wave frequency and cluster location along the anterior–posterior axis (Talairach coordinates [mm]).

Two notable theoretical neural models for traveling waves are the single-oscillator (SO) and excitable-network (EN) models (Ermentrout and Kleinfeld, 2001). Critically, both SO and EN models predict that traveling waves have a constant propagation speed, because the propagation is caused by neural conduction delays, which are constant. In contrast to the prediction of these models, we found a positive correlation between propagation speed and oscillation frequency—waves with faster temporal frequencies propagated more rapidly—which seemingly rejects these models. This positive correlation between frequency and speed could be seen both at the trial level, by comparing propagation speed and frequency across trials from the same electrodes (r = 0.34, p < 0.01; Fig. 6C), and at the group level, by comparing the mean properties of traveling waves between electrode clusters (r = 0.47, p < 10⁻⁷; Fig. 6E).

A third theoretical model is a network of weakly coupled oscillators (WCO) (Ermentrout and Kleinfeld, 2001), which have been used to model traveling waves in both neural and non-neural systems (Diamant and Bortoff, 1969; Ermentrout and Kopell, 1984). Traveling waves appear in a network of weakly coupled Kuramoto (1981) oscillators when their arrangement shows two properties: First, the oscillators must be arranged in a linear array with the strength of interoscillator phase coupling decreasing with distance. Second, there must be a spatial gradient in intrinsic frequency across the array. When these two criteria are satisfied, traveling waves appear and propagate towards oscillators with slower intrinsic frequencies (Ermentrout and Kopell, 1984). Critically, the WCO model predicts that oscillations with faster temporal frequencies propagate more rapidly (Fig. 6A–C), because the traveling wave is derived from coupling based on oscillatory phase rather than fixed time shifts (Ermentrout and Kopell, 1984; Ermentrout and Kleinfeld, 2001). Because we found a positive correlation between propagation speed and oscillation frequency (Fig. 6D–E), it supports the idea that human cortical traveling waves are driven by WCOs.

Furthermore, we found that the WCO model predictions matched the direction of wave propagation in our data. In the WCO model, traveling waves propagate towards oscillators with the slowest intrinsic frequencies (Ermentrout and Kopell, 1984). Similarly, in our data we observed a systematic decrease in mean oscillation frequency along the posterior-to-anterior axis (r = 0.34, p < 0.001, Fig. 6F), which also followed the mean direction of traveling wave propagation (Fig. 2A). These patterns indicate that human cortical traveling waves generally propagate in a posterior-to-anterior direction because they are coordinated by an overall decrease in intrinsic frequency from posterior to anterior regions (Voytek et al., 2010).

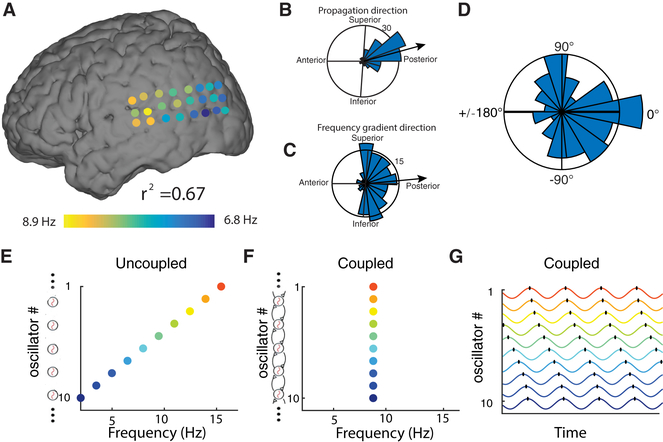
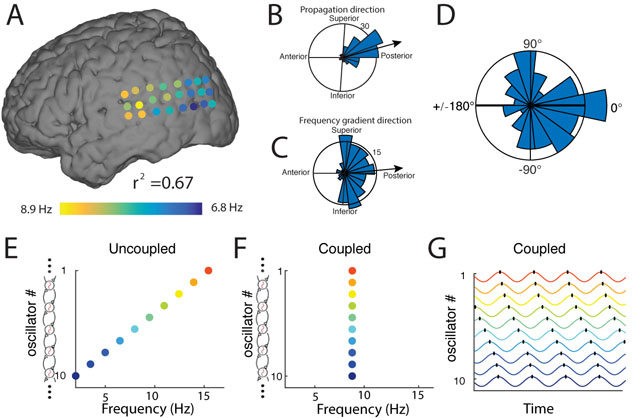
Although most traveling waves showed posterior-to-anterior propagation, some exceptional clusters reliably propagated in other directions (e.g., Fig. 1). We compared the directions of frequency gradients and propagation across clusters to test whether these factors were correlated, as predicted by the WCO model. If such a correlation existed, it would suggest that the exceptional propagation directions of some traveling waves were caused by corresponding distinctive frequency gradients. Such a pattern was evident in Patient 1, as seen in Figure 7B & C, which shows that the mean directions of the wave propagation and the frequency gradients both had anterior-to-posterior orientations. We assessed this correspondence statistically at the group level by testing for a correlation in the mean directions of frequency gradients and wave propagation. Across clusters, the distribution of pairwise directional differences was clustered near zero (Rayleigh test p < 0.01; Fig. 7D), which indicates that the direction of traveling-wave propagation is positively correlated with the orientation of the local oscillatory frequency gradient.

Figure 7: Mechanisms of traveling waves.

(A) The instantaneous frequency distribution across an oscillation cluster from Patient 1 on one trial (same as Fig. 1B), demonstrating an anterior-to-posterior decreasing spatial-frequency gradient (r² = 0.67). (B) Distribution of traveling-wave propagation directions on this electrode cluster across trials (reproduced from Fig. 1G). (C) Distribution of the directions of the spatial-frequency gradients across this cluster. In B & C, black lines indicate the mean directions, thus demonstrating a correspondence between the directions of phase and frequency gradients. (D) Distribution of angular differences, across oscillation clusters, between the mean direction of traveling-wave propagation and the mean direction of spatial frequency gradients. (E–G) Illustration of a model of weakly coupled oscillators (Ermentrout and Kopell, 1984) with parameters matched to our findings. Color warmth increases with intrinsic frequency. When there is no phase coupling (Panel E), individual oscillators demonstrate their intrinsic oscillation frequencies from 2 Hz (anterior) to 16 Hz (posterior). When phase coupling is present (Panels F–G), all oscillators have the same temporal frequency (F) and a traveling wave emerges (G).

In summary, these results indicate that WCO model provides a good model for human cortical traveling waves because it illustrates how the direction and speed of traveling waves can be predicted by the local oscillatory frequency gradients. The WCO model suggests that the existence and direction of traveling waves are modulated by two factors: the strength of local phase coupling and spatial gradients of intrinsic oscillation frequencies (Ermentrout and Kopell, 1984; Ermentrout and Kleinfeld, 2001). When phase coupling is absent, there are no traveling waves because oscillation frequencies differ between electrodes (Fig. 7E). When phase coupling is present, traveling waves emerge, propagating in the direction of decreasing oscillation frequency (Fig. 7F–G).

Discussion

Our findings demonstrate a new potential functional role for theta- and alpha-band oscillations by showing that they are often traveling waves. This expands our understanding of the types of functions that neural oscillations can support beyond phase coding (O’Keefe and Recce, 1993), modulating synaptic plasticity (Huerta and Lisman, 1995), and an array of other phenomena (Klimesch, 1999; Buzsáki and Draguhn, 2004). Researchers had previously known that oscillations modulated cortical interactions in a point-to-point fashion between specific cortical areas (Hyman et al., 2011; Liebe et al., 2012). Our results add to this work by demonstrating that theta and alpha oscillations can spatially and temporally organize neural processing throughout large contiguous extents of human cortex.

Our work shows that human cortical traveling waves can be modeled as a network of weakly coupled oscillators (WCOs). In addition to suggesting a mechanism underlying traveling waves, the WCO model has implications for understanding traveling-wave dynamics in behavior. A key part of the WCO model is the link between local oscillation frequency and the direction of wave propagation. Traditionally, the frequency of a brain oscillation has been considered to be important because it indicates the functional role of a given oscillation. For example, oscillations in the neighboring theta and alpha bands have been associated with memory and idling, respectively (Klimesch, 1999; Roux and Uhlhaas, 2014). Instead, our results suggest that—at least for the frequencies and regions we examined—the precise frequency of an oscillation could most closely relate to broad physiological factors such as the direction of wave propagation (Lisman and Jensen, 2013).

Going forward, it will be important to test the functional relevance of traveling waves in more detail. One key issue is characterizing the potential importance of the direction of wave propagation. Although most traveling waves propagated in a posterior-to-anterior direction, some subjects reliably showed traveling waves with the opposite direction of propagation. Given this variability, an important issue is whether traveling waves with different directions support distinct functional or physiological processes. In visual perception there is evidence that oscillations with anterior and posterior directional patterns support feedforward and feedback processing, respectively (Bastos et al., 2015). Likewise, it will be interesting to test whether human traveling theta and alpha waves move in different directions to support distinct physiological processes. An alternate possibility is that human traveling theta and alpha waves consistently support a single functional process and that the varying in propagation directions we observed reflect intersubject differences in the anatomy or frequency gradients.

Previous research suggested several potential computational roles for traveling waves (Ermentrout and Kleinfeld, 2001; Muller et al., 2018). One possibility is that traveling theta and alpha oscillations form carrier waves that represent detailed information about the current behavioral state via phase and amplitude modulation—this pattern has been observed for both beta and theta oscillations in the cortex and hippocampus, respectively (Freeman and Schneider, 1982; Agarwal et al., 2014). A different potential function for traveling waves is to spatially and temporally segment the neural representations of discrete behavioral states, such that individual oscillation cycles correspond to distinct neural patterns. Such a phenomenon was previously observed for alpha oscillations in cortex (VanRullen and Koch, 2003; Samaha and Postle, 2015) and for theta oscillations in the hippocampus (Jezek et al., 2011; Gupta et al., 2012). It is also likely that human cortical traveling waves correlate with the spatial propagation of high-frequency neural patterns, including both oscillations and neuronal spiking, owing to the phenomenon of cross-frequency phase coupling (CFC) (Canolty et al., 2006; Jacobs et al., 2007; Voytek et al., 2015). The coexistence of traveling waves and CFC suggests that spatial bands of high-frequency neural activity move across the human cortex during behavior (Bahramisharif et al., 2013). It will be useful going forward to test the potential functional role of these spatial bands (VanRullen and Lozano-Soldevilla, 2017), such as testing the idea that traveling waves guide the propagation of discrete “packets” of activity across the cortex (Freeman, 2003).

Finally, a different potential role for traveling waves is that they could relate to detailed features of neural coding. It is notable that several known neural coding schemes also exhibit posterior-to-anterior spatial gradients, such as the representation of spatial and temporal information in the hippocampus (Kjelstrup et al., 2008; Lubenov and Siapas, 2009), of task rules in the frontal lobe (Badre and D’Esposito, 2009), and of object abstractness in the visual system (Harry et al., 2016). Traveling waves that follow the structure of these networks could be important for these computational processes.

Although we believe it is likely that traveling waves are relevant for human cognition, there are several limitations of our results. Our data come from epilepsy patients, so it is possible that features of our results do not generalize beyond this clinical population. However, there are several reasons why we believe our results are likely to be widely relevant. Previous work showed that healthy subjects have the same types of task-related theta and alpha changes that we observed here (Jacobs et al., 2006), including spatial patterns consistent with the presence of traveling waves (Patten et al., 2012; VanRullen and Lozano-Soldevilla, 2017). Further, the spatial and temporal propagation patterns of interictal and seizure-related activity differ dramatically compared to the theta and alpha traveling waves we described (Liou et al., 2017). Although the ECoG recordings that we conducted measure human brain activity directly, it should be noted that these findings are correlational because our experiments did not manipulate traveling waves. Thus more work is necessary to establish a potential causal role for traveling waves. Further, our findings concern human cortical oscillations at 2–15 Hz during wakefulness, whereas neural traveling waves in other settings may have different properties (Massimini et al., 2004; Rubino et al., 2006; Sato et al., 2012).

Elements of the traveling theta and alpha waves we observed were noted in previous studies that used different types of methods to examine spatial characteristics of human brain signals (e.g., Patten et al. 2012; Bahramisharif et al. 2013; Alexander et al. 2013, among many others). A differentiating feature of our approach was that we identified traveling waves across multiple regions, directions, and frequencies directly in individual subjects at the single-trial level. Because different subjects exhibited widely varying types of traveling waves even in the same anatomical region, it suggests that there are substantial intersubject differences in the spatial and temporal structure of brain oscillations and traveling waves. These patterns may not be adequately appreciated because they are difficult to capture with typical group-average analyses.

In addition to traveling waves, the brain also exhibits other large-scale spatial patterns of oscillations, such as spirals (Muller et al., 2016) and “phase cones” (Freeman and Barrie, 2000), as well as smaller patterns at finer spatial scales (Freeman, 2003; Rubino et al., 2006). Together, this work suggests that there is potential for researchers and engineers to identify important new spatial patterns of brain dynamics across the cortical surface using improved high-resolution electrocorticographic electrodes (Viventi et al., 2011; Khodagholy et al., 2015) rather than necessarily requiring penetrating electrodes or single-cell recordings.

More broadly, because our results show that neuronal oscillations can be synchronized across large regions of cortex, researchers and clinicians examining noninvasive brain recordings should consider that aspects of their findings may result from large neural masses (Freeman, 1975, 2003) rather than precisely localizable point sources (Michel et al., 2004). Furthermore, whereas many electrical signals from the brain are commonly interpreted as event-related potentials or as task-induced power changes from local oscillators, instead it is possible that these signals could result from traveling waves that become transiently organized at a particular timepoint and phase across a cortical region (Alexander et al., 2013). Thus, single-trial analysis of traveling waves could be an intriguing new direction for scalp electroencephalography and magnetoencephalography.

In addition to demonstrating a new fundamental feature of human brain activity, our findings could have significant practical implications. The potential for non-invasively measuring traveling waves on a single-trial basis may be useful for the development of brain–computer interfaces (BCI). However, for traveling waves to be useful for BCIs, given the intersubject differences we observed, it seems important to characterize these patterns individually for each subject rather than averaging across individuals. Our results suggest a way to predict the mean direction of traveling wave propagation at the individual subject level, by measuring the spatial gradient of a subject’s intrinsic oscillatory frequencies. Measuring traveling waves’ instantaneous properties may provide a new tool for neural interfacing, by tracking a subject’s attention or cognitive state for timing stimulus presentation or neuromodulation (Ezzyat et al., 2017).

In summary, our findings show that traveling waves of theta and alpha oscillations comprise large spatiotemporal patterns across the human cortex (Livanov, 1977; Freeman, 2003). The existence of traveling waves that comply with WCO models indicates that an important component of large-scale brain connectivity are neuronal oscillations with precise spatial frequency characteristics. Traveling waves expand our understanding of cortical functional connectivity by showing that signal propagation across large brain networks can be rhythmic and dynamic (Kopell et al., 2014). We hypothesize that traveling-waves relate to the slower functional connectivity signals that have been identified with fMRI (Honey et al., 2007), based on the known link between fMRI activity and the power of neuronal oscillations (Debener et al., 2005), as well as convergent findings with calcium imaging (Matsui et al., 2016). More broadly, our findings emphasize that human cognition is supported by complex, large-scale neural patterns that are exquisitely organized across both time and space. Traveling waves may reveal one role of large-scale brain connectivity and oscillations in cognition, by showing when behavioral information is represented and where signals are propagating.

STAR METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests should be directed to and will be fulfilled by Dr. Joshua Jacobs (joshua.jacobs@columbia.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Subjects and Task.

We examined direct brain recordings from 77 epilepsy patients who had electrodes surgically implanted to guide seizure mapping. Individual patients were implanted with a configuration of electrodes customized according to their clinical needs, which included both electrocorticographic (ECoG) surface grid and strips as well as depth electrodes. The spacing between neighboring electrodes was 10 mm (center-to-center). Our data collection was a continuation of previous reported study (Jacobs and Kahana, 2009) and recordings were made at four hospitals (Thomas Jefferson University Hospital, Philadelphia; University of Pennsylvania Hospital Philadelphia; Children’s Hospital of Philadelphia, and University Hospital Freiburg). All patients consented to having their brain recordings used for research purposes and the research was approved by relevant Institutional Review Boards. For the work described here, we examined only ECoG grid and strip electrodes on the cortical surface. See Zhang and Jacobs (2015) for an analysis of traveling waves in recordings from depth electrodes.

During free time between clinical procedures, these patients performed the Sternberg working memory task (Sternberg, 1966) on a laptop computer at their bedside. Each trial of the task consisted of two phases. In the first phase they memorize a short list of items. The second phase involves memory retrieval. Here they view a probe item and press a key to indicate if the probe was present in the remembered list. Task performance was excellent, with patients having a mean accuracy of 90% and median reaction time of 1.16 s. Our data analyses examined brain recordings during memory retrieval because it let us compare properties of patients’ brain signals to their simultaneous behavioral performance (Jacobs et al., 2006).

Data acquisition.

The electrical activity from each electrode was recorded by a clinical recording system whose timing was synchronized with the task computer. We pre-processed the data by downsampling the recordings to 250 Hz and performing an anatomically weighted average re-referencing (Jacobs and Kahana, 2009). We identified the location of each recording electrode by co-registering a pre-surgical structural magnetic resonance image (MRI) image with a post-operative computed tomography (CT) image. From these images, we identified the location of each recording contact on the CT images and computed the electrode location in standardized Talairach coordinates (Talairach and Tournoux, 1988).

QUANTIFICATION AND STATISTICAL ANALYSIS

Identifying spatial clusters of electrodes with similar oscillations.

Given our interest in characterizing propagating traveling waves, we designed an algorithm to identify spatial clusters of electrodes with narrowband oscillations at very similar frequencies. This algorithm accounted for several complexities of human brain oscillations measured with ECoG signals, including differences in electrode positions across subjects and variations in oscillation frequencies across individuals (Fig. S2).

In this procedure, first we used Morlet wavelets (wave number 6) to compute the power of the neuronal oscillations throughout the task at 129 frequencies logarithmically spaced from 2 to 32 Hz. To identify narrowband oscillations at each site, we fit a line to each patient’s mean power spectrum in log–log coordinates using a robust linear regression (Fig. S1; Manning et al. 2009; Lega et al. 2012; Zhang and Jacobs 2015). We then subtracted the actual power spectrum from the regression line. This normalized power spectrum provides a “whitened” version of the signal that removes the 1/ f background signal and emphasizes narrowband oscillations as positive deflections. We identified narrowband peaks in the normalized power spectrum as any local maximum greater than one standard deviation above the mean (Zhang and Jacobs, 2015). We also used this normalized power spectrum to estimate the narrowband power of each traveling wave, minimizing the influence of the 1/ f background signal (Fig. 3B).

Next, we implemented a spatial clustering algorithm to identify oscillation clusters, which we defined as contiguous groups of electrodes in each subject that exhibited narrowband oscillations at a closely neighboring frequency. First, considering a series of 2-Hz intervals centered at 2 to 32 Hz in 1-Hz steps, we identified all the electrodes that exhibited a narrow-band oscillatory peak within that range. We counted the number of electrodes with oscillatory peaks at each frequency window, and computed local maxima as potential oscillation clusters. We then tested whether the electrodes that contributed to each local maximum comprised a spatially contiguous group. We found all the electrodes with a peak in the 2-Hz interval around each local maximum and created a pairwise-adjacency matrix to judge their spatial proximity. This matrix indicated whether each electrode pair was separated by less than 15 Talairach units (15 mm). Finally, we used this adjacency matrix to identify mutually connected spatial clusters of electrodes by computing the connected components of this graph (Tarjan, 1972). We included in our subsequent analyses only clusters with at least four electrodes.

A key feature of our spatial clustering algorithm is that it adapts to the specific anatomical orientation of each patient’s ECoG electrode organization by utilizing Talairach coordinates rather than labeled positions from clinical recordings. Thus, our methods are capable of identifying oscillation clusters that span multiple ECoG grids or strips (e.g., Fig. 1I), rather than being limited to identifying signals within regularly structured electrode arrays (Rubino et al., 2006; Lubenov and Siapas, 2009; Zhang and Jacobs, 2015).

Identifying traveling waves.

Having identified groups of electrodes with oscillations at the same frequency, we next sought to identify traveling waves. Intuitively, a traveling wave can be described as an oscillation that moves progressively across a region of cortex. Although many types of traveling waves are possible (Ermentrout and Kleinfeld, 2001; Muller et al., 2016), we focused our analyses here on one form of this phenomenon, the linear phase wave. Quantitatively, a traveling phase wave can be described as a set of simultaneously recorded neural oscillations at the same frequency whose instantaneous phases vary systematically with the location of the recording electrode so that the wave front can be modeled as a moving plane. This phenomenon would appear in our dataset as an oscillation cluster whose instantaneous relative phases exhibit a linear relationship with electrode location.

We followed the following procedure to identify plane waves in the phases from each oscillation cluster. First, we measured the instantaneous phases of the signals across each oscillation cluster by applying a Butterworth filter to the signals from each electrode at the cluster’s narrowband mean peak frequency (3-Hz bandwidth). Then we perform the Hilbert transform on each electrode’s filtered signal to extract the instantaneous phase at each timepoint (Freeman, 2007). To facilitate visualization, we normalize the phase distributions by rotating so that the smallest value is set to 0.

We used circular statistics to identify plane waves of phase progression across each oscillation cluster at each timepoint (Fisher, 1993). For each spatial phase distribution, we used a two-dimensional circular–linear regression to assess whether the observed phase pattern varied linearly with the electrode’s coordinates in 2-D. In this regression, for electrode i, x_i y_i and represent the 2-D coordinates and θ_i is the instantaneous phase. x and y are determined by projecting the 3-D Talairach coordinates for each cluster into the best-fitting 2-D plane. We projected the electrode coordinates into a 2-D space because it simplified visualizing and interpreting the data, following the model that traveling-wave propagation roughly follows the surface of the cortex.

A 2-D circular–linear model has three parameters to be fit: the phase slopes a and b, which each correspond to the rate of phase change (or spatial frequencies) in each dimension, and the phase offset ϑ. We converted this model to polar coordinates to simplify fitting. This polar model has two parameters: The angle of wave propagation α, defined as α = atan2(b,a), and the spatial frequency ξ, defined as $\xi =\sqrt{a^2+b^2}$. Circular–linear models do not have an analytical solution and must be fitted iteratively (Fisher, 1993). We fit α and ξ to the distribution of oscillation phases at each timepoint by conducting a grid search over α ∈ [0°,360°] and ξ ∈ [0,18] in increments of 5°and 0.5°/mm, respectively. (Note that ξ = 18 corresponds to the spatial Nyquist frequency of 18°/mm.)The model parameters for each timepoint are fitted to most closely match the phase observed at each electrode in the electrode cluster. For each value of α and ξ, the model’s predicts the phase ${\widehat{\theta }}_i$ at each electrode i as

$${\widehat{\theta }}_i=\left(a{x}_i+b{y}_i+\vartheta \right)\text{mod}{360}^{°},$$

where a = ξcos(α) and b = and ξsin(α). Then we compute the goodness of fit as the mean vector length $\overline{r}$ of the residuals between the predicted $\left({\widehat{\theta }}_i\right)$ and actual (θi) phases (Fisher, 1993),

$$\overline{r}=\sqrt{{\left[\frac{1}{n}\sum _{i=1}^n\text{cos}\left({\theta }_i-{\widehat{\theta }}_i\right)\right]}^2+{\left[\frac{1}{n}\sum _{i=1}^n\text{sin}\left({\theta }_i-{\widehat{\theta }}_i\right)\right]}^2}.$$

The selected values of α and ξ are chosen to maximize $\overline{r}$.

Figure S3 illustrates the results of performing this procedure for several trials from Patient 1. The fitted model coefficients indicate physical characteristics of any identified plane traveling wave, by showing the slope and direction of the spatial phase gradient: α is the wave’s instantaneous propagation direction and ξ is it’s spatial frequency (i.e., rate of phase change over space) in °/mm.

To measure the statistical reliability of each fitted traveling wave we examined the phase variance that was explained by the best fitting model. As in earlier work (Kempter et al., 2012), we adapted the r² goodness-of-fit measure from linear correlation for use with circular data. To do this, we computed the circular correlation ρ_cc between the predicted $(\widehat{\theta })$ and actual (θ) phases at each electrode (Kempter et al., 2012):

$${\rho }_{cc}=\frac{{\sum }_{i=1}^n\text{sin}\left({\theta }_i-\overline{\theta }\right)\text{sin}\left({\widehat{\theta }}_i-\overline{\widehat{\theta }}\right)}{\sqrt{{{\sum }_{i=1}^n\text{sin}}^2\left({\theta }_i-\overline{\theta }\right){{\sum }_{i=1}^n\text{sin}}^2\left({\widehat{\theta }}_i-\overline{\widehat{\theta }}\right)}},$$

where bar denotes averaging across electrodes. We squared the result to compute ${\rho }_{cc}^2$. Finally, we applied an adjustment to account for the number of fitted model parameters:

$${\rho }_{adj}^2=1-\frac{\left(1-{\rho }_{cc}^2\right)(n-1)}{n-k-1}.$$

where n is the number of electrodes, and k is number of independent regressors (k=3). We refer to ${\rho }_{adj}^2$ as phase gradient directionality (PGD) in the main text, similar to (Rubino et al., 2006).

Classification of traveling waves.

The procedure described above identifies the spatial gradients in a single instantaneous phase distribution. Next, we describe the procedure we used to measure the reliability of each phase gradient across trials, based on variations in PGD and directional consistency. First, we computed the median PGD for each trial and cluster. We computed the median PGD for each cluster (across trials) and compared this value with the distribution of PGDs estimated from a shuffling procedure (1,000 iterations). In each iteration of this shuffling procedure, we compute a single surrogate PGD value by repeating our main PGD calculation after randomly permuting the locations of individual electrodes within each cluster, while preserving other features of the data. We identify reliable traveling waves as electrode clusters in which the actual PGD value exceeds 95% of the distribution of the 1,000 surrogate PGD values from shuffling. Due to the spatial electrode permuting in this shuffling, this method ensures that the traveling waves we identify reliably exhibit spatially organized plane waves, rather than other types of phase patterns with less structure (Maris et al., 2016). For clusters with only four electrodes we used the unadjusted ${\rho }_{cc}^2$ to assess significance in this shuffling procedure, rather than the PGD $\left({\rho }_{adj}^2\right)$.

Finally, here we considered only the electrode clusters with traveling waves that propagated in a consistent direction over time. To do this, after identifying the clusters with reliable PGD values, we computed for each cluster the distribution of propagation directions across trials. The clusters we designate as exhibiting significant traveling waves have a non-uniform distribution of propagation directions across trials, as determined by the Rayleigh test (Fisher, 1993) at p < 0.05. We calculated the directional consistency (DC) of each cluster as the circular mean vector length of this distribution of propagation directions. Thus, a cluster with DC=1 would have traveling waves that always propagate in the same direction.

Statistical assessment of traveling-wave properties.

We performed a series of analyses to compare the properties of traveling waves between clusters from different brain regions. To compare directional propagation between different traveling waves, we first converted each cluster’s mean propagation direction into Talairach coordinates. Note that this sometimes caused directional plots to appear distorted, when the 2-D plane for each cluster was skewed relative to the Talairach axes (e.g., Fig. 1F). Then, to assess regional differences in propagation directions (Fig. 2B), we grouped each cluster according to whether it was in the frontal, temporal or occipitoparietal region. When a cluster spanned multiple areas, we labeled it to the lobe that contained the plurality of its electrodes.

We computed an estimate of the radius of individual clusters by using Welzl’s algorithm (Welzl, 1991), which computes the size of the smallest circle that contains all the electrodes in an oscillation cluster. We prefer this method, rather than reporting electrode counts per cluster, because it partially compensates for the irregular electrode sampling across patients. However, it is likely that this approach underestimates the size of individual oscillation clusters to some degree.

To measure the temporal frequency f of a traveling wave, we followed $f=d\overline{\theta }/dt$, where $\overline{\theta }$ is the average phase at each timepoint, taken as the circular mean across electrodes, and t is time. We used this approach to assess each wave’s propagation speed v as v = f / ξ, where f is instantaneous temporal frequency and ξ is the spatial frequency. To summarize the propagation speed for each wave (Fig. 6E), we computed the median propagation speed across all timepoints, excluding periods where the model fit was poor (i.e., mean PGD < 0.5; Rubino et al., 2006). Twenty one clusters had no timepoints with mean PGD ≥ 0.5 and thus were excluded from this analysis. We refined this approach to measure wave propagation speed on a single-trial basis, by only examining trials that clearly showed a robust traveling wave, as defined by a PGD value above 0.5 for at least the duration of one continuous oscillation cycle (Fig. 6C). To identify task-related changes in wave DC, we computed the trend of DC over time for each traveling wave cluster as the Pearson correlation between mean DC and time (Fig. 4F).

We considered the possibility that traveling waves could relate to stimulus-locked signals by calculating, for each cluster that showed a traveling wave, the mean phase resetting $\overline{R}$ and event-related potential (ERP) (Rizzuto et al., 2003). To identify the contribution of phase resetting to each cluster’s post-stimulus activity, we calculated the phase distribution at each point in time for the cluster’s mean frequency as in Rizzuto et al. (2003). We calculated the ERP for each cluster by first filtering the raw signal at 0.5–40 Hz, performing baseline correction (–200–0 ms), and finally identifying the individual electrode with the largest absolute ERP component.

To assess the role of traveling waves in behavior, for each cluster we compared the properties of traveling waves between trials where the patient had fast or slow responses to the probe in the memory task (median split). Then, for each cluster we computed the mean values of several properties of traveling waves separately for fast and slow trials: power, temporal frequency, PGD, spatial frequency, and directional consistency (Tab. S3). Unless otherwise specified, we used Student’s t-tests and ANOVAs to compare differences between regions, with rejection of the null hypothesis reported after FDR correction (Genovese et al., 2002) at q = 0.05

Model of traveling waves based on weakly coupled oscillators.

A linear array of weakly coupled Kuramoto oscillators (Kuramoto, 1981) produces traveling waves when it exhibits two properties: (1) weak phase coupling only between neighboring oscillators and (2) a spatial frequency gradient. In this spatial frequency gradient, the intrinsic frequency of each oscillator systematically varies with position along the array (Ermentrout and Kopell, 1984; Ermentrout and Kleinfeld, 2001). This configuration explains the appearance of traveling waves in the digestive system (Diamant and Bortoff, 1969) and is hypothesized to generate traveling waves in the cortex (Ermentrout and Kleinfeld, 2001).

We simulated this model to demonstrate that the frequency gradient we observed in our data (Fig. 7A) is feasible for producing traveling waves that propagate in the directions we observed (Fig. 1). As in earlier work (Ermentrout and Kleinfeld, 2001), we implemented the Kuramoto model as

$$\frac{d{\theta }_i}{dt}={\omega }_i+ϵ\left[\text{sin}\left({\theta }_{i-1}-{\theta }_i\right)+\text{sin}\left({\theta }_{i+1}-{\theta }_i\right)\right].$$

where i indexes separate oscillators, ω_i is an oscillator’s intrinsic frequency, θ_i is the instantaneous phase, and ϵ is the strength of phase coupling between neighboring oscillators. We used this model to simulate ten oscillators, which vary in frequency from 2 Hz to 16 Hz (ω_i =1.56i + 0.44 for i ∈ [1,10]), corresponding to a decreasing posterior-to-anterior frequency gradient from oscillator 10 to 1. Our simulations showed that when there is no phase coupling (ϵ = 0), each oscillator exhibits independent oscillations (Fig. 7E)—this resembles the spatial frequency gradients we observed in individual subjects (Fig. S6) and at the population level (Fig. 6D). When coupling is positive(ϵ ≫ 0), the same distribution of intrinsic frequencies produces a traveling wave propagating in a posterior-to-anterior direction (Fig. 7F–G). In this model the velocity of traveling wave propagation is fairly consistent except for a slowing near the edges due to boundary conditions (Cohen et al., 1982). Understanding and modeling edge effects in neural traveling waves is an active area of future work.

DATA AND SOFTWARE AVAILABILITY

Raw data for this paper are available at http://memory.psych.upenn.edu/. Analysis software are available from the authors upon request.

Supplementary Material

1

Movie 1. Animation of a traveling wave in one trial from Patient 1. (Related to Figure 1.)

3

Movie 2. Rotating animation showing the topography of traveling-wave propagation. (Related to Figure 2.) Format follows Figure 2A.

KEY RESOURCE TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Software and Algorithms
MATLAB R2015A	The MathWorks	RRID:SCR_001622
Python 2.7	python.org	RRID:SCR_008394
Custom MATLAB & Python scripts	This paper	Request from lead contact

Highlights.

• Theta and alpha oscillations are spatially clustered in the human neocortex.

• Clustered oscillations display traveling waves.

• Traveling waves generally propagate in a posterior-to-anterior direction.

• Traveling waves can be modeled as coupled oscillators.