Quantum Roaming in the Complex Forming Mechanism of the Reactions of OH with formaldehyde and methanol at Low Temperature and Zero Pressure: A Ring Polymer Molecular Dynamics Approach

Abstract

The quantum dynamics of the title reactions are studied using the Ring Polymer Molecular Dynamics (RPMD) method from 20 to 1200 K using recently proposed full dimensional potential energy surfaces which include long range dipole-dipole interactions. A V-shaped dependence of the reaction rate constants is found with a minimum at 200-300 K, in rather good agreement with the current experimental data. For temperatures above 300 K the reaction proceeds following a direct H-abstraction mechanism. However, below 100 K the reaction proceeds via organic-molecule⋯OH collision complexes, with very long lifetimes, longer than 10⁻⁷ s, associated to quantum roaming arising from the inclusion of quantum effects by the use of RPMD. The long lifetimes of these complexes are comparable to the time scale of the tunnelling to form reaction products. These complexes are formed at zero pressure due to quantum effects and not only at high pressure as suggested by Transition State Theory (TST) calculations for OH + methanol and other OH reactions. The zero-pressure rate constants reproduce quite well measured ones below 200 K, and this agreement opens the question of how important the pressure effects on the reaction rate constants are, as implied in TST-like formalisms. The zero pressure mechanism is the only applicable to very low gas density environments, such as the interstellar medium, unrepeatable by the experiments.

Hydroxyl radical, OH, is one of the main oxidants in the atmosphere^1,2 and in many combustion reactions.³ It reacts with many organic molecules with strong dipole moments, such as alcohols, ethers, etc, and the reaction rate constants increase enormously below 200 K.⁴ This increase has an enormous potential impact on astrochemistry, in which organic molecules are thought to be formed on ices^5–8 because at the low temperatures of interest, ≈ 10 K, barriers inhibit the reactions. However, the molecules formed on ices do not desorb at 10 K^9,10 and the question of how molecules, like formaldehyde and methanol, are detected in the gas phase in cold and dense molecular clouds is still under debate.

Using a uniform supersonic gas expansion technique (CRESU, acronym in French) Heard and co-workers¹¹ reported that the OH + CH₃OH reaction accelerates by 1-2 orders of magnitude when decreasing the temperature from 200-300 K to 100 K or below. This non-Arrhenius behavior was also found by other authors^12–14 and in many other reactions of OH with organic compounds^4,15–18 all using the CRESU technique. In these experiments, a V-shaped temperature dependence for the rate constant was found, with a minimum at about 200-300 K for all of the reactions, independently of the height of the reaction barrier. In all these cases the acceleration of the reaction below 100 K is explained by the formation of collision complexes between reactants and tunneling through the reaction barrier.⁴ However, some controversy still persists.

For OH + CH₃OH, Siebrand and co-workers¹⁹ found that the imaginary frequency at the saddle points used in Ref.11 was too large, and that, when using the proper one, the tunneling was too slow to reproduce the measured rate constants. As an alternative, they proposed a model based on the formation of methanol dimers during the expansion: when the dimers collide with OH they lead to the formation of the CH₃OH-OH complex, below the CH₃OH + OH re-dissociation limit, that can only be destroyed by tunneling towards the products. Siebrand and co-workers¹⁹ also predicted that the OH-reactivity of methanol dimers had to be much higher than that of the monomer. Within this model, a high density of dimers is necessary to reproduce the experimental data. The dimer density required in the simulations, however, seems to be too high according with the experimental conditions^20,21 to be responsible of the observed increase in the rate constant at T < 200 K.

The fast increase of the rate constant for the OH + methanol reaction with decreasing temperature can be explained by transition state theory (TST) assuming that the high pressure limit (HPL) is reached.^22,23 In these studies the low pressure limit for the reaction was described differently. Gao et al²² considered a direct H-abstraction process without any stabilized pre-reactive complex formed. On the contrary, Ocaña et al.²³ used RRKM calculations, where the complex energy is determined by the nascent energy distribution above the dissociation energy at the temperature considered.

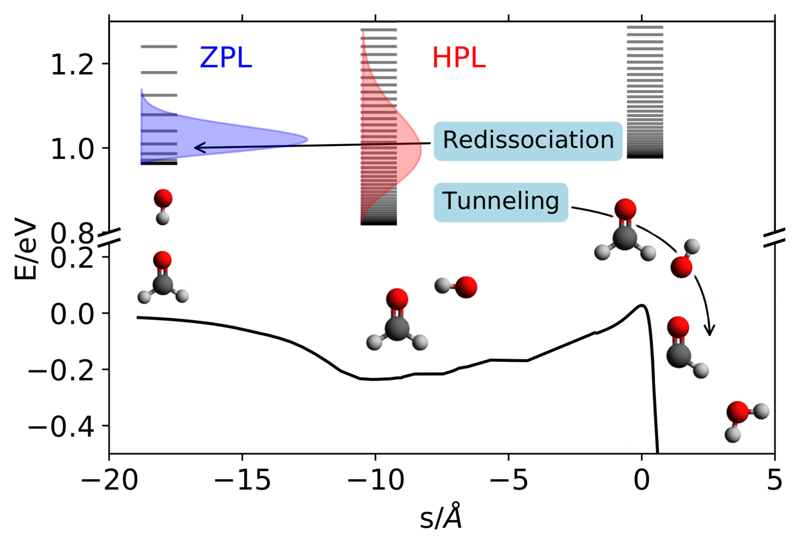
In the HPL situation, the pre-reactive complexes are stabilised by collisions with the buffer gas (BG) (more than three orders of magnitude more abundant than any reactant) used in the experiments, probably in a sequential way: first, the organic molecules (OM) complexes with the buffer gas forming OM⋯BG, and, second, the OH reactant, formed after the nozzle by photolysis, collides with this complex leading to the formation of the OM⋯OH collision complex. Since the BG can take some energy, the OM⋯OH complex has a broader energy distribution than at the zero pressure limit (ZPL), with a portion below the OM + OH redissociation limit (see Fig. 1 for the OH + H₂CO reaction). At the HPL, these complexes can live long enough to tunnel through the reaction barrier to form the products. This mechanism under HPL conditions can qualitatively explain the experimental observations and, in principle, would depend on the nature of the BG.

Figure 1.

Energy diagram of the H₂CO +OH → HCO + H₂O reaction.

Recently, quasi-classical trajectory (QCT) calculations on the reactions of H₂CO^17,24 and CH₃OH²⁵ with OH have been studied using full dimensional potential energy surfaces (PES). These studies indicate that for low temperatures the reactions take place through the formation of collision complexes, with lifetimes of several picoseconds. For H₂CO+OH it is found that the QCT rate constants are very similar to the measured ones^17,24 while for CH₃OH + OH they do not increase enough at low temperature.²⁵ Below 100 K, quantum effects are expected to play an important role, namely zero-point energy (ZPE) and tunneling effects. The aim of this work is then to re-evaluate the reaction mechanism under ZPL conditions by including quantum effects in full dimension dynamical simulations focussing in the reactions of OH with formaldehyde and methanol at low temperatures.

Given the high dimensionality of the reactions under examination, rigorous quantum methods are not feasible to study the reaction dynamics, and reduced dimension approaches are also expected not to be adapted because they reduce the density of states. In addition, complex forming reactions present additional difficulties for quantum dynamics as recently reviewed.²⁶ For these reasons, in this work we apply the Ring Polymer Molecular Dynamics (RPMD) method.^27–31 RPMD is a semiclassical formalism based on Path Integral Molecular Dynamics (PIMD) which includes quantum effects such as ZPE³² and tunneling,³³ and it has been demonstrated to be a very powerful technique to describe reaction dynamics for various profiles of reaction path including barriers an deep weels.³¹ In this work, we extend these RPMD studies to the title reactions which involves roaming reaction pathways and show the importance of including quantum effects for accurate estimation of reaction rate constants at low temperatures. We use the dRPMD program,³⁴ a direct version of the RPMD method based on the RPMDrate code,³⁵ which is parallelized specifically to describe long time dynamics. This direct RPMD trajectory approach involves two steps: thermalization and real-time dynamics.

The thermalization step is essentially a constrained PIMD simulation, performed in our case using the Andersen thermostat³⁶ and keeping constant the distance between the centers of mass of the two reactants, at 120 bohr in this case. After a thermalization time of 2-5 ps, the thermostat is removed, and the system is rotated so that the relative velocity vector is set parallel to the z-axis. Furthermore, a maximum impact parameter between centroids is also set, similarly to what is done in QCT approaches, to improve the statistics. In the second step, the real time dynamics is studied, with no thermostat, until the system reacts or becomes trapped. Some details of the convergence checks are described in the suplementary information (SI).

In the second real-time dynamics part, a system consisting of N_atoms × N_beads is propagated using a simplectic operator with a time step of 0.1 fs, needed to reproduce the high frequency modes (with N_atoms being the number of atoms, and N_beads the number of replica or beads of each atom). At the end of each RPMD trajectory the centroids are analyzed to determine whether or not the system has reacted. The rate constant is calculated according to the expression

$$k_{\beta }(T)=p_e(T)\sqrt{\frac{8k_{B}T}{\pi \mu }}\times \pi {\left[b_{\mathit{\text{max}}}^{\beta }(T)\right]}^2\times P_{\beta }(T).$$ (1)

The index β refers to either the reaction (hereafter called direct reaction rate constant, k_dir) or trapping (k_trap), where P_β (T) = N_β/N_max is the probability for channel β, with N_max being the total number of RPMD trajectories and N_β is the number of trajectories leading to products or trapped in the entrance channel until a maximum propagation time t_max. The parameters used in the calculations are listed in Table 1. $b_{\mathit{\text{max}}}^{\beta }(T)$ is the maximum impact parameter for channel β, reaction or trapping, at temperature T. Finally, p_e(T) = 1/[1 + exp(−200.3/T)] is the relative population of the ground ²Π_3/2 spin-orbit states of OH(²Π), which is introduced under the assumption that only the ground spin-orbit state reacts.

Table 1. Parameters of the direct RPMD trajectory calculations, and calculated rate constants.

T(K)	Nbeads	Ntot	tmax (ns)	$b_{max}^{react}$ (bohr)	$b_{max}^{trab}$ (bohr)	Pdir	Ptrap	kdir (cm3/s)	ktrap (cm3/s)
H2CO + OH
1400	48	10000	20	8.08	0	0.043	0.0	2.20 10–11	0.0
1200	48	10000	20	7.27	0	0.047	0.0	1.80 10–11	0.0
1000	64	12000	20	7.49	0	0.033	0.0	1.27 10–11	0.0
800	64	10000	20	7.60	0	0.030	0.0	1.06 10–11	0.0
600	64	10000	20	10.78	0	0.009	0.0	6.00 10–12	0.0
500	96	10000	20	10.43	0	0.009	0.0	5.09 10–12	0.0
400	96	10000	20	10.05	0	0.008	0.0	3.68 10–12	0.0
300	128	10000	20	10.59	0	0.007	0.0	3.72 10–12	0.0
200	256	10000	20	13.15	0	0.007	0.0	5.05 10–12	0.0
100	384	5000	20	13.40	16.00	0.008	0.20	5.10 10–12	1.77 10–10
50	768	3000	1	8.63	22.07	0.017	0.55	3.51 10–12	7.22 10–10
20	1920	3000	1	12.30	26.85	0.003	0.48	8.90 10–13	6.01 10–10
CH3OH + OH
500	96	20000	50	8.95	0	0.003	0.0	1.22 10–12	0.0
400	96	20000	50	8.00	0	0.003	0.0	8.70 10–13	0.0
300	128	20000	50	8.52	0	0.002	0.0	5.26 10–13	0.0
200	192	10000	5	5.66	11.91	0.008	0.32	1.01 10–12	1.80 10–10
100	384	2000	5	0.0	13.44	0.0	0.46	0.0	2.80 10–10
50	768	2000	5	0.0	17.54	0.0	0.37	0.0	3.06 10–10

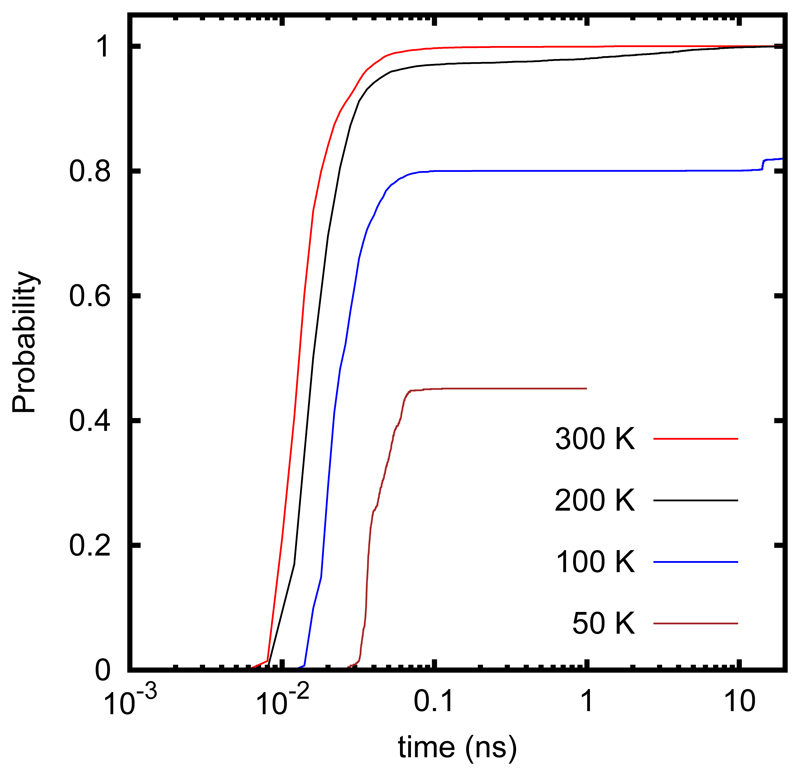
The direct reaction rate constants, k_dir (T), in Table 1 decreases monotonously with decreasing temperature. On the contrary, the trapping starts at 100-200 K and increases rapidly below this temperature. For formaldehyde, it drops again at 20K. These two mechanisms present very different time scales. In Fig. 2, the probability of finished trajectories versus the propagation time are shown for several temperatures to illustrate the different time scales of the direct reaction and trapping mechanisms for the case of H₂CO + OH reaction. For temperatures above 200 K, all trajectories finish before 0.1 ns. At 200 K, it can be observed that there is a second elbow for times longer than 1 ns, but it only accounts for less than 5 %. For formaldehyde at 100 K, this elbow seems to shift to even longer times and a large percentage of trajectories, ≈ 20%, remains trapped for times longer than 20 ns. Similar results are found for methanol at 200K. To make the calculations affordable, the maximum time has been reduced for temperatures where trapping dominates to make the calculations affordable. Many checks have been done at 100 K for the H₂CO + OH reaction, where the trapping mechanism starts to be important, as explained in the SI.

Figure 2.

Finished trajectories versus propagation time for the H₂CO + OH reaction.

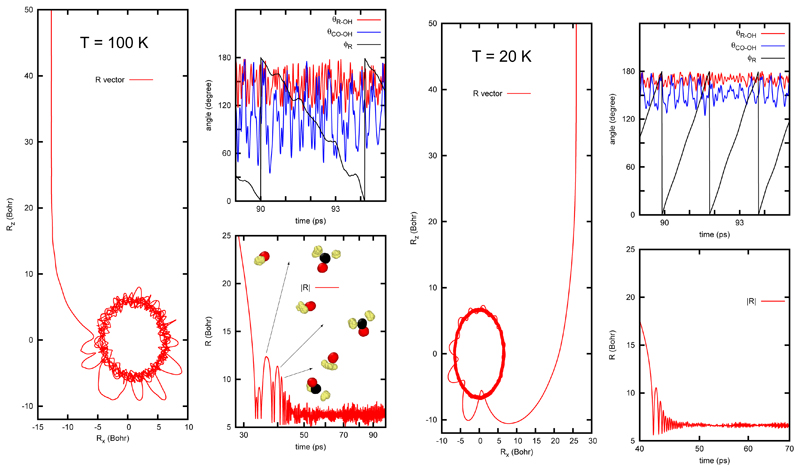
All trapped trajectories were found in the well of the reactants, with geometries in between the two insets shown in Fig. 1. One typical RPMD trajectory for OH+ H₂CO at 100K is shown in Fig. 3. The system starts an orbit, with relatively high end-over-end angular momentum. Along this orbit, the two systems are rotating initially and reoriented according to the long range dipole-dipole interaction. This first part of the trajectory, up to ≈ 30 ps, time at which the two reactants are at about 10 bohr, is the capture, which depends on the long range interaction. Dipole-dipole interaction is very effective in producing this capture, as already found with QCT calculations.^17,24,25

Figure 3.

Evolution of the vector R, between the centers-of-mass of reactants using the centroid for a RPMD trajectory at 100 K with initial impact parameter b^trap=13 bohr (left panels), and at 20 K with b^trap= 26 bohr (right panels). In the upper right panels, the evolution of the angles between R and r_OH and r_CO and r_OH are displayed for a short period of time. The angle ϕ_R = arctan (R_x/R_z) represents the end-over-end rotation of OH with respect to H₂CO. Similar roaming patterns are found for the OH + methanol case.

Once the two reactants get closer, they start to rotate with respect to each other with a couple of rebounds in which the distance, R, between the two centers-of-mass increases. After some time, these large amplitude trajectories, similar to classical roaming trajectories,^37–40 stop and the two subsystems, H₂CO and OH, rotate around each other in a rather narrow interval of R, as if the excess of energy is dissipated in the beads. This second process of the trajectory can be associated to trapping, because a periodic-orbit-like motion starts and lasts longer than ≈ 100 ns. Along these orbits, the mutual orientation oscillates rapidly, in a pendular-like motion sampling a region close to the potential well.

A similar situation is also found for the second trajectory shown in Fig. 3 for OH + H₂CO at T = 20 K. In this case, the number of high amplitude rebounds is lower, and the amplitude of the oscillations in θ_R−OH (R being the vector between the centers-of-mass of the two reactants) and θ_CO−OH is reduced, but the end-over-end rotation, represented by ϕ_R in the figure, is faster. This indicates that these long-lived complexes correspond to high rotational states, induced by reorientation of the two reactants along the orbit to approach each other, along the so-called capture process. This rotational excitation is “quantized” when using RPMD while in QCT calculations can be gradually switched on. This quantization introduces a constraint that at very low temperatures prevents the molecules from starting rotation at very long distances: in the RPMD case the available energy does not allow to increase an integer number the rotational quantum of the reactants needed to allow the reactants to reorient, reducing the capture probability. This explains why at 20 K, the trapping rate constant decreases, while in QCT calculation it continues growing.²⁴ The same roaming features are found for OH + CH₃OH reaction, showing a high rotational excitation with the relative position of the two reactants facing each other.

The fact that these trajectories are captured in the collision complex for such a long time is due to quantum effects. In the previous QCT study,^17,24,25 the lifetime of the collision complexes was analized, and never exceeded 50 ps, while in the present RPMD study this time is longer than 100 ns. According to the RRKM statistical theory,^41,42 the lifetime of the collision complex depends on the number of open channels, N_o(E), as

$$\tau =2\pi \hslash \frac{\rho \left(E\right)}{N_o\left(E\right)},$$ (2)

where ρ(E) is the density of states of the complex at energy E. In the RPMD, where quantum ZPE and tunneling effects are included, the number of accesible states of the reactants, N_o(E), is much lower than in the classical simulations, what explains why the RPMD collision lifetimes are much longer.

ρ(E) is associated to the bound states of the collision complex in the potential well. If the separation of these bound states Δ is lower than their width, Γ, associated to redissociation and tunneling, the statistical limit associated to large molecules is reached.^43–47 The initial state irreversibly decays in this dense manifold of bound states, and they rarely escape because of the low density of dissociation channels. This situation explains the results of the RPMD calculations. These bound states are rotationally excited, and only can redissociate back to the reactants by rotational predissociation. Because the angular momentum conservation law introduces many constraints, it is very unlikely to stop the rotations of the two reactants to nearly zero angular momenta by transfering their energy back to the relative kinetic energy.

The extremely long collision complex lifetimes get closer to the tunneling timescale necessary to react. In this sense, this ZPL model is similar to the dimer¹⁹ and HPL-TST models,^22,23 without needing to reduce the energy of the complex below the redissociation threshold by collisions with third bodies. Since in this zero pressure model the energy is higher than in the HPL model, the tunneling is also faster.

The total reaction rate constant is given by

$$k(T)=k_{dir}(T)+k_{CF}(T),$$ (3)

where k_dir(T) is the direct reaction rate constant defined above and k_CF (T) is the complex forming reaction rate constant given by

$$k_{CF}(T)=k_{trap}(T)\frac{k_{tunnel}(T)}{k_{tunnel}(T)+k_{rediss}(T)}.$$ (4)

The challenge is to calculate the tunneling rate constant, k_tunnel(T), and the redissociation rate, k_rediss(T), under similar conditions, since they involve different processes and degrees of freedom.

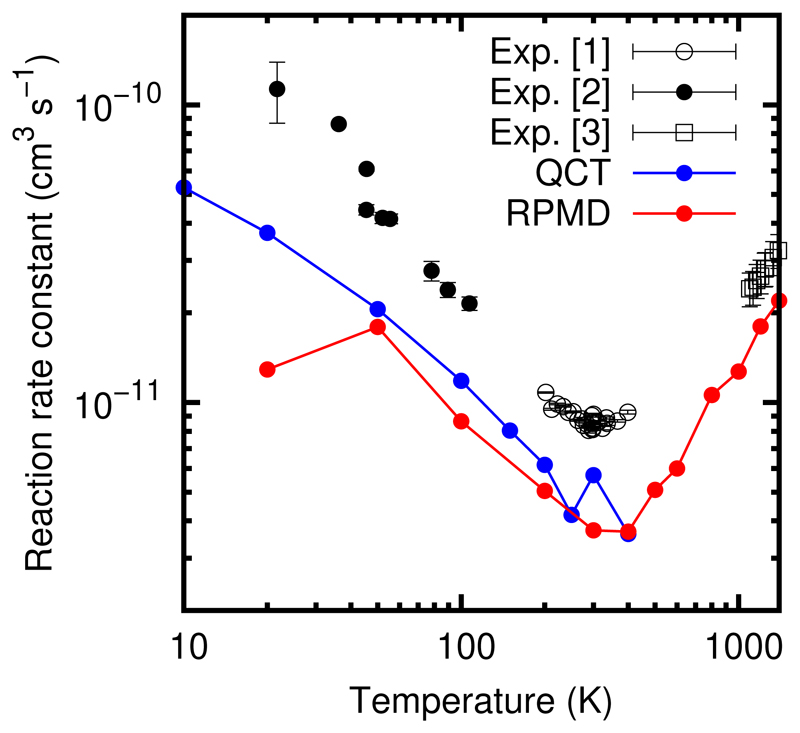
In the H₂CO+OH reaction the barrier is quite low, and we can assume that anharmonic effects can reduce it sufficiently to justify the classical results. For this reason, we consider that the k_tunnel/[k_tunnel + k_rediss] ratio can be approximated by the reaction probability found in the QCT calculations of Refs.^17,24. The QCT reaction probability is ≈ 2 % for energies below 5 meV (see Fig. 10 of Ref.24). Using this value, the total reaction rate constant obtained with the RPMD method, Eq. (3), is calculated and presented in Fig. 4, and is compared with the previous QCT results^17,24 and the available experimental data.^17,48,49 The RPMD results are in a rather good agreement with the QCT results from 50 to 300 K, while the reduction obtained at 20 K with the RPMD method is not reproduced by the QCT results, as discussed above. The good agreement above 50 K is explained by the trapping mechanism, which involves essentially rotational degrees of freedom, whose quantification only plays a role at the lowest temperature of 20 K. Also, the barrier is sufficiently low so that it may be considered as submerged by the anharmonic effects. The comparison with experimental data is also reasonable in H₂CO + OH, showing a semiquantitive agreement above 50 K, and a good qualitative behavior. The difference between the experiments and these calculations above 200 K by a factor between 2-3 is attributed to the accuracy of the PES, and work is currently in progress to improve it.

Figure 4.

RPMD rate constants for the H₂CO+ OH → HCO + H₂O reaction, obtained using Eq. (3). The QCT results are taken from Ref.17,24 Exp[1] are from Ref.48 Exp[2] are from Ref.17 Exp[3] are from Ref.49

The RPMD calculations performed for the CH₃OH + OH reaction show very similar features to that of H₂CO + OH, in particular the traping below 200 K following the same roaming mechanism. The direct reaction rate constant between 300 and 500 K is in very good agreement with the low pressure limit (LPL-CCUS) results of Gao and co-workers,²² and the transition to the trapping mechanism occurs at 200 K, where the two mechanisms coexist. Below 200 K, the direct mechanism is completely negligible, and the trapping mechanism dominates. As in the OH + H₂CO case, the lifetime of the collision complex is longer than 50 ns at 50 K, and this lifetime should increase at lower temperatures.

The RPMD trapping rate constants in Table 1 increase very sharply from 200 to 50 K. For lower temperatures, k_trap is expected to stabilize or decrease as for the H₂CO reaction. In this temperature regime, the RPMD k_trap(T) can be compared with the capture rate coefficients, $k_a^{TST}(T),$ calculated within a TST formalism by Ocaña et al.,²³ listed in their Table 4. $k_a^{TST}(T)$ in Ref.23 varies from the minimum at 150 K of 3.22 10⁻¹¹ cm³/s to 4.31 10⁻¹¹cm³/s at 30 K, while the RPMD trapping rate constants, 2.98 10 ⁻¹⁰ > k_trap(T) > 1.80 10 ⁻¹⁰ cm³/s, is ≈ 5 times larger. The RPMD method is considered to be more accurate,³¹ because it includes quantum effects (ZPE and tunneling), treats all degrees of freedom on an equal footing, and is based on real-time propagation of collision dynamics using the full PES, not only the stationary points.

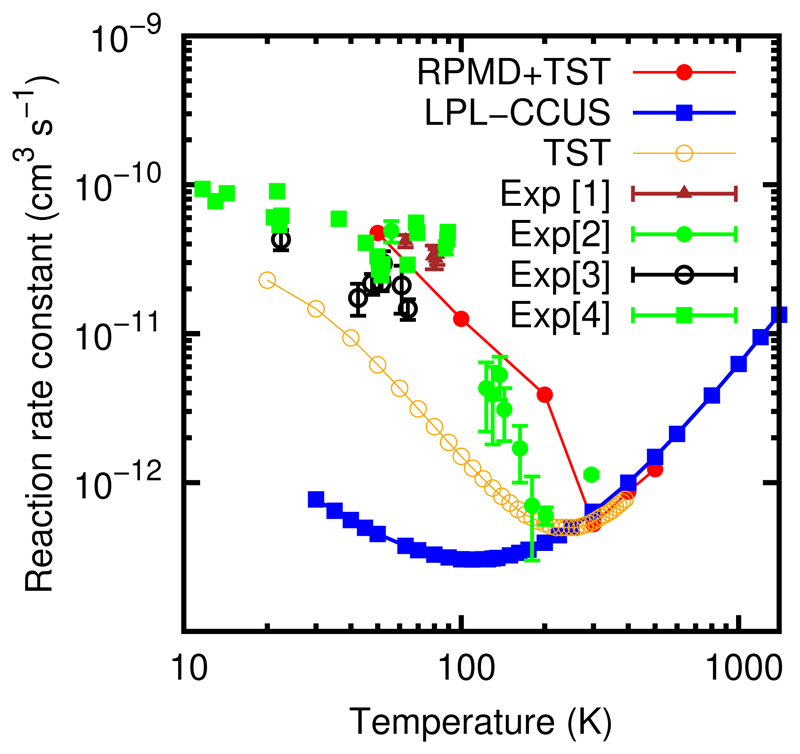
The low pressure rate constant, $k_{LPL}^{TST}(T),$ calculated in Ref.23 must then be multiplied by the same factor of 5, leading to a considerably larger reaction rate constant, much closer to the measured one. This implies firstly that the pressure effects are less important and secondly, and more important for astrochemical models, that the zero pressure reaction rate constant also increases when lowering temperature. In order to calculate the complex forming rate constant, k_CF(T), the ratio k_tunnel/[k_tunnel + k_rediss] has to be calculated. This branching ratio can be directly obtained from Ref.23 as k_LPL/k_a(T), from their Eq.(E6). The branching ratio takes the values of 0.16, 0.045 and 0.016 at T=50, 100 and 200 K, respectively. Using these values the total reaction rate constant in the zero pressure limit is obtained using Eqs.(3) and (4), where k_trap(T) and k_dir (T) are directly calculated with the RPMD method, and k_tunnel/[k_tunnel + k_rediss] = k_LPL/k_a(T) is taken from the TST calculations of Ref.,²³ and it is compared with the experimental data in Fig. 5.

Figure 5.

Total reaction rate constant for CH₃OH+OH reaction at the zero pressure limit calculated using Eq. (??) combining RPMD and TST results as explained in the text. The [1,2,3,4] experimental results are from Refs.,¹¹,¹²,¹⁴,²³ respectively. LPL–CCUS are taking from Ref.22 TST referes to the TST (RRKM) results obtained in the LPL in Ref.23

The agreement obtained with the experimental data for the CH₃OH + OH reaction is really good, but further theoretical analysis should be done to completely confirm the results. In particular, the calculation of the k_tunnel/[k_tunnel + k_rediss] ratio as a function of temperature has to be recalculated including more dimensions.

In summary, we can conclude that reactions of formaldehyde and methanol with OH at the ZPL proceed via very long lived collision complexes and the reaction rate constant increases at low temperatures. The present RPMD study shows that it is of paramount importance to include ZPE and tunneling quantum effects giving rise to new dynamical features such as quantum roaming which play a major role in the reaction mechanisms. The complex mechanism at the zero pressure limit is an alternative that must coexist with the high pressure models already used,^22,23 with many aspects in common. Since in these studies the relative weight of the LPL and HPL rate constants are fitted to the experimental results, it is of great interest to evaluate the LPL capture rate as accurately as possible. At this regard, the RPMD method used here is very accurate considering multidimensional quantum effects, and it is considered to yield better results than the TST approach beyond mono-dimensional model.

The behavior below 100 K, could also be explained by the pressure effects in the experiments, as suggested in previous TST studies.^22,23 In fact, the collision complexes live considerably longer than 100 ns, time of the order of magnitude of the collisions with the buffer gas. Under these conditions, it is therefore possible that the OM-OH complex collides with the BG, thus producing an energy change of the complex. If this energy increases, the reaction over the barrier is facilitated. If the energy decreases, the complex can only tunnel towards products, but at even longer time scales than the zero pressure mechanism presented here.

The extremely long lifetime of the collision complexes is then of high importance in interpreting the measurements. The reaction rate constants in CRESU experiments are obtained following the dissapareance of the OH radical by laser induced fluorescence (LIF) technique. The loss of OH radicals can be due not only to the reaction with formaldehyde or methanol, but also by complexation. An experimental evidence of products or collision complexes at very low temperatures would be desirable indeed. For the OH + methanol reaction, the Leeds group detected CH₃O radicals (one of the products) at 80 K, demonstrating that the reaction occurs at this low temperature.¹¹ However, quantification was not possible by LIF, which is necessary to determine the branching ratio of different products.

The CRESU experimental set up can follow the reaction dynamics in a limited time scale of around several hundreds of microseconds imposed by the uniformity length of the gas temperature and pressure. Therefore, if the trapped complexes, formed by either quantum LPL or HPL mechanisms, live longer, their fragmentation cannot be studied. In the present quantum LPL mechanism at 100K a lower limit of the complex lifetimes of > 200 or 50 ns are found in the two cases. For lower temperatures this complex lifetime is expected to increase significantly. The quantitative measurement of the products ratio would allow to address this point.

In astrophysical environments, the gas density is extremely low and high pressure conditions are not achieved. It is therefore of great importance to determine the individual rate constants of the quantum LPL for pressure-dependent reactions. This problem is a challenge for theory and experiment. For theory, the accurate determination of the full dimensional potential and the accuracy of RPMD or any other dynamical method to describe realistically the complex lifetimes are currently open questions. From the experimental side, the low gas densities of the interstellar medium are impossible to reach and the quantitative measurement of product branching ratios and the spectroscopic study of long-lived intermediates are now-a-days a challenge.