Abstract
We present a model of the whole visual train to estimate an individual’s visual acuity based on their eye’s physical properties. Our simulation takes into account the optics of the eye, neural transmission and noise, as well as the recognition process. Personalized input data are represented by the ocular wavefront aberration and pupil diameter, both either coming from in vivo measurements of a subject or being produced by optical design software using a schematic eye. This flexibility opens the door to a broad range of potential applications, such as objective visual acuity measurements and intraocular lens design. Our algorithm contains only two adjustable neural parameters: additive noise σ, and discrimination range δρ, with their values being experimentally calibrated by fitting the results of simulations to the outcome of real acuity tests performed on healthy young subjects with normal vision (visual acuity: 0…−0.3 logMAR range). It was established that by using fixed values of σ = 0.10 and δρ = 0.0025 for each person examined, the residual of the acuity simulations averaged over the calibration group reached its minimum at 0.045 logMAR.
Subject terms: Image processing, Biological physics
Introduction
Visual acuity is the single most important ophthalmological quantity describing the perceived resolving power of the human eye. Conventional acuity tests are performed using eye charts, for which purpose the Early Treatment Diabetic Retinopathy Study (ETDRS) chart, implemented with the Sloan characters, has become the standard1–3. In such tests, the subject’s task is to correctly recognize letters of different scales, where letter size is characterized by the visual angle α, of the stroke width. In line with the sensitivity of the human eye to lowering stimulation, in eye charts currently used the letter size decreases from line to line in a geometric progression with a ratio of 101/10 , 3–5. Thus, the visual acuity value V, is usually expressed in logMAR units (i.e. the decimal-base logarithm of the Minimum Angle of Resolution) such as:
| 1 |
where α0 denotes the visual angle in minutes of arc at the 50% recognition probability threshold by definition of the International Council of Ophthalmology (ICO) standard1,2. This measurement process is used to assess the entire visual system, as a result of which the acuity value depends not only on the optical parameters of the human eye, but is affected by factors such as retinal sampling, neural transfer, neural noise, and cortical recognition6,7. Accordingly, reliable visual acuity models should accurately take all these phenomena into consideration7–10.
The primary goal of vision models is to relate precisely measurable objective optical/mechanical parameters to the subjective visual acuity value7,10. In order to establish such a relationship, first the image quality of the eye has to be known. The “optically filtered” retinal image can be reconstructed from the monochromatic aberrations of the human eye11–14, which is measurable using Shack-Hartmann wavefront sensors15. As a next step, neural transfer simulates the post-retinal neural image, with additional neural noise being taken into account to determine the noisy image which is finally recognized by the visual cortex16,17. The recognition process is usually represented as a template-matching algorithm, which is known to be one of the simplest and oldest models of pattern vision18–20. By examining the correct/incorrect identifications of several letters of a given size, it is possible to estimate the recognition probability from one line to the next. Vision models use these data to calculate the psychometric function of vision by curve-fitting, from which the visual acuity value can be determined by thresholding7,9. The outline of a typical visual acuity model is depicted in Fig. 1.
Figure 1.
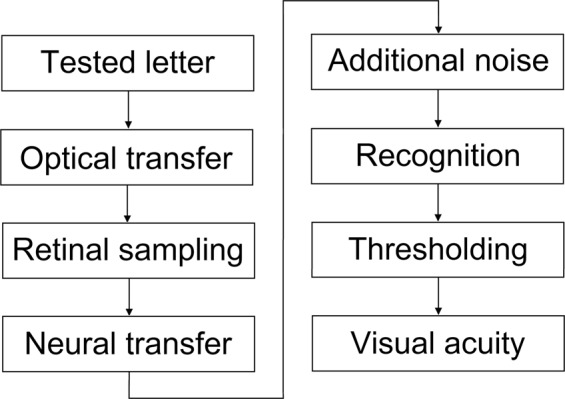
The outline of visual acuity models presented in the literature.
Most visual acuity models analyze optical aberrations and diffraction effects through the use of the monochromatic Point Spread Function, PSF. More elaborate implementations take into account the severe longitudinal chromatic aberration of the eye11,21,22 by integrating defocused PSFs for a few discrete monochromatic wavelengths10,21. However, we found that this was neither sufficiently precise nor very practical. Some other models utilize Bayesian probability theory to provide a more realistic description of recognition10,21,23, which increases simulation time, but does not address the individual characteristics of optical transfer. Another possibility is to model recognition with neural networks24,25, which has become widespread recently— especially for identifying handwritten digits26,27 or characters28–30. The main drawback of using artificial intelligence is that a huge number of samples are required during the training phase.
Given the stated limitations, we decided to develop a new personalizable visual acuity model based on those propounded in the literature7,9,10. Since most medical treatments attempt to restore the patients’ vision capability to a normal level, we focused our attention on studying the visual acuity of healthy people with near-emmetropic vision, examining only the ±0.5° field angle range of foveal vision. Our intention was to create a simple simulation tool having as few parameters as possible, in which one can modify the opto-mechanical structure and analyze the resulting effects. Thus, we implemented a physiologically correct schematic eye that can accurately describe the polychromatic imaging properties of any specific human eye, to which we added a simplified but realistic representation of the retina. We supplemented it with an improved numeric model of neural processes and cortical recognition, and integrated a novel algorithm that estimates the visual acuity value. The specific motivation for our research came from the field of cataract surgery: we were particularly interested in improving the design, measurement, and implantation of intraocular lenses (IOLs). Our practice shows that the comparison of different IOL types (e.g. aspheric, toric, or diffractive lenses) and also the evaluation of alternative designs of the same type would greatly benefit from a simulation tool that estimates post-operative visual acuity31,32. Moreover, the same model could be used to devise new visual acuity measurements to objectively assess the outcome of surgery33,34. Such objectives may not be universally required, but we expect that our model will prove useful for other areas of vision research, too.
In this paper, we present our model in detail and demonstrate its capability to algorithmically reconstruct the monocular visual performance of a small group of young subjects based on the measured optical properties of their eyes. Furthermore, we provide preliminary calibration values for the two adjustable neural parameters of the model. Sensitivity to changes in different construction parameters are discussed and a comparison with the former Watson-Ahumada model7 is outlined.
Methods
Basics of vision modeling: image formation and neural processing
Visual acuity models presented in the literature7,9,10 determine the generalized (complex) pupil function O(X, Y), using a simplified formula derived from wavefront aberration (i.e. Optical Path Difference, OPD):
| 2 |
where T(X, Y) describes the amplitude transmission of the pupil, X and Y denote coordinates on the exit pupil of the eye, and OPD is given in wavelength units of λ0 (the reference wavelength, e.g. that of the aberrometer). From O(X, Y), the PSF can be computed as the squared modulus of its Fourier transform. It should be noted that it is very common to formulate the wave function as if the phase advances in the direction of wave propagation. Since we follow this sign convention, in our case the Huygens-Fresnel diffraction integral specifies a Fourier transform and not its inverse.
Since biological visual systems are considered to be linear in terms of incoherent irradiance at the retina27, the foveal image of an arbitrary object can be obtained by convolving the ideal (paraxial) image with the PSF. As spatial domain convolution is equivalent to multiplication in the frequency domain, the calculations are usually implemented in the latter form35. In this way, the Optical Transfer Function, OT F, (being the inverse Fourier transform of the PSF) is used to characterize the optical system12. Consequently, the irradiance distribution RI(x, y), of the image at the retina can be calculated as:
| 3 |
where II(x, y) indicates the ideal image (magnified image of the object), while FT and IFT stand for Fourier transform and its inverse, respectively. In order to avoid any confusion that may arise from expressing the optical image of eyes having different focal length by spatial coordinates at the retina, we project the image back into the object space and present coordinates in angular units (x and y are expressed in degrees). Accordingly, fx and fy indicate angular frequencies in cycles/degree.
In visual acuity models, the optical transfer is followed by retinal sampling that characterizes the effects of the photoreceptor mosaic. According to anatomical studies, cones are arranged in a quasi-hexagonal lattice with approximately 50…60 cycles/degree Nyquist limit at the fovea centralis10,17,36. Therefore, the sampling process can be modeled using a low-pass filter whose prime function is to decrease spatial resolution. Nevertheless, according to previous experimental findings10,21, this effect is only significant for almost aberration-free, diffraction limited eyes; whilst in the case of average vision it is negligible.
There are certain models that take into account the contrast drop caused by light scattering that occurs at the cornea and the crystalline lens. Since at this phase of the project we deal only with healthy young subjects whose vision is affected by scattered light only in a minor extent37, for the time being we do not take it into consideration.
As a next step, the Neural Transfer Function, NTF, should be incorporated to model low-level retinal image processing. It can be either measured directly without optical effects, bypassing the optics by interferometric techniques, or derived from the Contrast Sensitivity Function, CSF, 7,9. The CSF is a radially symmetric band-pass filter composed of a low and a high-frequency lobe, from which low-pass filtering corresponds to convolution with a blurring mask21,28,29. Since in the frequency domain overall contrast is the product of the optical and neural filters, the NTF can be determined by dividing the CSF by the Mean Optical Transfer Function, MOTF:
| 4 |
The most accurate characterization of the MOTF— which represents the average optical transfer function of the best-corrected human eye— is presented by Watson38. Applying this, the shape of the resulting NTF curve corresponds to that of edge-enhancement filters. Analogously to optical filtering, the post-retinal neural image PI(x, y), can be expressed as:
| 5 |
The mathematical construction PI(x, y) represents the electrical signals that the retina sends towards the visual cortex. This takes us to the last step of image processing: the calculation of a noisy image, that is to be analyzed by the cortical recognition process. As with all biological organs, the visual system also has some temporal uncertainty16,17, which is usually modeled at one instant as additive noise:
| 6 |
In (6) NI(x, y) denotes the noisy image, and GWN(x, y) stands for the Gaussian white noise of a cell. In this expression “Gaussian” refers to the distribution of the added random values, being a normal distribution with 0 mean and σ2 variance, while “white” indicates that the stochastic activity of cones is independent of each other. The probability density p, of GWN can be formulated as:
| 7 |
New neuro-physiological vision model
Our new visual acuity model basically follows the steps described above, but also contains some substantial improvements. Instead of applying elementary monochromatic calculations described by (2), we characterize the complete, polychromatic optical transfer using a physiological eye model. In this way, both ray-tracing and scalar diffraction analysis are taken into account to accurately model the imaging system. Additionally, the schematic eye enables us to make modifications to its structure and analyze the resulting effects. This personalization can be realized in two ways. First, we can make a structurally correct model of a given person’s eye based on biometric measurements (using ultrasonometry, corneal topography etc.), by which it would be possible to design certain visual optical devices (such as IOLs) directly for improved visual acuity. Second, using a structurally average eye model we can customize it by appropriately inserting a given person’s wavefront map OPD(X, Y), measured at a given wavelength and let the model deal with polychromatic aberrations and diffraction. This approach makes it possible to develop e.g. new diagnostic methods by which visual acuity could be objectively determined from a quick wavefront measurement. In this paper we pursue this second way, as it better serves our aims with respect to model calibration (see the “Results” section).
Personalized physiological eye model
Our physiologically accurate average eye model is implemented in Zemax OpticStudio39. Its structure is kept simple, since individual wavefront aberration is to be introduced to the model directly from measurements. From the many existing schematic eyes, our choice fell on the well-known “historical” Gullstrand Exact (No. I) model40,41, which involves only spherical surfaces and simplifies the gradient-index crystalline lens to a central nucleus (core) of high refractive index, surrounded by a cortex of lower refractive index. Since longitudinal chromatic aberration plays important role in human vision11,21,22 and the Gullstrand Exact model excludes wavelength dispersion, we replaced its original fixed refractive indices with dispersion formulae based on Atchison and Smith’s measurements42. They used the Cauchy formula, but as it was not available in Zemax we fitted their dispersion curves42 using the Sellmeier 1 formula, which has an implementation in most optical design software:
| 8 |
Here n denotes the refractive index of the material, λ indicates the wavelength in vacuum (given in microns), while K1,2,3 and L1,2,3 are coefficients describing a specific material. Their fitted values are summarized in Table 1 for all media of the schematic eye. The result of the fit follows the profile given by Atchison and Smith42 with high accuracy: the standard deviation of the refractive indices determined by the Cauchy and the Sellmeier 1 formula being smaller than 0.0017 for all media of the eye model. Polychromatic illumination is weighted as a function of wavelength according to the photopic sensitivity curve of the human eye3. In total we apply 24 discrete wavelengths equally distributed across the visible spectral range.
Table 1.
The numerical values of the K1,2,3 and L1,2,3 coefficients used in the Sellmeier 1 formula to describe the wavelength dispersion of the different media of the eye model.
| Material | K1 [−] | K2 [−] | K3 [−] | L1 [μm2] | L2 [μm2] | L3 [μm2] |
|---|---|---|---|---|---|---|
| Cornea | 8.68·10−1 | 4.60·10−4 | 3.93·102 | 9.35·10−3 | 1.41·10−1 | 4.41·104 |
| Aqueous | 7.61·10−1 | 4.18·10−4 | 5.18·104 | 1.01·10−2 | 1.42·10−1 | 5.73·106 |
| Lens nucleus | 9.42·10−1 | 1.29·10−3 | 4.71·104 | 1.12·10−2 | 1.32·10−1 | 6.19·106 |
| Lens cortex | 1.26·10−3 | 8.87·10−1 | 3.63 | 1.31·10−1 | 1.15·10−2 | 4.88·102 |
| Vitreous | 7.61·10−1 | 2.73·10−4 | 4.30·104 | 1.01·10−2 | 1.43·10−1 | 5.61·106 |
The Styles-Crawford effect (i.e. the directional sensitivity of cones) is taken into account using a Gaussian apodization in the amplitude transmission factor T(X, Y), of the pupil function, see (2). Its single parameter, the 1/e radius equals 2.9 mm40. The schematic view of our Zemax model is shown in Fig. 2, its mechanical dimensions are presented by Gobbi40.
Figure 2.
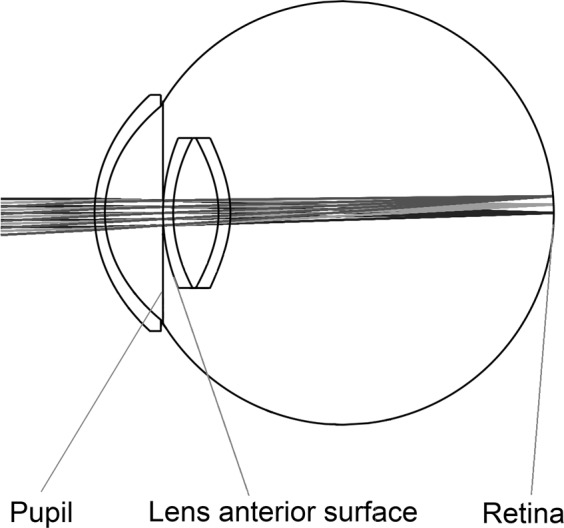
Schematic view of the physiological eye model.
In order to personalize the model, we use the wavefront aberration of a given subject measured by a medical Shack-Hartmann sensor. The outputs of the aberrometer are the coefficients of the Zernike polynomials fitted to the measured wavefront of the subject11,13–15. We use a tenth-order expansion, so that OPD is given by a set of 64 Zernike coefficients (the zero-order piston, the first-order horizontal and vertical tilts, and also the second-order defocus terms are ignored to exclude instrumental myopia15). After a necessary rearrangement (due to the different ordering of Noll’s sequential indices used in Zemax39 and OSA/ANSI standard indices used by wavefront sensors15), the coefficients can be directly imported to Zemax to characterize the target wavefront. To this end, the first surface of the lens (see Fig. 2) has been modified to be a so-called Zernike-surface, having variable coefficients.
As the first step of personalization, we adjust the entrance pupil diameter d, to the value measured by the Shack-Hartmann sensor. Then, we optimize the Zernike coefficients of the lens anterior surface, so that the monochromatic OPD equals the measured wavefront shape at the reference wavelength of the Shack-Hartmann sensor, i.e. λ0 = 555 nm. As a consequence, the model produces exact results at the reference wavelength. Thanks to the close-anatomical structure of the Gullstrand Exact model and the applied Atchison-Smith dispersion formulae, this model allows us to take the effects of chromatic aberrations into account.
After this process of personalization, we change the entrance pupil diameter to the specific value at which the visual acuity of the subject is to be determined. Pupil diameter is a very important parameter, thus we developed a custom arrangement for its real-time measurement during visual acuity tests43, see subsection “Experimental setup used for calibration”. For subjects having emmetropic or hypermetropic eyes we optimize the axial retina position for infinite object distance in order to ensure a sharp image. The optimization error function includes the diffraction Modulation Transfer Function, MTF, at two distinct spatial frequencies: 14.85 and 22.28 cycles/degree (50 and 75 cycles/mm at the retina, respectively). For subjects with negative refractive error the retina position optimization is performed using an extra paraxial lens (i.e. an ideal model of eyeglasses prescribed for best correction). In order to simulate their uncorrected visual acuity, which is our intention, the paraxial lens has to be removed afterwards. In terms of Zernike polynomials, their coefficient has a negative value.
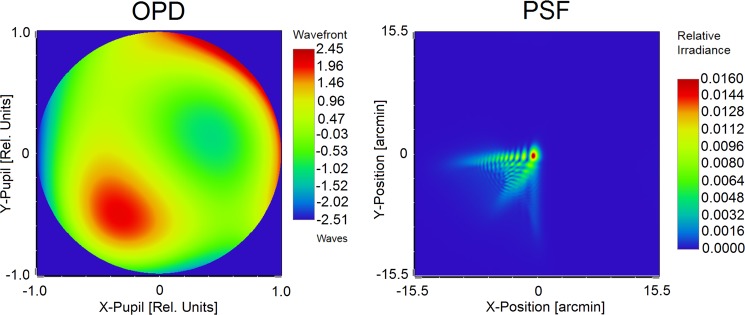
Finally, the polychromatic diffraction PSF of the eye is determined and normalized so that its surface integral equals unity. This is an important pre-processing procedure for character recognition29,30, that allows for the comparison of results from subjects having different optical aberrations. A representative OPD map and the corresponding high-accuracy PSF— determined by the personalized model of the subject’s eye at a typical entrance pupil diameter of 5.0 mm— is depicted in Fig. 3.
Figure 3.
The measured wavefront aberration OPD, of subject S. T.’s OD eye and the corresponding polychromatic PSF at d = 5.0 mm entrance pupil diameter derived from his personalized physiological eye model.
It can be argued that the effective focal length of our eye model equals the well-known average value of 17.1 mm22,40,41, which does not necessarily correspond to that measured on a given person. Having said that the examined letter size, the pupil diameter, and the wavefront aberration are all known in the object space, the focal length of the actual eye cannot affect the image quality in any respect.
The output of the eye model is the numerical matrix representation of the polychromatic diffraction PSF. In order to provide accurate angular sampling even for diffraction-limited PSFs, we defined the matrices of all filters and images so that the visual angle of one pixel corresponds to Δx = Δy = 5.724 arcsec. Since we implemented Fourier transform using the fast Fourier transform method44, FFT, the number of grid points N, must be a power of two. In order to ensure that the PSF of strongly aberrated eyes can also be evaluated, we set N = 1024. From this, the frequency-domain resolution can be calculated as:
| 9 |
Numeric model of neural image processing
The neural part of the model, which imitates the subsequent steps of image processing and character recognition, is implemented in MatLab45 to take advantage of its efficient numerical matrix calculations. All operations are accomplished in the frequency domain and the only piece of input data is the polychromatic diffraction PSF calculated using Zemax. From this the OTF is determined by inverse fast Fourier transform, IFFT, and is applied to the ideal image of the visual target object according to (3). Our target objects are single letters of different sizes, represented by 1024 × 1024 binary matrices. Black pixels of the letter strokes are represented by 0 and white background pixels are indicated by 1.
We use the average NTF described by (4) to obtain the post-retinal neural image. In our model, similarly to the PSF, the NTF is normalized so that the spatial domain surface integral of its Fourier transform equals unity, i.e. NTF(f = 0) = 1. Due to this normalization, the background value of the filtered images always remains unity. At this point, there is a numerical issue that needs to be mentioned. When a Fourier transform and its inverse are performed one after the other, both calculations have to be accomplished using the same algorithm in order to obtain the correct results. In the present case, we use IFFT for OTF calculation, but the NTF has not been determined this way. For this reason, we first apply a discrete Fourier transform, DFT, to the NTF, then we transform it back by IFFT to obtain the NTF', which we use in our algorithm:
| 10 |
The last step of neural image processing is the calculation of a noisy image, according to (6). In case of high-acuity human vision, one of the most important noise sources is the limited channel capacity of the retinal ganglion cells17,46. Thus, we decided to represent neural noise so that it corresponds to the individual cells of the retinal cone lattice, i.e. a hexagonal structure with 120 cycles/degree spatial frequency10,17,36. We apply additive Gaussian white noise according to (6) and (7). In order to differentiate between the subjects’ neural sensitivity, and to model temporal changes in their concentration ability, the standard deviation σ, of the applied normal distribution is a free parameter of the model that has to be optimized. Since the background of the images is unity, the numerical value of σ represents a signal-to-noise ratio relative to the noiseless image. The results of the successive steps of opto-neural image processing are illustrated in Fig. 4. The last sub-image (d) is used as input for the character recognition algorithm.
Figure 4.
The results of the successive image processing steps of our vision model: (a) ideal image of the examined letter, (b) retinal image, (c) post-retinal neural representation, (d) noisy image.
Template-matching model of cortical character recognition
The final phase of our vision model is character recognition. In order to provide a simple algorithm with great descriptive power, like many other authors18,19,35, we use template-matching. It quantifies similarity between the examined object and several templates by normalized cross-correlation18,20,47. In our model, subjects are considered as ideal observers limited by optical and neural filtering, as well as neural noise, which determines the noisy image as described above. However, the construction of template images requires special consideration.
Despite all distortions being caused by the complex multi-step visual process, people see objects equally sharp in a wide range of environmental conditions. This can be explained by the fact that the brain is able to store and retrieve different filtered images from prior experiences. These images are used as templates, and are compared to the actual noisy image during recognition. According to the literature19,24,48, human subjects (and even animals) can learn and memorize the permanent properties of multiple filtered images of an object at different scales and different positions, but cannot learn their variations. Consequently, subjects can form average templates for target objects that had passed through the steps of cortical image processing9. Therefore, in our model the template set contains optically and neurally filtered, but noiseless images of the same size as the tested image.
We determine the normalized cross-correlation of two matrices using Pearson’s correlation formula49,50. Its result is not a single scalar number, but a matrix with a linear size that equals the sum of the original linear sizes less one. Since correlation calculations are highly time-consuming and are called multiple times during a visual acuity simulation, they significantly affect the running time of the algorithm. Therefore, we estimate the lateral extension of the template images by taking two times their second momentum (root-mean-square value), and perform cross-correlation only on matrices covering this area. In this way, the correlation matrix size depends on the actual image size, but is strictly smaller than 200 × 200 (cf. the original 1024 × 1024), which boosts the calculation significantly. Furthermore, by cutting off the constant background borders, we eliminate the possibility of fake high correlation peaks corresponding to shifted positions where only the edges of the two matrices overlap. Finally, the correlation value ρ, is determined from the maximum element of the calculated cross-correlation matrix, which ensures translation invariance for recognition23,25,48.
In the case of a tested letter, the template-matching algorithm determines the above-described correlation value for all possible templates and sorts them in descending order to find the maximum: ρmax. Though simple recognition models define the response directly by ρmax7,9, we noticed that during visual acuity tests the subjects often become hesitant near the recognition threshold and start guessing from multiple choices. This suggests that differences below a certain threshold cannot be distinguished5,51. In order to reconstruct the decision-making method accordingly, we defined a discrimination range δρ, in which the identification of any differences is not possible. We consider indistinguishability bound to an absolute limit, thus we have determined δρ as a constant value, which is another free parameter of our visual acuity model. Accordingly, the output of our recognition process is a set of potential guesses corresponding to the correlation values within the [ρmax − δρ; ρmax] discrimination range. In this way, the vision model has only two independent parameters: σ and δρ, which we optimized based on our measurements, see “Experimental setup used for calibration” and “Results”.
Determination of the visual acuity value using correlation-based scoring
We have formerly introduced a correlation-based scoring scheme to reduce the statistical error of visual acuity tests52,53. As we make extensive use of it in the vision model, a brief summary is given below and some differences from the standard probability-based scoring are expressed. Further details and deeper explanations are presented in our former papers52,53.
During conventional visual acuity measurements, the examiner only registers whether the optotypes are identified correctly or not, i.e. the mere fact of recognition is tested. Thus, the responses are represented as binary scores, where 1 represents a correct recognition and 0 indicates a mistake. However, in some cases the examiner omits minor errors (e.g. misidentifying C as O, or R as P)5, which suggests that human visual perception is more complex than a simple binary scheme. In other words, whenever the subject makes a mistake, they might see some features of a specific letter, so it is worth characterizing how bad or good the guess is. Consequently, we have previously introduced a new quantity called Optotype Correlation, OC, as a measure of character similarity52,53. The quantification is based on Pearson’s normalized cross-correlation50 calculated on the non-distorted original images of letters. For a given character pair we take the correlation peak, which results in a single real number over the [−1; 1] interval. From this, OC is obtained after a linear transformation, so that the expected value of the statistics of OC for two randomly selected letters equals 1/26 (because we use all 26 letters of the English alphabet in our examinations), and correct recognitions are always represented by 1. In this way, OC is directly comparable to the conventional binary scheme of true/false identifications, but provides more information about the specific response. The OC values for all potential combinations of displayed-guessed characters can be tabulated as a two-dimensional array, the so-called OC matrix. This is similar to confusion matrices (used both in ophthalmology51 and machine learning26 to quantify the probability of misidentifications), since letter pairs with higher OC values are more likely to be confused.
The discrimination range may contain one or more potential responses in case of each single tested letter. Accordingly, our recognition model calculates the OC value for all these guesses and yields the output for the tested letter as their mean. In such ambiguous cases the averaging step represents the hesitation of the subject by summarizing the possible results of multiple acuity tests performed subsequently, thereby decreasing uncertainty error. The workflow of the entire process for the identification of one single letter, together with its main parameters, is depicted in Fig. 5.
Figure 5.
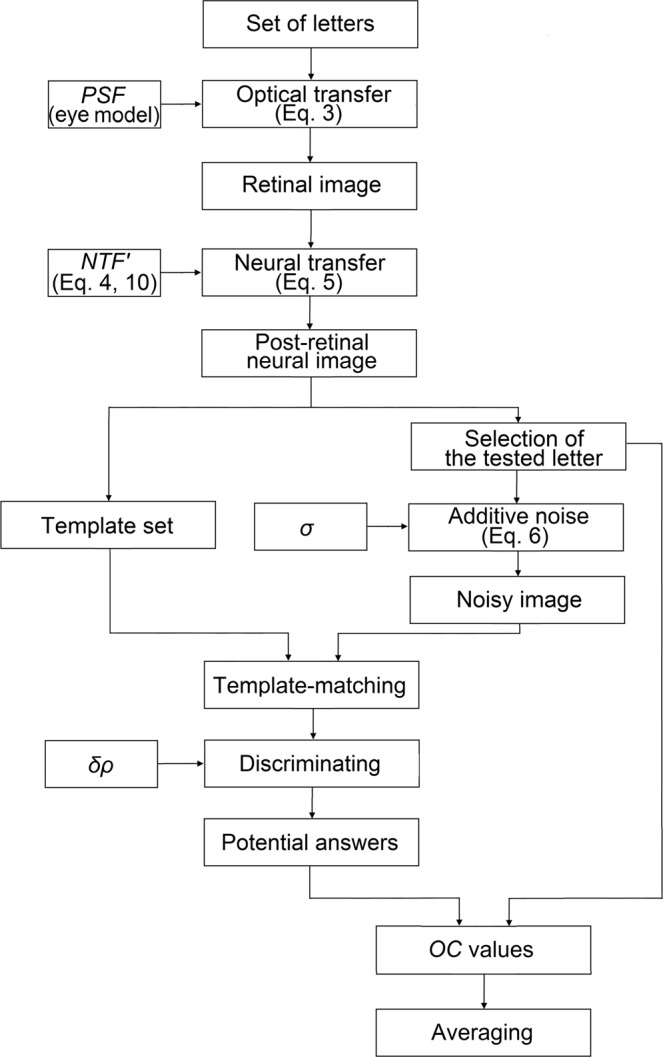
Workflow of our vision model describing the identification of one single letter. Main input parameters are indicated.
When testing multiple letters, the standard method characterizes perception quality at a given letter size by the recognition probability P. Instead of this, we have proposed a new quantity, the Rate of Recognition, RR, that better describes visual quality, but is still directly comparable to recognition probability52,53. For a fixed letter size s (i.e. the actual line of the ETDRS chart), RR is defined as the average OC value of the tested-identified character pairs:
| 11 |
After scoring the individual identifications and evaluating their distribution, the last step of our vision model is to determine the visual acuity value of the examined eye. In our former paper52 we concluded that thresholding the visual psychometric function of a given subject provides the most precise acuity result without any bias52,54. If we express the letter size s, in logMAR units:
| 12 |
where α denotes the visual angle of the stroke width of letters, then the relation represents the psychometric function of vision55–57. We describe its profile by the sigmoid-shape logistic function L(s), which is the most common two-parameter curve used to approximate any psychometric function55,56,58. We linearly transform the logistic function to ensure its limits correspond to the theoretically expected RR values, according to the total number of possible responses57 (i.e. all 26 letters of the English alphabet). Its mathematical formula is described by the following equation:
| 13 |
where smp sets the midpoint position of the sigmoid and k determines the steepness of the curve at this point.
Based on the calculated points RR(s), of the given subject, we determine the two parameters of the psychometric curve L(s), by logistic regression. Then, the visual acuity value V, is given by that letter size s0, at which the RR value equals the correlation threshold, RR0:
| 14 |
This method follows the idea of conventional visual acuity measurements evaluated using curve-fitting in terms of recognition probability, where only the probability threshold P0 = 0.5, of the ICO standard1,2 has to be replaced with an adequate value of RR0. We have formerly calibrated the threshold level by our high-precision measurements taken under special laboratory conditions: RR0 = 0.68 (for details see52). Figure 6 depicts the concept of curve-fitting-based evaluation using the average psychometric curves determined in our previous paper52 (LP: smp = −0.214 logMAR, k = 3.306 logMAR−1, and LRR: smp = −0.269 logMAR, k = 4.278 logMAR−1). Differences between the probability and correlation-based scoring methods are clearly visible.
Figure 6.
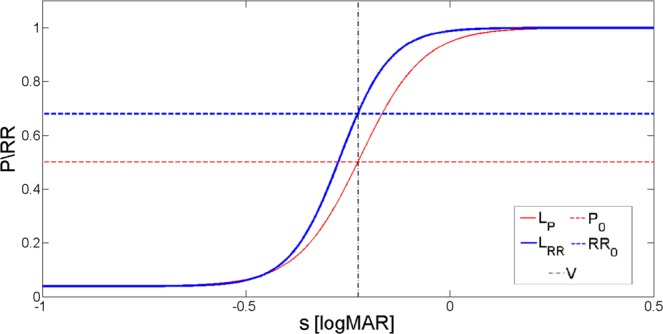
Average psychometric functions based on our high-precision measurements both in cases of probability and correlation-based scorings, together with the corresponding thresholds: P0 = 0.5 and RR0 = 0.6852.
Experimental setup used for calibration
So that we could provide accurate data for the calibration of the two free neural parameters of our vision model and demonstrate its operation, we performed visual acuity tests on real subjects. During these trials we used a special computer-controlled measuring system52 that is much more precise than standard visual acuity tests, thanks to the applied correlation-based scoring, increased number of tested characters, and denser letter-size sampling. Below a brief description of our measurement is given and some differences compared to conventional acuity tests are expressed. Further details and explanations are presented in our previous papers52,53.
In order to reduce statistical error, we examined not only five-letter lines printed on a standard ETDRS chart, but the complete extended Sloan font type59 comprising of all 26 letters of the English alphabet at each size. We used a Dell U2312HMT in-plane-switching LCD monitor for the visualization of optotypes. As there was not enough space to display all 26 letters on a single line, the black characters were presented individually, one after another in random order, in the middle of a solid white background. This is exactly the same way as our model simulates it. The subjects were told beforehand that they would be presented only with letters. Accordingly, in our model the template set comprised of the 26 letters of the English alphabet, each being a possible response. We examined 14 letter sizes ranging from 0.3 to −0.35 logMAR with steps of 0.05 logMAR. During the trial the subject verbally identified each displayed optotype and the examiner promptly typed the response on a keyboard. Right after the measurement the controller software automatically scored the test using OC, evaluated the collected data (11), and performed logistic regression (13) to determine the visual acuity value (14). A measurement trial lasted 30…40 minutes due to the large number of tested letters and dense size sampling.
It has long been known that pupil size significantly influences visual acuity1,3,38,60. Based on our simulations, 1.1 mm alteration in the pupil diameter could cause 0.05 logMAR change in the acuity value, which confirmed this observation. Accordingly, we paid special attention to control the surrounding illumination and to measure pupil size. As the human pupil diameter is larger under mesopic than photopic conditions, which emphasizes the imaging errors of the eye1,3,11,60, we implemented our measurement in a darkened room with an illuminance level of around 5…10 lux. Furthermore, during the trial the subject watched the monitor with one eye, while the other was covered with a transparent but opaque shield (i.e. a diffuser) to keep the pupil size at the specific value it was adapted to with both eyes open. In addition, we continuously measured the pupil diameter using our custom-made far-field machine vision system43. We applied infrared illumination to provide appropriate lighting conditions for high-resolution images and so as not to affect the dark-adapted pupil size. We monitored (but not controlled) the pupil using a digital camera and determined the accurate pupil diameter by our adaptive circular-Hough-transform-based algorithm corrected for magnification error43. The pupil size measurement and the acuity test were synchronized, hence we knew the exact pupil diameter dm, corresponding to each recorded response.
In order to simulate exactly the above-described acuity tests with our vision model, the wavefront aberration of the eyes of each individual subject was measured using a clinical Shack-Hartmann sensor (WASCA Asclepion Zeiss Wavefront Analyzer, SW 1.41.6; Carl Zeiss Meditec AG, Germany). The outputs of the wavefront sensor were the pupil diameter dw, recorded at the wavefront measurement, and the coefficients of the Zernike polynomials, which were needed to personalize the Zemax eye model. For the calculation of the polychromatic diffraction PSF we applied the pupil diameter dm, measured for each tested letter separately during the acuity trials. In our simulation we considered exactly the same letter sizes and character set as in our measurement, so that we could reconstruct the monocular visual acuity value of the examined subjects as precisely as possible.
We carried out our demonstrative trials through the cooperation of eight young subjects (ages of 22…40), none of whom wore prescription eyeglasses. Their visual acuity was between 0…−0.3 logMAR, close to the range of normal vision (−0.1…−0.2 logMAR3,61). They were selected to be close-emmetropic so that they could always sharply focus on the eyechart. The results of their wavefront measurement, including the pupil diameter dw, are summarized in Table 2. The refractive error RE, and the astigmatism Cyl, of the subjects’ eyes were measured using a TopCon autorefractor. Although we gathered all data for each of the subjects’ eyes, we only considered their right eyes (OD) in our analyses, as an individual’s eyes are often strongly correlated62,63 and do not, therefore, provide additional information.
Table 2.
Summary of the wavefront aberration measurements: the refractive error RE, the astigmatism Cyl, the pupil diameter dw, and the second, third, and fourth-order Zernike coefficients of the applied tenth-order expansion ( defocus term is considered to be zero, except for subject K. M. for whom ). λ0 = 555 nm.
| Subject | RE [D] | Cyl [D] | dw [mm] | [λ0] | [λ0] | [λ0] | [λ0] | [λ0] | [λ0] | [λ0] | [λ0] | [λ0] | [λ0] | [λ0] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| G. A. | 0.0 | −0.5 | 4.5 | −1.32·10−1 | −1.59·10−1 | −4.15·10−2 | −4.09·10−2 | −3.32·10−2 | 7.52·10−2 | 4.86·10−2 | 4.02·10−2 | 2.98·10−2 | −6.97·10−2 | 7.45·10−2 |
| M. T. | 0.25 | 0.5 | 6.2 | −3.57·10−2 | −2.54·10−1 | −2.68·10−1 | −3.81·103−1 | 6.28·10−2 | 1.40·10−1 | −4.13·10−2 | 5.40·10−3 | 9.23·10−2 | 6.07·10−2 | −7.46·10−2 |
| P. B. | 0.5 | 0.5 | 5.8 | 4.34·10−1 | 1.91·10−1 | 3.43·10−1 | −2.09·10−2 | −7.65·10−2 | −4.06·10−2 | 9.23·10−2 | −3.86·10−2 | 2.27·10−1 | 1.36·10−1 | 2.90·10−2 |
| S. T. | 0.25 | 0.0 | 5.4 | 1.42·10−1 | −1.39·10−1 | −6.18·10−2 | 2.02·10−1 | 2.93·10−1 | 8.87·10−2 | −4.35·10−2 | 5.55·10−3 | −5.71·10−2 | 5.94·10−2 | −3.04·10−2 |
| U. F. | 0.25 | −0.25 | 2.9 | −4.63·10−3 | 6.81·10−2 | −1.22·10−2 | 1.70·10−2 | 1.05·10−2 | −4.59·10−3 | 1.45·10−3 | 4.80·10−3 | 5.53·10−3 | 3.67·10−3 | 2.19·10−3 |
| K. M. | −0.5 | −1.25 | 6.3 | 1.82·10−1 | 1.15 | −1.63·10−2 | −7.06·10−2 | −1.06·10−1 | −1.20·10−2 | 4.61·10−3 | 4.35·10−2 | 9.13·10−2 | 1.20·10−2 | 6.06·10−2 |
| S. O. | 1.5 | 0.0 | 6.2 | 3.93·10−1 | −1.93·10−1 | −3.31·10−1 | 1.45·10−1 | −6.66·10−3 | 1.42·10−1 | −3.68·10−2 | 6.14·10−2 | 1.98·10−1 | −4.30·103−2 | −1.05·10−2 |
| G. T. | 0.0 | −0.25 | 6.2 | 2.11·10−1 | 2.21·10−2 | −3.29·10−2 | −2.31·10−1 | 5.65·10−2 | 5.84·10−2 | −4.91·10−2 | 4.53·10−2 | 1.21·10−1 | −5.39·10−2 | −7.90·10−3 |
Results
We calibrated the free neural parameters of our vision model by comparing the predictions of acuity simulations to the outcomes of the above-described visual acuity measurements. Using extremum detection over an appropriate parameter space we sought for that specific σ and δρ pair that minimized the root-mean-square difference ΔRR, between the simulated RRs(si), and the measured RRm(si), rate of recognition values (note: the same letter sizes were tested). For each given subject the fitting error takes the form of the following expression:
| 15 |
where i indicates the index of the letter sizes. This method provides a more comprehensive error figure than the pure difference in visual acuity, since that is only a single scalar number58. We performed the calibration for each person examined individually and also for the entire subject pool using common σ and δρ parameters.
Individual calibration of model parameters
The correct operation of our vision model can be best investigated by optimizing σ and δρ for all tested subjects independently of each other. We completed this individual calibration by performing simulations in the parameter space of σ = 0…0.15; δρ = 0…0.005, and compared the predictions of the model to the outcome of the measurement person by person. In order to avoid any bias, we determined both the simulated and the measured visual acuity values according to (14). A representative example for the measured/simulated RR values and the fitted psychometric curves is depicted in Fig. 7. The measured and the best-fit visual acuity values, together with the optimized parameters and the corresponding fitting error are presented in Table 3 for each subject.
Figure 7.
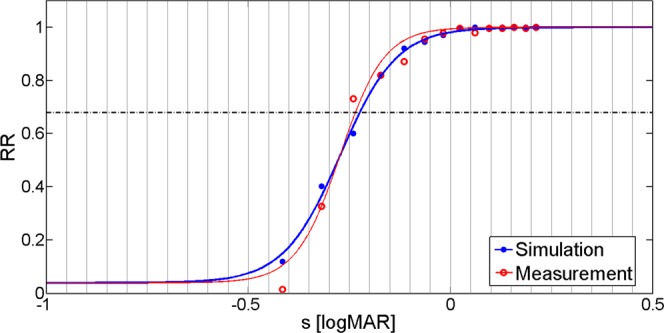
Visual acuity measurement and simulation results for subject S. O.’s OD eye. Filled and hollow circles represent registered values, while continuous curves show the psychometric functions obtained through logistic regression.
Table 3.
Summary of our individual calibration results: measured pupil diameter dm, averaged for a given subject, measured Vm, and best-fit simulated Vbf, visual acuity values, and fitting error ΔRR.
| Subject | dm [mm] | Vm [logMAR] | Vbf [logMAR] | ΔRR [−] | σ [−] | δρ [−] |
|---|---|---|---|---|---|---|
| G. A. | 4.6 | −0.27 | −0.26 | 0.025 | 0.075 | 0.002 |
| M. T. | 5.6 | −0.22 | −0.21 | 0.060 | 0.150 | 0.002 |
| P. B. | 4.8 | −0.18 | −0.16 | 0.047 | 0.125 | 0.003 |
| S. T. | 5.6 | −0.25 | −0.23 | 0.050 | 0.100 | 0.002 |
| U. F. | 3.8 | −0.31 | −0.30 | 0.033 | 0.150 | 0.003 |
| K. M. | 6.0 | −0.09 | −0.07 | 0.047 | 0.125 | 0.002 |
| S. O. | 5.0 | −0.24 | −0.23 | 0.039 | 0.150 | 0.003 |
| G. T. | 6.0 | −0.25 | −0.25 | 0.034 | 0.075 | 0.002 |
The optimized model parameter values are listed below σ and δρ.
The average difference between the best-fit simulated Vbf, and the measured Vm, visual acuity values is 0.010 logMAR, which approximates the systematic error of individual best-fit simulations, while the standard deviation equals 0.0055 logMAR. The sum of these two estimates the best achievable residual of our simulation over the calibration group: 0.016 logMAR. A comparative error analysis will be presented in the “Discussion” section, revealing that this value approximately equals the uncertainty of our high-precision acuity measurements52. This implies that the precision of the simulations is limited by the reference measurements, and demonstrates that proper adjustment of the model is feasible with only two free neural parameters.
Investigation of sensitivity to changes in model parameters
In order to examine the required complexity of our vision model, and to assess the role of optical effects and neural transfer, we subsequently performed additional simulations by omitting the PSF and the NTF. Based on the results we conclude that the free neural parameters cannot be calibrated if any part of the model is discarded. This confirms that both optical filtering and neural transfer are key elements of the simulation to accurately reconstruct visual acuity. Similarly, we performed the individual calibration by neglecting either σ or δρ, but in all cases the fitting error ΔRR, and the average difference between simulated and measured acuity values were larger than with both parameters optimized simultaneously.
We evaluated the reliability of our model by carrying out an inverse-sensitivity analysis. In this simulation we sought the change of construction parameters necessary to cause ΔV = 0.05 logMAR alteration in the visual acuity value. For this purpose, we varied the entrance pupil diameter d, and the two neural parameters. We also examined the effect of changes in the wavefront shape by introducing some artificial refractive error RE, corresponding to a small amount of defocus. The results of the analysis are presented in Table 4.
Table 4.
Results of the inverse-sensitivity analysis.
| Parameter | Average value ± standard deviation | Change required for ΔV = 0.05 logMAR |
|---|---|---|
| Pupil diameter (d) | 5.2 ± 0.77 mm | 1.1 mm |
| Refractive error (RE) | 0 D* | <0.25 D |
| Additive Gaussian white noise (σ) | 0.12 ± 0.03 | 0.15 |
| Discrimination range (δρ) | 0.0024 ± 0.0005 | 0.0012 |
Averages and standard deviations are given for the calibration group. *It is practically zero, since almost all our subjects could naturally focus on the eyechart.
These results confirm our expectation, that the vision model is highly sensitive to the optical input parameters. This means that their precise knowledge is essential to accurately simulate the acuity value of a specific eye. Moreover, it is observable that the model is considerably less sensitive to the adjustment of the neural parameters, which implies that it may be possible to achieve promising results by using average neural features together with personalized wavefront/pupil data. In this way, the lengthy individual calibration process might be eliminated. An investigation of a potential average neural model is presented below.
Optimum neural parameters for the average visual system
In order to determine the parameters of the average neural model, we performed global optimization considering all subjects simultaneously. We determined the fitting error ΔRRave, again using the root-mean-square deviation between the simulated and the measured RR values, but this time we calculated it for all examined eyes and analyzed their average over the subjects. We found the optimum parameters of the average neural model to be σave = 0.10 and δρave = 0.0025. These are close to the mean of the individual best-fit parameters listed in Table 3, however provide more precise estimates. The predictions of the average model, together with the outcomes of the measurement and the resulting fitting errors are presented in Table 5.
Table 5.
Comparison of the average neural model and the measurement: measured Vm, and simulated Vave, visual acuity values (σ = 0.10 and δρ = 0.0025).
| Subject | Vm [logMAR] | Vave [logMAR] | ΔRRave [−] |
|---|---|---|---|
| G. A. | −0.27 | −0.22 | 0.065 |
| M. T. | −0.22 | −0.21 | 0.067 |
| P. B. | −0.18 | −0.19 | 0.064 |
| S. T. | −0.25 | −0.21 | 0.070 |
| U. F. | −0.31 | −0.33 | 0.049 |
| K. M. | −0.09 | −0.05 | 0.069 |
| S. O. | −0.24 | −0.26 | 0.070 |
| G. T. | −0.25 | −0.21 | 0.069 |
ΔRRave indicates the root-mean-square difference between simulated and measured RR values.
The average difference between the Vave simulated and Vm measured visual acuity values is 0.013 logMAR (systematic error), while the standard deviation of the differences equals 0.032 logMAR (uncertainty). The sum of these two estimates the residual of our simulation over the calibration group: 0.045 logMAR, which is certainly larger than the residual of the best-fit model, as expected. Based on our detailed comparative error analysis to be presented in the next section, we conclude that the residual of our simulations using the average neural model over the calibration group is smaller than the error of conventional five-letter line-assignment-based visual acuity tests3,54,64.
Due to the small number of participants involved, we can only present the behavior of our model over the calibration group. Further experiments performed on an extended subject pool, including wider age bracket and participants with certain vision loss, are required to conclude general statements about its eventual accuracy.
Discussion
The accuracy of visual acuity simulations is affected by both systematic and random errors. The source of random error is twofold. First, it comes from neglecting the fine individual characteristics of cortical character recognition, such as learning capabilities, effects of fatigue, mood etc., that may even change over time. Second, it occurs during the simulation, since the additional Gaussian white noise implemented in the model represents a statistical quantity. In order to determine its effect on repeatability, we performed five separate simulations with the same parameter settings and determined the standard deviation of the resulting visual acuity values, in the same way as ophthalmic scientists check test-retest-variability54,64. Based on the results, this constituent of random error proved to be smaller than 0.0045 logMAR. This value is very close to the random error of our individual simulation results, providing a reasonable explanation for that and is negligible for all practical purposes.
Behind systematic errors there are those simplifications that we applied when constructing the model. In order to verify the relevance of our assumptions, and to assess their effects on accuracy, we compared our model to a scheme presented in the literature. Since Watson and Ahumada’s model7 is the closest to our work, we chose it as a basis for our comparison. From their set of remarkably complex and comprehensive models, we selected that version which agrees with ours in every aspects— except for the optical model of the eye and the decision-making step of the recognition process. To implement their approach, we started from our own vision model (M0) and then simply eliminated the differences one after the other. First, we changed the discrimination range to δρ = 0, in which case the recognized template is determined simply by the highest cross-correlation value ρmax (M1). Then, we discarded the effects of chromatic aberration by calculating optical transfer from the monochromatic PSF (M2), and finally we applied a fix pupil diameter d = 6 mm, across the entire model (M3). This last version corresponds exactly to the model described by Watson and Ahumada7. In order to achieve the best comparison of methods, we determined the optimum neural parameters for each subject independently. For the sake of consistency with the other parts of this paper, visual acuity values were evaluated using our correlation-based scoring scheme52,53 and logistic regression for all M0…M3 models. The statistics of neural parameters and fitting errors is presented in Table 6.
Table 6.
Comparison of simulations performed using modified vision models (for details see the text).
| Method | V [logMAR] | ΔRR [−] | σ [−] | δρ [−] |
|---|---|---|---|---|
| M0 | −0.21 ± 0.07 | 0.042 ± 0.011 | 0.12 ± 0.03 | 0.0024 ± 0.0005 |
| M1 | −0.23 ± 0.08 | 0.049 ± 0.016 | 0.24 ± 0.06 | 0 |
| M2 | −0.23 ± 0.07 | 0.052 ± 0.019 | 0.31 ± 0.12 | 0 |
| M3 | −0.21 ± 0.07 | 0.079 ± 0.067 | 0.34 ± 0.10 | 0 |
M0 refers to our solution, and M3 reconstructs the scheme presented by Watson and Ahumada7. All indicated values are averages ± standard deviations calculated over the calibration group.
Based on the fitting error ΔRR, we conclude that the subsequent M0 → M1 → M2 → M3 modifications of the model steadily deteriorate the goodness of fit to the reference measurements. The ΔRR value of M3 (which reconstructs the model presented by Watson and Ahumada7) is twice as large as that of M0, justifying our decision to include chromatic aberrations, discrimination range, and precise pupil diameter in the model. Additionally, the average neural noise parameter σ, increases with the modifications, which indicates that additive noise gradually takes over the role of other factors that affect image quality, as they are eliminated step by step from the system. The noise of 0.34 in the case of M3 is surprisingly close to the value presented by Watson and Ahumada7. However, according to the literature46,65, σ is somewhere between 0.03 and 0.08, to which our value in M0 is much closer.
The fitting error is perfectly suitable for the theoretical comparison of different models. However, from the point-of-view of applicability, our simulation has to be compared to other similar methods and real acuity measurements via the ΔV value, i.e. the sum of systematic and random errors. Correspondingly, the average residual of our calibration group, together with the accuracy of the Watson-Ahumada model7, our high-precision measurements52, and conventional visual acuity tests51,54,64 are summarized in Table 7. For the sake of completeness, we also share the duration of the analyses. Simulations were performed on a virtual PC with Intel Xeon E5 4620 processor (4 cores, 8 threads, 2.2 GHz) and DDR-3 RAM (1333 MHz) of a Dell PowerEdge R820 four-socket server.
Table 7.
Accuracy (residual) and duration of different methods used to determine visual acuity.
| Method | ΔV [logMAR] | t [min] | |
|---|---|---|---|
| Simulation | Individual best-fit neural parameters | 0.016 | ≈200* |
| Average neural parameters | 0.045 | 15…20 | |
| Watson and Ahumada model7 | 0.056…0.070 | n/a | |
| Measurement | Correlation-based scoring, 26 letters/size52 | 0.017 | 30…40 |
| Correlation-based scoring, 5 letters/size52 | 0.053 | 2…3 | |
| Conventional line-assignment-based ETDRS test51,54,64 | 0.06…0.15 | 1…2 |
*Optimization time included.
Based on the results, the personalized best-fit simulation provides approximately the same residual over the calibration group as our high-precision measurement using all 26 letters at each letter size and correlation-based scoring. However, personal optimization of the simulation parameters requires a substantial amount of computation time. The residual of simulations using the average neural model is comparable to the accuracy of our improved-precision measurements taken with five Sloan characters per line and correlation-based scoring52. This residual is still much less than the error of standard clinical line-assignment-based ETDRS trials51,54,64. Its 15…20 minutes duration may be too lengthy for certain applications, thus it needs to be reduced through further software/hardware optimization.
After a subsequent calibration to be conducted on a broader population sample— including older subjects as well as those with certain loss of vision— our long-term goal is to further refine the model such that it can be used to make efficient program extensions for standard optical design software. In this way, the design of visual optical devices (such as IOLs) directly for improved visual acuity would become possible. For example, by applying a more sophisticated eye scheme (i.e. one including topographic corneal data and biometric ocular dimensions) our simulations could estimate the post-operative visual acuity of patients destined for cataract surgery. Since our method apparently works fine with ocular wavefront-aberration measurements, it might also be translated to clinical practice. With its help new objective tests could be developed to determine the visual acuity in cases where traditional means are not feasible (e.g. testing illiterate adults or preschool children, etc.).
Acknowledgements
The authors are extremely grateful to the colleagues of the Department of Atomic Physics, Budapest University of Technology and Economics, and Medicontur Medical Engineering Ltd. who took time from their busy schedules to participate in the measurements. We would like to express our gratitude to the Ministry of National Development (NFM) for the support granted as a competitiveness and excellence contract for the project “Medical technological research and development on the efficient cure of cataract” (VKSZ-12-1-2013-80).
Author Contributions
G.E., I.K. and C.F. designed the project, G.E. and C.F. conceived the method, K.K. and C.F. conducted the experiments, C.F. and G.E. analyzed the results, C.F. wrote the manuscript. All authors reviewed the manuscript.
Data Availability
The datasets generated and analyzed in the study are available from the corresponding author on reasonable request.
Competing Interests
Erdei, G. and Fülep, C. Measuring visual acuity of a client. World Intellectual Property Organization WO/2018/020281 A1, PCT/HU2016/000050, patent pending (2018).
Footnotes
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Change history
11/22/2019
An amendment to this paper has been published and can be accessed via a link at the top of the paper.
References
- 1.Duane, T. Duane’s Clinical Ophthalmology (CD-ROM ed.) (Lippincott Williams and Wilkins, 2006).
- 2.International Council of Ophthalmology, Visual Functions Committee Visual acuity measurement standard, ICO 1984. Ital. J. Ophthalmol. 1988;II/I:1–15. [Google Scholar]
- 3.Rabbetts, R. B. Bennett and Rabbetts’ Clinical Visual Optics (Butterworth-Heinemann, Elsevier, 2007).
- 4.Bailey IL, Lovie JE. New design principles for visual acuity letter charts. Am. J. Optom. Physiol. Opt. 1976;53(11):740–745. doi: 10.1097/00006324-197611000-00006. [DOI] [PubMed] [Google Scholar]
- 5.Bailey IL, Lovie-Kitchin JE. Visual acuity testing. From the laboratory to the clinic. Vision Res. 2013;90:2–9. doi: 10.1016/j.visres.2013.05.004. [DOI] [PubMed] [Google Scholar]
- 6.Jackson AJ, Bailey IL. Visual acuity. Optometry in Practice. 2004;5:53–70. [Google Scholar]
- 7.Watson AB, Ahumada AJ., Jr. Predicting visual acuity from wavefront aberrations. J. Vis. 2008;8(4)(17):1–19. doi: 10.1167/8.4.17. [DOI] [PubMed] [Google Scholar]
- 8.Watson AB, Ahumada AJ., Jr. Modeling acuity for optotypes varying in complexity. J. Vis. 2012;12(10):1–19. doi: 10.1167/12.10.19. [DOI] [PubMed] [Google Scholar]
- 9.Faylienejad, A. A computational model for predicting visual acuity from wavefront aberration measurements. M.Sc. thesis in Vision Science (University of Waterloo, 2009).
- 10.Nestares O, Navarro R, Antona B. Bayesian model of Snellen visual acuity. J. Opt. Soc. Am. A. 2003;20(7):1371–1381. doi: 10.1364/josaa.20.001371. [DOI] [PubMed] [Google Scholar]
- 11.Thibos LN, Hong X, Bradley A, Cheng X. Statistical variation of aberration structure and image quality in a normal population of healthy eyes. J. Opt. Soc. Am. A. 2002;19(12):2329–2348. doi: 10.1364/josaa.19.002329. [DOI] [PubMed] [Google Scholar]
- 12.Marsack JD, Thibos LN, Applegate RA. Metrics of optical quality derived from wave aberrations predict visual performance. J. Vis. 2004;4(4):322–328. doi: 10.1167/4.4.8. [DOI] [PubMed] [Google Scholar]
- 13.Applegate RA, Ballentine C, Gross H, Sarver EJ, Sarver CA. Visual acuity as a function of Zernike mode and level of root mean square error. Optom. Vis. Sci. 2003;80(2):97–105. doi: 10.1097/00006324-200302000-00005. [DOI] [PubMed] [Google Scholar]
- 14.Liang J, Williams DR. Aberrations and retinal image quality of the normal human eye. J. Opt. Soc. Am. A. 1997;14(11):2873–2883. doi: 10.1364/josaa.14.002873. [DOI] [PubMed] [Google Scholar]
- 15.Liang J, Grimm B, Goelz S, Bille JF. Objective measurement of wave aberrations of the human eye with the use of a Hartmann-Shack wave-front sensor. J. Opt. Soc. Am. A. 1994;11(7):1949–1957. doi: 10.1364/josaa.11.001949. [DOI] [PubMed] [Google Scholar]
- 16.Watson AB, Ahumada AJ., Jr. Letter identification and the Neural Image Classifier. J. Vis. 2015;15(2):1–26. doi: 10.1167/15.2.15. [DOI] [PubMed] [Google Scholar]
- 17.Anderson, A. G., Olshausen, B. A., Ratnam, K. & Roorda, A. A neural model of high-acuity vision in the presence of fixational eye movements. IEEE Proceedings of the 50th Asilomar Conference on Signals, Systems and Computers, 588–592 (2016).
- 18.Lamghari, N., Charaf, M. E. H. & Raghay, S. Template matching for recognition of handwritten Arabic characters using structural characteristics and Freeman code. IJCSIS14(12) (2016).
- 19.Schuster S, Amtsfeld S. Template-matching describes visual pattern-recognition tasks in the weakly electric fish Gnathonemus petersii. J. Exp. Biol. 2002;205:549–557. doi: 10.1242/jeb.205.4.549. [DOI] [PubMed] [Google Scholar]
- 20.Shehu, G. S., Ashir, A. M. & Eleyan, A. Character recognition using correlation and Hamming distance. IEEE Proceedings of the 23rd Signal Processing and Communications Applications Conference (SIU), 755–758 (2015).
- 21.Dalimier E, Pailos E, Rivera R, Navarro R. Experimental validation of a Bayesian model of visual acuity. J. Vis. 2009;9(7)(12):1–16. doi: 10.1167/9.7.12. [DOI] [PubMed] [Google Scholar]
- 22.Thibos LN, Ye M, Zhang X, Bradley A. The chromatic eye: a new reduced-eye model of ocular chromatic aberration in humans. Appl. Opt. 1992;31(19):3594–3600. doi: 10.1364/AO.31.003594. [DOI] [PubMed] [Google Scholar]
- 23.Oliver NM, Rosario B, Pentland AP. A Bayesian computer vision system for modeling human interactions. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2000;22(8):831–843. [Google Scholar]
- 24.Chen, F. X., Roig, G., Isik, L., Boix, X. & Poggio, T. Eccentricity dependent deep neural networks: modeling invariance in human vision. AAAI 2017 Spring Symposium Series on Science of Intelligence: Computational Principles of Natural and Artificial Intelligence, 541–546 (2017).
- 25.Li RY, Xu M. Character recognition using a fast neural-net classifier. Patt. Rec. Lett. 1992;13(5):369–374. [Google Scholar]
- 26.Bayat AB. Recognition of handwritten digits using optimized adaptive neuro-fuzzy inference systems and effective features. Journal of Pattern Recognition and Intelligent Systems (PRIS) 2013;1(2):25–37. [Google Scholar]
- 27.Teow LN, Loe KF. Robust vision-based features and classification schemes for off-line handwritten digit recognition. Patt. Rec. 2002;35(11):2355–2364. [Google Scholar]
- 28.Liu CL, Nakashima K, Sako H, Fujisawa H. Handwritten digit recognition: benchmarking of state-of-the-art techniques . Patt. Rec. 2003;36(10):2271–2285. [Google Scholar]
- 29.Liu CL, Nakashima K, Sako H, Fujisawa H. Handwritten digit recognition: investigation of normalization and feature extraction techniques. Patt. Rec. 2004;37(2):265–279. [Google Scholar]
- 30.McDonnell MD, Tissera MD, Vladusich T, van Schaik A, Tapson J. Fast, simple and accurate handwritten digit classification by training shallow neural network classifiers with the ‘Extreme Learning Machine’ algorithm. PLoS One. 2015;10(8):1–20. doi: 10.1371/journal.pone.0134254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Eppig T, Scholz K, Langenbucher A. Assessing the optical performance of multifocal (diffractive) intraocular lenses. Ophthalmic Physiol. Opt. 2008;28(5):467–474. doi: 10.1111/j.1475-1313.2008.00582.x. [DOI] [PubMed] [Google Scholar]
- 32.Jinabhai, A. N., Young, G., Hall, L. A. & Wolffsohn, J. S. Clinical techniques to assess the visual and optical performance of intraocular lenses: A review. Cataracts and Cataract Surgery: Types, Risk Factors, and Treatment Options (Eye and Vision Research Development) (ed. Navarro, D.) (Nova Science, 2013).
- 33.Graney MJ, et al. A clinical index for predicting visual acuity after cataract surgery. Am. J. Ophthalmol. 1988;105(5):460–465. doi: 10.1016/0002-9394(88)90235-8. [DOI] [PubMed] [Google Scholar]
- 34.Koskin SA, Boiko EV, Shelepin YE. Modern methods of measuring the resolving power of the visual system. J. Opt. Tech. 2008;75(1):17–20. [Google Scholar]
- 35.Bonmassar G, Schwartz EL. Improved cross-correlation for template matching on the Laplacian pyramid. Patt. Rec. Lett. 1998;19(8):765–770. [Google Scholar]
- 36.Ratnam K, Domdei N, Harmening WM, Roorda A. Benefits of retinal image motion at the limits of spatial vision. J. Vis. 2017;17(1)(30):1–11. doi: 10.1167/17.1.30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.McLaren JW, Patel SV. Modeling the effect of forward scatter and aberrations on visual acuity after endothelial keratoplasty. Invest. Ophthalmol. Vis. Sci. 2012;53(9):5545–5551. doi: 10.1167/iovs.12-10011. [DOI] [PubMed] [Google Scholar]
- 38.Watson AB. A formula for the mean human optical modulation transfer function as a function of pupil size. J. Vis. 2013;13(6)(18):1–11. doi: 10.1167/13.6.18. [DOI] [PubMed] [Google Scholar]
- 39.Zemax LLC (Zemax, Washington, USA), www.zemax.com.
- 40.Gobbi, P. G. Modeling the Optical and Visual Performance of the Human Eye (SPIE Press, 2013).
- 41.Atchison, D. A. & Smith, G. Optics of the Human Eye (Butterworth-Heinemann, Elsevier, 2000).
- 42.Atchison DA, Smith G. Chromatic dispersions of the ocular media of human eyes. J. Opt. Soc. Am. A. 2005;22(1):29–37. doi: 10.1364/josaa.22.000029. [DOI] [PubMed] [Google Scholar]
- 43.Fülep, C. & Erdei, G. Far-field infrared system for the high-accuracy in situ measurement of ocular pupil diameter. IEEE Proceedings of the 10th International Symposium on Image and Signal Processing and Analysis (ISPA 2017), 31–36 (2017).
- 44.Frigo M, Johnson SG. FFTW: an adaptive software architecture for the FFT. IEEE Proceedings of the International Conference on Acoustics, Speech, and Signal Processing (ICASSP’98) 1998;3:1381–1384. [Google Scholar]
- 45.The MathWorks Inc. (MatLab: the language of technical computing), www.mathworks.com/products/matlab.
- 46.Barten, P. G. J. Contrast Sensitivity of the Human Eye and its Effects on Image Quality (SPIE Optical Engineering Press, 1999).
- 47.Sarmah, S. & Kalita, S. K. A correlation based band selection approach for hyperspectral image classification. IEEE Proceedings of the 6th International Conference on Advanced Computing (IACC), 271–274 (2016).
- 48.Han, Y., Roig, G., Geiger, G. & Poggio, T. Is the human visual system invariant to translation and scale? AAAI 2017 Spring Symposium Series on Science of Intelligence: Computational Principles of Natural and Artificial Intelligence, 564–568 (2017).
- 49.Goshtasby, A. A. Image Registration: Principles, Tools and Methods (Advances in Computer Vision and Pattern Recognition) (Springer, 2012).
- 50.Neto, A. M. et al. Image processing using Pearson’s correlation coefficient: applications on autonomous robotics. IEEE Proceedings of the 13th International Conference on Autonomous Robot Systems, 14–19 (2013).
- 51.Liu L, Klein SA, Xue F, Zhang JY, Yu C. Using geometric moments to explain human letter recognition near the acuity limit. J. Vis. 2009;9(1)(26):1–18. doi: 10.1167/9.1.26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Fülep C, Kov´acs I, Kr´anitz K, Erdei G. Correlation-based evaluation of visual performance to reduce the statistical error of visual acuity. J. Opt. Soc. Am. A. 2017;34(7):1255–1264. doi: 10.1364/JOSAA.34.001255. [DOI] [PubMed] [Google Scholar]
- 53.Erdei, G. & Fülep, C. Measuring visual acuity of a client. World Intellectual Property Organization WO/2018/020281 A1, PCT/HU2016/000050, patent pending (2018).
- 54.Vanden Bosch ME, Wall M. Visual acuity scored by the letter-by-letter or probit methods has lower retest variability than line assignment method. Eye (Lond) 1997;11(3):411–417. doi: 10.1038/eye.1997.87. [DOI] [PubMed] [Google Scholar]
- 55.Carkeet A, Lee L, Kerr JR, Keung MM. The slope of the psychometric function for Bailey–Lovie letter charts: defocus effects and implications for modeling letter-by-letter scores. Optom. Vis. Sci. 2001;78(2):113–121. doi: 10.1097/00006324-200102000-00012. [DOI] [PubMed] [Google Scholar]
- 56.Norton, T. T., Corliss, D. A. & Bailey, J. E. The Psychophysical Measurement of Visual Function (Ridgevue, 2014).
- 57.Tinning S, Bentzon MW. A new method for exact measurements of visual acuity. Determination of threshold curves for the resolving power of the eye by computerized curve fitting. Acta Ophthalmol. (Copenh) 1986;64(2):180–186. doi: 10.1111/j.1755-3768.1986.tb06897.x. [DOI] [PubMed] [Google Scholar]
- 58.Wichmann FA, Hill NJ. The psychometric function: I. Fitting, sampling, and goodness of fit. Percep. Psychophys. 2001;63(8):1293–1313. doi: 10.3758/bf03194544. [DOI] [PubMed] [Google Scholar]
- 59.Pelli, D. G., Robson, J. G. & Wilkins, A. J. The design of a new letter chart for measuring contrast sensitivity. Clin. Vision Sci. 2(3), 187–199, The Sloan font is available for noncommercial research use from GitHub, https://github.com/denispelli/Eye-Chart-Fonts/ (1988).
- 60.Campbell FW, Gregory AH. Effect of size of pupil on visual acuity. Nature. 1960;187(4743):1121–1123. doi: 10.1038/1871121c0. [DOI] [PubMed] [Google Scholar]
- 61.Elliott DB, Yang KC, Whitaker D. Visual acuity changes throughout adulthood in normal, healthy eyes: seeing beyond 6/6. Optom. Vis. Sci. 1995;72(3):186–191. doi: 10.1097/00006324-199503000-00006. [DOI] [PubMed] [Google Scholar]
- 62.Glynn RJ, Rosner B. Regression methods when the eye is the unit of analysis. Ophthalmic Epidemiol. 2012;19(3):159–165. doi: 10.3109/09286586.2012.674614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Murdoch IE, Morris SS, Cousens SN. People and eyes: statistical approaches in ophthalmology. Br. J. Ophthalmol. 1998;82(8):971–973. doi: 10.1136/bjo.82.8.971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Raasch TW, Bailey IL, Bullimore MA. Repeatability of visual acuity measurement. Optom. Vis. Sci. 1998;75(5):342–348. doi: 10.1097/00006324-199805000-00024. [DOI] [PubMed] [Google Scholar]
- 65.Gold J, Bennett PJ, Sekuler AB. Signal but not noise changes with perceptual learning. Nature. 1999;402(6758):176–178. doi: 10.1038/46027. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets generated and analyzed in the study are available from the corresponding author on reasonable request.