Fundamental bounds on learning performance in neural circuits

Significance

We show how neural circuits can use additional connectivity to achieve faster and more precise learning. Biologically, internal synaptic noise imposes an optimal size of network for learning a given task. Above the optimal size, addition of neurons and synaptic connections starts to impede learning and task performance. Overall brain size may therefore be constrained by pressure to learn effectively with unreliable synapses and may explain why certain neurological learning deficits are associated with hyperconnectivity. Beneath this optimal size, apparently redundant connections are advantageous for learning. Such apparently redundant connections have recently been observed in several species and brain areas.

Abstract

How does the size of a neural circuit influence its learning performance? Larger brains tend to be found in species with higher cognitive function and learning ability. Intuitively, we expect the learning capacity of a neural circuit to grow with the number of neurons and synapses. We show how adding apparently redundant neurons and connections to a network can make a task more learnable. Consequently, large neural circuits can either devote connectivity to generating complex behaviors or exploit this connectivity to achieve faster and more precise learning of simpler behaviors. However, we show that in a biologically relevant setting where synapses introduce an unavoidable amount of noise, there is an optimal size of network for a given task. Above the optimal network size, the addition of neurons and synaptic connections starts to impede learning performance. This suggests that the size of brain circuits may be constrained by the need to learn efficiently with unreliable synapses and provides a hypothesis for why some neurological learning deficits are associated with hyperconnectivity. Our analysis is independent of specific learning rules and uncovers fundamental relationships between learning rate, task performance, network size, and intrinsic noise in neural circuits.

In the brain, computations are distributed across circuits that can include many millions of neurons and synaptic connections. Maintaining a large nervous system is expensive energetically and reproductively (1–3), suggesting that the cost of additional neurons is balanced by an increased capacity to learn and process information.

Empirically, a “bigger is better” hypothesis is supported by the correlation of brain size with higher cognitive function and learning capacity across animal species (4–6). Within and across species, the volume of a brain region often correlates with the importance or complexity of the tasks it performs (7–9). These observations make sense from a theoretical perspective because larger artificial neural networks can solve more challenging computational tasks than smaller networks (10–15). However, we still lack a firm theoretical understanding of how network size improves learning performance.

Biologically it is not clear that there is always a computational advantage to having more neurons and synapses engaged in learning a task. During learning, larger networks face the problem of tuning greater numbers of synapses using limited and potentially corrupted information on task performance (16, 17). Moreover, no biological component is perfect, so unavoidable noise arising from the molecular machinery in individual synapses might sum unfavorably as the size of a network grows. Intriguingly, a number of well-studied neurodevelopmental disorders exhibit cortical hyperconnectivity at the same time as learning deficits (18–21). It is therefore a fundamental question whether learning capacity can grow indefinitely with the number of neurons and synapses in a neural circuit or whether there is some law of diminishing returns that eventually leads to a decrease in performance beyond a certain network size.

We address these questions with a general mathematical analysis of learning performance in neural circuits that is independent of specific learning rules and circuit architectures. For a broad family of learning tasks, we show how the expected learning rate and steady-state performance are related to the size of a network. The analysis reveals how connections can be added to intermediate layers of a multilayer network to reduce the difficulty of learning a task. This gain in overall learning performance is accompanied by slower per-synapse rates of change, predicting that synaptic turnover rates should vary across brain areas according to the number of connections involved in a task and the typical task complexity.

If each synaptic connection is intrinsically noisy, we show that there is an optimal network size for a given task. Above the optimal network size, adding neurons and connections degrades learning and steady-state performance. This reveals an important disparity between synapses in artificial neural networks, which are not subject to unavoidable intrinsic noise, and those in biology, which are necessarily subject to fluctuations at the molecular level (22–25).

For networks that are beneath the optimal size, it turns out to be advantageous to add apparently redundant neurons and connections. We show how additional synaptic pathways reduce the impact of imperfections in learning rules and uncertainty in the task error. This provides a potential theoretical explanation for recent, counterintuitive experimental observations in mammalian cortex (26, 27), which show that neurons frequently make multiple, redundant synaptic connections to the same postsynaptic cell. A nonobvious consequence of this result is that the size of a neural circuit can either reflect the complexity of a fixed task or instead deliver greater learning performance on simpler, arbitrary tasks.

Results

Modeling the Effect of Network Size on Learning.

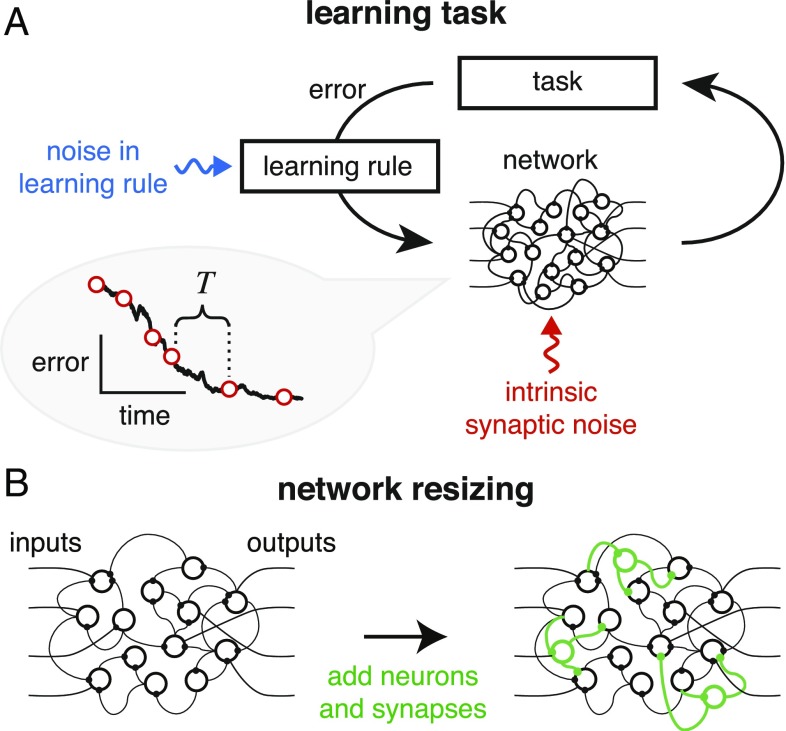
Our goal is to analyze how network size affects learning and steady-state performance in a general setting depicted in Fig. 1, which is independent of specific tasks, network architectures, and learning rules. We assume that there is some error signal that is fed back to the network via a learning rule that adjusts synaptic weights. We also assume that the error signal is limited both by noise and by a finite sampling rate quantified by some time interval $T$ (Fig. 1A). In addition to the noise in the learning rule, we also consider noise that is independently distributed across synapses (“intrinsic synaptic noise”). This models molecular noise in signaling and structural apparatus in a biological synapse that is uncorrelated with learning processes and with changes in other synapses. Network size is adjusted by adding synapses and neurons (Fig. 1B).

Fig. 1.

(A) Schematic of learning in a neural network. Information on task error is received by a learning rule which converts this information into synaptic changes that decrease task error. Biologically, the learning rule faces several challenges: It will be subject to noise and perturbations (blue arrow), and the synapses themselves may suffer from intrinsic noise (red arrow). Error information will be acquired only intermittently, as shown in the learning curve on the left, where $T$ specifies the intermittency of feedback (main text). (B) We analyze the effect of network size on learning performance by adding redundant neurons and synapses (green) to an existing network.

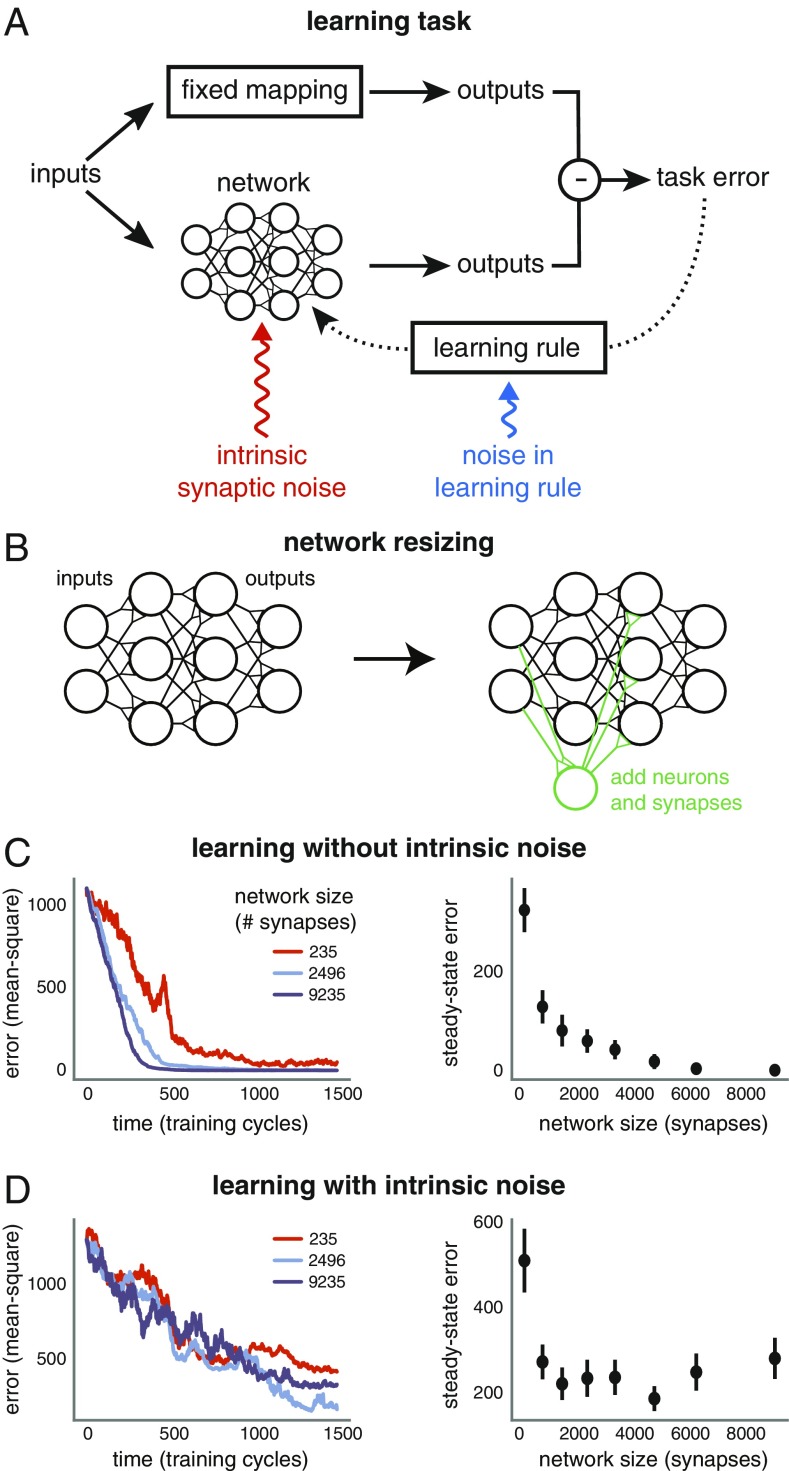
Before analyzing the general case, we motivate the analysis with simulations of fully connected, multilayer nonlinear feedforward neural networks that we trained to learn input–output mappings (Fig. 2A). We used the so-called student–teacher framework to generate tasks (e.g., refs. 28 and 29). A “teacher” network is initialized with random fixed weights. The task is for a randomly initialized “student” network to learn the input–output mapping of the teacher. This framework models learning of any task that can be performed by a feedforward neural network by setting the teacher as the network optimized to perform the task.

Fig. 2.

(A) Learning task. Neuronal networks are trained to learn an input–output mapping using feedback error and a gradient-based learning rule to adjust synaptic strengths. The feedback is corrupted with tunable levels of noise (blue), reflecting imperfect sensory feedback, imperfect learning rules, and task-irrelevant changes in synaptic strengths. Synaptic strengths are additionally subject to independent internal noise (red), reflecting their inherent unreliability. (B) Network size is increased by adding neurons and synapses to inner layers. (C) Three differently sized networks are trained on the same task, with the same noise-corrupted learning rule. A learning cycle consists of a single input (drawn from a Gaussian distribution) being fed to the network. The gradient of feedback error with respect to this input (i.e., the stochastic gradient) is then calculated and corrupted with noise (blue component in A). All networks have five hidden layers of equal size. We vary this size from 5 neurons to 45 neurons across the networks. (C, Right) Mean task error after 1,500 learning cycles, computed over 12 simulations. Error bars depict $\pm 1$ SEM. (C, Left) Task error over time for a single simulation of each network. (D) The same as C but each synapse is subject to internal independent noise fluctuations in addition to noise in the learning rule (red component in A).

The sizes of the student networks were set by incrementally adding neurons and connections to internal layers of a network with the same initial connection topology as that of the teacher (Fig. 2B and Materials and Methods). This generated student networks of increasing size with the guarantee that each student can in principle learn the exact input–output mapping of the teacher.

Learning was simulated by modifying synapses with noise-corrupted gradient descent to mimic an imperfect biological learning rule. We emphasize that we do not assume learning in a biological network occurs by explicit gradient descent. However, any error-based learning rule must induce synaptic changes that approximate gradient descent, as we show below (Eq. 1). We assume that learning must be performed online; that is, data arrive one sample at a time. We believe this captures a typical biological learning scenario where a learner gets intermittent examples and feedback.

The phenomena we wish to understand are shown in Fig. 2 C and D. We trained networks of varying sizes on the same task, with the same amount of learning-rule noise. Larger networks learn more quickly and to a higher steady-state performance than smaller networks when there is no intrinsic synaptic noise (Fig. 2C). This is surprising because the only difference between the smallest network and larger networks is the addition of redundant synapses and neurons, and the task is designed so that all networks can learn it perfectly in principle. Moreover, as shown in Fig. 2D, adding intrinsic noise to the synapses of the student networks results in a nonmonotonic relationship between performance and network size. Beyond a certain size, both learning and asymptotic performance start to worsen.

The simulations in Fig. 2 provide evidence of an underlying relationship between learning rate, task performance, network size, and intrinsic noise. To understand these observations in a rigorous and general way, we mathematically analyzed how network size and imperfections in feedback learning rules impact learning in a general case.

We note that in machine learning, noise processes such as dropout and stochastic regularization (e.g., refs. 30–32) can be applied to improve generalization from finite training data. Intrinsic synaptic noise is qualitatively different from these regularization processes. In particular, the per-synapse magnitude of intrinsic noise remains constant, independent of network size or training level. Moreover, our simulations use online learning, which is distinct from the common machine-learning paradigm where data are divided into training and test sets. The implications of our paper for this paradigm are considered in SI Appendix, Regularization and Generalization Error and Online Learning and Generalization Error, where we also show that regularization can be incorporated as learning-rule noise.

Learning Rate and Task Difficulty.

We define task error as a smooth function $F\left[\mathbf{w}\right]$ which depends on the vector $\mathbf{w}$ of $N$ synaptic weights in a network. We assume that learning rules use some (potentially imperfect) estimate of this error to adjust synaptic weights.

Biologically, it is reasonable to assume that learning-related synaptic changes occur due to old information. For example, a task-related reward or punishment may be supplied only at the end of a task, which itself takes time to execute. Similarly, even if error feedback is ongoing in time, there will always be some biochemically induced delay between acquisition of this error signal and its integration into plastic changes at each synapse.

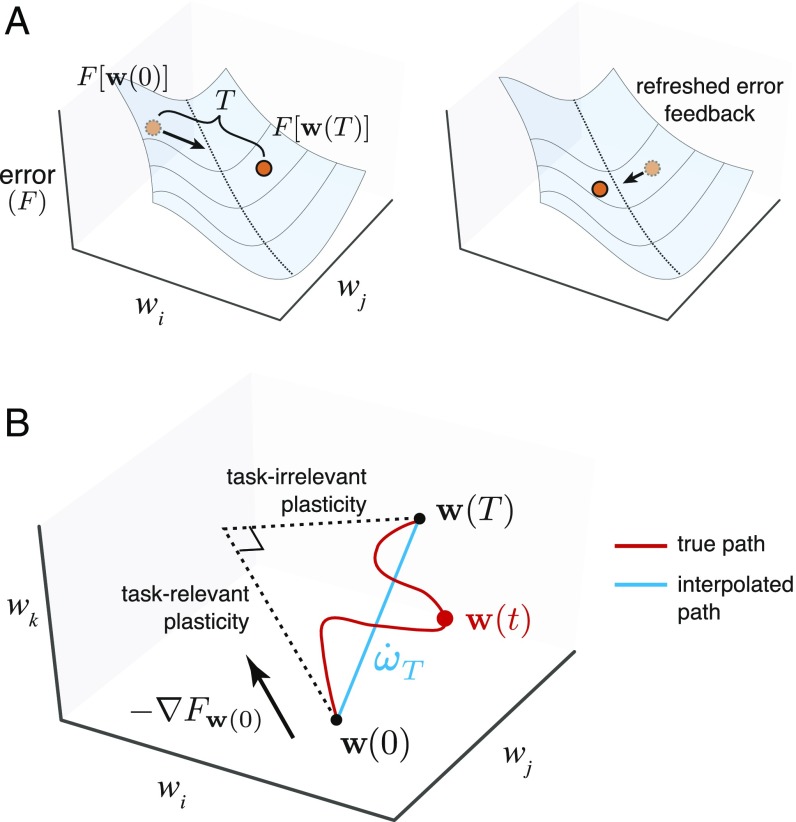
Thus, there will be a maximum rate at which task error information can be transmitted to synapses during learning, which for mathematical convenience can be lumped into discrete time points. Suppose feedback on task error occurs at time points 0 and $T$, but not in between, for some $T>0$ (Fig. 3A). If the network learned over the interval $\left[0,T\right]$, then $F\left[\mathbf{w}\left(T\right)\right]-F\left[\mathbf{w}\left(0\right)\right]<0$ by definition. We quantify learning rate during this interval as the value of $k$ such that

$$F\left[\mathbf{w}\left(T\right)\right]=\left(1-kT\right)F\left[\mathbf{w}\left(0\right)\right],$$

with $k<\frac{1}{T}$. A larger positive value of $k$ implies a faster rate of learning. We can write the total change in error over the interval $T$ (Fig. 3A) as

$$\begin{array}{ll}\hfill F\left[\mathbf{w}\left(T\right)\right]-F\left[\mathbf{w}\left(0\right)\right]& ={\int }_0^T⟨\nabla F\left[\mathbf{w}\left(t\right)\right],\dot{\mathbf{w}}\left(t\right)⟩\hspace{0.17em}dt\hfill \\ \hfill & =T\hspace{0.17em}{\mathbb{E}}_t\left[⟨\nabla F\left[\mathbf{w}\left(t\right)\right],\dot{\mathbf{w}}\left(t\right)⟩\right],\hfill \end{array}$$ [1]

where expectation is taken across a uniform distribution of time points in $\left[0,T\right]$, dots denote time derivatives, and angle brackets denote the (standard) inner product. Eq. 1 shows that synaptic changes, on average, must anticorrelate with the gradient for learning to occur. We can thus decompose net learning rate during the interval $T$ into contributions as follows (further details in SI Appendix, Learning Rate and Local Task Difficulty):

$$\begin{array}{ll}\hfill k& =\underset{\begin{array}{c}\text{gradient}\\ \text{strength}\end{array}}{\underbrace{\frac{-{\Vert \nabla F\left[\mathbf{w}\left(0\right)\right]\Vert }_2}{F\left[\mathbf{w}\left(0\right)\right]}}}\left[\stackrel{\begin{array}{c}\text{contribution}\\ \text{from gradient}\end{array}}{\overbrace{⟨{\dot{\mathit{\omega }}}_T,\nabla \widehat{F}\left[\mathbf{w}\left(0\right)\right]⟩}}+\underset{\begin{array}{c}\text{contribution}\\ \text{from curvature}\end{array}}{\underbrace{{\mathbf{G}}_F\left[{\dot{\widehat{\mathit{\omega }}}}_T\right]{\Vert {\dot{\mathit{\omega }}}_T\Vert }_2^{2}T}}\right]\hfill \\ \hfill & \hspace{1em}+\mathcal{O}\left(T^2\right),\hfill \end{array}$$ [2]

where

$${\mathbf{G}}_F\left[{\dot{\widehat{\mathit{\omega }}}}_T\right]≔\frac{1}{2{\Vert \nabla F\left[\mathbf{w}\left(0\right)\right]\Vert }_2}⟨{\dot{\widehat{\mathit{\omega }}}}_T,{\nabla }^{2}F\left[\mathbf{w}\left(0\right)\right]{\dot{\widehat{\mathit{\omega }}}}_T⟩.$$

Hats indicate unit length normalized vectors (i.e., $\widehat{x}=\frac{x}{{\Vert x\Vert }_2}$) and ${\dot{\mathit{\omega }}}_T$ denotes the average synaptic change over the time interval $\left[0,T\right]$, normalized by $T$:

$${\dot{\mathit{\omega }}}_T=\frac{\mathbf{w}\left(T\right)-\mathbf{w}\left(0\right)}{T}.$$ [3]

Note that we have made no assumptions on the size of $T$, so the $\mathcal{O}\left(T^2\right)$ term in Eq. 2 is not necessarily small. Nonetheless, we can gain useful insight for how error surface geometry affects learning by examining the other terms on the right-hand side of Eq. 2. The gradient strength scales the overall learning rate. Inside the brackets, the curvature term (which can change sign and magnitude during learning) can compete with the gradient term to slow down (or reverse) learning.

Fig. 3.

Geometry of error-based learning in arbitrary networks. (A) Schematic of task error as a function of (two) synaptic weights. Learning rule receives and processes task-relevant feedback to provide direction for each synapse to move in weight space. Direction must correlate with steepest-descent direction, resulting in initial improvement of task error. If no new feedback is received over a long time period $T$, this initially good direction may eventually go uphill, thus becoming bad. Frequent error feedback, a less “curvy” error surface, and a good correlation with the initial steepest-descent direction make learning faster. Local task difficulty captures these factors. (B) Schematic of changes in three weights over interval $\left[0,T\right]$. The true weight trajectory $\mathbf{w}\left(t\right)$ over time (red line) is summarized by an interpolated, linear trajectory ${\dot{\mathit{\omega }}}_T$ (blue line) between $\mathbf{w}\left(0\right)$ and $\mathbf{w}\left(T\right)$. We can decompose this interpolated trajectory into task-relevant and task-irrelevant plasticity components. The former is the initial steepest-descent direction $-\nabla F\left[\mathbf{w}\left(0\right)\right]$, and the latter is the remaining orthogonal component, which corresponds to the direction ${\widehat{\mathbf{n}}}_2+{\widehat{\mathbf{n}}}_3$.

Informally, the curvature term in Eq. 2 therefore controls the learning “difficulty” at each stage of learning. As we will show, this term can be tuned by changing the number of neurons and synaptic connections in the network.

The learning rate, $k$, is likely to remain positive during learning if the gradient direction changes gradually as the error surface is traversed (i.e., the error surface is almost linear). In this case a high rate of plasticity—due to a high gain between feedback error and synaptic change—will result in a high learning rate. However, if the descent direction changes rapidly due to the curvature of the error surface (i.e., the surface is crinkled up), then correlation with $-\nabla F\left[\mathbf{w}\left(0\right)\right]$ becomes a weaker predictor of learning over the entire time interval $T$. Effective learning therefore involves balancing error surface curvature and per-synapse rate of plasticity. This is illustrated in Fig. 3A, where the length of the leaps along the error surface indicates the rate of plasticity.

We next decompose the contributions to the overall synaptic change during a learning increment. First we assume that synapses are perfectly reliable, with no intrinsic noise fluctuations affecting their strengths. In this case, we can decompose ${\dot{\mathit{\omega }}}_T$ into two components that are parallel and perpendicular to the gradient at time 0, when error information was supplied to the network (Fig. 3B),

$${\dot{\mathit{\omega }}}_T=-{\gamma }_1\nabla \widehat{F}\left[\mathbf{w}\left(0\right)\right]+{\gamma }_2{\widehat{\mathbf{n}}}_2,$$

where ${\gamma }_1$ is the component of synaptic change that projects onto the error gradient direction and ${\gamma }_2$ is the component perpendicular to the gradient direction, with ${\widehat{\mathbf{n}}}_2$ denoting the unit vector in this direction. We call these two components, ${\gamma }_1$ and ${\gamma }_2$, the task-relevant plasticity and task-irrelevant plasticity, respectively.

Note that a learning rule could theoretically induce task-relevant synaptic changes in a direction that is not parallel to the gradient, $\nabla F\left[\mathbf{w}\left(0\right)\right]$, if information on the Hessian ${\nabla }^{2}F\left[\mathbf{w}\left(0\right)\right]$ were available. However, as mentioned previously we are assuming that such information is not available biologically and the best the network can do is follow the gradient. In fact, the results of this paper can be generalized to eliminate this assumption (SI Appendix, Task-Relevant Plasticity) but this complicates the presentation without adding insight.

There are several sources of task-irrelevant plasticity. First, there can be inherent imperfections in the learning rule: Information on task error may be imperfectly acquired and transmitted through the nervous system. Second, as we have emphasized above, the process of integrating feedback error and converting it into synaptic changes takes time. Therefore, any learning rule will be using outdated information on task performance, implying that the gradient information will have error in general, unless it is constant for a task. This is illustrated in Fig. 3A, where we see that during learning, the local information used to modify synapses leads to a network overshooting local minima in the error surface. Third, in a general biological setting, synapses will be involved in multiple task-irrelevant plasticity processes that contribute to ${\gamma }_2$ (Fig. 1A). For instance, the learning of additional, unrelated tasks may induce concurrent synaptic changes; so too could other ongoing cellular processes such as homeostatic plasticity. The common feature of all these components of task-irrelevant plasticity is that they are correlated across the network, but uncorrelated with learning the task.

We now consider the impact of intrinsic noise in the synapses themselves. Synapses are subject to continuous fluctuations due to turnover of receptors and signaling components. Some component of this will be uncorrelated across synapses so we can model these sources of noise as additional, independent white-noise fluctuations at each synapse with some total (per-synapse) variance ${\gamma }_{3}T$ over the interval $\left[0,T\right]$. Because this noise is independent across synapses, the total variance in the network will scale with the number of synapses. This gives another expression for synaptic weight change:

$$\begin{array}{ll}\hfill \mathbf{w}\left(T\right)-\mathbf{w}\left(0\right)& =-{\gamma }_{1}T\nabla \widehat{F}\left[\mathbf{w}\left(0\right)\right]+{\gamma }_{2}T{\widehat{\mathbf{n}}}_2+{\gamma }_3\sqrt{T}\sqrt{N}{\widehat{\mathbf{n}}}_3\hfill \\ \hfill & =T\left(-{\gamma }_1\nabla \widehat{F}\left[\mathbf{w}\left(0\right)\right]+{\gamma }_2{\widehat{\mathbf{n}}}_2+{\gamma }_3\sqrt{\frac{N}{T}}{\widehat{\mathbf{n}}}_3\right).\hfill \end{array}$$ [4]

Note that ${\gamma }_3$ describes the average degree of intrinsic noise per synapse, whereas ${\gamma }_1$ and ${\gamma }_2$ describe components of synaptic change over the entire network. This in turn gives the following expression for the average weight velocity over the learning interval:

$${\dot{\mathit{\omega }}}_T=-{\gamma }_1\nabla \widehat{F}\left[\mathbf{w}\left(0\right)\right]+{\gamma }_2{\widehat{\mathbf{n}}}_2+{\gamma }_3\sqrt{\frac{N}{T}}{\widehat{\mathbf{n}}}_3.$$ [5]

Note that the per-synapse fluctuation due to the ${\gamma }_3$ term is independent of network size. This is because $\Vert {\widehat{\mathbf{n}}}_3\Vert =1$, which implies that the expected magnitude of the $i$th component of ${\widehat{\mathbf{n}}}_3$ is $\sqrt{\frac{1}{N}}$. If we assume that each component is independent (see SI Appendix, Decomposition of Local Task Difficulty for justification), we can also write the magnitude of total synaptic rate of change across the network in a convenient form:

$${\Vert {\dot{\mathit{\omega }}}_T\Vert }_2^2={\gamma }_1^2+{\gamma }_2^2+{\gamma }_3^2\frac{N}{T}.$$ [6]

We see that the ${\gamma }_3$ term, which is a measure of per-synapse fluctuation magnitude, scales with the number of neurons. This stands in contrast to ${\gamma }_1$ and ${\gamma }_2$, which measure fluctuation sources over the network. Eqs. 5 and 6 allow us to rewrite Eq. 2:

$$\begin{array}{l}\hfill \mathbb{E}\left[k\right]=\frac{-{\Vert \nabla F\left[\mathbf{w}\left(0\right)\right]\Vert }_2}{F\left[\mathbf{w}\left(0\right)\right]}\left[-{\gamma }_1+{\mathbf{G}}_F\left[{\dot{\widehat{\mathit{\omega }}}}_T\right]{\Vert {\dot{\mathit{\omega }}}_T\Vert }_2^{2}T\right]+\mathcal{O}\left(T^2\right).\\ \hfill \end{array}$$ [7]

For given values of the ${\gamma }_i$ and $T$, we see from Eq. 7 that ${\mathbf{G}}_F$ controls the learning rate of a network: A higher value of ${\mathbf{G}}_F\left[{\dot{\widehat{\mathit{\omega }}}}_T\right]$ leads to slower or negative learning. For this reason, we refer to ${\mathbf{G}}_F$ as the local task difficulty. Again, the $\mathcal{O}\left(T^2\right)$ term may not be small. However, as mentioned, it is reasonable to assume this term cannot be controlled by the learning rule because it depends on higher-order derivatives of $F$ that synapses are unlikely to be able to compute. Therefore, we can reasonably say that learning requires the first term of Eq. 7 to be negative and ceases to occur when this term is zero. This implies

$${\mathbf{G}}_F\left[{\dot{\widehat{\mathit{\omega }}}}_T\right]\le \frac{{\gamma }_1}{T\left({\gamma }_1^2+{\gamma }_2^2+{\gamma }_3^2\frac{N}{T}\right)}.$$ [8]

This inequality relates the intrinsic “learnability” of a task (local task difficulty, ${\mathbf{G}}_F$), the rate of information on task error ($T$), the quality of the learning rule (relative magnitudes of ${\gamma }_1$ and ${\gamma }_2$), the network size ($N$), and the intrinsic noisiness of synapses (${\gamma }_3$).

If inequality Eq. 8 is broken, then learning stops entirely. At some point in learning, this breakage is inevitable: As $F\left[\mathbf{w}\right]$ approaches a local minimum, the gradient $\nabla F\left[\mathbf{w}\right]$ approaches zero, and the Hessian ${\nabla }^{2}F\left[\mathbf{w}\right]$ is guaranteed positive semidefinite. At a precise minimum of error, ${\mathbf{G}}_F$ becomes unbounded. This means that for a nonzero $T$, cessation of learning is preceded by an increase in local task difficulty, and learning stops just as inequality 8 above is broken.

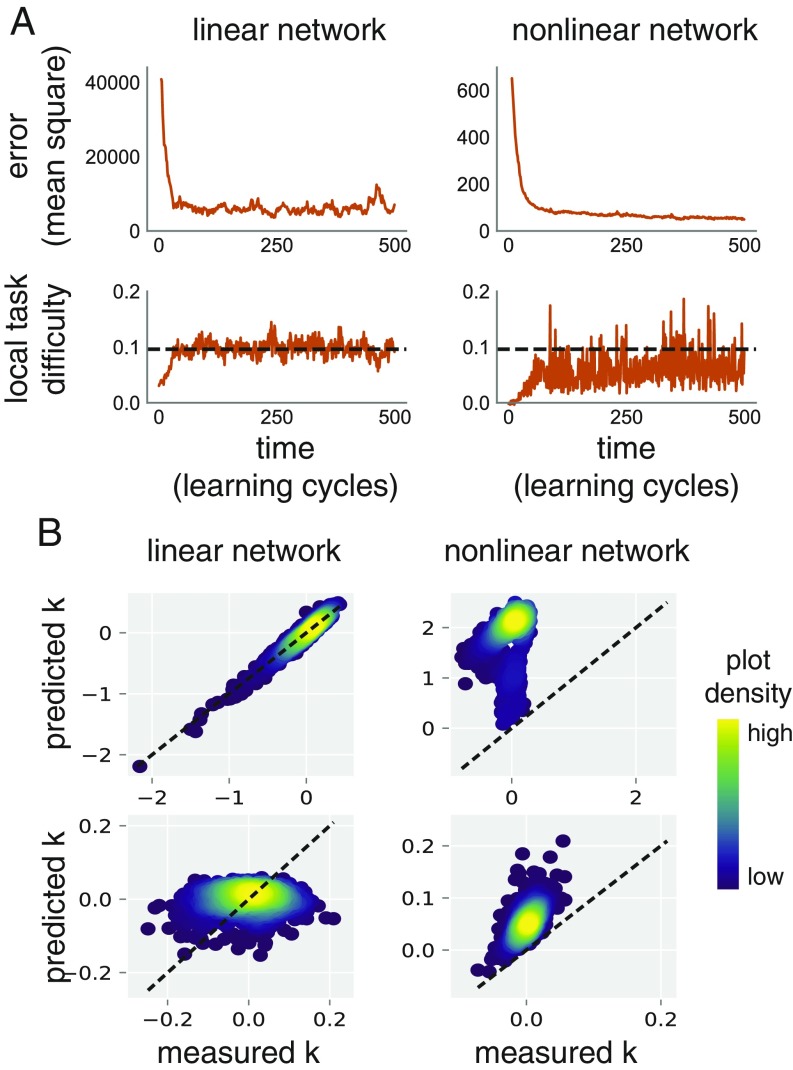
To validate our analysis we numerically computed the quantities in Eq. 7 in simulations (Fig. 4). In the case of a linear network with quadratic error the $\mathcal{O}\left(T^2\right)$ terms disappear, allowing us to verify that equality in Eq. 8 indeed predicts the steady-state value of ${\mathbf{G}}_F$. This agreement is confirmed in Fig. 4A.

Fig. 4.

Numerical validation of learning-rate calculations in simulated neural networks. (A) Local task difficulty and mean squared error over time for a linear network (Left) with quadratic error function and a nonlinear network (Right). Local task difficulty is low when the networks are in an untrained state. As performance improves, it rises, until reaching some steady-state level (black dashed lines). We can predict this steady state a priori, exactly for the quadratic error, and conservatively for the nonlinear error, using Eq. 8. Both networks are trained using a corrupted learning rule ($\overline{\gamma }=\left[0.2,\mathrm{1,0}\right]$, $T=2$; Materials and Methods). Network sizes are 200 synaptic weights (linear) and 220 synaptic weights (nonlinear, one hidden layer). (B) We use the same linear (Left) and nonlinear (Right) networks as in A. We compare the predicted value of the learning rate $k_{\text{pred}}$ (using Eq. 7 and $\gamma =\overline{\gamma }$) with the actual value, under low-noise (Top, $\overline{\gamma }=\left[\mathrm{1,0.05},0.05\right]$) and high-noise (Bottom, $\overline{\gamma }=\left[0.2,0.5,0.1\right]$) conditions. Dashed lines represent $k=k_{\text{pred}}$. Density plots of $\left\{k,k_{\text{pred}}\right\}$ are shown. Two sources of discrepancy exist. First, $k_{\text{pred}}$ is calculated from the mean values $\overline{\gamma }$ (Materials and Methods). Transient correlations between task-irrelevant sources of plasticity and the gradient lead to unbiased fluctuations of $\gamma$ around $\overline{\gamma }$. This is the only source of discrepancy in the linear case (Left). Thus, the density distributes equally on either side of the dashed line. In the nonlinear case (Right), there is an unknown, nonzero $\mathcal{O}\left(T^2\right)$ term (Eq. 7) unaccounted for in calculation of $k_{\text{pred}}$. This term almost always decreases learning rate, as $k_{\text{pred}}$ now consistently overestimates $k$. Thus, predicted steady-state local task difficulty (e.g., A, Bottom Right, dashed line) is consistently an overestimate.

For more general error functions, we have observed that Eq. 8 is always conservative in numerical simulations: Learning stops before local task difficulty reaches the critical value, implying that the $\mathcal{O}\left(T^2\right)$ term of Eq. 7 is usually negative. This is demonstrated in Fig. 4 A and B.

In summary, we have shown that local task difficulty ${\mathbf{G}}_F$ determines the learning rate as well as the steady-state learning performance of a network.

Note that in Fig. 4 (as well as in subsequent numerical simulations) we define the entire distribution of input–output pairs to be a finite set or “batch” generated from a fixed, random set of inputs. This a technical necessity that allowed us to numerically calculate true task error (i.e., the error over all inputs) and the true task gradient $\nabla F\left[\mathbf{w}\left(0\right)\right]$ and thus define specific values of ${\gamma }_i$ when applying the update of Eq. 5. We emphasize that this finite batch is considered to be the entire distribution, not a sample from a true (unknown) distribution. It is not possible to numerically specify the ${\gamma }_i$ in the simulations of Fig. 2, because we cannot explicitly calculate the true gradient in this case. Instead, learning occurred online by a single sample from an infinite number of potential inputs, producing a stochastic gradient estimate. Fortunately, conclusions drawn from the both simulation paradigms are interchangeable. Online learning using a stochastic gradient is mathematically equivalent to adding task-irrelevant (${\gamma }_2$) plasticity to the batch learning setup of Figs. 4 and 6. The amount by which ${\gamma }_2$ is increased depends on the task, but not the network size/architecture (see SI Appendix, Online Learning and Generalization Error for further details).

Fig. 6.

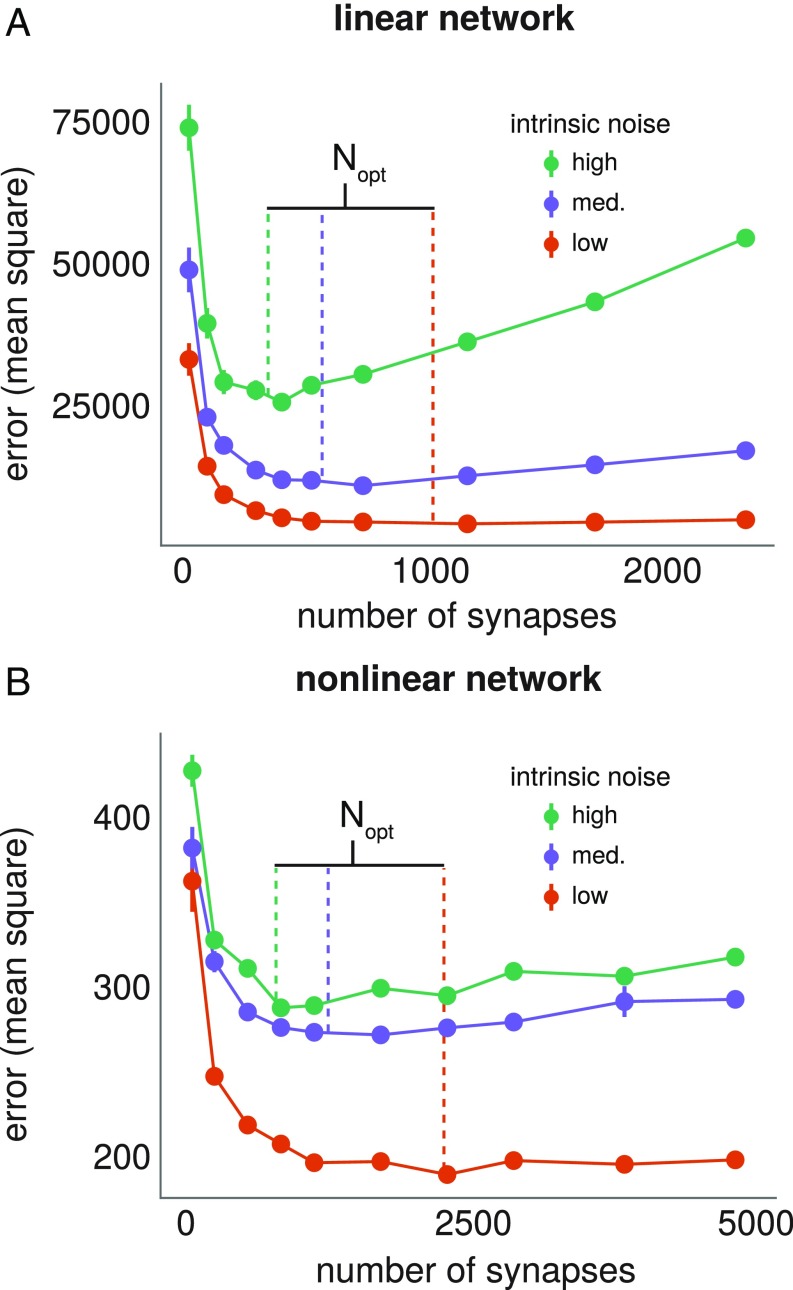
Testing analytic prediction of optimal network size for linear and nonlinear networks. (A and B) Linear (A) and nonlinear (B) networks of different sizes are trained for 1,500 learning cycles of length $T=1$. Mean steady-state error over 12 repeats is plotted against network size. Error bars denote $\pm 1$ SEM. Colored lines represent a priori predicted optimal network sizes using Eqs. 17 and 19 for the linear and nonlinear examples, respectively. (A) Linear networks all have a 2:1 ratio of inputs to outputs. On each repeat, networks of all considered sizes learn the same mapping, embedded in the appropriate input/output dimension (detailed in SI Appendix, Learning in a Linear Network). The learning rule uses $\overline{\gamma }=\left[0.07,\mathrm{1,0.03}\right]$ (low intrinsic noise), $\overline{\gamma }=\left[0.06,\mathrm{1,0.04}\right]$ (medium intrinsic noise), and $\overline{\gamma }=\left[0.05,\mathrm{1,0.05}\right]$ (high intrinsic noise). (B) Nonlinear networks have sigmoidal nonlinearities at each neuron and a single hidden layer (Materials and Methods). All networks have 10 input and 10 output neurons and learn the same task. The number of neurons in the hidden layer is varied from 5 to 120. The learning rules all use ${\overline{\gamma }}_1=0.04$ and ${\overline{\gamma }}_2=1.5$. The value of ${\overline{\gamma }}_3$ is set respectively at 0.03, 0.04, and 0.05, in the low, medium, and high intrinsic noise cases.

Local Task Difficulty as a Function of Network Size.

We next show precisely how network size influences the local task difficulty and thus learning rate and steady-state performance when other factors such as noise and the task itself remain the same.

Recall that ${\mathbf{n}}_2$ represents the direction in which synapses are perturbed due to error in the learning rule and other task-irrelevant changes that affect all synapses. Meanwhile ${\mathbf{n}}_3$ represents the direction of weight change due to intrinsic white-noise fluctuations at each synapse. For arbitrary tasks, networks, and learning trajectories we can model these terms as coming from mutually independent probability distributions that are independent of task error $F\left[\mathbf{w}\right]$ and its derivatives. Thus, we assume $\mathbb{E}\left[{\mathbf{n}}_2^T{\mathbf{n}}_3\right]=0$, which allows us to write an expression for expected local task difficulty:

$$\begin{array}{l}\hfill \mathbb{E}\hspace{0.17em}\left[{\mathbf{G}}_F\left[{\dot{\widehat{\mathit{\omega }}}}_T\right]\right]{\Vert {\dot{\mathit{\omega }}}_T\Vert }_2^2={\gamma }_1^2{\mathbf{G}}_F^1\left[\mathbf{w}\left(0\right)\right]+\frac{Tr\left({\nabla }^{2}F\left[\mathbf{w}\left(0\right)\right]\right)}{2{\Vert \nabla F\left[\mathbf{w}\left(0\right)\right]\Vert }_2}\left[\frac{{\gamma }_2^2}{N}+\frac{{\gamma }_3^2}{T}\right],\\ \hfill \end{array}$$ [9]

where

$$\begin{array}{l}\hfill {\mathbf{G}}_F^1\left[\mathbf{w}\left(0\right)\right]=\frac{1}{2{\Vert \nabla F\left[\mathbf{w}\left(0\right)\right]\Vert }_2}\langle \nabla \widehat{F}\left[\mathbf{w}\left(0\right)\right],{\nabla }^{2}F\left[\mathbf{w}\left(0\right)\right]\nabla \widehat{F}\left[\mathbf{w}\left(0\right)\right]\rangle .\\ \hfill \end{array}$$ [10]

This expression for the local task difficulty explicitly incorporates $N$, the number of synaptic weights. So too does the learning rate Eq. 7, as we see by substituting into it the expanded form of $\mathbb{E}\left[{\mathbf{G}}_F\left[{\dot{\widehat{\mathit{\omega }}}}_T\right]\right]{\Vert {\dot{\mathit{\omega }}}_T\Vert }_2^2$.

We can gain intuition into how Eq. 9 is derived without going through additional technical details (SI Appendix, Decomposition of Local Task Difficulty). Suppose that the weights were perturbed by a randomly chosen direction $\mathbf{n}$ over the time interval $\left[0,T\right]$. This gives

$$\begin{array}{cc}\hfill & F\left[\mathbf{w}\left(T\right)\right]=F\left[\mathbf{w}\left(0\right)+\mathbf{n}\right]=\hfill \\ \hfill & F\left[\mathbf{w}\left(0\right)\right]+⟨\nabla F\left[\mathbf{w}\left(0\right)\right],\mathbf{n}⟩+\frac{1}{2}⟨\mathbf{n},{\nabla }^{2}F\left[\mathbf{w}\left(0\right)\right]\mathbf{n}⟩+\mathcal{O}\left({\Vert \mathbf{n}\Vert }_2^2\right).\hfill \end{array}$$ [11]

If the direction $\mathbf{n}$ is drawn independently of task error and its derivatives, then

$$\mathbb{E}\left[⟨\nabla F\left[\mathbf{w}\left(0\right)\right],\mathbf{n}⟩\right]=0.$$

Therefore, it is the quadratic term of Eq. 11 that determines the effect of the perturbation on task error. Its contribution is

$$\begin{array}{ll}\hfill \mathbb{E}\left[⟨\mathbf{n},{\nabla }^{2}F\left[\mathbf{w}\left(0\right)\right]\mathbf{n}⟩\right]& ={\Vert \mathbf{n}\Vert }_2^2\mathbb{E}\left[⟨\widehat{\mathbf{n}},{\nabla }^{2}F\left[\mathbf{w}\left(0\right)\right]\widehat{\mathbf{n}}⟩\right]\hfill \\ \hfill & ={\Vert \mathbf{n}\Vert }_2^2\frac{Tr\left({\nabla }^{2}F\left[\mathbf{w}\left(0\right)\right]\right)}{N}.\hfill \end{array}$$

So the effect of random perturbations on learning grows with the ratio of $Tr\left({\nabla }^{2}F\left[\mathbf{w}\left(0\right)\right]\right)$ to the number of synapses, $N$. Eq. 9 tells us explicitly how local task difficulty (and thus expected learning rate and steady-state performance) can be modified by changing the size of a network, provided the size change leaves ${\mathbf{G}}_F^1\left[\mathbf{w}\left(0\right)\right]$ and $\frac{Tr\left({\nabla }^{2}F\left[\mathbf{w}\left(0\right)\right]\right)}{2{\Vert \nabla F\left[\mathbf{w}\left(0\right)\right]\Vert }_2}$ unchanged. For different network architectures there are many possible ways of adding neurons and connections while satisfying these constraints. This explains why the naive size increases in Fig. 2C generically increased learning performance and provides a general explanation for enhanced learning performance in larger networks.

Network Expansions That Increase Learning Performance.

We next give detailed examples of network expansions that increase learning rate and use the theory developed so far to compute the optimal size of a network when intrinsic noise is present. We first analyze a linear network and then apply insights from this to a more general nonlinear feedforward case.

Consider a linear network (i.e., a linear map, as shown in Fig. 5A) that transforms any input $u$ into an output $y=Wu$ for a matrix $W\in {\mathbb{R}}^{oi}$ of synaptic weights. The input-dependent error of the network is taken as a simple mean square error,

$$F\left[W\right]=\int F\left[W,u\right]\mathbb{P}\left(u\right)\hspace{0.17em}du=\int {\Vert y^{*}\left(u\right)-Wu\Vert }_2^2\mathbb{P}\left(u\right)\hspace{0.17em}du,$$

where the input vectors are drawn from some distribution $\mathbb{P}\left(u\right)$ (e.g., a Gaussian) and $y^{*}\left(u\right)$ is a target output generated by a linear mapping of the same rank and dimension.

Fig. 5.

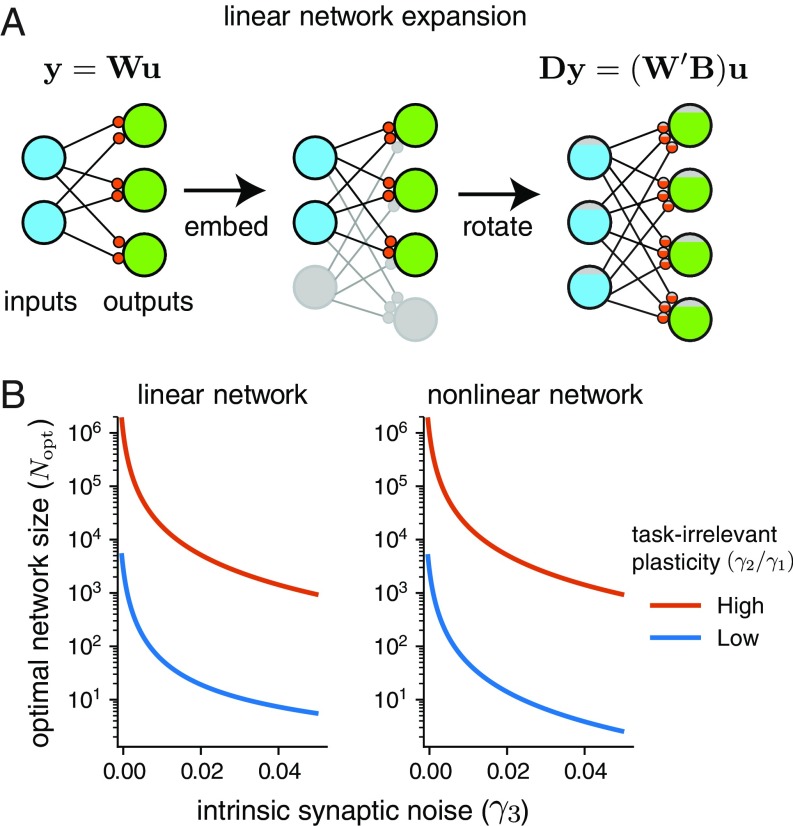
Optimal network size for linear and nonlinear networks in the presence of intrinsic synaptic noise. (A) Network expansion for a linear network, given by an embedding into a larger network, followed by a rotation of the weight matrix. This corresponds to transforming inputs $\mathbf{u}$ by a projection $\mathbf{B}$ and outputs $\mathbf{y}$ by a semiorthogonal mapping $\mathbf{D}$. (B) Plots show the dependence of $N_{\text{opt}}$ in linear and nonlinear networks using Eqs. 17 and 19. In both cases the learning rule has ${\gamma }_1=0.01$ and $T=2$. Low task-irrelevant plasticity corresponds to ${\gamma }_2=0.05$, while high task-irrelevant plasticity corresponds to ${\gamma }_2=1$.

We next embed this network in a larger network with $c_{1}i$ inputs, $c_{2}o$ outputs, and a synaptic weight matrix $W\prime$, for some integers $c_1$, $c_2>1$. We define the total number of weights as $Ñ=c_{1}i{c}_{2}o$. We take the transformation $u\prime =Bu\in {\mathbb{R}}^{c_{1}i}$, where $B\in {\mathbb{R}}^{c_{1}i\times i}$ is an arbitrary semiorthogonal matrix. (i.e., it satisfies $B^{T}B={\mathbb{I}}_i$). Geometrically, $B$ therefore represents the composition of a projection into the higher-dimensional space ${\mathbb{R}}^{c_{1}i}$ with a rotation. Note that this is an invertible mapping: If $u\prime =Bu$, then $B^{T}u\prime =u$. Similarly, we can take ${y\prime }^{*}\left(u\prime \right)=D{y}^{*}\left(u\right)\in {\mathbb{R}}^{c_{2}o}$, where $D^{T}D={\mathbb{I}}_o$. This is illustrated in Fig. 5A.

The expanded neural network with weights $W\prime \in {\mathbb{R}}^{c_{2}o\times c_{1}i}$ has to learn the same mapping as the original, but with respect to the higher-dimensional inputs. So the network receives inputs $u\prime \in B\mathcal{U}$ and transforms them to outputs $y\prime =W\prime u\prime$, with input-dependent error

$$\begin{array}{ll}\hfill F\prime \left[W\prime ,u\prime \right]& ={\Vert {y\prime }^{*}\left(u\prime \right)-W\prime u\prime \Vert }_2^2\hfill \\ \hfill & ={\Vert D{y}^{*}\left(u\right)-W\prime Bu\Vert }_2^2\hfill \\ \hfill & ={\Vert y^{*}\left(u\right)-D^{T}W\prime Bu\Vert }_2^2.\hfill \end{array}$$ [12]

For some weight configuration $W\prime$ in an expanded network, Eq. 12 tells us that if these weights are related to the original network weights by $W=D^{T}W\prime B\in {\mathbb{R}}^{oi}$, then we have

$$F\prime \left[W\prime \right]=F\left[W\right].$$

Explicit differentiation of $F\prime \left[W\prime \right]$ (see SI Appendix, Learning in a Linear Network) yields:

$$\begin{array}{ll}\hfill {\Vert \nabla F\prime \left[W\prime \right]\Vert }_2& ={\Vert \nabla F\left[W\right]\Vert }_2\hfill \\ \hfill Tr\left({\nabla }^{2}F\prime \left[W\prime \right]\right)& =2c_{2}o{\int }_{u\in \mathcal{U}}{\Vert u\Vert }_2^2\hspace{0.17em}\mathbb{P}\left(u\right)\hfill \\ \hfill & =c_{2}Tr\left({\nabla }^{2}F\left[W\right]\right).\hfill \end{array}$$ [13]

We now rewrite the weight matrices $W\prime$ and $W$ as vectors $\mathbf{w}\prime \in {\mathbb{R}}^{Ñ}$ and $\mathbf{w}\in {\mathbb{R}}^N$.We will assume that $\nabla \widehat{F\prime }\left[\mathbf{w}\prime \right]$ (which is a normalized vector) projects approximately equally onto the different eigenvectors of ${\nabla }^{2}F\prime \left[\mathbf{w}\prime \right]$. The latter is constant, whereas the former is a linear function of the (randomly chosen) $W\prime$, which justifies this assumption. In this case, Eq. 13 implies

$$\begin{array}{cc}\hfill \nabla \widehat{F\prime }{\left[\mathbf{w}\prime \right]}^T{\nabla }^{2}F\prime \left[\mathbf{w}\prime \right]& \nabla \widehat{F\prime }\left[\mathbf{w}\prime \right]\approx \hfill \\ \hfill & c_2\nabla \widehat{F}{\left[\mathbf{w}\right]}^T{\nabla }^{2}F\left[\mathbf{w}\right]\nabla \widehat{F}\left[\mathbf{w}\right].\hfill \end{array}$$ [14]

Bringing together Eqs. 13 and 14 and the formula Eq. 10 for ${\mathbf{G}}_F^1$, we see that

$${\mathbf{G}\prime }_{F\prime }^1\left[\mathbf{w}\prime \right]\approx c_2{\mathbf{G}}_F^1\left[\mathbf{w}\right],$$ [15a]

and similarly

$$\frac{Tr\left({\nabla }^{2}F\prime \left[\mathbf{w}\prime \right]\right)}{{\Vert \nabla F\prime \left[\mathbf{w}\prime \right]\Vert }_2}\approx c_2\frac{Tr\left({\nabla }^{2}F\left[\mathbf{w}\right]\right)}{{\Vert \nabla F\left[\mathbf{w}\right]\Vert }_2}.$$ [15b]

We can therefore write local task difficulty of the expanded network in terms of quantities of the smaller network:

$$\begin{array}{l}\hfill \mathbb{E}\left[{\mathbf{G}}_{F\prime }^{\prime }\left[{\dot{\widehat{\mathit{\omega }}}}_T^{\prime }\right]\right]{\Vert {\dot{\mathit{\omega }}}_T^{\prime }\Vert }_2^2\approx c_2{\mathbf{G}}_F\left[\mathbf{w}\right]+c_2\frac{Tr\left({\nabla }^{2}F\left[\mathbf{w}\right]\right)}{2{\Vert \nabla F\left[\mathbf{w}\right]\Vert }_2}\left[\frac{{\gamma }_2^2}{Ñ}+\frac{{\gamma }_3^2}{T}\right].\\ \hfill \end{array}$$ [16]

As long as the ratio $\frac{c_2}{c_1}$ is fixed, we can rewrite $Ñ$ in terms of $c_2$ and alter $c_2$ as an independent parameter in Eq. 16. Indeed this allows us to optimize the steady-state error of the network by changing $N$. To see how, recall that

$$\begin{array}{ll}\hfill \mathbb{E}\left[k\right]& =\frac{-{\Vert \nabla F\left[\mathbf{w}\left(0\right)\right]\Vert }_2}{F\left[\mathbf{w}\left(0\right)\right]}\left[-{\gamma }_1+\mathit{\delta }\right]+\mathcal{O}\left(T^2\right),\hfill \\ \hfill \text{where}\mathit{\delta }& ={\mathbf{G}}_F\left[{\dot{\widehat{\mathit{\omega }}}}_T\right]{\Vert {\dot{\mathit{\omega }}}_T\Vert }_2^{2}T,\hfill \end{array}$$

with $\mathcal{O}\left(T^2\right)\equiv 0$ for quadratic error. Suppose the network has reached steady-state error; i.e., $\mathbb{E}\left[k\right]=0$. If we decreased $\mathit{\delta }$, then $\mathbb{E}\left[k\right]$ would also decrease, and the network would learn further. Therefore, to derive the optimal $N^{*}$, we should minimize the expression for $\mathit{\delta }$ in $N$ (or equivalently, $c_2$). We differentiate $\mathit{\delta }$ in $c_2$ and note that a single stationary point exists, satisfying the equation

$$\begin{array}{ll}\hfill & N^{*}=\frac{{\gamma }_2^2}{C{\gamma }_1^2+\frac{{\gamma }_3^2}{T}}\hfill \\ \hfill & \text{where}C=\frac{⟨\nabla \widehat{F}\left[\mathbf{w}\left(0\right)\right],{\nabla }^{2}F\left[\mathbf{w}\left(0\right)\right]\nabla \widehat{F}\left[\mathbf{w}\left(0\right)\right]⟩}{Tr\left({\nabla }^{2}F\left[\mathbf{w}\left(0\right)\right]\right)}.\hfill \end{array}$$

Note that $C$ is unknown in general because it depends on the weight configuration of the network. However, we can take the heuristic $C\approx \frac{1}{N^{*}}$, since if the gradient $\nabla \widehat{F}\left[\mathbf{w}\left(0\right)\right]$ is uncorrelated with the Hessian ${\nabla }^2\widehat{F}\left[\mathbf{w}\left(0\right)\right]$, then it would project equally onto each of the eigenvectors of the latter, and thus the numerator of $C$ would be the mean eigenvalue, i.e., $\frac{Tr\left({\nabla }^2\widehat{F}\left[\mathbf{w}\left(0\right)\right]\right)}{N}$. This results in an approximate expression for $N^{*}$, the stationary point of $\mathit{\delta }$ in $N$:

$$N^{*}\approx \frac{T{\gamma }_2^2}{{\gamma }_3^2}\left(1-\frac{{\gamma }_1^2}{{\gamma }_2^2}\right).$$ [17]

Since $\underset{Ñ\to \infty }{lim}\mathit{\delta }=\infty$, we have that $\mathit{\delta }\left(Ñ\right)$ is monotonically increasing in $Ñ$, for $Ñ\ge N^{*}$. So if $N^{*}<N$, the size of the original network, then any extra redundancy hurts learning performance. If $N^{*}>N$, then the optimal network size $N_{\text{opt}}$ satisfies $N_{\text{opt}}=N^{*}$. Our formula is verified numerically in Fig. 6A, by evaluating the learning performance of transformed neural networks of different sizes, with different ${\gamma }_i$ values.

This estimate of the optimal network size is plotted in Fig. 5B, which shows the dependence on intrinsic synaptic noise levels. As noise decreases to zero, we see that the optimal network size grows arbitrarily. In addition, the optimal network size is smaller for a lower amount of task-irrelevant plasticity (i.e., a “better” learning rule). We validate the optimal network size estimate in Fig. 6A in simulations.

We next consider nonlinear multilayer, feedforward networks. Again, we use the student–teacher framework to generate learning tasks. We consider learning performance of a nominal and an expanded network, both with $l$ layers, and both using the same learning rule. The only difference between the two networks is the larger number of neurons in each hidden layer of the expanded network. We will use our theory to predict an optimal number of synapses (and consequently optimal hidden layer sizes) for the transformed network. As before, this size will depend on the learning rule used by the networks, which is defined by levels of task-relevant plasticity, task-irrelevant plasticity, per-synapse white-noise intensity, and frequency of task error feedback. Our predictions are validated in simulations in Fig. 6B.

We first describe the nominal network architecture. Given a vector $h^{\left(k-1\right)}$ of neural activities at layer $k-1$, the neural activity at layer $h^{\left(k\right)}$ is

$$h^{\left(k\right)}=\underset{\_}{\sigma }\left(W^{\left(k\right)}{h}^{\left(k-1\right)}\right).$$

Here, $W^{\left(k\right)}$ is the matrix of synaptic weights at the $k$th layer. The concatenation of the synaptic weight matrices across all layers is denoted $W$ and has $N$ elements. We interchangeably denote it as a vector $\mathbf{w}\in {\mathbb{R}}^N$. The function $\sigma$ passes its arguments elementwise through some nonlinearity (sigmoidal in simulations; Materials and Methods). The first layer of neurons receives an input vector $u$ in place of neural activities $h^{\left(0\right)}$. The output $y\left(W,u\right)$ is defined as neural activity at the final hidden layer.

For any given state $\mathbf{w}$ of the nominal network, we can construct a state $\varphi \left(\mathbf{w}\right)$ of the expanded network with the same input–output properties; i.e., $y\left(\mathbf{w},u\right)=y\prime \left(\varphi \left(\mathbf{w}\right),u\right)$, where $y\prime$ denotes expanded network output. We do this by setting synaptic weights of the added neurons in the expanded network to zero, so the neurons do not contribute at state $\varphi \left(\mathbf{w}\right)$. Nevertheless the extra neurons can affect expanded network behavior because once they are perturbed by the learning rule they contribute to the error gradient and higher derivatives.

Suppose the nominal network is at state $\mathbf{w}\left(0\right)$, and a learning rule picks the direction ${\dot{\mathit{\omega }}}_T$ for weight change over the time interval $\left[0,T\right]$. This direction will have some local task difficulty ${\mathbf{G}}_F\left[{\dot{\widehat{\mathit{\omega }}}}_T\right]$. If we map the state $\mathbf{w}\left(0\right)$ and the direction ${\dot{\mathit{\omega }}}_T$ to the transformed network via the transformation $\varphi$, then we can estimate local task difficulty ${\mathbf{G}}_F^{\prime }\left[\varphi \left({\dot{\widehat{\mathit{\omega }}}}_T\right)\right]$ of the transformed network (see SI Appendix, Learning in a Nonlinear, Feedforward Network for additional details). We get

$$\begin{array}{ll}\hfill & \mathbb{E}\left[{\mathbf{G}\prime }_{F\prime }\left[\varphi \left({\dot{\widehat{\mathit{\omega }}}}_T\right)\right]\right]{\Vert \varphi \left({\dot{\mathit{\omega }}}_T\right)\Vert }_2^2\hfill \\ \hfill & \hspace{1em}\approx \sqrt{\frac{N}{Ñ}}{\gamma }_1^2{\mathbf{G}}_F^1\left[\mathbf{w}\left(0\right)\right]+\sqrt{\frac{Ñ}{N}}\frac{Tr\left({\nabla }^{2}F\left[\mathbf{w}\left(0\right)\right]\right)}{2{\Vert \nabla F\left[\mathbf{w}\left(0\right)\right]\Vert }_2}\left[\frac{{\gamma }_2^2}{Ñ}+\frac{{\gamma }_3^2}{T}\right].\hfill \\ \hfill \end{array}$$ [18]

We can use Eq. 18 to minimize

$$\mathit{\delta }={\mathbf{G}}_{F\prime }^{\prime }\left[{\dot{\widehat{\mathit{\omega }}}}_T\right]{\Vert {\dot{\mathit{\omega }}}_T\Vert }_2^{2}T$$

in $Ñ$, the number of synapses. There is a single global minimum of $\mathit{\delta }$ in $Ñ$, for $Ñ>0$. It satisfies

$$N^{*}\approx \frac{T{\gamma }_2^2}{{\gamma }_3^2}\left[\frac{{\gamma }_1^2}{{\gamma }_2^2}\frac{N}{N^{*}}+1\right].$$ [19]

This gives an optimal size of the transformed network for minimizing steady-state task performance (validated in Fig. 6B).Note the dependence of $N^{*}$ on $N$, the number of weights in the nominal and the teacher networks. The teacher networks can generate arbitrary nonlinear mappings whose complexity grows with $N$. In this way Eq. 19 reflects the intrinsic difficulty of the task.

Discussion

It is difficult to disentangle the physiological and evolutionary factors that determine the size of a brain circuit (33–35). Previous studies focused on the energetic cost of sustaining large numbers of neurons and connecting them efficiently (2, 34–36). Given the significant costs associated with large circuits (3), it is clear that some benefit must offset these costs, but it is currently unclear whether other inherent tradeoffs constrain network size. We showed under broad assumptions that there is an upper limit to the learning performance of a network which depends on its size and the intrinsic volatility of synaptic connections.

Neural circuits in animals with large brains were presumably shaped on an evolutionary timescale by gradual addition of neurons and connections. Expanding a small neural circuit into a larger one can increase its dynamical repertoire, allowing it to generate more complex behaviors (37, 38). It can improve the quality of locally optimal behaviors arrived at after learning (39, 40). Less obviously, as we show here, circuit expansion can also allow a network to learn simpler tasks more quickly and to greater precision.

By directly analyzing the influence of synaptic weight configurations on task error we derived a quantity we called “local task difficulty” that determines how easily an arbitrary network can learn. We found that local task difficulty always depends implicitly on the number of neurons and can therefore be decreased by adding neurons according to relatively unrestrictive constraints. In simple terms, adding redundancy flattens out the mapping between synaptic weights and task error, reducing the local task difficulty on average. This flattening makes learning faster and steady-state task error lower because the resulting error surface is less contorted and easier to descend using intermittent task error information. Biological learning rules are unlikely to explicitly compute gradients. Regardless, any learning rule that uses error information must effectively approximate a gradient as the network learns.

As an analogy, imagine hiking to the base of a mountain without a map and doing so using intermittent and imperfect estimates of the slope underfoot. An even slope will be easier to descend because slope estimates will remain consistent and random errors in the estimates will average out over time. An undulating slope will be harder to descend because the direction of descent necessarily changes with location. Now consider the same hike in a heavy fog at dusk. The undulating slope will become far harder to descend. However, if it were possible to somehow smooth out the undulations (that is, reduce local task difficulty), the same hike would progress more efficiently. This analogy illustrates why larger neural circuits are able to achieve better learning performance in a given task when error information is corrupted.

In specific examples we show that adding neurons to intermediate layers of a multilayer, feedforward network increases the magnitude of the slope (gradient) of the task error function relative to its curvature. From this we provide a template for scaling up network architecture such that both quantities increase approximately equally. This provides hypotheses for the organizing principles in biological circuits which, among other things, predict a prevalence of apparently redundant connections in networks that need to learn new tasks quickly and to high accuracy. Recent experimental observations reveal such apparently redundant connections in a number of brain areas across species (26, 27, 41, 42).

Even if neurons are added to a network in a way that obeys the architectural constraints we derive, intrinsic synaptic noise eventually defeats the benefits conferred to learning. All synapses experience noisy fluctuations due to their molecular makeup (23–25, 43–45). These sources of noise are distinct from shared noise in a feedback signal that is used in learning. Such independent noise sources accumulate as a network grows in size, outcompeting the benefit of size on learning performance. An immediate consequence is an optimal network size for a given task and level of synaptic noise.

Furthermore, our results show that different noise sources in nervous systems impact learning in qualitatively different ways. Noise in the learning rule as well as external noise in the task error, which may arise from sensory noise or fluctuations in the task, can be overcome in a larger circuit. On the other hand, the impact of intrinsic noise in the synaptic connections only worsens as network size grows. Our results demonstrate the intuitive fact that insufficient connections impair learning performance. Conversely, and less obviously, excessive numbers of connections impair learning once the optimal network size is exceeded. This provides a hypothesis for why abnormalities in circuit connectivity may lead to learning deficits (18–21).

Our analysis allowed us to predict the optimal size of a network in theoretical learning tasks where we can specify the levels of noise in the learning rule and in synapses. Fig. 5 shows that the optimal network size decreases rapidly as the intrinsic noise in synapses increases. We speculate that the emergence of large neural circuits therefore depended on evolutionary modifications to synapses that reduce intrinsic noise. In particular, optimal network size increases explosively as intrinsic synaptic noise approaches zero. An intriguing and challenging goal for future work would be to infer noise parameters in synapses across different nervous systems and test whether overall network size obeys the relationships our theory predicts.

Materials and Methods

Full details of all simulations are provided in SI Appendix. We provide an overview here. Code related to paper is publicly accessible in ref. 46.

Network Architectures.

All tested neural networks have fully connected feedforward architectures. Unless otherwise specified networks are nonlinear with multiple hidden layers. Each neuron in these networks passes inputs through a sigmoidal nonlinearity $\sigma :\mathbb{R}\to \mathbb{R}$ of the form $\sigma \left(x\right)=\frac{1}{1+\exp \left(-x\right)}.$

Details of the Learning Tasks.

All training tasks used in simulation use the student–teacher framework. The basic setup is as follows: We first make a teacher network, which has the same basic network architecture as the student’s. We then initialize the teacher weights at fixed values, which are generated as follows (unless otherwise specified): At the $k$th layer of the teacher network, weights are distributed uniformly on the interval $\left[-a_k,a_k\right]$. Here $a_k$ is set so that the SD of weights on the layer is $\frac{4}{\sqrt{i}}$, where $i$ is the number of inputs to the layer. This scaling with $i$ ensures that the magnitude of hidden layer outputs does not increase with the size of hidden layer (47).

We then specify a set $\mathcal{U}$ consisting of 1,000 input vectors. We generate each vector $u\in \mathcal{U}$ componentwise, randomly drawing each component $u_i$ from the distribution $u_i\sim \mathcal{N}\left(\mathrm{0,1}\right)$. Note that in Fig. 2 this acts as a test set, which is not used when training the network (details in the next section).

The output vector of the teacher, given an input vector $u$, is denoted $y*\left(u\right)$. The task of the student network, with weights $\mathbf{w}$, is then to match its output to $y*\left(u\right)$, for all $u\in \mathcal{U}$. Therefore, the task error is

$$F\left[\mathbf{w}\right]=\sum _{u\in \mathcal{U}}{\Vert y*\left(u\right)-y\left(\mathbf{w},u\right)\Vert }_2^2,$$ [20]

where $y\left(\mathbf{w},u\right)$ denotes the output of the student given input $u$ and weights $\mathbf{w}$.

For the linear networks studied at the beginning of the section Network Expansions That Increase Learning Performance, the dimensionalities of the input and output vectors differ between the teacher and the students. However, fixed matrix transformations lift the teacher inputs/outputs into the appropriate dimensionality (Eq. 12). For all other networks, the number of network inputs/outputs is shared between the students and the teacher. Teacher and students also have the same number of hidden layers. At the $i$th hidden layer, each student has at least as many neurons as the teacher. This ensures that the teacher network forms a subset of each student network and therefore that each student network is theoretically capable of exactly recreating the input–output mapping $y*\left(u\right)$ of the teacher.

Network Training.

The theoretical analysis in this paper and the simulations in Fig. 2 pertain to online learning, where training data are sampled continuously from an (infinite) distribution defined by the input–output mapping of the teacher networks. However, in cases where we needed to compute a true gradient (specifically Figs. 4 and 6), we needed to define finite distributions to numerically evaluate the true gradient. Having the true gradient allows us to precisely specify values of task-relevant and task-irrelevant components of plasticity.

We emphasize (as we emphasized in the main text) that this differs from treating the finite set as a sample—or batch—from an infinite distribution, which would incur generalization issues because any finite sample will be necessarily biased. The relationship between the results of our paper and the latter scenario is described in SI Appendix, Regularization and Generalization Error.

In Figs. 4 and 6 learning is conducted on the finite input set $\mathcal{U}$ described in the previous section. At each learning cycle, we apply the weight update

$${\mathbf{w}}_{t+T}={\mathbf{w}}_t-T{\overline{\gamma }}_1\nabla \widehat{F}\left[{\mathbf{w}}_t\right]+T{\overline{\gamma }}_2{\widehat{\mathbf{n}}}_2^t+\sqrt{NT}{\overline{\gamma }}_3{\widehat{\mathbf{n}}}_3^t.$$ [21]

The parameters ${\left\{{\overline{\gamma }}_i\right\}}_{i=1}^3$ and $T$ specify the quality of the learning rule, the feedback delay, and the intrinsic, per-synapse noise (main text). $N$ is the number of synapses in the network. We calculate the gradient $\nabla F\left[{\mathbf{w}}_t\right]$ by taking the gradient of Eq. 21 using backpropagation. The normalized vectors ${\widehat{\mathbf{n}}}_2^t$ and ${\widehat{\mathbf{n}}}_3^t$ represent sources of task-irrelevant plasticity. The dynamics of the unnormalized vector ${\mathbf{n}}_2$ satisfy ${\mathbf{n}}_2^{t+1}=\sqrt{0.1}{\widehat{\mathbf{n}}}_2^t+\sqrt{0.9}\widehat{\nu }$, where $\nu$ is a Gaussian random variable, normalized such that ${\Vert \nu \Vert }_2=1$. ${\widehat{\mathbf{n}}}_3$, which models intrinsic synaptic noise, is a Gaussian random variable, normalized so that ${\Vert {\widehat{\mathbf{n}}}_3\Vert }_2=1$.

The network in Fig. 2 C and D is conducted online from an infinite distribution. At each learning cycle, we randomly draw a single input vector $u$ of Gaussian components; i.e., $u_i\sim \mathcal{N}\left(\mathrm{0,1}\right)$. We replace the term $\nabla \widehat{F}\left[{\mathbf{w}}_t\right]$ in the weight update Eq. 21 with $\nabla \widehat{F}\left[\mathbf{w},u\right]$, the (normalized) stochastic gradient, where $F\left[\mathbf{w},u\right]≔{\Vert y*\left(u\right)-y\left(\mathbf{w},u\right)\Vert }_2^2$. The overall error $F\left[\mathbf{w}\right]$ is then the expected error on the next input; i.e.,

$$F\left[\mathbf{w}\right]={\int }_{\mathrm{\Omega }}F\left[\mathbf{w},u\right]\mathbb{P}\left[u\right]\hspace{0.17em}du,$$

where $\mathbb{P}\left[u\right]$ is the componentwise Gaussian probability density function from which $u$ is drawn, with support $\mathrm{\Omega }$. We cannot exactly calculate $F\left[\mathbf{w}\right]$ in this setting; we therefore use the error function described above, which is constructed from 1,000 inputs, providing an estimate of $F\left[\mathbf{w}\right]$.