Muscle-like fatigue-resistant hydrogels by mechanical training

Significance

The combinational muscle-like properties including high fatigue resistance, high strength, superior compliance, and high water content are highly desirable for various applications of soft biomaterials such as hydrogels. These combinational properties, largely attributed to the aligned nanofibrils in natural muscles, have not been achieved in synthetic hydrogels. Here, we propose a strategy of mechanical training to impart hydrogels with an extremely high fatigue threshold (1,250 J/m²) and strength (5.2 MPa), while maintaining a high water content (84 wt %) and a low Young’s modulus (200 kPa), reaching combinational muscle-like properties with aligned nanofibrillar architectures. We further achieve isotropically enhanced properties by three-dimensionally printing the hydrogels into microstructures.

Abstract

Skeletal muscles possess the combinational properties of high fatigue resistance (1,000 J/m²), high strength (1 MPa), low Young’s modulus (100 kPa), and high water content (70 to 80 wt %), which have not been achieved in synthetic hydrogels. The muscle-like properties are highly desirable for hydrogels’ nascent applications in load-bearing artificial tissues and soft devices. Here, we propose a strategy of mechanical training to achieve the aligned nanofibrillar architectures of skeletal muscles in synthetic hydrogels, resulting in the combinational muscle-like properties. These properties are obtained through the training-induced alignment of nanofibrils, without additional chemical modifications or additives. In situ confocal microscopy of the hydrogels’ fracturing processes reveals that the fatigue resistance results from the crack pinning by the aligned nanofibrils, which require much higher energy to fracture than the corresponding amorphous polymer chains. This strategy is particularly applicable for 3D-printed microstructures of hydrogels, in which we can achieve isotropically fatigue-resistant, strong yet compliant properties.

Biological load-bearing tissues such as skeletal muscles commonly show J-shaped stress−strain behaviors with low Young’s modulus and high strength on the order of 100 kPa and 1 MPa, respectively (1, 2). Moreover, despite their high water content of around 75 wt % (3), skeletal muscles can sustain a high stress of 1 MPa over 1 million cycles per year, with a fatigue resistance over 1,000 J/m² (4). The combinational properties of skeletal muscles (i.e., high fatigue resistance, high strength, superior compliance, and high water content) are highly desirable for hydrogels’ nascent applications in soft biological devices, such as load-bearing artificial tissues (5), hydrogel bioelectronics (6–9), hydrogel optical fibers (10, 11), ingestible hydrogel devices (12), robust hydrogel coatings on medical devices (13–17), and hydrogel soft robots (18–20).

Although various molecular and macromolecular engineering approaches have replicated parts of biological muscles’ characteristics, none of them can synergistically replicate all these attributes in one single material system (SI Appendix, Table S1). For example, both strain-stiffening hydrogels (21, 22) and bottle brush polymer networks (1, 23) can mimic the J-shaped stress−strain behaviors, but their fracture toughness is still much lower than biological tissues, since no significant mechanical dissipation has been introduced in these materials for toughness enhancement. Although various tough hydrogels (24–26) have been developed by incorporating various dissipation mechanisms, they are susceptible to fatigue fracture under repeated mechanical loads, since the resistance to fatigue crack propagation after prolonged repeated mechanical loads is the energy required to fracture a single layer of polymer chains, unaffected by the additional dissipation (27). Recently, introduction of well-controlled nanocrystalline domains (28) has been shown to substantially increase a hydrogel’s fatigue threshold (i.e., the minimal fracture energy at which crack propagation occurs under cyclic loads), but the growth of nanocrystalline domains consumes interstitial amorphous polymer chains and therefore increases the Young’s modulus and reduces the water content of the hydrogel.

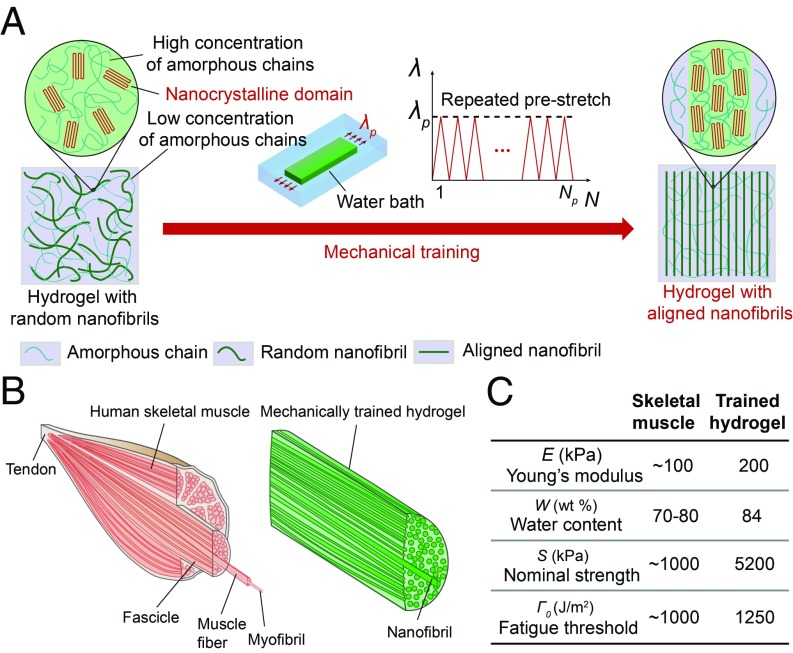
Here, we propose a strategy to achieve the combinational muscle-like properties in synthetic hydrogels via mechanical training (Fig. 1A). Using freeze-thawed polyvinyl alcohol (PVA) hydrogel as a model material, we successfully mimic the aligned nanofibrillar architectures in skeletal muscles (Fig. 1B). The developed hydrogels by mechanical training can achieve an extremely high fatigue threshold (1,250 J/m²) and nominal tensile strength (5.2 MPa), while maintaining a high water content (84 wt %) and low Young’s modulus (200 kPa), reaching combinational muscle-level properties (29) (Fig. 1C). In situ confocal microscopy of the hydrogels’ fracturing processes reveals that the fatigue-resistant (or anti–fatigue-fracture, endurant) mechanism for the hydrogels is the crack pinning by the aligned nanofibrils, which require much higher energy to fracture than the corresponding amorphous polymer chains. In situ X-ray scattering of the hydrogels under elongation further reveals that the low Young’s modulus of the hydrogels is attributed to the stretching of polymer chains, orientation of nanocrystalline domains, and sliding of aligned nanofibrils under moderate stretches.

Fig. 1.

Design of muscle-like hydrogels. (A) Schematic illustration of the microstructure of a PVA hydrogel with randomly oriented nanofibrils before mechanical training and a PVA hydrogel with aligned nanofibrils after mechanical training (i.e., cyclic prestretches). (B) Similar aligned nanofibrillar architectures of human skeletal muscles and mechanically trained hydrogels. (C) Comparison of combinational properties of human skeletal muscle and mechanically trained hydrogel.

Results

Design of Muscle-Like Hydrogels.

Fig. 1A schematically illustrates our strategy to design synthetic hydrogels with combinational properties comparable to skeletal muscles. The strategy first involves growing compliant nanofibrils in PVA hydrogels by forming two separated phases (30): (i) high concentration of polymer chains in the form of nanofibrils cross-linked by nanocrystalline domains and (ii) low concentration of amorphous polymer chains. PVA polymer chains possess abundant hydroxyl side groups, which can readily form intrachain/interchain hydrogen bonding. Upon exposure to a low temperature below freezing (i.e., −20 °C), the water freezes and forms ice crystals that can expel PVA chains to form regions of high polymer concentrations. As the PVA chains come into close contact with each other, nanocrystalline domains nucleate with the formation of hydrogen bonds (30–32). These interactions (i.e., hydrogen bonding) remain intact in the subsequent thawing process, leading to a physically cross-linked network of nanofibrils. The dendritic growth of ice crystals further leads to a random distribution of these nanofibrils (33). The process of freezing and thawing is repeated for five cycles to grow sufficient nanofibrils.

To form the aligned nanofibrillar structures, the pristine freeze-thawed hydrogels with randomly distributed nanofibrils are exposed to repeated prestretches in a water bath as mechanical training, similar to the exercise of skeletal muscles. Under repeated exercise, skeletal muscles get strengthened by self-growing, accompanied by the disruption of the nanofibrillar structures in skeletal muscle and growth of new muscle nanofibrils (34). Similarly, repeated prestretches applied on the hydrogels with randomly distributed nanofibrils are accompanied by the disruption of randomly oriented nanocrystalline domains, followed by gradual alignment of nanofibrils with newly formed aligned nanocrystalline domains (35). One merit of our training strategy is that it does not require any extra supply of building blocks (i.e., monomers) during the mechanical training (36).

Random and Aligned Nanofibrillar Structures.

We first use confocal laser scanning microscopy to visualize the nanofibrils in the pristine freeze-thawed PVA hydrogel. Fluorochromes are conjugated to the PVA macromolecules by immersing the freeze-thawed hydrogels in a reactive dye solution (37) (SI Appendix, Fig. S1). With the conjugated fluorochromes, the PVA-rich phases are visible in green in the form of randomly distributed nanofibrils (Fig. 2A), while regions with relatively low concentrations of PVA polymers (i.e., water-rich phase between adjacent nanofibrils) are dark. As a control, the chemically cross-linked PVA hydrogel shows green luminance with uniform brightness, indicating the uniform distribution of PVA amorphous chains (SI Appendix, Fig. S2).

Fig. 2.

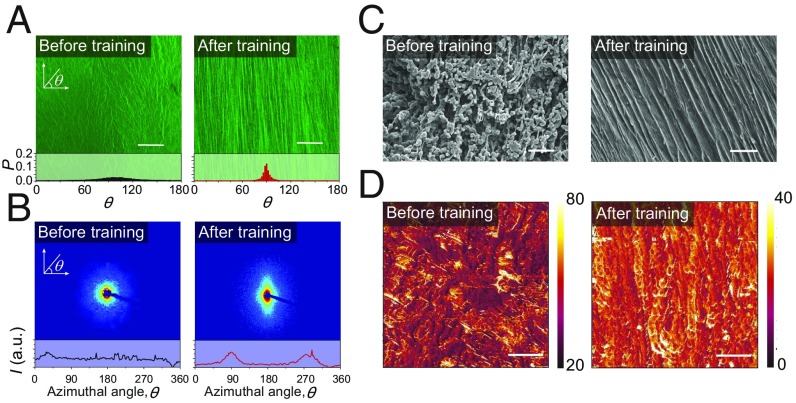
Microstructures of PVA hydrogels before and after mechanical training. (A) Confocal images and corresponding histograms of a hydrogel with randomly oriented nanofibrils before training (i.e., freeze-thawed PVA) and a hydrogel with aligned nanofibrils after training (i.e., prestretched PVA). P in the histograms represents the probability of nanofibrils at each aligned direction θ. (Scale bar: 50 µm.) (B) SAXS patterns and corresponding scattering intensity I vs. azimuthal angle θ curve of a hydrogel with randomly oriented nanofibrils before training (i.e., freeze-thawed PVA) and hydrogel with aligned nanofibrils after training (i.e., prestretched PVA); a.u., arbitrary units. (C) SEM images of a hydrogel with randomly oriented nanofibrils before training (i.e., freeze-thawed PVA) and a hydrogel with aligned nanofibrils after training (i.e., prestretched PVA). [Scale bars: 20 µm (Left), 10 µm (Right).] (D) AFM phase images of a hydrogel with randomly oriented nanofibrils before training (i.e., freeze-thawed PVA) and a hydrogel with aligned nanofibrils after training (i.e., prestretched PVA). (Scale bar: 100 nm.)

We next show that the freeze-thawed PVA hydrogel can form aligned nanofibrillar structures by repeated prestretches in a water bath (Fig. 2A and SI Appendix, Fig. S3A). The confocal images of the prestretched PVA hydrogel in Fig. 2A and SI Appendix, Fig. S3 confirm that the randomly distributed nanofibrils gradually reorient and align toward the direction of the applied prestretches. It is noted that, once the first cycle of prestretch is relaxed, the aligned nanofibrils mostly recover their previous random distribution elastically (SI Appendix, Fig. S4). As the cycle number increases, plastic deformation accumulates in the hydrogel, which gradually elongates along the prestretched direction, and finally preserves the alignment (SI Appendix, Fig. S5). The alignment of nanofibrils reaches a steady state after sufficient cycles of prestretches (i.e., 1,000 cycles of prestretches of 4.6). The alignment of the nanofibrils in the prestretched PVA hydrogels is also validated through scanning electron microscopy (SEM) images (Fig. 2C) and atomic force microscopy (AFM) phase images (Fig. 2D). Small angle X-ray scanning (SAXS) patterns (Fig. 2B) further reveal that the nanocrystalline domains in nanofibrils have been reoriented during the prestretches. In addition, the measured diameters of the nanofibrils range from ∼100 nm to ∼1 µm (Fig. 2 A and C and SI Appendix, Fig. S6).

Existing approaches to introduce ordered nanocrystalline domains and aligned structures in hydrogels include cold-drawing (38), prestretching in air (39), and constrained air-drying (40), which fail to retain their original high water contents, due to the formation of additional excessive nanocrystalline domains. By contrast, the prestretched PVA hydrogel obtained from our strategy can still maintain a high water content of 84 wt % (Fig. 3C), close to the pristine freeze-thawed PVA samples (88 wt %). The differential scanning calorimetry results further show that the crystallinity in the swollen state of the prestretched PVA hydrogel is only 2.8 wt % (SI Appendix, Fig. S8), slightly higher than the pristine freeze-thawed PVA hydrogel (1.8 wt %) (Fig. 3C). The slightly increased crystallinity could be attributed to the newly formed nanocrystalline domains during the nanofibrillar alignments under cyclic prestretches (41). Both high water content and low crystallinity in our prestretched PVA hydrogel indicate that our strategy could substantially suppress the undesirable excessive crystallization while maintaining water content and compliance of the hydrogels.

Fig. 3.

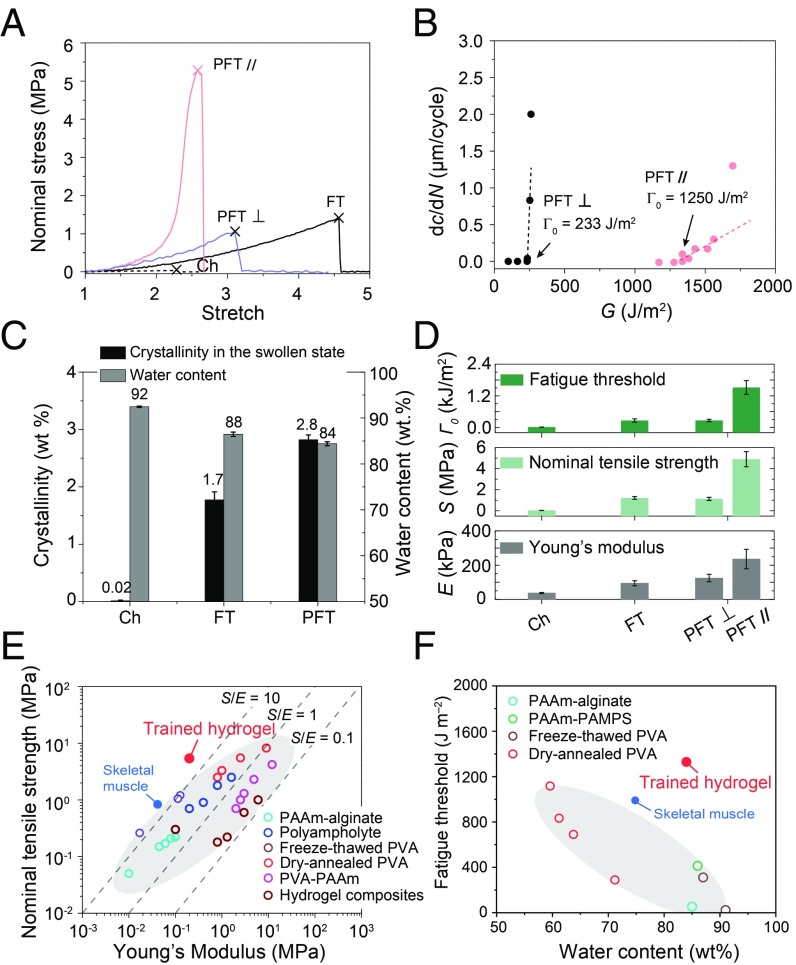
Mechanical properties of PVA hydrogels before and after mechanical training. (A) Nominal stress versus stretch curves of chemically cross-linked (Ch), freeze-thawed (FT), and prestretched PVA hydrogels parallel to (PFT //) and perpendicular to (PFT ⊥) nanofibrils. The X mark indicates the point of fracture. (B) Crack extension per cycle dc/dN versus applied energy release rate G of prestretched PVA hydrogels parallel to (PFT //) and perpendicular to (PFT ⊥) nanofibrils. (C) Summarized water contents and crystallinities in the swollen state of chemically cross-linked PVA (Ch), freeze-thawed PVA (FT), and prestretched PVA (PFT). (D) Summarized Young’s moduli E, ultimate nominal tensile strengths S, and fatigue thresholds ${\mathrm{\Gamma }}_0$ of chemically cross-linked (Ch), freeze-thawed (FT) and prestretched PVA hydrogels parallel to (PFT //) and perpendicular to (PFT ⊥) nanofibrils. (E) Comparison chart in the plot of nominal tensile strengths and Young’s moduli among tough hydrogels [e.g., PAAm-alginate (24), polyampholyte (47), freeze-thawed PVA (28), dry-annealed PVA (28), PVA-PAAm (48), and hydrogel composites (51)], biological tissues [e.g., skeletal muscle (1, 2)], and trained hydrogel (i.e., prestretched PVA). The dashed lines denote the linear relation between strength and modulus with strength−modulus ratio S/E of 0.1, 1, and 10. (F) Comparison chart in the plot of fatigue thresholds and water contents among tough hydrogels (44) [e.g., PAAm-alginate, PAAm-poly(2-acrylamido-2-methylpropanesulfonic acid) (PAMPS), freeze-thawed PVA] and nanocrystalline hydrogels (e.g., dry-annealed PVA) (28), biological tissues (e.g., skeletal muscle), and trained hydrogel (i.e., prestretched PVA). Data in C and D are means ± SD, n = 3.

Combinational Muscle-Like Properties.

We further demonstrate the combinational muscle-like mechanical properties in the prestretched PVA hydrogel (Fig. 3). At small stretches, the prestretched PVA hydrogel demonstrates a low Young’s modulus along directions both parallel (210 kPa) and perpendicular (140 kPa) to the aligned nanofibrils, similar to the pristine freeze-thawed PVA hydrogel (100 kPa) (Fig. 3 A and D). At high stretches, the prestretched PVA hydrogel stiffens drastically parallel to the aligned nanofibrils, exhibiting a J-shaped stress versus stretch curve, similar to that of skeletal muscles (1). In addition, the prestretched PVA hydrogel shows an extremely high ultimate nominal tensile strength of 5.2 MPa parallel to the aligned nanofibrils, which is 4.3 times the pristine freeze-thawed hydrogel’s strength (1.2 MPa) and 26 times the chemically cross-linked hydrogel’s strength (0.2 MPa) (Fig. 3 A and D). The ultimate nominal tensile strength of the prestretched PVA hydrogel perpendicular to nanofibrils is measured to be 1.1 MPa, close to the value of the pristine freeze-thawed hydrogel (i.e., 1.2 MPa). The prestretched PVA hydrogel also shows high resilience with negligible hysteresis when stretched along the aligned nanofibrils (SI Appendix, Fig. S9). The fatigue threshold of the prestretched PVA hydrogel measured along the aligned nanofibrils reaches a record-high value of 1,250 J/m² (Fig. 3B), orders of magnitude higher than those of existing tough hydrogels (∼10 J/m² to ∼100 J/m²) (42–44). To validate the high fatigue threshold of the prestretched PVA hydrogels parallel to the aligned nanofibrils, we also apply cyclic loads on a single-notch tensile specimen with an energy release rate of 1,250 J/m² and observe no crack extension over 30,000 cycles (SI Appendix, Fig. S10). Note that the resolution of measured dc/dN to determine this fatigue threshold is on the same order as the resolution in previous measurements of rubbers’ fatigue thresholds (27). By contrast, the fatigue threshold perpendicular to the aligned nanofibrils is 233 J/m², which is on the same order as that of the pristine freeze-thawed PVA hydrogel (i.e., 310 J/m²; SI Appendix, Fig. S11), but still much larger than that of the chemically cross-linked PVA hydrogel (i.e., 10 J/m²; SI Appendix, Fig. S11).

To compare our results with existing hydrogels and biological tissues, we summarize the nominal tensile strengths, Young’s moduli, fatigue thresholds, and water contents of various tough hydrogels (24, 25, 28, 40, 45–49) and biological tissues (1) in Fig. 3 E and F. The strength−modulus ratios S/E of existing tough hydrogels such as PAAm-alginate (24), PVA-PAAm (48), dry annealed PVA (28), freeze-thawed PVA (50), polyampholyte hydrogels (47), fiber-reinforced hydrogel composites (45, 51), wood hydrogels (46), and constrained air-drying hydrogels (40) are in the range of 0.1 to 10 (Fig. 3E). Remarkably, the strength−modulus ratio S/E of the prestretched PVA hydrogel is as high as 50, since the high strength of the prestretched PVA hydrogel is accompanied by its low Young’s modulus.

In addition to the challenge of designing synthetic hydrogels with superior compliance and high strength, the combinational properties of high fatigue threshold and high water content have not been achieved in existing hydrogels (Fig. 3F). By following our strategy, the fatigue threshold of the prestretched PVA hydrogel can achieve a high value of 1,250 J/m² along with a high water content of 84 wt %, outperforming existing hydrogels and biological tissues.

Mechanisms for Superior Compliance.

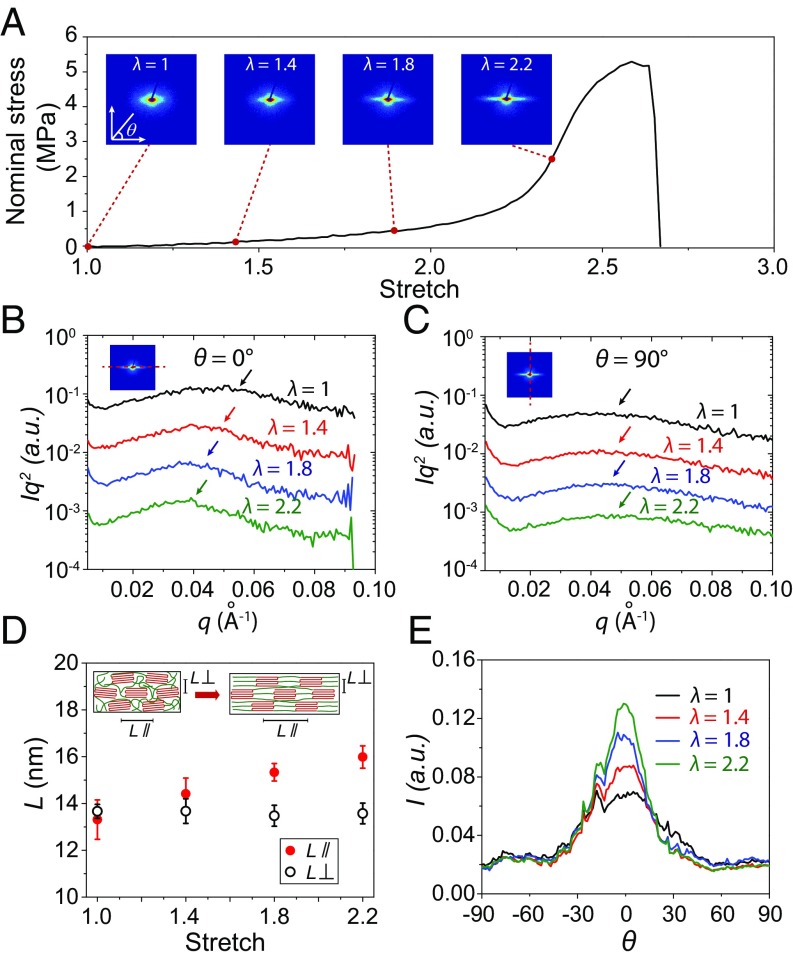
In situ SAXS measurements offer insights into the mechanisms for the superior compliance of the prestretched PVA hydrogel at small deformations (Fig. 4A). The nanocrystalline morphology in the prestretched PVA hydrogel (in the swollen state) is investigated by SAXS analysis at the applied stretch of 1, 1.4, 1.8, and 2.2. As shown in Fig. 4 B and D, the average distance between neighboring nanocrystalline domains parallel to aligned nanofibrils L∥ (i.e., θ = 0°) for the prestretched PVA hydrogel at undeformed state (i.e., λ = 1) is estimated to be 13.2 nm. As the applied stretch increases to 2.2, the average distance between neighboring nanocrystalline domains increases to 15.5 nm (Fig. 4D), which indicates the stretching of interstitial amorphous chains between the adjacent nanocrystalline domains in the nanofibrils. Since the stretch ratio of interstitial amorphous chains (e.g., 15.5 nm/13.2 nm) is much lower than the corresponding applied stretch (e.g., 2.2), sliding between nanofibrils may also occur during stretching. In comparison, the scattering curves show negligible difference at different stretches perpendicular to the aligned nanofibrils L⊥ (i.e., θ = 90°) (Fig. 4C), which implies the average distance between neighboring nanocrystalline domains perpendicular to the aligned nanofibrils L⊥ (i.e., θ = 90°) remains constant with negligible lateral contraction as the stretch increases.

Fig. 4.

Mechanisms for high compliance of prestretched PVA hydrogel with aligned nanofibrils. (A) Nominal stress versus stretch curve of prestretched PVA hydrogel with aligned nanofibrils and corresponding SAXS pattern at the stretch of 1, 1.4, 1.8, and 2.2. (B) The corrected scattering intensity Iq² versus vector q parallel to nanofibrils (i.e., θ = 0°) of prestretched PVA hydrogel at the stretch of 1, 1.4, 1.8, and 2.2. (C) The corrected scattering intensity Iq² versus vector q perpendicular to nanofibrils (i.e., θ = 90°) of prestretched PVA hydrogel at the stretch of 1, 1.4, 1.8, and 2.2. (D) Calculated average distance between adjacent nanocrystalline domains of prestretched PVA hydrogel parallel to nanofibrils L// (i.e., θ = 0°) and perpendicular to nanofibrils L⊥ (i.e., θ = 90°) at the stretch of 1, 1.4, 1.8, and 2.2. The Inset schematic of nanofibrils illustrates the average distance between adjacent nanocrystalline domains parallel to nanofibrils L//and perpendicuar to nanofibrils L⊥. (E) The measured scattering intensity I vs. Azimuthal angle θ curves of prestretched PVA hydrogel at the stretch of 1, 1.4, 1.8, and 2.2. Data in D are means ± SD, n = 3. The dashed red lines in Inset scattering pattern in B and C indicate the direction parallel to nanofibrils and perpendicular to nanofibrils, respectively.

We further plot the scattering intensity I versus direction θ to quantify the degree of orientation of nanocrystalline domains during stretching (Fig. 4E). At the undeformed state (i.e., λ = 1), there are peaks along the prestretched direction (i.e., θ = 0°), implying that the orientation of nanocrystalline domains along the prestretched direction exists in the undeformed sample. As the applied stretch increases, the peaks along the prestretched direction (i.e., θ = 0°) become more pronounced, indicating that the applied stretch can drive additional orientation of nanocrystalline domains. Overall, the stretching of interstitial amorphous chains, orientation of nanocrystalline domains, and sliding between nanofibrils account for the superior compliance of the prestretched PVA hydrogel at moderate deformations along the aligned nanofibrils.

Furthermore, the high compliance of the pristine freeze-thawed PVA hydrogel and the prestretched PVA hydrogel stretched perpendicularly to the aligned nanofibrils can be attributed to the orientation of randomly distributed nanofibrils and the stretching of amorphous polymer chains between adjacent nanofibrils, respectively.

Mechanisms for High Fatigue Threshold.

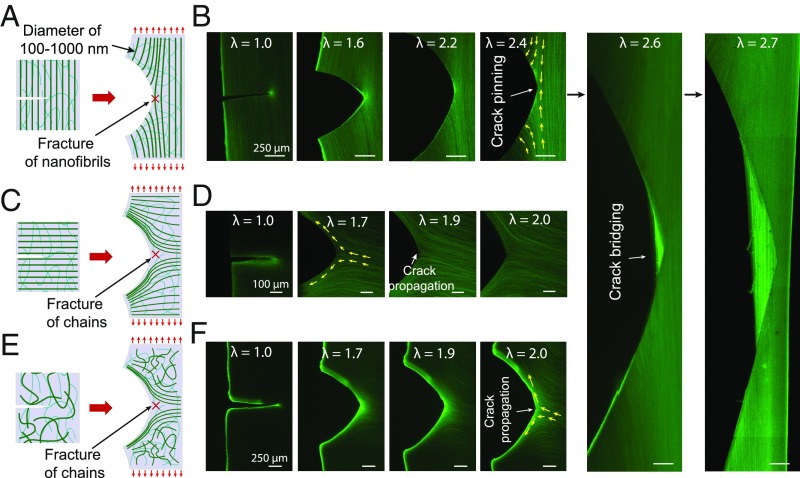
In situ confocal laser scanning microscopy further explains the mechanisms for the high fatigue threshold of the prestretched PVA hydrogel. As shown in Fig. 5 A and B, the aligned nanofibrils are perpendicular to the crack path and pin the crack due to the high strength of the nanofibrils. There is no observable crack propagation at the applied stretch of 2.4. As the applied stretch further increases to 2.6, the nanofibrils at the crack tip are pulled out from the hydrogel but still bridge the crack tip. As the crack propagates, the rupture of the nanofibrils requires a much higher energy per unit area than fracturing the corresponding amorphous polymer chains, giving rise to a much higher fatigue threshold (1,250 J/m²) than that of the amorphous polymer networks (10 J/m²). Notably, the crack pinned by the aligned nanofibrils does not branch or tilt under high static and cyclic loads (e.g., Fig. 5B and SI Appendix, Fig. S10), assuring the hydrogel’s high fatigue threshold. By contrast, crack branching and tilting has been observed in hydrogels reinforced by microscale phase separation (52) and in elastomers reinforced by macroscale fibers (53). It will be interesting to study the effects of the reinforcements across different length scales in future.

Fig. 5.

Mechanisms for high fatigue threshold of prestretched PVA hydrogel with aligned nanofibrils. Schematic illustration of nanofibril morphology in (A) notched prestretched PVA hydrogel where crack is perpendicular to the longitudinal direction of nanofibrils, (C) notched prestretched PVA hydrogel where crack is parallel to the longitudinal direction of nanofibrils, and (E) freeze-thawed PVA hydrogel. Corresponding confocal images of notched samples under different stretches for (B) prestretched PVA hydrogel where crack is perpendicular to the longitudinal direction of nanofibrils, (D) prestretched PVA hydrogel where crack is parallel to the longitudinal direction of nanofibrils, and (F) freeze-thawed PVA hydrogel. The yellow arrows in confocal images indicate the direction of aligned nanofibrils around crack tip. (Scale bars: B, 250 µm; D, 100 µm; F, 250 µm.)

When the crack is parallel to the aligned nanofibrils, the crack begins to propagate in between neighboring nanofibrils at the applied stretch of 1.5, fracturing interstitial amorphous chains between the adjacent nanofibrils (Fig. 5 C and D). Similarly, in pristine freeze-thawed PVA hydrogel, the initially randomly oriented nanofibrils gradually align parallel to the crack contour with the increase of the applied stretch, followed by fracturing interstitial amorphous chains (Fig. 5 E and F). In addition, due to the very long amorphous chains between the adjacent nanofibrils (27), the fatigue thresholds of the pristine freeze-thawed PVA hydrogel and the prestretched PVA hydrogel with a crack along the aligned nanofibrils are still moderately high (310 J/m² and 233 J/m², respectively; SI Appendix, Fig. S11).

Three-Dimensional Printing of Isotropically Fatigue-Resistant, Strong yet Compliant Micromeshes.

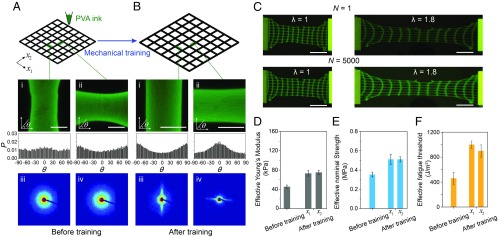
The aligned nanofibrils give notably anisotropic mechanical behaviors of the prestretched PVA hydrogel, similar to that of skeletal muscles. However, for many applications, it is desirable to achieve isotropically muscle-level properties. Here, we propose to three-dimensionally print microstructures of hydrogels and mechanically train the structures to achieve fatigue-resistant, strong yet compliant properties in both in-plane directions. To demonstrate such potential, we develop PVA ink and print microstructures with square meshes as shown in SI Appendix, Fig. S12A. The confocal image of the 3D-printed PVA filaments with a diameter of 750 µm shows random distributions of nanofibrils before mechanical training (Fig. 6A and SI Appendix, Fig. S12B). During mechanical training, the printed microstructure undergoes biaxial cyclic prestretches in a water bath (i.e., prestretch of 3.5 over 1,000 cycles). The trained PVA filaments with a reduced diameter of 500 µm (SI Appendix, Fig. S12B) show pronounced alignments of nanofibrils along the filaments from the confocal images and the SAXS patterns (Fig. 6B). We further measure the effective nominal stress (i.e., the force divided by the cross-sectional area of the microstructure) versus stretch of the PVA mesh before and after training. The effective Young’s moduli of the prestretched mesh along both in-plane directions are measured to be 70 kPa, which is slightly higher than that of the pristine mesh (Fig. 6D). The effective nominal strength of the prestretched mesh along both in-plane directions is measured to be 500 kPa, which is 1.5 times higher than that of the pristine mesh (Fig. 6E). We further apply cyclic loads on both meshes before and after training with a notch (Fig. 6C), evaluating their effective fatigue thresholds (i.e., the minimal energy release rate at which crack propagation occurs in the mesh under cyclic loads). The effective fatigue threshold of the prestretched mesh after training reaches 1,000 J/m² in both in-plane directions, 2 times higher than that of the pristine mesh (Fig. 6F).

Fig. 6.

Isotropically fatigue-resistant, strong yet compliant microstructures of PVA hydrogels by 3D printing and mechanical training. (A) Morphology characterization of 3D-printed freeze-thawed PVA mesh before mechanical training: i and ii are confocal images and histograms for filaments along both in-plane directions; iii and iv are SAXS patterns in filaments along both in-plane directions. (Scale bar, 250 µm.) (B) Morphology characterization of 3D-printed freeze-thawed PVA mesh after mechanical training: i and ii are confocal images and histograms for filaments along both in-plane directions; iii and iv are SAXS patterns in filaments along both in-plane directions. (Scale bar, 250 µm.) (C) Images of mechanically trained mesh with a precrack at the stretch of 1.0 and 1.8 under the first cycle and the 5,000th cycle of loads. (Scale bar: 1 cm.) (D) Effective Young’s moduli, (E) effective nominal tensile strengths, and (F) effective fatigue thresholds of PVA mesh before and after mechanical training. P in the histograms in A and B represents the probability of nanofibrils at each aligned direction θ.

Conclusions

The classical Lake−Thomas theory predicts that the fatigue threshold of a polymer network is the energy required to fracture a single layer of amorphous polymer chains, on the order of 1 J/m² to 100 J/m² (27, 54). We have proposed that the design principle for fatigue-resistant (or anti–fatigue-fracture, endurant) hydrogels is to make the fatigue crack encounter and fracture objects requiring energies per unit area much higher than that for fracturing a single layer of amorphous polymer chains (28). We have shown that high densities of nanocrystalline domains in hydrogels can act as the high-energy phase to effectively pin fatigue cracks and greatly enhance the fatigue threshold of nanocrystalline hydrogel up to 1,000 J/m², exceeding the Lake−Thomas limit (28). However, the nanocrystalline domains also significantly increase the Young’s modulus of the hydrogel, due to nanocrystalline domains’ high rigidity over 1 GPa (28).

While a much higher energy is also required to fracture nanofibrils than the corresponding amorphous polymer chains, the rigidity of nanofibrils under moderate stretches can be designed to be relatively low (55). In this paper, we further establish that aligning these nanofibrils in hydrogels by mechanical training can empower the integration of muscle-like performances, i.e., high fatigue threshold (1,250 J/m²), high strength (5.2 MPa), low Young’s modulus (200 kPa), and high water content (84 wt %), into one single hydrogel material. In addition, we achieve isotropically enhanced properties by three-dimensionally printing the hydrogel into microstructures followed by mechanical training. The capability of making strong, fatigue-resistant yet soft hydrogels can enable various biomedical applications that interact with the human body for long-lasting performances. This work also opens an avenue to mechanically engineer alignments of nanofibrils and orientations of nanocrystalline domains in hydrogels.

Methods

All details associated with sample preparations, in situ confocal imaging, in situ X-ray scattering, SEM imaging, AFM phase imaging, mechanical characterization, measurement of water content and crystallinity, and 3D printing of PVA meshes appear in SI Appendix.

Material Preparation.

The freeze-thawed PVA was fabricated by freezing 10 wt % of PVA solution at −20 °C for 8 h and thawing at 25 °C for 3 h with five repeated cycles. The mechanically trained PVA hydrogel was fabricated by cyclically prestretching the freeze-thawed hydrogel in a water bath using a mechanical stretcher (Cellscale).

Confocal Imaging of PVA Hydrogels.

To visualize the microstructures of the PVA hydrogels, a fluorescent dye {i.e., 5-[(4,6-dichlorotriazin-2-yl)amino]fluorescein hydrochloride [5-DTAF]} was used to label the PVA side groups. Specifically, PVA hydrogel samples were first immersed in a large volume of sodium bicarbonate solution (0.1 M, pH 9.0) for 12 h to equilibrate the pH within the samples. Then 5 mg of 5-DTAF dissolved in 1.0 mL of anhydrous dimethyl sulfoxide was further immersed into 100 mL of sodium bicarbonate solution (0.1 M, pH 9.0) to form a reactive dye solution. The pH-equilibrated PVA samples were immersed in the dye solution for 12 h at 4 °C in a dark environment to form conjugated fluorochromes. Finally, the hydrogel samples were rinsed several times with deionized water to wash away the nonconjugated dyes, before fluorescence imaging.

Mechanical Characterization.

All of the mechanical tests were performed using a U-stretch testing device (Cellscale) at a deformation rate of 0.3/s. Young’s modulus, strength, and fatigue threshold were measured in a water bath to prevent dehydration, following the method established in ref. 28.

Three-Dimensional Printing of PVA Hydrogels.

The prepared PVA inks were stored in 5-mL syringe barrels, which fit nozzles with diameters of 400 µm (Nordson EFD). To achieve stable and optimal printing, we chose 50 kPa of air pressure (Ultimus V; Nordson EFD) as the printing pressure, and 15 wt % PVA (146 kDa, 99% hydrolysis ratio) as the ink. After deposition, the printed samples were treated by five cycles of freezing (−20 °C for 8 h) and thawing (20 °C for 3 h) to achieve the final PVA hydrogel meshes.