Abstract
The position and orientation of the mitotic spindle is precisely regulated to ensure the accurate partition of the cytoplasm between daughter cells and the correct localization of the daughters within growing tissue. Using magnetic tweezers to perturb the position of the spindle in intact cells, we discovered a force-generating machinery that maintains the spindle at the cell center during metaphase and anaphase in one- and two-cell C. elegans embryos. The forces increase with the number of microtubules and are larger in smaller cells. The machinery is rigid enough to suppress thermal fluctuations to ensure precise localization of the mitotic spindle, yet compliant enough to allow molecular force generators to fine-tune the position of the mitotic spindle to facilitate asymmetric division.
The position and orientation of the mitotic spindle determines the plane of cell division, which, in turn, determines how the cytoplasmic contents are partitioned to the daughter cells (1), and how the daughter cells are localized within the tissue (2). After the spindle reaches the cell center prior to metaphase, its position and orientation must be precisely maintained (3) until the cell enters anaphase. The molecular forces underlying the maintenance of spindle position and orientation are not known.
Although much is known about how force is generated by purified proteins (4) and in cell extracts (5), little is understood about how molecular forces are integrated in vivo to serve complex cellular processes such as spindle positioning. This is due to the difficulties of exerting and measuring forces in intact cells. Indeed, with the exception of the landmark paper by Nicklas in 1983 (6) that measured forces associated with spindle elongation during anaphase, there has been no direct quantitative measurement of forces on mitotic spindles in cells (see 7, 8).
To measure mitotic forces in vivo, we injected 1.0-μm-diameter superparamagnetic beads (9) and used magnetic tweezers (10) to exert calibrated forces of up to 200 pN to mitotic spindles in one- and two-cell C. elegans embryos, a model system for studying mitosis (1) (Figure 1A, Fig. S1–S4 and see Methods). We applied forces of 20–60 pN to the centrosome at one of the spindle’s poles for up to 20 seconds during metaphase, when the spindle is in a relatively quiescent phase at the cell center (Fig. 1A). In response to force, the spindle rotated as the centrosome was displaced up to 3 μm from the anterior-posterior (AP) axis (Fig. 1B–1C; Movie S1). Thus, it was possible to perturb the position and orientation of the spindle using magnetic forces.
Fig. 1. Measurement of spindle centering forces using magnetic tweezers.
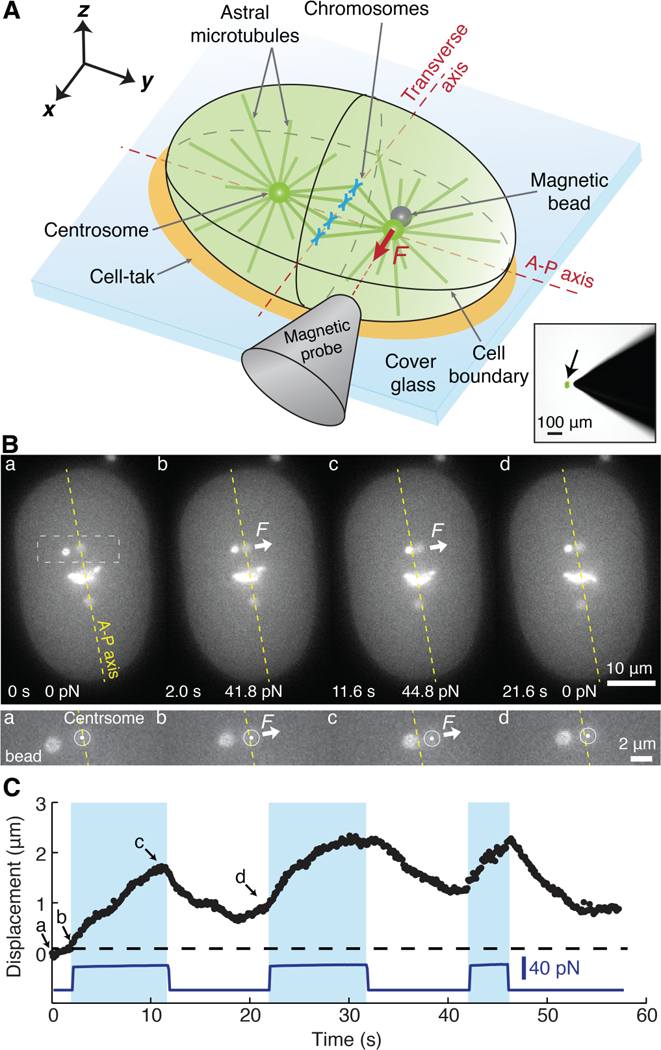
(A) The embryo (green) was glued to a cover glass using cell-tak© (orange). The bead was pulled into the array of the astral microtubules. Lower-right inset: an image of the probe next to an embryo expressing GFP in its cytoplasm (arrow). (B) Top: Video images of spindle displacement following force onset and return following force cessation. Times and forces are indicated on each frame. Bottom: Close up of the displacement. (C) Force and centrosome displacement are plotted against time. The dashed line corresponds to the A-P axis. The letters indicate when the images in B were taken. Blue shaded area indicates when the bead pushed on the centrosome.
The kinetics of spindle displacement indicated that the mitotic spindle is held at the cell center by viscoelastic forces. First, after the onset of the force, the centrosome moved with an approximately constant velocity during the first few seconds (Fig. 2A: average displacement), suggesting that the spindle is subject to viscous forces. Second, the displacement speed decreased after several seconds (Fig. 1C and2A), suggesting that there is an elastic force (i.e. a spring) that opposes the external force. Third, after cessation of the force, the centrosome partially relaxed back towards its initial position (Fig. 1C and2B), suggesting that the elastic element returns part of its stored mechanical energy. Finally, higher external forces were required to displace the centrosome through larger distances, as expected for an elastic element (Fig. S5).
Fig. 2. Viscoelasticity of the centering apparatus during metaphase.
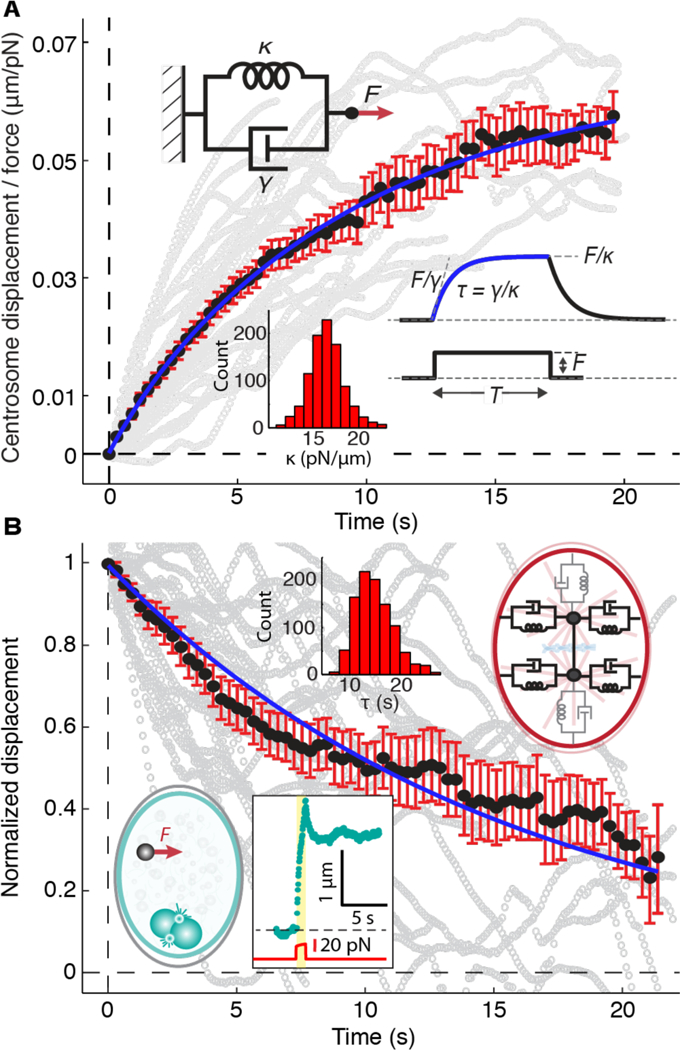
(A) The average movement of the spindle away from the AP axis in response to external forces (black circles). 34 displacement traces from 27 cells were averaged and scaled by the force, F(t). The gray traces in the background are the individual traces, smoothed using an 11-point window. The blue curve is x(t)/F(t) = (1/κ)(1 – exp (–tκ/γ), where κ is the stiffness and γ is the drag coefficient of a Voigt element (upper inset). (B) The average relaxation of the spindle back towards the AP axis following cessation of the force (black circles) superimposed on individual traces (gray). The blue curve is x(t) / x(0) = exp(–t / τ). The left inset shows the rising and relaxation phases of a 1.0 μm bead in the cytoplasm (see Fig. S6). The right inset shows a model comprising six Voigt elements; the four that were probed in the experiments shown in A and B are indicated in black. Histograms show parameter values obtained by bootstrapping. Errors are SEs.
To estimate the stiffness of the elastic element, we fit the spindle’s rising phase (Fig. 2A) with a Voigt model (Fig. 2A, left inset), in which a spring and a viscous damper are in parallel. A curve fit of the data to the Voigt model gave a stiffness (κ)of 16.4 ± 2.1 pN/μm (Table 1, uncertainties are SEs): 16 pN force on average was needed to displace the centrosome 1 μm from the AP axis. We call the force the centering force and the stiffness the centering stiffness. The drag coefficient (γ) of the damper was 137 ± 27 pN s/μm (Table 1). The associated time constant (κ/γ) was 8.1 ± 1.5 s. The time constant of the relaxation phase was 14.5 ± 2.8 s (Figure 2B, solid red line), longer than the rising phase (see discussion in Supplementary Text). The dynamics of the spindle are very different from the dynamics of beads in the cytoplasm, which relax incompletely and much more quickly (0.65 ± 0.08 s, Fig. 2B, Fig. S6, Movie S2). Thus, a centering machinery opposes motion of the spindle away from the cell center and has viscoelastic properties distinct from those of the cytoplasm.
Table 1.
Stiffness, drag coefficients and time constants under several different conditions.
| Rising phase | Falling phase | ||||||
|---|---|---|---|---|---|---|---|
| Group | n | Stiffness (κ, pN/μm) | Drag (γ, pNs/μm) | τ (s) | n | τ (s) | |
| Metaphase | Control | 34 | 16.4 ± 2.1 | 134 ± 17 | 8.1 ± 1.5 | 27 | 14.5 ± 2.8 |
| gpr-1/2 (all) | 33 | 29.1 ± 3.9 | 174 ± 19 | 6 ± 1 | 25 | 14.3 ± 1.9 | |
| gpr-½ | 10 | 30.6 ± 5.1 | 129 ± 35 | 4.2 ± 1.4 | 9 | 13.7 ± 3.9 | |
| gpr-½+fzy-1 | 23 | 27.7 ± 4.7 | 195 ± 28 | 7.1 ± 1.6 | 21 | 16.3 ± 3 | |
| klp-7 | 6 | 31.4 [24.1 – 44.1]* | 271 [75 – 491]* | 8.6 [3.1 – 11.1]* | 6 | 10.2 ± 1.3 | |
| P1 cell | 18 | 39.6 ± 7 | 137 ± 35 | 3.4 ± 1.1 | 17 | 5.8 ± 2.2 | |
| AB cell | 12 | 35.6 ± 10.5 | 116 ± 43 | 3.3 ± 1.6 | † | ||
| Anaphase | Control | 33 | 91.1 ± 17.9 | 522 ± 100 | 5.7 ± 1.6 | 30 | 4.4 ± 0.9 |
| gpr-½ | 27 | 119.4 ± 21.3 | 389 ± 81 | 3.3 ± 0.9 | 14 | 9.5 ± 3.6 | |
| P1 cell | 11 | 104.8 [43.6 – 178.3]* | 1134 [174 – 1713]* | 10.8 [3.99 – 19.6]* | ‡ | ||
Errors are SEs obtained from bootstrapping.
Values in brackets are 95% confidence intervals for asymmetric bootstrap distributions.
Not measured because the spindle rotated during late metaphase and anaphase.
Not measured because cytokinesis occurred shortly after anaphase onset.
We propose that the centering machinery acts like a set of four damped springs that oppose movements transverse to the AP axis (Fig. 2B, right inset, black). These springs orient the spindle so that when one centrosome is perturbed, the spindle pivots around the other centrosome (Fig. 1B). The machinery ensures that the cleavage plane is perpendicular to the A-P axis during cytokinesis.
As the cell cycle progresses from metaphase through anaphase, several morphological and mechanical changes take place (11–14). Concomitant with these changes, we found that the centering stiffness increased five-fold (Fig. 3A, Table 1, Fig. S7 and Movie S3): during anaphase, forces on the order of 100 pN were required to displace the spindle 1 μm. These forces are similar in magnitude to the forces measured during chromosome segregation by Nicklas in grasshopper cells (6). An increase in the centering force may help to stabilize spindle position against high centrifugal forces occurring the anaphase, such as those driving transverse oscillations (12–14).
Fig. 3. Spindle responses during anaphase in two-cell embryos and after klp-7 RNAi and gpr-½ RNAi.
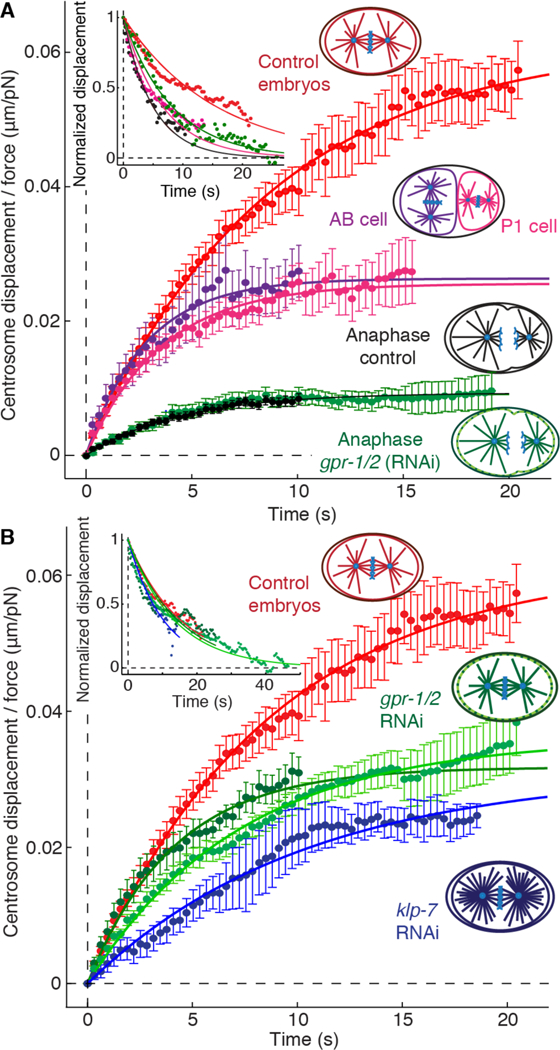
(A) Averaged rising phases during metaphase in one-cell (red) and two-cell (P1, pink; AB, purple) embryos and during anaphase of control (black) and gpr-½(RNAi) (green) embryos. (B) Averaged rising phases in klp-7 (RNAi) (blue), gpr-½ (RNAi) (dark green), gpr-½+fzy-1 (green) and control embryos (red). The solid lines show fits of the Voigt model. Upper left inset shows the corresponding falling phases. Errors are SEs.
Mitotic spindles remain centered throughout C. elegans development, during which cell and spindle size decrease (15). To study the influence of the cell size on the centering force, we performed the force experiments in the smaller cells of the two-cell embryo, P1 and AB (Fig. S7–8 and Movie S4), which have different cytoplasmic and cortical compositions (1). We found that the centering stiffness increased approximately 2-fold in both cells (Table 1), indicating that the relative precision of centering may be independent of cell size and cell type.
Dynein-based cortical force generators, which drive posterior spindle displacement during anaphase (12,14), are not necessary for the initial centration of the spindle (13) but have been proposed to contribute to the maintenance phase (4, 16). To the contrary, we found that the cortical force generators antagonize, rather than augment, the maintenance of centration: the centering stiffness in gpr½ (RNAi) embryos, in which the force generators are inactive, was approximately twice that in control embryos (Fig. 3B, Table 1). Consistent with the destabilizing effect, spindles arrested in metaphase using fzy-1 RNAi (3) were quiescent only when the cortical pulling forces were absent (gpr-½+fzy-1 (RNAi), Fig. S9). The gpr-½+fzy-1 (RNAi) embryos had similar high centering stiffness to gpr-½ (RNAi) embryos and they underwent almost complete recovery of the spindle position after 45s (Fig. 3B inset, Table 1, Fig. S6B and Movie S5), as expected for the Voigt model.
Finally, the centering stiffness did not change in gpr-½ (RNAi) embryos even during anaphase (Fig. 3A), when the cortical forces are strongest (12, 14). Together, these experiments show that the cortical force generators are not required for the maintenance of centration, and suggest instead that the cortical force generators play an anti-centering role, namely the posterior displacement of the spindle that leads to asymmetric division.
We used RNAi to explore the roles of microtubules in the centering machinery. When we increased the number of astral microtubules by RNAi against klp-7 (Fig. S10), which encodes a depolymerizing kinesin, we found that the centering stiffness increased approximately two-fold (Figure 3A, Table 1). Thus, the centering stiffness scales with the number of microtubules. We also found that the number of microtubules reaching the cortex in P1 cells, which have higher centering stiffness, was twice that in one-cell embryos (Fig. S11). Furthermore, the high centering stiffness of embryos during anaphase is associated with a combination of more microtubule nucleation (11) and longer times that microtubule ends remain at the cortex (17) (Fig. S12). Thus, the force-generating machinery appears to depend on microtubules.
The centering machinery is remarkably compliant. Microtubules are among the most rigid cellular polymers (Young’s modulus E ≈2 GPa, (18)) so that even a single microtubule (cross-sectional area A ≈ 200 nm2) spanning between the centrosome and the cortex (R = 15 μm) will have a static compressive stiffness of EA/R ≈ 25,000 pN/μm. This is more than one thousand times larger than the measured centering stiffness, which is associated with an entire microtubule array. This suggests that the centering stiffness is due to dynamical properties such as buckling of microtubules under compression or conversion of growing microtubules to shrinking ones (17, 19).
A dynamic array of astral microtubules that grow out from the centrosome and transiently push against the cortex can account for the centering machinery (17, 19). Such an array has spring-like properties: when the spindle moves away from the center, more microtubules push against the closer cortex as it takes less time for the microtubules to reach the closer cortex. This imbalance generates a net force–the centering force–that directs the spindle back to the cell center. The force imbalance increases with larger displacements away from the cell center, giving rise to spring-like behavior: the centering stiffness (17, 19). The predicted centering stiffness of an ensemble of M pushing microtubules is κ ≈ Mf /R (17, 19), where f ≈ 1 pN is the polymerization force (20) or the buckling force of a 15 μm microtubule (18). A stiffness of 16 pN/μm is therefore consistent with an average of ≈ 200 microtubules in contact with and pushing against the cortex at any time, as observed ((21) and see Methods). This number corresponds to about 10% of the total number of astral microtubules (22). The pushing model accounts for the high centering stiffness of klp-7 RNAi embryos (they have more microtubules) and the higher stiffness of smaller cells (Fig. 3) (they have a higher density of microtubule ends at the cortex, Fig. S11). The model also predicts drag forces: movement of the aster increases the rate of arrival of ends at one cortex and therefore leading to an effective drag force (17). The measured drag coefficient is in quantitative agreement with this prediction (see Supplementary Text). Thus, our results support a model in which microtubule polymerization against the cortex generates the centering force.
In a remarkable adaptation of mechanical properties to cellular function, the magnitudes of the stiffness and damping of the centering machinery are ideally suited for cellular function. A centering spring with stiffness 16 pN/μm is rigid enough to stabilize the spindle against thermal forces: the displacement fluctuations of a spring due to Brownian motion have a standard deviation of √ (kT/κ), which is about 16 nm for the single-cell embryo. Thus, the precision of centration is not limited by thermal fluctuations. Indeed, fluctuations from other sources, such as stochastic variation in the number of force generators (i.e. microtubules) with an expected standard deviation of R/√M ≈ 1000 nm (17), are expected to exceed the thermal fluctuations.
On the other hand, the centering spring is compliant enough to allow adjustments of spindle position by a small number of motor proteins. During metaphase, the spindle moves through d ≈ 3 μm along the AP axis into the posterior half of the embryo to set up asymmetric cell division (3). If the centering stiffness is similar along the AP axis as transverse to it (Fig. 2B, gray springs), which is reasonable given the symmetry of the microtubule asters, then such a posterior displacement requires a force imbalance of κd ≈ 50 pN. This could be exerted by as few as 10–20 cortical force generators (14). The drag coefficient is also well adapted. If it were much lower, then transient force imbalances due to motor stochasticity would not be smoothed out; if it were much higher, then it would prevent posterior displacement from being completed on the minute timescale.
In conclusion, a force-generating centration apparatus with spring-like properties maintains the spindle at the cell center. The centering stiffness is high enough to ensure the precise maintenance of spindle position against thermal and other fluctuations while spindle assembly is completed and the cell prepares for chromosome segregation. Yet it is low enough to allow force generators to fine-tune the position of the spindle to facilitate asymmetric cell division.
Supplementary Material
Acknowledgments:
We thank J. Alper, A. Hyman, S. Grill, H. Bowne-Anderson and F. Carrillo-Oesterreich for comments on the manuscript and R. Ma, C. Bruchatz, V. Thacker, J. Mücksch and V. Duran for discussion and assistance. CGC was funded by the European network MitoSys project. HF, CGC and JH designed the experiments. HF and CGC performed experiments and analyzed data. CGC and JH wrote the paper. All the authors discussed the results and commented on the manuscript. HF, CGC and JH declare no competing financial interest. We thank the Max Planck Society, Yale University and NIH GM110386 for support.
References and Notes:
- 1.Galli M, Van Den Heuvel S, Annu. Rev. Genet. 42, 389–411 (2008). [DOI] [PubMed] [Google Scholar]
- 2.Gillies TE, Cabernard C, Curr Biol 21, R599–R609 (2011). [DOI] [PubMed] [Google Scholar]
- 3.McCarthy Campbell EK, Werts AD, Goldstein B, Ahringer J, Ed. PLoSBiol. 7, e1000088 (2009). [Google Scholar]
- 4.Laan L et al. , Cell 148, 502–514 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Shimamoto Y, Maeda YT, Ishiwata S, Libchaber AJ, Kapoor TM, Cell 145, 1062–1074 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Nicklas RB, J Cell Biol 97, 542–548 (1983). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Dumont S, Mitchison TJ, Current Biology 19, R749–R761 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.McIntosh JR, Molodtsov MI, Ataullakhanov FI, Q. Rev. Biophys. 45, 147–207 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Daniels BR, Masi BC, Wirtz D, Biophysical Journal 90, 4712–4719 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kollmannsberger P, Fabry B, Rev. Sci. Instrum. 78, 114301 (2007). [DOI] [PubMed] [Google Scholar]
- 11.Srayko M, Kaya A, Stamford J, Hyman AA, Dev Cell 9, 223–236 (2005). [DOI] [PubMed] [Google Scholar]
- 12.Labbé J-C, McCarthy EK, Goldstein B, J Cell Biol 167, 245–256 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Pecreaux J et al. , Current Biology 16, 2111–2122 (2006). [DOI] [PubMed] [Google Scholar]
- 14.Grill SW, Howard J, Schaffer E, Stelzer EHK, Hyman AA, Science 301, 518–521 (2003). [DOI] [PubMed] [Google Scholar]
- 15.Hara Y, Kimura A, Mol Biol Cell 24, 1411–1419 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Grill SW, Hyman AA, Dev Cell 8, 461–465 (2005). [DOI] [PubMed] [Google Scholar]
- 17.Howard J, Phys Biol 3, 54–66 (2006). [DOI] [PubMed] [Google Scholar]
- 18.Gittes F, Mickey B, Nettleton J, Howard J, J Cell Biol 120, 923–934 (1993). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ma R, Laan L, Dogterom M, Pavin N, Jülicher F, New J Phys. 16, 013018 (2014). [Google Scholar]
- 20.Dogterom M, Yurke B, Science 278, 856–860 (1997). [DOI] [PubMed] [Google Scholar]
- 21.Kozlowski C, Srayko M, Nedelec F, Cell 129, 499–510 (2007). [DOI] [PubMed] [Google Scholar]
- 22.Müller-Reichert T, Mäntler J, Srayko M, O’Toole E, J Microsc 230, 297–307 (2008). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


