Summary
Decisions must be implemented through actions, and actions are prone to error. As such, when an expected outcome is not obtained, an individual should not only be sensitive to whether the choice itself was suboptimal, but also whether the action required to indicate that choice was executed successfully. The intelligent assignment of credit to action execution versus action selection has clear ecological utility for the learner. To explore this, we used a modified version of a classic reinforcement learning task in which feedback indicated if negative prediction errors were, or were not, associated with execution errors. Using fMRI, we asked if prediction error computations in the human striatum, a key substrate in reinforcement learning and decision making, are modulated when a failure in action execution results in the negative outcome. Participants were more tolerant of non-rewarded outcomes when these resulted from execution errors versus when execution was successful but reward was withheld. Consistent with this behavior, a model-driven analysis of neural activity revealed an attenuation of the signal associated with negative reward prediction error in the striatum following execution failures. These results converge with other lines of evidence suggesting that prediction errors in the mesostriatal dopamine system integrate high-level information during the evaluation of instantaneous reward outcomes.
eTOC BLURB
Failure to obtain a desired outcome could arise from selecting the wrong action, or errors in executing the correct action. McDougle et al. show that humans are sensitive to this distinction, down-weighting outcomes credited to motor error. Activity in the striatum, a subcortical region critical for reinforcement learning, reflects this behavior.
Introduction
When a desired outcome is not obtained during instrumental learning, the agent should be compelled to learn why. For instance, if an opposing player hits a home run, a baseball pitcher needs to properly assign credit for the negative outcome: The error could have been in the decision about the chosen action (e.g., throwing a curveball rather than a fastball) or the execution of that decision (e.g., letting the curveball break over the plate rather than away from the hitter, as planned). Here we ask if teaching signals in the striatum, a crucial region for reinforcement learning, are sensitive to this dissociation.
The striatum is hypothesized to receive reward prediction error (RPE) signals -- the difference between received and expected rewards -- from midbrain dopamine neurons [1–3]. The most common description of an RPE is as a “model-free” error, computed relative to the scalar value of a particular action, which itself reflects a common currency based on a running average of previous rewards contingent on that action [4]. However, recent work suggests that RPE signals in the striatum can also reflect “model-based” information [5], where the prediction error is based on an internal simulation of future states. Moreover, human striatal RPEs have been shown to be affected by a slew of cognitive factors, including attention [6], episodic memory [7,8], working memory [9], and hierarchical task structure [10]. These results indicate that the information carried in striatal RPEs may be more complex than a straightforward model-free computation, and can be influenced by various top-down processes. The influence of these additional top-down processes may serve the striatal-based learning system by identifying variables or features relevant to the task.
To date, studies examining the neural correlates of decision making have used tasks in which participants indicate their choices with button presses or lever movements, conditions that generally exclude execution errors. As such, the outcome can be assigned to the decision itself (e.g., choosing stimulus A over stimulus B), rather than its implementation (e.g., failing to properly acquire stimulus A). To introduce this latter negative outcome, we have recently conducted behavioral studies in which we modified a classic 2-arm bandit task, requiring participants to indicate their choices by physically reaching to the chosen stimulus under conditions where the arm movement was obscured from direct vision [11,12]. By manipulating the visual feedback available to the participant, we created a series of reward outcomes that matched those provided in a standard button-pressing control condition, but with two types of failed outcomes: “Execution failures” in the reaching task, and “selection errors” in the button press task. The results revealed a strong difference in behavior between the two conditions, manifest as a willingness to choose a stimulus that had a high reward payoff, but low execution success (i.e., participants were tolerant of unrewarded “execution error” trials). By using reinforcement-learning models, we could account for this result as an attenuation in value updating following execution errors relative to selection errors. That is, when reward was withheld due to a salient execution error, participants were unlikely to decrease the value of the stimulus that they had chosen.
This behavioral result is intuitive, but the underlying neural processes are not as clear. One hypothesis is that striatal prediction errors are primarily linked to the economic outcome of actions, and will thus be insensitive to whether a stimulus was properly queried or not. That is, the striatum will respond similarly if the absence of reward is the result of an execution or selection failure. On the other hand, prediction errors in the striatum may be sensitive to the source of the error. Given the results of our behavioral studies, we would expect the response following execution errors to be attenuated relative to selection errors. To test these hypotheses, we used fMRI to measure reward prediction errors in the striatum after both selection and execution errors.
Results
We developed a simple 3-arm “bandit task” in which, during fMRI scanning, the participant had to make a short reaching movement on a digital tablet to indicate their choice on each trial and to attempt to maximize monetary earnings (Figure 1). At the end of the movement, feedback was provided to indicate one of three outcomes, as follows: On Rew+ trials, the visual cursor landed in the selected stimulus (i.e., slot machine) and a money bag indicated that $.10 had been earned. On Rew− trials, the visual cursor landed in the selected stimulus but an X was superimposed over the money bag, indicating that no reward was earned. On Miss trials, the visual cursor was displayed outside the chosen stimulus, and no money was earned. We used a stationary bandit task in which the outcome probabilities associated with each stimulus was fixed for the duration of the experiment. The reward probability for each stimulus (“bandit”) was fixed at 0.4, but the probabilities of Rew− and Miss outcomes varied between the three stimuli (0.5/0.1, 0.3/0.3, 0.1/0.5 respectively; see Methods). To maintain the fixed probabilities for each stimulus, we varied whether the cursor feedback was veridical on a trial-by-trial basis. If the true movement outcome matched the probabilistically determined outcome — either because the participant accurately reached to the stimulus on a Rew+ or Rew− trial, or missed the stimulus on a Miss trial — the cursor position was veridical. However, if the true movement outcome did not match the probabilistically determined outcome, the cursor feedback was perturbed (see Methods). Deterministically controlling the outcomes of the trials was necessary to enforce the fixed outcome probabilities, consistent with prior studies [11,12].
Figure 1: Task Design.
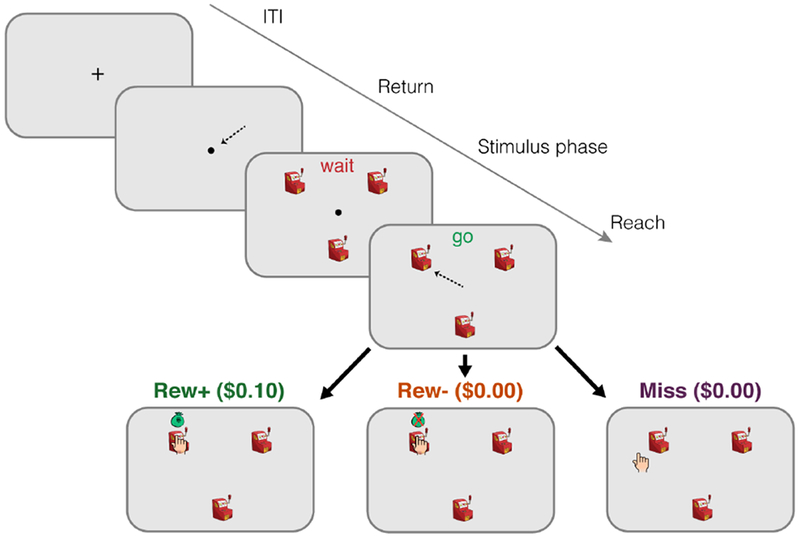
Participants selected one of three choice stimuli (slot machines) on each trial by reaching to one of them using a digital tablet in the fMRI scanner. Three trial outcomes were possible: On Rew+ trials (bottom left, green), the cursor hit the selected stimulus and a monetary reward was received; on Rew− trials (bottom middle, orange), the cursor hit the stimulus but no reward was received; on Miss trials (bottom right, purple), the cursor was shown landing outside the selected stimulus and no reward was received.
Behavior
In previous studies using a similar task, participants showed a bias for stimuli in which unrewarded outcomes were associated with misses (execution errors) rather than expected payoffs (selection errors), even when the expected value for the choices were held equal [11,12]. We hypothesized that this bias reflected a process whereby execution failures lead to attenuated negative prediction errors, with the assumption that “credit” for the negative outcome under such situations was attributed to factors unrelated to the intrinsic value of the chosen action. This behavior was formalized in a reinforcement learning model that included a unique learning rate parameter for each of the three outcomes ([11]; see Methods; Figures S1–S2).
In the current task, a similar bias should lead participants to prefer the high-Miss stimulus (0.5/0.1 ratio of Miss/Rew− outcome probabilities). Although the overall choice data showed only a weak bias over the three choice stimuli (Figure 2A, all ps > 0.11), simulations of the fitted model were in accord with this prediction (Figure 2B).
Figure 2: Behavioral and modeling results.
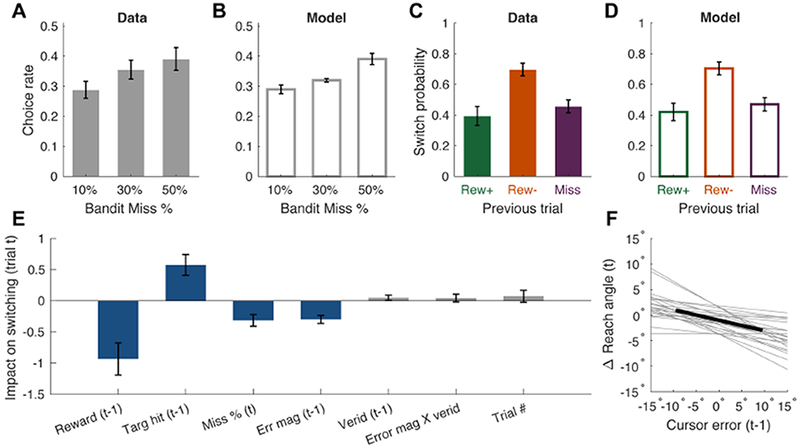
(A) Participants’ biases to select stimuli with different underlying chances of Miss trials. (B) Biases obtained from simulations of the fitted model. (C) Average switch probabilities separated by the outcome of the previous trial. (D) Switch probabilities from simulations of the fitted model. (E) Weights from the logistic regression on switch behavior, with blue bars reflecting statistically significant predictors. (F) Linear regression on change in reach angle as a function of signed cursor errors on the trial previous. This analysis is limited to trials in which the participant’s reach on trial t-1 was accurate, but the cursor was perturbed away from the stimulus (Miss trial). The dark line reflects the mean regression line, light grey lines are individual regression lines. Error bars = 1 s.e.m. See also Table S2 and Figures S1 and S2.
Trial-by-trial switching behavior offers a more detailed way to look at choice biases, as particular probabilistic trial outcomes are taken into account. Participants were more likely to switch to a different choice stimulus following Rew− trials compared to Miss trials (t23 = 5.02, p < 0.001; Figure 2C). Moreover, they were more likely to switch after Rew− trials compared to Rew+ trials (t23 = 4.77, p < 0.001), and showed no difference in switching rate after Rew+ and Miss trials (t23 = 1.32, p = 0.20). Overall, participants were, on average, more likely to switch following a non-rewarded trial (Rew− or Miss) than a rewarded one (Rew+; t23 = 2.97, p = 0.007), suggesting that they were sensitive to receiving a monetary reward from specific choice stimuli, even though the reward lottery was identical for each. Critically, simulations of the RL model replicated participants’ choice switching behavior as well (Figure 2D).
In sum, the switching behavior indicates that participants responded more negatively to Rew− outcomes compared to Miss outcomes, even though both yielded identical economic results. This finding is consistent with the hypothesis that cues suggesting a failure to properly implement a decision may affect how value updates are computed.
A logistic regression analysis was used to probe how various factors influenced switching behavior (Figure 2E). As expected, earning reward on trial t-1 negatively predicted switching on trial t (i.e., predicted staying over switching), reflecting reward sensitivity in the task (t-test for regression weight difference from o: t21 = 3.48, p = 0.002). In contrast, hitting the stimulus on trial t-1 had a positive impact on the probability of switching on trial t, driven by the aversive Rew− trials (t21 = 3.32, p = 0.003). Both effects were tempered by the Miss trials, which led to reduced switching (Figure 2C). Consistent with Figure 2A, the Miss probability regression coefficient negatively predicted switching (t21 = 3.23, p = 0.004).
Interestingly, the absolute magnitude of the cursor error on trial t-1 (unsigned error) negatively predicted switching on trial t; that is, after relatively large errors, participants were more likely to repeat the same choice again (t21 = 4.51, p < 0.001). This effect did not appear to be driven by the veridicality of errors, as neither the predictor for the veridicality of feedback, nor the interaction between veridicality and error magnitude, predicted switching (t21 = 1.16, p = 0.26 and t21 = 0.67, p = 0.51, respectively). Lastly, switching behavior did not appear to fluctuate over the duration of the experiment (“trial #” predictor; t21 = 0.72, p = 0.48).
Perturbed cursor feedback was often required to achieve the desired outcome probabilities for each stimulus, as those probabilities were fixed (see Methods). Although the regression analysis indicated that the veridicality of the feedback did not directly affect switching behavior, we conducted a few additional analyses to further explore the potential impact of false feedback on participants’ behavior. Results from the post-experiment questionnaire were equivocal: When asked if the feedback was occasionally altered, the mean response on a 7-point scale was 4.2, where 1 is “Very confident cursor location was fully controlled by me,” and 7 is “Very confident cursor location was partially controlled by me.” However, it is not clear if the question itself biased participant’s answers, so further analyses were conducted.
We examined if adjustments in reaching direction were responsive to non-veridical errors, as they would be expected to after veridical errors. We analyzed trial pairs in which the same stimulus was chosen on two consecutive trials where the first reach had been accurate but resulted in a false miss. The analysis showed that heading direction did indeed shift in the opposite direction of the perturbation on the subsequent trial (t23, = 6.83, p < 0.001; Figure 2F). This may result from implicit sensorimotor adaptation, explicit adjustments in aiming, or both [13]. Taken together, both the regression and movement analyses indicate that participants responded in a similar manner to veridical and perturbed feedback. (An additional analysis of the neural data adds further support to this conclusion; see below.)
Finally, previous studies have shown that movements toward high-value choices are more vigorous (i.e., faster) compared to low value choices [14–16]. Because we obtained continuous kinematic data, we could test if this phenomenon was present in our data. Indeed, modeled choice values negatively predicted MT (regression beta values relative to o: t23 = 3.27, p = 0.003; Figure S2). In other words, higher-value choices were accompanied by faster movements (shorter movement times). This result agrees with previous research on vigor and value, and provides additional model validation, with the model describing behavioral data that were not involved in the fitting procedure.
Imaging
Our first GLM analysis was focused on whole-brain response differences across the three trial outcomes. Figure 3A shows the results of the whole-brain contrasts for reward processing (Rew+ > Rew− and Miss), as well as execution errors (Miss > Rew−), and selection errors (Rew− > Miss). The reward contrast revealed four significant clusters spanning bilateral striatum, bilateral ventromedial prefrontal cortex (vmPFC), bilateral posterior cingulate (PCC), and a single cluster in left orbital frontal cortex (OFC; see Table S1). These ROIs are broadly consistent with areas commonly associated with reward [17,18]. The execution error contrast (Miss > Rew−) identified three broad clusters: A single elongated cluster spanning bilateral premotor cortex (PMC), supplementary motor area (SMA), and the anterior division of the cingulate (ACC), and two distinct clusters in the left and right inferior parietal lobule (IPL). This pattern is consistent with previous work on cortical responses to salient motor errors [19–21]. The reverse contrast, Rew− > Miss, revealed a bilateral cluster spanning several regions of visual cortex, perhaps due to the differences in visual feedback.
Figure 3: Whole-brain trial outcome contrasts.
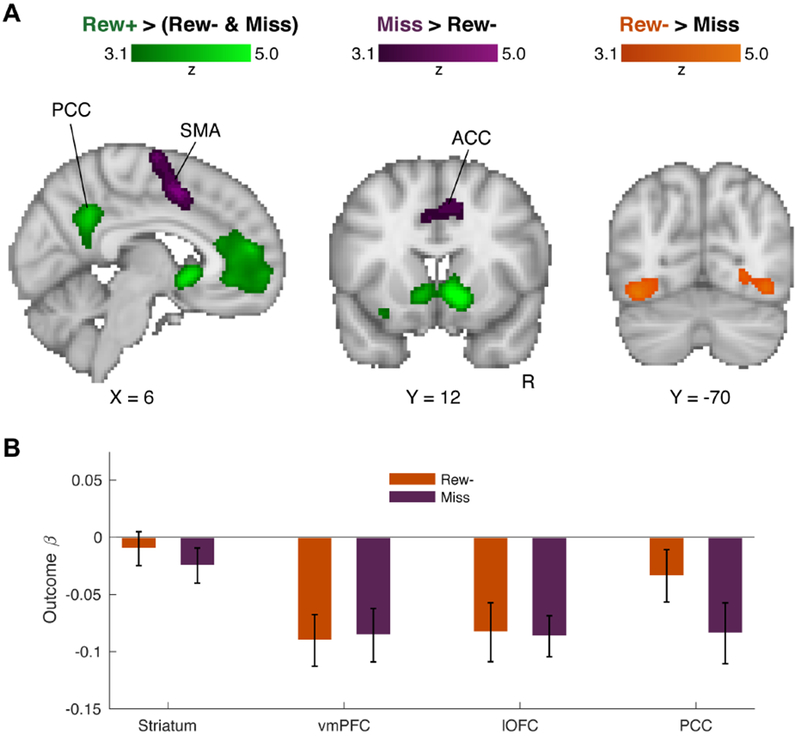
(A) Results of whole-brain contrasts for Rew+ trials > Rew− and Miss trials (green), Miss trials > Rew− trials (purple), and Rew− trials > Miss trials (orange). In the reward contrast (green), four significant clusters were observed, in bilateral striatum, ventromedial prefrontal cortex (vmPFC), left orbital-frontal cortex (OFC), and posterior cingulate cortex (PCC). For the Miss trial/motor error contrast (purple), three significant clusters were observed, one single cluster spanning bilateral premotor cortex, supplementary motor area (SMA), and the anterior division of the cingulate (ACC), as well as two distinct clusters in both the left and right inferior parietal lobule (not shown). The Rew− trials > Miss trials contrast showed a single cluster spanning visual cortex. (B) Beta weights extracted from each reward-contrast ROI for the (orthogonal) Rew− and Miss trial outcomes. Error bars = 1 s.e.m. See also Table S1 and Figures S3 and S4.
We examined feedback-locked betas on Rew− and Miss trials to assay gross differences in activity in the four reward-sensitive ROIs (Figure 3B), distinct from the more fine-grained parametric RPE modulations to be explored in the model-driven analysis (see below). Directly comparing the two negative outcome trial types showed that average activity in the four ROIs was similar for Rew− and Miss trials, with no significant differences seen in the striatum (t19 = 0.87, p = 0.40), vmPFC (t19 = 0.21, p = 0.84), nor OFC (t19 = 0.16, p = 0.88), and a marginal difference in the PCC (t19 = 1.92, p = 0.07).
To assess if the reward-related activity was influenced by our experimental manipulation of feedback, we performed a control whole-brain analysis comparing rewarded trials (Rew+) in which the feedback was either veridical or perturbed (we note that rewarded trials were used as power was too low to separate error outcomes by veridicality; see Methods). Here we re-ran the GLM but added a regressor that indicated the feedback type on Rew+ trials. No significant clusters were observed when contrasting these two trial types, even at a relaxed significance threshold (p < 0.05). Thus, our analysis of the neural data further indicates that the participants were insensitive to the motor feedback manipulation.
In our second GLM, separate parametric RPE regressors for the three possible trial outcomes were constructed by convolving trial-by-trial RPE values derived from the reinforcement learning model (see Methods) with the canonical hemodynamic response function. Beta weights for the three regressors were then extracted from the striatum ROI delineated by the first GLM.
As seen in Figure 4A, striatal activity was parametrically sensitive to trial-by-trial positive RPEs on Rew+ trials (t19 = 2.62, p = 0.017) and negative RPEs on Rew− trials (t19 = 2.16, p = 0.044). In contrast, striatal activity did not appear to code RPEs following Miss trials (t19 = 0.61, p = 0.55). Critically, the strength of RPE coding was significantly greater on Rew− trials than on Miss trials (t19 = 2.64, p = 0.016) and greater on Rew+ trials than on Miss trials (t19 = 2.23, p = 0.038), but not significantly different between the Rew+ and Rew− trials (t19 = 0.52, p = 0.61). Consistent with our hypothesis, that the striatum would be sensitive to the source of errors, these results suggest that striatal coding of RPEs is attenuated following execution failures. One consequence of this would be an attenuation of choice value updating on Miss trials, consistent with the observed behavioral biases (Figure 2).
Figure 4: Reward prediction errors in the striatum are sensitive to error type.
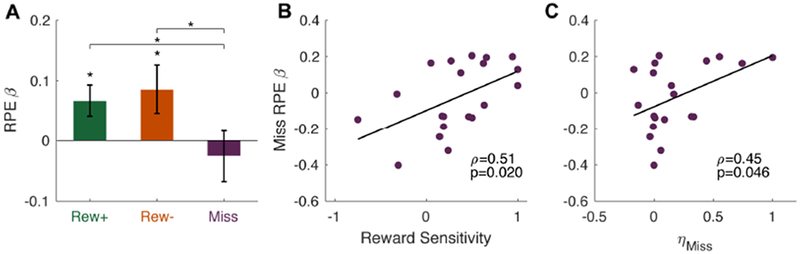
(A) Average reward prediction error (RPE) beta weights within the striatum ROI, separated by trial outcome. (B-C) Brain-behavior correlations between striatal RPE betas on Miss trials (y-axis), and (B) reward sensitivity values from the logistic regression on switching behavior, and (C) the fitted Miss-trial learning rate parameter from the winning reinforcement learning model. Error bars = 1 s.e.m. * p < 0.05. See also Figures S1 and S3.
To further test this hypothesis, we performed correlations between behavioral and neural parameters (we note that these analyses of individual differences have limited power due to the modest sample size). First, we correlated participants’ reward sensitivity, operationalized as the reward predictor in the logistic regression on switching behavior multiplied by negative one (Figure 2E), with the Miss-trial RPE betas from the striatum. This correlation was significant (ρ = 0.51, p = 0.020; Figure 4B), suggesting that participants with stronger negative RPEs on Miss trials were generally more sensitive to economic outcomes, and thus treated Miss trials as more aversive. As described in the Methods, this correlation was computed with sigmoid-transformed sensitivity values since two participants showed extreme parameter values in the logistic regression analysis due to a near-deterministic relationship between one or more predictors and switching probability. A similar correlation is observed if we exclude those two participants and repeat the analysis using the raw regression coefficients (ρ = 0.50, p = 0.035), or perform a nonparametric Spearman correlation with the two participants dummy-coded with maximum reward sensitivity values (ρ = 0.53, p = 0.018).
To further test the relationship between the behavioral and neural results, we also correlated the estimated Miss-trial learning rate parameter from the RL model (ηMiss; see Methods) with Miss-trial RPE betas from the striatum. This model parameter represents the degree to which a participant punishes a particular choice stimulus after a Miss trial. Here, too, we observed a positive correlation (ρ = 0.45, p = 0.046; Figure 4C) between the brain and behavioral measures.
One additional question concerns the specificity of our effects to the striatum. Do other regions show the same pattern of RPE effects? To address this question, we extracted RPE beta values from the other three reward-sensitive ROIs revealed by the first GLM (Figure 3). No significant differences between outcome RPE betas were found across the three areas, though activity in the vmPFC numerically mirrored the striatal results (Figure S3).
Finally, our task was designed to reveal brain areas sensitive to sensorimotor errors. As mentioned above, the Miss > Rew− contrast in the first GLM revealed areas sensitive to the presence of execution errors, controlling for reward (Figure 3A, purple). To investigate the effect of error magnitude, a fourth parametric regressor was included in the second GLM to reflect the size of unsigned cursor errors on Miss trials. Consistent with previous research [22,23], error magnitude on Miss trials was correlated with activity in anterior cingulate cortex, bilateral dorsal premotor (PMd) and primary motor cortices, bilateral superior parietal lobes (SPL), ipsilateral dorsal cerebellum (Cb; lobule VI), and primary and secondary visual cortex (VC; Figure S4; Table S1).
Discussion
The present results demonstrate that perceived movement execution errors influence reward prediction error (RPE) computations in the human striatum. When participants did not receive a reward but properly executed their decision, the striatum predictably represented the corresponding negative RPE, consistent with much previous experimental work (Figure 4A). However, on trials where a non-rewarded outcome was framed as the result of an action execution failure, the striatum did not reliably generate a corresponding negative RPE. These results indicate that the striatum may have access to information concerning whether a decision was properly implemented. This was reflected in participants’ choice behavior (Figure 2A, C), and can be described by a reinforcement learning model where decision execution errors demand a unique step size parameter ([11]; Figure 2B, D; Figures S1–S2). Moreover, individual differences in behavioral policies were correlated with differences in striatal RPE coding following execution errors (Figure 4B, C).
These findings fit into a broader reevaluation of the nature of RPEs in the mesostriatal dopamine system. While a reasonable hypothesis for our experiment would be that the striatum is primarily sensitive to economic outcomes separate from their cause, our results suggest that is not the case. Indeed, mounting evidence suggests that the striatum does not just signal a model-free prediction error, but is affected by high-level cognitive states, concerning, for instance, model-based predictions of future rewards [5], sampling from episodic memory [8], top-down attention to relevant task dimensions [6], and the holding of stimulus-response relationships in working memory [9]. We believe the present results add to this growing body of evidence, showing that contextual cues concerning the implementation of a decision affect if and how the value of that decision is updated by a prediction error.
We note that this putative “gating” phenomenon -- the diminished negative RPE in the striatum -- was not categorical; indeed, participants displayed varying degrees of gating both behaviorally and neurally (Figure 2, Figure 4B, D). One speculation could be that gating is a function of how optimistic a participant is that they could correct for their motor errors in the future. According to this hypothesis, gating is useful only if one is confident in their execution ability, and are likely to persist with a decision until successful execution allows them to glean information from the selected stimulus. On the other hand, if one is not confident in their ability to execute a movement, a strong negative RPE might be generated upon an execution error, steering them away from that choice and its associated action in the future. This trade-off suggests that other brain regions, perhaps upstream of the basal ganglia, act to modulate the coding of RPEs following movement errors. Future studies should be designed to identify these regions and investigate how they regulate RPE coding during reinforcement learning.
Differences in participant strategies could explain a curious result in a previous study [11]: Participants with degeneration of the cerebellum, which results in problems with both motor learning and motor execution, showed diminished “gating” behavior relative to controls; that is, they avoided decisions that were difficult to execute at the cost of larger rewards. We had hypothesized that the cerebellum may play a role in a putative gating mechanism, perhaps communicating sensory prediction errors to the basal ganglia via established bidirectional connections [24]. However, significant cerebellar activity only survived statistical correction in our analysis of cursor error size (Figure S4, Table S1), but not our main motor error contrast (Figure 3A). A recent behavioral follow-up to our previous study suggests that cerebellar-dependent motor error signals are likely not affecting choice behavior in this kind of task [12]; rather, participants’ may use a cognitive model of the causal structure of the task to guide their decisions [25]. It would be reasonable to assume that individuals with cerebellar degeneration may have a greater propensity to avoid choices associated with execution errors due to reduced confidence in their ability to successfully control and improve their movements.
Although we are interpreting the current results in the context of perceived motor execution errors, an alternative explanation is that participants did not fully believe the feedback they received because it was often perturbed. That is, participants may have tried to infer whether they truly “caused” an observed outcome, and the gating of striatal RPEs could reflect instances where participants inferred that the outcome was manipulated. However, we found no evidence of different physiological responses to veridical and perturbed feedback in terms of the striatal response on rewarded trials (there was insufficient power to perform the same analysis on unrewarded trials). Moreover, the behavioral results suggest that error veridicality was not a strong predictor of participants’ choices (Figure 2E), nor their movement kinematics (Figure 2F). Either way, future research could test the specificity of these results. Would the observed attenuation of RPEs happen if the lack of reward was attributed to a salient external cause, for instance, if the participant’s hand was knocked away by an external force? The results of this study may reflect a unique role of intrinsically-sourced motor execution errors in RPE computations, or a more general effect of any arbitrary execution failure, whether internally or externally generated.
Research on the computational details of instrumental learning has progressed rapidly in recent years, and the nature of one fundamental computation in learning, the reward prediction error, has been shown to be more complex than previously believed. Our results suggest that prediction errors update choice values in a manner that incorporates the successful implementation of those choices, specifically, by ceasing to update value representations when a salient execution failure occurs. These results may add to our understanding of how reinforcement learning proceeds in more naturalistic settings, where successful action execution is often not trivial.
STAR Methods
Contact for Reagent and Resource Sharing
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Samuel McDougle (mcdougle@berkeley.edu).
Experimental Model and Subject Details
Participants
A total of 24 participants were tested (11 female; age range: 18–42 years). The participants were fluent English speakers with normal or corrected-to-normal vision. They were all right-handed as confirmed by the Edinburgh Handedness Inventory [28]. Participants were paid $20.00 per hour for ~2 h of participation, plus a monetary bonus based on task performance (mean bonus = $12.00). The protocol was approved by the institutional review board at Princeton University and was performed in accordance with the declaration of Helsinki.
All 24 participants’ data were included in behavioral and modeling analyses. We excluded four participants from the imaging analysis due to excessive head motion (a priori maximum movement threshold = 3 mm), leaving a final imaging sample of 20 participants.
Method Details
Task and Apparatus
The experimental task was a modified version of a “multi-armed bandit” task commonly used in studies of reinforcement learning [29]. On each trial, three stimuli were presented, and the participant was required to choose one (Figure 1). The participant was instructed that each stimulus had some probability of yielding a reward and that they should try and earn as much money as possible. Critically, the participant was told that each trial was an independent lottery (i.e., that the outcome on trial t-1 did not influence the outcome on trial t), and that they had a fixed number of trials in the task over which to maximize their earnings.
In a departure from the button-press responses used in standard versions of bandit tasks, participants in the current study were required to indicate their decisions by making a wrist movement with the right hand toward the desired stimulus. The movement was performed by moving a wooden dowel (held like a pen) across an MRI-compatible drawing tablet. The right hand was positioned on the tablet, and the tablet rested on the participant’s lap, supported by pillow wedges. Participants were instructed to maintain this posture for the duration of the scanning session. The visual display was projected on a mirror attached to the MRI head coil, and the participant’s hand and the tablet were not visible to the participant. All stimuli were displayed on a black background.
To initiate each trial, the participant moved their hand into a start area, which corresponded to the center of the tablet and the visual display. The start area was displayed as a hollow white circle (radius 0.75 cm) and a message, “Go to Start”, was displayed until the hand reached the start position. To assist the participant in finding the start position, a white feedback cursor (radius 0.25 cm) corresponding to the hand position was visible when the pen was within 4 cm of the start circle. As soon as the cursor entered the start circle, the start circle filled in with white and the cursor disappeared, and the three choice stimuli were displayed along with the text “Wait” displayed in red font. The three choice stimuli were small cartoon images of slot machines (0.6 cm by 0.6 cm). They were presented at the same locations for all trials, with the three stimuli displayed along an invisible ring (radius 4.0 cm) at 30°, 150°, and 270° degrees relative to the origin. If the hand exited the start circle during the “Wait” phase, the stimuli disappeared and the “Go to Start” phase was reinitialized.
After an exponentially determined jitter (mean 2 s, truncated range = 1.5 s - 6 s), the “Wait” text was replaced with the message “GO!” in green font. Reaction time (RT) was computed as the interval between the appearance of the go signal and the moment when the participant’s hand left the area corresponding to the start circle. The participant had 2 s to begin the reach; if the RT was greater than 2 s, the trial was aborted and the message “Too Slow” appeared. Once initiated, a reach was considered complete at the moment when the radial amplitude of the movement reached 4 cm, the distance to the invisible ring. This moment defined the movement time (MT) interval. If the MT exceeded 1 s, the trial was aborted and the message “Reach Faster” was displayed.
The feedback cursor was turned off during the entirety of the reach. On trials in which the reach terminated within the required spatial boundaries (see below) and met the temporal criterion, reach feedback was provided by a small hand-shaped cursor (dimensions: 0.35 cm X 0.35 cm) that reappeared at the end of the reach, displayed along the invisible ring. The actual position of this feedback cursor was occasionally controlled by the experimenter (see below), although the participant was led to believe that it corresponded to their veridical hand position at 4 cm. To help maintain this belief, the trial was aborted if the reach was > ± 25° degrees away from any one of the three stimuli, and the message “Please Reach Closer” was displayed. The cursor feedback remained on the screen for 1.5 s, and the participant was instructed to maintain the final hand position during this period. In addition to the starting circle, slot machines, and, when appropriate, feedback cursor, the display screen also contained a scoreboard (dimensions: 3.3 cm × 1.2 cm), presented at the top of the screen. The scoreboard showed a running tally of participant’s earnings in dollars. At the end of the feedback period, the entire display was cleared and replaced by a fixation cross presented at the center for an exponentially jittered inter-trial interval (mean 3 s, truncated range = 2 - 8 s).
Assuming the trial was successfully completed (reach initiated and completed in a timely manner, and terminated within 25° of a slot machine), there were three possible trial outcomes (Figure 1). Two of these outcomes corresponded to trials in which the hand-shaped feedback cursor appeared fully enclosed within the chosen stimulus, indicating to the participant that they had been successful in querying the selected slot machine. On Rew+ trials, the feedback cursor was accompanied by the appearance of a small money-bag cartoon above the chosen stimulus and $0.10 would be added to the participant’s total. On Rew− trials, the feedback cursor was accompanied by the same money-bag overlaid with a red “X” and no money was added to the participant’s total. The third outcome consisted of “Miss” trials, in which the feedback cursor appeared outside the chosen stimulus, indicating an execution error. No money bag was presented on these trials and the monetary total remained unchanged, as in Rew− trials. Participants were informed at the start of the experiment that, like Rew− trials, no reward would be earned on trials in which their reach failed to hit the chosen stimulus. Importantly, the probabilities of each outcome for each choice stimulus were fixed (see below), and were not directly related to the actual reach accuracy of the participant.
In summary, of the three possible outcomes, one yielded a positive reward and two yielded no reward. For the latter two outcomes, the feedback distinguished between trials in which the execution of the decision was signaled as accurate but the slot machine failed to provide a payout (Rew−), and trials in which execution was signaled as inaccurate (Miss).
For all three stimuli, the probability of obtaining a reward (Rew+) was 0.4. Stimuli differed in their ratio of Rew− and Miss probabilities, with each of the three stimuli randomly assigned to one of the following ratios for these two outcomes: 0.5/0.1 (low miss), 0.3/0.3 (medium miss), and 0.1/0.5 (high miss). In this manner, the stimuli varied in terms of how likely they were to result in execution errors (and, inversely, selection errors), but not in the probability of obtaining a reward. Trial outcomes were probabilistically determined once a reach was initiated toward a particular stimulus. The positions of the choice stimuli assigned to the three Rew−/Miss probability ratios were counterbalanced across participants. Because of the fixed outcome probabilities, there is no optimal choice behavior in this task; that is, participants would earn the same total bonus (in the limit) regardless of their choices, consistent with our previous study [11]. Behavioral biases therefore reflected their attitude toward different kinds of errors.
To maintain fixed probabilities for each stimulus, we varied whether the cursor feedback was veridical on a trial-by-trial basis. Once a stimulus was selected (i.e., the participant initiated a reach towards the stimulus), the outcome (i.e. Rew+, Rew−, or Miss) was determined based on the fixed probabilities. If the true movement outcome matched the probabilistically determined outcome — either because the participant hit the stimulus on a Rew+ or Rew− trial, or missed the stimulus on a Miss trial — the cursor position was veridical. However, if the true movement outcome did not match the probabilistically determined outcome, the cursor feedback was perturbed: If the movement had missed the stimulus (>±3° from the center of the stimulus) on Rew+ and Rew− trials, the cursor was depicted to land within the stimulus. If the movement had hit the stimulus on a Miss trial, then the cursor was depicted to land outside the stimulus. The size of the displacement on Miss trials was drawn from a skewed normal distribution (mean 19 ± 2.3°), which was truncated to not be less than 3° (the stimulus hit threshold) or greater than 25° (the criterion required for a valid reach), thus yielding both a range of salient errors, but also keeping errors within the predetermined bounds (values were determined through pilot testing). If the participant reached accurately but a Miss trial was induced, the direction of the displacement from the stimulus was randomized.
Overall, we had to perturb the cursor position on 58.0% of trials. Most of these (46.9% of trials) were “false hits,” where the feedback cursor was moved into the stimulus region following an actual miss. 11.1% of trials were false misses, in which the cursor was displayed outside the stimulus following an actual hit. We had designed the Miss-trial perturbations to balance the goal of keeping the participants unaware of the feedback perturbations, while also providing large, visually salient execution errors. The mean size of the perturbed Miss trial errors was 10.98° larger than veridical Miss trial errors (t23 = 39.24, p < 0.001), raising the possibility that participants could be made aware of the perturbations. Given the difficulty of the reaching task (i.e., no feedback during the movement, a transformed mapping from tablet to screen, small visual stimuli, etc.) and the strict temporal (< 1 s) and spatial (within 25° of the stimulus) movement constraints, we expected that participants would be unaware of the feedback manipulation (see Results).
The experimental task was programmed in MATLAB (MathWorks), using the Psychophysics Toolbox [30]. Participants were familiarized with the task during the structural scan and performed 30 practice trials for which they were not financially rewarded. Participants received a post-experiment questionnaire at the end of the task to query their awareness of perturbed feedback.
fMRI data acquisition
Whole-brain imaging was conducted on a 3T Siemens PRISMA scanner, using a 64-channel head coil. MRI-optimized pillows were placed about the participant’s head to minimize head motion. At the start of the scanning session, structural images were collected using a high-resolution T1-weighted MPRAGE pulse sequence (1 × 1 × 1 mm voxel size). During task performance, functional images were collected using a gradient echo T2*-weighted EPI sequence with BOLD contrast (TR = 2000 ms, TE = 28 ms, flip angle = 90°, 3 × 3 × 3 mm voxel size; 36 interleaved axial slices). Moreover, a field map was acquired to improve registration and limit image distortion from field inhomogeneities (for one participant a field map was not collected).
Functional data were collected in a single run that lasted approximately 40 min. For one participant, the run was split into two parts due to a brief failure of the drawing tablet. Because of the self-paced nature of the reaching task (i.e., variable time taken to return to the start position for each trial, reach, etc.), the actual time of the run, and thus number of total TRs, varied slightly across participants. The run was terminated once the participant had completed all 300 trials of the task.
Quantification and Statistical Analysis
Behavioral variables and analysis
Trials were excluded from the analysis if the reach was initiated too slowly (RT > 2 s; 0.4 ± 0.7% of trials), completed too slowly (MT > 1 s; 2.4 ± 4.5% of trials), or terminated out of bounds (Reach terminated > 25° from a stimulus; 1.2 ± 2.0% of trials). For the remaining data, we first evaluated the participants’ choice biases: For each stimulus, the choice bias was computed by dividing the number of times the participant chose that stimulus by the total number of choice trials. Second, we looked at switching biases. These were computed as the probability that the participant switched to a different stimulus on trial t given the outcome of trial t-1 (Rew+, Rew−, or Miss). An additional switching analysis was conducted based on only the reward outcome of trial t-1 (i.e., rewarded versus non-rewarded trials) by collapsing Rewand Miss trials together. One-sample t-tests were used to evaluate if differences in choice and switching biases deviated significantly from each other.
To further evaluate potential predictors of switching, a logistic regression was conducted using choice switching on trial t as the outcome variable (1 for switch, 0 for stay). Seven predictors were entered into the regression: 1) The reward outcome of trial t-1 (1 for reward, 0 for no reward), 2) the movement execution outcome of trial t-1 (1 for a hit, 0 for a miss), 3) the Miss/Rew− trial probability ratio of the chosen stimulus on trial t, 4) the unsigned cursor error magnitude on trial t-1 (angular distance from feedback cursor to stimulus), 5) the veridicality of the feedback on trial t-1 (1 for veridical feedback, 0 for perturbed feedback), 6) the interaction of unsigned error magnitude X the veridicality of the feedback on trial t-1, and 7) the current trial number. The multiple logistic regression was computed using the MATLAB function glmfit, with a logit link function. All predictors were z-scored. One-sample t-tests were used to test for significant regression weights across the sample. For two out of the 24 participants, near complete “separation” was observed with the reward sensitivity regressor (e.g., they rarely switched after a Rew+ trial, or always switched after failing to receive a reward). These participants were excluded from the initial regression analysis (Figure 2E), although they were included in other analyses in which we normalized the regression parameters with a sigmoid function (Figure 4B; see Results).
We also analyzed how movement feedback altered reaching behavior to test if participants were actively attempting to correct their execution errors. In particular, we were interested in whether participants were sensitive to the non-veridical feedback provided on trials in which the feedback position of the cursor was perturbed. To assess this, we focused on trial pairs in which consecutive reaches were to the same stimulus and the first trial of the pair was accurate (< ± 3° from stimulus’s center), but the cursor feedback was displayed fully outside of the stimulus, indicating a Miss (the analysis was conducted this way to limit simple effects of regression to the mean reaching angle). A linear regression was performed with the observed signed cursor error on the first trial of the pair as the predictor variable and the signed change in reach direction on the second trial as the outcome variable. One-sample t-tests were used to test for significant regression weights.
Modeling analysis of choice behavior
A reinforcement-learning analysis was conducted to model participants’ choice data on a trial-by-trial basis and generate reward prediction error (RPE) time-courses for later fMRI analyses. We tested a series of temporal difference (TD) reinforcement-learning models [31], all of which shared the same basic form:
| (1) |
| (2) |
where the value (Q) of a given choice (a) on trial t is updated according to the reward prediction error (RPE) δ on that trial (the difference between the expected value Q and received reward r), with a learning rate or step-size parameter η. All models also included a decay parameter γ [32], which governed the decay of the three Q-values toward their initial value (assumed to be 1/the number of actions, or 1/3) on every trial:
| (3) |
The decay parameter was important for model fitting, likely due to both the lack of any optimal slot machine and the stationary reward probabilities – many participants switched their choices often. Models without the decay parameter performed significantly worse than those with this parameter (data not shown).
Our previous results showed that participants discount Miss trials, suggesting a tendency to persist with a given choice following a perceived execution error [11,12] more often than following a choice error (Rew− trials). However, it is not known if this tendency is driven by RPE computations, or can also arise from a different source. To model an additional route to “Miss discounting,” we included a persistence parameter, Φ, in the softmax computation of the probability of each choice (P),
| (4) |
where “miss_prev” and “choice_prev” are indicator vectors, indicating, respectively, whether the previous trial was a Miss (1 for Miss, 0 for Rew+/Rew−) and which action was chosen, and β is the inverse temperature parameter. If Φ is positive, the learner is more likely to repeat the same choice after a Miss trial (a bonus of Φ is given to that option). If Φ is negative, the learner is more likely to switch after a Miss due to a penalty of Φ. This parameter represents a bias factor distinct from RPE-driven value updating [8], as the bonus (or penalty) is fixed regardless of the value of the chosen option.
We modeled reinforcement learning based on trial outcomes as follows: In the Standard(2η]) model, distinct learning rates, η, were included to account for updating following negative RPEs (unrewarded trials) and positive RPEs (rewarded trials),
| (5) |
where ηRew+ and ηMiss/Rew− are the learning rates for updates following Rew+ or Miss/Rew− trials, respectively. Allowing positive and negative RPEs to update Q values at different rates has been shown to provide better fits to human behavior compared to models in which a single learning rate is applied after all trials [33,34]. We also included a second variant of this model, the Standard(no-Φ) model, that was identical to the Standard(2η) model but did not include the Φ parameter.
Two other models were included, based on our previous study in which negative outcomes could result from execution or selection errors [11]. One model, the 3η model (or the “gating” model), was similar to the Standard(2η) model, except that it had unique learning rates for each of the three possible trial outcomes(ηRew+, ηRew−, and ηMiss). This model allows for values to be updated at a different rate following execution errors (Miss) or selection errors (Rew−). Lastly, the Probability model separately tracked the probability of successful execution (E) for each stimulus and the likelihood (V) of receiving a reward if execution was successful:
| (7) |
| (8) |
| (9) |
where δt,prob, and δt,payoff represent, respectively, prediction errors for whether the current action was successfully executed (where r = 1 on Rew+/Rew− trials and r = 0 on Miss trials), and if a reward was received given that execution was successful.
Using the MATLAB function fmincon, all models were fit to each participant’s observed choices outcomes by finding the parameters that maximize the log posterior probability of the choice data given the model. To simulate action selection, Q-values in all models were converted to choice probabilities using a softmax logistic function (equation 4). All learning rate parameters (η) were constrained to be between −1 and 1; negative values were permitted given that we did not have an a priori reason to assume ηMiss would be positive, and thus opted to be consistent across all learning-rate parameters and models. The persistence parameter (Φ) was constrained to be between −5 and 5, based on constraints for a similar parameter in a recent study characterizing empirical priors in RL models [35]. The decay parameter (γ) was constrained to be between 0 and 1, reflecting the range from no decay (0) to maximum decay (1). The inverse temperature parameter (β) was constrained to be between 0 and 50 [35], and a Gamma(2,3) prior distribution was used to discourage extreme values of this parameter [6]. Q-values for each stimulus were initialized at 1/3.
The fitting procedure was conducted 100 times for each model to avoid local minima during optimization, using different randomized starting parameter values for each iteration. The resulting best fit model was used in further analyses. Model fit quality was evaluated using the Akaike information criteria [36,37].
After model fitting and comparison, we performed a simulate-and-recover experiment on each of the four models to assess model confusability [38]. Choices were simulated for each model using the best-fit parameters of each of the 24 participants, yielding 24 simulations per model over 10 total iterations. Simulated data were then fit with each model (using 20 randomized vectors of starting parameters for each fit to avoid local minima) to test whether the correct models were recovered. Confusion matrices were created comparing differences in summed Aikake weights [39], as well as the percent of simulations fit best by each model.
Simulated choice data (from the winning model) were created to investigate the model’s ability to replicate the main behavioral findings (Figure 2B, D). Simulated choice data were generated 100 times for each participant, using that participant’s optimized parameters. Choice preferences (Figure 2B) and switch probabilities (Figure 2D) were extracted and averaged over the 100 simulations. For visualization purposes, standard errors were computed on the mean choice preferences and switch probabilities obtained for each simulated participant, using the true sample size (24).
fMRI data analysis
Preprocessing and data analysis were performed using FSL v. 5.98 (FMRIB) and SPM12. Given the movement demands of the task, multiple steps were taken to assess and minimize movement artifacts. After manual skull-stripping using FSL’s brain extraction tool (BET), we performed standard preprocessing steps, registering the functional images to MNI coordinate space using a rigid-body affine transformation (FLIRT), applying the field map correction, performing slice timing correction, spatially smoothing the functional data with a Gaussian kernel (8 mm FWHM), and attaining six realignment parameters derived from standard motion correction (MCFLIRT). To identify and remove components identified as head-motion artifacts, we then applied the independent components motion-correction algorithm ICA-AROMA [27] to the functional data. As a final preprocessing step, we temporally filtered the data with a 100 s high-pass filter. Based on visual inspection of the data, four participants were excluded from the imaging analysis, before preprocessing, due to excessive (>3 mm pitch, roll, or yaw) head motion.
Three GLM analyses were performed. For all GLMs, we imposed a family-wise error cluster-corrected threshold of p < 0.05 (FSL FLAME 1) with cluster-forming threshold p < 0.001. Task-based regressors were convolved with the canonical hemodynamic response function (double Gamma), and the six motion parameters were included as regressors of no interest.
The first GLM was designed to functionally define ROIs that were sensitive to reward. Trial outcome regressors for the three trial types (Rew+, Rew−, Miss) were modeled as delta functions concurrent with visual presentation of the trial outcome. Task regressors of no interest included boxcar functions that spanned the wait and reach periods, and invalid trials (i.e., excessive RT or MT, or reaches angled too far from a stimulus). The contrast Rew+ > (Rew− and Miss) was performed to identify reward-sensitive ROIs. Resulting ROIs were visualized, extracted, and binarized using the xjview package for SPM12 (http://www.alivelearn.net/xjview). Beta weights were extracted from the resulting ROIs using FSL’s featquery function. To identify areas sensitive to different error types, while controlling for reward, we also tested two additional trial outcome contrasts: Miss > Rew− and Rew− > Miss.
A second GLM was used to measure reward prediction errors (RPEs). Three separate parametric RPE regressors, corresponding to RPE time courses for each outcome (delta functions at the time of feedback), were entered into the GLM to account for variance in trial-by-trial activity not captured by the three binary outcome regressors (which were also included in the model as delta functions at the identical time points). Beta weights for each RPE regressor were extracted from the functional reward ROIs obtained from the first GLM using FSL’s featquery function. A fourth parametric regressor was entered into the GLM to identify brain areas parametrically sensitive to unsigned motor execution error magnitude. The regressor of interest here was limited to Miss trials, and included a single parametric unsigned cursor error regressor, which tracked the magnitude of angular cursor errors on Miss trials. Nuisance regressors included the wait period, reach period, invalid trials, and the three outcome regressors.
A third GLM was constructed as a control analysis to measure potential neural effects of feedback perturbations on reward processing. This GLM was identical to the first GLM, but was designed to compare Rew+ trials where the cursor feedback was veridical (the hand passed within the bounds of the stimulus), to Rew+ trials where the cursor feedback was perturbed (the hand missed the stimulus but the feedback signaled an accurate reach). Here, outcome regressors for Rew+ trials were separated by feedback veridicality (a similar analysis on perturbed versus veridical execution error trials was not performed due to insufficient power).
All voxel locations are reported in MNI coordinates, and all results are displayed on the average MNI brain.
Data and Software Availability
Raw behavioral and imaging data, and model code, will be placed at https://osf.io/d564h/ upon publication.
Supplementary Material
Key Resources Table
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Software and algorithms | ||
| MATLAB 2017b | MathWorks | http://www.mathworks.com |
| FSL 5.98 | FMRIB, Oxford, UK | http://fsl.fmrib.ox.ac.uk |
| SPM 12 | [26] | http://www.fil.ion.ucl.ac.uk/spm |
| ICA-AROMA | [27] | http://github.com/maartenmennes/ICA-AROMA |
| Psychophysics Toolbox | [30] | http://psychtoolbox.org |
| Deposited Data | ||
| Raw data | This paper | http://osf.io/d564h |
HIGHLIGHTS.
Humans devalue choices less following execution versus selection errors
Reward prediction errors in the striatum are attenuated following execution errors
Different error classes have distinct neural signatures
Acknowledgments
This work was supported by the National Institute of Neurological Disorders and Stroke-National Institute of Health, Grant NS092079 to R.B.I. and Grant NS084948 to J.A.T. We thank Krista Bond for help with data collection, and Anne Collins for helpful comments.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Declaration of Interests
The authors declare no competing interests.
References
- 1.Barto AG (1995). Adaptive Critics and the Basal Ganglia In Models of information processing in the basal ganglia, Houk D, JL JC and Beiser DG, eds. (Cambridge, MA: MIT Press; ), pp. 215–232. [Google Scholar]
- 2.Montague PR, Dayan P, and Sejnowski TJ (1996). A framework for mesencephalic dopamine systems based on predictive Hebbian learning. J. Neurosci 16, 1936–1947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Schultz W, Dayan P, and Montague PR (1997). A neural substrate of prediction and reward. Science 275, 1593–1599. [DOI] [PubMed] [Google Scholar]
- 4.Langdon AJ, Sharpe MJ, Schoenbaum G, and Niv Y (2017). Model-based predictions for dopamine. Curr. Opin. Neurobiol 49, 1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Daw ND, Gershman SJ, Seymour Ben, Dayan P, and Dolan RJ (2011). Model-Based Influences on Humans’ Choices and Striatal Prediction Errors. Neuron 69, 1204–1215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Leong YC, Radulescu A, Daniel R, DeWoskin V, and Niv Y (2017). Dynamic Interaction between Reinforcement Learning and Attention in Multidimensional Environments. Neuron 93, 451–463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wimmer GE, Braun EK, Daw ND, and Shohamy D (2014). Episodic Memory Encoding Interferes with Reward Learning and Decreases Striatal Prediction Errors. J. Neurosci 34, 14901–14912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Bornstein AM, Khaw MW, Shohamy D, and Daw ND (2017). Reminders of past choices bias decisions for reward in humans. Nat. Commun 8, 15958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Collins AGE, Ciullo B, Frank MJ, and Badre D (2017). Working Memory Load Strengthens Reward Prediction Errors. J. Neurosci 37, 4332–4342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ribas-Fernandes JJF, Solway A, Diuk C, McGuire JT, Barto AG, Niv Y, and Botvinick MM (2011). A Neural Signature of Hierarchical Reinforcement Learning. Neuron 71, 370–379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.McDougle SD, Boggess MJ, Crossley MJ, Parvin D, Ivry RB, and Taylor JA (2016). Credit assignment in movement-dependent reinforcement learning. Proc. Natl. Acad. Sci 113, 6797–6802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Parvin DE, McDougle SD, Taylor JA, and Ivry RB (2018). Credit assignment in a motor decision making task is influenced by agency and not sensorimotor prediction errors. J. Neurosci, 3601–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Taylor JA, Krakauer JW, and Ivry RB (2014). Explicit and Implicit Contributions to Learning in a Sensorimotor Adaptation Task. J. Neurosci 34, 3023–3032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Reppert TR, Lempert KM, Glimcher PW, and Shadmehr R (2015). Modulation of Saccade Vigor during Value-Based Decision Making. J. Neurosci 35, 15369–15378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Seo M, Lee E, and Averbeck BB (2012). Action selection and action value in frontal-striatal circuits. Neuron 74, 947–960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Niv Y, Daw ND, Joel D, and Dayan P (2007). Tonic dopamine: opportunity costs and the control of response vigor. Psychopharmacology (Berl.) 191, 507–520. [DOI] [PubMed] [Google Scholar]
- 17.McClure SM, York MK, and Montague PR (2004). The neural substrates of reward processing in humans: the modern role of FMRI. The Neuroscientist 10, 260–268. [DOI] [PubMed] [Google Scholar]
- 18.Schultz W (2015). Neuronal Reward and Decision Signals: From Theories to Data. Physiol. Rev 95, 853–951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Krakauer JW, Ghilardi M-F, Mentis M, Barnes A, Veytsman M, Eidelberg D, and Ghez C (2004). Differential cortical and subcortical activations in learning rotations and gains for reaching: a PET study. J. Neurophysiol 91, 924–933. [DOI] [PubMed] [Google Scholar]
- 20.Diedrichsen J, Hashambhoy Y, Rane T, and Shadmehr R (2005). Neural correlates of reach errors. J. Neurosci 25, 9919–9931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Seidler RD, Kwak Y, Fling BW, and Bernard JA (2013). Neurocognitive mechanisms of error-based motor learning. Adv. Exp. Med. Biol 782, 39–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Anguera JA, Seidler RD, and Gehring WJ (2009). Changes in performance monitoring during sensorimotor adaptation. J. Neurophysiol 102, 1868–1879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Grafton ST, Schmitt P, Horn JV, and Diedrichsen J (2008). Neural substrates of visuomotor learning based on improved feedback control and prediction. Neuroimage 39, 1383–1395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bostan AC, Dum RP, and Strick PL (2013). Cerebellar networks with the cerebral cortex and basal ganglia. Trends Cogn. Sci 17, 241–254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Green CS, Benson C, Kersten D, and Schrater P (2010). Alterations in choice behavior by manipulations of world model. Proc. Natl. Acad. Sci 107, 16401–16406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Friston KJ, Penny WD, Ashburner JT, Kiebel SJ, and Nichols TE (2011). Statistical Parametric Mapping: The Analysis of Functional Brain Images (Amsterdam: Elsevier; ). [Google Scholar]
- 27.Pruim RHR, Mennes M, Buitelaar JK, and Beckmann CF (2015). Evaluation of ICA-AROMA and alternative strategies for motion artifact removal in resting state fMRI. Neuroimage 112, 278–287. [DOI] [PubMed] [Google Scholar]
- 28.Oldfield RC (1971). The assessment and analysis of handedness: the Edinburgh inventory. Neuropsychologia 9, 97–113. [DOI] [PubMed] [Google Scholar]
- 29.Daw ND, O’Doherty JP, Dayan P, Seymour B, and Dolan RJ (2006). Cortical substrates for exploratory decisions in humans. Nature 441, 876–879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Brainard DH (1997). The psychophysics toolbox. Spat. Vis, 433–436. [PubMed] [Google Scholar]
- 31.Sutton RS, and Barto AG (1998). Reinforcement learning: An introduction (Cambridge, MA: MIT Press; ). [Google Scholar]
- 32.Collins AG, Brown JK, Gold JM, Waltz JA, and Frank MJ (2014). Working memory contributions to reinforcement learning impairments in schizophrenia. J. Neurosci 34, 13747–13756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Niv Y, Edlund JA, Dayan P, and O’Doherty JP (2012). Neural prediction errors reveal a risk-sensitive reinforcement-learning process in the human brain. J. Neurosci 32, 551–562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Gershman SJ (2015). Do learning rates adapt to the distribution of rewards? Psychon. Bull. Rev 22, 1320–1327. [DOI] [PubMed] [Google Scholar]
- 35.Gershman SJ (2016). Empirical priors for reinforcement learning models. J. Math. Psychol 71, 1–6. [Google Scholar]
- 36.Akaike H (1974). A new look at the statistical model identification. IEEE Trans. Autom. Control 19, 716–723. [Google Scholar]
- 37.Schwarz G (1978). Estimating the Dimension of a Model. Ann. Stat 6, 461–464. [Google Scholar]
- 38.Wilson RC, Nassar MR, and Gold JI (2013). A Mixture of Delta-Rules Approximation to Bayesian Inference in Change-Point Problems. PLOS Comput. Biol. 9, e1003150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Wagenmakers E-J, and Farrell S (2004). AIC model selection using Akaike weights. Psychon. Bull. Rev 11, 192–196. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Raw behavioral and imaging data, and model code, will be placed at https://osf.io/d564h/ upon publication.


