From Complexity to Distinctiveness: The Effect of Expertise on Letter Perception

Abstract

Fluent, adult readers of alphabetic languages encounter hundreds of millions of individual letters. What is the impact of such extensive experience on the perception and identification of letters? Recent evidence indicates that expert and naïve observers perceive letters differently. Here, we focus on the relationship between expertise and letter complexity (number of visual features) and distinctiveness (overlap in features with the other letters of the alphabet). Using a same-different letter judgement task, we examined the performance of individuals with high levels of expertise with Roman letters, but with different amounts of experience with the Arabic alphabet. The results reveal a trade-off between letter complexity and distinctiveness, such that while naïve individuals are sensitive only to letter complexity and not distinctiveness, the opposite is true for individuals with high expertise with an alphabet. These findings reveal a learning trajectory in which, with increasing experience, the influence of letter complexity is supplanted by distinctiveness, which requires an understanding of the relationship of each letter to the other possible letter shapes in the alphabet as a whole.

Introduction

Letter perception and identification require processing a letter’s component visual features (Grainger, Rey, & Dufau, 2008). For example, Pelli and colleagues (Pelli, Burns, Farell, & Moore-Page, 2006) examined a number of different alphabets and scripts, and determined that letters are identified based on 7 ± 2 visual features. While core properties of the human visual system certainly determine how and which visual features are used in letter identification, there is increasing evidence that the extent and type of experience with letters also influence how the visual system processes them.

Wiley, Wilson, & Rapp (2016) examined the effects of both alphabet and expertise on Arabic letter perception by comparing same/different letter judgments of expert, biscriptal Arabic English readers, and naïve, monoscriptal English-only readers. Among the findings was that letter complexity, defined as the number of visual features in each Arabic letter, was associated with slower/less accurate responses for naïve observers and with faster/more accurate responses for expert observers. That naïve observers are slower on more complex relative to simple letters is not surprising, given that they have no experience with the letters. Presumably, letters with more features require more time to process, if all features are exhaustively processed. In contrast, the finding that expert viewers exhibited an apparent “complexity benefit” was more intriguing, and the nature of this apparent relationship between letter complexity and processing speed deserved more scrutiny and, thus, forms the focus of the current paper.

According to the principle of “feature detection,” letters are identified via component features such as oriented lines and curves, as opposed to whole-letter templates (Palmer, 1999). However, given only this principle, it is not clear why expert compared to naïve letter processing would be influenced differently by letter complexity. Potentially relevant to this question is evidence that experts use only a subset of a letter’s component features for identification (see Fiset et al., 2008, 2009; Wolfe & Horowitz, 2004). It is possible that fluent readers, having seen millions of instances of letters, come to know which features are most useful for letter identification. Thus, for example, while uppercase letter ‘B’ likely has more visual features than lowercase ‘l’, ‘B’ may be identified on the basis of only a few of its features, with its other features being redundant. This suggests that the distinctiveness of letters vis a vis other letters may play a key role in letter identification. The finding that expert observers process complex letters more easily than simpler ones could be explained if complexity is highly correlated with distinctiveness. However, although more complex letters may tend to also be more distinctive, these two variables are not identical. Critically, distinctiveness and complexity differ in that while complexity can be defined in absolute terms (e.g., numbers of features), distinctiveness is necessarily defined relative to a reference set (e.g., the set of Arabic letters). Notably, a reference set is necessarily learned and, thus, distinctiveness could be expected to play a role in letter identification based on the extent to which the reference set has been learned.

The goal of the current study was to better understand how the mental representation of letters changes due to expertise, specifically with regard to the roles of complexity and distinctiveness. To do so we further examined the complexity benefit for expert viewers reported in Wiley et al. (2016), investigating if it is a true complexity effect or attributable, instead, to distinctiveness. In order to investigate this issue, in two experiments we compared the behavior of groups of individuals with varying amounts of expertise with Arabic letters, using a same/different letter judgment task. In Experiment 1, we compared two different measures of the letters’ visual properties, complexity and distinctiveness, and report here on how those two measures relate to the perception of both Roman and Arabic letters by monoscriptal (Roman alphabet-only) observers. We replicated the Wiley et al. (2016) finding of a positive relationship between complexity and RT for naïve observers in viewing the Arabic alphabet. However, for viewing the Roman alphabet, with which all participants were experts, we found that it is distinctiveness, a measure of how similar a letter is relative to all other letters within a set, which accounts for differences in RT. In Experiment 2, we examined the performance of three populations in viewing both Roman and Arabic letters: monoscriptal (Roman alphabet-only) observers, and low- and high-proficiency biscriptal (Arabic-Roman) observers. The results strengthen the conclusion that letter distinctiveness, and not complexity, predicts RT for expert over less experienced observers, regardless of the alphabet.

Examining both Arabic and Roman letters allows further consideration of whether specific properties of alphabet determine whether letter complexity or distinctiveness affect letter perception. The Arabic writing system is an abjad, not a true alphabet, because the letters represent only consonants and not vowels (Daniels & Bright, 1996). More technically, modern Arabic, like Hebrew, is an “impure” abjad, because some of the vowels are written with letters (while others are written optionally as diacritic marks above or below the letters). Compared to Roman letters, Arabic letters are more visually complex and are less-efficiently detected by the human visual system (see Pelli et al., 2003). One of the most distinctive aspects of Arabic letters that does not exist for Roman letters is that most letters have one to four “sisters” (Wiley et al., 2016) that share the same basic shape, differing only in the number and location of diacritic marks (dots). For example, the letter-shapes ت, ب, and ث (“ba”, “ta”, and “tha”). These diacritic marks have been demonstrated to be essential visual features for letter/word recognition in Arabic (Perea et al., 2016), and naïve observers have been shown to quickly learn their importance (Wiley et al., 2016). Therefore, given the greater complexity of Arabic letters relative to Roman letters, the importance of diacritic marks in Arabic letters, and the fact that those visual features do not exist in Roman letters¹, it is particularly important to consider whether the “complexity benefit” reported for Arabic letters might be unique to that alphabet.

Experiment 1

Experiment 1 examines the role of complexity and distinctiveness in monoscriptal individuals, using a same/different letter judgment task with either Arabic or Roman letters. As the participants are unfamiliar with Arabic, the former corresponds to the Naïve Observer Condition, whereas the latter corresponds to the Expert Observer Condition.

Participants

188 participants were recruited online via Amazon’s Mechanical Turk, receiving payment of $7.50/hour for their participation. 92 participants completed the task with Roman letters and 96 with Arabic letters. In total, 38 participants were removed from the analyses for the following reasons: reported knowledge of a non-Roman script (18), failure to complete the task (17), or mean RT or accuracy ± 2 standard deviations from the mean (3). The remaining 150 participants (81 for Arabic and 69 for Roman letters) were all monoscriptal (MS, Roman-only).

Stimuli

A set of 23² letter-shapes from the Arabic alphabet was presented in Adobe Arabic, in font size 24 (stimuli subtended 0.17°−0.31° and 0.05°−0.35° of visual angle, respectively in the vertical and horizontal dimensions). A set of 23 letter-shapes (including both uppercase and lowercase), from the Roman alphabet was also presented, in Arial font size 16, approximately equating the size range of the two alphabets. For each letter, measures of complexity and distinctiveness were computed.

1) Letter complexity was defined as the total number of visual features in each letter. The set of visual features included has been previously proposed in the literature on letter detection and identification (Palmer, 1999; Courrieu, Farioli & Grainger, 2004; Fiset et al., 2008, 2009; Wiley et al., 2016). The procedure for determining each individual letter’s visual features followed the procedure of Wiley et al. (2016) for the Arabic alphabet, and was repeated here for the Roman alphabet. All of the following features³ observable within a 4-pixel diameter (proportional to the window within which terminations and intersections have previously been identified in the Roman alphabet; see Fiset et al., 2008, 2009) were identified for each letter-shape, with lines considered to be slanted only if ≥20° off the horizontal or vertical: straight lines (horizontal, vertical, slants left and right), curved lines (open to the left, right, top and bottom), intersections (L, T, and X), terminations (left, right, top and bottom), cyclicity, and closed space.

(2) Letter distinctiveness was defined based on feature overlap. First, each letter’s feature overlap with each other letter was computed:

$$\frac{sharedfeatures\left(letter1\&letter2\right)}{totalfeatures\left(letter1\right)}$$

For the 23 letter-shapes included for each alphabet, this resulted in an asymmetrical 23×23 matrix, each row corresponding to one letter’s proportion of shared features with each of the other 22. For example, for the pair ‘c Q’, 80% of the features in ‘c’ overlap with those in ‘Q’, whereas only 44% of ‘Q’s features overlap with those in ‘c’. The distinctiveness of ‘c’ within the set of 23 letter-shapes is the average of the values from all pairwise comparisons of ‘c’ with the 22 other letters in the set. The final measures of distinctiveness were changed to 1 minus this value, so that the values range from 0 (very non-distinct, a letter-shape that shares all its features with every other shape) to 1 (completely distinct, shares no feature with any other shape).

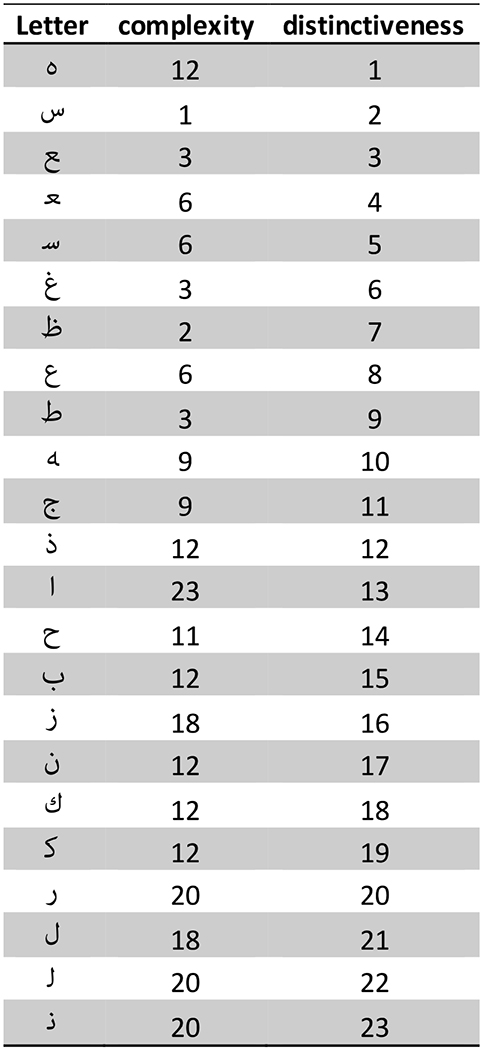
The list of letters included and their rankings by both letter complexity and distinctiveness are presented in Table 1 (Roman letters) and Table 2 (Arabic letters).

Table 1.

Roman letters and their ranking by letter complexity (1 = most complexity) and distinctiveness (1 = most distinct).

Letter	complexity	distinctiveness
w	5	1
x	13	2
E	2	3
t	5	4
B	1	5
A	5	6
Q	5	7
j	19	8
s	16	9
T	13	10
R	2	11
D	19	12
i	19	13
c	16	14
G	13	15
a	2	16
g	5	17
o	19	18
b	10	19
J	23	20
d	10	21
r	16	22
q	10	23

Table 2.

Arabic letters and their ranking by letter complexity (1 = most complexity) and distinctiveness (1 = most distinct).

Procedure

Each trial began with a central fixation cross (250ms), which disappeared and was replaced by a pair of letters simultaneously on either side of fixation, 48 pixels apart. Each pair of letters was presented until a response of “same” or “different” (by pressing “a” or “l” the keyboard) was recorded. After a response there was a 500ms intertrial blank screen. Participants completed the task either with Roman or Arabic letters but not both. Only “same” trials were analyzed, because of the previous finding of a relationship between RT and letter complexity on “same” decisions (Wiley et al., 2016). There were a total of 184 same trials (8 trials/letter) and the ratio of same to different trials was 40/60.

Analysis

All analyses were conducted using linear mixed-effects modeling (LMEM) using R (R Core Team, 2017), package lme4 (Bates, Mächler, Bolker, & Walker, 2015). RT on correct responses to “same” trials in the same/different judgment was modeled as a gamma distribution with generalized LMEM (Lo & Andrews, 2015). Arabic and Roman letters were analyzed separately.

Regression predictors: For the fixed-effects, two predictors of interest were included: letter complexity and distinctiveness. Two additional predictors were included: Trial Order and Previous RT (RT on the preceding trial), to control for trends in RT across the duration of the experiment. For the random-effects, a random intercept and random slopes for both letter complexity and distinctiveness were included by-participants, as was a random intercept by-items (i.e., letter-shapes).

The two measures, letter complexity and distinctiveness, are positively correlated with one another, both for the set of 23 Arabic letters (Spearman correlation = 0.81) and 23 Roman letters (Spearman correlation = 0.36). Nonetheless, when entered into simultaneous regression, multicollinearity was not problematic (as measured by variance inflation factor, all VIF < 4). Both measures were therefore kept in the LMEM in order to determine the unique contributions of complexity and distinctiveness to RT in the task.

Results

The results are reported in Table 3 and Figure 1. The 95% confidence intervals are based on the standard-normal distribution for the fixed-effects estimates, as returned by the R package effects (Fox, 2003). Accuracy was high for both the Arabic letters (mean: 95.4%, sd: 5.4%) and the Roman letters (mean: 96.7%, sd: 2.6%).

Table 3.

Results of the LMEM for Experiment 1 (monoscriptal participants), with Arabic letters (left) and Roman letters (right). β = estimated beta coefficient, z = z-value for beta coefficient, p = p-value for beta coefficient. *** p < 0.001, ** p < 0.01, * p < 0.05.

Arabic letters						Roman letters
Predictor	β	z	P			Predictor	β	z	P
(Intercept)	935.69	7.3	< 0.001	***		(Intercept)	821.96	274.6	< 0.001	* * *
Trial Order	−21.70	2.4	< 0.001	***		Trial Order	−6.29	−2.8	0.005	**
Previous RT	17.52	3.1	< 0.001	***		Previous RT	14.32	7.6	< 0.001	* * *
Complexity	12.53	4.20	0.003	**		Complexity	−3.20	−1.0	0.316
Distinctiveness	−3.16	4.1	0.442			Distinctiveness	−6.08	−2.3	0.024	*

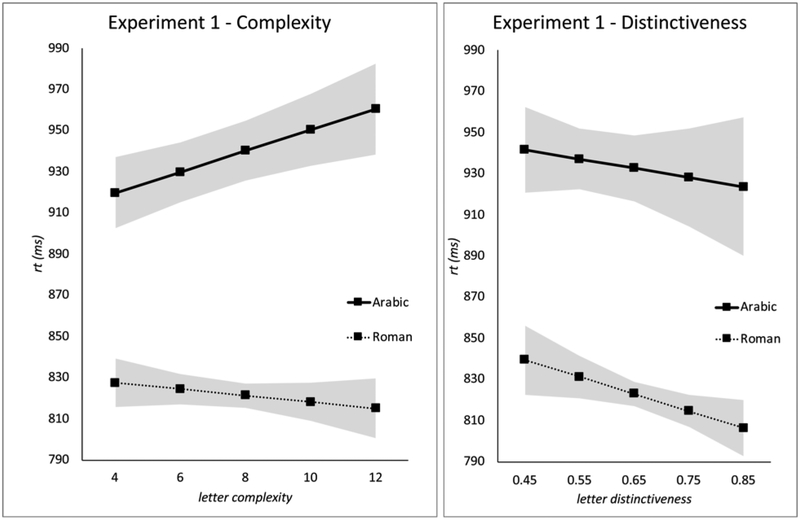
Figure 1. : Complexity and distinctiveness effects for monoscriptal participants.

Experiment 1 Left panel: RT (ms) on the y-axis, as a function of letter complexity in the Arabic (solid line) and Roman (dashed line) alphabets. Right panel: RT as a function of letter distinctiveness in the Arabic (solid line) and Roman (dashed line) alphabets. Error bands reflect 95% confidence interval around the fixed-effects estimates.

With regard to complexity (Figure 1 left), we replicate the finding of a significant positive relationship between letter complexity and RT among naïve observers of the Arabic alphabet (Wiley et al., 2016) with an effect size of 5.1ms increase in RT per additional visual feature (Table 3 left, p = 0.003). The previously reported “complexity benefit” (Wiley et al., 2016) for expert observers of the Arabic alphabet is also found here for expert observers of the Roman alphabet, with an effect size of −3.0ms/feature (p < 0.001). However, this is only if letter distinctiveness is not included as a regressor in the LMEM. When both letter complexity and letter distinctiveness are entered into simultaneous regression, there is no significant effect of letter complexity for the Roman alphabet (effect size of −1.6ms/feature, p = 0.316; Table 3 right and Figure 1 left).

With regard to distinctiveness, there is a significant effect (Figure 1 right, Table 1 right, p = 0.024) for the expert observers of the Roman alphabet. However, the naïve observers of the Arabic alphabet do not exhibit a significant effect of distinctiveness (Figure 1 right, Table 1 left, p = 0.442). In terms of effect size, for the Roman alphabet this equates to an 82ms faster response to a highly distinct letter (distinctiveness = 1) versus a highly non-distinct letter (distinctiveness = 0), compared to a non-significant 45ms benefit for the same comparison for the unfamiliar Arabic letters.

Summary:

We replicated the finding reported by Wiley et al. (2016) that naïve observes are slower to respond to more complex letters, whereas expert observers show an apparent effect in the opposite direction. However, we also showed that this effect of complexity disappears when controlling for letter distinctiveness. This finding indicates that the apparent “complexity benefit” is explained by the fact that complex letters tend to be relatively more distinct, although the variables are not entirely co-linear. The effect of distinctiveness is not found for naïve observers of the Arabic alphabet, which supports the hypothesis that it arises only after extensive experience with the entire set of letters. Finally, the findings reveal that the effect of distinctiveness that arises from expertise in one alphabet (Roman) does not transfer to an unfamiliar alphabet.

Experiment 2

Experiment 2 further investigates the role of distinctiveness and expertise, by including both monoscriptal participants (as in Experiment 1) as well as biscriptal participants with expertise with both alphabets. The biscriptal individuals had varying levels of expertise with Arabic, allowing us to examine if and how the amount of experience impacts the development of sensitivity to distinctiveness. The experimental procedures were the same as those described for Experiment 1, with differences as noted. In addition to evaluating effects of complexity and distinctiveness using the feature-based measures used in Experiment 1, we carry out a second set of analyses of the data set based on low-level visual metrics of complexity and distinctiveness, to determine the extent to which the findings are tied to a specific approach to defining complexity and distinctiveness.

Participants

82 participants, all from the Johns Hopkins University community, took part in one-hour sessions, receiving either course credit or $20 for their participation. The participants were categorized into three groups: Low-Proficiency Biscriptal (L-BS, n = 23): individuals who received instruction in reading and writing with the Roman alphabet during elementary school, and had completed fewer than 4 years of Arabic study; High-Proficiency Biscriptal (H-BS, n = 18): individuals with the same background as the L-BS group except with more than 4 years of experience with Arabic; and Monoscriptal (MS, n = 41): individuals who received instruction in reading and writing the Roman alphabet during elementary school, and reported no knowledge of Arabic or any language written in that script. The cutoff of 4 years of Arabic study was adopted based on analysis of an Arabic test of writing and reading by Wiley et al. (2016), indicating a marked difference in ability level after 4 years of study (likely distinguishing those who learned Arabic entirely from college course work, versus native or heritage speakers).

Procedure

The stimuli were the same as Experiment 1, but were presented using E-Prime 2.0 (Psychology Software Tools, Pittsburg, PA). 33 participants (17 MS, 9 L-BS, 7 H-BS) completed the experiment with both Roman and Arabic letters. The two alphabets were administered separately on two different days (with the order counterbalanced across participants). The remaining participants completed the experiment only with Arabic letters. There was a 50/50 ratio of same to different trials, and a total of 1,012 trials per session. Thus, for this analysis there were 22 “same” judgments of each letter.

Analysis 1: Feature-based metrics of complexity and distinctiveness

The same analysis was used as Experiment 1, with the additional regression predictors of Group and the interactions of Group X Complexity and Group X Distinctiveness. The Group variable was simple-coded with the MS as the reference level. A follow-up LMEM was conducted to compare the L-BS and H-BS separately (sum-coded).

In addition, the signal detection theory measures of sensitivity (d’) and bias (β) were also computed for each individual participant (Stanislaw & Todorov, 1999), using information from both the “same” and the “different” judgments. This allows for an evaluation of the possibility that differences in the effects of letter complexity or distinctiveness could be driven, at least in part, by different biases across the three groups to respond “same” or “different”. One-way ANOVAs were conducted for each of the measures (d’ and β) with the planned contrasts of MS versus L-BS and L-BS versus H-BS.

Results

Roman alphabet:

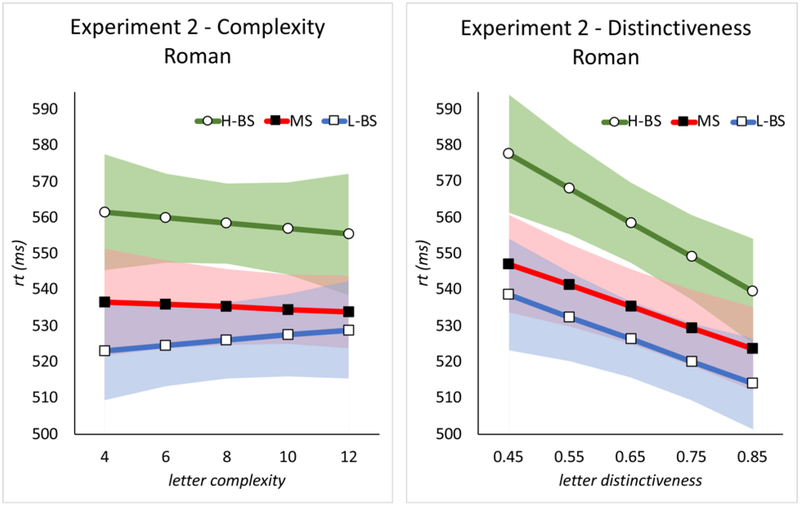
Accuracy was high for all groups (mean: 92%, 95%, and 94% for the MS, LBS, and H-BS, respectively). As in Experiment 1, when both letter complexity and distinctiveness were included in simultaneous regression (Table 4), the effect of complexity was not significant overall (p = 0.85), nor was there any significant interaction with Group (MS versus L-BS, p = 0.92, MS versus H-BS, p = 0.18). However, there was a significant main effect of distinctiveness (p < 0.001), again with no significant interaction with Group (MS versus L-BS, p = 0.38, MS versus H-BS, p = 0.82). As depicted in Figure 2 (right), the results are very similar to those obtained in Experiment 1 with the Roman alphabet—with which all three groups have high levels of expertise—the MS, L-BS, and H-BS participants all showed a positive effect of letter distinctiveness (effect size of 59ms, 62ms, and 96ms, respectively), but no effect of complexity (Figure 2 left).

Table 4.

Results of the LMEM for Experiment 2, with Roman letters. Group sum-coded (BS +1, MS −1). β = estimated beta coefficient, z = z-value for beta coefficient, p = p-value for beta coefficient. *** p < 0.001, ** p < 0.01, * p < 0.05.

Predictor	β	z	p
(Intercept)	539.99	125.57	< 0.001	***
Trial Order	−7.48	−1.85	0.06	.
Previous RT	16.54	8.58	< 0.001	***
Complexity	−0.32	−0.19	0.85
Distinctiveness	−8.13	−4.55	< 0.001	***
MS vs. L-BS	−9.07	−1.95	0.05
MS vs. H-BS	23.12	4.59	0.00	***
Complexity: MS vs. L-BS	−0.31	−0.11	0.92
Complexity: MS vs. H-BS	−4.14	−1.34	0.18
Distinctiveness: MS vs. L-BS	2.57	0.87	0.38
Distinctiveness: MS vs. H-BS	−0.98	−0.22	0.82

Figure 2. : Complexity and distinctiveness effects for Roman letters in monoscriptal, and low and high-proficiency biscriptal participants.

Experiment 2 Left panel: RT (ms) on the y-axis, as a function of letter complexity in the Roman alphabet. Right panel: RT (ms) on the y-axis, as a function of letter distinctiveness in the Roman alphabet. MS = monoscriptals, L-BS = low-proficiency biscriptals, H-BS = high-proficiency biscriptals. Error bands reflect 95% confidence interval around the fixed-effects estimates.

In terms of sensitivity, d’ was 3.44, 3.75, and 3.56 respectively for the MS, L-BS, and H-BS, and a one-way ANOVA revealed no significant effect of Group on d’ (F(2,30) = 1.54, p ≈ 0.23). In terms of bias, β was 0.43, 0.53, and 0.51 for the MS, L-BS, and H-BS, respectively. A one-way ANOVA revealed no significant effect of Group on β (F(2,30) = 0.51, p ≈ 0.60). Thus, the signal detection theory measures reveal no differences between the groups in terms of either their sensitivity or bias in performing the same/different judgment task with Roman letters.

Arabic alphabet:

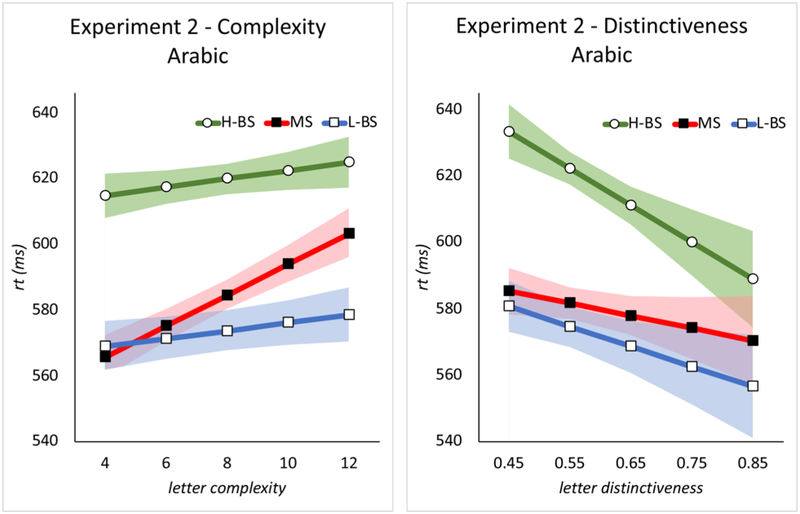
Accuracy was high for all groups (mean: 90%, 94%, and 95% respectively for the MS, L-BS, and H-BS). Unlike the results for the Roman alphabet, when both letter complexity and distinctiveness were included in simultaneous regression (Table 5), the effect of complexity remained significant (p < 0.001), however this was modulated by significant interactions with Group, such that the effect was greater in the MS compared to both the L-BS and H-BS (p’s < 0.001). There was also a significant main effect of distinctiveness (p < 0.001), but this too was modulated by a significant interaction with Group, specifically such that the effect was larger for the H-BS compared to the MS (p < 0.001) but not for the L-BS compared to the MS (p = 0.33). As can be seen in Figure 3 (left), these interactions reveal that there is a strong positive relationship between RT and letter complexity for the naïve, MS observers of Arabic, which is significantly weaker among the expert L-BS and H-BS observers. In contrast, the effect of letter distinctiveness (Figure 3 left panel) is strongest among those with the most expertise, the H-BS group.

Table 5.

Results of the LMEM for Experiment 2, with Arabic letters. Group sum-coded (BS +1, MS −1). β = estimated beta coefficient, z = z-value for beta coefficient, p = p-value for beta coefficient. *** p < 0.001, ** p < 0.01, * p < 0.05.

Predictor	β	z	p
(Intercept)	590.59	252.44	< 0.001	***
Trial Order	−8.72	−5.25	< 0.001	***
Previous RT	30.79	40.34	< 0.001	***
Complexity	5.84	4.19	< 0.001	***
Distinctiveness	−4.86	−3.52	< 0.001	***
MS vs. L-BS	−7.75	−4.49	< 0.001	***
MS vs. H-BS	38.31	18.49	< 0.001	***
Complexity: MS vs. L-BS	−8.64	−7.22	< 0.001	***
Complexity: MS vs. H-BS	−8.40	−6.27	< 0.001	***
Distinctiveness: MS vs. L-BS	−1.57	−0.98	0.33
Distinctiveness: MS vs. H-BS	−5.15	−3.75	< 0.001	***

Figure 3. : Complexity and distinctiveness effects for Arabic letters in monoscriptal, and low and high-proficiency biscriptal participants.

Experiment 2 Left panel: RT (ms) on the y-axis, as a function of letter complexity in the Arabic alphabet. Right panel: RT (ms) on the y-axis, as a function of letter distinctiveness in the Arabic alphabet. MS = monoscriptals, L-BS = low -proficiency biscriptals, H-BS = high-proficiency biscriptals. Error bands reflect 95% confidence interval around the fixed-effects estimates.

In terms of sensitivity, d’ was equal to 3.04, 3.54, and 3.67 respectively for the MS, L-BS, and H-BS groups. A one-way ANOVA revealed a significant effect of Group on d’ (F(2,79) = 4.14, p ≈ 0.02). Planned contrasts further indicated that d’ was significantly lower for the MS compared to the L-BS (p < 0.05), with no significant difference between the L-BS and H-BS (p > 0.1). In terms of bias, β was equal to 0.70, 0.83, and 0.69 respectively for the MS, L-BS, and H-BS. A one-way ANOVA revealed no significant effect of Group on β (F(2,79) = 1.51, p ≈ 0.23). Thus, the signal detection theory measures revealed that indeed, the biscriptal participants were more sensitive when processing Arabic letters compared to the monoscriptal participants, whereas there were no significant differences across the groups in bias to respond “same” or “different”. Overall, the results of the d’ analyses indicate that the reported differences in the effects of complexity or distinctiveness were not driven by differences in bias.

Amount of experience:

For the Roman alphabet, there was no significant interaction between either letter complexity or distinctiveness and Group—this is consistent with the fact that all three groups have extensive experience processing Roman letters; indeed, a sign of their expertise is that they show an effect of letter distinctiveness but not of complexity. For the Arabic alphabet, however, the letter complexity effect was significantly larger for the naïve observers (MS) compared to the experts (both L-BS and H-BS). With regard distinctiveness, those with the most expertise (H-BS) differed significantly compared to the MS observers, while those with less expertise (L-BS) did not.

In order to further evaluate a possible relationship between degree of expertise and magnitude of the effects of letter complexity and distinctiveness, a separate LMEM was carried out with only the two biscriptal groups, to test interactions between Group (L-BS versus H-BS) and letter complexity and distinctiveness. Reported in Table 6, the results of this LMEM confirm what can be seen in Figure 3: there is no effect of letter complexity for the expert Arabic observers, and no difference between the L-BS and H-BS (main effect of complexity, p = 0.32, interaction with Group, p = 0.99). However, the main effect of distinctiveness (p = 0.01) is driven by the H-BS group, with an effect size of 116ms for the H-BS compared to just 18ms for the L-BS (interaction with Group, p = 0.03).

Table 6.

Results of the LMEM for Experiment 2, comparing low- versus high-proficiency biscriptal participants’ judgments of Arabic letters. Group sum-coded (low −1, high +1). β = estimated beta coefficient, z = z-value for beta coefficient, p = p-value for beta coefficient. *** p < 0.001, ** p < 0.01, * p < 0.05.

Predictor	β	z	p
(Intercept)	599.1581	209.38	< 0.001	***
Trial Order	−9.81532	−4.7	< 0.001	***
Previous RT	31.30571	27.09	< 0.001	***
Complexity	1.66481	0.98	0.32558
Distinctiveness	−4.66873	−2.59	0.00959	**
L-BS vs. H-BS	16.6245	5.27	5.27	***
Complexity: L-BS vs. H-BS	−0.01002	−0.01	0.99448
Distinctiveness: L-BS vs. H-BS	−3.38939	−2.2	0.02747	*

Summary:

We replicated the finding that expert observers show a significant effect of letter distinctiveness, but not of letter complexity. However, this was found to be true only for highly-proficient individuals: while those with fewer than 4 years of Arabic differed from the naïve observers in showing a significantly reduced effect of letter complexity, they showed a much smaller effect of letter distinctiveness compared to highly proficient individuals. In fact, an analysis of the L-BS group alone shows that neither the effects of letter complexity nor distinctiveness were significant (p’s > 0.1).

Analysis 2: Low-level visual metric of letter complexity and distinctiveness

Although the visual features used to quantify letter complexity and distinctiveness have various degrees of empirical support (see e.g., Wolfe, 2000), there is certainly no clear consensus regarding what visual features are used for letter processing or even whether letter processing is based on visual feature detection versus template-matching (Grainger, Rey, & Dufau, 2008). Further, there is some degree of ambiguity in defining the specific features present within individual letter-shapes (e.g., what precisely is the distinction between slanted and horizontal/vertical lines? Does “S” contain a slanted line as well as curved lines? etc.).

Therefore, in order to provide alternative measures of letter complexity and distinctiveness that do not depend on defining visual features, we computed complexity and distinctiveness based on low-level visual information. Specifically, as an alternative measure of letter complexity we computed “parametric complexity” (perimeter squared divided by area; Pelli et al., 2006) and, as an alternative measure of letter distinctiveness, we used pixel overlap (proportion of shared black pixels) instead of the proportion of shared visual features⁴. Although we believe that these lowerlevel visual measures are less likely to be the appropriate level at which letter identification is taking place, they nonetheless provide some information regarding the extent to which the results are tied to the specific visual feature set and complexity/distinctiveness calculations we used.

We analyzed Experiment 2 as already described, replacing the visual feature-based measures with the pixel-based measures. The results (Supplementary Materials, Tables S1–S3) show a highly similar pattern of results, with only two exceptions. First, the non-significant interaction term of Group (MS vs. L-BS) X distinctiveness for Arabic letters (reported in Table 5) is significant when based on pixel overlap (p < 0.05; see Table S2). Second and relatedly, the significant interaction between the L-BS and H-BS in terms of letter distinctiveness for Arabic letters (reported in Table 6) is not significant when measured by pixel overlap (p ≈ 0.47). Thus, these two findings suggest that the lower-level measure of letter distinctiveness (i.e., pixel overlap) is a relatively stronger predictor for the L-BS participants than is the feature overlapbased measure.

Overall, the interpretation remains the same when the measures of complexity and distinctiveness are derived from lower-level visual information: greater letter complexity is associated with slower RT only for naïve observers, whereas greater letter distinctiveness is associated with faster RT only for observers with some expertise.

Discussion

We investigated the role expertise plays in the visual processing of letter-shapes. Specifically, we sought to determine how letter complexity and distinctiveness contribute to the perceptual processing of letters. We examined the effects for both Roman and Arabic letters among groups of individuals with different amounts of experience. Our findings can be summarized as follows. First, we found that among expert observers there is an effect of letter distinctiveness of similar magnitude for both alphabets, such that distinctiveness contributes significantly to processing time. Second, for naïve viewers, complexity contributes significantly to processing time. Third, we found that letter complexity was not a significant effect for experts when included in simultaneous regression with letter distinctiveness. Thus, the complexity benefit for expert viewers reported by Wiley et al. (2016) would seem to be due to the strong correlation between complexity and distinctiveness. While more complex letters tend to be more distinctive, it is knowledge of a letter’s distinctiveness relative to the other shapes within the set of letters that best explains expert letter processing. Fourth, we found strong evidence that expert letter processing requires extensive experience, given that biscriptal participants who had only a few years’ experience with Arabic did not show an effect of letter distinctiveness. Furthermore, consistent with their intermediate expertise between experts and naïve viewers, low-proficiency individuals also did not show the effect of complexity exhibited by the naïve monoscriptal participants. Finally, it is also worth pointing out that we found that expertise with one script (Roman) does not seem to transfer to another (Arabic). This result is all the more striking, given that the set of Arabic letter-shapes used in this experiment were chosen to be those that are most visually similar to Roman letters (such as Arabic ‘ط’ and Roman ‘b’).

The visual features used to define letter complexity and distinctiveness include those that have long been proposed in the literature on feature detection (see Palmer, 1999), with some more contemporary additions, such as “diacritic marks” that are critical for letter recognition in Arabic (e.g., Perea et al., 2016; Wiley et al., 2016). The process used to decompose the letters into a list of visual features, which was first applied by Wiley et al. (2016) to the Arabic alphabet, was applied here to the Roman alphabet. The fact that we find the same relationships between letter complexity and distinctiveness for experts regardless of the alphabet makes it less likely that the results are an artifact of the choice of visual features, or the way in which complexity and distinctiveness were computed. Nonetheless, we considered whether alternative, low-level visual measures of complexity and distinctiveness would yield similar results. Using perimetric complexity and pixel overlap, we still found effects of complexity for naïve observers only, and distinctiveness for expert observers only. While this convergence may be interpreted as indicating that pixel- and feature-based measures are equally relevant, we would argue that this is not necessarily the case. Instead, it may be that the two classes of measures are relevant at different processing stages, and will explain more or less variance depending on the task. Furthermore, one advantage of feature-based measures is that they are relatively invariant to changes in font, whereas pixel-based measures will be highly specific to stimulus format. In other words, there can be increased confidence that feature-based measures will generalize across a larger range of stimuli, whereas pixel-based measures must be re-computed for each stimulus set and may be greatly affected by font.

Overall, we see a learning trajectory in which feature complexity plays an early role while increasing knowledge of the learning set provides the basis for distinctiveness-based processing. The finding that letter distinctiveness influences the performance of expert observers on same/different judgments is all the more striking, given that knowledge about what other shapes exist within the set (i.e., the alphabet as whole) is not relevant to the task, as evidenced by the fact that naïve observers very accurately complete the task without this knowledge. It would be important to understand the learning mechanisms that underlie these representational changes. While some have reported that experts attend to only a subset of features within a letter (e.g., Fiset et al., 2008, 2009), this evidence considers only a set of pre-defined elementary features such as lines and curves, and cannot rule out that experts use other features as well. One possibility is that expertise leads to the detection of new visual features. This type of expertise effect is consistent with findings in perceptual learning research (e.g. Goldstone, 1998; Kellman & Garrigan, 2009; Sireteanu & Rettenbach, 2000).

The possibility that experts may learn to detect different and/or more visual features suggests that the dimensionality of letter representations (in psychological space) might change with expertise. Relevant to this, Rouder (2001, 2004) reported a striking difference between the effect of set size for unidimensional stimuli (i.e., horizontal lines) versus multidimensional stimuli (i.e., letters) in an absolute identification task. Rouder reported that for unidimensional stimuli, identification performance was hindered with increasing set size: two horizontal lines differing only in length were less accurately identified when they were part of a set of 6 compared to a set of 2. In other words, the psychological distance between the horizontal lines decreased when they formed part of a larger set. This result is readily explained by limited processing capacity. The unexpected result was that the reverse was found for letters—letters were more readily perceived when they were identified within a set of 6 versus 2 letters, indicating that the psychological distance between the letters increased with the larger set size. Rouder (2001) indicates that he did not have an explanation for this very interesting phenomenon and, to the best of our knowledge, this phenomenon remains unexplained.

Following up on this idea, we evaluated the possibility that dimensionality increases with increasing expertise by conducting a principal component analysis (PCA)⁵ based on median RT to the “different” pairs of Arabic letters (following the procedure of Courrieu, Farioli, & Grainger, 2004) for both the naïve (MS) and expert (combined L-BS and H-BS) observers (see Supplementary Materials).

There are two results worth highlighting. Most directly relevant to this issue: overall, more variance is explained in fewer dimensions for the naïve versus the expert observers. Not only does the first dimension alone explain more for the naïve observers (23%) compared to the experts (17%), more than half (51%) of the variance is explained cumulatively by the first three dimensions for the naïve observers, whereas the top three dimensions explain just 40% for the experts (five dimensions are required to explain more than 50% of the variance for the experts). With regard to an interpretation of the dimensions, we found that the correlation between the naïve and expert observers on the first dimension is high (0.80), indicating very similar loadings for the letters along this dimension for both groups. A qualitative interpretation of this dimension suggests a representation of curves oriented to the right or left. The correlation between the groups decreases across the subsequent dimensions. This could be either because the dimensions are ranked differently for expert and naïve observers in terms of relative importance, or because the content of the representations differs between the groups.

These PCA results suggest that although expert and naïve observers may share dimensions of letter representations, experts’ letter knowledge is distributed across more dimensions, with less information carried by any single dimension, relative to naïve observers. Taken together with the findings from the two experiments reported on here, the implication is that expert letter perception entails processing different/additional visual features, which seem to be determined, at least in part, by the distribution of features across the set of letters in the alphabet. These findings further our understanding of the nature of letter processing, and more generally provide insight into the nature of the perceptual changes provided by expertise. One possibility raised by these results is that Rouder’s findings (2001, 2004) might be at least partly explained by expertise differences, namely that participants are likely to have had extensive experience with letters compared to much less experience with horizontal lines of slightly different lengths (a novel task).

Finally, in future research, among other things it will be important to understand if and how experts’ perceptual representations of letters affect their performance in other letter-based tasks such as word reading.