A Gradient in Metaphase Tension Leads to a Scaled Cellular Response in Mitosis

Summary

During mitosis, motor proteins associate with microtubules to exert pushing forces that establish a mitotic spindle. These pushing forces generate opposing tension in the chromatin that connects oppositely attached sister chromatids, which may then act as a mechanical signal to ensure the fidelity of chromosome segregation during mitosis. However, the role of tension in mitotic cellular signaling remains controversial. In this study, we generated a gradient in tension over multiple isogenic budding yeast cell lines by genetically altering the magnitude of motor-based spindle forces. We found that a decreasing gradient in tension led to an increasing gradient in the rates of kinetochore detachment and anaphase chromosome mis-segregration, and in metaphase time. Simulations and experiments indicated that these tension responses originate from a tension-dependent kinetochore phosphorylation gradient. We conclude that the cell is exquisitely tuned to the magnitude of tension as a signal to detect potential chromosome segregation errors during mitosis.

Introduction

Eukaryotic cells must faithfully segregate their chromosomes to daughter cells during mitosis. Failure to properly segregate results in aneuploidy, an improper chromosome number condition associated with certain cancers as well as birth defects (Kops et al., 2005). During metaphase, replicated chromosomes are aligned at the center of a mitotic spindle, and each sister chromatid must be bi-oriented, i.e. connected to microtubules emanating from opposite spindle poles, to ensure proper segregation following anaphase (Walczak et al., 2010). To prevent chromosome segregation errors during mitosis, cells employ a fail-safe mechanism to detect and correct bi-orientation errors prior to anaphase onset (Hepperla et al., 2014; Khodjakov and Pines, 2010; Lew and Burke, 2003; Maresca and Salmon, 2010; Musacchio and Salmon, 2007; Pinsky and Biggins, 2005).

We hypothesize that a key difference between properly and improperly oriented chromosomes is the magnitude of the tension that builds up from the stretching of the chromatin that connects sister kinetochores during metaphase. Properly bi-oriented sister chromatids are pulled apart from each other, i.e., towards opposite spindle poles, by pole-separating forces that are generated by molecular motors within the mitotic spindle. Recent work suggests that tension, which builds in opposition to these pole-separating forces, is substantial (Chacon et al., 2014; Ye et al., 2016). In contrast, for erroneous syntelic attachments, in which both sister chromatids are attached to the same pole, the magnitude of tension is predicted to be much lower, due to the loss of pole-separating spindle forces on the improperly connected sister chromatid pair. Although reports in the literature suggest that cells may sense and respond to tension as a readout of chromosome orientation (Biggins and Murray, 2001; Stern and Murray, 2001), this issue remains controversial (Chmátal et al., 2015; Magidson et al., 2016; Ye et al., 2015).

Early reports found that in meiotic cells, the metaphase to anaphase transition could be rapidly effected by applying external forces to chromosomes (Li and Nicklas, 1997; Nicklas, 1997; Nicklas and Koch, 1969), an observation that has since been confirmed using a different modality of force application (Itabashi et al., 2012). These studies provided a basis for hypothesizing that tension could act as a mechanical error detection signal during mitosis. A subsequent series of studies in budding yeast demonstrated that cells entering mitosis with unreplicated (and thus tensionless) chromosomes elicited an error correction pathway response, similar to that of improperly oriented chromosomes (Biggins and Murray, 2001; Pinsky et al., 2006; Stern and Murray, 2001). However, the applicability of this mechanism in cells entering a normal mitosis with duplicated chromosomes remains unknown. Other studies have examined whether an error correction pathway response could be elicited when tension was lowered, but not completely abrogated, by using the microtubule stabilizing drug Taxol (Elowe et al., 2007; Waters et al., 1998). However, Taxol-mediated stabilization of microtubule dynamics may itself disrupt the error correction process, and the discovery that Taxol may also destabilize kinetochore-microtubule attachments, similar to an error correction response, complicates the interpretation of these studies (Rizk et al., 2009). Finally, recent work has now argued that cells use other factors, such as the positioning of chromosomes relative to the spindle equator, as readouts for improper chromosome orientation (Chmátal et al., 2015; Ye et al., 2015). Therefore, the importance of tension as a direct mechanical signal that allows the cell to detect potential chromosome segregation errors during mitosis remains controversial.

In our previous work, we used a microscopy-based technique to determine whether the magnitude of metaphase tension in budding yeast was large enough to act as a mechanical signal that could allow the cell to detect chromosome orientation errors during mitosis. Tension builds up in the region between sister kinetochores (Fig 1A, left), and is manifested as the stretching of the chromatin material in a manner analogous to the stretching of a spring (Fig 1A, right, “inter-kinetochore spring”). The magnitude of tension (F_tension) for properly attached sister chromosomes must be larger than random, thermal forces in order for tension to act as a mechanical signal that could be detected by the cell (Fig. 1B). We previously developed an optical method that allowed for estimation of tension during mitosis in unperturbed, living cells by motion tracking of fluorescent, centromere-associated lacO arrays (Chacon et al., 2014). Our results demonstrated that F_tension ~ 4–5 pN in budding yeast (Fig. 1C), which is nearly three orders of magnitude larger than is predicted for random thermal forces (F_thermal ~ 0.01 pN) (Chacon et al., 2014). Thus, tension is substantial, well above the minimum thermal noise threshold, and so is large enough to potentially provide a tension-based mechanical signal to ensure the fidelity of chromosome segregation during mitosis in budding yeast. However, whether the magnitude of tension is read out by the cell and transduced into an important chemical signal during mitosis remains an open question.

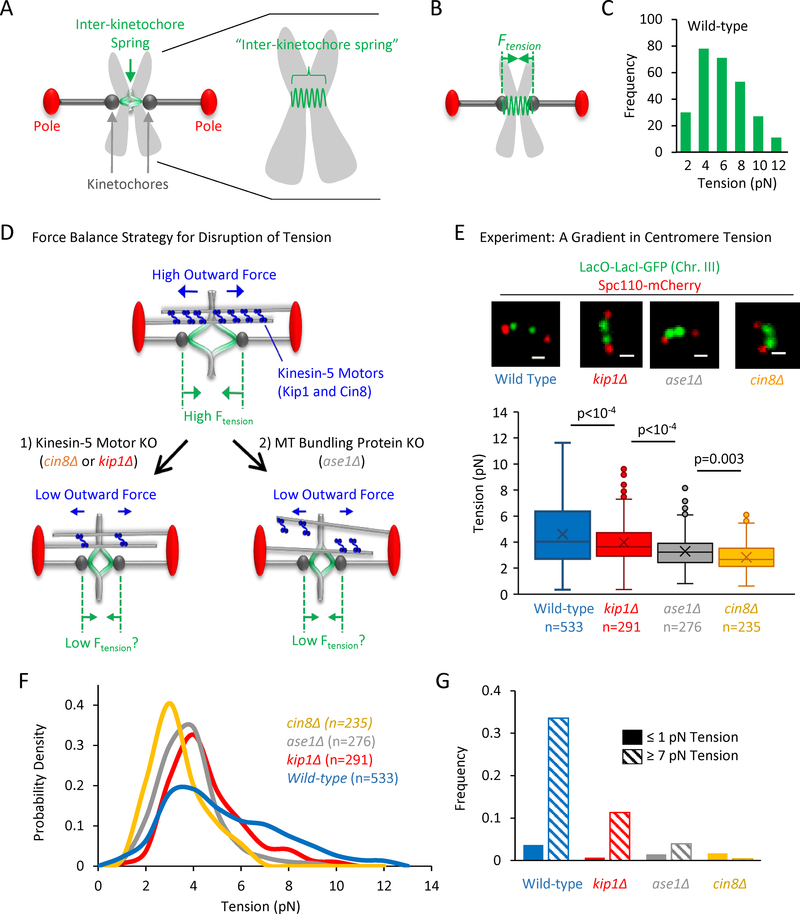
Figure 1: Generation and measurement of a tension gradient.

(A) Left: Cartoon of a budding yeast metaphase spindle. Right: Detailed cartoon of duplicated sister chromsomes, including the inter-kinetochore spring that connects the two sister kinetochores. (B) Left: F_tension (green) represents tension that is generated in the inter-kinetochore spring as a result of molecular motors that push apart the spindle poles (red). (C) Distribution of tension magnitudes as measured in wild-type cells (see materials and methods and (Chacon et al., 2014)). (D) Cartoon highlighting a strategy for suppressing tension by experimentally reducing outward forces. Top: Generation of outwardly directed spindle forces by Kinesin-5 motors (blue) that crosslink antiparallel spindle microtubules (grey) leads to tension (green). Bottom-left: One strategy for reducing outward motor-based forces was to selectively delete Kinesin-5 motor protein genes. Bottom-right: A second strategy involved disrupting microtubule bundling (Fig. S1A), therefore reducing the force-producing crosslinking of Kinesin-5 motors. (E) Top: Representative images of lacO spot spacings in wild type and mutant budding metaphase spindles (scale bar, 500 nm). Bottom: Measured tension in these strains reveals a decreasing gradient in average metaphase tension (p-values calculated from a least squares means multiple comparison procedure using a Bonferonni correction; bars: quartiles, marker: average, box: 1^st quartile, line in center of box: median; see also Fig. S1B–H). (F) Tension probability density function for the wild-type strain and each tension mutant (12 bins in each histogram, smoothed lines shown). (G) Relative frequency of low tension magnitudes (≤ 1 pN) vs high tension magnitudes (≥ 7 pN) in each strain.

In this study, we generated a gradient in tension across multiple isogenic cell lines by genetically altering the molecular motor-based pole-separating spindle forces. This gradient allowed us to quantitatively demonstrate the presence of a highly sensitive, tension-based error detection pathway in yeast metaphase spindles. These results were obtained from cells that had robust microtubule dynamics and proper chromosome replication, and in the absence of drug treatments. We found that a decreasing gradient in tension magnitudes led to an increasing gradient in population-wide kinetochore detachments, and this gradient depended upon functional Aurora B kinase. In computational simulations, we predicted that our experimentally observed tension-dependent kinetochore detachment gradient could occur as a result of a gradient in kinetochore phosphorylation. Using both phosphorylation westerns and mass spectrometry, we observed a gradient of increasing phosphorylation with decreasing tension for the critical kinetochore protein Dam1. Thus, the cell is exquisitely and sensitively tuned to the magnitude of tension during mitosis, with lower values of tension eliciting an increased cellular response.

Results

Genetic manipulation of metaphase tension in budding yeast

In order to test the role of tension as a mechanical signal for chromosome orientation, we sought to modulate the magnitude of metaphase tension during budding yeast mitosis. Outwardly directed forces from Kinesin-5 motors are transmitted to the chromosomes via kinetochore microtubules, leading to stretching of the inter-kinetochore chromatin spring (Fig. 1D, top), and giving rise to an inwardly directed tension (Fig. 1B). Therefore, to modulate tension, we directed our efforts at Kinesin-5 molecular motors, the active source of the forces against which tension is generated (similar to previous work. (Vallot et al., 2017)). We reasoned that by targeting outward force generation by Kinesin-5 motors, tension could be modulated without disruptions to chromosome structure or replication, alterations to kinetochore structure, or suppression of kinetochore microtubule dynamics, which would provide a powerful method for quantitatively evaluating the sensitivity of the cell to tension as a mechanical signal during mitosis.

To modulate outward force generation by Kinesin-5 motors, we first individually knocked out each of the two force-generating Kinesin-5 molecular motors in budding yeast, Cin8 and Kip1 (Fig. 1D, bottom left) (Hildebrandt and Hoyt, 2000). Second, we knocked out Ase1, an important microtubule bundling protein in the yeast mitotic spindle (Janson et al., 2007; Schuyler et al., 2003). The absence of Ase1 leads to increased spacing between spindle microtubules (Gardner et al., 2008), (Fig. S1A; t = −2.87, p = 0.0043), likely facilitating a reduction in the dynamic crosslinking of Cin8 and Kip1 between antiparallel microtubules (Fig. 1D, bottom right). We predicted that reduced Kinesin-5 crosslinking would lower the Kinesin-5 mediated outward force generation in the metaphase spindle without any change in the overall expression levels of the Kinesin-5 motors (Fig. 1D, bottom right) (Hepperla et al., 2014).

To test whether the mutants as described above would lead to reduced metaphase tension, we first verified our previous results by measuring average metaphase tension in the wild-type budding yeast cells (F_tension= 4.6 pN) (Chacon et al., 2014), and then used our published protocol to measure metaphase tension for each of the mutants (Fig. 1E; Fig. S1B–H). Here, we note that while bipolar metaphase spindles were included in our analysis, the spindles with spatially separated pole markers but non-separated centromere-associated lacO arrays were counted as spindles with detached kinetochores, and so were not included in the tension measurements. We found that each of the mutants had a unique tension magnitude in metaphase, such that cin8Δ cells had the lowest average tension (Fig. 1E, bottom, 2.8 pN), while ase1Δ and kip1Δ cells had average tension magnitudes that were between the wild-type and cin8Δ values (Fig. 1E, bottom, ase1Δ = 3.3 pN; kip1Δ = 4.0 pN). The differences in mean tension were statistically significant between the strains (F_3,1069 = 70.31, p<0.0001), and, importantly, the average tension magnitudes trended downward for the motor mutants (p < 0.0001 wild-type vs kip1Δ, p < 0.0001 kip1Δ vs ase1Δ, and p = 0.003 ase1Δ vs cin8Δ). We note that the decreasing magnitudes of mean tension across our motor mutants were correlated with decreased average spacings between lacO-lacI-GFP spots in these strains (Fig 1E, top), consistent with the hypothesis that tension is proportional to inter-kinetochore spring stretch distance (Fig. 1E, bottom). We then examined the dynamic range of tensions in the wild-type and in the tension mutant cells. As shown in the histograms of tension magnitudes for each cell type (Fig 1F), the dynamic range of tensions was unique for each strain, but, interestingly, the higher tension “tail” of the distribution was most affected in the mutant cells. Specifically, the wild type cells had a long tail of higher tension magnitudes, which was gradually eliminated in the tension mutants. Thus, we compared the frequency of cells with low tension (≤ 1 pN), to the frequency of cells with high tension (≥ 7 pN) (new Fig. 1G). We found that while the frequency of cells with low tension (≤1 pN) was relatively unchanged across the cell lines, the frequency of cells with high tension (≥7 pN) was strongly reduced in a dose-dependent fashion in our low tension cell lines (Fig. 1G). Thus, we then used this tension gradient as tool to explore the response of the cell to moderate, step-wise decreases in the magnitude of metaphase tension.

Kinetochore detachment scales with tension in a dose-dependent fashion

To explore the response of the cells to a step-wise decrease in the average tension magnitudes, we reasoned that if the cell did indeed sense tension to detect errors in chromosome orientation during mitosis, the cell might interpret the low tension in our mutants as a signal of improperly oriented chromosomes (Fig. 2A). We therefore tested whether the cellular response to our low tension mutants would resemble the cellular response to improperly attached chromosomes, similar to previous work with unreplicated chromosomes (Biggins and Murray, 2001; Pinsky et al., 2006; Stern and Murray, 2001). The primary response to an error in chromosome orientation is the destabilization of kinetochore-microtubule attachments (Kapoor et al., 2000), thereby creating detached kinetochores (O’Connell et al., 2008; Pinsky et al., 2006). Thus, we asked whether the incidence of detached kinetochores was increased in our tension mutants (Fig 2A).

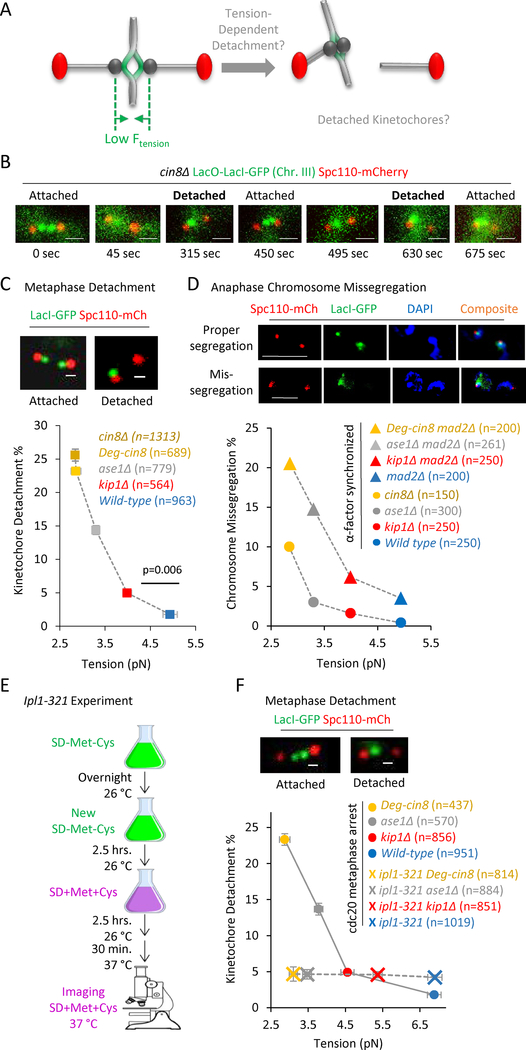
Figure 2: A decreasing gradient in tension leads to an increasing gradient in both detached kinetochores at metaphase, and mis-segregation of chromosomes in anaphase.

(A) Cartoon demonstrating a potential cellular response to low tension: a low metaphase tension (left) could lead to an increase in detached kinetochores (right). (B) Images from time series in metaphase cin8Δ mutants demonstrating dynamic attachment (see also Fig. S3A) (scale bars, 1 μm). (C) Top: Representative images of lacO-lacI-GFP spots in cells with properly attached kinetochores (left), and detached kinetochores (right) in budding yeast (scale bars, 500 nm). Bottom: Detachment rate vs tension in wild type and mutant strains. The tension and detachment rate in the Degron-Cin8 cells (dark yellow) was similar to that in cin8Δ cells (light yellow) (see also Fig. S2A, B). The detachment rate increased substantially with decreasing tension (z = −15.49, p < 0.0001, Cochran-Armitage trend test), and the detachment rate was significantly increased even when average tension was decreased by as little as 0.9 pN (Χ² = 11.91, p = 0.006). (D) Top: Representative images of lacO-lacI-GFP spots (green) and chromosomes (blue, DAPI) in anaphase cells with proper chromosome segregation (top), and representative images of lacO-lacI-GFP spots (green) and chromosomes (blue, DAPI) in anaphase cells with improper, missegregated chromosomes (bottom) (scale bars, 5 μm). Bottom: Anaphase chromosome missegregation rate vs tension in a mad2Δ strain background (triangles; z=−6.16, p<0.0001, Cochran-Armitage trend test). Note that detachment rates were similar regardless of the presence or absence of Mad2 (Fig. S3C). The anaphase missegregation rate was reduced in cells with normal Mad2 expression (circles; Χ² = 36.61, p < 0.0001). (E) Experimental protocol for deactivating Ipl1 in ipl1–321 experiments. (F) Top: Representative images of lacO-lacI-GFP spots in cells with properly attached kinetochores (left), and detached kinetochores (right) in budding yeast strains harboring the ipl-321 allele (scale bars, 500 nm). Bottom: Detachment rate vs tension in wild type and tension mutant strains in Cdc20 arrested cells at 37 °C (circles; tension measurements in Fig. S2D–E), and detachment rate vs tension in wild type and tension mutant strains in cells that harbored the ipl1–321 allele, and that were Cdc20 arrested at 37°C (crosses; tension measurements in Fig. S2D,F). The detachment rate increased substantially with decreasing tension for the Cdc20 arrested cells (Χ² = 169.70, p < 0.0001), but the inactivation of Ipl1 abrogated this dependence (Χ² = 0.27, p = 0.966). All panels: error bars=SEM.

To detect kinetochore detachments using a microscope-based assay, we noted that properly attached chromosomes/kinetochores appeared as two separated green spots between the red spindle poles in our strains with a lacI-GFP expressing strain and 33 lacO repeats inserted 1.1 kb 3′ to CEN3 (Fig. 2B, top left) (Pearson et al., 2001). In contrast, we reasoned that when one chromosome/kinetochore became detached, the separated lacO spots would collapse into a single, diffraction-limited spot, proximal to the spindle pole associated with the remaining attachment (Fig 2B, top right) (O’Toole et al., 1999). This reasoning is consistent with (1) observations that lacO spots collapse into a single diffraction-limited spot in the absence of microtubules (i.e., with Nocodazole treatment) (Chacon et al., 2014), and (2) our measurements of lacO-lacI-GFP fluorescence intensity measurements for the single lacO spots, which were approximately twice as bright as two separated lacO spots in the same field of view (Fig. S2C). To verify that kinetochore detachments occurred dynamically during metaphase, we performed time-lapse microscopy, and observed detachment and reattachment events in the mutant strains. (Fig 2B and Fig. S3A).

To determine the relative rates of kinetochore detachment in our wild-type and tension mutant cells, we collected images of individual metaphase spindles for each strain (n > 500 images for each strain), and then counted the number of metaphase spindles with two separated lacO spots (e.g., attached kinetochores), and the number of spindles with a single, off-axis lacO spot near to one pole (e.g., at least one kinetochore detached) (Fig. 2C, top). We found that the ratio of detachments varied significantly across strains (Χ² = 248.13, p < 0.0001), and was higher in all of the motor mutant strains as compared to wild type cells (Fig. 2C; p ≤ 0.0006 all comparisons). Further, there was a statistically significant increase in detachments even when average tension was decreased by as little as 0.9 pN (Χ² = 11.91, p = 0.006, wild type to kip1Δ). Strikingly, the detachment rate scaled with tension in a dose-dependent manner: the mutants with lower average tension magnitudes had a higher detachment rate, and those with higher tension had a reduced detachment rate (Fig 2C; z = −15.49, p < 0.0001, Cochran-Armitage trend test). These results suggest that metaphase cells are exquisitely sensitive to tension, leading to a population-wide, dose-dependent kinetochore detachment response that directly scales with the magnitude of average tension.

Uncorrected kinetochore detachments persist into anaphase in low tension mutants

To verify that our lacO microscopy assay was effective in properly detecting detached chromosomes/kinetochores, we reasoned that if cells with detached kinetochores were allowed to enter anaphase, the chromosomes with detached kinetochores may be mis-segregated. Thus, we measured the anaphase chromosome mis-segregation rates in wild-type cells, and in our tension mutant cell lines.

To allow the cells to enter anaphase regardless of attachment status, the spindle assembly checkpoint protein Mad2 was knocked out in all of our cell lines (Cimini et al., 2003; Gorbsky et al., 1998; Li and Murray, 1991). Because cin8Δ-mad2Δ cells were not viable, we used a previously described Cin8-degron mutant (Kotwaliwale et al., 2007), which, under conditions of Cin8 degradation, had a similar tension magnitude (F_2,554 = 0.25, p = 0.77, Fig. S2A–B) and detachment rate (Χ² = 0.82, p = 0.36, Fig. 2C) as compared to the cin8Δ cells (See STAR methods for details).

To detect mis-segregated chromosomes during anaphase in synchronized mad2Δ cells, we adapted a previously described assay (Miller et al., 2016) in which we released mutant and wild type cells from an alpha factor arrest, and, once the population had entered anaphase, we fixed the cells, stained with DAPI, and then scored cells for unequal distribution of green Chr. III lacO spots into the nuclei of each daughter cell (Fig 2D, top). We found that in the mad2Δ strain background there was a dose-dependent increase in anaphase mis-segregation rates with decreasing tension (Fig. 2D, bottom, triangles; z=−6.16, p<0.0001, Cochran-Armitage trend test). Of note, our observed anaphase chromosome mis-segregation rates in mad2Δ cells (Fig. 2D, triangles) were similar to our metaphase kinetochore detachment rates as described above (Fig. 2C), which further validated our metaphase detachment results via an alternative, previously published approach. Persistent low tension in our tension mutants therefore led to large-scale mis-segregation of chromosomes in the mad2Δ background cell lines, due to increased rates of metaphase kinetochore detachment. As would be expected, the overall magnitude of anaphase chromosome mis-segregation was lower with Mad2 present as compared to our mad2Δ cells (Fig 2D; Χ² = 36.61, p < 0.0001, Mad2 background main effect). However, the metaphase kinetochore detachment rate was unaffected by the presence or absence of Mad2 (Fig S2H; Χ² = 0.09, p = 0.76, Mad2 background main effect).

Tension-dependent detachment gradient depends on Aurora B

We then asked whether our observed tension-dependent detachment phenotype could be a specific consequence of the cell activating its error correction machinery in response to low tension. Aurora B has been shown to play a key role in destabilizing incorrect kinetochore microtubule attachments during metaphase, perhaps in response to a low tension signal (Biggins and Murray, 2001; Cimini et al., 2006; Hauf et al., 2003; Kallio et al., 2002; Lampson and Cheeseman, 2011; Lampson et al., 2004). The yeast homolog of Aurora B is Ipl1, which is essential for cell survival (Biggins et al., 1999; Carmena and Earnshaw, 2003). To test the role of Ipl1 in our observed tension-dependent detachment gradient, we used a well-characterized temperature sensitive allele, ipl1-321, which leads to inactivation of Ipl1 when cells are shifted to the restrictive temperature of 37 °C (Biggins et al., 1999; Keating et al., 2009). However, deactivating Ipl1 in asynchronous populations of cells causes defects that accumulate at earlier stages of mitosis (Jin et al., 2012; Marco et al., 2013; Tanaka et al., 2002). To prevent these defects from complicating our analysis, we depleted Cdc20 to arrest our cells in metaphase before shifting temperatures to 37 °C to deactivate Ipl1 (Fig. 2E). Cdc20 depletion was accomplished by shifting yeast cells harboring Cdc20 under the control of the Met promoter into media containing high concentrations of methionine and cysteine, as previously described (Fig. 2E) (Keating et al., 2009).

Using this protocol, we first evaluated both metaphase detachment and tension in cells that were arrested in metaphase via Cdc20 depletion and then shifted to 37 °C (Fig. 2F (circles, detachment rates); Fig S2E (tension)). Differences in mean tension between the cell lines remained statistically significant within the Cdc20 arrested strains (F_3,665 = 124.05, p<.0001, Fig. S2D,E), and, similar to our previous observations (Fig. 2C), we observed a trend of increasing metaphase detachment rates with decreasing average tension for the control Cdc20 metaphase-arrested cells (Fig. 2F, circles; z = −12.79, p < 0.0001, Cochran-Armitage trend test). These results were also similar to cells that had the ipl1-321 allele, but were measured at the 26 °C permissive temperature, allowing Ipl1 to remain active (Fig. S3B; z = −8.14, p < 0.0001, Cochran-Armitage trend test). Importantly, we then measured tension and detachment rates for Cdc20 metaphase-arrested cells that harbored the ipl1-321 allele, and that were shifted to 37 °C, thus inactivating Ipl1 (Fig. 2F (crosses, detachment rates); Fig. S2D,F (tension)). We found that the dose-dependent relationship between detachment and tension was lost when ipl1 was deactivated (Χ² = 0.27, p = 0.966) (Fig. 2F, crosses), even though tension differences remained statistically significant across the ipl1 restrictive tension mutant strains (Fig. S2F; F_3,1151 = 139.43, p<.0001). Here, the cells with inactivated Ipl1 had a characteristic basal detachment rate that remained constant regardless of tension magnitude (Fig 2F, crosses). Similarly, in cells with the ipl1–321 allele, the anaphase mis-segregation rate was independent of tension (Fig S3E).

Taken together, our metaphase kinetochore detachment and anaphase chromosome mis-segregation results strongly suggest that small reductions in tension activate the cellular error correction machinery in a dose-dependent manner. Ipl1 has been previously implicated in tension-dependent error correction (Biggins and Murray, 2001; Cimini et al., 2006; Hauf et al., 2003; Kallio et al., 2002; Lampson and Cheeseman, 2011; Lampson et al., 2004), and so the loss of the tension-dependent detachment and the anaphase chromosome mis-segregation rate gradients upon inactivation of Ipl1 strongly suggests that our observed gradient in detachment rates is a direct and specific response to decreasing tension magnitudes.

Mad2-dependent metaphase time scales with tension in a dose-dependent fashion

To further investigate the cellular response to decreasing tension, we predicted that an increase in detachment rate may lead to a concurrent increase in metaphase time, since the spindle assembly checkpoint would likely cause a delay in anaphase onset in response to detached kinetochores (Foley and Kapoor, 2013; Lew and Burke, 2003; Musacchio and Salmon, 2007). Therefore, we tested whether there was a metaphase delay in our tension mutants. We measured metaphase time by performing time-lapse imaging in which we followed the spindles poles of yeast cells from pole duplication to anaphase, and then we plotted spindle length vs time for each of our cells (Fig 3A). These plots were then used to measure the average time spent in metaphase (Fig 3A).

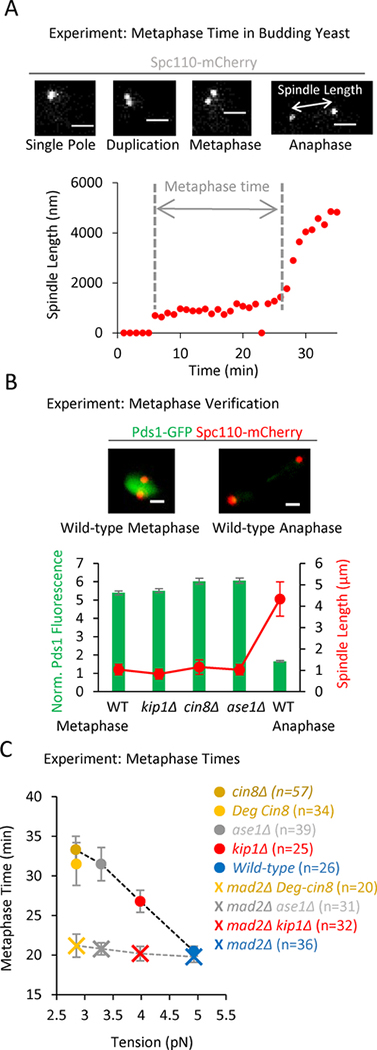
Figure 3: A decreasing gradient in tension leads to an increasing gradient in metaphase times.

(A) Top: Representative images of budding yeast Spc110-mCherry spindle pole markers taken from a time lapse series of a cell going through mitosis (scale bars, 1500 nm). Bottom: Plot of spindle length vs time. Recorded metaphase time shown in grey. (B) Top: Representative images of Pds1-GFP fluorescence in budding yeast cells at metaphase (left) and anaphase (right) (scale bars, 1500 nm). Bottom: Quantification of Pds1-GFP intensity at metaphase-like spindle lengths in wild type and mutant cells. This plot suggests that the spindle lengths designated as metaphase in the spindle length vs time experiments were indeed in metaphase, since Pds1-GFP fluorescence was still present in high levels. (C) Average metaphase time vs tension for the wild-type and tension mutant cells (circles; F_4,187 = 7.77, p<0.0001, linear trend p <0.0001), and metaphase time for the wild-type and tension mutant cells when Mad2 was additionally knocked out (crosses, corresponds to the detachment data in Fig. S3C). Metaphase times remain near wild-type levels for all mutants in the absence of Mad2 (F_3,126 = 0.45, p=0.72), despite reduced tension and increased incidence of detachments (Fig. S3C). All panels: error bars=SEM.

To first verify that cells with metaphase-like spindle lengths were indeed in metaphase, we quantified the average nuclear Pds1 intensity as a marker for mitotic progression (Lu et al., 2014), using cells with representative spindle lengths for the wild-type strain and each of the mutants. While we could readily detect a sharp drop-off in Pds1 intensity in anaphase cells, as has been previously reported (Lu et al., 2014), our mutant cells with metaphase-like spindle lengths did not show reduced Pds1 intensity (Fig 3B). We therefore confirmed that cells with metaphase-like spindle lengths were indeed in metaphase, and so we then measured metaphase time for the wild-type and mutant cells.

We found that our low tension mutants spent more time in metaphase than wild type cells (Fig 3C, circles; F_4,187 = 7.77, p<0.0001; Fig. S3D), and, consistent with our metaphase detachment results, the average metaphase time also scaled with tension in a dose-dependent manner (Fig 3C, circles; p<0.0001, linear trend). To test whether the observed metaphase delays were a specific consequence of spindle assembly checkpoint activation, we evaluated metaphase times in the mad2Δ background cell lines, which did not have a functioning spindle assembly checkpoint. As noted above, the cin8Δ-mad2Δ cells were not viable, so we used a previously described Cin8-degron mutant for these experiments (Kotwaliwale et al., 2007). Consistent with the idea that the observed metaphase delays were mediated by Mad2, the gradient in average metaphase times was no longer observed in the tension mutants when Mad2 was absent (Fig 3C, crosses; F_3,126 = 0.45, p=0.72), even though a gradient in kinetochore detachment rates was still observed (Fig. S3C). These results suggest that the primary response of the cell to low tension was the creation of detachments, and that the spindle assembly checkpoint acted downstream of this primary response to delay cells in metaphase.

Simulations with a tension-dependent kinetochore phosphorylation rate constant can explain detachment gradient

To investigate a mechanism for how the kinetochore detachment rate could gradually increase in response to decreasing magnitudes of tension, we used a simulation-based approach. Specifically, we tested whether a tension-dependent kinetochore phosphorylation rate constant could account for the increasing gradient in kinetochore detachment rates with decreasing tension (Fig. 2B). It has been shown that Aurora B mediated phosphorylation of key microtubule binding proteins in the kinetochore, such as Dam1 and Ndc80, acts to destabilize kinetochore-microtubule connections to facilitate error correction (Asbury et al., 2006; Cheeseman et al., 2001, 2006; DeLuca et al., 2006; Lampert et al., 2010; Tanaka et al., 2002; Tien et al., 2010; Welburn et al., 2010). Since phosphorylation of these substrates increases when chromosome orientation is incorrect (Keating et al., 2009; Welburn et al., 2010), we introduced a rule into our simulation in which decreasing tension would lead to an increased substrate phosphorylation rate constant (Fig 4B). This allowed us to ask whether a tension-dependent kinetochore phosphorylation rate could account for the experimentally observed gradient in detachment rates with decreasing tension.

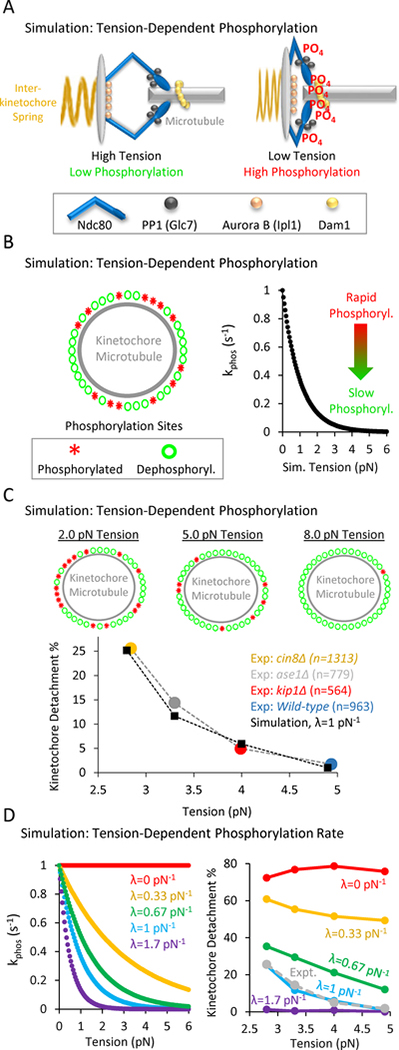
Figure 4: In computational simulations, a tension-dependent phosphorylation rate can explain tension-dependent detachment gradient.

(A) Speculative cartoon showing the architecture of a budding yeast kinetochore under high tension (left) and low tension (right). (B) The simulation tests whether a tension-dependent phosphorylation rate constant can explain our experimentally observed gradient in detachment rates. Left: Schematic of simulation: each kinetochore has N_sites = 50 phosphorylation sites, which can stochastically switch between a phosphorylated state (red asterisks) and a dephosphorylated state (green circles). Right: The phosphorylation rate constant in the simulation is exponentially sensitive to tension (Eqn. 1), such that rapid phosphorylation occurs when tension is high, and slower phosphorylation occurs when tension is low. (C) Top: Representative images of the relationship between tension and the number of phosphorylated kinetochore sites in the simulation. Low tension leads to an increased number of phosphorylated sites on the kinetochore (left), while higher tension decreases the number of phosphorylated sites on the kinetochore (right) (see also Movie S1). Bottom: Plots showing the dependence of detachment rate on tension, as was experimentally observed (colored circles) and as predicted by simulation (black diamonds). The simulation can explain the observed gradient in detachment by using a tension-dependent phosphorylation rate as shown in Fig. 4B, right and Eqn. 1. (D) Left: λ was the scaling factor that determined the influence of tension on the phosphorylation rate constant (pN⁻¹) in Eqn. 1, such that for λ=0, there was no influence of tension on the phosphorylation rate constant (red), and for λ>0, increased tension would act to exponentially decrease the phosphorylation rate constant per Eqn. 1. Right: The best fit between experiment and simulation was for λ=1 pN⁻¹ (light blue, experimental data shown as dotted grey line).

Specifically, an individual kinetochore-microtubule attachment structure with N_sites= 50 phosphorylation sites was included in each simulation (Fig. 4B, left; results are similar for N_sites = 2–150; Fig. S4C) (Cheeseman et al., 2001, 2002, 2006; Joglekar et al., 2006). Each site could be phosphorylated (Fig. 4B, left, red), or dephosphorylated (Fig. 4B, left, green). In the simulation, the rate of switching between phosphorylation states at each site was regulated by rate constants, in which k_phos was the phosphorylation rate constant per site (s⁻¹), and k_dephos was the dephosphorylation rate per site (s⁻¹). Importantly, the phosphorylation rate constant decreased exponentially with increasing tension, according to:

$$k_{phos}=k_{phos,0}{e}^{-\lambda F_{tension}}$$ (1)

Where k_phos,0 was the basal phosphorylation rate constant in the absence of tension, F_tension was the tension (pN), and λ was the scaling factor that determined the influence of tension on the phosphorylation rate constant (pN⁻¹), such that for λ=0, there was no influence of tension on the phosphorylation rate constant, and for λ>0, increased tension would act to exponentially decrease the phosphorylation rate constant (Fig. 4B, right, λ=1 pN⁻¹).

Thus, for each separate simulation, a different tension was imposed on the kinetochore-microtubule attachment structure. At each time point (Δt_step=0.01 s), the individual phosphorylation sites stochastically switched between a phosphorylated or dephosphorylated state, according to the rate constants as described above. Thus, with increasing tension, a smaller number of sites tended to be phosphorylated (Fig 4C, top-right; Movie S1).

To directly compare our simulation results to experiments, we then allowed detachment events to occur, where the probability of a kinetochore detachment event (pr_det) depended upon the fraction of phosphorylated sites (Tien et al., 2010; Zaytsev et al., 2015):

$$p{r}_{\text{det}}=\beta \left(\frac{N_{phos}}{N_{sites}}\right)$$ (2)

Here, N_phos represented the number of phosphorylated sites, and β was a sensitivity factor that linearly scaled the fraction of phosphorylated sites with the probability of detachment. In order to allow the simulation to achieve a steady-state level of detachments for each given tension value, any detached kinetochore was automatically reattached at a similar tension magnitude after an elapsed time that was consistent with published observations (Kalinina et al., 2013) (see simulation methods for details).

Using the rules and the parameter values as described above, the simulation recapitulated the experimentally observed relationship between detachment and tension (Fig 4C, bottom). This result was most sensitive to the parameter value for λ, which relates the sensitivity of k_phos to tension (Fig. 4D, Eqn. 1). For example, when λ=0, k_phos was insensitive to tension (Fig. 4D, left, red), and a gradient in detachment rate with tension was not observed (Fig. 4D, right, red). The best fit between experiment and simulation was for λ=1 pN⁻¹ (Fig. 4D, left, cyan), which led to a clear gradient in detachment rate vs tension that was similar to experimental results (Fig. 4D, right, dotted grey line is experimental data; parameter sensitivity analysis for other simulation parameters in Fig. S4). Thus, we conclude from our simulations that a tension-dependent kinetochore phosphorylation rate could explain our experimentally observed gradient in detachment rates with tension.

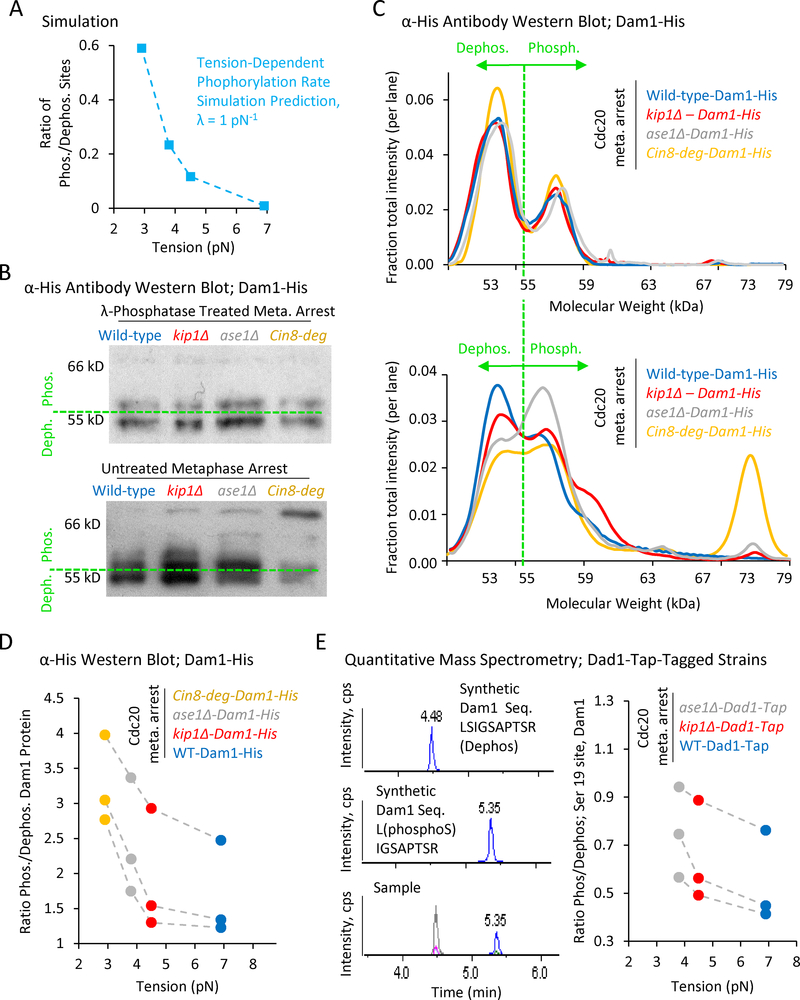
Phosphorylation levels of Dam1 scale with tension

Using a tension-dependent kinetochore phosphorylation rate constant (Eq. 1), our simulations predicted that we would observe an increasing gradient in kinetochore phosphorylation with decreasing tension (Fig. 5A). Since Dam1 is a key budding yeast kinetochore protein that is implicated in microtubule attachment (Joglekar et al., 2010) we then asked whether there was an increasing gradient in Dam1 phosphorylation with decreasing tension, as was predicted by our simulations (Fig. 5A).

Figure 5: A decreasing gradient in tension leads to an increasing gradient in Dam1 phosphorylation.

(A) Simulation prediction for the ratio of phosphorylated kinetochore sites vs tension. (B) Top: Anti-His western blots of Dam1-His purified from Cdc20-arrested wild-type and mutant cells, and then treated with λ-phosphatase. Bottom: Anti-His western blots of Dam1-His purified from Cdc20-arrested wild-type and mutant cells in the presence of phosphatase inhibitors. A shift towards higher molecular weights is indicative of increased phosphorylation. (C) Quantification of relative band intensities for each lane in λ-phosphatase treated samples (top), and in samples purified with phosphatase inhibitors (bottom). (D) The ratio of phosphorylated (> 55 kDa) to dephosphorylated (≤ 55 kDa) Dam1 protein as calculated from western blot band intensities demonstrates increasing phosphorylation with decreasing tension (p=0.043, single-factor ANOVA, 3 individual trials shown). (E). Left: Mass spectrometry scans of synthetic proteins (top and middle) and a typical experimental protein sample (bottom). Right: Quantitative mass spectrometry demonstrates an increasing gradient in the phosphorylation ratio at serine 19 of Dam1 with decreasing tension (3 individual trials shown, p=0.015, single-factor ANOVA, 3 groups).

First, we leveraged the previously reported shift in electrophoretic mobility of phosphorylated Dam1 (Kang et al., 2001), to quantify the relative abundance of phosphorylated and dephosphorylated forms of Dam1 in wild type cells, as well as in our three tension mutants. Thus, wild type and tension mutant cells were arrested at metaphase by depletion of Cdc20, and then 6-His-tagged Dam1 was purified using a nickel column.

We first purified metaphase-arrested Dam1-His from all strains in the absence of phosphatase inhibitors, and then treated each sample with λ-phosphatase (Fig. 5B, top). In a western blot against the His tag, we observed a high intensity band at < 55 kDa, and, in addition, a second, dimmer, slightly higher molecular-weight band in all of the λ-phosphatase treated Dam1 samples, perhaps suggesting incomplete dephosphorylation by λ-phosphatase, or the presence of another modification. We then purified Dam1-His from metaphase-arrested cells in the presence of phosphatase inhibitors, (Fig. 5B, bottom), allowing us to examine the Dam1 phosphorylation state of each mutant during metaphase. A western blot against the His tag revealed a shift towards higher molecular weights, and therefore higher phosphorylation levels, going from wild type cells to the mutants with decreasing tension (Fig. 5B, bottom). Consistent with this shift, the intensity of the second, dimmer band in the λ-phosphatase treated samples was strongly increased in the phosphatase-inhibited samples. This observation is consistent with previously reported results (Kang et al., 2001), and suggests that the lowest band (below 55 kDa) represents the de-phosphorylated form of Dam1, while the upper bands (above 55 kDa) were progressively more phosphorylated.

We then quantified the relative intensities within each respective lane for the λ-phosphatase-treated samples (Fig. 5C, top), and for the phosphatase-inhibited samples (Fig. 5C, bottom). The relative intensities of the two peaks in the λ-phosphatase treated samples were nearly identical for the wild-type and tension mutant strains (Fig. 5C, top). However, for the phosphatase-inhibited samples, we observed an increasing number and relative intensity of peaks to the right of the 55 kDa cutoff for the tension mutants as compared to the wild-type cells (Fig. 5C, bottom vs top). To compare the ratio of phosphorylated to dephosphorylated Dam1 in each case, we summed the total band intensity below 55 kDa (dephosphorylated Dam1), and above 55 kDa (phosphorylated Dam1), for each lane, and then plotted the ratio of phosphorylated to dephosphorylated Dam1 against average metaphase tension for each strain (Fig 5D, three replicate experiments shown). Strikingly, we observed an increasing gradient in the ratio of phosphorylated to dephosphorylated Dam1 with decreasing tension (p=0.043, single-factor ANOVA), similar to simulation predictions (Fig. 5D vs 5A).

Second, to independently test our phosphorylation results using another method, we measured the relative abundance of phosphorylated vs dephosphorylated Dam1 using tandem mass spectrometry. Phosphorylation of Dam1 has been previously observed (Cheeseman et al., 2002), and in vitro experiments have shown that the affinity of Dam1 for microtubules is greatly reduced when the protein is phosphorylated by Aurora B (Gestaut et al., 2008). Of the four known phosphorylation sites on Dam1, increased phosphorylation at three sites was previously detected using mass spectrometry (Sarangapani et al., 2013). Therefore, we selected one of these Dam1 phosphorylation sites, Serine 19, and used Multiple Reaction Monitoring (MRM) mass spectrometry to detect and quantify phosphorylation on Serine 19 of Dam1 (See Materials and Methods for details).

For the mass spectrometry experiments, Dad1-Tap tagged protein was used to pull down unlabeled Dam1 protein from Cdc20 metaphase-arrested cells for all strains except Cin8-degron, which was inviable in the presence of the Dad1-tap tag (Shimogawa et al., 2006). To precisely quantify phosphorylation at Serine 19, targeted MRM mass spectrometry methods for analyzing the peptides LSIGSAPTSR and L(phosphoS)IGSAPTSR were first developed using synthetic peptides (Fig. 5E, left; Fig. S5). Then, the quantities of each of the peptides L(phosphoS)IGSAPTSR and LSIGSAPTSR were measured using MRM mass spectrometry (Fig. 5E, left, bottom). Similar to the western blot analysis for Dam1 as a whole, quantitative mass spectrometry demonstrated an increased phosphorylation ratio at Serine 19 of Dam1 with decreased tension (Fig. 5E, right; p=0.015, single-factor ANOVA, 3 groups).

These results support a mechanism of tension sensing in which decreasing tension leads to increasing phosphorylation of key kinetochore proteins, thus increasing the probability of detachment events.

Discussion

In this study, we leveraged the balance of forces in the yeast mitotic spindle to generate a gradient in metaphase tension using a series of isogenic mutants that were genetically altered to modulate the magnitude of motor-based spindle forces. This methodology allowed us to examine the role of tension during mitosis in spindles with robust microtubule dynamics and properly duplicated chromosomes. Overall, all of the observed spindle phenotypes in our mutant cells were relatively mild, and we did not observe large scale changes in spindle structure. In addition, all of our measurements and observations were performed using properly formed bipolar spindles. However, we cannot exclude the possibility that microtubule lengths, organization, or numbers were changed in our mutant spindles, that kinetochore-microtubule attachment configurations were altered under low tension conditions, or that there were other potential upstream and downstream effects of the motor disruptions in the mutant cells. Regardless, all of the tension mutants had significantly altered tension as compared to each other, and to wild-type cells (Fig. 1C). In addition, the minimum observed mean tension (~2.8 pN in cin8Δ) was still orders of magnitude larger than thermal forces (~0.01 pN), and so tension remained large enough to potentially act as mechanical signal during mitosis. This approach allowed us to ask whether cells would respond in a dose-dependent manner to moderate changes in the magnitude of tension. We found that the cellular response to a tension gradient was dose-dependent, such that the severity of the cellular response directly scaled with the average magnitude of metaphase tension (Fig. 2). Thus, our results suggest that mitotic tension-sensing mechanisms within the cell are exquisitely sensitive, which may be particularly important in mammalian systems with multiple microtubule attachments per kinetochore, where tension could vary with the number of incorrectly oriented connections. This tension sensitivity could potentially allow mammalian cells to detect both syntelic and merotelic attachments via a tension-based mechanism (Cimini et al., 2003; Knowlton et al., 2006).

Our observation of increasing detachment rates with decreasing tension strongly suggests that error detection and tension sensing are part of the same pathway. We also demonstrated that the generation of kinetochore detachments in response to low tension was dependent on the activity of Aurora B, a protein that likely plays a crucial role in turnover of improper kinetochore-microtubule attachments (Fig. 2E) (Hauf et al., 2003; Kapoor et al., 2000; Tanaka et al., 2002). Recent work has found that the microtubule-associated protein Stu2 also plays a role in tension-dependent stabilization of kinetochore-microtubule attachments (Miller et al., 2016). We speculate that while Aurora B-dependent kinetochore phosphorylation may be critically important for weakening the strength of kinetochore microtubule attachments, robust microtubule plus-end dynamics could also be important downstream of Aurora B for physically separating the loosened kinetochores from their associated microtubule plus-ends, which may involve the interaction of Stu2 with dynamic microtubule plus-ends. (Miller et al., 2016). Recent data has shown that the primary role of Aurora B during error correction in meiosis I is the creation of kinetochore detachments, especially on chromosomes that show reduced inter-kinetochore distances, and that spindle assembly checkpoint activation occurs downstream of the detachments (Vallot et al., 2017). Our data suggests that a similar process operates in mitosis, and we build on this model to demonstrate that the error detection process may originate as a result of highly sensitive tension sensing by the cell.

In recent work, Cane and coworkers manipulated expression of the chromokinesin NOD in Drosophila S2 cells, thus directly increasing the polar ejection forces that push chromosome arms away from the poles, leading to a putative increase in tension force at the centromere (Cane et al., 2013). Here, the authors found that increased polar ejection forces at the chromosome arms led to stabilization of kinetochore-microtubule connections in a dose dependent manner (Cane et al., 2013). Therefore, consistent with our conclusions in yeast, kinetochore-microtubule connections in Drosophila S2 cells that are subjected to smaller forces may be selectively destabilized as compared to those subjected to greater forces.

We used computational modeling to investigate a potential mechanism to explain our experimentally observed dose-dependent response to low tension. We found that our probabilistic model could faithfully recapitulate our experimental observations of a dose-dependent kinetochore detachment response to decreasing average tension magnitudes if (1) the kinetochore phosphorylation rate was tension dependent, and (2) the strength of the kinetochore-microtubule binding interface was directly reduced by an increasing fraction of phosphorylated sites (Gestaut et al., 2008). In support of this model, we found that a decreasing gradient in tension was correlated with an increasing gradient in phosphorylation of the kinetochore protein Dam1. Therefore, it is likely that decreases in tension lead to increased phosphorylation of the outer kinetochore in order to detach microtubule connections.

Interesting future work will involve dissecting the mechanism for how low tension translates into a higher phosphorylation rate, for example, by evaluating changes to the tension-dependent detachment rate gradient in mutants with altered numbers of active kinetochore phosphorylation sites (Akiyoshi et al., 2009; Sarangapani et al., 2013; Tien et al., 2010). In addition, the underlying physical mechanism of a tension-dependent kinetochore phosphorylation rate may involve the kinetochore itself stretching under high tension (Joglekar et al., 2009; Maresca and Salmon, 2010; Nannas and Murray, 2014) and limiting the accessibility of Aurora B to its substrates (Fig 4A) (Liu et al., 2009; Maresca and Salmon, 2009), but this mechanism remains controversial (Dumont et al., 2012; Magidson et al., 2016). Thus, interesting future work could also center on the origin of a tension-dependent phosphorylation rate constant, since we predict that alterations in component(s) that mediate a tension-dependent kinetochore phosphorylation rate would directly alter our experimentally observed gradient in detachment rate as a function of tension.

STAR Methods

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Melissa K. Gardner (klei0091@umn.edu)

EXPERIMENTAL MODEL AND SUBJECT DETAILS

The experimental model used for these studies was budding yeast, in a W303 background.

Growth Conditions and Media Used

To obtain lacO spacings, spindle lengths, and to assay for detachments, yeast strains were grown overnight in SDC at 26 °C, diluted into fresh SDC and grown for 4 hours at 30°C to mid-log phase before imaging at 26 °C.

Cells that had Cin8 under the control of the Gal promoter were grown overnight in SD containing 4% raffinose as the carbon source. Cells were diluted into SDC (with glucose as the carbon source), grown for 4 hours at 30°C until the majority of the population was in mid-log phase, and then imaged. Cells harboring the Cin8-degron were grown overnight in SDC and diluted into fresh SDC. After 2 hours of growth at 30°C, cells were washed twice, and shifted to SD containing galactose to induce Ubr1 expression, allowing for subsequent degradation of Cin8, for an additional 2 hours prior to imaging. Imaging was performed in SD containing galactose. Cells harboring the pMet-Cdc20 construct were grown overnight in SD lacking Methionine and Cysteine. They were diluted into fresh SD lacking Methionine and Cysteine for 2.5 hours, before being shifted to SD containing excess Methionine and Cysteine for 3 hours prior to imaging. Imaging was done in SD with excess of Methionine and Cysteine.

For cells harboring both the pMet-Cdc20 construct and ipl-321 allele, the growth protocol was as described above, with cells shifted to 37°C for the last 30 minutes of growth before imaging. Imaging was done at 37°C using an objective heater and heated stage.

For cells harboring the Degron-Cin8, pMet-Cdc20 constructs and the ipl-321 allele, the growth conditions were as follows. Cells were grown overnight in SD containing glucose, but lacking Methionine and Cysteine. Cells were diluted into SD containing glucose but lacking Methionine and Cysteine and allowed to grow for 2.5 hours at 30°C. Cells were then washed twice and shifted into SD containing galactose, and an excess of Methionine and Cysteine, and allowed to grow for a further 2.5 hours at 30°C. Cells were then shifted to 37°C for 30 min before imaging at 37°C.

For longer time-lapse movies to detect metaphase time, cells were grown overnight in SDC at 26°C, diluted into fresh SDC and grown for 3 hours at 30°C to mid-log phase before imaging at 30°C. Imaging was done at 10 X-Y locations in the red channel at one minute intervals for 3 hours. For cells containing the Degron-Cin8 construct, cells were grown overnight at 26°C, diluted into fresh SDC and grown for 2 hours. Cells were then washed twice and transferred to SD containing galactose for 2 hours prior to imaging. The imaging modality was as described. No additional projection lenses were used for longer time-lapse imaging.

To assay chromosome mis-segregation, cells were grown overnight in SDC at 26°C, then diluted into fresh SDC and grown for 2 hours at 30°C. Alpha factor was added to the culture and cells were allowed to grow for 2.5 hours before release. After release from alpha factor, cells were grown for an additional 2 hours to allow the population to enter anaphase, and then fixed and stained with DAPI prior to imaging. A previously described fixing protocol (Miller et al., 2016) designed to preserve the fluorescence of the GFP labeled lacO spots and mCherry labeled spindle pole bodies was used. Imaging was done in three channels.

To assay chromosome mis-segregation in the absence of Aurora B activity, cells harboring the ipl1–321 allele as well as Cdc20 under the control of the repressible methionine promoter (pMet-Cdc20) were grown overnight in SDC lacking Methionine and Cysteine at 26°C, then diluted into fresh SDC lacking Methionine and Cysteine and grown for 2 .5 hours at 26°C. Cells were then washed twice and shifted to SDC media containing excess of Methionine and Cysteine, for 2 hours at 26°C. Cells harboring the Degron-cin8 construct were shifted to SD medium containing an excess of Methionine and Cysteine along with Galactose as the primary carbon source, for 2 hours at 26°C. Cells were then shifted to 37 °C for 30 min before being washed twice and transferred to SDC lacking Methionine and Cysteine to facilitate entry to anaphase. Cells harboring the Degron-cin8 construct were transferred to SD lacking Methionine and Cysteine , along with Galactose as the primary carbon source. Cells were incubated at 37 °C, before being fixed and stained and assayed for mis-segregation as described below.

METHOD DETAILS

Imaging Protocols

Cells were imaged on a TIRF microscope (Nikon Eclipse Ti) using 405 nm, 488 nm and 561 nm laser lines. Yeast cells were adhered to a cover slip and then imaged using a pseudo-TIRF setup (i.e, the laser angle was adjusted to increase penetration of the evanescent field into the sample while optimizing the signal to noise ratio). An EMCCD camera (iXon3, Andor Technologies) was used to capture images. Additional projection lenses were used depending on specific modes of imaging as described in following sections.

Flow chambers for imaging live yeast cells were constructed as follows. A coverslip (1.5, 22 mm × 22 mm) was soaked overnight in 1M NaOH, and rinsed thoroughly with nanopure water prior to imaging. It was then secured to our imaging chamber using screws and metal retainers at the edges of the cover slip. Strips of parafilm were laid across the lower coverslip and overlaid with an untreated coverslip. The parafilm was then melted on a hot plate and allowed to cool. This treatment adhered the two coverslips to each other and created a flow chamber between the upper and lower cover slips. 30μL Concanavalin A was then flowed into a dry prepared chamber and incubated for 10–20 minutes. The chamber was then washed of excess Concanavalin A, and the yeast cells introduced to the flow chamber and allowed to adhere to the surface. Excess cells were vacuumed out after a 5–10 min incubation time, and the media replaced with a sugar source and water for optimal imaging.

To obtain lacO spacings, spindle lengths, and to assay for detachments, imaging was done using a rapid switching triggered acquisition setup, which allowed for near simultaneous imaging in red and green channels. Cells tagged with red and green were imaged continuously with 200 ms exposure time per channel, using TIRF with a Nikon CFI Apochromat 100X 1.49 NA oil objective. For this imaging modality, the camera was fitted with a 2.5x projection lens for an effective pixel size of 64 nm per pixel.

To assay for spring constant, growth conditions were as described above. Imaging was done in the green channel at 30 frames per second using both an additional 1.5x and 2.5X projection lens for an effective pixel size of 42nm per pixel. Individual cells were imaged for 3 seconds or less.

Two-color, live cell imaging was performed to capture kinetochore detachment and reattachment events. Imaging was performed at 45 second intervals, with three 750nm Z-stacks in each channel.

Image Analysis

To analyze live yeast spindles, images of in-plane spindles were selected for analysis. All analysis of mitotic spindles was done in MATLAB (Mathworks, Natick, MA) using custom-made programs. For spindle length measurements and for calculating distance between lacO-lacI-GFP spots, a background-subtracted image was created from the raw image by filtering with a coarse-grain Gaussian filter, and then by subtracting this image from the noise-corrected image. A custom image analysis program written in MATLAB used Gaussian fitting to find the center of each spindle pole or lacO-lacI-GFP spot and then calculated the distance between the two spindle poles or lacO-lacI-GFP spots.

For metaphase time analysis, we used movies where a single cell was observed to undergo a pole duplication event, enter metaphase, and finally undergo anaphase. For each time point in the movie, spindle lengths were calculated using the algorithm described above. Metaphase time was estimated to be the interval between pole separation and anaphase onset.

For analysis of detachments and mis-segregation, individual spindles were cropped to form an image series, which were then manually scored.

To estimate the ratio in fluorescence intensity between detached diffraction-limited lacO-lacI-GFP spots and attached, separated lacO spots, we started by collecting images in which a spindle with a detached chromosome and a spindle with an attached chromosome were in the same field of view. (Fig S2C, images). The cin8Δ mutant was used to maximize the chances of such pairs occurring in any given imaging chamber. We imaged both lacO spots and spindle poles and collected 7 Z-series images of 300 um width in both channels. A maximum projection was used for intensity analysis. We then estimated the background-corrected fluorescence intensity of the detached lacO spots and the averaged, background-corrected fluorescence intensity of the two lacO spots. Comparing two cells in the same field of view allowed us to control for day to day variations in fluorescence intensity. We also measured the average background-corrected fluorescence intensity of the spindle pole bodies. The ratio of these intensities acted as a correction factor to account for the inhomogeneity of the TIRF field, and for slight variations in spindle z-position tilt. The final formula to calculate intensity ratio was as follows. We reported the average of the ratio of all our measurements.

$$R=\left(\frac{I_{lacO,Det}}{I_{lacO,Att}}\right)\left(\frac{I_{SPB,Att}}{I_{SPB,Det}}\right)$$ (S1a)

Where I_lacO,Det represented the fluorescence intensity (A.U.) of detached lacO-lacI-GFP spots, I_lacO,Att represented the average fluorescence intensity (A.U.) of attached lacO-lacI-GFP spots, I_SPB,Att represented the average fluorescence intensity (A.U.) of spindle poles in cells with attached lacO spots, and I_SPB,Det represented the average fluorescence intensity (A.U.) of spindle poles in cells with detached lacO spots.

Estimation of Tension

Metaphase tension was estimated for all strains and growth conditions in the manuscript according to our previously published method for quantitatively evaluating metaphase tension in budding yeast (Chacon et al., 2014). In this previously published work, careful methods validation was completed, and a complete explanation for the method rationale is included. Thus, the following explanation of the tension estimation method is a brief summary of previous work. For more details please see (Chacon et al., 2014).

Briefly, it is assumed that the inter-kinetochore chromatin acts as a Hookean spring (for an extensive and detailed discussion of the rationale and justification for this approach, including a spring linearity analysis, see (Chacon et al., 2014). Thus, tension (F_tension) was estimated via the equation for Hooke’s law, as follows:

$$F_{tension}=\kappa (\Delta x-\Delta x_{rest})$$ (S1)

Here, κ is the stiffness of the inter-kinetochore spring, and κ was estimated using the methods summarized below. Δx_rest is the rest length of the inter-kinetochore spring, i.e., the distance between the sister centromere lacO-lacI-GFP spots when no forces are pulling them apart. For Δx_rest we used previously published values that were estimated as described in (Chacon et al., 2014) using cells treated with Nocodazole to depolymerize microtubules, thus eliminating all forces on the chromosomes. For spindles treated with Nocodazole, the separated sister centromere lacO-lacI-GFP spots collapse to a single diffraction-limited spot, and so the rest length was estimated as the theoretical microscope resolution, based on the numerical aperature of the microscope lens (Chacon et al., 2014). Δx is the average metaphase stretch distance of the inter-kinetochore spring, as represented by the average distance between lacO-lacI-GFP spots with properly bioriented kinetochores at metaphase (Fig. S1B, left). Here, we used strains with a LacO-lacI-GFP construct, where a LacI-GFP fusion was localized to a tandem array of 33 lacO repeats inserted 1.1 kb 3′ to CEN3 (Pearson et al., 2001). The stretch distance was measured by collecting many still images of metaphase spindles, and then by evaluating the center-to-center distance between the two lacO-lacI-GFP spots (Fig. S1B, right) on pairs of sister chromatids of the same chromosomes (Chr 3 in our studies). For any given strain, we obtained a set of measurements of lacO-lacI-GFP distances (Δx) across multiple cells on at least three different imaging days.

Estimation of Spring Constant

The final measured parameter that was required in order to estimate tension was the stiffness of the inter-kinetochore spring (κ). The inter-kinetochore spring stiffness is a measure of its resistance to force-induced stretching, and an extensive and detailed discussion of the rationale and justification for our approach to estimating inter-kinetochore spring stiffness is included in (Chacon et al., 2014). Briefly, while the inter-kinetochore stretch distance (Δx) is a measure of the mean lacO-lacI-GFP spot spacing over many metaphase spindles, the stiffness of the inter-kinetochore spring is estimated by measuring the variance in distance between lacO-lacI-GFP spots over time, according to:

$$\kappa =\frac{k_{B}T}{<{\sigma }^2>}$$ (S2)

Here, the general principle is that the stiffness of the spring (κ) is reflected by the amount of energy that is available to move the lacO-lacI-GFP spots on the inter-kinetochore spring (k_BT), divided by the variance in motion that is observed as a result of this energy (<σ²>). In general, the available amount of thermal energy is defined as k_BT, which is the Boltzmann constant (k_B) multiplied by the temperature (T). Thus, in order to use this relationship, the measured variance in motion of the lacO-lacI-GFP spots should reflect thermal forces, and not active, directed forces by microtubules and motors. In our previous work, we reasoned that thermal forces occur on a fast time scale relative to active forces (Fig. S1C, left), and so we collected rapid time-lapse movies (33 frames/s) of the LacI-GFP tags (Fig. S1C, right) to visualize the rapid fluctuations of the tags with respect to each other over small time scales of ~1 second total. In our previous work, this approach was verified using drugs to halt active forces (Chacon et al., 2014). After movie collection, the center of each LacO-LacI GFP spot for every time frame was accurately localized using 2D Gaussian fitting, thus limiting measurement noise to ~20 nm, and the distance between pairs of lacI-GFP tags on sister chromatids (Δx_i) was measured for each time point (Fig S1C, right).

To quantify the variability in distance between pairs of sister lacO-lacI-GFP tags over time, the distance measurements were converted to Mean Squared Displacement (MSD) values for increasing intervals of time (Δt), as follows:

$$MSD=\frac{1}{n}{\sum }_{j=1}^n{\left[{\sum }_{i=j}^{j+\left(\frac{\Delta t}{t_{frame}}\right)-1}\Delta x_i\right]}^2$$ (S3)

Here, t_frame is the time between image frames in the movies (30 ms under our imaging conditions), and n is the number of displacements within the time interval (eg, n=Δt/t_frame). The MSD values were then plotted for increasing time intervals (up to ~2 sec maximum) and the plots were used to find the plateau value of MSD, (<σ²>), where < σ²> = MSD_plateau - MSD(Δt₁). A representative plot (Fig S1D) of MSD vs Δt shows a plateau characteristic of constrained diffusion. Here, the height of this plateau above the Y intercept represents (<σ²>). To calculate the stiffness of the inter-kinetochore spring (κ), the value for <σ²> was then substituted into Eqn. S3.

To estimate the spring constant of the interkinetochore spring, cells harboring the lacO-CEN3/lacI-GFP system were grown and immobilized on cover slips as described above. 90 to 120 images were acquired for each cell using continuous single color acquisition at 30 fps. Imaging at high frame rates ensures that the observed movement of lacO-lacI-GFP spots relative to each other, as shown in a representative kymograph (Fig S1C, right) is due to thermal forces and not active forces such as those exerted by motors and microtubule dynamics. A custom MATLAB script was used for image analysis. For each frame, individual lacO spots were localized with sub-pixel resolution using Gaussian mixture model fitting (Fig S1B), and the distance between two lacO-lacI-GFP spots was calculated. The movement of the lacO spots from one frame to the next was calculated (termed first difference) and the effect of drift was removed by fitting a line through a plot of the first differences over time for each cell. Residuals from this line were then used for the remainder of the analysis. To find the MSD for the entire population of cells for wild-type and mutant cells, the residuals for all cells were pooled, similar to previous work (Chacon et al., 2014).

Protein Purification for Western Blots

1.2 L cultures containing the Dam1-His6x and pMet-Cdc20 yeast strain, were grown at 30 °C in SD without methionine or cysteine (SD-met-cys) to log phase, and then Met and Cys were added to a final concentration of 10 mM and 2 mM respectively. Growth continued for another 3 hrs. to arrest the cells in metaphase. Cells containing the PGal-degron-Cin8 construct were grown to log phase in SD + 2% raffinose, and then galactose added to 2% at the time that Met and Cys were added, which allowed Cin8 to degrade for 3 hrs.

Cells were harvested by centrifugation and resuspended in 20 ml lysis buffer (20mM Hepes pH 7.4 / 300mM NaCl / 0.5% Triton x-100 / 5mM B-mercaptoethanol) plus protease inhibitors (1mM PMSF / 1mM AEBSF / 10uM pepstatin A / 10uM E-64 / 0.3uM aprotinin / 1mM benzamidine) and phosphatase inhibitors (10mM sodium pyrophosphate / 10mM B-glycerophosphate / 10mM NaF / 1mM Na3VO4). The cells were then lysed by liquid nitrogen freeze-grinding in a Retch RM100 mortar mill. Lysates were then centrifuged at 14000 xg, 4 °C for 1 hr., and the soluble supernatant was mixed with 1 ml of Talon metal affinity resin (Clontech labs) for 2 hr. at 4 °C. Resin was washed extensively with lysis buffer + protease and phosphatase inhibitors, and protein was eluted from the resin by adding 1 ml of the same buffer containing 400 mM imidazole pH7, incubating for 15 min at 4 °C, and then collecting the eluate by slow speed centrifugation through a fritted filter column.

Phosphatase Treatment

Phosphatase treatment of the affinity purified samples was similar to the protocol above except that the phosphatase inhibitors were left out of all buffers and additional washing of the Talon resin 2x with 4ml of phosphatase buffer (50mM Hepes pH 7.5 / 100mM NaCl / 0.01% Brij35) plus 0.1x protease inhibitors was done. Proteins were eluted from the resin with 400ul phosphatase buffer containing 400mM imidazole by incubation and centrifugation through a filter as above.

Eluates were heated 95° for 6 min and then put on ice to denature proteins. MnCl₂ buffer was added to 1mM, DTT was added to 2mM and 2ul (800 units) lambda phosphatase (New England Biolabs) was added. Samples were incubated at 30° for 4 hr., then at 10° for 12 hours.

Western blotting

5x reducing electrophoresis sample buffer was added to samples to 1x. Samples were boiled for 6 min and added to a 12% acrylamide gel, transferred to PVDF membrane and detected with mouse monoclonal anti-6HIS antibody (clone 6-His, BioLegend), HRP-anti-mouse secondary and Supersignal West Fempto chemiluminescence reagent (ThermoFisher).

Protein Purification for Mass Spectrometry

Cell growth, arrest, harvesting and lysis was done as described above, except that the strains contained the Dad1-TAP tag construct (gift of T. Davis) instead of the Dam1-HIS6x. In addition, the lysis buffer and phosphatase inhibitors were as described above, but the protease inhibitors were 2mM PMSF / 2mM AEBSF / 20uM Pepstatin A / 20uM E-64 / 2mM EDTA / 0.6uM aprotinin / 20uM leupeptin / 200uM TPCK.

Soluble lysates were mixed with 200 ul of rabbit IgG-agarose resin (Sigma-Aldrich) for 1 hr. at 4° C. The resin was washed extensively with lysis buffer + protease and phosphatase inhibitors, and then washed extensively with TEV buffer (40mM Hepes pH 7.4 / 200mM NaCl / 1mM EDTA / 1mM DTT / 1mM sodium pyrophosphate / 1mM NaF / 1mM B-glycerophosphate). Resin was then mixed in 200 ul of TEV buffer with 5 ul of TEV at 2 U/ul at 4 °C for 14 hr. The eluate was collected, the resin washed with and additional 100ul of TEV buffer and both eluates combined and sent for trypsin digestion and mass spectrometry.

Mass Spectrometry

Samples (2 μL containing 1 μg protein) for SRM analysis were subjected to injection using a manual injection loop with an analytical Eksigent HALO fused-core C18 2.7 μm, 0.3 × 100 mm connected to the Applied Biosystems 5500 iontrap fit with a turbo V electrospray source fitted for micro-flow. The samples were subjected to a gradient of 26 minutes with an Agilent 1100 micro-flow HPLC. The samples were subjected to the following gradient at a flow rate of 8 μL/minute: 0–1 minute at 5% B; 3–18 minutes a gradient to 46% B; 18–21 minutes at 95% B; and equilibrated from 21–23 minutes at 5% B, (Buffer A: Water, 0.1% formic acid; Buffer B: high-performance liquid chromatography grade acetonitrile (Fisher Scientific, Pittsburg, PA, USA), 0.1% formic acid). Transitions monitored are listed below. These were established using the instrument optimization mode with direct injection of synthetic phosphorylated and unphosphorylated peptides representing their tryptic digest of DAM1 protein. The entrance potential (EP) was 10 V with a collision energy (CE) of 28.0 V and collision cell exit potential (CXP) of 15.0. The data were analyzed using MultiQuant™ (ABI Sciex, Framingham, MA, ). The peak area ratio of phosphorylated/unphosphorylated DAM1 peptide was used to determine the percent of phosphorylation peptide in the reaction. Samples were run in triplicate and randomized.

SRM Monitored Transitions

ID	Q1 Mass (Da)	Q3 Mass (Da)	Time (msec)	DP (Volts)
DAM1 (P) Y7	535.0	675.5	100.0	63.9
DAM1 (P) Y8	535.0	788.6	100.0	64.8
DAM1 (P) Y9	535.0	955.6	100.0	63.9
DAM1 Y7	495.0	675.4	100.0	64.8
DAM1 Y8	495.0	788.6	100.0	64.8
DAM1 Y9	495.0	875.4	100.0	64.8

Modeling Methods

A stochastic simulation was used to investigate potential mechanisms to explain how the kinetochore detachment rate could gradually increase in response to decreasing magnitudes of centromere tension. Specifically, we tested whether a tension-dependent kinetochore phosphorylation rate could account for an increasing gradient in detachment rates with decreasing tension (Fig. 3A). This allowed us to directly ask whether a tension-dependent kinetochore phosphorylation rate could account for an increasing gradient in detachment rates with decreasing tension. Detailed simulation methods are as follows.

Modeling Methods: Simulation Initiation

The simulation was initiated by establishing a tension value (F_tension), matched to an average experimental value for both wild-type and tension mutants. This tension value remained constant throughout each simulation.

During each simulation, 500 kinetochores were independently simulated, each kinetochore with N_sites number of phosphorylation sites, for a duration of t_dur, which was typically 20 minutes. At the start of the simulation, all kinetochores started in the “attached” state, and all phosphorylation sites on each kinetochore started in the “dephosphorylated” state.

Modeling Methods: Simulation Process

At each time point in the simulation, the following activities occurred (in order):

For ATTACHED kinetochores:

1. The phosphorylation rate constant is calculated based on tension, according to:

   $$k_{phos}=k_{phos,0}{e}^{-\lambda F_{tension}}$$ (MS1)

   Here, the basal phosphorylation rate constant (k_phos,0) and the tension scaling factor (λ) are both free parameters, held constant for each F_tension value in each simulation (parameter sensitivity analysis shown in Fig. S4).

2. Probability of phosphorylation (pr_phos) (for dephosphorylated sites) is calculated as follows:

   $$p{r}_{phos}=1-e^{-k_{phos}\Delta t_{step}}$$ (MS2)

   Where Δt_step is the simulation time step size (Δt_step=0.01 s), and k_phos depends on tension, as in Eqn. S1.

3. Probability of dephosphorylation (pr_dephos) (for phosphorylated sites) is calculated as follows:

   $$p{r}_{dephos}=1-e^{-k_{dephos}\Delta t_{step}}$$ (MS3)

   Where Δt_step is the simulation time step size (Δt_step=0.01 s), and k_dephos remained constant throughout the simulation (k_dephos = 1 s⁻¹).

4. Then, each individual phosphorylation site on each kinetochore either changed its phosphorylation state, or remained unchanged, based on comparison of a uniform random number between 0 and 1 to the probabilities as calculated above. Here, if the random number was less than the calculated probability, then the phosphorylation state would switch. Otherwise, the phosphorylation state would remain unchanged.

5. Once all of the phosphorylation sites either changed states or remained unchanged, then the probability of detachment for each attached kinetochore (pr_det) was calculated, as follows

   $$p{r}_{\det }=\beta \left(\frac{N_{phos}}{N_{sites}}\right)$$ (MS4)

   Where N_phos represents the number of phosphorylated sites within a kinetochore, N_sites represents the total number of phosphorylation sites available, and β is the detachment sensitivity factor, which scales the sensitivity of detachment with the fraction of phosphorylated sites.

6. Then, each kinetochore either detached, or remained attached, based on comparison of a uniform random number between 0 and to 1 the probability as calculated above. Here, if the random number was less than the calculated probability, then the kinetochore would detach. Otherwise, the kinetochore would remain attached.

For DETACHED kinetochores:

1. Immediately upon kinetochore detachment, a “reattach time” (Δt_reattach) is calculated for that kinetochore, which represents the time that a particular kinetochore will remain detached prior to automatically attaching again. The reattach time (Δt_reattach, in sec.) is calculated according to:

   $$\Delta t_{reattach}=(3.5\ast 60)+randn\ast 60$$ (MS5)

   This time is based on previous reports that the reattach time for kinetochores in yeast is ~3.5 minutes (Kalinina, Nandi et al. 2013). To introduce noise into this value, rand, which generates a normally distributed random number with mean = 0 and standard deviation = 1, is multiplied by 60 s and added to the mean experimentally reported value.

2. A detached kinetochore remains in a detached state for its entire Δt_reattach time period.

3. Then, after Δt_reattach has elapsed, the kinetochore automatically reattaches. At the time of reattachment, all phosphorylation sites on a kinetochore are initialized in the dephosphorylated state.

Modeling Methods: Simulation Results Reporting

After the total elapsed time is greater than or equal to t_dur, the stochastic simulation is complete. Then, the simulation results are reported as follows:

1. The total number of detached kinetochores is calculated, and then the detachment fraction (frac_Detach) is calculated according to:

   $$fra{c}_{Detach}=\frac{N_{kinetochores}-N_{Detached}}{N_{kinetochores}}$$ (MS6)

   Where N_kinetochores represents the total number of kinetochores simulated (typically ~500), and N_Detached represents the total number of kinetochores that were detached at the completion of the simulation.

2. In order to directly compare the simulation results to experimental results, the simulated detachment fraction (for a single kinetochore) is scaled to account for detachment events inside of cells (frac_Detach,obs), which is observed if one of two kinetochores are detached in the spindle, as follows:

   $$fra{c}_{Detach,obs}=2(fra{c}_{Detach})-{(fra{c}_{Detach})}^2$$ (MS7)

3. To compare experimental and simulation results, frac_Detach,obs was recorded for each experimental tension value (F_tension), and plotted alongside experimental percent detachment results for each tension value. To quantitatively compare simulation to experiments for different simulation parameter values, a sum of squared error (SSE) was calculated for each parameter set, in which the difference between the experimental and the simulated detachment fraction was calculated and then squared for each tension, and then the values were summed across all tension value.

Model Parameters

Symbol	Description	Value	Reference
kphos,0	Basal Phosphorylation Rate Constant per site when Ftension= 0	1 s−1	This study: matched to experimental detachment data in wild-type cells. See parameter sensitivity analysis Fig. S4D.
λ	Scaling factor that determines the influence of tension on the phosphorylation rate constant	1 pN−1	Free parameter, see sensitivity analysis in Fig. S4A and Fig. 4D.
Ftension	Centromere tension	2.8, 3.3, 44.9 pN	Matched to experimental average tension values for wild-type and tension mutant cells
β	Sensitivity factor that scaled the fraction of phosphorylated sites with the probability of detachment	10−4	This study: matched to experimental detachment data in wild-type cells. See sensitivity analysis Fig. S4B.
Nsites	Total number of phosphorylation Sites in the kinetochore	1–50	Simulation is insensitive to this parameter (Fig. S4); see sensitivity analysis Fig. S4C.
Nphos	Number of phosphorylated sites	1–50	Determined based on phosphorylation event; varies at each time step in simulation
Δtstep	Simulation time step size	0.01 s	N/A
kdephos	Dephosphorylation rate constant	1 s−1	This study: matched to experimental detachment data in wild-type cells
Δtreattach	Time to reattach a detached kinetochore	210+(rand*60) sec; where rand = uniformly distributed random number between 0 and 1	(Kalinina et al., 2013)
tdur	Simulation duration	20 min	Metaphase time in budding yeast. (Pearson et al., 2001)

Model Assumption Summary

Behavior	Model Assumption	Reference or Explanation
Tension-Dependent Phosphorylation Rate	Increasing tension causes an exponential decrease in phosphorylation rate of Aurora B substrates at the outer kinetochore.	(Kelly and Funabiki, 2009)
Phosphorylation dependent Kinetochore Detachments	Increasing the fraction of phospho-sites that are phosphorylated increases the probability of detachment.	(Asbury et al., 2006; Cheeseman et al., 2006; Sarangapani et al., 2013)
Tension Independent Dephosphorylation	Phosphatases at the outer kinetochore de-phosphorylate Aurora B substrates.	(Lampson and Cheeseman, 2011; Pinsky et al., 2009; Wurzenberger and Gerlich, 2011)
Reattachment	Detached kinetochores re-attach via microtubule search and capture.	(Kalinina et al., 2013)

QUANTIFICATION AND STATISTICAL ANALYSIS

All experiments were performed in different (independent) cells for each sample, and each experiment was replicated/performed over a minimum of 3–5 different days/experiments. Sample sizes for single image snap-shots were >100 minimum per experiment, and sample sizes for more involved experiments were as large as possible to minimize error bars.

Statistical analyses were performed by SAS 9.4 (SAS Institute, Cary, NC). All p values were 2-sided, and p < .05 was used to indicate statistical significance unless otherwise noted. All results for main effects and post hoc tests included in the text or figure legends were drawn from models which yielded a significant global hypothesis test.

A student’s t test with pooled (equal) variances was used to evaluate the difference in spindle width between wild-type and ase1Δ cells.

One way analysis of variance (ANOVA) models were used to compare mean tension across strains (wild-type, kip1Δ, ase1Δ, and cin8Δ or degron-cin8) within a single genetic background or condition (wild type, mad2Δ, ipl1–321, or cdc20-restrictive). Similarly, a one way ANOVA was used to test for differences in tension across the three motor mutant strains with varying cin8 modifications (i.e. cin8Δ, Pgal-cin8, degron-cin8). Post hoc testing for pairwise comparisons between strains was conducted using the least squares means multiple comparison procedure with a Bonferroni correction (α = 0.05/n_tests). To test the effect of both strain and background (e.g. wild-type vs mad2Δ) on tension, multivariate linear regression models were conducted with corresponding main effects. Equivalent models were used to test the effect of either strain or strain and background on metaphase time. A trend analysis with orthogonal polynomial contrast coefficients for unequally spaced factor levels was used to test for a linear or quadratic trend in increasing metaphase time with decreasing mean tension. All results are summarized as F statistics and associated p values.

Pearson chi-square analyses were used to test the associated between strain (i.e. wild type and motor mutants, or varying Cin8 modifications) and either kinetochore detachment or mis-segregation. Cochran-Armitage tests were used to evaluate for trends across strains, with levels ordered by the strains estimated mean tension values. Statistical significance for post hoc pairwise comparisons was determined by using a Bonferroni correction. Multivariate logistic regression models with two main effects were used to test the effect of both strain and background on either detachment or missegregation. Results are summarized as either X² (global or main effects) or z (trend analysis) statistics and associated p values.

Supplementary Material

Supplemental Movies

Movie S1: Simulation Output: Related to Figure 4. Movie S1 is an output from the simulation demonstrating the effect of different tension magnitudes on the overall phosphorylation state of the kinetochore (red = phosphorylated site; green = dephosphorylated site).

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Mouse anti-HIS6 antibody, clone 6-His	Biolegend	Cat # 906101
Rabbit IgG-agarose beads	Sigma Aldrich	Cat # A2909
HRP-goat-anti-mouse secondary antibody	Santa Cruz Biotechnology	Cat # sc-2005
Chemicals, Peptides, and Recombinant Proteins
Yeast SD Media	Meth Enzymology 1987. 152 pp.481–504	NA
Sodium Pyrophosphate	Sigma-Aldrich	Cat # S-9515
Sodium Fluoride	VWR	Cat # SS0535
Sodium Vanadate	Fisher	Cat # S454–50
B-glycerophosphate	Sigma-Aldrich	Cat # G-6376
Talon CellThru metal affinity resin	Clontech / Takara	Cat # 635509
Lambda Phosphatase	New England Biolabs	Cat # P0753S
Supersignal West Fempto chemiluminescence reagent	ThermoFisher	Cat # 34095
Liquid Chromatography grade Acetonitrile	Fisher Scientific	Cat A955–500
Experimental Models : Organisms/Strains (All S. cerevisiae background W303, unless otherwise stated)
MATa ura3–1 ade2–1 his3–11,−15 leu2–3,112 ade3Δ can1–100 trp1–1 CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX)	T. Davis; MMWY61n2a (Wargacki et al., 2010)	YMG005
MATa CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) kip1Δ::Ura3	This Study	YMG163
MATa CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) cin8Δ::Natmx4 bar1Δ ura3 ade1 leu2 his2 trp1	This Study	YMG172 (15D background)
MATa bar1::HisG pds1::PDS1-GFP-URA3 SPC42-mCherry::HIS3	David O Morgan DL009P (Lu et al., 2014)	YMG191
MATa CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) ase1Δ::Natmx4	This Study	YMG197
MATα ura3–1 ade2–1 his3–11,−15 leu2–3,−112 can1–100 trp1–1 CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX)	This Study	YMG200
MATa bar1::HisG pds1::PDS1-GFP-URA3 SPC42-mCherry::HIS3 cin8Δ::TRP1	This Study	YMG203
MATa bar1::HisG pds1::PDS1-GFP-URA3 SPC42-mCherry::HIS3 kip1Δ::TRP1	This Study	YMG208
MATa CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) cin8Δ::NATmx	This Study	YMG218
MATa ipl1–321 ade2–1 can1–100 his3–11,−15 leu2–3,−112 trp1–1 ura3–1	Trisha Davis; SFY-233–2D (Shimogawa et al., 2010)	YMG223
MATa ipl1–321 CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX)	This Study	YMG233
MATa ipl1–321 CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) ase1Δ::TRP1	This Study	YMG234
MATa ipl1–321 CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) kip1Δ::TRP1	This Study	YMG237
MATa CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) LacI-GFP:HIS3 SPC110::SPC110-mCherry(hphMX) mad2Δ::TRP1	This Study	YMG240
MATa CEN3:lacO×33(Kan), his3::GFP-lacI(HIS3) LacI-GFP:HIS3, SPC110::SPC110-mCherry(hphMX) mad2Δ::TRP1, kip1Δ::URA3	This Study	YMG242
MATa CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) LacI-GFP:HIS3 SPC110::SPC110-mCherry(hphMX) mad2Δ::TRP1 ase1Δ::NATmx	This Study	YMG244
MATa bar1::HisG pds1::PDS1-GFP-URA3 SPC42-mCherry::HIS3 ase1Δ::TRP1	This Study	YMG261
MATa CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) mad2Δ::URA3	This Study	YMG264
MATα CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) kip1Δ::TRP1	This Study	YMG281
MATα CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) ase1Δ::TRP1	This Study	YMG283
MATa CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) cin8Δ::NATmx, plasmid pGal-CIN8-TRP (p58)	This Study	YMG295
MATa cdc20::pMET3-CDC20::TRP1	Tomoyuki Tanaka; T4032 (Keating et al., 2009)	YMG302
MATα ipl1–321, cdc20::pMET3-CDC20::TRP1 CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX)	This Study	YMG309
MATa ura3–1 ade2–1 his3–11,15 leu2 trp1–1 can1–100 LYS2 GAL-UBR1 myc::HIS3, Cup1p-Nd-CIN8::URA3, SPC42-GFP::TRP	Sue Biggins; SBY3884 (Kotwaliwale et al., 2007)	YMG314
MATa CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) cdc20::pMET3-CDC20::TRP1	This Study	YMG316
MATa CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) GAL-UBR1myc::HIS3 Cup1p-Nd-CIN8::URA3	This Study	YMG317
MATα ipl1–321, CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX)	This Study	YMG318
MATa CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) GAL-UBR1myc::HIS3, Cup1p-Nd-CIN8::URA3 mad2Δ::TRP1	This Study	YMG320
MATα CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) ipl1–321 GAL-UBR1myc::HIS3 Cup1p-Nd-CIN8::URA3	This Study	YMG322
MATa CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) cdc20::pMET3-CDC20::TRP1 kip1Δ::TRP1	This Study	YMG323
MATa CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) cdc20::pMET3-CDC20::TRP1 ipl1–321	This Study	YMG325
MATα, CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) cdc20::pMET3-CDC20::TRP1 ipl1–321	This Study	YMG326
MATα CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) cdc20::pMET3-CDC20::TRP1 ase1Δ::TRP1	This Study	YMG327
MATa CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) cdc20::pMET3-CDC20::TRP1 ase1Δ::TRP1	This Study	YMG328
MATα CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) cdc20::pMET3-CDC20::TRP1	This Study	YMG329
MATa CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) cdc20::pMET3-CDC20::TRP1 ipl1–321 GAL-UBR1myc::HIS3 Cup1p-Nd-CIN8::URA3	This Study	YMG332
MATa CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) cdc20::pMET3-CDC20::TRP1 GAL-UBR1myc::HIS3 Cup1p-Nd-CIN8::URA3	This Study	YMG334
MATα CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) kip1Δ:: cdc20::pMET3-CDC20::TRP1 ipl1–321	This Study	YMG336
MATa CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) ase1Δ::NATmx cdc20::pMET3-CDC20::TRP1 ipl1–321	This Study	YMG337
MATa CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) ipl1–321 GAL-UBR1myc::HIS3 Cup1p-Nd-CIN8::URA3	This Study	YMG338
MATa CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110::SPC110-mCherry(hphMX) GAL-UBR1myc::HIS3, Cup1p-Nd-CIN8::URA3 mad2Δ::TRP1	This Study	YMG342
MATa CEN3:lacO×33(Kan) SPC110-mCherry::hphMX DAD1-TAP-KanMx TRP1-pMET-CDC20	This Study	YMG412
MATα CEN3:lacO×33(Kan) SPC110-mCherry::hphMX DAD1-TAP-KanMx TRP1-pMET-CDC20	This Study	YMG413
MATα, CEN3:lacO×33(Kan) kip1Δ::TRP1 SPC110-mCherry::hphMX DAD1-TAP-KanMx TRP1-pMET-CDC20	This Study	YMG414
MATα, CEN3:lacO×33(Kan) kip1Δ::TRP1 SPC110-mCherry::hphMX DAD1-TAP-KanMx TRP1-pMET-CDC20	This Study	YMG415
MATα, CEN3:lacO×33(Kan) SPC110-mCherry::hphMX DAD1-TAP-KanMx ase1Δ::NATmx TRP1-pMET-CDC20	This Study	YMG418
MATa DAM1::6HIS-Kanmx TRP1-pMET::CDC20	This Study	YMG434
MATα CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110-mCherry::hphMX DAM1::6HIS-Kanmx GAL UBR1myc::HIS3, Cup1p-Nd-CIN8::URA3 TRP1::pMET-CDC20	This Study	YMG442
MATA CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110-mCherry::hphMX, kip1Δ::TRP1, TRP1::pMET-CDC20,DAM1–6HIS::Kanmx	This Study	YMG444
MATA CEN3:lacO×33(Kan) his3::GFP-lacI(HIS3) SPC110-mCherry::hphMX ase1Δ::TRP1, TRP1::pMET-CDC20 DAM1–6HIS::Kanmx	This Study	YMG446
MAT A DAD1::TAP-KanMx	Trisha Davis	JBY103–4A
Software and Algorithms
ImageJ (Fiji)	NIH	N/A
MATLAB	Mathworks, Inc.	N/A
The R Project for Statistical Computing	R Foundation	N/A
Excel	Microsoft	N/A