Mechanoadaptive Responses in the Periodontium Are Coordinated by Wnt

Abstract

Despite an extensive literature documenting the adaptive changes of bones and ligaments to mechanical forces, our understanding of how tissues actually mount a coordinated response to physical loading is astonishingly inadequate. Here, using finite element (FE) modeling and an in vivo murine model, we demonstrate the stress distributions within the periodontal ligament (PDL) caused by occlusal hyperloading. In direct response, a spatially restricted pattern of apoptosis is triggered in the stressed PDL, the temporal peak of which is coordinated with a spatially restricted burst in PDL cell proliferation. This culminates in increased collagen deposition and a thicker, stiffer PDL that is adapted to its new hyperloading status. Meanwhile, in the adjacent alveolar bone, hyperloading activates bone resorption, the peak of which is followed by a bone formation phase, leading ultimately to an accelerated rate of mineral apposition and an increase in alveolar bone density. All of these adaptive responses are orchestrated by a population of Wnt-responsive stem/progenitor cells residing in the PDL and bone, whose death and revival are ultimately responsible for directly giving rise to new PDL fibers and new bone.

Introduction

The clinical literature is replete with examples of how tissues adapt to physical forces. In the craniomaxillofacial skeleton, tooth loss predictably leads to alveolar bone atrophy (Canger and Celenk 2012) and a thinning of the periodontal ligament (PDL; Denes et al. 2013; Krieger et al. 2013). Conversely, hyperloading of the dentition causes a thickening of the PDL (Mortazavi and Baharvand 2016) and alveolar bone accrual (Carlsson 2004). Clearly, the PDL and bone must function as a unit to absorb and transmit mechanical loads—but precisely how are these tissue-level responses coordinated? Prior to the onset of occlusal forces, the PDL is a disorganized collection of fibroblasts, but shortly after occlusion begins, fibroblasts rearrange themselves and align their cytoplastic projections tangential to the force vector (Huang, Salmon, et al. 2016). This rearrangement is instigated in response to tensile strains in the PDL as it transfers the force produced by occlusion to the alveolar bone (Qian et al. 2009). Then, in a balanced occlusion, an equilibrium is somehow maintained between masticatory forces and bone/PDL health, but how this homeostasis is achieved is largely in the realm of speculation.

In the event of tooth loss, there is a disruption in this balanced state (Witter et al. 2001), and presumably, a new occlusal equilibrium is established to contend with differences in force distribution. This adjustment is critical because any strategy to replace the dentition (e.g., with implants) should emulate the physiologic loading environment that maintained tissue homeostasis. This, then, was the starting point for our study: we sought to understand how the alveolar bone and PDL adapt to hyperloading situations, reasoning that once we had clues into how this was achieved, we could use this knowledge to optimize the design of implant-supported prostheses or improve orthodontic tooth movement procedures.

To guide our investigation, we began with some general assumptions. First, we anticipated that whatever signals were responsible for coordinating alveolar bone and PDL responses to loading, they would to be under tight temporal and spatial control (Rios et al. 2008; Takimoto et al. 2015). Therefore, comparisons to a “ground state” representing a balanced, homeostatic status would be warranted. Second, we assumed that because the PDL transfers force to the alveolar bone, molecular/cellular changes would occur first in the PDL and later in bone. Third, we expected that the responses in the PDL and bone would be coordinated with one another.

With these guiding principles in mind, we considered in vitro and in vivo models of loading (Rios et al. 2008; Oortgiesen et al. 2012; Ho et al. 2013). Because our interest was primarily in the coordinated responses of bone and PDL, we opted for an in vivo model and settled on a modified method whereby masticatory forces are concentrated on a tooth by virtue of the extraction of surrounding teeth (Kondo and Wakabayashi 2009). The idea behind this model is simple: when a tooth is lost, masticatory forces that once were shared by the entire dentition are now borne by fewer teeth. Using this model in mice, we first asked, were robust, reproducible, reliable changes detectable in the PDL and alveolar bone in response to hyperloading? Second, were any of the observed changes reminiscent of the response of human periodontium to hyperloading? With affirmative answers to both questions in hand, we then undertook a series of experiments using FE modeling coupled with molecular, cellular, and genetic analyses to determine how and when the PDL and alveolar bone dynamically respond to changes in their mechanical environment.

Materials and Methods

Animals

Experimental protocols followed ARRIVE guidelines and were approved by the Stanford Committee on Animal Research (13146). Wild-type, Axin2^CreERT2/+ (018867), and R26R^mTmG/+ (007576) mice were purchased from Jackson Laboratories. All mice were 5 wk old. To induce Cre expression in Axin2^CreERT2/+;R26R^mTmG/+ mice, tamoxifen (4 mg/25 g) was delivered intraperitoneally for 5 consecutive days.

Tooth Extraction

Mice were anesthetized, and maxillary second and third molars (mxM2s and mxM3s) were extracted with microforceps. Bleeding was controlled by local compression. Subcutaneous injection of buprenorphine (0.1 mg/kg) was used to control postoperative discomfort. Mice were fed with a regular hard-food chow (2918; Envigo), and body weight was recorded weekly (Appendix Table).

Vital Dye Double Labeling

Animals were divided into 3 groups: hyperloading group 1, hyperloading group 2, and an intact dentition group. In hyperloading group 1, mice were given a single intraperitoneal injection of calcein (25 mg/kg; Sigma-Aldrich) 2 d prior to mxM2 and mxM3 extraction. Five days after tooth extraction, mice were given an alizarin red (AR) (25 mg/kg; Sigma-Aldrich) injection. Two days later, mice were sacrificed, and mandibular bones were harvested for analysis. In hyperloading group 2, mice were given an injection of calcein 5 d following mxM2 and mxM3 extraction. Twelve days after tooth extraction, mice were given an injection of AR. Two days after the last injection, mice were sacrificed, and mandibular bones were harvested. An intact dentition group was used as control, and age-matched mice with intact dentition were given the same injections with an exact 7-d interval.

FE Method

Following the micro–computed tomography (µCT) scanning at 10.5-μm voxel size (70 kV, 115 μA, 300-ms integration time), the relevant portion of the mouse mandible and molar was developed. Multiplanar reconstruction and volume rendering were carried out with Avizo Fire 8.1.1 (FEI) and ImageJ (1.51w; National Institutes of Health) software. Further analysis was carried out with ScanIP (N-2019.03-SP1; Synopsys). A restricted threshold value was determined to select the molar and alveolar bone structure. Boolean operations were performed to eliminate fine details of the bone/tooth structure and socket. Recursive Gaussian filtering and mean filtering were used to smooth surfaces. The model was exported from ScanIP in .stl file format and then imported into Comsol 5.4 (Multiphysics) for subsequent FE analysis. With Boolean operations, the region between the molar and the alveolar bone socket was filled with a solid assigned to be the PDL. The molar, bone, and PDL were modeled as linear elastic materials with Young’s elastic moduli of 20 GPa, 100 MPa, and 20 MPa, respectively, and Poisson’s ratios of 0.45, 0.33, and 0.45, respectively (Nishihira et al. 2003; Fill et al. 2012). The top surface of the molar tooth was flattened in the model to allow a simpler application of net downward forces on the tooth, which consisted of the “normal” load of 1.36 N and a “hyperload” of 5 N (Niver et al. 2011). The bottom surface of the cube of alveolar bone that surrounded the PDL and molar was fixed at its base. The FE model was run with geometric nonlinearity (39,497 elements, 178,716 degrees of freedom).

Statistical Analysis

Results were presented as mean ± SD. All statistical analyses were performed with GraphPad 7.0 (GraphPad Software). Comparison of cell density in PDL was analyzed with a 2-tailed Student’s t test. Comparison of other histomorphometric data was based on a one-way analysis of variance, followed by Tukey’s post hoc testing. Significance was attained at P < 0.05.

For µCT, molecular analyses, and histomorphometric analysis, see the Appendix.

Results

A Hyperloading Model That Causes Excessive Attrition and Amplifies PDL Stress and Strain

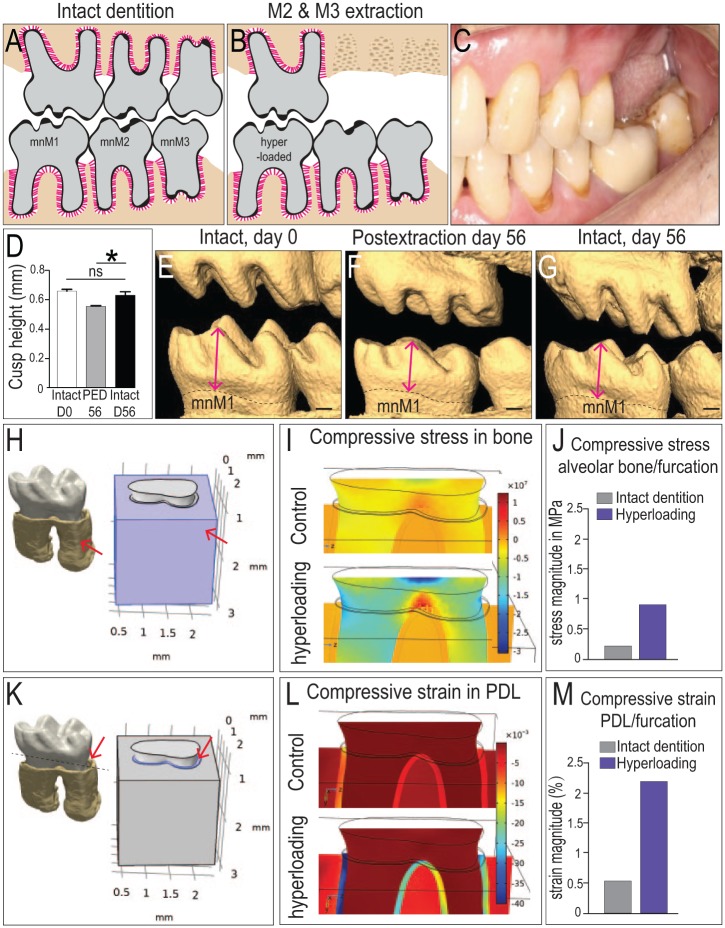
To simulate a hyperloading condition, mxM2s and mxM3s were extracted (Fig. 1A, B). This experimental scenario mimics a common clinical situation (Fig. 1C) where removal of an opposing dentition results in hyperloading of the remaining teeth (Kondo and Wakabayashi 2009). To ascertain whether the mandibular first molar (mnM1) was indeed subjected to excessive loads, we examined attrition on mnM1. In comparison with mnM1s from animals with intact dentition (Fig. 1D, E), mnM1s from the extraction group exhibited significantly more attrition by postextraction day 56 (Fig. 1F, G).

Figure 1.

Biological and mechanical validation of a murine model of hyperloading. Dentition in (A) an intact state and (B) after mxM2 and mxM3 extraction, with the intention to hyperload mnM1. (C) An analogous condition in a patient who has lost mxM1 and mxM2. (D) Quantification of cusp height from (E–G) 3-dimensional (3D) micro–computed tomography (µCT) reconstructions of representative dentitions. Cusp height of mnM1 was measured from the tip of the buccal-middle cusp to the cementoenamel junction (arrows). (H) A 3D µCT reconstruction of mnM1 used in a 3D finite element model; arrow indicates alveolar bone surrounding mnM1, which was assigned appropriate material properties (see Methods). (I) Compressive stress distributions in the alveolar bone under normal occlusal load (top) and under hyperocclusal load (bottom). (J) Magnitude of the stress in alveolar bone of the furcation region. (K) A 3D µCT reconstruction of mnM1, where the PDL is assigned appropriate material properties (arrow). (L) Compressive strain distributions in the PDL under normal occlusal load (top) and under hyperocclusal load (bottom). (M) Calculated strains in the PDL occupying the furcation region. Scale bars = 200 µm. Values are presented as mean ± SD. *P < 0.05. mnM, mandibular molar; ns, not significant; PED, postextraction day; PDL, periodontal ligament.

To estimate the magnitude of the increased occlusal load, we began with the force required by the mouse to break a hard chow pellet, which is ~5 N (Niver et al. 2011). The jaw acts as a class III lever, which influences the distribution of this bite force on the teeth (Wysocki and Tseng 2018). We determined the distance of the molars from the temporomandibular joint and then computed that the third mandibular molar experiences the highest percentage of the total force (38.4%, 1.92 N) and mnM1, the lowest percentage of the total force (27.2%, 1.36 N). Following removal of mxM2 and mxM3, the total force was now concentrated solely on mnM1, which translated into a 3.7-fold increase in occlusal force on that single tooth. These force data coupled with the µCT data were used to formulate a 3-dimensional FE model to estimate the stress and strain states in the PDL of mnM1 and its surrounding bone (Fig. 1H).

The first observation is that compressive strains were distributed among all 3 tissues of the periodontium. In bone underlying the furcation, normal occlusal loading produced a stress magnitude of ~0.25 MPa (Fig. 1I, J). Under hyperloading conditions, the stresses quadrupled, to ~1.0 MPa (Fig. 1I, J). We next examined the PDL (Fig. 1K) where normal occlusal loading produced a strain magnitude of ~0.5% (Fig. 1L, M). Under hyperloading, the strain magnitude again quadrupled, to >2.0% (Fig. 1L, M).

Hyperloading Instigates a Series of Catabolic and Anabolic Reactions in the PDL

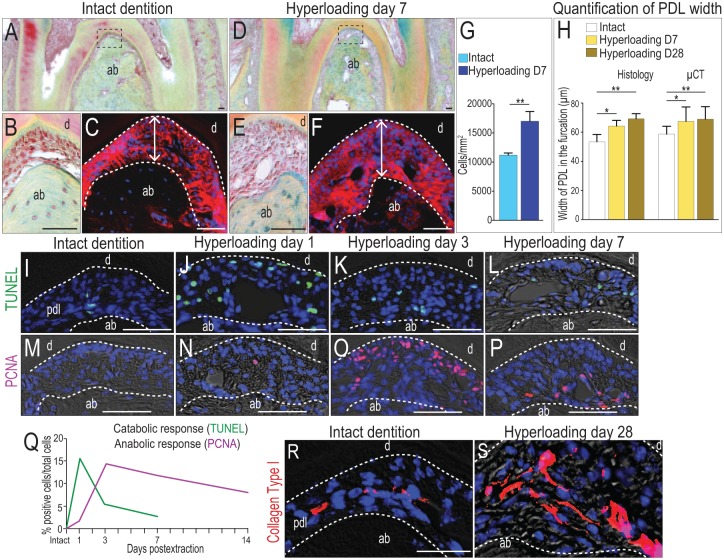
We analyzed the biological responses in the PDL initiated by the elevated strain. We used mnM1 PDLs from intact dentition as a control (Fig. 2A, B). Periostin immunostaining was used to demarcate the PDL and allow measurement of its width (Fig. 2C). One week after initiating hyperloading, the mnM1 PDL was significantly more cellular (Fig. 2D, E) and significantly wider (Fig. 2F) than mnM1 PDLs from intact dentition. Histomorphometric quantification revealed that in the hyperloading group, cell density was increased almost 1.5 times above that of controls (Fig. 2G). These measurements, coupled with µCT analyses, demonstrated that relative to the intact state, PDL width significantly increased as a function of hyperloading (Fig. 2H).

Figure 2.

Hyperloading causes local apoptosis in the periodontal ligament (PDL), followed by robust proliferation. (A) Pentachrome staining of a representative sagittal tissue section through mnM1 from mice with intact dentition. (B) Higher magnification of boxed area in panel A. (C) Periostin immunostaining of the PDL. (D) Representative sagittal section through mnM1 after 7 d of hyperloading caused by extraction of the opposing dentition. (E) Higher magnification of boxed area in panel D. (F) Periostin immunostaining of the PDL. (G) Quantification of cell density in the PDL of the furcation area. (H) Quantification of PDL width from immunostaining staining and µCT data. (I–L) Cell apoptosis detected by TUNEL staining and (M–P) cell proliferation detected by PCNA immunostaining in the PDL at time points indicated. (Q) Quantification of TUNEL^+ve (n = 3) and PCNA^+ve cells (n = 3) in the furcation PDL, as a function of time. Immunostaining for type I collagen in the PDL of mice with (R) intact dentition and (S) following 28 d of hyperloading. Scale bars = 50 µm. Values are presented as mean ± SD. *P < 0.05. **P < 0.01. ab, alveolar bone; d, dentin; PCNA, proliferating cell nuclear antigen; µCT, micro–computed tomography.

To explore the cellular mechanisms responsible for this increase in PDL width, we undertook a detailed molecular/cellular analysis, conducted at multiple time points after hyperloading. For example, in intact dentition, few TUNEL^+ve cells were detectable in the PDL (Fig. 1I), but within 1 d of hyperloading, programmed cell death was rampant in the mnM1 PDL (Fig. 2J). The proportion of TUNEL^+ve cells per total PDL cells quickly decreased over the next 48 h (Fig. 2K), and by day 7 (Fig. 2L), few TUNEL^+ve cells were detectable, similar to the levels seen in the intact state.

Mitotic activity, however, was on the rise. In intact dentition, the PDL is a quiescent tissue (Huang, Liu, et al. 2016). Proliferating cell nuclear antigen (PCNA) immunostaining of the mnM1 PDL confirmed the scarcity of proliferating cells in the PDLs of mice with intact dentition (Fig. 2M). In a hyperloaded PDL, the proportion of PCNA^+ve cells per total PDL cells increased from baseline (Fig. 2N), reached its dramatic peak on day 3 (Fig. 2O) and then remained elevated for a considerable time (Fig. 2P; quantified in 2Q).

We compared the timing of these 2 cellular responses. Hyperloading instigated in the PDL an immediate catabolic response in the form of apoptotic cells (green line, Fig. 2Q). The peak of this catabolic response, 24 h after the initiation of hyperloading, coincided with the onset of an anabolic response, such as cell proliferation in a tissue that is mitotically quiescent in a homeostatic state (purple line, Fig. 2Q). The prolonged nature of this anabolic response (Fig. 2Q) culminated in a densely cellular, thicker, collagen matrix-rich PDL by day 7 (compare Fig. 2R with S).

Bone Displays a Synchronized Response to Hyperloading

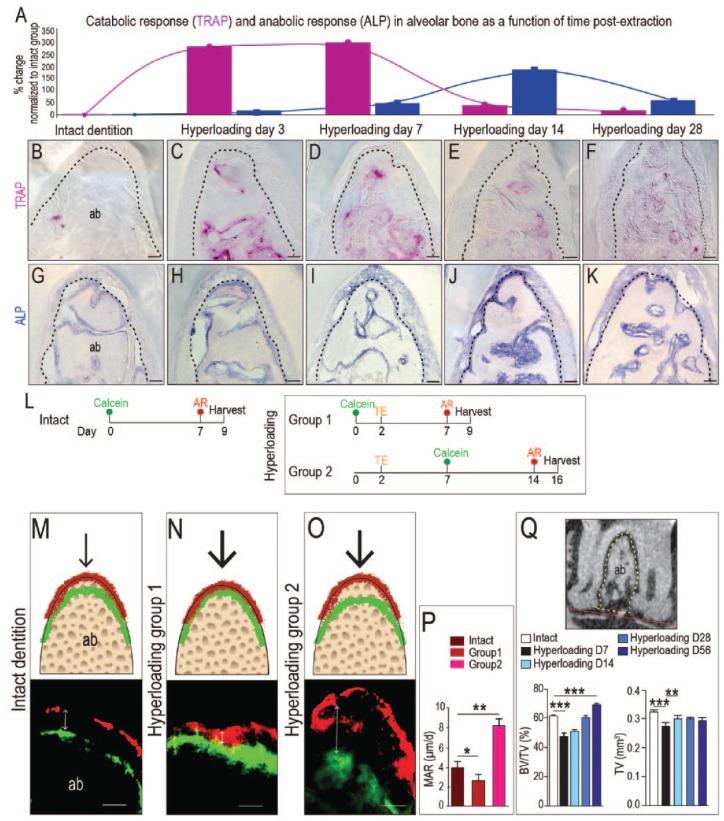
The force generated by hyperloading is initially borne by the PDL and is then transferred to the alveolar bone. Since most bony changes manifest as alterations in osteoclast and osteoblast function, we followed these cellular activities first. Tartrate-resistant acid phosphatase (TRAP) and alkaline phosphatase (ALP) activities are balanced in healthy animals (Prideaux et al. 2016; Fig. 3A, B). By day 3 of hyperloading, TRAP activity was significantly (2.5-fold) elevated in interradicular bone (Fig. 3C). TRAP activity remained elevated at day 7 (Fig. 3A, D). By day 14, TRAP activity had almost returned to levels seen in intact dentition (Fig. 3E). By day 28, TRAP activity was indistinguishable from baseline TRAP activity (Fig. 3F).

Figure 3.

Hyperloading initially activates bone resorption, which in response triggers an increase in mineral apposition and alveolar bone accrual. (A) Quantification of TRAP and ALP activity in alveolar bone in response to hyperloading. Values are normalized to TRAP and ALP levels in an intact dentition. (B–F) TRAP activity and (G–K) ALP activity in alveolar bone in the furcation area at time points indicated. (L) Vital dye double-labeling experiment to evaluate mineral apposition rate (MAR) in alveolar bone in response to hyperloading. (M) In mice with intact dentition, calcein (green) dye was injected first, and 7 d later, AR (red) was injected. Two days after the last injection, tissues were harvested. (N) In hyperloading group 1, calcein was injected 2 d before tooth extraction, and AR was injected on day 7 (postextraction day 5). (O) In hyperloading group 2, calcein was injected on day 7 (postextraction day 5), and AR was injected on day 14 (postextraction day 12). Black arrows indicate the load. Double arrows indicate the distance between labels. (P) Quantification of MARs. (Q) The ratio of bone volume (BV) to total volume (TV) and the absolute TV were calculated and compared. The red line connects the lowest points of two roots. The TV was measured above this line and under the furcation (dotted line area). Scale bars = 50 µm. Values are presented as mean ± SD. *P < 0.05. **P < 0.01. ***P < 0.0001. ab, alveolar bone; ALP, alkaline phosphatase; AR, alizarin red; TE, tooth extraction; TRAP, tartrate-resistant acid phosphatase. This figure is available in color online.

The peak catabolic TRAP response coincided with the onset of an anabolic response, visualized by ALP staining. For example, relative to the intact state (Fig. 3A, G), hyperloading caused an increase in ALP activity (see Fig. 3H, I) that peaked on day 14 and then gradually returned to baseline levels by day 28 (Fig. 3J, K). Collectively, these TRAP and ALP data suggested that hyperloading initially instigated a catabolic response that caused bone loss and then an immediate anabolic response. From these analyses, however, it was not clear whether this series of events ultimately culminated in a net alveolar bone loss or a net bone gain.

To address this question, we monitored mineral apposition rates (MARs). Calcein and AR were delivered with a 7-d interval (Fig. 3L), and the MAR was calculated for mice with intact dentition (intact group). In this case, the calcein- and AR-labeled bone was separated by ~30 µm (Fig. 3M); therefore, the MAR was ~4 µm/d. We then considered the hyperloading cases. In hyperloading group 1, calcein was given 2 d prior to hyperloading, and AR was given after a same 7-d interval (Fig. 3L). There was no separation in the calcein- and AR-stained bone (Fig. 3N).

In hyperloading group 2, calcein was given 5 d after hyperloading was initiated, and AR was given after a 7-d interval (Fig. 3L). A separation of 59 µm was observed between the calcein- and AR-stained bone (Fig. 3O). Collectively, these data demonstrated that hyperloading caused an initial catabolic response in bone that eliminated mineral apposition, but this was transient. Shortly afterward, an anabolic response ensued, in which MAR increased (Fig. 3P). Imaging (µCT) data confirmed that in the interradicular space, bone became significantly denser in response to hyperloading (Fig. 3Q).

Wnt-Responsive Stem/Progenitor Cells Coordinate the Functional Adaptation of PDL and Alveolar Bone to Hyperloading

At the beginning of our study, we speculated that the molecular signals coordinating the PDL and bone responses to hyperloading would likely be shared between the tissues. A good candidate for this coordinating activity was the Wnt pathway: Wnt signaling is involved in cell proliferation and bone mineralization (Wu et al. 2018) and is critical for PDL homeostasis and response to injury (Yuan, Pei, Zhao, Tulu, et al. 2018).

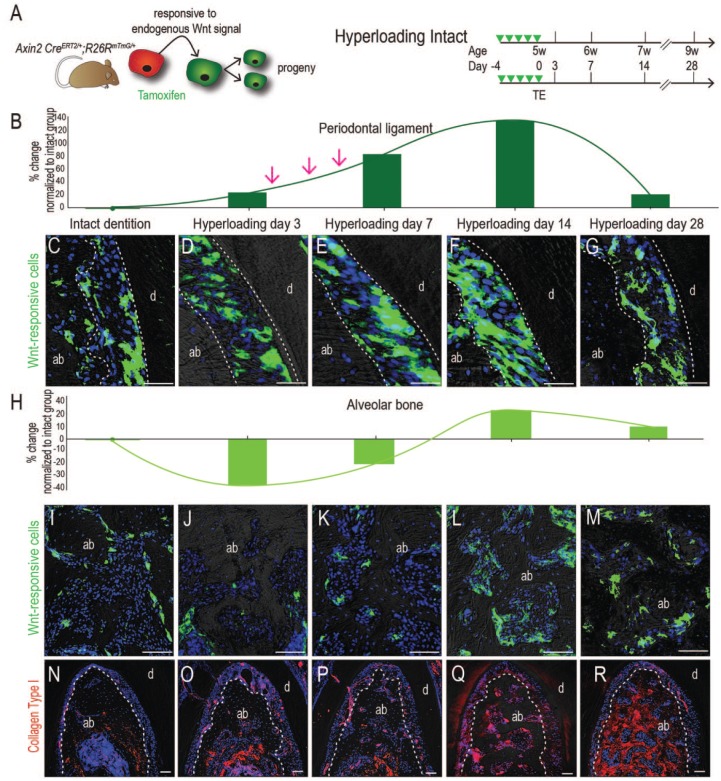
We used Axin2^CreERT2/+; R26R^mTmG/+ mice (Yuan, Pei, Zhao, Li, et al. 2018) in which Wnt-responsive stem/progenitor cells and their descendants are labeled with green fluorescent protein (GFP; Fig. 4A) to characterize their distribution in the PDL of mice with intact dentition (Appendix Fig. 2); these data established a baseline against which we could compare the hyperloading group. Relative to controls (Fig. 4C), hyperloading stimulated an immediate increase in the number of Wnt-responsive cells in the PDL (quantified in Fig. 4B, see also D–G). Coimmunostaining with GFP and PCNA confirmed that Wnt-responsive stem/progenitor PDL cells were mitotically active (Appendix Fig. 3). Over time, the number of Wnt-responsive descendants in the PDL was reduced, back to the numbers observed in the PDL of the intact dentition group (Fig. 4D–G).

Figure 4.

Wnt-responsive stem/progenitor cells are directly responsible for giving rise to new force-induced periodontal ligament (PDL) and alveolar bone. (A) Experiment design. Tamoxifen was delivered to Axin2^CreERT2/+; R26R^mTmG/+ mice prior to tooth extraction and examined at days 3, 7, 14, and 28. Cells’ response to Wnt signaling were converted from membrane tomato expressing (red) to membrane GFP expressing (green) in the presence of tamoxifen. (B) Quantification of Wnt-responsive cells in the PDL, normalized to the GFP^+ve area in the intact group. (C–G) GFP immunostaining in the PDL at time points indicated. (H) Quantification of Wnt-responsive cells in alveolar bone, normalized to the GFP^+ve area in the intact group. (I–M) GFP immunostaining in alveolar bone at time points indicated. (N–R) Immunostaining for collagen I at time points indicated. Scale bars = 50 µm. ab, alveolar bone; d, dentin; GFP, green fluorescent protein. This figure is available in color online.

A similar adaptive response was noted in bone (Fig. 4H). In the intact dentition group, most GFP^+ve stem/progenitor cells lined the bone surfaces of the vascular spaces (Fig. 4I). Hyperloading reduced this population (Fig. 4J), coincident with the catabolic phase of bone resorption (Fig. 3). The remaining Wnt-responsive pool then expanded again (Fig. 4K–M), which coincided with the anabolic bone response observed previously. This coordinated mechanoadaptive response to hyperloading culminated in an increase in collagen type I deposition in the PDL and alveolar bone (compare Fig. 4N with O–R).

Discussion

When does loading of the dentition become hyperloading? In its simplest form, “hyper” describes a condition that is “in excess of, or exceeds, the normal status.” According to the literature, murine molars are subjected to ~5 N during the mastication of hard food (Niver et al. 2011). If the total occlusal surface that bears this load is reduced via extraction of mxM2 and mxM3, the remaining mxM1 bears the full load by itself; therefore, we state that mxM1 is hyperloaded.

Another model of hyperloading involves the creation of premature occlusal contact, which triggers a robust catabolic reaction (Walker et al. 2008; Goto et al. 2011; Tsutsumi et al. 2013; Tsuzuki et al. 2016; Tsutsumi et al. 2018). Unlike our study, however, a subsequent anabolic response (Figs. 2–4) was not reported. This might be explained by the fact that the time points for analysis in the preceding studies were short (e.g., ≤7 d; Goto et al. 2011; Tsutsumi et al. 2013; Tsuzuki et al. 2016; Tsutsumi et al. 2018) and an anabolic effect that followed the catabolic response might have been missed. In our experiments, collagen content increased in response to hyperloading (Figs. 2, 4). As the collagen content of a tissue increases, so too does its elastic modulus (Wenger et al. 2007; Dutov et al. 2016). What this means is that the hyperloaded PDL becomes thicker and stiffer (Fig. 5) and the hyperloaded alveolar bone becomes thicker and denser (Fig. 3). As a consequence of this biological adjustment in collagen content, both tissues have an increased strain tolerance, thus reducing strains back to levels observed in intact dentition (Fig. 5).

Figure 5.

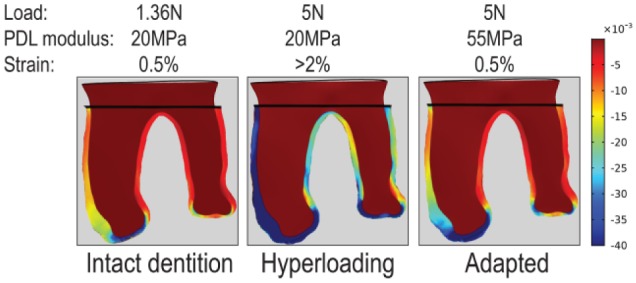
FE modeling demonstrates an adaptive response of periodontal ligament (PDL) to hyperloading. In an intact dentition, the PDL is loaded with 1.36 N and has a modulus of 20 MPa, which results in 0.5% strain at the furcation region. In a hyperloading condition, the same PDL is subjected to an increased load (5 N), which produces higher strain (>2%) at the furcation. In response, the PDL accumulates collagen and becomes thicker, thereby increasing its elastic modulus to 55 MPa. Now, the 5-N load produces strain at the furcation of ~0.5%, demonstrating that the adaptive response of the PDL acclimates the tissue to its new loaded condition. The stain distribution in the bone is not shown.

A second possible explanation for a failure by others to observe an adaptive response in the periodontium could be that the forces delivered by premature occlusal contact may actually exceed the “physiologic envelope” of the periodontium. None of the referenced studies estimated the magnitude of the force produced by premature occlusal contact, so it is difficult to directly compare results. This brings up an important question, though: when does hyperloading of the dentition become overloading? The simple answer is, we don’t know. There is no a priori reason to think that the 2 conditions are synonymous; in fact, our data demonstrate the opposite (Figs. 2, 3). Overloading does occur though, and clinical literature is replete with examples of how excessive forces can irreversibly damage tissues. For example, forces associated with tooth concussion and subluxation can lead to permanent damage of the pulp (Hermann et al. 2012). The PDL, however, appears to be a remarkably resilient tissue. Even after it has undergone hyalinization because of excessive orthodontic force, the PDL can recover (Feng et al. 2016). Tissue overloading must therefore take into account not only the magnitude and duration of a force but also the material properties of the tissue and its regenerative capacity.

With regard to this last point, there is another biological variable to consider: our study used young mice, and young tissues typically exhibit robust, adaptive responses to injury. What if older animals were subjected to hyperloading? We know that the proliferative activity associated with tissue repair decreases with age (Lossdorfer et al. 2010; Lim et al. 2014), and we speculate that the adaptive responses observed in the young periodontium will be attenuated in older animals. If this proves to be true, then we will be one step closer toward understanding the biomechanical limits of alveolar bone and its associated structures. This information can in turn be used to build smarter biomaterials to replace damaged and/or diseased tissues.

Author Contributions

Q. Xu, contributed to conception, design, data acquisition, analysis, and interpretation, drafted and critically revised the manuscript; X. Yuan, contributed to conception, design, data acquisition, analysis, and interpretation, critically revised the manuscript; X. Zhang, J. Chen, contributed to data acquisition, analysis, and interpretation, critically revised the manuscript; Y. Shi, J.B. Brunski, contributed to data analysis and interpretation, critically revised the manuscript; J.A. Helms, contributed to conception, design, data analysis and interpretation, drafted and critically revised the manuscript. All authors gave final approval and agree to be accountable for all aspects of the work.