Abstract
Proton-coupled electron-transfer (PCET) steps play a key role in energy conversion reactions. Molecular PCET reactions are well-described by “square schemes” in which the overall thermochemistry of the reaction is broken into its constituent proton-transfer and electron-transfer components. Although this description has been essential for understanding molecular PCET, no such framework exists for PCET reactions that take place at electrode surfaces. Herein, we develop a molecular square scheme framework for interfacial PCET by investigating the electrochemistry of molecularly well-defined acid/base sites conjugated to graphitic electrodes. Using cyclic voltammetry, we first demonstrate that, irrespective of the redox properties of the corresponding molecular analogue, proton transfer to graphite-conjugated acid/base sites is coupled to electron transfer. We then show that the thermochemistry of surface PCET events can be described by the pKa of the molecular analogue and the potential of zero free charge (zero-field reduction potential) of the electrode. This work provides a general framework for analyzing and predicting the thermochemistry of interfacial PCET reactions.
Short abstract
The thermochemistry of proton-coupled electron-transfer steps at electrode surface sites can be described by the pKa of the molecular analogue and the potential of zero free charge of the electrode.
Introduction
Proton-coupled electron-transfer (PCET) reactions are central to energy conversion processes across chemical and biological systems.1−78 These same reactions take place at the surfaces of materials,25−27 playing a key role in corrosion,28 sensing,29,30 and catalysis.31−36 Consequently, interfacial PCET reactions underlie a wide array of energy conversion technologies, including flow batteries,37,38 supercapacitors,39,40 fuel cells,41−44 and solar fuels devices.45,46 Thus, a molecular-level understanding of the factors that control the energetics of interfacial PCET is critical to designing improved materials for energy conversion.
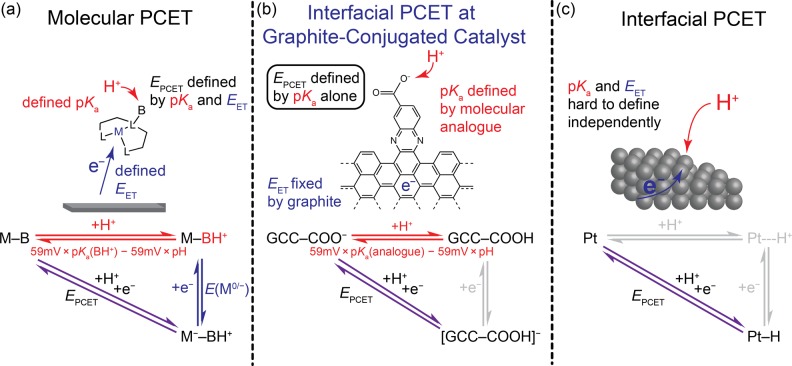
In molecular and biological systems, the overall thermochemistry of a PCET reaction is well described by the sum of the free energies for the constituent proton-transfer (PT) and electron-transfer (ET) reactions (Figure 1a).18,47 In aqueous media, the free energy of the PT step is proportional to the difference between the pKa of the proton acceptor, pKa(BH+), and the pH of the solution. The free energy of the ET step is given by the standard reduction potential of the molecule in the absence of proton transfer (E(M0/–)). This thermodynamic partitioning is usually depicted in a “square scheme,” wherein the horizontal legs of the square represent PT steps, the vertical legs represent ET steps, and the diagonal represents the overall PCET reaction.18,47 A partial square scheme is shown for molecular PCET in Figure 1a. The square scheme framework is particularly useful for molecular PCET reactions because, in most cases, at least two of the three parameters in the thermodynamic cycle are independently measurable. Furthermore, this framework enables the rational design of molecular PCET agents and catalysts via tuning of ΔG for PT and ET through changes to the pKa and E(M0/–), respectively.5,48−57
Figure 1.
(a) Partial square scheme for the molecular proton-coupled electron-transfer (PCET) reaction M–B + H+ + e– → M––BH+. The horizontal leg represents the thermochemistry of the proton-transfer step, determined by the pKa of the proton acceptor and the pH of the solution. The vertical leg represents the thermochemistry of the electron-transfer step, determined by the reduction potential of the protonated molecule, M–BH+, in the absence of proton transfer. The diagonal represents the thermochemistry of the overall reaction, which is the sum of the two legs. (b) Partial square scheme for PCET at a GCC–COOH site. The pKa in the horizontal leg is taken as that of a molecular phenazine analogue, and the vertical leg is grayed out because the parameter defining it was unknown prior to this work. (c) Partial square scheme for a PCET reaction to form a bond at a Pt surface. The horizontal and vertical legs of the scheme defining these legs were unknown prior to this work.
There is no corresponding approach for partitioning the thermochemistry of an interfacial PCET reaction at the surface of an electrode (Figure 1c). This knowledge gap exists for two reasons. First, the identity of the surface site involved in the PCET reaction is usually not known with precision. Most metal surfaces exhibit a heterogeneous distribution of sites that can engage in PCET reactions, making it difficult, if not impossible, to correlate PCET redox features to the local structure and physicochemical properties of the site undergoing the reaction. Second, only the diagonal of the square scheme is directly measurable electrochemically because PT is always coupled to ET for a metallic surface held at constant potential. This obligatory PCET arises because the surface active sites are in constant electrostatic equilibrium with the rest of the solid. When a proton is transferred to the surface, the electron density instantaneously redistributes to compensate for the charge on the proton, leading to electron flow from the external circuit in order to hold the potential at the electrode constant.58 If the electrode is disconnected from an external circuit such that compensating charge cannot flow, each proton transfer to the surface will augment the surface charge and alter the proton affinity for subsequent PT events (see below). Thus, it is unclear which physical descriptors should be used to describe the horizontal and vertical legs of the square scheme, and they are grayed out in Figure 1c. These factors have impeded the development of an analogous square scheme framework for interfacial PCET. This knowledge gap could be resolved if the surface site undergoing PCET had a molecular analogue with a known pKa.
We have developed a strategy for incorporating molecularly well-defined active sites into graphitic electrodes using conjugated aromatic pyrazine linkages. We have previously established that the resulting graphite-conjugated catalysts (GCCs) are strongly electronically coupled to the electrode and behave like metallic active sites.59 This bottom-up synthetic method allows us, for the first time, to correlate interfacial PCET reactions with the properties of analogous molecular species.
Herein, we use the GCC platform to develop a square scheme framework for interfacial PCET reactions. Using cyclic voltammetry, we first demonstrate that the redox behavior of acid/base sites on GCCs is radically different than that of their molecular analogues. Remarkably, at acid/base sites on GCCs, PT is always coupled to ET, even if the corresponding molecular analogue is redox inactive. Furthermore, we discover that the potential at which the PCET reaction occurs at a GCC site correlates to the pKa of the molecular analogue with an ∼60 mV per pKa unit scaling. From these data, we construct a model for the thermochemistry of interfacial PCET at GCC sites based on the pKa of the molecular analogue and the potential of zero free charge (zero-field reduction potential) of the electrode (Figure 1b). This model provides a general framework for analyzing and predicting the thermochemistry of interfacial PCET reactions more broadly.
Synthesis of Graphite-Conjugated Catalysts
GCC electrodes were prepared via treatment of carbon surfaces with o-phenylenediamine derivatives following procedures described previously (Scheme 1).59−61 Graphitic carbon electrodes have o-quinone groups native to the surface edge planes of the graphite sheets that react to form pyrazine linkages.62−65 Other oxygenic functional groups, including ketones, alcohols, and carboxylic acids, are also native to carbon surfaces.62−65 Since our study aims to understand PCET processes at the added surface sites, the experiments described herein were conducted on glassy carbon plates with minimal background electrochemical activity. (Full synthetic details and X-ray photoelectron spectroscopy characterization are provided in the Supporting Information.)
Scheme 1. Synthesis of GCCs.

Proton Transfer at GCCs Is Coupled to Electron Transfer
Cyclic voltammograms (CVs) indicate that the redox properties of GCC sites are fundamentally different than those in molecules. CVs of GCC-phenazine in 0.1 M NaOH display a broad redox feature at −0.65 V (all potentials are vs the normal hydrogen electrode (NHE)) (Figure 2), previously attributed to the two-proton, two-electron reduction of the surface pyrazine unit to dihydropyrazine.59,60 This wave occurs 0.35 V positive of the redox feature associated with the two-proton, two-electron reduction of phenazine to dihydrophenazine in solution.66
Figure 2.

Cyclic voltammogram (100 mV s–1) of GCC-phenazine recorded in 0.1 M NaOH.
Interestingly, the electrochemical behaviors of GCC-phen-COOH and GCC-phen-NH2 are strikingly different than those of the molecular analogues. In CVs of GCC-phen-COOH in 0.1 M NaOH, the pyrazine wave is still observed at −0.65 V, but we also observe a second reversible wave at −0.46 V (Figure 3a). The E1/2 values for these redox features shift −63 and −61 mV per pH unit, respectively (Figure S1), indicating that both waves arise from PCET reactions involving an equal number of protons and electrons.47 Similarly, CVs of GCC-phen-NH2 in 0.1 M NaOH display both a pyrazine-based redox feature at −0.75 V and a second redox feature at −0.47 V (Figure S2). These waves shift by −65 and −59 mV per pH unit, respectively (Figure S3), again indicating that these redox features both arise from PCET processes in which an equal number of protons and electrons are transferred. The PCET behavior of GCC sites is in stark contrast to that of the molecular analogues. The base-soluble molecular analogues, quinoxaline-6-carboxylate and 6-quinoxalinamine, each display only one redox feature, attributed to the proton-coupled pyrazine reduction, at −0.87 V and −1.03 V, respectively (Figures 3b and S4). These observations reveal a unique feature of redox processes at GCCs: acid/base sites give rise to redox waves irrespective of the redox behavior of the corresponding molecular analogue.
Figure 3.

Cyclic voltammograms (100 mV s–1) recorded in 0.1 M NaOH of (a) GCC-phen-COOH and (b) quinoxaline-6-carboxylate.
This unusual redox behavior is also observed for other acid/base moieties on GCCs. A GCC bearing an OH group meta to the pyrazine ring, GCC-phen-m-OH, gives rise to a pyrazine wave at −0.71 V as well as a second proton-coupled wave at −0.26 V in 0.1 M NaOH (Figures 4a and S5). Likewise, a GCC bearing an OH group ortho to the pyrazine ring, GCC-phen-o-OH, displays two proton-coupled redox waves at −0.71 V and −0.17 V (Figures S6 and S7). Molecular phenols are redox active, and CVs of OH-substituted molecular pyrazines, 6-quinoxalinol and 5-quinoxalinol, each display a second oxidative feature due to phenol oxidation along with the quasi-reversible pyrazine waves (Figures 4b and S8). However, the phenol oxidation waves are fundamentally distinct from either wave observed at GCC-phen-m-OH or GCC-phen-o-OH. The molecular OH oxidation waves for 5-quinoxalinol and 6-quinoxalinol are both irreversible and display anodic peak potentials at 0.56 and 0.99 V, respectively, >0.7 V positive of the reversible waves observed for GCC-phen-o-OH and >1.2 V positive of the reversible waves observed for GCC-phen-m-OH. These dramatic differences in both reversibility and wave position indicate that the redox waves observed in GCC-phen-o-OH and GCC-phen-m-OH are fundamentally different than those observed in the molecular quinoxalinol compounds.
Figure 4.
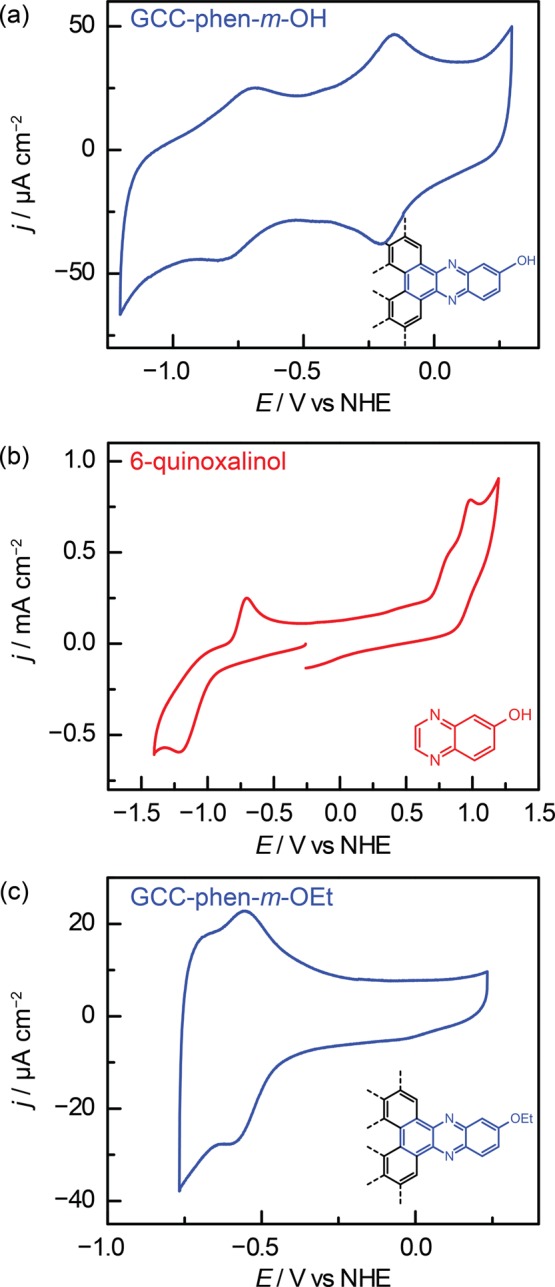
Cyclic voltammograms (100 mV s–1) recorded in 0.1 M NaOH of (a) GCC-phen-m-OH, (b) 6-quinoxalinol, and (c) GCC-phen-m-OEt.
Alkylating the hydroxyl moiety eliminates the corresponding redox wave. GCC-phen-m-OEt and GCC-phen-o-OEt each only give rise to one proton-coupled redox feature (Figures 4c and S9–S11), suggesting that the second waves observed in GCC-phen-m-OH and GCC-phen-o-OH are a direct consequence of the OH site on the surface.
Together, our data indicate that, irrespective of the redox properties of the corresponding molecular analogues, acid/base functional groups on GCCs host interfacial PCET reactions.
Safety
No unexpected or unusually high safety hazards were encountered.
Thermochemistry of Interfacial PCET
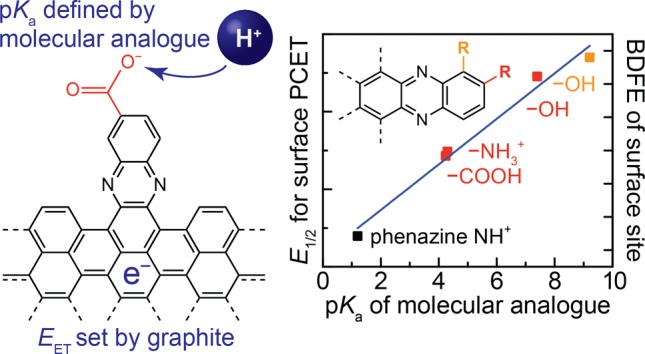
The wide range of conjugated acid/base functional groups examined above provides the basis for understanding the thermochemistry of interfacial PCET reactions. The electrochemical data for GCC-phenazine, GCC-phen-COOH, GCC-phen-NH2, GCC-phen-m-OH, and GCC-phen-o-OH are summarized in the Pourbaix diagram in Figure 5a. We see that all the GCC moieties give rise to PCET reactions with Nernstian pH scaling and are vertically displaced roughly parallel to each other on the Pourbaix diagram.
Figure 5.
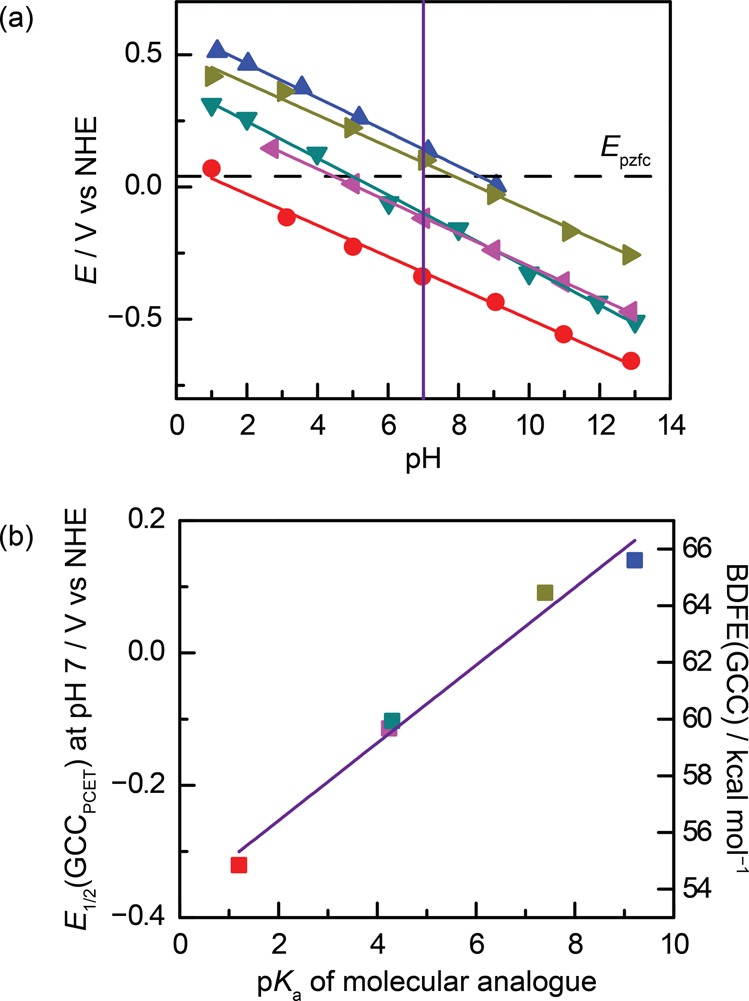
(a) Pourbaix diagram showing pH-dependence of interfacial proton-coupled electron-transfer (PCET) waves for GCC-phenazine (red), GCC-phen-NH2 (purple), GCC-phen-COOH (dark green), GCC-phen-m-OH (olive green), and GCC-phen-o-OH (blue). The purple vertical line shows the interpolated data points from which panel b was constructed. The dotted line shows the computed potential of zero free charge (EPZFC), which is discussed in greater detail below. (b) Plot of the potential of the PCET wave for each GCC at pH 7 vs the pKa of the corresponding acidic site on a molecular phenazine analogue. Values of the pKa for molecular analogues were taken from the literature for phenazine,67 phenazine-2-carboxylic acid,68 phenazin-2-amine,69 phenazin-2-ol,69 and phenazin-1-ol.70
To gain further insight into the factors governing the thermochemistry of PCET reactions at GCC sites, we plotted the potential at which we observe the PCET wave for the GCC (E1/2(GCCPCET)) at pH 7 (vertical line, Figure 5a) vs the pKa of the corresponding moiety on a substituted phenazine molecular analogue (Figure 5b).67−70 Owing to the Nernstian behavior of all of these waves, nearly identical plots are obtained across the pH range (Figure S12). Remarkably, the potentials at which we observe these PCET waves are also linearly correlated with the pKa of the corresponding molecular analogue with a slope of ∼60 mV per pKa unit.
Since each of these processes corresponds to the simultaneous transfer of a proton and an electron, we can convert the E1/2(GCCPCET) values to effective bond dissociation free energies (BDFEs) using the following equation (units are kcal mol–1):
| 1 |
The H2 BDFE value taken from the literature was 104 kcal mol–1.71 These values are plotted on the right y-axis in Figure 5b and highlight the dramatic difference in BDFE between the conjugated moieties and the molecular analogues. For example, the O–H BDFE of an aryl carboxylic acid is ∼110 kcal mol–1,71 whereas the BDFE of the same exact moiety in GCC-phen-COOH is ∼60 kcal mol–1. The strong linear correlation between the BDFEs of the GCC sites and the pKa values of the analogues further highlights the remarkable difference between GCCs and their molecular counterparts.
Mechanistic Model: Field-Driven PCET
In Figure 6, we present a cartoon model of PCET at GCC electrode surface sites at four different applied potentials. In each diagram, the metallic carbon electrode consists of filled states (gray) and unfilled states (purple), and the transition between the two corresponds to the Fermi level of the electrode. The Fermi level, denoted EF, is the electrochemical potential of the electrons in the electrode, which is the potential directly measured by a potentiostat relative to a reference electrode. Importantly, this value has contributions both from the intrinsic chemical potential of electrons in the solid, defined by the composition of the solid material and approximated by its work function, and also from the electrostatic potential drop between the electrode and the solution.58 In this paper, we refer to the “chemical potential” and the “electrostatic potential” explicitly, and all other uses of the word “potential” refer to the electrochemical potential. The rough spatial extent of the electrostatic potential drop is demarcated with a dotted vertical line representing the electrical double layer (EDL), the dotted red line represents the electrostatic potential drop across the double layer, and the gradient of the electrostatic potential drop at the EDL is the interfacial electric field. The potential at which there is no free charge in the double layer and therefore no electrostatic potential drop between the electrode and the solution is denoted as EPZFC, the potential of zero free charge.58 Charging the electrode raises EF with respect to EPZFC, but leaves the chemical potential of the electrons in the solid largely unchanged.58 In Figure 6, this concept is depicted by showing all of the electronic states in the electrode shifting with respect to EPZFC in accordance with the magnitude of the electrostatic potential drop. In particular, we note that the high degree of electronic coupling between the conjugated site and the electrode ensures that changes in EF lead to similar changes in the electrostatic potential of the conjugated surface functional groups.59
Figure 6.
Putative interfacial free energy diagrams for GCC-phen-COOH when the pH of the solution is less than the pKa of the surface COOH in the absence of an external field. In each panel, the gray denotes the filled band states of the electrode, the purple denotes the unfilled band states, and the dotted horizontal black line between the filled and unfilled states denotes the Fermi level of the electrode, EF. The approximate edge of the electrical double layer, EDL, is denoted by a vertical dotted black line, and the free energy required to bind a proton to a surface COO– in the absence of an electric field is shown with a vertical blue bar labeled Δμ. The electrostatic potential of the metal, ψM, and solution, ψsoln, are in red, and the difference between them, Δψ, is indicated by a vertical red bar. The electrostatic potential profile across the EDL is indicated by a dotted red line in each diagram. Across all four diagrams, the electrochemical potential required to protonate the surface COO– site, E(GCCPCET), and the potential of zero free charge, EPZFC, are denoted by dotted gray lines. The four panels correspond to the situations in which (a) EF < E(GCCPCET), (b) EF = EPZFC, (c) EF = E(GCCPCET), and (d) EF > E(GCCPCET). In each case, varying EF changes the magnitude of the electrostatic potential, which consequently alters the driving force for proton transfer across the double layer to or from the surface COO–.
Varying the applied potential at the metallic electrode varies the strength of the electric field in the double layer, which in turn alters the driving force for ions such as H+ to cross the double layer. Figure 6 shows snapshots of this process for GCC-phen-COOH sites at four different values of EF for the situation in which the solution pH is lower than the pKa of the surface site in the absence of an external field. Under these conditions, we expect the surface sites to be protonated when EF = EPZFC and the electrostatic potential drop is 0 across the EDL, as shown in Figure 6b. At this potential, the free energy for binding a proton to the surface COO– group is simply given by the difference between the pKa of the surface site, and the pH in solution and is denoted by vertical blue bars, Δμ. Δμ represents a chemical potential difference, which for purposes of this discussion includes all contributions to the free energy of binding protons to the surface that are independent of the externally applied field, including local and surface dipole contributions. This chemical potential contribution to the free energy of binding protons to the surface remains constant as the applied potential is varied, and thus the magnitude of Δμ is constant across all panels in Figure 6. When EF is negative of EPZFC, as shown in Figure 6a, the electrode is negatively charged. This negative charge leads to an electrostatic potential drop between the metal phase and the solution phase, Δψ (ψM – ψsoln, red vertical bar in Figure 6), that adds to Δμ to bind the H+ more strongly to the surface COO– groups. When EF is positive of EPZFC (Figure 6c,d) the electrode is positively charged, which creates an electrostatic potential drop that subtracts from Δμ to bind the H+ less strongly to the surface COO– groups.
At sufficiently positive values of EF, the electric field drives protons bound to surface carboxylate groups across the EDL and into solution (Figure 6c,d). When the PT reaction occurs, in order to maintain EF, electrons must flow to the external circuit to compensate for the positive charge on the proton.58 This compensatory current is observed as a surface redox wave in CVs and occurs any time an ion specifically adsorbs to or desorbs from an electrode, irrespective of the redox properties of the molecular analogue of the surface site. The equilibrium potential for the PT reaction at surface COOH sites is the potential at which the surface sites are half-protonated and is denoted as E(GCCPCET) in Figure 6. We note that when EF = E(GCCPCET) (Figure 6c), the electrostatic potential drop that repels protons from the surface is equal and opposite to the chemical potential difference that binds protons to the surface (Δμ = −Δψ).
In order for the interfacial electric field to drive proton transfer, there must be an electrostatic potential drop between the site of protonation and solution. For GCCs, strong electronic coupling between the protonation site and the band states of the solid ensures that this electrostatic potential drop occurs between the conjugated site and the solution rather than between the electrode and the site.59 Field-driven protonation has also been documented in densely packed self-assembled monolayers (SAMs) terminated with non-redox-active acidic groups over narrow potential/pH ranges.72−74 In cases for which these redox processes are observed at SAMs, although there is negligible electronic coupling between the moiety and the electrode, the layer of densely packed aliphatic chains effectively blocks ions, forcing the majority of the electrostatic potential drop to occur between the edge of the SAM layer and the solution.26 Physisorbed perylene units with COOH substituents also give rise to redox processes driven by the protonation and deprotonation of the acidic site,75 which may occur due to electronic coupling between the perylene unit and the surface and/or the inability for ions to penetrate the perylene layer. GCCs provide a robust platform with which to generalize this phenomenon because they ensure, through strong electronic coupling, that the appended acid/base moiety is truly part of the electrode.
Mathematical Model for the Thermochemistry of Interfacial PCET
In the above model, the interfacial electric field drives proton transfer to the surface site. Notably, the proton is the only particle that transits through this interfacial field in the reaction; the electron does not. Consequently, to extract the field strength required to drive PT and the electrochemical potential that corresponds to that field, we simply consider the surface PT equilibrium. The following derivation closely follows that for the protonation/deprotonation of a carboxylate in a mixed-monolayer SAM.26 As an example, we examine the deprotonation of GCC-phen-COOH:
| 2 |
At equilibrium,
| 3 |
where μ̅i represents the electrochemical potential for species i. GCC moieties on the electrode surface are denoted with *. The definition of electrochemical potential nicely separates μ̅i into the chemical potential (μi° + RT ln ai), which consists of all contributions independent of the externally applied electric field, and the electrostatic potential (ziFψ j), which consists of field-dependent contributions:
| 4 |
where μi° is the standard chemical potential, R is the gas constant, T is the temperature, ai is the activity of species i, zi is the charge number on i, F is Faraday’s constant, and ψ j is the electrostatic potential in phase j. We can use eq 4 to describe the electrochemical potential for each species in eq 3.
| 5 |
| 6 |
| 7 |
In these expressions, θCOOH* and θCOO–* represent the surface coverages of COOH sites that are protonated and deprotonated, respectively, and ψM and ψsoln are the electrostatic potentials at the metal surface and in solution, respectively, as shown in Figure 6. For the solution species, H+, the substitution of eq 4 into eq 3 is straightforward: The chemical potential is rigorously defined by the standard chemical potential, μH+ο, the proton activity, aH+, and the charge on the proton, +1. For a surface-adsorbed species, the activity of the species is defined by the surface coverage, θ.76 Strictly speaking, the standard state for an adsorbed species is dependent on the isotherm and the strength of any lateral interactions between adsorbed species. Direct comparisons can only be made among surface species governed by the same isotherm.76 For this derivation, we assume a Langmuirian isotherm, and the standard electrochemical potentials of the neutral COOH* and negatively charged COO–* are described by μCOOH* + RT ln(θCOOH*) + 0FψM and μCOO−*o + RT ln(θCOO−*) − FψM, respectively.
Substituting the electrochemical potentials written out in eq 5–7 into eq 3, we obtain
| 8 |
We now rearrange and consolidate the terms in eq 8:
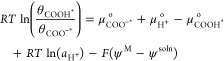 |
9 |
Since pH = −log(aH+), we can rewrite eq 9 as a function of pH:
| 10 |
The chemical potential difference (μCOO–*o + μH+ – μCOOH*o) is reflective of the intrinsic affinity for protons at the COO– surface sites, excluding contributions from an external field. We define this intrinsic affinity in terms of the “0-field pKa” of the surface site (pKa-surface-0field):
| 11 |
Indeed, from eq 11 we see that when the 0-field pKa of
the surface site is equal to the pH of the solution and there is no external field, the surface coverage of protonated sites
(θCOOH*) is equal to the surface coverage of deprotonated
sites (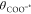 ).
).
From this expression, it is clear that there are two ways to shift the ratio of protonated to deprotonated surface carboxylate groups. The first is the one we are most familiar with from solution-phase chemistry: changing the H+ activity by changing the pH. The second is changing the magnitude of the interfacial electrostatic potential drop (ψM – ψsoln) by varying the applied potential. The qualitative impact of varying the applied potential is illustrated in Figure 6.
The electrostatic potential drop across the double layer, (ψM – ψsoln), is equal to the difference between EF and EPZFC, as depicted in Figure 6, so
| 12 |
Since each proton transfer to the surface leads
to compensatory
electron transfer, the half-wave potentials determined from CVs, E1/2(GCCPCET), corresponds to the
potential, EF, at which the surface sites
are half-protonated, i.e., θCOOH* = 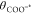 . Thus:
. Thus:
| 13 |
| 14 |
Equation 14 constitutes a general expression for surface PCET waves in terms of the following thermodynamic descriptors: the 0-field pKa of the site, the pH of the solution, and the EPZFC of the electrode. We stress that while we derived this expression for GCCs, the final result is general for any PCET reaction occurring at the surface of a polarized metallic electrode.
Unfortunately, for most surfaces, the analysis must stop here because either the site identity is not known, or its 0-field pKa is not easily measurable. At GCC sites, we can extend the analysis further because we do know the site identity, and we can estimate the 0-field pKa of the site using the pKa of the molecular analogue (pKa-molecular-analogue):
| 15 |
The efficacy of this approximation is shown in Figure 5. In Figure 5a, we observe ∼−60 mV per pH unit shift in E1/2(GCCPCET) for all GCC waves examined, in line with the pH-dependent term in eq 15. Figure 5b plots the data at a constant pH, and we observe a linear relationship between E1/2(GCCPCET) and the pKa of a molecular analogue with a slope of ∼60 mV per pKa unit, in line with the pKa-dependent term in eq 15. Importantly, this 60 mV per pKa unit shift indicates that any difference between the true 0-field pKa of the surface site and the pKa of the molecular analogue must be roughly constant across all of the acid/base sites we investigated. In the limit that the 0-field pKa of the surface site is identical to that of the molecular analogue, the EPZFC can be calculated directly from eq 15. Using eq 15, the intercept in Figure 5b is equal to EPZFC + 0.059 V (pH), and from the data at pH 7, we calculate EPZFC = 0.04 V. The EPZFC value can also be approximated using the difference between the measured work function of graphite, for which typical values fall between 4.3 and 4.6,77 and the ∼4.5 eV conversion value between the NHE and vacuum.18 Remarkably, this independent calculation returns EPZFC values between −0.2 and 0.1 V, very much in line with the ∼0.0 V value that eq 15 predicts for EPZFC across the entire pH range. Furthermore, the fact that similar EPZFC values are obtained from our data at all pH values indicates that for these GCCs, EPZFC does not change significantly with pH.
Square Scheme Model for Interfacial PCET
The foregoing analysis effectively partitioned the thermochemistry of interfacial PCET reactions into the zero-field proton affinity of the site, the pH, and the potential of zero free charge of the electrode. This partitioning closely mirrors the partitioning used in square schemes that describe molecular PCET reactions (Figure 1a). As stated above, the thermochemistry of a molecular one-proton, one-electron PCET reaction can be described as the sum of its PT and ET constituents.18,47 For the reaction shown in Figure 1a:
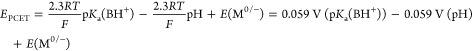 |
16 |
We note that eq 16 takes the same form as eq 15, indicating that interfacial PCET, like molecular PCET, can be partitioned into its PT and ET constituents. Both equations contain a term that depends on the pKa of the site in question in the absence of an external field and a term that depends on the pH of the solution, indicating that we can describe the PT components of molecular and interfacial PCET using the same parameters. In molecular PCET (eq 16), the remaining term, E(M0/–), defines the ET component of the square scheme. Since we have defined the pKa of the surface site at 0 field, we expect the vertical leg in the interfacial PCET square scheme to be the potential at which an electron is added to the solid in the absence of an electrostatic field. That value is, by definition, EPZFC, and indeed it is the remaining term in eq 11. The square scheme for interfacial PCET that results from this analysis is depicted in Scheme 2.
Scheme 2. Partial Square Scheme for Interfacial Proton-Coupled Electron Transfer (PCET) at GCC-phen-COOH as an Example Reaction.
Our model partitions the potential for PCET (diagonal leg) into a horizontal leg, defined as the difference between the 0-field pKa of the surface site and the pH of the solution, and a vertical leg, defined as the potential of zero free charge, EPZFC, of the electrode.
A unique outcome of the above analysis is that for GCCs, the contribution of the ET component to the overall thermochemistry of the reaction (Scheme 2, vertical leg) remains unchanged as the surface functional groups are modified. This highlights the dramatically divergent behavior of GCCs relative to molecules. For molecules, changing the acid/base moiety typically changes both the pKa and the reduction potential.47 In contrast, for GCCs, changing the surface acid/base moiety changes the pKa of the site, but does not dramatically change EPZFC. This phenomenon is a result of the high density of electronic states in the electrode. Due to the high density of states, changes in a small number of proton donor/acceptor states at the surface do not dramatically alter the overall band structure. Thus, for GCCs, the change in the 0-field pKa of the surface site is the sole predictor of the change in potential for the surface PCET reaction.
Conclusion
We have shown that the redox properties of acid/base sites on GCCs are fundamentally different than those in molecular analogues. In particular, we have demonstrated that, irrespective of the redox properties of the molecular analogue, acid/base functional groups on GCCs host interfacial PCET reactions, and we have used this unique behavior to develop a square scheme framework for understanding the thermochemistry of interfacial PCET. Specifically, we have demonstrated that, at a constant pH, E1/2(GCCPCET) is linearly correlated to the pKa of the molecular analogue with a slope of ∼60 mV per pKa unit. This relationship indicates that the PT component of the square scheme can be defined by the 0-field pKa of the moiety and the pH of the solution. When the PT component is defined in this fashion, the ET component is defined by the reduction potential of the uncharged solid, EPZFC, which remains constant across changes in the identity of the acid/base group and the solution pH. The quantitative relationship shown here provides a framework with which to use the GCC platform to design active sites at the molecular level using the pKa of the molecular analogue as a powerful descriptor.
Our analysis also has implications for surface PCET reactions beyond GCCs. In particular, we note the following:
PCET reactions can occur at all acid/base sites on electrode surfaces. A wide range of metallic electrode materials contain surface acid/base groups, including carbons, oxides, chalcogenides, and pnictides, which are used widely in pseudocapacitors, supercapacitors, and catalysts. The results shown here indicate that, provided that the electrode material has a high density of electronic states at the Fermi level, even surface acid/base moieties that are redox inactive as molecules can host PCET reactions on the surface. Furthermore, our studies show that the effective BDFEs of these surface acid/base sites differ dramatically from those of their molecular analogues. In the context of catalysis, the low BDFEs suggest that these surface acid/base sites not only have the ability to act as proton donors/acceptors, but also have the ability to transfer H-atom equivalents to molecules in solution or surface-bound intermediates.
While GCCs provide a platform with which to develop a quantitative model, the principles established here are generalizable across all electrode surface PCET reactions. In particular, we show that knowledge of the proton binding affinity of the surface site and the work function of the electrode (a correlate of EPZFC) can be used to predict the thermochemistry of the surface PCET process. Changing either of these parameters will change the potential at which the surface PCET reaction occurs, accordingly. Our model extends even to surfaces for which a molecular analogue that would provide an independent measurement of the 0-field pKa does not exist. Using eq 15, we can estimate the pKa of any surface site, provided we know the potential at which the PCET reaction occurs and the value of the electrostatic potential drop at that site. The model put forward here highlights that the pKa of the surface site and the EPZFC or work function of the material can be used to tune the potential of interfacial PCET.
Our analysis also explains how surface sites and surface-bound reaction intermediates can be protonated at pH values that do not lead to protonation of a molecular analogue. On a surface, varying the potential directly alters the free energy for PT, and at sufficiently negative potentials, even very acidic sites can be readily protonated. This recognition has broad implications for the construction of viable mechanistic models for surface electrocatalysis.
The analysis put forward here, enabled by the molecular precision and strong electronic coupling of GCCs, provides a powerful paradigm for understanding and designing interfacial PCET reactions at the molecular level.
Acknowledgments
We gratefully acknowledge Henry White, Cyrille Costentin, James Mayer, and Jaeyune Ryu for fruitful discussions. This research was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Award Number DE-SC0014176. M.L.P. was supported by a postdoctoral fellowship from the NIH (F32GM130071). Y.S. acknowledges the Sloan Foundation, Research Corporation for Science Advancement (Cottrell Scholar), and the Canadian Institute for Advanced Research (CIFAR Azrieli Global Scholar).
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.9b00114.
Full experimental details, X-ray photoelectron spectroscopy data, and additional electrochemical data (PDF)
The authors declare the following competing financial interest(s): M.N.J. and Y.S. are inventors on patent application 15/236,963, submitted by the Massachusetts Institute of Technology, that covers the graphite-conjugated materials described in this work.
Supplementary Material
References
- Reece S. Y.; Nocera D. G. Proton-Coupled Electron Transfer in Biology: Results from Synergistic Studies in Natural and Model Systems. Annu. Rev. Biochem. 2009, 78 (1), 673–699. 10.1146/annurev.biochem.78.080207.092132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hammes-Schiffer S.; Iordanova N. Theoretical Studies of Proton-Coupled Electron Transfer Reactions. Biochim. Biophys. Acta, Bioenerg. 2004, 1655 (1–3), 29–36. 10.1016/j.bbabio.2003.07.009. [DOI] [PubMed] [Google Scholar]
- Roubelakis M. M.; Bediako D. K.; Dogutan D. K.; Nocera D. G. Proton-Coupled Electron Transfer Kinetics for the Hydrogen Evolution Reaction of Hangman Porphyrins. Energy Environ. Sci. 2012, 5 (7), 7737–7740. 10.1039/c2ee21123h. [DOI] [Google Scholar]
- Rountree E. S.; Dempsey J. L. Reactivity of Proton Sources with a Nickel Hydride Complex in Acetonitrile: Implications for the Study of Fuel-Forming Catalysts. Inorg. Chem. 2016, 55 (10), 5079–5087. 10.1021/acs.inorgchem.6b00885. [DOI] [PubMed] [Google Scholar]
- Rountree E. S.; Martin D. J.; McCarthy B. D.; Dempsey J. L. Linear Free Energy Relationships in the Hydrogen Evolution Reaction: Kinetic Analysis of a Cobaloxime Catalyst. ACS Catal. 2016, 6 (5), 3326–3335. 10.1021/acscatal.6b00667. [DOI] [Google Scholar]
- Carver C. T.; Matson B. D.; Mayer J. M. Electrocatalytic Oxygen Reduction by Iron Tetra-Arylporphyrins Bearing Pendant Proton Relays. J. Am. Chem. Soc. 2012, 134 (12), 5444–5447. 10.1021/ja211987f. [DOI] [PubMed] [Google Scholar]
- Rosenthal J.; Nocera D. G. Role of Proton-Coupled Electron Transfer in O−O Bond Activation. Acc. Chem. Res. 2007, 40 (7), 543–553. 10.1021/ar7000638. [DOI] [PubMed] [Google Scholar]
- Costentin C.; Drouet S.; Robert M.; Savéant J.-M. A Local Proton Source Enhances CO2 Electroreduction to CO by a Molecular Fe Catalyst. Science 2012, 338 (6103), 90–94. 10.1126/science.1224581. [DOI] [PubMed] [Google Scholar]
- Wilson A. D.; Fraze K.; Twamley B.; Miller S. M.; DuBois D. L.; DuBois M. R. The Role of the Second Coordination Sphere of [Ni(PCy2NBz2)2](BF4)2 in Reversible Carbon Monoxide Binding. J. Am. Chem. Soc. 2008, 130 (3), 1061–1068. 10.1021/ja077328d. [DOI] [PubMed] [Google Scholar]
- Rakowski DuBois M.; DuBois D. L. Development of Molecular Electrocatalysts for CO2 Reduction and H2 Production/Oxidation. Acc. Chem. Res. 2009, 42 (12), 1974–1982. 10.1021/ar900110c. [DOI] [PubMed] [Google Scholar]
- Mora S. J.; Odella E.; Moore G. F.; Gust D.; Moore T. A.; Moore A. L. Proton-Coupled Electron Transfer in Artificial Photosynthetic Systems. Acc. Chem. Res. 2018, 51 (2), 445–453. 10.1021/acs.accounts.7b00491. [DOI] [PubMed] [Google Scholar]
- Costentin C.; Drouet S.; Robert M.; Saveant J.-M. A Local Proton Source Enhances CO2 Electroreduction to CO by a Molecular Fe Catalyst. Science 2012, 338 (6103), 90–94. 10.1126/science.1224581. [DOI] [PubMed] [Google Scholar]
- Hammes-Schiffer S.; Soudackov A. V. Proton-Coupled Electron Transfer in Solution, Proteins, and Electrochemistry. J. Phys. Chem. B 2008, 112 (45), 14108–14123. 10.1021/jp805876e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Helm M. L.; Stewart M. P.; Bullock R. M.; DuBois M. R.; DuBois D. L. A Synthetic Nickel Electrocatalyst with a Turnover Frequency Above 100,000 s–1 for H2 Production. Science 2011, 333 (6044), 863–866. 10.1126/science.1205864. [DOI] [PubMed] [Google Scholar]
- Chang C. J.; Loh Z.; Shi C.; Anson F. C.; Nocera D. G. Targeted Proton Delivery in the Catalyzed Reduction of Oxygen to Water by Bimetallic Pacman Porphyrins. J. Am. Chem. Soc. 2004, 126 (32), 10013–10020. 10.1021/ja049115j. [DOI] [PubMed] [Google Scholar]
- Chang C. J.; Chng L. L.; Nocera D. G. Proton-Coupled O-O Activation on a Redox Platform Bearing a Hydrogen-Bonding Scaffold. J. Am. Chem. Soc. 2003, 125 (7), 1866–1876. 10.1021/ja028548o. [DOI] [PubMed] [Google Scholar]
- Nichols E. M.; Derrick J. S.; Nistanaki S. K.; Smith P. T.; Chang C. J. Positional Effects of Second-Sphere Amide Pendants on Electrochemical CO2 Reduction Catalyzed by Iron Porphyrins. Chem. Sci. 2018, 9 (11), 2952–2960. 10.1039/C7SC04682K. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayer J. M. Proton-Coupled Electron Transfer: A Reaction Chemist’s View. Annu. Rev. Phys. Chem. 2004, 55 (1), 363–390. 10.1146/annurev.physchem.55.091602.094446. [DOI] [PubMed] [Google Scholar]
- Weinberg D. R.; Gagliardi C. J.; Hull J. F.; Murphy C. F.; Kent C.; Westlake B. C.; Paul A.; Ess D. H.; McCafferty D. G.; Meyer T. J. Proton-Coupled Electron Transfer. Chem. Rev. 2012, 112 (7), 4016–4093. 10.1021/cr200177j. [DOI] [PubMed] [Google Scholar]
- Huynh M. H. V; Meyer T. Chem. Rev. 2007, 107, 5004–5064. 10.1021/cr0500030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nocera D. G. Chemistry of Personalized Solar Energy. Inorg. Chem. 2009, 48 (21), 10001–10017. 10.1021/ic901328v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hammes-Schiffer S. Proton-Coupled Electron Transfer: Moving Together and Charging Forward. J. Am. Chem. Soc. 2015, 137 (28), 8860–8871. 10.1021/jacs.5b04087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saveant J.-M.Elements of Molecular and Biomolecular Electro-Chemistry: An Electrochemical Approach to Electron Transfer Chemistry; John Wiley & Sons, Inc.: Hoboken, NJ, 2006. [Google Scholar]
- Rakowski DuBois M.; DuBois D. L. The Roles of the First and Second Coordination Spheres in the Design of Molecular Catalysts for H2 Production and Oxidation. Chem. Soc. Rev. 2009, 38 (1), 62–72. 10.1039/B801197B. [DOI] [PubMed] [Google Scholar]
- Sutin N.; Brunschwig B. S.; Creutz C.; Winkler J. R. Pure Appl. Chem. 1988, 60 (12), 1817–1830. 10.1351/pac198860121817. [DOI] [Google Scholar]
- Schrauben J. N.; Hayoun R.; Valdez C. N.; Braten M.; Fridley L.; Mayer J. M. Titanium and Zinc Oxide Nanoparticles Are Proton-Coupled Electron Transfer Agents. Science 2012, 336 (6086), 1298–1301. 10.1126/science.1220234. [DOI] [PubMed] [Google Scholar]
- Smith C. P.; White H. S. Voltammetry of Molecular Films Containing Acid/Base Groups. Langmuir 1993, 9 (1), 1–3. 10.1021/la00025a001. [DOI] [Google Scholar]
- Levine S.; Smith A. Theory of the Differential Capacity of the Oxide/Aqueous Electrolyte Interface. Discuss. Faraday Soc. 1971, 52, 290–301. 10.1039/df9715200290. [DOI] [Google Scholar]
- Pourbaix M.Atlas of Electrochemical Equilibria in Aqueous Solutions; National Association of Corrosion Engineers: Houston, TX, 1974. [Google Scholar]
- Cobb S.; Ayres Z. J.; Newton M. E.; Macpherson J. V. Deconvoluting Surface-Bound Quinone Proton Coupled Electron Transfer in Unbuffered Solutions: Towards a Universal Voltammetric pH Electrode. J. Am. Chem. Soc. 2019, 141 (2), 1035–1044. 10.1021/jacs.8b11518. [DOI] [PubMed] [Google Scholar]
- Ryu J.; Wuttig A.; Surendranath Y. Quantification of Interfacial pH Variation at Molecular Length Scales Using a Concurrent Non-Faradaic Reaction. Angew. Chem., Int. Ed. 2018, 57 (30), 9300–9304. 10.1002/anie.201802756. [DOI] [PubMed] [Google Scholar]
- Jackson M. N.; Surendranath Y. Donor-Dependent Kinetics of Interfacial Proton-Coupled Electron Transfer. J. Am. Chem. Soc. 2016, 138 (9), 3228–3234. 10.1021/jacs.6b00167. [DOI] [PubMed] [Google Scholar]
- Wuttig A.; Liu C.; Peng Q.; Yaguchi M.; Hendon C. H.; Motobayashi K.; Ye S.; Osawa M.; Surendranath Y. Tracking a Common Surface-Bound Intermediate during CO2-to-Fuels Catalysis. ACS Cent. Sci. 2016, 2 (8), 522–528. 10.1021/acscentsci.6b00155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoon Y.; Hall A. S.; Surendranath Y. Tuning of Silver Catalyst Mesostructure Promotes Selective Carbon Dioxide Conversion into Fuels. Angew. Chem., Int. Ed. 2016, 55 (49), 15282–15286. 10.1002/anie.201607942. [DOI] [PubMed] [Google Scholar]
- Hall A. S.; Yoon Y.; Wuttig A.; Surendranath Y. Mesostructure-Induced Selectivity in CO2 Reduction Catalysis. J. Am. Chem. Soc. 2015, 137 (47), 14834–14837. 10.1021/jacs.5b08259. [DOI] [PubMed] [Google Scholar]
- Schreier M.; Yoon Y.; Jackson M. N.; Surendranath Y. Competition between H and CO for Active Sites Governs Copper-Mediated Electrosynthesis of Hydrocarbon Fuels. Angew. Chem., Int. Ed. 2018, 57 (32), 10221–10225. 10.1002/anie.201806051. [DOI] [PubMed] [Google Scholar]
- Li C. W.; Ciston J.; Kanan M. W. Electroreduction of Carbon Monoxide to Liquid Fuel on Oxide-Derived Nanocrystalline Copper. Nature 2014, 508, 504–507. 10.1038/nature13249. [DOI] [PubMed] [Google Scholar]
- Huskinson B.; Marshak M. P.; Suh C.; Er S.; Gerhardt M. R.; Galvin C. J.; Chen X.; Aspuru-Guzik A.; Gordon R. G.; Aziz M. J. A Metal-Free Organic-Inorganic Aqueous Flow Battery. Nature 2014, 505 (7482), 195–198. 10.1038/nature12909. [DOI] [PubMed] [Google Scholar]
- Lin K.; Chen Q.; Gerhardt M. R.; Tong L.; Kim S. B.; Eisenach L.; Valle A. W.; Hardee D.; Gordon R. G.; Aziz M. J.; et al. Alkaline Quinone Flow Battery. Science 2015, 349 (6255), 1529–1532. 10.1126/science.aab3033. [DOI] [PubMed] [Google Scholar]
- Singh C.; Paul A. Physisorbed Hydroquinone on Activated Charcoal as a Supercapacitor: An Application of Proton-Coupled Electron Transfer. J. Phys. Chem. C 2015, 119 (21), 11382–11390. 10.1021/acs.jpcc.5b01322. [DOI] [Google Scholar]
- Costentin C.; Porter T. R.; Savéant J.-M. Conduction and Reactivity in Heterogeneous-Molecular Catalysis: New Insights in Water Oxidation Catalysis by Phosphate Cobalt Oxide Films. J. Am. Chem. Soc. 2016, 138 (17), 5615–5622. 10.1021/jacs.6b00737. [DOI] [PubMed] [Google Scholar]
- Falkowski J. M.; Surendranath Y. Metal Chalcogenide Nanofilms: Platforms for Mechanistic Studies of Electrocatalysis. ACS Catal. 2015, 5 (6), 3411–3416. 10.1021/acscatal.5b00449. [DOI] [Google Scholar]
- Yan B.; Concannon N. M.; Milshtein J. D.; Brushett F. R.; Surendranath Y. A Membrane-Free Neutral pH Formate Fuel Cell Enabled by a Selective Nickel Sulfide Oxygen Reduction Catalyst. Angew. Chem., Int. Ed. 2017, 56 (26), 7496–7499. 10.1002/anie.201702578. [DOI] [PubMed] [Google Scholar]
- Braten M. N.; Gamelin D. R.; Mayer J. M. Reaction Dynamics of Proton-Coupled Electron Transfer from Reduced ZnO Nanocrystals. ACS Nano 2015, 9 (10), 10258–10267. 10.1021/acsnano.5b04222. [DOI] [PubMed] [Google Scholar]
- Yan B.; Krishnamurthy D.; Hendon C. H.; Deshpande S.; Surendranath Y.; Viswanathan V. Surface Restructuring of Nickel Sulfide Generates Optimally Coordinated Active Sites for Oxygen Reduction Catalysis. Joule 2017, 1 (3), 600–612. 10.1016/j.joule.2017.08.020. [DOI] [Google Scholar]
- Walter M. G.; Warren E. L.; McKone J. R.; Boettcher S. W.; Mi Q.; Santori E. A.; Lewis N. S. Solar Water Splitting Cells. Chem. Rev. 2010, 110 (11), 6446–6473. 10.1021/cr1002326. [DOI] [PubMed] [Google Scholar]
- Lewis N. S.; Nocera D. G. Powering the Planet: Chemical Challenges in Solar Energy Utilization. Proc. Natl. Acad. Sci. U. S. A. 2006, 103 (43), 15729–15735. 10.1073/pnas.0603395103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warren J. J.; Tronic T. a.; Mayer J. M. Thermochemistry of Proton-Coupled Electron Transfer Reagents and Its Implications. Chem. Rev. 2010, 110 (12), 6961–7001. 10.1021/cr100085k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCarthy B. D.; Dempsey J. L. Decoding Proton-Coupled Electron Transfer with Potential-pKa Diagrams. Inorg. Chem. 2017, 56 (3), 1225–1231. 10.1021/acs.inorgchem.6b02325. [DOI] [PubMed] [Google Scholar]
- Elgrishi N.; Kurtz D. A.; Dempsey J. L. Reaction Parameters Influencing Cobalt Hydride Formation Kinetics: Implications for Benchmarking H2-Evolution Catalysts. J. Am. Chem. Soc. 2017, 139 (1), 239–244. 10.1021/jacs.6b10148. [DOI] [PubMed] [Google Scholar]
- Elgrishi N.; McCarthy B. D.; Rountree E. S.; Dempsey J. L. Reaction Pathways of Hydrogen-Evolving Electrocatalysts: Electrochemical and Spectroscopic Studies of Proton-Coupled Electron Transfer Processes. ACS Catal. 2016, 6 (6), 3644–3659. 10.1021/acscatal.6b00778. [DOI] [Google Scholar]
- Bourrez M.; Steinmetz R.; Ott S.; Gloaguen F.; Hammarström L. Concerted Proton-Coupled Electron Transfer from a Metal-Hydride Complex. Nat. Chem. 2015, 7 (2), 140–145. 10.1038/nchem.2157. [DOI] [PubMed] [Google Scholar]
- Liu T.; Guo M.; Orthaber A.; Lomoth R.; Lundberg M.; Ott S.; Hammarström L. Accelerating Proton-Coupled Electron Transfer of Metal Hydrides in Catalyst Model Reactions. Nat. Chem. 2018, 10 (8), 881–887. 10.1038/s41557-018-0076-x. [DOI] [PubMed] [Google Scholar]
- Costentin C.; Savéant J. M. Towards an Intelligent Design of Molecular Electrocatalysts. Nat. Rev. Chem. 2017, 1 (11), 0087. 10.1038/s41570-017-0087. [DOI] [Google Scholar]
- Costentin C.; Drouet S.; Robert M.; Savéant J.-M. Turnover Numbers, Turnover Frequencies, and Overpotential in Molecular Catalysis of Electrochemical Reactions. Cyclic Voltammetry and Preparative-Scale Electrolysis. J. Am. Chem. Soc. 2012, 134 (27), 11235–11242. 10.1021/ja303560c. [DOI] [PubMed] [Google Scholar]
- Hu X.; Brunschwig B. S.; Peters J. C. Electrocatalytic Hydrogen Evolution at Low Overpotentials by Cobalt Macrocyclic Glyoxime and Tetraimine Complexes. J. Am. Chem. Soc. 2007, 129 (29), 8988–8998. 10.1021/ja067876b. [DOI] [PubMed] [Google Scholar]
- Wakerley D. W.; Reisner E. Development and Understanding of Cobaloxime Activity through Electrochemical Molecular Catalyst Screening. Phys. Chem. Chem. Phys. 2014, 16 (12), 5739–5746. 10.1039/C4CP00453A. [DOI] [PubMed] [Google Scholar]
- Pegis M. L.; McKeown B. A.; Kumar N.; Lang K.; Wasylenko D. J.; Zhang X. P.; Raugei S.; Mayer J. M. Homogenous Electrocatalytic Oxygen Reduction Rates Correlate with Reaction Overpotential in Acidic Organic Solutions. ACS Cent. Sci. 2016, 2 (11), 850–856. 10.1021/acscentsci.6b00261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmickler W.; Santos E. In Interfacial Electrochemistry; Springer-Verlag: Berlin, 2010; pp 51–65, 145–162. [Google Scholar]
- Jackson M. N.; Oh S.; Kaminsky C. J.; Chu S. B.; Zhang G.; Miller J. T.; Surendranath Y. Strong Electronic Coupling of Molecular Sites to Graphitic Electrodes via Pyrazine Conjugation. J. Am. Chem. Soc. 2018, 140 (3), 1004–1010. 10.1021/jacs.7b10723. [DOI] [PubMed] [Google Scholar]
- Fukushima T.; Drisdell W.; Yano J.; Surendranath Y. Graphite-Conjugated Pyrazines as Molecularly Tunable Heterogeneous Electrocatalysts. J. Am. Chem. Soc. 2015, 137 (34), 10926–10929. 10.1021/jacs.5b06737. [DOI] [PubMed] [Google Scholar]
- Oh S.; Gallagher J. R.; Miller J. T.; Surendranath Y. Graphite-Conjugated Rhenium Catalysts for Carbon Dioxide Reduction. J. Am. Chem. Soc. 2016, 138 (6), 1820–1823. 10.1021/jacs.5b13080. [DOI] [PubMed] [Google Scholar]
- Boehm H. P.; Diehl E.; Heck W.; Sappok R. Surface Oxides of Carbon. Angew. Chem., Int. Ed. Engl. 1964, 3 (10), 669–677. 10.1002/anie.196406691. [DOI] [Google Scholar]
- McCreery R. L. Advanced Carbon Electrode Materials for Molecular Electrochemistry. Chem. Rev. 2008, 108 (7), 2646–2687. 10.1021/cr068076m. [DOI] [PubMed] [Google Scholar]
- Wildgoose G. G.; Abiman P.; Compton R. G. Characterising Chemical Functionality on Carbon Surfaces. J. Mater. Chem. 2009, 19, 4875. 10.1039/b821027f. [DOI] [Google Scholar]
- Thorogood C. A.; Wildgoose G. G.; Crossley A.; Jacobs R. M. J.; Jones J. H.; Compton R. G. Differentiating between Ortho- and Para-Quinone Surface Groups on Graphite, Glassy Carbon, and Carbon Nanotubes Using Organic and Inorganic Voltammetric and X-Ray Photoelectron Spectroscopy Labels. Chem. Mater. 2007, 19 (20), 4964–4974. 10.1021/cm071412a. [DOI] [Google Scholar]
- Kaye R. C.; Stonehill H. I. 619. The Polarographic Reduction of Pyridine, Quinoline, and Phenazine. J. Chem. Soc. 1952, 3240. 10.1039/jr9520003240. [DOI] [Google Scholar]
- Albert A.; Phillips J. N. 264. Ionization Constants of Heterocyclic Substances. Part II. Hydroxy-Derivatives of Nitrogenous Six-Membered Ring-Compounds. J. Chem. Soc. 1956, 1294. 10.1039/jr9560001294. [DOI] [Google Scholar]
- Brisbane P. G.; Janik L. J.; Tate M. E.; Warren R. F. Revised Structure for the Phenazine Antibiotic from Pseudomonas Fluorescens 2–79 (NRRL B-15132). Antimicrob. Agents Chemother. 1987, 31 (12), 1967–1971. 10.1128/AAC.31.12.1967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown K. C.; Corbett J. F.; Loveless N. P. Spectrophotometric Studies on the Protonation of Hydroxy and Aminophenazines in Aqueous Solution. Spectrochim. Acta Part A Mol. Spectrosc. 1979, 35 (5), 421–423. 10.1016/0584-8539(79)80155-5. [DOI] [Google Scholar]
- Kidani Y.; Inagaki K.; Koike H. [Studies on Metal Chelate Compounds of Phenazine Derivatives. 8. Metal Complex of 1-Hydroxyphenazine (Author’s Transl)]. Yakugaku Zasshi 1973, 93 (9), 1089–1093. 10.1248/yakushi1947.93.9_1089. [DOI] [PubMed] [Google Scholar]
- Blanksby S. J.; Ellison G. B. Bond Dissociation Energies of Organic Molecules. Acc. Chem. Res. 2003, 36 (4), 255–263. 10.1021/ar020230d. [DOI] [PubMed] [Google Scholar]
- Rosendahl S. M.; Burgess I. J. Electrochemical and Infrared Spectroscopy Studies of 4-Mercaptobenzoic Acid SAMs on Gold Surfaces. Electrochim. Acta 2008, 53 (23), 6759–6767. 10.1016/j.electacta.2007.11.020. [DOI] [Google Scholar]
- Pillay J.; Agboola B. O.; Ozoemena K. I. Electrochemistry of 2-Dimethylaminoethanethiol SAM on Gold Electrode: Interaction with SWCNT-Poly(m-Aminobenzene Sulphonic Acid), Electric Field-Induced Protonation-Deprotonation, and Surface pKa. Electrochem. Commun. 2009, 11 (6), 1292–1296. 10.1016/j.elecom.2009.04.028. [DOI] [Google Scholar]
- White H. S.; Peterson J. D.; Cui Q.; Stevenson K. J. Voltammetric Measurement of Interfacial Acid/Base Reactions. J. Phys. Chem. B 1998, 102 (98), 2930–2934. 10.1021/jp980035+. [DOI] [Google Scholar]
- Gan S.; Zhong L.; Gao L.; Han D.; Niu L. Electrochemically Driven Surface-Confined Acid/Base Reaction for an Ultrafast H+ Supercapacitor. J. Am. Chem. Soc. 2016, 138 (5), 1490–1493. 10.1021/jacs.5b12272. [DOI] [PubMed] [Google Scholar]
- Bockris J. O.; Amulya K. N.; Reddy M. G.-A.. Modern Electrochemistry 2A. In Fundamentals of Electrodics; Springer: Boston, MA, 2000; pp 933–938. [Google Scholar]
- Ivey H. F. Thermionic Electron Emission from Carbon. Phys. Rev. 1949, 76 (4), 567. 10.1103/PhysRev.76.567. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.