Generation of photonic spin-controlled accelerating light beams along arbitrary curved trajectories

Abstract

Bending light along arbitrary curvatures is a captivating and popular notion, triggering unprecedented endeavors in achieving quasi-diffraction-free propagation along a curved path in free-space. Much effort has been devoted to achieving this goal in homogeneous space, which solely relies on the transverse acceleration of beam centroid exerted by a beam generator. Here, based on an all-dielectric metasurface, we experimentally report a synthetic strategy of encoding and multiplexing arbitrary acceleration features on a freely propagating light beam, synergized with photonic spin states of light. Independent switching between two arbitrary visible frequency accelerating light beams with distinct acceleration directions and caustic trajectories is achieved. This proof-of-concept recipe demonstrates the strengths of the designed metasurface element: a subwavelength pixel size, independent control over light beam curvature, multi-wavelength operation in the visible, and ultrathin scalable planar architecture. Our results open up the possibility of creating ultra-compact, high-pixel density and flat-profile nanophotonic platforms for efficient generation and dynamical control of structured light beams.

Bending light beams along engineered curvatures could enable many intriguing phenomena as well as applications that include optical camouflaging [1], cloaking [2], three-dimensional imaging [3], and nanoparticle curved conveyance [4]. However, generating curved light beams usually requires a background media of engineered gradient refractive index [5-6]. The curved trajectory typically expires quickly in a homogeneous medium due to the absence of transverse acceleration of the beam centroid. One solution entails imprinting the incident light beam with a nonlinearly distributed phase profile to realize approximated accelerating light beams (ALBs). As a fascinating caustic-wave phenomenon, ALBs do not diffract while propagating along curved trajectories. For example, optical Airy beams, one representative form of ALB, have shape-preserving nature and their peak intensity follows a continuous parabolic curve as they propagate in free-space [7-8]. Their spatial evolution can be simply described by the paraxial Helmholtz equation, which has a mathematical equivalence with its counterpart Schrödinger equation within the framework of quantum mechanics [9].

Since the first experimental demonstration of optical Airy beams [8], there have been numerous investigations on generalized ALBs that propagate along arbitrary convex trajectories [10], including equivalent demonstrations in other field of physics such as with acoustic beams [11], electron beams [12] or surface plasmon polaritons [13]. Thanks to their unique quasi-non-diffractive nature, ALBs are a subject of intense current interest and have potential for applications in high-resolution microscopy [14], optical manipulation of biological cells [15], generation of light-induced curved plasma channels [16], laser machining of curved microstructures [17] and generation of light bullets [18].

To date, most ALBs are generated by using a commercial spatial light modulator (SLM) [8,10,14-17, 19-21]. However, the large pixel size and pitch of SLMs inherently limits the available range of phase gradient, and its accuracy. As a result, it is difficult to generate ALBs using SLMs with both fine spatial resolution and high precision. Moreover, its bulky footprint and high-cost poses a challenge for their integration within a compact nanophotonic platform. In addition, the ability to control and multiplex propagation characteristics of an ALB, such as its acceleration direction and caustic trajectory, has long been a challenge. Although some progress has been made towards achieving dynamical control of the propagation trajectory of an ALB using second harmonic generation or three-wave mixing in a nonlinear medium [22-23], these schemes only work at specific frequencies, and impose a stringent requirement on the ALB generation process. Hence, there is a need for realizing efficient generation mechanisms and arbitrary conversion platforms for ALBs that offer subwavelength pixel sizes, compact footprint, low cost and multi-wavelength operation.

In this report, we experimentally realize an ultrathin all-dielectric optical device to circumvent the aforementioned limitations, and provide an efficient platform for both the generation and control of ALBs. In synergy with the photonic spin states of incident light, distinctively generated ALBs can propagate along pre-defined trajectories, independently. Inspired by the classical control methods that utilize phase and polarization of light, we implement an equivalent strategy by using metasurfaces [24-31] – arrays of planar subwavelength optical nanostructures – and controlled by the handedness of the circularly polarized incident light. For experimental proof-of-concept, two all-dielectric metasurface devices operating at visible frequencies are fabricated, exhibiting generation of optical Airy beams with switchable opposite acceleration directions, and dynamic ALBs interchangeable between a natural logarithmic and biquadratic caustic trajectory. The spin state of incident light plays a coordinated role with the encoded polarization-dependent nonlinear phase profile of the dielectric metasurface to generate the requisite ALBs.

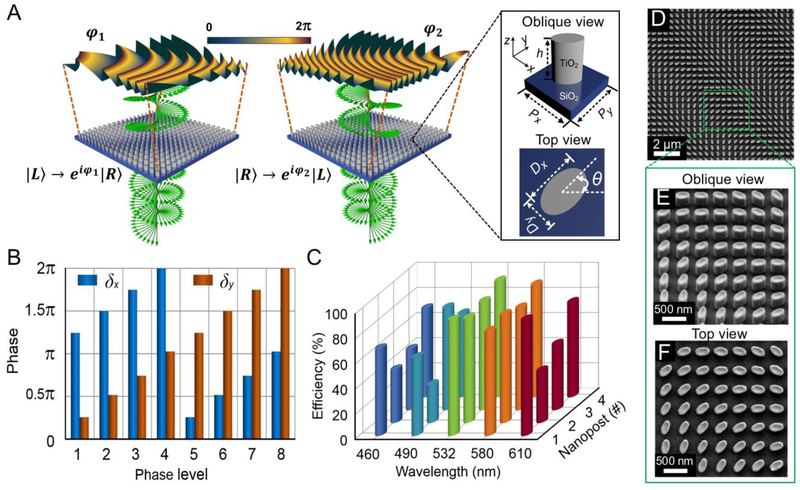
Figure 1A depicts an artistic rendering of the metasurface, consisting of an array of subwavelength elliptical dielectric nanoposts. The normally incident light onto the metasurface is assumed to be in two orthogonal spin states: $\mid R\rangle =\left[\begin{array}{c}\hfill 1\hfill \\ \hfill -i\hfill \end{array}\right]$ and $\mid L\rangle =\left[\begin{array}{c}\hfill 1\hfill \\ \hfill i\hfill \end{array}\right]$, where ∣R⟩ and ∣L⟩ denote right-circularly polarized (RCP) and left-circularly polarized (LCP) states, respectively. To generate two switchable accelerating beams (ALB₁ and ALB₂), the metasurface is required to provide two independent phase profiles φ₁(x, y) and φ₂(x, y) corresponding to the incident RCP and LCP spin states, respectively. Hence the metasurface can be described by a Jones matrix J(x, y) such that it simultaneously satisfies J(x, y) ∣R⟩ = e^iφ₁(x,y)∣L⟩ and J(x, y) ∣L⟩=e^iφ₂(x,y)∣R⟩ [32-33]. Therefore, the Jones matrix J(x, y) takes the form:

$$J(x,y)=\frac{1}{2}\left[\begin{array}{cc}\hfill e^{i{\phi }_1(x,y)}+e^{i{\phi }_2(x,y)}\hfill & \hfill i{e}^{i{\phi }_2(x,y)}-i{e}^{i{\phi }_1(x,y)}\hfill \\ \hfill i{e}^{i{\phi }_2(x,y)}-i{e}^{i{\phi }_1(x,y)}\hfill & \hfill -e^{i{\phi }_1(x,y)}-e^{i{\phi }_2(x,y)}\hfill \end{array}\right]$$ (1)

Fig. 1. Photonic spin-controlled ALB metasurface generator.

(A) Schematic diagram of the metasurface device capable of providing two independent phase profiles, φ₁ and φ₂, respectively for normally incident LCP and RCP light. Inset: perspective and top view of the metasurface unit cell formed by elliptical amorphous TiO₂ nanopost sitting on a silica substrate. (B) Calculated phase shifts, δ_x and δ_y, for different phase levels at a free-space wavelength of 532 nm. Each level corresponds to a specific TiO₂ nanopost birefringent wave-plate. (C) Calculated polarization conversion efficiency of the chosen nanopost structures at five different wavelengths (460 nm, 490 nm, 532 nm, 580 nm and 610 nm) across the visible range. (D)-(F) SEM images of the fabricated metasurface device. The SEM image respectively show (D) a top view of large area, (E) zoomed view at an oblique angle and (F) corresponding top view for the same area.

Based on the eigenvalues and eigenvectors of the Jones matrix in eq. (1), analytical solutions can be obtained for the required orientation angle for each constituent nanopost of the metasurface in the x-y plane, θ(x, y), relative to the reference coordinate as: θ(x, y) = [φ₁(x, y) – φ₂(x, y)]/4. The corresponding phase shifts along the elliptical nanoposts’ two perpendicular symmetry axes can then be expressed as: δ_x(x, y) = [φ₁(x, y) + φ₂(x, y)]/2 and δ_y(x, y) = {[φ₁(x, y) + φ₂(x, y)]/2} – π, respectively (detailed calculations are shown in the supplementary section SI). Therefore, it is imperative to find a set of nanoposts with proper orientation angle θ (x, y) and phase shifts δ_x(x, y) and δ_y(x, y) covering an entire 2π phase range.

Inset of Fig. 1A shows the artistic rendering of an individual unit-cell of the designed metasurface, composed of elliptical titanium dioxide (TiO₂) nanoposts on a fused-silica substrate. We choose TiO₂ as the constituent material because of its large index of refraction and low loss at visible frequencies [34-36]. The TiO₂ nanoposts are designed to have identical heights of 600 nm but differ in their lateral dimensions D_x and D_y. According to the calculated transmission coefficient and phase shift of cross-polarized scattered light for TiO₂ elliptical nanoposts at a free-space wavelength of 532 nm (supplementary Fig. S1), a set of eight nanostructures, including four fundamental nanoposts with different width (D_x, D_y) and their mirror structures with width (D_y, D_x), is designed which provide eight phase levels covering the 2π phase range for δ_x and δ_y. as shown in Fig. 1B. These structural parameters are optimized such that the nanoposts’ polarization conversion efficiencies are relatively high for five different wavelengths across the entire visible range (Fig. 1C), which is a prerequisite for efficient generation of ALBs at multiple wavelengths. All nanoposts are organized in a square array with a lattice constant of P_x = P_y = 450 nm along the x and y directions, respectively. This lattice constant is approximately two- to three- orders of magnitude smaller than the current commercial SLMs for visible light [37]. Thanks to high refractive index of TiO₂, optical fields are mainly confined within individual nanoposts, and hence each onecan be regarded as an independent stand-alone cylindrical waveguide (supplementary Fig. S2). Figure 1D-F show the top-view and perspective-view scanning electron microscope (SEM) images of the fabricated TiO₂ metasurface. The complete fabrication process is described in the supplementary section SII.

We first demonstrate a metasurface device capable of generating and switching the acceleration direction of an optical Airy beam. The mapping between the incident and transmitted light through the metasurface follows ∣L⟩ → ∣A_l⟩ and ∣R⟩ → ∣A_r⟩. where ∣A_l⟩ (∣A_r⟩) represents the state of Airy beam accelerating towards the left (right). According to the geometrical properties of the optical caustics, ALBs along arbitrary convex trajectories can be generated by direct application of a spatial phase profile on an incident beam [10, 38-39]. Here, we impose a spatial phase function on an incident plane wave to obtain the required phase profile of the metasurface, and generate a two-dimensional Airy beam, expressed as:

$${\phi }_1(x,y)=-\frac{4}{3}\sqrt{n}k(x^{\frac{3}{2}}+y^{\frac{3}{2}})$$ (2)

where n is the acceleration coefficient associated with the contour of the Airy beam (here, n = 4 m⁻¹), k = 2π/λ₀ is the free-space wavevector and λ₀ is the free-space wavelength of operation. The parabolic caustic trajectory of the Airy beam can be expressed as a form of space curve: $\{\begin{array}{c}x=n{z}^2\hfill \\ y=n{z}^2\hfill \end{array}\phantom{\}}$. The phase profile to generate an Airy beam with opposite acceleration direction can be obtained by ${\phi }_2(x,y)={\phi }_1(\sqrt{2}w-x,\sqrt{2}w-y)$, where w is the side length of the square sample ensuring that the output positions of the two Airy beams are centrosymmetric.

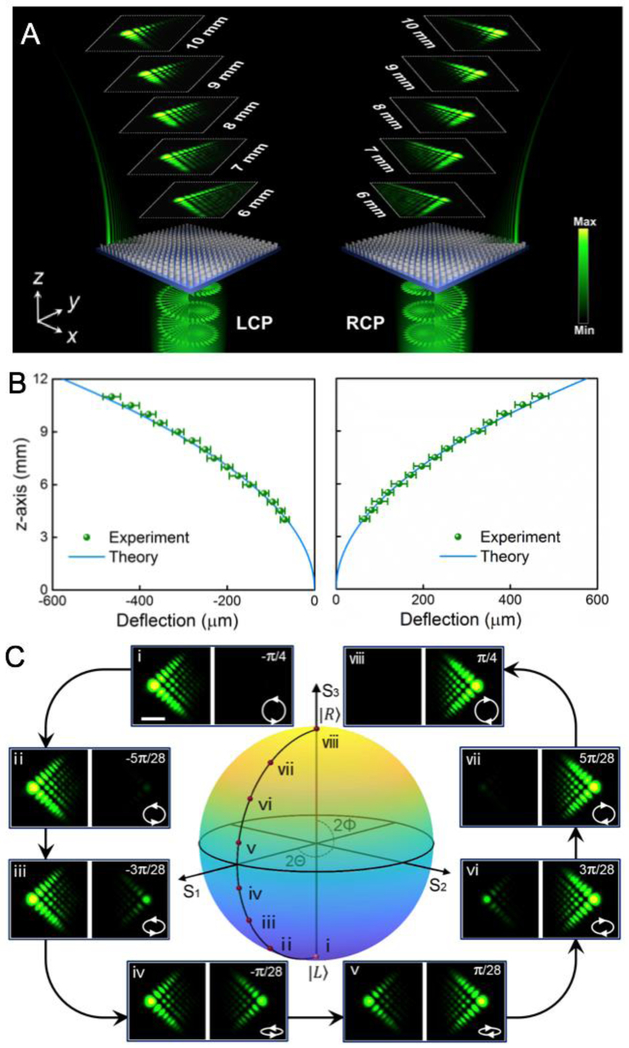
The designed metasurface composed of a TiO₂ nanopost array is fabricated with a lateral footprint of 450 μm × 450 μm on a fused-silica substrate. To characterize its performance, a normally incident collimated circularly polarized laser beam at a free-space wavelength of λ₀ = 532 nm is impinged on the metasurface from the substrate side. A schematic diagram of the measurement setup is shown in supplementary Fig. S3. The parabolic trajectories of the generated accelerating light beam is recorded by mapping the transverse intensity profiles of the transmitted light beam, with a charge-coupled device (CCD) camera, at different x-y planes on the exit side of the metasurface (z > 0, Figure 2A). Under LCP illumination, the metasurface generates an Airy beam with a parabolic trajectory exhibiting a transverse acceleration towards the left side. The main lobe of the Airy beam maintains a spot size of (30 ± 1) μm up to a propagation distance of ≈ 10 mm, clearly demonstrating the quasi-diffraction-free nature of an ALB propagating along a curved trajectory. The uncertainty in the measurement of the spot size is 1 standard deviation in fitting the full-width half-maximum of the main lobe of the Airy beam. As expected, when the spin state of the incident light is switched from LCP to RCP, a mirrored Airy beam with similar propagation trajectory but opposite acceleration direction is observed. The propagation characteristics and trajectories for both the left- and right- propagating Airy beams match well with the theoretical predictions (shown in Fig. 2B). The experimentally measured Airy beam generation efficiency of the metasurface, defined as the ratio of the optical intensity of the generated ALB to the optical intensity of the incident light beam, is (52 ± 2) %. The uncertainty in the calculated efficiency is 1 standard deviation based on propagation of uncertainty from the measurements of optical intensities of the transmitted and incident beams using the CCD detectors.

Fig. 2. Generation of switchable optical Airy beams with opposite acceleration directions.

(A) Schematic diagram of the experimental generation of optical Airy beams by the metasurface. The images in the white dashed frame show measured output intensities in the x-y plane along propagation trajectories for the incident light in LCP (left) and RCP (right). The wavelength of the incident light is 532 nm. (B) Experimentally measured (sphere) and theoretically calculated (solid line) Airy beams’ propagation trajectories. The uncertainties are one standard deviation of deflection distance for repeated experimental measurements (four in total). (C) Evolution of the output beams versus incident spin states. All the intensity profiles are taken at z = 8 mm. The circles with arrows on the Poincaré sphere show eight experimental incident spin states corresponding to intensity profiles i-viii. Scale bar for all the optical intensity images in (C), 50 μm.

Figure 2C depicts the continuous evolution of the transverse light field at a distance of z = 8 mm from the exit surface of the metasurface (z = 0 mm) as the spin state of incident light is gradually modified from LCP to RCP using a quarter wave plate (QWP) with a rotation angle α relative to its fast axis increasing from − π/4 to + π/4. Since input light with an arbitrary elliptical spin state on the Poincaré sphere is the superposition of two orthogonal spins ∣L⟩ and ∣R⟩, the two output states, ∣Ψ_l(α)) and ∣Ψ_r(α)⟩, from the metasurface can be respectively expressed as:

$$\mid {\Psi }_l(\alpha )\rangle =\cos (\alpha +\frac{\pi }{4})\cdot e^{-i(\alpha +\frac{\pi }{4})}\mid L\rangle \mid A_l\rangle$$ (3)

$$\mid {\Psi }_r(\alpha )\rangle =\sin (\alpha +\frac{\pi }{4})\cdot e^{i(\alpha -\frac{\pi }{4})}\mid R\rangle \mid A_r\rangle$$ (4)

The optical intensity ratio K between these two states can be expressed as $K(\alpha )={\tan }^2(\alpha +\frac{\pi }{4})$. We extract the experimentally measured intensity ratio K for the two opposite Airy beams as a function of α (supplementary Fig. S4), and find it to be in good agreement with the theoretically predicted values. These results indicate that the intensities of the two generated Airy beams can be tuned by simply changing the spin state of incident light, making it beneficial for the trapping and release of multiple objects during an in situ optical manipulation experiment.

In addition to controlling the acceleration direction of ALBs, it is possible to achieve generation and switching between two arbitrary accelerating light beams that follow different caustic trajectories in free-space. As a proof-of-concept, here we report for the first time, a metasurface design that generates two output ALBs, one following a natural logarithmic and another a quartic caustic trajectory, expressed as space curve ${\mathrm{C}}_1:\{\begin{array}{c}x=\text{aln}(bz)\hfill \\ y=\text{aln}(bz)\hfill \end{array}\phantom{\}}\text{and}{\mathrm{C}}_2:\{\begin{array}{c}x=c{z}^4\hfill \\ y=c{z}^4\hfill \end{array}\phantom{\}}$, respectively. The acceleration coefficients a, b and c are freely used as arbitrarily chosen constants, and here a = −10⁻⁴ m, b = 8×10³ m⁻¹, and c = 6.7×10⁴ m⁻³. The photonic spin-dependent phase profiles of the metasurface corresponding to LCP and RCP incident excitation are respectively expressed as:

$${\phi }_1(x,y)=e^{-1}{a}^{2}bc[2-ex{p}^{(-\frac{x}{a})}-ex{p}^{(-\frac{y}{a})}]$$ (5)

$${\phi }_2(x,y)=-\frac{16}{21}\sqrt[4]{3c}k(x^{\frac{7}{4}}+y^{\frac{7}{4}})$$ (6)

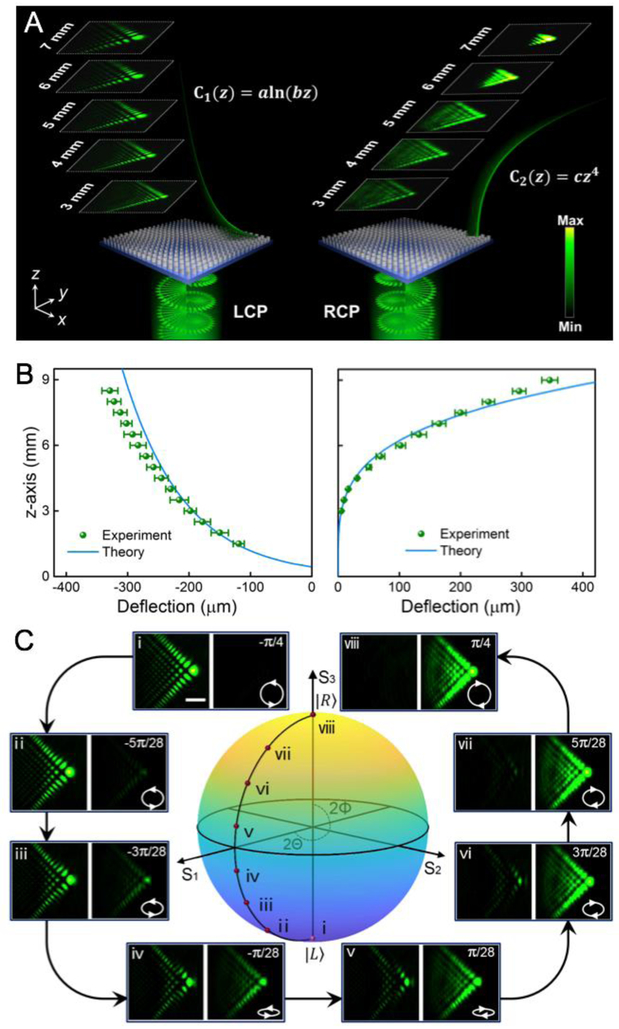
Figure 3 shows the experimental results for this metasurface device illuminated with normally incident circularly polarized light at a free-space wavelength of 532 nm. Figure 3A shows the measured transverse field profiles of two generated ALBs for various x-y planes at different z positions on the exit-side of the metasurface (z > 0). Two-dimensional quasi-diffraction-free fields are measured along with their evolution dynamics. When illuminated with a LCP incident light, the accelerating beam generated by the metasurface follows the predesigned natural logarithm trajectory. When the incident light is switched to RCP, the generated beam propagates along a biquadratic curvature. In the latter case, the intensity cross-section of the beam diminishes as the beam propagates farther away from the metasurface exit surface. This occurs because all the side lobes experience rapid deflection, due to the biquadratic transverse acceleration, and begin to converge with the main lobe [10]. Nevertheless, the propagation trajectories of these generated beams, after passing through an ultrathin dielectric metasurface, validate the theoretical predictions (Fig. 3b). The experimentally measured generation efficiencies for ALBs following natural logarithm and biquadratic caustic trajectories are (57 ± 2) % and (49 ± 1) %, respectively. The uncertainty in the calculated efficiency is 1 standard deviation based on propagation of uncertainty from the measurements of optical intensities of the transmitted and incident beams using the CCD detectors.

Fig. 3. Generation of switchable ALBs with different caustic trajectories.

(A) Schematic diagram of the experimental generation of ALBs respectively following natural logarithm and biquadratic caustic trajectories by metasurface. The images in the white dashed frame show measured output intensities in the x-y plane along propagation trajectories for the incident light with LCP (left) and RCP (right). (B) Experimentally measured (sphere) and theoretically calculated (solid line) two ALBs’ propagation trajectories for LCP and RCP light. The uncertainties are one standard deviation of deflection distance for repeated experimental measurements (four in total). (C) Evolution of the output beams versus incident spin states. All the intensity profiles are taken at z = 5 mm. The circles with arrows on the Poincaré sphere show 8 experimental incident spin states corresponding to intensity profiles i-viii. Scale bar for all the intensity images in (C), 50 μm.

Figure 3c shows the continuous evolution of transverse intensity profile at a distance of z = 5 mm from the exit surface of the metasurface as the spin state of incident light is gradually changed from LCP to RCP. A gradual monotonic transition between the two distinct accelerating trajectories is clearly evident. Similar to the demonstration with Airy beams discussed above, the intensities of the two arbitrary ALBs can be tuned by changing the spin state along the Poincaré sphere. The theoretical and experimentally measured intensity ratio K(α) for the two ALBs as a function of rotation angle α of the QWP are discussed in supplementary Fig. S4.

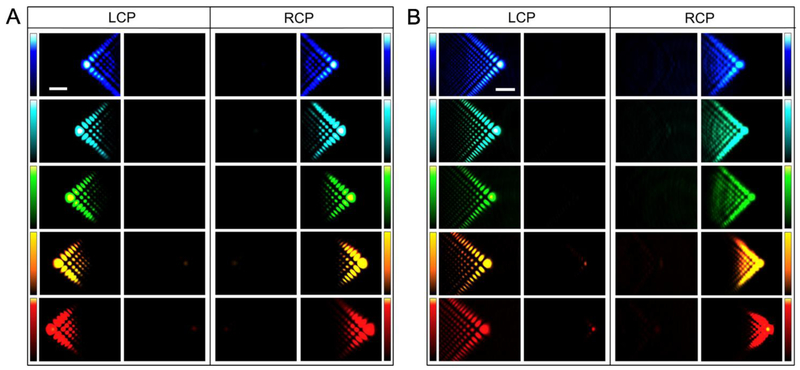
Figure 4 shows the experimental results for the two metasurface devices, discussed in the previous sections, illuminated at five different free-space wavelengths across the visible region (λ₀ = 460 nm, 490 nm, 532 nm, 580 nm, 610 nm). It is clearly evident from the lateral intensity profiles that the transmitted beam still exhibits a two-dimensional Airy-like interference pattern except that the position of main lobe at each wavelength is shifted laterally. The corresponding propagation trajectories for the three types of ALBs are summarized in supplementary Fig. S5-S7. In principle, a two-dimensional ALB can be treated as a superposition of two one-dimensional ALBs travelling along two orthogonal directions. Under the paraxial approximation, for a two-dimensional ALB with a caustic trajectory $C(z):\{\begin{array}{c}x=g(z)\hfill \\ y=f(z)\hfill \end{array}\phantom{\}}$, the required phase at the exit surface (z = 0) is given by [39]

$$\phi (x,y)=k[\int g^{{}^{\prime }}(z)dx+\int f^{{}^{\prime }}(z)dy]$$ (7)

where g(z) and f(z) are two continuous functions and respectively indicate the projection of the caustic trajectory of two-dimensional ALB in x-z and y-z plane. As shown in supplementary Fig. S8, the phase profiles of the TiO₂ metasurface are very similar for the selected multi-wavelengths. Therefore, based on eq. (7), by increasing the free-space wavelength λ₀ hence decreasing k, φ(x, y) increases, resulting in a larger deflection for the generated ALB. This prediction agrees well with the experimental observations shown in Fig. 4 and supplementary Fig. S5-S7. The experimentally measured generation efficiencies of the two metasurfaces for ALBs at different wavelengths ranges from (22 ± 1) % to (57 ± 2) %. The uncertainty in the calculated efficiency is 1 standard deviation based on propagation of uncertainty from the measurements of optical intensities of the transmitted and incident beams using the CCD detectors.

Fig. 4. Multi-wavelength generation and control of ALBs.

Experimentally measured intensity profiles of the generated (A) optical Airy beams (z = 8 mm) and (B) generalized acceleration light beams (z = 5 mm) by the two designed metasurface devices at free-space wavelengths of λ₀ = 460 nm, 490 nm, 532 nm, 580 nm, 610 nm. Scale bar for all the intensity images is 50 μm.

Furthermore, as shown in Fig. 4, the acceleration direction and caustic trajectories of the generated ALBs at these multiple incident wavelengths still depend on the spin states of incident light. This occurs because TiO₂ nanoposts have relatively high polarization conversion efficiencies at these wavelengths and can be treated as half-wave plates. As a result, they can generate geometrical phases for the incident light solely based on their rotation angle θ. These wavelength-insensitive geometrical phases are associated with the eigenvectors of the Jones matrix J(x, y) of the metasurfaces, and enable the photonic spin-control functionality [32-33]. Our results explicitly show that these metasurface devices can simultaneously achieve efficient generation and dynamic control of ALBs at multiple wavelengths across the visible region, which are not readily achievable from conventional methods based on SLM.

In conclusion, we have demonstrated an ultrathin all-dielectric metasurface device that can achieve robust generation and arbitrary control of accelerating light beams at multiple wavelength across the visible region. The propagation characteristics of the metasurface-assisted ALBs, including acceleration direction and caustic trajectory, can be well controlled and manipulated. Compared with previous demonstrations of ALB generation, the single layer and ultrathin architecture of the metasurfaces realized here enables an efficient, scalable and integration friendly platform for structured light generation, and its applications.