Abstract
Task-based functional Magnetic Resonance Imaging (fMRI) has been widely used to determine population-based brain activations for cognitive tasks. Popular group-level analysis in fMRI is based on the general linear model and constitutes a univariate method. However, univariate methods are known to suffer from low sensitivity for a given specificity because the spatial covariance structure at each voxel is not taken entirely into account. In this study, a spatially constrained local multivariate model is introduced for group-level analysis to improve sensitivity at a given specificity for activation detection. The proposed model is formulated in terms of a multivariate constrained optimization problem based on the maximum log likelihood method and solved efficiently with numerical optimization techniques. Both simulated data mimicking real fMRI time series at multiple noise fractions and real fMRI episodic memory data have been used to evaluate the performance of the proposed method. For simulated data, the area under the receiver operating characteristic curves in detecting group activations increases for the subject and group level multivariate method by 20%, as compared to the univariate method. Results from real fMRI data indicate a significant increase in group-level activation detection, particularly in hippocampus, parahippocampal area and nearby medial temporal lobe regions with the proposed method.
Keywords: Functional Magnetic Resonance Imaging (fMRI), group-level analysis, constrained multivariate method, maximum log likelihood, numerical optimization
1. Introduction
Task-based functional magnetic resonance imaging (fMRI) studies have been widely used to understand brain activations for cognitive tasks (Adleman et al., 2002; Kwong et al., 1992; Peterson et al., 1999; Reagh and Yassa, 2014). In a task-based fMRI experiment, series of brain images are collected while the subject is performing a task. To obtain group-level inference, multiple subjects are studied and common activations among these subjects specify a group map (Lindquist, 2008). Data analysis in task-based fMRI studies usually consist of a two-level model. A subject-level analysis detects the activation of each individual subject for a contrast of interest and a second group-level analysis localizes common activations among multiple subjects (Beckmann et al., 2003; Ferreira da Silva, 2011; Friston et al., 2005; Holmes and Friston, 1998; Penny and Holmes, 2003; Road, 1996; Woolrich et al., 2004; Worsley et al., 2002).
In the subject-level analysis, the experimental paradigm for each subject is modeled as a matrix with multiple columns (Buxton, 2009). Each column corresponds to a specific task condition, with 1 representing time points when the task is “on” and 0 when the task is “off”. The binary task functions are then convolved with an appropriate hemodynamic response function (HRF) to represent the fMRI signal. The resulting functions containing the signal regressors as columns then define the design matrix for the subject (Friston et al., 1998; Lindquist et al., 2009). The univariate general linear model (GLM) is a widely used method that fits the collected time series to the subject-specific design matrix by minimizing the Gaussian-distributed residual error. The signal magnitude in response to each single task condition is computed during this fitting process and is defined as the effect of each task condition. A contrast vector that constitutes a linear combination of one or multiple condition effects can then be defined to estimate the signal magnitude in response to either a single condition, an average effect over multiple conditions or a difference effect between two conditions. The subject’s response to the same task condition may vary from trial to trial and this variation is known as the within subject variance. Statistical inferences for a specific contrast of interest is computed for each subject (Lindquist, 2008).
In the group-level analysis, individual subjects are considered as random samples from a targeted population and brain activation effects for the same task vary from subject to subject. To draw conclusions on brain activations for a population in response to a specific task condition, between-subject variances need to be considered and a group analysis based on a random-effects model is preferred (Friston et al., 2002; Woolrich et al., 2004). In the random-effects model, activation effects from every single subject are taken as inputs and are fitted to a binary group design matrix where an entry with a 1 represents subjects belonging to a specific group. The group-level GLM could also be used to linearly model the group effect. This model is widely recognized as the summary statistics method (Holmes and Friston, 1998). The group-level GLM has been solved by using a) a direct Moore-Penrose inverse operation that assumes Gaussian noise (Friston et al., 2005), b) a fully Bayesian method (Woolrich et al., 2004), or c) a maximum likelihood estimation with an expectation trust region algorithm (Li et al., 2014). A group contrast vector detects activation effects averaging over multiple subjects in one group or detects difference effects between multiple groups. Statistical inferences are then computed for the group effects.
Another group-level analysis method in fMRI relies on combining hypothesis tests from each individual subject (Lazar et al., 2002). Subject-level activation is tested using parametric statistical tests and corresponding p-values are computed for each individual subject. Group analysis methods, such as Fisher’s data fusion method (Fisher, 1992), are used to generate group inferences from subjects’ p-values. Combining of p-value information is easy to implement but difficult to interpret. The null hypothesis of such a group-level analysis is that “no effect can be observed for any subject’. In Fisher’s data fusion method, this null hypothesis could be rejected on the basis of a non-zero effect in only one subject (Lazar et al., 2002) and therefore the computed group-level activation effects are prone to false positives. Additional group-level analysis involves using information across individual samples to assist in the recovery of group-level connections among different regions of interests (ROIs) (Friston, 2011; Gates and Molenaar, 2012; Smith et al., 2011). Instead of localizing the group-level common or different activated regions during a cognitive task, these group-level methods focus on constructing network connections between ROIs.
Both single subject and group-level analysis are performed independently for every voxel, and therefore are univariate in nature. However, each voxel has a different spatial covariance structure which is not taken into full consideration by a univariate method because a univariate method assumes neighboring voxels to be independent and therefore is not sensitive enough to detect activation effects especially for fMRI data with low signal-to-noise ratio (SNR). To improve the sensitivity of activation detection, isotropic spatial Gaussian smoothing is typically performed as a preprocessing step in most univariate methods. However, an improper smoothing kernel size that does not match the spatial activation pattern exactly may eliminate the detection of activation (Yang et al., 2018). Specifically, an extended isotropic smoothing kernel can be problematic to cortical regions with thin and folded grey-matter structures (Cordes et al., 2012; Zhuang et al., 2017).
CCA (Hotelling, 1936) applied to local neighborhoods to obtain adaptive spatial filter kernels has been successfully applied to fMRI subject-level analyses and shown improved sensitivity in activation detection (Friman et al., 2001). To obtain rotationally adaptive filter kernels in local CCA, each voxel time series can be convolved with spatially anisotropic basis functions with optimized weight coefficients determined by the data (Friman et al., 2003, 2002, 2001). These low-pass spatial basis functions with optimized weight coefficients determine the underlying spatial covariance structure at each voxel and therefore can better capture arbitrarily-shaped activation patterns. Subject-level activation status is then computed by maximizing the canonical correlation between the filtered time series within each neighborhood of a voxel time series and the task design matrix. Statistical inferences are finally computed for a specific contrast of interest an assigned to the center voxel of each neighborhood. Compared to a univariate analysis method, local CCA has higher degrees of freedom and therefore spatial constraints are needed in estimating weights of the spatial basis functions to improve the specificity of the activation pattern (Cordes et al., 2012; Zhuang et al., 2017). More accurate subject-level activation maps with improved sensitivity at a given specificity have been computed with locally constrained CCA (cCCA) methods (Yang et al., 2018; Zhuang et al., 2017).
In this study, we introduce the cCCA model for fMRI group-level analysis, where local neighboring voxels are incorporated with optimized spatial weights at each voxel to obtain neighborhood-specific spatial filter kernels. However, due to the particular structure of the group-level design matrix which is different for a 1st level design matrix involving cCCA, the solution of the group cCCA model is performed differently than a subject-level cCCA. In group-level analysis, a binary design matrix is used with 1s representing subjects belong to a specific group. In this case, the design matrix is a vector with all 1s for within-group activation detection and a two-column binary matrix for between-group difference detection. Since the design matrix is a constant matrix with covariance equal to zero for within-group activation detection, a covariance-based analysis cannot be directly carried out. To prevent potential singularity problems in group-level cCCA, we convert the group-level cCCA problem to a maximum log-likelihood problem and solve it with nonlinear optimization techniques. Specifically, we form an optimization problem at each voxel with subject-level effects of interest from center voxel and its neighboring voxels as inputs. Group inferences of the center voxel, between-subject variance and optimum weight coefficients of each neighboring voxels are estimated simultaneously. Using simulations, we show the improvements of the proposed cCCA method over standard univariate group analysis methods such as univariate summary statistics and Fisher’s data fusion with the same subject-level analysis as input. We further apply the cCCA group model to real fMRI data and demonstrate superior performance over other analysis methods in group activation detection.
2. Materials and Methods.
2.1. Theory
2.1.1. Univariate group analysis in fMRI
Subject-level univariate analysis and variance structures.
In a two-level univariate general linear model, the subject-level analysis for the kth subject is modeled as
| (1) |
where is a random vector of continuous variables representing the time course (t time points) from a single voxel u, and represents n functions used to model the blood oxygenation level-dependent (BOLD) response. Subscripts k in Eq. (1) denotes the subject index and subscript u for βk and ∊k represents effects and residuals for a single voxel. The single voxel residual vector follows a Gaussian distribution with and . With a known covariance , the best linear unbiased estimator of is (Searle et al., 1992)
| (2) |
where + indicates the pseudo inverse. Eq. (2) can be further simplified to
| (3) |
The covariance structure of is then computed as
| (4) |
Without loss of generality, we can re-parameterize xk to be an effective design matrix corresponding to a specific contrast c of interest, i.e. n = 1. Then, the vector becomes a scalar quantity and represents the subject-level activation effect that will be estimated.
Group-level univariate analysis and variance structures.
The group-level group univariate analysis is modeled as
| (5) |
where represents effects from N subjects at a single voxel and XG is the design matrix modeling either within-group activation detection or between-group difference detection . The vector represent the Gaussian-distributed residual error term of group activation with a mean vector of 0 and variance-covariance matrix , where denotes the between subjects random effects variance and IN is a N × N identity matrix. We use the subscript G in Eq. (5) to denote the group label. The mean and covariance structure of the random variable βu in Eq. (5) is then given by
| (6) |
In practice, the second level model uses estimated effects from the subject-level as inputs instead of the true (but not observable) parameters (Beckmann et al., 2003). This modification leads to
| (7) |
where indicates the estimated vector of βu and the remaining error vector. According to Eq. (3), we replace each with and obtain
| (8) |
with and . Following the same derivation as in Eq. (6), we can write . The variance-covariance matrix of , i.e. , in Eq. (8) consists of both within-subject variance Ru and between-subjects variance at a single voxel, i.e.:
| (9) |
where and , respectively. from Eq. (4), we can write and therefore, Ru takes the form of:
| (10) |
Furthermore, for within-group activation detection, we have
| (11) |
For between-group difference detection, XG is defined to be
| (12) |
The non-diagonal terms vanish since all subject data are assumed to be independent observations.
Maximum likelihood formulation in univariate second-level fMRI analysis.
The vector in Eq. (7) follows a Gaussian distribution with and . The probability density function of is a multivariate Gaussian distribution (Li et al., 2014) according to
| (13) |
Taking the natural log on both sides of Eq. (11) gives
| (14) |
By maximizing the log-likelihood objective function in Eq. (14) with nonlinear optimization techniques, we determine the solutions of unknown parameters and . Note that is either parameterized by (Eq.11) or (Eq.12).
2.1.2. Multivariate group analysis in fMRI with local CCA.
With local CCA, activation status of the center voxel of a neighborhood is determined by incorporating its neighboring voxels. The two-level mixed effects model applies here.
Subject-level local CCA analysis and variance structures.
In local CCA analysis, the subject-level multivariate model for subject k can be written as
| (15) |
where is the design matrix as before and is a matrix of time courses (t time points) of M voxels (e.g., M = 9 for 3×3 regions in a 2D slice and M =27 for a 3D 3×3×3 neighborhood). We use superscripts 1,2, …M to denote indices of voxels. Using optimization theory, we find spatial weight vectors and multivariate weight vectors that maximize the canonical correlation between Yk and Xk. With a proper normalization term (var(Ykαk) = 1), the subject-level CCA model can be converted to an equivalent multivariate multiple regression model (Zhuang et al., 2017) given by
| (16) |
where is the regression weight vector and is the residual error vector. In this case, βk 2 and ∊k are linear combinations of and from the local neighborhood, and therefore, ∊k also follows a Gaussian distribution with E(∊k) = 0 and . We can further compute the best linear unbiased estimator of βk with a known covariance matrix Vk to be
| (17) |
The mean and covariance structure of is then computed as and .
Group-level multivariate analysis and covariance structures.
Using the same concept of incorporating local neighboring voxels, the group-level CCA can be modeled as
| (18) |
where is a matrix that represents subject-level activation effects of M voxels from N subjects in a local neighborhood of a center voxel (labeled as voxel 1 in superscript) and XG is the group analysis design matrix. We convert the group-level local CCA model to a multivariate multiple regression model according to
| (19) |
where the vector βG is the group inference weight vector and ηG is the residual error vector. In this case, βG and ηG are linear combinations of and from the univariate model for local neighborhood voxels i ∊{1,..,M} defined by
| (20) |
Therefore, ƞG follows a multivariate Gaussian-distribution with E(ηG) = 0 and for the within-group scenario or for the between-group scenario. In practice, the group-level multivariate model takes estimated effects from the subject-level as input instead of the true (but not observable) parameters, i.e. Eq. (19) is modified to
| (21) |
Where , and . similar to Eq. (8), . The variance-covariance of consists of both within-subject variance-covariance RG and between-subject variance-covariance QG.RG takes the following form:
| (22) |
where
| (23) |
and is the element in αG of the mth voxel in the local neighborhood.
To sum up, for within-group activation detection, we have
| (24-1) |
For between-group difference detection,
| (24-2) |
2.1.3. Maximum likelihood formulation in multivariate second-level fMRI analysis.
The main focus of this paper is to solve the multivariate second level analysis in fMRI, i.e. estimate αG, βG in Eq. (21) and or in Eqs. (24-1, 24-2). The quantities and are computed from the subject-level analysis, where k denotes the index of subjects and m is the voxel index. As discussed in section 2.1.2, in Eq. (21) follows a Gaussian distribution with and . The probability density function of takes the form of the multivariate Gaussian distribution (Li et al., 2014) according to
| (25) |
Taking natural log on both sides of Eq. (25) gives:
| (26) |
By maximizing the log-likelihood objective function in Eq. (26) with nonlinear optimization techniques, we determine the solutions of unknown parameters αG,βG and or .
2.1.4. Normalization of the term .
A normalization term is further added to in Eq. (21) to guarantee the estimated βG with different voxel configurations (αG) are scale invariant and therefore the computed statistical inference with various number of neighboring voxels are comparable to the univariate statistic computed from only the center voxel. In this case, Eq. 21 further turns into
| (27) |
where is the L2-norm of the combined effect of the local neighborhood. As stated above, follows a Gaussian distribution with and , therefore, after normalization, the same Gaussian distribution will be followed.
2.1.5. Constraints in multivariate second-level analysis.
In the subject-level analysis, CCA without any spatial constraint has been shown to yield a significant smoothing artifact, as activations of strongly active voxels tend to bleed into the neighboring voxels. This artifact leads to a low specificity (Cordes et al., 2012; Friman et al., 2002). The same problem also occurs for the group-level multivariate analysis due to the extra degrees of freedom introduced by αG.
The constrained CCA (cCCA) model has been applied to the subject-level fMRI analysis to guarantee the dominance of the center voxel in each local neighborhood (Cordes et al., 2012; Zhuang et al., 2017). As before, we use the notation that α(1) is the weight of the center voxel and α(m) the weight of the mth neighboring voxel in each local neighborhood. A dominant weight of the center voxel will reduce the smoothing artifact and increase the specificity of the multivariate analysis method. In the following we use a sum-constraint previously proposed (Cordes et al., 2012) with paramter K in the group-level multivariate analysis in this study, which we solve for the most important case where the dominant constraint becomes an inequality constraint, i.e.
| (28) |
2.1.6. Solving the optimization problem of multivariate group-level analysis.
By combining Eq. (26), Eq. (27) and Eq. (28), the full optimization problem in multivariate group-level analysis becomes
| (29-1) |
for within-group activation detection and
| (29-2) |
for between-group difference detection. The objective function in Eqs. (29) is convex since VG is positive definite and therefore optimization techniques like the Broyden–Fletcher–Goldfarb–Shanno (BFGS) with self-scaling (Nocedal and Wright, 2006; Shanno, 1985) method can be applied to solve Eqs. (29). BFGS is an iterative gradient descent method where the search direction in each step is facilitated with a backtracking line search algorithm (Nocedal and Yuan, 1998). In each optimization step, α(1) is replaced by and the non-negative constraint is satisfied by substituting α(m) = (θ(m)2), i.e. spatial weights of all other neighboring voxels are represented by nonnegative variables (0m)2, j = 2, …, M.
2.1.7. Statistical analysis:
T statistics were used to determine the group inference of the center voxel for a specific contrast c of interest, given by
| (30) |
Statistical thresholds for significance are computed from the null distribution non-parametrically. For within-group activation detection, all of the above analysis is repeated on wavelet-resampled resting-state time courses (Breakspear et al., 2004) until a stable maximum statistic is obtained. Specifically, the spatial structure of the wavelet resampled resting-state time series is kept the same as the spatial structure of the original fMRI data by using the same random permutation of the wavelet coefficients for the entire brain. Breakspear et al. (2004) have demonstrated that constrained temporal resampling of the resting-state data in the wavelet domain allows construction of bootstrapped data with the following essential properties: (1) spatial and temporal correlations are preserved; (2) the irregular geometry of the intracranial images is maintained; (3) there is adequate type I error control; and (4) expected experiment-induced correlations are included. Therefore, the spatiotemporal resampled data in the wavelet domain can be further used in testing the null hypothesis of within-group activation.
For between-group difference detection, a permutation test (Nichols and Holmes, 2002) was performed to generate the null distribution of the t statistic in Eq. (26). We randomly shuffled the group assignment of the subjects in two groups and then repeated the same type analysis again until a stable maximum statistic was obtained. The null hypothesis for the two-group analysis here is that no activation differences existed between groups.
2.2. Data collection.
Subjects.
Eight subjects diagnosed with amnestic mild cognitive impairment (aMCI, 4 Males; Age: 60.9±3.2 years; Years of education: 16.9±1.9 years) and eight normal control subjects (NC, 5 Males; Age 60.6±8.3 years; Years of education: 16.9±2.1 years) were recruited with Institutional Review Board approval and scanned using a 3.0 T GE scanner at the University of Colorado, Denver. All subjects were right-handed, and their demographics were listed in Table 1. Diagnosis of aMCI was made by trained professionals based on Petersen Criteria (Petersen et al., 2001). Clinical dementia rating for MCI subjects and Mini-Mental State Examination scores for all subjects were also included in Table 1.
Table 1.
Subject demographics. Abbreviations: CDR: Clinical Dementia Rating; MMSE: Mini- Mental State Examination.
| NC | aMCI | Group difference | |
|---|---|---|---|
| Number of subjects | 8 (5 Males) | 8 (4 Males) | Not significant |
| Age (years) | 60.6±8.3 | 60.9±3.2 | Not significant |
| Years of education (years) | 16.9±2.1 | 16.9±1.9 | Not significant |
| CDR | 0±0 | 0.5±0 | p=0 |
| MMSE | 29.6±0.5 | 28.1±1.1 | p=0.0041 |
Table 1. Subject demographics.
MRI data collection.
One resting-state and one episodic memory fMRI data set were collected with the following parameters: TR 2000 ms, TE 30 ms, parallel imaging factor of 2, 25 slices (coronal oblique, perpendicular to the long axis of hippocampus), slice thickness/gap=4.0 mm/1.0 mm, in-plane resolution 96×96 interpolated to 128×128, voxel size of 1.72×1.72 ×5 mm3, 288 time frames (total scan duration 9.6 mins, both resting-state run and episodic memory task run). Subjects were instructed to relax and refrain from executing any task with eyes closed during the resting-state data collection. High resolution structural images were also acquired including a T1-weighted image (0.86×0.86×1 mm3) and a coplanar T2-weighted image (0.43×0.43×2.5 mm3) using a standard acquisition protocol.
Episodic memory task.
The episodic memory task involved encoding and recognition activity using stimuli of human faces paired with occupations (face-occupation task). The task consisted of six periods of encoding, distraction, recognition activity, and short instructions where words on the screen reminded subjects of the task component ahead. The encoding task consisted of seven novel visual stimuli, and the recognition task consisted of fourteen stimuli, half novel and half identical to the items seen in the previous encoding task. An active control task (button press responding to the letter “Y” or “N”) was used as a distraction task between each pair of encoding and recognition activity. A detailed task description can be found in Cordes et al. (2012).
2.3. fMRI data preprocessing.
The first 5 time frames of the EPI data (10 seconds) were removed to avoid incomplete steady-state magnetization. All other time frames were slice-timing corrected and realigned to the mean EPI image in SPM12 (http://www.fil.ion.ucl.ac.uk/spm/), further co-registered to the subject T1 space using affine transformation, and then non-linearly normalized to the standard MNI-152 2mm-template using ANTs software (http://stnava.github.io/ANTs/). The normalized data were further smoothed using 3D Gaussian filters with full-width-half-maximum (FWHM) of 2mm, 4mm and 6mm, respectively. All voxels were high-pass filtered using cosine basis functions with a cut-off frequency of 1/120 Hz to remove temporal drift (Holmes et al., 1997).
2.4. Subject-level analysis.
A univariate GLM analysis was first performed at the subject-level. For each subject (k), a design matrix was constructed by first modeling the episodic memory task design with 4 regressors for conditions {instruction, encoding, distraction and recognition}, and further convolving the task design with the standard canonical hemodynamic response function. Both unsmoothed and smoothed time series were fitted to this design matrix separately. A voxel-wise effect map for contrast encoding v/s control was computed for every subject and a voxel-wise variance map of this effect was also obtained. A subject-level t-statistic map for contrast encoding v/s control was also computed for each subject. The corresponding p-value map for subject’s t-statistics was then determined parametrically, with a degree of freedom equal to the number of time frames in the task fMRI data minus the number of regressors in the design matrix (Xk).
A 3D local constrained CCA (cCCA) model was also applied to each subject. Optimum parameters in this local cCCA model of the same dataset were determined in Zhuang et al (2017) and applied to each subject. A voxel-wise effect map for contrast encoding v/s control was computed and a voxel-wise variance map of this effect was also obtained.
2.5. Simulation.
Realistic simulated data were generated to evaluate the sensitivity and specificity of the proposed method and other existing methods for group-level analysis with a known ground truth. For within-group activation analysis, 500 5×5 neighborhoods with active center voxels and 500 5×5 neighborhoods with inactive center voxels were simulated for 16 subjects. The group-level analysis is carried out for the center voxel only within each simulated neighborhood.
2.5.1. Generation of simulated data.
Determine number of active neighbors in each neighborhood.
The distribution of active neighbors in each local neighborhood followed the empirical distribution of unsmoothed real fMRI data analyzed with subject-level univariate GLM analysis plus the group-level univariate summary statistics method (Holmes and Friston, 1998). Specifically, effect maps of contrast encoding v/s control for all subjects computed from unsmoothed time series were input into a group-level univariate summary statistics analysis. A voxel-wise t-map was computed for the group inferences, i.e. an activation map for within-group activation detection. A t-threshold corresponding to an uncorrected p-value of 1e-5 was used to label active voxels in the group maps. The empirical distribution of active neighbors in each local neighborhood was then computed by counting how many of the neighboring voxels were also active given an active or inactive center voxel. Activation patterns in simulated neighborhoods were then generated by randomly sampling from this empirical distribution so that the activation patterns in the simulated data represent real data.
Generate simulated time series in each neighborhood.
Simulated time series for each neighborhood at multiple noise levels were generated for all 16 subjects. Time frames for simulated neighborhoods were obtained from neighborhoods in unsmoothed real data with the same 5×5 neighborhood arrangement. For each simulated neighborhood, both resting-state and task fMRI time frames of the real data fMRI neighborhoods were obtained for all 16 subjects, which preserves the spatial dependency within each simulated 5×5 neighborhoods as in real data. Specifically, wavelet-resampled resting-state time courses (ynull) were added to the task activated time series (ytask) with different noise fractions (f) to simulate time courses at different noise levels for the entire neighborhood using
| (27) |
We varied the noise fraction f from 0.45 to 0.95 in steps of 0.1 to cover a wide range of noise levels in fMRI data. The corresponding ranges from 1.22 to 0.05.
2.5.2. Analyze simulated data.
Subject-level analysis.
Univariate GLM analysis (single voxel analysis (SV)) was first performed on each simulated neighborhood for all 16 subjects. Time series of each voxel were linearly fitted to the subject-specific design matrix Xk. The effect and its variance of contrast encoding v/s control were determined for every voxel in each neighborhood. The corresponding t-statistics were computed and p-values were determined parametrically. Gaussian filters with FWHMs equal 2mm, 4mm and 6mm were then used to smooth the middle 3×3 voxels in each simulated 5×5 neighborhood, respectively. Univariate GLM analysis was performed and the effect and its variance of the middle 3×3 voxels were computed for each smoothed neighborhood with various FWHMs, respectively (SVGS). Parametric p-values were then determined. The subject-level local constrained CCA method (cCCA) was also applied to the middle 3×3 voxels in each simulated 5×5 neighborhood. The effect and its variance were determined for the same contrast.
Group-level analysis.
The effect and its variance of the center voxel in each simulated 5×5 neighborhood computed from every subject-level analysis method were input to the group-level univariate summary statistics method (SV+SV and SVGS+SV). Group inferences were estimated by solving Eq. (14) and t-statistic was computed following Eq. (30). Uncorrected p-values of the effect of the center voxel in each simulated neighborhood were input to the Fisher’s data fusion (SV+Fisher) method. The group inferences were computed as , N = 16. The effect and its variance of the middle 3×3 voxels in each simulated 5×5 neighborhood were input to the proposed multivariate group-level analysis (SV+cCCA) method. By solving Eq. (29-1), the group inferences of the center voxel were determined and t-statistics were computed following Eq. (30). Table. 2 summarizes all methods performed to analyze the simulated data, with subject-level smoothing kernel size, both subject-level and group-level analysis methods and their abbreviations.
Table 2.
Maximum log-likelihood formulations of both univariate and multivariate methods applied in the group-level analysis.
| Univariate | Multivariate | |
|---|---|---|
| Group analysis model | ||
| Inputs to group level analysis | Subject-level effects from N subjects ; Within-subject variances of the effect (1st part of ); | Subject-level effects of m voxels in a local neighborhood from N subjects ; Within-subject variances of the effect (1st part of ); |
| Estimated parameters | Univariate group inference ; Between-subject variance of the effect (2nd part of ) | Group inference assigned to the center voxel (βG); Between-subject variance of the effect (2nd part of VG) |
| Objective function |
Evaluating model performance.
Receiver operating characteristic (ROC) curve was used to evaluate the performance of each method by comparing the computed group inferences of each center voxel with the simulated ground truth. The fractions of true positives (TPR) and false positives (FPR) were computed at each threshold. Area under the ROC curves (AUC), integrating from FPR of 0 to 0.1 were computed for all analysis methods and plotted against noise fractions for selected methods. AUC for all methods applied to simulated data with a noise fraction that is close to real fMRI data (f = 0.85, SNR = 0.18) were also computed to make comprehensive comparisons of all methods.
Significance analysis of multivariate and univariate group-level analysis methods.
To conduct the significance analysis between univariate and multivariate group-level methods, we repeated our simulation procedure (detailed in Section 2.5.1) 10 times to generate 10 sets of different simulated data at the noise fraction of 0.85. Subject-level univariate analysis (SV) was performed. Group-level univariate (SV+SV) and multivariate (SV+cCCA) methods were then applied to compute the group-level activation for each data set. AUCs, integrating over FPR ∊ [0, 0.1], were finally computed and compared between these two methods (SV+SV and SV+cCCA).
2.6. Group-level analysis of task fMRI data.
Both univariate and the proposed multivariate methods were applied to detect brain activations within-group as well as the differences between groups during the episodic memory task. In the within-group activation detection, we include all 16 subjects (8 NC and 8 aMCI subjects) to achieve a larger sample size. For all analysis methods, the group design matrix XG is set to be for one group activation detection and to be for between-group difference detection.
Univariate summary statistics as described in section 2.1.1 were first applied to compute group inferences. A voxel-wise effect map for contrast encoding v/s control ( in Eq. (14)) and the corresponding variance map ( in Eq. (14)) computed from both unsmoothed (SV+SV) and smoothed (SVGS+SV) time series were input to the group-level analysis. The effect and its variance computed from the subject-level optimum cCCA model were also input to the univariate group-level analysis (cCCA+SV). By maximizing the log-likelihood function in Eq. (14), we obtained the group inferences and the group variance . The corresponding t-statistics were computed as , where c = 1 for one group analysis and c = [1, −1] for between-group analysis.
The proposed multivariate group-analysis method was then applied. The inputs to Eq. (30) were the voxel-wise effect map and the corresponding variance map of contrast encoding v/s control inside each local 3×3×3 neighborhood computed from subject-level univariate (SV+cCCA) and multivariate (cCCA+cCCA) methods. The group inference of the center voxel was determined of this neighborhood. By solving Eq. (30) with BFGS optimization techniques, we obtained multivariate group inferences βG, the optimum weight coefficients αG and the one group variance or the two-group variances . T-statistics (tG) for each center voxel were computed following Eq. (30), where c = 1 for one group analysis and c = [1, −1] for between-group analysis.
Fisher’s data fusion was also applied to generate a voxel-wise within-group activation map using unsmoothed time series (SV+Fisher). We combined subject-level independent tests from N subjects at each voxel by following Fisher’s data fusion (1992) rule as , N = 16. The combined group-level test statistics follows a χ2 distribution with 2N degrees of freedom. By combining tests this way, we cannot obtain information on the direction of the group-level activation. For between-group difference detection, the null hypothesis was that no activation differences existed between groups. Since the group difference hypothesis cannot be computed at subject-level, the Fisher’s data fusion model was not applicable in this case.
Statistical threshold for significance levels of group inferences , tG and tF for each analysis method were computed non-parametrically as described in section 2.1.7. Specifically, we repeated the exact analysis on wavelet-resampled resting-state time series from all 16 subjects by using at least 200 iterations to achieve a stable null distribution for within-group activation detection. For between-group difference detection, NC and aMCI subjects were randomly assigned to each group and the exact analysis was carried out on the shuffled groups. At least 200 iterations of randomly shuffling were performed to achieve a stable null distribution. We used the , tG and tF value at the αth percentile of the null distribution with all statistical values to be the thresholds of the uncorrected p-value of . We used the distribution of the maximum statistics to correct for multiple comparisons and obtain the statistical thresholds at a family-wise-error-rate (FWE) corrected p<0.05 (R. Nandy and Cordes, 2004) for all analysis methods.
2.7. Evaluating group-analysis methods with task fMRI data.
Activation maps.
We thresholded each within-group activation map obtained from different analysis methods using a significance threshold of p=0.05 (corrected for multiple comparisons) and computed an activation percentage for each Automated Anatomical Labeling (AAL) region (Tzourio-Mazoyer et al., 2002). Activation percentage in targeted medial temporal regions (bilateral hippocampus, para-hippocampal gyrus and fusiform gyrus, further detailed in section 4.1.2) then provide quantitative measurements to directly make the comparison among different methods. We then ranked the regions according to descending values of activation percentages and compared the activation status in each region among different analysis methods. The between-group difference maps computed with various methods were thresholded at p<0.01 (uncorrected), with a minimum cluster size of 15. The number of voxels passing the threshold were also counted and the percentage for each AAL regions was computed.
Modified ROC curve.
In real fMRI activation detection, since the ground-truth is unknown, the ROC method cannot be applied directly. In our previous studies, we have shown that the ROC method can be modified and applied to real fMRI data, termed “modified ROC curves” (Cordes et al., 2012; Nandy and Cordes, 2003; Nandy and Cordes, 2004). The modified ROC curve has been demonstrated to always be the lower bound of traditional ROC curve and the ordinate of both ROC methods are linearly related (Cordes et al., 2012). Specifically, instead of fractions of true positives (TPR) and false positives (FPR), we estimated the fraction of active positives (AP) using task-activated fMRI time series and the fraction of resting positives (RP) using resting-state time series. FPR is then approximated using RP and the upper bound of TPR is estimated using AP as detailed in Nandy and Cordes, (2003). Modified ROC curves were generated here to compare different analysis methods in within-group activation detection. Area under the modified ROC curve (AUC), integrated from false positive rate of 0 to 0.1, was computed for each method. The correlation between sequences of AUCs computed from simulated data and real fMRI data with multiple analysis methods was computed.
3. Results
Table 2 summarizes maximum log-likelihood formulations of both univariate and multivariate group-analysis methods.
Table 2. Univariate and multivariate group analysis methods.
3.1. Simulation.
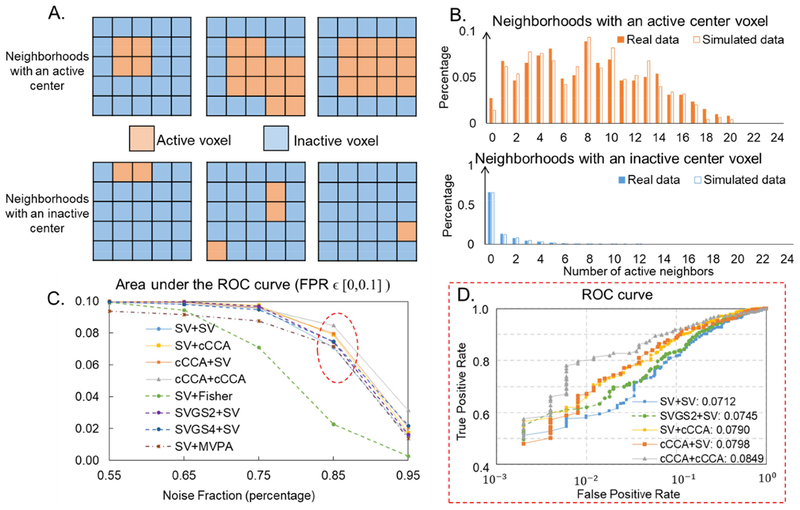
Simulation of within-group activation results are summarized in Fig. 1, Table 3 and Table 4. Six typical simulated activation patterns in local 5×5 neighborhoods are shown in Fig. 1(A), three with active center voxels (top) and three with inactive center voxels (bottom). Fig. 1(B) shows the empirical distribution of active neighbors with an active (top) or inactive (bottom) center voxel for the real data (solid bars) and simulated data (unfilled bars). The active voxels are labeled as described in section 2.5.1. As shown in Fig. 1(B), the empirical distribution of active neighbors with an active or inactive center voxel for the real data and simulated data are approximately matched, with Pearson correlations between these two distributions of 0.96 (p-value<0.001) for neighborhoods with active center voxels and 0.99 (p-value<0.001) for neighborhoods with inactive center voxels.
Figure 1.
Simulation: Within-group activation detection. (A). Examples of simulated 5×5 neighborhoods with an active (top) or inactive (bottom) center voxel. (B). The distribution of number of active neighbors with an active (top) or inactive (bottom) center voxel in both real data (filled) and simulated data. (C). Area under the ROC curves (AUC), integrated over FPR ∊ [0, 0.1] for different analysis methods applied to simulated data with different noise levels. (D). ROC curves for different analysis methods applied to simulated data with a noise fraction of 0.85 (SNR = 0.18) which is close to the real fMRI data (dotted red ellipse in (C)). Areas under ROC curves, integrated over FPR ∊ [0, 0.1] for each method are listed in the legend.
Table 3.
Smoothing kernel sizes (column 2), subject-level (column 3) and group-level (column 4) analysis methods used in simulation and the corresponding AUCs (column 5) of each method when analyzing simulated data with a noise fraction of 0.85 (SNR = 0.18).
| Abbreviations | Subject-level smoothing kernel size (FWHM) | Subject-level analysis method | Group-level analysis method | Area under the ROC curve (integrating over FPR ∈ [0,0.1]) |
|---|---|---|---|---|
| SV+SV | 0 mm | Univariate | Univariate | 0.0712 |
| SV+cCCA | 0 mm | Univariate | Multivariate Method | 0.0790 |
| cCCA+SV | 0 mm | Sum-cCCA | Univariate | 0.0798 |
| cCCA+cCCA | 0 mm | Sum-cCCA | Multivariate Method | 0.0849 |
| SVGS2+SV | 2 mm | Univariate | Univariate | 0.0745 |
| SVGS4+SV | 4 mm | Univariate | Univariate | 0.0748 |
| SVGS6+SV | 6 mm | Univariate | Univariate | 0.0681 |
| SV+Fisher | 0 mm | Univariate | Fisher’s data fusion | 0.0227 |
Table 4.
Area under the ROC curves integrated over FPR ∊ [0, 0.1]) for all combinations of subject-level and group-level univariate and multivariate analysis methods.
| Univariate summary statistics (SV) | Group-level analysis method Univariate Fisher’s data fusion (Fisher) | Multivariate cCCA | ||
|---|---|---|---|---|
| Subject-level analysis method | GLM on unsmoothed time series (SV) | 0.0712 | 0.0227 | 0.0790 |
| cCCA on unsmoothed time series (cCCA) | 0.0798 | N/A | 0.0849 | |
| GLM on smoothed time series with FWHM = 2mm (SVGS2) | 0.0745 | 0.0259 | 0.0812 | |
| GLM on smoothed time series with FWHM = 4mm (SVGS4) | 0.0748 | 0.0377 | 0.0801 | |
| GLM on smoothed time series with FWHM = 6mm (SVGS6) | 0.0681 | 0.0348 | 0.0729 |
Table 3 lists details of each method used to analyze the simulated data. The area under the ROC curves (AUC), integrated for false positive rates 0 to 0.1, at multiple noise levels methods are plotted in Fig. 1(C). AUC for each analysis method at the noise fraction of 0.85 (dotted red circle in Fig. 1(C)), corresponding to an SNR of 0.18 that is close to the real fMRI data, is listed in Table 3. As shown in Fig. 1(C) and Table 3, applying multivariate analysis at group-level shows an increased AUC of 12% at high noise fractions (f=0.85, SV+cCCA, solid yellow curve in Fig. 1(C)) when compared to the univariate method (SV+SV, solid blue curve in Fig. 1(C)). Subject-level Gaussian smoothing with proper kernel sizes (FWHM ≤ 4mm) increase the group-level performance at high noise levels (f ≥0.75, SVGS+SV, dashed green and purple curves in Fig. 1(C)), compared to the same analysis performed on unsmoothed time series (SV+SV). However, SVGS+SV is still less accurate than either level constrained multivariate models (solid yellow and orange curves in Fig. 1(C)) in activation detection. Furthermore, applying both level constrained multivariate methods (solid grey curve in Fig. 1(C)) further increases the AUC by 13% at the noise level of 0.85 (Table 3), as compared to only applying multivariate method at either subject-level or group-level (SV+cCCA or cCCA+SV). Last, Fisher’s data fusion gives the worst performance at high noise fractions (f ≥0.65).
Fig. 1(D) plots the ROC curves for different analysis methods of simulated data with a noise fraction of 0.85 (dotted red circle in Fig. 1(C)). As we can see in Fig. 1(D), given a specificity (1-FPR), the multivariate methods show higher sensitivities (TPR, solid grey, yellow and orange curves), which demonstrates optimum performance of the proposed multivariate method at high noise levels. Table 4 lists AUCs integrated from FPR of 0 to 0.1, computed for all analysis methods with simulated data at the noise level of 0.85. AUCs were computed for combinations of subject-level (SV, SVGS and cCCA) and group-level (SV, cCCA and Fisher) univariate and multivariate analysis methods. As shown in Table 4, with results from the same subject-level analysis method as inputs, multivariate methods at group-level can always increase the model performance in activation detection.
Fig. 1. Simulation: Within-group activation detection.
Table 3. Details of methods used to analyze the simulated data at noise fraction of 0.85.
Table 4. AUCs for all analysis methods.
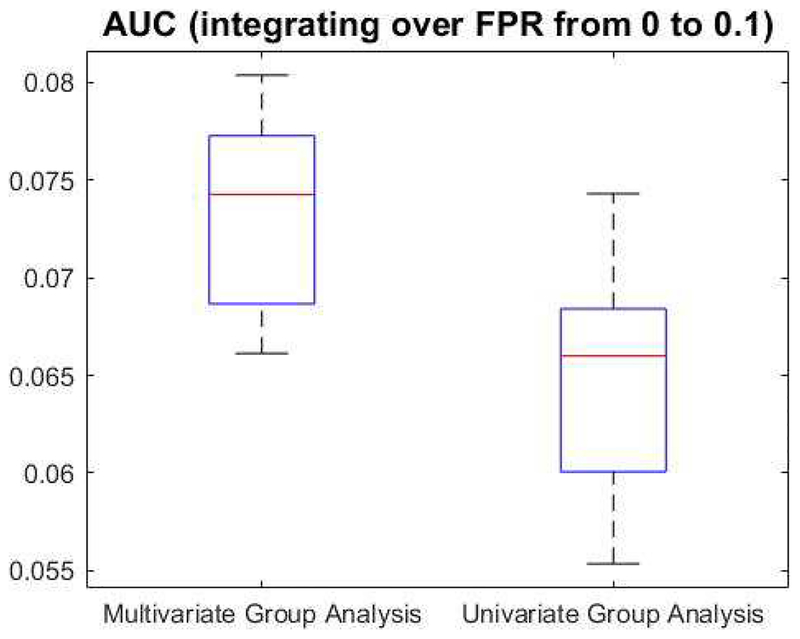
Fig. 2 plots the AUCs computed from univariate (SV+SV) and multivariate (SV+cCCA) group-level analysis methods for 10 different simulated data sets at noise fraction of 0.85. The average AUC is 0.0737 ± 0.0048 for the proposed multivariate group-level method (SV+cCCA) and is 0.0652±0.0057 for the univariate group-level method (SV+SV). Significant between-group difference is observed (p-value=0.0023).
Figure 2.
Significance analysis between multivariate (SV+cCCA) and univariate (SV+SV) group-level analysis methods using simulated data with a noise fraction of 0.85. Areas under the ROC curves (AUCs), integrating over false positive rate (FPR) from 0 to 0.1, are plotted for multivariate (left) and univariate (right) group-level analysis methods. Significant between-group difference is observed (p=0.0023).
Fig. 2 Significance analysis between SV+SV and SV+cCCA methods.
3.2. Episodic memory fMRI data analysis.
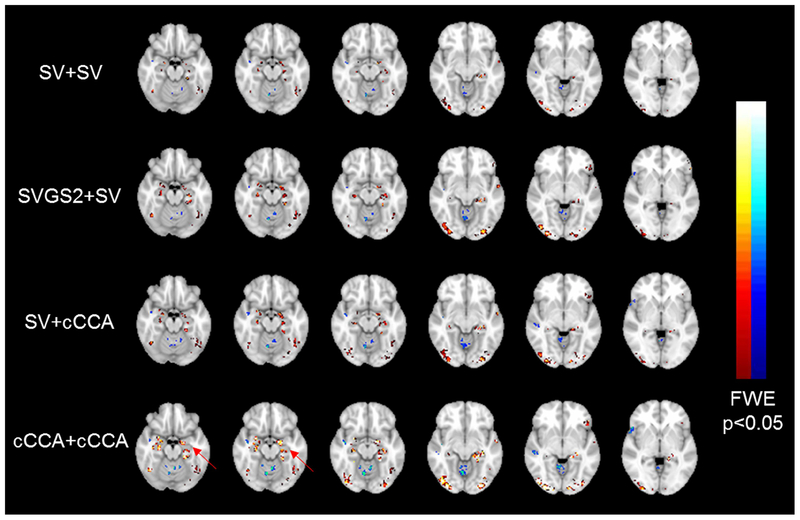
Fig. 3 shows the within-group activation maps of contrast encoding v/s control for the episodic memory task, produced by: 1) subject-level univariate GLM analysis on unsmoothed time series plus group-level univariate summary statistics (SV+SV); 2) subject-level univariate GLM analysis on smoothed time series plus group-level univariate summary statistics (SVGS+SV); 3) subject-level univariate GLM analysis plus group-level multivariate method (SV+cCCA)); and 4) subject-level optimum cCCA model (3D 3×3×3 neighborhood) plus group-level multivariate method (cCCA+cCCA)). The subject-level smoothing kernel size in SVGS+SV is selected to be FWHM= 2mm and is determined from both the simulated data performance and the fMRI raw resolution (1.7×1.7×5mm3).
Figure 3.
Within-group activation map of contrast encoding v/s control, computed for different analysis methods. Selected slices with hippocampus, para-hippocampal areas and fusiform gyrus are shown.
T-statistic described in section 2.1.7 is used to display the activation maps. All activation maps are thresholded at p<0.05 (FWE corrected) and overlaid on the MNI-152 2-mm anatomical template. Selected slices with hippocampus, para-hippocampal areas and fusiform gyrus are shown. Table 5 lists the top 20 AAL regions that have the largest positive activation percentages at the same statistical threshold for all analysis methods. As shown in Fig. 3 and Table 5, the proposed group-level multivariate methods (SV+cCCA and cCCA+cCCA) detect larger and more accurate activations in bilateral hippocampus, bilateral fusiform gyrus and bilateral para-hippocampal areas (highlighted in red in Table 5), as compared to the univariate methods (SV+SV and SVGS+SV). The statistical values are also higher for group-level multivariate methods (highlighted by red arrows in Fig. 3 and in red in Table 5), as compared to the univariate methods.
Table 5.
Top 20 AAL regions with the largest activation percentages, computed for the within-group activation maps of contrast encoding v/s control for different analysis methods, thresholded at p<0.05 and family-wise error rate corrected.
| SV+SV | SVGS2+SV | SV+cCCA | cCCA+cCCA | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AAL region | # of Active voxels | Activation percentage | AAL region | # of Active voxels | Activation percentage | AAL region | # of Active voxels | Activation percentage | AAL region | # of Active voxels | Activation percentage | |
| 1 | Occipital Inf R | 122 | 12.34% | Occipital Inf R | 222 | 22.45% | Occipital Inf R | 184 | 18.60% | Occipital Inf R | 248 | 25.08% |
| 2 | Angular L | 81 | 6.91% | Angular L | 178 | 15.17% | Angular L | 131 | 11.17% | Hippocampus L | 156 | 16.74% |
| 3 | Occipital Inf L | 55 | 5.84% | Occipital Inf L | 106 | 11.26% | Hippocampus L | 87 | 9.33% | Angular L | 183 | 15.60% |
| 4 | Hippocampus L | 54 | 5.79% | Hippocampus L | 102 | 10.94% | Occipital Inf L | 83 | 8.82% | Amygdala L | 27 | 12.27% |
| 5 | Amygdala L | 7 | 3.18% | Amygdala R | 17 | 6.85% | Amygdala L | 12 | 5.45% | Occipital Inf L | 110 | 11.69% |
| 6 | Hippocampus R | 25 | 2.64% | Hippocampus R | 56 | 5.92% | Hippocampus R | 39 | 4.12% | Amygdala R | 23 | 9.27% |
| 7 | Frontal Inf Tri L | 56 | 2.21% | Amygdala L | 13 | 5.91% | Amygdala R | 10 | 4.03% | Hippocampus R | 74 | 7.82% |
| 8 | Cingulate Post L | 10 | 2.16% | Frontal Inf Tri L | 115 | 4.55% | Calcarine L | 74 | 3.28% | ParaHippocampal L | 54 | 5.52% |
| 9 | Amygdala R | 5 | 2.02% | Calcarine L | 100 | 4.43% | Fusiform L | 72 | 3.12% | Calcarine L | 95 | 4.21% |
| 10 | Calcarine L | 43 | 1.90% | Cingulate Post L | 20 | 4.32% | Frontal Inf Tri L | 75 | 2.97% | ParaHippocampal R | 41 | 3.62% |
| 11 | Fusiform L | 39 | 1.69% | Frontal Inf Orb 2 L | 34 | 4.18% | Cingulate Post L | 12 | 2.59% | Frontal Inf Tri L | 79 | 3.12% |
| 12 | Cingulate Mid L | 32 | 1.65% | Fusiform L | 72 | 3.12% | Cingulate Mid L | 42 | 2.16% | Fusiform L | 68 | 2.94% |
| 13 | Fusiform R | 33 | 1.31% | Calcarine R | 48 | 2.58% | Fusiform R | 54 | 2.14% | Cingulate Mid L | 55 | 2.83% |
| 14 | Precuneus L | 45 | 1.28% | Occipital Mid R | 52 | 2.48% | Frontal Inf Orb 2 L | 15 | 1.84% | Fusiform R | 67 | 2.66% |
| 15 | Frontal Inf Orb 2 L | 6 | 0.74% | Fusiform R | 61 | 2.42% | Precuneus L | 59 | 1.67% | Frontal Sup Medial L | 67 | 2.24% |
| 16 | ParaHippocampal R | 8 | 0.71% | Cingulate Mid L | 47 | 2.42% | Vermis 7 | 3 | 1.55% | Frontal Inf Orb 2 L | 18 | 2.21% |
| 17 | Frontal Sup 2 L | 31 | 0.64% | Frontal Sup Medial L | 61 | 2.04% | ParaHippocampal L | 14 | 1.43% | Frontal Sup 2 L | 96 | 1.97% |
| 18 | Frontal Sup Medial L | 18 | 0.60% | ParaHippocampal L | 19 | 1.94% | Frontal Sup 2 L | 61 | 1.25% | Precuneus L | 59 | 1.67% |
| 19 | Temporal Inf L | 18 | 0.56% | Frontal Sup 2 L | 88 | 1.81% | ParaHippocampal R | 12 | 1.06% | Vermis 7 | 3 | 1.55% |
| 20 | Frontal Mid 2 L | 25 | 0.55% | Precuneus L | 62 | 1.76% | Frontal Sup Medial L | 30 | 1.00% | Cerebelum Crus2 R | 28 | 1.32% |
Fig. 3. Within-group activation map of contrast encoding v/s control, computed for different analysis methods.
Table 5. Top 20 AAL regions with the largest activation percentages, computed for the Within-group activation maps of contrast encoding v/s control with different analysis methods.
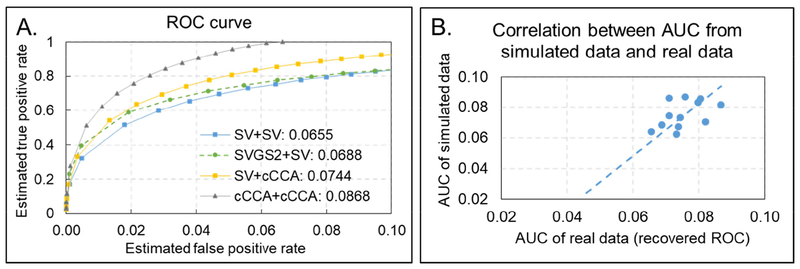
Fig. 4(A) plots the modified ROC curves for these four analysis methods. Areas under the modified ROC curves (AUCs), integrated of FPR from 0 to 0.1, are listed in Table 6. As shown in Table 6, applying group-level multivariate method (SV+cCCA) increases the AUC by 14%, as compared to univariate analysis at both levels (SV+SV). Applying both level multivariate analysis methods (cCCA+cCCA) further increases the AUC by another 16%.
Figure 4.
(A). Modified ROC curves for different analysis methods. Areas under modified ROC curves, integrated over FPR ∊ [0, 0.1] for each method are listed in the legend. (B). Correlation between the sequence of AUC computed from simulated data and real fMRI data.
Table 6.
Smoothing kernel sizes (column 2), subject-level (column 3) and group-level (column 4) analysis methods used in real fMRI data analysis and the corresponding AUCs (column 5) computed from the modified ROC curve for each method.
| Analysis method | Subject-level smoothing kernel size (FWHM) | Subject-level analysis method | Group-level analysis method | Area under the modified ROC curve of real data (integrating over FPR ∈ [0,0.1]) |
|---|---|---|---|---|
| SV + SV | 0 mm | Univariate | Univariate | 0.0655 |
| SV + cCCA | 0 mm | Univariate | Multivariate Method | 0.0744 |
| cCCA+ SV | 0 mm | Sum-cCCA | Univariate | 0.0732 |
| cCCA + cCCA | 0 mm | Sum-cCCA | Multivariate Method | 0.0868 |
| SV_GSs2 + SV | 2 mm | Univariate | Univariate | 0.0688 |
| SV_GSs4 + SV | 4 mm | Univariate | Univariate | 0.0709 |
| SV_GSs6 + SV | 6 mm | Univariate | Univariate | 0.0739 |
| SV + Fisher | 0 mm | Univariate | Fisher’s data fusion | 0.0459 |
Furthermore, all analysis methods listed in Table 3 are applied to real fMRI data and each method generate a within-group activation map. Table 6 lists details of each method and corresponding AUCs computed from the modified ROC curves. As shown in Fig. 4(B) and Table 6, we obtain a Pearson correlation of 0.92 (p-value=0.001) between sequence of AUCs computed from the simulated data at the noise fraction 0.85 and sequence of AUCs computed from the real fMRI data. This high positive correlation demonstrates the linear dependence between the performance of the proposed method in analyzing real fMRI data and simulated pseudo-real data, further validating the simulation method and the proposed analysis method.
Fig. 4. (A) Modified ROC curves for real fMRI data and (B) correlation between the sequences of AUCs computed from simulated and real data.
Table 6. Area under the modified ROC curve, integrated over FPR ∈ [0, 0.1] for eachanalysis method.
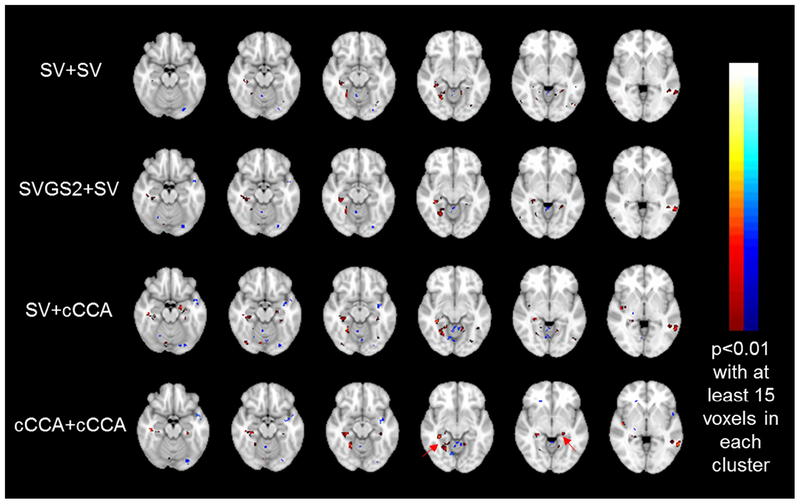
Fig. 5 shows the between-group difference maps (NC v/s MCI) for the contrast encoding v/s control, computed for univariate summary statistics (SV+SV and SVGS+SV,) and proposed multivariate group-level methods (SV+cCCA and cCCA+cCCA). T-statistics maps, thresholded at p<0.01(uncorrected) with at least 15 voxels in each cluster, are shown. Activation percentages for each AAL region at the same thresholds are listed in Table 7. Larger between-group differences are seen in hippocampus and fusiform gyrus (Table 7) using the multivariate group-level analysis method, as compared to the univariate methods. The statistical values are also higher in the multivariate group-level methods (see red arrows in Fig. 5), as compared to the univariate methods.
Figure 5.
Between-group difference map (NC v/s MCI) for contrast encoding v/s control, computed for different analysis methods. Selected slices with hippocampus, para-hippocampal area and fusiform gyrus are shown.
Table 7.
Top 20 AAL regions with the largest between-group difference (in percent), computed for the between-group difference maps of contrast encoding v/s control for different analysis methods, thresholded at p<0.01 with at least 15 voxels in each cluster.
| SV+SV | SVGS2+SV | SV+cCCA | cCCA+cCCA | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AAL region | # of Active voxels | Activation percentage | AAL region | # of Active voxels | Activation percentage | AAL region | # of Active voxels | Activation percentage | AAL region | # of Active voxels | Activation percentage | |
| 1 | Cerebelum 9 R | 43 | 5.32% | Cerebelum 9 R | 67 | 8.28% | Cerebelum 9 R | 83 | 10.26% | Cerebelum 9 R | 91 | 11.25% |
| 2 | ParaHippocampal R | 43 | 3.80% | ParaHippocampal R | 77 | 6.80% | ParaHippocampal R | 74 | 6.54% | ParaHippocampal R | 72 | 6.36% |
| 3 | Cerebelum 7b R | 15 | 2.81% | Parietal Sup L | 113 | 5.47% | Fusiform R | 123 | 4.88% | Hippocampus R | 44 | 4.65% |
| 4 | Occipital Sup R | 38 | 2.69% | Occipital Sup R | 65 | 4.60% | Cerebelum 9 L | 37 | 4.26% | Cerebelum 9 L | 40 | 4.60% |
| 5 | Occipital Inf L | 19 | 2.02% | Cerebelum 7b R | 21 | 3.93% | Hippocampus R | 39 | 4.12% | Fusiform R | 111 | 4.41% |
| 6 | Occipital Mid L | 66 | 2.02% | Occipital Mid L | 125 | 3.82% | Hippocampus L | 30 | 3.22% | Paracentral Lobule R | 29 | 3.47% |
| 7 | Frontal Inf Tri R | 41 | 1.91% | Hippocampus R | 35 | 3.70% | Occipital Mid L | 100 | 3.06% | Occipital Sup R | 49 | 3.47% |
| 8 | Supp Motor Area L | 40 | 1.86% | Fusiform R | 80 | 3.18% | Paracentral Lobule R | 25 | 2.99% | Occipital Mid L | 95 | 2.91% |
| 9 | Temporal Mid L | 82 | 1.66% | Cerebelum 9 L | 22 | 2.53% | Frontal Inf Tri R | 59 | 2.74% | Occipital Mid R | 53 | 2.53% |
| 10 | Lingual R | 38 | 1.65% | Lingual R | 49 | 2.13% | Occipital Sup R | 37 | 2.62% | Supp Motor Area L | 54 | 2.52% |
| 11 | Cerebelum 9 L | 14 | 1.61% | Occipital Mid R | 43 | 2.05% | Supp Motor Area L | 54 | 2.52% | Cerebelum Crus2 R | 53 | 2.50% |
| 12 | Occipital Mid R | 29 | 1.38% | Frontal Inf Tri R | 42 | 1.95% | Lingual R | 53 | 2.30% | Frontal Inf Tri R | 53 | 2.46% |
| 13 | Fusiform R | 34 | 1.35% | ParaHippocampal L | 19 | 1.94% | Temporal Mid L | 111 | 2.25% | Hippocampus L | 18 | 1.93% |
| 14 | Parietal Sup L | 25 | 1.21% | Temporal Mid L | 92 | 1.86% | Insula R | 38 | 2.15% | Parietal Sup L | 39 | 1.89% |
| 15 | Frontal Sup 2 L | 57 | 1.17% | Parietal Sup R | 39 | 1.76% | Occipital Mid R | 40 | 1.91% | Cerebelum Crusl R | 50 | 1.89% |
| 16 | Lingual L | 24 | 1.15% | Supp Motor Area L | 35 | 1.63% | Occipital Inf L | 17 | 1.81% | Temporal Mid L | 91 | 1.84% |
| 17 | Calcarine L | 24 | 1.06% | Occipital Sup L | 20 | 1.46% | Frontal Sup 2 L | 83 | 1.70% | Lingual R | 41 | 1.78% |
| 18 | ParaHippocampal L | 10 | 1.02% | Lingual L | 27 | 1.29% | Cerebelum Crus2 R | 34 | 1.61% | Frontal Sup 2 L | 85 | 1.74% |
| 19 | Hippocampus R | 9 | 0.95% | Rolandic Oper R | 12 | 0.90% | Cerebelum 7b R | 8 | 1.50% | Insula R | 30 | 1.69% |
| 20 | Rolandic Oper R | 10 | 0.75% | Calcarine L | 20 | 0.89% | Lingual L | 30 | 1.43% | ParaHippocampal L | 14 | 1.43% |
Fig. 5. Between-group difference map (NC v/s MCI) for contrast encoding v/s control, computed with different analysis methods.
Table 7. Top 20 AAL regions with the largest between-group difference (in percent), computed for the between-group difference maps of contrast encoding v/s control with different analysis methods.
4. Discussion
This study introduces a constrained multivariate model for group-level analysis and shows that it provides improved detection of activations. The proposed method incorporates local neighboring voxels with optimal spatial weights to determine group activations. The proposed method simultaneously estimates spatial weights and group-level effect and variance using numerical optimization techniques. The group-level cCCA model is validated by both simulation studies (Fig. 1, 2, Table 3 and 4) and real episodic memory fMRI data for 8 aMCI subjects and 8 NCs (Fig. 3, 4 and Table 5, 6 and 7). Results demonstrate superior performance of the group-level cCCA model over univariate analysis methods.
4.1. Performance of group-level cCCA model.
The proposed cCCA model is compared to two widely used group analysis methods, namely the univariate summary statistics (Friston et al., 2005; Holmes and Friston, 1998) and Fisher’s data fusion method (Fisher, 1992).
4.1.1. Simulated data.
The comparison is first done using unsmoothed simulated data where the ground truth is known. Specifically, the univariate GLM analysis is performed at subject-level using unsmoothed time series. The effect and its variance map were then input to the group analysis and the group-level activation status of the center voxel within each simulated 5×5 neighborhood were computed with different analysis methods. We computed the area under the ROC curves (AUC), integrated over false positive rate (FPR) ∊ [0, 0.1], which is a range that is most important in fMRI activation detection to provide a quantitative measurement of the overall model performance for method SV+SV, SV+cCCA and SV+Fisher. As shown by the solid blue (SV+SV), solid yellow (SV+cCCA) and dashed brown(SV+Fisher) curves in Fig. 1(C), all three methods show decent performance with AUC close to 0.1 for high SNRs (f <0.6, Fig. 1(C)). Incorporating neighboring voxels in this case would not provide much additional improvements because the SNR is already high. As the noise level increases in the simulated data (f >0.8), univariate methods (SV+SV) lose sensitivity in activation detection, as indicated by a decreasing AUC (solid blue curve in Fig. 1(C)). On the contrary, the proposed multivariate method still shows high AUC (solid yellow curve in Fig. 1(C)) since incorporating local neighboring information increases the sensitivity of activation detection while the constraint in the model preserves the specificity of activation detection. This improvement in AUC of SV+cCCA method is significant as compared to the SV+SV (p<0.005), as plotted in Fig. 2. Furthermore, Fisher’s data fusion starts performing poorly at lower noise levels (f>0.65, dashed brown curve in Fig. 1(C)), mainly due to the way independent tests for each subject are combined. The null hypothesis of no effect in all subjects in this case could be easily rejected on the basis of a nonzero effect in just one subject (Lazar et al., 2002). More specifically, if the p-value is large (near 1) for some subjects, then the combined tF is close to zero and the value of the statistic is nearly unchanged. If the p-value is small (close to 0) on the other hand, a small change of p-value in a single subject will affect the combined statistics potentially leading to false positives.
We next compare the proposed multivariate group analysis method (SV+cCCA) with the univariate methods using smoothed simulated time series (SVGS+SV). Specifically, for SVGS+SV, neighboring voxels were incorporated at subject-level with an isotropic Gaussian smoothing kernel. Multiple kernel sizes were used in our analysis to conduct a thorough comparison. As shown in Fig. 1(C), applying Gaussian smoothing with proper kernel sizes (FWHM=2mm and 4mm) at subject-level analysis can improve the AUC of the group-level univariate method at high noise levels (f>0.8, dashed purple curve). Furthermore, an extended isotropic smoothing kernel (FWHM=6mm) may decrease the activation detection power at medium to high noise levels (0.55<f<0.95), as indicated by the dashed dark blue curve in Fig. 1(C)). The proposed constrained multivariate method optimizes the weights of incorporated neighboring voxels at group-level so that a common neighborhood configuration that matches actual spatial activation patterns among all subjects can be determined, especially for fMRI data with high noise fractions. Therefore, as shown by the solid yellow curve in Fig. 1(C), the proposed method improves the group-level activation detection performance at high noise levels (f>0.8), as compared to SVGS+SV.
We further compare the performance of SVGS+cCCA and SVGS+SV using simulated data with the noise fraction of 0.85. As listed in Table 4, with effect and variance maps from the same subject-level analysis method as inputs, multivariate group-level analysis method (last column) always outperforms univariate methods (3rd and 4th columns) since incorporating neighboring voxels in this case improves the sensitivity in group-level activation detection. At the same time, the constraint put in the multivariate method guarantees the dominance of the center voxel in each local neighborhood so that the smoothing artifact is limited.
Previous studies have shown that in subject-level activation detection, the local cCCA method optimizes weights of incorporated neighboring voxels and therefore outperforms univariate methods with or without Gaussian smoothing (Cordes et al., 2012; Zhuang et al., 2017). The optimum performance of the subject-level cCCA has also been demonstrated in our analysis using group-level activation detection. As shown by the orange curve in Fig. 1(C), applying constrained multivariate method at subject-level (cCCA+SV) also improves the group-level activation detection performance, as compared to SV+SV and SVGS+SV. Furthermore, applying both level constrained multivariate analysis methods (cCCA+cCCA) will further increase the AUC at high noise levels (f >0.8, solid grey curve in Fig. 1(C)), since subject-level cCCA optimizes weights of neighboring voxels to match subject-specific activation patterns and group-level constrained multivariate method determines an optimum neighborhood configuration that matches common activation patterns among all subjects.
In summary, applying constrained multivariate methods at group-level analysis will incorporate the local spatial activation information while keep the appropriate dominance of the center voxel; therefore are able to more accurately detect activations in noisy data, as compared to the univariate analysis methods with the same subject-level inputs.
4.1.2. Episodic memory activation.
Within-group activation detection.
We compared the selected univariate and multivariate methods using real fMRI data of an episodic memory task, namely: SV+SV, SVGS+SV, SV+cCCA and cCCA+cCCA. We set the size of the isotropic Gaussian smoothing kernel during preprocessing for SVGS+SV method to be FWHM=2mm for our episodic memory task data. We choose this conservative smoothing kernel size because 1) simulation results have demonstrated an optimum performance of SVGS2+SV, as compared to SV+SV; and 2) the targeted activated medial temporal regions are with thin cortical thicknesses and folded grey-matter structures; therefore an extended isotropic smoothing kernel may contaminate activated voxels in this area with nearby non-grey matter structures and further eliminate the detection of activation or produce false positives in nearby non-grey matter regions. Furthermore, we set the window-size for multivariate group-level analysis to be 3×3×3 based on the fMRI resolution and to incorporate only the nearest neighbors. This 3D 3×3×3 window-size is also comparable with the Gaussian smoothing kernel size (FWHM=2mm) in SVGS2+SV. In addition, an optimum cCCA model determined in (Zhuang et al., 2017) is used for subject-level analysis in cCCA+cCCA.
We have repeated the group-level multivariate method with a 3D 5×5×5 spatial neighborhood using real fMRI data. We would like to test if a 3D 5×5×5 spatial neighborhood could further improve the model performance on real fMRI data and therefore, the first level analysis remains the constrained cCCA method. The computation time doubled with this larger neighborhood (will be further discussed in section 4.3). Greater activations have been observed in the targeted medial temporal lobe, as compared to the analysis with cCCA+cCCA method with 3×3×3 neighborhood. The area under the modified ROC curve, integrated from FPR 0 to 0.1, is 0.0886, which shows a further increase of 2%, as compared to cCCA+cCCA method with 3×3×3 neighborhood. Therefore, in joint consideration of model performance improvement and computation time increase, we have reported results of cCCA+cCCA method with 3×3×3 neighborhood on real fMRI data in this manuscript.
Episodic memory is a type of declarative memory that involves conscious recollection of previous experiences together with their context in terms of time, place, and associated emotions (https://en.wikipedia.org/wiki/Episodic memory). Previous studies have shown that episodic memory is facilitated by neural pathways in the medial temporal lobe (MTL), which includes hippocampus, para-hippocampal areas and other nearby regions (Squire et al., 2004; Zeineh et al., 2003a). In particular, using a face-name encoding and retrieval task, Zeineh et al. (2003) have shown that strong activation can be detected in hippocampal sub-regions including Cornu Ammonis (CA) fields and Dentate Gyrus (DG) during encoding while fusiform is active regardless of encoding and retrieval. Therefore, regions of activation during a face-occupation memory task should involve bilateral hippocampus, para-hippocampal areas and fusiform gyrus (pointed to in Fig. 3 and highlighted in red in Table 5). However, activation detection in these regions is often complicated due to the low SNR caused by susceptibility artifacts and the anatomically small size of hippocampal subfields. As can be seen from Fig. 3 and Table 5, univariate summary statistics (SV+SV) detects less active voxels and misses part of the activations in hippocampus or para-hippocampal areas at a significance level of p<0.05 (FWE corrected). SVGS+SV detects large activations in bilateral hippocampus, bilateral fusiform gyrus, but misses part of the activations in para-hippocampal area. Both SV+cCCA and cCCA+cCCA find bilateral hippocampus, bilateral fusiform gyrus and bilateral para-hippocampal areas within the top 20 activated regions, which is more accurate and as expected in our memory task. In addition, activations in other brain regions such as occipital areas involved in visual processes and frontal areas involved in cognitive process are also better detected with the proposed method (column 3 and 4 in Table 5), as compared to univariate methods (column 1 and 2 in Table 5).
Furthermore, the modified ROC curve provides a more comprehensive way to make comparisons among all analysis methods at multiple sensitivity and specificity levels. The multivariate method incorporates multiple time series with optimal weights in each local neighborhood and is thus more sensitive to detect activations. On the other hand, the constraint term in the cCCA model reduces the extra degrees of freedom introduced by the multivariate method and therefore preserves specificity at the same time. In this case, as shown in Fig. 4(A), applying both level multivariate analysis methods (cCCA+cCCA) improves the sensitivity (TPR) extensively at a given specificity (1-FPR), as compared to SV+SV and SVGS+SV.
We further computed the area under the ROC curves (AUC) by integrating FPR from 0 to 0.1, as a quantitative measurement to compare different methods. As shown in Fig. 4(B), a significant linear dependency (p=0.001) between sequences of AUCs computed from simulated data and real fMRI data has been observed, which validates the conclusion we draw from the comparisons using simulated data. Based on our observations, we expect that the proposed method will detect group-level activations more accurately in noisy fMRI data.
We included all 16 subjects (8 NC and 8 MCI) for within-group activation detection to obtain a larger sample size with increased power of activation detection. We also computed the within-group activation maps for all three analysis methods for the NC group and the aMCI group separately. For both groups, we observe more activations in hippocampus, para-hippocampal areas and other medial temporal lobe regions using the proposed method when compared to the univariate summary statistics method.
Between-group difference detection.
Previous studies on MTL functional changes in MCI subjects reported diverse results, with either increased MTL activation found during encoding and retrieval phases (Dickerson et al., 2005; Selkoe et al., 2006) or hypoactivation in MTL regions reported (Machulda et al., 2003) in MCI subjects. In this study, we observe less activation in MTL regions for the contrast encoding v/s control during the episodic memory task in MCI subjects, as compared to the normal subjects. These observations are consistent with results in Jin et al. (2012), where functional abnormalities in the same set of amnestic MCI subjects during three different episodic memory tasks (word-name, picture-name and face-occupation) are reported. More importantly, in this study, a between-group analysis is conducted to compare performances in cross-group difference detection between the proposed method and univariate methods. As shown in Fig. 5 and Table 7, greater between-group differences are found in MTL regions with the proposed multivariate method, as compared to univariate methods.
4.2. Other multivariate modeling methods in group analysis.
In the past decade, multivariate pattern analysis (MVPA) has become one of the most popular multivariate modeling methods in fMRI analysis (Allefeld and Haynes, 2014; Haxby, 2012; Haxby et al., 2001). MVPA examines several voxels simultaneously but the signs of the contrast for each individual subject are neglected. A classification process is then carried out for multiple subjects. Therefore, MVPA is different from the methods proposed and described in this study since our proposed method can detect both within-group activations and between-group differences.
Gilron et al. (2017) proposed a directional MVPA to detect similar multivariate spatial patterns of activity over subjects. In their method, the Srivastava-Du (2008) statistic is used for directional analysis at the group-level and common differences between two effects are being detected. Both directional MVPA and the proposed multivariate model are related to searchlight (Allefeld and Haynes, 2014; Kriegeskorte et al., 2006) methods that incorporates local neighborhood information in the group-level analysis. The statistics in the directional MVPA is not adjusted by the variance at the single subject-level and may suffer from power losses (Gilron et al., 2017). We applied the directional MVPA method to simulated data (SV+MVPA) at noise fraction of 0.85 and obtained an AUC of 0.0718 by integrating FPR from 0 to 0.1. MVPA in group-level analysis (SV+MVPA) slightly improves the performance in activation detection, as compared to SV+SV (with AUC of 0.0712) but is still less accurate than proposed multivariate methods (SV+cCCA, with AUC of 0.0790). Furthermore, the statistic used in the proposed cCCA model is easier to compute and statistically significant levels in the proposed method are determined non-parametrically, which are more accurate and easier to interpret.
Kriegeskorte et al. (2006) introduced a searchlight based MVPA method, which is known as information-based functional brain mapping method, to determine the subject-level center voxel activation status by incorporating information from the local neighborhood. We applied the Kriegeskorte’s searchlight method to group-level analysis using the Mahalanobis distance defined as: , where represents estimated subject-level effects of a local neighborhood (with q voxels) from Nsub subjects, and represents the average estimated effects (over subjects) of this local neighborhood. Applying the Kriegeskorte’s searchlight method to simulated data (SV+Kriegeskorte’s MVPA) at noise fraction of 0.85 with a 3×3 window gives an AUC of 0.0738 by integrating FPR from 0 to 0.1. Kriegeskorte’s searchlight in group-level analysis (SV+Kriegeskorte’s MVPA) improves the performance in activation detection, as compared to SV+SV (with AUC of 0.0712); and is comparable to the performance of SVGS2+SV (with AUC of 0.0745); but is still less accurate than the proposed multivariate method (SV+cCCA, with AUC of 0.0790). Both MVPA methods in Gilron et al. (2017) and Kriegeskorte et al. (2006) incorporate neighboring voxels with equal weights. Therefore, for an active center, both inactive neighbors and active neighbors are treated equivalently. In this case, the effect of incorporating neighboring voxels is similar to apply a smoothing kernel but adjusted for the spatial noise covariance. In the proposed cCCA method, however, neighboring voxels are incorporated with optimum weights, so that active neighboring voxels could contribute greater to the statistics of the active center voxel, as compared to the inactive neighbors. Therefore, the proposed method outperforms both searchlight-based MVPAs.
Correa et al. (2010) proposed a multiset-CCA (mCCA) method to analyze multiple data set for a single modality for group inferences. In their method, similar to widely used independent component analysis (ICA, Calhoun et al., 2001) method, fMRI time series from all subjects are stacked together and blind-source-separation based on mCCA is performed. The resulting group inferences are group source components with the maximal between-set correlation values. In this case, the mCCA model is a data decomposition method whereas the proposed cCCA model is a data modeling technique.
4.3. Technical aspects of multivariate group-level analysis.
Group-level multivariate analysis is different from subject-level cCCA.
In this study, we modeled and solved the group-level multivariate problem based on the maximum log likelihood method by considering the joint distribution of all unknowns, which is different from the traditional CCA (Friman et al., 2001; Hotelling, 1936) that maximizes the correlation between two canonical variables (ρ(Yα,Xβ) in Eq. (15)). The design matrix in group-level cCCA (Xg) is a constant vector with all ones for within-group activation detection, which is rank deficient and leads to a covariance of zero. In this case, maximizing ρ(Yα,Xβ) is not possible. Cordes et al.(2012) proves that the CCA model can be converted into an equivalent multivariate multiple regression problem under proper normalization terms (var(Yα) = 1). In this study, we utilized the same concept by forming a multiple regression problem and introduced α as an unknown multivariate vector that incorporates neighboring voxels in the model. In this case, the estimated group-inference is not scale invariant among different voxel configurations and therefore, a proper normalization term is necessary. Group-level activation status, optimum weights of neighboring voxels (α) and the group-level variance are estimated simultaneously.
Computational time.
All calculations are performed in MATLAB (The Mathworks, Inc., version R2018b) on a Dell-workstation with Intel Xeon E5–2687W architecture running at a clock speed of 3.4GHz and equipped with 96GB of memory. Under this hardware setting, the average computational time for SV+cCCA method with a 2D 3×3 window to detect the group-level whole brain activation is around 600 seconds. Extending the window-size to 3D 3×3×3 takes around 1000 seconds to finish a whole brain multivariate group-level analysis. Further increasing the window-size to a 3D 5×5×5 neighborhood doubles the computation time, as compared to the 3×3×3 neighborhood size. Applying both level multivariate methods (cCCA+cCCA) requires a longer computational time since the subject-level cCCA model takes about 600 seconds (1000 seconds for 3D window) per subject. In this case, cCCA+cCCA needs 600 × (Nsub + 1) seconds to compute one group activation map. The computational time of cCCA+cCCA needs to be taken into consideration when selecting the analysis method, because the statistical significance needs to be determined non-parametrically.
4.4. Future directions.
In this study, we have tested the performance of a local cCCA model using 3×3×3 in-plane neighborhoods for group-level analysis. CCA can link multiple datasets by maximizing the correlation among canonical components. We have not tested these algorithms in multiple groups. In the future, performance of combining cCCA modeling technique and a mCCA data fusion method will also be evaluated for group-level analysis.
Furthermore, as we stated above, the group-level design matrix Xg for within-group activation detection is rank deficient, which limits the usage of kernel based cCCA methods (Yang et al., 2018) in group-level analysis. In the future, for within-group activation detection, we could form a second group using wavelet resampled resting-state time series. In that case, the null hypothesis will be to detect the differences between the real task group and the null group and the design matrix will be a binary matrix with two columns of input. Therefore, kernel CCA could also be applied.
5. Conclusion.
We have introduced a constrained multivariate method to incorporate local neighboring voxels for fMRI group-level analysis. Using simulation, we have demonstrated better performance for activation detection of the proposed method over univariate techniques with the same subject-level inputs. Applying the proposed method to real fMRI episodic memory data, larger within-group activation in hippocampus, fusiform gyrus, para-hippocampal areas and stronger between-group differences in hippocampus and fusiform gyrus have been found. Furthermore, we have shown that applying both level constrained multivariate methods further increases the power of group-level activation detection, but also significantly increases the computational time.
6. ACKNOWLEDGEMENTS
This research project was supported by the NIH (grant 1R01EB014284 and COBRE grant 5P20GM109025), a private grant from Peter and Angela Dal Pezzo, and the Young Scientist Award at Cleveland Clinic Lou Ruvo Center for Brain Health. We also would like to thank the anonymous reviewers for their helpful comments, which have allowed us to significantly improve our manuscript.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Adleman NE, Menon V, Blasey CM, White CD, Warsofsky IS, Glover GH, Reiss AL, 2002. A developmental fMRI study of the Stroop color-word task. Neuroimage 16, 61–75. 10.1006/nimg.2001.1046 [DOI] [PubMed] [Google Scholar]
- Allefeld C, Haynes JD, 2014. Searchlight-based multi-voxel pattern analysis of fMRI by cross-validated MANOVA. Neuroimage 89, 345–357. 10.1016/j.neuroimage.2013.11.043 [DOI] [PubMed] [Google Scholar]
- Beckmann CF, Jenkinson M, Smith SM, 2003. General multilevel linear modeling for group analysis in FMRI. Neuroimage 20, 1052–1063. 10.1016/S1053-8119(03)00435-X [DOI] [PubMed] [Google Scholar]
- Breakspear M, Brammer MJ, Bullmore ET, Das P, Williams LM, 2004. Spatiotemporal wavelet resampling for functional neuroimaging data. Hum. Brain Mapp 23, 1–25. 10.1002/hbm.20045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buxton RB, 2009. Introduction to functional magnetic resonance imaging: principles and techniques. Cambridge university press. [Google Scholar]
- Calhoun VD, Adali T, Pearlson GD, Pekar JJ, 2001. Spatial and temporal independent component analysis of functional MRI data containing a pair of task-related waveforms. Hum. Brain Mapp 13, 43–53. 10.1002/hbm.1024 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordes D, Jin M, Curran T, Nandy R, 2012. Optimizing the performance of local canonical correlation analysis in fMRI using spatial constraints. Hum. Brain Mapp 33, 2611–2626. 10.1002/hbm.21388 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Correa NM, Adali T, Li Y, Calhoun VD, 2010. Canonical Correlation Analysis for Data Fusion and Group Inferences. IEEE Signal Process Mag 27, 39–50. 10.1109/MSP.2010.936725.Canonical [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dickerson BC, Salat DH, Greve DN, Chua EF, Rentz DM, Bertram L, Mullin K, Tanzi RE, Blacker D, Albert MS, Sperling RA, 2005. Increased hippocampal activation in mild cognitive impairment compared to normal aging and AD 404–411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferreira da Silva AR, 2011. A Bayesian multilevel model for fMRI data analysis. Comput. Methods Programs Biomed 102, 238–252. 10.1016/j.cmpb.2010.05.003 [DOI] [PubMed] [Google Scholar]
- Fisher RA, 1992. Statistical methods for research workers, in: Breakthroughs in Statistics. Springer, pp. 66–70. [Google Scholar]
- Friman O, Borga M, Lundberg P, Knutsson H, 2003. Adaptive analysis of fMRI data. Neuroimage 19, 837–845. 10.1016/S1053-8119(03)00077-6 [DOI] [PubMed] [Google Scholar]
- Friman O, Borga M, Lundberg P, Knutsson H, 2002. Detection of neural activity in fMRI using maximum correlation modeling. Neuroimage 15, 386–395. 10.1006/nimg.2001.0972 [DOI] [PubMed] [Google Scholar]
- Friman O, Cedefamn J, Lundberg P, Borga M, Knutsson H, 2001. Detection of neural activity in functional MRI using canonical correlation analysis. Magn. Reson. Med 45, 323–330. [DOI] [PubMed] [Google Scholar]
- Friston KJ, 2011. Functional and Effective Connectivity: A Review. Brain Connect. 1, 13–36. 10.1089/brain.2011.0008 [DOI] [PubMed] [Google Scholar]
- Friston KJ, Fletcher P, Josephs O, Holmes A, Rugg MD, Turner R, 1998. Event - Related fMRI: Characterizing Differential Responses. Neuroimage 7, 30–40. 10.1006/nimg.1997.0306 [DOI] [PubMed] [Google Scholar]
- Friston KJ, Glaser DE, Henson RNA, Kiebel S, Phillips C, Ashburner J, 2002. Classical and Bayesian inference in neuroimaging: Applications. Neuroimage 16, 484–512. 10.1006/nimg.2002.1091 [DOI] [PubMed] [Google Scholar]
- Friston KJ, Stephan KE, Lund TE, Morcom A, Kiebel S, 2005. Mixed-effects and fMRI studies. Neuroimage 24, 244–252. 10.1016/j.neuroimage.2004.08.055 [DOI] [PubMed] [Google Scholar]
- Gates KM, Molenaar PCM, 2012. Group search algorithm recovers effective connectivity maps for individuals in homogeneous and heterogeneous samples. Neuroimage 63, 310–319. 10.1016/j.neuroimage.2012.06.026 [DOI] [PubMed] [Google Scholar]
- Gilron R, Rosenblatt J, Koyejo O, Poldrack RA, Mukamel R, 2017. What’s in a pattern? Examining the type of signal multivariate analysis uncovers at the group level. Neuroimage 146, 113–120. 10.1016/j.neuroimage.2016.11.019 [DOI] [PubMed] [Google Scholar]
- Haxby JV, 2012. Multivariate pattern analysis of fMRI: The early beginnings. Neuroimage 62, 852–855. 10.1016/j.neuroimage.2012.03.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haxby JV, Gobbini MI, Furey ML, Ishai A, Schouten JL, Pietrini P, 2001. Distrubuted and Overlapping Representations of Face and Objects in Ventral Temporal Cortex. Science (80-.). 293, 2425–2430. 10.1126/science.1063736 [DOI] [PubMed] [Google Scholar]
- Holmes A, Josephs O, Buchel C, Friston K, 1997. Statistical modeling of low- frequency confounds in fMRI. Neuroimage 5. [Google Scholar]
- Holmes AP, Friston KJ, 1998. Generalisability, Random Effects and Population Inference. Neuroimage 7, S754. [Google Scholar]
- Hotelling H, 1936. Relations between two sets of variates. Biometrika 28, 321–377. [Google Scholar]
- Jin M, Pelak VS, Curran T, Nandy RR, Cordes D, 2012. A preliminary study of functional abnormalities in aMCI subjects during different episodic memory tasks. Magn. Reson. Imaging 30, 459–470. 10.1016/j.mri.2011.12.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kriegeskorte N, Goebel R, Bandettini P, 2006. Information-based functional brain mapping. Proc. Natl. Acad. Sci 103, 3863–3868. 10.1073/pnas.0600244103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwong KK, Belliveau JW, Chesler DA, Goldberg IE, Weisskoff RM, Poncelet BP, Kennedy DN, Hoppel BE, Cohen MS, Turner R, 1992. Dynamic magnetic resonance imaging of human brain activity during primary sensory stimulation. Proc. Natl. Acad. Sci. U. S. A 89, 5675–5679. 10.1073/pnas.89.12.5675 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lazar NA, Luna B, Sweeney JA, Eddy WF, 2002. Combining Brains: A Survey of Methods for Statistical Pooling of Information. Neuroimage 16, 538–550. 10.1006/nimg.2002.1107 [DOI] [PubMed] [Google Scholar]
- Li X, Coyle D, Maguire L, McGinnity TM, 2014. Maximum likelihood estimation for second level fMRI data analysis with expectation trust region algorithm. Magn. Reson. Imaging 32, 132–149. 10.1016/j.mri.2013.10.007 [DOI] [PubMed] [Google Scholar]
- Lindquist MA, 2008. The Statistical Analysis of fMRI Data. Stat. Sci 23, 439–464. 10.1214/09-STS282 [DOI] [Google Scholar]
- Lindquist MA, Loh JM, Atlas LY, Wager TD, 2009. Modeling the Hemodynamic Response Function in fMRI: Efficiency, Bias and Mis-modeling. Neuroimage 45, S187–S198. 10.1007/s10955-011-0269-9.Quantifying [DOI] [PMC free article] [PubMed] [Google Scholar]
- Machulda MM, Ward HA, Borowski B, Gunter JL, Cha RH, Brien PCO, Petersen RC, Boeve BF, Knopman D, Wai DFT, Ivnik RJ, Smith GE, Tangalos EG, Jack CR, 2003. Comparison of memory fMRI response among normal, MCI, and Alzheimer’s patients. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nandy R, Cordes D, 2004. Improving the spatial specificity of canonical correlation analysis in fMRI. Magn. Reson. Med 52, 947–952. 10.1002/mrm.20234 [DOI] [PubMed] [Google Scholar]
- Nandy RR, Cordes D, 2004. New approaches to receiver operating characteristic methods in functional magnetic resonance imaging with real data using repeated trials. Magn. Reson. Med 52, 1424–1431. 10.1002/mrm.20263 [DOI] [PubMed] [Google Scholar]
- Nandy RR, Cordes D, 2003. Novel ROC-type method for testing the efficiency of multivariate statistical methods in fMRI. Magn. Reson. Med 49, 1152–1162. 10.1002/mrm.10469 [DOI] [PubMed] [Google Scholar]
- Nichols TE, Holmes APAP, 2002. Nonparametric permutation tests for functional neuroimaging: A primer with examples. Hum. Brain Mapp. 15, 1–25. 10.1002/hbm.1058 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nocedal J, Wright SJ, 2006. Numerical Optimization, Numerical Optimization. Springer. [Google Scholar]
- Nocedal J, Yuan Y, 1998. Combining trust region and line search techniques. Adv. Nonlinear Program. 153–175. [Google Scholar]
- Penny W, Holmes A, 2003. Random-Effects Analysis. Hum. Brain Funct. Second Ed 843–850. 10.1016/B978-012264841-0/50044-5 [DOI] [Google Scholar]
- Petersen RC, Doody R, Kurz A, Mohs RC, Morris JC, Rabins PV, Ritchie K, Rossor M, Thal L, Winblad B, 2001. Current Concepts in Mild Cognitive Impairment. Arch. Neurol 58(12), 1985–1992. [DOI] [PubMed] [Google Scholar]
- Peterson BS, Skudlarski P, Gatenby JC, Zhang H, Anderson AW, Gore JC, 1999. An fMRI study of stroop word-color interference: Evidence for cingulate subregions subserving multiple distributed attentional systems. Biol. Psychiatry 45, 1237–1258. 10.1016/S0006-3223(99)00056-6 [DOI] [PubMed] [Google Scholar]
- Reagh ZM, Yassa MA, 2014. Object and spatial mnemonic interference differentially engage lateral and medial entorhinal cortex in humans. Proc. Natl. Acad. Sci 111, E4264–E4273. 10.1073/pnas.1411250111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Road WP, 1996. AFNI: Software for Analysis and Visualization of Functional Magnetic Resonance Neuroimages 173, 162–173. [DOI] [PubMed] [Google Scholar]
- Selkoe DJ, DePeau K, Sperling RA, Atri A, Blacker D, Rentz DM, Calhoun VD, Celone KA, Dickerson BC, Chua EF, Albert MS, Miller SL, 2006. Alterations in Memory Networks in Mild Cognitive Impairment and Alzheimer’s Disease: An Independent Component Analysis. J. Neurosci 26, 10222–10231. 10.1523/jneurosci.2250-06.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shanno DF, 1985. On broyden-fletcher-goldfarb-shanno method. J. Optim. Theory Appl. 46, 87–94. [Google Scholar]
- Smith SM, Miller KL, Salimi-Khorshidi G, Webster M, Beckmann CF, Nichols TE, Ramsey JD, Woolrich MW, 2011. Network modelling methods for FMRI. Neuroimage 54, 875–891. 10.1016/j.neuroimage.2010.08.063 [DOI] [PubMed] [Google Scholar]
- Squire LR, Stark CEL, Clark RE, 2004. the Medial Temporal Lobe. Annu. Rev. Neurosci 27, 279–306. 10.1146/annurev.neuro.27.070203.144130 [DOI] [PubMed] [Google Scholar]
- Srivastava MS, Du M, 2008. A test for the mean vector with fewer observations than the dimension. J. Multivar. Anal 99, 386–402. 10.1016/j.jmva.2006.11.002 [DOI] [Google Scholar]
- Tzourio-Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, Joliot M, 2002. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage 15, 273–289. 10.1006/nimg.2001.0978 [DOI] [PubMed] [Google Scholar]
- Woolrich MW, Behrens TEJ, Beckmann CF, Jenkinson M, Smith SM, 2004. Multilevel linear modelling for FMRI group analysis using Bayesian inference. Neuroimage 21, 1732–1747. 10.1016/j.neuroimage.2003.12.023 [DOI] [PubMed] [Google Scholar]
- Worsley KJ, Liao CH, Aston J, Petre V, Duncan GH, Morales F, Evans AC, 2002. A general statistical analysis for fMRI data. Neuroimage 15, 1–15. 10.1006/nimg.2001.0933 [DOI] [PubMed] [Google Scholar]
- Yang Z, Zhuang X, Sreenivasan K, Mishra V, Curran T, Byrd R, Nandy R, Cordes D, 2018. 3D spatially-adaptive canonical correlation analysis: Local and global methods. Neuroimage 169, 240–255. 10.1016/j.neuroimage.2017.12.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeineh MM, Engel SA, Thompson PM, Bookheimer SY, 2003a. Dynamics of the Hippocampus during encoding and retrieval of face[ndash]name pairs. Sci 299, 577–580. [DOI] [PubMed] [Google Scholar]
- Zeineh MM, Engel SA, Thompson PM, Bookheimer SY, 2003b. Dynamics of the Hippocampus during encoding and retrieval of face-name pairs. Science (80-.). 299, 577–580. [DOI] [PubMed] [Google Scholar]
- Zhuang X, Yang Z, Curran T, Byrd R, Nandy R, Cordes D, 2017. A family of locally constrained CCA models for detecting activation patterns in fMRI. Neuroimage 149, 63–84. 10.1016/j.neuroimage.2016.12.081 [DOI] [PMC free article] [PubMed] [Google Scholar]