A Wrinkling-Based Method for Investigating Glassy Polymer Film Relaxation as a Function of Film Thickness and Temperature

Abstract

We investigate the relaxation dynamics of thin polymer films at temperatures below the bulk glass transition T_g by first compressing polystyrene films supported on a polydimethylsiloxane substrate to create wrinkling patterns, and then observing the slow relaxation of the wrinkled films back to their final equilibrium flat state by small angle light scattering. As with recent relaxation measurements on thin glassy films reported by Fakhraai and coworkers, we find the relaxation time of our wrinkled films to be strongly dependent on film thickness below an onset thickness on the order of 100 nm. By varying the temperature between room temperature and T_g (≈ 100 °C), we find that the relaxation time follows an Arrhenius-type temperature dependence to a good approximation at all film thicknesses investigated, where both the activation energy and the relaxation time pre-factor depend appreciably on film thickness. The wrinkling relaxation curves tend to cross at a common temperature somewhat below T_g, indicating an entropy-enthalpy compensation relation between the activation free energy parameters. This compensation effect has also observed recently in simulated supported polymer films in the high temperature Arrhenius relaxation regime rather than the glassy state. In addition, we find that the film stress relaxation function, as well as the height of the wrinkle ridges, follow a stretched exponential time dependence and the short-time effective Young’s modulus derived from our modeling decreases sigmoidally with increasing temperature—both characteristic features of glassy materials. The relatively facile nature of the wrinkling-based measurements in comparison to other film relaxation measurements makes our method attractive for practical materials development, as well as fundamental studies of glass formation.

I. INTRODUCTION

Understanding the properties of nanoscale thin polymer films is imperative to material design in many emerging nanotechnologies. A large body of evidence indicates that the properties of thin polymer films can differ markedly from their bulk counterparts,^1,2,3where the scale at which these changes in properties occur (e.g., glass transition temperature, glassy modulus) is typically on the order of 100 nm.^4,5 Unfortunately, there are limited direct measurements on the relaxation of glassy polymer films since the long time-scales involved make many experimental methods unsuitable.

Fakhraai and coworkers have made significant progress on this problem by developing new experimental methods for studying slow relaxation processes in both polymeric^6,7,8,9 and non-polymeric films.^10,11 Their measurements were primarily based on two methods: hole-filling of nano-indentations produced by nanoparticle embedding and dissolution, and ellipsometric determination of the glass transition temperature. More recently, the dynamics of thin glassy film was determined by measuring the rate of film dewetting as function of film thickness and temperature.¹⁰ Despite the rather dissimilar nature of these measurements, they collectively revealed a rather general pattern of thin film relaxation below the bulk glass transition temperature (T_g). First, the relaxation processes were found to be nearly Arrhenius, as noted in previous bulk measurements on glassy materials below T_g,^12,13 and the activation energy for relaxation decreased in a sigmoidal fashion as the film thickness was reduced, reaching a value near zero for the thinnest films. They also observed that the Arrhenius relaxation curves have the striking property of intersecting near a common temperature that is somewhat below the bulk T_g.^7,9,10 The intersection of relaxation curves in this fashion is termed ‘entropy-enthalpy compensation’, and implies that the entropy and enthalpy of activation vary in a proportional fashion.^14,15 Entropy-enthalpy compensation has also recently been observed in simulations of thin polymer films as a function of film thickness in the high temperature fluid regime where the polymer dynamics again becomes Arrhenius.¹⁶ This correspondence is natural since the string model of relaxation indicates that the high and low temperature activation free energy parameters are typically related by a factor of 4 to 5.¹⁷ Hanakata et al.15^,18,19 attribute this change in activation energy to a reduction in the cohesive interaction with geometrical confinement and the effect of the polymer-substrate interactions, the basic physical origin of the shift of the melting point of materials with confinement, i.e., the Gibbs-Thompson effect.²⁰ Hanakata et al.^15,18 also suggest that shifts in T_g and other film properties are mainly consequences of these changes in thermodynamic properties with confinement.

Previously, we have shown that the elastic (glassy) modulus (E_f) of amorphous polymer thin films can be robustly measured by simply compressing the thin film supported on a relatively soft, elastic substrate (e.g., polydimethylsiloxane (PDMS)) and measuring the resulting wavelength of the wrinkling instability that occurs.^21,22,23 In those measurements, the wrinkling instabilities were induced at temperatures well below the bulk T_g so that the wrinkling patterns were relatively stable over time and the modulus deduced from the wrinkling wavelength could safely be assumed to represent the glassy modulus of the polymer film. In the present paper, we extend this wrinkling-based metrology to study confinement-induced changes in relaxation behavior of polymer thin films for a temperature range below T_g, where the wrinkling patterns are observed to relax over time. Specifically, we measure the relaxation of the wrinkling wavelength and amplitude back to the equilibrium (flat) state over a range of temperature (T) and film thickness (h_f). We expect that the results from our experiments should provide an independent method to validate (or not) the observations made by Fakhraai et al. ^9,10 Indeed, our measurements confirm trends in variation of film relaxation with T and h_f reported by Fakhraai et al. Additionally, our results provide new information about the time dependence of the relaxation process, the temperature dependence of thin film modulus, and the temperature breadth of the glass transition. It should be noted that Russell et al. observed similar relaxation of surface wrinkles for a highly plasticized polymer film floating on a fluid, where the T_g of the film is significantly suppressed.²⁴ Our wrinkling-based method is thus a robust technique to measure relaxation in polymer thin films and other glassy materials utilized in many nanotechnology and medical applications.

II. EXPERIMENTAL

Thin films of polystyrene (M_w = 654.4 kg mol⁻¹, M_w/M_n = 1.09; M_w and M_n are mass- and number-average molecular mass, respectively; Polymer Source Inc.) were spin-cast from dilute toluene (99.8 %; Sigma-Aldrich) solutions (0.25 % to 5.0 % by polymer mass) onto Si substrates and their thicknesses were measured by reflectance interferometry (Model F20, Filmetrics). PDMS sheets (Sylgard 184; Dow Chemical Co.) were prepared by hand-mixing an oligomeric base and a curing agent (10:1 by mass) and casting onto glass plates. After curing at 75 °C for 2 h, the cross-linked PDMS sheets (thickness ≈ 2 mm) were cut into 25 mm × 75 mm strips. The modulus of PDMS was measured using a conventional tensile test (Texture Analyzer, Model TAXT2i; Texture Technologies). To prepare samples for the relaxation studies, a small piece of as-cast (i.e. unannealed) PS film (≈ 1 cm²) was transferred from the Si substrate onto the surface of the PDMS substrate that had previously been mounted on a computer-controlled motorized translation stage, as described previously.²⁵ The whole setup was placed inside a custom-built, temperature-controlled environmental chamber (Figure 1(a)), and all the samples tested in this study were allowed to dry under ambient conditions for ≈ 2 h prior to measurements.

FIG. 1.

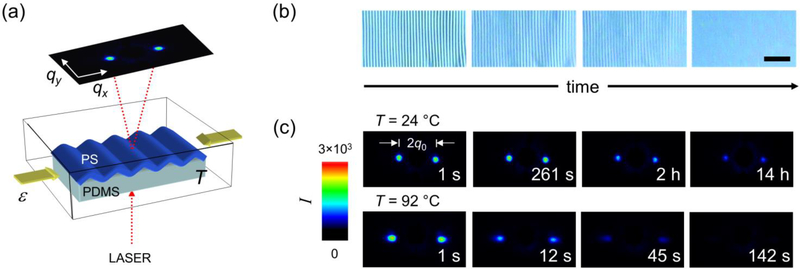
(a) Schematic illustration of the custom-built SALS apparatus equipped with a temperature-controlled chamber and a strain stage for measuring the temporal evolution of a pre-wrinkled polymer film on a compliant substrate. A laser beam is passed through the wrinkled film, and the resulting scattering pattern is projected onto a screen and acquired by a CCD camera. Arrows indicate the direction of compressive strain. (b) Representative optical microscopy images for a 31 nm thick PS film wrinkled at T = 92 °C as a function of time, depicting the wrinkling amplitude decay (scale bar = 10 μm). (c) Time-sequential SALS images of a 31 nm-thick PS film at a temperature of T = 24 °C (upper row) and T = 92 °C (lower row), clearly indicating the decay of scattering intensity as a function of the annealing time.

The evolution of wrinkling patterns was measured by monitoring the intensity and wavenumber of scattered light using a custom-built small angle light scattering (SALS) instrument²⁶ equipped with a temperature-controlled chamber. The sample was heated at a rate of ≈ 5 °C / min to a target temperature (T < T_g) for about 2 h. Once thermal equilibrium was attained (i.e., ΔT < 1 °C), a uniaxial compressive strain ε > 0.02 (above the critical strain for wrinkling,²⁶ which is typically less than 0.01) was applied to the sample at a strain rate of $\dot{\epsilon }$ ≈ 0.1 s⁻¹ using a linear actuator (Model 850G series; Newport Co.) to generate wrinkling patterns on the PS films. SALS was performed on samples in transmission mode with a low-power helium-neon laser (wavelength = 633 nm, beam diameter = 0.52 mm; Melles Griot). Time-resolved images of the scattered light from SALS were obtained by using a charge-coupled-device (CCD) camera (RTE/CCD-1300-Y/HS; Roper Scientific Inc.) with an exposure time of 0.05 s to 0.2 s. Note that the present experimental setup was limited to a time interval of about 1 s between each image due to low data transfer rates. The images were processed and analyzed using the WinView/32 imaging software (Princeton Instruments). Only one sample/film was measured at each thickness and temperature combination.

III. RESULTS AND DISCUSSION

Narrow polydispersity polystyrene (PS) is often taken as a model material for glass-formation in both bulk polymer materials and thin polymer films, and we focus our initial study on PS since we can compare our results with various other techniques in the literature for measuring the properties of PS. We follow the relaxation of wrinkled PS films that were prepared by spin-casting onto silicon wafers and subsequently transferred onto PDMS substrates via an aqueous immersion method²¹ to produce a supported PS film. After equilibration at a given temperature, a small compressive strain was applied to the PS/PDMS laminate to induce surface wrinkling. Immediately after wrinkle formation, the relaxation of wrinkle patterns was measured by tracking time-dependent changes in the intensity of scattering pattern and the position of the 1st order diffraction spot (Figure 1(a)).

In Figure 1(b), we present a time series of optical micrographs for wrinkled PS films (h_f = 31 nm) at a constant T under a fixed compressive strain, showing a typical time-dependent behavior of the wrinkle patterns. As discussed below, the gradual decay of the wrinkle patterns over time (t), particularly with respect to its wrinkling amplitude (A), is attributed to the stress relaxation of the polymer film under shear induced by local bending. The wavelength of the wrinkles is typically on the order of (1 to 5) μm, while the amplitude of the wrinkles is on the order of (10 to 100) nm. In Figure 1(c), we present a sequence of representative SALS images of wrinkled PS films (h_f = 31 nm) at T = 24 °C (upper row) and T = 92 °C (lower row), showing the time- and temperature-dependent behavior of the scattering intensity (I ~ A²) and the dominant wavenumber (q₀ = 2π/λ) of the scattering peaks. We observe that I decays much faster near the T_g of bulk PS (≈ 105 °C) as compared to the decay at lower T and disappears after about t = 140 s. However, the wrinkling wavelength (as evidence by the location of the diffraction spot) does not change appreciably.

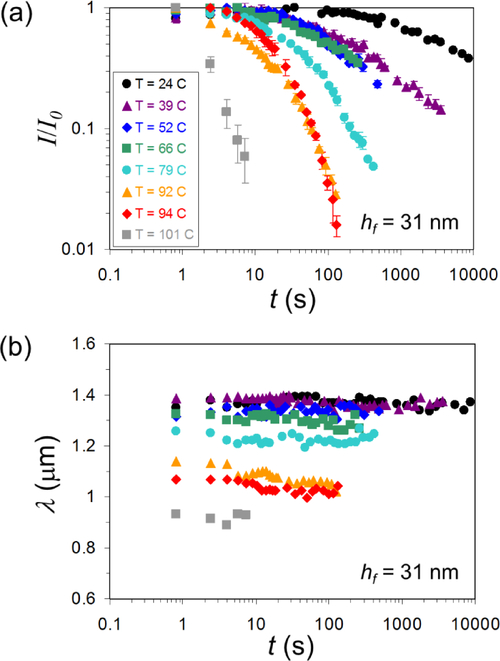
In Figure 2, we plot the values of the normalized scattered intensity (I/I₀, where I₀ denotes the initial intensity at t = 1 s) and the wrinkling wavelength (λ) as a function of t and T for h_f = 31 nm. Again, I/I₀ decays faster over time at higher T, while λ remains roughly constant with t. The wavelength of the wrinkles decreases with increasing T, indicative of a decrease in the apparent Young’s modulus (E_f) since E_f ~ λ³.^21,22 This model assumes that the wrinkled polymer film is an ideal Hookean solid material rather than a non-linear viscoelastic material, but the wavelength is representative of the short time-scale response of the film and is subsequently referred to be in a post-buckled state. Recent measurements and simulations have shown that molecular mobility can be orders of magnitude higher at the surface compared to the interior of glassy films²⁷, raising the question of whether the relaxation of the wrinkles in our measurements is dominated by this mobile interfacial layer or the film as a whole. While it is difficult for us to account for this mobile interfacial layer in our modeling of the time evolution of the wrinkle relaxation process based on a continuum model, we do observe that the relaxation of the wrinkled film depends strongly on the film thickness, while Zhang and Fakhraai²⁸ observe that the mobility at the polymer-air interface of a glassy film is strikingly insensitive to the film thickness. One way to account for a mobile interfacial layer would be to include a surface region of some thickness (e.g., h* = 2 nm) displaying much faster dynamics. This would impact the magnitude of the initial stress ($\langle {\widehat{\sigma }}_0\rangle$) induced by the wrinkles via a reduced effective thickness of the polymer film; however, we use the normalized stress ($\langle \widehat{\sigma }\rangle /\langle {\widehat{\sigma }}_0\rangle$) in the film as a function of time to calculate a relaxation time. Additionally, if the relaxation of the mobile surface layer is rapid and the remaining parts of the film remain ‘bulk-like’, then we would observe a thickness-independent relaxation time. This would seem to imply that the wrinkle relaxation relates to the dynamics of the film as a whole, and thus we treat the film as an effective medium. This model also assumes perfect bonding between the PS film and the PDMS substrate, a reasonable assumption given the low strains applied. We designate our estimates of film stiffness as apparent Young’s moduli since this idealized model has primarily been used to describe polymer films in the glassy state. Our previous estimates of E_f in the glassy state accord well with independent measurement methods,^29,30 but most other studies make similar assumptions about the rheological nature of these complex materials. In our measurements, we acknowledge that the relaxation may reflect contributions from both the polymer-substrate interactions and a coupling of the film relaxation to the elastomeric PDMS substrate. Nevertheless, our analysis assumes that the contribution of the PDMS substrate to wrinkle relaxation process to be relatively small, as evidenced by many measurements indicating no change in the effective elastic modulus in the temperature range studied here.^31,32 We must acknowledge that recent simulation studies have indicated that the polymer-substrate interaction and the rigidity of the substrate can influence the dynamics of supported polymer films,¹⁵ thus the properties of polymer films inevitably depend somewhat on the substrate on which the films are cast, in addition to the effect of changes in film thickness studied here.

FIG. 2.

(a) Measured normalized scattering intensity (I/I₀) as a function of time (t) and temperature (T) (film thickness, h_f = 31 nm). The error bars indicate one standard deviation of the data, which is taken as the experimental uncertainty of the measurement. (b) Measured wrinkling wavelength (λ) as a function of t and T (h_f = 31 nm). λ is given by 2π/q₀, where the dominant wavenumber (q₀) is measured from the location of the scattering peaks [legend shown in (a)].

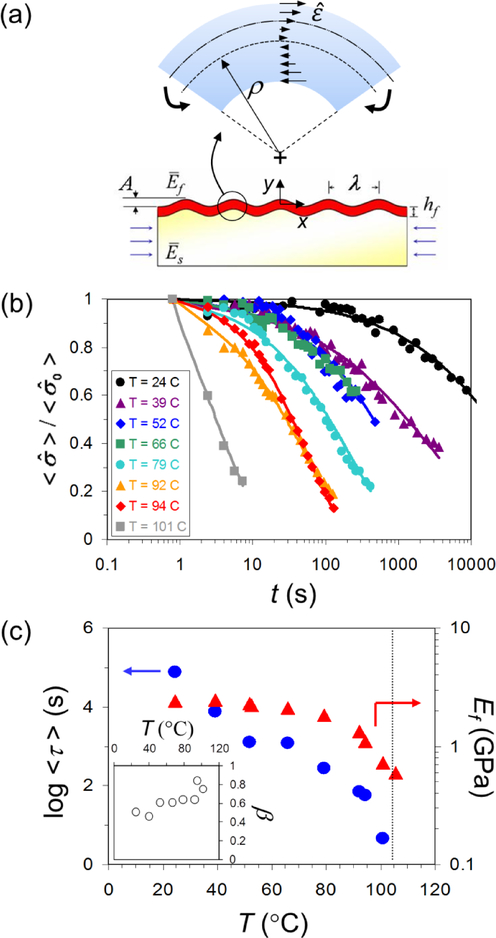
We then propose that the driving force for wrinkle relaxation arises primarily from the shear stress induced by local surface bending caused by the wrinkling instability. We illustrate our model of the imposition of film stress by wrinkling in Figure 3(a) where the crests of the wrinkles are in tension and the valleys in compression. This is the same picture as shown in previous studies where no wrinkle relaxation was assumed.²¹ The magnitude of the average strain applied to the film ($\langle \widehat{\epsilon }\rangle$) depends on the average radius of curvature (ρ_ave) of the wrinkled surface:³³ $\langle \widehat{\epsilon }\rangle =2/h_f{\int }_0^{h_f/2}y/{\rho }_{ave}dy=h_f/4{\rho }_{ave}$. If we further assume a sinusoidal surface undulation of the buckled surface with a wavelength of λ and an amplitude of A and λ ≫ A, then 1/ρ_ave = 8π A/λ². The assumption that the film is linearly elastic (i.e., $\langle \widehat{\sigma }\rangle =E\langle \widehat{\epsilon }\rangle$), noted before, implies the average stress applied to the film equals, $\langle \widehat{\sigma }\rangle \approx 2\pi h_f{E}_{f}A/{\lambda }^2$. For typical initial parameter values used in this study (E_f ≈ 1 GPa, A ≈ 50 nm, and λ ≈ 1 μm for h_f ≈ 30 nm), an initial stress due to the surface undulations is calculated to be $\langle \widehat{\sigma }\rangle$ ≈ 10 MPa. This value is below the yield stress of bulk PS (≈ 30 MPa).⁶ Yielding of the polymer film would lead to irrecoverable deformation of the film, which could result in the wrinkled film never fully relaxing back to the flat state. Our measurements based on SALS cannot definitively show this; a more surface sensitive technique such as atomic force microscopy would need to be employed. It should also be noted that the films studied here were unannealed prior to film transfer and measurements. The residual stress in spin-cast films has previously been reported to be thickness-dependent²⁶ and might serve as an additional driving force for wrinkle relaxation. However, annealing a polymer film above T_g on a solid support removes some but not all residual stress in the film (e.g., thermal expansion mismatch between film and substrate after vitrification), so obtaining an accurate value for the residual stress is elusive. The impact of residual stress on the wrinkle relaxation is an exciting yet challenging area to be explored.

FIG. 3.

(a) Schematic of the local shear stress fields induced by local bending along a wavy surface. (b) Normalized average stress ($\langle \widehat{\sigma }\rangle /\langle {\widehat{\sigma }}_0\rangle$) applied to PS films (h_f = 31 nm) as a function of t, showing the relaxation of the wrinkle pattern at various T below T_g. The solid lines are stretched exponential fits. (c) Average relaxation time (τ: circles) and high frequency Young’s modulus (E_f: triangles) for PS films (h_f = 31 nm) as a function of T. The vertical dotted line indicates the bulk T_g of PS, and the inset shows the plot of stretched exponential coefficient (β) vs. T.

To quantify the wrinkle relaxation, we consider the normalized average stress applied to the polymer film as $\langle \widehat{\sigma }\rangle /\langle {\widehat{\sigma }}_0\rangle \approx \sqrt{I/I_0}(\lambda /{\lambda }_0)$ where $\langle {\widehat{\sigma }}_0\rangle$ is the ‘initial’ average stress at t = 1 s. We then have $A/A_0=\sqrt{I/I_0}$ and E_f/E_f0 = (λ/λ₀)³,²⁶ where λ₀ and A₀ denote the initial wavelength and amplitude at t = 1 s, respectively. We note that the relative change in h_f during relaxation of polymer films examined in this study (25 nm < h_f < 200 nm, T < T_g) will likely be very small,³⁴ and this change is thus not considered. Using our model of film wrinkling, we may deduce the T-dependence of the film stress relaxation in our thin PS films by measuring the two quantities, $\sqrt{I/I_0}$ and λ/λ₀, using small angle light scattering to probe the wrinkle patterns. In Figure 3(b), the stress decay $\psi \left(t\right)\equiv \langle \widehat{\sigma }\rangle /\langle {\widehat{\sigma }}_0\rangle$ for 31 nm-thick PS films is plotted as a function of t and T using the results shown in Figure 2. We see that ψ(t) decreases progressively with t for the whole temperature range studied and this decay occurs faster at higher T. We find that the relaxation of the wrinkling patterns can be well-described by a stretched exponential, ψ(t) = exp[−(t/τ)^β], where τ is an “unwrinkling” relaxation time and β lies in the interval (0, 1). This type of non-exponential structural relaxation is typical of glass-forming liquids and is normally attributed to a distribution of relaxation times associated with dynamic heterogeneity within the material, where greater heterogeneity normally identified with a smaller β.^35,36,37 We find that β decreases at lower T, which is again normal for glass-forming liquids; β vs. T for PS films with h_f = 31 nm is shown in the inset of Figure 3(c). We calculate the average relaxation time using $\langle \tau \rangle ={\int }_0^{\infty }\mathrm{e}\mathrm{x}\mathrm{p}[-{\left(t/\tau \right)}^{\beta }]dt=\tau \mathrm{\Gamma }\left(1/\beta \right)/\beta$, where Γ is the gamma function.³⁶ Figure 3c summarizes τ as function of T. We see that the T dependence of τ is rather strong, and its values are nearly equivalent to the relaxation time calculated from the decay of the wrinkle amplitude so that ψ(t) ≈ A/A₀ (data not shown). This quantity is often considered to describe relaxation of nanoscale deformation of polymer film surfaces.^37,38

The wrinkling wavelength (λ) measured at different T (Figure 2(b)) also provides a quantitative estimate of the temperature-dependent Young’s modulus of thin glassy polymer films. For an ideal elastic film, the (effective) Young’s modulus (E_f) is related to the wavelength, film thickness, and substrate modulus (E_s) through the established relation: ${\overline{E}}_f(T)=3{\overline{E}}_s{\left[\lambda \left(T\right)/2\pi h_f\right]}^3$, where $\overline{E}=E/\left(1-{\nu }^2\right)$ is the plane-strain modulus, ν is the Poisson’s ratio, and the subscripts f and s denote the film and substrate, respectively.²¹ We take E_s, ν_s and ν_f as 1.8 MPa, 0.50 and 0.33, respectively, as in prior work.²¹ Figure 3(c) plots the calculated values of the effective E_f using the results shown in Figure 2(b) for h_f = 31 nm. We note the strong dependence of E_f on T, particularly near T_g. It should be noted that while the modulus of the PDMS substrate could change at elevated temperatures, the fact that we calculate a Young’s modulus of (2 to 3) GPa for PS serves as an internal check that suggests the PDMS modulus is not changing significantly over the time scale of the experiment. The variation of the wrinkle wavelength with time is rather weak at a fixed T, as illustrated in Figure 2(b). Our analysis of the film wrinkling assumes that the glassy film is an ‘elastic solid’ material. We know that above T_g the relaxation time exhibits a rapidly growing stress relaxation time upon cooling that is non-Arrhenius over a large T range.

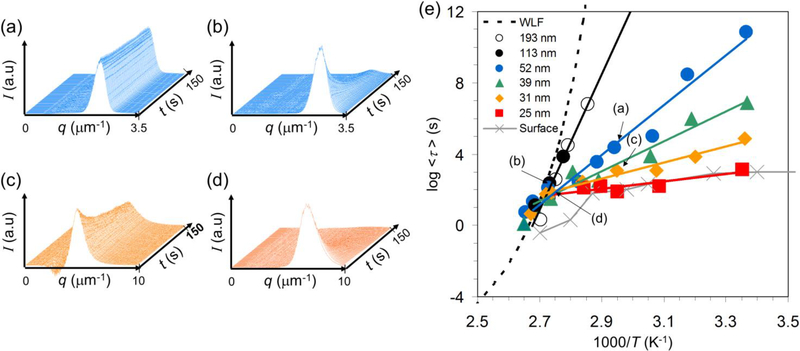
Based on our film wrinkling relaxation approach, we now examine the effect of film thickness on the relaxation dynamics of thin PS films. Figures 4(a)–(d) represent three-dimensional (3D) plots of the temporal and spatial evolution of scattering patterns in the relaxation of wrinkled PS films, clearly showing a thickness and temperature dependent structural relaxation in ultrathin glassy polymer films. Figure 4(e) summarizes ⟨τ⟩ values as a function of T for film thicknesses ranging from 25 nm to 200 nm. We observe that ⟨τ⟩ exhibits a strong dependence on h_f and a striking linear variation with 1/T below T_g. Film relaxation is well-described by an Arrhenius temperature dependence³⁹, $\tau ={\tau }_0{e}^{-E_a/RT}$, where τ₀ is the relaxation time prefactor, R is the gas constant, and E_a is a film thickness dependent activation energy, a quantity observed before by Fakhraai and coworkers for relaxation in thin glassy films.^7,9,10 It should be noted that the relaxation curves as a function of T converge to a common temperature, T*, ≈368 K (94 °C ± 2 °C), or about 10 °C below the bulk glass transition temperature of PS (T_g = 105 °C), and a corresponding relaxation time, τ*, of about (35 to 45) s. We contrast this Arrhenius relaxation with the Vogel-Fulcher-Tammann (VFT) T-dependence of relaxation that is normally observed in the relaxation of glass-forming materials such as PS above T_g.^40,41,42 The VFT curve for bulk relaxation is indicated by a dashed line in Figure 4(e). Note that even relatively thick ‘bulk-like’ films having a h_f > 100 nm exhibit an apparent Arrhenius relaxation. A transition between VFT to Arrhenius relaxation below T_g has been reported in previous studies,^12,13 so this phenomenon is not specific to thin films.

FIG. 4.

(a)−(d) Representative 3D plots of the temporal and spatial variation of scattering patterns in the relaxation of PS films with different thicknesses (h_f) at different temperatures (T): (a) h_f = 52 nm, T = 67 °C; (b) h_f = 52 nm, T = 93 °C; (c) h_f = 31 nm, T = 66 °C; and (d) h_f = 31 nm, T = 92 °C. (e) A plot of the average relaxation times ⟨τ⟩ for PS films with different h_f as a function of T. The straight lines indicate Arrhenius fits to the corresponding experimental data (see text for details). For comparison, the ‘WLF’ curve is displayed as a black dashed line, which is reproduced from ref. 33. Grey cross symbols (‘Surface’) are measurements of the near-surface dynamics reproduced from ref. 6; the lines are a guide for the eye.

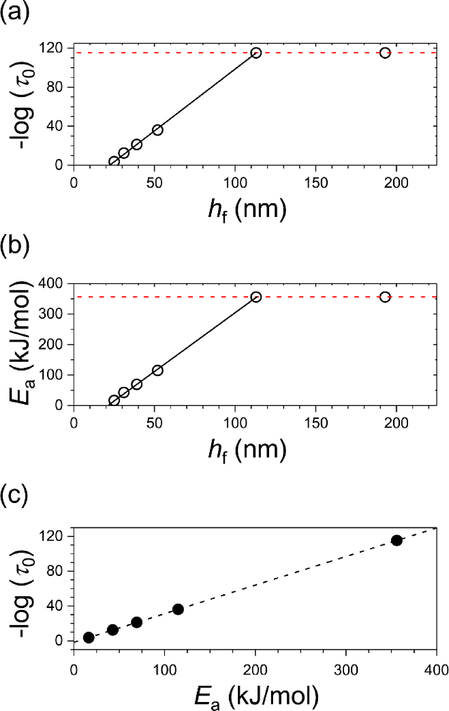
The resulting prefactors (τ₀) and activation energies (E_a) from Arrhenius fits to the data in Figure 4(e) are plotted as a function of h_f in Figures 5(a) and 5(b). It should be noted that in the theory of activated transport¹⁴ ${\tau }_0=A{e}^{(-\mathrm{\Delta }{S}_a/k_b)}$, where A is a constant and ΔS_a is the activation entropy. Thus, −log(τ₀) is linear in the activation entropy. Therefore, we plot −log(τ₀) as a function of E_a in Figure 5(c), where a linear correlation is indicative of entropy-enthalpy compensation (discussed in more detail below). For films having h_f > 100 nm, there appears to be no appreciable effect of film thickness on τ, and both E_a and −log(τ₀) are nearly independent of h_f in this bulk-like film regime. The plateau value (E_a ≈ 350 kJ mol⁻¹) has a magnitude comparable to previously reported bulk values of the segmental relaxation time of PS in the glassy state.^43,44 In contrast, for films having h_f < 100 nm, both the entropy and enthalpy of activation decrease as the films becomes thinner, making τ appreciably smaller than its bulk value. Our observations are remarkably consistent with nano-hole filling experiments in PS films,⁶ where a similar reduction of E_a is observed in the glassy state. This reduction of E_a in ultrathin glassy films also accords with the film dewetting measurements of Fakhraai et al.¹⁰ and accords qualitatively with other reported polymer film measurements.^7,45,46 A decrease of E_a with geometrical confinement and a crossing of the relaxation curves near a fixed compensation temperature below T_g has also been observed in glassy materials confined to nanopores,^47,48,49 so this type of confinement effect on activated dynamics seems to be rather general.

FIG. 5.

Thickness dependence of the (a) apparent activation entropy (ΔS_a, or −log(τ₀)) and (b) apparent activation energy (E_a) calculated from the Arrhenius fits in Figure 4(e). The solid lines are the linear fit to the data below h_f = 100 nm and the horizontal dashed lines are a guide for the eye, indicative of the bulk-limit value above h_f = 100 nm. (c) A plot of the prefactor (−log(τ₀)) as a function of E_a reveals that the relaxation data exhibit entropy-enthalpy compensation. The slope of this plot determines the temperature where the Arrhenius curves intersect in Figure 4(e).

Although molecular dynamics (MD) simulation cannot directly address the long time-scales required to estimate relaxation times in thin glassy films, MD simulation in conjunction with the string model of relaxation^16,17 does allow for extrapolation of simulation data into the glassy regime based on fits of this model to simulation data over a wide temperature range in which equilibrium simulation is possible. In particular, the string model of relaxation¹⁷ predicts that the structural relaxation time τ has an Arrhenius temperature dependence at both elevated temperatures, where the fluid is dynamically homogeneous, and in the low temperature glassy dynamics regime (T < T_g), where relaxation is extremely slow; in between these regimes, there is a broad glass transition regime where the activation free energy increases monotonically upon cooling, directly reflecting the growth of string-like collective motion with cooling. The magnitude of the activation energy in the low temperature regime is normally a factor of about 4 to 5 times larger than its corresponding values in the high temperature regime^17,50 so that only a modest change in the extent of collective motion is required to explain the extremely large changes in the observed relaxation times in glassy materials. These theoretical predictions, in conjunction with the MD simulation observation of a decrease in the high temperature activation enthalpy and activation entropy with confinement, imply that the entropy-enthalpy compensation effect relating the activation (enthalpy) energy and activation entropy should also be observed in polymer films in their glassy state (see supplementary material for further discussion). In the physical literature, the term entropy-enthalpy compensation effect is defined by this crossing phenomena in Arrhenius relaxation, chemical rate and diffusion curves. Within transition state theory, this phenomenon arises from the enthalpy and entropy of activation varying in a linear way with the compensation temperature itself being the constant of proportionality required by dimensional consistency that relates these energetic parameters. The term compensation temperature reflects the fact that the enthalpic and entropic contributions to the activation free energy vanish at this temperature. An increase in the relaxation time prefactor as the film is made thinner is a result of a decrease in the entropy of activation. For the curves to intersect when the activation energy decreases with confinement, the prefactor must be increasing (i.e. the entropy of activation is decreasing as well). The decrease in the activation energy with film thickness, approaching zero when the film is sufficiently thin, and the observation of entropy-enthalpy compensation (the intersection of the Arrhenius relaxation curves at nearly a common point) are both features exhibited by our measurements and by earlier observations by Fakhraai and coworkers on both polymeric^6,7,8,9 and non-polymeric films.^10,11 These predicted changes in the dynamics of glassy polymer films with confinement are discussed by Hanakata et al.¹⁸

Additionally, the initial wavelength of wrinkling at t = 1 s (see Figure 2(b)) allows to estimate the temperature dependent glassy plateau modulus^51,52 based on the relation ${\overline{E}}_f(T)=3{\overline{E}}_s{\left[\lambda \left(T\right)/2\pi h_f\right]}^3$, as discussed above. Figure 6(a) shows effective E_f estimates for PS films having a thickness range from 25 nm < h_f < 200 nm over a temperature range from room temperature to near T_g. E_f normally exhibits a sigmoidal variation with T for a broad range of amorphous solids in general,^53,54 and polystyrene specifically.^55,56,57 Our measurements of the reduced Young’s modulus (E_f/E_f0), where E_f0 is the apparent modulus at room temperature, shown in Figure 6(b) for different h_f exhibit this characteristic type of variation. Correspondingly, we find that E_f/E_f0 can be fit rather well by a model of the shear modulus of amorphous solids developed by Lin et al.,⁵³ E_f/E_f0 = 1/{1 + exp[(ΔH − TΔS)/RT]}, where ΔH and ΔS are the energetic fitting parameters. While the significance of these energetic parameters is not yet clear to us, this fitting procedure clearly indicates that there is a significant broadening of the T range over which E_f/E_f0 varies when h_f is decreased. This result is consistent with numerous previous observations indicating a broadening of the glass transition in thin polymer films.

FIG. 6.

(a) Measured high frequency Young’s modulus (E_f) for PS films with different thicknesses (h_f) as a function of temperature (T). (b) Normalized Young’s modulus (E_f/E_f0) as a function of T and h_f. The symbols are the same as in (a). The dotted curves represent model fits to the data using E_f/E_f0 = 1/{1 + exp[(ΔH − TΔS)/RT]} with the following fitting parameters: h_f > 39 nm (ΔH = −171 kJ mol⁻¹, ΔS = −472 J mol⁻¹ K⁻¹); h_f = 39 nm (ΔH = −125 kJ mol⁻¹, ΔS = −342 J mol⁻¹ K⁻¹); h_f = 31 nm (ΔH = −84 kJ mol⁻¹, ΔS = −231 J mol⁻¹ K⁻¹); and h_f = 25 nm (ΔH = −52 kJ mol⁻¹, ΔS = −150 J mol⁻¹ K⁻¹).

IV. CONCLUSIONS

The measurement of structural relaxation in nanoconfined materials below T_g is difficult by standard experimental methods because of long relaxation times involved. Thus, many experimental studies have focused on the onset regime above T_g, where relaxation is rapidly growing upon cooling and normally non-Arrhenius. In the present study, we investigate both the thickness and temperature dependence of the relaxation of wrinkle patterns in polymer films by following the relaxation process by small angle light scattering. Previously, this method was used to measure the high frequency Young’s modulus of ultrathin glassy films, and relaxation of the wrinkles were not observed due to the relatively short time scales of those experiments. Here, we extended the previous wrinkling-based approach to a temperature range below the bulk T_g of the material where wrinkle relaxation is apparent over reasonable time scales (up to several hours). For PS thin films, this corresponded to a temperature range between room temperature and T_g (≈ 100 °C). We observe a decrease of the activation energy upon confinement and a tendency of the relaxation curves to intersect near a common temperature, corresponding to entropy-enthalpy compensation. Recent molecular dynamics simulations have also indicated the existence of entropy-enthalpy compensation in the structural relaxation of polymer liquids in the high temperature polymer regime where relaxation is also Arrhenius.^16,17,18 Furthermore, we found that stress relaxation of the film could be fit with a decaying stretched exponential function with a stretching exponent that decreases with decreasing temperature. Our findings are remarkably consistent with other film relaxation measurements using disparate measurement methods,^6,45 demonstrating the validity of our technique and the generality of the measurement trends. Our measurements also highlight the importance of the activation energy changes in understanding changes of the dynamics of thin polymer films.