Biophysical Modeling of Large-Scale Brain Dynamics and Applications for Computational Psychiatry

Abstract

Noninvasive neuroimaging has revolutionized the study of the organization of the human brain and how its structure and function are altered in psychiatric disorders. A critical explanatory gap lies in our mechanistic understanding of how systems-level neuroimaging biomarkers emerge from underlying synaptic-level perturbations associated with a disease state. We describe an emerging computational psychiatry approach leveraging biophysically based computational models of large-scale brain dynamics and their potential integration with clinical and pharmacological neuroimaging. In particular, we focus on neural circuit models, which describe how patterns of functional connectivity observed in resting-state functional magnetic resonance imaging emerge from neural dynamics shaped by inter-areal interactions through underlying structural connectivity defining long-range projections. We highlight the importance of local circuit physiological dynamics, in combination with structural connectivity, in shaping the emergent functional connectivity. Furthermore, heterogeneity of local circuit properties across brain areas, which impacts large-scale dynamics, may be critical for modeling whole-brain phenomena and alterations in psychiatric disorders and pharmacological manipulation. Finally, we discuss important directions for future model development and biophysical extensions, which will expand their utility to link clinical neuroimaging to neurobiological mechanisms.

A central research challenge in clinical neuroscience is to develop a mechanistic understanding of how molecular and synaptic-level disturbances in the human brain propagate across levels to analysis to impact systems-level neural activity, and ultimately cognitive computations, in neuropsychiatric disorders. At the level of microcircuitry, the field is generating hypotheses related to cell types and synaptic processes, such as disrupted balance between synaptic excitation and inhibition. For instance, histological studies have revealed alterations in synaptic densities in schizophrenia (1,2). At the molecular level, transcriptome mapping has characterized alterations in cortical expression levels of genes regulating synaptic and neuronal processes across multiple disorders (3-6), implicating microcircuit dysfunction in psychiatric neuropathologies. However, it is unclear how such deficits impact distributed computations in large-scale brain networks, which subserve cognitive functions.

At a vastly different level of analysis, clinical neuroscience has leveraged noninvasive neuroimaging techniques to discover disorder-related biomarkers in the large-scale organization of anatomical structure and functional dynamics in the human brain. Altered evoked and intrinsic neural activity across distributed brain systems can be observed from modalities including functional magnetic resonance imaging (fMRI), electroencephalography (EEG), and magnetoencephalography (MEG). Resting-state fMRI has emerged as a powerful tool for characterizing the intrinsic functional organization of brain network dynamics in terms of functional connectivity (FC), the statistical covariation of neural activity (7-10), with widespread application to psychiatric disorders (11).

One promising effort to bridge this gap is the multidisciplinary field of computational psychiatry, which uses theoretical neuroscience models to study how disruptions at lower levels propagate upward to produce dysfunction at higher levels of behavior and function. Computational psychiatry encompasses a wide range of modeling approaches, from biophysical simulation of microcircuit dynamics, to connectionist modeling of distributed neural computation, to normative models of learning and decision making. In turn, these distinct levels of computational modeling connect to different types of neural and behavioral measurements. A number of recent articles and books have surveyed the progress and challenges in the emerging field of computational psychiatry (12-18).

Among computational psychiatry approaches, biophysically based modeling of neural circuit dynamics is well suited to link synaptic-level disruptions to emergent brain dysfunction (12,15,19-21). Circuit models can simulate neural population activity and computations, incorporating key properties of neurons and synaptic connectivity (22). Simulated activity patterns can then be related to empirical measures of neural activity, or in some cases even behavior. Perturbation of specific synaptic parameters can simulate hypothesized disease mechanisms and pharmacological manipulations, generating predictions for their impacts on neural activity and behavior (23-25). Such model results can then be related to experimental findings from clinical populations, pharmacological challenge, or animal models of disease states. Through mechanistically linking molecular, cellular, circuit, and ultimately behavioral levels of analysis, biophysically based modeling has the potential to inform rational design of pharmacological therapies.

We provide a targeted review of progress in biophysically based circuit modeling of large-scale neural dynamics in the human brain and application of these whole-brain neural circuit models to understanding findings in clinical neuroimaging. Dynamical modeling has been applied to a variety of neuroimaging phenomena, including in psychiatric disorders; a more general overview of this field can be found in several recent review articles (14,26,27). In particular, a number of studies have used brain network models to study how the FC of neural activity across brain areas emerges from the interplay between their anatomical structural connectivity and intrinsic dynamics (27-33).

We focus here on whole-brain dynamical models that attempt to bridge from the level of synapses and neurons to that of spatiotemporal dynamics in distributed brain systems. These models can incorporate key features of neuronal and synaptic processes and integrate data from multimodal human neuroimaging (32). They can therefore study how synaptic-level physiological perturbations impact large-scale organization of functional dynamics. For computational psychiatry applications, we focus on studies relating these models to schizophrenia (34-37). Schizophrenia is a disorder thought to involve large-scale dysconnectivity (38,39) as well as alterations in local cortical excitation-inhibition (E-I) physiology (40-43) and therefore poses important research questions that are amenable to this level of computational modeling.

We also highlight opportunities in computational psychiatry that will require further development of this class of models. In particular, we emphasize the importance of regional heterogeneity of neural microcircuitry, including across cortical areas (33), which can be informed by empirical measurements such as large-scale transcriptome mapping (44-46). Increasing neurobiological detail in the model’s microcircuitry is important to address synaptic-level hypotheses related to psychiatric disorders, yet this also poses critical challenges for how such model features can be adequately constrained and tested with neuroimaging data. Pharmacological neuroimaging may provide an important test bed for future model development and validation (47-50). Whole-brain circuit modeling can thereby provide a translational bridge to advance clinical neuroscience.

COMPUTATIONAL MODELS OF LARGE-SCALE RESTING-STATE DYNAMICS AT THE WHOLE-BRAIN LEVEL

Computational neuroscience has focused primarily on modeling phenomena at levels from neurons to small microcircuits, rather than large-scale neural systems (22). Dynamical modeling of brain networks has a rich history integrating developments from fields including neurophysiology, statistical physics, and nonlinear dynamics. In particular, the field has been strongly influenced by analysis of synchronization of coupled oscillators (51-54). [For a useful overview, see (27).]

Computational modeling of large-scale brain dynamics has been limited by experimental techniques to characterize neural structure and function at the whole-brain level. Progress in resting-state fMRI has played an important role in development of a class of neural circuit models that explicitly relate to resting-state FC. Whole-brain models — which typically do not actually model the entire brain, but, for instance, a cortical hemisphere—operate at the level of large-scale neural systems and address questions such as how distributed structural connectivity shapes FC through dynamical interactions of neuronal populations across brain regions (26,27,55).

Whole-brain models of resting-state dynamics typically represent a brain as a network of interconnected discrete nodes (Figure 1A), with each node simulating a region, e.g., parcellated cortical area. The model architecture requires two key elements: 1) a structural connectivity matrix defining coupling between areas, which can be derived from empirical data, typically diffusion MRI, and 2) equations governing neural dynamics of each local node, which can be constrained by known neurophysiology (55). The net input to each node can contain contributions from local recurrent connections, long-range connections from other nodes, and fluctuating background input (31,32,56). As nodes respond to inputs, their activity fluctuates in time. Owing to long-range coupling, fluctuations are correlated across nodes, generating spatiotemporal patterns that can be characterized via measures such as FC. The resultant FC pattern is thereby shaped not only by underlying structural connectivity but also by dynamical properties of local nodes.

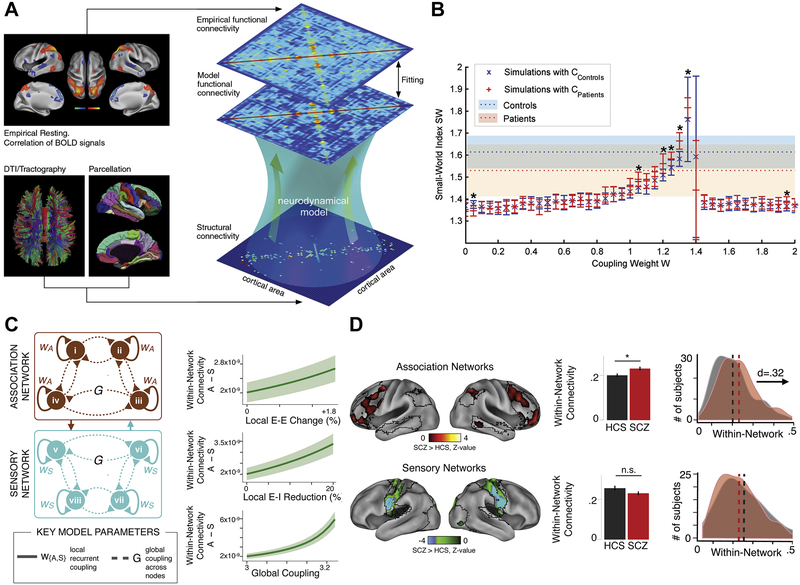
Figure 1.

Computational circuit models of resting-state dynamics in the human brain and their application to study of functional dysconnectivity in schizophrenia. (A) Modeling framework. The neurodynamical model simulates dynamical activity of interconnected microcircuits, each representing a parcellated brain area. Structural connectivity, defining the strengths of long-range connections between local areas, is derived from diffusion magnetic resonance imaging tractography. The simulated blood oxygen level–dependent (BOLD) signal yields a model functional connectivity pattern, which can be compared with empirical functional connectivity patterns. The biophysical parameters of the model (e.g., local or long-range synaptic strengths) can then be fitted to optimize this correspondence. (B) Application of the model to study structural and functional dysconnectivity in schizophrenia. The graph-theoretic small-world index is calculated on the simulated functional connectivity, using distinct structural connectivity matrices for control subjects and patients with schizophrenia, as a function of the global coupling strength, and compared with empirically measured values (dotted lines). (C) Expansion of the model to incorporate hierarchical heterogeneity of local circuit properties, specifically stronger recurrent excitation (W) in association with cortical networks compared with sensory cortical networks. Elevated excitation-inhibition ratio increases preferential dysconnectivity in association networks in the model. The difference between association and sensory measures (A – S) of within-network connectivity (covariance) is plotted. (D) Empirical measures of within-network connectivity in schizophrenia reveal preferential increase in connectivity in association networks. DTI, diffusion tensor imaging; E-E, excitatory-to-excitatory; E-I, excitatory-to-inhibitory; HCS, healthy control subjects; n.s., not significant; SCZ, schizophrenia (patients). [(A) Modified with permission from Deco et al. (31); (B) modified with permission from Cabral et al. (37); (C) and (D) modified with permission from Yang et al. (35).]

Neural activity in each node can generate simulated blood oxygen level–dependent signals via hemodynamic models, such as the Balloon-Windkessel model (57), enabling more direct comparison with fMRI measures (58). Empirical neuroimaging data (e.g., fMRI resting-state FC matrices, MEG spectral power maps) can be used to quantitatively fit model parameters to optimize the similarity between simulated and empirical FC patterns (31-33).

Structural connectivity describes long-range inter-areal connections through which nodes interact. In nonhuman primates, these projections can be quantified and compiled through invasive tract-tracing methods (59,60). Such measurements have been used in models of monkey cortex (28,30,61). In models of human cortex, for which tract tracing is unavailable, diffusion MRI can be used to derive a structural connectivity matrix through diffusion tractography (31-35,56,62,63). In models, elements of the structural connectivity matrix set the strength of coupling between nodes. A fundamental limitation of diffusion MRI is that it can yield only symmetric structural connectivity estimates. Loss of directionality in long-range connectivity can impact network properties (64). One approach to mitigate this limitation is to estimate directional effective connectivity for a model by its fit to empirical data (65,66).

A second key element needed to link structural connectivity to FC is the choice for the model generating the local dynamics of the nodes, which differs substantially across computational studies (27,55,67). Owing to the spatiotemporal resolution of neuroimaging, these models typically eschew computationally intensive simulation of spiking neurons in favor of simulating each area with a small number of dynamical variables, which may describe the effective activity levels in neural populations. Models of local cortical nodes differ in their level of detail and correspondence of their parameters to neurophysiology. Most node models exhibit intrinsic dynamical regimes described either as an oscillator or as a point attractor state, and fluctuating background input can perturb the state of the node around these trajectories.

Several early seminal studies of whole-brain models simulated each area as a reduced excitable neural system whose dynamical regime intrinsically generates coherent oscillations, instantiated via a conductance-based neuronal model (28,68), a FitzHugh-Nagumo neuronal model (29), or a Wilson-Cowan excitatory-inhibitory model (30). Intrinsic oscillations can also be directly imposed as in the Kuramoto phase-oscillator model (36,69), in which each node is represented by a single dynamical variable, the phase of the oscillator. The Kuramoto model can be considered an abstraction or reduction of an oscillatory neural system, and its nodal simplicity facilitates tractable analyses of synchronization phenomena in networks (70). An important question is the degree to which oscillators describe spontaneous dynamics of local microcircuits in awake cortex (71). Recent review articles provide a more comprehensive survey of various local node models (27,55,72).

For computational psychiatry applications, models should be able to instantiate perturbations to parameters that correspond to hypothesized neurobiological alterations in disease-related states (12,15,73). For these purposes, it is advantageous for the local node model to have greater biophysical fidelity, neurophysiologically interpretable parameters, and dynamical regimes in correspondence with in vivo neural activity. Simulation of each node as a large population of spiking neurons is computationally expensive, limiting its applicability (27,56,74). A substantial advance has been development of whole-brain models whose local nodes follow biophysically based mean-field dynamics derived from recurrent networks of excitatory and inhibitory neurons in a cortical microcircuit (31,32). The mean-field equations track aggregate levels of synaptic activity and firing rate in populations of asynchronously spiking neurons, such as excitatory pyramidal neurons of inhibitory interneurons in the local circuit (75). Stochastic background input to the mean-field population induces fluctuations in the dynamical variables describing activity in the population. This aggregate description is computationally tractable and well matched to the coarse spatiotemporal resolution of neuroimaging modalities (27,55).

Mean-field models make simplifying assumptions about circuit activity to reduce the dimensionality and complexity of the system. [For reviews of mean-field and neural field models and applications to neuroimaging, see (27,72).] For instance, typically mean-field models assume asynchronous spiking across the neuronal population, and they therefore cannot model neuronal circuit mechanisms that rely on precise spike timing. Further simplifying assumptions allow greater reduction of the system’s dynamics, which may be favorable to match the coarseness of corresponding experimental measures. Of note, these reductions also pose challenges for parameter identifiability, as many biophysical parameters jointly shape the simplified dynamical properties.

Dynamical mean-field models have been applied to study how the physiological state of cortical circuits shapes FC (31,32). In these models, FC emerges from local asynchronous spontaneous fluctuations of areas that are driven by stochastic background input and coupled through structural connectivity. Computational tractability of mean-field models enables efficient analysis of how network dynamics are shaped by synaptic parameters. Deco et al. (31,32). fitted the long-range coupling strength parameter to maximize the similarity between simulated and empirical FC (Figure 1A). They found that the best fit occurred when the network’s dynamical regime exhibits stable attractor dynamics in its baseline state but is near a bifurcation point where baseline activity destabilizes. Slightly below this point, the system exhibits modes of correlated fluctuations that are strong and broadly distributed across nodes, as observed in resting-state neuroimaging.

APPLICATIONS OF WHOLE-BRAIN CIRCUIT MODELS TO SCHIZOPHRENIA

In recent years, biophysically based models of resting-state dynamics have been applied to study circuit mechanisms underlying neuroimaging biomarkers. Here we focus on applications to schizophrenia, a neurodevelopmental disorder that is thought to involve large-scale dysconnectivity (38,39) and disruptions in the synaptic E-I balance of local cortical microcircuits (40-43,76). This provides an important test bed in which whole-brain modeling can simulate how synaptic-level perturbations shape large-scale dysconnectivity (73). As shown by whole-brain models described above, FC is shaped both by anatomical structural connectivity and by the dynamics of local circuit activity. Therefore, FC alterations in a psychiatric disorder could be driven jointly by differences in long-range anatomical projections or in local circuit physiology. Biophysically based whole-brain modeling is well suited to examine the respective contributions of these mechanisms.

Schizophrenia is associated with alterations in structural connectivity, as measured by diffusion-weighted imaging of white matter (77-79). To examine how this impacts functional dysconnectivity in schizophrenia, Cabral et al. (37) analyzed a whole-brain model, based on asynchronous attractor dynamics, using structural connectivity matrices from patients with schizophrenia and matched control subjects (Figure 1B). They calculated graph-theoretic measures of the model-simulated FC and compared them with values from resting-state fMRI in patients and control subjects (80). Interestingly, the empirically measured structural connectivity alterations did not produce the functional dysconnectivity observed in patients. In contrast, the graph-theoretic features of functional dysconnectivity in schizophrenia could be captured by changing the global parameter scaling to all long-range connections, which can be interpreted as a synaptic strength (37). This study highlights that FC is shaped by more than structural connectivity and that synaptic disruptions may play a profound role in disease-related dysconnectivity.

As noted, a leading hypothesis for cortical dysfunction in schizophrenia is disruption in the synaptic E-I balance. In a series of studies, Yang et al. (34,35) applied whole-brain models to study the large-scale impact of alterations in the E-I ratio in cortical circuits, relating these effects to resting-state fMRI biomarkers in schizophrenia. Increasing the effective strength of connectivity at either the local or the long-range level, resulting in an elevated E-I ratio, can capture the elevated local and global neural variability observed in schizophrenia (34,81,82). Interestingly, the empirical functional dysconnectivity was preferential in association cortical networks compared with sensory networks. This raises the question of how a global E-I perturbation can give rise to preferential deficits in association networks. One possibility is that local circuit properties differ between association and sensory cortex, which contributes to a preferential vulnerability to E-I imbalance in association cortex. Instantiating this hypothesis in the model, Yang et al. (35) found that endowing association nodes with strong recurrent connectivity resulted in preferential dysconnectivity under elevated E-I ratio perturbations, in line with observations in schizophrenia. These studies highlight the importance of local synaptic properties on large-scale FC and suggest that heterogeneity of local properties across cortical areas may shape the whole-brain organization of dysconnectivity in psychiatric disorders.

A future challenge and opportunity for computational psychiatry concerns how to link anatomical or physiological biomarkers to the level of cognitive functions and behavior at which symptoms are manifested and disorders are diagnosed. For instance, schizophrenia is not defined as a disorder of resting-state FC, but is defined by characteristic symptoms including delusions and disorganized thinking, which may arise from aberrant inference computations (83-85). Behavioral modeling has proposed circuit mechanisms by which false inferences in schizophrenia could arise from imbalanced excitatory-inhibitory interactions in hierarchical processing (86,87). Further research is needed to make connections between circuit-level models and psychological-level models, which may in turn help to link psychiatric biomarkers to symptoms.

IMPORTANCE OF CORTICAL HETEROGENEITY

Most biophysically based circuit models of human resting-state FC have treated all of the cortex as homogeneous, simulating all cortical areas as nodes with identical local circuit properties. Yet cortical microcircuitry varies across cortex in large-scale gradients (88-90); indeed, early areal parcellations were based on regional variation in cytoarchitecture and myeloarchitecture (91). Clinical neuroimaging effects show regional specificity (e.g., differential alterations in association vs. sensory cortical networks) (35,92-94). Therefore, an important direction for translational research in whole-brain modeling will be to incorporate heterogeneity of local circuit properties across cortical areas in principled ways. Such progress will enable greater applicability of these models to pressing challenges in clinical neuroscience. Below we describe examples of recent studies characterizing and modeling cortical heterogeneity.

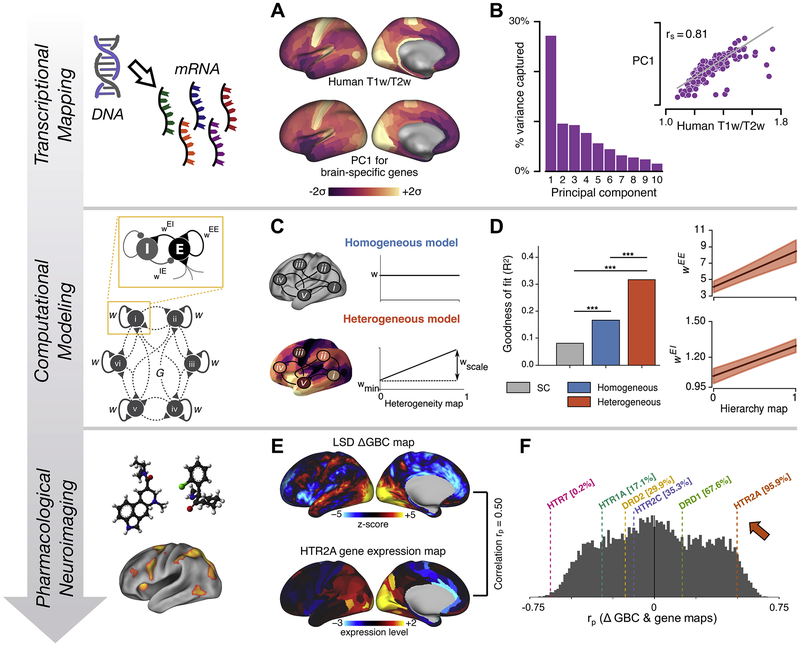
An influential principle for the large-scale organization of cortex is sensory-to-association hierarchy. In nonhuman primates, anatomical hierarchy is defined by laminar patterns of long-range projections among areas (95,96), and this neural axis captures functionally defined processing hierarchies (95,97-100). To study hierarchical specialization of microcircuitry across human cortex, Burt et al. (46) analyzed transcriptional, anatomical, and neuroimaging data from humans and monkeys. They found that the structural MRI-derived T1-weighted (T1w)/T2-weighted (T2w) map (91,101) provides a noninvasive proxy of anatomical hierarchy in primate cortex. By correlating the human T1w/T2w map to spatial profiles of gene expression from the Allen Human Brain Atlas (44,45), they found strong hierarchical gradients in expression of genes related to synaptic physiology, cell types, and cytoarchitecture. Remarkably, there is close topographic alignment between the T1w/T2w map and the dominant spatial pattern of gene expression variation across human cortex (Figure 2A, B).

Figure 2.

Heterogeneity of local circuit properties across human cortex shapes large-scale functional dynamics: insights from transcriptional mapping, computational modeling, and pharmacological neuroimaging. (A) (Top) Structural magnetic resonance imaging–derived T1-weighted (T1w)/T2-weighted (T2w) map over human cortex. The T1w/T2w map exhibits a hierarchical topography, with high values in primary sensorimotor areas and low values in higher-order association areas. (Bottom) The first principal component (PC1) of transcriptional expression levels across human cortex for brain-specific genes. PC1 is the spatial map that captures the maximal gene expression variance across cortical areas. (B) PC1 captures a dominant proportion of gene expression variance (left), and the T1w/T2w map is highly correlated with PC1 (right). (C) Computational modeling of hierarchical heterogeneity in the large-scale model. In contrast to a homogeneous model with uniform values for local circuit parameters across areas (top), in the heterogeneous model, values for local circuit parameters (e.g., recurrent excitatory strength) are scaled according to a heterogeneity map. The heterogeneity map shown is based on the T1w/T2w map to capture specialization along a sensory-association axis related to cortical hierarchy. (D) Hierarchical heterogeneity of local circuit parameters improves the fit to empirical functional connectivity, compared with the homogeneous model or the structural connectivity (SC) (left). The heterogeneous model improves the fit through a gradient of increasing recurrent excitatory strengths along cortical hierarchy (right). (E) (Top) Change in global brain connectivity (GBC) (i.e., mean functional connectivity) on resting-state functional magnetic resonance imaging induced by administration of lysergic acid diethylamide (LSD). (Bottom) Transcriptional expression levels for the gene HTR2A, which codes for the serotonergic 5-hydroxytryptamine 2A receptor. These maps are correlated (r_p = .50), with both exhibiting high values in occipital visual cortex. (F) Distribution across genes of the correlation between the transcriptional expression map and the LSD ΔGBC map. Among putative LSD-related receptor genes, HTR2A exhibits the highest similarity with the LSD ΔGBC map and is in the top 5% of all genes. E-E, excitatory-to-excitatory; E-I, excitatory-to-inhibitory; mRNA, messenger RNA. [(A) and (B) modified with permission from Burt et al. (46); (C) and (D) modified with permission from Demirtaş et al. (33); (E) and (F) modified with permission from Preller et al. (47).]

How can whole-brain models incorporate heterogeneity of local circuit properties in a principled way that is constrained by empirical data? To address this, Demirtaş et al. (33) developed a large-scale cortical circuit model incorporating hierarchical heterogeneity of local microcircuit properties. Model parameters were quantitatively fitted to multimodal human neuroimaging data, using approximate Bayesian computation and population Monte Carlo sampling to estimate posterior distributions for parameter estimates. To instantiate a hierarchical gradient, areal variation in local recurrent strengths was parametrized according to a predefined heterogeneity map, derived from the T1w/T2w map topography, which thereby constrains the topography of local circuit specialization without the need to fit separate parameters for each node in the network.

Compared with a model with homogeneous microcircuit properties (32), the T1w/T2w–derived heterogeneity map substantially improves the fit to empirical resting-state FC patterns, capturing important sensory-association differences (33). In this model comparison, the heterogeneous model may have an improved fit simply as a result of its extra degrees of freedom, raising the question of whether the T1w/T2w–derived hierarchical heterogeneity map provides a preferential axis of cortical specialization compared with other possible heterogeneity maps. The authors found that the T1w/T2w–derived map indeed yielded substantially improved fits compared with randomized surrogate heterogeneity maps. These findings identify the T1w/T2w map as a preferential axis for heterogeneity shaping FC (102,103). More broadly, this study provides a useful path forward in hypothesis-driven whole-brain modeling by using the topography of a heterogeneity map to parametrize local circuit properties across brain areas. For instance, to simulate a pharmacological perturbation, a whole-brain model can explicitly simulate the regional expression pattern of the drug target by using the corresponding gene expression map.

The studies described above provide convergent evidence that hierarchical gradients of microcircuit properties shape large-scale specialization of cortical function (90). One circuit mechanism for temporal processing hierarchies (97-99) is regional gradients in local synaptic properties (61,104), consistent with microanatomical measurements of dendritic spines on pyramidal neurons (46,61,105,106). Interestingly, the hierarchical organization of the structural connectome can give rise to temporal hierarchies even in networks with homogeneous node properties (107). Future analyses are needed to understand the how interplay between gradients in local properties and network organization of structural connectomes shapes large-scale brain dynamics (61).

Pharmacological neuroimaging may provide a unique test bed for development and validation of whole-brain models with regional heterogeneity in properties such as receptor densities. One can test for correspondence between neuroimaging effects of a drug and the regional topography of its receptor expression. Preller et al. (47) characterized regional topography of acute lysergic acid diethylamide (LSD) effects on fMRI resting-state FC. LSD robustly induced hyperconnectivity predominately in sensory areas, especially the occipital visual cortex, and hypoconnectivity in higher-order association areas (Figure 2E). These neural effects as well as psychedelic effects of LSD were absent after pretreatment with a selective antagonist of the 5-hydroxytryptamine 2A receptor. The expression map for the gene 5HT2A, which codes for the 5-hydroxytryptamine 2A receptor, exhibits a strong positive correlation with the change in mean FC (change in global brain connectivity), exceeding the correlation for other candidate LSD-associated receptor genes (47) (Figure 2E, F). Biophysically based whole-brain models can directly integrate gene expression maps to simulate the neuroimaging effects of pharmacology (33). A growing literature links transcriptomic specialization across cortex with the organization of structural connectivity and FC (45,46,108-111). Integration of transcriptomics with connectomics in whole-brain models can potentially open new opportunities to explore the circuit bases of large-scale structure-function relationships.

FUTURE DIRECTIONS

Future model development is needed to address critical questions in clinical neuroscience. As described above, the local nodes of current whole-brain models are highly simplified in their description compared with the neurobiological complexity involved in the cellular and synaptic mechanisms hypothesized to underlie disorder-related states (27,72). Current mean-field models can incorporate key neurobiological details, such as biophysically constrained dynamics and recurrent connection strengths between excitatory pyramidal neurons and inhibitory interneurons (32). This level of resolution is sufficient for simulating the effects of relatively coarse perturbations, such as overall E-I imbalance or reductions in net synaptic strength (34-37,81). However, many hypothesized disruptions in psychiatric disorders involve more fine-grained aspects of neural microcircuits, such as distinct inhibitory interneuron cell types or specific cortical layers.

With more complex models, a key computational challenge will be how to map between model parameters and simulated neural features. The effects of multiple synaptic-level perturbations may converge on a common effective circuit disruption, such as E-I imbalance. Effective degeneracies may arise if different circuit alterations similarly impact the mesoscopic aggregate measures of neural activity, as are measured with current neuroimaging modalities. Therefore, the level of the modeling should be matched to the spatiotemporal resolution of the experimental data to which it will be related. Constraining complex neural models may be facilitated through integration of multimodal functional modalities, such as combining the spatial resolution of fMRI with the temporal resolution of EEG.

Model extensions to include additional fine-grained elements can be informed by basic neurobiology and will need to relate model predictions to the limited spatial and temporal resolution of different human neuroimaging modalities. For instance, inhibitory interneuron classes in cortex differentially contribute to different oscillatory modes of circuit dynamics; disorder-related perturbations to each interneuron class should therefore make dissociable predictions for oscillations in cortical electrophysiology (112,113). These dynamics are too fast to resolve with blood oxygen level–dependent imaging but are amenable to methods such as EEG and MEG (114-116). EEG spectral features have motivated neural models such as the influential Jansen-Rit model (117) and developments incorporating further neurobiological detail (118,119).

Cortical layers differ in their oscillatory dynamics, which in turn shapes the frequency channels used in feedforward and feedback projections across the cortical hierarchy (100,120), as observed in human MEG (121). These spectral properties of hierarchical interactions were recently simulated in a laminar circuit model of monkey cortex (122), and future modeling can extend such phenomena to human neuroimaging findings. Experimentally constrained extensions of local cortical circuit models, embedded in large-scale network simulations, will expand the range of computational psychiatry questions these models can address.

Another promising direction for model extension is to incorporate subcortical substructures, such as thalamus. Dynamical neural models of a thalamocortical loop can capture key aspects of the resting-state dynamics, such as the temporal statistics of the alpha rhythm in occipital cortex from EEG (123,124). An open question is how thalamus shapes the spatial patterns of resting-state FC in cortex. Distinct thalamic nuclei interact with different regions of cortex in a bidirectional manner. Future large-scale modeling can be extended to include nodes for thalamic nuclei, with distinct projection patterns with cortex for different nuclei. These models should simulate thalamic nodes differently than cortical nodes in their local dynamics and parametrization, as the thalamus differs in its local synaptic connectivity and neuronal properties (125). The thalamus is a prominent site of dysconnectivity in schizophrenia, with preferential alterations in mediodorsal thalamus, which is interconnected with prefrontal cortex (126-133). Circuit modeling is well suited to study how disruptions of subcortical structures affect functional dynamics at the whole-brain level through large-scale recurrent cortical-subcortical interactions.

There is an acute need for computational psychiatry approaches to parse the individual variation across patients within a diagnostic category. Most prior biophysically based whole-brain models applied to psychiatric disorders have been fitted at the group level (34-37). Recent studies have found that fitting dynamical neural models to fMRI data at the individual level can yield personalized parameter estimates that correlate with clinically relevant behavioral measures (134,135). Individual-level fitting of biophysically based models has the potential to guide hypotheses of variation in neurophysiological state and characterize dimensional variation or clustering within a diagnostic category (136).

In summary, biophysically based whole-brain models of human resting-state dynamics are well positioned to impact the nascent field of computational psychiatry. This emerging modeling framework has the potential to integrate multimodal clinical neuroimaging findings and link them with translational knowledge of neurophysiology and hypothesized synaptic-level alterations in psychiatric disorders.