Enhancing Sidechain Rotamer Sampling Using Non-Equilibrium Candidate Monte Carlo

Abstract

Molecular simulations are a valuable tool for studying biomolecular motions and thermodynamics. However, such motions can be slow compared to simulation timescales, yet critical. Specifically, adequate sampling of sidechain motions in protein binding pockets is crucial for obtaining accurate estimates of ligand binding free energies from molecular simulations. The timescale of sidechain rotamer flips can range from a few ps to several hundred ns or longer, particularly in crowded environments like the interior of proteins. Here, we apply a mixed non-equilibrium candidate Monte Carlo (NCMC)/molecular dynamics (MD) method to enhance sampling of sidechain rotamers. The NCMC portion of our method applies a switching protocol wherein the steric and electrostatic interactions between target sidechain atoms and the surrounding environment are cycled off and then back on during the course of a move proposal. Between NCMC move proposals, simulation of the system continues via traditional molecular dynamics. Here, we first validate this approach on a simple, solvated valine-alanine dipeptide system and then apply it to a well-studied model ligand binding site in T4 lysozyme L99A. We compute the rate of rotamer transitions for a valine sidechain using our approach and compare it to that of traditional molecular dynamics simulations. Here, we show that our NCMC/MD method substantially enhances sidechain sampling, especially in systems where the torsional barrier to rotation is high (≥ 10 kcal/mol). These barriers can be intrinsic torsional barriers or steric barriers imposed by the environment. Overall, this may provide a promising strategy to selectively improve sidechain sampling in molecular simulations.

Graphical TOC Entry

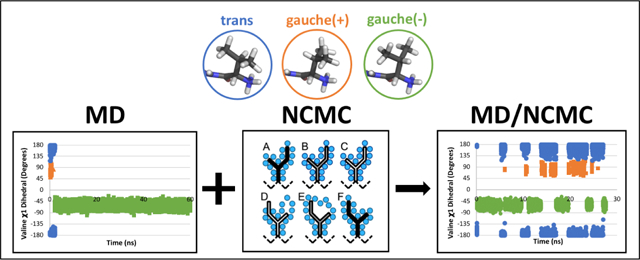
1. Introduction

Proteins are highly dynamic as they interact with hormones, ions, and other types of signaling molecules as well as other proteins. The motions that mediate these interactions comprise both large and small remodeling events, such as the shifting of domains to facilitate access to a catalytic site or the flipping of sidechain rotamers in an active site to accommodate a binding event. Classical molecular simulations have proven a valuable tool for understanding these motions, and in some cases, quantitatively predicting properties like binding affinity or the kinetics for structural transitions.^1–4

Unfortunately, some of these motions are difficult to model and predict even as advances in computing power make longer timescale motions more accessible. In some cases, simulation timescales are still not long enough to capture the relevant motions, and such difficulties are often called “sampling problems”.

Some motions are expected to be slow. For example, allosteric remodeling, protein unfolding, and ligand binding can often take microseconds to seconds. In contrast, simple sidechain rotations are often faster in comparison but can still take anywhere from ps to several hundred ns, or even longer in the interior of proteins⁵ — thus, they too can present sampling problems. Such motions are often simpler to detect and more tractable for sampling improvements than larger-scale rearrangements in biomolecules. As such, our particular focus here is on accelerating sidechain motions with our enhanced sampling methodology.

Adequately sampling the populations of local conformational states and understanding the impact of ligand binding on local configurational entropy is critical for accurate free energy predictions. Although rotamer flips may occur on accessible timescales, predicting the correct population distribution of a set of sidechain rotamer states still presents challenges, particularly if only a handful of transitions are observed over the course of a simulation. Thus, poor sampling of these transitions can bias free energy calculations used for predicting ligand binding, leading to inaccurate results.^6,7 Previous studies on T4 lysozyme L99A have demonstrated that insufficient sampling of sidechain motions during simulations for free energy calculations can lead to errors of several kcal/mol.^8–10

Sidechain rotamer states play a pivotal role in ligand binding. An extensive analysis of a carefully curated library of protein structures in the Protein Data Bank revealed that sidechain rotamer flips in binding sites are both common and critical to binding. Among the >1000 distinct apo/holo pairs evaluated for conformational changes, nearly 90% of those structures undergo at least one rotamer flip in the binding site upon ligand binding; reconfiguration of five or fewer side chains account for 90% of those cases. ¹¹

Here our focus is on accelerating sampling of sidechain rearrangements in proteins. Although conventional Monte Carlo (MC) can facilitate transitions of sidechain rotamers across energy barriers, acceptance rates of such MC move proposals are particularly low for crowded systems. Thus, here, we use non-equilibrium candidate Monte Carlo (NCMC)¹² to improve acceptance of these MC moves. By mixing NCMC sidechain sampling moves with classical molecular dynamics (MD) simulations, we improve sidechain rotamer sampling in solvated systems relative to standard MD.

2. Theory

Ultimately, one of our long-term goals is to accurately predict binding thermodynamics, even when accompanied by protein conformational change. However, such predictions require that the representative states of the system be sampled with their correct populations. Thus, slow sidechain rearrangements can pose substantial problems for accurate predictions. By focusing on enhancing sidechain sampling in biomolecular simulations, our goal is to ultimately improve the accuracy of downstream applications used for prediction of binding modes and binding thermodynamics.

2.1. Other methods can be used to observe sidechain flips

Sidechain rotamer flips are observed both deliberately and incidentally by many simulation methods. Depending on the system and the magnitude of torsional energy barriers, classical MD may sample sidechain rotamer flips and rearrangements. However, obtaining accurate populations requires simulating long enough to obtain many transitions of all relevant sidechain rotamers, which could in some cases be prohibitively long.

Monte Carlo (MC) schemes can accelerate sampling across energy barriers by allowing hops over barriers (given suitable move proposals) rather than having barrier-crossing times be limited by normal kinetics. However, MC is not well suited for solvated or other crowded systems (eg. interior of proteins) as the overwhelming majority of proposed moves result in clashes and hence will be rejected. Thus for sidechains, while very small rotational moves may be accepted, larger moves are very likely to result in collisions with the surrounding atoms and be rejected.

Since direct simulation using MD or MC is relatively impractical for improving sampling of sidechain rotamer transitions, given the exponential dependence of barrier-crossing rates on the barrier height, biased or enhanced sampling techniques such as umbrella sampling may be more suited to this problem. Umbrella sampling applies biasing techniques to augment the sampling of selected motions and can be used to enhance sidechain sampling^8,13 Although it is an efficient tool for generating the free energy landscape (or potential of mean force, PMF) of individual sidechain rotamers, its utility declines as simulations and systems become more complex.

Specifically, umbrella sampling is challenging to apply to larger systems because of practical considerations arising from the difficulty of biasing more than one or two degrees of freedom at a time; even applications to sample rearrangement of a few sidechain rotamers quickly becomes intractable. Imagine umbrella sampling an arginine sidechain where we need to sample the rotation of multiple torsions simultaneously; this would require construction of a multidimensional PMF which, while tractable, involves substantial computational cost. The situation would be further complicated if the arginine neighbored another residue that we also needed to umbrella sample. Furthermore, integrating with other types of simulations would be laborious – for example, a simulation which sampled across ligand binding modes might need a separate umbrella sampling study and associated PMF for each binding mode.

Beyond logistical challenges related to implementation, a final challenge for umbrella sampling is that it requires advance knowledge about which sidechains in a binding pocket are likely to rotate (in order to avoid wasting time umbrella sampling unimportant motions). Ideally one would like a tool which automatically determines which motions are most likely to occur. Thus, while umbrella sampling is a valuable tool, its application can quickly become complex and require considerable human intervention and planning.

Tempering and annealing MD methods, wherein the simulation temperature is allowed to vary between high and low values to help overcome energy barriers, can also be applied to enhance sampling of sidechain rearrangements. However, for slow motions, very high temperatures can be required in order to drive transitions over high energy barriers; this can lead to instability or unfolding of other regions of the system. Furthermore, raising the temperature shifts the equilibrium distribution, meaning that samples from higher temperature simulations require re-weighting for accurate free energy calculations. Methods such as replica exchange with solute tempering (REST/REST2)^8,14 provide an alternate approach for enhancing sampling that preserves ensemble distributions; in REST2, the intramolecular potential energy for regions of the protein can be scaled so as to alchemically decrease energy barriers and facilitate exploration of alternate states. Typically, REST2 is applied in binding free-energy calculations whereas here, we seek to develop a more general tool for enhanced sidechain sampling in molecular simulations.

2.2. Non-equilibrium candidate Monte Carlo provides potentially a more general tool

Here, we apply non-equilibrium candidate Monte Carlo (NCMC) to improve sampling of sidechain rotamer moves.

While related, MC and NCMC moves are executed and evaluated differently. In MC, a move is instantaneously attempted and accepted or rejected according to its impact on the potential energy of the system. For NCMC, a move proposal proceeds via a non-equilibrium switching protocol¹² consisting of a series of perturbation and propagation steps wherein the structural and thermodynamic degrees of freedom are progressively sampled. During this stepwise process, the surrounding environment of the system can react to the perturbation before the move is accepted or rejected. This is especially useful for condensed phase systems as the surrounding solvent can make way for the repositioning of other atoms. Unlike MC, move acceptance depends not on the resultant potential energy, but rather the (nonequilibrium) work performed over the course of the NCMC move. The total work is tallied and the move is either accepted or rejected according to an acceptance criterion; this ensures the resulting states are sampled from the Boltzmann distribution and are representative of the equilibrium populations. If the simulation were done at constant volume and energy (NVE), the work done in this case would simply be the total change in potential energy as in conventional Metropolis Monte Carlo; however, because we use Langevin dynamics here, dissipative work is also done in the process and contributes to the total, so the total work is not equal to the change in potential energy. Rather, we accumulate the protocol work for the proposed perturbation (the work done in the context of making the perturbation) and accept or reject based on this work.^12,15

In our case, a sidechain rotational move proposal proceeds via a series of smaller steps in which the steric and electrostatic interactions between the sidechain and the rest of the system are alchemically turned off, the sidechain is rotated, and then the interactions are progressively cycled back on (Figure 1). The move is either accepted or rejected based on the nonequilibrium work done during this process.

Figure 1: Atom interactions cycled off/on during execution of NCMC sidechain move.

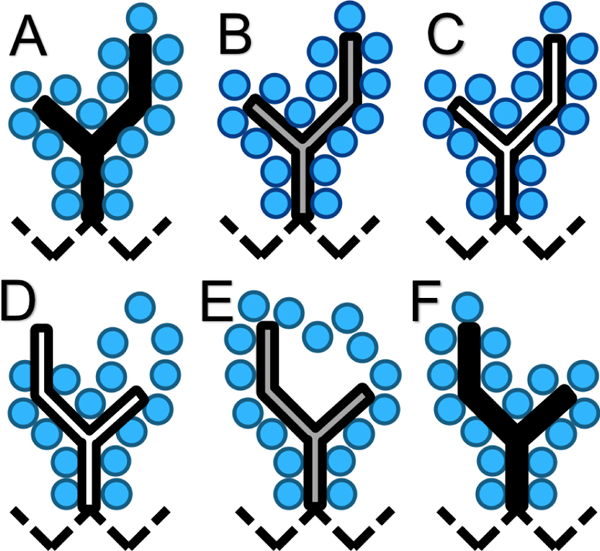
The branched isoleucine sidechain is depicted with a solid black outline while the backbone atoms are represented by a black dashed line. The blue circles represent all atoms proximal to the sidechain, including the surrounding solvent. The fill color of the branched sidechain reflects the degree of interaction with the surrounding atoms: black – full interaction, white – no interaction, and gray – partial interaction. A) The sidechain is fully interacting with the environment. B) The sidechain’s interactions are partially off, allowing gradual relaxation of the surrounding atoms. C) The sidechain’s interactions are fully turned off. D) The sidechain is randomly rotated around a significant rotatable bond; its interactions remain off. E) The sidechain’s interactions are partially turned on and the NCMC propagation steps facilitate relaxation of the rotated sidechain to resolve clashes. F) At the end of the NCMC protocol the sidechain fully interacts with the surrounding environment in a new orientation. The NCMC move is then accepted or rejected based on the work performed.

Breaking the move into smaller, discrete segments allows the system to gradually relax and respond to the perturbation, thereby facilitating more frequent acceptance of larger positional perturbations. Particularly, nonequilibrium relaxation in NCMC mitigates steric clashes and other difficulties which would result in rejection of proposals in traditional MC, allowing for more ambitious move proposals.

This is not the first study to apply NCMC to sidechain sampling; another recent study applied it with some success but limited overall benefit, using a different protocol than that employed here. Particularly, in the prior study, the nonequilibrium switching protocol only addressed the sampling of structural degrees of freedom without perturbing interact-tions within the system,¹⁶ meaning that rotation of sidechains across energy barriers involved applying a force to rotate the sidechain across any torsional barrier and past any steric obstacles. In contrast, we apply NCMC to sidechain rotations where we perturb thermodynamic properties — particularly, the strength of the interactions between the sidechain and the rest of the system — removing steric barriers to rotation (though still retaining any inherent torsional barriers).

2.3. We implement NCMC sidechain rotations as an extension of BLUES

BLUES¹⁵ is a simulation package designed to enhance sampling of ligand binding modes by combining NCMC move proposals with intervals of standard MD. When applied to a model T4 lysozyme L99A system, the BLUES approach of mixing random NCMC ligand rotation move proposals with MD enhances binding mode sampling efficiency by more than two orders of magnitude, as compared with classical MD.

2.3.1. Implementation of NCMC and MD in BLUES

NCMC moves are implemented in BLUES by first cycling off the interactions between the target and surrounding atoms prior to the move. The electrostatic and then steric interactions are turned off and on by scaling λ (a variable controlling the strength of interactions between the sidechain and the rest of the system) over a given number of n NCMC steps. First, the interactions are scaled from 1 to 0 over a series of $\frac{n}{2}$ steps, where λ=1 corresponds to full interactions and λ=0 corresponds to no interactions. When all interactions are turned off (at $\frac{n}{2}$), the target atoms are re-positioned — in this case, a sidechain is rotated — and the interactions are scaled back on in reverse order (steric and then electrostatic) from λ=0 to λ=1 over $\frac{n}{2}$ steps. The total work of decoupling, repositioning and recoupling of the atoms is summed and used to accept or reject the move. NCMC moves are alternated with intervals of traditional molecular dynamics to allow the system to undergo normal dynamics and relax further before attempting additional moves. The number of intermediate MD steps is specified by the user. BLUES also provides options for adding extra NCMC steps immediately preceding and following the rotational move (via an option called nprop) as well as freezing atoms distant from the region being perturbed during the NCMC simulation to help limit unintended motion and reduce variance in the work distribution, thereby improving move acceptance.^12,15,16 More robust documentation and details as well as the full BLUES package are freely available on GitHub at https://github.com/MobleyLab/blues, in the BLUES documentation (https://mobleylab-blues.readthedocs.io), and detailed in the work of Gill et al.¹⁵

2.3.2. Addition of sidechain moves to BLUES

Here, we build upon the existing BLUES framework by introducing a new move type, wherein selected sidechains are rotated by way of NCMC move proposals. Given a list of residue indices, BLUES identifies all significant rotatable bonds within the selected sidechains, where a significant rotatable bond is here defined to mean a rotatable bond for a torsion for which neither terminal atom is a hydrogen. We use Open-Eye’s OEChem Toolkit to traverse and interrogate bonds in the target residues.¹⁷ For each NCMC move proposal, one significant rotatable bond is randomly selected and rotated after scaling off interactions between the downstream atoms and the surrounding environment. During this process, the work done during the NCMC move proposal is tracked and the move is either accepted or rejected accordingly using the Metropolis acceptance criterion.

2.3.3. We bias our moves according to known sidechain rotamer states

Sidechain moves can be proposed in various ways, such as to random torsional angles, or via selection from a potential torsional distribution which is biased in some way. In the case of sidechain rotations, random moves would likely result in many proposed moves being rejected because they would place the torsion in a state with a particularly high energy. Because each NCMC move proposal has an associated cost, regardless of whether the move is ultimately accepted or not, it is advantageous to propose rational moves (i.e. moves to favorable rotameric states) rather than random ones. In addition to avoiding move proposals to high energy states, we also want to avoid using NCMC to attempt small, favorable moves within the same rotamer state; while small moves are more likely to be accepted, they are readily (and more economically) accessed using traditional MD.

Fortunately in the case of sidechain flips, the rotamer states are well-known; the structural conformations of the 20 natural amino-acids have been extensively characterized;^18–23 here we use this a priori knowledge of low energy rotamer states to conditionally bias move proposals to known, alternate rotamer states.

Move proposal biasing however, if applied haphazardly, can disrupt detailed balance, distorting the resulting distribution of states sampled. In order to ensure the reversibility of our move proposals, a biased move is only proposed when the rotamer is in one of the pre-defined favored states, so that move proposals and their corresponding reverse rotations have equivalent probabilities (Figure 2). For the random rotations of ligands in BLUES, the intermixing of NCMC and MD proceeds in an alternating fashion — every m MD steps, an NCMC move is proposed (e.g., NCMC→MD→NCMC→MD). When using BLUES with biased sidechain rotations, however, move proposals may be more irregular (Figure 3). Specifically, after m MD steps, an NCMC move is only proposed if the current rotamer state falls within one of the favored rotamer states, otherwise more another round of m MD steps is executed executed and the process is repeated until the condition is satisfied (eg. MD→NCMC→MD→MD→MD→NCMC→MD).

Figure 2: Move biasing is based on known sidechain rotamer states.

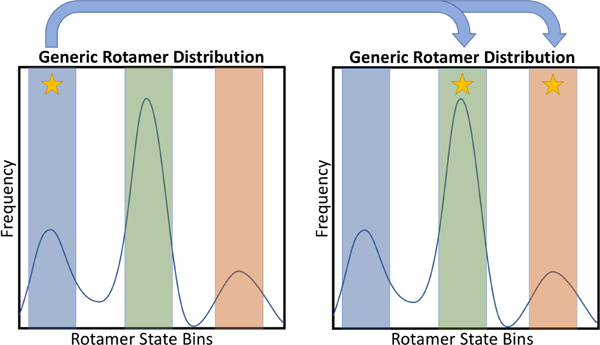
Shown here is a generic rotamer distribution possessing three dominant states. From these dominant states, one can define three equivalently sized bins highlighted in blue, green and yellow. In order for a biased move to be executed, the rotamer must start from one of these three bins. If the rotamer is in the blue state (starred on left plot), a move is randomly proposed to one of the two alternate states (starred on right plot). To ensure reversibility of biased moves, the final state of the rotamer following NCMC propagation must still fall within the defined region of one of these two alternate states. Although overall move acceptance decreases (as smaller, inconsequential moves are no longer attempted), sidechain move biasing ultimately helps enhance efficiency by ensuring that only substantial moves that sample alternate rotamer states are attempted.

Figure 3: Workflow illustration of BLUES sidechain proposals.

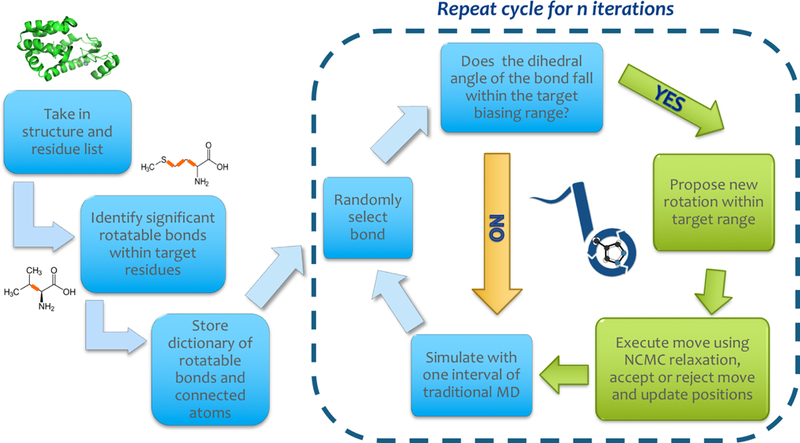
Prior to executing any sidechain type moves, a dictionary of target bonds and associated atoms is generated according to user inputs (outside of dashed box). Given the structure and a list of residue ID numbers, BLUES identifies significant rotatable bonds in those residues; these are bonds for which neither terminus is a hydrogen. It also identifies all upstream atoms that would move as a result of each significant bond being rotated. This information is compiled and stored in a dictionary. Thereon, BLUES cycles through a series of steps as it executes n NCMC sidechain rotation move proposals (shown in the dashed box). First a bond is randomly selected from the dictionary. If the angle falls within one of the rotamer bins (as described in Figure 2), a move to a new rotamer bin is proposed and executed via the NCMC protocol (represented by green path). Otherwise (yellow path), the sidechain move proposal is skipped and an additional round of molecular dynamics is executed before restarting the cycle by randomly selecting a bond.

To preserve move reversibility, the collection of starting states must match the states considered in rotational move proposals (Figure 2). Thus if, at the point of evaluation, the sidechain rotamer is within the pre-defined range of favorable states, an NCMC move is proposed to another favorable state; if not, no move is proposed and we follow up with another round of m MD steps (Figure 3). Relatedly, if an NCMC move is executed and the resulting state (after relaxation) falls outside of the range of favorable states, the move is immediately rejected. This scenario arises because the physical rotation of the atoms occurs at the midpoint of the NCMC switching protocol; as the intermolecular interactions are turned back on, the sidechain atoms can move and sometimes fall outside of the acceptable range.

As noted previously, we bias our move proposals towards “large” rotations to ensure that NCMC is efficiently enhancing sampling alternate rotamer states; NCMC rotational moves are only proposed to a rotameric state that differs from the starting state, as shown in Figure 2. For example, in the case of valine, a rotamer in the trans (χ₁ ≈ 180°) state will be limited to move proposals that would result in it occupying either the gauche(−) (χ₁ ≈ −60°) or gauche(+) (χ₁ ≈ 60°) rotameric state.

While rotamer biasing minimizes proposals to high energy states and increases the overall acceptance of larger moves (to alternate rotamer states), the overall acceptance rate suffers. Small rotational moves within the same starting state, which have a higher likelihood of acceptance, are never proposed, resulting in an overall lower acceptance rate relative to unbiased moves. It is worth noting that, in contrast to conventional MC (and as in our previous work) the acceptance ratio is NOT the key criteria for efficiency here. Specifically, we are much more interested in the acceptance rate of substantial moves than in the overall acceptance rate; one protocol might result in high overall acceptance rate but very poor acceptance of substantial torsional moves, whereas a protocol with a lower overall acceptance rate might result in much better acceptance of substantial moves. So here we examine not just overall acceptance rate but acceptance rate of substantial moves.

3. Validation

To validate NCMC with MD for sidechain rotations, we tested our method on a simple model system and compared it with brute force MD as well as umbrella sampling. Ultimately, we were interested in whether our BLUES with sidechain rotations produces correct rotamer populations consistent with those obtained from umbrella sampling.

3.1. We use a valine-alanine dipeptide as our model system

Our chosen test system consists of a valine-alanine dipeptide, explicitly solvated in water. We chose to focus our tests on a simple dipeptide because this minimizes backbone motions and reduces the possibility of the sidechains interacting with one another, which could make sampling more challenging and complicate validation or conflate sampling challenges with implementation errors.

Alanine dipeptide is a commonly used model system for molecular simulations;^24–31 however the absence of rotatable bonds involving central heavy atoms in the alanine sidechain makes it unsuited for our purposes. The next simplest dipeptide option is valine-alanine, which possesses a single significant rotatable bond in the valine sidechain that has 3 distinct rotamers as shown in Figure 4. Initially a valine-valine system was tested, but there were challenges associated with controlling for the interdependence and influence of one residue’s rotamer state on the other when generating reference results for comparison with BLUES (data not shown). A valine-glycine system was also explored, however the absence of a glycine sidechain resulted in the dipeptide backbone collapsing on itself.

Figure 4: Valine has three distinct rotamer states.

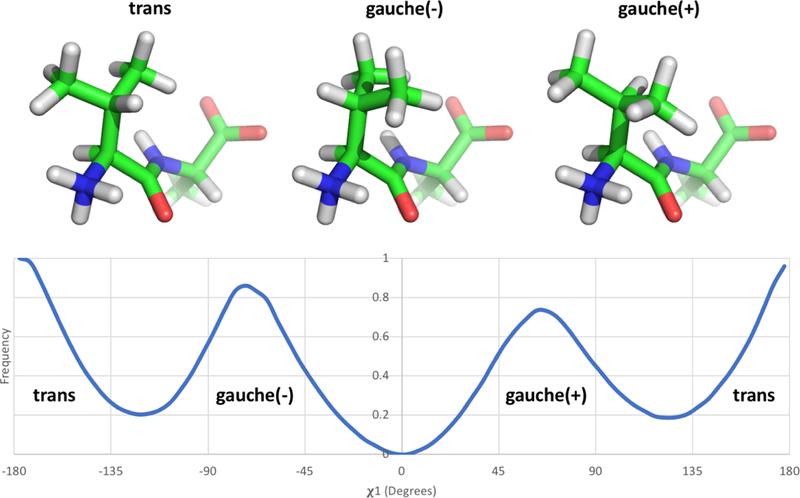
The valine-alanine dipeptide structure is represented here with the N-terminus and valine sidechain positioned at the front and the C-terminus and alanine sidechain at the posterior. The three structures show the valine sidechain χ₁ rotamer in each of its three states [trans, gauche(−), and gauche(+)]. The bottom panel shows the frequency of occurrence of the different states indicated above from simulations in solution; the data shown here is based on umbrella sampling of the valine-alanine peptide which is described and discussed further in Section 3.2 and Figure 5. While the qualitative rotameric preferences of valine are expected to remain consistent whether the sidechain is in solution or in a binding site, the actual frequency of each state is likely to vary substantially depending on its surroundings.

We opted to include explicit water in our model system so as to better represent the typical solvated state of biological systems. We also sought to evaluate whether this method is viable in a solvated system; while previous BLUES ligand rotations were carried out in an explicitly solvated system,¹⁵ the ligand itself is buried in a binding pocket mostly devoid of local solvent molecules. Further, in recent work, others have encountered challenges when performing rotational moves on valine and methionine sidechains in explicit solvent using a hybrid MD and NCMC approach,¹⁶ providing an opportunity to see whether the approach employed here might fare better.

Here, in our valine-alanine dipeptide system, we use BLUES with sidechain rotations to sample rotamer states for the valine sidechain and compute the populations. We compare these results with populations obtained from a separate set of umbrella sampling simulations performed with more conventional techniques in order to validate our BLUES-based approach.

3.1.1. Preparation of valine-alanine input files

The input files for valine-alanine were prepared using tleap from AmberTools 15.³² A linear valine-alanine peptide was generated with an N-terminal valine and a C-terminal alanine and parameterized using ff99SBildn.³³ The dipeptide was explicitly solvated in tleap with a 14Å rectangular box of TIP3P water, extending from the surface of the peptide to the box edge, and chloride ions were added to neutralize the charge of the system. The system was then minimized using sander from AMBER14³² with steepest descents running for 20,000 steps with 2fs timesteps and heated from 100K to 300K with constant volume for 25,000 steps using 2fs timesteps. Equilibration proceeded with sander for 500,000 steps and 2fs timesteps under constant pressure with positional restraints initially applied on all non-water atoms with a force constant of 50 kcal/mol/Ų and progressively lifted in increments of 5 kcal/mol/Ų over ten 50,000 step segments. The resulting topology and coordinate files of valine-alanine were used as inputs for umbrella sampling, MD, and BLUES runs.

3.1.2. Umbrella sampling methods

Umbrella sampling was executed in OpenMM 7.1.0³⁴ using a Langevin integrator with a 1fs timestep and a friction coefficient of 10/picosecond. The dipeptide backbone atoms were restrained with a force constant of 5 kcal/mol/Ų. The atoms forming the dihedral angle of the valine χ₁ were harmonically restrained with a force constant of 200 kcal/mol/Ų for 36 10°χ₁ simulation windows (0°−350°). The simulation length for each umbrella window was 3ns (3,000,000 steps).

For analysis, the reduced potential energy — a dimensionless generalized form of the potential as a function of inverse temperature, pressure, volume, chemical potential and number of particles — was computed from the trajectory of each umbrella sampling window and the multistate Bennett acceptance ratio (MBAR) was used to estimate free energies.³⁵ The reduced potential is used by MBAR to help ensure the framework can easily extend to different ensembles without reformulation.

The resulting free energy profile is shown in Figure 5. Full details are available in scripts deposited in the SI.

Figure 5: Umbrella sampling of valine-alanine peptide in explicit solvent.

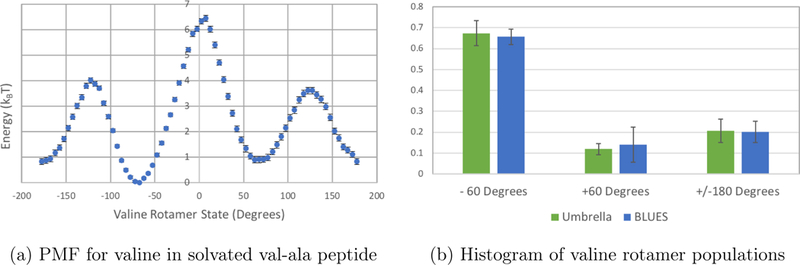
(a) As expected, the PMF analysis of the solvated valine-alanine system reflects energy valleys at the three dominant valine rotamer states (Figure 4). Error bars were generated using estimates of the standard error from MBAR analysis as provided by the pymbar package. (b) Here the populations of each valine rotamer state from umbrella sampling are plotted in green and populations from BLUES are plotted in blue. Umbrella sampling populations were estimated from the PMF using the Boltzmann relationship (Equation 1) Uncertainties were estimated by splitting the umbrella data into 10 chunks and splitting the BLUES data into 5 chunks prior to analysis, and computing the standard deviation in the population estimate across chunks.

3.1.3. MD simulation details

MD simulations were executed with OpenMM 7.1.0³⁴ using a Langevin integrator with a 2fs timestep and a friction coefficient of 10/picosecond. Backbone atoms were restrained with a force constant of 5 kcal/mol/Ų. For simulations wherein the torsional barrier was inflated (further details below), the periodic torsion force constant on the valine χ₁ dihedral was increased by 2.6X (from 3.8 to 10 kcal/mol) to mimic the highest barrier to rotation found for valine in the crowded environment of a binding pocket where the surroundings provide a steric barrier to rotation.³⁶

3.1.4. BLUES simulation details

BLUES with sidechain rotations was executed for 50,000 iterations, where an iteration is defined as one attempted NCMC move followed by at least one round of MD. Backbone atoms were restrained with a force constant of 5 kcal/mol/Ų. After each NCMC move, at least 2ps of MD was carried out before the valine χ₁ dihedral angle was evaluated. If the angle fell within the favorable range, an NCMC move was proposed and attempted; otherwise additional rounds consisting of 2ps of MD were run, with the angle re-evaluated after each, until the angle fell within specified favorable range, in which case an NCMC move was proposed. The three favorable dihedral angles for the χ₁ rotamer of valine are approximately centered near −60°, +60°, and ±180°; for these simulations, three equivalently sized rotamer biasing bins for the valine sidechain were defined as: [−74°to −52°], [52°to 74°], and [169°to −169°] as conceptually illustrated in Figure 2.

3.2. BLUES generates accurate rotamer populations

Umbrella sampling was used to obtain a potential mean of force (PMF) for the valine sidechain in the dipeptide and to obtain reference rotamer populations to validate our BLUES-based approach.

The output from umbrella sampling is the free energy landscape as a function of dihedral angle, which we can invert to estimate the population of particular rotameric states (Figure 5). The population is proportional to the negative exponential of the free energy divided by the Boltzmann factor:³⁷

$$F\left({\chi }_1\right)\alpha e^{-G/k_{B}T}$$ (1)

where F(χ₁) is the frequency of a given rotamer state χ₁, G is the energy of that state, k_B is Boltzmann’s constant and T thermodynamic temperature. To minimize population discrepancies arising from differences in backbone sampling using the different methods, the dipeptide backbone was restrained during the simulations.

Here, populations for each of the three dominant rotamer states for valine were estimated directly from the PMF and normalized to 1. The ranges for each dihedral rotamer bin were defined as gauche(−): [−115°, 0°], gauche(+): [0°, 115°], and trans: [−115°, −180°] and [115°, 180°]. When compared to the normalized rotamer states sampled by BLUES (Figure 5b), the populations agreed within statistical uncertainty. We expect these results to be independent of the selected bin ranges as the state populations should be comparable between the two simulation methods (after convergence). We have confirmed this by recomputing populations using alternate bin ranges (data not shown). This serves to validate that BLUES with sidechain rotations is indeed sampling the correct rotamer distribution and is implemented correctly.

3.3. We use the number of force evaluations to compare sampling efficiency

To compare the efficiency of classical MD and BLUES, we must account for the non-trivial cost of performing the NCMC switching protocol.

Because BLUES includes intervals of both MD and NCMC, we consider the total number of force evaluations resulting from each simulation type when comparing with MD rather than comparing the total simulation time run. In terms of wallclock time, this may not be strictly comparable – e.g. alchemical perturbations in NCMC can incur some additional costs relative to force evaluations in standard MD, but also can be made faster by holding some parts of the system fixed. However accounting for force evaluations still provides a good starting point for examination of efficiency.

For each perturbation or propagation step, NCMC executes one force evaluation. Hence a BLUES simulation consisting of MD and NCMC will have a total cost, in force evaluations (FEs) of:

$$FEs=(N+M)\times n+K$$ (2)

where N is the number of MD steps per move, M is the number of NCMC steps per move, n is the number of proposed NCMC moves, and K is the number of additional MD steps added for iterations where a rotamer is in a state outside of the target states (see yellow path in Figure 3).

For classical MD, the calculation is much simpler:

$$FEs\text{=}K$$ (3)

where K is the total number of MD steps.

3.4. MD outperforms BLUES for simple valine-alanine system

To compare the sampling efficiency of BLUES versus MD, we compute and compare the number of transitions per nanosecond of simulation time as well as the transitions per million force evaluations, accounted as described above.

Here, we define a transition as being a move of the valine χ₁ rotamer from one stable conformational state to another (eg. when χ₁ transitions from gauche(−) to trans or −60°to ±180°).

For this particular system, BLUES confers no advantage over classical MD (Figure 6c). There is no significant difference in the number of transitions per nanosecond of simulation time (1.9±0.3 vs 2.1±0.3 for BLUES and MD, respectively), but classical MD is significantly more efficient at sampling rotamer states by our metric of transitions per million force evaluations (2.3±0.4 vs 4.2±0.6 for BLUES and MD, respectively). As evidenced by the relatively high frequency of rotamer transitions for both BLUES and MD (Figure 6), the valine sidechain in our dipeptide is one that is quite mobile and readily sampled by classical MD and thus unlikely to benefit from methods that specifically enhance sidechain rotamer sampling at an added cost. As such, it is not a good test case for evaluating the potential benefits of BLUES in systems when transition barriers are large.

Figure 6: Valine-Alanine rotamer transition data where k = 3.8 kcal/mol.

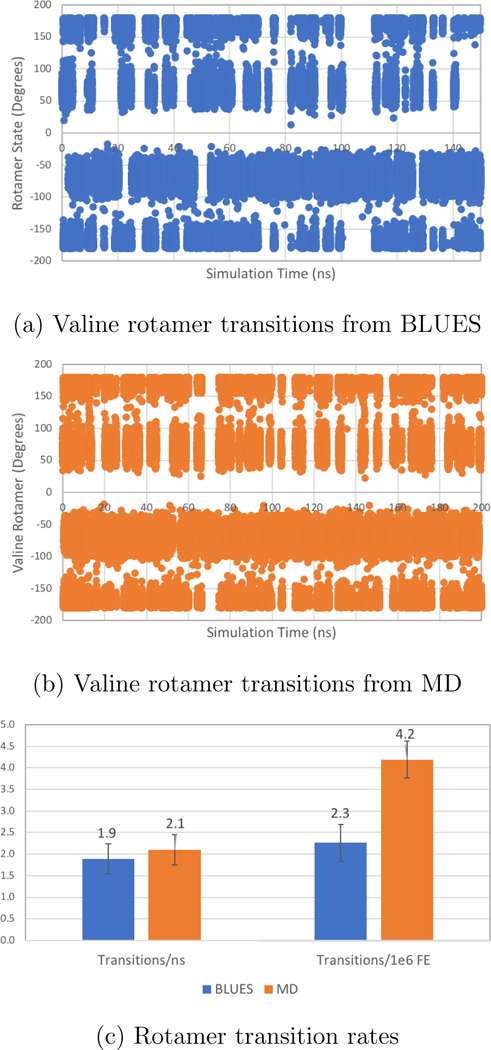
Rotamer data for valine χ₁ in solvated val-ala dipeptide system shown for BLUES and MD simulations. The x axes of (a) and (b), while different, represent roughly equivalent numbers of force evaluations (FE) when accounting for the costs of NCMC sidechain moves. Each measurement represents 2ps of simulation time. (a) The dihedral angles of the valine χ₁ rotamer from the BLUES simulation are plotted in blue. (b) The dihedral angles of the valine χ₁ rotamer from the MD simulation are plotted in orange. (c) The transition frequencies from one rotamer state to another (eg. from trans to gauche(−)) are plotted for both BLUES (in blue) and MD (in orange). On the left are the transitions per ns and on the right are the transitions per 1e6 FEs. Error bars were generated by splitting the data into five chunks for analysis.

As noted above however, there are systems or regions of systems where sidechain transitions are slow and the benefit of applying enhanced sidechain sampling methods can perhaps in some cases outweigh the costs. In the interior of proteins (e.g. as in the case of the valine 111 sidechain in the widely-studied L99A mutant of T4 lysozyme L99A^8,38,39) the maximal barrier to rotation can be >10kcal/mol due to tight packing of the surroundings such as neighboring sidechains.³⁸ To assess the relative performance of BLUES versus MD when barrier heights are higher (e.g. when torsional rotation is hindered by steric interactions with the surroundings) we updated our model system to have a higher barriers to sidechain rotation. Specifically, by artificially elevating the torsional barriers for valine χ₁ (by increasing the torsional force constants), we can use the valine-alanine system as a test case for BLUES sidechain sampling.

3.5. BLUES confers an advantage in systems where the torsion barriers are high

In the binding pocket of T4 lysozyme L99A, torsional rotation is blocked by the surrounding environment—leading to very high barriers to rotamer swaps.³⁸ Here, to mimic this phenomenon, we increase the periodic torsion force constant for the valine χ₁ by a factor of 2.6 (from 3.8 kcal/mol) such that the highest barrier to rotation is roughly equivalent to 10kcal/mol. Given the periodicity of the torsion being rotated, the maximum barrier to rotation may not represent the rate limiting barrier; nonetheless, by increasing the torsional force constant and thus the height of all barriers, we decrease the rotational mobility of the valine χ₁ and increase the typical timescale for rotation.

Compared to our unmodified valine-alanine system, there is a reduction in the total number of observed transitions between rotamer states as well as in the rates of transitions (Figure 7). When comparing transitions per nanosecond and transitions per force evaluation, BLUES exhibits a more favorable transition rate by both metrics when compared with MD (1.4±0.1 transitions/ns and 1.6±0.1 transitions/1e6 FEs for BLUES versus 0.50±0.04 transitions/ns and 1.1±0.1 transitions/1e6 FEs for MD). Thus, roughly as expected, BLUES becomes a better option for enhanced sidechain sampling as barriers to rotation grow larger.

Figure 7: Valine-Alanine rotamer transition data where k = 10 kcal/mol.

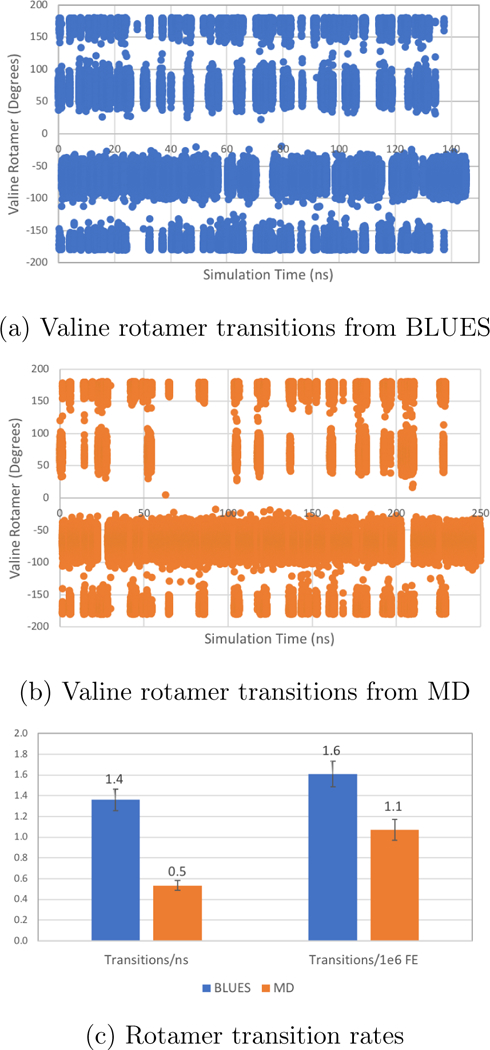
Rotamer data for valine χ₁ in solvated val-ala dipeptide system is plotted for BLUES and MD simulations where the torsional force constant (k) of valine χ₁ has been increased to 10 kcal/mol. The x axes of (a) and (b), while different, represent roughly equivalent numbers of force evaluations (FE) when accounting for the costs of NCMC sidechain moves. Each measurement represents 2ps of simulation time. (a) The dihedral angles of the valine χ₁ rotamer from the BLUES simulation are plotted in blue. (b) The dihedral angles of the valine χ₁ rotamer from the MD simulation are plotted in orange. (c) The frequency of transitions from one rotamer state to another (eg. from gauche(+) to gauche(−)) are plotted for both BLUES (in blue) and MD (in orange). Bars on the left reflect the number of transitions per ns while the transitions per 1e6 FEs are shown on the right. Error bars were generated by analyzing the data in five chunks and computing the standard deviation across chunks.

While we have demonstrated that sidechain moves in BLUES can be used to enhance rotamer sampling, they should not be blindly applied to every system. NCMC can be costly, especially for sidechain rotations where move acceptance is low, and one must first evaluate whether there is a likely barrier to rotation that is significant enough to be worth the additional cost. When barriers are low, standard MD may be more efficient than NCMC.

4. Testing on a protein binding site

In line with our ultimate goal of improving accuracy of binding free energy calculations in pharmaceutically relevant systems, we are interested in applying NCMC sidechain rotations to the binding sites of receptors, enzymes, and other biomolecules. Thus, we sought to assess the impact of our method on sampling of a sidechain rotamer in a ligand binding site.

4.1. We use T4 lysozyme L99A as a model system

T4 lysozyme’s L99A mutant (which forms a simple buried binding site that binds a series of nonpolar ligands) was chosen because it has studied extensively both crystallographically and as a computational model.^{6,8,9,39–42} A cursory search of the RCSB PDB⁴³ for T4 lysozyme L99A returns over 120 structures containing nearly more than 90 distinct ligands and recently, absolute binding free energy calculations were calculated between T4 lysozyme L99A and 141 distinct ligands, using results from a more careful search.⁴⁴

Previously it has been observed that a valine sidechain in the binding pocket of T4 lysozyme L99A remodels its rotamer state in the presence of p-xylene, as compared with other ligands like toluene.^6,8,9 With benzene and toluene bound, valine 111 (Val111) adopts a trans conformation (χ₁=180°); however in the presence of modestly larger ligands like p-xylene and o-xylene, the Val111 rotamer flips to the gauche(−) conformation (χ₁=−60°). This particular rotamer rearrangement has been used previously to test methods for sampling sidechain rearrangement on ligand binding,^6,9,14 and has proven challenging to adequately sample with standard MD simulations, driving applications of umbrella sampling⁶ and Hamiltonian replica exchange.^8,14

4.1.1. Preparation of input files for T4 lysozyme L99A with p-xylene system

The input files for T4 lysozyme L99A structure with p-xylene bound were prepared from the crystal structure (PDBID: 187L) retrieved from the RCSB Protein Data Bank. Waters were removed and hydrogens were added to the system using pdb4amber from AmberTools15.³² P-xylene was parameterized using antechamber from AmberTools15³² with GAFF version 1.7 and AM1-BCC charges. Missing atoms of the lysozyme structure were added using tleap in AmberTools15,³² and parameterized using ff99SBildn.³³ The system was explicitly solvated in tleap with a 10Å rectangular box of TIP3P water, extending from the surface of the protein to the box edge, and chloride ions were added to neutralize the charge of the system.

The system was then minimized using sander from AMBER14³² with steepest descents running for 20,000 timesteps of 2 fs each and heated from 100K to 300K with constant volume for 25000 timesteps of 2fs. Equilibration continued using sander for 500,000 timesteps of 2 fs under constant pressure with positional restraints initially applied on all non-water atoms at 50 kcal/mol/Ų and progressively lifted in increments of 5 kcal/mol/Ų over ten 50,000 step segments. The resulting topology and coordinate files of T4 lysozyme L99A with p-xylene bound were used as inputs for MD and BLUES runs.

4.2. A microsecond simulation of T4 lysozyme L99A provides baseline for comparison with BLUES

We first performed a baseline classical MD simulation of T4 lysozyme L99A bound with p-xylene for 1 microsecond and analyzed the rotamer state transitions and populations for Val111.

4.2.1. MD simulation details

Using the input files described above, we ran the microsecond production phase using PMEMD from Amber14.³² The simulation ran at 300K with a Berendsen thermostat to maintain temperature and with isotropic position scaling and a Monte Carlo barostat to maintain pressure. Further details can be found in the scripts deposited in the SI.

4.2.2. Analysis of Val111 rotamer in classical MD

Over the course of the microsecond simulation, there were 44 transitions of the Val111 χ₁ rotamer amongst the 3 possible states. The transition rate is 0.09±0.05 transitions/1e6 force evaluations or 0.04±0.03 transitions/ns. Interestingly, the transition frequency appears to decline over the course of the simulation with fewer rotameric state transitions occurring at the latter time points as shown in Figure 8. Also, the residence time in the alternate rotameric state appears very short (100–500 ps).

Figure 8: Val111 χ₁ rotamer data for microsecond MD simulation of T4 lysozyme L99A in explicit solvent.

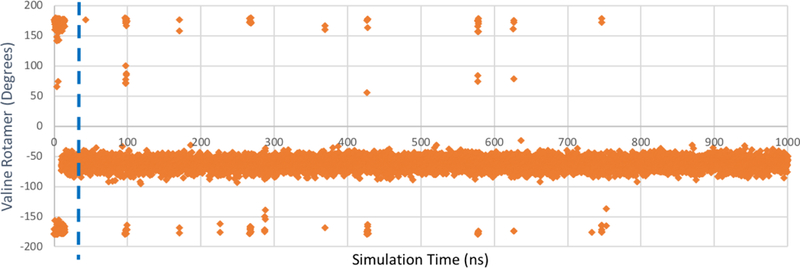
The dihedral angles of the Val111 χ₁ rotamer are plotted in orange. A total of 44 transitions of Val11 χ₁ are recorded over 1000 ns of simulation time with 500 × 10⁶ FEs. The dashed blue line reflects the approximate timescale of the associated BLUES simulations ( 25–30ns).

4.3. BLUES enhances sampling of Val111 rotamer transitions in T4 lysozyme L99A

To compare with our microsecond MD simulation, two short repetitions of BLUES were run on T4 lysozyme L99A bound to p-xylene wherein the Val111 χ₁ rotamer was targeted for enhanced sidechain sampling.

4.3.1. BLUES simulation details

Two repetitions for BLUES were run for 10,000 iterations. Between each NCMC move, we conducted at least 1000 steps (2ps in total) of MD before the state of the Val111 χ₁ dihedral was assessed, with increments of 2ps of MD added as needed until the rotamer fell within the biased dihedral range, as described previously. Each NCMC move was executed for 2200 steps with nprop = 3; nprop is a parameter in BLUES that adds additional NCMC propagation steps during the middle phase (lambda 0.2 to 0.8) of the NCMC switching protocol. The final result was that in this case, 200 steps were used between lambda values 0.0 to 0.2 (1000 steps per lambda unit), 1800 steps were used from lambda 0.2 to 0.8 (3000 steps per lambda unit), and 200 steps were used in lambda 0.8 to 1.0 (1000 steps per lambda unit). This approach increases the relative number of NCMC steps used during the alchemical cycling of the steric interactions; previously we have found that this increases move acceptance of ligand rotations in BLUES. For this system, we have also chosen to freeze atoms during the NCMC simulation to reduce the added computational cost and increase the acceptance of proposed moves. The freeze distance parameter was set to 5Å such that all atoms located 5Å or more from the sidechain were immobilized during the NCMC portion of the BLUES simulation. Further simulation details are available in scripts deposited in SI. General information about the function of nprop, freeze distance and other parameters can be found in the GitHub repository for BLUES (http://github.com/MobleyLab/blues) and in the BLUES documentation (https://mobleylab-blues.readthedocs.io).

4.3.2. BLUES results and comparison with MD

Compared to the 500 million FEs performed in the microsecond MD simulation, there were approximately 35 million FEs for each of the two BLUES runs comprising just under 30ns of simulation time as shown in Table 1. The total number of Val111 χ₁ rotamer transitions in each of these two simulations was 71 and 61. The rate of transitions (Figure 10) for these BLUES simulations were 2.0±0.8 and 1.7±1.0 transitions/1e6 FEs and 2.7±1.0 and 2.3±1.4 transitions/ns. The rotamer transition frequency per million FEs of BLUES shows nearly 20 fold improvement over traditional MD. However, because of the peculiarities in the microsecond trajectory noted previously, (eg - decrease in transitions over time, low residence time at alternate rotamer states), we decided it was necessary to further analyze these simulations.

Table 1:

Data summary for simulations of T4 Lysozyme L99A with p-xylene from alternate starting conformations.

Method [Starting Conformation]	Acceptance Rate	# of Trans	Time (ns)	FEs (106)	Trans/ 106 FEs
MD [T0] Blues [T0]	n/a 0.11%	15 91	60.0 27.7	30.0 23.9	0.5 3.8
MD [T250] Blues [T250]	n/a 0.04%	0 47	60.0 25.3	30.0 22.7	0.0 2.1
MD [T1000] Blues [T1000]	n/a 0.08%	0 30	60.0 24.8	30.0 22.5	0.0 1.3

Figure 10: Val111 χ₁ transition rates in T4 lysozyme L99A bound to p-xylene for BLUES and MD.

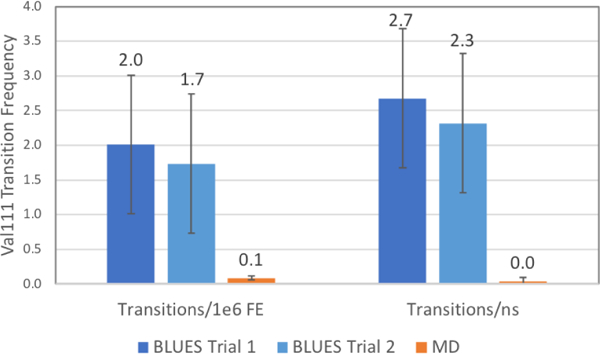
Rotamer state transition rates for two replicates of BLUES simulations are shown in dark blue and light blue while those for MD are shown in orange. On the left are transitions per 1 × 10⁶ FEs and on the right are transitions per ns of simulation time. Error bars for transition rates were generated by splitting the simulation data into 3 chunks and computing the standard deviation across chunks.

4.4. Slow relaxation of T4 lysozyme L99A backbone impacts sampling of the Val111 χ₁ rotamer

To further analyze the trajectory of T4 lyzoyme bound to p-xylene, we used MDTraj to compute the backbone RMSDs of the whole system, of the local residues, and of Val111 for both the microsecond simulation and one of the BLUES simulations.

4.4.1. Details of MDTraj analysis

For all RMSD calculations, the initial input coordinates for T4 lysozyme L99A with p-xylene were used as the reference state; all simulations started from this state. The global backbone RMSD was computed using all backbone atoms in the system. The local backbone RMSD was computed using backbone atoms from all residues within 5Å of the Val111 sidechain and the Val111 backbone RMSD was computed using the Val111 backbone atoms.

4.4.2. Analysis of backbone trajectories for T4 lysozyme L99A with p-xylene in MD and BLUES

While there were no obvious differences for the backbone of the Val111 residue or backbones of residues local to the binding site (Supplementary Figure 1), there appears to be some larger systemic relaxation that occurs over the course of the longer MD simulation (Figure 11). Previous long-timescale simulations (5 μs) of the T4 lysozyme L99A mutant in its apo form capture larger conformational changes as the protein transitions from a ground state to an excited state. During this conformational shift, the binding pocket expands and the χ₁ of phenylalanine 114⁴⁵ relaxes to an alternate rotamer state. Here, in our much shorter microsecond simulation, we may be observing some relaxation towards either the excited or ground states; further analysis is needed to determine if and how the motions we see relate to those previously reported.

Figure 11: RMSDs of T4 lysozyme L99A backbone atoms in BLUES and MD simulations.

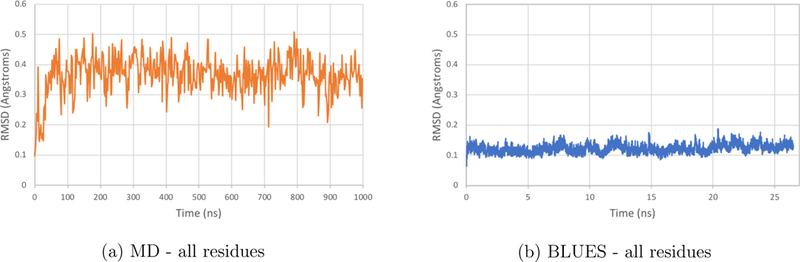
RMSDs of backbone atoms from the microsecond MD simulation of T4 lysozyme L99A with p-xylene bound are plotted in orange while those from the shorter BLUES simulations are plotted in blue. (a) and (b) RMSDs of all backbone atoms in T4 lysozyme L99A bound to p-xylene.

Overlaying the whole backbone RMSDs of BLUES and MD simulations (Figure 12) suggests that the BLUES simulations have not yet transitioned to this alternate state in the relatively short simulation time. As such, it could imply that the improvement in sidechain sampling of Val111 by BLUES may be somewhat attributable to the fact that it is limited to sampling a particular conformational state when compared with MD, a topic we address further below.

Figure 12: Overlay of backbone RMSDs of T4 lysozyme L99A for BLUES and MD (first 100ns).

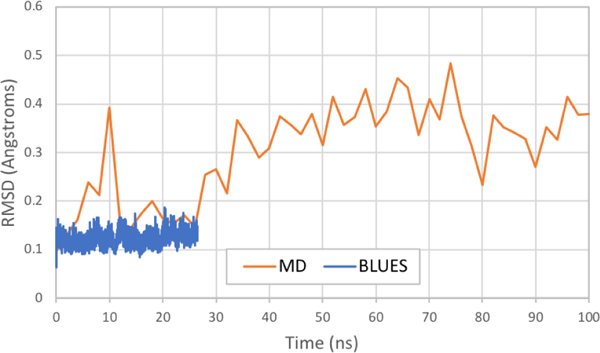
The backbone RMSDs for all residues in T4 lysozyme L99A for the BLUES simulation (Figure 11b) are plotted in blue while those from the first 100ns of the MD simulation (Figure 11a) are plotted in orange.

4.5. BLUES enhances Val111 rotamer sampling in T4 lysozyme L99A at alternate conformational starting points

In order to more clearly explore and evaluate the performance of BLUES as compared to MD given the observed backbone remodeling, simulations of T4 lysozyme L99A were run using different snapshots from the microsecond trajectory as starting points. The first set was run using the initial input coordinates for the system (time 0). The next set commenced from the 250ns point, just after the observed backbone transition. And the last set of simulations was run using a snapshot from the end point of the microsecond simulation. Hereafter, these starting points will be referred to as T0, T250, and T1000, respectively. For each starting point, 60ns of classical MD data was generated such that the trajectory frames were written with the same frequency as BLUES; this was important for ensuring that no fast transitions were missed as a result of differences in reporting frequency (as could have also affected the prior comparison for the microsecond simulation).

4.5.1. MD and BLUES simulation details for protein relaxation tests

The three sets of starting coordinates were generated from the microsecond trajectory of T4 lysozyme L99A bound to p-xylene, with the first being the input coordinates (T0), the second being a snapshot after 250ns (T250), and the third from the final state after 1 microsecond of simulation (T1000). MD was executed in OpenMM 7.1.0³⁴ using a Langevin integrator with a 2fs timestep and a friction coefficient of 10/picosecond.

BLUES simulations were run for 10,000 iterations with 2ps increments of MD between each Val111 dihedral state evaluation, repeated as needed until the rotamer fell within the biased dihedral range described previously. Each NCMC move was executed for 1004 steps with nprop = 3, such that NCMC steps were weighted toward the middle (lambda 0.2 to 0.8) of the NCMC switching protocol as described previously.

Each BLUES simulation consisted of 22–24 million FEs comprising 24 – 28ns of simulation time. Comparatively, each MD simulation ran for 30 million FEs, equivalent to 60 ns of simulation time. See Table 1 for specific FE and timescale data. Full details are available in scripts deposited in the SI.

4.5.2. Comparison of MD and BLUES from three starting conformations

As shown in Figure 13 and Table 1, the Val11 χ₁ rotamer transition frequency decreases for the simulations that start after the backbone relaxation (T250, T1000).

Figure 13: Val111 χ₁ state transitions per 10⁶ FEs from simulations from 3 distinct starting conformations of p-xylene bound T4 lysozyme L99A.

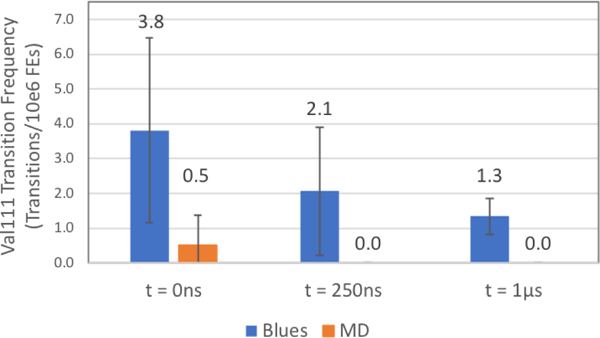
The rotamer transition rate for the 3 BLUES and 3 MD simulations are plotted in blue and orange, respectively and are in units of transitions per million FEs. As shown in Supplementary Figures (SI) 2d and 2f, there are 0 recorded transitions for MD simulations starting from the 250ns frame as well as the 1 μs frame. Error bars for transition rates were generated by splitting the simulation data into 3 chunks and computing the standard deviation across chunks.

For the MD simulations, transitions are only observed in the T0 simulation using the original input files. For all three starting points, BLUES exhibits a marked improvement in sampling the rotamer states compared to MD, with MD showing one or zero transitions to the alternate rotamer state. However, as observed in our long MD simulation, there is a decline in rotamer transition rate (and associated move acceptances) for the T250 and T1000 simulations, compared to T0. (Table 1). Thus, the rotamer transitions per million force evaluations in BLUES drops from 3.8 to 2.1 after the backbone relaxation and down to 1.3 in simulations starting from the final structure (Figure 13). This further suggests that some sort of system relaxation is causing an increase in the torsional barrier for Val111. Nonetheless, BLUES still performs favorably compared to standard MD, dramatically accelerating rotamer transitions.

For both BLUES and MD, the gauche(−) rotamer is the dominant state regardless of the starting point; however, the increase in the Val111 torsional barrier post-backbone relaxation is reflected in the relative increase in occupancy of this state. For BLUES, the relative occupancies of the gauche(−) conformation for T0, T250, and T1000 are 0.58, 0.78 and 0.88 respectively (with not enough data yet collected for convergence). By comparison, the relative occupancy of the gauche(−) rotamer state for the MD simulations is 0.97, 1.0, and 1.0, though the occupancies computed from MD are even further from convergence than those from BLUES since the number of transitions is far lower. Overall, it seems that some slow protein relaxation is impacting at least the likelihood of rotamer transitions, but potentially also the relative preference of different rotameric states.

From this data we can see the BLUES is effectively enhancing the sampling of the Val111 χ₁ rotamer. However, in the absence of efficient backbone sampling, the improvements to binding free energy calculations may be limited. While we think the slow backbone relaxation observed here may be relatively uncommon amongst receptor-ligand systems, further study of this observed relaxation and its impact on ligand binding and binding free energy calculations now seem warranted.

Despite this challenge, our results clearly show that BLUES provides accelerated sampling of sidechain motions in systems with substantial barriers to rotation. This was modestly true in our model dipeptide system, but is especially borne out for sidechain sampling in the case of p-xylene bound the T4 lysozyme L99A mutant.

5. Discussion and Future Work

Sidechain BLUES enhances sampling of sidechain rotamer states, as compared with classical MD, for systems where there is an existing (or artificially inflated) high torsional barrier. Here we have demonstrated an increase in sampling efficiency for both our valine-alanine dipeptide as well as our larger T4 lysozyme L99A/p-xylene system which has known sidechain sampling problems,^6,8,14 and this improved sampling has the potential to improve binding free energy calculations. However, in the case of the T4 lysozyme L99A/p-xylene system studied here, without long exploratory classical simulations, alternate backbone configurations could be missed; in classical MD, these appear to essentially lock the relevant sidechain in a single rotameric state by increasing the transition barrier, whereas with BLUES, transitions are still possible. Nonetheless, the BLUES framework readily allows for integration of various move types and in the future, sidechain sampling could be combined with enhanced backbone sampling.

In our work here, the application of sidechain BLUES has been limited to sampling of a single valine sidechain with one significant rotatable χ bond; most amino acid sidechains, however, have multiple rotatable bonds. Furthermore, rotamer flips in a binding pocket are not always isolated but often coupled with remodeling of neighboring amino acid rotamers. ¹¹ Moving forward we are interested in evaluating how this method performs in sampling more complex residues as well multiple sidechains in a single simulation.

As written, the sidechain BLUES method can be used to sample multiple χ angles in a given sidechain, as well as multiple such angles from several sidechains; this is implemented in our existing BLUES framework by randomly and sequentially applying the NCMC procedures to these target bonds, as described below. Given a user-input list of residues, all significant rotatable bonds are identified (Figure 3). Each sidechain bond torsion or χ_i has an associated distribution of states (where i is the selected chi index in a given sidechain): valine has one χ with three predominant states; lysine has four χ each with three prevailing states; phenylalanine has two χ, one with three dominant states and the other with two states (the aromatic bonds are not rotatable and thus are ignored). The preferred rotamer states for each of the 20 natural amino acids has been described previously and is readily obtained from the literature.^18–20,23 The biasing ranges are set by identifying the favored angles for each χ and then then creating a range (eg.±15°) around those angles. Currently, only one χ is rotated per move proposal.

So let’s imagine we are interested in specifically sampling a lysine sidechain in our BLUES simulation. For each NCMC move proposal, one of the four χ within lysine would be randomly chosen and a move would be proposed to an angle within 15° of the three favored angles for that selected χ_i. In simulations where multiple residues are sampled, all χ torsions are identified prior to simulation and one is randomly selected for each NCMC move proposal. For example, a series of move proposals where Val111 and Lys104 are sampled might proceed as follows: Move Proposal 1 - Val111 χ₁ rotated to 63°; Move Proposal 2 - Lys104 χ₄ rotated to −170°; Move Proposal 3 - Lys104 χ₂ rotated to - 91°. In the future, we may bias moves according to a continuous rotamer library and also rotate more than one bond at a time.

Given the flexibility of its implementation, BLUES can be used to explore and more readily identify residues in a protein binding site that are most likely to undergo some sort of conformational reformation, and sample such rearrangements much more efficiently than MD. It can also be mixed with different BLUES move types (some established and some in development) such as ligand flips and internal bond rotations, ligand translocations, and water translocations.

As noted, BLUES is not practical or beneficial for all applications (ie. sampling of solvent exposed residues as in our simple dipeptide), and one should think carefully about whether and how to apply the method. In practice, one may not know which residues may have high barriers to rotation and would thus benefit from enhanced sampling. In these cases, we suggest running short exploratory MD simulations for which the binding pocket residue dihedrals are plotted and evaluated to identify those with few or no transitions. This analysis could be further aided by examination of existing crystal structures (if available) of the target protein; any sidechains with slow transition rates in-silico that have alternate orientations in crystals would most likely benefit by enhanced sampling by NCMC/MD.

Furthermore, the rotamer state of a given sidechain may depend on the positions of surrounding residues. Increasing the number of MD steps between NCMC move proposals can help facilitate transient exploration of alternate conformations of the proteins and may allow for some degree of coupling among sidechain conformations. However, in its current form, sidechain moves in BLUES may not be suited for systems with sidechains that must rotate simultaneously. Future work will include testing on a system wherein a series of sidechains in the binding pocket are known to rotate in concert to assess how well BLUES works for such problem.

While NCMC is an exciting way to accelerate sampling of specific degrees of freedom known to be problematic within MD simulations, one remaining challenge is that, given the high cost of NCMC and low acceptance of sidechain moves, more work may need to be done to improve acceptance of these move types and/or reduce the additional computational cost. One potential side benefit that remains to be explored, despite the challenge of low move acceptances, can be derived from the Jarzynski relationship, which relates differences in free energies between states to the irreversible work done in moving between them. Currently BLUES tracks the work done in turning on and off interactions between the sidechain and the surrounding system, regardless of whether an NCMC move is accepted. The accumulation of this data could be used to readily identify favored or unfavored rotamer states in a system regardless of the rate of acceptance, via the Jarzynski nonequilibrium free energy relationship. ⁴⁶

As noted, further studies of lysozyme L99A binding may be needed to assess the impact of the long-timescale protein relaxation observed here and by others,⁴⁵ and it may have implications for the diverse modeling studies of binding which have previously been conducted on this lysozyme binding site.

Figure 9: Val111 χ₁ rotamer data for BLUES simulations of p-xylene bound T4 lysozyme L99A in explicit solvent.

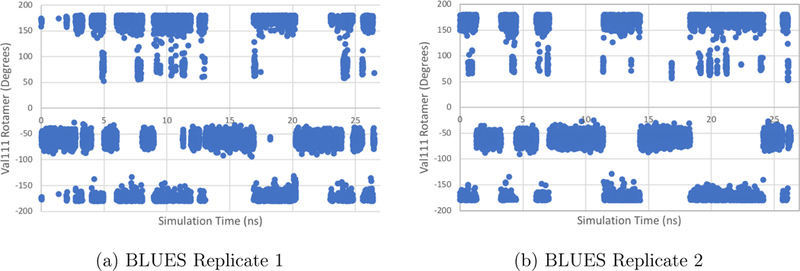
Here, Val111 χ₁ angle data is plotted for two BLUES simulations with identical user inputs for T4 lysozyme L99A in explicit solvent. Initial velocities were assigned using different random seeds in these two trials, so simulation results are distinct given the rapid divergence in trajectories which results. (a) The dihedral angles of the Val111 χ₁ rotamer for the first replicate are plotted in dark blue. A total of 71 transitions of Val11 χ₁ are recorded over 26.5 ns of simulation time with 35 × 10⁶ FEs. (b) The dihedral angles of the Val111 χ₁ rotamer for the second replicate are plotted in light blue. A total of 61 transitions of Val11 χ₁ are recorded over 26.3 ns of simulation time with 35 × 10⁶ FEs.