DeepPET: A deep encoder–decoder network for directly solving the PET image reconstruction inverse problem

Abstract

The purpose of this research was to implement a deep learning network to overcome two of the major bottlenecks in improved image reconstruction for clinical positron emission tomography (PET). These are the lack of an automated means for the optimization of advanced image reconstruction algorithms, and the computational expense associated with these state-of-the art methods.

We thus present a novel end-to-end PET image reconstruction technique, called DeepPET, based on a deep convolutional encoder–decoder network, which takes PET sinogram data as input and directly and quickly outputs high quality, quantitative PET images. Using simulated data derived from a whole-body digital phantom, we randomly sampled the configurable parameters to generate realistic images, which were each augmented to a total of more than 291,000 reference images. Realistic PET acquisitions of these images were simulated, resulting in noisy sinogram data, used for training, validation, and testing the DeepPET network.

We demonstrated that DeepPET generates higher quality images compared to conventional techniques, in terms of relative root mean squared error (11%/53% lower than ordered subset expectation maximization (OSEM)/filtered back-projection ( FBP), structural similarity index (1%/11% higher than OSEM/FBP), and peak signal-to-noise ratio (1.1/3.8 dB higher than OSEM/FBP). In addition, we show that DeepPET reconstructs images 108 and 3 times faster than OSEM and FBP, respectively. Finally, DeepPET was successfully applied to real clinical data. This study shows that an end-to-end encoder–decoder network can produce high quality PET images at a fraction of the time compared to conventional methods.

1. Introduction

Positron emission tomography (PET) is widely used for numerous clinical, research, and industrial applications, due to its ability to image functional and biological processes in vivo. PET can detect radiotracer concentrations as low as picomolar. In cancer care, this extreme sensitivity enables earlier and more precise diagnosis and staging, which is greatly correlated with early treatment intervention and better patient outcome. The benefits of PET rely strongly on quantitative PET images, necessitating a reliable method that produces high image quality.

Tomographic PET projection data (sinograms) cannot be directly interpreted by an observer, but must first be reconstructed into images. However, random process noise in the data makes this relationship ill-posed, and the reconstruction of the tracer’s distribution function can be solved as an inverse problem. Various PET reconstruction techniques exist, the most common being analytical filtered back-projection (FBP), and iterative maximum-likelihood (ML) methods. The latter includes maximum-likelihood expectation maximization (MLEM) or its incremental update version, ordered subset expectation maximization (OSEM). Typically however, images resulting from these standard methods suffer from data/model mismatches, data inconsistency, and data over-fitting, which can manifest as artifacts such as streaks and noise in the reconstructed images. In the case of ML methods, regularization can be used to overcome the ill-posedness and reduce the fitting noise in the final images. However, though regularization for PET image reconstruction has been around for a long time (Fessler, 1994; Lange and Fessler, 1995), regularization requires many iterations to make its benefits apparent. As a result, methods based on earlier work (Nuyts et al., 2002; Ahn and Fessler, 2003) have only recently been implemented clinically (Ross, 2014). Regularization is still an open problem in PET image reconstruction, and many approaches have been proposed (Sidky et al., 2012; Teng et al., 2016; Schmidtlein et al., 2017). However, there is no clear consensus on how to choose between them, or automate the regularization strength.

The use of a deep network carries some advantages, because it can be trained to at once learn the inverse of the physical model, the appropriate statistical model, and the regularization that best fits the character of the noisy data. Another advantage is its potential for computational efficiency. Viewing the deep network as a regularized inverse to the PET system model, one can envision it as performing a single forward step, as opposed to iteratively back- and forward-projecting the data numerous times (e.g., gradient descent). Hence, we propose an encoder– decoder network that uses supervised learning to solve the PET reconstruction inverse problem directly.

1.1. Related work

In recent years, deep learning has been shown to have great potential in many medical image restoration, segmentation, and analysis applications. In particular, encoder–decoder architectures have been readily used for these purposes. Convolutional encoder–decoder (CED) models are capable of stepwise compressing the input image data into a latent space representation, and then stepwise rebuilding that representation into a full dataset. CEDs and generative adversarial networks have been used to restore low dose computed tomography (CT) images (Chen et al., 2017; Wang et al., 2018; Shan et al., 2018), estimate full view from sparse view FBP images (Jin et al., 2017; Zhang et al., 2018), and reduce metal artifacts in CT (Zhang and Yu, 2018). Furthermore, neural networks have also been used to generate synthetic CT from magnetic resonance (MR) images (Liu et al., 2018), improve maximum a posteriori (MAP) PET reconstructions (Yang et al., 2018a), and improve dynamic PET MLEM reconstructions (Cui et al., 2017).

All the works above are post processing methods using reconstructed images as network input to restore image quality. It is less explored how to use deep learning methods within the PET image reconstruction process itself, i.e., as part of generating PET images directly from PET sinogram data. A number of studies have used convolutional neural networks ( CNNs ) as a regularizer in iterative CT reconstruction. In Chen et al. (2018b) an auxiliary variable was introduced to allow splitting where the iterative algorithm alternates between updating the image (deblurring) via a conventional system model and updating the auxiliary regularization variable (denoising) using a CNN autoencoder. In Chen et al. (2018a), a learned experts’ assessment-based reconstruction network was used via a 3-layer CNN to create the sparse transform matrix and the potential function or sparsity matrix. Another study by Gong et al. (2019) proposed a residual convolutional autoencoder within an ML framework to denoise PET images. Their approach is based on using the CNN to mimic a kernel representation of the image. Using an augmented Lagrangian format, the alternating direction method of multipliers (ADMM) algorithm was used to solve the resulting minimization problem. For each of the studies Chen et al. (2018b), Chen et al. (2018a), and Gong et al. (2019), although the CNN is part of the reconstruction, they still utilize a mostly conventional regularized iterative approach where the CNN is the regularizer in the reconstruction loop. This is in contrast to our proposed approach, where the network has implicitly learned the problem inverse. Yang et al. (2018b) used a CNN for regularization in MR reconstruction, and Shen et al. (2018) used deep enforcement learning for parameter tuning in iterative CT reconstruction. In a recent end-to-end approach similar to the work presented here, Zhu et al. (2018) studied image reconstruction for various medical imaging modalities by deep learning the transform between sensor and image domain. However, this work focused on MR, providing only a single low resolution example for PET data without testing or analysis. Adler and Oktem (2018) proposed an iterative end-to-end trained CNN, applied to CT image reconstruction, where they learned the primal and dual proximal updates using the primal dual hybrid gradient algorithm. Gupta et al. (2018) also used an iterative end-to-end approach for CT, where they used a CNN to project the gradient descent of a chosen objective function into the space of the underlying object (i.e., the universe of all CT images). In both cases, these methods utilize a known system model within an iterative scheme. In particular, Gupta et al. explicitly defines a noise model for the learning algorithm.

In this work we propose a novel deep CED architecture that we named DeepPET, which directly and quickly reconstructs PET sinogram data into high quality, quantitative images. To the best of our knowledge, this will be the first systematic, full-scale, end-to-end work for PET in the new field of direct deep learningbased tomographic image reconstruction. An early version of this work can be found on arXiv (Häggström et al., 2018).

2. Methods

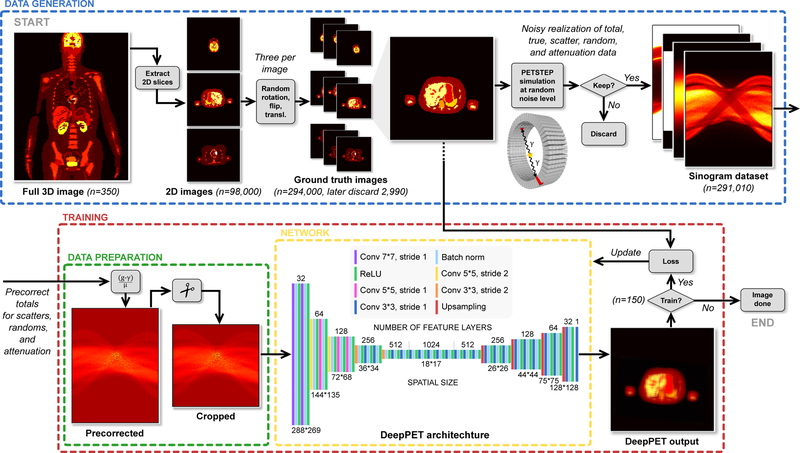
A schematic illustration of the data generation, and PET reconstruction, as well as the detailed DeepPET encoder–decoder architecture is depicted in Fig. 1.

Figure 1.

Schematic illustration of the reconstruction pipeline and the DeepPET convolutional encoder–decoder architecture. The data generation process is depicted on top. It includes the generation of 1D humanoid phantom images, followed by simulation of realistic PET scans with PETSTEP, resulting in multiple sinogram datasets at different noise levels. Experimental setup of the network training procedure is shown on the bottom, where the sinogram data is first precorrected for scatters, randoms and attenuation, and cropped before being inputted to DeepPET. Details of the DeepPET architecture is shown on the bottom middle.

2.1. Emission computed tomography image reconstruction

Traditional emission computed tomography image reconstruction is based on a Poisson noise model given by

$$g=\text{Poisson}\{Af+\gamma \},$$ (1)

where g is the measured sinogram data, A is the linear projection operator, f is the unknown activity distribution (image) to be estimated, and γ is the additive counts from random and scatter events. This model can be solved by minimizing the residual of the Kullback-Leibler (KL) divergence of the data model and a regularization term, which results in the minimization problem given by

$$f=\underset{f}{\arg \min }\left\{\langle Af,1\rangle -\langle \log Af+\gamma ,g\rangle +\lambda R(f)\right\},$$ (2)

where $\langle \cdot ,\cdot \rangle$ is the inner product, R(f) is a regularization function, and λ the regularization weight. In this form, the physical aspects of the model (e.g., geometry and statistical distribution) are accounted for by the KL-divergence term. However, the model in (2) contains many assumptions. These include the approximation of the geometric relationship between the image and detectors, the associated point spread function, the estimate of the additive count distribution, the validity of the Poisson statistical model as applied to the actual data, and the functional form of the regularizer. In particular, the optimal regularization function R is not generally known, nor is the regularization weight λ, and is an active area of research (Sidky et al., 2012; Teng et al., 2016; Schmidtlein et al., 2017).

On the other hand, a deep neural network has the potential to learn each of these aspects of the model from the data itself. The network learns the correct geometric, statistical, and regularization models, provided that the training examples are sufficiently realistic. As a result, knowledge of all these properties do not need to be explicitly included in our proposed network model. We note here that this study uses simulated PET data for network training, which also relies on assumptions such as the Poisson noise and forward models to generate synthetic data. Further consideration on this matter is found in section 4.1.

In this study, precorrected data is used, where the i^th precorrected data element is given by

$${\widehat{g}}_i=\frac{g_i-{\gamma }_i}{{\mu }_i},$$ (3)

where µ_i is the attenuation in the i^th coincidence count. Precorrecting the data mixes its statistical properties and, as a result, is generally avoided in the inverse problem formulation due to its explicit use of a particular statistical model (Poisson in the case of PET). For this study however, the solution is not explicitly dependent on any a priori data noise model making precorrection applicable. Alternatively, additional network inputs ( attenuation map and scatter+randoms estimate) could be used. However, using precorrected data instead decreases the network size, and thus memory usage and computation time, as well as reduces the risk of overfitting.

2.2. Dataset generation

The major bottleneck in many deep learning experiments is the limited size of available datasets and lack of labeled data. This problem was circumvented by generating labeled data synthetically. The open-source PET simulation software PET Simulator of Tracers via Emission Projection (PETSTEP) (Berthon et al., 2015; Häggström et al., 2016), which was implemented in MATLAB® (www.matlab.com), and was here used to simulate PET scans and generate realistic PET data. PETSTEP has previously been validated by the Geant4 Application for Tomographic Emission (GATE) Monte Carlo (MC) software (Jan et al., 2004). It includes the effects of scattered and random coincidences, photon attenuation, Poisson counting noise, and image system blurring. For this study, a GE D710/690 PET/CT scanner was modeled, with sinogram data of 288 angular ×381 radial bins. This approach is more realistic than only adding Poisson noise to sinogram data, and thus should better enable transferability of the trained network to clinical data.

In this study, the deformable humanoid XCAT digital phantom was used to produce random, patient realistic whole-body three-dimensional (3D) phantoms with 280 slices of transaxial size 128 × 128 pixels over a 700 mm field of view FOV) (Segars et al., 2010). The generation of one 3D XCAT phantom uses several hundreds of user adjustable parameters regarding the geometry, position (e.g., 3D rotations and translations), patient and organ shape and size, gender, arms up or down, as well as tracer activity of each organ and tissue. Here, these parameters were randomized within realistic ranges to generate a diverse population of 350 patients, making a total of 350·280 = 98,000 unique two-dimensional (2D) activity images (with associated attenuation µ-maps). Data augmentation was achieved by generating three realizations of each 2D phantom image by randomly right/left flipping, translating (±30 pixels in x and y-dir), and rotating (±10°) the images. Pixels outside a 700 mm circular FOV were set to zero. PET acquisitions of these phantom images were then simulated using PETSTEP, where the activity (noise) level of each image slice was randomized, and the random and scatter fractions were randomly drawn from normal distributions around realistic values for the given activity level and object size. The resulting activity distribution sinograms were then used as the Poisson parameters for generating the random counts. This ensured that the noise used in all simulation data were independently distributed. The simulation resulted in projection datasets containing noisy total, trues, scatters, randoms, and attenuation factors. The data sets with a noisy total count of < 2·10⁵ or > 8·10⁶ were discarded to stay within a clinically relevant count range. 291,010 projection datasets were kept, and the noisy total sinogram data had, on average, 10⁶ total counts. The original 291,010 phantom images were used as ground truth.

2.3. Data preparation

Precorrection for scatters, randoms, and attenuation of the simulated total projection data was done according to (3), using the scatter and randoms estimate, and attenuation data from the PETSTEP simulation. Finally, the circular 700 mm FOV leaves the image corners empty, and thereby the first and last 56 radial projection data bins also remain empty. These bins were subsequently cropped (from a total of 381 to 269) to reduce the number of network elements, before using the sinograms as network input. The use of precorrected data in DeepPET is discussed in more detail in section 4.

2.4. Convolutional encoder–decoder architecture

The encoder and decoder of the final model loosely mimicked the VGG16 network architecture(Simonyan and Zisserman, 2014), with modifications, and is depicted in detail in Fig. 1. The sinogram input data is of size 288 × 269 × 1, and the output in image space is of size 128 × 128 × 1. The encoder contracts the input data in a manner typical to CNNs. It consists of sequential blocks of convolutions with stride 2 and a factor 2 increase in the number of output feature layers, followed by batch normalization (BN) and activation by a rectified linear unit (ReLU). The convolution filter size decreases throughout the encoder, starting with the two first layers of 7 × 7, followed by 5 layers of 5 × 5, and the rest are of 3 × 3. The encoder output consists of 1024 feature maps of size 18 × 17. Each feature is a non-linear function of an extensive portion of the input sinogram. This is of special interest in this PET scenario because single points in the reconstructed image domain are represented by sinusoidal traces in the input domain. In other words, a large spread out portion of the input image data is needed to infer each reconstructed image pixel. This also motivated the initially larger convolution filter sizes of the encoder. The decoder upsamples the contracted feature representation from the encoder into PET images. Each step in the decoder path consists of an upsampling layer, increasing the image size by a factor of 1.7, a 3 × 3 convolution that halves the number of feature layers, a BN layer, followed by a ReLU. The total number of convolutional layers of the whole encoder–decoder was 31.

Several different CED designs were implemented and explored, with a different number of convolutional layers and feature layer depths, varying spatial sizes and convolution filter sizes, as well as optimization by stochastic gradient descent (SGD) with momentum on mini-batches and learning rate decay, and Adam stochastic gradient descent (Kingma and Ba, 2014). The hyperparameters learning rate and mini-batch BN momentum were individually optimized for each architecture, and the models were evaluated by comparing reconstructed image quality on the validation set. The most relevant models/settings investigated are denoted M1 through M8, as well as the ultimately chosen model named DeepPET, and are shown in Table 1.

Table 1:

Parameterization of the eight most relevant encoder–decoder architectures denoted M1 through M8, in comparison to DeepPET. Hyperparameters (learning rate and batch normalization momentum) were individually optimized. The last column shows the minimum (optimal) validation set mean squared error loss after 150 training epochs.

Name	Conv layers	Feature layers	Filter size	Optimizer	Val loss
M1	29	512	3×3	Adam	0.231
M2	29	1024	3×3	Adam	0.206
M3	31	512	3×3	SGD	0.219
M4	31	512	3×3	Adam	0.202
DeepPET	31	1024	7×7	Adam	0.187
M5	31	1024	3×3	SGD	0.219
M6	31	1024	3×3	Adam	0.199
M7	31	2048	3×3	SGD	0.211
M8	31	2048	3×3	Adam	0.197

2.5. DeepPET implementation and training procedure

The PETSTEP simulated dataset was randomly divided on a patient level into three splits. Out of the total 350 randomly generated XCAT patients (291,010 2D sinogram datasets), 245 were used for training (n = 203,305, 70%), 52 for validation (n = 43,449, 15%), and 53 for testing (n = 44,256, 15%). The three sets were kept separate throughout the study.

The network was implemented in PyTorch (www.pytorch.org), trained on NVIDIA DGX-1 graphics processing units (GPUs), and tested on a NVIDIA GTX 1080Ti GPU. The mean squared error (MSE) between model output and ground truth image was used as loss function,

$$\text{MSE}=\frac{1}{n}\sum _{i=1}^n{(x_i-y_i)}^2,$$ (4)

where x is the model image, y the ground truth, and n the number of image pixels. Because SGD was found to yield poorer results, the model was optimized using the Adam optimization method. Training hyperparameters were: learning rate 10⁻⁴; weight decay 10⁻⁵; batch size 70; BN momentum 0.3; bilinear upsampling. Different learning rates and momentums were explored, and the optimal (on the validation set) ones were those used in the final model. The model was optimized on the 291,010/70 = 4158 mini-batches of the training set over 150 epochs, and the MSE was calculated on the validation set every 5th epoch. After finishing training, the model with optimal performance on the validation set was used on the test set.

2.6. Image reconstruction

The precorrected and cropped test set PET sinograms were reconstructed into images by a single forward pass through the trained DeepPET. In addition, the sinograms were also reconstructed using conventional techniques implemented in PETSTEP ( here on a GPU); FBP using precorrected data and a 0.5 frequency scale factor for a Shepp-Logan filter, and OSEM with 5 iterations and 16 subsets using in-loop corrections to avoid altering the statistical distribution of data. For both methods, the images were post-filtered with a 9.0 mm full width half maximum (FWHM) Gaussian. The FBP and OSEM reconstruction settings (0.5–1 frequency scale factor in steps of 0.1, 1–15 iterations, and 0–30 mm post-filter FWHM in steps of 0.5 mm) were optimized using 100 unique activity images generated in the same way as described previously in section 2.2. Each image was then simulated 10 times with PETSTEP using the same noiseless count, into 10 independent noise replicates (total 1,000 images). These 1,000 images were used solely for this optimization. The optimal settings (later used on the test set) were deemed the ones yielding the minimum relative root MSE (rRMSE),

$$\text{rRMSE}=\sqrt{\text{MSE}}/\overline{y},$$ (5)

where ȳ is the ground truth average pixel value.

2.7. Application on clinical data

As a final qualitative test, the trained DeepPET model was applied to real data from two separate GE D690 PET/CT patient scans. The clinical 3D PET data was first precorrected, then converted into stacks of 2D slice sinograms by single slice rebinning, and then inputted to DeepPET. As before, the sinograms were also reconstructed with FBP and OSEM.

2.8. Image quality evaluation

For image quality evaluation, three metrics were used. The first was the structural similarity index (SSIM) (Wang et al., 2004), used for visually perceived image quality where image structure is taken more into account. The higher SSIM value the better, where 0 ≤ SSIM ≤ 1 and SSIM = 1 if and only if the compared image is identical to the reference (ground truth). For the second metric we used rRMSE according to (5). We finally used the peak signal-to-noise ratio (PSNR) as the third metric, providing similar information as the RMSE,

$$\text{PSNR}=20\cdot {\log }_{10}\left(\frac{y_{\max }}{\sqrt{\text{MSE}}}\right),$$ (6)

but in units of dB. Here, y_max is the maximum value of the ground truth image.

3. Results

The average loss of the training and validation sets as a function of training epoch is depicted in Fig. 2. As shown, the loss decreases as a result of the network learning to better represent the features of the data.

Figure 2.

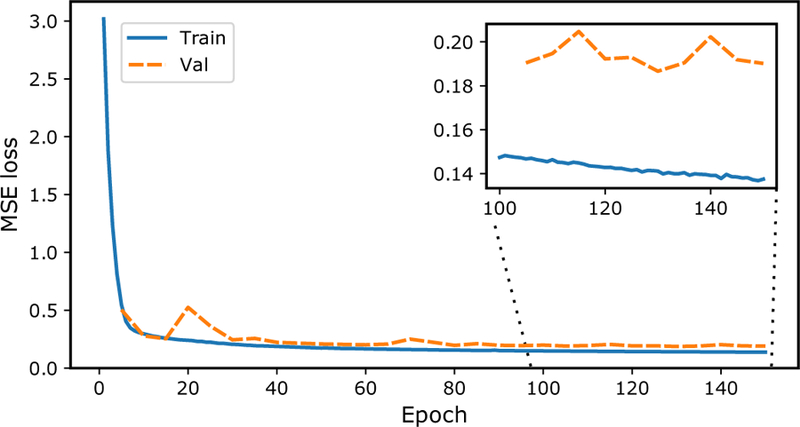
Convergence behavior of average mean squared error (MSE) calculated between the ground truth simulation and the reconstructed images. Depicted is the training error (blue) and validation error (orange) for each epoch, showing that the error decreases as the network learns to represent the data features.

The average bias (MSE minus variance) versus noise (variance between noise replicates) for the 100 ×10 images of the different OSEM iteration numbers, and FBP frequency scales for the optimal postfilter FWHM of 9 mm, in comparison to DeepPET, is seen in Fig. 3. As seen, DeepPET places superior to both FBP and OSEM with comparatively lesser noise and bias. The average (n = 44,256) reconstruction time per image in the test set, together with the average SSIM and rRMSE using FBP, OSEM, and DeepPET are found in Fig. 4. With an average execution speed of 6.47±0.01 ms per image, DeepPET compared favorably to the conventional methods of FBP at 19.9±0.2 ms (3 times slower), and OSEM at 697.0±0.2 ms (108 times slower). Furthermore, the resulting image quality of DeepPET also outperformed the conventional methods in terms of SSIM, being 0.97958±0.00005 for DeepPET, compared to 0.8729±0.0004 for FBP (11% lower), and 0.9667±0.0001 for OSEM (1% lower). In addition, the average rRMSE of DeepPET was the lowest at 0.6012±0.0009, with values of 0.922±0.001 for FBP (53 % higher), and 0.6669±0.0007 for OSEM (11% higher). The PSNR was highest for DeepPET at 34.69(2) dB, while 30.85±0.02 dB for FBP (3.84 dB lower), and 33.59±0.02 dB for OSEM (1.09 dB lower). Standard errors of the means are noted in parentheses. Comparing the 44,256 test set images one-by-one, DeepPET had a higher SSIM than FBP and OSEM for 100% and 80% of the images, respectively. Equivalently, DeepPET had a lower rRMSE than FBP and OSEM for 100% and 75% of the images (same numbers for PSNR). In terms of reconstruction speed, DeepPET was faster than both FBP and OSEM for 100% of the images.

Figure 3.

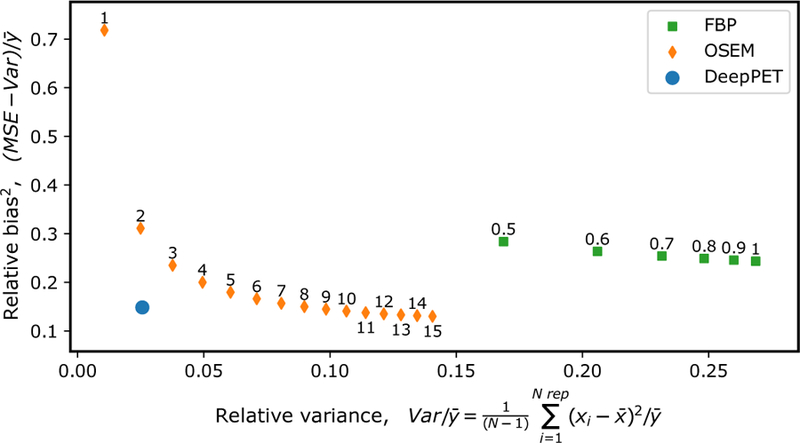
Average bias (relative MSE) versus noise (relative variance) for 100 unique images with 10 noise replicates each, for the optimal postfilter of 9.0 mm. FBP points are labeled with their frequency scale, and OSEM points with the number of iterations. Here, N=number of replicates (10), x=reconstructed image, y=ground truth.

Figure 4.

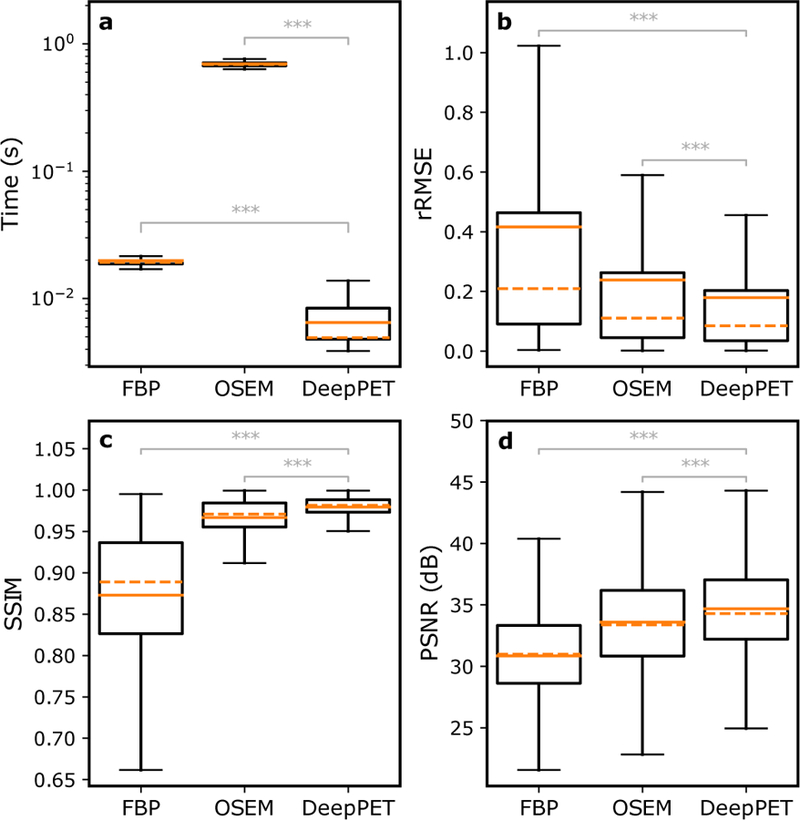
The average (n = 44,256) reconstruction time per image (a), as well as average relative root mean squared error (rRMSE) (b), structural similarity index (SSIM) (c), and peak signal-to-noise ratio (PSNR) (d) in the test set for the different reconstruction methods, showing that DeepPET outperforms both FBP and OSEM (ANOVA p<10⁻¹⁰) in terms of image quality (lowest rRMSE, highest SSIM, highest PSNR) as well as reconstruction speed. The plots depict the mean (solid orange) and median (dashed orange) values, the interquartile range (IQR, box), and the 25/75% quartile −/+ 1.5 IQR (whiskers).

Since the same sinogram data was reconstructed using different methods, a repeated measures one-way ANOVA test with Bonferroni correction was used to confirm that the improvements observed using DeepPET over both FBP and OSEM, in terms of reconstruction speed, SSIM, rRMSE, and PSNR were statistically significant (p<10⁻¹⁰).

The SSIM values for the images are high (close to 1) for OSEM and DeepPET since each value is calculated as the average over the entire image, and there is a lot of background in the images that is correctly reconstructed for these methods. Masked SSIM values, i.e. the SSIM over only those pixels with nonbackground ground truth, were 0.8816±0.0002 for DeepPET, 0.8729±0.0004 for FBP (1% lower), and 0.8136±0.0004 for OSEM (8% lower). Corresponding values for rRMSE are 0.2163±0.0003, 0.3019±0.0005 (40% higher), and 0.2441±0.0003 (13% higher) for DeepPET, FBP and OSEM, respectively. The superior performance of DeepPET over FBP and OSEM thus still holds for masked SSIM (ANOVA p<10⁻¹⁰). As expected, the performance of FBP relative the other methods increases when masking off the background, which for FBP contains notorious streak artifacts.

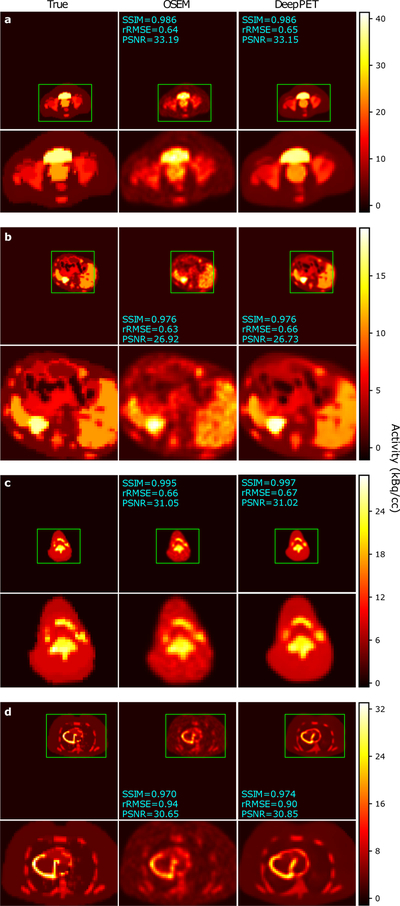
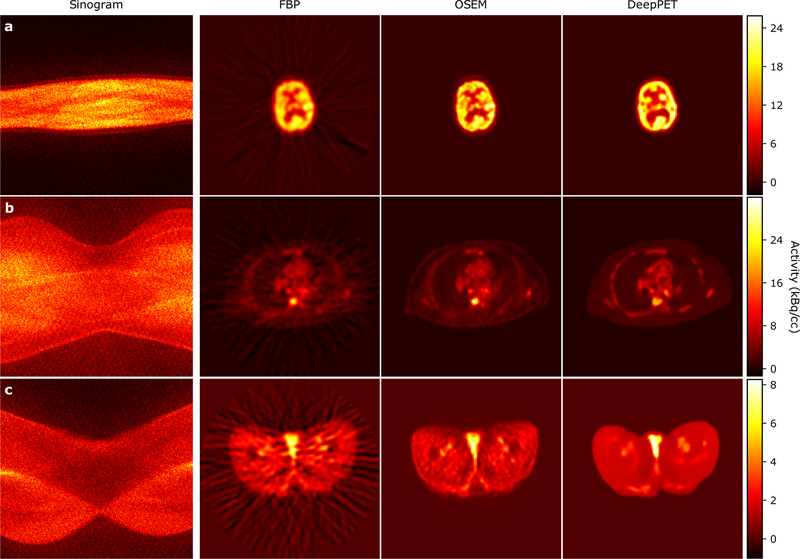
Example FBP, OSEM, and DeepPET reconstructions from the test set are shown in Fig. 5. The images were randomly chosen with constraints on body location to obtain diverse images. As shown, DeepPET generated less noisy images while preserving edges, which is especially apparent in large homogeneous areas (e.g. Fig. 5c, g). Qualitative differences between OSEM and DeepPET are more discernible in Fig. 6. For this figure we purposely chose to show cases where OSEM has similar image quality to DeepPET based on the rRMSE and/or SSIM measures to show that even in these cases, the OSEM images appear noisier, less detailed, and having less sharp edges. The same or better performance of OSEM with these metrics appears incongruous with the visual quality of the images wherein fine details appear to be better preserved with less noise with our DeepPET-based method.

Figure 5.

Random test set reconstructions using both conventional methods, as well as the proposed deep learning-based method. Left to right: PET sonogram (network input prior to precorrection), ground truth, FBP, OSEM, and the DeepPET reconstruction. Sinograms are labeled with their total counts, and images with SSIM, rRMSE, and PSNR relative ground truth.

Figure 6.

Test set reconstructions where OSEM is nearly equal to DeepPET in terms of image quality metrics, albeit mostly appearing noisier and less detailed. Left to right: Ground truth, OSEM, and the DeepPET reconstruction. Images are labeled with SSIM, rRMSE, and PSNR relative ground truth.

As a proof of concept, in Fig. 7 we show DeepPET reconstructions using the clinical data. Because this was real patient data, there was no ground truth for comparison. Despite the fact that DeepPET was trained using simulated data, when using real patient data it produced perceptually smoother and more detailed images compared to either OSEM or FBP. It should be noted that the patient sinogram data was noisy due to the extraction of 2D slices from the 3D data. A more in depth discussion of the results and their significance is given in the next section.

Figure 7.

Reconstructions of three real patient sinograms (hence no ground truth available). Left to right: PET sinogram (network input prior to precorrection), FBP, OSEM, and the DeepPET reconstruction. As shown, DeepPET produces smoother images while keeping a high level of sharpness and detail, compared with the other methods.

4. DISCUSSION

The use of deep learning methods for medical imaging applications is rapidly increasing, and tomographic medical image reconstruction is no exception, with new approaches being proposed on an accelerated time line. However, the vast majority of these approaches are post-processing approaches, where a noisy initial image is denoised/restored. Alternatively, a few groups working with CT sinogram data are exploring the iterative schemes where deep learning methods augment the iterative process (Adler and Oktem, 2018; Gupta et al., 2018). These methods require the use of a tomographic projection operator, increasing their computational effort. In this study, we instead propose an end-to-end deep learning image reconstruction that directly uses the sinogram data to create images without the need of a projection operator. In fact it is precisely for these reasons, that there are no forward- or back-projection operations, nor any iterations, that make DeepPET’s reconstructions so fast.

As shown in the results, DeepPET was 108 times faster than standard OSEM and 3 times faster than FBP. DeepPET only requires one pass to reconstruct an image from sinogram data, whereas traditional techniques require multiple iterations. Regularized iterative reconstruction methods were not compared in this study, but the speed gain is expected to be far greater due to the larger number of iterations typically used to ensure more uniform image convergence, and likely longer computations per iteration for regularized methods. On a clinical system ( here a GE D690/710), with the vendor algorithms implemented on a dedicated reconstruction computer, a typical clinically used OSEM reconstruction takes approximately 90 s for a 3D sinogram (553 times more data than 2D), roughly equivalent to 163 ms for 2D, which is 25 times longer than DeepPET. Furthermore, although our network was trained on state-of-the-art Volta GPUs on NVIDIA DGX-1 compute nodes, testing was done on a common NVIDIA GTX 1080Ti GPU. For clinical practice, only single forward passes are required for image reconstruction, limiting the demand for large memory and computational power, enabling the use of a simple GPU. For full 3D reconstruction, due to oblique projections, the sinogram data size increases by a factor of more than 500, which limits the use of some GPUs due to memory issues.

The bias versus variance trade-off depicted in Fig. 3 shows that neither FBP nor OSEM are capable of producing images that simultaneously have the same low bias and variance as DeepPET. Hence, according to our results, images of the same quality as those produced by DeepPET are unobtainable using conventional, unregularized image reconstruction methods (i.e., FBP and OSEM). DeepPET reconstructions (Fig. 5, and 6), especially in comparison with FBP and OSEM, are consistent with our conjecture that the DeepPET model learns not only the mapping from sinogram to image, but also the appropriate noise model, effectively regularizing the ill-posedness of the inverse problem. This is important because it allows the use of precorrected data, which results in a simpler CED architecture and a smaller memory footprint, both contributing to improved reconstruction speed. We add that this may also improve images from acquisitions with a lot of deadtime, where the Poisson noise model is less accurate. As a result, the projection data noise is suppressed during the forward pass, producing smooth images while preserving resolution.

The application of the trained model on real patient data (Fig. 7) shows the potential for clinical use of the DeepPET system, where it can reconstruct smooth images while preserving edges. However without ground truth it is difficult to make quantitative claims, or judge the authenticity of structures that are made apparent with DeepPET. Furthermore, since PET data is acquired in 3D, individual 2D slices were extracted to use in DeepPET, and no time-of-flight information was used. The clinical data thus had higher noise, and the resulting images were likely of lesser quality than those resulting from full 3 D data.

One major benefit with PET over many other modalities is that it is inherently quantitative. Hence, the network input and output, though differing in size and structure (as they come from different data domains: sinogram vs. image), are related to one another, where pixel units go from sinogram counts ( registered photon pairs) on the input side, to image pixels in activity concentration (Bq/cc) as output. In addition, the spatial correlation between neighboring bins (pixels) in the sinograms (related via system model) are not the same as those in the reconstructed image. The use of a convolutional encoder is therefore not as intuitive as when working with ordinary image input. Due to memory, time, and over-fitting limitations, a fully connected network on the other hand is difficult or even infeasible for large 2 D (and 3D) data due to the huge number of network weights. As an example, a single fully connected layer taking one sinogram of 288×381 to a 128×128 image requires about 2 billion weights.

Furthermore, although this work focuses on PET, the methodology presented is also valid for other types of tomographic data, SPECT and CT being the most relevant examples. SPECT data is even noisier than PET data and has poorer intrinsic resolution making a prime candidate for our approach. CT data is much less noisy than PET, and has higher spatial resolution, also making it a suitable candidate for our approach.

4.1. Limitations

In this study we use synthetic data instead of real patient data. This is necessary to provide ground truth for the training data. In particular, the simulations used in this study use a forward projection operator and noise models as described in the PETSTEP papers (Berthon et al., 2015; Häggström et al., 2016), and source distributions defined by the XCAT model. While the use of PETSTEP provides the benefit of allowing us to rapidly generate ground truth images and simulated projection data, it implicitly introduce both system and noise models into the training data. Furthermore, it is possible that the network will learn the simplifications and assumptions used in the simulations, which may not be accurately reflected in real patient data.

These issues can be alleviated by using a full MC simulation model such as GATE, which could provide a more accurate representation of the sinogram data. However, the use of MC can be computationally expensive, where such simulations can take days, weeks, or even months to produce the projection data for one realization. For a deep learning study of this scale, using hundreds of thousands of images, this is impractical. We note that PETSTEP has been validated against GATE MC and proven to provide realistic results, which gives us confidence that our approach is reasonable.

With regard to the synthetic patient source distributions, in this study the XCAT phantom was used. Although this phantom is realistic, and we randomly set its adjustable geometry, shape, material and activity parameters, such population is not quite the same as real patient population. Nevertheless, the training, testing, and validation data used here that are based on XCAT do have a wide ranges of appearances and contrasts, containing everything from highly detailed regions to smooth homogeneous ones, as well as large, small, hot, and cold structures. Furthermore, application on real patient data (Fig. 7) shows that DeepPET performs well in clinical scenarios after training on We have not included any comparisons to regularized iterative techniques. Because this work represents a proof of concept, we believe it is enough to only compare DeepPET to recon-XCAT.

We have not included any comparisons to regularized iterativetechniques. Because this work represents a proof of concept, we believe it is enough to only compare DeepPET to reconstruction methods that are widely available in the clinic, namely OSEM. Another reason we have not compared DeepPET to regularized image reconstruction is that regularization weights are often difficult to automate, especially when the underlying source distribution varies both in and between patients ,and often requires user oversight and input (Schmidtlein et al., 2017). For tens of thousands of images like in this study, this makes this approach challenging or even infeasible. DeepPET on the other hand has an inherent regularizer learned from the training data that utilized many diverse anatomies and noise levels.

Finally, others have pointed out that end-to-end networks for tomographic image reconstruction, such as the one described in this paper, can have generalization errors that do not have a well defined bound (Gupta et al., 2018). As a result, there is no guarantee that any particular data used in this type of network will produce artifact free images. However, because of the nature of this approach, using large and diverse test data sets, one can statistically quantify the probability distribution of large local errors (e.g., the ℓ_∞-norm) and giving the frequency and size of the reconstruction errors. We conjecture that this type of approach, when outliers can be shown to be acceptably rare, will provide clinicians with confidence in the resulting images.

5. Conclusions

To the best of our knowledge, this paper presents the first systematic study of an end-to-end deep learning model that is capable of directly reconstructing quantitative PET images from sinogram data without the need of system and noise models. The major contributions of this work are four-fold: (i) We proposed a novel encoder–decoder architecture for PET sinogram data, (ii) that does not rely on any assumptions with respect to the physical system, noise distributions nor regularization model, (iii) which on average increases the reconstruction speed over the conventional OSEM image reconstruction by a factor of 108, (iv) while also improving image quality by on average 1% (SSIM), 11% (rRMSE), and 1.1 dB (PSNR) respectively. We are confident that our approach shows the potential of deep learning in this domain and is part of a new branch in tomographic image reconstruction. Ultimately the gain in quality and speed should lead to higher patient throughput, as well as more reliable and faster diagnoses and treatment decisions, and thus better care for cancer patients.