SUMMARY
The cerebellum has long been implicated in tasks involving precise temporal control, especially in the coordination of movements. Here we asked whether the cerebellum represents temporal aspects of oscillatory neuronal activity, measured as instantaneous phase and difference between instantaneous phases of oscillations in two cerebral cortical areas involved in cognitive function. We simultaneously recorded Purkinje cell (PC) single-unit spike activity in cerebellar lobulus simplex (LS) and Crus I and local field potential (LFP) activity in the medial prefrontal cortex (mPFC) and dorsal hippocampus CA1 region (dCA1). Purkinje cells in cerebellar LS and Crus I differentially represented specific phases and phase differences of mPFC and dCA1 LFP oscillations in a frequency-specific manner, suggesting a site- and frequency-specific cerebellar representation of temporal aspects of neuronal oscillations in non-motor cerebral cortical areas. These findings suggest that cerebellar interactions with cerebral cortical areas involved in cognitive functions might involve temporal coordination of neuronal oscillations.
In Brief
The cerebellum has long been implicated in tasks involving precise temporal control, especially in the coordination of movements. McAfee et al. show that the cerebellar principal neurons, Purkinje cells, represent precise temporal information about the phase and phase differences of neuronal oscillations occurring in two non-motor-related cerebral cortical structures.
Graphical Abstract

INTRODUCTION
Cerebellar function has long been linked to tasks involving precise timing and temporal coordination (Braitenberg, 1967; Ivry et al., 2002) in sensory-motor tasks. Popa and colleagues have shown that cerebellar inactivation disrupts the coherence, i.e., the stability of phase relationships between oscillations in cerebral cortical sensory-motor circuits (Popa et al., 2013). These findings implicate the cerebellum in the temporal or phase alignment of oscillatory activities between cerebral cortical structures. Watson et al. (2014) showed increased theta coherence between the medial prefrontal cortex (mPFC) and the cerebellar fastigial nucleus in freely moving rats during locomotion, but not when the rats were at rest. Granger causality analysis revealed a directionality of the coherence in the fastigial-mPFC direction, suggesting that cerebellar output could modulate the phase of mPFC theta oscillations in a behavior-dependent manner (Watson et al., 2014).
Here we tested whether the phase of spontaneous local field potential (LFP) oscillations in the mPFC and dorsal hippocampal CA1 region (dCA1) is represented in cerebellar Purkinje cell (PC) spike activity in awake, head-fixed mice. We use the term representation in the sense of PC activity reflecting the occurrence of specific oscillation phases or phase differences. Our reasoning behind targeting these three areas is based on their potential joint involvement in spatial working memory (SWM) (Lefort et al., 2015) and on findings of increased coherence between mPFC and dCA1 during the decision-making process in a SWM task (Gordon, 2011).
We asked whether phase and/or phase relationship of oscillations in the mPFC and CA1 are represented in the cerebellum and investigated whether representations in lobulus simplex (LS) and Crus I would show site-specific differences with respect to the representation of phase or phase differences. To address this question, we recorded PC simple spike activity in LS or Crus I while simultaneously recording LFP activity in mPFC and dCA1.
RESULTS
Link between Oscillation Phase and PC Activity
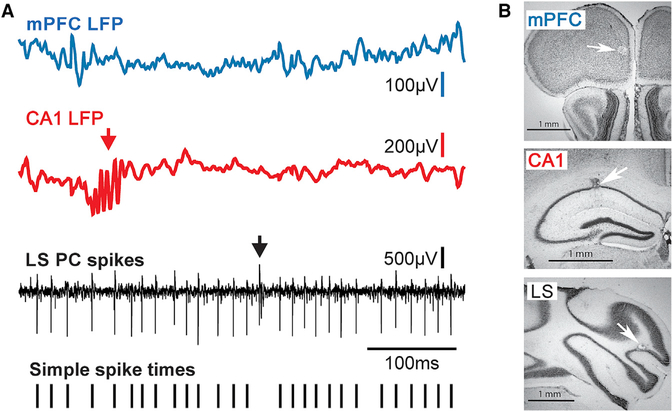
We obtained recordings of LFP activities in the mPFC and dorsal CA1 region while simultaneously recording PC simple spike activity in the cerebellar LS or Crus I. Raw data examples of LFP activity recorded in the mPFC and CA1 and single-unit PC spike activity in LS are shown in Figure 1.
Figure 1. Raw LFP and Single-Unit Spike Signals and Anatomical Reconstructions of Recording Sites.
(A) Raw LFPs recorded in the mPFC (blue trace) and CA1 (red trace), and raw single-unit PC spike activity recorded in the cerebellar LS (black trace). The arrow in the LFP recording from the CA1 region points to a sharp wave ripple event, a brief high-frequency oscillation characteristic for the hippocampus. The presence of sharp wave ripples in the LFP recordings was used for online verification of electrode tip placement within CA1. The arrow in the trace of raw PC spike activity marks the occurrence of a complex spike, which reflects input from the inferior olive. Complex spikes are characteristic for PCs and were used for online identification of PC activity. The bottom trace shows tick marks representing the time sequence of simple spikes extracted from the raw trace and used for subsequent analysis.
(B) Photomicrographs of Nissl-stained sections of the mPFC, CA1, and cerebellar LS showing microlesions at recording sites (white arrows).
Scale bars in all three panels are 1 mm.
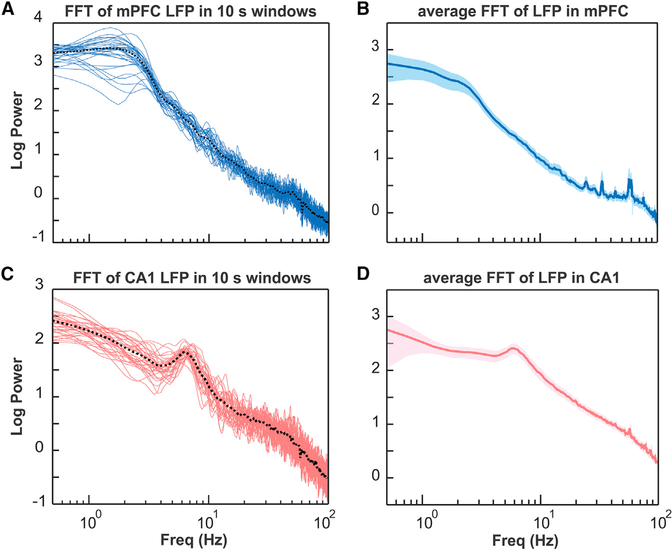
All recordings were performed in awake, head-fixed mice at rest. Results from a fast Fourier transform (FFT) analysis of the power spectral densities of LFP activities in the mPFC and hippocampal CA1 region are compatible with awake-state brain activity with limited variability (Figure 2), consistent with previous findings in similar head-fixed recording conditions (Ito et al., 2014).
Figure 2. FFT Analysis of LFP Activity Recorded in the mPFC and Hippocampal CA1 Region at Different Times during the Recording and Averaged across Recording Time.
(A) Power spectral density of LFP activity in the mPFC calculated for subsequent 10 s wide time windows (blue lines) for a 5.5 min recording session in one mouse. Dotted black line represents average FFT for the entire recording session.
(B) FFT of LFP recorded in the mPFC averaged across all mice (n = 11). Shaded area represents SEM.
(C) Power spectral density of LFP activity recorded in the hippocampal CA1 region calculated for subsequent 10 s wide time windows (red lines) for a 5.5 min recording session in one mouse. Dotted black line represents average FFT for the entire recording session.
(D) FFT of LFP recorded in the hippocampal CA1 region averaged across all mice (n = 11). Shaded area represents SEM.
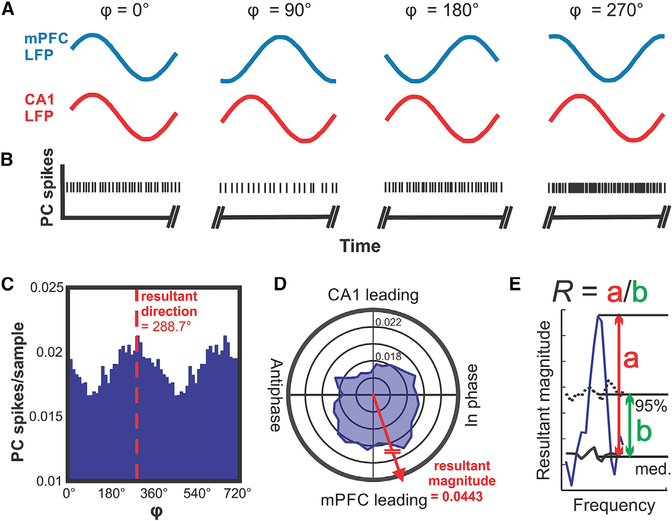
To determine whether the simple spike activity of PCs in LS was correlated with the instantaneous phase of LFP oscillations in the mPFC or CA1, we quantified PC spike activity as a function of the instantaneous phase for frequencies between 0.5 and 100 Hz. An illustration describing the principle of the spike-phase difference analysis is shown in Figure 3, using single-unit PC spike activity recorded in LS.
Figure 3. Conceptual Illustration of the Data Analysis Applied to Determine the Correlation between Phase Differences of mPFC-CA1 Oscillatory LFP Activity and Those of PC Simple Spike Activity in LS.
(A) Illustration of hypothetical oscillations at a specific frequency occurring simultaneously in the mPFC (blue traces) and CA1 (red traces) and displaying different phase relationships (φ) at different times. The phase relationship φ is defined as the phase difference relative to the mPFC oscillation.
(B) Hypothetical PC spikes recorded simultaneously with the LFP activity in the mPFC and CA1 shown in (A). The rate modulation of this hypothetical PC shows a significant increase in spike firing when the phase difference between mPFC and CA1 oscillations reaches values around 270°.
(C) Phase histogram of real PC simple spike activity. The histogram shows spike activity as a function of mPFC-CA1 phase differences at 11 Hz. The simple spike activity of the PC in this example was significantly modulated as a function of mPFC-CA1 phase difference, with a preference of 288.7°.
(D) Same data as in (C) represented in polar coordinates. Vectors composed of the angular value φ and the magnitude of the spikes per sample were summated to determine the angular preference of PC activity. The resultant vector magnitude was taken to quantify the degree of modulation and tested against surrogate results for statistical significance.
(E) Illustration of the quantitative evaluation of the strength of representation (R) of the mPFC-CA1 phase difference in PC spike trains. The solid blue line represents the resultant vector magnitude plotted as a function of frequency. The solid black line (med., median) and dotted black line (95%) represent the bootstrap-statistics-derived median and 95th percentile boundary of the surrogate distribution, respectively. Resultant magnitude peak values exceeding the 95th percentile boundary were expressed as the ratio (R) of the peak resultant magnitude value minus the surrogate median (red double arrow a) and the difference between the surrogate distribution’s 95th percentile and the median values (green double arrow b) for the corresponding frequency.
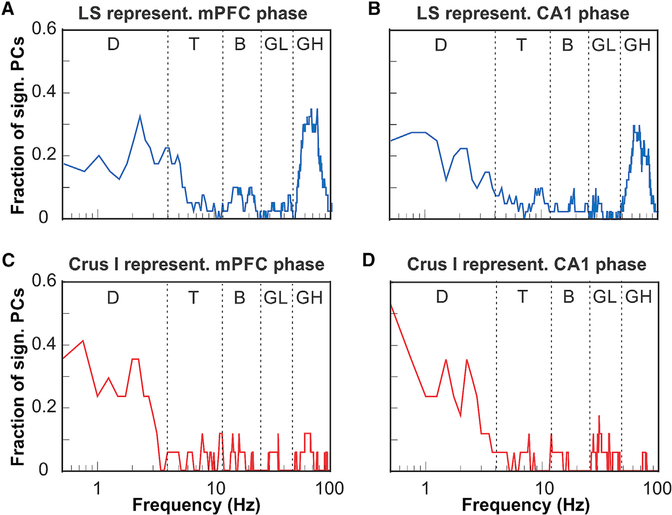
The representation of the instantaneous phase of mPFC LFP oscillations across the population of PCs in LS showed two distinct peaks at 2.5 and 68 Hz, corresponding to the conventional delta (0.5–4 Hz) and high gamma (50–100 Hz) frequency bands, respectively (Figure 4A). The representation of the instantaneous phase of LFP oscillations in CA1 across the population of PCs in LS was similar to that of the mPFC, showing distinct peaks at 1 and 60 Hz (Figure 4B).
Figure 4. Representations of the Phase of Oscillatory LFP Activity in the mPFC and CA1 by Cerebellar PCs in Lobulus Simplex and Crus I.
(A) Fraction of PCs in LS (n = 32) whose simple spike activity was significantly modulated by the oscillatory phase plotted as a function of mPFC oscillation frequency (plotted on a log-10 scale). The function shows two peaks at the delta frequency range (0.5–4 Hz) and the high gamma range (50–100 Hz).
(B) As in (A) but showing fractions of LS PCs significantly modulated by the phase of oscillatory activity in CA1.
(C) Fraction of PCs in Crus I (n = 17) whose simple spike activity was significantly modulated by the oscillatory phase in mPFC plotted as a function of LS oscillation frequency. The function shows a single peak at the delta frequency range (0.5–4 Hz).
(D) As in (C) but showing fractions of Crus I PCs significantly modulated by the phase of oscillatory activity in CA1.
D, delta; T, theta; B, beta; LG, low gamma; HG, high gamma.
The representation of the instantaneous phase of mPFC LFP oscillations across the population of PCs in Crus I showed distinct peaks at 0.5 and 2.5 Hz, both within the delta frequency range. In contrast to LS, the Crus I PC population representation lacked a distinct peak in the gamma frequency range (Figure 4C). The representation of the instantaneous phase of CA1 LFP oscillations across the population of PCs in LS was similar to the mPFC, showing distinct peaks around 0.5, 1.5, and 2.5 Hz, all within the delta frequency range (Figure 4D).
Link between PFC-CA1 Phase Differences and Spike Rate in Individual PCs in LS and Crus I
To determine whether the simple spike activity of PCs in LS is correlated with phase differences between LFP oscillations in the mPFC and CA1, we quantified PC spike activity as a function of mPFC-CA1 oscillation phase difference for frequencies between 0.5 and 100 Hz. The relationship between spike rate and phase difference was quantified for each frequency band by calculating a vector with a direction corresponding to a preferred mPFC-CA1 phase difference and a length representing how strongly spike activity reflected that particular phase difference for PCs in LS (Figures 5A and 5B) and in Crus I (Figures 5C and 5D). The statistical significance of spike modulation as a function of mPFC-CA1 phase difference was determined using bootstrap statistical methods (see the STAR Methods section for details). Significant firing rate modulation with mPFC-CA1 phase differences was found in 29 of 32 PCs (90.6%) in LS and in 14 of 17 PCs (82.35%) in Crus I.
Figure 5. Individual Examples of PCs from LS and Crus I, Showing mPFC-dCA1 Phase Difference Representation in PC Simple Spike Activity.
(A) Results for a representative PC recorded in LS. The blue line shows the depth of PC spike modulation, as measured by the resultant vector magnitude. Significance cutoffs represent the 95th percentile and 99th percentile boundaries, respectively, of the surrogate result distributions for each frequency obtained by shifting the PC spike recording in time relative to LFPs 200 times. Asterisks indicate frequencies with significant modulation (p < 0.01).
(B) Pseudocolor plot shows LS PC spike density as a function of phase difference (φ) between mPFC and CA1 LFP oscillations across frequencies between 0.5 and 100 Hz. Analysis was performed within frequency bands with a 0.5–10 Hz width, in steps of 0.25 Hz.
(C and D) Results for a representative PC recorded in Crus I. Plots are as in (A) and (B) but for a PC recorded in Crus I.
PC Activity Modulation Occurs across the Frequency Spectrum of mPFC and dCA1 Oscillations
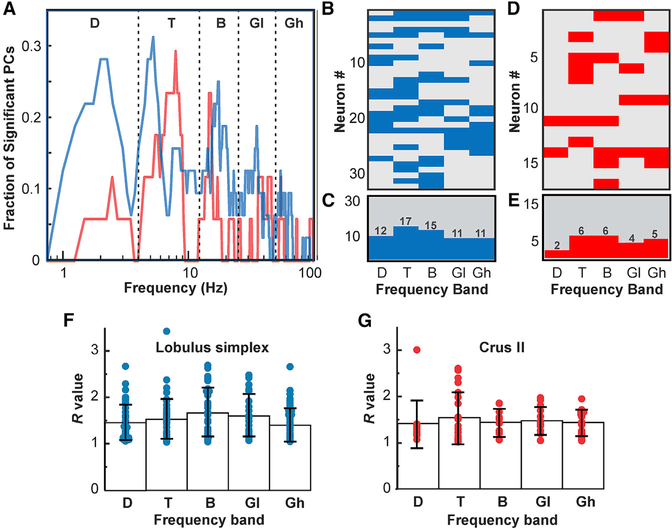
In an analysis of group data, we asked what fraction of PCs showed significant phase-difference-related rate modulations at each analyzed frequency (Figure 6). The results suggest that there are clear preferred frequencies in both LS and Crus (Figure 6A), whose phase differences are represented by large proportions of observed PCs, while other frequencies are not represented. The analysis of LS data revealed that spike rates were most commonly modulated by phase differences in the theta band, with the highest number of PCs representing phase differences for 5 Hz oscillations (Figures 6B and 6C). Significant results also clustered into modes within each of the other conventional frequency bands: delta (2 Hz), beta (17.5 Hz), low gamma (35 Hz), and high gamma (55 Hz).
Figure 6. Summary of the Representation of mPFC-dCA1 Phase Differences in PC Spike Activity and Evaluation of Representation Strength for PCs in LS and Crus I Grouped by Frequency Band.
(A) Plot depicting the fraction of PCs with significantly modulated simple spike activity (p < 0.01) within each 0.25 Hz frequency step between 0.5 and 100 Hz in LS (blue graph, n = 32) and Crus I (red graph, n = 17). Modal peaks were observed within each of the conventional frequency bands: delta (D; 0.5–4 Hz), theta (T; 4–12 Hz), beta (B; 12–25 Hz), low gamma (GL; 25–45 Hz), and high gamma (GH; 45–100 Hz).
(B) Pseudocolor matrix with rows representing individual PCs and columns representing frequency bands. Blue fields indicate a significant correlation between PC simple spike activity in LS and mPFC-dCA1 phase differences in each frequency band (p < 0.01). Gray fields indicate no significant correlation.
(C) Histogram showing the number of PCs with significant spike-phase difference correlations within each frequency band.
(D and E) Pseudocolor matrix (D) and histogram (E) are as (B) and (C), respectively, but representing results from Crus I.
(F) Strength of mPFC-dCA1 phase difference representation by PCs in LS. R expresses resultant vector magnitude as the ratio of the vector length to the 95th percentile boundary, each relative to the median surrogate value. R values were grouped by frequency band. Each dot represents the resultant vector magnitude of a PC. Bars represent the mean R for each frequency band. Error bars represent SD.
(G) As in (F) but showing results for Crus I.
PCs in Crus I also represented phase differences only for specific mPFC and CA1 oscillations, with different preferred frequencies, compared to LS PCs (Figures 6D and 6E). In Crus I, the modal frequencies were 2.5 Hz (delta), 8 Hz (theta), 15.25 Hz (beta), and 45 Hz (low gamma).
We evaluated the strengths of the representation of mPFC-CA1 phase differences for each conventional frequency band for PCs in LS and Crus I by expressing resultant vector length as the ratio (R) of the vector length minus the surrogate distribution median and the difference between the surrogate median and the surrogate 95th percentile values (see STAR Methods and Figure 3E). For further analysis, R values were grouped by the conventional frequency bands for PCs recorded in LS and Crus I (Figures 6F and 6G). A comparison of R value distributions revealed no differences between LS and Crus I for any frequency band (Wilcoxon rank-sum test) (results not shown). The average R values across all frequency bands were 1.52 ± 0.43 (mean ± SD) and 1.46 ± 0.41 (mean ± SD) for LS and Crus I, respectively. Comparison among frequency bands within each structure revealed no differences among R value distributions in different frequency bands with LS or Crus I (Wilcoxon rank-sum test) (results not shown).
DISCUSSION
Here we report that PC simple spike activity in LS and Crus I of awake, head-fixed mice represents the instantaneous phase and phase differences of LFP oscillations in the mPFC and dCA1. When evaluating the representation of phase across the populations of PCs, we found that the phase of delta band (0.5–4 Hz) oscillations in mPFC and dCA1 was represented by more than 30% of PCs in both LS and Crus I (Figure 4). By comparison, the phase of most other frequencies was represented by 10% or less of PCs in both cerebellar sites. However, the representation of the instantaneous phase of high gamma band (50–100 Hz) oscillations clearly differentiated between PCs recorded in LS and Crus I. More than 30% of LS PCs represented the instantaneous phase of gamma band oscillations in both mPFC and dCA1. There was no corresponding representation of mPFC or dCA1 gamma phase in Crus I, in which the fraction of PCs representing gamma phase was around or below 10% (compare Figures 4A and 4B with Figures 4C and 4D).
These findings document that the phase of neuronal oscillations in cerebral cortical areas is represented in cerebellar PC spike activity and that the representation is site and frequency band specific, suggesting that oscillations in different cerebral cortical areas are differentially represented in cerebellar cortical sites. Whether such a phase- and frequency-dependent map of the cerebral cortex exists in the cerebellum will have to be determined in additional experiments.
In addition to the representation of the instantaneous phase, we found that PCs in both LS and Crus I represented phase differences between mPFC and dCA1 oscillations in one or more of the conventional frequency bands. As for the instantaneous phase, phase differences were not represented equally for all frequencies. We found differences between LS and Crus I in terms of preferred frequencies whose phase differences were represented by the largest proportions of PCs, as reflected in distinct peaks in the plots of fractions of PCs representing phase differences versus frequency (Figure 6). In LS, those preferred frequencies were 2 Hz (delta), 5 Hz (theta), 17.5 Hz (beta), 35 Hz (low gamma), and 55 Hz (high gamma). In Crus I, the preferred frequencies were 2.5 Hz (delta), 8 Hz (theta), 15.5 Hz (beta), and 45 Hz (low gamma). In addition, in Crus I, three PCs represented phase differences in high gamma but with each cell representing a different frequency. The most prominent difference that distinguishes the activity of PCs in the LS compared to Crus I is the smaller portion of PCs representing delta band phase differences, with 28% of PCs in LS versus 11.7% of PCs in Crus I.
We evaluated the strength of the representation of phase differences between frequency bands within each structure or between the two structures (Figures 6F and 6G). There were no significant differences in the strengths of representation of phase differences between LS and Crus I. Thus, although there were differences between LS and Crus I regarding the preferred frequencies for which phase differences are represented in PC spike trains, there were no differences with respect to the strengths of these representations.
LS and Crus I are adjacent to each other in the cerebellar cortex. Functional imaging studies suggest that the two lobules have different, as well as common, functional properties. For example, both have been implicated in verbal working memory (Desmond et al., 2005). However, Crus I (together with Crus II) was found to be part of the default mode network that did not include LS (Halko et al., 2014). Tracing studies showed reciprocal connections between Crus I and II and the prefrontal cortex in primates (Bostan et al., 2013) and rodents (Suzuki et al., 2012) but no such connections for LS. However, based on findings of extensive functional connectivity patterns in fMRI studies (Buckner, 2013), future studies are likely to reveal unexpected connections. For example, Watson et al. (2014) showed that the rat cerebellar fastigial nucleus, long believed to interact solely or predominantly with spinal cord circuits, has strong functional connections with the medial prefrontal cortex. We have no conclusive understanding of the similarities and differences between Crus I and LS based on connectivity patterns and involvement in behaviors. Our findings suggest distinct roles for the two areas with respect to the neuronal representation of the oscillatory phase and phase differences in the mPFC and CA1 region.
Although primates and rodents share evolutionarily conserved features in protein expression, neural circuit projection patterns, and gross anatomy, specific adaptations exist, such as expansion of lobules and the functional maps therein. Therefore, although a direct extrapolation of our data into other higher-order species may be challenging, the fundamental basis of how the cerebellum is organized and how it interacts with other brain regions is predicted to share significant homology across mammals (Luo et al., 2017; Sugihara, 2018).
Coherent oscillations between the cerebellum and the cerebral cortex, especially sensory cerebral cortical areas, have been reported previously. O’Connor et al. (2002) showed that coherence of 1–20 Hz oscillations in cerebral and cerebellar whisker-related areas were modulated by behavior, because they increased during active whisking. However, the authors did not investigate the directionality of influence between the two structures. Later, Ros et al. (2009) and Rowland et al. (2010) showed a directionality of influence for low-frequency (<10 Hz) coherence with sensory cerebral cortical areas driving cerebellar cortex and nuclei oscillations.
How cerebellar PC simple spike activity comes to represent phase and phase differences of neuronal oscillations in the mPFC and dCA1 remains to be determined. The phase of cerebral cortical oscillations could be present in the activity of mossy fibers, driven by phase-locked neuronal activity in the mPFC or dCA1. Such a representation could be supported by resonance properties of the Golgi cell network, which would be limited to frequencies of up to 30 Hz (Dugué et al., 2009). However, phase differences would have to be computed either within upstream structures, such as the pontine nuclei, or within the cerebellar network. Considering that any phase difference can be represented as a time interval, a possible neuronal mechanism, at least for higher frequencies, can be derived from the cerebellar network architecture. Parallel fibers could serve as delay lines, transforming phase-difference encoding delays between mossy fiber spike events into synchronous inputs to PCs as proposed by Braitenberg et al. (1997).
Although the behavioral significance of our findings remains to be determined, we would like to point out that the cerebellum, mPFC, and dCA1 are jointly implicated in spatial processing and SWM (Lefort et al., 2015; Spellman et al., 2015) and the process of decision-making in working memory involves temporary stabilization of phase differences (i.e., increased coherence) between mPFC-dCA1 oscillations (Gordon, 2011). How the cerebellum contributes to SWM is not understood, but our results uncover the compelling possibility of a cerebellar role in modulating mPFC-dCA1 coherence, which is concordant with findings by Popa et al. (2013), who showed that normal coherence between sensory and motor cortical areas requires an intact cerebellum. Coherence has been proposed as a mechanism for the coordination of neuronal communication between brain regions (Bastos et al., 2015). Our findings thus suggest cerebellar involvement in the temporal coordination of oscillatory phase relationships, a function that would be in line with the long-standing notions of cerebellar timing and temporal coordination functions (Braitenberg, 1961; Ivry et al., 2002).
STAR★METHODS
CONTACT FOR REAGENT AND RESOURCE SHARING
Further information and requests for resources and data should be directed to and will be fulfilled by Dr. Samuel S. McAfee (Stuart.McAfee@STJUDE.ORG) or Dr. Detlef H. Heck (dheck@uthsc.edu).
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Experiments were performed on a total 11 adult male C57BL/6J (B6) mice, (> 8 weeks old, 18–25 g body weight). Mice were housed in a breeding colony with 12-hour light/dark cycles in standard cages with ad libitum access to food and water. All experiments were performed during the light cycle, between 12:00 noon and 17:00 hours. None of the mice had undergone any previous experimental procedure. All animal experimental procedures adhered to guidelines approved by the University of Tennessee Health Science Center Animal Care and Use Committee. Principles of laboratory animal care (NIH publication No. 86–23, rev. 1996) were followed. Founder animals were originally purchased at Jackson Labs (Stock # 000664).
METHOD DETAILS
Surgical procedures
Mice were initially anesthetized in an induction chamber with 3% Isoflurane in oxygen controlled by a vaporizer (Highland Medical Equipment, CA) and then transferred to a stereotaxic head frame. Anesthesia was maintained at the lowest concentration at which mice failed to show toe-pinch reflexive withdrawal, typically 1%−2.5% Isoflurane in oxygen. Core body temperature was maintained at 37°C using a feedback-controlled heating pad with a rectal thermometer (FHC Inc., Bowdoinham, ME).
The skull was exposed and craniotomies were made over the left mPFC (lat. 0.5 mm, ant. 2.8 mm) and dCA1 (lat. 2.0 mm, ant. −2.3 mm) and over the right cerebellar LS (lat. 2.0 mm, ant. −5.52 mm, 6 mice) or right Crus I (2.5 mm, ant. −6.25 mm, 5 mice). Cylindrical recoding chambers were placed over each craniotomy. Recording chambers and a head fixation bar were anchored to the skull with three small skull screws and acrylic cement (Co-Oral-Ite Manufacturing, USA). Mice recovered for 3 to 4 days prior to recording.
Electrophysiological recordings
Recording procedures were as described previously (Liu et al., 2017). A 7-electrode micromanipulator (System Eckhorn; Thomas Recording, Germany) with a custom-made set of guiding tubes was used to record simultaneously from the three brain areas. Extracellular recording electrodes (3–7 MΩ) were advanced through the intact dura. In this system the metal guiding tubes serve as the electrical reference forthe extracellular recordings. Guiding tubes are immersed in saline, which is used to fill the recording chambers during experiments and established electrical contact between the guiding tubes and the surface of the targeted brain area. Hippocampal recording electrodes were advanced until sharp wave ripples (SWRs), a high-frequency local field potential (LFP) oscillation characteristic for the hippocampus (Buzsaki, 2015), were detected (Figure 1A). Cerebellar PCs were identified by the presence of complex spikes (Thach, 1968). Prefrontal cortical sites were targeted following stereotaxic coordinates (Paxinos and Franklin, 2001) and verified anatomically using small electrolytic lesions.
LFPs and spike signals were separated by band-pass filtering at 0.1 to 200 Hz and at 200 Hz to 8 kHz, respectively (FA32; Multi Channel Systems, Germany), digitized (sampling rate: > 20 kHz for action potentials and > 1 kHz for LFPs) and stored on hard disk, using a 16 bit A/D converter (CED power1401) and Spike2 software (both Cambridge Electronic Design, UK). Electrode depths were adjusted to obtain stable LFP recordings in mPFC and dCA1 and single unit PC activity in the cerebellum.
Recording sessions were repeated on three successive days for each mouse. After completion of each recording session, the chambers were rinsed and re-filled with triple antibiotic ointment and mice were returned to their home cages.
Histology
At the end of the last recording sessions electrolytic lesions were created at the final recording sites in the mPFC, dCA1 and LS by passing a small current (5 μA/10 s) through the recording electrodes (Figure 1B). Within 12 hours of creating the lesion, mice were euthanized and then transcardially perfused. After perfusion, the brain was removed and post-fixed in 4% formaldehyde for 24 h. Brain tissue was cut into 50 μm thick coronal sections, which were mounted and stained with cresyl violet. The location of lesion sites was determined using a stereotaxic atlas of the mouse brain (Paxinos and Franklin, 2001).
Analysis of PC activity
Single-unit spike activity was recorded from 32 PCs located in LS (6 mice) and 17 located in Crus I (5 mice). PCs were identified based on location, firing characteristics and the presence of complex spikes (Thach, 1970) (Figure 1). Simple spike activity was identified offline using a shape-based spike-sorting algorithm of the Spike2 software. PCs simple spike firing rates ranged from 36.5 to 157.9Hz, with a mean of 89.1 Hz, consistent with previously reported rates in awake mice (Cao et al., 2012) and primates (Thach, 1970). Complex spikes were excluded from the analysis because their low frequency (~1 Hz) resulted in too small a number of incidents for a meaningful evaluation.
Pre-preprocessing of LFPs
Only sections of data with stable single-unit spike isolation and LFP recordings, which were free of movement artifacts, were included in analysis. dCA1 recording sites were included only if they showed clear sharp wave ripples (Figure 1, dCA1 LFP). 60Hz noise was diminished using a hum-removal algorithm in Spike2 that subtracted 60Hz components rather than applying a notch-filter, which left the power spectrum of LFP signals at that frequency intact (Figure 2).
QUANTIFICATION AND STATISTICAL ANALYSIS
Analysis of LFP power spectral density
Power spectral density for LFP activity recorded in the mPFC and hippocampal CA1 regions were calculated using Fast Furier Transform (FFT) in MATLAB. FFT analysis was applied to subsequent, non-overlapping 10 s wide windows for individual recordings to determine temporal variability of power spectral density as a measure of brain states. The average power spectral density was also calculated across all datasets from all 11 mice, expressing the variability power spectral density across the group as standard error of the mean (SEM).
Estimation of LFP phase and phase relationships
In order to determine phase and phase relationships of LFP oscillations in PFC anddCA1 overtime, LFPs were band-pass filtered for frequencies between 0.5–100Hz. FIR filters were applied in frequency steps of 0.25Hz with bandwidth ranging from 0.5–10Hz with increasing frequency. Filter order was determined to be the number of samples within 5 cycles of the center frequency. The Hilbert transform was performed on each band-pass-filtered signal, and instantaneous phase values were defined as the angular value derived from the complex-valued analytic signal. The frequency specific phase relationship between mPFC and dCA1 oscillations was determined by subtracting the instantaneous mPFC phase from dCA1 phase.
Instantaneous phase and phase difference values were analyzed using an angular binning approach to produce a mean spike incidence (spike density) value for each phase. The choice to implement vector mean analysis over more conventional vector sum statistics was made primarily to account for potential inherent bias in the distribution of observed phase relationships (i.e., mPFC-dCA1 phase relationship preferences), and isolate the statistical relationship between spike rate and phase. Furthermore, the vector mean test can reveal significant PC silence during frequently-observed phases, which may be functionally relevant.
The phase or phase difference values were designated into 30 angular bins of 12° width, and the corresponding spikes within each bin were counted. The spike count in each bin was divided by the total number of angular samples in the bin to return a measure of spike density. Each bin was then treated as a vector with an angular value of the phase or phase difference and magnitude of the spike density in order to calculate a resultant vector with magnitude reflecting degree of modulation and direction of preferred phase or phase difference.
Statistical analysis
Bootstrap statistical analysis of the relationship between spike activity and PFC-CA1 phase/phase differences was performed by calculating vector lengths for 200 surrogate datasets. Each surrogate dataset was created by randomly shifting the spike sequence, leaving the original spike sequence unchanged. The resulting 200 surrogate vector values were rank-ordered for each frequency and the 95th and 99th percentile values were determined. Real vector values greater than the 95th percentile of the surrogate vector distribution were considered statistically significant, and those greater than the 99th percentile were selected for further group analysis. The magnitude of all significant resultant vectors was further quantified by first subtracting the surrogate median from each vector value and the corresponding 95 percentile boundary values and then calculating the ratios of those two values, as illustrated in Figure 3. The resulting ratio was termed R. For further analysis R values were grouped by frequency bands and evaluated separately for LS and Crus I PCs (Figures 6F and 6G).
KEY RESOURCES TABLE.
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Experimental Models: Organisms/Strains | ||
| C57BL/6J | Jackson Labs | Stock # 000664 |
| Software and Algorithms | ||
| MATLAB R2017a/b | MathWorks (USA) | N/A |
| Spike2, Version 7 | Cambridge Electronic Design (UK) | N/A |
| Spike2, Version 7 Hum removal script used to remove 60 Hz mains hum (HumRemoveExpress.s2s) | Cambridge Electronic Design (UK) | N/A |
| Custom Code for Phase/Phase difference analysis written in MATLAB R2017a/b | Developed by SSM | N/A |
Highlights.
Cerebellar Purkinje cells represent phase information of neuronal oscillations
Represented oscillations occur in medial prefrontal cortex and hippocampus
Representations of phase and phase differences are frequency specific
Representation of phase information differs between lobulus simplex and Crus I
ACKNOWLEDGMENTS
We thank Shuhua Qi for technical assistance, Micheal Nguyen for custom machined parts, and Brittany Correia and Aspen Robinson for help with data analysis. Support was provided by the UTHSC College of Medicine, the Neuro-science Institute, and the Department Anatomy and Neurobiology. R.V.S. is supported by R01NS089664, R01NS100874, and U54HD083092 (Neuropathology Core) and D.H.H., R.V.S., and Y.L. are supported by R01MH112143.
Footnotes
DECLARATION OF INTERESTS
The authors declare no competing interests.
REFERENCES
- Bastos AM, Vezoli J, and Fries P (2015). Communication through coherence with inter-areal delays. Curr. Opin. Neurobiol 31, 173–180. [DOI] [PubMed] [Google Scholar]
- Bostan AC, Dum RP, and Strick PL (2013). Cerebellar networks with the cerebral cortex and basal ganglia. Trends Cogn. Sci 17, 241–254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braitenberg V (1961). Functional Interpretation of Cerebellar Histology. Nature 190, 539–540. [Google Scholar]
- Braitenberg V (1967). Is the Cerebellar Cortex a Biological Clock in the Millisecond Range? Prog. Brain Res 25, 334–346. [DOI] [PubMed] [Google Scholar]
- Braitenberg V, Heck D, and Sultan F (1997). The detection and generation of sequences as a key to cerebellar function: experiments and theory. Behav. Brain Sci 20, 229–245, discussion 245–277. [PubMed] [Google Scholar]
- Buckner RL (2013). The cerebellum and cognitive function: 25 years of insight from anatomy and neuroimaging. Neuron 80, 807–815. [DOI] [PubMed] [Google Scholar]
- Buzsáki G (2015). Hippocampal sharp wave-ripple: A cognitive biomarker for episodic memory and planning. Hippocampus 25, 1073–1188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao Y, Maran SK, Dhamala M, Jaeger D, and Heck DH (2012). Behavior-related pauses in simple-spike activity of mouse Purkinje cells are linked to spike rate modulation. J. Neurosci 32, 8678–8685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Desmond JE, Chen SH, and Shieh PB (2005). Cerebellar transcranial magnetic stimulation impairs verbal working memory. Ann. Neurol 58, 553–560. [DOI] [PubMed] [Google Scholar]
- Dugué GP, Brunel N, Hakim V, Schwartz E, Chat M, Lévesque M, Courtemanche R, Léna C, and Dieudonné S (2009). Electrical coupling mediates tunable low-frequency oscillations and resonance in the cerebellar Golgi cell network. Neuron 61, 126–139. [DOI] [PubMed] [Google Scholar]
- Gordon JA (2011). Oscillations and hippocampal-prefrontal synchrony. Curr. Opin. Neurobiol 21, 486–491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halko MA, Farzan F, Eldaief MC, Schmahmann JD, and Pascual-Leone A (2014). Intermittent theta-burst stimulation of the lateral cerebellum increases functional connectivity of the default network. J. Neurosci 34, 12049–12056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ito J, Roy S, Liu Y, Cao Y, Fletcher M, Lu L, Boughter JD, Grün S, and Heck DH (2014). Whisker barrel cortex delta oscillations and gamma power in the awake mouse are linked to respiration. Nat. Commun 5, 3572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivry RB, Spencer RM, Zelaznik HN, and Diedrichsen J (2002). The cerebellum and event timing. Ann. N Y Acad. Sci 978, 302–317. [DOI] [PubMed] [Google Scholar]
- Lefort JM, Rochefort C, and Rondi-Reig L; Group of L.R.R. is member of Bio-Psy Labex and ENP Foundation (2015). Cerebellar contribution to spatial navigation: new insights into potential mechanisms. Cerebellum 14, 59–62. [DOI] [PubMed] [Google Scholar]
- Liu Y, McAfee SS, and Heck DH (2017). Hippocampal sharp-wave ripples in awake mice are entrained by respiration. Sci. Rep 7, 8950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo Y, Fujita H, Nedelescu H, Biswas MS, Sato C, Ying S, Takahashi M, Akita K, Higashi T, Aoki I, and Sugihara I (2017). Lobular homology in cerebellar hemispheres of humans, non-human primates and rodents: a structural, axonal tracing and molecular expression analysis. Brain Struct. Funct 222, 2449–2472. [DOI] [PubMed] [Google Scholar]
- O’Connor SM, Berg RW, and Kleinfeld D (2002). Coherent electrical activity between vibrissa sensory areas of cerebellum and neocortex is enhanced during free whisking. J. Neurophysiol 87, 2137–2148. [DOI] [PubMed] [Google Scholar]
- Paxinos G, and Franklin KBJ (2001). The Mouse Brain in Stereotaxic CoordinatesVolume 2 (Academic Press; ). [Google Scholar]
- Popa D, Spolidoro M, Proville RD, Guyon N, Belliveau L, and Léna C (2013). Functional role of the cerebellum in gamma-band synchronization of the sensory and motor cortices. J. Neurosci 33, 6552–6556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ros H, Sachdev RN, Yu Y, Sestan N, and McCormick DA (2009). Neocortical networks entrain neuronal circuits in cerebellar cortex. J. Neurosci 29, 10309–10320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rowland NC, Goldberg JA, and Jaeger D (2010). Cortico-cerebellar coherence and causal connectivity during slow-wave activity. Neuroscience 166, 698–711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spellman T, Rigotti M, Ahmari SE, Fusi S, Gogos JA, and Gordon JA (2015). Hippocampal-prefrontal input supports spatial encoding in working memory. Nature 522, 309–314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugihara I (2018). Crus I in the Rodent Cerebellum: Its Homology to Crus I and II in the Primate Cerebellum and Its Anatomical Uniqueness Among Neighboring Lobules. Cerebellum 17, 49–55. [DOI] [PubMed] [Google Scholar]
- Suzuki L, Coulon P, Sabel-Goedknegt EH, and Ruigrok TJ (2012). Organization of cerebral projections to identified cerebellar zones in the posterior cerebellum of the rat. J. Neurosci 32, 10854–10869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thach WT (1968). Discharge of Purkinje and cerebellar nuclear neurons during rapidly alternating arm movements in the monkey. J. Neurophysiol 31, 785–797. [DOI] [PubMed] [Google Scholar]
- Thach WT (1970). Discharge of cerebellar neurons related to two maintained postures and two prompt movements. II. Purkinje cell output and input. J. Neurophysiol 33, 537–547. [DOI] [PubMed] [Google Scholar]
- Watson TC, Becker N, Apps R, and Jones MW (2014). Back to front: cerebellar connections and interactions with the prefrontal cortex. Front. Syst. Neurosci 8, 4. [DOI] [PMC free article] [PubMed] [Google Scholar]